Теорема пифагора
Определение теоремы пифагора
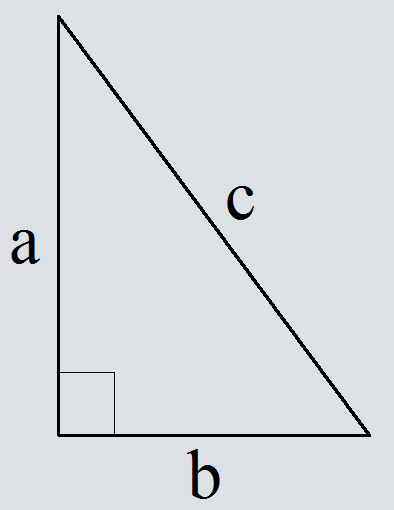
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Обозначив гипотенузу буквой — c, катеты буквами a и b получим следующее равенство
c2=a2+b2
Расчёт катета по теореме пифагора
Введите гипотенузу
c =
Введите катет
b =
Формула пифагора для катета
Где a, b — катеты прямоугольного треугольника,
с — гипотенуза прямоугольного треугольника
Расчёт гипотенузы по теореме пифагора
Введите первый катет
a =
Введите второй катет
b =
Формула пифагора для гипотенузы
Где a, b — катеты прямоугольного треугольника,
с — гипотенуза прямоугольного треугольника
Доказательство теоремы пифагора
Дано
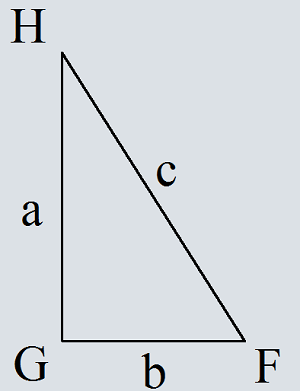
Прямоугольный треугольник с катетами a, b и гипотенузой c.
Доказать
c2=a2+b2
Доказательство
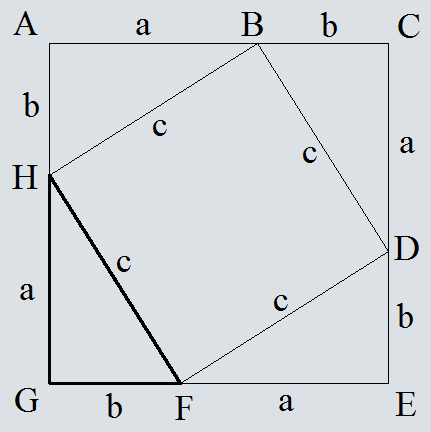
Достроим треугольник HFG до квадрата со стороной a+b.
Запишем площадь получевшегося квадрата двумя способами
S=(a+b)2
S=4*0.5*a*b +c2
Приравняем площади
(a+b)2=4*0.5*a*b +c2
a2+2*a*b +b2=2*a*b +c2
a2+b2=c2
Теорема доказана
Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² — b²
b = √c² — a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² — 4² = √25 — 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
См. также
В публикации представлены онлайн-калькуляторы и формулы для нахождения катета и гипотенузы в прямоугольном треугольнике по теореме Пифагора.
Инструкция по использованию: введите длины двух известных сторон треугольника (одного из катетов и гипотенузы или двух катетов), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина третьей стороны.
Содержание
скрыть
- Нахождение катета
- Нахождение гипотенузы
Нахождение катета
Формулы расчета
Нахождение гипотенузы
Формула расчета
Это смотря какие данные нам даны для решения.
Например есть теорема Пифагора:
по ней, если катеты a и b, а гипотенуза c, то:
a²+b²=c²
Отсюда можно найти катет, зная длину гипотенузы и второго катета:
a²=c²-b²
a=√(c²-b²)
Также находим и b:
b=√(c²-a²)
Ещё можно найти катет через тригонометрические функции, то есть зная угол через синусы, косинусы, тангенсы, котангенсы и т.д.
Если представить треугольник как вписанный в круг, то зная угол и размер гипотенузы можно найти катеты.
В рассматриваемом треугольнике, вписанном в круг, гипотенуза будет радиусом круга и приравнивается к 1 (к единице). А катеты — это синус и косинус, они меньше единицы.
Допустим зная угол α можно вычислить sin(α) и cos(α).
Синус соответствует вертикальному катету, а косинус горизонтальному.
Теперь, чтобы найти длины этих катетов, нужно перевести их из коэффициентов, которые меньше единицы, в реальные длины. Для этого их нужно домножить на длину гипотенузы:
Если:
Y — вертикальный катет, а X — горизонтальный катет (см. картинку) a Z — гипотенуза, то:
Y=Z*sin(α)
X=Z*cos(α)
Можно найти катет и зная лишь длину второго катета, а также угол.
Допустим знаем Y и угол α.
Тогда запросто находим гипотенузу, выражая её из предыдущей формулы:
Z=sin(α)/Y
А затем уже находим второй катет: X=Z*cos(α)
Если же наоборот знаем только X катет (горизонтальный, относительно приведённого рисунка), то находим гипотенузу так:
Z=X/cos(α)
А затем уже находим катет Y: Y=Z*sin(α)
Теорема Пифагора
О важности теоремы Пифагора высказался Иоганн Кеплер: «Геометрия обладает двумя великими сокровищами: теоремой Пифагора и делением отрезка в крайнем и среднем отношении; первое можно сравнить с мерой золота, второе назвать драгоценным камнем»
Теорема Пифагора актуальна в заданиях как базового, так и профильного ЕГЭ по математике. За верное решение задач базового уровня дается 1 балл, за задания повышенного уровня начисляется 3 балла. В статье мы рассмотрим доказательство теоремы и решим пару задач по теме. Благодаря качественному изучению этого материала экзаменуемый справится с рядом заданий и получит за них наивысший балл.
Что такое теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Важно!
Сторону прямоугольного треугольника, противолежащую прямому углу, называют гипотенузой, а стороны, прилежащие к прямому углу, — катетами. Гипотенуза больше любого из катетов («Геометрия. 8 класс. Учебник», А. Г. Мерзляк).
Формула теоремы Пифагора
c² = a² + b²
Из этой формулы выводятся следующие:
с = √a² + b²
a = √c² — b²
b = √c² — a²
Доказательство теоремы Пифагора

Дано:
△АВС — прямоугольный;
<АСВ = 90⁰.
Доказать:
АВ² = АС² + ВС².
Доказательство:
Проведем высоту СН.
АН, НВ — проекции катетов АС и ВС на гипотенузу. По теореме о метрических соотношениях в прямоугольном треугольнике, квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу. Значит,
АС² = АВ × АН; ВС² = АВ × НВ.
Сложим почленно эти равенства:
АС² + ВС² = АВ × АН + АВ × НВ = АВ × (АН + НВ) = АВ ×АВ = АВ².
Что и требовалось доказать.
Задачи на теорему Пифагора
Переходим к решению задач с помощью теоремы Пифагора.
Задача №1
Центр окружности, описанной около треугольника КРH, лежит на стороне КН. Радиус окружности равен 10. Найдите КР, если РН равен 12

Дано:
Описанная окружность с центром в точке О.
О ∈ КН;
R = 10;
РН = 12.
Найти: КР.
Решение:
Так как окружность описанная, то все вершины треугольника лежат на ней. Следовательно, угол <КРН — вписанный.
По условию задачи центр окружности О ∈ КН, значит, хорда КН является диаметром.
КН = 2R = 2 ✕ 10 = 20.
Вписанный угол <КРН, опирающийся на диаметр, — прямой, значит, треугольник КРН — прямоугольный.
По теореме Пифагора:
КР = √КН² — РН²,
КР = √400-144 = √256 = 16
Ответ: КР = 16
Теорема о трех перпендикулярах
Доказательство и формулировка теоремы о трех перпендикулярах
подробнее
Задача №2
Дано:
Пирамида МАВС с высотой МА. Известно, что в основании лежит прямоугольный треугольник с прямым углом С.
Найти:
1) Угол между ребрами МС и ВС. Ответ дайте в градусах.
2) МВ, если МС = 12, ВС = 5.
Решение:
1) Так как по условию задачи МА — высота пирамиды, то МА ⟂ (АВС). АС — проекция наклонной МС на плоскость АВС. Так как АС ⟂ ВС, то, по теореме о трех перпендикулярах, МС ⟂ ВС, следовательно, угол между МС и ВС равен 90° (градусов).
Ответ: 90°.
2) Так как из пункта 1 МС ⟂ ВС ⇒ треугольник МСВ — прямоугольный ⇒ по теореме Пифагора: МВ = √МС² + ВС² ⇒ МВ = √144 + 25 = √169 = 13.
Ответ: МВ = 13.
Популярные вопросы и ответы
Почему теорему Пифагора изучают на геометрии в 8 классе?
Потому что это необходимый теоретический материал для решения задач с помощью данной теоремы: квадратные уравнения, арифметический квадратный корень, подобие треугольников и другие. Эти темы изучаются именно в 8 классе.
Где и когда возникла теорема Пифагора?
Согласно сирийскому историку Ямвлиху, Пифагора познакомили с учителем математики Фалесом Милетским и его учеником Анаксимандром. После известно, что Пифагор отправился в Египет для продолжения своих исследований, был захвачен во время вторжения Камбиса II из Персии в 525 году до н. э. и доставлен в Вавилон. Пифагор вскоре поселился в Кротоне (ныне Кротон, Италия) и основал школу или, говоря современным языком, монастырь, где все члены дали строгий обет хранить тайну, а все новые математические результаты на протяжении нескольких столетий приписывались его имени. Таким образом, до конца неизвестно первое доказательство теоремы, а также есть некоторые сомнения в том, что сам Пифагор действительно ее доказал. Она была одной из первых теорем, пришедших из древних цивилизаций.
Теорема Пифагора — самый известный математический вклад ученого. Согласно одной из легенд, он был так счастлив, когда решил доказательство, что принес в жертву 100 быков.
Также при изучении вавилонских клинописных табличек и древнекитайских рукописей было установлено, что знаменитая теорема была известна задолго до Пифагора, возможно несколько тысячелетий до него. Так, немецкий математик Кантор выяснил, что равенство 32 + 42 = 52 было известно египтянам около 2300 лет до н. э., еще во времена царя Аменехмета (согласно папирусу 6 619 Берлинского музея). Такой треугольник со сторонами 3, 4, 5 получил название «египетский треугольник». Одни предполагают, что Пифагор дал теореме полноценное доказательство, а другие считают по-другому. Например, доказательство в «Началах Евклида» (Предложение 47), по утверждению Прокла, принадлежит самому Евклиду, а не Пифагору.
Где в жизни можно применить теорему Пифагора?
Широкое применение имеет теорема при решении геометрических задач: нахождении длин, расстояний в прямоугольном треугольнике. Большой спектр применения есть у этой великой теоремы в физике, астрономии, строительстве, архитектуре, литературе.
Как звучит обратная теорема Пифагора?
Если квадрат длины одной стороны треугольника равен сумме квадратов длин двух других сторон, то треугольник является прямоугольным.
Изображения на странице: wikipedia.org, Наталия Юмагулова.