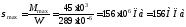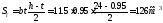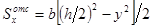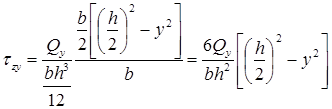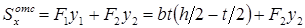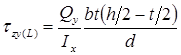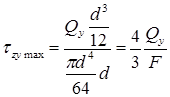В этой статье начнем говорить о кручении. Это одна из базисных тем в сопромате, как и растяжение-сжатие. Знания этой темы помогут тебе при изучении более сложных тем курса «сопротивление материалов».
Кручение – это такой вид деформации, при котором в сечениях стержня возникают крутящие моменты (T).
На кручение, как правило, работают детали, которые называются валами. Детали, которые широко используются в машиностроении.
Что такое крутящий момент?
Крутящий момент – это внутренний силовой фактор, возникающий в сечениях стержней испытывающих деформацию кручения.
На практике же стержни не работают исключительно на кручение, они могут и растягиваться, и изгибаться. Но это уже более продвинутые темы – сложное сопротивление. В этом же разделе будем рассматривать чистое кручение.
В чем измеряется крутящий момент и как обозначается?
Крутящие моменты обозначаются буквой – T (сокращённое с английского: Torque – крутящий момент), однако, часто в другой литературе ты можешь встретить обозначение — Мкр. Ты можешь использовать любое обозначение, какое больше нравиться, либо которое использует твой преподаватель.
В задачах тебе будут даны крутящие моменты, скорее всего, в Н·м либо кН·м.
Построение эпюры крутящих моментов
В этой статье расскажу, как строить эпюры при кручении: крутящих моментов, максимальных касательных напряжений и углов закручивания (углов поворотов).
На самом деле, многие рассматриваемые здесь принципы сильно похожи на те, что мы изучали ранее в уроке про построение эпюр при растяжении (сжатии). Здесь фактически будем делать всё то же самое, только оперировать другими обозначениями и названиями. После изучения того урока, с кручением у тебя точно не возникнет никаких трудностей.
В качестве примера, возьмём следующую расчётную схему:

Будем считать, что стержень изготовлен из стали (G = 8 · 1010 Па), а диаметры ступеней равны: d1=150 мм, d2=200 мм, d3=300 мм.
Под действием внешних моментов (M), их еще часто называют вращающими или скручивающими моментами, в поперечных сечениях стержня возникают внутренние моменты – крутящие (T).

Правило знаков для крутящих моментов
Чтобы построить эпюру крутящих моментов, необходимо задаться каким-то правилом знаков для крутящих моментов. В этой статье я буду использовать следующее правило:
- Если внешний момент (M), в плоскости сечения, поворачивает ПРОТИВ часовой стрелки, то крутящий момент (T) – положительный.

- Если внешний момент (M), в плоскости сечения, поворачивает ПО часовой стрелке, то крутящий момент (T) – отрицательный.

Можно учитывать знак крутящего момента ровно наоборот. Главное, придерживаться этого правила при расчёте всех участков и ориентироваться по полученным эпюрам: в какую сторону у тебя будут направлены внешние моменты, внутренние – крутящие моменты, куда будут поворачиваться сечения. Как видишь, знаки здесь нам нужны, чтобы задать определённые правила игры, а правило знаков – условное и не имеет физического смысла.
Расчёт крутящих моментов
Что же, давай, наконец, приступим к расчёту крутящих моментов. Пронумеруем расчётные участки:

Используя правило знаков, описанное выше, рассчитаем крутящие моменты на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Построение эпюры касательных напряжений при кручении
Касательные напряжения по высоте круглого сечения, будут распределены следующим образом:

Как видишь, касательные напряжения будут максимальны на поверхности стержня, они нас и будут интересовать больше всего, т. к. по ним выполняются прочностные расчёты, для них и будем строить эпюру – максимальных касательных напряжений.
Расчёт максимальных касательных напряжений
Максимальные касательные напряжения в поперечном сечении, можно определить по формуле:

где Wp — полярный момент сопротивлния, T — крутящий момент.
Полярный момент сопротивления для круглого сечения определяется по формуле:

Поэтому формулу для нахождения максимальных касательных напряжений для круглого поперечного сечения, можно записать в следующем виде:

По условию задачи диаметры участков известны. Осталось вычислить максимальные касательные напряжения на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Построение эпюры углов закручивания (поворотов)
Под действием внешних – скручивающих моментов, поперечные сечения стержня будут поворачиваться на определенный угол (φ). В этом разделе будем учиться определять эти углы закручивания (поворотов) поперечных сечений и строить эпюру.
Обозначим точки в характерных сечениях стержня:

Расчёт начинаем от жёсткой заделки и сразу можем записать, что в точке A, угол поворота равен нулю, т. к. здесь заделка ограничивает любые повороты сечения:
Чтобы рассчитать поворот сечения B, нужно учесть поворот предыдущего сечения:
А также, угол закручивания участка между расчётными сечениями:
Угол закручивания участка можно посчитать по формуле:

где l – длина участка; Ip – полярный момент инерции; G – модуль сдвига.
G – модуль сдвига (модуль упругости 2 рода) – определяется при испытании образцов на кручение, тем самым зависит от материала образца.
Модуль сдвига (G) известен, по условию задачи.
Формула для определения полярного момента инерции для круглого сечения следующая:

Зная диаметры, сразу вычислим полярные моменты инерции для каждого участка:

Определим угол закручивания сечения B, с учётом вышеуказанных формул:

Также можно перевести это значение в привычные градусы:

Для двух других сечений расчёт производится аналогичным образом.
Угол поворота сечения С

Угол поворота сечения D

По рассчитанным значениям, построим эпюру углов закручивания поперечных сечений:

Таким образом, свободный торец стержня, повернётся на 0.58 градуса, относительно неподвижного сечения A.
Расчеты на прочность при кручении
При кручении расчёты на прочность в целом похожи на расчёты при растяжении. Только здесь вместо нормальных напряжений расчёт ведётся по касательным напряжениям.
На кручение, как правило, работают детали, которые называются валами. Их назначение – передача крутящего момента от одного элемента к другому. При этом вал по всей длине имеет либо круглое сечение, либо кольцевое.
Условие прочности
За допустимое касательное напряжение [τ], часто в задачах по сопромату, принимают напряжение в два раза меньше, чем допустимое нормальное напряжение [σ]:

Максимальные касательные напряжения (τmax) в сечениях можно найти по формуле:

где T – крутящий момент в сечении;
Wp – полярный момент сопротивления сечения.
Полярные моменты сопротивления можно посчитать этим формулам.
В
произвольной
точке прямоугольного поперечного
сечения балки (рис.
3.6) касательное напряжение определяют
по формуле Д.
И. Журавского:
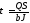
где
Q
—
поперечная сила в рассматриваемом
сечении;

момент относительно нейтральной осиz
части
площади сечения,
рис.
5. лежащей по одну
сторону от уровня у,
на
котором определяется
напряжение; b—ширина
сечения и J
= bh3/12—момент
инерции площади сечения относительно
оси x.
Наибольшие
касательные напряжения получаются
в точках нейтральной оси (у=0). Они имеют
значение
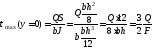
где
F=bh—площадь
поперечного сечения балки.
По
формуле (3.10) приближенно можно подсчитывать
составляющие касательных напряжений,
перпендикулярные нейтральной оси, для
балок непрямоугольного сечения, понимая
под b
ширину
сечения
на уровне рассматриваемой точки.
Результирующие касательные
напряжения в точках контура сечения
направлены по касательным
к контуру сечения, а в других точках
сечения они как-то
наклонены к плоскости действия сил.
Точно
найти касательные напряжений в балках
произвольной формы
сечения весьма сложно. Приближенное их
определение основано на некоторых
произвольных допущениях о направлении
касательных
напряжений внутри сечения.
Прочность
балки по касательным напряжениям
проверяется в точках
с максимальными касательными напряжениями
того поперечного
сечения, в котором действует наибольшая
по абсолютному значению
поперечная сила Qmax.
Проверке
следует подвергать короткие балки,
балки с тонкой и
высокой стенкой сечения, балки,
изготовленные из материала,
плохо сопротивляющегося
сдвигу и балки, несущие
большие
нагрузки вблизи опор. Проверочная
формула имеет вид
где
SQ—статический
момент
относительно нейтральной
оси части поперечного
сечения, лежащей
по одну сторону линии
действия ттах;
bо—
ширина
сечения на линии
действия ттах.
Для большинства проверяемых сечений
ттах
действует в точках
нейтральной оси.
Допускаемое
касательное напряжение

берут равным0,5—0,7
от [
Например, для СтОС и Ст2

100 МПа, для сосны и ели
Пример:
Дано: М1
=
40 кНм, М2
=
20 кНм,
М3
=
10 кНм, а=1
м;
6 = 4 cm;
h
=12
см (рис. 6). Определить
аА
и
хл
в
сечении
Решение.
Реакции опор
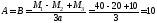
Эпюры
Q
и
М
показаны
на рис. 3.11. В сечении тп
М=-
(30
+ 20)/2 = — 25 кН-м; Q
=
10 кН.
Так
как точка А
находится
в растянутой зоне сечения, то по формуле
(3.3) находим
Рис
6
Для
прямоугольного сечения
Для
рассматриваемой точки А
поэтому
Па
= 130 МПа.
По
формуле (3.10),
5.4. Главные напряжения и полная проверка прочности балок
В
произвольной точке поперечного сечения
балки, находящейся на расстоянии у
от
нейтральной оси г, нормальные

напряжения
определяют по формулам

момент инерции и статический
момент относительно нейтральной оси
х
Элемент,
выделенный около этой точки бесконечно
близкими поперечными сечениями на
расстоянии dх
друг от друга и бесконечно близкими
продольными сечениями, параллельными
нейтральному слою,
на расстоянии dу
друг
от друга, испытывает плоское напряженное
состояние вида, указанного на рис. 3.14.
Нормальные
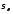
касательные

сечения,проходящей
через эту точку (рис. 3.15), имеют значения
Две
взаимно перпендикулярные наклонные
плоскости являются главными
плоскостями напряжений в данной точке
балки, когда

(3.14)
Главные
напряжения а£
и а3
находят из выражения
Рис
9
Экстремальные
касательные напряжения определяют
по
формуле
Графическое
определение значений и направлений
главных напряжений для четырех возможных
вариантов напряженных состояний
элементов, выделенных из балки, показано
на рис. 3.16,
а—г.
Если
в одном и том же поперечном сечении
балки одновременно
действуют максимальный изгибающий
момент и максимальная
поперечная сила или величины М
и
Q,
близкие
к максимальным,
то в этом сечении
производят проверку прочности
балки по главным напряжениям.
Прочность
по главным
напряжениям
проверяют только для
балок, поперечное
сечение
которых имеет тонкую стенку,
резко расширяющуюся вблизи крайних
волокон. Проверку
прочности производят
в точках перехода от малой
ширины сечения к большой.
Балки из пластичного материала
проверяют по третьей гипотезе
прочности по формуле
Балки
из хрупкого материала проверяют по
первой гипотезе прочности
согласно условию
Полный
расчет на прочность статически
определяемой балки дадим
в примере
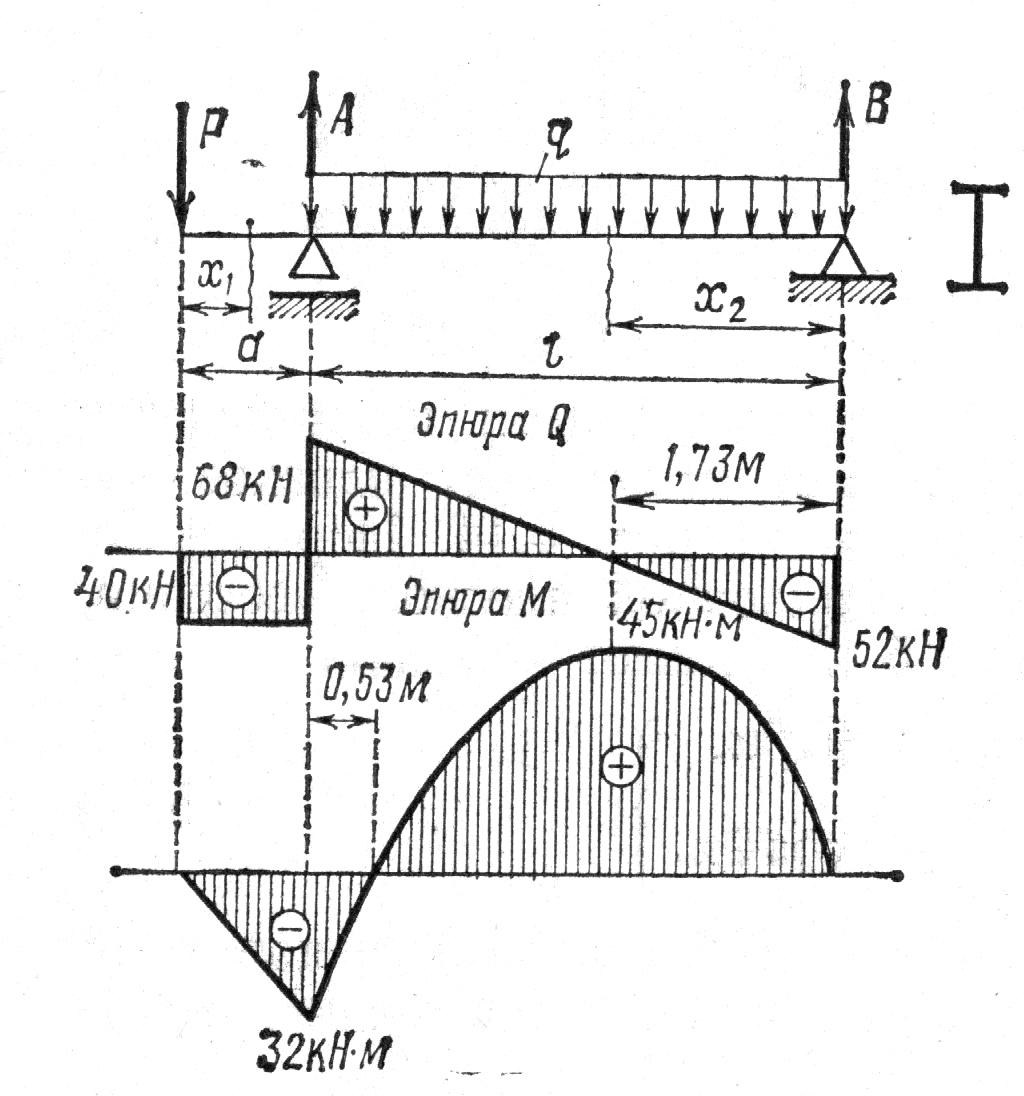
Пример
Дано:
Р = 40 кН, q
= 30 кН/м,
а = 0,8 м, l
= 4м,

160МПа,
100МПа (рис. 3.17). Определитьномер
двутавровой балки.
Решение.
1. Определение
опорных реакций:
2.
Построение
эпюр Q
и М. На
консоли
В
пролете между опорами
Так
как Qx2=-
52 + 30x2
= 0 при x2
= 52/30=
1.73м, то

По
этим данным на рис. 3.17 построены эпюры
Q
и М.
3.
Подбор
сечения двутавровой балки. Так
как Мтах
= 45кН-м, то
По сортаменту для двутавра № 22а W
=
254 см3
(пере
напряжение)
Для
двутавра № 24 W= 289 см3,

Выбираем
двутавр № 24, для которого W
=
289 см3,J
= 3460 см4,
S0=163cm3,
h
= 24 см, b=
11,5см,
t
= —
0.95 см
d
= b0
= 0 56 см. h0
=h
-2t
=22,1
см (рис. 3.18). Этот двутавр будет работать
при максимальном нормальном напряжении
в крайнем волокне опасного сечения
4.
Проверка
сечения балки по касательным
напряжениям. Так
как Qmах
= 68кН,то
5.
Построение
эпюр нормальных

главных
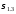
экстремальных
касательных

в
неблагоприятном
сечении балки и определение их направлений.
В
отношении главных напряжений
неблагоприятным является сечение
над левой опорой (при
подходе к ней справа), в котором М=
—32кН*м и Q
= 68kH
Нормальное
напряжение в произвольной точке,
находящейся на
расстоянии у
от
нейтральной оси,

Статический
момент площади полки относительно оси
Статический
момент части площади стенки по одну
сторону от
ординаты
Статический
момент части сечения по одну сторону
ординаты
Касательные
напряжения для точек полки, согласно
формуле (3.10),

а
для точек стенки

QS/(bJ). (в)
По
формулам (а),
(б),
(в), (3.14), (3.15), (3.16) вычислены значения-



для
у, отвечающего девяти точкам
сечения. Полученные значения сведены
в следующую таблицу:
|
Номер |
У см |
|
|
|
|
|
tg |
|
|
|
МПа |
|||||||||
|
1 |
12,00 |
111 |
0 |
±55,5 |
111 |
0 |
—0,00 |
0°0′ |
90°0′ |
|
2 |
11,05 |
102 |
2 |
±51 |
102 |
0 |
—0,0392 |
—1°7′ |
88°53′ |
|
3 |
11,05 |
102 |
44 |
±67 |
118 |
-16 |
—0,863 |
—20°24′ |
69°36′ |
|
4 |
5,52 |
51 |
53 |
±59 |
84 |
-34 |
—2,08 |
—32° |
57°50′ |
|
5 |
0,00 |
0 |
56 |
±56 |
56 |
-56 |
00 |
45°0′ |
45°0′ |
|
6 |
—5,52 |
—51 |
53 |
±59 |
34 |
-84 |
2,08 |
32°10′ |
122°10′ |
|
7 |
— |
— |
44 |
±67 |
16 |
-118 |
0,863 |
20°24′ |
110°24′ |
|
8 |
—11,05 |
—102 |
2 |
±51 |
0 |
-102 |
0,0392 |
1°7′ |
91°7′ |
|
9 |
—12,00 |
— |
0 |
±55,5 |
0 |
-111 |
0,00 |
0°0′ |
90°0′ |
Эпюры
напряжений изображены на рис. 5.19.
Направления главных
напряжений в рассмотренных точках
сечения показаны на
рис. 5.20. На рис..21 произведено графическое
определение значений и направлений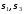
5.5.
Проверка
прочности балки по главным напряжениям.
Наиболее
опасной точкой в неблагоприятном сечении
является точка 3.
В
этой точке

МПа и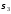
в этой точке по третьей гипотезе прочности
согласно неравенству

Так как118+
16=
134
< 160,
то
выбранное сечение
прочно и по главным напряжениям.
Рис.
136.
Проверка
прочности балки по главным напряжениям.
значений
и направлений главных напряжений Gt
и
a3
в точках 4,
5 и
5.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эпюры касательных напряжений для прямоугольного, двутаврового, круглого сечений
Эпюры касательных напряжений прямоугольного сечения
При выводе формулы Журавского предполагалось: балка имеет прямоугольное поперечное сечение (рис. 7.11), поэтому
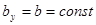
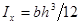
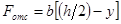
где y – расстояние от точки, в которой определяется касательное напряжение, до нейтральной оси x.
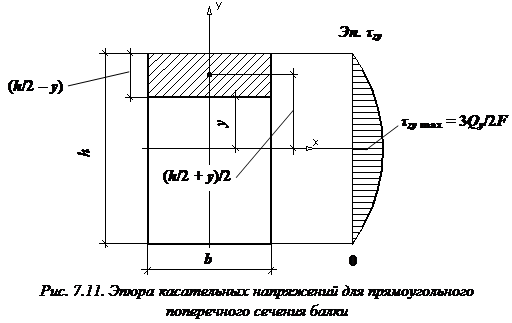
Касательные напряжения изменяются по высоте поперечного сечения по закону квадратичной параболы (см. рис. 7.11).
При 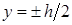
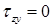
Для точек, расположенных на нейтральной оси (при 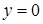
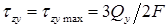
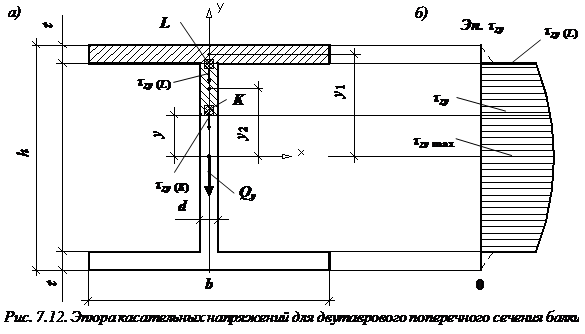
Эпюры касательных напряжений двутаврового сечения
Характерная особенность двутаврового сечения: резкое изменение ширины поперечного сечения (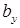
Определим касательное напряжение в некоторой точке K (рис. 7.12), проведя через нее сечение, ширина которого равна толщине стенки: 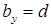
Рассмотрим верхнюю отсеченную часть поперечного сечения (заштрихована на рис. 7.12), статический момент инерции которой относительно нейтральной оси x равен сумме статических моментов инерции полки и заштрихованной части стенки:
Эпюра касательных напряжений для двутаврового сечения представлена на рис. 7.12, б.
Касательные напряжения 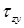
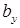
Формула касательного напряжения в точке L ( где полка соединяется со стенкой):
Наибольшие касательные напряжения возникают в точках, лежащих на нейтральной оси x.
Эпюры касательных напряжений круглого сечения
Для построения эпюры касательных напряжений круглого сечения выясним направление касательных напряжений при изгибе, возникающих в некоторой точке контура поперечного сечения стержня.
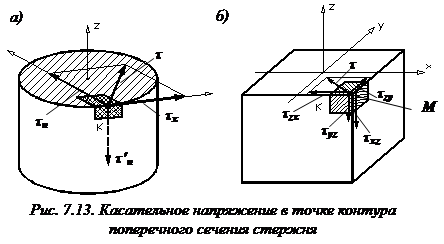
Предположим: в некоторой точке контура К касательное напряжение при изгибе 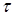
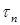
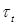
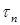
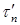
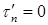
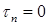
Таким образом, в точке контура поперечного сечения, поверхность которого не нагружена продольными внешними нагрузками, касательное напряжение при изгибе направлено по касательной к контуру.
Покажем, что в вершине угла поперечного сечения стержня касательное напряжение равно нулю (рис. 7.13, б).
Предположим, что в вершине угла (в точке M) возникает касательное напряжение 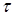
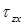
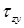
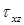
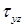
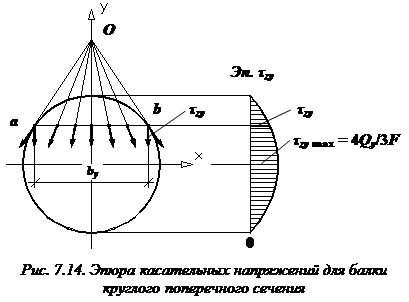 |
Задача вычисления касательных напряжений в произвольной точке балки круглого поперечного сечения усложняется. Однако если сделать предположение: в точках, расположенных на некоторой линии ab (рис. 7.14), касательные напряжения 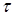
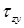
Наибольшие касательные напряжения, возникающие в точках, расположенных на нейтральной оси x, вычисляются по формуле:
В прошлой части мы выяснили, какие нормальные напряжения будут возникать при изгибе. Однако это не все воздействия, которые есть в сечении. Также необходимо учесть и касательные напряжения. Последние обычно возникают либо если сечение скручивают, либо если в нем возникают поперечные силы. О скручивании будет написано в других частях, а сегодня мы обсудим влияние поперечной силы на изгибающийся стержень. Для вычисления изменения поперечной силы и момента нам потребуется теорема Журавского, а для нахождения касательных напряжений формула Журавского
Какие силы действуют в изгибаемом стержне
В случае если на конструкцию давит сила или по ней распределена нагрузка, в ней возникают поперечные силы. Как мы уже говорили, момент – это произведение силы на плечо. И вполне естественно, что действующие в конструкциях поперечные силы будут приводить и к возникновению момента.
Для того, чтобы выяснить, как именно этот момент возникает, проведем мысленный эксперимент:
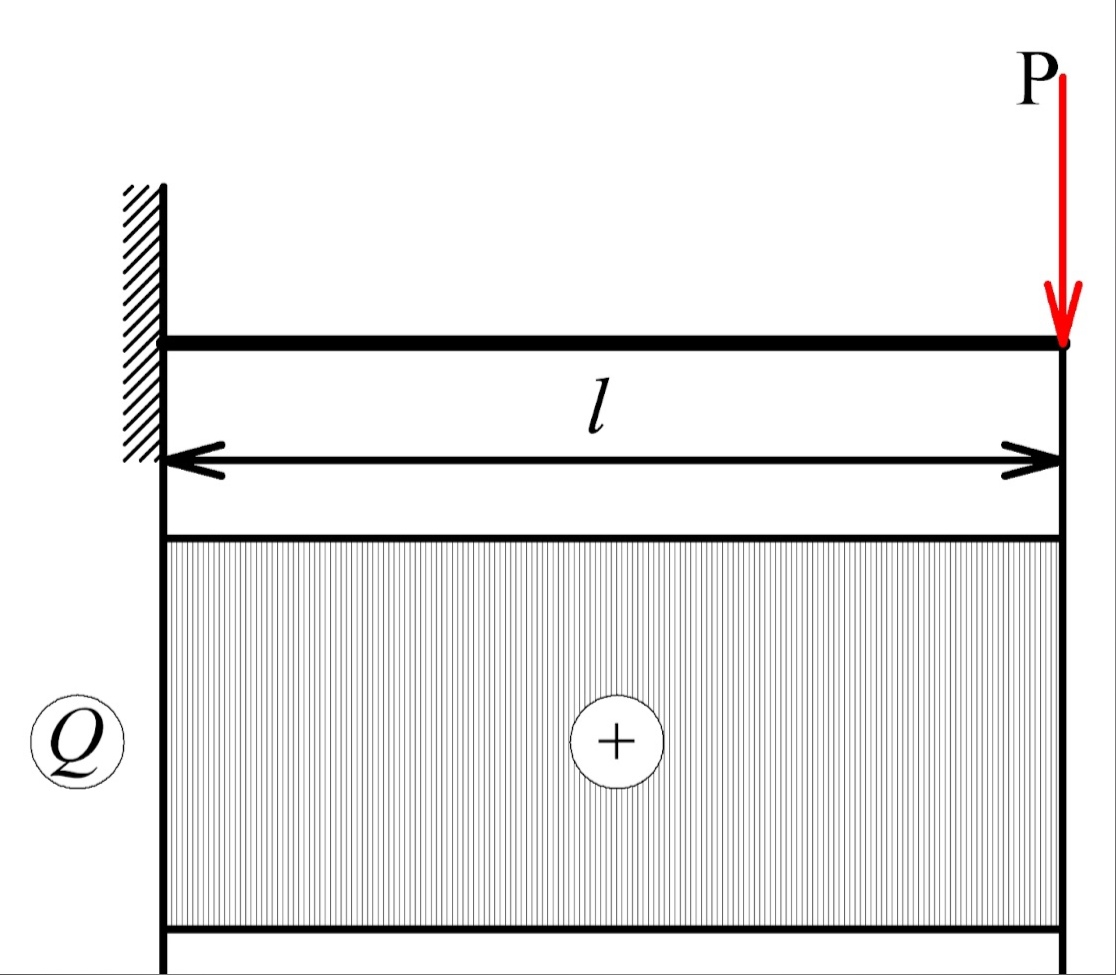
Жестко (чтобы не менял угол наклона в месте закрепления, противодействовал моменту) закрепим некоторый стержень на стене и надавим на его конец:
Теперь разделим стержень на бесконечное количество пластинок с практически нулевой шириной dx:
Сила P будет пытаться сдвинуть самую крайнюю пластинку вниз. В компенсацию этой силе в стержне возникает поперечная сила сопротивления материала Qy, направленная в противоположную приложенной сторону по плоскости сечения. По закону Ньютона, где действие, там противодействие. И по этому закону в компенсацию поперечной силы сопротивления возникает ей противоположная сила, которая будет воздействовать на следующую пластинку:
В итоге получаем достаточно прозаичную формулу распределения поперечной силы:
Qy=P
Не менее прозаично будет выглядеть и эпюра продольных сил:
Численно она будет равна приложенной к концу стержня силе. При этом, так как между центрами пластинок будет некоторое расстояние dx, на следующий элемент будет передаваться момент равный произведению силы на dx:
Итого, на первой пластинке, так как сила будет приложена к ее центру, момента m1 не будет. Момент m2 на второй пластинке будет равен произведению силы на расстояние между центрами пластинок:
m2=P*dx=P*dx
Момент третьей пластинки будет складываться из момента, который перейдет со второй пластинки и момента возникающего под действием силы:
m3=m2+P*dx=2*P*dx
В конечном счете, каждый раз, когда мы будем смещаться в сторону от места приложения силы на одну пластинку, будет меняться лишь множитель. Общая формула для момента m n-ной пластинки будет выглядеть так:
mn=n*P*dx
Ну если мы умножаем количество пластинок n на их ширину dx, то получаем расстояние от места приложения силы c. В итоге, эпюра момента под действием силы P будет выглядеть вот так:
Впрочем, помимо сил нам может попасться и распределенная нагрузка. Как в таком случае будет изменяться момент?
Рассуждения нашим будут абсолютно аналогичны. Разделим стержень на много тоненьких пластинок.
На каждую пластинку ширины dx будет действовать небольшая сила q и поперечная сила от соседней пластинки:
Сила взаимодействия между пластинками в таком случае будет накапливаться.
Найти ее можно просто перемножив расстояние от начала действия распределенной нагрузки до интересующей нас точки на величину распределенной нагрузки:
Qy=q*n*dx=q*l
Теперь разберемся с моментом. На первой пластинке момента не будет, по допущению, что сила q действует по ее середине.
На вторую пластинку же по касательной будет действовать сила q. Так как между центрами пластинок есть расстояние dx, в ней возникнет момент равный произведению q на dx:
m2=q*dx.
На третью пластинку будет действовать по касательной уже вдвое большая сила. Как следствие, для этой пластинки момент увеличится уже на 2q*dx:
dm2-3=2q*dx
Суммарный момент третьей пластинки будет складываться из момента передавшегося со второй пластинки и момента возникающего под действием нагрузки:
m3=m2+2q*dx=(2+1)dx*q
Если мы будем продолжать данную операцию и дальше, то получим общую формулу для момента m n-ной пластинки:
mn=(n+…+2+1)dx*q
Многочлен Sn=(n+…+2+1)dx- это сумма арифметической прогрессии. Ее находят как полусумму первого и последнего элемента умноженную на количество элементов:
S_n=frac{a_1+a_n}{2}cdot n
Примечание: желающие могут взглянуть на вывод этой формулы в числах (в общем виде вывод практически аналогичен, но на числах он нагляднее), с сайта umath.ru[7]:

По легенде эту формулу вывел Карл Гаусс, когда школьный учитель математики решил подшутить над учениками, заставив посчитать сумму чисел от 1 до 100.
Подставляем нашу последовательность x1=ndx+…+2dx+dx и получаем:
xn=ndx+…+2dx+dx=(dx+ndx)*ndx/2=(n+n2)dx2/2
Так как число пластинок мы сделали ну очень большим (практически бесконечным), по сравнению с n2 обычное n будет пренебрежительно мало. Например, если мы разделим стержень на 1000 пластинок, n2 от n2+n будет отличаться на одну тысячную.
В итоге, получившуюся формулу можно представить как простейшее n2/2.
Подставляем все в исходную формулу:
mn=(n+…+2+1)*q*dx=n2*dx2*q/2=ql2/2
А эпюра момента под равномерно-распределенной нагрузкой будет выглядеть как полупарабола:
Теорема Журавского
Обобщает и упрощает расчет интегрирование. А метод нахождения поперечных сил и моментов известен как теорема Журавского. Для того, чтобы найти момент в определенной точке, необходимо взять интеграл от поперечной силы по длине:
Поперечная сила не всегда постоянна на всем протяжении участка, как это, например, бывает при распределенной нагрузке. Чтобы найти поперечную силу, если балка находится под воздействием распределенной нагрузки, необходимо последнюю проинтегрировать:
Ну а для нахождения момента при распределенной нагрузке, нужно эту нагрузку дважды проинтегрировать:
M_z=int_{0}^{x}int_{0}^{x}q_y dx
Если обобщить, то для нахождения момента в сечении надо дважды проинтегрировать распределенную нагрузку, сложить это с интегралом силы по расстоянию до опоры и с моментами, которые мы приложили к этом сечении.
Теорема Журавского в дифференциальной форме выглядит так:
q=frac{dQ_y}{dx}=frac{d^2M_z}{dx^2}
Теорема Журавского позволяет вычислять попереченые силы и моменты. Отрезок балки под воздействием сложной системы сил:
Изображение расчета балки взято из онлайн-калькулятора.
Подробнее почитать о построении эпюр можно в соответствующей статье.
Выражены формулы взаимосвязи распределенной нагрузки, поперечных напряжений и моментов были Дмитрием Ивановичем Журавским и обобщаются как теорема Журавского.
Формула Журавского
В процессе проектирования железнодорожных мостов деревянные балки часто давали скол. На тот момент не было теоретического аппарата для выяснения точных значений касательных напряжений в сечении. Их либо не учитывали, либо, по аналогии с нормальными напряжениями при растяжении/сжатии, считали равномерно-распределенными по всему сечению (т.е. τ=Qy/F).
Однако реальность упорно не хотела следовать расчетам: конструкции разрушались, хотя не должны были.
При этом нормальных напряжений явно было недостаточно для скола. Журавский данную проблему решил за счет добавления в уравнение касательных напряжений и нашёл закон их распределения по сечению. Попробуем и сами вывести закон распределения касательных напряжений (более известный как формула Журавского).
У нас есть балка произвольного сечения под нагрузкой:

В этом стержне, под действием распределенной нагрузки изменяются момент и нормальные напряжения:
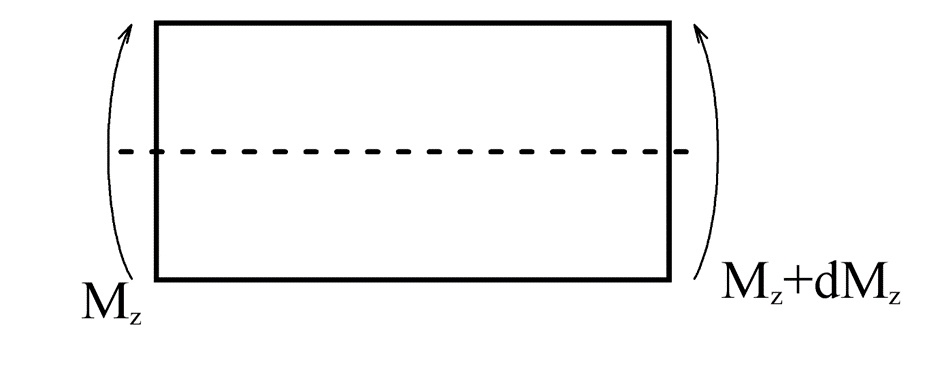

Если мы отсечем верхнюю или нижнюю часть стержня (так, чтобы линия среза была параллельна нейтральной линии), на данном участке возникнет нескомпенсированная продольная сила:

Журавский предположил, что ключом к ответу на вопрос, как именно распределяются по сечению касательные напряжения, может стать решение проблемы этой нескомпенсированной силы.
Разберемся в том, как касательные напряжения вообще могут распространяться в материале.
Для этого вырежем из какой-то не разрушившейся конструкции куб с пренебрежительно малыми сторонами. Затем приложим к одной из его граней силу по касательной. Для того, чтобы куб уравновесить, необходимо приложить к поверхности этой грани касательную силу, но в другом направлении:

От касательных сил возникнет момент. А так как мы вырезаем куб из целой, не разрушенной конструкции, все силы и моменты должны быть скомпенсированы. Поэтому на соседних гранях возникнут такие же касательные напряжения с противоположным моментом:

Иными словами, если конструкция сохраняет свою форму, каждое касательное напряжение по оси x на одной из сторон куба будет уравновешено точно таким же, но в обратном направлении на противоположной стороне куба. А получившийся момент будет скомпенсирован касательными напряжениями по оси y.
Так как касательные напряжения по y приведут к возникновению точно таких же касательных напряжений по x, разумно предположить, что приращение нормальных напряжений можно скомпенсировать касательными напряжениями.
Возвращаемся к нашему стержню. Мы вырезали некоторую его часть и хотим компенсировать избыток продольной силы, за счет касательных напряжений приложенных к поверхности горизонтального сечения:

Для того, чтобы система оставалась неподвижной, необходимо, чтобы продольные и касательные силы в сумме давали ноль:
-N+(N+dN)-τ*b(y)=0
dN-τ*b(y)=0
dN=τ*b(y)
Остается дело за малым: выяснить чему будет равно изменение продольной силы на отсеченной нами части. Для этого нам нужно просуммировать все напряжения в ней возникающие:
dN=∑dσ=∫dσdF
Подставляем формулу из прошлой части для нахождения нормальных напряжений при изгибе и изменения момента под действием поперечной силы из этой:
dσ=ydMz/Jz, dMz=Qy
Примечание: дальше мы будем использовать такие понятия как момент инерции I и статический момент S. Если вы хотите поподробнее узнать про то, откуда появились данные величины, каков их физический смысл и как их находить, то вы можете это сделать прочитав наши статьи:
- Статический момент
- Момент инерции
- Момент сопротивления изгибу
В итоге избыток продольной силы будет равен:
dN=frac{Q_ycdot dx}{I_z} int y dF
Fотс.∫ydF — это статический момент инерции отсеченной фигуры Sотс. Таким образом формулу можно записать чуть элегантнее:
dN=frac{Q_ycdot S_{отс.}cdot dx}{I_z}
Как мы уже говорили, чтобы тело находилось в равновесии необходимо, чтобы избыточная продольная сила компенсировалась касательной:
dN-τcdot bcdot dx=dx(frac{Q_ycdot S_{отс.}}{I_z}-τcdot b)=0;
Или:
τcdot b=frac{Q_ycdot S_{отс.}}{I_z}
Теперь мы можем сказать, по какому закону будут распределяться касательные напряжения при изгибе:
τ=frac{Q_ycdot S_{отс.}}{I_zcdot b}
Вычисление касательных напряжений по формуле Журавского
Разберем распределение касательных нагрузок на простейшем примере. На прямоугольном брусе.
Нам нужно выяснить, какие касательные напряжения будут в каждой точке сечения. Величина Qy нам задана. Ширина b тоже. Момент инерции Iz мы тоже для всего сечения мы тоже знаем:
I_z=frac{bcdot h^3}{12}
Остаётся найти момент отсеченной части. В данном случае мы отсекаем все, что снизу:

Статический момент (посмотреть как вычисляется можно по ссылке) равен произведению площади на центр масс:
Sотс=F*l
Где l расстояние до центра масс (в данном случае до середины) отсеченной фигуры, а F площадь, которую можно найти перемножив высоту отсекаемого прямоугольника (h/2-y) на его ширину b. Расстояние до центра масс же можно найти сложив верхнюю (h/2) и нижнюю (y) границу и поделив это выражение на два (потому-что нам интересно найти середину):
I_z=frac{frac{h}{2}+y}{2}
S_{отс.}=Fcdot l=frac{b(frac{h}{2}+y)(frac{h}{2}-y)}{2}
Получаем напряжение в середине:
τ=frac{Q_ycdot S_{отс.}}{bcdot I_z}=frac{12cdot Q_y cdot bcdot(frac{h^2}{4}-y^2)}{2cdot b^3cdot h^3}=frac{6cdot Q_y cdot (frac{h^2}{4}-y^2)}{b^2cdot h^3}
Теперь остается только подставить в уравнение получившуюся для этого сечения поперечную силу Qy и можно посчитать, какие касательные напряжения будут возникать на каждом расстоянии y от нейтральной линии.
Так как в уравнении меняться будет только y, выражение можно представить в виде:
τ=C-B*y^2
Где B и C константы, а при y=h/2 τ=0.
Ну и, очевидно, что когда y=0 (т.е. посередине сечения), напряжение максимально.

Т.е. изменяться касательные напряжения будут по параболе, где максимум будет на средней линии, а ноль на верхней и нижней грани сечения.

Если сечение не прямоугольное, ширину b надо будет представить как некую функцию b(y).
τ=frac{Q_y cdot S_{отс.}(y)}{b(y)cdot I_z}
Форма эпюры напряжений могут меняться, но характер будет будет остаться прежним: по мере движения к центру напряжения будут расти.

Ещё в прошлой части мы вывели закон распределения нормальных напряжений при изгибе: напряжения изменяются по линейному закону от своего минимального (максимальное сжатие) до максимального (максимальное растяжение) значения.

А сейчас мы выяснили, как распределяются по сечению касательные напряжения. Если стержень имеет одинаковую ширину на всей высоте сечения, то напряжения меняются по параболе. Но в прошлой части мы также говорили, что для экономии материала гораздо целесообразнее использовать сечения сложной формы (для нахождения моментов инерции гуглить “сортамент, прокатные профили”).
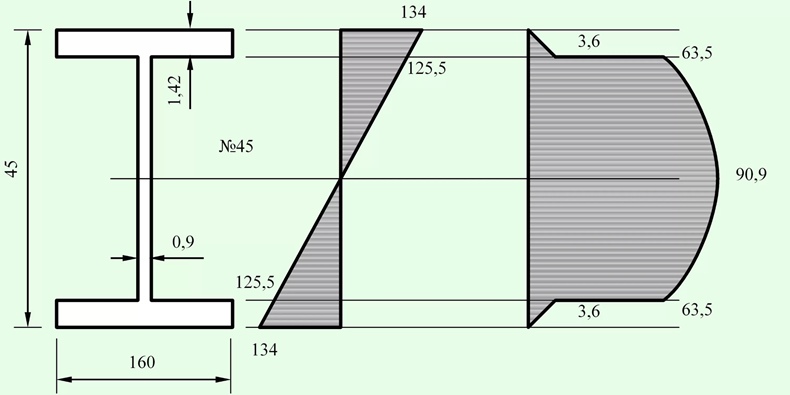
Например двутавр, у которого максимальная ширина по краям, где нормальные напряжения максимальны. Как мы уже выяснили, касательные напряжения сильно зависят от ширины сечения. Есть точки, где ширина уменьшается и происходит увеличение касательных напряжений, но нормальные напряжения все ещё велики. Их следует проверить, точно ли они выдержат нагрузки. И необходим математический аппарат для предсказания прочности, учитывающий эти два вида нагрузок.
И на него нет однозначного, исчерпывающего ответа. Но есть ответы практические, каждый справедливый для своих границ применимости. И эти ответы называются теориями прочности. И о них мы расскажем в будущем.
В рамках темы изгиба наибольшую применимость имеет теория «Наибольших касательных напряжений» (Третья теория прочности). Чаще всего её используют для металлов или материалов, плохо сопротивляющихся сдвигу.
Для того, чтобы понять, выдержит ли материал, в рамках теории наибольших касательных напряжений, нормальные и касательные напряжения приводят к эквивалентным напряжениям, которые должны быть меньше предельных напряжений при растяжении/сжатии по определенной формуле. Ее вывод мы сейчас производить не будем, предлагаем просто поверить на слово, что эквивалентные напряжения должны быть меньше опасных и рассчитываются так:
σэкв.=√(σ2+4τ2)<[σ]
Возвращаемся к двутавру. Какие у него будут самые опасные точки, которые надо проверить? Такие, где возникают максимальные напряжения и где высокие и нормальные и касательные напряжения:
Из прошлой части мы знаем, что наибольшие нормальные напряжения находятся на самых удаленных от нейтральной линии участках сечения. Так как там отсутствуют касательные напряжения, достаточно чтобы нормальные напряжения были меньше опасных:
134МПа<[σ]
Максимальные касательные напряжения возникают в середине сечения. Так как нормальные напряжения будут равны нулю, формула σэкв.=√(σ2+4τ2) превращается в простейшее σэкв.=√(4τ2)=σэкв.=2τ
Подставляем значение и оказывается, что материал должен выдерживать аж 182 МПа:
2τ=91*2=182МПа<[σ]
Если данный материал такие напряжения выдерживать не способен, придется выбирать другой прокатный профиль (например, с большей шириной промежуточной полки). Ну а если способен, надо рассчитать третью точку. Она будет находиться на месте, где промежуточная узкая полка переходит в широкую. Подставляем в формулу значения нормальных и касательных напряжений:
σэкв.=√(σ2+4τ2)=√(1342+4*642)=√(19.000+4*4.100)=√35400=188,2 МПа<[σ]
Если допускаемые напряжения меньше, значит сечение подходит. Если нет, значит придется искать сечение с лучшей способностью сопротивления касательным и нормальным напряжениям. Например, следующий номер двутавра.
Для того, чтобы выяснить, выдержит ли деталь нагрузку, необходимо проверять эквивалентные напряжения (с чем поможет формула Журавского и третья теория прочности) в максимумах моментов и поперечных сил (с чем поможет теорема Журавского), а также на местах, где совпадают большие моменты и поперечные силы:
Вот мы и разобрались с ещё одним источником опасности для прочности конструкции: с касательными напряжениями от поперечных сил. Главный инструмент в поиске поперечных сил, моментов — теорема Журавского. А найти касательные напряжения поможет формула Журавского.
Теперь в теме изгиба нам остаётся только научиться считать, как будет деформироваться балка под действием момента.
Информация о произведении
Автор: К.А.Овчинников
Редактор, факт-чекер: Д.А. Сабуров, Марк Ершов
Иллюстратор: Михаил Корнев [I]
Информация о произведении:
Условия использования: свободное некоммерческое использование при условии указания людей участвовавших в его создании и ссылку на первоисточник (статьи на действующем сайте интернет-журнала «Стройка Века»).
Для коммерческого использования — обращаться на почту:
buildxxvek@gmail.com
Источники
- Лекции по сопротивлению материалов в СПбПУ им. Петра Великого
- Горшков А. Г., Трошин В. Н., Шалашилин В. И. Сопротивление материалов. – Физматлит, 2002. – С. 548-548.
- iSopromat Формула Журавского // https://youtu.be/4rsFdn5fSrU
- Kirsanov2011 Формула Журавского // https://youtu.be/AZE70B9m2lA
- Основные теории прочности // http://sopromat.in.ua/handbook/teorii-prochnosti
- Гипотезы прочности // http://k-a-t.ru/tex_mex/5-sochetanie_defor2/index.shtml
- https://umath.ru/theory/posledovatelnosti/arifmeticheskaya-progressiya/
5 792
Определение касательных напряжений в двутавровом сечении. Рассмотрим сечение двутавра. Sx=96,9 см3; Yх=2030 см4; Q=200 кН
Для определения касательного напряжения применяется формула Д.И. Журавского ,где Q — поперечная сила в сечении, Sx0 – статический момент части поперечного сечения, расположенной по одну сторону от слоя, в котором определяются касательные напряжения, Ix – момент инерции всего поперечного сечения, b – ширина сечения в том месте, где определяется касательное напряжение
Вычислим максимальное касательное напряжение:
Вычислим статический момент для верхней полки:
Теперь вычислим касательные напряжения:
Строим эпюру касательных напряжений:
Касательные напряжения в балке двутаврового сечения