Как найти какое число точнее

1. Задачи на вычисление погрешностей

1. Определить, какое равенство точнее:

9/11 =
0.818
4.24

Находят значения
данных выражений с большим числом
десятичных знаков:

a₁
= 9/11 = 0.81818… a₂
=
4.2426…

Вычисляют предельные
абсолютные погрешности, округляя их с
избытком:

Предельные
абсолютные погрешности составляют:

%

%

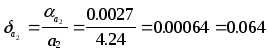
Так как
,
то 9/11=0.818 является более точным.

2. Определить сомнительные цифры числа, оставив верные знаки: а) в узком смысле; б) в широком смысле. Определить абсолютную погрешность результата:

а)
72.353 (0.026)
б) 2.3544 =0.2%.

а) Пусть
72.353 ( 
0.026) = а. Согласно условию, погрешность
_а
= 0.026 <
0.05
. Это означает, что в числе 72.353 верными
в узком смысле являются цифры 7, 2, 3. По
правилам округления находят приближенное
значение числа, сохранив десятые доли:

а₁
= 72.4;

Полученная
погрешность больше 0.05; значит, нужно
уменьшить число цифр в приближенном
числе до двух:

а₂
= 72;

Так как
<
0.5, то
обе оставшиеся цифры верны в узком
смысле.

б) Пусть
а = 2.3544; _а
= 0.2%; тогда _а
= а * _а
=
0.00471. В данном числе верными в широком
смысле являются три цифры, поэтому
округляем его, сохраняя эти три цифры:

а₁
= 2.35;

Значит, и в
округленном числе 2.35 все три цифры верны
в широком смысле.

3. Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры: а) в узком смысле; б) в широком смысле.

а) 0.4357 б)
12.384

а) Так
как все четыре числа а = 0.4357 верны в узком
смысле, то абсолютная погрешность _а

= 0.00005, а относительная погрешность _а
= 1 / (2 * 4 * 10³)
= 0.000125 = 0.0125% .

б) Так
как все пять цифр числа а = 12.384 верны в
широком смысле, то _а

= 0.001, а относительная погрешность _а
= 1 / (1 * 10⁴)
= 0.0001 = 0.01% .

4. Вычислить и определить погрешности результата:

где m
= 28.3 (
0.02), n = 7.45 (
0.01), k = 0.678 (
0.003)

Вычисляют

m²
= 800.9; _m
= 0.02 / 28.3 = 0.00071

n³
= 413.5; _n
= 0.01 / 7.45 = 0.00135

_k
= 0.003 / 0.678 = 0.00443

Тогда

_X
= 2 _m
+ 3 _n
+ 0.5 _k
= 0.00142 + 0.00405 + 0.00222 = 0.00769 = 0.77%

_X
= 4.02 10⁵
* 0.0077 = 3.1 10³

Ответ:
X = 4.02 10⁵
(
3.1 10³)
; _X
= 0.77%

5. Вычислить и определить погрешности результата:

где n
= 3.0567 (
0.0001) , m = 5.72 (
0.02)

Имеем
n — 1 = 2.0567
(
0.0001) ; m + n = 5.72 (
0.02) + 3.0567 (
0.0001) = 8.7767 (
0.0201) ; m — n = 5.72 (
0.02) — 3.0567 (
0.0001) = 2.6633 (
0.0201) .

%

Ответ:
N 
2.54 (
0.044): _N
= 1.74% .

6. Вычислить, пользуясь правилами подсчета цифр

,
где h
= 11.8 и
R = 23.67

V = 3.142 * 11.8²
* (23.67 — 3.933) = 3.142 * 11.8²
* 19.737 = 3.142 * 139.2 * 19.737 = 437.37 * 19.737 = 8630 
8.63 10³
.

Соседние файлы в папке 2

• #
• #
• #
• #
• #
• #
• #
• #

Что может быть проще (сложнее), чем упорядочивание чисел?

Предположим, вы программист и у вас есть два числа. Вы хотите узнать, какое из чисел больше. Если оба числа имеют одинаковый тип, то почти в любом языке программирования решение будет тривиальным. Для этой операции обычно даже есть специальный оператор <=. Вот пример на Python:

>>> "120" <= "1132"
False

Сравнение двух чисел на Brainfuck оставим в качестве упражнения для читателя.

Ой. Ну, строго говоря, это строки, а не числа, а строки обычно сортируются лексикографически. Но это всё-таки числа, хотя и представленные в виде строк. Это может показаться глупым, но такая проблема очень распространена в интерфейсах пользователя, например, в списках файлов. Именно поэтому нужно отбивать числовые имена файлов нулями (frame-00001.png) или использовать описания, сохраняющие лексикографический порядок, например, ISO 8601 для дат.

Впрочем, я отклонился от темы. Предположим, числа действительно представлены числовыми типами. Тогда всё просто и <= отлично работает:

>>> 120 <= 1132
True

Но так ли это?

Сравнения разных целочисленных типов

Что если два сравниваемых числа не имеют одного типа? Первым делом мы можем всё равно попробовать использовать <=. Вот пример на C++:

std::cout << ((-1) <= 1u) << "n";  // Выводит 0.

Ой. C++ автоматически преобразовал -1 в unsigned int, из-за чего значение превратилось в максимальное значение типа (которое очевидно больше 1). Но, по крайней мере, современный компилятор по умолчанию ведь предупреждает о таких вещах?

$ g++ -std=c++20 main.cpp && ./a.out
0

Любопытно было бы прочитать исследование о том, сколько багов возникло из-за сравнения разных целочисленных типов. Не удивился бы, что их довольно много, особенно на C.

Отлично. Ещё одна причина не забывать включать предупреждения (-Wall -pedantic).

Попробуем Rust:

let x: i32 = -1; let y: u32 = 1;
println!("{:?}", x <= y);

error[E0308]: mismatched types
 --> src/main.rs:4:22
  |
4 | println!("{:?}", x <= y);
  |                      ^ expected `i32`, found `u32`
  |
help: you can convert a `u32` to an `i32` and panic if the converted value doesn't fit

Ну, по крайней мере, он не выполняет втихомолку ошибочную компиляцию… Однако предлагаемое решение ужасно. Нет никаких причин для паники. Наиболее эффективное решение здесь — преобразовать оба значения в тип, являющийся надмножеством обоих. Например:

println!("{:?}", (x as i64) <= (y as i64)); // Выводит true.

Но что если типа, являющегося надмножеством обоих, не существует? По крайней мере, для типов integer это не проблема. Например, в Rust нет типа, являющегося надмножеством i128 и u128. Но мы знаем, что i128 при неотрицательности соответствует u128, а если он отрицателен, то всегда меньше:

fn less_eq(x: i128, y: u128) -> bool {
    if x <= 0 { true } else { x as u128 <= y }
}

Всё это может вызывать ошибки, да и попросту раздражает. Сравнения между разными типами integer всегда малозатратны, поэтому я не вижу веских причин того, что компилятор не генерирует показанный выше код автоматически. Например, на Apple ARM показанное выше для i64 <= u64 компилируется в три команды:

example::less_eq:
        cmp     x0, #1
        ccmp    x0, x1, #0, ge
        cset    w0, ls
        ret

Компилятор должен сам делать всё правильно, а не заставлять людей выполнять вручную преобразования, которые могут быть и ошибочными, или, хуже того, втихомолку генерировать неверный код. По крайней мере, в C++20 появились новые функции сравнения integer для сравнений между разными типами integer, но обычные операторы сравнения по-прежнему столь же опасны.

Числа с плавающей запятой точны

Прежде чем углубляться в сравнения разных типов с плавающей запятой, надо вкратце вспомнить, что же такое плавающая запятая. Когда я говорю о плавающей запятой, то подразумеваю двоичные числа с плавающей запятой, определяемые стандартом IEEE 754, в частности, binary32 (также известный как f32 или float) и binary64 (также известный как f64 или double). Последняя версия стандарта имеет DOI 10.1109/IEEESTD.2019.8766229.

А вы знали о существовании Sci-Hub? Это важный проект, устраняющий преграды и paywall перед человеческим знанием. Обычно, если у вас есть DOI-ссылка, то документ можно найти всего за пару кликов! (В некоторых юрисдикциях это может быть незаконным.)

Вспомним IEEE 754

Этот формат чисел с плавающей запятой имеет множество странностей, но с большой вероятностью машина, на которой вы читаете мою статью, использует его в качестве нативной реализации floating point. В этом формате число состоит из одного бита знака,

битов экспоненты и

завершающих битов мантиссы. Для f32

, а

, для f64

. Также есть смещение экспоненты

, которое равно

для f32 и

для f64; оно используется для получения отрицательных экспонент.

Чтобы расшифровать число с плавающей запятой (пока забудем о разных NaN и бесконечностях), мы сначала смотрим на

битов и декодируем три беззнаковых двоичных целых числа

,

и

:

Тогда если

, значение числа будет равно

а в противном случае

Именно поэтому это называется завершающими битами мантиссы: первая цифра мантиссы определяется экспонентой. Когда поле экспоненты равно нулю (до применения смещения), мантисса начинается с

, в противном случае она начинается с

. Когда мантисса начинается с

, это называется денормализованным числом. Они важны, потому что закрывают пробел между нулём и первым числом с плавающей запятой. Хорошенько понять всё это вам помогут эксперименты с приложением Float Toy.

Неточность

После того, как мы с этим разобрались, нужно сказать следующее: типы с плавающей запятой стандарта IEEE 754 определяют множество точных чисел. В них нет никакой двусмысленности (за исключением двух видов нуля,

и

), как нет и потери точности, нечёткости, интервальных представлений и так далее. Например,

точно представлено в f32 значением 0x3f800000, а следующее по величине число f32 — это 0x3f800001 со значением

.

Пример на Rust:

println!("{}", f32::from_bits(0x3f800001));
1.0000001

Ой. Я что, соврал? Нет, лжёт именно Rust:

let full = format!("{:.1000}", f32::from_bits(0x3f800001));
println!("{}", full.trim_end_matches('0'));
1.00000011920928955078125

Это не баг и не случайность. Rust (и, на самом деле, большинство языков программирования) пытается выводить как можно меньше цифр, чтобы гарантировать корректность round-trip. И в самом деле:

println!("0x{:x}", "1.0000001".parse::<f32>().unwrap().to_bits());
0x3f800001

Однако это имеет неприятные последствия, если вы затем парсите число как тип с более высокой точностью:

"1.0000001".parse::<f64>().unwrap() == 1.00000011920928955078125
false

Помните, что значение

точно представимо и в f32, и в f64 (потому что f32 является строгим подмножеством f64), однако мы теряем точность, выводя число как f32 и выполняя его парсинг как f64. Причина в том, что хотя 1.0000001 — это самое короткое десятичное число, которое округляется до

в формате чисел с плавающей запятой f32, в формате f64 оно округляется до

.

Иронично то, что в данном случае было бы точнее выполнить парсинг как f32 и преобразовать значение в f64, потому что Rust гарантирует корректность round-trip:

"1.0000001".parse::<f32>().unwrap() as f64 == 1.00000011920928955078125
true

То есть f32 -> f64 выполняется без потерь, как и f32 -> String -> f32 -> f64. Однако при f32 -> String -> f64 точность теряется.

Для выявления и отладки проблем с плавающей запятой критически важно понять вышеизложенное. При вводе числа в исходном коде языки программирования втихомолку округляют число с плавающей запятой до ближайшего числа, которое можно представить, втихомолку округляют его при парсинге и втихомолку округляют его при выводе. Способы округления в разных языках отличаются, они могут отличаться даже в зависимости от типа.
На каждом этапе пути вам потенциально могут врать.

Учитывая объёмы незаметного округления, я не буду винить вас, если у вас сложилось впечатление о числах с плавающей запятой как о «нечётких». Они создают иллюзию существования типа «вещественного числа». Однако в реальности внутри языка значения являются точным конечным множеством чисел.

Сравнения разных типов с плавающей запятой

Почему я делаю такой большой упор на точность чисел с плавающей запятой стандарта IEEE 754? Потому что она означает (за исключением NaN), что сравнение целых чисел и чисел с плавающей запятой тоже определено чрезвычайно точно и без всяких двусмысленностей. В конечном итоге, все они являются точными числами, помещёнными на прямую вещественных чисел.

Прежде чем вы продолжите чтение, предлагаю вам задачу: попробуйте написать корректную реализацию следующей функции:

/// x <= y
fn is_less_eq(x: i64, y: f64) -> bool {
    todo!()
}

Если вы хотите попробовать сделать это на Rust, то я написал набор тестов (не исчерпывающий) в песочнице Rust. Можно вставить туда свою реализацию, которая покажет вам, при каких входных данных функция даёт сбой. Если вы хотите попробовать сделать это на другом языке, то помните, что язык программирования может лгать вам по умолчанию! Например:

let x: i64 = 1 << 58;
let y: f64 = x as f64; // 2^58, можно представить в точном виде.
println!("{x} <= {y}: {}", x as f64 <= y);
288230376151711744 <= 288230376151711740: true

Это может показаться плохим сравнением или преобразованием из i64 в f64, но на самом деле это не так. Проблема целиком связана с округлением при форматировании.

Основная сложность заключается в том, что для многих сочетаний типов (например, i64 и f64) в языке программирования не существует нативного типа, являющегося надмножеством обоих. Например,

можно точно представить как f64, но не как i64. А

точно представимо в i64, но не в f64. Поэтому мы не можем просто преобразовать одно в другое и закончить на этом, однако так поступают очень многие люди. На самом деле, это настолько распространено, что даже ChatGPT научился это делать:

Бесполезно просить ChatGPT устранить баг с явным контрпримером, он будет болтать какую-то чушь об f64::EPSILON и сравнивать разницу с ним.

Приведённая выше тестовая среда показывает, что проверка x as f64 <= y не проходит, поскольку мы выяснили, что

9007199254740993 as f64 <= 9007199254740992.0

а это очевидно ошибочно. Проблема в том, что значение 9007199254740993 (то есть

) нельзя представить в f64 и оно округляется до

, после чего сравнение выполняется успешно.

Корректная реализация i64 <= f64

Чтобы реализовать

корректно, нужно выполнить операцию в целочисленной области определения после округления числа с плавающей запятой до ближайшего целочисленного, поскольку для целочисленного

мы имеем

Нам не нужно беспокоиться о том, что округление числа с плавающей запятой вверх или вниз до ближайшего целого произойдёт неверно и мы пропустим целое число, поскольку для IEEE 754 функции floor / ceil точны. Так происходит потому, что в части числовой прямой, где числа с плавающей запятой IEEE 754 являются дробными, целые числа тоже расположены плотно.

Но нам всё равно стоит беспокоиться о том, что значение с плавающей запятой не соответствует целочисленному типу. К счастью, когда такое происходит, сравнение выполняется тривиально. К несчастью, целочисленные типы имеют другой интервал в положительной и отрицательной областях определения, поэтому всё равно нужно быть немного осмотрительными, особенно потому что мы не можем сравнивать с

(максимальное значение i64) в области определения с плавающей запятой.

fn is_less_eq(x: i64, y: f64) -> bool {
    if y.is_nan() { return false; }
    if y >= 9223372036854775808.0 { // 2^63
        true // y всегда больше.
    } else if y >= -9223372036854775808.0 { // -2^63
        x <= y.floor() as i64  // y находится в [-2^63, 2^63)
    } else {
        false // y всегда меньше.
    }
}

Возможно, вы подумаете, что можно обойтись без floor, поскольку сразу после него мы выполняем преобразование в целое число. Увы, as i64 выполняет округление в сторону нуля, но нам нужно выполнять в сторону отрицательной бесконечности, в противном случае мы заявим, что -1 <= -1.5.

Обобщение

Отлично, мы можем выполнять сравнение

. А как насчёт

? Мы не можем снова использовать ту же реализацию, поменяв порядок аргументов, поскольку их типы различаются. Однако мы можем создать новую реализацию с нуля, применив тот же принцип; при этом придётся использовать ceil вместо floor:

fn is_greater_eq(x: i64, y: f64) -> bool {
    if y.is_nan() { return false; }
    if y >= 9223372036854775808.0 { // 2^63
        false // y всегда больше.
    } else if y >= -9223372036854775808.0 { // -2^63
        x >= y.ceil() as i64  // y находится в [-2^63, 2^63)
    } else {
        true // y всегда меньше.
    }
}

Но что если мы хотим строгого неравенства? Теперь наш трюк с floor/ceil добавляет проблемы, связанные с равенством. Решить их можно отдельной проверкой на равенство в области определения целых чисел, а затем проверкой на неравенство в области определения чисел с плавающей запятой:

fn is_less(x: i64, y: f64) -> bool {
    if y.is_nan() { return false; }
    if y >= 9223372036854775808.0 { // 2^63
        true
    } else if y >= -9223372036854775808.0 { // -2^63
        let yf = y.floor(); // y находится в [-2^63, 2^63)
        let yfi = yf as i64;
        x < yfi || x == yfi && yf < y
    } else {
        false
    }
}

Принцип понятен. Возможно, есть более умные и/или эффективные способы решения задачи, но, по крайней мере, этот работает.

Заключение

Итак, насколько сложным может быть упорядочивание чисел? Я бы сказал, что довольно-таки сложным, если язык, с которым вы работаете, не поддерживает его нативно. Судя по тому, как разные люди решали задачу корректной реализации is_less_eq, никто не может сделать это правильно с первой попытки. И это после того, как им чётко сказали, что сложность в том, чтобы сделать это корректно для всех входных данных. Цитата из стандартной библиотеки Python: «сравнение — это настоящий кошмар».

Из всех рассмотренных мной языков с чётким разделением на типы целых чисел и чисел с плавающей запятой это правильно реализовано в Python, Julia, Ruby и Go. Отличная работа! Некоторые языки по умолчанию предупреждают или просто не разрешают выполнять сравнения между разными типами, однако, например, Kotlin просто говорит, что 9007199254740993 <= 9007199254740992.0 является true.

Я создал для Rust крейт num-ord, позволяющий корректно сравнивать два любых встроенных числовых типа. Но мне бы хотелось, чтобы в этом и других языках всё делалось правильно нативно. Потому что если этого не будет, то людям придётся решать такую задачу самостоятельно, на что они чаще всего неспособны.

20 < m < 30.

Заменив потом гирю  10 г  гирей  5 г, и убедимся, что масса детали больше  25 г,

То есть

25 < m < 30.

Положив на чашу весов с гирьками еще  2 г, заметим, что масса
детали меньше чем  27 г.

25 < m < 27.

Поскольку более мелких гирь нет, то процесс определения
массы на этом этапе закончим.

Взвешиваниями мы нашли приближенные значения массы детали
в граммах:

26 г – приближённое значение с
недостачей,

27 г – приближённое значение с излишком.

Другими словами, мы установили границы значения массы в
граммах. Число  26 – нижняя граница, число 
27 –
верхняя граница.

Заметим, что когда бы наименьшая гиря была бы равна  2
г, то границами значения массы детали в граммах были бы числа  25 г  и  27 г, то есть масса была бы определена менее точно.

Зная пределы
значения некоторой величины, можно оценить значение другой величины, которая
зависит от первой.

ПРИМЕР:

Пусть известны приближенные значения (в см) с недостачей и с излишком длины  а  стороны равностороннего треугольника:

5,4 ≤ а ≤ 5,5.

Надо найти пределы периметра  Р.

РЕШЕНИЕ:

Периметр равностороннего треугольника вычисляется по
формуле:

Р = 3а.

Из условия, что  а ≥ 5,4  выплывает, что  3а
≥ 16,2.

Из условия, что  а ≤ 5,5  выплывает, что  3а
≤ 16,5.

Числа  16,2  и  16,5
– приближенные значения периметра  (в см)  с недостачей и излишком:

16,2 ≤ Р ≤ 16,5.

Записать решение можно и так:

5,4 ≤ а ≤ 5,5,

5,4 ∙ 3 ≤ 3а ≤ 5,5 ∙ 3,

то есть

16,2 ≤ Р ≤ 16,5.

ПРИМЕР:

Пусть известны границы какого-то числа  х:

3 < х < 6.

Надо оценить значение выражения  ¹/_х.

РЕШЕНИЕ:

Из условия задачи определяем, что  х –
число положительное.

Поскольку  х ˃ 3, то

¹/_х < ¹/₃.

Поскольку  х < 6, то

¹/_х ˃ ¹/₆.

Выходит, что

¹/₆ < ¹/_х < ¹/₃.

Заменим границы значения выражения  ¹/_х  десятичными дробями. Число  ¹/₆  можно заменить лишь меньшим числом (любым приближением
с недостачей), а число ¹/₃ –
лишь больше (приближением с излишком). Поскольку

¹/₆ =
0,166…   

¹/₃ =
0,333… ,

то границами значения выражения  ¹/_х  могут быть десятичные дроби  0,1  и  0,4.

0,1 < ¹/_х < 0,4.

Заменив нижнюю границу
числом  0,1, а верхнюю – числом  0,4, мы
расширили промежуток, которому принадлежат значения выражения  ¹/_х.

Если бы мы сделали иначе, округлив бесконечные десятичные
дроби

0,166…  и  0,333…

по известным правилам округления, то получили бы, что

0,2 < ¹/_х < 0,3.

Но тогда неизвестное нам точное значение выражения  ¹/_х  могло бы очутиться вне полученных границах.

Способ записи приближённых чисел.

Приближённые
значения обычно записывают так, чтобы по записи можно было судить о точности
приближения.

ПРИМЕР:

На рулоне обоев написано, что его длина равна 

18 ±
0,3 м.

Эта запись означает, что длина рулона равна  18
м  с точностью до  0,3
м, то есть точное значение длины может отличаться от
приближённого значения, равного  18 м, не более чем на 
0,3 м.
Другими словами длина рулона должна находиться между 

18
– 0,3 = 17,7 м  и 

18
+ 0,3 = 18,3 м.

 ПРИМЕР:

Если измеряя длину 
х 
некоторой рейки, выявили, что она больше чем  6,427
м  и меньше чем  6,429
м, то записывают:

х = 6,428 ± 0,001 м.

Говорят, что значение длины рейки найдено с точностью
до 

0,001 м (одного миллиметра).

ПРИМЕР:

При приближённых вычислениях отличают запись  2,4  от  2,40, запись  0,02  от  0,0200  и так далее.

Запись  2,4  означает,
что верны только цифры целых и десятых, истинное же значение числа может быть,
например, 2,43 или  2,38 (при отбрасывании цифры  8  происходит округление в сторону увеличения
предшествующей цифры).

Запись  2,40  означает,
что верны и сотые доли, истинное число может быть  2,403  или  2,398, но не  2,421  и
не  2,382.

То же отличие производится и для целых чисел. Запись  382  означает, что все цифры верны, если же за
последнюю цифру ручаться нельзя, то число округляется, но записывается не в
виде  380,
а в виде  38
∙ 10. Запись же  380  означает, что
последняя цифра  (0)  верна.

Если в числе  4720  верны лишь первые
две цифры, его нужно записать в виде  47 ∙ 10²,
или это число можно также записать в виде 
4,7 ∙
10³  и так далее.

Значащими
цифрами называются все верные цифры числа, кроме нулей, стоящих впереди числа.

ПРИМЕР:

В числе 
0,00385  три значащие цифры.

В числе 
0,03085  четыре значащие цифры,

В числе 
2500 – четыре,

В числе 
2,5 ∙
10³ – две.

Число
значащих цифр некоторого числа называется его значностью.

Через то, что мы не
можем выполнить бесконечного процесса деления, то мы должны прекратить деление
на каком-либо десятичном знаке, то есть выполнить приближенное деление. Мы
можем, например, прекратить деление на первом десятичном знаке, то есть
ограничиться десятыми частями; в случае потребности мы можем остановиться на
втором десятичном знаке, ограничиться сотыми частями, и так далее. В таких
случаях говорят о приближенном превращении обычных дробей в десятичные. В этих
случаях говорят, что мы округляем бесконечную десятичную дробь. Округление
делается с той точностью, которая нужна для решения данной задачи.

Вычисления с приближенными
данными.

Вычисления с
приближенными данными постоянно используется в практических задачах, при этом
результат вычислений обычно округляют. Результат действий с приближёнными
числами есть тоже приближённое число. Выполняя некоторые действия над точными числами,
можно так же получить приближённые числа.

При сложении и вычитании приближённых чисел в
результате следует сохранять столько десятичных знаков, сколько их в
приближённом данном с наименьшим числом десятичных знаков, то есть оставляют в
результате столько знаков после запятой, сколько их содержится в менее точном
данном числе.

ПРИМЕР:

Пусть 

х ≈ 17,2  и  у
≈ 8,407.

Найдём приближённое значение суммы  х 
и  у.

РЕШЕНИЕ:

Имеем:

х +
у ≈ 25,607.

Из данных приближённых значений  17,2 
и  8,407 
менее точным является первое. Округлив результат по первому данному, то
есть до десятых, получим:

х + у ≈ 25,6.

ПРИМЕР:

Пусть 

х ≈ 6,784  и 

у ≈ 4,91.

Найдём приближённое значение разности  х 
и  у.

РЕШЕНИЕ:

Имеем:

х –
у ≈ 1,874.

Из данных приближённых значений  6,784 
и  4,91 
менее точным является второе. Округлив результат по второму данному, то есть.
до сотых, получим:

х –
у ≈ 1,87.

ПРИМЕР:

Найдите разность приближенных значений 

х = 1,52
± 0,01  и 

у = 0,27
± 0,02.

РЕШЕНИЕ:

Данным приближенным значением отвечают двойные
неравенства

1,51 ≤ х ≤ 1,53  и 

0,25 ≤ у ≤ 0,29.

Умножим все части последнего двойного неравенства на  –1, получим

–0,29 ≤ –у ≤ –0,25.

Прибавив это двойное неравенство к первому, получим

1,22 ≤ х – у ≤ 1,28, или  

х – у = 1,25
± 0,03.

Несколько иначе
поступают при умножении и делении приближённых значений. Здесь округление
производится с учётом относительной точности данных. В
этом случае находят произведение или частное приближённых значений, и результат
округляют по менее точному данному, имея ввиду относительную точность. Для
этого исходные данные и полученный результат записывают в стандартном виде 

а × 10ⁿ,

и множитель  а  результата округляют, оставляя в нём столько
знаков после запятой, сколько их имеет соответствующий множитель в менее точном
данном.

ПРИМЕР:

Пусть 

х ≈ 0,86  и 

у ≈ 27,1.

Найдём приближённое значение произведения  х  и  у.

РЕШЕНИЕ:

Перемножив  0,86  и  27,1,  получим:

ху ≈
23,306.

Запишем данные числа и результат в стандартном виде:

0,86 = 8,6 × 10^-1;   

27,1 = 2,71 × 10¹;   

23,306 = 2,3306 × 10¹.

В множителе  8,6  одна цифра после запятой, а в множителе  2,71
две цифры после запятой. Округлим число  2,2306  по первому данному, то есть до десятых.
Получим:

ху ≈ 2,3 × 10¹ = 23.

ПРИМЕР:

Пусть 

х ≈ 60,2  и 

у ≈ 80,1.

Найдём приближённое значение произведения  х  и  у.

РЕШЕНИЕ:

Известно, что все выписанные цифры верны, так что
истинные величины могут отличаться от приближённых лишь сотыми, тысячными и так
далее долями.

В произведении получаем 
4822,02. Здесь
могут быть неверными не только цифры сотых и десятых, но и цифры единиц.

Пусть, например, сомножители получены округлением точных
чисел  60,23  и  80,14.
Тогда точное произведение будет  4826,8322, так что цифра единиц в приближённом произведении (2)
отличается от точной цифры  (6)  на  4  единицы.

ПРИМЕР:

Пусть 

х ≈ 563,2  и 

у ≈ 32.

Найдём приближённое значение частного  х  и  у.

РЕШЕНИЕ:

Разделив  563,2  на  32, получим:

х :
у ≈ 17,6.

Запишем данные числа и результат в стандартном виде:

563,2 = 5,632 × 10²;   

32 = 3,2 × 10;   

17,6 = 1,76 × 10.

Из этой записи видно, что число  1,76 
следует округлить по второму данному, то есть до десятых. Получим:

х :
у ≈ 1,8 × 10
≈ 18.

При умножении и делении приближённых чисел нужно в
результатах сохранять столько значащих цифр, сколько их было в приближённом
данном с наименьшим числом значащих цифр.

Таким образом, при
сложении, вычитании, умножении и делении приближённых значений результат
округляется по менее точному данному. При этом при сложении и вычитании данные
числа записываются в десятичных дробях и менее точное данное определяется по
абсолютной точности, а при умножении и делении данные числа записываются в
стандартном виде и менее точное данное определяется по относительной точности.

Теория приближённых
вычислений позволяет:

– зная степень точности данных, оценить степень
точности результатов ещё до выполнения действий;

– брать данные с надлежащей степенью точности,
достаточной для обеспечения требуемой точности результата, но не слишком
большой, чтобы избавить вычислителя от бесполезных расчётов;

– рационализировать сам процесс вычисления,
освободив его от тех выкладок, которые не окажут влияния на точные цифры
результата.