Как найти изохорную теплоемкость идеального газа - AvtoShod.ru

to continue to Google Sites

Not your computer? Use Guest mode to sign in privately. Learn more

Теплоемкость идеального газа — это отношение тепла, сообщенного газу, к изменению температуры δТ, которое при этом произошло.

${displaystyle C={frac {delta Q}{delta T}}}$

Молярная теплоемкость

Молярная теплоемкость — теплоемкость 1 моля идеального газа.

${displaystyle C_{M}={frac {1}{nu }}{frac {delta Q}{Delta T}}}$

Теплоемкость идеального газа в процессах

Адиабатический

В адиабатическом процессе теплообмена с окружающей средой не происходит, т.е. δQ=0. Следовательно, теплоемкость идеального газа в адиабатическом процессе также равна нулю: С_адиаб=0.

Изотермический

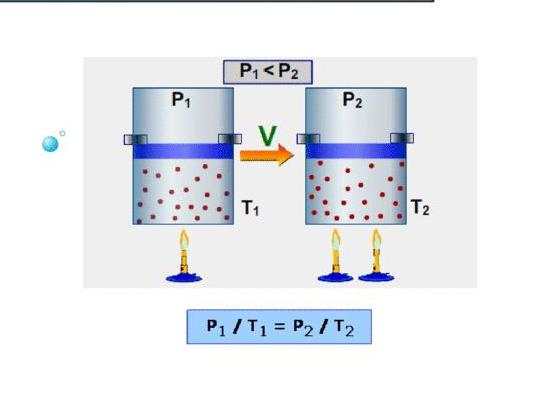
В изотермическом процессе постоянна температура, т.е. . Следовательно, теплоемкость идеального газа стремится к бесконечности:

Изохорический

В изохорическом процессе постоянен объем, т.е. . Элементарная работа газа равна произведению изменения объема на давление, при котором происходит изменение (). Первое Начало Термодинамики для изохорического процесса имеет вид:

${displaystyle dU=delta Q=C_{V}Delta T}$

А для идеального газа

${displaystyle dU={frac {i}{2}}nu RDelta T}$

Таким образом,

${displaystyle C_{V}={frac {i}{2}}nu R,}$

где — число степеней свободы частиц газа.

Изобарический

В изобарическом процессе ():

${displaystyle delta Q=dU+PdV=nu C_{V}Delta T+nu RDelta T=nu (C_{V}+R)Delta T=nu C_{P}Delta T}$

C_P=δQ/νΔT=C_V+R=(5/2)*R

Вывод формулы для теплоемкости в данном процессе

Согласно 1 началу термодинамики существует 2 способа изменить внутреннюю энергию тела (в нашем случае идеального газа): передать ему тепло или совершить над ним работу.

dU=δQ+δA, где δA — работа окр. среды над газом.

δA_{окр.среды}=-δA_газа

δQ=dU+δA_газа

В расчете на 1 моль:

С=δQ/ΔT=(ΔU+pΔV)/ΔT

ΔU=C_V*ΔT

C=C_V+(pΔV/ΔT)_{в данном процессе}

См. также

Идеальный газ
Первое начало термодинамики
Теплоемкость

Ссылки

1. Открытый Колледж
2. CГГА
3. Статья в «Кванте», формат djvu

Источник

В термодинамике при изучении переходов из начального в конечное состояние некоторой системы важно знать тепловой эффект процесса. С этим эффектом тесно связано понятие теплоемкости. В данной статье рассмотрим вопрос, что понимают под изохорной теплоемкостью газа.

Идеальный газ

Идеальным называется такой газ, частицы которого считаются материальными точками, то есть не имеют размеров, но обладают массой, и у которого вся внутренняя энергия состоит исключительно из кинетической энергии движения молекул и атомов.

Любой реальный газ в идеале никогда не будет удовлетворять описанной модели, поскольку его частицы все же имеют некоторые линейные размеры и взаимодействуют между собой с помощью слабых ван-дер-ваальсовых связей или химических связей другого типа. Однако при низких давлениях и высоких температурах расстояния между молекулами велики, а их кинетическая энергия превышает потенциальную в десятки раз. Все это позволяет применять с высокой степенью точности идеальную модель для реальных газов.

Внутренняя энергия газа

Внутренняя энергия любой системы — это физическая характеристика, которая равна сумме потенциальной и кинетической энергии. Поскольку в идеальных газах можно пренебречь потенциальной энергией, то для них можно записать равенство:

U = E_k.

Где E_k — энергия кинетическая системы. Используя молекулярно-кинетическую теорию и применяя универсальное уравнение состояния Клапейрона-Менделеева, несложно получить выражение для U. Оно записано ниже:

U = z/2*n*R*T.

Здесь T, R и n — абсолютная температура, газовая постоянная и количество вещества соответственно. Величина z — это целое число, показывающее количество степеней свободы, которыми обладает молекула газа.

Изобарная и изохорная теплоемкость

В физике теплоемкостью называется количество теплоты, которое необходимо предоставить изучаемой системе, чтобы нагреть ее на один кельвин. Справедливо также и обратное определение, то есть теплоемкость — это количество теплоты, которое система выделяет при охлаждении на один кельвин.

Проще всего для системы определить изохорную теплоемкость. Под ней понимают теплоемкость при постоянном объеме. Поскольку система в таких условиях работу не совершает, то вся энергия расходуется на повышение внутренних энергетических запасов. Обозначим изохорную теплоемкость символом C_V, тогда можно записать:

dU = C_V*dT.

То есть изменение внутренней энергии системы прямо пропорционально изменению ее температуры. Если сравнить это выражение, с записанным в предыдущем пункте равенством, то приходим к формуле для C_V в идеальном газе:

С_V = z/2*n*R.

Данной величиной на практике неудобно пользоваться, поскольку она зависит от количества вещества в системе. Поэтому было введено понятие удельной изохорной теплоемкости, то есть величины, которую рассчитывают либо на 1 моль газа, либо на 1 кг. Обозначим первую величину символом C_Vⁿ, вторую — символом C_V^m. Для них можно записать такие формулы:

C_Vⁿ = z/2*R;

C_V^m = z/2*R/M.

Здесь M — молярная масса.

Изобарной называется теплоемкость при поддержании постоянного давления в системе. Примером такого процесса является расширение газа в цилиндре под поршнем при его нагревании. В отличие от изохорного, во время изобарного процесса подводимое к системе тепло расходуется на повышение внутренней энергии и на выполнение механической работы, то есть:

H = dU + P*dV.

Энтальпия изобарного процесса представляет собой произведение изобарной теплоемкости на изменение температуры в системе, то есть:

H = C_P*dT.

Если рассмотреть расширение при постоянном давлении 1 моль газа, то первое начало термодинамики запишется в виде:

C_Pⁿ*dT = C_Vⁿ*dT + R*dT.

Последнее слагаемое получено из уравнения Клапейрона-Менделеева. Из этого равенства следует связь между изобарной и изохорной теплоемкостями:

C_Pⁿ = C_Vⁿ + R.

Для идеального газа удельная молярная теплоемкость при постоянном давлении всегда больше соответствующей изохорной характеристики на величину R=8,314 Дж/(моль*К).

Степени свободы молекул и теплоемкость

Выпишем еще раз формулу для удельной молярной изохорной теплоемкости:

C_Vⁿ = z/2*R.

В случае газа одноатомного величина z = 3, поскольку атомы в пространстве могут перемещаться лишь в трех независимых направлениях.

Если же речь идет о газе, состоящем из двухатомных молекул, например, кислород O₂ или водород H₂, то, помимо поступательного движения, эти молекулы могут еще вращаться вокруг двух взаимно перпендикулярных осей, то есть z будет равно 5.

В случае более сложных молекул для определения C_Vⁿ следует использовать z=6.

Источник

Теплоемкость идеального газа

Определение теплоемкости

Теплоемкость – это количество тепла, которое затрачивается для того, чтобы повысить температуру тела на один кельвин. Теплоемкость зависит от массы вещества, условий при которых системе сообщают теплоту. Уравнение (1) – это определение теплоемкости через интегральные параметры. Иногда удобнее использовать следующее определение теплоемкости:

$[C=frac{delta Q}{dT} qquad (2) ]$

где – бесконечно мало количество плоты, которое получает тело; dT – приращение температуры тела.

При единичной массе тела теплоемкость называют удельной. Обозначают ее обычно маленькой буквой c. Еще используют молярную теплоемкость ( $c_{mu}$ ) – это теплоемкость одного моля вещества.

Теплоемкость и первое начало термодинамики

Используя первое начало термодинамики в интегральной записи, теплоёмкость можно найти как:

$[C=frac{Delta U+A}{Delta T} qquad (3) ]$

где – изменение внутренней энергии термодинамической системы; A – работа системы над внешними силами. Для идеального газа имеем:

$[C=frac{frac{i}{2}frac{m}{mu}RDelta T+A}{Delta T} qquad (4) ]$

где m – масса газа; – молярная масса газа; R – универсальная газовая постоянная.

В дифференциальном виде:

$[C=frac{dU+pdV}{dT} qquad (5) ]$

Для идеального газа теплоемкость равна:

$[C=frac{frac{i}{2}frac{m}{mu}RdT+pdV}{dT}=frac{i}{2}frac{m}{mu}R+pfrac{dV}{dT} qquad (6) ]$

Теплоемкость для процессов, проводимых в идеальном газе

Теплоемкость связана с характером процесса. Она может изменяться от бесконечных отрицательных величин до бесконечных положительных.

Рассмотрим изохорный процесс . При проведении изохорного процесса газ работы не совершает, поэтому теплоемкость газа в изохорном процессе () равна:

$[C_V=frac{Delta U}{Delta T}qquad (7); C_V=frac{dU}{dT} qquad (8) ]$

Или:

$[C_V=frac{i}{2}frac{m}{mu}R=frac{i}{2}R nu qquad (9) ]$

При изобарном процессе () теплоемкость обозначают как . Она равна:

$[C_p=frac{Delta U+pDelta V}{Delta T}qquad left(10right); C_p=frac{dU+pdV}{dT} qquad (11)]$

Или:

$[C_p=frac{i+2}{2}R nu qquad (12)]$

Теплоемкости, при постоянных давлении и объеме, являются функциями состояний. Надо отметить, что независимость теплоемкости от температуры не подтвердили эксперименты.

В изотермическом процессе теплоемкость идеального газа считают бесконечной:

В адиабатном процессе теплоемкость равна нулю.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Источник

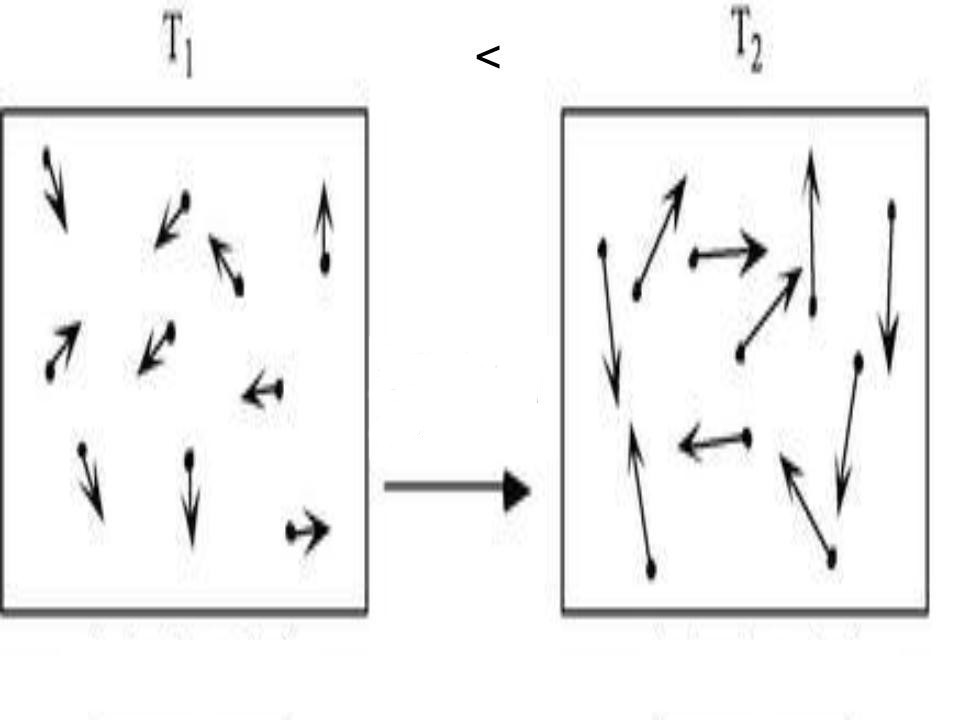
Перевод термодинамической системы (например, порции идеального газа) из состояния `1` в состояние `2` можно осуществить разными способами. На рис. 12 показаны графики двух возможных процессов (`1-«а»-2` и `1-«в»-2`), позволяющих осуществить такой перевод. Изменение внутренней энергии системы в том и в другом случае одинаково (оно определяется положениями точек `1` и `2` на -диаграмме), а работа, совершённая системой над окружающими телами, различна (площадь фигур под графиками процессов `1-«а»-2` и `1-«в»-2` разная, площадь под графиком процесса `1-«в»-2` больше).

Следовательно, и количество теплоты, затраченное на перевод системы из состояния `1` в `2` ( $$ Q=Delta U+{A}^{text{‘}}$$ ), будет разным.

Теплоёмкостью $$ C$$ термодинамической системы (тела) называют отношение бесконечно малого количества теплоты $$ Delta Q$$, переданного системе, к изменению $$ Delta T$$ его температуры, вызванного этим количеством теплоты.

$$ C={displaystyle frac{Delta Q}{Delta T}}$$ — теплоёмкость тела (системы).

Единицей измерения этой величины будет $$ left[Cright]={displaystyle frac{1mathrm{Дж}}{mathrm{К}}}$$.

Численное значение теплоёмкости тела показывает, какое количество теплоты потребуется для изменения температуры всего тела на `1` градус по шкале Цельсия (Кельвина).

При расчётах чаще пользуются удельной теплоёмкостью (теплоёмкостью `1` кг вещества).

называют отношение теплоёмкости тела (системы) к массе этого тела (системы):

$$ {c}_{mathrm{уд}}={displaystyle frac{C}{m}}={displaystyle frac{Delta Q}{m· Delta T}}$$ — удельная теплоёмкость тела (системы).

(1)

Единицей измерения этой величины будет $$ left[cright]={displaystyle frac{1mathrm{Дж}}{mathrm{кг}·mathrm{К}}}$$.

называют отношение теплоёмкости тела (системы) к количеству вещества в этом теле (системе):

$$ {c}_{mathrm{мол}}={displaystyle frac{C}{nu }}={displaystyle frac{Delta Q}{ Delta T·nu }}$$ — молярная теплоёмкость тела (системы).

(2)

Единицей измерения этой величины будет $$ left[{c}_{mathrm{мол}}right]={displaystyle frac{1mathrm{Дж}}{mathrm{моль}·mathrm{К}}}$$.

Получим соотношение между удельной и молярной теплоёмкостями:

$$ {c}_{mathrm{мол}}={displaystyle frac{Q}{ Delta T·frac{m}{M}}}={displaystyle frac{Q·M}{ Delta T·m}}={c}_{mathrm{уд}}·M$$ — соотношение между молярной и удельной теплоёмкостями

(3)

Теперь найдём молярную теплоёмкость идеального газа при изобарном и при изохорном процессах.

При изобарном процессе присутствуют и $$ Delta U$$, и $$ {A}^{text{‘}}$$, следовательно:

$$ {c}_{p}={displaystyle frac{Q}{nu · Delta T}}={displaystyle frac{Delta U+Atext{‘}}{nu · Delta T}}={displaystyle frac{Delta U}{nu Delta T}}+{displaystyle frac{Atext{‘}}{nu Delta T}}={displaystyle frac{frac{i}{2}nu R Delta T}{nu Delta T}}+{displaystyle frac{nu R Delta T}{nu Delta T}}={displaystyle frac{iR}{2}}+R=R{displaystyle frac{i+2}{2}}$$,

$${c}_{p}=R{displaystyle frac{i+2}{2}}$$ — молярная теплоёмкость газа при изобарном процессе.

При изохорном процессе работа не совершается, $$ {A}^{text{‘}}=0$$, следовательно:

$$ {c}_{V}={displaystyle frac{Q}{nu Delta T}}={displaystyle frac{Delta U+{A}^{text{‘}}}{nu Delta T}}={displaystyle frac{Delta U}{nu Delta T}}={displaystyle frac{frac{i}{2}nu R Delta T}{nu Delta T}}={displaystyle frac{iR}{2}}$$

$$ {c}_{V}=R{displaystyle frac{i}{2}}$$ — молярная теплоёмкость газа при изохорном процессе.

Соотношение между $$ {c}_{V}$$ и $$ {c}_{р}$$ можно записать в двух формах:

1) $$ {c}_{p}={c}_{V}+R$$ — закон Майера, и

2) $$ gamma ={displaystyle frac{{c}_{p}}{{c}_{V}}}$$ — коэффициент Пуассона.

Т. к. мы уже знаем, чему равно число степеней свободы у разных молекул, то можем вычислить и значения $$ {с}_{р}$$ и $$ gamma $$:

	формула	Одноатомные `(i = 3)`	Двухатомные `(i = 5)`
`c_p`	`R((i+2)/2)`	`5/2 R`	`20,775 «Дж»/(«моль»*»К»)`	`7/2 R`	`29,085 «Дж»/(«моль»*»К»)`
`gamma`	`(i+2)/i`	`5/3`	`1,66667`	`7/5`	`1,4`

Воздух представляет собой смесь газов, преимущественно двухатомных азота и кислорода, потому для него эксперименты дают значение $$ gamma approx mathrm{1,4}$$.

Для твёрдых тел теплоёмкости $$ {с}_{р}$$ и $$ {c}_{V}$$ будут почти одинаковыми. Это можно показать следующим образом. По определению $$ C={displaystyle frac{Delta Q}{ Delta T}}$$, но $$ Delta Q= Delta U+pDelta V$$, тогда

$$ {C}_{p}={displaystyle frac{Delta U+pDelta V}{ Delta T}}={displaystyle frac{Delta U}{ Delta T}}+{displaystyle frac{pDelta V}{ Delta T}}={C}_{V}+{displaystyle frac{pDelta V}{ Delta T}}$$.

При нагревании твёрдых или жидких тел изменение объёма составляет около $$ {10}^{-6}$$ первоначального объёма, поэтому вторым слагаемым можно пренебречь по сравнению с первым, что и позволяет говорить о равенстве $$ {c}_{p}={c}_{V}$$.

Для газов $$ frac{ Delta V}{V}$$ на два порядка больше, чем для твёрдых или жидких тел, потому пренебрегать вторым слагаемым нельзя, более того, оно будет составлять заметную долю теплоёмкости $$ {c}_{p}$$.

Источник

Молярная теплоемкость

Теплоемкость идеального газа в процессах

Адиабатический

Изотермический

Изохорический

Изобарический

Вывод формулы для теплоемкости в данном процессе

См. также

Ссылки

Идеальный газ

Внутренняя энергия газа

Изобарная и изохорная теплоемкость

Степени свободы молекул и теплоемкость

Теплоемкость идеального газа

Определение теплоемкости

Теплоемкость и первое начало термодинамики

Теплоемкость для процессов, проводимых в идеальном газе

Примеры решения задач

Не пропустите также: