Как найти похожую картинку, фотографию, изображение в интернет
12.07.2019
Допустим у Вас есть какое-то изображение (рисунок, картинка, фотография), и Вы хотите найти такое же (дубликат) или похожее в интернет. Это можно сделать при помощи специальных инструментов поисковиков Google и Яндекс, сервиса TinEye, а также потрясающего браузерного расширения PhotoTracker Lite, который объединяет все эти способы. Рассмотрим каждый из них.
Поиск по фото в Гугл
Тут всё очень просто. Переходим по ссылке https://www.google.ru/imghp и кликаем по иконке фотоаппарата:
Дальше выбираем один из вариантов поиска:
- Указываем ссылку на изображение в интернете
- Загружаем файл с компьютера
На открывшейся страничке кликаем по ссылке «Все размеры»:
В итоге получаем полный список похожих картинок по изображению, которое было выбрано в качестве образца:
Есть еще один хороший способ, работающий в браузере Chrome. Находясь на страничке с интересующей Вас картинкой, подведите к ней курсор мыши, кликните правой клавишей и в открывшейся подсказке выберите пункт «Найти картинку (Google)»:
Вы сразу переместитесь на страницу с результатами поиска!
Статья по теме: Поисковые сервисы Google, о которых Вы не знали!
Поиск по картинкам в Яндекс
У Яндекса всё не менее просто чем у Гугла 
Укажите адрес картинки в сети интернет либо загрузите её с компьютера (можно простым перетаскиванием в специальную области в верхней части окна браузера):
Результат поиска выглядит таким образом:
Вы мгновенно получаете доступ к следующей информации:
- Какие в сети есть размеры изображения, которое Вы загрузили в качестве образца для поиска
- Список сайтов, на которых оно встречается
- Похожие картинки (модифицированы на основе исходной либо по которым алгоритм принял решение об их смысловом сходстве)
Поиск похожих картинок в тинай
Многие наверняка уже слышали об онлайн сервисе TinEye, который русскоязычные пользователи часто называют Тинай. Он разработан экспертами в сфере машинного обучения и распознавания объектов. Как следствие всего этого, тинай отлично подходит не только для поиска похожих картинок и фотографий, но их составляющих.
Проиндексированная база изображений TinEye составляет более 10 миллиардов позиций, и является крупнейших во всем Интернет. «Здесь найдется всё» — это фраза как нельзя лучше характеризует сервис.
Переходите по ссылке https://www.tineye.com/, и, как и в случае Яндекс и Google, загрузите файл-образец для поиска либо ссылку на него в интернет.
На открывшейся страничке Вы получите точные данные о том, сколько раз картинка встречается в интернет, и ссылки на странички, где она была найдена.
PhotoTracker Lite – поиск 4в1
Расширение для браузера PhotoTracker Lite (работает в Google Chrome, Opera с версии 36, Яндекс.Браузере, Vivaldi) позволяет в один клик искать похожие фото не только в указанных выше источниках, но и по базе поисковика Bing (Bing Images)!
Скриншот интерфейса расширения:
В настройках приложения укажите источники поиска, после чего кликайте правой кнопкой мыши на любое изображение в браузере и выбирайте опцию «Искать это изображение» PhotoTracker Lite:
Есть еще один способ поиска в один клик. По умолчанию в настройках приложения активирован пункт «Показывать иконку быстрого поиска». Когда Вы наводите на какое-то фото или картинку, всплывает круглая зеленая иконка, нажатие на которую запускает поиск похожих изображений – в новых вкладках автоматически откроются результаты поиска по Гугл, Яндекс, Тинай и Бинг.
Расширение создано нашим соотечественником, который по роду увлечений тесно связан с фотографией. Первоначально он создал этот инструмент, чтобы быстро находить свои фото на чужих сайтах.
Когда это может понадобиться
- Вы являетесь фотографом, выкладываете свои фото в интернет и хотите посмотреть на каких сайтах они используются и где возможно нарушаются Ваши авторские права.
- Вы являетесь блогером или копирайтером, пишите статьи и хотите подобрать к своему материалу «незаезженное» изображение.
- А вдруг кто-то использует Ваше фото из профиля Вконтакте или Фейсбук в качестве аватарки на форуме или фальшивой учетной записи в какой-либо социальной сети? А ведь такое более чем возможно!
- Вы нашли фотографию знакомого актера и хотите вспомнить как его зовут.
На самом деле, случаев, когда может пригодиться поиск по фотографии, огромное множество. Можно еще привести и такой пример…
Как найти оригинал заданного изображения
Например, у Вас есть какая-то фотография, возможно кадрированная, пожатая, либо отфотошопленная, а Вы хотите найти её оригинал, или вариант в лучшем качестве. Как это сделать? Проводите поиск в Яндекс и Гугл, как описано выше, либо средствами PhotoTracker Lite и получаете список всех найденных изображений. Далее руководствуетесь следующим:
- Оригинальное изображение, как правило имеет больший размер и лучшее качество по сравнению с измененной копией, полученной в результате кадрирования. Конечно можно в фотошопе выставить картинке любой размер, но при его увеличении относительно оригинала, всегда будут наблюдаться артефакты. Их можно легко заметить даже при беглом визуальном осмотре.
Статья в тему: Как изменить размер картинки без потери в качестве.
- Оригинальные фотографии часто имеют водяные знаки, обозначающие авторство снимка (фамилия, адрес сайта, название компании и пр.). Конечно водяной знак может добавить кто угодно на абсолютно на любое изображение, но в этом случае можно поискать образец фото на сайте или по фамилии автора, наверняка он где-то выкладывает своё портфолио онлайн.
- И наконец, совсем простой признак. Если Ваш образец фото черно-белый (сепия и пр.), а Вы нашли такую же, но полноцветную фотографию, то у Вас явно не оригинал. Добавить цветность ч/б фотографии гораздо более сложнее, чем перевести цветную фотографию в черно-белую
Уважаемые читатели, порекомендуйте данный материал своим друзьям в социальных сетях, а также задавайте свои вопросы в комментариях и делитесь своим мнением!
Похожие публикации:
- Как включить новый дизайн Фейсбук и темную тему
- Какие программы можно без опасений удалить с компьютера?
- Как заряжать смартфон быстрее – 7 полезных советов
- Что о Вас знает Яндекс и как удалить свои персональные данные?
- TFW – что это значит и когда употребляется
Понравилось? Поделитесь с друзьями!
Сергей Сандаков, 42 года.
С 2011 г. пишу обзоры полезных онлайн сервисов и сайтов, программ для ПК.
Интересуюсь всем, что происходит в Интернет, и с удовольствием рассказываю об этом своим читателям.
Рассмотрим
простейшие приемы нахождения оригинала
по известному изображению. Один из них
основан на использовании таблицы
изображений, которая в этом случае
рассматривается в обратном порядке, и
правил операционного исчисления. В
первую очередь это относится к теореме
смещения, интегрированию и дифференцированию
изображения и изображению свертки
функций.
Пример
12.
Найти оригинал f(t),
если
.
Решение.
Исходным можно взять соответствие
.
Операции
смещения на а
в области изображений соответствует
операция домножения на
в области оригиналов. Поэтому при а=1
имеем
.
Операции
домножения на
в области изображений соответствует
запаздывание на =2
в области оригиналов. Следовательно,
Пример
13.
Найти оригинал изображения
.
Решение.
Выделим в знаменателе полный квадрат
.
Воспользуемся
равенством
,
а также теоремой смещения. В результате
получим
.
Пример
14.
Найти оригинал, соответствующий
изображению
.
Решение.
Можно поступить так: за исходное взять
соотношение
.
Затем
воспользуемся тем, что делению на р
в области изображений соответствует
операция интегрирования в области
оригиналов:

Это же свойство
применим повторно:
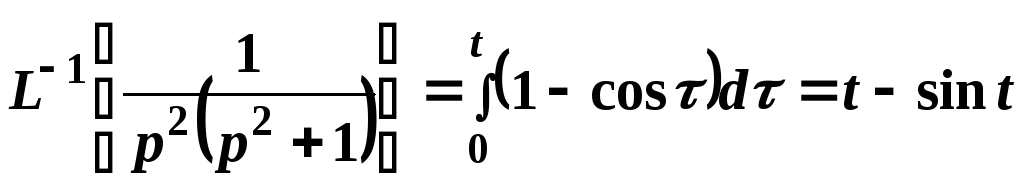
Заметим,
что оригинал указанного изображения
проще можно было бы найти, если разложить
его на простейшие дроби:
.
Согласно
свойству линейности имеем
.
Пример
15.
Найти оригинал изображения
.
Решение.
Представим изображение в виде
.
Произведению
изображений
и
соответствует свертка их оригиналов
и
.
Поэтому
.
Для
этого изображения оригинал можно найти
проще, если воспользоваться тем, что
операции дифференцирования в области
изображений соответствует операция
домножения на (-t)
в области оригиналов. Поэтому

Очень
часто при решении практических задач
возникает необходимость нахождения
оригиналов изображений, которые
представляются в виде дробно рациональной
функции
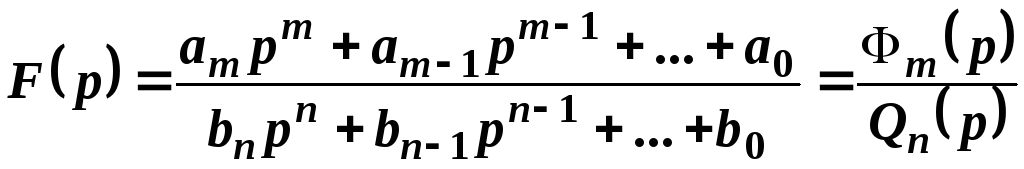
в
которой старшая степень числителя
меньше старшей степени знаменателя
переменной р.
При
нахождении оригинала такой дроби
разлагают ее на сумму простых дробей с
помощью метода неопределенных
коэффициентов, известного из интегрального
исчисления. Затем находят оригиналы
для каждой простой дроби.
Пример
16.
Найти оригинал, соответствующий
изображению
.
Решение.
Разложим данную дробь на сумму простейших
дробей. Для этого, прежде всего, найдем
корни знаменателя, решив уравнение
.
Проверкой убеждаемся, что
один из его корней. Разделим кубический
многочлен
на двучлен р+1.
В частном получим
.
Дискриминант этого трехчлена —
отрицательный, на действительные
множители он не разлагается. Разложение
данного изображения на простейшие дроби
имеет вид:
.
Отсюда
.
Полагая
в этом равенстве
,
находим
.
Затем приравниваем коэффициенты при
одинаковых степенях р:
,
.
Таким
образом,
.
В
знаменателе второй дроби выделим полный
квадрат, а в числителе — двучлен
:
.
Используя
свойство линейности , переходим в область
оригиналов. Получим
.
Заметим,
что в данном случае, прежде чем приступать
к разложению изображения на простейшие
дроби, было бы полезно воспользоваться
теоремой смещения. Для этого в исходном
изображении выделим двучлен
:
.
Тогда
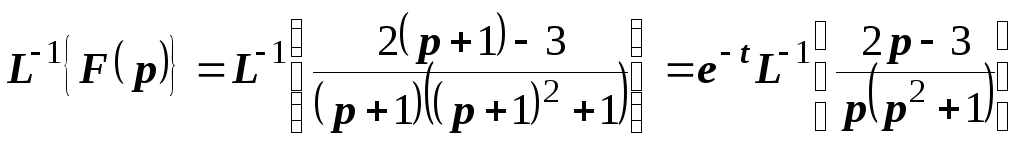
Разложение
полученного изображения на простейшие
дроби проще, чем исходного:
;
;
;
.
Оригиналом
будет функция
или
.
Задача
нахождения оригиналов, соответствующих
дробно-рациональным изображениям
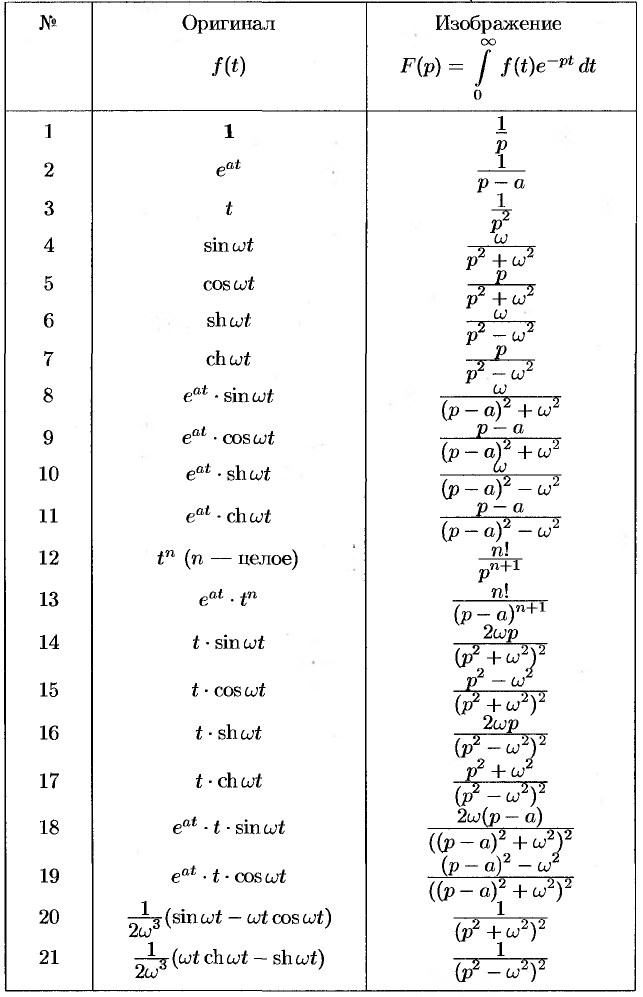
упрощается, если воспользоваться
следующей краткой таблицей (табл. 3).
Таблица 3 –
Изображение – оригинал
|
№ |
Изображение |
Оригинал |
|||
|
1 |
2 |
3 |
|||
|
1 |
|
|
|||
|
2 |
|
|
|||
|
3 |
|
|
|||
|
4 |
|
|
|||
|
5 |
|
|
|||
|
6 |
|
|
|||
|
7 |
|
|
|||
|
8 |
|
|
|||
|
9 |
|
|
|||
|
1
0 |
|
|
Продолжение табл.
3
|
1 |
2 |
3 |
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Преобразование Лапласа и его свойства
Основные определения
1. Оригинал — это комплекснозначная функция действительного аргумента
, которая удовлетворяет следующим условиям:
а) при
;
б) на любом конечном отрезке функция
имеет не более чем конечное число точек разрыва первого рода;
в) имеет ограниченный рост, т.е. возрастает не быстрее показательной функции: существуют такие постоянные
и
, что
при
.
Замечания 5.1
1. Величина называется показателем роста функции
. Для любой ограниченной функции, являющейся оригиналом, можно принять
.
2. Обозначим , если пределы существуют и конечны.
3. Совокупность всех оригиналов называется пространством оригиналов.
4. В точке разрыва первого рода функция имеет конечные односторонние пределы:
.
Пример 5.1
2. Изображение функции — функция
комплексного переменного
, определяемая равенством
(5.1)
Область существования этой функции определяется областью сходимости интеграла Лапласа, стоящего в правой части равенства (5.1). Исследование интeгpaлa позволяет определить эту область и установить свойства функции . Имеет место следующее утверждение.
Утверждение 5.1. Если функция , является оригиналом, то интеграл Лапласа сходится абсолютно в области
(рис. 5.1) , где
— показатель роста оригинала. Внутри этой области, т.е. на любом замкнутом подмножестве
, интеграл сходится равномерно и определяет аналитическую функцию
.
Замечания 5.2
1. Утверждение 5.1 аналогично свойствам степенных рядов, сходящихся в круге и равномерно сходящихся внутри этого круга, где сумма ряда является аналитической функцией.
2. Свойство аналитичности изображения имеет важное значение в теории и практике применения преобразования Лапласа, так как позволяет использовать в пространстве изображений методы теории аналитических функций, в частности разложения функций в ряды и теорию вычетов.
3. Совокупность всех изображений называется пространством изображений.
4. Переход, определяющий изображение по оригиналу
, называется преобразованием Лапласа:
(5.2)
Запись означает, что оригиналу
соответствует изображение
.
5. Оригинал по изображению находится с помощью обратного преобразования Лапласа по формуле обращения
(5.3)
где путь интегрирования — любая прямая , параллельная мнимой оси и лежащая правее прямой
(рис. 5.1).
Непосредственное применение формулы обращения часто затруднительно. Поэтому на практике пользуются методами, изложенными ранее.
Замечания 5.3
1. Для преобразования Лапласа используются различные обозначения, на пример и
, что означает: оригиналу
соответствует изображение
и изображению
соответствует оригинал
. В некоторых учебниках вместо аргумента
применяется
, то есть
и
.
2. Для компактной записи оригиналов используется единичная ступенчатая функция
(5.4)
где — точка приложения (рис. 5.2). Так как во многих практических задачах аргумент
имеет смысл текущего времени, то
также называется моментом приложения единичной ступенчатой функции. В системах автоматического регулирования и управления функция
рассматривается как типовой входной сигнал.
При функция
является функцией Хевисайда:
(5.5)
Тогда, если функция удовлетворяет условиям «б», «в» в определении оригинала (п. 1), но не удовлетворяет условию «а», то функция
будет оригиналом, так как
Далее под заданной с помощью аналитической формулы функцией , там, где это не вызывает недоразумений, будем понимать произведение этой функции на функцию Хевисайда, а множитель
опускать.
3. Функции , являющиеся изображениями, удовлетворяют необходимому условию: если
есть изображение, то
при
. Поэтому функции
не являются изображениями. Однако в практических задачах функции типа
и другие встречаются. Это требует расширения понятий оригинала и изображения.
Класс оригиналов можно расширить, включив в него функции, которые могут быть не ограничены в окрестности некоторых конечных точек, но такие, что интеграл Лапласа от них, тем не менее, сходится абсолютно в некоторой полуплоскости . К числу таких обобщенных оригиналов относятся степенная функция
при
и некоторые другие.
4. Во всякой точке , являющейся точкой разрыва функции
, правая часть формулы (5.3) равна
.
Примеры 5.2-5.3
Пример 5.2. Найти изображение единичной функции Хевисайда .
Решение. Так как функция ограничена, то в качестве показателя роста можно положить
. По формуле (5.2) имеем
так как из равенства следует, что
при
.
Пример 5.3. Найти изображение функции , где
— действительное число.
Решение. Показателем роста можно считать . По формуле (5.2)
так как из равенства следует, что
при
.
Свойства преобразования Лапласа
Будем предполагать, что рассматриваемые далее функции являются оригиналами. Соответствующие им изображения (при
) обозначим
.
1. Линейность. Если — оригиналы, то для любых комплексных чисел
, функция
также является оригиналом и справедливо равенство
(5.6)
Заметим, что для функции существенно, что все слагаемыс являются оригиналами, так как, например, функция
является оригиналом, а слагаемые
и
не являются.
Справедливо и обратное утверждение: если — изображения, то
Здесь также важно, что слагаемые функции являются изображениями, поскольку из того, что
— изображение, не следует, что
— изображения. Например, функция
является изображением, а слагаемые
и
не являются.
Примеры 5.4-5.5
Пример 5.4. Найти изображение функции .
Решение. Из примера 5.2 имеем , а из примера 5.3 при
имеем
. Тогда согласно свойству линейности для оригинала
получаем
.
Пример 5.5. Найти изображение функции .
Решение. Используя формулу Эйлера (2.11), получаем .
Из примера 5.3 при и
следует:
. Тогда по свойству линейности
2. Подобие (теорема подобия). Для любого из
следует
(5.7)
и обратно: .
Пример 5.6
Найти изображение функции .
Решение. Из примера 5.5 следует, что . Тогда по теореме подобия
3. Смещение (теорема смещения). При любом комплексном из
следует
(5.8)
то есть умножению оригинала на соответствует смещение изображения на
.
Пример 5.7
Найти изображение функции .
Решение. Из примера 5.6 следует . Тогда по теореме смещения
.
Запаздывание оригинала
4. Запаздывание (теорема запаздывания). Для любого из
следует
(5.9)
где (рис. 5.3), т.е. запаздыванию оригинала на
соответствует умножение изображения на
.
Примеры 5.8-5.10
Пример 5.8. Найти изображение функции .
Решение. В примере 5.5 получено . По теореме запаздывания при
имеем
.
Пример 5.9. Найти оригиналы по изображениям: a) ; б)
.
а) Из примера 5.7 следует, что при изображению
соответствует оригинал
. Тогда по теореме запаздывания при
имеем
б) По формуле 3 из табл. 5.1 .По теореме запаздывания при
получаем
. Заметим, что для похожего, но отличного от полученного, оригинала
(его можно записать в виде
) изображение имеет вид
.
Пример 5.10. Найти изображение функции , график которой представлен на рис. 5.4.
С учетом (5.4) представим функцию в виде
.
Из примера 5.2 имеем . Применяя свойства линейности и запаздывания, получаем
Заметим, что, находя предел при в последнем выражении, можно получить изображение δ-функции
Замечание 5.4. Дельта-функция часто встречается в инженерных приложениях как идеализация импульса конечной длительности. В теории автоматического регулирования и управления δ-функция вместе с единичной ступенчатой являются типовыми входными воздействиями.
Очевидно, изображение дельта-функции не удовлетворяет необходимому условию (п.2 замечаний 5.3). Этот факт свидетельствует о практическом требовании расширения понятия оригинала. Дельта-функция относится к обобщенным функциям и задается соотношением
(5.10)
Дифференцирование оригинала
5. Если функции являются оригиналами и
, то
(5.11)
где .
Примеры 5.11-5.12
Пример 5.11. Найти изображение , если
.
Решение. Из примера 5.7 следует, что при имеем
.
Найдем . Согласно (5.11)
.
Пример 5.12. Найти изображение выражения с начальными условиями
.
Решение. Пусть , тогда
. В примере 5.2 получено
. Используя свойство линейности, имеем
Интегрирование оригинала
Если функция является оригиналом и
, то
(5.12)
т.е. интегрированию оригинала соответствует деление изображения на .
Пример 5.13
Найти изображение интеграла от функции
.
Решение. Из примера 5.6 следует, что . Тогда
, то есть
.
Дифференцирование изображения
Если функция является оригиналом и
. то
(5.13)
Примеры 5.14-5.15
Интегрирование изображения
Если функция является оригиналом, то из
следует
(5.14)
Пример 5.16
Найти изображение функции .
Решение. Функция является оригиналом, так как
(условие «в») и точка
является точкой разрыва первого рода (условие «б»). Из примера 5.13 следует
.
Отсюда .
Умножение изображений (теорема Бореля)
Из и
следует
(5.15)
т.е. свертке оригиналов соответствует произведение изображений. Функция определяется формулой
(5.16)
и называется сверткой оригиналов и
.
Пример 5.17
Найти оригинал, соответствующий изображению .
Решение. Представим в виде произведения изображений:
.
Из примеров 5.6 и 5.13 следует .
Согласно (5.15),(5.16) получаем искомый оригинал:
Дифференцирование свертки (интеграл Дюамеля)
10. Согласно свойствам 9 и 5 найдем преобразование Лапласа от производной свертки двух функций:
С другой стороны,
или, применяя правило дифференцирования интеграла, зависящего от параметра, имеем
Здесь при дифференцировании интеграла, зависящего от параметра, применялась формула Лейбница, которая для общего случая имеет вид
Объединяя полученные результаты, можно записать:
(5.17)
Формула (5.17) называется интегралом Дюамеля. Интеграл Дюамеля применяется для решения дифференциальных уравнений.
Пример 5.18
Найти оригиналы, соответствующие изображениям: a) ; б)
.
Решение. а) Заметим, что здесь нельзя непосредственно воспользоваться теоре мой Бореля, так как в произведении множитель
не является изображением (не выполняется необходимое условие).
Представим изображение в виде произведения . Из примера 5.3 вытекает
Тогда по формуле (5.17) имеем
Можно решить этот пример с помощью теоремы Бореля, представив изображение в виде
Тогда, используя свойство линейности и теорему Бореля, получаем
б) Представим изображение в виде произведения:
Из примера 5.6 при и
следует
Тогда по формуле (5.17) получаем
Теорема о связи «начальных» и «конечных» значений оригинала и изображения
Начальное значение оригинала находится по формуле
(5.18)
Если существует конечный предел , то
(5.19)
Из соотношений (5.18),(5.19) следует, что для нахождения начальных и конечных значений оригинала не требуется знания оригинала, а достаточно иметь соответствующее изображение. На практике соотношение (5.19) применяется, например, для нахождения установившегося значения выходного сигнала в системах автоматического регулирования.
Пример 5.19
Найти начальное и конечное значения оригинала, которому соответствует изображение .
Решение. Согласно (5.18) и (5.19) имеем
С другой стороны, из примера 5.7 следует, что
поэтому легко убедиться в правильности полученного результата.
Полученные решения примеров 5.2–5.17 позволяют сформировать таблицу преобразования Лапласа. Табл. 5.1 является фрагментом более полных таблиц, используемых далее при решении примеров и задач.
Нахождение изображения по оригиналу
Для нахождения изображения требуется применить свойства преобразования Лапласа Так, чтобы к функции или ее составляющим можно было применить результаты, содержащиеся в табл. 5.1.
Таблица 5.1. Таблица основных преобразований Лапласа
Посмотреть
Пример 5.21
Найти изображения функций:
a) ; б)
;
в) ; г)
;
д) ; е)
;
ж) ; з)
.
Решение
а) Согласно формуле 12 из табл. 5.1 . По свойству дифференцирования изображения (формула (5.13) при
):
или
.
Поэтому .
Можно решать иначе, используя формулу 10 из табл. 5.1 при а = 3 и свойство смещения при
и
.
б) Применим свойства линейности и интегрирования изображения. Так как в силу формул 1 и 9 из табл. 5.1 , то согласно (5.14)
в) По формуле 9 из табл. 5.1 . Функцию fit) можно записать, используя единичную ступенчатую функцию:
. Поэтому для нахождения изображения следует применить теорему запаздывания (5.9) к оригиналу
при
г) Согласно теореме смещения (5.8) и с учетом результата п. «в» имеем
, так как
.
д) По теореме запаздывания (5.9) при и по формуле 7 из табл. 5.1 при
получаем
е) Используя свойства линейности, запаздывания и формулы 6,1,8 из табл. 5.1, получаем
ж) По формуле 19 из табл. 5.1 находим . По свойству интегрирования изображения (формула (5.14)):
По свойству интегрирования оригинала (5.12): .
з) Используем формулу косинуса разности и запишем оригинал в виде суммы:
По свойству линейности получаем:
Заметим, что здесь и результаты пп. «в» и «з» различны так как оригиналами являются разные функции.
Нахождение изображений функций, заданных графиком
При решении прикладных задач оригинал часто задан графиком. Это может быть, например, входной сигнал, действующий на систему автоматической регулирования. В этом случае рекомендуется сначала записать аналитическое выражение оригинала с помощью единичной ступенчатой функции (5.4), привести полученное выражение к виду, удобному для применения табл. 5.1 и свойстве преобразования Лапласа.
Пример 5.22
Найти изображения функций, заданных графиками на рис. 5.5.
Решение.
а) Представим функцию в виде .
По формуле 3 из табл.5.1 и теореме запаздывания (формула (5.9) при )
б) Запишем функцию в виде .
По формулам 1,3 из табл. 5.1 и (5.6), (5.9) имеем .
в) Запишем изображенную функцию в виде .
По формулам 1,3 из табл. 5.1 и (5.6), (5.9) имеем .
г) Представим функцию в виде
По формулам 3 из табл. 5.1 и (5.6), (5.9) имеем .
д) Запишем функцию в форме
По формулам З из табл. 5.1 и (5.6), (5.9) .
е) Представим изображенную функцию в виде
По формулам 1,3 из табл. 5.1 и (5.6), (5.9) .
ж) Запишем функцию в форме .
По формуле 8 из табл. 5.1 и по теореме запаздывания .
з) Представим функцию в виде .
По формуле 6 из табл. 5.1 при и (5.9) при
имеем
и) Представим функцию в виде .
Используя формулы 2 из табл. 5.1 и (5.6), (5.9), получаем .
Нахождение изображений периодических функций
Во многих приложениях используются оригиналы, являющиеся периодическими функциями.
Пусть — оригинал с периодом
(рис. 5.6,в), образованный повторением функции
(рис. 5.6,б):
Для нахождения изображения периодической функции
следует:
1. Найти изображение функции .
2. Найти изображение по формуле
(5.20)
Пример 5.23.
Найти изображения функций, представленных на рис. 5.7.
Решение
а) По графику (рис. 5.7,в) получаем
Поэтому .
Поскольку , по формуле (5.20) находим
б) По графику (рис. 5.7,б) имеем , тогда
. По формуле (5.20) при
имеем
в) Функция, изображенная на рис. 5.7,в , имеет период . Запишем аналитическое выражение для
и соответствующее изображение
По формуле (5.20) получаем .
г) Для функции, изображенной на рис. 5.7,г, изображением для является
(см. пример 5.22 п.»ж»). Тогда по формуле (5.20) при
получаем
.
Нахождение оригинала по изображению
Непосредственное применение формулы обращения (5.3) затруднительно, поэтому для нахождения оригинала применяются теоремы разложения и правила преобразования изображения к виду, представленному в табл. 5.1.
Применение теорем разложения
Теорема 5.1 (первая теорема разложения). Если функция аналитична в некоторой окрестности бесконечно удаленной точки и ее разложение в ряд по степеням
имеет вид
, то функция (5.21) является оригиналом, соответствующим изображению
.
(5.21)
Теорема 5.2 (вторая теорема разложения). Если изображение является однозначной функцией и имеет лишь конечное число особых точек
лежащих в конечной части плоскости, то
(5.22)
Замечания 5.5
1. Формула (5.21) может быть записана в виде . Задача нахождения оригинала при выполнении условий теоремы сводится к нахождению коэффициентов разложения функции в ряд Лорана в окрестности бесконечно удаленной точки.
2. Формула (5.22) принимает наиболее простой вид в случае — рационального изображения, т.е.
, где
— многочлены степеней /пил соответственно, не имеющие общих корней. Если все полюсы
функции
простые, то по формуле (4.24) получаем
, а формула (5.22) принимает вид
(5.23)
3. Если при выполнении условий п.2 коэффициенты многочлена — лействительные числа, то его комплексные корни, как известно, являются по парно сопряженными. Нахождение суммы вычетов в таких точках можно заме нить нахождением действительной части вычета в одной из них. Действительио, вычет в точке
, используя свойства сопряженных чисел, можно записать следующим образом:
Это означает, что вычет в точке есть число, сопряженное вычету в точке
, а сумма таких чисел равна их удвоенной действительной части:
Пример 5.24
Найти оригиналы для функций:
a) ;
б) .
Решение. В случае «а» для решения задачи используем теорему 5.1, а в случае «б» — теорему 5.2.
а) Используем типовые разложения
Для заданных изображений получаем:
Согласно первой теореме разложения
б) Представим в виде
где — простые полюсы функции
. По второй теореме разложения
Тот же результат можно получить, пользуясь пп. 2 и 3 замечаний 5.5:
Функция имеет четыре простых полюса:
.
Так как вычет в простом полюсе находится по формуле , то по второй теореме разложения
Функция имеет два полюса: простой
и полюс второго порядка
.
По второй теореме разложения . Находим вычеты
получаем окончательный ответ .
Применение таблицы и свойств преобразования Лапласа
Приведем ряд известных приемов нахождения оригинала.
1. Если изображение отличается от табличного на постоянный множитель, то его следует умножить и одновременно поделить на этот множитель, а затем воспользоваться свойством линейности.
Пример 5.25
2. Изображение, заданное в виде дроби , разлагается на сумму дробей.
Пример 5.26
Найти оригинал для функций: а) ; б)
; в)
.
Решение. Представим дроби в виде суммы двух слагаемых, а затем воспользуемся свойством линейности и формулами из табл. 5.1:
а) ;
б) .
в) представим в виде
. По формулам 4,6 из табл. 5.1 находим
.
3. Если знаменатель дроби содержит квадратный трехчлен, то в нем выде ляется полный квадрат: . При этом числитель дроби представляется в виде многочлена от
.
Пример 5.27
Найти оригиналы для функций: a) ; б)
.
Решение. а) Выделим полный квадрат в знаменателе дроби и воспользуемся табл. 5.1 (по формуле 12 из табл. 5.1 при ):
б) Используем представление
По формулам 19,20 из табл. 5.1 и по теореме смещения (формула (5.8))
Можно решить эту задачу иначе, используя вторую теорему разложения (см. п. «б» примера 5.24):
4. Если оригинал представляет собой правильную рациональную дробь, то следует разложить ее на простейшие дроби и для каждой из полученных дробей найти оригинал.
Примеры 5.28-5.29
Пример 5.28. Найти оригиналы для функций:
а) ; б)
; в)
; г)
.
Решение. а) Представим в виде
, где
— неопределенные коэффициенты.
Отсюда следует равенство .
Приравнивая коэффициенты при одинаковых степенях , получаем систему уравнений для нахождения неопределенных коэффициентов:
Решая ее, получаем
и
По формулам 1,12,13 из табл. 5.1 .
б) Представим в виде
, где
— неопределенные коэффициенты.
Отсюда .
Подставляя последовательно , получаем
и поэтому
По формулам 6,7 из табл. 5.1 находим .
в) Представим изображение в виде . Отсюда
При получаем
, поэтому
По свойству линейности и по формуле 6 из табл. 5.1 получаем
Можно решить эту задачу иначе, используя вторую теорему разложения (см. п. «б» примера 5.24):
г) Представим в виде
, где
— неопределенные коэффициенты.
Из равенства при
получаем
, поэтому
.
По формуле 6 из табл. 5.1 имеем .
Можно также решить эту задачу иначе, используя вторую теорему разложения (см. п. «б» примера 5.24 и п. «в» данного примера):
Пример 5.29. Найти оригиналы для функций: a) ; б)
.
Решение. а) Решим пример различными способами.
Первый способ. Воспользуемся разложением дроби на элементарные:
По формулам 2,3,6,7 из табл. 5.1 получаем .
Второй способ. Применим вторую теорему разложения, учитывая, что и
— полюсы второго порядка функции
Третий способ. Обозначим . Тогда
. Рассмотрим функцию
. По свойству интегрирования оригинала (формула (5.12)) получаем
Заметим, что . Применяя еще раз свойство интегрирования оригинала, имеем
Четвертый способ. Представим изображение в виде произведения
, где
.
По формулам 3 и 7 из табл. 5.1 . Далее по теореме Бореля (формула (5.15))
б) Решим пример также несколькими способами.
Первый способ. Воспользуемся разложением дроби на элементарные:
По формуле 9 из табл. 5.1 получаем .
Второй способ. Применим вторую теорему разложения с учетом пп. 2,3 замечаний 5.5:
Третий способ. Представим изображение в виде произведения:
Отсюда . По теореме Бореля
Четвертый способ. Используем формулу 37 из табл. 5.1. При получаем
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Свойства преобразования Лапласа
Находить изображения, пользуясь только определением изображения, не всегда просто и удобно. Свойства преобразования Лапласа существенно облегчают задачу нахождения изображений для большого числа разнообразных функций, а также задачу отыскания оригиналов по их изображениям.
Линейность
Линейной комбинации оригиналов соответствует такая же линейная комбинация изображений, т. е. если 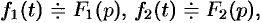
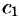
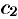
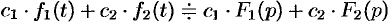
Используя свойства интеграла, находим
Пример №78.4.
Найти изображения функций 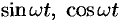
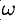
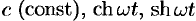
Решение:
Пользуясь свойством линейности, формулой (78.3), находим:
т.е.
Аналогично получаем формулу
Далее, 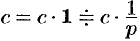
Наконец, 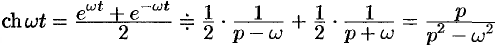
Аналогично получаем формулу
Подобие
Если 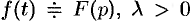
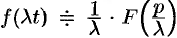
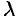
По формуле (78.1) имеем
(так как безразлично, какой буквой обозначена переменная интегрирования).
Например, пусть 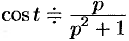
Смещение (затухание)
Если 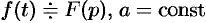
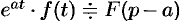
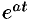
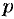
В силу формулы (78.1) имеем
Благодаря этому свойству можно расширить таблицу соответствия между оригиналами и их изображениями:
Пример №78.5.
Найти оригинал по его изображению
Решение:
Преобразуем данную дробь так, чтобы можно было воспользоваться свойством смещения:
(См. формулы (78.9), (78.10) и свойство линейности.)
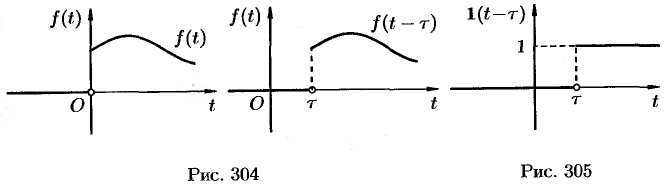
Запаздывание
Если 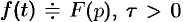
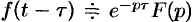
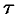
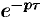
Положив 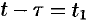
Поясним термин «запаздывание». Графики функции 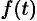
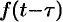
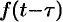
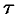
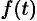
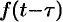
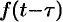
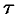
Свойство запаздывания удобно применять при отыскании изображения функций, которые на разных участках задаются различными аналитическими выражениями; функций, описывающих импульсные процессы.
Функция 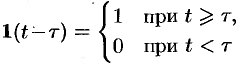
Так как 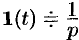
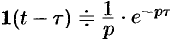
Запаздывающую функцию
можно записать так: 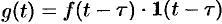
Пример №78.6.
Найти изображение 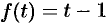
Решение:
Для того чтобы быть оригиналом, функция 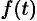
Если понимать функцию 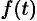
т. е. 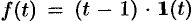
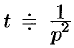
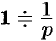
Если же понимать функцию 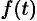
т. е. 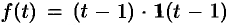
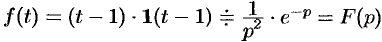
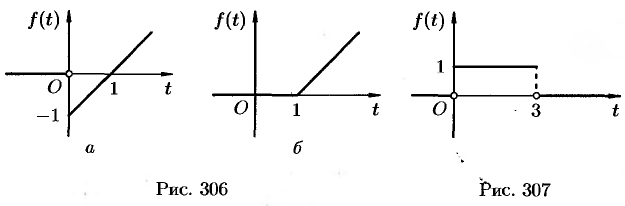
Пример №78.7.
Найти изображение функции
Решение:
Данная функция описывает единичный импульс (см. рис. 307), который можно рассматривать как разность двух оригиналов: единичной функции 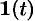
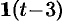
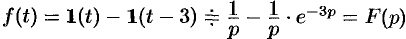
Пример №78.8.
Найти изображение функции
Решение:
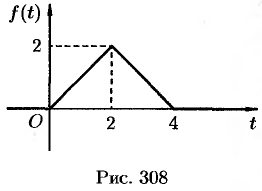
Функция-оригинал изображена на рис. 308. Запишем ее одним аналитическим выражением, используя функции Хевисайда 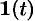
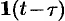
т.е.
Раскроем скобки и приведем подобные слагаемые:
Изображение функции 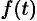
Замечания.
- Изображение периодического оригинала с периодом, равным
, есть
.
- Свойство опережения
применяется значительно реже.
Дифференцирование оригинала
Если 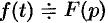
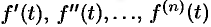
По определению изображения находим
Итак, 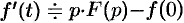
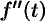
Аналогично найдем изображение третьей производной 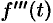
Применяя формулу (78.11) 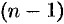
Замечание. Формулы (78.11)—(78.14) просто выглядят при нулевых начальных условиях: если 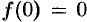
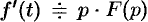
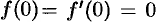
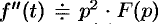
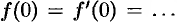
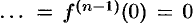
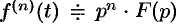
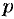
Рассмотренное свойство дифференцирования оригинала вместе со свойством линейности широко используется при решении линейных дифференциальных уравнений.
Пример №78.9.
Найти изображение выражения
если 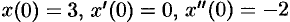
Решение:
Пусть 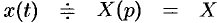
Следовательно,
Дифференцирование изображения
Если 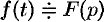
т. e. дифференцированию изображения соответствует умножение его оригинала на 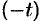
Согласно теореме 78.1 существования изображения, 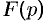
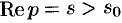
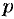
т.е. 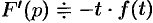
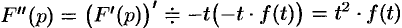
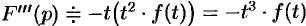
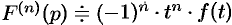
Пример №78.10.
Найти изображения функций 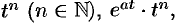
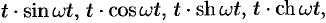
Решение:
Так как 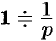
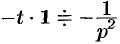
Далее находим 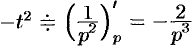
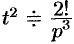
С учетом свойства смещения получаем
Согласно формуле (78.5), 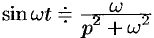
т. e. 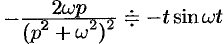
Аналогично, используя формулы (78.6), (78.7) и (78.8), находим
С учетом свойства смещения и формул (78.15) и (78.16), получаем
Интегрирование оригинала
Если 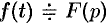
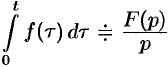
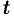
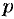
Функция 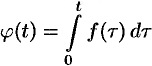
Пусть 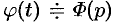
(так как 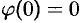
то 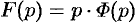
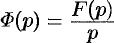
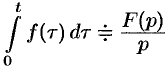
Интегрирование изображения
Если 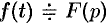
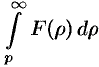
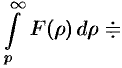
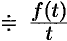
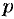
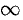
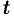
Используя формулу (78.1) и изменяя порядок интегрирования (обоснование законности этой операции опускаем), получаем
Пример №78.11.
Найти изображение функции 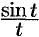
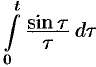
Решение:
Так как 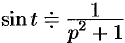
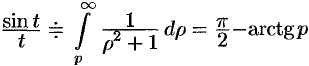
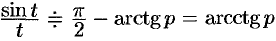
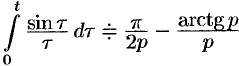
Умножение изображений
Если 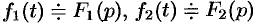
Можно показать, что функция 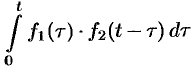
Используя преобразование Лапласа (78.1), можно записать
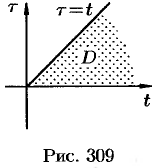
Область 
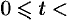
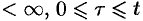
Изменяя порядок интегрирования и полагая 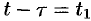
Интеграл в правой части формулы (78.17) называется сверткой функции 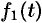
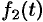
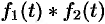
Можно убедиться (положив 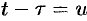
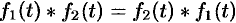
Итак, умножение оригиналов равносильно их свертыванию, т. е.
Пример №78.12.
Найти оригинал функций
Решение:
Так как 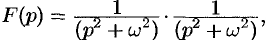
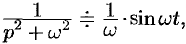
т.е.
Аналогично получаем
Следствие 78.2. Если 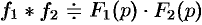
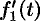
Запишем произведение 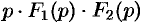
или
Первое слагаемое в правой части есть произведение изображений, соответствующих оригиналам 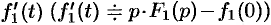
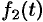
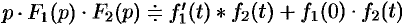
Формула (78.18) называется формулой Дюамеля.
На основании свойства переместительности свертки формулу Дюамеля можно записать в виде
Формулу Дюамеля можно применять для определения оригиналов по известным изображениям.
Пример №78.13.
Найти оригинал, соответствующий изображению
Решение:
Так как
то на основании формулы Дюамеля (78.18) имеем
Умножение оригиналов
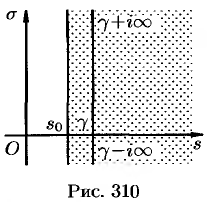
Если 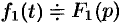
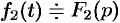
где путь интегрирования — вертикальная прямая 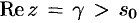
Резюме
Рассмотренные свойства преобразования Лапласа представляют собой основные правила (аппарат) операционного исчисления. Для удобства пользования перечислим эти свойства.
- Линейность:
.
- Подобие:
.
- Смещение:
.
- Запаздывание:
.
- Дифференцирование оригинала:
- Дифференцирование изображения
- Интегрирование оригинала:
.
- Интегрирование изображения:
.
- Умножение изображений:
.
- Умножение оригиналов:
.
Таблица оригиналов и изображений
Составим краткую таблицу, устанавливающую соответствие между некоторыми оригиналами (часто встречающимися на практике) и их изображениями. Достаточно полная таблица оригиналов и изображений, позволяющая по заданному оригиналу находить изображение и наоборот, есть, в частности, в книге «Справочник по операционному исчислению» (авторы В. А. Диткин и П. И. Кузнецов).
Таблица оригиналов и изображений
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
Примеры решений задач по операционному исчислению (преобразованию Лапласа)
Операционное (символическое) исчисление – это один из методов математического анализа, позволяющий в
некоторых случаях свести исследование и решение дифференциальных, псевдодифференциальных, интегральных уравнений, к более простым алгебраическим задачам.
Изучая преобразование Лапласа, мы вводим оригинал функции $f(t)$ и ее изображение $F(p)$, находимое по формуле:
$$F(p) = int_0^infty f(t) e^{-pt}dt$$
Для быстроты и удобства решения задач составлена таблица изображений и оригиналов, которая, наряду с теоремами (линейности, подобия, смещения, запаздывания), свойствами и правилами дифференцирования и интегрирования изображения/оригинала, постоянно используется в решении примеров.
В этом разделе вы найдете готовые задания разного типа: восстановление оригинала или изображения функции, нахождение свертки функций, решение ДУ, систем ДУ или интегральных уравнений с помощью преобразования Лапласа и т.д.
Полезная страница? Сохрани или расскажи друзьям
Как найти изображение функции
Задача 1. Найти изображение данного оригинала, или оригинала, удовлетворяющего данному уравнению
$$f(t)=frac{e^{2t}-e^{-3t}}{t}.$$
Задача 2. Пользуясь определением, найти изображение функции $f(t)=3^t$.
Задача 3. Найти изображение функции: $int_0^t cos tau cdot e^{-3tau}dtau. $
Задача 4. Найти изображение оригинала $f(x)$ двумя способами:
1) Вычислив интеграл $F(p) = int_0^infty f(x) e^{-px}dx$;
2) Воспользовавшись таблице изображений и свойствами преобразования Лапласа.
Оригинал задается формулой (курсочно-линейная функция, см. файл).
Как найти оригинал функции
Задача 5. Найти оригинал изображения $F(p)$, где
$$F(p)=frac{2p-1}{(p^2-4p+13)^2}.$$
Задача 6. Найти оригинал изображения
$$F(p)=frac{15p^2+3p+34}{(p^2+4p+8)(p^2-6p+5)}.$$
Задача 7. Найти оригинал для функции с помощью вычетов
$$F^*(p)=frac{1}{e^{4p}-625}.$$
Как решить ДУ (систему ДУ) операционным методом
Задача 8. Найти частное решение дифференциального уравнения с заданными начальными условиями операторным методом
$$x’+x=4e^t, x(0)=2.$$
Задача 9. Найти решение задачи Коши методами операционного исчисления
$$x»+2x’+2x=te^{-t}, quad x(0)=0, x'(0)=0.$$
Задача 10. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.
$$x’=x-y,\
y’=x+y,\
x(0)=2, y(0)=1.$$
Задача 11. Методом операционного исчисления найти решение задачи Коши для ДУ 3-го порядка
$$x»’+x»-2x’-5x=5e^t, quad x(0)=0, x'(0)=1, x»(0)=2.$$
Задача 12. Решите задачу Коши для системы дифференциальных уравнений с помощью преобразования Лапласа.
$$frac{dx}{dt}=x-2y,\
frac{dy}{dt}=x+3y,\
x(0)=0, y(0)=1. $$
Задача 13. C помощью формулы Дюамеля найти решение уравнения
$$x»’+x’=tg t, quad x(0)=x'(0)=x»(0)=0.$$
Задача 14. Решить систему ДУ с помощью преобразования Лапласа
$$
x’=-y+z,\
y’=z, quad x(0)=1, \
z’=-x+z;\
y(0)=z(0)=1/2.
$$
Как решить интегральное уравнение
Задача 15. Методом операционного исчисления найти решение интегрального уравнения
$$ y(t)=cos t +int_0^t (t-tau)^2 y(tau)d tau. $$
Задача 16. Решить интегральное уравнение
$$ int_0^t ch (tau) x(t-tau)d tau = t. $$
Как найти свертку функций
Задача 17. Найти свертку функций $f(t)=1$ и $phi(t)=sin 5t$.
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей, оформление производится в Word, срок от 1 дня.
Подробнее о решении заданий с преобразованием Лапласа
Дополнительная информация
- Онлайн-помощь по математическому анализу
- Дифференциальные уравнения — задачи с решениями
- Как решать ДУ с помощью операционного исчисления










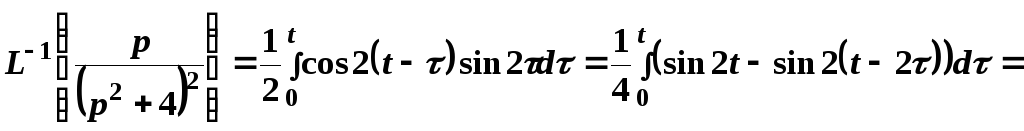

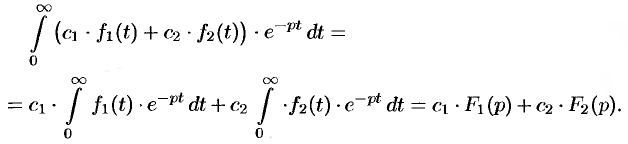
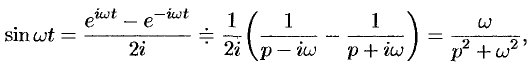


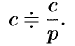


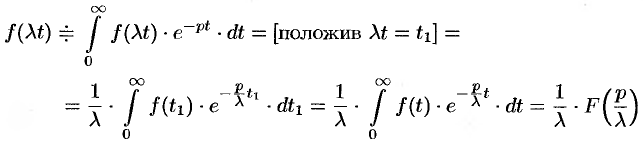
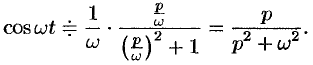
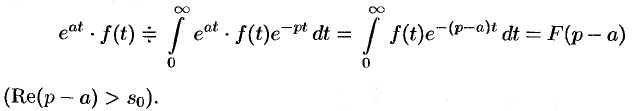
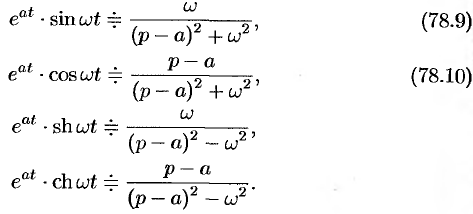
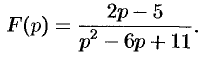
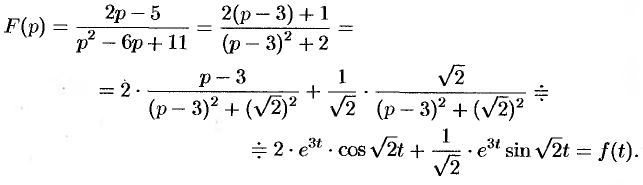
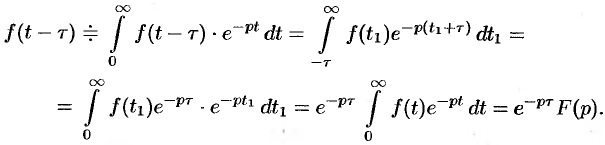
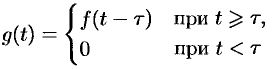
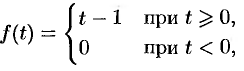
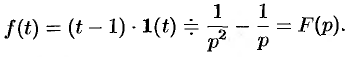
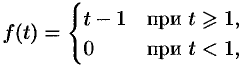


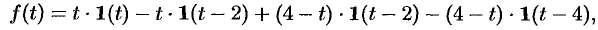
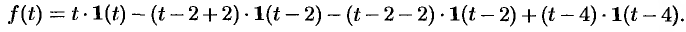
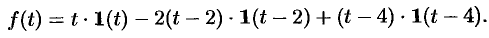
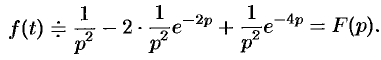
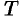 , есть
, есть 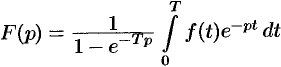 .
.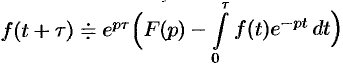
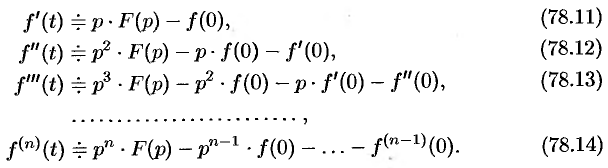
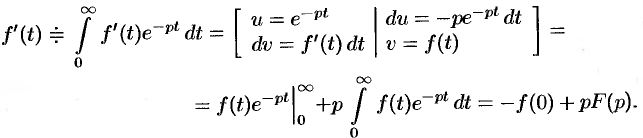
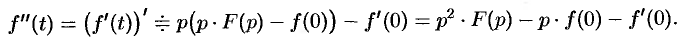
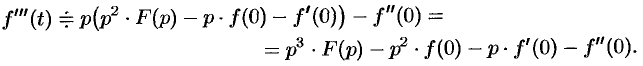
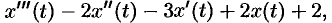
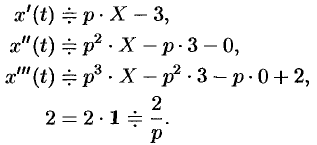
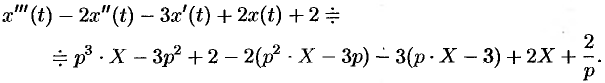
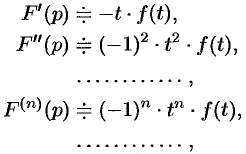
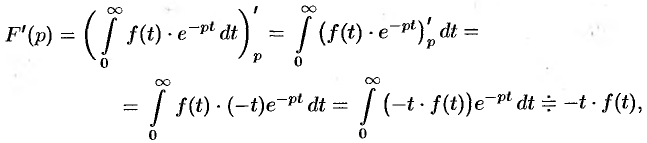
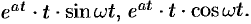
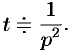
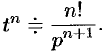
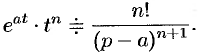
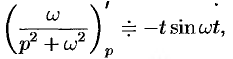
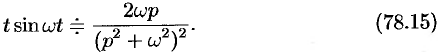
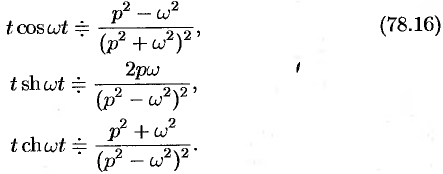
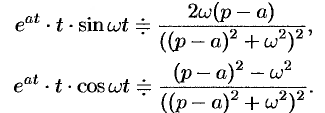
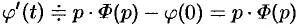
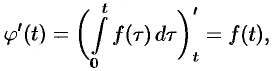
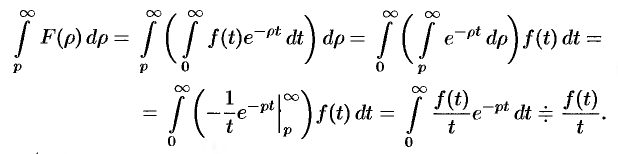
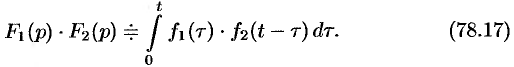
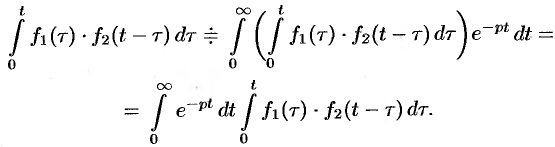
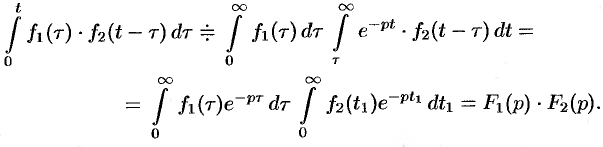
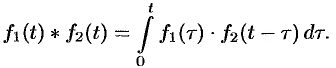
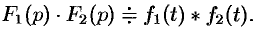
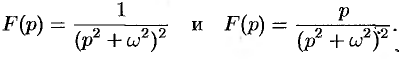
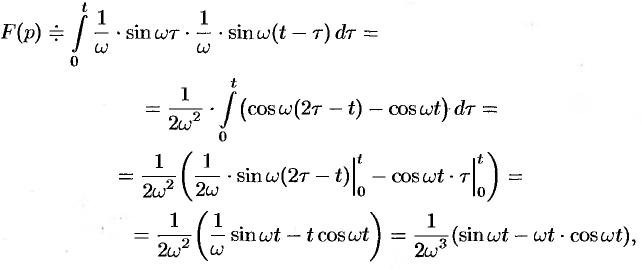
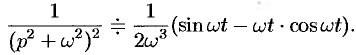
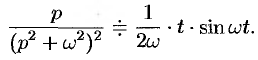
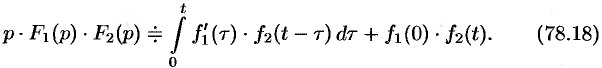
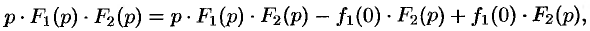
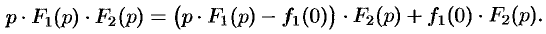
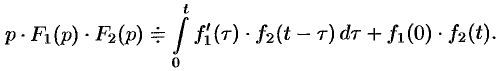
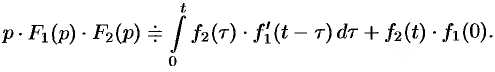
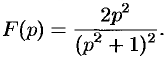
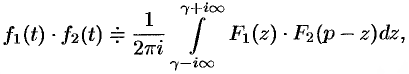
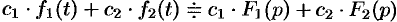 .
.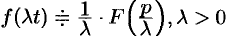 .
.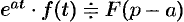 .
.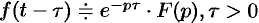 .
.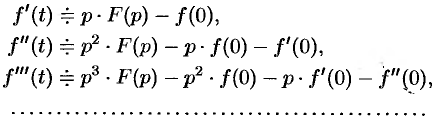
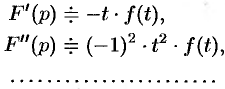
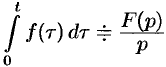 .
.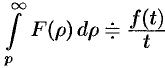 .
.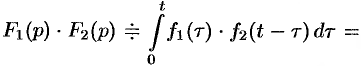
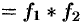 .
.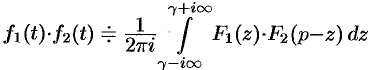 .
.