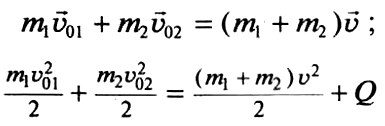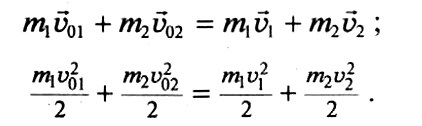Как найти изменение механической энергии - AvtoShod.ru

Энергия.

Работа.
Мощность.
Механическая энергия.
Кинетическая энергия.
Потенциальная энергия тела вблизи поверхности Земли.
Потенциальна яэнергия деформированной пружины.
Закон сохранения механической энергии.
Закон изменения механической энергии.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа силы, мощность, кинетическая энергия, потенциальная энергия, закон сохранения механической энергии.

Мы приступаем к изучению энергии — фундаментального физического понятия. Но предварительно нужно разобраться с другой физической величиной — работой силы.

к оглавлению ▴

Работа.

Пусть на тело действует постоянная сила vec F и тело, двигаясь прямолинейно по горизонтальной поерхности, совершило перемещение vec s . Сила vec F не обязательно является непосредственной причиной перемещения (так, сила тяжести не является непосредственной причиной перемещения шкафа, который передвигают по комнате).

Предположим сначала, что векторы силы и перемещения сонаправлены (рис. 1; остальные силы, действующие на тело, не указаны)

Рис. 1.A=Fs

В этом простейшем случае работа определяется как произведение модуля силы на модуль перемещения:

A=Fs . (1)

Единицей измерения работы служит джоуль (Дж): Дж=Н cdot м. Таким образом, если под действием силы 1 Н тело перемещается на 1 м, то сила совершает работу 1 Дж.

Работа силы, перпендикулярной перемещению, по определению считается равной нулю. Так, в данном случае сила тяжести и сила реакции опоры не совершают работы.

Пусть теперь вектор силы образует с вектором перемещения острый угол alpha (рис. 2).

Разложим силу vec F на две составляющие: $vec F _{parallel }$ (параллельную перемещению) и $vec F _{perp }$ (перпендикулярную перемещению). Работу совершает только $vec F _{parallel }$ . Поэтому для работы силы vec F получаем:

$A=vec F _{parallel }s=Fcosalpha cdot s$ . Итак,

. (2)

Если вектор силы образует с вектором перемещения тупой угол alpha , то работа по-прежнему определяется формулой (2). В этом случае работа оказывается отрицательной.

Например, работа силы трения скольжения, действующей на тело в рассмотренных ситуациях, будет отрицательной, так как сила трения направлена противоположно перемещению. В этом случае имеем:

$alpha=180^{circ}, cos alpha=-1$ , и для работы силы трения получаем:

$A_{TP}=-F_{TP}s=-mu mgs$ ,

где — масса тела, — коэффициент трения между телом и опорой.

Соотношение (2) означает, что работа является скалярным произведением векторов силы и перемещения:

Это позволяет вычислять работу через координаты данных векторов:

$A=F_{displaystyle x}s_{displaystyle x}+F_{displaystyle y}s_{displaystyle y}+F_{displaystyle z}s_{displaystyle z}$ .

Пусть на тело действуют несколько сил $vec F_{1},vec F_{2},..,vec F_{n}$ и vec F — равнодействующая этих сил. Для работы силы vec F имеем:

$A=vec F vec s=(vec F_{1}+vec F_{2}+...+vec F_{n})vec s=vec F_{1}vec s+vec F_{2}vec s+...+vec F_{n}vec s$ ,

или

$A=A_{1}+A_{2}+...+A_{n}$ ,

где $A_{1}, A_{2},...,A_{n}$ — работы сил $F_{1}, F_{2},...,F_{n}$ . Итак, работа равнодействующей приложенных к телу сил равна сумме работ каждой силы в отдельности.

к оглавлению ▴

Мощность.

Часто имеет значение быстрота, с которой совершается работа. Скажем, на практике важно знать, какую работу сможет выполнить данное устройство за фиксированное время.

Мощность — это величина, характеризующая скорость совершения работы. Мощность есть отношение работы ко времени , за которое эта работа совершена:

$N=frac{displaystyle A}{displaystyle t}$ .

Мощность измеряется в ваттах (Вт). 1 Вт = 1 Дж/с, то есть 1 Вт — это такая мощность, при которой работа в 1 Дж совершается за 1 с.

Предположим, что силы, действующие на тело, уравновешены, и тело движется равномерно и прямолинейно со скоростью vec v . В этом случае существует полезная формула для мощности, развиваемой одной из действующих сил vec F .

За время тело совершит перемещение . Работа силы vec F будет равна:

Отсюда получаем мощность:

или

где alpha -угол между векторами силы и скорости.

Наиболее часто эта формула используется в ситуации, когда vec F — сила «тяги» двигателя автомобиля (которая на самом деле есть сила трения ведущих колёс о дорогу). В этом случае , и мы получаем просто:

N=Fv .

к оглавлению ▴

Механическая энергия.

Энергия является мерой движения и взаимодействия любых объектов в природе. Имеются различные формы энергии: механическая, тепловая, электромагнитная, ядерная. . .

Опыт показывает, что энергия не появляется ниоткуда и не исчезает бесследно, она лишь переходит из одной формы в другую. Это самая общая формулировка закона сохранения энергии.

Каждый вид энергии представляет собой некоторое математическое выражение. Закон сохранения энергии означает, что в каждом явлении природы определённая сумма таких выражений остаётся постоянной с течением времени.

Измеряется энергия в джоулях, как и работа.

Механическая энергия является мерой движения и взаимодействия механических объектов (материальных точек, твёрдых тел).

Мерой движения тела является кинетическая энергия. Она зависит от скорости тела. Мерой взаимодействия тел является потенциальная энергия. Она зависит от взаимного расположения тел.

Механическая энергия системы тел равна сумме кинетической энергии тел и потенциальной энергии их взаимодействия друг с другом.

к оглавлению ▴

Кинетическая энергия.

Кинетической энергией тела (принимаемого за материальную точку) называется величина

$K=frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ ,

где — масса тела, — его скорость.

Кинетической энергией системы из тел называется сумма кинетических энергий каждого тела:

$K=frac{displaystyle m_{displaystyle 1}v_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}+frac{displaystyle m_{displaystyle 2}v_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}+...+frac{displaystyle m_{displaystyle N}v_{displaystyle N}^{displaystyle 2}}{displaystyle 2}$ .

Если тело движется под действием силы vec F , то кинетическая энергия тела, вообще говоря, меняется со временем. Оказывается, именение кинетической энергии тела за некоторый промежуток времени равно работе силы vec F . Покажем это для случая прямолинейного равноускоренного движения.

Пусть $vec{v_{1}}$ — начальная скорость, $vec{v_{2}}$ — конечная скорость тела. Выберем ось вдоль траектории тела (и, соответственно, вдоль вектора силы vec F ). Для работы силы vec F получаем:

$A=vec{F}vec{s}=F_{x}s_{displaystyle s}=ma_{displaystyle x}s_{displaystyle x}= ma_{displaystyle x}frac{{v_{displaystyle 2x}}^{displaystyle 2}-{v_{displaystyle 1x}}^{displaystyle 2}}{displaystyle 2a_{displaystyle x}}=frac{{displaystyle mv_{displaystyle 2x}}^{displaystyle 2}-{displaystyle mv_{displaystyle 1x}}^{displaystyle 2}}{displaystyle 2}$ .

(мы воспользовались формулой для $s_{x}$ , выведенной в статье «Равноускоренное движение»). Заметим теперь, что в данном случае проекция скорости отличается от модуля скорости разве что знаком; поэтому ${v_{displaystyle 1x}}^{displaystyle 2}={v_{displaystyle 1}}^{displaystyle 2}$ и ${v_{displaystyle 2x}}^{displaystyle 2}={v_{displaystyle 2}}^{displaystyle 2}$ . В результате имеем:

$A=frac{displaystyle mv_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}-frac{displaystyle mv_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}=K_{displaystyle 2}-K_{displaystyle 1}=Delta K$ ,

что и требовалось.

На самом деле соотношение справедливо и в самом общем случае криволинейного движения под действием переменной силы.

Теорема о кинетической энергии. Изменение кинетической энергии тела равно работе, совершённой приложенными к телу внешними силами за рассматриваемый промежуток времени.

Если работа внешних сил положительна, то кинетическая энергия увеличивается (, тело разгоняется).

Если работа внешних сил отрицательна, то кинетическая энергия уменьшается (, тело замедляет движение). Пример — торможение под действием силы трения, работа которой отрицательна.

Если же работа внешних сил равна нулю, то кинетическая энергия тела за это время не меняется. Нетривиальный пример — равномерное движение по окружности, совершаемое грузом на нити в горизонтальной плоскости. Сила тяжести, сила реакции опоры и сила натяжения нити всегда перпендикулярны скорости, и работа каждой из этих сил равна нулю в течение любого промежутка времени. Соответственно, кинетическая энергия груза (а значит, и его скорость) остаётся постоянной в процессе движения.

Задача. Автомобиль едет по горизонтальной дороге со скоростью и начинает резко тормозить. Найти путь , пройденный автомобилем до полной остановки, если коэффициент трения шин о дорогу равен .

Решение. Начальная кинетическая энергия автомобиля $K_{displaystyle 1}=frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ , конечная кинетическая энергия $K_{displaystyle 2}=0$ . Изменение кинетической энергии $Delta K=K_{displaystyle 2}-K_{displaystyle 1}=-frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ .

На автомобиль действуют сила тяжести m vec g , реакция опоры vec N и сила трения vec f . Сила тяжести и реакция опоры, будучи перпендикулярны перемещению автомобиля, работы не совершают. Работа силы трения:

Из теоремы о кинетической энергии теперь получаем:

$Delta K=A Rightarrow - frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}=- mu mgs Rightarrow s=frac{displaystyle v^{displaystyle 2}}{displaystyle 2 mu g}$ .

к оглавлению ▴

Потенциальная энергия тела вблизи поверхности Земли.

Рассмотрим тело массы , находящееся на некоторой высоте над поверхностью Земли. Высоту считаем много меньше земного радиуса. Изменением силы тяжести в процессе перемещения тела пренебрегаем.

Если тело находится на высоте , то потенциальная энергия тела по определению равна:

W=mgh

где — ускорение свободного падения вблизи поверхности Земли.

Высоту не обязательно отсчитывать от поверхности Земли. Как мы увидим ниже (формулы (3), (4)), физическим смыслом обладает не сама по себе потенциальная энергия, но её изменение. А изменение потенциальной энергии не зависит от уровня отсчёта. Выбор нулевого уровня потенциальной энергии в конкретной задаче диктуется исключительно соображениями удобства.

Найдём работу, совершаемую силой тяжести при перемещении тела. Предположим, что тело перемещается по прямой из точки , находящейся на высоте $h_{1}$ , в точку , находящуюся на высоте $h_{2}$ (рис. 3).

Рис. 3.A=mg(h1-h2)[/math]

Угол между силой тяжести m vec g и перемещением тела vec s обозначим alpha . Для работы силы тяжести получим:

Но, как видно из рис. 3, $s cos alpha=h_{1}-h_{2}$ . Поэтому

$A=mg(h_{1}-h_{2})=mgh_{1}-mgh_{2}$ ,

или

$A=W_{1}-W_{2}$ . (3)

Учитывая, что $W_{1}-W_{2}=-(W_{2}-W_{1})=- Delta W$ , имеем также:

. (4)

Можно доказать, что формулы (3) и (4) справедливы для любой траектории, по которой тело перемещается из точки в точку , а не только для прямолинейного отрезка.

Работа силы тяжести не зависит от формы траектории, по которой перемещается тело, и равна разности значений потенциальной энергии в начальной и конечной точках траектории. Иными словами, работа силы тяжести всегда равна изменению потенциальной энергии с противоположным знаком. В частности, работа силы тяжести по любому замкнутому пути равна нулю.

Сила называется консервативной, если при перемещении тела работа этой силы не зависит от формы траектории, а определяется только начальным и конечным положением тела. Сила тяжести, таким образом, является консервативной. Работа консервативной силы по любому замкнутому пути равна нулю. Только в случае консервативной силы возможно ввести такую величину, как потенциальная энергия.

к оглавлению ▴

Потенциальна яэнергия деформированной пружины.

Рассмотрим пружину жёсткости . Начальная деформация пружины равна $x_{1}$ . Предположим,
что пружина деформируется до некоторой конечной величины деформации $x_{2}$ . Чему равна при этом работа силы упругости пружины?

В данном случае силу на перемещение не умножишь, так как сила упругости меняется в процессе деформации пружины. Для нахождения работы переменной силы требуется интегрирование. Мы не будем приводить здесь вывод, а сразу выпишем конечный результат.

Оказывается, сила упругости пружины также является консервативной. Её работа зависит лишь от величин $x_{1}$ и $x_{2}$ и определяется формулой:

$A=frac{kx_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}-frac{displaystyle kx_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}$ .

Величина

$W=frac{displaystyle kx^{displaystyle 2}}{displaystyle 2}$

называется потенциальной энергией деформированной пружины (x — величина деформации).

Следовательно,

$A=W_{1}-W_{2}=- Delta W$ ,

что полностью аналогично формулам (3) и (4).

к оглавлению ▴

Закон сохранения механической энергии.

Консервативные силы называются так потому, что сохраняют механическую энергию замкнутой системы тел.

Механическая энергия тела равна сумме его кинетической и потенциальной энергий:

E=K+W .

Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии их взаимодействия друг с другом.

Предположим, что тело совершает движение под действием силы тяжести и/или силы упругости пружины. Будем считать, что трения нет. Пусть в начальном положении кинетическая и потенциальная энергии тела равны $K_{1}$ и $W_{1}$ , в конечном положении — $K_{2}$ и $W_{2}$ . Работу внешних сил при перемещении тела из начального положения в конечное обозначим .

По теореме о кинетической энергии

$K_{2}-K_{1}=A$ .

Но работа консервативных сил равна разности потенциальных энергий:

$A=W_{1}-W_{2}$ .

Отсюда получаем:

$K_{2}-K_{1}=W_{1}-W_{2}$ ,

или

$K_{1}+W_{1}=K_{2}+W_{2}$ .

Левая и правая части данного равенства представляют собой механическую энергию тела в начальном и конечном положении:

$E_{1}=E_{2}$ .

Следовательно, при движении тела в поле силы тяжести и/или на пружине механическая энергия тела остаётся неизменной при отсутствии трения. Справедливо и более общее утверждение.

Закон сохранения механической энергии. Если в замкнутой системе действуют только консервативные силы, то механическая энергия системы сохраняется.

При этих условиях могут происходить лишь превращения энергии: из кинетической в потенциальную и наоборот. Общий запас механической энергии системы остаётся постоянным.

к оглавлению ▴

Закон изменения механической энергии.

Если между телами замкнутой системы имеются силы сопротивления (сухое или вязкое трение), то механическая энергия системы будет уменьшаться. Так, автомобиль останавливается в результате торможения, колебания маятника постепенно затухают и т. д. Силы трения неконсервативны: работа силы трения очевидным образом зависит от пути, по которому перемещается тело между данными точками. В частности, работа силы трения по замкнутому пути не равна нулю.

Снова рассмотрим движение тела в поле силы тяжести и/или на пружине. Вдобавок на тело действует сила трения, которая за рассматриваемый промежуток времени совершает отрицательную работу $A_{TP}$ . Работу консервативных сил (тяжести и упругости) по-прежнему обозначаем .

Изменение кинетической энергии тела равно работе всех внешних сил:

$K_{2}-K_{1}=A+A_{TP}$ .

Но $A=W_{1}-W_{2}$ , следовательно

$K_{2}-K_{1}=W_{1}-W_{2}+A_{TP}$ .

Отсюда

$K_{2}+W_{2}-(K_{1}+W_{1})=A_{TP}$ ,

или

$E_{2}-E_{1}=A_{TP}$ .

В левой части стоит величина $Delta E=E_{2}-E_{1}$ — изменение механической энергии тела:

$Delta E=A_{TP}$ .

Итак,при движении тела в поле силы тяжести и/или на пружине изменение механической энергии тела равно работе силы трения. Так как работа силы трения отрицательна,изменение механической энергии также отрицательно: механическая энергия убывает.
Справедливо и более общее утверждение.

Закон изменения механической энергии. Изменение механической энергии замкнутой системы равно работе сил трения, действующих внутри системы.

Ясно, что закон сохранения механической энергии является частным случаем данного утверждения.

Конечно, убыль механической энергии не противоречит общефизическому закону сохранения энергии. В данном случае механическая энергия превращается в энергию теплового движения частиц вещества и их потенциальную энергию взаимодействия друг с другом, т. е. переходит во внутреннюю энергию тел системы.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Энергия.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Если
частица массы m
движется со скоростью v,
то ее кинетическая
энергия
может быть представлена в виде

.
(1.3.57)

Кинетическая
энергия системы
частиц – величина аддитивная и
представляет собой сумму кинетических
энергий всех частиц системы:

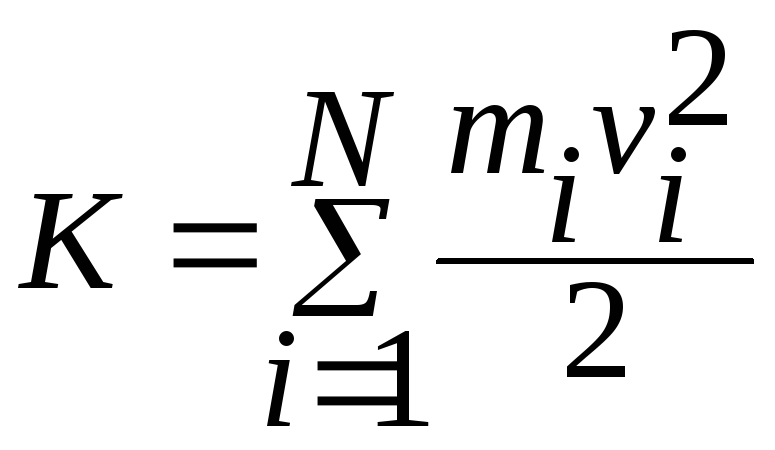
где
N
– число частиц в системе, m_i
– масса i-той
частицы, v_i
– скорость i-той
частицы.

*
Сила,
работа которой не зависит от формы и
длины пути (от
траектории точки приложения силы),
называется консервативной
силой.
Математически условие консервативности
силы выражается в виде:

что
означает:

*
циркуляция
консервативной силы по любому замкнутому
контуру равна нулю.

Из
определения консервативной силы следует:

работу
консервативной силы можно представить
как убыль некоторой скалярной функции

,
зависящей только от положения тела
(частицы), которая называется потенциальной
энергией:

Последняя
формула является определением
потенциальной энергии:

*
Потенциальная
энергия определена с точностью до
произвольной постоянной.

Так
как определена только разность
потенциальной энергии, то к выражению
для потенциальной энергии можно добавить
или вычесть любую постоянную величину.
Поэтому в каждом конкретном случае
договариваются о начале отсчета
потенциальной энергии (в какой именно
точке считают U
= 0).

Полная
механическая энергия частицы
– это сумма ее кинетической и потенциальной
энергий:

Если на частицу
действуют только консервативные силы,
то с одной стороны dA
= – dU
, с другой (из второго закона Ньютона):
dA
= dK

– dU
= dK,

d(K
+ U)
= dE=0 

Е = const
(1.3.58)

Выражение
(1.3.58) – это закон сохранения полной
механической энергии, который гласит:

*
механическая
энергия частицы, подверженной действию
только консервативных сил, сохраняется.

Неконсервативные
силы
– силы, работа которых зависит от длины
и формы пути. То есть, работа неконсервативных
сил на замкнутом пути не равна нулю, с
ними не связана потенциальная энергия.

Примеры:
сила трения скольжения, сила вязкого
трения.

Работа
силы трения скольжения зависит не от
перемещения тела, а от длины пути: A_тр
= – Nl,
и не равна
нулю при возвращении тела в исходную
точку.

Если
на частицу действуют как консервативные,
так и неконсервативные силы, то полная
механическая энергия этой частицы
сохраняться
не будет:

dE
= d(K
+ U)
= dA_неконс.
(1.3.59)

Выражение
(1.3.59) является математическим выражением
закона
изменения полной механической энергии:

*
Изменение полной механической энергии
частицы равно работе всех действующих
на нее неконсервативных сил:

Потенциальная
энергия системы
частиц
складывается из собственной
потенциальной энергии
U_соб
(энергия взаимодействия частиц системы
между собой) и внешней
потенциальной энергии
U_внешн:

U_сист
= U_соб
+ U_внешн,

где

Здесь
U_ij
– потенциальная энергия взаимодействия
i-той
и j-той
частиц системы; коэффициент 1/2
учитывает тот факт, что каждое слагаемое
в двойной сумме учитывается дважды.

Если
на каждую частицу системы действуют,
кроме внутренних, также внешние силы,
пусть тоже консервативные, то их работа
равна убыли внешней энергии dA
= – dU_внешн,

где .

Здесь
U_i
– потенциальная энергия i-той
частицы во внешнем поле. Она зависит от
положений всех частиц во внешнем поле
и является аддитивной (в отличие от
собственной энергии U_соб).

В
таком случае, полная механическая
энергия системы частиц запишется так:

E
= K_сист
+ U_соб
+ U_внешн.

*
Консервативной
называется система, полная механическая
энергия которой сохраняется:
E_сист
= сonst.
В такой
системе отсутствуют любые неконсервативные
силы (и внешние, и внутренние).

Заметим,
что консервативность системы и закон
сохранения энергии никак не связаны с
замкнутостью системы.

Закон
изменения полной механической энергии
системы:

*
Изменение
полной механической энергии системы
равно суммарной работе всех неконсервативных
сил:

dE_сист
= dA_неконс.

Кинетическая
энергия вращающегося вокруг закрепленной
оси твердого тела:

,
(1.3.60)

где
m_i
– масса i-той
частицы, R_i
– радиус окружности, по которой вращается
i-тая
частица, 
– угловая скорость вращения тела.

Продифференцируем
по времени формулу (1.3.60) и получим закон
изменения кинетической энергии
вращающегося вокруг закрепленной оси
твердого тела:

то
есть,

*
скорость
изменения кинетической энергии
вращательного движения равна мощности
результирующего момента сил относительно
оси вращения.

Отсюда

dK_вращ= M_zdt
= M_zd  K

K₂
– K₁
= 
M_zd,

то
есть,

*
изменение
кинетической энергии вращательного
движения равно работе момента сил.

Движение
твердого тела, при котором центр масс
перемещается в фиксированной плоскости,
а ось вращения тела, проходящая через
его центр масс, остается перпендикулярной
к этой плоскости, называется плоским
движением.
Типичным примером такого движения
является качение симметричного тела.

Это
движение можно свести к совокупности
поступательного движения и вращения
вокруг неподвижной
(закрепленной) оси.

Кинетическая
энергия тела, совершающего плоское
движение, запишется в виде

.
(1.3.61)

Здесь
V_С
– скорость движения центра масс тела.

Пример
22. Однородный
диск массы 1 кг и радиуса 1 м катится без
трения и проскальзывания. Скорость
центра масс диска составляет 1 м/с. Найти
кинетическую энергию диска.

Дано:
m
= 1 кг;

R
= 1 м;

V_C
= 1 м/с.

Найти:
К_плоск.

Решение.
Данное движение диска является плоским,
поэтому для кинетической энергии диска
запишем формулу (1.3.61):

Найдем
момент инерции диска, вращающегося
относительно оси, проходящей через его
центр масс из (1.3.52):

I_C
= (1/2)
mR²,

а
угловую скорость вращения диска из
(5.17): v
= R.

Имеем:

=
=

=
0,75 (Дж).

Ответ:
0,75 Дж.

Пример
23. Небольшая
шайба массы 1 кг, имея начальную скорость
10 м/с, останавливается, пройдя путь,
равный 5 м. Найти силу трения, действующую
на шайбу.

Дано:
m
= 1 кг;

V₀
= 1 м/с;

S
= 5 м.

Найти:
F_тр.

Решение.
В силу того, что во время движения на
шайбу действует сила трения, полная
механическая энергия шайбы изменяется,
причем из (1.3.59) имеем:

dE
= d(K
+ U)
= dA_неконс или
в интегральной форме, расшифровывая
работу силы трения,

Е
= A_неконс
= F_тр
Scos
= – F_тр
S,
(1.3.62)

так
как вектор силы трения противонаправлен
перемещению шайбы, то есть 
= 180,
cos180
= – 1.

Запишем,
чему равно изменение полной механической
энергии шайбы, используя (1.3.62):

,
откуда

= 10
(Н).

Ответ: 10 Н.

Пример 24.
Резиновая шайба массы 1 кг, двигаясь со
скоростью 1 м/с, соскальзывает с горки
высотой 1 м и приобретает скорость V
у подножия горки. Во время движения над
шайбой была совершена работа сил трения
А_тр
= 1 Дж. Считая, что ускорение свободного
падения составляет 10 м/с²,
найти скорость шайбы V.

Дано:
m
= 1 кг;

V₀
= 1 м/с;

А_тр
= 1 Дж;

g
= 10 м/с².

Найти: V.

Решение. Поскольку
во время движения шайбы на нее по условию
задачи действует сила трения, полная
механическая энергия шайбы изменяется.
Запишем закон изменения полной
механической энергии в интегральной
форме:

E
= Е₂
– Е₁
= A_тр.

Изменение
полной механической энергии:

,
откуда выразим
скорость, которую приобретает шайба у
подножия горки:

= 4,36 (м/с).

Ответ:
4,36 м/с.

Источник

Полная механическая энергия

Содержание:

Что такое полная механическая энергия тела
Закон изменения и сохранения полной механической энергии
Чему равна полная энергия, как изменяется по времени

Что такое полная механическая энергия тела

Энергия тела — физическая величина, которая показывает работу, совершаемую рассматриваемым телом в течение любого, в том числе неограниченного периода времени.

Объект, который совершает положительную работу, расходует частично энергию. В случае, когда положительную работу совершают над телом, его энергия возрастает. Если рассматривается отрицательная работа, то эффект будет противоположным. Таким образом, энергия выражается через физическую величину, характеризующую способность тела или системы взаимодействующих объектов совершать работу. Единицей измерения энергии в СИ является Джоуль (Дж).

Кинетическая энергия — это энергия тел, находящихся в движении.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В качестве движущихся тел рассматриваются не только перемещающиеся тела, но и объекты, которые вращаются. Кинетическая энергия возрастает по мере увеличения массы тела и скорости, с которой оно движется, то есть перемещается, либо вращается в пространстве. Кинетическая энергия определяется телом, по отношению к которому проводят измерения скорости рассматриваемого объекта. Для расчета кинетической энергии Ек тела, масса которого составляет m, движущегося со скоростью v, используют следующую формулу:

(E_{k}=frac{mv^{2}}{2})

Потенциальная энергия — энергия тел или их частей, которые взаимодействуют друг с другом.

Потенциальная энергия тел отличается в зависимости от силы, которая на них воздействует:

сила тяжести;
сила упругости;
архимедова сила.

Любая потенциальная энергия определяется силой взаимодействия и расстоянием между взаимодействующими телами или их частями. Для расчета потенциальной энергии выбирают какой-то условный нулевой уровень. В качестве примера потенциальной энергии можно рассмотреть энергию, которой будет обладать груз, поднятый на определенную высоту над поверхностью Земли, или сжатая пружина. Потенциальная энергия рассчитывается по формуле:

(E_{p}=mgh)

Энергия может трансформироваться из одного вида в другой. Так кинетическая энергия объекта может преобразоваться в его потенциальную энергию, и наоборот.

Механическая энергия тела — это сумма его кинетической и потенциальной энергий.

Механическая энергия любого тела определяется несколькими факторами:

Объект, относительно которого выполняют измерение скорости рассматриваемого тела.
Условные нулевые уровни, присущие всем разновидностям имеющихся у тела потенциальных энергий.

Данная величина является одной из основных характеристик тела. С помощью механической энергии определяют способность тела или системы объектов совершать работу по причине изменений скорости тела, либо взаимного положения тел, находящихся во взаимодействии.

Закон изменения и сохранения полной механической энергии

Закон сохранения и превращения энергии: энергия не может возникать ниоткуда, либо исчезать бесследно. Можно лишь наблюдать переход одного вида энергии в другой, либо от одного тела к другому.

Закон сохранения механической энергии: когда тела системы испытывают на себе воздействие силы тяжести или силы упругости, сумма кинетической и потенциальной энергии не будет изменяться, таким образом, механическая энергия сохраняется.

Изменение механической энергии системы тел определяется, как сумма работы внешних по отношению к системе тел и работы внутренних сил трения и сопротивления. Формула для расчета имеет следующий вид:

(Delta W;=;Aвнешн;+;Адиссип)

В случае замкнутой системы тел ее полная механическая энергия будет изменена только в том случае, когда совершается работа внутренних диссипативных сил системы таких, как сила трения:

Aвнешн = 0, то ΔW = Адиссип

Когда рассматривают консервативную систему тел, то есть при отсутствии сил трения и сопротивления, полная механическая энергия системы тел изменяется при работе внешних, относительно системы тел, сил:

(Атр = 0)

(ΔW = Aвнешн)

Чему равна полная энергия, как изменяется по времени

Полная механическая энергия тела определяется суммой его кинетической и потенциальной энергии. Определение полной механической энергии справедливо в случае действия закона сохранения энергии, и ее постоянном значении.

В ситуации, когда тело движется без влияния внешних сил, включая отсутствие взаимодействия с другими телами, силы трения и силы сопротивления, полная механическая энергия тела не меняется со временем. С помощью формулы это утверждение можно записать следующим образом:

(Епот;+;Екин;=;const)

Примечание

В реальном мире нельзя смоделировать таких идеальных ситуаций, в условиях которых объект полностью сохраняет свою энергию. Причиной этому является постоянное взаимодействие тела с другими телами, к примеру с молекулами воздуха или сопротивлением воздуха.

В случаях, когда сила сопротивления минимальна, и поступательное или другое движение наблюдают в относительно короткое время, подобную систему можно принять за теоретически идеальную. Как правило, закон сохранения полной механической энергии справедлив для тела, совершающего свободное падение, при вертикальном подбрасывании объекта или в случае колебательного движения тела такого, как маятник.

К примеру, во время вертикального подбрасывания тела наблюдают сохранение его полной механической энергии. Кинетическая энергия объекта при этом трансформируется в потенциальную, и наоборот. Амплитуда изменений энергий представлена на графике.

Энергия

В зависимости от точки нахождения тела энергия будет рассчитываться следующим образом:

самая верхняя точка при (h = max), (Eпот = mgh), (Eкин = 0), (Eполная = mgh);
средняя точка при (h = средняя), (Eпот = mgh), (Eкин = mv2/2), (Eполная = mgh + mv2/2);
самая нижняя точка при (h = 0), (Eпот = 0), (Eкин = mv2/2), (Eполная = mv2/2).

В начале пути тело обладает кинетической энергией, которая будет равна его потенциальной энергии в верхней точке траектории движения. Исходя из этого, можно использовать еще несколько полезных формул. При известном значении максимальной высоты, на которую поднимется тело, максимальная скорость движения будет определена следующим образом:

(v_{max}=sqrt{2gh_{max}})

При известном значении максимальной скорости, с которой движется тело, можно рассчитать максимальную высоту подъема тела, брошенного вверх. Формула будет иметь такой вид:

(h_{max}=frac{v^{2}_{max}}{2g})

Источник

Екатерина Владимировна Мосина

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Механической энергией называют энергию, которая связана с движением тел, их возможностью совершать механическую работу, взаимодействовать.

Подчеркнем, что наличие энергии у тела объясняют две причины:

Перемещение тела с некоторой скоростью.
Пребывание тела в потенциальном поле сил.

Энергия, связанная с движением тела называется кинетической энергией.

Потенциальную энергию называют энергией положения, она связывается с нахождением тела в поле сил.

Находят механическую энергию как сумму:

кинетической энергии тела (системы тел) ($E_k$) и
потенциальной энергии тела (системы) $E_p$.

Кинетическая энергия

Допустим, что материальная точка, имеющая массу $m$, перемещается. Ее скорость равна $vec v$. Это тело воздействует на второе тело (рис.1), которое соприкасается с первым, с силой $vec F$.

Рисунок 1. Кинетическая энергия. Автор24 — интернет-биржа студенческих работ

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

За промежуток времени $dt$ точка, к которой приложена сила (точка $A$ рис.1) совершит перемещение, равное:

$dvec s=vec v dt (1)$.

Это означает, что сила (материальная точка 1) совершает над телом 2 работу, равную:

$dA=vec F dvec s =vec F vec v dt(2).$

Материальная точка 1 выполняет работу, поскольку имеет запас энергии, мы знаем, что она перемещается, и, значит, у нее есть кинетическая энергия. При отсутствии движения мы имели бы $ds=0$, следовательно, была бы равна нулю работа $dA=0$.

На этом основании работу, которую совершает тело 1, будем считать равной уменьшению его кинетической энергии:

$dA=-dE_{k1}(3).$

Учитывая формулу (2) получим:

$ dE_{k1}=-vec F vec v dt (4)$.

Из третьего закона Ньютона имеем (рис.1):

$vec F’ =- vec F (5),$

в результате скорость материальной точки 1 изменяется на величину $dvec v$ за отрезок времени $dt$:

$ dvec v = frac {1}{m}vec F’ dt=-frac {1}{m}vec F dt (6).$

Запишем скалярное произведение обеих частей уравнения (6) на величину $mvec v$:

$mvec v dvec v=-vec F cdot vec v dt (7).$

«Закон изменения механической энергии с формулами» 👇

Выполним сравнение выражений (2) и (7), имеем:

$d E_k=d(frac{m v^2}{2}) (8).$

Формула (8) показывает, что кинетическая энергия материальной точки определяется как:

$E_k=frac{m v^2}{2} = frac {p^2}{2m}(9),$

где $p$ — модуль импульса тела.

Закон изменения кинетической энергии

Работа, которую совершают над телом ($A’$), равна увеличению его кинетической энергии:

$Delta E_k=E_{k2}-E_{k1}=A’(10).$

Для доказательства данного утверждения следует воспользоваться выражением для элемента работы, которое мы запишем в виде:

$dA’=vec F’vec v dt (11),$

где $vec F’$ — сила, которая совершает работу над телом; $vec v$ — скорость тела. Используем второй закон Ньютона в виде:

$frac {dvec p}{dt}=vec F’ (12),$

следовательно, $m dvec v=vec F’ dt (13).$

Учитывая полученное в (13), имеем:

$dA’=mvec v dvec v=mvdv=d(frac {mv^2}{2})=d E_k (14)$.

Интегрирования выражения (14) приводит к результату:

$A’=Delta E_k (15).$

Потенциальная энергия

Определение 1

Потенциальным полем называют силовое поле, которое выражается при помощи скалярной потенциальной функции ($U(x,y,z,t)$), зависящей от пространственных координат и времени. Данную функцию называют потенциальной. При этом сила, оказывающая воздействие на частицу, и потенциальная функция связаны соотношением:

$vec F(x,y,z,t)=-(frac{partial U(x,y,z,t)}{partial x}vec i+frac{partial U(x,y,z,t)}{partial y}vec j+frac{partial U(x,y,z,t)}{partial y}vec k)=-grad U (16)$.

Градиент скалярной функции – это вектор, который направлен в сторону наиболее быстрого увеличения данной функции, равный по величине скорости ее увеличения в этом направлении. Знак минус в формуле (16) показывает то, что сила имеет направление в сторону наиболее быстрого уменьшения функции $U$.

Частным случаем потенциальных полей являются поля, которые не зависят в явном виде от времени. Такие поля именуют консервативными. Для консервативных полей $U=U(x,y,z)$.

Иначе говорят, что тело (частица) находится состоянии стационарных внешних условий, например, в постоянном поле гравитации. В этом случае потенциальную функцию $U$ называют потенциальной энергией частицы во внешнем консервативном поле.

Обозначим потенциальную энергию как $E_p$, в таком случае выполняется равенство:

$vec F=- grad E_p (x,y,z)(17).$

Конкретный вид потенциальной энергии зависит от характера силового поля, в котором находится тело.

Потенциальную энергию имеют:

система тел, находящихся во взаимодействии;
тело в состоянии упругой деформации.

Закон изменения потенциальной энергии

Работа в потенциальном поле сил не зависит от пути.

Рассмотрим материальную точку, находящуюся в потенциальном поле сил. Каждую точку поля будем характеризовать значением $E_p(vec r)$, где $vec r$ — радиус – вектор точки поля.

Допустим, что величина функции $E_p(vec r)$ в начальной точке равна:

$E_p(0)=E_{p0}.$

Для получения величины $ E_{p1} (vec r_1)$ в некоторой точке 1 выполним следующее действие:

$E_{p1}(vec r_1)= E_{p0}+A_{10}(18),$

где $ A_{10}$ — работа, которую совершают над материальной точкой силы поля, когда перемещают ее из начальной точки в точку 1.

Так как работа в поле потенциальных сил не зависима от пути, то величина E_{p1} является однозначной. Для второй точки по аналогии запишем:

$E_{p2}(vec r_2)= E_{p0}+A_{20}(19).$

Найдем разность $ E_{p1}- E_{p2}$, используя формулы (18) и (19), принимая во внимание, что $A_{20}=-A_{02}$

$ E_{p1}- E_{p2}= A_{10}- A_{20}= A_{10}+A_{02}(20), $

где $ A_{10}+A_{02}$ — работа, которую выполняют силы поля, если совершают перемещения тела из точки 1 в точку 2 через начальную точку. Но мы помним, что работа консервативных сил не будет зависеть от траектории движения тела, то есть работа при непосредственном перемещении из 1 в 2 будет такой же как из1 в 0, а потом в 2. Поэтому:

$ A_{10}+A_{02}=A_{21} (21)$.

В результате мы имеем:

$ E_{p1}- E_{p2}=A_{12} (22)$.

Выражение (22) показывает нам, что при помощи потенциальной энергии имеется возможность найти работу, которую силы потенциального поля совершают над телом при любом пути из точки 1 в точку 2. Данная работа будет равна уменьшению потенциальной энергии.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Обновлено: 28.05.2023

Полную механическую энергию рассматривают в тех случаях, когда действует закон сохранения энергии и она остаётся постоянной.

Если на движение тела не оказывают влияния внешние силы, например, нет взаимодействия с другими телами, нет силы трения или силы сопротивления движению, тогда полная механическая энергия тела остаётся неизменной во времени.

Разумеется, что в повседневной жизни не существует идеальной ситуации, в которой тело полностью сохраняло бы свою энергию, так как любое тело вокруг нас взаимодействует хотя бы с молекулами воздуха и сталкивается с сопротивлением воздуха. Но, если сила сопротивления очень мала и движение рассматривается в относительно коротком промежутке времени, тогда такую ситуацию можно приближённо считать теоретически идеальной.

Закон сохранения полной механической энергии обычно применяют при рассмотрении свободного падения тела, при его вертикальном подбрасывании или в случае колебаний тела.

При вертикальном подбрасывании тела его полная механическая энергия не меняется, а кинетическая энергия тела переходит в потенциальную и наоборот.

Исходя из того, что в начале движения величина кинетической энергии тела одинакова с величиной его потенциальной энергии в верхней точке траектории движения, для расчётов могут быть использованы ещё две формулы.

Если известна максимальная высота, на которую поднимается тело, тогда можно определить максимальную скорость движения по формуле:

Если известна максимальная скорость движения тела, тогда можно определить максимальную высоту, на которую поднимается тело, брошенное вверх, по такой формуле:

На графике синей пунктирной линией показано изменение потенциальной энергии. В средней точке рампы потенциальная энергия равна (нулю). Зелёной пунктирной линией показано изменение кинетической энергии. В верхних точках рампы кинетическая энергия равна (нулю). Жёлто-зелёная линия изображает полную механическую энергию — сумму потенциальной и кинетической — в каждый момент движения и в каждой точке траектории. Как видно, она остаётся (неизменной) во всё время движения. Частота точек характеризует скорость движения — чем дальше точки расположены друг от друга, тем больше скорость движения.

На графике видно, что значение потенциальной энергии в начальной точке совпадает со значением кинетической энергии в середине рампы.

В реальной ситуации всегда происходят потери энергии, так как часть энергии выделяется в виде тепла под влиянием сил трения и сопротивления.

Поэтому для того, чтобы автомобиль двигался с равномерной и неизменной скоростью, необходимо постоянно подводить дополнительную энергию, которая компенсировала бы энергетические потери.

Физика — такая клевая наука, в которой ничего не исчезает бесследно. В том числе энергия. Вернее: особенно энергия. О том, куда она девается, если не бесследно — в этой статье.

О чем эта статья:

Энергия: что это такое

Поэтому давайте условимся здесь и сейчас, что энергия — это запас, который пойдет на совершение работы.

Энергия бывает разных видов: механическая, электрическая, внутренняя, гравитационная и так далее. Измеряется она в Джоулях (Дж) и чаще всего обозначается буквой E.

Механическая энергия

Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.

Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.

Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим 😂), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.

Кинетическая энергия

Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.

Кинетическая энергия

Е_к — кинетическая энергия [Дж]

m — масса тела [кг]

Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.

Задачка раз

Определить кинетическую энергию собаченьки массой 10 кг, если она бежала за мячом с постоянной скоростью 2 м/с.

Решение:

Формула кинетической энергии

Ответ: кинетическая энергия пёсы равна 20 Дж.

Задачка два

Найти скорость бегущего по опушке гнома, если его масса равна 20 кг, а его кинетическая энергия — 40 Дж

Решение:

Формула кинетической энергии

Ответ: гном бежал со скоростью 2 м/с.

Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!

Потенциальная энергия

В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.

Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.

Потенциальная энергия деформированной пружины

Е_п — потенциальная энергия [Дж]

k — жесткость [Н/м]

x — удлинение пружины [м]

Потенциальная энергия в поле тяжести

Е_п = mgh

Еп — потенциальная энергия [Дж]

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g ≃ 9,8 м/с 2

Задачка раз

Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с 2 .

Решение:

Формула потенциальной энергии Е_п = mgh

E_п = 0,1 · 9,8 · 2500 = 2450 Дж

Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.

Задачка два

Найти высоту горки, с которой собирается скатиться лыжник массой 65 кг, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с 2 .

Решение:

Формула потенциальной энергии Е_п = mgh

Переведем 637 кДж в Джоули.

637 кДж = 637000 Дж

Ответ: высота горы равна 1000 метров.

Задачка три

Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E₁ и E₂. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.

Решение:

Потенциальная энергия вычисляется по формуле: E = mgh

По условию задачи

Таким образом, получим, что

Закон сохранения энергии

В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии.

Закон сохранения энергии

Полная механическая энергия замкнутой системы остается постоянной.

Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так:

Закон сохранения энергии

Е_{полн. мех.} — полная механическая энергия системы [Дж]

Е_п — потенциальная энергия [Дж]

Е_к — кинетическая энергия [Дж]

const — постоянная величина

Задачка раз

Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза?

Решение:

Должен выполняться закон сохранения энергии:

В начальный момент времени высота равна нулю, значит Е_п = 0. В этот же момент времени Е_к максимальна.

В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты.

Это можно описать соотношением:

Разделим на массу левую и правую часть

Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза.

Ответ: высота увеличится в 4 раза

Задачка два

Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v₀, поднялось на максимальную высоту h₀. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h?

Решение

По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Е_мех = Е_п = mgh₀.

Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Е_мех = mgh₀.

Задачка три

Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь.

Решение:

Переведем массу из граммов в килограммы:

m = 100 г = 0,1 кг

У поверхности земли полная механическая энергия мяча равна его кинетической энергии:

На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии:

Ответ: мяч имел скорость 2 м/с на высоте 1,6 м

Переход механической энергии во внутреннюю

Внутренняя энергия — это сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. То есть та энергия, которая запасена у тела за счет его собственных параметров.

Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путем совершения механической работы над телом. Например, если сгибать и разгибать проволоку — она будет нагреваться.

Или если кинуть мяч в стену, часть энергии при ударе перейдет во внутреннюю.

Задачка

Какая часть начальной кинетической энергии мяча при ударе о стену перейдет во внутреннюю, если полная механическая энергия вначале в два раза больше, чем в конце?

Решение:

В самом начале у мяча есть только кинетическая энергия, то есть Е_мех = Е_к.

В конце механическая энергия равна половине начальной, то есть Е_мех/2 = Е_к/2

Часть энергии уходит во внутреннюю, значит Е_полн = Е_мех/2 + Е_внутр

Ответ: во внутреннюю перейдет половина начальной кинетической энергии

Закон сохранения энергии в тепловых процессах

Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую.

Вот что сформулировал Фурье:

При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия.

Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы.

Дальше Карно установил, что тепловую энергию, которой обладает нагретое тело, непосредственно невозможно превратить в механическую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры.

Закон сохранения энергии в тепловых процессах

При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом.

Математически его можно описать так:

Уравнение теплового баланса

Q_отд — отданное системой количество теплоты [Дж]

Q_пол — полученное системой количество теплоты [Дж]

Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом:

Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен.

Чтобы разобраться в задачках, читайте нашу статью про агрегатные состояния вещества.

Задачка раз

Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии.

Удельная теплота сгорания спирта 2,9 · 10₇ Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг · °С).

Решение:

При нагревании тело получает количество теплоты

где c — удельная теплоемкость вещества

При сгорании тела выделяется энергия

где q — удельная теплота сгорания топлива

По условию задачи нам известно, что на нагревание воды пошло 20% энергии, полученной при горении спирта.

Ответ: масса сгоревшего топлива равна 33,6 г.

Задачка два

Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг · ℃, удельная теплота плавления льда равна 3,3 · 10 5 Дж/кг.

Решение:

Для нагревания льда до температуры плавления необходимо:

Q_нагрев = 2100 · 0,5 · (10 − 0) = 10 500 Дж

Для превращения льда в воду:

Q_пл = 3,3 · 10 5 · 0,5 = 165 000 Дж

Таким образом, для превращения необходимо затратить:

Q = Q_нагрев + Q_пл = 10 500 + 165 000 = 175 500 Дж = 175,5 кДж

Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла.

Механическая энергия.
Закон сохранения энергии

Раздел ОГЭ по физике: 1.18. Механическая энергия. Закон сохранения механической энергии. Формула для закона сохранения механической энергии в отсутствие сил трения. Превращение механической энергии при наличии силы трения.

1. Энергия тела – физическая величина, показывающая работу, которую может совершить рассматриваемое тело (за любое, в том числе неограниченное время наблюдения). Тело, совершающее положительную работу, теряет часть своей энергии. Если же положительная работа совершается над телом, энергия тела увеличивается. Для отрицательной работы – наоборот.

Энергией называют физическую величину, которая характеризует способность тела или системы взаимодействующих тел совершить работу.
Единица энергии в СИ 1 Джоуль (Дж).

2. Кинетической энергией называется энеpгия движущихся тел. Под движением тела следует понимать не только перемещение в пространстве, но и вращение тела. Кинетическая энергия тем больше, чем больше масса тела и скорость его движения (перемещения в пространстве и/или вращения). Кинетическая энеpгия зависит от тела, по отношению к которому измеряют скорость рассматриваемого тела.

3. Потенциальной энергией называется энергия взаимодействующих тел или частей тела. Различают потенциальную энергию тел, находящихся под действием силы тяжести, силы упругости, архимедовой силы. Любая потенциальная энергия зависит от силы взаимодействия и расстояния между взаимодействующими телами (или частями тела). Потенциальная энергия отсчитывается от условного нулевого уровня.

Потенциальной энергией обладают, например, груз, поднятый над поверхностью Земли, и сжатая пружина.
Потенциальная энергия поднятого груза Е_п = mgh .
Кинетическая энергия может превращаться в потенциальную, и обратно.

4. Механической энергией тела называют сумму его кинетической и потенциальной энергий. Поэтому механическая энеpгия любого тела зависит от выбора тела, по отношению к которому измеряют скорость рассматриваемого тела, а также от выбора условных нулевых уровней для всех разновидностей имеющихся у тела потенциальных энергий.

Механическая энергия характеризует способность тела или системы тел совершить работу вследствие изменения скорости тела или взаимного положения взаимодействующих тел.

5. Внутренней энергией называется такая энергия тела, за счёт которой может совершаться механическая работа, не вызывая убыли механической энергии этого тела. Внутренняя энеpгия не зависит от механической энергии тела и зависит от строения тела и его состояния.

6. Закон сохранения и превращения энергии гласит, что энеpгия ниоткуда не возникает и никуда не исчезает; она лишь переходит из одного вида в другой или от одного тела к другому.

Закон сохранения механической энергии: если между телами системы действуют только силы тяготения и силы упругости, то сумма кинетической и потенциальной энергии остается неизменной, то есть механическая энергия сохраняется.

7. Изменение механической энергии системы тел в общем случае равно сумме работы внешних по отношению к системе тел и работы внутренних сил трения и сопротивления: ΔW = А_внешн + А_диссип

Если система тел замкнута (А_внешн = 0), то ΔW = А_диссип, то есть полная механическая энергия системы тел меняется только за счёт работы внутренних диссипативных сил системы (сил трения).

Если система тел консервативна (то есть отсутствуют силы трения и сопротивления А_тр = 0), то ΔW = А_внешн, то есть полная механическая энергия системы тел меняется только за счёт работы внешних по отношению к системе сил.

8. Закон сохранения механической энергии: В замкнутой и консервативной системе тел полная механическая энергия сохраняется: ΔW = 0 или W_п1 + W_к1 = W_п2 + W_к2 . Применим законы сохранения импульса и энергии к основным моделям столкновений тел.

Абсолютно неупругий удар (удар, при котором тела движутся после столкновения вместе, с одинаковой скоростью). Импульс системы тел сохраняется, а полная механическая энергия не сохраняется:

Абсолютно упругий удар (удар, при котором сохраняется механическая энергия системы). Сохраняются и импульс системы тел, и полная механическая энергия:

Удар, при котором тела до соударения движутся по прямой, проходящей через их центры масс, называется центральным ударом.

Схема «Механическая энергия.
Закон сохранения энергии. Углубленный уровень«

В начале этого раздела мы с вами отмечали то, что энергия, подобно импульсу, – величина сохраняющаяся. Однако на предыдущих уроках мы с вами убедились, что работа всех сил, действующих на тело, приводит к изменению кинетической и потенциальной энергии тела, однако не получили закон сохранения энергии. На этом уроке мы выведем закон сохранения полной механической энергии, а также поговорим о том, при каких условиях он справедлив.

Читайте также:

Что такое внешняя культура кратко

Какое участие ученики вашей школы принимают в работе по охране природы

План открытого урока по английскому языку 10 класс

Что такое вокзал кратко

Кто разрабатывает образовательную программу доу ответ на вопрос

Источник

Энергия.

Работа.

Мощность.

Механическая энергия.

Кинетическая энергия.

Потенциальная энергия тела вблизи поверхности Земли.

Потенциальна яэнергия деформированной пружины.

Закон сохранения механической энергии.

Закон изменения механической энергии.

Полная механическая энергия

Что такое полная механическая энергия тела

Закон изменения и сохранения полной механической энергии

Чему равна полная энергия, как изменяется по времени

Кинетическая энергия

Закон изменения кинетической энергии

Потенциальная энергия

Закон изменения потенциальной энергии

Энергия: что это такое

Механическая энергия

Кинетическая энергия

Потенциальная энергия

Закон сохранения энергии

Переход механической энергии во внутреннюю

Закон сохранения энергии в тепловых процессах

Механическая энергия. Закон сохранения энергии

Не пропустите также:

Механическая энергия.
Закон сохранения энергии