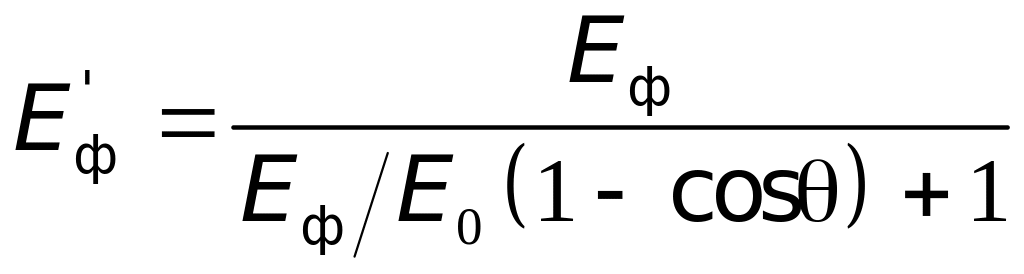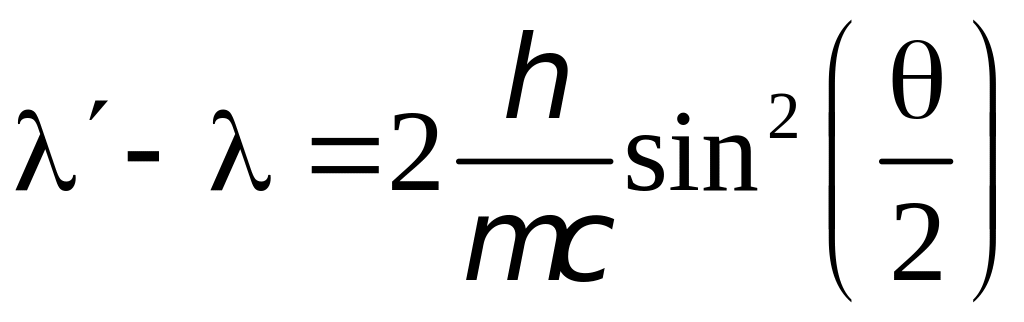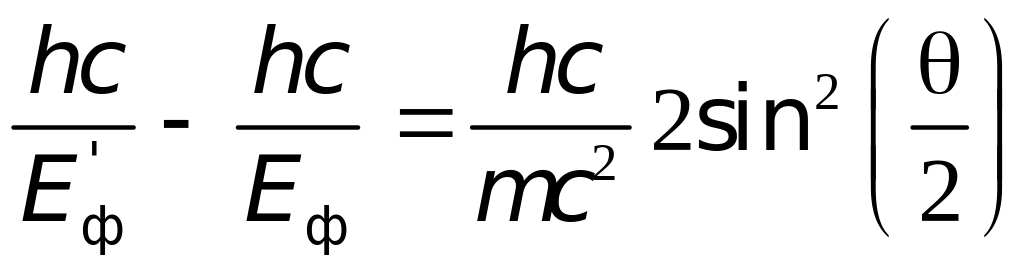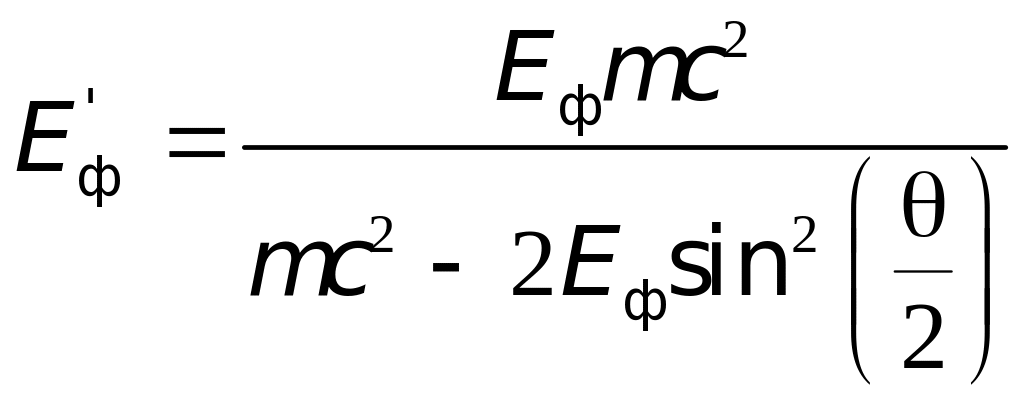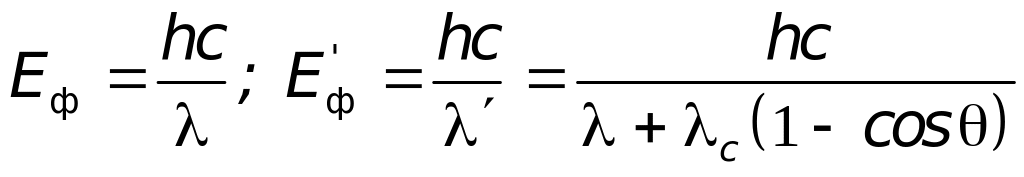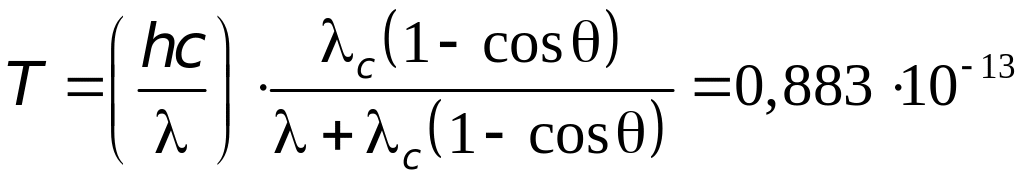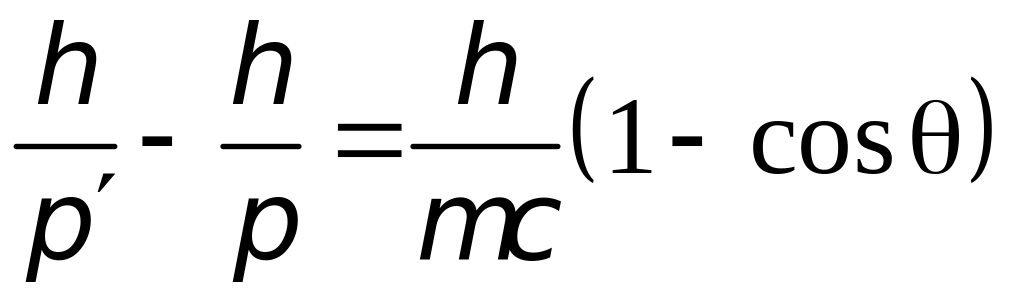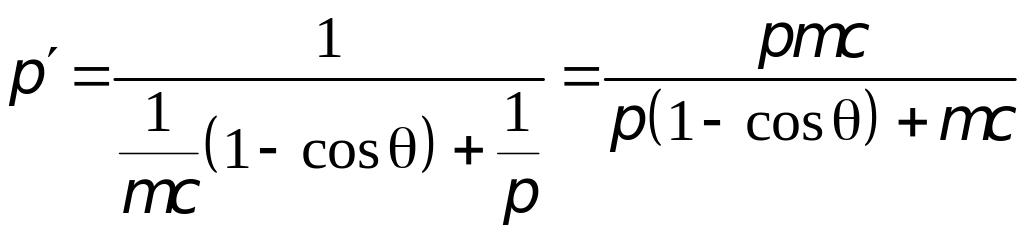В
1922 году А. Комптон, исследуя рассеяние
рентгеновского излучения различными
веществами обнаружил, что в нем наряду
с исходной длиной волны
появляется смещенная линия с длиной
волны
>
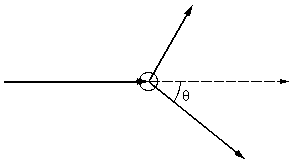
(Рис.8).

Рис.8 Схема установки
по изучению эффекта Комптона
Это
изменение длины волны получило название
комптоновского смещения, а само явление
эффекта Комптона. Комптоновское смещение
не зависит от длины волны
и от природы рассеивающего вещества и
определяется формулой:
,
где
– масса электрона или другой заряженной
частицы,
—
комптоновская длина волны этой частицы,
и
— длины волн
падающего и рассеянного излучения;
–угол
рассеяния. Для электрона
2,42пм.
Все
закономерности эффекта Комптона можно
объяснить, если рассмотреть упругое
столкновение рентгеновского кванта с
покоящимся электроном, слабо связанным
с атомом. Происходит процесс, напоминающий
удар двух биллиардных шаров, когда один
шар (рентгеновский квант) налетает на
покоящийся шар (электрон) и в результате
абсолютно упругого удара шары (рассеянный
квант и электрон) разлетаются под
некоторым углом. Налетающий квант с
энергией
передает часть своей энергии электрону,
поэтому рассеянный квант имеет меньшую
энергию и, следовательно, большую длину
волны. Энергия рентгеновского кванта
(десятки кэВ) на несколько порядков
превосходит энергию связи электрона в
атоме (десятки эВ), поэтому наиболее
слабо связанные с атомом электроны
внешних оболочек можно считать свободными
и покоящимися.
Законы
сохранения энергии при комптоновском
упругом рассеянии.
Закон сохранения
импульса имеет вид:
,
где
и
– волновые векторы падающего и рассеянного
фотонов (модуль волнового вектора равен
).
Графическая иллюстрация закона сохранения
импульса приведена на Рис. 9. Закон
сохранения энергии записывается в виде:
(
используется
релятивистская формула, т.к. энергия
падающего кванта сравнима в энергией
покоя электрона). Здесь
–постоянная
Планка, с –
скорость света,
– масса электрона,
– импульс электрона,
и
– длины падающей и рассеянной волн.
Рис.9
Графическая иллюстрация закона сохранения
импульса в эффекте Комптона
В
эффекте Комптона участвуют только
свободные электроны, которые слабо
связаны с атомами. Если же энергия связи
электрона больше энергии фотона, то
такой электрон не будет свободным и
эффект Комптона не возникает. В этом
случае фотон взаимодействует с жестко
связанной системой электрон – ядро и
«отскакивает» от нее, практически не
изменяя своей энергии и длины волны. В
реальном веществе фотоны сталкиваются
как со свободными, так и с сильно
связанными электронами, поэтому и
возникают оба компонента рассеяния с
длинами волн
и
.
Эффект
Комптона не может происходить под
действием квантов видимого света (с
длинами волн 400 – 700 нм), поскольку их
энергия составляет 3 – 1,8 эВ соответственно,
что на 5 порядков меньше энергии покоя
электрона – 511000 эВ.
Кинетическая
энергия электрона отдачи:
,
где
– энергия падающего фотона и
– энергия рассеянного фотона.
Соотношение
между энергией падающего
и рассеянного
фотонов при комптоновском рассеянии:
,
откуда
,
где
= 0,511 МэВ
– энергия покоя электрона.
Примеры решения задач
Задача
1. В результате
эффекта Комптона фотон при соударении
с электро-ном был рассеян на угол 90.
Энергия
рассеянного фотона равна 0,4 МэВ.
Опре-делите энергию фотона
до рассеяния.
Решение.
Выразим в
формуле Комптона
длины волн
и
через энергии
и
соответствующих фотонов, воспользовавшись
соотношением
,
,
откуда
=
1,85 Мэв,
где
= 0,51 МэВ, 1 МэВ = 1,6·10-13
Дж.
Задача
2. Гамма-фотон
с длиной волны 1,2 пм в результате
комптоновского рассеяния на свободном
электроне отклонился от первоначального
направления на угол 60.
Определите кинетическую энергию и
импульс электрона отдачи. До столкновения
электрон покоился.
Решение.
Из закона
сохранения энергии кинетическая энергия
электрона отдачи равна
,
где
и
– энергия падающего и рассеянного
фотонов.
Выражая
энергию падающего и рассеянного фотона
через его длину волны и используя формулу
изменения длины волны фотона при
комптоновском рассеянии, получим:
.
Для
кинетической энергии электрона находим
Дж.
= 0,521 МэВ.
пм
– комптоновская длина волны электрона.
Кинетическая энергия электрона сравнима
с его энергией покоя
,
поэтому его импульс найдем по
релятивистской формуле
=
4,8·10-22кг·м/c.
Задача
3. Фотон с
импульсом 5,4410–22
кгм/с
в результате эффекта Компто-
на
был рассеян на свободном электроне на
угол 30.
Найти импульс рассеянного фотона.
Решение.
Выражая
импульс фотона через его длину волны и
используя формулу изменения длины волны
при эффекте Комптона получим:
,
или
,
откуда
= 4,310–22
кгм/с.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Электрон переместился в ускоряющем электрическом поле из точки с потенциалом 200 В в точку с потенциалом 300 В. Найти кинетическую энергию электрона, изменение потенциальной энергии и приобретенную скорость. Начальную скорость считать равной нулю.
Источник: задачник 10-11 класс, А. П. Рымкевич.
Решение.
Φ1 − Φ2 = А / q.
A = q (Φ1 − Φ2).
A = 1.6 × 10−19 × (200 − 300) = −1.6 × 10−17.
A = −ΔWp.
Wp = Ek = 1.6 × 10−17.
E = mc2.
m = E / c2.
m = 1.6 × 10−17 / (2.99 × 108) = 0.54 × 10−25.
v = (√2) E / m.
v = (√2) 1.6 × 10−17 / (0.54 / 10−25) = 24300.
|
ДАНО: τ r1 = 0,01 м r2 = 0,005 |
АНАЛИЗ. Электростатическое поле образовано заряженной нитью. |
|
|
В результате
потенциальная энергия поля WP убывает. Она переходит в
кинетическую энергию электрона WK , причем ∆WK
= — ∆WP , где ∆WK — приращение
кинетической энергии электрона. Очевидно, убыль потенциальной энергии
Разность
потенциалов найдем, пользуясь связью напряженности и потенциала.
РЕШЕНИЕ.
Приращение кинетической энергии равно 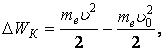
поэтому
Очевидно,
скорость электрона равна
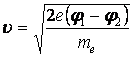
(2.1.12)
Для
нахождения разности потенциалов в неоднородном поле, создаваемом положительно
заряженной нитью, воспользуемся выражением для напряжённости поля нити
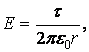
и связью напряженности и
потенциала . Заряд распределен вдоль силовой
линии, поэтому и
.
Проинтегрировав, получаем