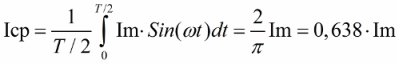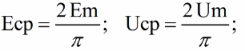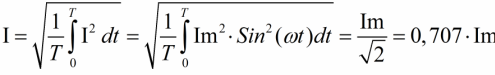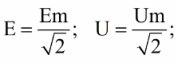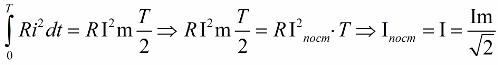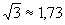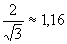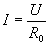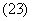Как найти истинное значение тока в цепи - AvtoShod.ru

Действующие значения тока и напряжения

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.

Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.

Действующее значение переменного тока — это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.

Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.

Мощность Р постоянного тока I , проходящего через сопротивление r , будет Р = Р 2 r .

Мощность переменного тока выразится как средний эффект мгновенной мощности I 2 r за целый период или среднее значение от ( Im х sin ω t ) 2 х r за то же время.

Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √ M ,

Величина I называется действующим значением переменного тока.

Среднее значение i2 при переменном токе определим следующим образом.

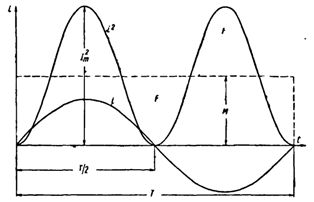
Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.

Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (- i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины.

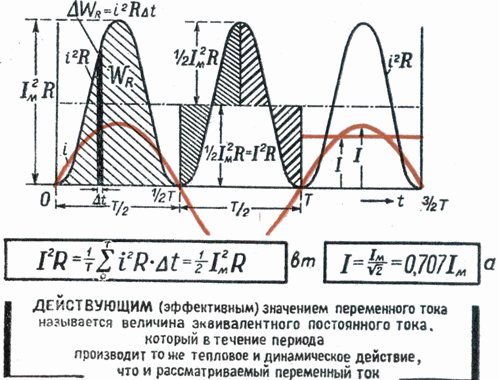
Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно 1/2I 2 m . Следовательно, М = 1/2I 2 m

Так как действующее значение I переменного тока равно I = √ M , то окончательно I = Im / √ 2

Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:

Действующие значения переменных величин обозначаются прописными буквами без индексов ( I , U, Е).

На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.

При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √ 2 раз. От этого расположение векторов на диаграмме не изменяется.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Что такое действующее, среднеквадратичное, эффективное напряжение или ток

Среднее значение переменного синусоидального напряжения или тока

Говоря о величине, изменяющейся по синусоидальному (гармоническому) закону, можно за половину периода определить ее среднее значение. Поскольку ток в сети у нас в подавляющем большинстве случаев синусоидальный, то для этого тока также легко может быть найдена средняя его величина (за половину периода), достаточно прибегнуть к операции интегрирования, установив пределы от 0 до Т/2. В результате получим:

Подставив Пи = 3,14, найдем среднюю, за половину периода, величину синусоидального тока в зависимости от его амплитуды. Аналогичным образом находится среднее значение синусоидальной ЭДС или синусоидального напряжения U:

Действующее значение тока I или напряжения U

Однако среднее значение не так широко применяется на практике, как действующее значение синусоидального тока или напряжения. Действующее значение синусоидально меняющейся во времени величины — есть среднеквадратичное, другими словами — эффективное ее значение.

Эффективное (или действующее) значение тока или напряжения находится так же, путем интегрирования, но уже по отношению к квадратам, и с последующим извлечением квадратного корня, причем пределы интегрирования теперь — целый период синусоидальной функции.

Итак, для тока будем иметь:

Подставив значение корня из 2, получим формулу для нахождения эффективного (действующего, среднеквадратичного) значения тока, напряжения, ЭДС — по отношению к амплитудному значению. Эту формулу можно встретить очень часто, ее используют всюду в расчетах, связанных с цепями переменного синусоидального тока:

С практической точки зрения, если сравнить тепловое действие тока переменного синусоидального с тепловым действием тока постоянного непрерывного, на протяжении одного и того же периода времени, на одной и той же активной нагрузке, то выяснится, что выделенная за период синусоидального переменного тока теплота окажется равна выделенной за это же время теплоте от тока постоянного, при условии, что величина постоянного тока будет меньше амплитуды тока переменного в корень из 2 раз:

Это значит, что действующее (эффективное, среднеквадратичное) значение синусоидального переменного тока численно равно такому значению постоянного тока, при котором тепловое действие (выделяемое количество теплоты) этого постоянного тока на активном сопротивлении за один период синусоиды равно тепловому действию данного синусоидального тока за тот же период.

Аналогичным образом находится действующее (эффективное, среднеквадратичное) значение синусоидального напряжения или синусоидальной ЭДС.

Подавляющее большинство современных портативных измерительных приборов, измеряя переменный ток или переменное напряжение, показывают именно действующее значение измеряемой величины, то есть среднеквадратичную величину, а не ее амплитуду и не среднее значение за полпериода.

Если других уточняющих настроек на приборе нет, а стоит значок

U – измерены будут действующие значения тока и напряжения. Обозначения для конкретно амплитуды или конкретно действующего — Im (m — maximum – максимум, амплитуда) или Irms (rms — Root Mean Square – среднеквадратичное значение).

Источник

Как найти истинное значение напряжения

Метод и средства для измерения напряжения и тока.

При измерении напряжения и тока используют прямые и косвенные способы. Прямые измерения основаны на сравнении измеряемой величина с мерой этой величины или на непосредственной оценке измеряемой величины по отчетному устройству измерительного прибора. Косвенные измерения основаны на прямых измерениях другой величины, функционально связанной с измеряемой величиной. Например, косвенное измерение тока выполняют при помощи вольтметра, измеряющего напряжение на известном сопротивлении R0, и расчете тока по формуле

Погрешность косвенного метода измерения зависит от погрешности прямого измерения и погрешности расчета по функциональной зависимости (23). Сопротивление, используемое при косвенном измерении тока, называют шунтом. Дополнительная погрешность при косвенных измерениях обусловлена перераспределением тока между шунтом и вольтметром при изменении температуры окружающей среды. Для снижения температурной погрешности применяют специальные схемы компенсации,

В зависимости от рода тока приборы делят на четыре группы;

1) вольтметры постоянного напряжения (группа В2),
2) вольтметры переменного напряжения (группа ВЗ),
3) вольтметры импульсного напряжения (группа В4),
4) вольтметры селективные (группа В6).

Универсальные приборы, предназначенные для измерения постоянного и импульсного напряжения и тока, выделены в группу В7.

Программа работы

1. Определение основной погрешности, вариация показаний и поправку вольтметра.
2. Определение чувствительности и цены деления вольтметра.
3. Определение входного сопротивления вольтметра.
4. Определение частотного диапазона вольтметра.
5. Исследование влияния формы напряжения на показание вольтметра.
6. Определение погрешности при прямых и косвенных измерениях тока.

Порядок выполнения работы.

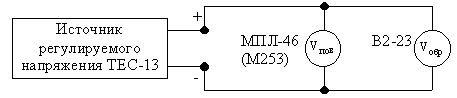
1. Определение основной погрешности, вариация показаний и поправки вольтметра выполняют по схеме, изображенной на рис. 1. В качестве поверяемого прибора используют вольтметр типа МПЛ-46, а образцовый служит цифровой вольтметр типа В2-23. Перед проведением измерений прибор В2-23 включить в сеть и выждать 10…15 мин. Затем произвести установку нуля и калибровку вольтметра И2-23 в соответствии с инструкцией по пользованию прибором. Кроме того, необходимо выполнить установку нуля вольтметра МПЛ-46, пользуясь корректором.

Для выполнения п.1 программы поверяемый вольтметр МПЛ-46 устанавливают на диапазон 15 В и измеряют напряжение на всех оцифрованных делениях шкалы, изменяя входное напряжение регулируемого источника ТЕС-13. Измерение напряжения на каждом оцифрованном делении шкалы МПЛ-46 производят дважды: один раз при возрастании напряжения (показание образцового вольтметра U’_обр), а второй раз при убывание напряжения (показание образцового вольтметра U’’_обр). При этом на образцовом вольтметре В2-23 необходимо выбрать поддиапазон, обеспечивающий не менее трех значащих цифр. Результаты измерений занести в ф.1.

Действительные значения на оцифрованных делениях шкалы поверяемого вольтметра определяют как среднее значение двух измерений U_ср=(U’_обр+U’’_обр)/2.
Расчет погрешности измерений выполняют по формулам:
Абсолютная погрешность U=U_пов-U_ср,
Относительная погрешность 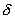=(U/ U_пов)*100%,
Приведенная погрешность _п=(U/ U_ном) *100%,
где U_ном=15 В – номинальное значение напряжения поверяемого.
Вариацию показаний вольтметра определяют по формулам:
Абсолютное значение вариации U=U’_обр-U’’_обр,
Приведенное значение вариации _в=(U_обр/ U_ном)*100%,
Поправку вольтметра вычисляют по формуле П=-U.
Из полученных значений _п и _в необходимо выбрать наибольшее и сравнить их с классом точности К_u поверяемого вольтметра. Если _{п макс} и _{в макс} окажутся больше К_u, то поверяемый вольтметр нельзя использовать с указанным классом точности.

Источник

Действующее значение тока и напряжения

Переменный ток, протекая по проводнику, нагревает его так же, как и постоянный ток. Силу переменного тока удобно оценивать по его тепловому действию (эффекту) или, как говорят, по действующей, эффективной его величине.

Действующее или эффективное значение переменного тока равно силе такого постоянного тока, который, протекая по данному проводнику, выделяет в нем ежесекундно то же количество энергии в виде тепла, что и переменный ток.

Тепловой эффект тока, а значит, и действующие (эффективные) значения переменного тока зависят не только от наибольших значений, которых достигает переменный ток, но и от формы тока.

Вообще говоря, в электротехнике, и особенно в радиотехнике, приходится иметь дело с токами довольно сложной формы. Но все эти токи могут быть представлены в виде суммы нескольких синусоидальных токов с различными частотами, амплитудами и начальными фазами. Поэтому очень важную роль играет связь между амплитудным и действующем значениями для синусоидального тока.

Если известна амплитуда переменного синусоидального тока, то действующее или эффективное его значение определяется по формуле:

то есть эффективное значение синусоидального тока в раз меньше его амплитудного значения.

Аналогичная формула применяется и для вычисления эффективного значения синусоидального напряжения:

Протекая по проводнику, переменный ток создает в нем эффективное падение напряжения, равное произведению эффективного значения силы тока на сопротивление проводника, что эквивалентно закону Ома для постоянного тока, то есть:

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Источник

Источник

Истинное значение — ток

Cтраница 1

Истинные значения токов, протекающих через сопротивления более 104 кОм, ничтожно малы — они выражаются наноамперами. Незначительная по абсолютному значению ошибка в вычислении токов в процессе решения уравнений может привести к большой погрешности определения напряжений на указанных сопротивлениях. В результате падение напряжения на сопротивлении, вычисленное исходя из данного тока, будет резко отличаться от напряжения на р — — переходе.
[1]

По вычисленным истинным значениям тока определяется погрешность прибора. В ходе проверки необходимо периодически убеждаться в неизменяемости рабочего тока потенциометра и напряжения на зажимах ваттметра.
[2]

Для определения истинного значения тока нужно суммировать найденные токи алгебраически, если речь идет об определении мгновенных значений тока и построении графика i ( t), и воспользоваться ( 12 — 16), вычислив предварительно действующее значение каждой гармоники для определения действующего значения тока.
[3]

При некоторых условиях уравнение Ильковича не дает истинного значения тока диффузии. Так, при уменьшении периода падения капель менее 3 — 4 сек, ток становится больше, чем получается по уравнению Ильковича, и воспроизводимость результатов ухудшается. Это явление связано с перемешиванием электролита быстро падающими каплями и нарушением диффузионного слоя.
[4]

Значения тока, вычисленные по формуле (2.1), всегда больше истинных значений тока в цепи коррозионной пары.
[5]

Завершая рассмотрение особенностей использования характеристик анодных кривых при анализе поведения титановых сплавов, нельзя не упомянуть о том, что для получения истинных значений токов растворения сплава при каком-либо значении потенциала необходимо учитывать и вносить поправку на ток возможного сопряженного электрохимического процесса. Например, для получения истинных значений гкр ( см. рис. 2.2 и 2.4) необходимо ввести поправку на катодный ток сопряженного процесса восстановления ионов гидроксония при Епп. Обычно этот ток определяют посредством экстраполяции тафелевского участка катодной кривой до рассматриваемого потенциала анодной кривой. Отметим, что для кислот ( НС1 и H2SO4) поправка очень незначительна и ею можно пренебрегать. Как следует из приведенных на рис. 2.1 и 2.4 кривых, в области потенциалов активного растворения титана на суммарной анодной кривой отсутствует тафелевский участок. С учетом же того, что, несмотря на высокую термодинамическую активность, титан в кислых хлоридных ( равно как и в сульфатных) растворах растворяется со скоростью, намного меньшей чем железо, можно предполагать, что титан и в активном состоянии частично запассивирован.
[7]

Приведенные соотношения могут быть использованы также для расчета экстремальных значений токов электризации реактивных топ-лив при различных сочетаниях очистных аппаратов в технологических схемах, при этом следует иметь в виду, что истинное значение тока электризации может быть значительно меньше полученного расчетом.
[8]

Для получения приближенного выражения для скорости движения капли предположим, что изменение поверхностного натяжения вдоль капли мало по сравнению с его абсолютным значением, так что отклонением формы капли от сферической можно пренебречь, Предположим, далее, что зависимостью диффузионного тока от угла 0 также можно пренебречь, заменив в выражении ( 75 1) истинное значение тока его средним значением по капле.
[9]

Метод контурных токов позволяет при составлении системы уравнений для расчета электрических цепей не записывать уравнения по первому закону Кирхгофа и тем самым уменьшить общее количество уравнений, необходимых для расчета. Истинные значения токов в ветвях электрической цепи определяются по значениям контурных токов.
[10]

Необходимо отметить, что величина тока, вычисленная по ( 10 — 59), приведена к базисной ступени напряжения. Для базисной ступени этот ток представляет собой истинное значение тока к.
[11]

Если источник питания не регулируется, то постоянное по величине напряжение подается поочередно к регулировочным отводам трансформатора. Полученные значения откладываются на кривой, при этом истинное значение тока и потерь, соответствующее номинальному напряжению, получится путем интерполирования или экстраполирования полученной кривой, причем экстраполирование допускается в пределах не более 10 % от крайнего опытного значения в любую сторону.
[12]

Тогда возможны два способа оценки интенсивности линий спектра. Второй ( более сложный) способ связан с оценкой площади, ограниченной производной данной линии, для нахождения истинного значения тока оже-электронов регистрируемой линии. Как правило, ли — нии оже-электронов ( особенно низко — g энергетические, обладающие доста — точной шириной) наблюдаются на плавно меняющемся фоне вторичных электронов. Очевидно, что экспери — ментальная интенсивность линии в данном случае получается несколько заниженной. В общем случае учет влияния фона — проблема сложная. Однако в первом приближении линейного закона изменения фона истинное значение интенсивности линии равно сумме экспериментального значения и А — величины изменения интенсивности фона между двумя экстремальными точками линии оже-электронов.
[14]

Схема, изображенная на рис. 324, непригодна для точных измерений. При расстоянии PN, большом по сравнению с размерами Р и N, не удается перехватить все электроны, освобожденные светом ( получить истинное значение тока насыщения), и затруднительно установить точное значение V, определяющего скорость фотоэлектронов. Удобной является установка, в которой Р к N образуют с ф е р и ы е-с к и и конденсатор: Р — небольшой шарик в центре сферы, поверхность которой образует электрод N. С такой установкой ( П. И. Лукир-ский) можно надежно определить величину тока насыщения и величину задерживающего потенциала V, в следовательно, определить фототек и максимальную скорость вылетающих электронов.
[15]

Страницы:

Источник

Главная
→
Примеры решения задач ТОЭ
→
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Основные положения и соотношения

1. Источники электрической энергии

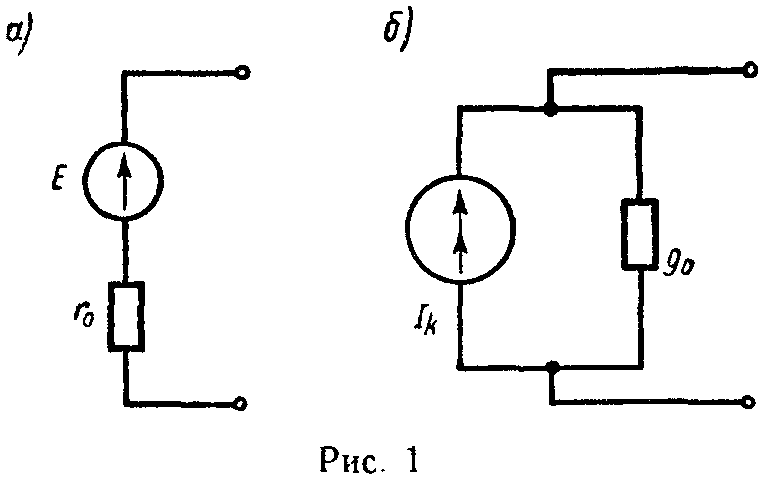
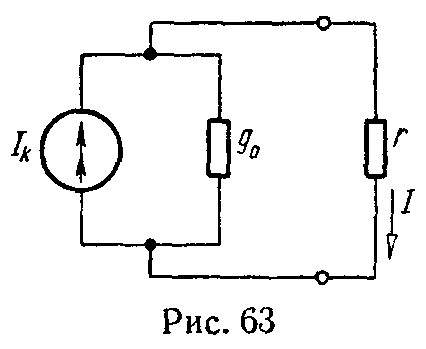
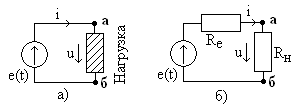
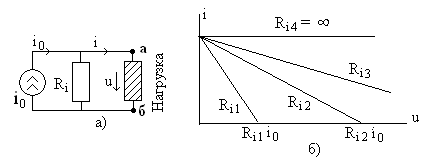
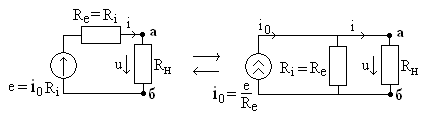
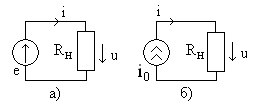
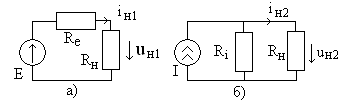
Реальный источник электрической энергии можно изобразить двояко: а) в виде генератора напряжения, который характеризуется э.д.с. Е, численно равной напряжению холостого хода источника, и включенной последовательно с сопротивлением r₀ (рис. 1, а), б) в виде генератора тока, который характеризуется током I_к, численно равным току короткого замыкания реального источника, и параллельно соединенной проводимостью g₀ (рис. 1, б).

Переход от генератора напряжения к эквивалентному генератору тока осуществляется по формулам

I к = E r 0 , g 0 = 1 r 0 , (1)

а обратный переход от генератора тока к эквивалентному генератору напряжения по следующим формулам

E= I к g 0 , r 0 = 1 g 0 . (2)

У идеального генератора напряжения внутреннее сопротивление равно нулю, тогда как у идеального генератора тока внутренняя проводимость равна нулю.

2. Закон Ома

Закон Ома применяется для ветви или для одноконтурной замкнутой цепи (не имеющей разветвлений).

Для написания закона Ома следует прежде всего выбрать произвольно некоторое положительное направление для тока.

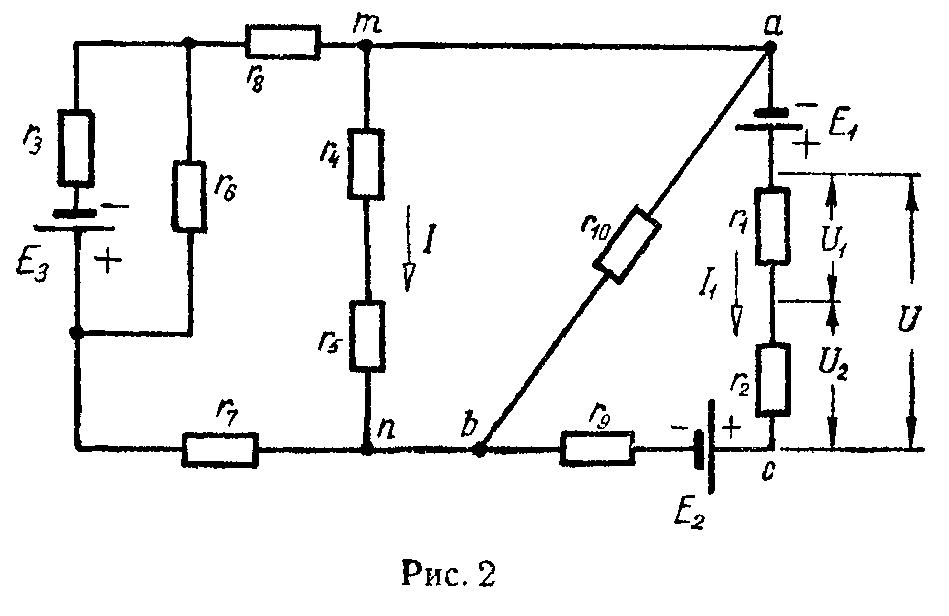
а) Для ветви, состоящей только из сопротивлений и не содержащей э.д.с. (например, для ветви mn на рис. 2), при положительном направлении для тока от точки m к точке n ток равен

I= φ m − φ n r mn = U mn r mn . (3)

Здесь φ_m и φ_n — потенциалы точек m и n, U_mn = φ_m — φ_n — разность потенциалов или напряжение между точками m и n, r_mn = r₄ + r₅ — полное сопротивление ветви между точками m и n.

Пример — в задаче 17.

б) Для замкнутой одноконтурной цепи

I= ΣE Σr , (4)

где Σr — арифметическая сумма всех внешних и внутренних сопротивлений цепи, ΣE — алгебраическая сумма ее электродвижущих сил.

Со знаком плюс берут те э.д.с., направления которых совпадают с выбранным положительным направлением для тока, и со знаком минус — э.д.с. с противоположными направлениями.

Примеры — в задачах 15 и 17.

в) Для ветви, содержащей э.д.с. и сопротивления (например, для ветви acb на рис. 2),

I 1 = φ a − φ b +ΣE Σ r ab = U ab + E 1 − E 2 r 1 + r 2 + r 9 , (5)

где U_ab = φ_a — φ_b — напряжение на концах ветви acb, отсчитываемое по выбранному положительному направлению тока, ΣE — алгебраическая сумма э.д.с., находящихся в этой ветви, а Σr — арифметическая сумма ее сопротивлений.

Формулу (5) называют обобщенным законом Ома.

Примеры — в задачах 15 и 17.

3. Законы Кирхгофа

Для написания законов Кирхгофа следует прежде всего задаться положительными направлениями для токов в каждой ветви.

Первый закон Кирхгофа

∑ k=1 n I k =0, (6)

Алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю. Токи, притекающие к узлу, условно принимаются положительными, а вытекающие из него — отрицательными (или наоборот).

Второй закон Кирхгофа

∑ k=1 n I k ⋅ r k = ∑ k=1 n E k . (7)

Алгебраическая сумма падений напряжений любого замкнутого контура равна алгебраической сумме э.д.с. в нем.

Направление обхода контура выбирается произвольно. При записи левой части равенства со знаком плюс берутся падения напряжения в тех ветвях, в которых положительное направление тока совпадает с направлением обхода (независимо от направления э.д.с. в этих ветвях), и со знаком минус — падения напряжения в тех ветвях, в которых положительное направление, тока противоположно направлению обхода. При записи правой части равенства э.д.с., направления которых совпадают с выбранным направлением обхода (независимо от направления тока, протекающего через них), принимаются положительными, а э.д.с., направленные против выбранного направления обхода, принимаются отрицательными.

Пример — в задаче 29.

Распределение напряжений при последовательном соединении двух сопротивлений (см. рис. 2)

I 1 = U 1 r 1 = U 2 r 2 = U r 1 + r 2 ,

U 1 =U⋅ r 1 r 1 + r 2 , U 2 =U⋅ r 2 r 1 + r 2 . (8)

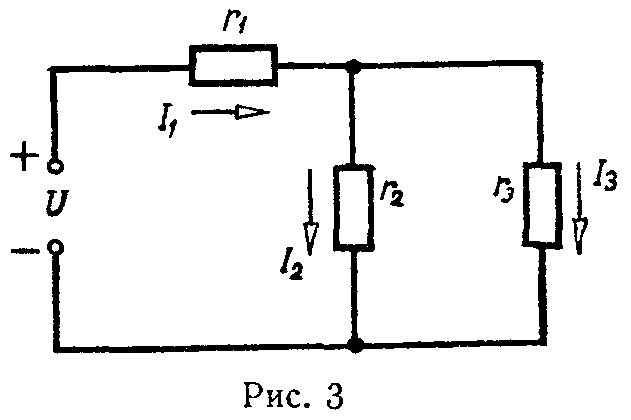
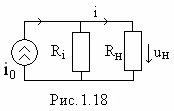
Распределение токов в двух параллельных ветвях — формула разброса токов или формула делителя токов (рис. 3)

U 2 = U 3 = U 2,3 , I 2 ⋅ r 2 = I 3 ⋅ r 3 = I 1 ⋅ r 2,3 = I 1 ⋅ r 2 ⋅ r 3 r 2 + r 3 ,

I 2 = I 1 ⋅ r 3 r 2 + r 3 , I 3 = I 1 ⋅ r 2 r 2 + r 3 . (9)

Распределение напряжений при последовательном соединении n сопротивлений

U k =U⋅ r k ∑ k=1 n r k .

Распределение токов в n параллельных ветвях

I k =I⋅ g k ∑ k=1 n g k .

4. Методы расчета сложных цепей постоянного тока

Пусть электрическая цепь состоит из p ветвей и имеет q узлов.

Применение законов Кирхгофа

Прежде всего, устанавливается число неизвестных токов, которое равно числу ветвей (p). Для каждой ветви задаются положительным направлением для тока.

Число n₁ независимых уравнений, составляемых по первому закону Кирхгофа, равно числу узлов без единицы

n₁ = q – 1.

Число n₂ независимых уравнений, составляемых по второму закону Кирхгофа, равно числу ячеек (контуров)

n₂ = p — q + 1.

Общее число уравнений n, составляемых по первому и второму законам Кирхгофа, равно числу неизвестных токов

n = n₁ + n₂ = p.

Решение этой системы уравнений дает значения искомых токов.

Пример — в задаче 29.

Метод контурных токов (МКТ, Максвелла).

Число n независимых контуров цепи равно числу уравнений по второму закону Кирхгофа

n = n₂ = p — q + 1.

Расчет цепи методом контурных токов, состоящей из n независимых контуров, сводится к решению системы из n уравнений, составляемых для контурных токов I₁₁, I₂₂, …, I_nn; ток в каждой ветви находится как алгебраическая сумма контурных токов, обтекающих эту ветвь.

Выбор направлений контурных токов произволен. Каждая из ветвей сложной электрической цепи должна войти хотя бы в один контур.

Система уравнений МКТ для n контурных токов имеет вид

{ r 11 ⋅ I 11 + r 12 ⋅ I 22 +…+ r 1n ⋅ I nn = E 11 ; r 21 ⋅ I 11 + r 22 ⋅ I 22 +…+ r 2n ⋅ I nn = E 22 ; ………………………………………………. r n1 ⋅ I 11 + r n2 ⋅ I 22 +…+ r nn ⋅ I nn = E nn . (10)

Здесь r_kk — собственное сопротивление контура k (сумма сопротивлений всех ветвей, входящих в контур k), r_kl — общее сопротивление контуров k и l, причем r_kl = r_lk; если направления контурных токов в ветви, общей для контуров k и l, совпадают, то r_kl положительно (r_kl > 0), в противном случае r_kl — отрицательно (r_kl < 0); E_kk — алгебраическая сумма э.д.с., включенных в ветви, образующие контур k.

Пример — в задаче 41.

Метод узловых потенциалов (МУП)

Число n независимых узлов цепи равно числу уравнений по первому закону Кирхгофа

n = n₁ = q — 1.

Для определения потенциалов всех узлов электрической схемы, имеющей q узлов, следует принять потенциал одного из узлов равным нулю, а для определения потенциалов остальных n = q — 1 узлов составляется следующая система уравнений

{ φ 1 ⋅ g 11 + φ 2 ⋅ g 12 +…+ φ n ⋅ g 1n = ∑ 1 Eg ; φ 1 ⋅ g 21 + φ 2 ⋅ g 22 +…+ φ n ⋅ g 2n = ∑ 2 Eg ; ……………………………………………….. φ 1 ⋅ g n1 + φ 2 ⋅ g n2 +…+ φ n ⋅ g nn = ∑ n Eg . (11)

Здесь g_ss — сумма проводимостей ветвей, присоединенных к узлу s; g_sq — сумма проводимостей, соединяющих узел s с узлом q; – алгебраическая сумма произведений э.д.с. ветвей, примыкающих к узлу s, на их проводимости (т.е. токов короткого замыкания этих ветвей); при этом со знаком плюс берутся те из произведений Eg, в ветвях которых э.д.с. действуют в направлении узла s, и со знаком минус — в направлении от узла.

Определив потенциалы узлов, находят токи в ветвях посредством закона Ома.

Этим методом рекомендуется пользоваться в тех случаях, когда число уравнений здесь будет меньше числа уравнений, составленных по методу контурных токов.

Примеры — в задачах 44 и 45.

Метод наложения

Ток в любой ветви может быть рассчитан как алгебраическая сумма токов, вызываемых в ней каждой э.д.с. в отдельности. При этом надо иметь в виду, что когда ведется расчет для какой-либо одной действующей э.д.с., то вместо остальных источников должны быть включены сопротивления, равные внутренним сопротивлениям этих источников.

Примеры — в задачах 47 и 49.

Метод эквивалентных преобразований

Во всех случаях применения метода эквивалентных преобразований замена одних схем другими, им эквивалентными, не должна привести к изменению токов или напряжений на участках цепи, не подвергшихся преобразованию.

1) Замена последовательных сопротивлений одним эквивалентным. Сопротивления последовательны, если они обтекаются одним и тем же током. Например, на схеме цепи, изображенной на рис. 2, сопротивления r₁, r₂ и r₉ соединены последовательно; так же последовательны сопротивления r₇ и r₈.

Эквивалентное сопротивление цепи, состоящей из n последовательно соединенных участков, равно сумме этих сопротивлений этих участков

r э = r 1 + r 2 +…+ r n = ∑ k=1 n r k . (12)

2) Замена параллельных сопротивлений одним эквивалентным. Сопротивления параллельны, если все они присоединены к одной паре узлов. Например (рис. 2), сопротивления r₄₅ = r₄ + r₅ и r₁₀ параллельны.

Эквивалентная проводимость цепи, состоящей из n параллельно соединенных ветвей равна сумме этих проводимостей этих ветвей. Эквивалентное сопротивление такой цепи находится как величина обратная эквивалентной проводимости этой цепи

1 r э = 1 r 1 + 1 r 2 +…+ 1 r n = ∑ k=1 n 1 r k . (13)

В частном случае параллельного соединения двух сопротивлений r₁ и r₂ эквивалентное сопротивление

r э = r 1 ⋅ r 2 r 1 + r 2 . (14)

3) Замена смешанного соединения сопротивлений одним эквивалентным. Смешанное соединение — это сочетание последовательного и параллельного соединения сопротивлений. Например, сопротивления r₁, r₂ и r₃ (рис. 3) находятся в смешанном соединении. Их эквивалентное сопротивление равно

r э = r 1 + r 2,3 = r 1 + r 2 ⋅ r 3 r 2 + r 3 . (15)

При смешанном соединении сопротивлений токи ветвей цепи (рис. 3):

по закону Ома

I 1 = U r э , (16)

по формуле разброса токов (делителя токов)

I 2 = I 1 ⋅ r 3 r 2 + r 3 , I 3 = I 1 ⋅ r 2 r 2 + r 3 .

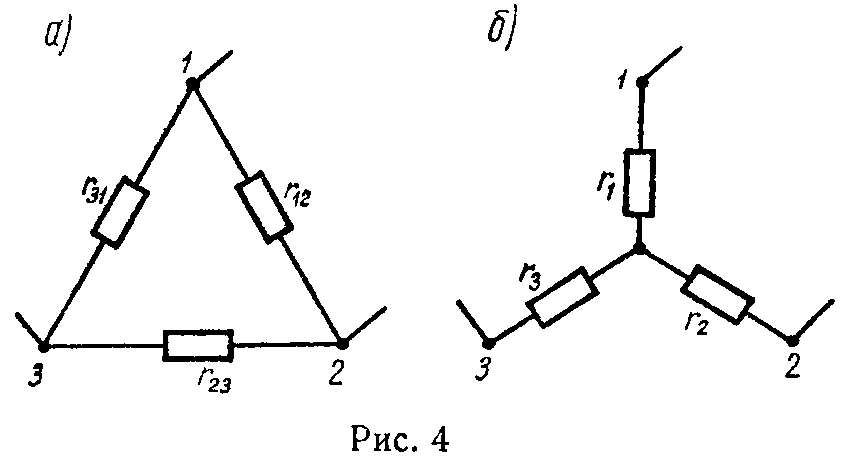
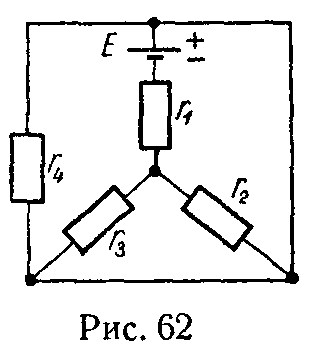
4) Формулы преобразования треугольника сопротивлений (рис. 4, а) в эквивалентную звезду сопротивлений (рис. 4, б) и наоборот имеют вид

{ r 1 = r 12 ⋅ r 31 r 12 + r 23 + r 31 ; r 2 = r 23 ⋅ r 12 r 12 + r 23 + r 31 ; r 3 = r 31 ⋅ r 23 r 12 + r 23 + r 31 , (17)

{ g 12 = g 1 ⋅ g 2 g 1 + g 2 + g 3 ; g 23 = g 2 ⋅ g 3 g 1 + g 2 + g 3 ; g 31 = g 3 ⋅ g 1 g 1 + g 2 + g 3 , (18)

где g — проводимость соответствующей ветви.

Формулы (18) можно записать через сопротивления так

r 12 = r 1 + r 2 + r 1 ⋅ r 2 r 3 ; r 23 = r 2 + r 3 + r 2 ⋅ r 3 r 1 ; r 31 = r 3 + r 1 + r 3 ⋅ r 1 r 2 . (19)

Пример — в задаче 51.

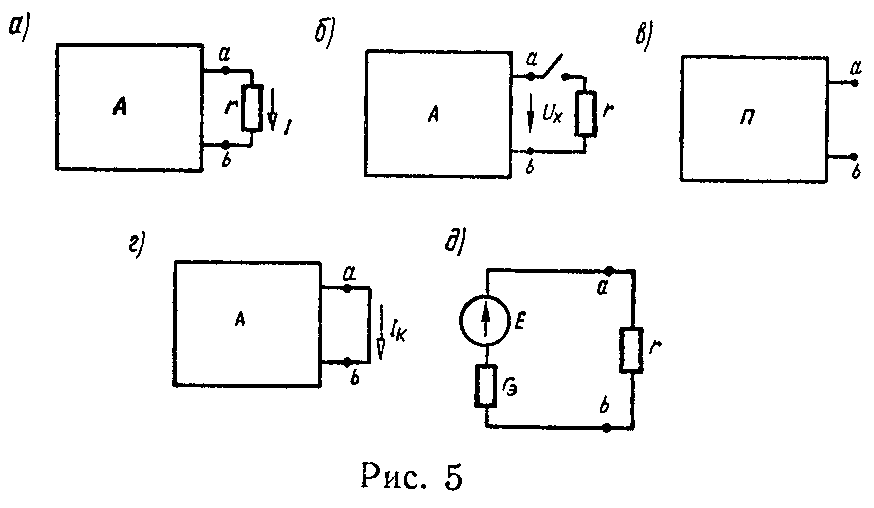
Метод эквивалентного генератора напряжения (метод холостого хода и короткого замыкания или метод активного двухполюсника)

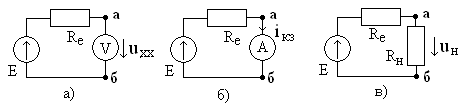
Для нахождения тока I в ветви ab, сопротивление которой r (рис. 5, а, буква А на рисунке обозначает активный двухполюсник), надо разомкнуть эту ветвь и при этом найти (любым способом) разность потенциалов на зажимах разомкнутой ветви — U_х (рис. 5, б). Затем надо вычислить сопротивление короткого замыкания r_к, равное эквивалентному сопротивлению всей остальной цепи, вычисленному в предположении, что в ней отсутствуют э.д.с. (при этом внутренние сопротивления источников сохраняются) и что она питается от постороннего источника, присоединенного непосредственно к зажимам a и b (рис. 5, в; буква П на рисунке обозначает пассивный двухполюсник).

Сопротивление r_к может быть вычислено либо непосредственно по схеме рис. 5, в, либо из соотношения

r к = U х I к , (20)

где I_к — ток короткого замыкания, протекающий по ветви ab, если ее сопротивление r сделать равным нулю (рис. 5, г).

Заданная схема (рис. 5, а) может быть заменена эквивалентным генератором напряжения с э.д.с. E = U_х и внутренним сопротивлением r_э = r_к, присоединенным к зажимам ab сопротивления r (рис. 5, д).

Ток в искомой ветви, имеющей сопротивление r, определяется из формулы закона Ома

I= U х r+ r к . (21)

Примеры — в задачах 55 и 56.

Метод эквивалентного генератора тока

В предыдущем пункте показано, как в любой сложной цепи можно получить эквивалентный генератор напряжения с э.д.с. E и внутренним сопротивлением r_к. Этот генератор напряжения (рис. 5, д) на основании формул (1) может быть заменен эквивалентным генератором тока (рис. 1, б) по формулам

I к = U х r к , g 0 = 1 r к . (22)

где I_к — ток эквивалентного генератора тока, равный току короткого замыкания в той ветви, по отношению к которой производится эквивалентное преобразование всей остальной части цепи, g₀ — внутренняя проводимость, равная эквивалентной проводимости всей остальной цепи между зажимами ab, к которым присоединен приемник энергии, в предположении, что э.д.с. всех генераторов равны нулю.

Пример — в задаче 65.

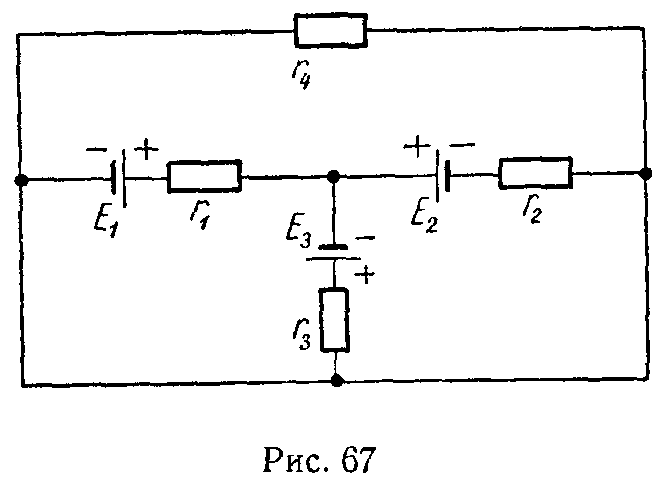
Метод замены нескольких параллельных генераторов напряжения одним эквивалентным

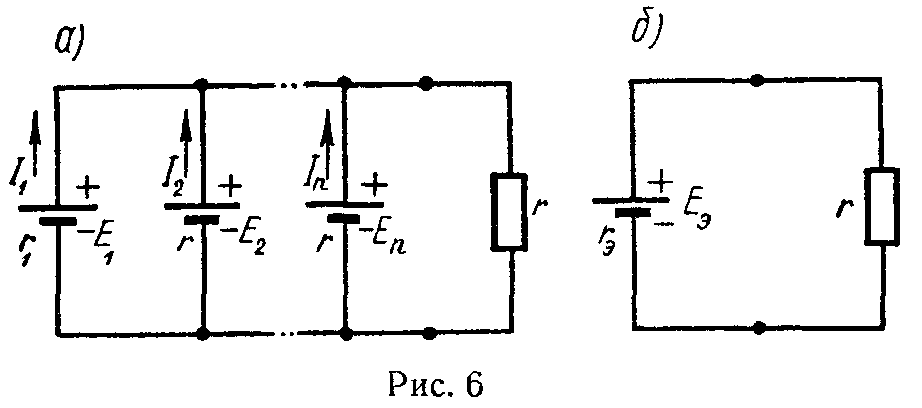
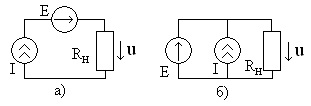
Если имеется несколько генераторов напряжения с э.д.с. E₁, E₂, …, E_n и внутренними сопротивлениями r₁, r₂, …, r_n, работающие параллельно на общее сопротивление нагрузки r (рис. 6, а), то они могут быть заменены одним эквивалентным генератором напряжений, э.д.с. которого E_э, а внутреннее сопротивление r_э (рис. 6, б),

при этом

{ E э = ∑ k=1 n E k g k ∑ k=1 n g k ; 1 r э = 1 r 1 + 1 r 2 +…+ 1 r n ; g k = 1 r k . (23)

Ток в сопротивлении r определится по формуле

I= E э r+ r э . (24)

Ток в каждой из ветвей находится по формуле

I k = E k −U r k , (25)

где U = I·r.

Пример — в задаче 60.

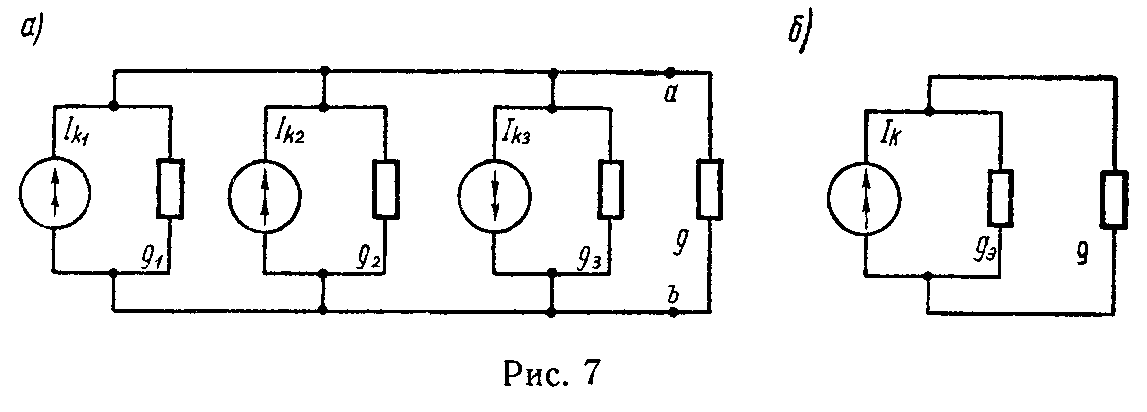
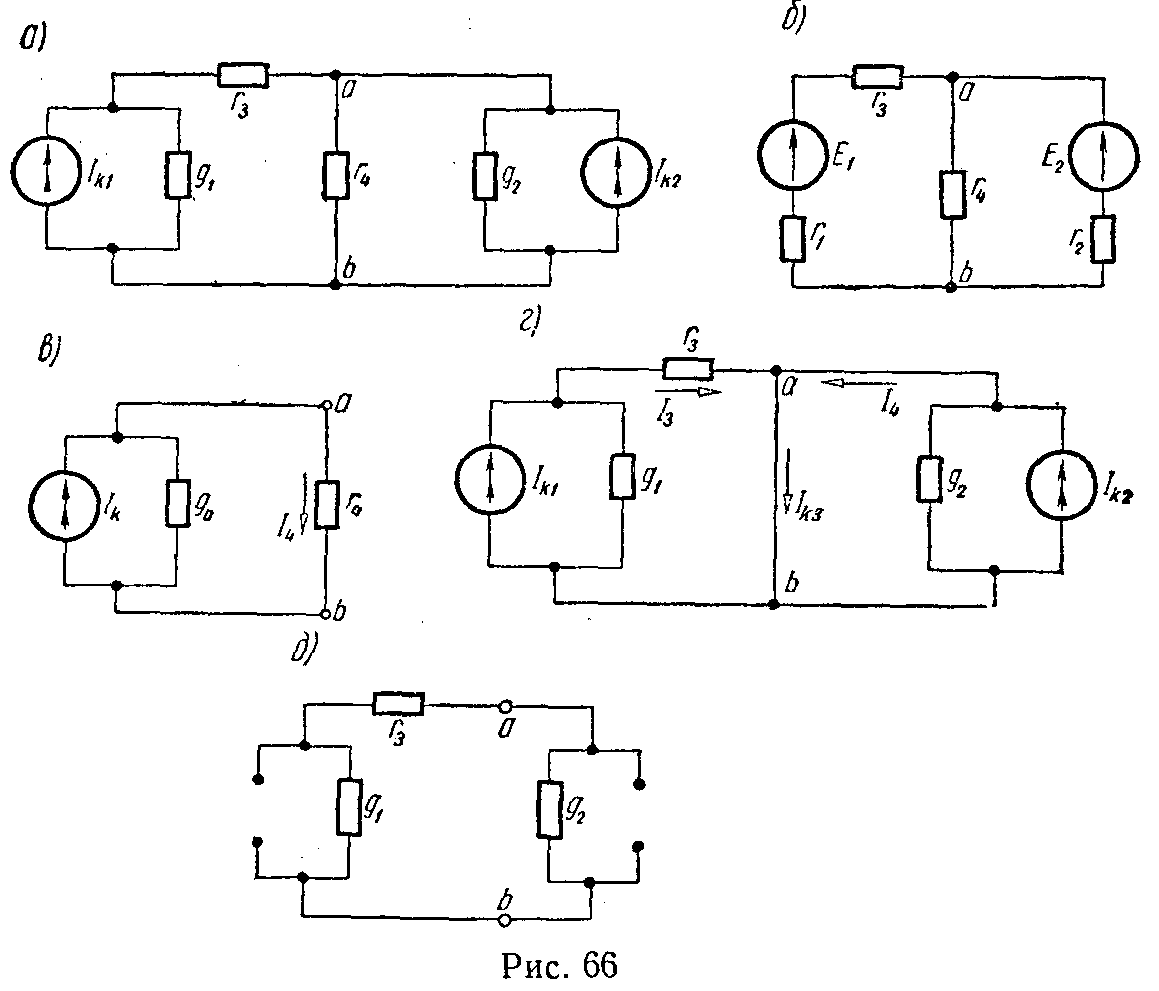
Метод замены параллельно соединенных генераторов тока одним эквивалентным

Если несколько генераторов тока с токами I_k₁, I_k₂, …, I_kn и внутренними проводимостями g₁, g₂, …, g_n соединены параллельно (рис. 7, а) и работают на общий приемник энергии с проводимостью g то они могут быть заменены одним эквивалентным генератором тока (рис. 7, б), ток которого I_k равен алгебраической сумме токов, а его внутренняя проводимость равна сумме внутренних проводимостей отдельных генераторов

I k = I k1 + I k2 − I k3 +…= ∑ m=1 n I km , (26)

g э = g 1 + g 2 + g 3 +…= ∑ m=1 n g m . (27)

5. Принцип взаимности

Принцип взаимности гласит: если э.д.с. E, находящаяся в ветви ab сколь угодно сложной цепи, вызывает ток в другой ветви cd этой же цепи, то при переносе этой э.д.с. в ветвь cd она вызовет в ветви ab такой же ток I.

6. Принцип компенсации

Принцип компенсации: любое сопротивление в электрической цепи может без изменения распределения токов в ее ветвях быть заменено э.д.с., численно равной падению напряжения в заменяемом сопротивлении и направленной навстречу току.

7. Входное сопротивление цепи относительно ветви

Входное сопротивление цепи относительно ветви k определяется как отношение э.д.с. E_k, действующей в этой ветви, к току I_k в этой же ветви при э.д.с. в остальных ветвях равных нулю

r kk = E k I k . (28)

Входная проводимость ветви k — величина обратная входному сопротивлению этой ветви

g kk = 1 r kk . (29)

Взаимное сопротивление (передаточное сопротивление) ветвей k и l — отношение э.д.с. E_k, действующей в ветви k, к току I_l, проходящему по ветви l при э.д.с. в остальных ветвях равных нулю

r kl = E k I l . (30)

Взаимная проводимость ветвей k и l — величина обратная взаимному сопротивлению тех же ветвей

g kl = 1 r kl . (31)

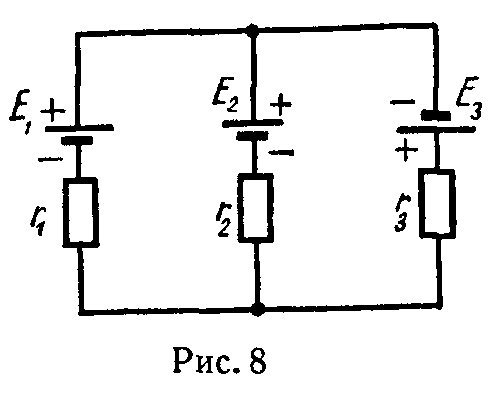
Пример. Для схемы рис. 8 входные сопротивления цепи относительно ветвей 1, 2 и 3 соответственно равны

r 11 = D r 2 + r 3 , r 22 = D r 1 + r 3 , r 33 = D r 1 + r 2 ,

а взаимные сопротивления ветвей 1 и 2, 2 и 3, 3 и 1 соответственно равны

r 12 = r 21 = D r 3 , r 23 = r 32 = D r 1 , r 13 = r 31 = D r 2 ,

где D = r₁·r₂ + r₁·r₃ + r₂·r₃.

8. Баланс мощностей

Для любой замкнутой электрической цепи сумма мощностей, развиваемых источниками электрической энергии, равна сумме мощностей, расходуемых в приемниках энергии

ΣP_ист = ΣP_потреб, или ΣEI = ΣI²r (32)

где ΣEI — алгебраическая сумма; здесь положительны те из слагаемых, для которых направления действия э.д.с. E и соответствующего тока I совпадают, в противном случае слагаемое отрицательно (при выборе положительных направлений токов в ветвях с э.д.с. выбираем направление тока совпадающим с действием соответствующей э.д.с.); ΣI²r — арифметическая сумма; здесь должны быть учтены как внешние сопротивления, так и сопротивления самих источников энергии.

Упражнения и задачи

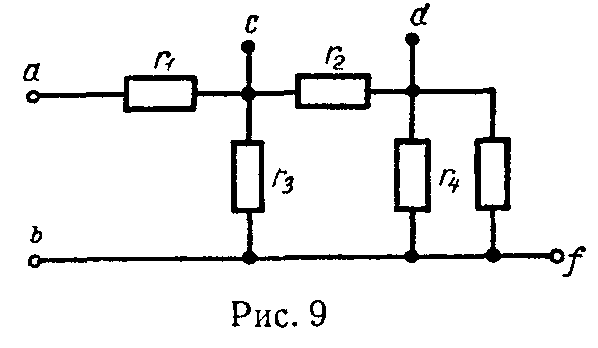
Задача 1. Для цепи (рис. 9) найти эквивалентные сопротивления между зажимами a и b, c и d, d и f, если r₁ = 6 Ом, r₂ = 5 Ом. r₃ = 15 Ом, r₄ = 30 Ом, r₅ = 6 Ом.

Решение

Расчет сопротивления r_ab.

Эквивалентное сопротивление соединенных параллельно сопротивлений r₄ и r₅ найдем по формуле (14)

r 45 = r 4 ⋅ r 5 r 4 + r 5 = 30⋅6 30+6 =5 Ом;

оно соединено последовательно с r₂; их общее сопротивление

r’ = r₂ + r₄₅ = 5 + 5 = 10 Ом.

Сопротивление цепи состоит из сопротивления r₁, последовательно с которым соединены два параллельных сопротивления r’ и r₃

r ab = r 1 + r ′ ⋅ r 3 r ′ + r 3 =6+ 10⋅15 10+15 =12 Ом.

Расчет сопротивления r_cd.

Сопротивления r₄ и r₅ теперь соединены параллельно друг другу; сопротивление r₃ к ним включено последовательно

r ″ = r 3 + r 4 ⋅ r 5 r 4 + r 5 =15+ 30⋅6 30+6 =20 Ом.

Сопротивление r_cd состоит из двух параллельно соединенных сопротивлений r₂ и r» и равно

r cd = r 2 ⋅ r ″ r 2 + r ″ = 5⋅20 5+20 =4 Ом.

Расчет сопротивления r_df.

Эквивалентное сопротивление цепи между точками d и f состоит из трех параллельно соединенных сопротивлений: r₅, r₄ и r₂ + r₃ и может быть определено по формуле (13)

1 r df = 1 r 5 + 1 r 4 + 1 r 2 + r 3 = 1 6 + 1 30 + 1 20 = 1 4 ,

откуда r_df. = 4 ом.

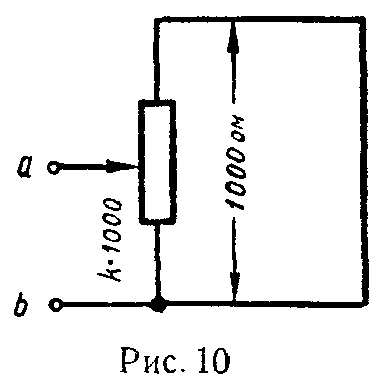
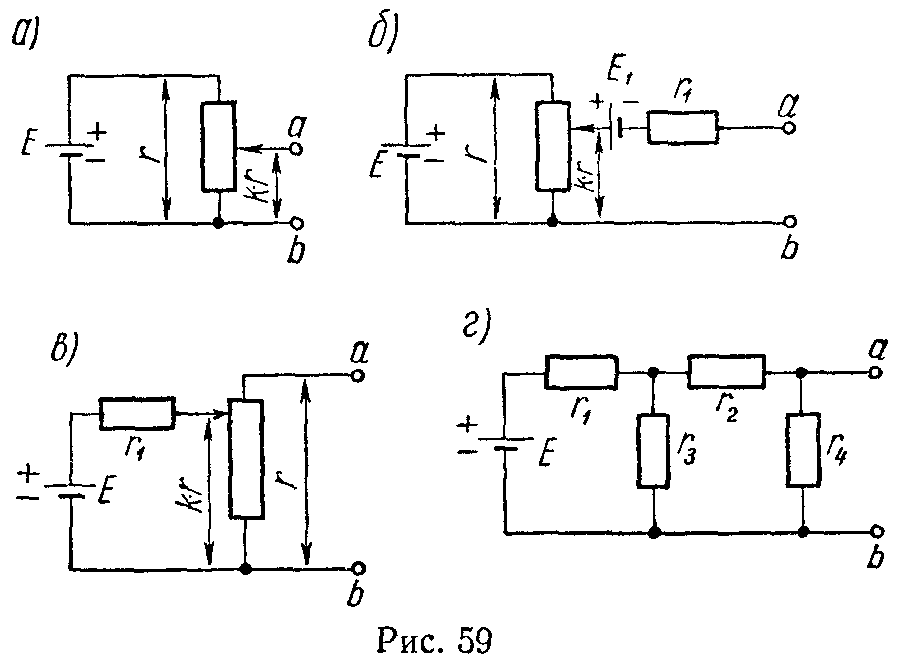
Задача 2. Для цепи (рис. 10) начертить кривую зависимости эквивалентного сопротивления между точками a и b как функцию от k (0 ≤ k ≤ 10).

Ответ: при k = 0 и k = 1 r_ab = 0; при k = 0,5 r_ab_макс = 250 Ом.

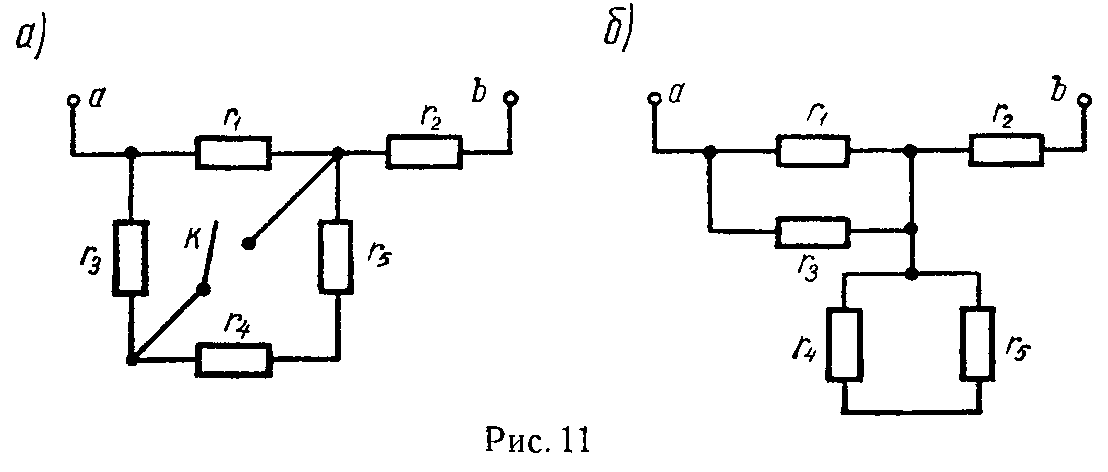
Задача 3. Цепь, схема которой изображена на рис. 11, а, состоит из пяти одинаковых сопротивлений r₁ = r₂ = r₃ = r₄ = r₅ = 10 кОм.

Чему равно сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К?

Решение

Ключ разомкнут.

Сопротивления r₃, r₄ и r₅ соединены между собой последовательно; заменяющее их эквивалентное сопротивление является параллельным к сопротивлению r₁; величина сопротивления, заменяющего r₃, r₄, r₅ и r₁, равна

r ′ = r 1 ⋅ ( r 3 + r 4 + r 5 ) r 1 + ( r 3 + r 4 + r 5 ) = 10⋅30 40 =7,5 кОм.

Искомое сопротивление цепи

r_ab = r’ + r₂ = 7,5 + 10 = 17,5 кОм.

Ключ замкнут.

В этом случае сопротивления r₁ и r₃ соединены параллельно друг другу, а сопротивления r₄ и r₅ закорочены (рис. 11, б). Искомое сопротивление цепи будет

r ab = r 1 ⋅ r 3 r 1 + r 3 + r 2 = 10⋅10 20 +10=15 кОм.

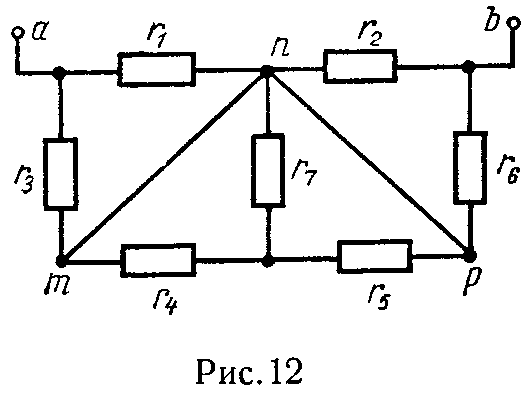
Задача 4. Вычислить эквивалентное сопротивление цепи (рис. 12) между зажимами a и b, если все семь ее сопротивлений одинаковы:

Указание. Обратить внимание на закорачивающие проводники mn и np.

Ответ: 10 Ом.

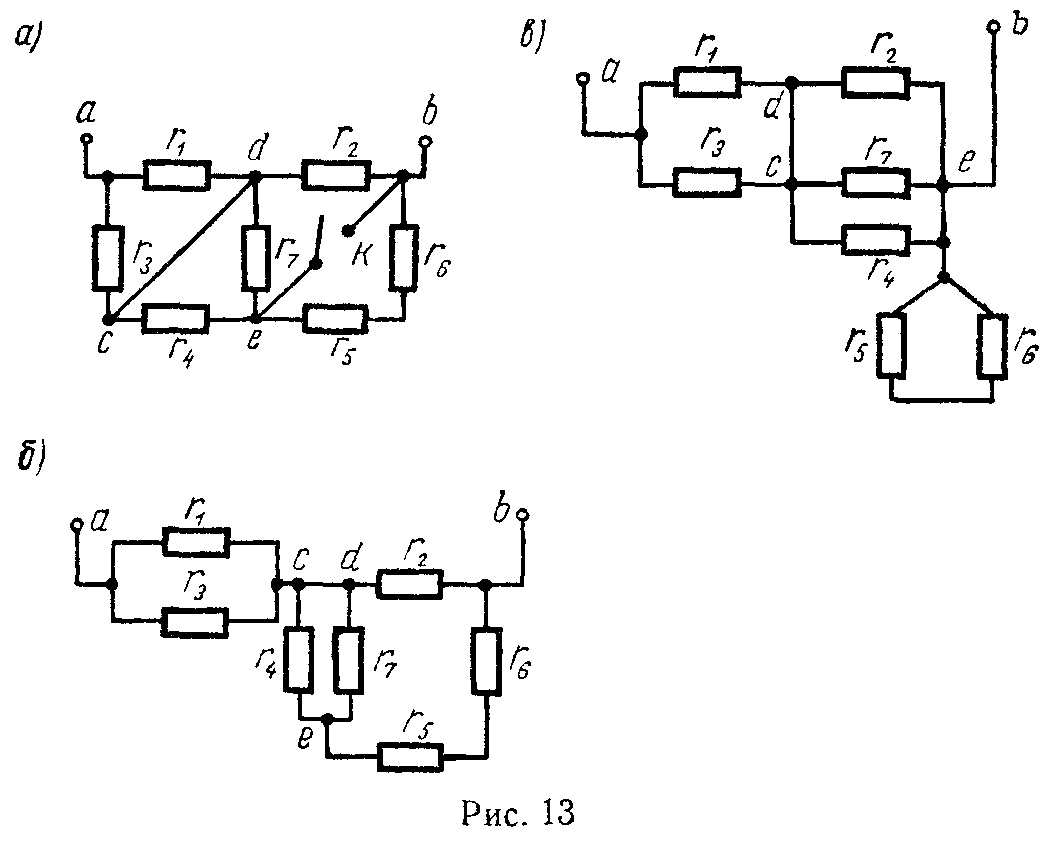
Задача 5. Определить эквивалентное сопротивление цепи между точками a и b при разомкнутом и замкнутом ключе К (рис. 13, а): r₁ = r₂ = r₃ = r₄ = r₅ = r₆ = r₇ = 10 Ом.

Решение

При разомкнутом ключе заданная схема может быть изображена согласно рис. 13, б.

Искомое сопротивление

r ab = r 1 ⋅ r 3 r 1 + r 3 = ( r 5 + r 6 + r 4 ⋅ r 7 r 4 + r 7 )⋅ r 2 r 5 + r 6 + r 4 ⋅ r 7 r 4 + r 7 + r 2 =5+ 25⋅10 35 =12,1 Ом.

При замкнутом ключе заданная схема имеет вид, изображенный на рис. 13, в.

Сопротивление цепи равно сумме двух сопротивлений

r ′ = r 1 ⋅ r 3 r 1 + r 3 10⋅10 20 =5 Ом,

и r», определяемого из формулы

1 r ″ = 1 r 4 + 1 r 7 + 1 r 2 ,

откуда r’ = 3,33 Ом. Таким образом,

r ab = r ′ + r ″ =5+3,33=8,33 Ом.

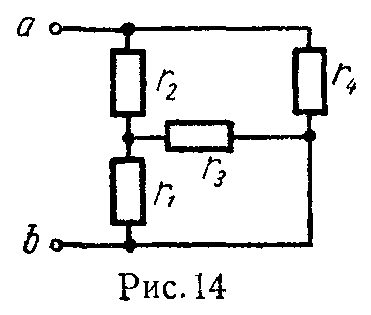
Задача 6. Найти эквивалентное сопротивление между зажимами a и b для схемы рис. 14. Даны: r₁ = 600 Ом, r₂ = 360 Ом, r₃ = 400 Ом, r₄ = 300 Ом.

Ответ: 200 Ом.

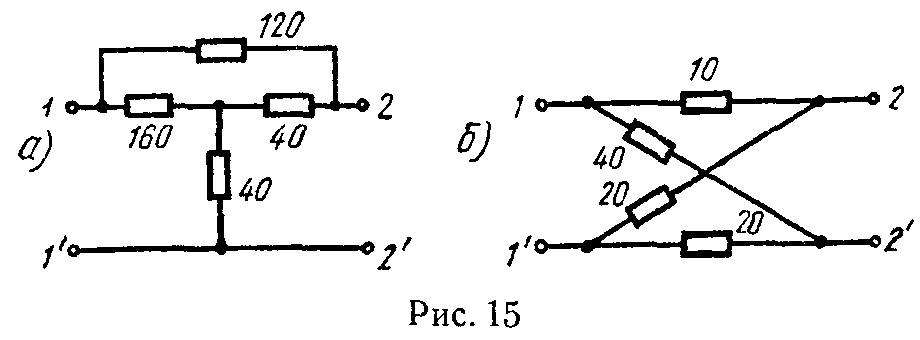
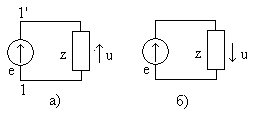
Задача 7. Определить сопротивление каждой из цепей (рис. 15, а и б) между зажимами 1–1′ при холостом ходе (точки 2 и 2′ разомкнуты) и при коротком замыкании (точки 2 и 2′ закорочены). Сопротивления в омах даны на схеме.

Ответ: а) r_1х = 120 Ом, r_1к = 72 Ом; б) r_1х = 20 Ом, r_1к = 18 Ом.

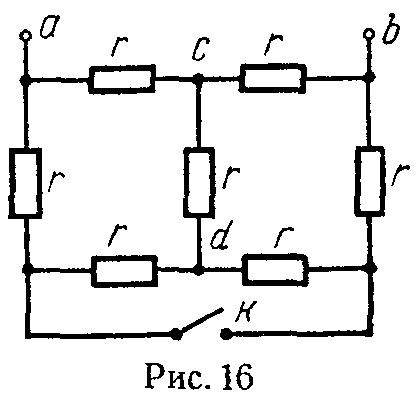
Задача 8. Вычислить сопротивление между зажимами a и b для схемы рис. 16 при разомкнутом и замкнутом ключе К. Все семь сопротивлений одинаковы и каждое равно r = 30 Ом.

Указание. Учесть, что точки c и d равнопотенциальны.

Ответ: При разомкнутом ключе r_ab = 40 Ом; при замкнутом — r_ab = 30 Ом.

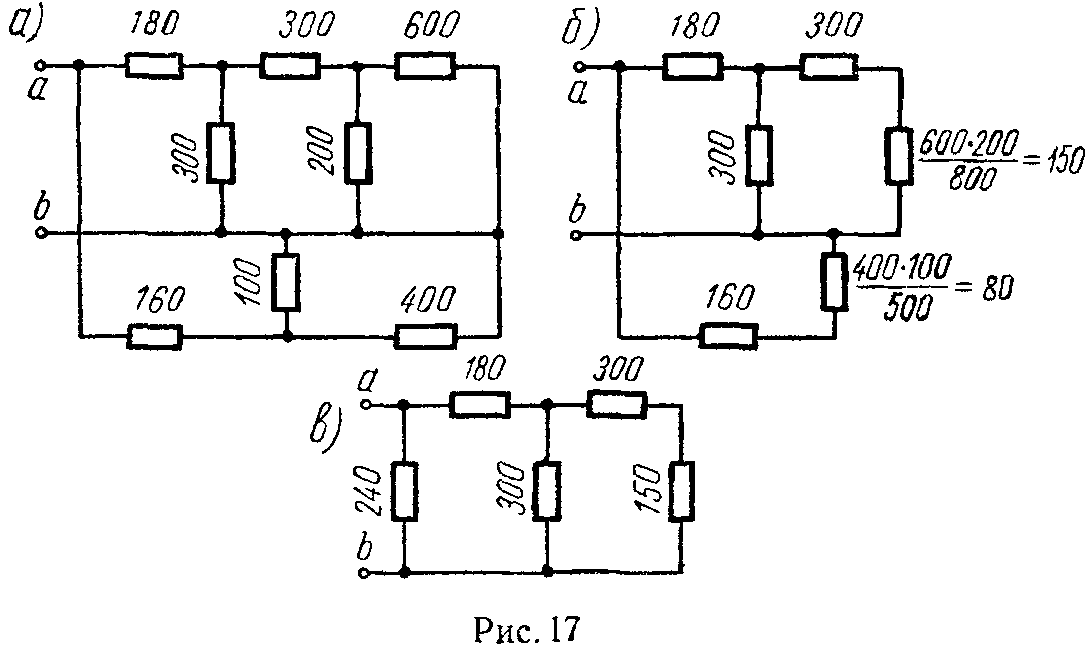
Задача 9. Найти сопротивление между зажимами a и b для схемы рис. 17, а. Значения сопротивлений в омах даны на схеме.

Решение

От данной схемы можно перейти к более простым схемам, изображенным на рис. 17, б и в. Искомое сопротивление

r ab = 240⋅ ( 180+ 300⋅450 750 ) 240+180+ 300⋅450 750 =144 Ом.

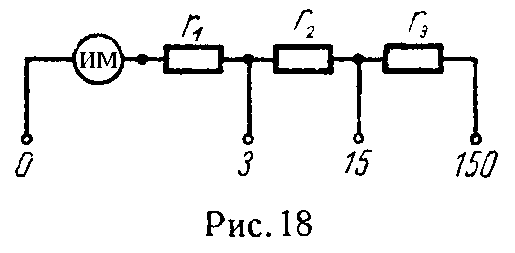
Задача 10. Имеется вольтметр, который может быть включен па три предела измерения: 3; 15 и 150 В (рис. 18). Максимально допустимый ток в измерительном механизме 30 мА.

Найти сопротивления r₁, r₂ и r₃.

Решение

Полагаем внутреннее сопротивление измерительного механизма (ИМ) равным нулю.

На пределе измерения 3 В: ток 30 мА, сопротивление r₁ = 3/0,030 = 100 Ом.

На пределе измерения 15 В: ток 30 мА, сопротивление r₁ + r₂ = 15/0,030 = 500 Ом, а сопротивление r₂ = 500 — 100 = 400 Ом.

Аналогично находится r₃ = 4500 Ом.

Задача 11. Два вольтметра, пределы измерения которых равны 150 и 100 В и внутренние сопротивления — 15000 и 7500 Ом, соединенные последовательно друг с другом и с добавочным сопротивлением 2500 Ом, подключены к сети 220 В. Чему равно показание каждого вольтметра?

Ответ: 132 и 66 В.

Задача 12. Батарея, э.д.с. которой E = 6,4 В и внутреннее сопротивление r₀ = 0,1 Ом, присоединена к сопротивлению r = 3,1 Ом. Найти ток батареи и напряжение на ее зажимах.

Решение

Применяя формулу закона Ома для замкнутой цепи (формула 4), находим ток

I= E r+ r 0 = 6,1 3,1+0,1 =2 А.

Напряжение на зажимах батареи может быть найдено двумя путями: или

U = E — I·r₀ = 6,4 — 2·0,1 = 6,2 В,

или

U = I·r = 2·3,1 = 6,2 В.

Задача 13. Напряжение холостого хода батареи равно 16,4 В. Чему равно внутреннее сопротивление батареи, если при токе во внешней цепи, равном 8 А, напряжение на ее зажимах равно 15,2 В?

Ответ: 0,15 Ом.

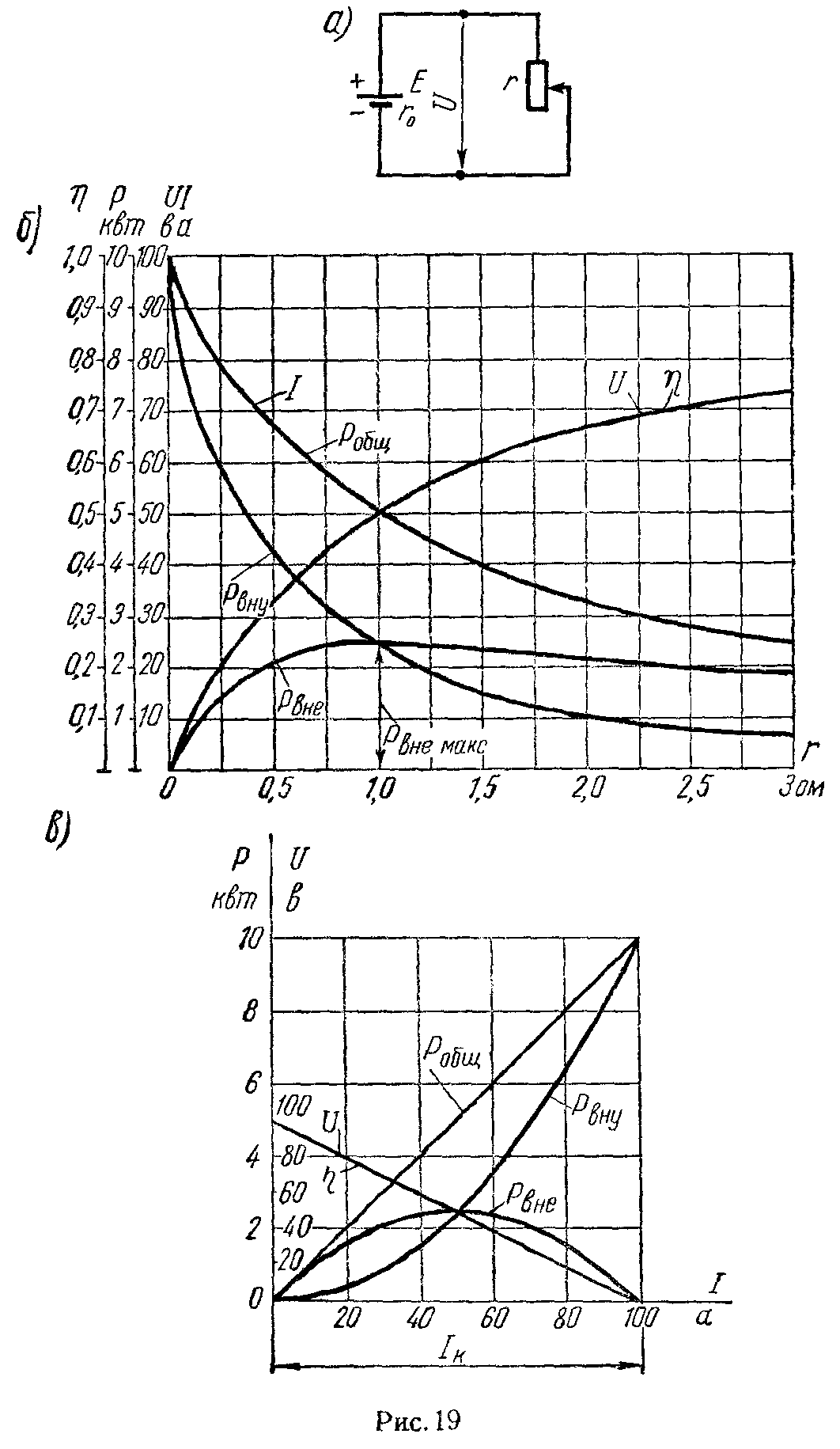
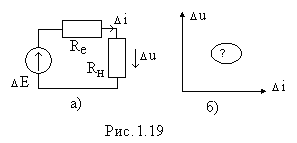
Задача 14. Источник с э.д.с. E = 100 В, внутренним сопротивлением r₀ = 1 Ом замкнут на внешнее сопротивление r, которое меняется от нуля до бесконечности (рис. 19, а). Определить в функции этого сопротивления: 1) ток I; 2) напряжение на зажимах источника U; 3) мощность, отдаваемую источником во внешнюю цепь P_внеш; 4) мощность, затрачиваемую в самом источнике P_внутр; 5) общую мощность P_общ; 6) коэффициент полезного действия η. При каком внешнем сопротивлении P_внеш будет максимальным? Чему оно равно?

Построить кривые I = F₁ (r), U = F₂ (r), P_внеш = F₃ (r), P_внутр = F₄ (r), P_общ = F₅ (r), η = F₆ (r).

Написать уравнения и построить кривые зависимостей U, P_внеш, P_внутр, P_общ и η в функции тока I.

Решение

I= E r+ r 0 = 100 r+1 ;

I=I⋅r= E⋅r r+ r 0 = 100⋅r r+1 ;

P внеш = I 2 ⋅r= E 2 ⋅r ( r+ r 0 ) 2 = 10000⋅r ( r+1 ) 2 ;

P внутр = I 2 ⋅ r 0 = E 2 ⋅ r 0 ( r+ r 0 ) 2 = 10000 ( r+1 ) 2 ;

P общ = I 2 ⋅ ( r+ r 0 )= E 2 ( r+ r 0 ) = 10000 r+1 ;

η= P внеш P общ = r r+ r 0 = r r+1 .

Определим r, при котором P_внеш будет максимально. Для этого вычислим производную от P_внеш по r и приравняем ее нулю

d P внеш dr = E 2 d dr r ( r+ r 0 ) 2 = E 2 d dr r⋅ ( r+ r 0 ) 2 −r⋅ d dr ( r+ r 0 ) 2 ( r+ r 0 ) 4 = = E 2 ( r+ r 0 ) 2 −r⋅2 ( r+ r 0 ) ( r+ r 0 ) 4 = E 2 r 0 −r ( r+ r 0 ) 3 =0.

Взяв вторую производную, можно убедиться, что она отрицательна. Это соответствует условию максимума.

Отсюда найдем, что r = r₀, т.е. при внешнем сопротивлении равном внутреннему сопротивлению, мощность, поступающая во внешнюю цепь, будет максимальна. При этом, по уравнению (6), коэффициент полезного действия равен 0,5. Величина максимальной мощности, поступающей во внешнюю цепь при r = r₀, по уравнению (3) равна

P внеш.макс = [ E 2 ⋅r ( r+ r 0 ) 2 ] r= r 0 = E 2 4r =2500 Вт.

По написанным выше уравнениям на рис. 19, б построены кривые.

Искомые уравнения зависимостей в функции тока имеют вид

U=E−I⋅ r 0 ; P внеш =E⋅I− I 2 ⋅ r 0 ; P внутр = I 2 ⋅ r 0 ; P общ =E⋅I; η=1− I⋅ r 0 E .

По этим уравнениям на рис. 19, в построены кривые.

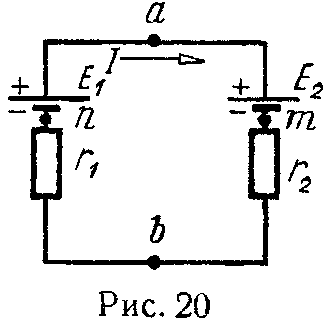
Задача 15. В схеме (рис. 20) э.д.с. E₁ = 120 В, E₂ = 40 В, а сопротивления r₁ = 12 Ом, r₂ = 8 Ом. Внутренние сопротивления источников энергии равны нулю. Определить напряжение между точками a и b.

Решение

Задавшись положительным направлением тока по часовой стрелке, на основании закона Ома (формула 4) имеем

I= E 1 − E 2 r 1 + r 2 = 120−40 12+8 =4 А.

Так как результат оказался положительным, то, следовательно, фактическое направление тока совпадает с выбранным. Напряжение между точками a и b можно найти по закону Ома (формула 5), примененному к участку amb

I= U ab − E 2 r 2 ,

откуда

U ab = E 2 +I⋅ r 2 =40+4⋅8=72 В.

Такой же результат можно получить, если применить ту же формулу к участку bna

I= U ba + E 1 r 1 ,

откуда

U ba =I⋅ r 1 − E 1 =4⋅12−120=−72 В,

а, следовательно, U_ab = 72 В.

Замечание. Следует запомнить, что если на участке цепи, содержащем э.д.с. и сопротивление, ток и э.д.с. совпадают по направлению, то напряжение на зажимах участка меньше э.д.с. на величину падения напряжения в сопротивлении участка, а если направление тока противоположно направлению э.д.с., то напряжение на зажимах участка больше э.д.с. на величину падения напряжения в рассматриваемом участке.

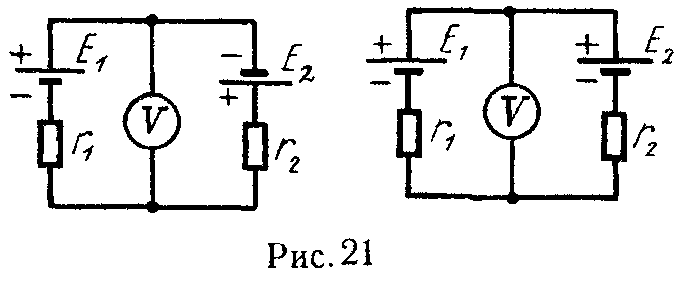
Задача 16. Определить показание вольтметра (рис. 21), сопротивление которого весьма велико по сравнению с r₁ и r₂.

Для обоих случаев даны: E₁ = 40 В, E₂ = 10 В, r₁ = r₂ = 5 Ом. Внутренними сопротивлениями источников энергии пренебречь.

Ответ: а) 15 В, б) 25 В.

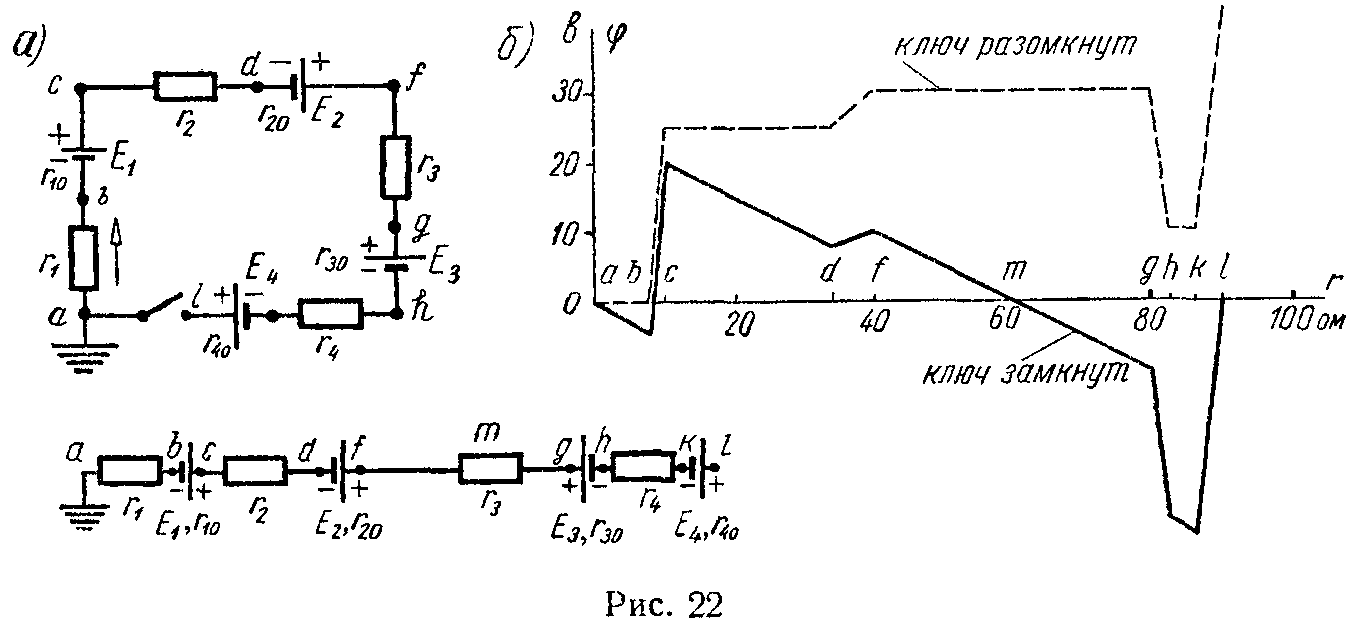
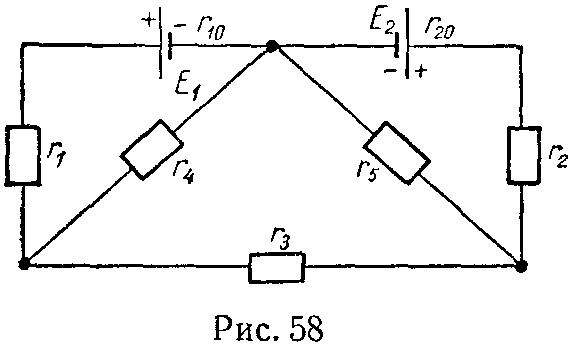
Задача 17. Построить график изменения потенциала вдоль цепи, изображенной на рис. 22, а, при замкнутом ключе и при разомкнутом ключе, предполагая в обоих случаях, что точка a заземлена (φ_a = 0).

В схеме найти точку, равнопотенцнальную точке a. Определить, потенциал какой точки следует принять равным нулю, чтобы потенциалы всех остальных точек были положительны (при замкнутом ключе).

Электродвижущие силы равны: E₁ = 25 В, E₂ = 5 В, E₃ = 20 В, E₄ = 35 В.

Внешние сопротивления имеют следующие значения: r₁ = 8 Ом, r₂ = 24 Ом, r₃ = 40 Ом, r₄ = 4 Ом. Внутренние сопротивления источников электрической энергии равны: r₁₀ = 2 Ом, r₂₀ = 6 Ом, r₃₀ = 2 Ом, r₄₀ = 4 Ом.

Решение

Ключ замкнут. Задавшись положительным направлением тока по часовой стрелке, на основании закона Ома (формула 4) найдем ток

I= E 1 + E 2 − E 3 + E 4 r 1 + r 10 + r 2 + r 20 + r 3 + r 30 + r 4 + r 40 = 45 90 =0,5 А.

Пользуясь формулами (3) и (5), вычислим потенциалы всех точек, обходя контур тока по часовой стрелке

φ a =0; φ b = φ a −I⋅ r 1 =0−0,5⋅8=−4 B; φ c = φ b + E 1 −I⋅ r 10 = ( −4 )+25−0,5⋅2=20 B; φ d = φ c −I⋅ r 2 =20−0,5⋅24=8 B; φ f = φ d + E 2 −I⋅ r 20 =8+5−0,5⋅6=10 B; φ g = φ f −I⋅ r 3 =10−0,5⋅40=−10 B; φ h = φ g − E 3 −I⋅ r 30 = ( −10 )−20−0,5⋅2=−31 B; φ k = φ h −I⋅ r 4 = ( −31 )−0,5⋅4=−33 B; φ a = φ k + E 4 −I⋅ r 40 = ( −33 )+35−0,5⋅4=0.

На рис. 22, б начерчен потенциальный график. По оси абсцисс отложены величины сопротивлений отдельных участков цепи, а по оси ординат — значения потенциалов в отдельных точках цепи.

Найдем точку, равнопотенциальную точке a. Из графика видно, что искомая точка m находится на участке сопротивления fg, так как в этой точке прямая падения потенциалов пересекает ось абсцисс, потенциал которой равен φ_a = 0. Обозначая участок сопротивления между точками f и m через r_fm и применяя к участку abcdfm формулу закона Ома (5) и учитывая, что φ_a = φ_m, найдем

I= φ a − φ m + E 1 + E 2 r 1 + r 10 + r 2 + r 20 + r fm ,

или

0,5= 30 40+ r fm ,

откуда r_fm = 20 Ом, т.е. точка m находится на середине сопротивления r₃.

Для нахождения точки, потенциал которой следует принять равным нулю при условии, чтобы потенциалы всех остальных точек были положительны, следует обратиться к потенциальному графику, из которого видно, что такой точкой является точка k.

Ключ разомкнут. Тока в цепи нет, поэтому точки a и b равнопотенциальны, т. е. φ_a = φ_b = 0. Потенциал точки c превышает потенциал точки b на величину э.д.с. E₁ и φ_c = E₁ = 25 В; рассуждая аналогично, найдем

φ d = φ c =25 B; φ f = φ d + E 2 =25+5=30 B; φ g = φ f =30 B; φ h = φ g − E 3 =30−20=10 B; φ k = φ h =10 B; φ l = φ k + E 4 =10+35=45 B.

На основе полученных результатов на рис. 22, б начерчен график изменения потенциала при разомкнутом ключе.

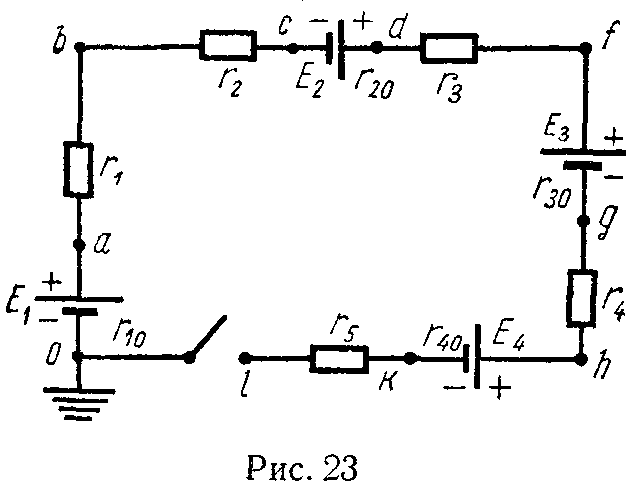
Задача 18. Для схемы рис. 23 построить потенциальные графики 0abcdfghkl при разомкнутом и замкнутом ключе, если E₁ = 60 В, E₂ = 40 В, E₃ = 25 В, E₄ = 15 В, r₁₀ = 6 Ом, r₂₀ = 4 Ом, r₃₀ = 3 Ом, r₄₀ = 2 Ом, r₁ = 24 Ом, r₂ = 16 Ом, r₃ = 25 Ом, r₄ = 22 Ом, r₅ = 18 Ом.

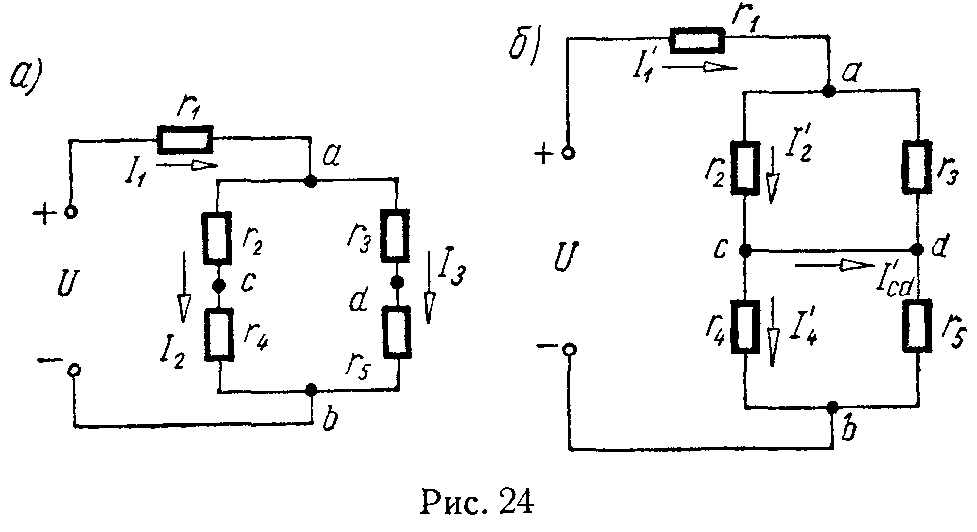
Задача 19. Определить токи в ветвях цепи (рис. 24, а) и напряжение между точками c и d и показание амперметра, включенного между точками c и d. Сопротивление амперметра считать равным нулю. Сопротивления элементов цепи r₁ = 10 Ом, r₂ = r₃ = r₅ = 25 Ом, r₄ = 50 Ом, а приложенное к ней напряжение U = 120 В.

Решение

Эквивалентное сопротивление всей цепи (рис. 24, а) равно

r= r 1 + ( r 2 + r 4 )⋅ ( r 3 + r 5 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =10+ 75⋅50 125 =40 Ом.

В неразветвленной части цепи протекает ток

I= U r = 120 40 =30 А.

Токи, протекающие через сопротивления r₂ + r₄ и r₃ + r₅, можно найти различными способами.

1) В параллельных ветвях токи распределяются обратно пропорционально их сопротивлениям (формулы 9)

I 2 = I 1 ⋅ ( r 3 + r 5 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =3⋅ 50 125 =1,2 А, I 3 = I 1 ⋅ ( r 2 + r 4 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =3⋅ 75 125 =1,8 А.

2) Найдем напряжение на зажимах параллельных ветвей

U ab = I 1 ⋅ ( r 2 + r 4 )⋅ ( r 3 + r 5 ) ( r 2 + r 4 )+ ( r 3 + r 5 ) =3⋅ 75⋅50 125 =90 В.

Токи в ветвях с сопротивлениями r₂ + r₄ и r₃ + r₅ равны

I 2 = U ab r 2 + r 4 = 90 75 =1,2 А, I 3 = U ab r 3 + r 5 = 90 50 =1,8 А.

Напряжение на зажимах параллельных ветвей может быть найдена как разность между приложенным напряжением и падением напряжения на сопротивлении r₁

U ab =U− I 1 ⋅ r 1 =120−3⋅10=90 В.

Найдем напряжение между точками c и d

U cd =− I 2 ⋅ r 2 + I 3 ⋅ r 3 =−1,2⋅25+1,8⋅25=15 В.

Наконец, вычислим ток, проходящий через амперметр, он равен току короткого замыкания I’_cd (рис. 24, б). Для его нахождения вычислим токи

I ′ 1 = U r 1 + r 2 ⋅ r 3 r 2 + r 3 + r 4 ⋅ r 5 r 4 + r 5 = 144 47 А, I ′ 2 = I ′ 1 ⋅ r 3 r 2 + r 3 = 144 47 ⋅ 1 2 = 72 47 А, I ′ 4 = I ′ 1 ⋅ r 5 r 4 + r 5 = 144 47 ⋅ 25 75 = 48 47 А.

Искомый ток, проходящий через амперметр, равен

I A = I ′ cd = I ′ 2 − I ′ 4 = 72 47 − 48 47 = 24 47 =0.51 А.

Задача 20. Для измерения тока применены амперметры, пределы измерений которых равны 5 и 2,5 А, и шунт, сопротивление которого неизвестно. Первый амперметр, включенный с шунтом в некоторую цепь, показал 3,6 А, второй — с тем же шунтом показал в той же цепи ток 2 А. Сопротивления амперметров r₁ = 0,002 Ом и r₂ = 0,004 Ом. Чему равен ток в цепи?

Ответ: 18 А; r_ш = 0,0005 А.

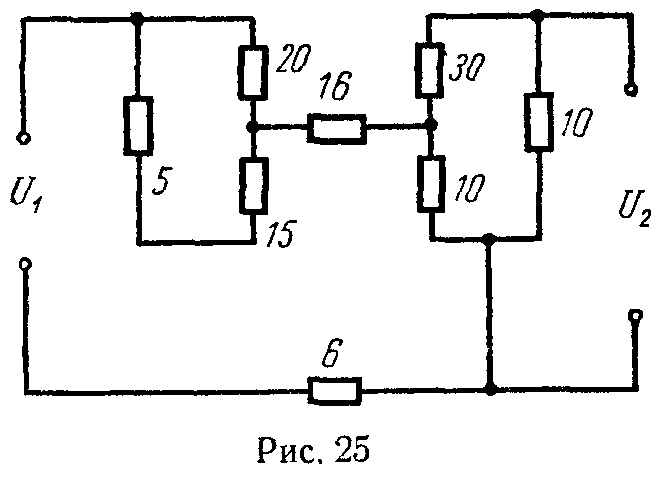
Задача 21. Для цепи рис. 25 определить отношение напряжения на выходе U₂ к напряжению на входе цепи U₁. Сопротивления отдельных ветвей цепи в омах указаны на схеме.

Ответ: U₂: U₁ = 0,05.

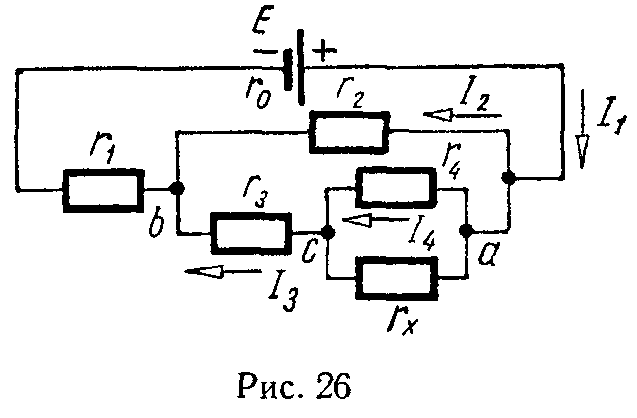
Задача 22. В схеме (рис. 26) найти сопротивление r_x, если I₁ = 2,6 А, I₃ = 0,6 А, r₁ = 0,5 Ом, r₂ =1,4 Ом, r₃ = 3 Ом, r₄ = 2,5 Ом. Найти э.д.с. батареи E, если ее внутреннее сопротивление r₀ = 0,1 Ом.

Решение

На основании первого закона Кирхгофа найдем

I₂ = I₁ — I₃ = 2,6 — 0,6 = 2 А.

По закону Ома, примененному к участку, содержащему сопротивление r₂, найдем

U_ab = I₂·r₂ = 2·1,4 = 2,8 В.

Применяя закон Ома к участку цепи ab, содержащему э.д.с. E и сопротивления r₁ и r₀, найдем искомую э.д.с.

E = U_ab + I₁· (r₁ + r₀) = 2,8 + 2,6·0,6 = 4,36 В.

Теперь найдем напряжение на параллельных ветвях с сопротивлениями r₄ и r_x и токи в них

U_ac = U_ab — I₃·r₃ = 2,8 — 0,6·3 = 1 В;

I₄ = U_ac/r₄ = 1/2,5 = 0,4 А;

I_x = I₃ — I₄ = 0,6 — 0,4 = 0,2 А.

Искомое сопротивление

r_x = U_ac/I_x = 1/0,2 = 5 Ом.

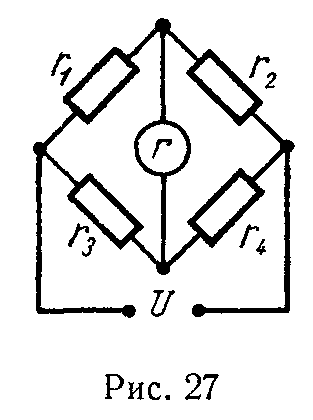
Задача 23. В схеме мостика (рис. 27) известны сопротивления r₁ = 1300 Ом, r₂ = 800 Ом, r₃ = 400 Ом. Сопротивление гальванометра r_г = 600 Ом. Через, сопротивление r₁ протекает ток I₁ = 1 мА. К мостику приложено напряжение U = 2,5 В.

Найти сопротивление r₄.

Ответ: 750 Ом.

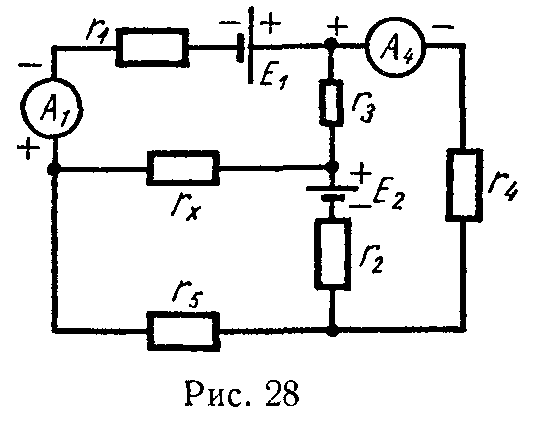
Задача 24. В цепи (рис. 28) найти E₁ и r_x, если E₂ = 3 В, r₁ = r₂ = 1 кОм, r₃ = 4 кОм, r₄ = 2 кОм, r₅ = 1 кОм. Внутренние сопротивления батарей принять равными нулю.

Амперметр А₁ показывает 4 мА, а А₄ — 3 мА; полярности приборов показаны на схеме, а их сопротивлениями можно пренебречь.

Ответ: E₁ = 12 В, r_x = 2 Ом.

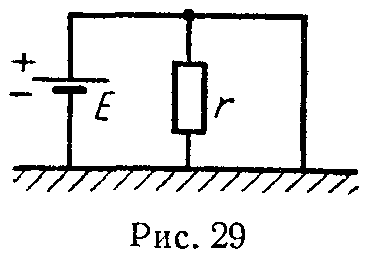
Задача 25. Однопроводная линия с сопротивлением r₀ на единицу длины, питаемая батареей с э.д.с., равной E, закорочена на приемном конце (рис. 29).

В каком месте линия должна иметь утечку с сопротивлением r, чтобы ток I на приемном конце был минимальным?

Ответ: по середине линии.

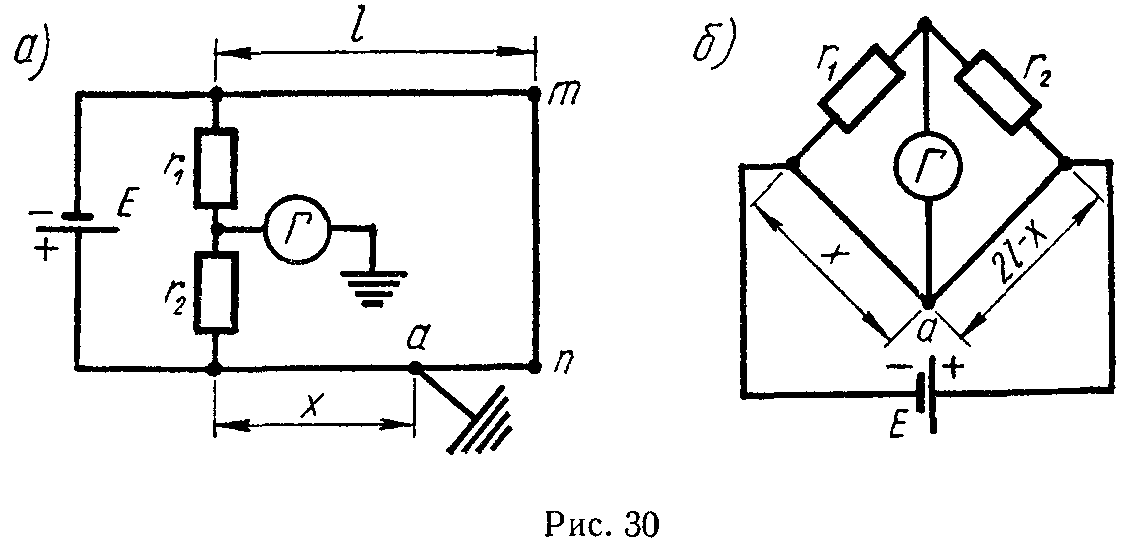
Задача 26. Для определения места повреждения изоляции линии применяется схема, изображенная на рис. 30, а; r₁ и r₂ — магазины сопротивлений.

Правый зажим гальванометра заземлен. Свободные концы тип линии соединены между собой накоротко. Подбором сопротивлений r₁ и r₂ добиваются отсутствия тока в гальванометре.

Показать, что если сечения обоих проводов одинаковы, то расстояние от места повреждения изоляции a до начала линии равно

2l⋅ r 2 r 1 + r 2 .

Указание. Заданная схема может быть заменена схемой рис. 30, б.

Задача 27. При проверке постоянной C счетчика оказалось, что при силе тока 10 А и напряжении 120 В якорь его в продолжение 30 сек сделал 37 оборотов. Определить ошибку в показаниях счетчика, если на счетчике указано, что 1 ГВт·ч соответствует 400 оборотам счетчика.

Примечание. Постоянной счетчика называется число ватт-часов, приходящихся на один оборот счетчика.

Ответ: 7,5%.

Задача 28. Каково должно быть сечение медных проводов линии для передачи потребителю мощности P = 16 кВт при условии, что потеря мощности не превысит p = 5%, если длина линии l = 180 м и напряжение в конце линии равно U = 220 В?

Ответ: точное значение 41,8 мм², по ГОСТ надо взять 50 мм².

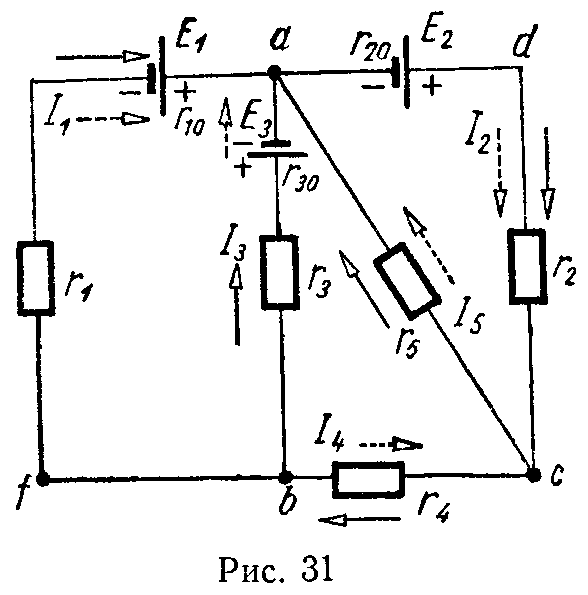
Задача 29. Для схемы (рис. 31), пользуясь законами Кирхгофа, найти токи и проверить баланс мощностей, если E₁ = 15 В, E₂ = 70 В, E₃ = 5 В, r₁₀ = r₂₀ = 1 Ом, r₃₀ = 2 Ом, r₁ = 5 Ом, r₁ = 5 Ом, r₂ = 4 Ом, r₃ = 8 Ом, r₄ = 2,5 Ом, r₅ = 15 Ом.

Решение

Всего узлов в схеме три (a, b, c), следовательно, число независимых уравнений, составляемых по первому закону Кирхгофа, будет на единицу меньше, т.е. два. Число контуров равно трем, следовательно, по второму закону Кирхгофа можно составить три взаимно независимых уравнения. Таким образом, общее число независимых уравнений, составляемых по первому и второму законам Кирхгофа, равно числу неизвестных токов в пяти ветвях схемы.

Выберем положительные направления для токов, которые обозначены пунктирными стрелками, и составим систему уравнений Кирхгофа:

для узла a

I₁ — I₂ + I₃ + I₅ = 0; (1)

для узла b

–I₁ — I₃ — I₄ = 0; (2)

для контура abfa

E₁ + E₃ = I₁· (r₁ + r₁₀) — I₃· (r₃ + r₃₀); (3)

для контура abca

E₃ = –I₃· (r₃ + r₃₀) + I₄·r₄ + I₅·r₅; (4)

для контура adca

E₂ = I₂· (r₂ + r₂₀) + I₅·r₅. (5)

Уравнения (1) — (5) после подстановки в них числовых значений будут иметь следующий вид

I₁ — I₂ + I₃ + I₅ = 0,

I₁ + I₃ + I₄ = 0,

6I₁ — 10I₃ = 20,

–10I₃ + 2,5I₄ + 15I₅ = 5,

5I₂ + 15I₅ = 70.

Решая эту систему уравнений, получим

I₁ = 5 А; I₂ = 8 А; I₃ = 1 А; I₄ = –6 А; I₅ = 2 А.

Отрицательный знак для тока I₄ означает, что истинное направление этого тока противоположно принятому. При проверке баланса мощностей надо иметь в виду, что в тех ветвях цепи, где истинное направление тока совпадает с направлением э.д.с., соответствующая э.д.с. будет являться источником энергии, а в тех участках, где направления э.д.с. и тока противоположны, э.д.с. будет являться потребителем энергии. Все сопротивления как внешние, так и самих источников, независимо от направления протекающего через них тока, будут являться потребителями энергии.

Баланс мощностей для рассматриваемой схемы будет

E₁·I₁ + E₂·I₂ + E₃· (–I₃) = I₁²· (r₁ + r₁₀) + I₂²· (r₂ + r₂₀) + I₃²· (r₃ + r₃₀) + I₄²·r₄ + I₅²·r₅,

или

15·5 + 70·8 — 5·1 = 5²·6 + 8²·5 + 1²·10 + 6²·2,5 + 2²·15,

получено тождество 630 Вт = 630 Вт.

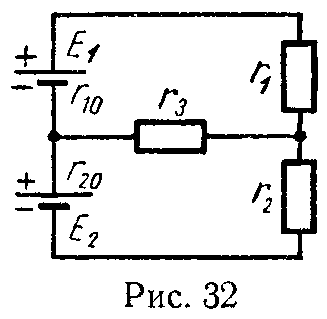
Задача 30. В схеме (рис. 32) найти все токи, если известны: E₁ = 20 В, E₂ = 1,1 В, r₁₀ = 0,2 Ом, r₂₀ = 0,4 Ом, r₁ = r₂ = 5 Ом, r₃ = 7 Ом.

Ответ: 2,5 А, 1,5 А, 1 А.

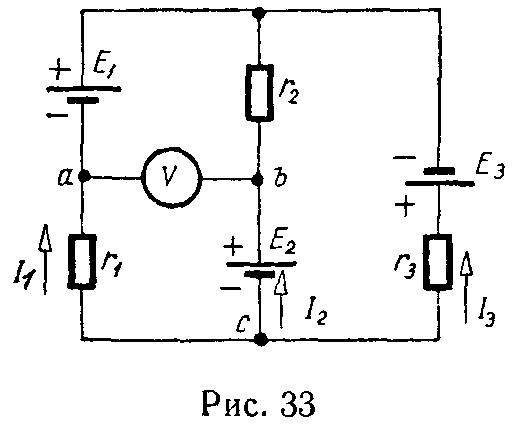
Задача 31. Для цепи, изображенной на рис. 33, рассчитать токи и определить показание вольтметра, если E₁ = 40 В, E₂ = 5 В, E₃ = 25 В, r₁ = 5 Ом, r₂ = r₃ = 10 Ом.

Внутренними сопротивлениями источников энергии и током, протекающим через вольтметр, можно пренебречь.

Ответ: I₁ = 5 А, I₂ = 1 А, I₃ = 4 А, U_ba = 30 В.

Задача 32. Аккумуляторная батарея из 20 последовательно соединенных элементов работает параллельно с генератором на сеть, имеющую нагрузку 30 А. Каждый аккумулятор имеет э.д.с. 1,82 В и сопротивление 0,001 Ом. Э.д.с. генератора 36,4 В и его сопротивление 0,04 Ом. Определить нагрузку генератора и батареи (т. е. отдаваемые ими токи) и напряжение на их зажимах.

Какую э.д.с. должен развивать генератор, чтобы нагрузка распределилась поровну между генератором и батареей?

Ответ: 20 А, 10 А, 36 В, 36,7 В.

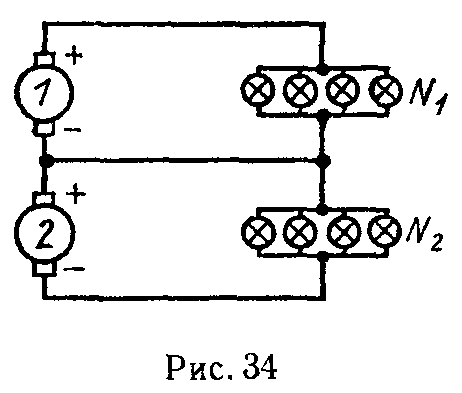
Задача 33. По трехпроводной линии длиной 0,5 км (рис. 34) от двух генераторов 1 и 2 питаются две группы ламп 50 Вт, 110 В.

В первой группе — N₁ = 200 ламп, а во второй — N₂ = 600 ламп. Сечение крайних проводов q = 35 мм², а сечение среднего (нулевого) провода q₀ = 16 мм². Каждый генератор имеет внутреннее сопротивление 0,01 Ом и развивает э.д.с. 120 В. Определить токи во всех проводах линии и напряжение на зажимах каждой группы ламп, сопротивления которых считать постоянным. Материал проводов линии — медь.

Ответ: I₁ = 98 А, I₂ = 144 А, I₀ = 46 А, U₁ = 102 В, U₂ = 71 В.

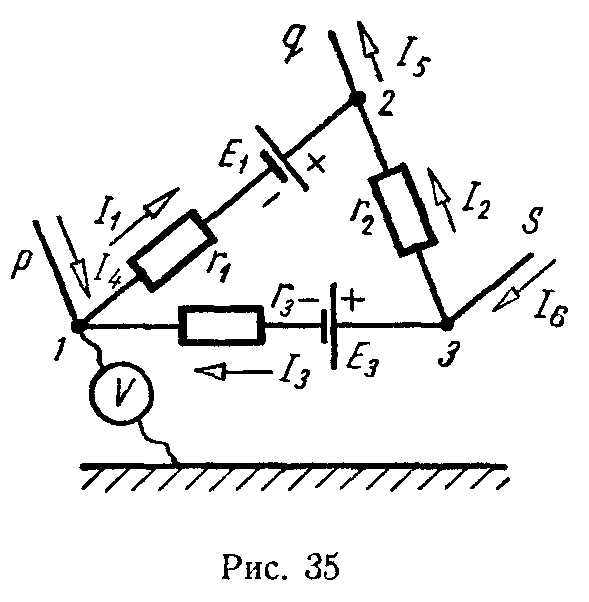
Задача 34. Напряжения, измеренные электростатическим вольтметром, между узловыми точками схемы и землей, равны: U₁₀ = –15 В, U₂₀ = 52 В, U₃₀ = 64 В (рис. 35).

Определить токи в ветвях и отходящих проводах при следующих данных: E₁ = 80 В, E₃ = 70 В, r₁ = 5 Ом, r₂ = 10 Ом, r₃ = 12 Ом.

Решение

Вычислим напряжения между точками 1 и 2, 2 и 3, 3 и 1

U₁₀ — U₂₀ = U₁₂ = (–15) — 52 = –67 В,

U₂₀ — U₃₀ = U₂₃ = 52 — 64 = –12 В,

U₃₀ — U₁₀ = U₃₁ = 64 — (–15) = 79 В.

Применяя к ветвям 1–2, 2–3, 3–1 закон Ома, найдем токи

I 1 = U 12 + E 1 r 1 = ( −67 )+80 5 =2,6 А, I 2 = U 32 r 2 = 12 10 =1,2 А, I 3 = U 31 − E 3 r 3 = 79−70 12 =0,75 А.

Так как все токи оказались положительными, то они имеют направления в соответствии с только что записанными уравнениями и нанесены на рис. 35.

Токи в ответвлениях от узловых точек 1–p, 2–q, 3–s находим по первому закону Кирхгофа

I₄ = I₁ — I₃ = 1,85 А, I₅ = I₁ + I₂ = 3,8 А, I₆ = I₂ + I₃ = 1,95 А.

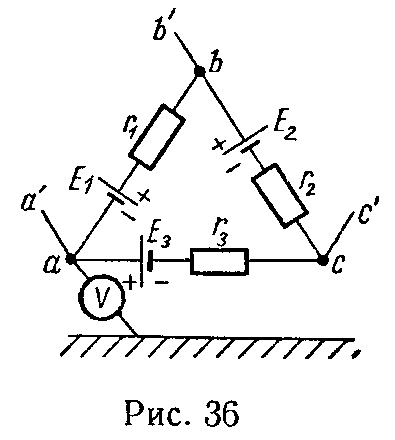
Задача 35. В цепи (рис. 36) известны э.д.с. E₁ = 120 В, E₂ = 40 В, E₃ = 70 В и сопротивления r₁ = 20 Ом, r₂ = 10 Ом, r₃ = 40 Ом.

Потенциалы точек a, b и c относительно земли соответственно равны (определены посредством вольтметра): U_a₀ =160 В, U_b₀ = 180 В, U_c₀ = 50 В. Определить токи в ветвях ab, bc, ca и в проводах aa’, bb’ и cc’, подходящих к точкам a, b и c.

Ответ: I₁ = 5 А, I₂ = 9 А, I₃ = 1 А.

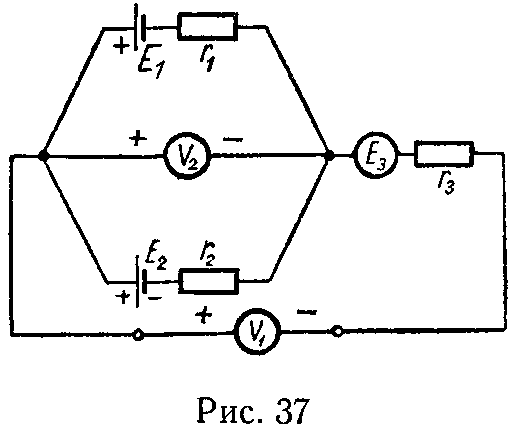
Задача 36. В цепи (рис. 37) известны э.д.с. E₁ = 40 В, E₂ = 30 В.

Сопротивления элементов схемы r₁ = 8 Ом, r₂ = 5 Ом, r₃ = 10 Ом. Показания вольтметров соответственно равны: U₁ = 125 В, U₂ = 60 В; полярность зажимов вольтметров показана на схеме. Пренебрегая внутренними сопротивлениями источников электрической энергии и считая потребляемые вольтметрами токи приближенно равными нулю, определить величину и полярность э.д.с. E₃. Найти все токи.

Ответ: E₃ = 20 В, I₁ = 2,5 А, I₂ = 6 А, I₃ = 8,5 А.

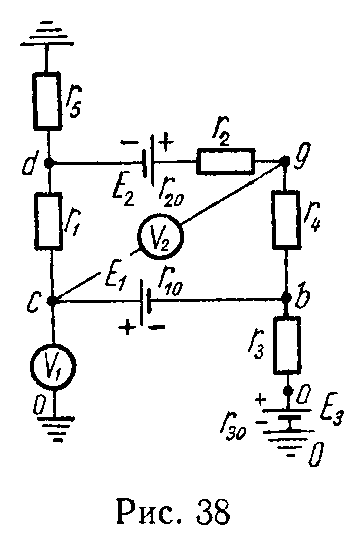
Задача 37. В цепи, изображенной на рис. 38, найти токи и показания вольтметров, включенных между точками 0 и c, c и g, если известно, что E₁ = 32 В, E₂ = 64 В, E₃ = 72 В, r₁ = 9 Ом, r₁₀ = 1 Ом, r₂ = 5 Ом, r₂₀ = 1 Ом, r₃ = 2 Ом, r₃₀ = 1 Ом, r₄ = 2 Ом, r₅ = 1 Ом. Сопротивления вольтметров весьма велики по сравнению с сопротивлениями элементов цепи.

Ответ: I₁ = 5 А, I₂ = 9 А, I₃ = 1 А.

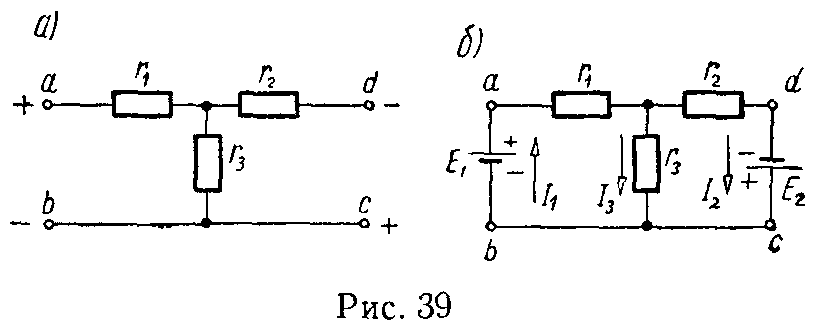
Задача 38. Для схемы (рис. 39, а) найти токи и проверить баланс мощностей, если U_ab = 12 В, U_cd = 5,6 В, r₁ = 4 Ом, r₂ = 5 Ом, r₃ = 3 Ом.

Решение

Данная схема может быть заменена эквивалентной, в которой между точками a и b, а также c и d включены э.д.с., численное значение которых E₁ = U_ab и E₂ = U_cd, а их внутренние сопротивления равны нулю (рис. 39, б). Обращаем внимание на то, что при включении э.д.с. следует соблюдать заданные полярности напряжений.

Задавшись направлениями для токов, составим систему уравнений Кирхгофа

I₁ — I₂ — I₃ = 0,

E₁ = I₁·r₁ + I₃·r₃,

E₂ = I₂·r₂ — I₃·r₃.

Подставляя сюда числовые значения и решая систему уравнений, найдем:

I₁ = 2,4 А, I₂ = 1,6 А, I₃ = 0,8 А.

Для проверки баланса мощностей составим уравнение

U_ab·I₁ + U_cd·I₂ = I₁²·r₁ + I₂²·r₂ + I₃²·r₃,

12·2,4 + 5,6·1,6 = 2,4²·4 + 1,6²·5 + 0,8²·3;

получено тождество 37,76 = 37,76.

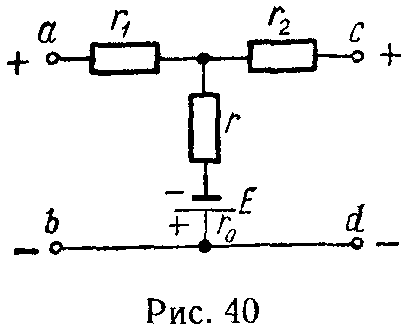
Задача 39. В цепи (рис. 40) найти токи и проверить баланс мощностей, если U_ab = 16 В, U_cd = 11,2 В, E = 5 В, r₀ = 0, r = 10 Ом, r₁ = 5 Ом, r₂ = 4 Ом.

Ответ: I₁ = 1,2 А, I₂ = 0,3 А, I = 1,5 А.

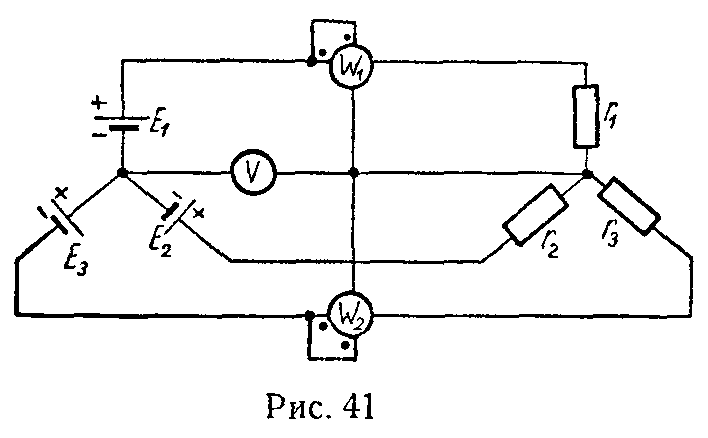
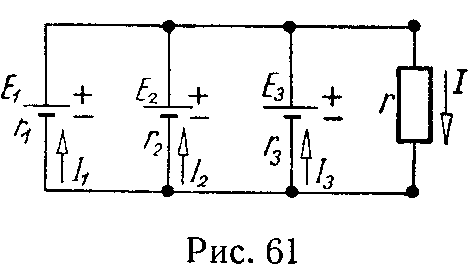
Задача 40. Чему равно показание вольтметра на рис. 41, если током вольтметра можно пренебречь по сравнению с токами в нагрузках? Внутренние сопротивления батарей принять равными нулю.

Определить показания ваттметров и убедиться в том, что их сумма равна сумме мощностей, расходуемых в сопротивлениях r₁, r₂ и r₃. Потерями в катушках ваттметров пренебречь.

Дано: E₁ = 30 В, E₂ = 21 В, E₃ = 5 В, r₁ = 5 Ом, r₂ = 10 Ом, r₃ = 50 Ом.

Ответ: 25 В, P₁ = 9 Вт, P₂ = 15,6 Вт.

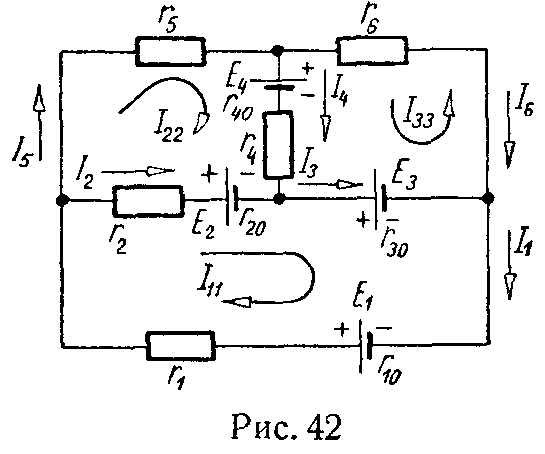
Задача 41. Методом контурных токов найти токи в цепи, схема которой изображена на рис. 42; даны: E₁ = 100 В, E₂ = 30 В, E₃ = 10 В, E₄ = 6 В, r₁ = 10 Ом, r₂ = 10 Ом, r₄ = 6 Ом, r₅ = 5 Ом, r₆ = 15 Ом, r₁₀ = r₂₀ = r₃₀ = 0, r₄₀ = 1 Ом.

Решение

Выберем направления контурных токов, которые обозначим через I₁₁, I₂₂, I₃₃.

Составим систему уравнений для контуров

E₁ — E₂ — E₃ = I₁₁· (r₁ + r₁₀ + r₂ + r₂₀ + r₃₀) — I₂₂· (r₂ + r₂₀) + I₃₃·r₃₀,

E₂ — E₄ = I₂₂· (r₂ + r₂₀ + r₅ + r₄ + r₄₀) + I₃₃· (r₄ + r₄₀) — I₁₁· (r₂ + r₂₀),

–E₃ — E₄ = I₃₃· (r₃₀ + r₆ + r₄ + r₄₀) + I₂₂· (r₄ + r₄₀) + I₁₁·r₃₀.

После подстановки числовых значений будем иметь

60 = 20·I₁₁ — 10·I₂₂ + 0·I₃₃,

24 = –10·I₁₁ + 22·I₂₂ + 7·I₃₃,

–16 = 0·I₁₁ + 7·I₂₂ + 22·I₃₃.

Решив эту систему уравнений, найдем контурные токи

I₁₁ = 5 А, I₂₂ = 4 А, I₃₃ = –2 А.

Теперь найдем истинные токи во всех ветвях.

В ветви, где действует э.д.с. E₁, истинный ток I₁ имеет направление контурного тока I₁₁ и равен

I₁ = I₁₁ = 5 А.

В ветви с сопротивлением r₅ истинный ток I₅ имеет направление контурного тока I₂₂ и равен

I₅ = I₂₂ = 4 А.

В ветви с сопротивлением r₆ истинный ток I₆ имеет направление, противоположное контурному току I₃₃, и равен

I₆ = –I₃₃ = — (–2) = 2 А.

В ветви с сопротивлением r₂ истинный ток I₂ получится от наложения контурных токов I₁₁ и I₂₂ и будет иметь направление большего контурного тока I₁₁;

I₂ = I₁₁ — I₂₂ = 5 — 4 = 1 А.

В ветви с сопротивлением r₄ истинный ток I₄ получится от наложения контурных токов I₂₂ и I₃₃ и будет иметь направление контурного тока I₂₂;

I₄ = I₂₂ + I₃₃ = 4 + (–2) = 2 А.

В ветви, где действует э.д.с. E₃, истинный ток I₃ получится от наложения контурных токов I₁₁ и I₃₃ и будет иметь направление тока I₁₁;

I₃ = I₁₁ + I₃₃ = 5 + (–2) = 3 А.

Эта же задача может быть решена методом определителей. Для этого уравнения для контурных токов следует записать в форме (10), а именно

{ r 11 ⋅ I 11 + r 12 ⋅ I 22 + r 13 ⋅ I 33 = E 11 ; r 21 ⋅ I 11 + r 22 ⋅ I 22 + r 23 ⋅ I 33 = E 22 ; r 31 ⋅ I 11 + r 32 ⋅ I 22 + r 33 ⋅ I 33 = E 33 ,

где контурные сопротивления

r₁₁ = r₁ + r₁₀ + r₂ + r₂₀ + r₃₀ = 20 Ом;

r₂₂ = r₂ + r₂₀ + r₅ + r₄ + r₄₀ = 22 Ом;

r₃₃ = r₃₀ + r₆ + r₄ + r₄₀ = 22 Ом,

взаимные сопротивления контуров

r₁₂ = r₂₁ = — (r₂ + r₂₀) = –10 Ом;

r₁₃ = r₃₁ = r₃₀ = 0;

r₂₃ = r₃₂ = r₄ + r₄₀ = 7 Ом,

контурные э.д.с.

E₁₁ = E₁ — E₂ — E₃ = 60 В;

E₂₂ = E₂ — E₄ = 24 В;

E₃₃ = –E₃ — E₄ = –16 В.

Получим численную систему уравнений метода контурных токов

{ 20⋅ I 11 − 10⋅ I 22 + 0⋅ I 33 =60; −10⋅ I 11 +22⋅ I 22 + 7⋅ I 33 =24; 0⋅ I 11 + 7⋅ I 22 +22⋅ I 33 =−16,

или в матричной форме записи

( 20 −10 0 −10 22 7 0 7 22 )⋅ ( I 11 I 22 I 33 )= ( 60 24 −16 ).

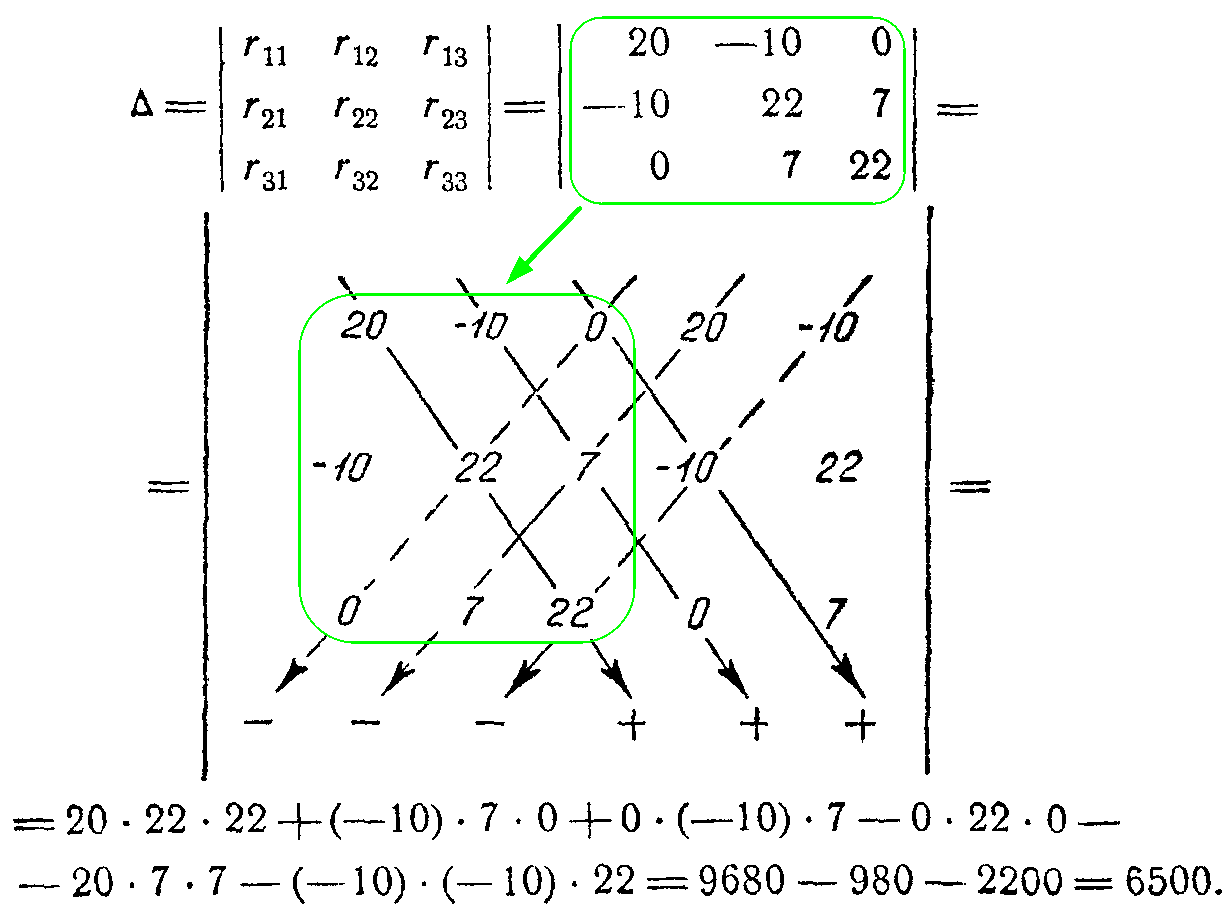
Составим главный определитель системы? и вычислим его значение

Вычислим значения вспомогательных определителей

Δ 11 =| E 11 r 12 r 13 E 22 r 22 r 23 E 33 r 32 r 33 |=| 60 −10 0 24 22 7 −16 7 22 |=32500; Δ 22 =| r 11 E 11 r 13 r 21 E 22 r 23 r 31 E 33 r 33 |=| 20 60 0 −10 24 7 0 −16 22 |=26000; Δ 33 =| r 11 r 12 E 11 r 21 r 22 E 22 r 31 r 32 E 33 |=| 20 −10 60 −10 22 24 0 7 −16 |=−13000.

Искомые контурные токи определяем по формулам

I 11 = Δ 11 Δ = 32500 6500 =5 А; I 22 = Δ 22 Δ = 26000 6500 =4 А; I 33 = Δ 33 Δ = −13000 6500 =−2 А.

Мы получили те же результаты, что и ранее.

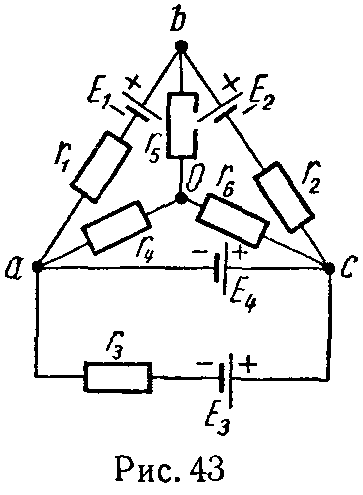
Задача 42. Найти все токи и определить потенциалы точек a, b, c и 0 относительно земли (рис. 43).

Задачу решить методом контурных токов, Внутренние сопротивления источников электрической энергии считать равными нулю: E₁ = 85 В, E₂ = 84 В, E₃ = 5 В, E₄ = 12 В, r₁ = 8 Ом, r₂ = 10 Ом, r₃ = 10 Ом, r₄ = 10 Ом, r₅ = 10 Ом, r₆ = 4 Ом.

Ответ: I₁ = 2 А, I₂ = 2,7 А, I₃ = 0,7 А, I₄ = 2,2 А, I₅ = 4,7 А, I₆ = 2,5 А.

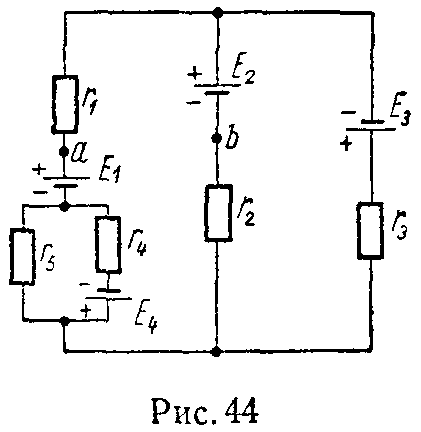
Задача 43. Для схемы (рис. 44) найти токи и U_ab, если E₁ = 70 В, E₂ = 5 В, E₃ = 15 В, E₄ = 10 В, r₁ = 5 Ом, r₂ = r₃ = 10 Ом, r₄ = 5 Ом, r₅ = 3 Ом.

Задачу решить методом контурных токов. Внутренние сопротивления источников энергии равны нулю.

Ответ: I₁ = 6 А, I₂ = 2 А, I₃ = 4 А, I₄ = 1 А, I₅ = 5 А.

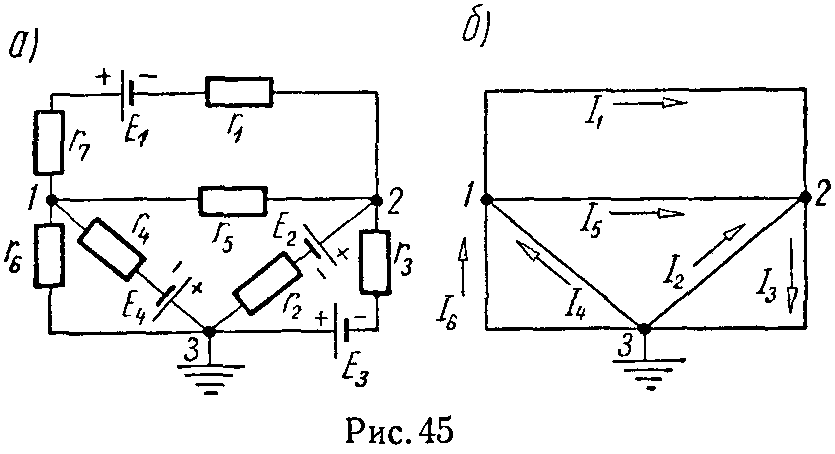
Задача 44. Для схемы, изображенной на рисунке 45, а, пользуясь методом узловых потенциалов, определить все токи. Данные схемы: E₁ = 30 В, E₂ = 10 В, E₃ = 200 В, E₄ = 56 В, r₁ = 20 Ом, r₂ = 30 Ом, r₃ = 6 Ом, r₄ = 8 Ом, r₅ = 15 Ом, r₆ = 40 Ом, r₇ = 10 Ом. Внутренние сопротивления источников напряжения равны нулю.

Решение

Примем потенциал точки 3 равным нулю. Тогда, на основании формулы (11), запишем систему уравнений для определения потенциалов точек 1 и 2

φ 1 ⋅ g 11 + φ 2 ⋅ g 12 = ∑ 1 E⋅g , (1) φ 1 ⋅ g 21 + φ 2 ⋅ g 22 = ∑ 2 E⋅g . (2)

Подсчитаем g₁₁ — сумму проводимостей, присоединенных к узлу 1

g 11 = 1 r 1 + r 7 + 1 r 5 + 1 r 4 + 1 r 6 = 1 30 + 1 15 + 1 8 + 1 40 =0,25 1 Ом .

Аналогично g₂₂ — сумма проводимостей, присоединенных к узлу 2

g 22 = 1 r 1 + r 7 + 1 r 5 + 1 r 2 + 1 r 3 = 1 30 + 1 15 + 1 30 + 1 6 =0,3 1 Ом .

Взаимные проводимости первого и второго узлов

g 12 = g 21 =− ( 1 r 1 + r 7 + 1 r 5 )=− 1 30 − 1 15 =−0,1 1 Ом .

Подставим в уравнения (1) и (2) числовые значения

0,25⋅ φ 1 + ( −0,1 )⋅ φ 2 =30⋅ 1 30 −56⋅ 1 8 =−6, ( −0,1 )⋅ φ 1 +0,3⋅ φ 2 =−30⋅ 1 30 +10⋅ 1 30 −200⋅ 1 6 =−34.

Решив последние два уравнения, найдем потенциалы точек 1 и 2

φ₁ = –80 В; φ₂ = –140 В.

Наконец, применяя закон Ома для отдельных ветвей, определим искомые токи

I 1 = φ 1 − φ 2 − E 1 r 1 = ( −80 )− ( −140 )−30 30 =1 А; I 2 = φ 3 − φ 2 + E 2 r 2 = 0− ( −140 )+10 30 =5 А; I 3 = φ 2 − φ 3 + E 3 r 3 = ( −140 )−0+200 6 =5 А; I 4 = φ 3 − φ 1 − E 4 r 4 = 0− ( −80 )−56 8 =3 А; I 5 = φ 1 − φ 2 r 5 = ( −80 )− ( −140 ) 15 =4 А.

Направления найденных токов указаны на скелетной схеме (рис. 45, б).

Рекомендуем читателю решить ту же задачу, приняв за нуль потенциал узловой точки 1.

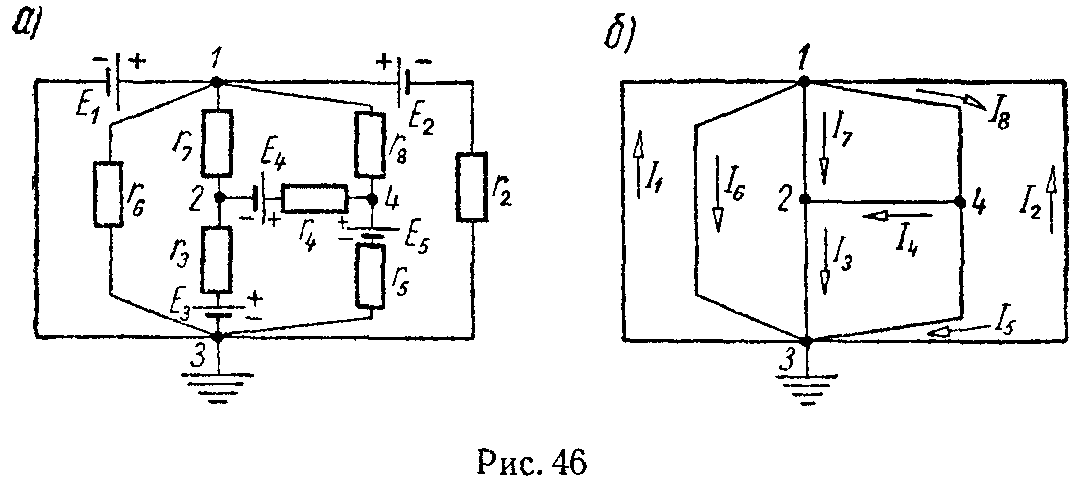
Задача 45. Методом узловых потенциалов определить токи во всех ветвях схемы, изображенной на рис. 46, а; заданы: E₁ = 20 В, E₂ = 30 В, E₃ = 2 В, E₄ = 1,2 В, E₅ = 5,6 В, r₂ = 50 Ом, r₃ = 10 Ом, r₄ = 20 Ом, r₅ = 10 Ом, r₆ = 100 Ом, r₇ = 50 Ом, r₈ = 20 Ом.

Внутренние сопротивления источников напряжения считать равными нулю.

Решение

В тех случаях, когда в цепи имеется ветвь с э.д.с., но не содержащая сопротивления, целесообразно принять равным нулю потенциал одной из узловых точек, к которой подходит указанная ветвь.

В нашем случае примем потенциал узла 3 равным нулю (φ₃ = 0). Тогда потенциал точки 1 имеет значение, равное E₁, т.е. φ₁ = 20 В. Общее число уравнений уменьшается и равняется числу узлов минус два. В нашей задаче достаточно составить всего два уравнения для узлов 2 и 4.

Определим сумму проводимостей, присоединенных к узлу 2

g 22 = 1 r 3 + 1 r 4 + 1 r 7 =0,17 1 Ом ,

и, соответственно, к узлу 4

g 44 = 1 r 4 + 1 r 5 + 1 r 8 =0,2 1 Ом .

Найдем взаимные проводимости узлов 2 и 1, 2 и 4, 4 и 1

g 12 = g 21 =− 1 r 7 =−0,02 1 Ом , g 24 = g 42 =− 1 r 4 =−0,05 1 Ом , g 14 = g 41 =− 1 r 8 =−0,05 1 Ом .

Вычислим суммы произведений э.д,с. на проводимости, присоединенные соответственно к узлам 2 и 4

∑ 2 E⋅g = E 3 ⋅ g 3 − E 4 ⋅ g 4 =0,14 В Ом , ∑ 4 E⋅g = E 4 ⋅ g 4 + E 5 ⋅ g 5 =0,62 В Ом .

Составим систему уравнений на основании формул (11) для узла 2:

φ 1 ⋅ g 21 + φ 2 ⋅ g 22 + φ 4 ⋅ g 24 = ∑ 2 E⋅g ,

для узла 4

φ 1 ⋅ g 41 + φ 2 ⋅ g 42 + φ 4 ⋅ g 44 = ∑ 4 E⋅g .

Подставляя сюда числовые значения, получим

0,17⋅ φ 2 + ( −0,05 )⋅ φ 4 =0,54, ( −0,05 )⋅ φ 2 +0,2⋅ φ 4 =1,62.

Решая эту систему уравнений, найдем

φ₂ = 6 В; φ₄ = 9,6 В.

Наконец, применяя к отдельным ветвям формулы закона Ома, получим значения всех токов, которые нанесены на скелетной схеме (46, б)

I₂ = 0,2 А, I₃ = 0,4 А, I₄ = 0,12 А, I₅ = 0,4 А, I₆ = 0,2 А, I₇ = 0,28 А, I₈ = 0,52 А.

Ток I₁ определяется на основании первого закона Кирхгофа

I₁ = I₃ + I₅ + I₆ – I₂ = 0,8 А.

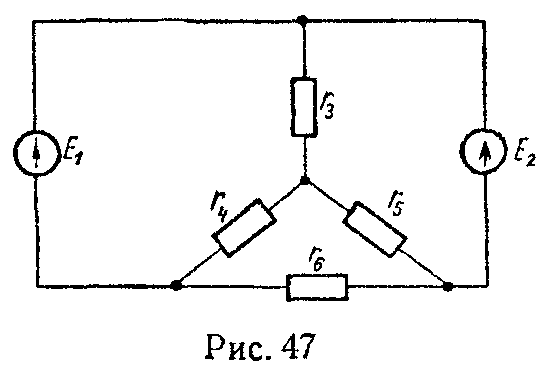
Задача 46. Методом узловых потенциалов рассчитать токи в цепи (рис. 47). Даны: E₁ = 160 мВ, E₂ = 300 мВ, r₃ = r₄ = 100 Ом, r₅ = 150 Ом, r₆ = 40 Ом. Внутренние сопротивления генераторов напряжения равны нулю.

Указание. Для решения задачи достаточно составить всего одно уравнение, так как в схеме имеется две ветви с э.д.с., но не содержащие сопротивления, а узлов в схеме четыре.

Ответ: I₁ = 2,25 мА, I₂ = 1,4 мА, I₃ = 0,85 мА, I₄ = 0,75 мА, I₅ = 0,1 мА, I₆ = 1,5 мА.

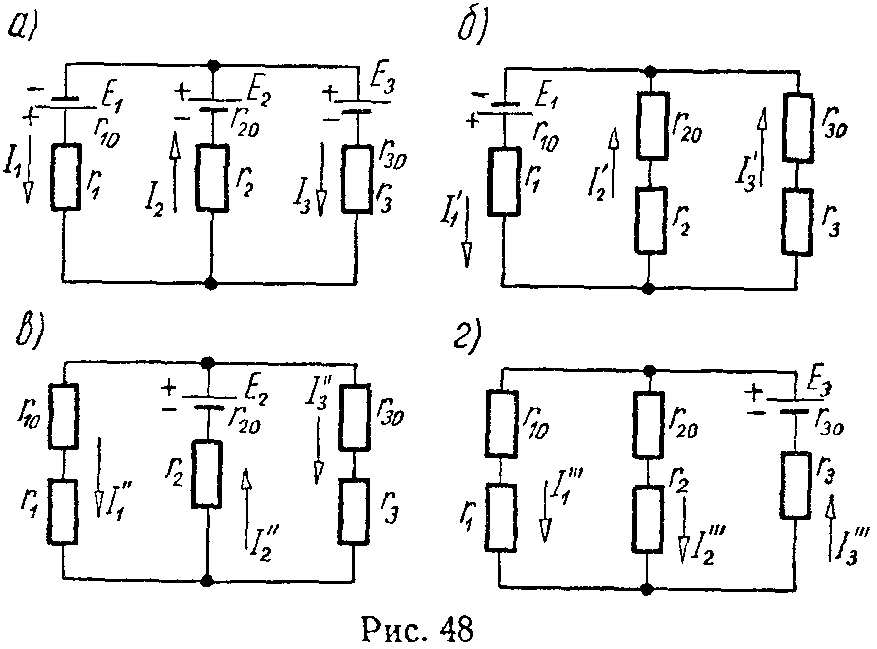
Задача 47. Методом наложения рассчитать токи в схеме (рис. 48. а), если E₁ = 10 В, E₂ = 40 В, E₃ = 5 В, r₁₀ = 5 Ом, r₂₀ = r₃₀ = 2 Ом, r₁ = 30 Ом, r₂ = 3 Ом, r₃ = 8 Ом.

Решение

Сначала предполагаем, что действует только э.д.с. E₁, а э.д.с. E₂ и E₃ считаем недействующими (рис. 48, б), тогда

I ′ 1 = E 1 r 1Э ,

где

r 1Э = r 1 + r 10 + ( r 2 + r 20 )⋅ ( r 3 + r 30 ) ( r 2 + r 20 )+ ( r 3 + r 30 ) =35+ 5⋅10 15 = 115 3 Ом.

Ток

I ′ 1 = E 1 r 1Э = 10 115/3 = 6 23 А.

Токи в параллельных ветвях найдем согласно формуле (9)

I ′ 2 = I ′ 1 ⋅ ( r 3 + r 30 ) ( r 2 + r 20 )+ ( r 3 + r 30 ) = 6 23 ⋅ 10 15 = 4 23 А, I ′ 3 = I ′ 1 ⋅ ( r 2 + r 20 ) ( r 2 + r 20 )+ ( r 3 + r 30 ) = 6 23 ⋅ 5 15 = 2 23 А.

Теперь проведем расчет, предполагая, что действует э.д.с. E₂, а э.д.с. E₁ и E₃ считаем недействующими (рис. 48, в)

I ″ 2 = E 2 r 2Э ; r 2Э = r 2 + r 20 + ( r 1 + r 10 )⋅ ( r 3 + r 30 ) ( r 1 + r 10 )+ ( r 3 + r 30 ) = 115 9 Ом; I ″ 2 = E 2 r 2Э = 40 115/9 = 72 23 А; I ″ 1 = I ″ 2 ⋅ ( r 3 + r 30 ) ( r 1 + r 10 )+ ( r 3 + r 30 ) = 72 23 ⋅ 10 45 = 16 23 А; I ″ 3 = I ″ 2 ⋅ ( r 1 + r 10 ) ( r 1 + r 10 )+ ( r 3 + r 30 ) = 72 23 ⋅ 35 45 = 56 23 А.

Аналогично рассчитываем величины токов при действии только одной э.д.с. E₃ (рис. 48, г)

I ? 3 = E 3 r 3Э ; r 3Э = r 3 + r 30 + ( r 1 + r 10 )⋅ ( r 2 + r 20 ) ( r 1 + r 10 )+ ( r 2 + r 20 ) = 115 8 Ом; I ? 3 = E 3 r 3Э = 5 115/8 = 8 23 А; I ? 1 = I ? 3 ⋅ ( r 2 + r 20 ) ( r 1 + r 10 )+ ( r 2 + r 20 ) = 8 23 ⋅ 5 40 = 1 23 А; I ? 2 = I ? 3 ⋅ ( r 1 + r 10 ) ( r 1 + r 10 )+ ( r 2 + r 20 ) = 8 23 ⋅ 35 40 = 7 23 А.

Истинное значение тока в каждой ветви найдется как алгебраическая сумма токов, определяемых каждой э.д.с. в отдельности.

Ток в первой ветви

I 1 = I ′ 1 + I ″ 1 + I ? 1 = 6 23 + 16 23 + 1 23 =1 А.

Ток во второй ветви

I 2 = I ′ 2 + I ″ 2 − I ? 2 = 4 23 + 72 23 − 7 23 =3 А.

Ток в третьей ветви

I 3 =− I ′ 3 + I ″ 3 − I ? 3 =− 2 23 + 56 23 − 8 23 =2 А.

Направления этих токов показаны на рис. 48, а.

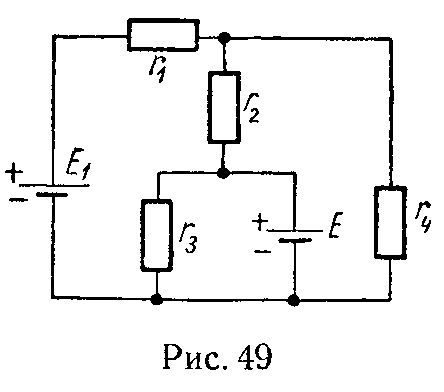
Задача 48. Найти токи в ветвях цепи, изображенной на рис. 49, если известны E₁ = 125 мВ, E = 120 мВ, r₁ = 40 Ом, r₂ = 36 Ом, r₃ = r₄ = 60 Ом. Внутренними сопротивлениями источников пренебречь. Задачу решить методами наложения и контурных токов.

Ответ: I₁ = 0,8 А, I₂ = 0,75 А, I₃ = 2 А, I₄ = 1,55 А, I = 2,75 А.

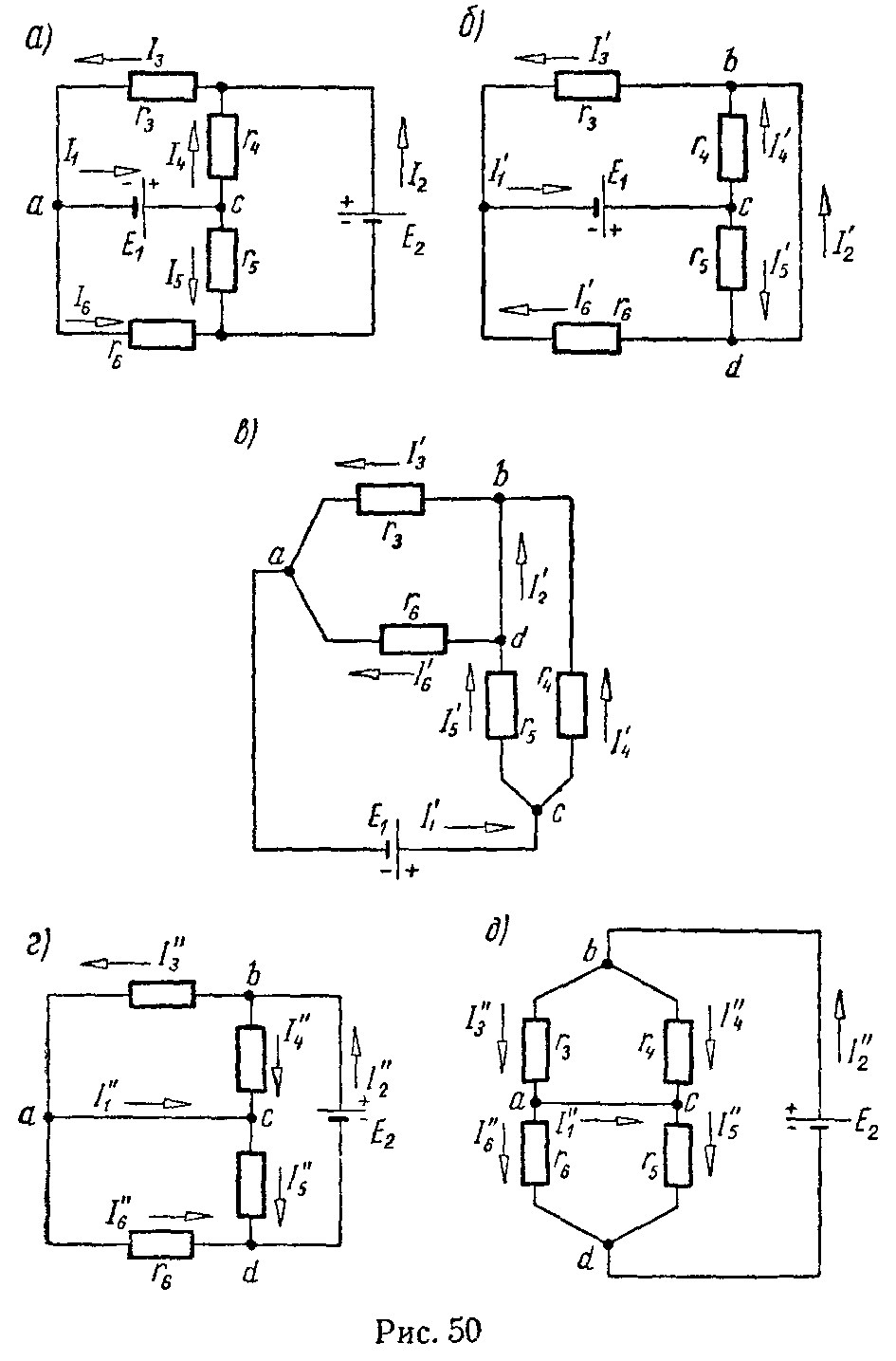
Задача 49. В схеме (рис. 50, а) методом наложения найти все токи. Внутренние сопротивления источников э.д.с. принять равными нулю. Электродвижущие силы и сопротивления элементов цепи имеют следующие значения: E₁ = 96 В, E₂ = 75 В, r₃ = 3 Ом, r₄ = 15 Ом, r₅ = 10 Ом, r₆ = 6 Ом.

Решение

Положим, что действует только э.д.с. E₁, а э.д.с. E₂ не действует. В этом случае схема примет вид, изображенный на рис. 50, б. Так как внутреннее сопротивление э.д.с. E₂ равно нулю, то на его месте между точками b и d показано короткое замыкание. Для большей наглядности схему рис. 50, б можно начертить в виде, показанном на рис. 50, в.

Полное сопротивление этой схемы равно

r 1экв = r 3 ⋅ r 6 r 3 + r 6 + r 4 ⋅ r 5 r 4 + r 5 = 3⋅6 9 + 15⋅10 25 =8 Ом.

Определим все токи

I ′ 1 = E 1 r 1экв = 96 8 =12 А, I ′ 3 = I ′ 1 ⋅ r 6 r 3 + r 6 =12⋅ 6 9 =8 А; I ′ 6 = I ′ 1 − I ′ 3 =4 А; I ′ 4 = I ′ 1 ⋅ r 5 r 4 + r 5 =12⋅ 10 25 =4,8 А; I ′ 5 = I ′ 1 − I ′ 4 =7,2 А; I ′ 2 = I ′ 3 − I ′ 4 =8−4,8=3,2 А или I ′ 2 = I ′ 5 − I ′ 6 =3,2 А .

Теперь положим, что действует только э.д.с. E₂, а э.д.с. E₁ считаем недействующей (рис. 50, г).

Схему (рис. 50, г) для большей наглядности можно представить в виде, показанном на рис. 50, д. Ее полное сонротивление

r 2экв = r 3 ⋅ r 4 r 3 + r 4 + r 5 ⋅ r 6 r 5 + r 6 = 3⋅15 18 + 6⋅10 16 =6,25 Ом.

Вычислим все токи

I ″ 2 = E 2 r 2экв = 75 6,25 =12 А, I ″ 3 = I ″ 2 ⋅ r 4 r 3 + r 4 =12⋅ 15 18 =10 А; I ″ 4 = I ″ 2 − I ″ 3 =2 А; I ″ 6 = I ″ 2 ⋅ r 5 r 5 + r 6 =12⋅ 10 16 =7,5 А; I ″ 5 = I ″ 2 − I ″ 6 =4,5 А; I ″ 1 = I ″ 3 − I ″ 6 =10−7,5=2,5 А .

Складывая алгебраически токи, полученные от действия каждой э.д.с. в отдельности (рис. 50, б и 50, г), найдем истинные токи в каждой ветви (они нанесены на рис. 50, а)

I 1 = I ′ 1 + I ″ 1 =12+2,5=14,5 А, I 2 = I ′ 2 + I ″ 2 =3,2+12=15,2 А, I 3 = I ′ 3 + I ″ 3 =8+10=18 А, I 4 = I ′ 4 − I ″ 4 =4,8−2=2,8 А, I 5 = I ′ 5 + I ″ 5 =7,2+4,5=11,7 А, I 6 = I ′ 6 − I ″ 6 =7,5−4=3,5 А.

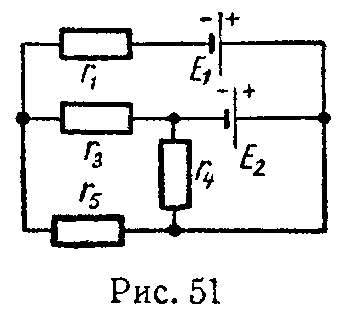
Задача 50. Для схемы (рис. 51) методами наложения, контурных токов и при помощи законов Кирхгофа найти все токи. Внутренние сопротивления источников электрической энергии считать равными нулю.

Дано: E₁ = 90 В, E₂ = 54 В, r₁ = 30 Ом, r₃ = 60 Ом, r₄ = 24 Ом, r₅ = 20 Ом.

Ответ: I₁ = 1,7 А, I₂ = 2,5 А, I₃ = 0,25 А, I₄ = 2,25 А, I₅ = 1,95 А.

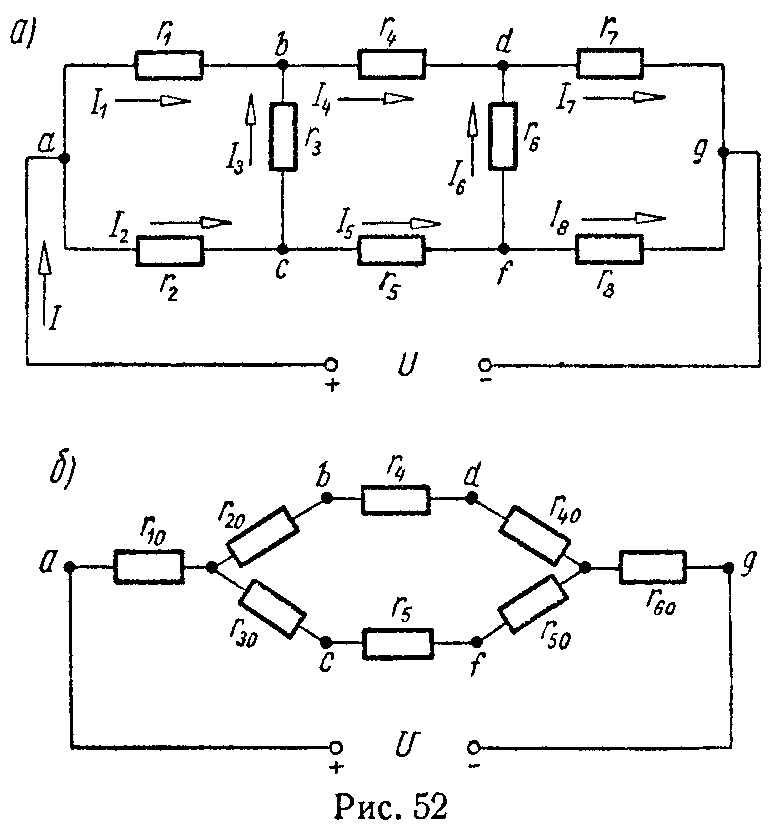
Задача 51. Найти эквивалентное сопротивление цепи (рис. 52, а) и все токи, если U = 114 В, r₁ = 30 Ом, r₂ = r₃ = 10 Ом, r₄ = 26 Ом, r₅ = 11 Ом, r₆ = 10 Ом, r₇ = 40 Ом, r₈ = 50 Ом. Задачу решить методом преобразования треугольника сопротивлений в эквивалентную звезду.

Решение

Заменим треугольники сопротивлений abc и dfg эквивалентными звездами (рис. 52, б).

Подсчитаем сопротивления лучей звезды r₁₀, r₂₀ и r₃₀, эквивалентной треугольнику abc сопротивлений r₁, r₂ и r₃ (формулы 17)

r 10 = r 1 ⋅ r 2 r 1 + r 2 + r 3 =6 Ом, r 20 = r 1 ⋅ r 3 r 1 + r 2 + r 3 =6 Ом, r 30 = r 2 ⋅ r 3 r 1 + r 2 + r 3 =2 Ом.

Сопротивления лучей звезды r₄₀, r₅₀, r₆₀ эквивалентной треугольнику dfg сопротивлений r₆, r₇, r₈, равны

r 40 = r 6 ⋅ r 7 r 6 + r 7 + r 8 =4 Ом, r 50 = r 6 ⋅ r 8 r 6 + r 7 + r 8 =5 Ом, r 60 = r 7 ⋅ r 8 r 6 + r 7 + r 8 =20 Ом.

Эквивалентное сопротивление всей схемы

r Э = r 10 + r I ⋅ r II r I + r II + r 60 =38 Ом,

где

r I = r 20 + r 4 + r 40 =36 Ом, r II = r 3 + r 5 + r 50 =18 Ом.

Ток в неразветвленной части цепи

I= U r Э = 114 38 =3 А.

Токи в параллельных ветвях I’ (r₂₀r₄r₄₀) и I» (r₃₀r₅r₅₀)

I ′ =I⋅ r II r I + r II =3⋅ 18 36+18 =1 А; I ″ =I⋅ r I r I + r II =3⋅ 36 36+18 =2 А.

Теперь найдем токи в сопротивлениях заданной цепи. Для этого предварительно из схемы (рис. 52, б) найдем напряжения между точками a и b, a и c, b и c, d и g, f и g, d и f

U ab =I⋅ r 10 + I ′ ⋅ r 20 =3⋅6+1⋅6=24 В; U ac =I⋅ r 10 + I ″ ⋅ r 30 =3⋅6+2⋅2=22 В; U ab − U ac = ( φ a − φ b )− ( φ a − φ c )= φ c − φ b = U cb =24−22=2 В; U dg = I ′ ⋅ r 40 +I⋅ r 60 =1⋅4+3⋅20=64 В; U fg = I ″ ⋅ r 50 +I⋅ r 60 =2⋅5+3⋅20=70 В; U fg − U dg = ( φ f − φ g )− ( φ d − φ g )= φ f − φ d = U fd =70−64=6 В.

искомые токи будут

I 1 = U ab r 1 = 24 30 =0,8 А, I 2 = U ac r 2 = 22 10 =2,2 А, I 3 = U cb r 3 = 2 10 =0,2 А, I 4 = I ′ =1 А, I 5 = I ″ =2 А, I 6 = U fd r 8 = 6 10 =0,6 А, I 7 = U dg r 7 = 64 40 =1,6 А, I 8 = U fg r 8 = 70 50 =1,4 А.

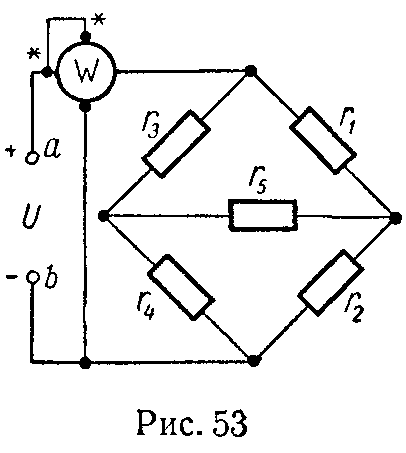
Задача 52. В схеме (рис. 53) найти токи, применив преобразование треугольника в звезду. Определить эквивалентное сопротивление между точками a и b.

Приложенное напряжение U = 30 В; сопротивления: r₁ = 60 Ом, r₂ = 120 Ом, r₃ = 180 Ом, r₄ = 80 Ом, r₅ = 120 Ом.

Определить показание ваттметра и убедиться в том, что оно равно сумме мощностей, расходуемых во всех сопротивлениях.

Ответ: I = 0,3 А, I₁ = 0,2 А, I₂ = 0,15 А, I₃ = 0,1 А, I₄ = 0,15 А, I₅ = 0,05 А, r_ab = 100 Ом, P = 9 Вт.

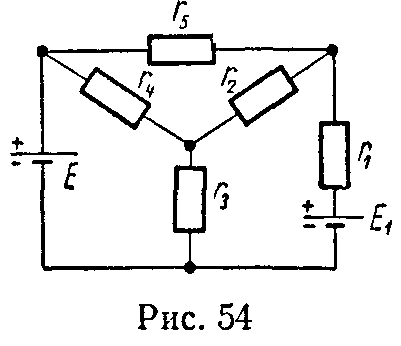
Задача 53. Вычислить токи, проходящие во всех ветвях схемы (рис. 54), если E = 213 В, E₁ = 90 В, r₁ = 6 Ом, r₂ = 40 Ом, r₃ = 10 Ом, r₄ = 100 Ом, r₅ = 60 Ом.

Задачу решить преобразованием треугольника в эквивалентную звезду. Внутренними сопротивлениями источников напряжения пренебречь.

Определить входное сопротивление относительно ветви r₁ и взаимное сопротивление ветвей r₁ и r₂.

Ответ: I = 3,8 А, I₁ = 0,5 А, I₂ = 1,5 А, I₃ = 3,3 А, I₄ = 1,8 А, I₅ = 2 А, r₁₁ = 33 Ом, r₁₂ = 60 Ом.

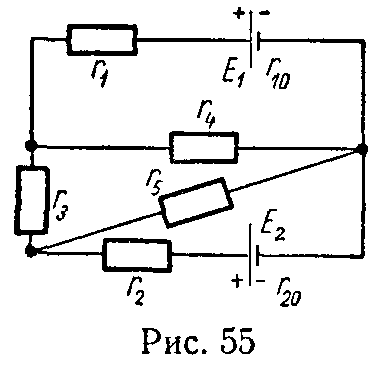
Задача 54. Определить величины токов, проходящих по цепи, схема которой показана на рис. 55.

Данные цепи: E₁ = 100 В, E₂ = 140 В, r₁ = 15 Ом, r₂ = 5 Ом, r₃ = 10 Ом, r₄ = 4 Ом, r₅ = 50 Ом, r₁₀ = r₂₀ = 0.

Задачу решить методами контурных токов и узловых потенциалов.

Ответ: I₁ = 4 А, I₂ = 8 А, I₃ = 6 А, I₄ = 10 А, I₅ = 2 А.

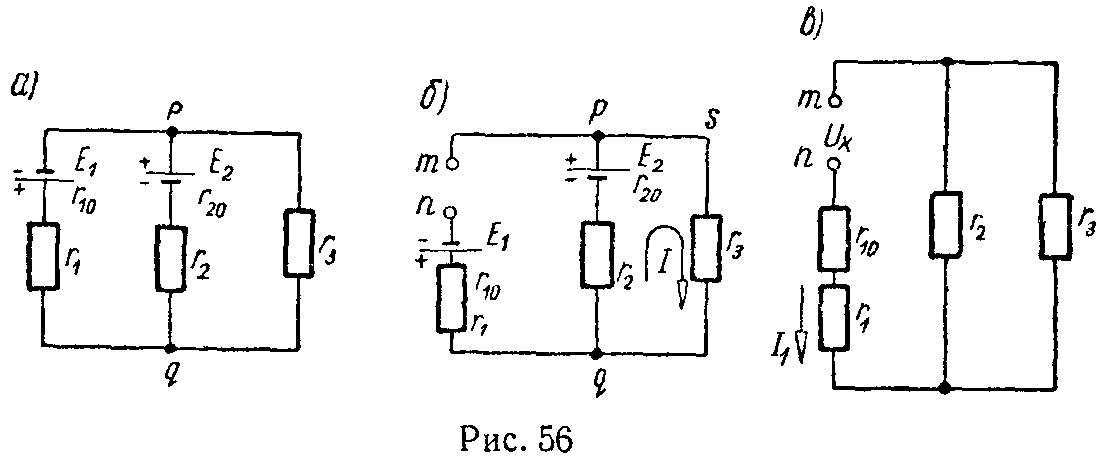
Задача 55. Для схемы (рис. 56, а) найти методом эквивалентного генератора напряжения ток в ветви с сопротивлением r₁, если E₁ = 18 В, E₂ = 21 В, r₁₀ = 1 Ом, r₁ = 2 Ом, r₂₀ = 0, r₂ = 9 Ом, r₃ = 6 Ом.

Решение

Разомкнем цепь, содержащую сопротивление r₁, и найдем напряжение между точками m и n (рис. 56, б).

Очевидно, что в разомкнутой ветви тока нет, точки m и p равнопотенциальны (φ_m = φ_p), а потенциал точки q превышает потенциал точки n на величину φ_q — φ_n = E₁.

Имея это в виду, определим U_x = U_mn

φ_m = φ_p, φ_n = φ_q — E₁,

φ_m — φ_n = φ_p — φ_q + E₁, U_mn = U_pq + E₁.

Найдем напряжение U_pq. Для этого сначала определим ток в контуре psqp

I= E 2 r 2 + r 20 + r 3 = 21 15 =1,4 А.

По закону Ома

U_pq = I·r₃ = 1,4·6 = 8,4 В.

Окончательно

U_x = U_mn = U_pq + E₁ = 8,4 + 18 = 26,4 В.

Для нахождения тока в ветви r₁ сначала определим сопротивление короткого замыкания (рис. 56, в)

r k = r 2 ⋅ r 3 r 2 + r 3 = 9⋅6 15 =3,6 Ом.

Искомый ток

I 1 = U x r 1 + r 10 + r k = 26,4 1+2+3,6 =4 А.

Этот ток течет от точки m к точке n.

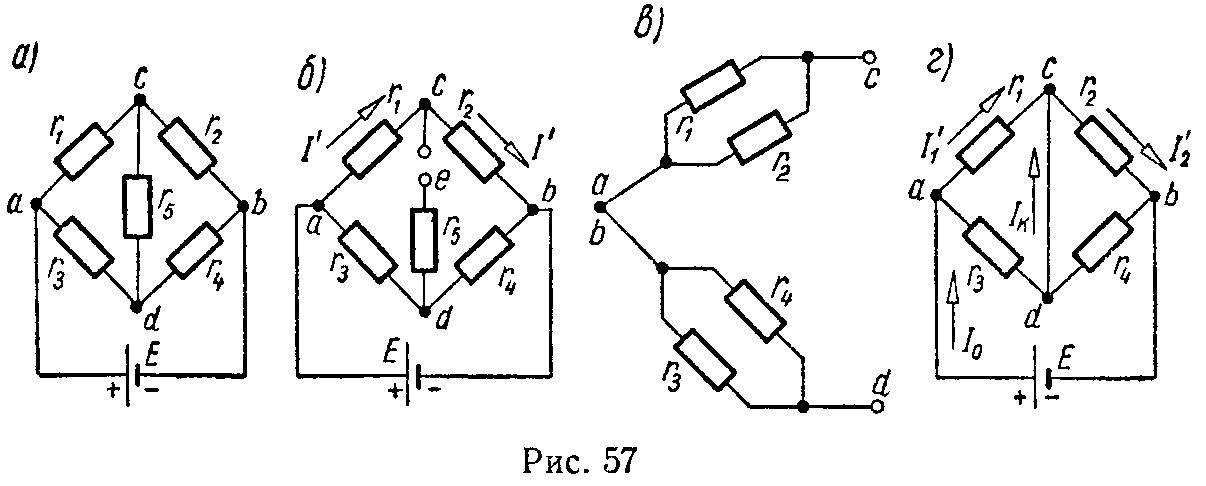
Задача 56. Методом эквивалентного генератора напряжения найти ток (рис. 57, а), проходящий через сопротивление r₅, если E = 120 В, r₁ = 60 Ом, r₂ = 15 Ом, r₃ = 90 Ом, r₄ = 60 Ом, r₅ = 12 Ом. Внутреннее сопротивление источника напряжения равно нулю.

Решение

Разомкнем сопротивление r₅ и. найдем напряжение между точками c и e (рис. 57, б).

Через сопротивления r₁ и r₂ протекает ток I’, а через r₃ и r₄ ток I»

I ′ = E r 1 + r 2 = 120 75 =1,6 А, I ″ = E r 3 + r 4 = 120 150 =0,8 А, φ a − φ c = U ac = I ′ ⋅ r 1 =1,6⋅60=96 В, φ a − φ d = U ad = I ″ ⋅ r 3 =0,8⋅90=72 В, ( φ a − φ c )− ( φ a − φ d )= φ d − φ c = U dc =24 В.

Но так как φ_d = φ_e, то U_dc = U_ec. Итак, напряжение холостого хода U_x = 24 В.

Теперь найдем сопротивление короткого замыкания. Определим его двумя способами.

1) Путем непосредственного подсчета по схеме.

В этом случае надо э.д.с. выключить, оставив ее внутреннее сопротивление, равное в данном случае нулю (рис. 57, в). Сопротивление короткого замыкания двухполюсника равно сопротивлению цепи между точками c и d

r k = r 1 ⋅ r 2 r 1 + r 2 + r 3 ⋅ r 4 r 3 + r 4 = 60⋅15 75 + 90⋅60 150 =48 Ом.

2) То же сопротивление можно найти и другим путем. Для этого надо замкнуть точки c и d накоротко, вычислить ток I_к, протекающий через короткозамкнутый участок (рис. 57, г), и сопротивление короткого замыкания определить по формуле (20).

Сопротивление схемы равно

r cx = r 1 ⋅ r 3 r 1 + r 3 + r 2 ⋅ r 4 r 2 + r 4 = 60⋅90 150 + 15⋅60 75 =48 Ом.

Найдем токи в ветвях

I 0 = E r cx = 120 48 =2,5 А, I ′ 1 = I 0 ⋅ r 3 r 1 + r 3 =2,5⋅ 90 150 =1,5 А, I ′ 2 = I 0 ⋅ r 4 r 2 + r 4 =2,5⋅ 60 75 =2 А.

Отсюда

I k = I ′ 2 − I ′ 1 =0,5 А.

Сопротивление короткого замыкания (формула 20) равно

r k = U x I k = 24 0,5 =48 Ом.

Искомый ток находим по формуле (21)

I 5 = U x r 5 + r k = 24 12+48 =0,4 А.

Задача 57. Для схемы (рис. 58) методом эквивалентного генератора напряжений найти ток в ветви с сопротивлением r₃, если E₁ = 5 В, E₂ = 7 В, r₁ = 7,5 Ом, r₂ = 2,5 Ом, r₃ = 5 Ом, r₄ = 2 Ом, r₅ = 25 Ом, r₁₀ = r₂₀ = 0.

Ответ: I₃ = 0,6 А.

Задача 58. Пользуясь методом эквивалентного генератора напряжений, найти э.д.с. и внутреннее сопротивление источников, эквивалентных каждой из схем (рис. 59 а, б, в и г; 0 < k < 1). Внутренние сопротивления источников энергий равны нулю.

Ответ: 1) U₀ = k·E, r_k = k· (1 — k)·r; 2) U₀ = k·E — E₁, r_k = r₁ + k· (1 — k)·r;

3) U 0 = k⋅E⋅r r 1 +k⋅r , r k = ( 1−k )⋅r+ k⋅r⋅ r 1 k⋅r+ r 1 ;

4) U 0 = E⋅ r 3 r 4 r 1 r 2 + r 1 r 3 + r 1 r 4 + r 2 r 3 + r 3 r 4 , r k = r 4 ⋅ ( r 1 r 2 + r 1 r 3 + r 2 r 3 ) r 1 r 2 + r 1 r 3 + r 1 r 4 + r 2 r 3 + r 3 r 4 .

Задача 59. По показаниям приборов, полученным из двух опытов, найти э.д.с. и внутреннее сопротивление источника электрической энергии, эквивалентного схеме (рис. 60), в случаях:

1)	U, B	I, A	2)	U, B	I, A	3)	U, B	I, A
	20	2		20	12		20	3
	30	3		30	14		30	5

Примечание. В части схемы, обведенной на рис. 60 четырехугольником абвг и называемой двухполюсником, в действительности может быть включено большое количество различных э.д.с. и сопротивлений так, что полный расчет занял бы слишком много времени. Поэтому решено ограничиться экспериментальным исследованием двухполюсника, результаты которого помещены в таблице данных.

Ответ: 1) сопротивление 10 Ом. 2) источник энергии с э.д.с. 40 В и внутренним сопротивлением 5 Ом. 3) источник энергии с э.д.с. 5 В и внутренним сопротивлением 5 Ом.

Задача 60. Три генератора напряжений, э.д.с. которых E₁ = 48 В, E₂ = 45 В, E₃ = 45 В, а внутренние сопротивления r₁ = 1,2 Ом, r₂ = 1 Ом, r₃ = 1,5 Ом, работают параллельно на общую нагрузку, сопротивление которой r = 4,2 Ом (рис. 61).

Произвести замену заданных генераторов напряжений одним эквивалентным, определив его э.д.с. и внутреннее сопротивление. Чему равны токи, протекающие через каждый генератор и нагрузку?

Решение

Значения э.д.с. и внутреннего сопротивления эквивалентного генератора напряжения могут быть определены по формулам (23)

E Э = E 1 ⋅ 1 r 1 + E 2 ⋅ 1 r 2 + E 3 ⋅ 1 r 3 1 r 1 + 1 r 2 + 1 r 3 = 115 2,5 =46 В, 1 r Э = 1 r 1 + 1 r 2 + 1 r 3 =2,5 1 Ом , r Э = 1 2,5 =0,4 Ом.

Ток в нагрузке

I= E Э r+ r Э = 46 4,2+0,4 =10 А.

Напряжение на нагрузке

U=I⋅r=10⋅4,2=42 В.

Таково же напряжение на каждой из параллельных ветвей. Ток в каждой из ветвей найдем по формуле (25)

I 1 = E 1 −U r 1 = 48−42 1,2 =5 А, I 2 = E 2 −U r 2 = 45−42 1 =3 А, I 3 = E 3 −U r 3 = 45−42 1,5 =2 А.

Проверка показывает, что ток в нагрузке I равен сумме трех токов: I₁, I₂ и I₃.

Задача 61. Для цепи, изображенной на рис. 62, проверить принцип взаимности, если э.д.с. E переместить в ветвь с сопротивлением r₃.

Даны: E = 80 В, r₁ = 8 Ом, r₂ = 20 Ом, r₃ = 30 Ом, r₄ = 12 Ом.

Задача 62. Определить ток, проходящий через сопротивление r = 5 Ом, подключенное к генератору тока (рис. 63), параметры которого имеют следующие величины: ток I_k = 6 мА, внутренняя проводимость g₀ = 0,04 1/Ом.

Решение

Внутреннее сопротивление генератора тока

r 0 = 1 g 0 = 1 0,04 =25 Ом.

Ток I_k распределяется по двум параллельным ветвям r и r₀ обратно пропорционально их сопротивлениям. Поэтому искомый ток

I= I k ⋅ r 0 r 0 +r =6⋅ 25 25+5 =5 мА.

Задача 63. Пользуясь теоремой об эквивалентном генераторе тока, определить ток I₃ в ветви r₃ = 12 Ом (рис. 64, а). Электродвижущие силы генераторов напряжения равны E₁ = 120 В, E₂ = 100 В, их внутренние сопротивления r₁ = 6 Ом, r₂ = 4 Ом.

Решение

Из теории известно, что ток эквивалентного генератора тока равен току короткого замыкания I_кз, проходящему между короткозамкнутыми зажимами m и n, к которым подключена данная ветвь (рис. 64, б)

I кз = E 1 r 1 + E 2 r 2 =45 А,

а внутренняя проводимость генератора тока равна проводимости пассивной цепи между зажимами m и n при разомкнутой ветви r₃ (рис. 64, в)

g 0 = 1 r 1 + 1 r 2 = 5 12 1 Ом , r 0 = 1 g 0 =2,4 Ом.

Схема эквивалентного генератора тока представлена на рис. 64 г.

Искомый ток

I 3 = I кз ⋅ r 0 r 0 + r 3 =45⋅ 2,4 2,4+12 =7,5 А.

Задача 64. Генератор тока создает в цепи ток I_k = 30 мА (рис. 65). Внутренней проводимостью генератора можно пренебречь.

Чему равны токи в ветвях, сопротивления которых равны r₁ =1,8 кОм, r₂ = 3 кОм, r₃ = 1,5 кОм, r₄ = 2 кОм.

Ответ: I₁ = 10 мА, I₂ = 4 мА, I₃ = 20 мА, I₄ = 6 мА.

Задача 65. Два генератора тока соединены в цепь, показанную на рис. 66, а. Ток первого генератора I_k₁ = 3 мА, его внутренняя проводимость g₁ = 0,05 1/Ом, второго — I_k₂ = 2 мА, g₂ = 0,01 1/Ом. Сопротивления равны: r₃ = 5 Ом, r₄ = 30 Ом.

Определить ток, проходящий через сопротивление r₄.

Решение

1-й способ. Преобразуем генераторы тока в эквивалентные генераторы напряжения, получим схему рис. 66, б. Э.д.с. и внутренние сопротивления генераторов напряжения находим по формулам (2)

E 1 = I k1 g 1 = 3 0,05 =60 мВ, r 1 = 1 g 1 = 1 0,05 =20 Ом, E 2 = I k2 g 2 = 2 0,01 =200 мВ, r 2 = 1 g 2 = 1 0,01 =100 Ом.

Далее, любым способом находим искомый ток. Обозначим

По методу узловых потенциалов находим

U ab = E 1 ⋅ 1 r 1 + r 3 + E 2 ⋅ 1 r 2 1 r 1 + r 3 + 1 r 2 + 1 r 4 = 60⋅ 1 20+5 +200⋅ 1 100 1 20+5 + 1 100 + 1 30 =52,8 мВ.

Искомый ток

I 4 = U ab r 4 = 52,8 30 =1,76 мА.

2-й способ. Решим задачу методом эквивалентного генератора тока. Для этого заменим всю цепь, за исключением ветви с r₄ эквивалентным генератором тока (рис. 66, в). Для определения его параметров I_k и g₀ сначала исключим ветвь с r₄, а точки a и b закоротим (рис. 66, г). Найдем ток короткого замыкания I_кз. Предварительно определим токи I₃ и I₄

I 3 = I k1 ⋅ 1 g 1 1 g 1 + r 3 =3⋅ 20 25 =2,4 мА, I 4 = I k2 =2 мА .

Следовательно, ток эквивалентного генератора тока

I_k = I₃ + I₄ = 2,4 + 2 = 4,4 А.

Теперь определим внутреннюю проводимость эквивалентного генератора тока g₀ между точками a и b. Для этого исключим генераторы токов и оставим лишь их внутренние сопротивления (рис. 66, д)

g 0 = g ab = 1 1 g 1 + r 3 + g 2 = 1 20+5 +0,01=0,05 См .

Ток в искомой ветви (рис. 66, в) равен

I 4 = I k ⋅ 1 g 0 1 g 0 + r 4 =4,4⋅ 20 20+30 =1,76 мА .

Задача 66. В схеме рис. 67 простейшим способом вычислить токи. Даны: E₁ = 100 В, E₂ = 80 В, E₃ = 40 В, r₁ = 10 Ом, r₂ = 10 Ом, r₃ = 20 Ом, r₄ = 30 Ом.

Внутренние сопротивления источников напряжения равны нулю.

Ответ: I₁ = 3,6 А, I₂ = 1,6 А, I₃ = 5,2 А, I₄ = 0.

В начало статьи Линейные электрические цепи постоянного тока

генератор тока,
Генератор напряжения,
закон Ома,
обобщенный закон Ома,
Законы Кирхгофа,
первый закон Кирхгофа,
второй закон Кирхгофа,
метод контурных токов,
метод узловых потенциалов,
метод наложения,
Метод эквивалентных преобразований,
метод эквивалентного генератора,
метод активного двухполюсника,
принцип взаимности,
принцип компенсации,
входная проводимость,
взаимная проводимость,
баланс мощностей

Источник

ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ

Во
всех радиотехнических устройствах
действуют физические процессы, изучаемые
в разделе «Электричество» курса физики.
Эти знания дают общие представления об
электрических устройствах и принципах
их действия, однако их недостаточно для
специалистов.

Так
как учебные дисциплины «Основы теории
цепей» и «Дополнительные разделы теории
цепей» относится к естественным наукам,
то для них применим основной метод
исследования – метод моделирования.
Суть его заключается в том, что для
изучения какого-либо физического явления
необходимо математическое представление
его свойств, которое называется моделью.
Модели
физических явлений могут обладать
различной степенью достоверности
описания исследуемых процессов. Так,
физические явления в электромагнитном
поле могут быть описаны с помощью
уравнений теории
поля, но
такое описание слишком громоздко.
Поэтому для инженерных радиотехнических
расчетов, там, где это возможно,
используется теория
электрических цепей,
основанная на понятиях тока, напряжения
и электродвижущей силы (ЭДС).

Электрическим током называется
направленное движение заряженных
частиц. Так как в металлах носителями
заряда являются свободные электроны,
то ток в металлах определяется как
направленное движение электронов. В
полупроводниках имеется два типа
зарядов: электроны, имеющие отрицательный
заряд, и дырки с положительным зарядом.
За положительное направление токапринято направление движенияположительных зарядов.

В теории цепей часто невозможно определить
истинное направление тока
в участке цепи, поэтому ввелиусловно-положительное направление
тока,которое в дальнейшем

будем
называть простоположительным
направлением(рис.1.1).

Направление тока характеризуется

Рис. 1.1 знаком. Понятие положительный
или отри-

цательный ток имеет смысл,
если только сравнивать направление
тока в проводнике с некоторым заранее
выбранным ориентиром – положительнымнаправлением тока. Поэтому, если в
результате расчета ток будет иметь знак
плюс (i>0), то это означает, что его
направление совпадает с выбранным
положительным направлением. Если же
значение тока i<0, то его истинное
направление противоположно выбранному.

Таким образом, выбранное положительное
направление тока не означает, что
электрические заряды в реальной цепи
текут в этом направлении. Оно только
придает смысл знаку тока.

Количественно
ток оценивают по величине зарядаq(t),
проходящего через какое-либо сечение
S проводника (рис. 1.2). Положим, что в
момент времени t через поперечное
сечениеS

прошел заряд q(t),
а в момент (t +t)
Рис. 1.2

соответственно q(t+t).
Тогда ток

в момент времени t будет равен

i(t)
=
=
. (1.1)

Из выражения (1.1) видно, что ток численно
равен скорости изменения заряда,
протекающего через заданное сечение
проводника S. Никоим образом ток не
равен скорости перемещения зарядов.

Вобщем случае ток является функцией
времени. Временная зависимость тока
может подчиняться различным законам.
В частном случае, когда зависимость
заряда от времени представляет собой
линейную функцию(временная диаграмма приведена на рис.
1.3) скорость изменения заряда во времени
представляет собой постоянную величину
I. Из (1.1) видно, что в таком случае

i(t) =
=
=I=const.

В этом случае ток называется

Рис. 1.3 постоянным.Во всех остальных

случаях временных
диаграмм q(t) ток

будет называться переменным.

В Международной системе единиц (СИ)
заряд выражается в кулонах (Кл), время
всекундах (с), а ток вамперах (А).

И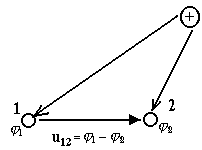з
физики известно, что на всякий заряд,
помещенный в электрическом поле,
действует сила, которая зависит от
напряженности электрического поля,
величины заряда и его знака. При движении
единичного положительного заряда из
бесконечности в точку 1 (рис. 1.4) будет
затрачена (источником электри-ческого
поля) или выделена энергия, которая
носит назва-

Рис. 1.4 ние потенциалточки 1.

Аналогично можно ввести понятие
потенциала
для точки 2.

Напряжениемu₁₂между точками 1 и 2 называется разность
потенциалов

u₁₂=
—,
(1.2)

представляющая собой
работу по переносу единичного
положительного заряда из точки 1 в точку
2, которая совершается электрическим
полем или внешней силой.

Напряжение может быть определено как
предел отношения энергии
w,
затрачиваемой на перемещение зарядаиз точки 1 в точку 2,

u₁₂=
=
.
(1.3)

Из определения напряжения следует, что
если потенциал точки 1 больше потенциала
точки 2, то напряжение u₁₂будет положительным.Напряжение будет
положительным, если оно направлено
таким образом, что при переносе
положительного заряда
увеличивается расход энергиина его перенос от точки с большим
потенциалом к точке с меньшим потенциалом.

З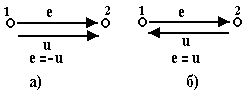а
положительное направление напряжения
принимается направление от точки с
большим потенциалом к точке с меньшим
потенциалом. При расчете электрических
цепей чаще всего не удается заранее
определить направление напряжения,
поэтому до начала расчета вводятусловно-положительное направление
напряжения.

Относительно
выбранного положительного направления
сравнивают полученный результат. Если
полученное напряжение положительно,
то истинное направление напряжения
совпадает с выбранным. Если же результат
будет отрицательным, то истинное
направление напряжения будет
противоположным.

Из
сказанного следует, что перед началом
расчета обязательнодолжны быть
указаны положительные направления
напряжений – только в этом случае
возможно иходнозначное определение.
Положительные направления напряжений
выбираются произвольно и независимо
от направлений других напряжений и
токов в цепи.

В
Международной системе единиц напряжение
имеет размерность вольт (В), а
работа (энергия) –джоуль
(Дж).

Для того чтобы образовать в цепи
электрический ток, необходимо какой-либо
вид энергии преобразовать в энергию
электрического поля от некоторого
источника. Например, энергия вращения
турбины на электростанции преобразуется
в электрическую энергию, подаваемую в
розетку потребителя, которая для него
выступает источником электроэнергии.
Такой источник характеризуется
электродвижущей силой (ЭДС), которая
может быть определена как работасторонних сил, затрачиваемая на
перемещение единичного положительного
заряда внутри источника. Так как ЭДС –
это энергия, которую затрачивают
сторонние силы на перенос зарядоввнутри
источника, а напряжение – энергия,
расходуемая источником на перенос
зарядов в нагрузке, чтобы подчеркнуть
их разную сущность, приняли за положительное
направление ЭДС направлениеот точкис меньшим потенциалом к точке с большим
потенциалом.

Если в цепи положительные направления
ЭДС и напряжения на источнике совпадают,
то принимают e(t)=
— u(t)
(рис. 1.6а), а если положительные
направления ЭДС и напряжения направлены

Рис. 1.5
навстречу друг другу

(рис.
1.6б), то e(t)
= u(t).

Электродвижущая сила (ЭДС) в Международной
системе единиц определяется в вольтах.

Из выражения (1.2) можно получить

dw = u
dq.(1.4)

Учитывая равенство (1.1), имеем

dw = u
i dt. (1.5)

Значение энергии dw называется элементарной
работой, которую совершает электрическое
поле за промежуток времени dt на перенос
элементарного заряда dq.

Как известно из физики, производная
энергии по времени называется мгновенной
мощностью

p(t)
=
. (1.6)

Из
(1.6) видно, что мгновенная мощность в
электрической цепи может быть как
положительной, так и отрицательной.
Так, при dw>0 мощность p(t) положительная,
а при dw<0 мощность p(t) – отрицательная.

Из
выражения (1.3) имеем, что

p(t)
= u i,
(1.7)

Чтобы определить энергию, поступившую
в цепь к моменту времени t, необходимо
выражение (1.6) проинтегрировать по
времени

w(t) =.
(1.8)

Нижний предел интеграла принят равным
(-
),
чтобы учесть

всю предысторию поступления электрической
энергии в цепь. Если энергия в цепи до
момента времени t = t₁была равна
нулю, то интеграл (1.8) может быть разбит
на два интеграла

w(t) =
=
,
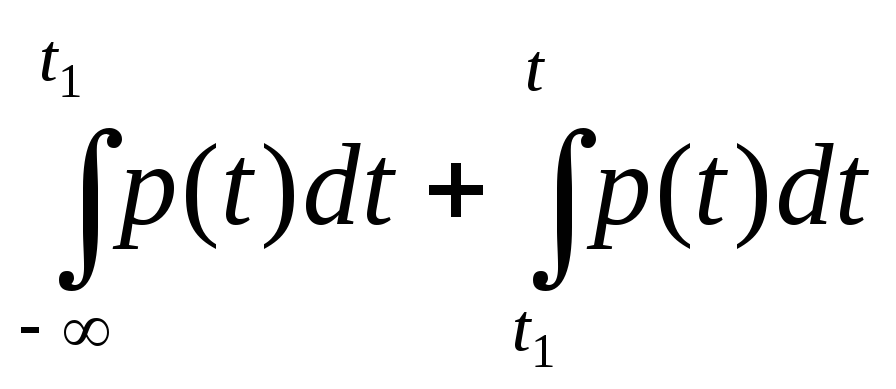
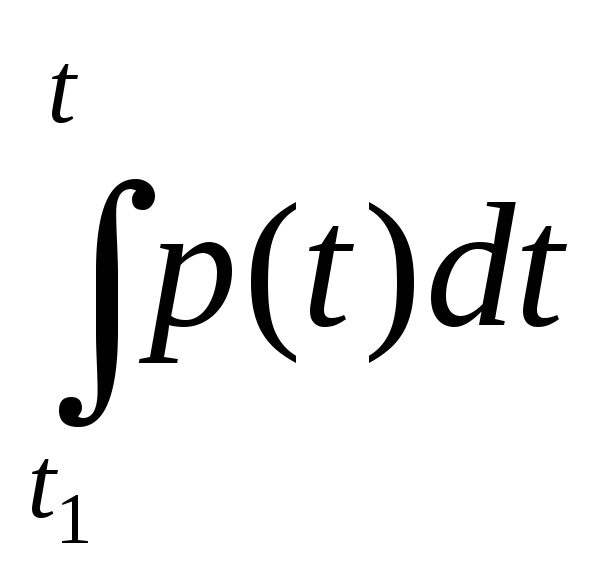
(1.9)

так как первый интеграл суммы равен
нулю.

Необходимо помнить, что значения
энергии всегда положительны.

Чтобы определить энергию, поступившую
в цепь за промежуток времени [t_1;;t₂], интегрируется
выражение (1.6) в пределах от t₁доt₂:

W[t₁;t₂] =
. (1.10)

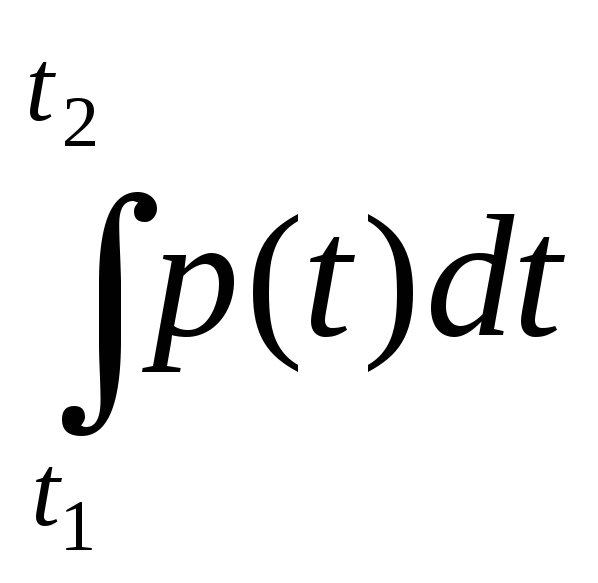
И, наконец, введем еще одну энергетическую
характеристику периодическихэлектрических процессов в цепи –среднюю
мощность Р, выделившуюся в цепи за
период колебаний
.
В математике вводится понятиесреднего
значения периодической функции

=
.

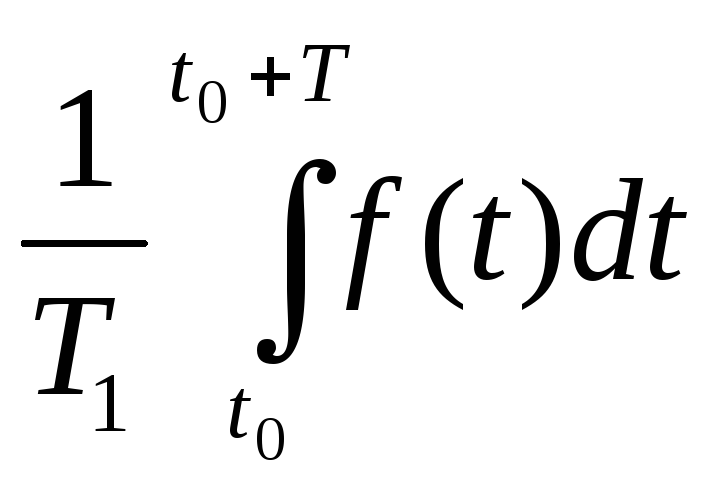
тогда по аналогии получаем

P=

.
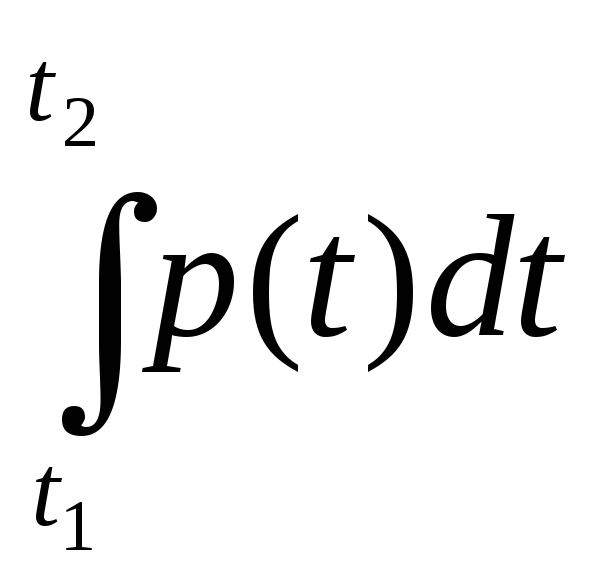
(1.11)

В системе единиц СИ мощность выражают
в ваттах (Вт).

В технике используются разнообразные
источники электрической энергии:
химические и солнечные батареи,
аккумуляторы, генераторы высокочастотных
колебаний и так далее. В теории нет
необходимости конкретизировать источники
по физическим признакам — вводятся и
наделяются определенными свойствами
некоторые абстрактные устройства —
модели источников, в той или иной мере
соответствующие действительно применяемым
на практике. Удобно пользоваться двумя
типами таких моделей в виде источников
напряжения и источников тока.

Идеальным источникомнапряженияназывается источник ЭДСe
(обозначается кружком с ориентирной
стрелкой внутри, рис. 1.6), без внутренних
потерь напряжения, независимо от
присоединяемой к нему нагрузки и
возникающего токаi. Разность
потенциалов между точкамиa,bопределяется только
ЭДС и остается неизменной при отсоединенной
нагрузке («холостой ход» источника)
и при любом ее сопротивлении, теоретически,
вплоть до нуля (режим короткого замыкания).

Рис. 1.6

У реального источника напряжения
разность потенциалов между выводами в
той или иной мере уменьшается с увеличением
зависящего от нагрузки тока i.
(Вспомните, при включении стартера в
автомашине свет меркнет). Для отражения
этого факта в модельреального источника напряжения

(рис. 1.6б)) вводят последовательное по
отношению к e(t)внутреннее сопротивление источника
R_e.
Теперь напряжение на выходе источника
(его нагрузке) оказывается равным

Тогда можно записать выражение для
зависимости тока от напряжения

.
(1.12)

которую принято называть вольтамперной
характеристикой реального источника
напряжения.

Величина R_e— фиктивная (расчетная), условно
существующая в виде некоторого
эквивалентного элемента цепи только
в модели реального источника напряжения.
Не вздумайте потрошить батарейку или
аккумулятор в поисках их внутреннего
сопротивления…

Выражение (1.12) представляет собой
уравнение прямой i=f(u)с отрицательным угловым коэффициентом.
Семейство таких прямых при различных
внутренних сопротивленияхR_eприведено на рис.1.7.

Рис.
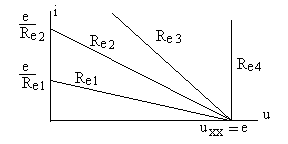
1.7

Присмотритесь к прямым (рис. 1.7), сообразуясь
с уравнением (1.12). При каком R_eвольтамперная характеристика соответствует
идеальному источнику напряжения? Какое
из неравенств справедливо:

а) R_e1<R_e2<R_e3<R_e4,

б) R_e1>R_e2>R_e3>R_e4
?

Максимальное напряжение u_xx=eимеет место прихолостом ходеисточника,
,
максимальный ток
— прикоротком замыканииего выводов.
Внутреннее сопротивление может быть
определено из очевидного равенства

(1.13)

Его можно найти экспериментально
посредством двух опытов — холостого
хода (измерение напряжения при разомкнутых
выводах источника) и короткого замыкания
(измерение тока источника при
короткозамкнутых выводах), если это
физически допустимо.

Будьте осторожны при выполнении опыта
короткого замыкания источника — его
можно производить лишь при уверенности,
что внутреннее сопротивление источника
достаточно велико и ток не превысит
допустимого для источника или амперметра
значения.

Источником токаназывается устройство,
модель которого с обозначенным током
приведена на рис. 1.8а,вольтамперная
характеристика— на рис. 1.8б,R_j– внутреннее сопротивление источника
тока.

Рис. 1.8

У идеального источника тока внутреннее
сопротивление
— из схемы его следует убрать. Идеальный
источник тока отличается тем, что
генерируемый им токне зависит от
сопротивлениянагрузкиR_H,
а следовательно, и от напряжения на
нагрузкеu, о чем
говорит горизонтальная прямая прина рис.1.8б. У реального источника
происходит перераспределение токов
черезR_iиR_нв пользу нагрузки
с уменьшением ее сопротивления.

Уравнение вольтамперной характеристики
источника тока выражается равенством

,
(1.14)

где
— внутренняя проводимость источника
тока. Уравнения (1.14) и (1.12) дуальны в том
смысле, что одно из них может быть
получено из другого путем заменыeнаiиR_eнаG_i.Соответственно этому, источники
напряжения и тока называются дуальными.

Источник тока ведет себя по отношению
к выходному току i
(через нагрузку) так, как источник
напряжения по отношению к выходному
напряжениюu.

Реальный источник тока тем ближе к
идеальному, чем больше его внутреннее
сопротивление R_i,
в отличие от источника напряжения, у
которого для этого требуется, чтобыR_eбыло возможно меньше (в пределеR_e=0).
Можно подобрать такие значения токаи ЭДСу реальных источников, чтобы при
одинаковыхR_i=R_e=R_истих действие на нагрузку (напряжение на
нагрузке и протекающий через нее ток)
было одинаковым, как показано на рис.
1.9. Условия эквивалентности таковы:

(1.15)

Рис. 1.9

Таким образом, один и тот же «живой»
(физический) источник в зависимости от
удобства анализа может быть представлен
либо в форме реального источника
напряжения, либо источника тока.

В качестве источников сигналов часто
выступают, кроме генераторов, усилители
напряжения и тока. Рассматриваются не
абсолютные значения напряжений и токов,
а их приращениеи соотношения между
ними. Электронные усилители могут быть
представлены в виде эквивалентных по
действию на нагрузку реальных источников
тока или напряжения. В силу того, что
приращения напряжений и токов в усилителях
зависят от управляющих напряжений или
токов, такого рода источники называютсяуправляемыми.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.1. ЭДС источника eв
цепи на рис.1.10а изменяется по законуe(t)=10cos10³tB.

Рис. 1.10

Укажите, потенциал какой точки: 1 или
1′, выше в моменты времени t₁=1
мс иt₂=3 мс.

Чему равно напряжение uна элементе цепиz
(рис.1.10) приe=e(t₁)=5,4
В:

а) при ориентирной стрелке для u(рис. 1.10,а)), проведенной снизу вверх (в
том же направлении, что иe);

б) при ориентирной стрелке для u
(рис. 1.10,б)), проведенной сверху вниз
(противоположноe)?

1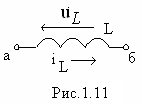.2.
Вычисленное значение напряжения на
индуктивностиL
(рис. 1.11) в некоторый момент времениtравноu_L=10
В.

Покажите посредством знаков (+) и (-),
потенциал какого конца индуктивности,
а или б, выше в этот момент времени.

В каком направлении течет ток через
индуктивность (рис. 1.11), слева направо
или справа налево, если известно, что
значение его в момент времени t равноi_L=0,1
А?

1.3. Напишите два выражения для закона
Ома (оба справедливые) для двух выбранных
направлений ориентирных стрелок uиiна рис. 1.12,а и б
соответственно.

1.4. В цепи на рис. 1.13 при положительном
напряжении между пластинами конденсатора
u, токiтечет в положительном направлении (по
стрелке). Какой знак имеет при этом
мгновенная мощностьP?
Происходит ли при этом отбор энергии
нагрузкой (конденсатором) от источника,
или наоборот?

Рис. 1.12 Рис 1.13

Разберите случай, когда при том же uмгновенная мощность отрицательна (p<0).
Какой знак имеет при этом ток? Какого
рода энергетический процесс имеет при
этом место – перекачка энергии в
нагрузку или возвращение источнику
накопленной в нагрузке энергии?

1.5. На рис. 1.14 приведены вольтамперные
характеристики двух реальных источников
напряжения 1 и 2. У какого из источников
— первого или второго — внутреннее
сопротивление меньше? Какой из них по
своим качествам ближе к идеальному?
Напишите, исходя из схемы реального
источника, выражения для вольтамперной
характеристики.

1.6. На рис. 1.15 приведены две вольтамперные
характеристики источников тока. К
какому значению внутреннего сопротивления
следует стремиться у источника тока с
целью его приближения к идеальному?
Какая из характеристик, 1 или 2, ближе к
характеристике идеального источника?

Напишите уравнение вольтамперных
характеристик источника тока. Какой
вид имеет вольтамперные характеристика
идеального источника тока? Почему
источники напряжения и тока называются
дуальными?

Рис.1.14 Рис. 1.15

1.7. Как изменятся напряжение
на нагрузкеuи ток
,
если увеличить сопротивление нагрузкиR_Hв два раза:

а) у идеального источника напряжения
(рис. 1.16,а));

б) у идеального источника тока (рис.
1.16,б))?

Рис. 1.16

ЗАДАЧИ

1.1(2 балла). Напряжение между
разомкнутыми выводамиaиb (рис.1.17а)) при
холостом ходе (отсутствии нагрузки)
при измерении его посредством вольтметраVоказалось равнымu_xx=2^G·NВ.

Рис. 1.17

Ток короткого замыкания I_кз,
измеренный (рис. 1.17б)) посредством
амперметра с нулевым собственным
сопротивлением, оказался равнымi_кз=(4N+8G)(2+(-1)^N⁺^G)
А. Постройте по указанным данным
характеристикуu=f(i)
источника. Определите:

1) ЭДС источника E(В);

2) внутреннее сопротивление источника
R_e(Ом);

3)
угол наклона характеристики к оси
абсцисс
(рад).

Вычислите величину, равную

и внесите ее для проверки в АКОС
(инструкция к вводу данных в АКОС
приведена в конце пособия).

1.2(2 балла). Постройте вольтамперную
характеристику и найдите ток короткого
замыкания реального источника напряжения
(рис. 1.17в)), для которого известно, что
при подсоединении к нему нагрузкиR_H=5G+N(2+(-1)^N⁺^G)
кОм напряжение на ней стало равнымu_H=(15GN+8)
В. ЭДС источника Е=(20GN+20) В. Значение тока
короткого замыканияI_кз(мА) внесите для проверки в АКОС.

1.3(3 балла). Рассчитайте и постройте
вольтамперную характеристику источника
тока (рис. 1.18)i=f(u_H),
для которого известно, что ток его
короткого замыкания равенI_кз=(2+0,1N)
ампер, а внутреннее сопротивлениеR_i=(0,1N*(4+(-1)^N⁺^G)+70)Oм.

Определите по характеристике ток через
нагрузку iи ее
сопротивлениеR_Hв Омах, если известно, что напряжение
на ней равноu_H=(135+G·N/2
)B. Внесите найденное
сопротивление нагрузкиR_Hв омах в АКОС.

1.4 (3 балла). Постройте вольтамперную
характеристику источника (рис. 1.19а) дляприращенийнапряжений и токовΔu(Δi)(рис. 1.19б), если известно, чтоΔU— линейная функцияΔI.
При нулевом значении приращения токаΔi=0 приращение
напряжения равно
B. При нулевом приращении
напряжения (Δu=0)
приращение тока равно
мА.

Какой вид имеет уравнение вольтамперной
характеристики Δu(Δi)в данном случае? Напишите его.

Определите по характеристике или
уравнению приращение тока Δi,
если известно, что напряжение возросло
на величинуΔu=(20+G+N)B.

Внесите величину Δiв миллиамперах для проверки в АКОС.

1.5(1 балл). Укажите, какое значение
токаIнеобходимо
установить у источника (рис. 1.20б) для
того, чтобы действие источников напряжения
(рис. 1.20а)) и тока (рис. 1.20б)) на нагрузку
было одинаковым, то есть, чтобы токи и
напряжения на одинаковых сопротивлениях
нагрузкиR_Hбыли равны:,.

Рис. 1.20

Примите при расчетах:

R_i=R_e=(G+0,2N)
Ом,R_н=7NG кОм,

E=200(G+2) + (-1)^N·GN
В.

Необходимое для эквивалентности
источников значение тока в амперах у
источника (рис. 1.20б) внесите в АКОС для
проверки.

1.6(1 балл). Определите напряжениеU_Hна нагрузке у источника тока (рис.1.18) с
внутренним сопротивлениемR_i=(2G+N)
Ом при величинеR_H=(600+N)
Ом и токе источника, равномi₀=[15+(-1)^N·G]
А.

Внесите величину U_Hв вольтах в АКОС для проверки.

ДЛЯ ПЫТЛИВЫХ

1.1. Как изменится напряжение uна нагрузкеR_H,
если:

1) последовательно с идеальным источником
тока I (рис. 1.21,а))
включить источник напряженияE;

2) параллельно источнику напряжения E(рис. 1.21,б)) включить источник токаI
?

Рис. 1.21

ОСНОВНЫЕ ФОРМУЛЫ

ЛИТЕРАТУРА

[1, с. 8 — 36].

Источник

SunRise03
5 лет назад

Светило науки — 182 ответа — 776 раз оказано помощи

Пусть абсолютная погрешность X
Истинное значение I₁ = 5,33 А
Измеренное I₂ = 5,4 А
Формула для абсолютной погрешности
X = I₂-I₁
X = 5,4 — 5,33 = 0,07 А
Для относительной
X = (I₂-I₁) / I₁
X = (5,4-5,33) / 5,33 = 0,07 А / 5,33 А = 0,0131 = 1,3%

(0 оценок)

Источник