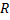Как найти иобщ в физике

Закон ома I=U/R из него U=I*R, при параллельном соединении сопротивлений 1/Rобщ=1/R1+1/R2+1/R3+1/R4, при последовательном соединении сопротивлений Rобщ=R1+R2+R3+R4, находим общее (эквивалентное) сопротивление и результат подставляем в закон ома и высчитываем ток или напряжение

если ответ лучший отметь
- Комментировать
- Жалоба
- Ссылка

Найди верный ответ на вопрос ✅ «Как находить I общую и U общую, при параллельном и последовательном соединении? (Известно R общая) …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Главная » Физика » Как находить I общую и U общую, при параллельном и последовательном соединении? (Известно R общая)

Источник

Смешанное соединение проводников. Расчёт электрических цепей

Повторение. Факты про последовательное и параллельное соединение проводников.

1. При последовательном соединении проводников общее сопротивление участка равно сумме сопротивлений проводников:

2. При последовательном соединении проводников силы тока в каждом из проводников равны и равны общей силе тока на участке цепи:

3. При последовательном соединении проводников сумма напряжений равна общему напряжению на участке цепи:

4. При параллельном соединении проводников общая проводимость участка равна сумме проводимостей проводников:

5. При параллельном соединении проводников сумма сил токов равна общей силе тока на участке цепи:

6. При параллельном соединении проводников напряжения в каждом из проводников равны и равны общему напряжению на участке цепи:

Задача 1

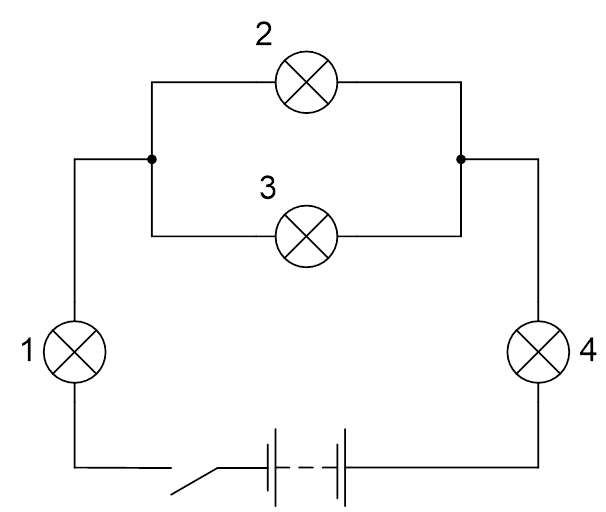
Четыре одинаковые лампы подключены к источнику постоянного напряжения (см. Рис. 1). Определите силу тока в каждой лампе, если напряжение на источнике составляет 30 В.

Дано: ;

Найти: , , ,

Решение

Рис. 1. Иллюстрация к задаче

На рисунке 1 изображена электрическая цепь со смешанным соединением проводников: лампы 2 и 3 соединены параллельно, а лампы 2 и 4 соединены последовательно с участком цепи, состоящим из ламп 2 и 3.

Проводимость участка цепи, состоящего из ламп 2 и 3, равна:

Следовательно, сопротивление этого участка равно:

Так как лампы 1 и 4 соединены последовательно с участком цепи, состоящим из ламп 2 и 3, то общее сопротивление ламп будет равно:

Согласно закону Ома, сила тока всей цепи равна:

Так как при последовательном соединении проводников силы тока в каждом из проводников равны и равны общей силе тока на участке цепи, то:

Необходимо найти силу тока на лампах 2 и 3. Для этого вычислим напряжение на участке цепи, который состоит из ламп 2 и 3:

Так как лампы 2 и 3 соединены параллельно, то напряжения на этих лампах равны:

Отсюда сила тока в каждой лампе равна:

Ответ: ;

Задача 2

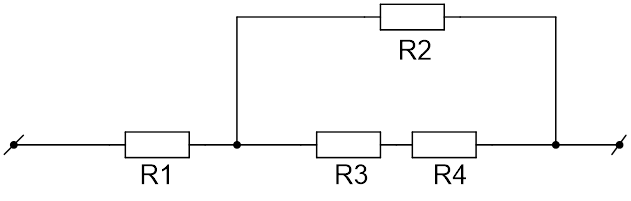
Участок цепи, который состоит из четырёх резисторов, подключён к источнику с напряжением 40 В (см. Рис. 2). Вычислите силу тока в резисторах 1 и 2, напряжение на резисторе 3. Сопротивление первого резистора равно 2,5 Ом, второго и третьего – по 10 Ом, четвёртого – 20 Ом.

Дано: ; ; ;

Найти: , ,

Решение

Рис. 2. Иллюстрация к задаче

Через резистор течёт такой же ток, как и через весь участок (), следовательно, согласно закону Ома:

То есть для нахождения нужно вычислить сопротивление (R) всего участка цепи, который состоит из двух последовательно подключённых частей, одна часть с резистором , другая часть с резисторами :

Резистор соединён параллельно резисторам и , следовательно:

Резисторы и соединены последовательно, поэтому:

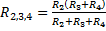
Следовательно, сопротивление всей цепи равно:

Подставим данное значение в формулу для нахождения тока в резисторе :

Так как при параллельном соединении проводников напряжения в каждом из проводников равны и равны общему напряжению на участке цепи, то:

Отсюда:

При последовательном соединении силы тока одинаковы, поэтому:

Получили систему уравнений:

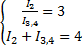
Решив эту систему получим, что:

Так как и соединены последовательно:

Напряжение на резисторе равно:

Ответ: ; ;

Задача 3

Найдите полное сопротивление цепи (см. Рис. 3), если сопротивление резисторов , , . Найдите силу тока, идущего через каждый резистор, если к цепи приложено напряжение 36 В.

Дано: ; ; ;

Найти: , , , , , , ;

Решение

Рис. 3. Иллюстрация к задаче

Резисторы , , соединены последовательно, поэтому сопротивление на этом участке равно:

Резистор подключён параллельно участку с резисторами , , , поэтому сопротивление на участке с резисторами ,, , равно:

Резисторы и соединены с участком цепи с резисторами ,, , последовательно, то есть общее сопротивление цепи равно:

Через резистор и () неразветвлённой цепи течёт весь ток цепи, поэтому:

По закону Ома этот ток равен:

Общее напряжение цепи будет состоять из напряжений , так как ,, соединены последовательно (, потому что и параллельны):

Согласно закону Ома:

Резисторы , , соединены последовательно, следовательно:

Ответ: ; ; ;

Разветвление: Задача на бесконечную электрическую цепь

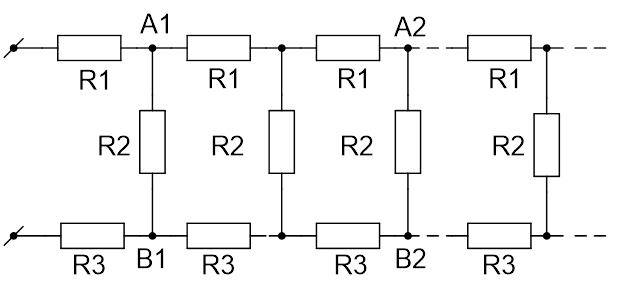
Найдите сопротивление R бесконечной цепи, показанной на рисунке 4.

Рис. 4. Иллюстрация к задаче

Решение

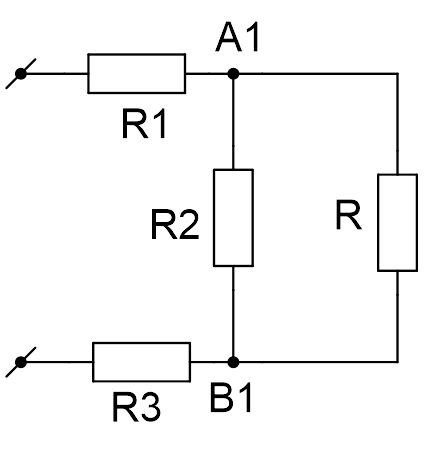
Поскольку рассматриваемая в задаче цепь бесконечна, удаление одной «ячейки», состоящей из резисторов и , не влияет на её сопротивление. Следовательно, вся цепь, находящаяся правее звена , тоже имеет сопротивление R. Это позволяет нарисовать эквивалентную схему цепи (см. Рис. 5) и записать для неё уравнение.

Рис. 5. Иллюстрация к задаче

Получили квадратное уравнение относительно R. Решая это уравнение и отбрасывая отрицательный корень (отрицательного сопротивления не существует), получаем формулу для общего сопротивления цепи:

Проанализировав данную формулу, можно заметить, что если , то общее сопротивление цепи . То есть резистор с малым сопротивление практически закоротит всю последующую бесконечную цепь.

Ответ:

Итоги

Мы рассмотрели различные задачи на смешанное сопротивление проводников, а также на расчёт электрических цепей.

Разветвление: Задача из ЕГЭ

Сопротивление каждого резистора в цепи (см. Рис. 6) равно 100 Ом. Участок подключён к источнику постоянного напряжения выводами AиB. Напряжение на резисторе равно 12 В. Найти напряжение между выводами схемы на участке A–B(варианты ответа: а) 12 В; б) 18 В; в) 24 В; г) 36 В.

Дано: ;

Найти:

Решение

Рис. 6. Иллюстрация к задаче

Резисторы расположены последовательно, значит, силы тока на этих резисторах равны:

Так как, по условию, 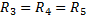, то и напряжения на этих резисторах будут равны:

Следовательно, общее напряжения на участке, состоящем из резисторов , будет равно:

Так как участок с резисторами соединён с участком с резисторами параллельно, то напряжения на этих участках равны между собой и равны общему напряжению на участке A–B:

Ответ: г) 36 В

Данную задачу, как видим, можно решить, не зная значений сопротивления, а зная только то, что они равны. Также эту задачу можно решить, зная значение сопротивлений , даже если они не равны.

Вопросы к конспектам

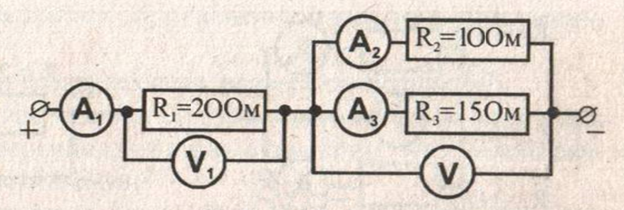
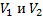
Участок электрической цепи состоит из трех сопротивлений: ; ; (см. Рис. 7). Определите показания вольтметров и амперметров , если амперметр показывает силу тока 2 А.

Рис. 7. Иллюстрация к задаче

Как нужно соединить четыре резистора, сопротивления которых 0,5 Ом, 2 ОМ, 3,5 Ом и 4 Ом, чтобы их общее сопротивление было 1 Ом?

Источник

Загрузить PDF

Элементы электрической цепи можно соединить двумя способами. Последовательное соединение подразумевает подключение элементов друг к другу, а при параллельном соединении элементы являются частью параллельных ветвей. Способ соединения резисторов определяет метод вычисления общего сопротивления цепи.

1

Определите, является ли цепь последовательной. Последовательное соединение представляет собой единую цепь без каких-либо разветвлений. Резисторы или другие элементы расположены друг за другом.
2
Сложите сопротивления отдельных элементов. Сопротивление последовательной цепи равно сумме сопротивлений всех элементов, входящих в эту цепь.^[1] Сила тока в любых частях последовательной цепи одна и та же, поэтому сопротивления просто складываются.
- Например, последовательная цепь состоит из трех резисторов с сопротивлениями 2 Ом, 5 Ом и 7 Ом. Общее сопротивление цепи: 2 + 5 + 7 = 14 Ом.
3
Вычислите сопротивление по известной силе тока и напряжению. Если сопротивление каждого элемента цепи не известно, воспользуйтесь законом Ома: V = IR, где V – напряжение, I – сила тока, R – сопротивление. Сначала найдите силу тока и общее напряжение.
- Сила тока в любых частях последовательной цепи одна и та же.^[2] Поэтому можно использовать известное значение силы тока на любом участке последовательной цепи.
- Общее напряжение равно напряжению источника тока. Оно не равно напряжению на каком-либо элементе цепи.^[3]
4
Подставьте известные значения в формулу, описывающую закон Ома. Перепишите формулу V = IR так, чтобы обособить сопротивление: R = V/I. Подставьте известные значения в эту формулу, чтобы вычислить общее сопротивление.
- Например, напряжение источника тока равно 12 В, а сила тока равна 8 А. Общее сопротивление последовательной цепи: R_O = 12 В / 8 А = 1,5 Ом.
Реклама

1
Определите, является ли цепь параллельной. Параллельная цепь на некотором участке разветвляется на несколько ветвей, которые затем снова соединяются. Ток течет по каждой ветви цепи.
- Если цепь включает элементы, расположенные до или после разветвления, или если на одной ветви два и более элементов, перейдите к третьему разделу этой статьи (такая цепь является комбинированной).
2

Вычислите общее сопротивление на основе сопротивления каждой ветви. Каждый резистор уменьшает силу тока, проходящего через одну ветвь, поэтому она оказывает небольшое влияние на общее сопротивление цепи. Формула для вычисления общего сопротивления: ${frac {1}{R_{O}}}={frac {1}{R_{1}}}+{frac {1}{R_{2}}}+{frac {1}{R_{3}}}+...{frac {1}{R_{n}}}$ , где R₁ – сопротивление первой ветви, R₂ – сопротивление второй ветви и так далее до последней ветви R_n.
3
Вычислите сопротивление по известной силе тока и напряжению. Сделайте это, если сопротивление каждого элемента цепи не известно.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи.^[4] Поэтому достаточно знать значение напряжение на любой ветви цепи. Общее напряжение также равно напряжению источника тока.
- В параллельной цепи сила тока на каждой ветви разная. Поэтому необходимо знать значение общей силы тока, чтобы найти общее сопротивление.
4
Подставьте известные значения в формулу закона Ома. Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I.
- Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: R_O = 9 В / 3 А = 3 Ом.
5
Поищите ветви с нулевым сопротивлением. Если у ветви параллельной цепи вообще нет сопротивления, то весь ток будет течь через такую ветвь. В этом случае общее сопротивление цепи равно 0 Ом.
- В реальной жизни это означает, что резистор неисправен или шунтирован (замкнут); в этом случае большая сила тока может повредить другие элементы цепи.^[5]
Реклама

1
Разбейте комбинированную цепь на последовательную и параллельную. Комбинированная цепь включает элементы, которые соединены как последовательно, так и параллельно. Посмотрите на схему цепи и подумайте, как разбить ее на участки с последовательным и параллельным соединением элементов. Обведите каждый участок, чтобы упростить задачу по вычислению общего сопротивления.
- Например, цепь включает резистор, сопротивление которого равно 1 Ом, и резистор, сопротивление которого равно 1,5 Ом. За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи.
2

Найдите сопротивление параллельной цепи. Для этого воспользуйтесь формулой для вычисления общего сопротивления параллельной цепи: ${frac {1}{R_{O}}}={frac {1}{R_{1}}}+{frac {1}{R_{2}}}+{frac {1}{R_{3}}}+...{frac {1}{R_{n}}}$ .
3
Упростите цепь. После того как вы нашли общее сопротивление параллельной цепи, ее можно заменить одним элементом, сопротивление которого равно вычисленному значению.
- В нашем примере избавьтесь от двух параллельных ветвей и замените их одним резистором с сопротивлением 1,875 Ом.
4
Сложите сопротивления резисторов, соединенных последовательно. Заменив параллельную цепь одним элементом, вы получили последовательную цепь. Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.
- После упрощения цепи она состоит из трех резисторов со следующими сопротивлениями: 1 Ом, 1,5 Ом и 1,875 Ом. Все три резистора соединены последовательно: $R_{O}=1+1,5+1,875=4,375$ Ом.
5

Воспользуйтесь законом Ома, чтобы найти неизвестные величины. Если сопротивление каждого элемента цепи не известно, попытайтесь вычислить его. Вычислить сопротивление по известной силе тока и напряжению можно по закону Ома: R = V/I.

Реклама

1
Запомните формулы, включающие мощность. Электрическая мощность – это величина, которая характеризует скорость преобразования электроэнергии и скорость ее передачи (например, к лампочке).^[6] Общая мощность цепи равна произведению общего напряжения на общую силу тока. Формула: P = VI.^[7]
- Запомните: чтобы вычислить общее сопротивления, нужно знать общую мощность. Значение мощности на одном элементе цепи для этих целей не подходит.
2
Вычислите сопротивление по известным значениям мощности и силы тока. В этом случае можно объединить две формулы, чтобы найти сопротивление.
- P = VI (мощность = напряжение х сила тока)
- Закон Ома: V = IR.
- В первую формулу вместо V подставьте произведение IR: P = (IR)I = I²R.
- Обособьте переменную R: R = P / I².
- Сила тока в любых частях последовательной цепи одна и та же. Это не так в параллельной цепи.
3
Вычислите сопротивление по известным значениям мощности и напряжения. В этом случае можно объединить две формулы, чтобы найти сопротивление. Учитывайте общее напряжение в цепи, которое равно напряжению источника тока.
- P = VI
- Перепишите закон Ома так: I = V/R
- В первой формуле замените I на V/R: P = V(V/R) = V²/R.
- Обособьте переменную R: R = V²/P.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи. Это не так в последовательной цепи, где общее напряжение не равно напряжению на одном элементе цепи.
Реклама

Советы

Мощность измеряется в ваттах (Вт).
Напряжение измеряется в вольтах (В).
Сила тока измеряется в амперах (А) или в миллиамперах (мА). 1 мА = $1*10^{{-3}}$ A = 0,001 А.
В приведенных формулах переменная Р – это мгновенная мощность, то есть мощность в определенный момент времени. Если цепь подключена к источнику переменного тока, мощность постоянно меняется. Поэтому для цепей с источником переменного тока специалисты вычисляют среднюю мощность; для этого используется формула: P_СР = VIcosθ, где cosθ – это коэффициент мощности цепи.^[8]

Об этой статье

Эту страницу просматривали 408 676 раз.

Была ли эта статья полезной?

Источник

Элементы цепи могут быть подключены двумя способами:

последовательно
параллельно

Проиллюстрируем данные подключения на примере двух конденсаторов (рис. 1).

последовательное соединение конденсаторов

Рис. 1. Последовательное соединение конденсаторов

Логическая зарядка конденсаторов происходит как показано на рис.1. Приходя из цепи, электрон останавливается на левой обкладке (пластине) конденсатора. При этом, благодаря своему электрическому полю (электризация через влияние), он выбивает другой электрон с правой обкладки, уходящий дальше в цепь (рис. 1.1). Этот образовавшийся электрон приходит на левую обкладку следующего конденсатора, соединённого последовательно. И всё повторяется снова. Таким образом, в результате «прохождения» через последовательную цепь конденсаторов «одного» электрона, мы получаем заряженную систему с одинаковыми по значению зарядами на каждом из конденсаторов (рис. 1.2).

Кроме того, напряжение на последовательно соединённой батареи конденсаторов есть сумма напряжений на каждом из элементов (аналог последовательного сопротивления проводников).

Рис. 2. Последовательное соединение конденсаторов

Часть задач школьной физики касается поиска общей электроёмкости участка цепи, логика такого поиска: найти такую электроёмкость, которым можно заменить цепь, чтобы параметры напряжения и заряда остались неизменными (рис. 2). Пусть заряд на обоих конденсаторах — $displaystyle {{C}_{1}}$ (помним, что они одинаковы), электроёмкости — $displaystyle {{C}_{2}}$ , $displaystyle {{U}_{1}}$ и соответствующие напряжения — $displaystyle {{U}_{2}}$ и $displaystyle {{U}_{2}}$ .

Учитывая определение электроёмкости:

$displaystyle C=frac{q}{U}$ (1)

Тогда:

$displaystyle {{U}_{1}}=frac{q}{{{C}_{1}}}$ (2)

где

$displaystyle {{U}_{2}}=frac{q}{{{C}_{2}}}$ (3)

где

$displaystyle {{U}_{0}}=frac{q}{{{C}_{0}}}$ (4)

где

Памятуя о том, что конденсаторы соединены последовательно, получаем:

$displaystyle {{U}_{0}}={{U}_{1}}+{{U}_{2}}$ (5)

Тогда:

$displaystyle Rightarrow frac{1}{{{C}_{0}}}=frac{1}{{{C}_{1}}}+frac{1}{{{C}_{2}}}$ $displaystyle Rightarrow frac{1}{{{C}_{0}}}=frac{1}{{{C}_{1}}}+frac{1}{{{C}_{2}}}$ (6)

Или в общем виде:

$displaystyle frac{1}{{{C}_{0}}}=sumlimits_{i}{frac{1}{{{C}_{i}}}}$ (7)

где

Для цепи из двух последовательных соединений:

$displaystyle {{C}_{0}}=frac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}+{{C}_{2}}}$ (8)

параллельное соединение конденсаторов

Рис. 3. Параллельное соединение конденсаторов

Параллельное подключение конденсаторов представлено на рисунке 3. При внесении электрона в систему, у него есть выбор: пойти на верхний или нижний конденсатор. При большом количестве электронов заполнение обкладок конденсатора происходит прямо пропорционально электроёмкости конденсаторов.

Рис. 4. Параллельное соединение конденсаторов. Поиск полной электроёмкости

Опять попробуем решить задачу по поиску полной ёмкости конденсаторов (рис. 4). Помним, что при параллельном подключении напряжения на элементах одинаковы, тогда:

$displaystyle {{q}_{1}}={{C}_{1}}U$ (9)

где

$displaystyle {{q}_{2}}={{C}_{2}}U$ (10)

где

$displaystyle {{q}_{0}}={{C}_{0}}U$ (11)

где

С учётом того, что $displaystyle {{q}_{0}}={{q}_{1}}+{{q}_{2}}$ , получим:

$displaystyle {{C}_{0}}U={{C}_{1}}U+{{C}_{2}}U$ (12)

Сокращаем:

$displaystyle {{C}_{0}}={{C}_{1}}+{{C}_{2}}$ (13)

Или в общем виде:

$displaystyle {{C}_{0}}=sumlimits_{i}{{{C}_{i}}}$ (14)

где

Вывод: в задачах, в которых присутствует цепь, необходимо рассмотреть, какое конкретно соединение рассматривается, а потом использовать соответствующую логику рассуждений:

для последовательного соединения
для параллельного соединения

Источник

Словами этот закон сохранения можно сформулировать так:

В замкнутой системе сумма импульсов тел не меняется со временем.

Формула:

[ large boxed{ vec{p_{1}} + vec{p_{2}} + vec{p_{3}} + ldots + vec{p_{n}} = const}]

Помним, что при сложении векторов учитываем их направления.

Примечания:

Импульс иногда называют количеством движения. Рекомендую освежить в памяти, какие виды импульсов есть в физике и что такое импульс.
Формулировку закона сохранения импульса можно упростить:

В замкнутой системе вектор ( vec{p_{text{общ}}}) не меняется.

Математики данный факт запишут таким способом:

[ large boxed{ vec{p_{text{общ}}} = const}]

Дополнительно читайте о том, какие системы можно считать замкнутыми, и какие виды систем в физике есть.

Пояснения к формуле закона сохранения импульса

Пусть, несколько тел двигаются в замкнутой системе.

В начальный момент времени сложим векторы ( vec{p} ) импульсов всех тел, входящих в систему.

В результате получим новый вектор, обозначим его ( vec{p_{text{общ}}} ). Этот вектор – импульс всей системы, как единого целого.

Время идет. Тела продолжают двигаться и соударяться. При ударах их импульсы будут меняться (и по направлению, и по модулю).

После каждого удара будем с помощью геометрии складывать новые импульсы тел.

При этом выяснится следующее: складывая новые импульсы тел, мы будем получать все тот же вектор ( vec{p_{text{общ}}} ), который был получен нами в начале.

Импульс сохраняется, на примере бильярдных шаров

Предположим, мы склонились над гладким бильярдным столом и смотрим на него сверху. Рассмотрим три бильярдных шара на столе (рис. 1). Массы шаров одинаковые.

( m_{1} = m_{2} = m_{3})

Рис. 1. Шар 1 движется по направлению к покоящимся шарам 2 и 3

Шары под номерами 2 и 3 покоятся. Значит, их начальные скорости и импульсы равны нулю.

Шар №2: ( vec{v_{2text{до}}} = 0), импульс ( vec{p_{2text{до}}} = 0)

Для третьего шара ( vec{v_{3text{до}}} = 0) и ( vec{p_{3text{до}}} = 0)

Еще один шар движется со скоростью ( vec{v_{1text{до}}} ) по направлению к шарам 2 и 3.

Его вектор импульса обозначен ( vec{p_{1text{до}}} ) на рисунке.

Сложим импульсы всех шаров, чтобы найти общий вектор импульса системы

[ vec{p_{1}} + vec{p_{2}} + vec{p_{3}} ]

[ vec{p_{1}} + 0 + 0 = vec{p_{1}} ]

То есть, импульс первого шара равен импульсу всех шаров системы (рис. 2) до удара

[ vec{p_{1}} = vec{p_{text{общ.до}}} ]

Рис. 2. До удара вектор импульса системы шаров равен вектору импульса первого шара

Во время удара шар 1 подействовал на шары 2 и 3 силой и передал им импульс.

После удара шар под номером 1 остановился, а шары 2 и 3 пришли в движение.

Примечание: в бильярде иногда бывает такое, шар передает свой импульс полностью шару, о который он ударяется.

Направления, в которых двигаются шары 2 и 3, указаны векторами их импульсов ( vec{p_{2text{после}}} ) и ( vec{p_{3text{после}}} ) на рисунке 3.

Рис. 3. После удара шар 1 остановился, шары 2 и 3 пришли в движение, стрелками указано направление движения шаров

Рассмотрим векторы импульсов шаров 2 и 3 подробнее. Совместим их начала и дорисуем параллелограмм (рис. 4), чтобы сложить импульсы ( vec{p_{2text{после}}} ) и ( vec{p_{3text{после}}} ).

Рис. 4. Совместим начала векторов импульса шаров 2 и 3 после удара для их сложения

В результате сложения получим вектор, обозначенный на рисунке 5 красной стрелкой и символом ( vec{p_{text{общ.после}}} )

Рис. 5. Общий вектор импульса системы получим, складывая векторы импульса шаров 2 и 3 после удара

Сравним векторы ( vec{p_{text{общ.до}}} ) и ( vec{p_{text{общ.после}}} ). Как видно из рисунка 6, у векторов совпадают длины и направления. Если у векторов совпадают обе характеристики, то векторы равны. О равенстве векторов подробно написано тут.

Рис. 6. Сравнивая вектор импульса системы до удара с вектором импульса системы послу удара обнаружим их равенство

Запишем математически равенство векторов:

[ vec{p_{text{общ.до}}} = vec{p_{text{общ.после}}} ].

Общий импульс системы до удара = общему импульсу системы после удара.

Это выражение и есть закон сохранения импульса.

Далее, советую почитать о способе решения задач, связанных с только что изученной темой. Переходите по ссылке, чтобы правильно составить формулу закона сохранения для двух случаев — абсолютно упругий и абсолютно неупругий удар (откроется в новой вкладке).

Источник

Смешанное соединение проводников. Расчёт электрических цепей

Повторение. Факты про последовательное и параллельное соединение проводников.

Задача 1

Задача 2

Задача 3

Разветвление: Задача на бесконечную электрическую цепь

Решение

Итоги

Разветвление: Задача из ЕГЭ

Вопросы к конспектам

Советы

Похожие статьи

Об этой статье

Была ли эта статья полезной?

Пояснения к формуле закона сохранения импульса

Импульс сохраняется, на примере бильярдных шаров

Не пропустите также:

Смешанное соединение проводников. Расчёт электрических цепей

Повторение. Факты про последовательное и параллельное соединение проводников.

Задача 1

Задача 2

Задача 3

Разветвление: Задача на бесконечную электрическую цепь

Ре­ше­ние

Итоги

Разветвление: Задача из ЕГЭ

Вопросы к конспектам

Советы

Похожие статьи

Об этой статье

Была ли эта статья полезной?

Пояснения к формуле закона сохранения импульса

Импульс сохраняется, на примере бильярдных шаров

Не пропустите также:

Решение