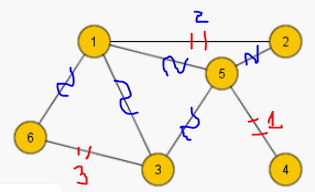
ПЗ
10. Графы (часть 2)
Инварианты
графа. Число вершин. Число ребер. Число
граней. Остовное дерево. Толщина.
Независимое множество. Клика и плотность
графа. Граф дополнения. Число доминирования.
9.1.
Инварианты графа
Два
графа называются изоморфными,
если у них одинаковое число вершин
(обозначим его n) и вершины каждого из
них можно занумеровать так числами от
1 до n, что в первом графе две вершины
соединены ребром тогда и только тогда,
когда вершины с такими же номерами во
втором графе соединены.
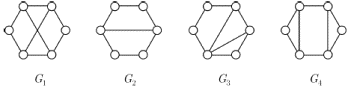
G1,
G2,
G3
– изоморфны.
Рис.
9, 10, 11 – неизоморфны.
Рис.
12 – изоморфны
Рис.
13 – неизоморфны
|
G1
|
|
|
|
|
|
Рис. |
|
|
Какие
|
Степень
вершины
– 1)
для неорграфа количество инцидентных
к вершине ребер, петля учитывается
дважды: 2) для орграфа количество выходящих
ребер, петля учитывается единожды.
Инвариантом
графа
называется некоторая характеристика
графа G,
которая принимает одно и то е значение
для любого графа, изоморфного G.
Существуют
следующие инварианты графов
-
Количество
вершин n. -
Количество
ребер r. -
Количество
граней f. -
Число
связности k. -
Толщина
графа t(G). -
Плотность
графа q(G). -
Число
независимости
-
Число
вершинного покрытия
-
Число
паросочетания
. -
Число
реберного покрытия
. -
Число
доминирования
-
Хроматическое
число
-
Реберно-хроматическое
число
-
Коцикломатическое
число
-
Цикломатическое
число
Количество
граней можно найти для плоского связного
графа.
Плоский
граф
– граф, который укладывается на плоскости
так, что никакие два его ребра не
пересекаются нигде, кроме как в инцидентной
им обоим вершине.
Граф
называется связным,
если между любыми его вершинами существует
цепь.
Грань
– область плоскости, ограниченная
ребрами, любые две точки которой могут
быть соединены линией, не пересекающей
ребра графа.
Неограниченная
часть плоскости — тоже грань, так
называемая внешняя
грань.
Любой
граф можно разбить на подграфы, каждый
из которых окажется связным. Минимальное
число таких связных компонент называется
числом связности графа.
Толщина
графа
– минимальное количество его плоских
подграфов, при наложении которых
образуется исходный граф.
—
формула для поиска толщины графа.
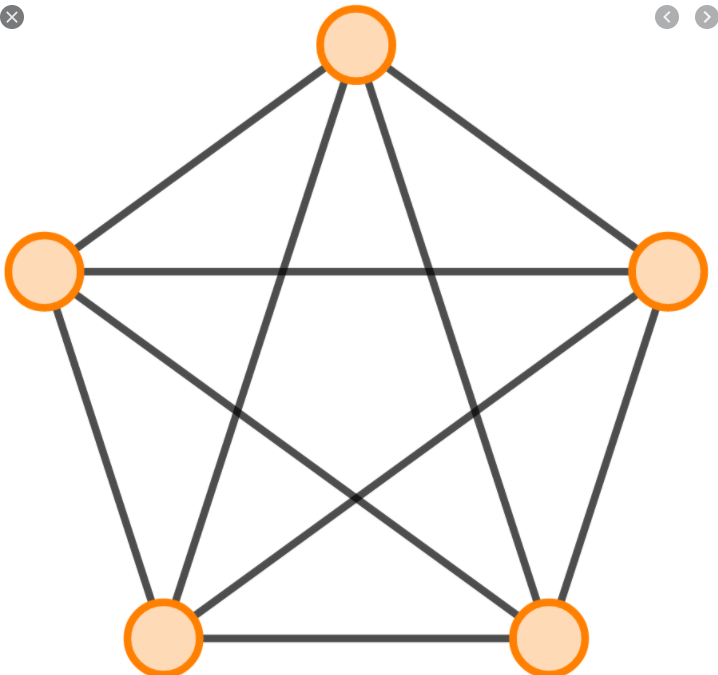
Клика
– полный подграф графа G.
Количество
вершин максимальной клики графа
называется плотностью
графа.
Независимое
множество вершин
—
множество вершин графа, никакие две
вершины которого не инцидентны.
Максимальное
независимое множество вершин
—
независимое
множество вершин,
которое не содержится ни в каком другом
независимом
множестве вершин.
Наибольшее
независимое множество вершин
— независимое
множество вершин максимальной
мощности.
Независимое
множество ребер,
или паросочетание
— множество ребер графа, никакие два
ребра которого не инцидентны.
Мощность
наибольшего независимого
множества вершин называется
числом
независимости
графа (а также неплотностью,
числом
внутренней устойчивости или
числом
вершинной упаковки
графа).
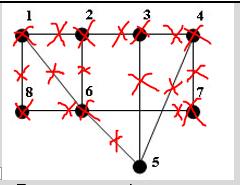
Нахождение
наибольшего
независимого множества
(алгоритм):
1.
В графе выбрать вершину с наименьшей
степенью в качестве элемента исходного
множества.
2.
Удалить выбранную вершину из графа
вместе с ее окрестностью (смежные вершины
и инцидентные им ребра).
Шаги
1—2 повторять до тех пор, пока множество
вершин не станет пустым.
Доминирующее
множество вершин
—
такое множество вершин графа, что каждая
вершина графа либо принадлежит
доминирующему
множеству вершин,
либо инцидентна некоторой вершине из
него.
Число
доминирования графа.
Мощность наименьшего доминирующего
множества называется числом
доминирования
графа.
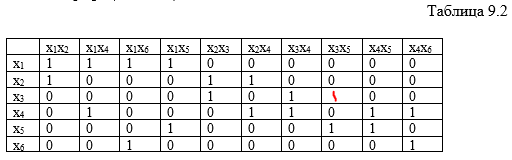
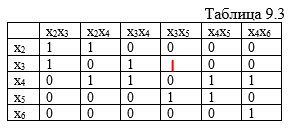
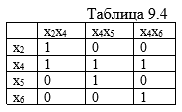
Для
решения задачи о нахождении числа
доминирования
графа применяется следующий алгоритм:
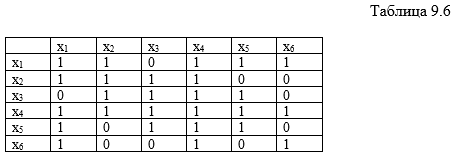
1.
Дополнить матрицу смежности единицами
по главной диагонали.
2.
Выбрать из матрицы смежности строку с
наибольшим числом единиц и ввести ее в
искомое покрытие.
3.
Вычеркнуть строку из матрицы и столбцы,
покрываемые этой строкой.
Повторять
шаги 2 и 3 до тех пор, пока в матрице
множество столбцов не окажется пустым.
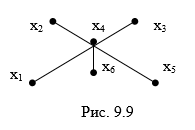
Алгоритм
поиска наибольшего паросочетания:
1.
Выбираем ребро с наименьшей степенью
(число инцидентных вершин) и включаем
в искомое паросочетание. Если таковых
несколько, выбираем то из них, для
которого степень второй граничной
вершины наименьшая.
2.
Удаляем из графа это ребро и ребра,
смежные с ним.
Шаги
1—2 повторять до тех пор, пока множество
ребер не станет пустым.
|
Задача
|
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 марта 2013;
проверки требуют 4 правки.
Инвариант графа в теории графов — некоторое обычно числовое значение или упорядоченный набор значений (хэш-функция), характеризующее структуру графа 
Содержание
- 1 Примеры инвариантов
- 2 Полный инвариант
- 3 Трудоемкость вычисления
- 4 Применение в компьютерной химии
- 5 См. также
- 6 Примечания
Примеры инвариантов[править | править вики-текст]
К инвариантам графа относятся:
- Диаметр графа
— длина кратчайшего пути (расстояние) между парой наиболее удаленных вершин.
- Инвариант Колен де Вердьера.
- Индекс Винера — величина
, где
— минимальное расстояние между вершинами
и
.
- Индекс Рандича — величина
.
- Индекс Хосойи — число паросочетаний ребер графа плюс единица.
- Мини-
и макси-код
матрицы смежности, получаемые путем выписывания двоичных значений матрицы смежности в строчку с последующим переводом полученного двоичного числа в десятичную форму. Мини-коду соответствует такой порядок следования строк и столбцов, при котором полученное значение является минимально возможным; макси-коду — соответственно максимальным.
- Минимальное число вершин, которое необходимо удалить для получения несвязного графа.
- Минимальное число ребер, которое необходимо удалить для получения несвязного графа.
- Минимальное число вершин, необходимое для покрытия ребер.
- Минимальное число ребер, необходимое для покрытия вершин.
- Неплотность графа
— число вершин максимального по включению безреберного подграфа (наибольшее количество попарно несмежных вершин). Несложно заметить, что
и
.
- Обхват графа — число ребер в составе минимального цикла.
- Определитель матрицы смежности.
- Плотность графа
— число вершин максимальной по включению клики.
- Упорядоченный по возрастанию или убыванию вектор степеней вершин
— при использовании переборных алгоритмов определения изоморфизма графов в качестве предположительно-изоморфных пар вершин выбираются вершины с совпадающими степенями, что способствует снижению трудоемкость перебора. Использование данного инварианта для k-однородных графов не приводит к снижению вычислительной сложность перебора, так как степени всех вершин подобного графа совпадают:
.
- Упорядоченный по возрастанию или убыванию вектор собственных чисел матрицы смежности графа (спектр графа). Сама по себе матрица смежности не является инвариантом, так как при смене нумерации вершин она претерпевает перестановку строк и столбцов.
- Число вершин
и число дуг/ребер
.
- Число компонент связности графа
.
- Число Хардвигера
.
- Характеристический многочлен матрицы смежности.
- Хроматическое число
.
В качестве инварианта можно рассматривать не одно из приведенных выше чисел, а их кортеж (супериндекс) вида 
суммирование ведется до последнего отличного от нуля значения 
Системы инвариантов графа, зависящие от двух и более параметров, можно записать в виде многочленов от нескольких формальных переменных 
Совпадение инвариантов является необходимым, но не достаточным условием наличия изоморфизма[1]
Полный инвариант[править | править вики-текст]
Инвариант называется полным, если совпадения инвариантов графов необходимо и достаточно для установления изоморфизма. Например, каждое из значений 


Трудоемкость вычисления[править | править вики-текст]
Инварианты различаются по трудоемкости вычисления. Инварианты 









В настоящее время полный инвариант графа, вычислимый за полиномиальное время, неизвестен, однако не доказано, что он не существует. Попытки его отыскания неоднократно предпринимались в 60-х — 80-х годах XX века, однако не увенчались успехом.
Применение в компьютерной химии[править | править вики-текст]
Многие инварианты (топологические индексы) используются в компьютерной химии для решения широкого круга общих и специальных задач[2]. К этим задачам относятся: поиск веществ с заранее заданными свойствами (поиск зависимостей типа «структура-свойство», «структура-фармакологическая активность»), первичная фильтрация структурной информации для бесповторной генерации молекулярных графов заданного типа и ряд других. Часто при этом наряду с топологическими индексами (зависящими только от структуры молекулы) используется информация и о химическом составе соединения[3].
См. также[править | править вики-текст]
- Изоморфизм графов
- Инвариант (математика)
- Топологический индекс
Примечания[править | править вики-текст]
- ↑ Зыков А. А. Основы теории графов. — М.: Наука, 1986. — 384 с. — ISBN 978-5-9502-0057-1.
- ↑ Химические приложения топологии и теории графов = Chemical Applications of Topology and Graph Theory / Под ред. Р. Кинга. — М.: Мир, 1987. — 560 с.
- ↑ М. И. Трофимов, Е. А. Смоленский, Известия Академии наук. Серия химическая, 2005, 2166—2176.
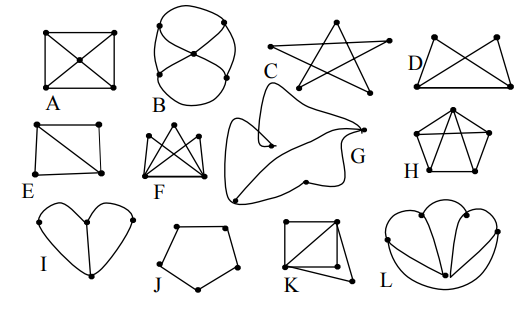
Инварианты
В общем случае узнать, изоморфны ли два графа, достаточно сложно. Если
буквально следовать определению, то нужно перебрать все биекции множества
вершин одного из них на множество вершин другого и для каждой из этих
биекций проверить, является ли она изоморфизмом. Для 
имеется 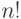
невыполнимой уже для не очень больших 
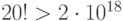
Однако во многих случаях бывает довольно легко установить, что два данных
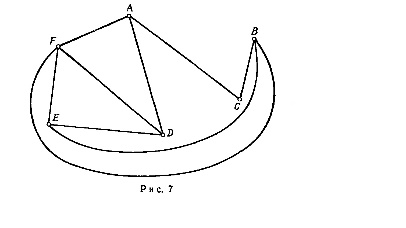
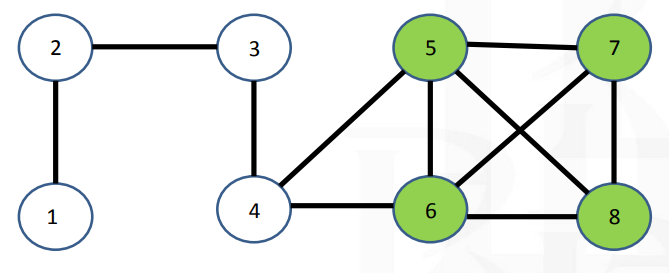
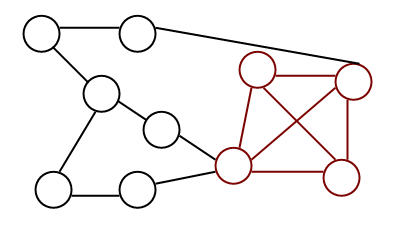
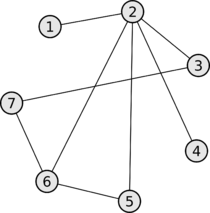
графа неизоморфны. Рассмотрим, например, графы, изображенные
на рис. 1.9.
Так как при изоморфизме пара смежных вершин переходит в пару смежных,
а пара несмежных — в пару несмежных, то ясно, что число ребер у двух
изоморфных графов должно быть одинаковым. Поэтому сразу можно сказать, что
графы 
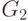
ребер,
неизоморфны. У графов 
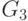
число ребер, но
они тоже неизоморфны. Это можно установить, сравнивая степени вершин.
Очевидно, при изоморфизме каждая вершина переходит в вершину той же
степени. Следовательно, изоморфные графы должны иметь одинаковые наборы
степеней, а у графов 
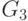
различны. С графами 
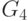
сложнее — у них и наборы степеней одинаковы. Все же и эти графы неизоморфны: можно заметить,
что в графе 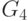

циклов нет. Ясно, что при изоморфизме каждый цикл длины 3 переходит в цикл
длины 3.
Рис.
1.9.
Характеристики графов, которые сохраняются при изоморфизме, называются инвариантами. В этом примере
мы видели некоторые простые
инварианты — число ребер, набор степеней, число циклов
заданной длины, в дальнейшем
будут введены еще некоторые другие. Если удается установить, что для двух
исследуемых графов некоторый инвариант принимает разные значения, то эти
графы неизоморфны. Для того чтобы доказать, что два графа изоморфны,
необходимо предъявить соответствующую биекцию.
Операции над графами
Для получения новых графов можно использовать разнообразные операции над
графами. Здесь мы рассмотрим два вида операций — локальные, при
которых заменяются, удаляются или добавляются отдельные элементы графа,
и алгебраические, когда
новый граф строится по определенным правилам
из нескольких имеющихся.
Локальные операции
Простейшая операция — удаление ребра. При удалении ребра сохраняются
все вершины графа и все его ребра, кроме удаляемого. Обратная
операция — добавление
ребра.
При удалении вершины
вместе с вершиной удаляются и все инцидентные
ей ребра. Граф, получаемый из графа 


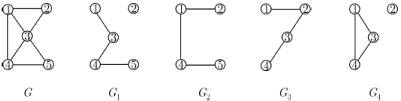
новая изолированная вершина. С помощью операций добавления вершин и ребер
можно «из ничего», то есть из графа 
любой граф.
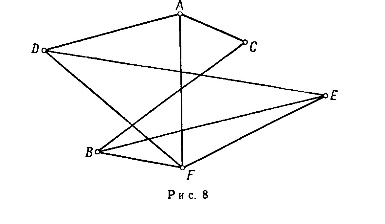
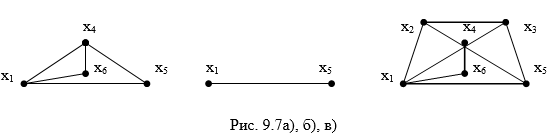
Операция стягивания
ребра 
следующим образом. Вершины 

графа, к нему добавляется новая вершина 
с каждой вершиной, с которой была смежна хотя бы одна из вершин 
Операция подразбиения
ребра 
следующим образом. Из графа удаляется это ребро, к нему добавляется новая
вершина 
и 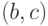
изображены исходный граф 
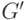
полученный из него стягиванием ребра 
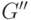
полученный подразбиением того же ребра. В обоих случаях вновь
добавленная вершина обозначена цифрой 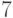
Рис.
1.10.
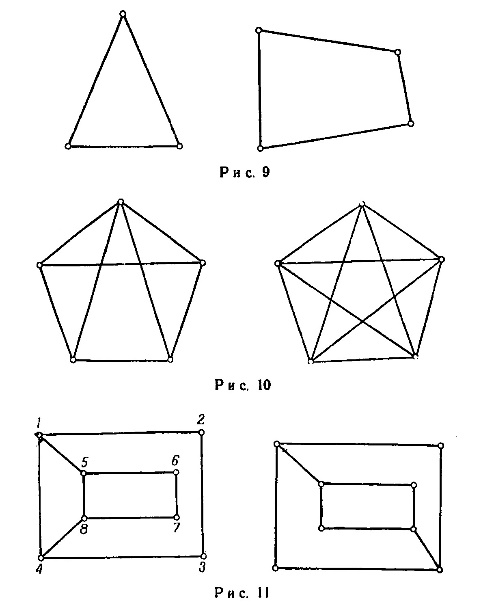
Подграфы
Граф 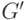

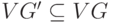
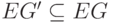
подграф может быть получен
из графа удалением некоторых вершин и ребер. На рис. 1.11
изображены граф 

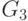
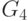
Рис.
1.11.
Подграф 


некоторых ребер, вершины же остаются в неприкосновенности. На рис. 1.11 

а 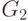
и 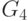
Другая важная разновидность подграфов — порожденные подграфы. Пусть
задан граф 
вершин 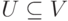
подграф 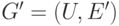
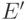
ребер графа 

Говорят,
что этот подграф порожден множеством вершин 
Он обозначается через 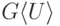
подграф может быть получен из графа удалением «лишних» вершин,
т.е. вершин, не принадлежащих 
Можно определить также подграф, порожденный множеством ребер 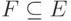
из всех вершин, инцидентных ребрам из 
На рис. 1.11 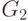

множеством
вершин 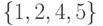
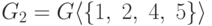
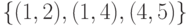
подграф 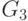
но порождается множеством
ребер 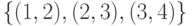
является ни остовным, ни порожденным в каком-либо смысле.
From Wikipedia, the free encyclopedia
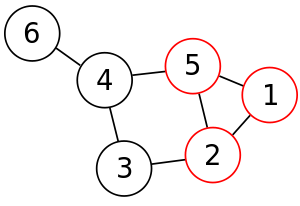
An example graph, with the properties of being planar and being connected, and with order 6, size 7, diameter 3, girth 3, vertex connectivity 1, and degree sequence <3, 3, 3, 2, 2, 1>
In graph theory, a graph property or graph invariant is a property of graphs that depends only on the abstract structure, not on graph representations such as particular labellings or drawings of the graph.[1]
Definitions[edit]
While graph drawing and graph representation are valid topics in graph theory, in order to focus only on the abstract structure of graphs, a graph property is defined to be a property preserved under all possible isomorphisms of a graph. In other words, it is a property of the graph itself, not of a specific drawing or representation of the graph.
Informally, the term «graph invariant» is used for properties expressed quantitatively, while «property» usually refers to descriptive characterizations of graphs. For example, the statement «graph does not have vertices of degree 1» is a «property» while «the number of vertices of degree 1 in a graph» is an «invariant».
More formally, a graph property is a class of graphs with the property that any two isomorphic graphs either both belong to the class, or both do not belong to it.[1] Equivalently, a graph property may be formalized using the indicator function of the class, a function from graphs to Boolean values that is true for graphs in the class and false otherwise; again, any two isomorphic graphs must have the same function value as each other. A graph invariant or graph parameter may similarly be formalized as a function from graphs to a broader class of values, such as integers, real numbers, sequences of numbers, or polynomials, that again has the same value for any two isomorphic graphs.[2]
Properties of properties[edit]
Many graph properties are well-behaved with respect to certain natural partial orders or preorders defined on graphs:
- A graph property P is hereditary if every induced subgraph of a graph with property P also has property P. For instance, being a perfect graph or being a chordal graph are hereditary properties.[1]
- A graph property is monotone if every subgraph of a graph with property P also has property P. For instance, being a bipartite graph or being a triangle-free graph is monotone. Every monotone property is hereditary, but not necessarily vice versa; for instance, subgraphs of chordal graphs are not necessarily chordal, so being a chordal graph is not monotone.[1]
- A graph property is minor-closed if every graph minor of a graph with property P also has property P. For instance, being a planar graph is minor-closed. Every minor-closed property is monotone, but not necessarily vice versa; for instance, minors of triangle-free graphs are not necessarily themselves triangle-free.[1]
These definitions may be extended from properties to numerical invariants of graphs: a graph invariant is hereditary, monotone, or minor-closed if the function formalizing the invariant forms a monotonic function from the corresponding partial order on graphs to the real numbers.
Additionally, graph invariants have been studied with respect to their behavior with regard to disjoint unions of graphs:
- A graph invariant is additive if, for all two graphs G and H, the value of the invariant on the disjoint union of G and H is the sum of the values on G and on H. For instance, the number of vertices is additive.[1]
- A graph invariant is multiplicative if, for all two graphs G and H, the value of the invariant on the disjoint union of G and H is the product of the values on G and on H. For instance, the Hosoya index (number of matchings) is multiplicative.[1]
- A graph invariant is maxing if, for all two graphs G and H, the value of the invariant on the disjoint union of G and H is the maximum of the values on G and on H. For instance, the chromatic number is maxing.[1]
In addition, graph properties can be classified according to the type of graph they describe: whether the graph is undirected or directed, whether the property applies to multigraphs, etc.[1]
Values of invariants[edit]
The target set of a function that defines a graph invariant may be one of:
- A truth-value, true or false, for the indicator function of a graph property.
- An integer, such as the number of vertices or chromatic number of a graph.
- A real number, such as the fractional chromatic number of a graph.
- A sequence of integers, such as the degree sequence of a graph.
- A polynomial, such as the Tutte polynomial of a graph.
Graph invariants and graph isomorphism[edit]
Easily computable graph invariants are instrumental for fast recognition of graph isomorphism, or rather non-isomorphism, since for any invariant at all, two graphs with different values cannot (by definition) be isomorphic. Two graphs with the same invariants may or may not be isomorphic, however.
A graph invariant I(G) is called complete if the identity of the invariants I(G) and I(H) implies the isomorphism of the graphs G and H. Finding an efficiently-computable such invariant (the problem of graph canonization) would imply an easy solution to the challenging graph isomorphism problem. However, even polynomial-valued invariants such as the chromatic polynomial are not usually complete. The claw graph and the path graph on 4 vertices both have the same chromatic polynomial, for example.
Examples[edit]
Properties[edit]
- Connected graphs
- Bipartite graphs
- Planar graphs
- Triangle-free graphs
- Perfect graphs
- Eulerian graphs
- Hamiltonian graphs
Integer invariants[edit]
- Order, the number of vertices
- Size, the number of edges
- Number of connected components
- Circuit rank, a linear combination of the numbers of edges, vertices, and components
- diameter, the longest of the shortest path lengths between pairs of vertices
- girth, the length of the shortest cycle
- Vertex connectivity, the smallest number of vertices whose removal disconnects the graph
- Edge connectivity, the smallest number of edges whose removal disconnects the graph
- Chromatic number, the smallest number of colors for the vertices in a proper coloring
- Chromatic index, the smallest number of colors for the edges in a proper edge coloring
- Choosability (or list chromatic number), the least number k such that G is k-choosable
- Independence number, the largest size of an independent set of vertices
- Clique number, the largest order of a complete subgraph
- Arboricity
- Graph genus
- Pagenumber
- Hosoya index
- Wiener index
- Colin de Verdière graph invariant
- Boxicity
Real number invariants[edit]
- Clustering coefficient
- Betweenness centrality
- Fractional chromatic number
- Algebraic connectivity
- Isoperimetric number
- Estrada index
- Strength
Sequences and polynomials[edit]
See also[edit]
- Hereditary property
- Logic of graphs, one of several formal languages used to specify graph properties
- Topological index, a closely related concept in chemical graph theory
References[edit]
- ^ a b c d e f g h i Lovász, László (2012), «4.1 Graph parameters and graph properties», Large Networks and Graph Limits, Colloquium Publications, vol. 60, American Mathematical Society, pp. 41–42, ISBN 978-1-4704-1583-9.
- ^ Nešetřil, Jaroslav; Ossona de Mendez, Patrice (2012), «3.10 Graph Parameters», Sparsity: Graphs, Structures, and Algorithms, Algorithms and Combinatorics, vol. 28, Springer, pp. 54–56, doi:10.1007/978-3-642-27875-4, ISBN 978-3-642-27874-7, MR 2920058.
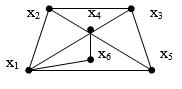
Экспресс-анализ метрических параметров графов
Время на прочтение
11 мин
Количество просмотров 3.9K
«А лохматость у меня повысилась.»
Итак, у нас на руках есть граф. Часто анализ графа сводят к его визуализации, поскольку «глаз — лучший инструмент». Не отрицая полезности вывода графа как картинки, отметим все же, что не все свойства графа можно увидеть. Некоторые надо считать.
Можно взять готовый пакет для работы с графами (например, NetworkX) и воспользоваться уже реализованными в нем функциями. Некоторые параметры графов имеют исключительно комбинаторный характер, и поэтому не подходят для графов с дробными значениями связей. Более универсальными характеристиками являются те, которые имеют метрическую основу. Далее мы приведем несколько таких параметров, способы их расчета и примеры использования.
Общие замечания
Арность
Параметр графа — это функция, которая возвращает действительное число. Данная функция может зависеть от аргументов. Количество аргументов функции называется арностью. Соответственно, параметры графа тоже характеризуются арностью (или рангом). В качестве аргументов выступают вершины графа.
Параметры 0-й арности характеризуют сам граф в целом, часто такие параметры называют инвариантами. Существуют инварианты, которые позволяют сравнивать между собой разные графы независимо от количества их вершин.
Параметры 1-й арности (1-го ранга, одинарные) характеризуют вершины графа. Наиболее известным из них является степень вершины — суммарное количество ее связей (в направленных графах входящие и исходящие степени будут разными). Другой известной характеристикой вершин является центральность, причем существуют разные центральности. Центральности можно считать разновидностью степеней вершин, адаптированных для оценки центра/периферии графа. Если у вас есть граф сотрудников вашей компании, то ключевые сотрудники скорее всего будут иметь наибольшее значение центральности.
Бинарные параметры зависят от двух вершин. Связь между вершинами — это бинарный параметр графа. На основе матрицы смежности можно сформировать пары вершин с наибольшей связью — это интересный параметр.
Ну и так далее. Можно рассчитать для графа и тернарные характеристики (3-го ранга), значение которых зависит от трех вершин.
Двойственность
Максимальная арность параметров равна количеству вершин графа. Но когда арность превышает половину от общего количества вершин вступает в силу принцип двойственности. Пусть граф имеет
вершин. Тогда дополнительной арностью для параметра
-ой арности является
-я арность. Поскольку вместо того, чтоб указывать, какие аргументы (вершины графа) используются для получения значения параметра, можно указать те, которые не используются. Это и порождает дополнительную арность.
Если параметр имеет максимальную арность (используются все вершины графа), то это эквивалентно дополнительной 0-й арности. Такой параметр характеризует весь граф целиком (а не подмножество его вершин). Если арность параметра на 1 меньше максимальной
, то дополнительная арность равна 1. Такой параметр можно рассматривать как свойство вершин. Однако надо иметь в виду, что смысл значения параметра при этом меняется на противоположный. Например, связность всех вершин графа, кроме одной, можно трактовать как несвязность данной вершины.
Параметры близости и дальности
Рассматриваем ненаправленные графы, величина связей между вершинами которых может быть произвольным действительным числом (обычно положительным). Метрические параметры графа характеризуют либо некую близость, либо дальность вершин графа. Считаем, что связи графа заданы матрицей смежности, которую обозначим как
.
Связность и остовное число
Величина близости связана со степенью связи вершин, — чем более вершины связаны, тем они ближе. Количественную оценку степени связи множества вершин назовем связностью. Данный параметр может иметь арность от 2 до
. Связность двух вершин — это величина связи между ними, задается его матрицей смежности графа. Связность 3-х вершин можно рассчитать на основе 2-связности:
Связность всех
вершин графа называется его остовным числом
. Комбинаторная интерпретация остовного числа — это количество остовных деревьев, которые можно построить на связях графа. В соответствии с матричной теоремой о деревьях остовное число можно рассчитать как определитель минора лапласиана графа. Если с какой-либо вершиной графа нет связи (это означает наличие в графе нескольких компонент), то остовное число графа (его общая связность) равно нулю.
В соответствии с принципом двойственности дополнительная арность остовного числа графа равна нулю, поэтому остовное число можно считать характеристикой всего графа.
Отсюда также следует, что связность подмножества вершин графа равна остовному числу подграфа, построенного на данном подмножестве вершин. Например, приведенная выше формула для 3-х вершин — это явное выражение остовного числа графа из 3-х вершин.
Наконец отметим также, что остовное число можно связать обратно пропорционально квадрату объема симплекса, построенного на вершинах графа. Чем больше связность — тем меньше объем:
Здесь
— мерность пространства графа из
вершин.
Резистивная метрика
Дальность (расстояние, дистанция) является обратным понятием близости, но это не просто обратная величина связности. Как уже отмечалось в предыдущей статье, между любыми вершинами существует резистивная дистанция, даже если эти вершины напрямую не связаны.
Способ расчета матрицы резистивных дистанций
Определим матричное преобразование дистанции над произвольной матрицей
как
Матрица резистивных дистанций
может быть получена несколькими способами.
1) Можно использовать псевдообращение лапласиана графа и получить матрицу Грина:
, после чего преобразование дистанции над матрицей Грина даст резистивную матрицу:
. Минус данного способа в необходимости использовании алгоритма псевдообращения (поскольку лапласиан — вырожденная матрица).
2) Можно использовать обращение минора лапласиана и получить фундаментальную матрицу:
. Преобразование дистанции над мажором фундаментальной матрицы также даст резистивную матрицу:
. Мажор здесь означает добавление элемента (который удалили для получения минора лапласиана) в базисное множество фундаментальной матрицы. Плюс данного способа — в использовании обычного матричного обращения.
Резистивная метрика может иметь различную арность — от двух до максимальной. Резистивная дистанция (эффективное сопротивление) является бинарным параметром, поскольку для определения значения резистивной дистанции надо задать две вершины. Значение резистивной дистанции эквивалентно квадрату линейного расстояния (квадрансу). Но помимо геометрической резистивная дистанция имеет также комбинаторную трактовку. Ее значение в простых графах отражает относительное изменение остовного числа графа
при добавлении (или удалении) связи между данными вершинами:
Значение числителя
равно детерминанту минора лапласиана, из которого удалены вершины
(двойственность — удаляем две вершины из множества, а не извлекаем).
Резистивной метрике 3-ей арности (тристанция?) соответствует квадрат двойной площади треугольника:
. Для ее получения можно детерминант минора лапласиана, из которого удалены три вершины, разделить на остовное число графа. Также как и для 3-связности существует выражение 3-дальности через резистивные дистанции. Приведем для справки:
Параметры описанной сферы
Поскольку граф можно трактовать как базис пространства, то геометрические характеристики данного пространства можно использовать для определения параметров графа. Известно, что вокруг невырожденного симплекса произвольного порядка всегда можно описать сферу. Такая сфера характеризуется: 1) положением центра и 2) радиусом. Положение центра задается барицентрическими координатами
относительно вершин симплекса, квадрат радиуса
— числом.
Параметры сферы имеют помимо геометрической комбинаторную интерпретацию. Более подробно рассмотрены здесь.
Остовная степень и центральность
Обратимся к одинарным (унарным) параметрам, — то есть к характеристикам вершин.
Как уже отмечалось, любой граф можно разложить на сумму деревьев (остовов). В каждом таком дереве вершина исходного графа может иметь различную степень. Тогда можно сложить степени вершин по всем деревьям графа и получить среднюю остовную степень вершин, обозначим ее как
(обычные степени вершин графа принято обозначать через
, degree). Оказывается, что координаты центра описанной сферы
и средняя остовная степень связаны между собой соотношением:
Данное выражение связывает геометрию с комбинаторикой. Видим, что координаты центра описанной сферы можно получить, просто считая степени вершин деревьев, на которые можно разложить граф.
С точки зрения прикладного анализа удобнее оперировать с центральностями вершин. Значения центральности можно трактовать как близость (или дальность) положения вершины относительно некоего центра графа. Центральность самых удаленных вершин должна быть нулевой. Из этого требования, а также из свойства барицентрических координат
вытекает следующее определение центральности (для того, чтобы отличать ее от других, назовем ее остовной);
Достоинство остовной центральности в том, что ее можно рассчитать на основе стандартных матричных операций. Приведем для справки соответствующие формулы:
Здесь
— матрица смежности графа,
— матрица резистивных дистанций (сопротивлений),
— обозначает адамарово (поточечное) произведение матриц.
На основе остовной центральности можно выделить центральные вершины графа и его периферию. Если значение центральности вершины больше 1, то она относится к центру. Если меньше — к периферии.
К сожалению в пакете networkX расчет остовной центральности не реализован, но зато в нем есть несколько других центральностей, которые тоже можно использовать.
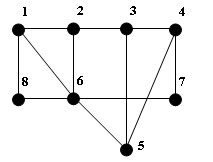
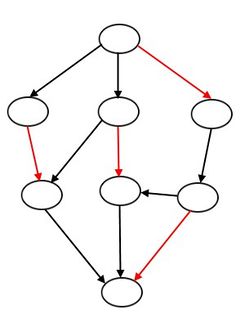
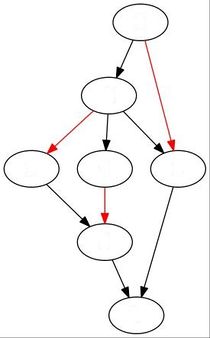
На рисунке показаны для сравнения две центральности для графа из Википедии. Слева a) — остовная центральность вершин, справа b) — betweenness centrality. Значения приведены к целым числам.
Целые значения остовной центральности интерпретируются просто — это разность (превышение) между суммой степеней вершины по всем остовам графа и общим количеством остовов. Рассмотрим, например, фиолетовую вершину. Поскольку она конечная, то ее степень во всех остовах равна 1. Поэтому общая сумма ее степеней совпадает с количеством остовов, в итоге получаем для нее нулевую центральность.
Немного странно, что алгоритм betweenness centrality дает также нулевое значение для красной вершины. Визуально очевидно, что положения красной и фиолетовой вершин совсем не равноправны.
Норма, связность и плотность графа
Размер описанной сферы характеризует граф в целом. Поскольку по определению все вершины графа принадлежат сфере, то ее диаметр задает максимально возможное значение резистивных дистанций (а, значит, и эффективных сопротивлений) между вершинами графа. Величину квадрата радиуса сферы назовем резистивной нормой графа
.
В отличие от остовного числа, которое имеет мультипликативный характер, норма графов аддитивна. Это проявляется, например, в операции сочленения графов (соединение в вершине). Норма результирующего графа равна сумме исходных графов, а остовное число — произведению.
Поскольку норма любого графа независимо от его порядка всегда является «квадратом расстояния», то нормы можно использовать чтобы сравнивать между собой графы разного порядка.
Однако в качестве топологической характеристики значение резистивной нормы графа не подходит. При увеличении величины связей в k раз его резистивная норма уменьшается во столько же раз, хотя очевидно, что топология (структура связей) при этом не изменилась.
Конструируем параметры плотности и разреженности графа
Для того, чтобы на основании нормы определить топологическую характеристику, необходимо умножить ее на величину какой-либо связности графа. В качестве такой связности подойдет средняя степень его вершин
.
Умножая резистивную норму на связность графа получаем некий безразмерный параметр, который назовем индексом разреженности
:
Величину, обратную данному индексу, назовем индексом компактности (плотности):
Но это еще не все. Хорошо бы привязать введенные нами индексы к какому-то стандарту, например, к полному графу. Тогда мы бы могли сказать, насколько отличается плотность (или разреженность) от полного графа. Для этого введем понятие несмещенных оценок. Несмещенная оценка получается умножением инварианта на фактор
(подобный трюк есть в статистике при определении дисперсии). Несмещенные оценки пометим звездочкой:
Тогда несмещенная оценка разреженности получается из обычной умножением на квадрат фактора — следствие определения (6):
Наконец-то мы добрались до финального выражения.
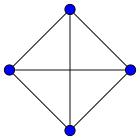
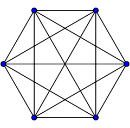
В полном графе
несмещенные индексы разреженности и компактности равны 1 — это предельные значения данных параметров. Из этого следует, что плотность (компактность) всех остальных графов будет меньше, чем плотность полного графа, а разреженность соответственно больше.
Например, несмещенная оценка плотности приведенного выше графа из Википедии равна 0.495. Данный граф примерно в два раза менее плотен, чем полный граф.
Спектральный и кластерный анализ
Особняком стоит анализ графов на основе спектров его матриц. В качестве матрицы обычно используется либо матрица смежности, либо лапласиан. Среди прочего спектр лапласиана используют для поиска кластеров вершин в графе, то есть выделения обособленных (слабо связанных) групп — этому посвящено большое количество работ.
Здесь нет возможности сильно вдаваться в подробности (да тут и не подходящее место для этого). Но считаем нужным отметить следующее для тех, кто будет использовать спектральный анализ для своих графов.
Обычно для поиска кластеров берут слой спектра лапласиана графа с наименьшим весом (наименьшим собственным значением) и формируют кластеры на основе близости значений соответствующего собственного вектора (вектор Фидлера). Но на практике (для графов с различными по величине связями) значение минимального собственного числа будет плохо обусловленным, — зависит от погрешностей данных. Да и вообще большинство слоев спектра обычно «плохо звенит», — направление таких слоев сформировано относительно небольшим числом вершин графа (это те, компоненты которых отличны от нуля в данном слое).
Поэтому для кластеризации надо сначала определить подходящие слои спектра. Такими слоями являются слои с наибольшей поляризацией вершин. Компоненты собственных векторов таких слоев должны быть заметно отличны от нуля (по абсолютному значению). Сами вершины делятся на кластеры по знаку компоненты. Соответственно для одного слоя получим два возможных кластера вершин. Если слоев два, то можно найти 4 кластера и т.д. При этом следует учитывать величину собственного числа слоя — оно определяет его мощность.
Сервис для анализа связности букв на основе корпуса слов
Чтобы разбавить унылую теорию веселой практикой, мы опубликовали сервис, который выполняет экспресс-анализ связности букв русского языка на основе заданного текста. Буквы связаны между собой неявным образом посредством слов, которые они образуют. На основании текстового файла сервис строит граф связности букв и выводить некоторые параметры из тех, которые описаны выше.
Используя данный сервис, можно выяснить, как меняются связи букв со временем. Мы сравнили графы букв, полученные по двум сказкам Пушкина «Сказка о мертвой царевне…» и «Сказка о царе Салтане», и более современное произведение Леонида Филатова «Сказ про Федота-стрельца».
Полученные центральности букв близки к общей частотности букв русского языка. Но заметны некоторые исторические особенности. Например, видно, что буква «ф» во времена Пушкина только народилась, — в «Сказке о мертвой царевне…» она вообще не встречается, а в «Сказке о царе Салтане» — только в единственном слове «флот».
Интересно, что значения центральностей букв связаны с их делением на кластеры (группы). Кластерный анализ текстов сказок (на основе спектра лапласиана графа букв) показал, что группы букв просто разбивают множество букв по степени их центральности. При этом существуют три основные группы (слоя) (показаны слои «по Филатову»):
Основная: [о, е, а, т, н, р, и, с, л, д*]
Промежуточная: [у, ь, к, в*, м, п, б, я]
Редкая: [ы, з, г, й, ч, ш, х, ж, ю, ц, ф, щ, э, ъ]
Внутри группы буквы отсортированы по степени убывания остовной центральности. Буквы основной группы можно отнести к центру (их центральности > 1), а промежуточной и редкой (центральность < 0.5) — к периферии.
Буквы «д» и «в» — беглые. За прошедшее время они поменялись местами. Роль буквы «д» повысилась, она перешла из промежуточного слоя в основной. А значимость «в» наоборот — понизилась. У Пушкина она была в основной группе, у Филатова — в промежуточной.
Наиболее связанные пары букв тоже известны. Вот первая десятка пар по степени убывания связи:
[е, н], [о, т], [е, т], [а, н], [а, к], [о, н], [а, р], [о, р], [а, л], [о, д]
Напомним, что граф ненаправленный, поэтому положение буквы внутри пары не имеет значения: [е, н] = [н, е]. Связность пары [о, д] в два раза меньше связности [е, н].
Отметим, что одна буква в парах данного списка всегда гласная, а другая согласная. Первая пара с двумя гласными находится на 11-м месте — это пара [е, о], а первая пара с двумя согласными — на 25-м: [с, т]. Отсюда ясно, что триплеты (три буквы) максимальной связности (см. формулу (1)) будут включать в себя буквы «е» и «о». Вот первые триплеты максимальной связности:
[ето], [оне], [неа], [ато], [нет], [рот], [сто], [она], [тон], [ора], [ока], [вот], [сет],…
От связности 3-й арности перейдем к 0-й и рассмотрим значение плотности/разреженности графа букв. Напомним, что минимальную разреженность (максимальную плотность) имеет полный граф. Все остальные графы намного более разрежены. Анализ показывает, что в современной сказке о Федоте разреженность равна примерно 39, в сказке о Салтане — 112, а в сказке о мертвой царевне — 222. Скорее всего более высокая плотность букв в сказке о Федоте объясняется ее большим объемом, то есть там просто больше разных слов и соответственно больше связей между разными буквами, которых нет у Пушкина.
Конечно, этот экспресс-анализ не претендует на широкие обобщения, поскольку выполнен на базе всего лишь трех текстов. Если взять более широкий корпус, то выводы могут быть другими.
Связность букв — лишь пример возможного анализа графа. Вы можете провести подобный анализ для своей компании на основании собственных данных.
Благодарю Сергея Аверкиева (averkij) за помощь в подготовке и публикации сервиса.


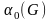
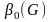
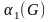
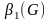
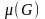
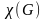
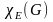
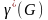
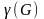




 — длина кратчайшего пути (расстояние) между парой наиболее удаленных вершин.
— длина кратчайшего пути (расстояние) между парой наиболее удаленных вершин. , где
, где  — минимальное расстояние между вершинами
— минимальное расстояние между вершинами  и
и  .
. .
. и
и  .
. — при использовании переборных алгоритмов определения изоморфизма графов в качестве предположительно-изоморфных пар вершин выбираются вершины с совпадающими степенями, что способствует снижению трудоемкость перебора. Использование данного инварианта для k-однородных графов не приводит к снижению вычислительной сложность перебора, так как степени всех вершин подобного графа совпадают:
— при использовании переборных алгоритмов определения изоморфизма графов в качестве предположительно-изоморфных пар вершин выбираются вершины с совпадающими степенями, что способствует снижению трудоемкость перебора. Использование данного инварианта для k-однородных графов не приводит к снижению вычислительной сложность перебора, так как степени всех вершин подобного графа совпадают:  .
. и число дуг/ребер
и число дуг/ребер  .
.