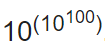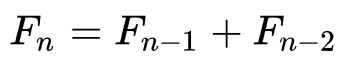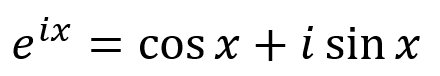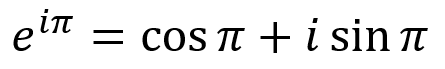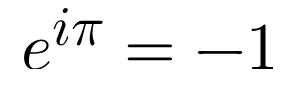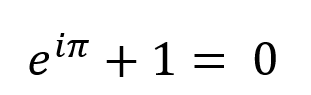О числах и математических терминах, которые будут интересны не только математикам.

Нередко числа находятся с помощью красивых уравнений и формул. А еще они могут обладать математической красотой. Это значит, что их свойства ведут к непредсказуемому результату — привлекательному как визуально, так и интеллектуально.
Ниже мы обсудим 13 удивительных чисел и понятий, от бесконечности до золотого сечения, которые доказывают, что математика — тоже своего рода искусство.
13. Алеф-ноль ℵ0
Алеф-ноль — это наименьшее бесконечное кардинальное число. Возможно, вы подумаете: как же так? Ведь бесконечность — это всего лишь понятие, а не множество бесконечных чисел. В конце концов, если и существует бесконечность, которая больше другой бесконечности, то первая — уже определенно не бесконечность.
Сейчас разберемся. Предположим, у нас есть базовое представление о том, что такое бесконечность (см. пункт 12). Алеф-ноль — это множество натуральных чисел (0, 1, 2, 3 и т. д.). Это понятие (или число) велико по размеру и, в общем-то, бесконечно.
Что, если мы пересчитаем все натуральные числа два или три раза? После завершения первого множества мы получим числа, выходящие за рамки натуральных чисел по порядку. Итак, нам понадобится порядок чисел или порядковый номер. Следующее число после Алеф-ноль — это омега (ω). Затем идет ω + 1. Эти два последних числа — не кардинальные числа, а порядковые (ординалы): то есть они показывают положение элементов относительно горизонтальной оси. График ниже — их упрощенное представление.
Каждое множество чисел может представлять набор множеств натуральных чисел с мощностью ℵ0. Если добавить к первому множеству единицу — это не изменит количество элементов (вы даже можете просто изменить порядок, и у вас все равно останется мощность Алеф-ноль).
Wikipedia
Это позволяет рассматривать их как порядковые величины (ординалы). Следовательно, первое порядковое трансфинитное число после набора — это то, что мы обсуждали выше — омега «ω». Интересно и то, что число ω + 1 необязательно больше ω — оно просто идет после него.
Да, возможно, это слишком для мгновенного понимания. Это то, о чем следует размышлять и к чему следует возвращаться. Поэтому ниже мы расписали все, что вам нужно знать:
- Бесконечность и Алеф-ноль — две разные вещи. Первое — это просто идея крайнего предела, лежащая на числовой оси, а второе — размер множества (его мощность).
- Кардинальное число — это мощность множества, его размер с точки зрения количества элементов (1, 2, 459, 1002 и т. п.). В то время как ординал или порядковое число — это порядковый тип множества (1-й, 2-й, 66-й и т. д.).
- Подобно бесконечным кардиналам, существуют и бесконечные ординалы. И первое бесконечное (несчетное) порядковое число — это омега ω. Его мы обсуждали чуть выше.
- Следуя этой логике, Алеф-один является мощностью омеги ω.
А Алеф-ноль — всего лишь первый кардинал из огромного множества других «Алефов».
12. Бесконечность ∞
Это скорее идея или концепция, чем число. Этот символ часто называют лемнискатой. Прежде чем обсуждать характеристики и интересные факты о бесконечности, важно отметить, что число π (см. пункт 4) считается одной из ее форм. Конечно, под этим мы подразумеваем диапазон чисел после запятой в 3,14159… Вот почему бесконечность — это понятие, а не то, что можно выразить количественно. Другой пример: прекрасное поле фракталов. Возьмем, к примеру, простую снежинку Коха, которую можно разделить на бесконечно малые «хлопья» одинаковой формы.
tenor.com
Интересно и то, что, когда мы думаем о бесконечности, мы представляем постоянно растущую меру, но она не расширяется и не становится больше. Она такая, какая есть.
Обсудим две простые темы, связанные с бесконечностью (те, которые не требуют мощной мозговой активности):
Верно ли, что 0,99999 = 1?
Учитывая, что после запятой у нас есть девятки, которые стремятся к бесконечности, мы можем предположить, что 0,99999 приблизительно равно 1. Но существует и алгебраическое доказательство:
Если x = 0,9999, то
10x = 9,9999
Если вычесть x с каждой стороны, то получим:
9x = 9,9999 — 0,9999
9x = 9
Разделим обе стороны на 9 и получим, что:
x = 1
Немного странно, вы не находите?
А то, что ∞ — ∞ = 0?
Любое число, вычтенное из самого себя, даст ноль. Но ведь бесконечность — это не число. Значит, попробуем провести «тест»:
∞ — ∞ = 0
Добавим по 1 с каждой стороны:
∞ — ∞ + 1 = 0 + 1
Зная, что ∞ + 1 = ∞, упростим уравнение:
∞ — ∞ = 1
Мы получили совершенно другой результат. С помощью этого метода мы можем получить бесконечность минус бесконечность, равную любому числу, которое мы хотим. Таким образом, мы не знаем ответ на ∞ — ∞ — он не определен.
В школе нас также учат, что мы не можем делить на 0. Нам говорят, что 1 : 0 не имеет смысла. Что ж, это утверждение нельзя назвать неверным, но в то же время оно не отражает всей истины. Просто подумайте: если вы разделите 1 яблоко на 0 человек, сколько людей вам понадобится, чтобы съесть фрукт? Это форма бесконечности, которая никогда не разрушается.
Итак, получается 1 : 0 = ∞. Тогда почему нас учат, что результат не определен и не имеет смысла?
Когда мы делим 1 на положительные числа, стремящиеся к нулю, легко установить, что 1 : 0 = ∞. Дело в том, что бесконечность — это положительная бесконечность. А если мы разделим 1 на отрицательные числа, которые стремятся к нулю, можно также предположить, что 1 : 0 = -∞. Так что в итоге? 1 : 0 = ∞ или 1 : 0 = -∞? Ответ не определен!
Итоговая таблица для вычислений с бесконечностью:
∞ + ∞ = ∞
-∞ + -∞ = -∞
∞ × ∞ = ∞
-∞ × -∞ = ∞
-∞ × ∞ = -∞
11. i
Буква i обозначает мнимое число. Это такое число, квадрат которого дает отрицательный результат. Это не то, о чем мы обычно думаем при возведении чисел в квадрат, потому что мы знаем, что умножение двух одинаковых чисел всегда дает положительный результат. Но это не мешает нам создать аксиому, которая бы изменила правила игры. Мы называем их воображаемыми, потому что их просто не должно быть.
Чему равен квадратный корень из -6? Мы не знаем. Калькулятор выдаст нам ошибку: в конце концов, какие два числа надо перемножить, чтобы получить отрицательное число? Но прелесть математики в том, что в отличие от других научных инструментов, можно предположить, что некоторые вещи существуют, и менять их характеристики, если они вам не подходят.
Концепция мнимых чисел проста. Мы представляем, что они существуют. Чем они полезны? Мы можем решать уравнения, для которых нужен квадратный корень из отрицательного числа.
Вот пример:
- Чему равен √4? Это просто: 2.
- А √-4? Уже немного сложнее. Ответ будет: — 2i.
Мы добавляем i, чтобы обозначить мнимое число — таким образом мы делаем так, что 2 во второй степени будет равно -4. Давайте разберем очень простое уравнение, которое обычно не имеет решения, и посмотрим, как оно решается с использованием мнимых чисел:
x2 + 1 = 0
Очевидно, что x, возведенный в степень 2, никогда не даст отрицательное число (в нашем случае -1), поэтому мы просто предположим, что ответ будет умноженным на i.
x2 = — 1
x = ± i
Мы можем представить квадратный корень из -1 (√-1) как исходное мнимое число. Как в цифре 1 для действительных чисел.
Есть и другое использование мнимых чисел: их объединяют с натуральными для получения комплексных чисел (например, 7i + 12), а также используют в электричестве.
10. Гугол
Гугол — это число в десятичной системе счисления, который изображается единицей со 100 нулями. И вот так оно выглядит: 10, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000. Или:
А еще его можно представить в виде факториала 70! — то есть 70 x 69 x 68 x 67 x 66 x 65 x 64 x 63 x 62 x 61 x 60 x 59… х 1
Чтобы еще больше вас запутать, существует число под названием «гуголплекс». Это 10 в степени гугол:
Интересный факт: название компании Google представляет собой неправильное написание числа. Хитроумный способ назвать поисковую систему. Число в основном используется в астрономических исследованиях, в частности, в альтернативе теории Большого Взрыва — в Большом замораживании.
9. Цифра 9
Любимое число всех маркетологов (вспомните ценники) и красивое визуально и математически. В геометрии оно часто прячется во многих местах. Например, возьмем круг:
- В окружности — 360 градусов (3 + 6 + 0 = 9)
- Если разрезать ее пополам, то каждая половина будет равна 180 градусам (1 + 8 + 0 = 9)
- Если разрезать на четвертинки, каждая из них будет равна 90 градусам (9 + 0 = 9)
- Теперь разрежем окружность на 8 частей. Каждая часть — 45 градусов (4 + 5 + 0 = 9)
- Разрежем на 16 частей. Каждая часть получится по 22,5 градуса (2 + 2 + 5 = 9)
- Наконец, разрежем его на 32 части. Каждая часть будет равна 11,25 градусов (1 + 1 + 2 +5 = 9)
- А теперь начертим внутри окружности правильный многоугольник. Каждый его угол будет равен 60 x 3 (180 = 1 + 8 = 9).
- И квадрат. Каждый его угол будет равен 90 x 4 (360 = 3 + 6 + 0 = 9)
Еще несколько фигур с обозначением углов:
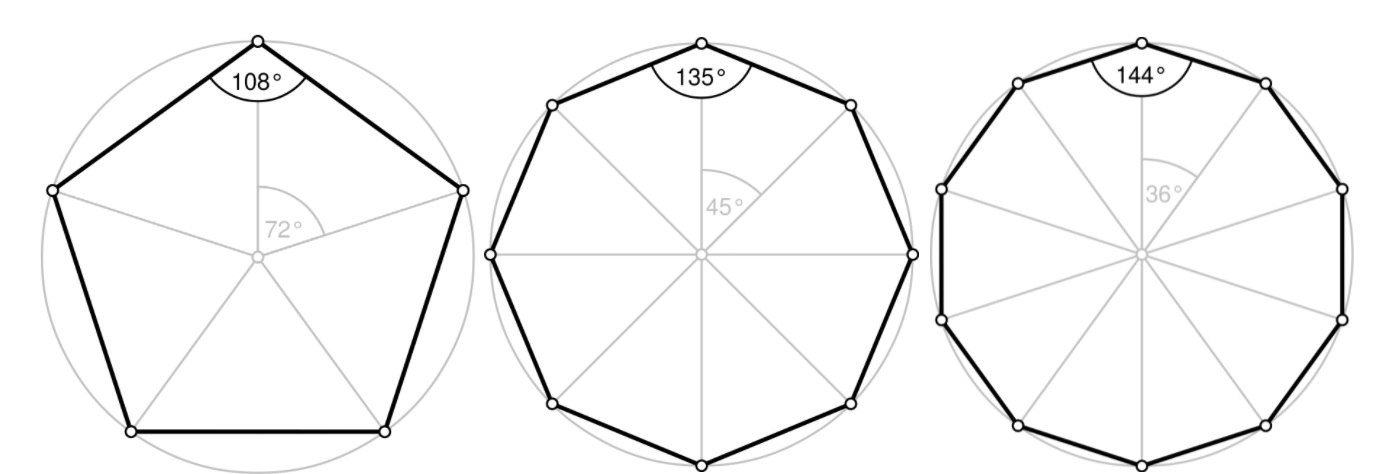
wikipedia.org
Слева направо: Пентагон, Октагон, Декагон.
- Пентагон = 108 = 1 + 0 + 8 = 9 // 72 = 7 + 2 = 9
- Восьмиугольник = 135 = 1 + 3 + 5 = 9 // 45 = 4 + 5 = 9
- Десятиугольник = 144 = 1 + 4 + 4 = 9 // 36 = 3 + 6 = 9
Отвлечемся от геометрии. Если сложить цифры, которые предшествуют девяти, то получим 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36. И вновь: 3 + 6 = 9
Если умножить цифры, предшествующие 9, на девять и сложить их элементы, сумма будет всегда равна 9. А вот и примеры:
- 9 х 1 = 9
- 9 х 3 = 27 = 2 + 7 = 9
- 9 х 7 = 63 = 6 + 3 = 9
- 9 х 9 = 81 = 8 + 1 = 9
Разделив цифры на 9, мы всегда получим одну и ту же цифру, повторяющуюся до бесконечности:
- 1/9 = 0,11111
- 3/9 = 0,33333
- 7/9 = 0,77777
8. Число 73
Если вы фанат «Теории Большого взрыва», то, должно быть, вы помните, как Шелдон Купер объяснял, почему 73 — идеальное число:
«Самое замечательное число — 73. Вы, скорее всего, теряетесь в догадках почему. 73 — это 21-ое простое число. Его зеркальное отражение 37 является 12-ым, чье отражение 21 является результатом умножения, не упадите, 7 и 3».
«В двоичной системе 73 — еще палиндром. 1001001, что справа налево читается, как 100100».
Все эти цитаты — из 10 серии 4-го сезона сериала, которая, по определенному стечению обстоятельств, ялвяется 73-м эпизодом сериала (а еще годом рождения Джима Парсонса, актера, сыгравшего Шелдона).
7. Число Эйлера
Названное в честь Леонарда Эйлера, e — иррациональное число и основание натуральных логарифмов. Интересно, что число Эйлера известно с точностью до 1 триллиона цифр. А найти его можно с помощью этой формулы:
Когда n приближается к бесконечности, мы получаем более ясное представление о значении e. Когда n = 100000, e = 2,71827.
Еще одно удивительное свойство e — его наклон является его же значением. Оно также используется в финансах для расчета сложных процентов.
6. Последовательность Фибоначчи
Леонардо Боначчи, также известный как Фибоначчи (это прозвище, означающее «сын Боначчи»), создал одну из самых увлекательных последовательностей в нашей вселенной. И для этого он использовал простые методы сложения, наблюдая за популяциями кроликов.
Несмотря на то, что есть несколько свидетельств, которые говорят о том, что индийские математики вывели последовательность намного раньше, предлагаем придерживаться широко признанного факта, что ее автор — Фибоначчи.
Получить числа Фибоначчи можно с помощью простой формулы для n > 2:
Так, мы получаем последовательность, которая уходит в бесконечность:
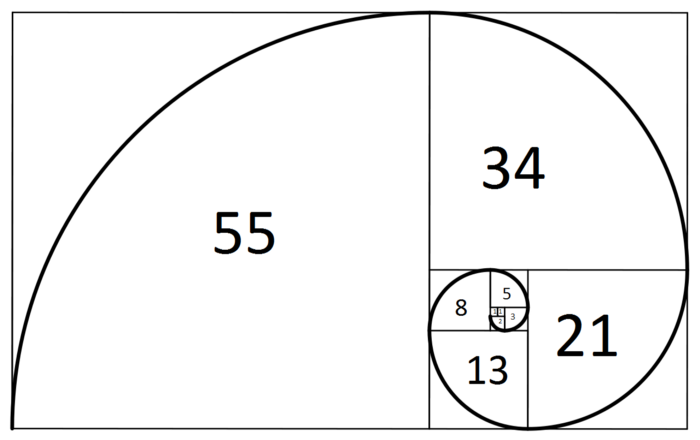
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,….
Ее прелесть в том, что она связана с природой. Например, ее можно обнаружить в цветении артишока и некоторых цветов вроде ромашек.
А что насчет Галактики? Гэри Б. Мэйснер выдвинул интересное и фактически обоснованное предположение, согласно которому размеры Земли и Луны находятся в соотношении Фи, образуя Треугольник, основанный на 1,618.
Но что такое Фи, и что за 1,618?
Wikipedia
Если взять два любых последовательных числа в последовательности, их отношение (Xn / Xn-1) приблизится к 1,618. Это число называется Фи — в честь древнегреческого скульптора и архитектора Фидия — или «золотым числом»:
3 : 2 = 1,5
13 : 8 = 1,666
55: 34 = 1,61764
233 : 144 = 1,61805
…
317 811 : 196 418 = 1,61803
Стремясь к бесконечности, значения отношений приближаются к 1,618.
5. Число 23
Наверное, многие видели фильм «Роковое число 23», в котором Джим Керри играет Уолтера Спэрроу — человека, который становится одержимым числом 23, после того как читает о нем в книге. Считается, что это число таинственным образом совпадает со многими событиями по всему миру, и, хотя это можно назвать наглядным примером Апофении, все-таки интересно перечислить некоторые «случайности»:
- Трагические события 11 сентября можно суммировать до 23, если записать полную дату следующим образом: 9 + 11 + 2 + 0 + 0 + 1 = 23.
- Согласно парадоксу дня рождения, 23 — это наименьшее количество случайно выбранных людей, необходимое для получения как минимум 50% вероятности, что в комнате будут хотя бы два человека с одним днем рождения. Любопытства ради: если в комнате будут 70 человек, этот шанс увеличится до 99,99%.
- Уильям Шекспир родился 23 апреля и 23 апреля скончался. Конечно, точная дата его рождения неизвестна (он крестился 26-го числа), но широко распространено мнение, что этот день — именно 23 апреля.
- Титаник затонул 15 апреля 1912 года. Если сложить все числа в дате (включая месяц), то мы получим: 1 + 5 + 4 + 1 + 9 + 1 + 2 = 23. Конечно, это начинает напоминать искусственный поиск закономерностей, потому что мы сами выбираем даты, которые удачно складываются, и отсеиваем те, что не суммируются так, как надо.
- Угол наклона земной оси равен 23,5°. Пусть вас не смущает 5: мы можем представить число в виде суммы 2 + 3, ведь так интереснее.
- Послание Аресибо состоит из 1679 бит, разбитых на 73 строки по 23 символа. Конечно, оно придумано людьми, но все же. Послание Аресибо — это радиосигнал, который был отправлен с Земли в космос в поисках разумной жизни.
- У человека 23 пары хромосом.
- Сумма первых 23 простых чисел равна 874, что делится на 23. Спасибо, Википедия.
- Бомба на Хиросиму была сброшена в 8:15. 8 + 15 = Трагическое событие, унесшее тысячи жизней. А еще 8 + 15 = 23.
- 23 — наименьшее простое число, которое состоит из последовательных цифр.
- У рыцарей-тамплиеров было 23 гроссмейстера.
- В среднем человеческая кровь циркулирует по всему телу каждые 23 секунды.
4. Пи (π) и Тау (τ)
Знаменитое иррациональное число, представляющее отношение длины окружности к ее радиусу. Сложно найти человека, который никогда его не видел.
Если мы нарисуем круг диаметром 1, тогда длина окружности будет равна 3,14159… что просто обозначается буквой π. Это длина окружности по диаметру.
А теперь к интересным свойствам:
- Его цифры идут до бесконечности в случайном порядке, без каких-либо закономерностей и паттернов.
- 3,14 — это примерно 22/7. Почему примерно? Число π нельзя представить в виде обыкновенной дроби, потому что оно иррационально.
А причем здесь Тау? Некоторые математики спорят над «полезностью» π и предлагают использовать вместо него тау (τ), которое равно 2π. По их словам, оно лучше подходит для вычисления кругов. Если вникнуть в детали, интуиция их не подводит. Но разве можно не любить π?
Кстати, ежегодно 14 марта отмечается день числа Пи (дата в США пишется в виде MM / DD — получается, 3/14).
3. Тождество Эйлера
А вот и главная причина, по которой в заголовке статьи фигурирует слово «красота». Сочетание красивейших математических концепций обычно дает простые результаты. Но для начала вспомним, о каких концепциях идет речь и как мы собираемся их объединить:
Число Эйлера e
Мнимая единица
Число π
Удивительно, но вместе все три образуют уравнение, которое дает простой результат -1:
mathsisfun.com
Но как это вышло?
Как мы уже говорили, i в степени 2 = -1. Леонард Эйлер применил к i ряд Тейлора (разложение функции в бесконечную сумму степенных функций) и вывел следующее уравнение (опустим детали, ведь они выходят далеко за рамки этой статьи):
Если переместить приведенную выше формулу Эйлера на комплексную плоскость (с настоящими и мнимыми числами), мы получим окружность. Включив в уравнение радиус r, мы сможем преобразовать точки в другую форму, например, возведя re в степень ix.
Если мы предположим, что x = π, то получим следующее:
Зная, что cos π = -1 и sin π = 0 — i справа исчезнет:
Мы можем вновь изменить это уравнение, чтобы сделать его более красивым, и добавить еще одно простое число:
2. Число 6174
Это число, также известное как Постоянная Капрекара, имеет отличительную особенность. Вы поймете, какую, когда выполните следующие шаги:
- Возьмите любое четырехзначное число (минимум две цифры в нем должны отличаться).
- Расположите цифры в порядке убывания и возрастания — вы должны получить два новых четырехзначных числа.
- Теперь вычтите меньшее число из большего.
- Повторите шаг 2.
Если вы будете повторять эти шаги, вы всегда будете получать 6174 — и это настоящая загадка.
Почему всегда выходит 6174, независимо от того, с каких чисел вы начнете? Давайте разберемся.
Возьмем, к примеру, 2714:
- 7421 — 1247 = 6174
Или 3687:
- 8763 — 3678 = 5085;
- 8550 — 0558 = 7992;
- 9972- 2799 = 7173;
- 7731 — 1377 = 6354;
- 6543 — 3456 = 3087;
- 8730 — 0378 = 8352;
- 8532 — 2358 = 6174
Теперь, когда мы получили 6174, мы больше не сдвинемся с этой точки. Потому что 7641-1467 = 6174.
А еще 6174 — число Харшада. Это значит, что оно делится на сумму его составляющих: 6174 / (6 + 1 + 7 + 4) = 6174/18 = 343.
Круто!
1. Золотое сечение
Пожалуй, это самое важное соотношение в мире. Напоминаем: его вывели греки. А вот список его основных характеристик:
- Его обратное значение 0,618 равно 1 + 0,618. Следовательно, 1 / ϕ ≈ 1 + ϕ
- Золотое сечение встречается в дикой природе. И некоторые деревья — тому подтверждение. Главный ствол пускает ветвь. На следующий год он отдыхает, а через год пускает еще одну ветвь. Получается, изначально есть главный ствол, через год — две ветви, еще через год — три, затем пять, восемь, тринадцать. Учитывая старые и новые ветви, выходит число Фибоначчи.

Источник: https://in.pinterest.com/pin/415034921892322849/
- Считается, что золотое сечение олицетворяет красоту. И хотя это убеждение не доказано, мы думаем, интересно узнать, как человек вообще распознает красоту. Например, лицо. Существует 10-балльная шкала, согласно которой 10 — самый красивый человек. По этой шкале, лица большинства людей оцениваются от 4 до 6. Чтобы получить результат, необходимо измерить длину и ширину лица. Оптимальное значение равно 1,618. Это значит, что длина лица красивого человека должна быть на 1,618 больше его ширины. Позже вычисляются и другие соотношения: нижняя часть носа и нижняя часть подбородка. Наконец, для более точного результата проводятся тесты симметрии. По словам автора шкалы, доктора Шмида, помимо соответствия других характеристик, длина уха на идеальном лице должна быть равна длине носа.
- Считается, что соотношение между средним пальцем и мизинцем тоже равно числу золотого сечения (ϕ).
- Золотое сечение присутствует и в геометрии. С его учетом выполнены многие здания и произведения искусства. Яркий пример: древнегреческий Парфенон.
- Еще один пример золотого сечения — пентаграмма.
Бонус
На самом деле самое большое число из существующих — 40. А вот и доказательство:
vsauce
Обложка: shutterstock.com
Источник статьи: 13 Fascinating Numbers Around Us — When Beauty Meets Math
Будем называть четырёхзначное число интересным, если среди четырёх цифр в его десятичной записи нет нулей, а одна из этих цифр равна сумме трёх других из них. Например, интересным является число (3111).
а) Приведите пример двух интересных четырёхзначных чисел, разность между которыми равна (17).
б) Найдутся ли два интересных четырёхзначных числа, разность между которыми равна (109)?
в) Найдите наименьшее простое число, для которого не существует кратного ему интересного четырёхзначного числа.
а) Приведите пример двух интересных четырёхзначных чисел, разность между которыми равна (17).
Рассуждения:
1) Интересное:
— без нулей
— четырехзначное
— одна цифра сумма трёх других
— пример: (3111) т.к. (3=1+1+1).
2) Разность равна (17) (→) если к меньшему прибавить (17) получится большее.
3) Пробуем перебор:
Комментарий: существует (5) пар подходящих чисел и около (100) интересных чисел. Поэтому это только вопрос времени найти нужную пару.
Пункт а) в 19 задаче часто решается простым перебором, поэтому советую его не боятся и решать всем, кто осилил первую часть на ЕГЭ.
В бланк ответов:
(1438-17=1421).
Ответ: (1438) и (1421).
б) Найдутся ли два интересных четырёхзначных числа, разность между которыми равна (109)?
Рассуждения:
1) Разность равна (109) (→) если к меньшему прибавить (109) получится большее.
2) Какие есть закономерности?
Очевидно, что (1) не может быть последней цифрой у первого «интересного» — тогда второе получается с нулём на конце, а значит точно не будет «интересным».
Вторая закономерность: последняя цифра будет уменьшаться на (1), а третья и четвертая цифра — увеличиваться на (1). Как это оформить на языке математике?
3) Обозначим цифры в меньшем числе как (a), (b), (c), (d), значит само число записывается как: (overline{abcd}).
4) Если к (overline{abcd}) прибавить (109), то получится число (overline{a(b+1)(c+1)(d-1)}).
5) Сумма цифр первого: (a+b+c+d).
Сумма цифр второго: (a+(b+1)+(c+1)+(d-1)=a+b+c+d+1).
6) А чему в принципе равны суммы цифр интересных чисел?
(1+7+3+3=14) ( (7 cdot 2) тоже равно (14))
(4+8+2+2=16 ) ( (8 cdot 2) равно (16))
(5+2+2+1=10) ((5 cdot 2=10))
(3+1+1+1=6) ((3 cdot 2=6))
Хм… Получается, что сумма цифр любого интересного числа всегда равна наибольшей цифре этого числа, умноженной на два. И это логично, ведь сумма трех других цифр равна наибольшему, значит все вместе они дадут два наибольших.
Тогда получается, что для любого интересного числа сумма (a+b+c+d) – четная, но тогда (a+b+c+d+1) – нечетное (→) (a+b+c+d+1) – не может быть «интересным».
В бланк ответов:
Обозначим меньшее «интересное» число, как (overline{abcd}), если к нему прибавить (109), то получится:

Значит сумма цифр второго числа равна (a+(b+1)+(c+1)+(d-1)=a+b+c+d+1).
Сумма цифр (a+b+c+d) – четная, т.к. одна цифра является суммой трех остальных, а значит их сумма равна двум наибольшим.
Следственно сумма (a+b+c+d+1) – не четная, значит и «интересным» оно быть не может. Пришли к противоречию, получается 2 «интересных» с разницей (109) быть не может.
в) Найдите наименьшее простое число, для которого не существует кратного ему интересного четырёхзначного числа.
Рассуждения:
1) Что тут написано? Что имеется в виду?
Расшифровываем:
Простое число – целое число, которое делится только само на себя и на единицу.
Кратное число – число, которое делится на данное целое без остатка, т.е. при делении интересного на кратное будет получаться некоторое целое. Можно даже нарисовать схемку:
Или если немного преобразовать:

Попробуем найти нужное нам наименьшее простое число перебором – будем брать их по очереди, начиная с самого маленького и проверять есть ли кратные им интересные числа. Если есть – такое простое число нам не подходит, и надо искать дальше.
2) Наименьшее из всех простых – число (2). Проверяем есть ли кратное ему интересное. Признак деления на (2) – число должно оканчиваться на четное, т.е. любое интересное оканчивающееся на (2),(4),(6) или (8) будет кратно (2). Таким является, например, интересное число (1124 → 2) не подходит.
3) Следующей проверяем (3). Признак деления на (3) – сумма цифр делится на (3). Из пункта б) становится ясно, что наибольшая цифра в таком интересном числе должна быть либо (3), либо (6), либо (9). Например, (3111:3 = 1037 → 3) также не подходит.
4) (4) – не простое число (оно делится на (2)), а вот (5) – простое. Проверяем его. Чтоб число делилось на (5) оно должно заканчиваться на (5) или (0). На ноль интересные числа заканчиваться не могут по условию (→) оканчиваются на (5). Например, (2185:5 = 437 →) и (5) мимо.
5) (6) – не простое, (7) -простое. У (7) нету признака деления, поэтому пробуем найти среди интересных чисел то, что делится на (7).

Долго искать не пришлось. (1113:7=159).
6) (8), (9), (10) – составные. (11) – простое. Признак деления на (11): если число делится на (11), то суммы цифр на четных и нечетных местах равны или отличаются на число, кратное (11) (подробности смотрите в предыдущей задаче).
Сумма цифр на четных местах и сумма цифр на нечетных местах в четырёхзначном числе не может отличаться больше чем на (18) (крайний случай (9090)) (→) в искомом суммы цифр на четных и нечетных местах равны (случай 1) или отличаются на (11) (случай 2). Рассмотрим их подробнее.
Случай 1: пусть (a) наибольшая цифра в интересном числе (overline{abcd}) (если наибольшим будет (b), (c) или (d) все рассуждения будут аналогичны).
Т.к. суммы равны, то (a+c=b+d);
Иными словами, (a=b+d-c).
С другой стороны, (a=b+d+c) (ведь (a) – наибольшее и значит равно сумме трех других). Т.к. (c) не ноль, то возникает противоречие (→ a+c≠b+d) в интересном числе. Первый случай – невозможен.
Случай 2: вновь полагаем (a) наибольшей цифрой числа.
Если суммы отличаются на (11), то (a+c=b+d+11).
С другой стороны, (a=b+d+c).
Подставляем (a) в первое равенство и получаем:
(b+d+c+c=b+d+11)
(2c=b+d+11-b-d)
(2c=11)
(c=frac{11}{2}).
Но (c) не может быть дробным, ведь это цифра числа! Опять противоречие (→) второй случай также невозможен.
Получается интересных чисел кратных (11) не бывает.
В бланк ответов:
Интересное число кратное (2) – (1124).
Интересное кратное (3) – (3111).
Интересное кратное (5) – (2185).
Интересное кратное (7) – (1113).
Докажем, что (11) — наименьшее простое, для которого нет кратного интересного. Для этого докажем, что нет интересного числа, которое делится на (11).
Признак деления на (11): разница между суммами цифр, стоящими на четных и нечетных местах, равна (0) или кратна (11). Так как мы рассматриваем четырехзначные числа, то максимальная разница между суммами цифр на четных и на нечетных местах, кратная (11), равна (11) ((22), (33) и т.д. получится не может, т.к. из четырехзначных максимальную разницу между такими суммами имеет число (9090), и эта разница равна (18)).
Таким образом, имеем два возможных случая:
— суммы цифр равны (разница между ними – ноль)
— суммы цифр отличаются на (11).
Пусть (k) – наибольшая из цифр интересного числа, (m) – находится через цифру от (k) (то есть является ее парой при подсчете сумм на четных и нечетных местах). (f) и (e) – другие две цифры интересного числа.
Случай 1 – суммы равны. Тогда (k+m=f+e). С другой стороны, в интересном числе: (k=m+f+e). Получается:
(m+f+e+m=f+e)
(2m=0)
(m=0)
Но по условию в интересном числе нет нулей, следовательно, суммы цифр на четных и нечетных местах равны быть не могут.
Случай 2 – разница равна (11). Тогда (k+m=f+e+11)
С другой стороны, (k=m+f+e). Получается:
(m+f+e+m=f+e+11)
(2m=11)
(m=frac{11}{2})
Но (m) не может быть дробным, ведь это цифра числа.
Таким образом, оба варианта невозможны, а значит нет интересного числа, кратного (11).
Ответ: (11)

Александр Клименков
кандидат технических наук, Tech Lead Bercut
Шелдон Купер — человек, который обожает свой разум
Сериал «Теория Большого взрыва» мало кого оставил равнодушным, как и его главный герой Шелдон Купер — гениальный физик-теоретик и доктор наук, программист с эйдетической памятью и интроверт, большой любитель правил и систематизации, идеального порядка и чистоты. Кстати, в нашей нынешней реальности зацикленность Шелдона на гигиене, обработка рук санитайзером и распыление антисептика на своих коллег и знакомых с малейшими признаками простуды нам уже не кажутся такими уж эксцентричными действиями.
Шелдон не только влюблён в науку, но и как истинный последователь Ричарда Фейнмана, постоянно изобретает множество увлекательных вещей, игр и занятий. Например, он придумал игру «Камень — ножницы — бумага — ящерица — Спок», трёхмерные шахматы и карнавальный костюм эффекта Доплера (его, правда, на той вечеринке все принимали за зебру).
Ещё Шелдон обожает пошутить (вспомним его «Бугагашеньку!» — Bazinga!), и по всем вопросам во Вселенной у него есть своё оригинальное мнение. Например: «Когда мы убиваем в детях способность критически мыслить, говоря, что кролики появляются из шляп, мы создаём взрослых, которые верят в астрологию и гомеопатию». Или как тут не вспомнить его замечательное высказывание «На моём новом компьютере стоит Windows 7. В ней более дружелюбный интерфейс, чем в Windows Vista. Мне это не нравится…».
Естественно, Шелдон, как и любой настоящий учёный, обожает математику и числа. Однажды он сказал, что «чувствует себя как функция арктангенса, которая приближается к асимптоте». В сериале есть множество смешных моментов, посвященных науке, и конечно же математических шуток. Одна из них — про любимое число Шелдона Купера.
Лучшее число — 73
Давайте вспомним, какие аргументы привёл Шелдон в защиту этого смелого утверждения. Итак:
- 73 — это 21-е простое число;
- зеркальные отражения, или переставленные местами разряды, 73 и 21 — это 37 и 12;
- при этом 37 — это 12-е простое число;
- перемножив цифры 73, можно получить 21;
- двоичное представление 73 — это 1001001, что является палиндромом.
В сериале это звучит эффектно, особенно в исполнении харизматичного Шелдона. Но, если это напечатать и перечитать внимательно, то аргументы выглядят не особо убедительно. Сразу возникает вполне резонный вопрос: почему сценаристы сериала выбрали именно это число в качестве любимого числа Шелдона? Неужели такой умный и гениальный учёный, в будущем лауреат Нобелевской премии, не смог найти число поинтереснее?
Ответ на этот вопрос я нашёл в книге Дэйва Зобеля «Теория Большого взрыва: наука в сериале». Оказывается, таким нехитрым способом сценаристы решили отметить 73-ий эпизод сериала, а заодно и упомянуть год рождения исполнителя главной роли Джима Парсонса — 1973. Всё встало на свои места, но число 73 от этого не стало более уникальным. Конечно, сами свойства числа выглядят занимательными. Более того, математики доказали, что 73 — это единственное число, обладающее указанными Шелдоном свойствами. Но можно ли подобрать более интересное число, у которого будет еще больше особенностей?
Лучшее число — 89
Новогодние каникулы — самое подходящее время для того, чтобы решать подобные задачи. Сначала у меня возникла идея написать программу, которая последовательно проверяла бы все числа на соответствие разным гипотезам. Гипотезы могли бы быть самыми разными. Самые простые: это вхождение числа в известные последовательности. Например, в ряд простых чисел или чисел Фибоначчи. Можно было придумать и что-нибудь посложнее. Например, сумма цифр числа является простым числом. Также интересно проверить на «особенность» первые вхождения рассматриваемого числа в дробную часть чисел e и pi. Таких гипотез можно придумать очень много. В итоге самым интересным будет число, для которого подтвердится наибольшее число гипотез.
Но неожиданно программу писать не пришлось. Чтобы поэкспериментировать с числами, я взял первое попавшееся число до 100, которое одновременно является простым числом и числом Фибоначчи. Им оказалось число 89. Для него я начал проверять разные пришедшие в голову гипотезы, и вот, что у меня получилось:
- 89 — это простое число.
- 89 — это 11-е число Фибоначчи. 11 — это тоже простое число.
- Сумма цифр 8 + 9 = 17 — это тоже простое число.
- 89² = 7921 — это число, хоть и не простое, но сумма его чисел — простое число 19.
- Но, что интереснее, если число 7921 записать наоборот, то получится число 1297 — оно тоже простое.
- В дробной части числа e число 89 впервые встречается на месте 218. Сумма цифр этого числа — тоже простое число 11. Кстати, про число 11 — смотри пункт 2.
- Угадайте, на каком месте число 89 впервые встречается в дробной части числа π? На 11-м!
- В двоичной форме число 89 записывается как 1011001. Если прочитать это двоичное число наоборот, то получится 1001101. Это число 77, которое является суммой первых восьми простых чисел. Согласен, по сравнению с предыдущими, этот пункт выглядит натянутым, но всё равно интересно.
Это те гипотезы, которые я проверил сразу. На моё удивление, все они дали положительный результат. Если само полученное число было ничем не примечательным, то я прибегал к уже испытанному Шелдоном способу — придумывал различные производные от числа (как, например, в случае с квадратом числа 89). Осечка случилась только в одной гипотезе — перемножение цифр 8 и 9 дало число 72. С ним я ничего такого сделать не смог. Хотя, постойте, давайте проверим, какое там 72-е простое число. Нет, опять мимо — 359 нам никак не подходит.
На этом идеи у меня кончились, и я пошёл в Википедию за дополнительной информацией. Оттуда я почерпнул ещё два пункта:
- 89 равняется сумме 8 в первой степени и 9 во второй степени.
- 89 — это число Маркова — вместе с числами 1 и 34 оно является решением уравнения x²+y²+z²=3xyz.
Думаю, моё число является гораздо более замечательным, чем число Шелдона Купера! Заметьте, я специально не выбирал число, просто взял первое, показавшееся мне интересным. Как сказал Леонард Хофстедтер, сосед и лучший друг Шелдона в сериале, это было настоящее «чудо сатурналий».
Так что теперь моё любимое число теперь — 89. Пока я не нашёл другое, ещё более интересное.
Лучшее число — x
На самом деле, таким образом можно экспериментировать практически с любыми числами. У многих есть такое любимое или «счастливое» число с детства, например, удачный номер билета на экзамене. Можно поупражняться в преобразовании этого числа. В результате тех или иных изменений с этим числом будут получаться всякие интересные результаты, которые можно записать в список. Например, можно проверить число 42, которое, как известно, является «ответом на главный вопрос жизни, вселенной и всего такого». Причины «интересности» числа могут быть самыми неожиданными. Мир чисел — это вообще крайне загадочная и захватывающая вещь, как и вся математика в целом.
Я думаю, что если всё же написать программу проверки разных гипотез, то можно найти и ещё более интересные числа. Для простых гипотез можно использовать обычные программные вычисления, а для проверки более сложных гипотез подойдут уже готовые массивы чисел в текстовых файлах. Например, такие:
- Огромные списки простых чисел от 10 тысяч до 2 миллиардов штук.
- Число e с точностью от 2 до 10 миллионов знаков.
- Число π с точностью до миллиардного знака.
Только нужно учесть, что файлы будут немаленькими. Например, текстовый файл с числом π (последний в списке) имеет размер 954 мегабайта.
Последовательность чисел Фибоначчи можно получить с помощью несложной программы. Кстати, Tproger недавно описывал получение такой последовательности как одну из задач для начинающих программистов.
Идеи для разных гипотез можно почерпнуть на ещё одном интересном ресурсе: онлайн-энциклопедии целочисленных последовательностей (сокращённо OEIS) — oeis.org. В этой энциклопедии собрано множество разных последовательностей, в которые складываются целые числа. В ней есть не только известные последовательности, такие как простые числа или числа Фибоначчи, но и менее известные, как, например, числа Белла.
Кстати, гипотезы для проверки чисел не обязательно забивать напрямую в программный код. Возможно, их можно было бы генерировать случайным образом.
Лучшее число — дата рождения
Поиск закономерностей в числах — это вообще очень результативное и интересное занятие. Такие закономерности встречаются далеко не так редко, как может показаться на первый взгляд. Для примера рассмотрим даты рождения. Ведь для многих дата рождения — это и есть то самое счастливое любимое число. Например, красивая дата 22.02.77 выглядит очень лаконично и легко преобразуется в простое число 22277, входящее во множество чисел-близнецов.
Наверняка, вы найдете для «своих» чисел много интересных особенностей. Например, в дробной части числа π можно найти не только ответы на все «главные вопросы жизни», но и любую дату. Кстати, это весьма оригинальный способ бросить жребий. Записываем дни рождения каждого участника в заранее оговорённом формате. Можно использовать любой: хоть ДДММГГГГ, хоть ГГГГММДД, а можно сократить год до двух цифр. Затем просто ищем, чьё число встречается раньше в дробной части числа π. Или позже — это уж как договоритесь. Для этого можно использовать готовый текстовый файл (см. выше) или, например, этот сайт.
Конечно, метод дат рождения срабатывает только один раз. В последующих розыгрышах нужно либо называть другие даты, либо использовать любые другие достаточно большие числа с заданным числом цифр. Главное, чтобы среди загадывающих не было того, кто знает большое количество цифр числа π наизусть.
Ещё одна закономерность, связанная с датами, называется «парадокс дней рождения». Он формулируется следующим образом: в группе, состоящей из 23 или более человек, вероятность совпадения числа и месяца рождения хотя бы у двух людей превышает 50%. На первый взгляд это утверждение противоречит здравому смыслу: в голове не укладывается, что в такой маленькой группе настолько вероятно появление одинаковых чисел из ряда от 1 до 365. А знаете, какова вероятность этого события для группы из 57 человек? Наверное, вы мне не поверите, но она равна 99 процентам. Подробный разбор этого парадокса есть в Википедии. Кстати, если у вас есть доступ к достаточно большому массиву дат рождений (например, список сотрудников вашей компании), то вы можете проверить этот парадокс экспериментально. В компании Bercut, на нашем корпоративном портале размещено много полезной информации для сотрудников. Например, у нас есть удобная страница для просмотра дней рождения сотрудников (конечно, без указания года рождения). Проверка по этому списку полностью подтвердила существование парадокса дней рождения.
В математике нет ничего неважного
Оказывается, в мире чисел совпадения и закономерности — это не такое редкое событие, как может показаться на первый взгляд. Главное — не забывать о бритве Оккама и не делать далеко идущих выводов в стиле нумерологии, астрологии или новой хронологии. Не будем множить сущности без необходимости.
Исследование различных числовых множеств — это не просто интересная задача и еще один подходящий повод заняться программированием. Возможно, очередная найденная закономерность приведёт к появлению нового интересного алгоритма. Вот как об этом пишет в своей книге Дэйв Зобель:
У многих чисел есть подобные странные свойства, которые оказались полезными в неожиданных ситуациях. […] Однажды кто-нибудь превратит [их] в сложный шифр, или в отличный способ упаковки предметов в твёрдые контейнеры…
Так, например, стало с простыми числами, которые теперь широко используются в криптографии. Математика — такая наука, в которой любое развлечение приносит свою пользу. Надо только немного пораскинуть мозгами, чтобы эту пользу отыскать.
Арифметика на грани астрологии.
27 января 20239
Дизайнеры всего мира знают: черный — цвет скорби, зеленый — цвет спокойствия, а голубой — цвет динамичного развития компании, молодой коллектив которой бесстрашно смотрит в будущее и не боится задержек зарплаты. И дизайнерам всего мира приходится с этими догмами работать.
Такая же история и с числами. В Китае не бывает 4-го этажа (звучит как «смерть»), 18-й — самый долгожданный день рождения, а длина и радиус одной окружности никогда не будут целыми числами одновременно. Список из самых интересных и загадочных чисел прилагается.
Пи: 3,14
Известная всем со времен школы константа, определяющая коэффициент отношения длины окружности к радиусу. Единственное число в списке, имеющее собственный праздник: 14 марта (то есть 3-й месяц, 14-е число).
Число действительно очень интересное, математики продолжают изучать его свойства до сих пор. Например, пи — удивительно нормальное число, то есть в его десятичной записи на 200 млн знаков после запятой примерно равномерно встречаются все десять цифр.
Число Эйлера (е): 2,71
Еще одна школьная константа, более известная как основание логарифма. Так же, как и пи, вызывает неугасающий интерес ученых и примерно те же самые вопросы. Кроме того, математикам так и не удалось обосновать какую-то связь пи и e.
666
В Библии фигурирует как «число, под которым скрыто имя зверя Апокалипсиса». «Здесь мудрость. Кто имеет ум, тот сочти число зверя, ибо число это человеческое; число его шестьсот шестьдесят шесть». (Отк. 13:18). Какого именно зверя — не очень ясно, потому что в «Откровении Иоанна Богослова» их четыре: орел, лев, ангел и бык. Число стало символизировать что угодно антихристианское, и его немедленно забронировали себе в качестве официального атрибута сатанисты.
Как считают некоторые теологи, в числе зашифровано имя, но какое именно — не ясно.
К слову, в Библии три шестерки встречаются четыре раза, в «Ветхом завете» — три.
13
Историки не могут точно сказать, откуда взялась боязнь числа 13, но, чтобы не выглядеть глупо, придумали явлению название — «трискайдекафобия». Самая известная версия — это отсылка к Библии: на Тайной вечере Иуда был 13-м.
Уровень боязни числа прямо пропорционален религиозности страны: больше всего попыток заменить число 13 разными способами (12+1, 12B и т.п.) в Италии и США.
18
Возраст совершеннолетия в самом большом количестве стран. Чаще всего после этого возраста молодым людям разрешают голосовать, заключать браки, начинать собственное дело и платить налоги.
Очевидно, что 18 оборотов вокруг Солнца, которые сделал гражданин, никак не гарантируют его дееспособность, поэтому число 18 до сих пор остается предметом спора.
Гугол
Это единица с сотней нулей после нее. Название в шутку придумал математик Эдвард Казнер в 1938 году, когда гулял с племянниками, а те донимали его вопросом, какое самое большое число. Спустя 60 лет два молодых человека назвали так собственный поисковый движок.
Ноль
Самое важное, что нужно знать про ноль, — это то, что его нельзя делить. На компьютерах и калькуляторах эта функция заблокирована, потому что может сломать Вселенную.
8
7 — счастливое число в западной культуре (тоже по библейским мотивам), но надежды, возлагаемые на него, не могут сравниться с тем, как боготворят восьмерку китайцы. На мандарине цифра 8 (八) читается как «ба», что созвучно с иероглифом 发, который читается как «фа». У него невероятное количество значений, но китайца больше всего интересует комбинация 发财 — богатеть. Почти все цены в Китае заканчиваются на восьмерку, а половина работодателей выплачивает зарплату суммами, заканчивающимися на 88, потому что восьмерок в Китае много не бывает.
Золотое сечение: 1,618
Самое творческое число, популяризованное Леонардо да Винчи. Встречается практически везде: и в химических структурах, в биологии, физиологии и т.д.
В реальной жизни начали применять еще до изобретения самого термина «математика». Самый известный пример — пропорции египетских пирамид.
Числа Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21…
Ряд Фибоначчи — это, по сути, выраженное числами золотое сечение. Записывается очень легко: первые два числа — это единицы, а каждое последующее — это сумма предыдущих.
Последовательность придумали в Древней Индии, но в Европе ее популяризовал Леонардо Пизанский в XI веке н.э. Эта последовательность чисел очень часто встречается в природе: согласно этой формуле располагаются семена подсолнуха, семена в шишках, ячейки ананаса и т.д. Даже длины фаланг пальцев у человека подчинены этой последовательности.
43252003274489856000
Количество комбинаций трехсекционного кубика Рубика. Нынешний рекорд сборки составляет 3,47 секунды, то есть нынешний чемпион сможет перебрать их все всего за 4,8 млрд лет.
12
Дюжина долгое время претендовала на то, чтобы стать основой для универсальной системы исчисления. Отсюда и такое количество рядов с двенадцатью пунктами: часы, месяцы, апостолы (Иуда не считается), боги в греческом пантеоне, ступень колеса в буддизме, имамы в буддизме, дюймы в футе, пункты в кегле, пенсы в шиллинге и т.д.
Есть мнение, что десятеричная система закрепилась только из-за того, что у нас на руках 10 пальцев, но для двенадцатеричной системы существовал свой способ демонстрации чисел: по количеству фаланг на четырех (кроме большого) пальцах руки.
42
42 — это ответ на главный вопрос жизни, вселенной и всего такого по версии писателя-фантаста Дугласа Адамса. Получен в результате вычисления семи с половиной миллионов лет непрерывных вычислений на специальном компьютере «Думатель». Ответ должен был решить практически все проблемы Вселенной.
Развитые расы, получившие ответ 42, были несколько разочарованы, тогда «Думатель» предложил создать еще более совершенный компьютер, который найдет Окончательный Вопрос. Компьютер назвали «Земля». Что было дальше — читай в романах серии «Автостопом по Галактике».
Существуют ли не интересные числа? На этот вопрос мэтр популярной математики Мартин Гарднер дает отрицательный ответ с обоснованием: разделим все числа на две части – интересные и не интересные. Самое маленькое число из не интересной части автоматически становится интересным и переходит в «интересную» часть. Продолжаем процесс до бесконечности… Это, конечно, шутка, но, тем не менее, предлагаю вашему вниманию первую сотню интересных чисел. Это начало более крупной задумки, ее, как теперь модно говорить, «демо-версия», возможны неточности в терминологии или даже ошибки.
0 (нуль) Величайшее изобретение человеческого разума, давшего исходный импульс развитию математике как таковой. Согласитесь – невероятно трудно придумать «ничего», дать ему имя и использовать в вычислениях. Интересная статья Роберта Каплана об истории «нуля» напечатана в октябрьском номере этого года Scientific American и начинается с таинственных закорючек в клинописных посланиях Месопотамии 5000 летней давности. Самые интересные свойства – на нуль нельзя делить, нуль, будучи показателем степени, приравнивает любое число к единице. Умножение на нуль дает нуль. Сложение и вычитание его результат не меняет. Использование нуля позволяет создавать позиционные системы счисления (в отличие, например, от римских цифр, обходившихся без нуля). О следующих числах предельно кратко.
1 Дает тождество при умножении. Равно любому числу в нулевой степени.
2 Единственное четное простое число.
3 Число размерностей пространства, в которых мы живем. Единственное число, равное сумме всех меньших чисел – естественно, речь все время идет о целых числах. Имеет горизонтальную ось симметрии.
4 Наименьшее число цветов для раскраски карты на плоскости. Тетраэдальное число.
5 Число Платоновых многогранников. Пятое число из последовательности Фибоначчи. Пирамидальное число.
6 =3! Наименьшее совершенное число. Треугольное число.
7 Наименьшее число сторон многоугольника, которым нельзя замостить плоскость. Шестиугольное число.
8 Наибольший куб в последовательности Фибоначчи. Имеет горизонтальную и вертикальную оси симметрии.
9 Максимальное число кубов, необходимое для представления в виде их суммы любого положительного целого числа.
10 Основание нашей системы счисления. Число топологически различных фигур из 5 спичек. Тетраэдальное и треугольное число.
11 Наибольшее количество кусков, на которые делят круг 4 прямые линии. Имеет горизонтальную ось симметрии.
12 Наименьшее число, имеющее 4 делителя. Количество плиток пентамино.
13 Число Архимедовых многогранников. Число из последовательности Фибоначчи. Перестановочное (с 31) простое число.
14 Четвертое число Каталана. Пирамидальное число.
15 Четвертое число последовательности Белла. Треугольное число. Произведение первых трех нечетных чисел. Количество сочетаний четырех чисел из шести.
16 Единственное число (кроме 1), выражаемое в форме xy=yx , а именно 24=42.
17 Количество вариантов узоров, построенных с использованием сдвигов, поворотов и отражений. Перестановочное (с 71) простое число.
18 Единственное число, равное удвоенной сумме его цифр.
19 Максимальное число четвертых степеней чисел, с помощью суммы которых можно выразить любое число. Шестиугольное число.
20 Число топологически различных фигур из 6 спичек. Тетраэдальное число. Количество сочетаний трех чисел из шести.
21 Число из последовательности Фибоначчи. Треугольное число. Количество сочетаний двух или четырех чисел из шести.
22 Количество кусков, на которые делят круг 6 прямых линий.
23 Количество деревьев с восемью звеньями.
24 =4! Самое большое число, которое делится на все числа, меньшие корня из него.
25 Наименьшее число, которое можно представить как сумму двух квадратов.
26 Наименьшее число не-палиндром, квадратом которого является палиндром.
27 Единственное (возможно?) число, у которого сумма цифр (9) суммы кубов цифр (8+343=351) с суммой цифр (18) куба суммы цифр (729) равна самому числу.
28 Второе совершенное и одновременно треугольное число.
29 Седьмое число Люка.Наибольшее количество кусков, на которые делят круг 7 прямых линий.
30 Самое большое число, у которого все числа меньшие его и взаимно простые с ним простые. Пирамидальное число.
31 Простое число Мерсенна. Перестановочное (с 13) простое число.
32 Наименьшая 5-ая степень числа (исключая 1)
33 Самое большое число, не равное сумме разных треугольных чисел. Имеет горизонтальную ось симметрии.
34 Наименьшее число такое, что имеет равное количество делителей с ближайшими соседними числами. Число из последовательности Фибоначчи
35 Количество плиток гексамино. Тетраэдальное число. Количество сочетаний трех или четырех чисел из семи.
36 Наименьшее число (кроме 1), которое одновременно и квадратное и треугольное.
37 Максимальное количество 5х степеней чисел, необходимое для выражения их суммой любого числа. Количество кусков, на которые делят круг 8 прямых линий. Шестиугольное число. Перестановочное (с 73) простое число. Последнее на этой странице.
38 Наибольшее римское число (по длине) в лексикографической записи (XXXVIII).
39 Три делителя этого числа пишутся одними и теми же цифрами.
40 Максимальное число сфер, касающихся каждой сферы при плотнейшей упаковке их в пятимерном пространстве. Количество расстановок 7 ферзей на доске 7*7 не угрожающих друг другу.
41 Наименьшее число, не выражаемое в форме |2x – 3y|. А его квадрат содержит в написании два квадрата.
42 Пятое число Каталана. Количество вариантов плоскостей гексагексафлексагона.
43 Количество гептиамондов. (Фигуры из 7 правильных треугольников)
44 Количество вариантов перемешивания пяти предметов.
45 число Капрекара. Треугольное число. Количество сочетаний двух или восьми чисел из десяти.
46 Количество участков, на которые делят круг 9 прямых линий.
47 Наибольшее число кубов, из которых нельзя сложить куб. Количество деревьев с девятью звеньями.
48 Наименьшее число,имеющее 10 делителей.
49 Наименьшее число такое, что оно само и его ближайшие соседи имеют среди делителей квадраты.
50 Наименьшее число, которое можно представить как сумму квадратов двумя способами. Число вариантов складывания полоски из 5 марок.
51 Шестое число Мотзкина.
52 Это пятое число Белла.
53 Является одним из чисел n, которые служат делителем суммы n первых простых чисел.
54 Наименьшее число, которое может быть представлено суммой трех квадратов тремя способами.
55 Наибольшее треугольное число среди чисел Фибоначчи. Пирамидальное число.
56 Количество вариантов Латинских квадратов. Тетраэдальное число.
57 = 111 по основанию 7.
58 Половина, сумма цифр и сумма квадратов цифр – простые числа.
59 Наименьшее число, представляемое четвертыми степенями чисел в форме a4+b4-c4.
60 Наименьшее число, имеющее своими делителями все числа от 1 до 6.
61 Это шестое число Эйлера. Шестиугольное число.
62 Наименьшее число, которое может быть представлено суммой трех квадратов двумя способами.
63 Количество вариантов упорядочивания множества из 5 элементов.
64 Наименьшее число, имеющее 7 делителей.
65 Еще одно (как и 50) число, которое можно представить как сумму квадратов двумя способами.
66 Треугольное число. Количество сочетаний двух или десяти чисел из двенадцати.
67 Наименьшее число, которое будет палиндромным, если его представить по основанию 5 или 6.
68 Попытка проследить последовательные суммы квадратов цифр сразу обрывается, так как ряд замыкается.
69 интересно тем, что n2 и n3 вместе содержат все цифры.
70 Количество сочетаний четырех элементов из восьми.
71 Делитель суммы всех простых чисел, меньших его самого. Перестановочное (с 17) простое число.
72 Максимальное число сфер, касающихся каждой сферы при плотнейшей упаковке их в шестимерном пространстве.
73 Наименьшее из чисел(исключая 1), которое меньше удвоенного числа с перевернутыми цифрами (37*2=74). Перестановочное (с 37) простое число.
74 Одно из чисел с таким свойством, что сумма его с перевернутым числом равна квадрату суммы его цифр (74+47=11^2). Число областей, на которые делят плоскость 9 пересекающихся окружностей.
75 Если сложить сумму цифр с их произведением и повторять эту операцию, то вскоре зациклимся на числе 39.
76 Количество треугольников, которые можно сложить из зубочисток 6 цветов.
77 Наибольшее число, которое не может быть представлено суммой ряда чисел, начиная с 1.
78 Наименьшее число, которое может быть представлено суммой четырех квадратов тремя вариантами. Треугольное число. Количество сочетаний двух или одиннадцати чисел из тринадцати.
79 Перестановочное простое число, так как 97 тоже простое.
80 Наименьшее число n такое, что n и n+1 оба являются произведениями четырех и более простых чисел.
81 Квадрат суммы цифр.
82 Пятиугольное число.
83 Еще одно из чисел с таким свойством, что сумма его с перевернутым числом равна квадрату суммы его цифр.
84 Тетраэдальное число. Количество сочетаний трех или шести чисел из девяти. Количество областей, на которые делят пространство 7 сфер.
85 Если взять сумму квадратов цифр и повторять эту операцию, то вскоре попадем в замкнутое кольцо, в котором, что самое интересное, число 85 не участвует.
86 = 222 по основанию 6.
87 Единственное ничем не примечательное число в первой сотне, этим и интересно 
88 Единственное число из двух одинаковых цифр, квадрат которого содержит две пары одинаковых цифр. Имеет горизонтальную и вертикальную оси симметрии.
89 = 81 + 92 Число из последовательности Фибоначчи.
90 Число десятков равно количеству делителей (не считая 1)
91 Запишется как 10101 по основанию 3. Шестиугольное число. Самое большое число, для которого выполняется равенство 12+22+32+…+n2 = 1+2+3+…+m, поэтому оно пирамидальное и еще и треугольное число.
92 Число расстановок восьми ферзей на шахматной доске так, чтобы они не угрожали друг другу. Число областей, на которые делят плоскость 10 пересекающихся окружностей.
93 = 333 по основанию 5.
94 Половина, сумма цифр и сумма квадратов цифр – простые числа.
95 Количество вариантов разделения плоскости на 10 областей
96 Наименьшее число,которое можно представить как сумму квадратов четырьмя способами.
97 Наименьшее из чисел, три первых кратных которого содержат цифру 9. Перестановочное (с 79) простое число.
98 Наименьшее из чисел, пять первых кратных которого содержат цифру 9.
99 Число Капрекара, так как 992=9801, а 98+01=99.
100 Наименьший квадрат, равный сумме кубов четырех последовательных чисел.