В дальнейшем эту функцию будем называть искомой функцией. Процесс нахождения решения ОДУ называется интегрированием дифференциального уравнения.
Определение 1. Задача, в которой требуется найти решение дифференциального уравнения F(x, y, y′)= 0 или y′ = f (x, y), удовлетворяющее начальному условию y(x0 )= y0 , называется
задачей Коши.
Теорема существования и единственности решения
|
задачи Коши. |
Пусть дано дифференциальное |
уравнение |
|
|
y′ = f (x, y), где |
функция f (x, y) |
определена в |
некоторой |
области D плоскости Oxy , содержащей точку (x0 , y0 ). Если функция f (x, y) удовлетворяет условиям:
1)f (x, y) есть непрерывная функция двух переменных x
иy в области D;
2)f (x, y) имеет частную производную ∂∂fy , ограниченную
в области D,
тогда найдется интервал (x0 − h,x0 + h), на котором существует
|
единственное |
решение |
y = ϕ(x) |
данного |
уравнения, |
удовлетворяющее условию ϕ(x0 )= y0 .
Доказательство теоремы в данном курсе опускается ввиду сложности. С ним можно ознакомиться в монографии [8].
Определение 2. Функция y = ϕ(x,C), где C — произвольная
|
постоянная, называется общим решением |
уравнения |
|
F(x, y, y′)= 0 , если |
|
|
1) она является решением этого уравнения |
при любых |
|
допустимых значениях произвольной постоянной C ; |
2) каково бы ни было начальное условие y(x0 )= y0 , где точка (x0 , y0 ) принадлежит области, в которой выполняются
10
условия существования и единственности решения задачи Коши, можно подобрать такое единственное значение C0 постоянной
C , что ϕ(x0 ,C0 )= y0 .
Определение 3. Функция Φ(x, y,C)= 0 называется общим
интегралом уравнения, если она задает общее решение уравнения в неявном виде.
Определение 4. Решение, в каждой точке которого нарушается единственность решения задачи Коши, называется особым решением.
Определение 5. Решение, полученное из общего при некотором допустимом значении произвольной постоянной, называется частным решением.
Замечание. Частное решение может быть получено из общего решения при некотором значении константы C . Особое решение не может быть получено из общего ни при каком значении произвольной постоянной C .
|
Пример 1. Найти интегральную кривую дифференциального |
||
|
уравнения y′ = 2x , проходящую через точку M (1;1). |
||
|
Решение. Общим решением уравнения является функция |
||
|
вида y = x2 +C , |
где C |
— произвольная константа. |
|
Действительно, y′ = 2x , отсюда y = ∫2xdx = x2 +C . |
||
|
Функции y = x2 , |
y = x2 +1 , |
y = x2 + 2 , полученные из |
общего решения при конкретных значениях C , являются частными решениями данного уравнения.
Построив графики решения при различных значениях C , получим бесконечное множество непересекающихся интегральных кривых, которое будем называть семейством интегральных кривых (рис. 2).
11

y
1 M
1 
Рис. 2. Интегральные кривые уравнения
|
Построим |
интегральную кривую, проходящую через точку |
||||
|
M (1;1). Для этого требуется решить задачу Коши с начальным |
|||||
|
условием y(1)=1. |
|||||
|
Подставим |
значения |
x0 =1, y0 |
=1 в |
общее |
решение. |
|
Полученное |
равенство |
1 =1 +C |
решим |
относительно |
|
|
произвольной |
постоянной |
C , получим |
C = 0 . |
Таким |
образом, |
|
решением поставленной задачи Коши является функция |
y = x2 . |
|||||
|
На |
рис. 2. это интегральная кривая, |
проходящая |
через точку |
|||
|
M |
(1;1), ее график выделен жирной линией. |
|||||
|
Данное |
уравнение не |
имеет особых решений, |
так как |
|||
|
f (x, y)= 2x |
непрерывная |
функция |
и частная |
производная |
||
|
∂f |
= 0 ограничена. |
|||||
|
∂y |
Пример 2. Построить интегральные кривые уравнение y′=2 y . Решение. Данное уравнение можно записать в виде
|
1 |
y или x |
′ |
1 |
||
|
x′ = 2 |
= 2 y . |
||||
|
Найдем для f (x, y)= 2 |
y |
производную |
|||
|
∂f |
= |
∂(2 y ) |
= |
1 . |
|
|
∂y |
∂y |
y |
|||
|
12 |

y(x0 )= 0 , то
При y = 0 нарушается условие теоремы о существовании и единственности решения задачи Коши. Уравнение может иметь особое решение вида y = 0 .
Общим решение данного дифференциального уравнения является x = y +C . Заметим, что при этом преобразовании мы
|
могли потерять решение y = 0 . |
|
|
Частным решением уравнения являются функции |
x = y при |
|
C = 0 , x = y +1 при C =1 и т.д. Семейство |
интегральных |
кривых показано на рис. 3.
Рассмотрим функцию y = 0 . Она является решением исходного
уравнения, которое не может быть получено из общего ни при каких значениях произвольной постоянной. Следовательно, это особое решение, в каждой точке такого решения нарушается единственность задачи Коши.
Действительно, если задать начальное условие
поставленная задача Коши будет иметь два решения. Одно получится из общего решения. Если в формуле общего решения
положить x = x0 , y = 0 , то C = x0 и решением задачи Коши
|
является функция x = y + x0 . |
Это решение проходит через точку |
|
|
(x0 ,0). |
Вторым решением, проходящим через эту точку, является |
|
|
функция |
y = 0 . Таким образом, |
в каждой точке решения y = 0 |
нарушается единственность задачи Коши. Такое решение является особым.
y = 0
Рис. 3.
13
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Дифференциальное уравнение первого порядка
(1)
определяет в каждой точке , где существует функция
, значение
, т.е. угловой коэффициент касательной к интегральной кривой в этой точке.
Если в каждой точке области задано значение некоторой величины, то говорят, что в области
задано поле этой величины. Таким образом, дифференциальное уравнение (1) определяет поле направлений.
Тройка чисел определяет направление прямой, проходящей через точку
. Совокупность отрезков этих прямых дает геометрическую картину поля направлений.
Задача интегрирования дифференциального уравнения (1) может быть теперь истолкована так: найти такую кривую, чтобы касательная к ней в каждой точке имела направление, совпадающее с направлением поля в этой точке.
Задача построения интегральной кривой часто решается введением изоклин. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым имеют одно и тоже направление. Семейство изоклин дифференциального уравнения (1) определяется уравнением
(2)
где — параметр. Придавая параметру
близкие числовые значения, получаем достаточно густую сеть изоклин, с помощью которых можно приближенно построить интегральные кривые дифференциального yравнения (1).
Замечание 1. Нулевая изоклина дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых.
Для большей точности построения интегральных кривых находят также геометрическое место точек перегиба. Для этого находят в силу уравнения (1):
(3)
и приравнивают ее нулю. Линия, определяемая уравнением
(4)
и есть возможное геометрическое место точек перегиба.
Пример 1. С помощью изоклин построить приближенно интегральные кривые дифференциального уравнения .
Решение. Для получения уравнения изоклин положим , тогда
или
.
Изоклинами являются параллельные прямые. При получим изоклину
. Эта прямая делит плоскость
на две части, в каждой из которых производная
имеет один и тот же знак (рис. 6).
Интегральные кривые, пересекая прямую , переходят из области убывания функции
в область возрастания, и наоборот, а значит на этой прямой находятся точки экстремума интегральных кривых, именно точки минимума.
Возьмем еще две изоклины: и
.
Касательные, проведенные к интегральным кривым в точках пересечения с изоклинами и
, образуют с осью
углы в
и
соответственно. Найдем далее вторую производную
.
Прямая , на которой
, является изоклиной, получаемой при
, и в то же время интегральной линией, в чем можно убедиться подстановкой в уравнение. Так как правая часть данного уравнения
удовлетворяет условиям теоремы существования и единственности во всей плоскости
, то остальные интегральные кривые не пересекают эту изоклину. Изоклина
, на которой находятся точки минимума интегральных кривых, расположена над изоклиной
, а поэтому интегральные кривые, проходящие ниже изоклины
, не имеют точек экстремума.
Прямая делит плоскость
на две части, в одной из которых (расположенной над прямой)
, а значит интегральные кривые обращены вогнутостью вверх, а в другой
и, значит, интегральные кривые обращены вогнутостью вниз. Интегральные кривые не пересекают прямой
, значит, она не является геометрическим местом точек перегиба. Интегральные кривые данного уравнения не имеют точек перегиба.
Проведенное исследование позволяет нам приближенно построить семейство интегральных кривых уравнения (рис.6).
Пример 2. Методом изоклин построить приближенно интегральные кривые дифференциального уравнения .
Решение. Полагая , где
, получаем уравнение изоклин
, причем
. При
получим
, откуда
(5)
Интегральные кривые в точках пересечения с этими изоклинами имеют горизонтальные касательные.
Определим, имеют ли интегральные кривые на изоклинах экстремум. Для этого найдем вторую производную:
При имеем
Если четное, то
, и, значит, в точках пересечения с изоклинами
, интегральные кривые имеют минимум; если же
нечетное, то
и интегральные кривые в точках пересечения с изоклинами имеют максимум. Находим изоклины:
(6)
(7)
Изоклинами являются параллельные прямыми с угловым коэффициентом, равным –1 , т. е. изоклины пересекают ось под углом
. Легко убедиться в том, что изоклины
, являются интегральными кривыми данного дифференциального уравнения (для этого достаточно подставить функции
в уравнение
).
Во всех точках плоскости правая часть данного уравнения, т.е. функция
, удовлетворяет всем условиям теоремы существования и единственности, а поэтому интегральные кривые не пересекаются, и, следовательно, не пересекают изоклины
. Производная
обращается в ноль при
, т.е. на изоклинах (6), и при
, т. е. на изоклинах (6) и (7). При переходе (слева направо) через изоклины (7)
меняет знак с плюса на минус. Например, если рассмотреть полосу, заключенную между изоклинами
и
, то на изоклине
производная
, причем под изоклиной
. Значит, интегральные кривые обращены вогнутостью вверх, а над изоклиной
, значит, интегральные кривые обращены вогнутостью вниз. Таким образом, изоклины (7) являются геометрическим местом точек перегиба интегральных кривых. Полученные данные позволяют приближенно построить семейство интегральных кривых данного уравнения. Для более точного построения следует нанести еще несколько изоклин (рис. 7).
Пример 3. Методом изоклин построить интегральные кривые уравнения .
Решение. Положим . Тогда уравнение изоклин будет
, или
.
Изоклинами являются параболы с вертикальной осью симметрии . Среди изоклин нет интегральных кривых. В самом деле, подставляя в данное уравнение
и
, будем иметь
, или
. Но это равенство ни при каком значении
не может выполняться тождественно относительно
.
Пусть , тогда в точках пересечения с изоклиной
интегральные кривые будут иметь горизонтальные касательные. Изоклина
разбивает плоскость
на две части: в одной из них
(решения
убывают), а в другой
(решения
возрастают). И так как эта изоклина не является интегральной кривой, то на ней находятся точки экстремума интегральных кривых, именно на той части параболы
, где
— точки минимума, а на другой части этой параболы, где
— точки максимума. Интегральная кривая, проходящая через точку
, т.е. через вершину параболы
, в этой точке не имеет экстремума. В точках изоклин
и
касательные к интегральным кривым имеют угловые коэффициенты, соответственно равные 1 и –1.
Для исследования направления вогнутости интегральных кривых найдем вторую производную:
Она обращается в ноль только в точках, лежащих на параболе . В точках плоскости
, координаты которых удовлетворяют условию
, интегральные кривые вогнуты вниз
, а в точках, где
, они вогнуты вверх
. Точки пересечения интегральных кривых с параболой
являются точками перегиба этих кривых. Итак, парабола
есть геометрическое место точек перегиба интегральных кривых.
Правая часть исходного уравнения во всех точках плоскости
удовлетворяет условиям теоремы существования и единственности, поэтому через каждую точку плоскости проходит единственная интегральная кривая уравнения.
Используя полученные сведения, строим приближенно семейство интегральных кривых данного уравнения (рис. 8).
Замечание 2. Точки пересечения двух или нескольких изоклин могут быть особыми точками дифференциального уравнения (1), т.е. такими точками, в которых правая часть уравнения (1) не определена.
Рассмотрим уравнение . Семейство изоклин определяется уравнением
. Это семейство прямых, проходящих через начало координат, так что в начале координат пересекаются изоклины, отвечающие различным наклонам касательных к интегральным кривым. Нетрудно убедиться, что общее решение данного уравнения имеет вид
и точка
является особой точкой дифференциального уравнения. Здесь изоклины являются интегральными кривыми уравнения (рис. 9).
Пример 4. Методом изоклин построить интегральные кривые уравнения .
Решение. Полагая , получаем уравнение семейства изоклин
. Таким образом, изоклинами являются прямые, проходящие через начало координат
.
При получим изоклину
, при
— изоклину
, при
— изоклину
.
Рассматривая обратное уравнение найдем изоклину
, во всех точках которой интегральные кривые имеют вертикальные касательные.
В точке пересекаются все изоклины данного уравнения (особая точка уравнения). С помощью полученных изоклин строим интегральные кривые (рис. 10).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
Дифференциальным уравнением 

где 

Дифференциальным уравнением первого порядка называют уравнение вида:

Например, 





Общим решением уравнения 8.2 называется функция

как семейство интегральных кривых на плоскости, зависящих от произвольной постоянной 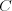
Например: 1) убедимся в том, что функция 
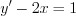



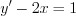


Если общее решение уравнения получено в неявном виде

то его называют общим интегралом.
Например, 

Решить задачу Коши – значит найти интегральную кривую, проходящую через заданную точку 

удовлетворяющее начальным условиям 
Некоторые виды уравнений первого порядка
1. Дифференциальное уравнение с разделенными переменными имеет вид:

Чтобы решить уравнение 8.6, необходимо проинтегрировать его обе части. Например, решим уравнение 


2. Дифференциальное уравнение с разделяющимися переменными имеет вид:

Чтобы решить уравнение 8.7, необходимо разделить переменные и проинтегрировать обе его части.
3. Дифференциальное однородное уравнение имеет вид:

где 



Например: 


Чтобы решить уравнение 8.8, необходимо применить подстановку:



4. Дифференциальное линейное уравнение имеет вид:

Чтобы решить уравнение 8.10, необходимо применить подстановку:




Пример 1. Решите уравнение 
Решение. Поскольку 





Ответ: 
Пример 3. Решите уравнение 
Решение. Запишем уравнение в виде 
Функции 



Следовательно, имеем однородное дифференциальное уравнение первого порядка 8.8. Полагая 






Разделим переменные и проинтегрируем полученное равенство:








Учитывая, что 


Ответ: 
Пример 4. Решите уравнение 
Решение. Имеем линейное уравнение 8.10 Полагая 



Сгруппируем слагаемые, содержащие множитель 


Если положим 

Запишем систему уравнений:
Решим первое уравнение системы: 




Подставим полученное значение 






Так как 
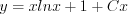
Ответ: 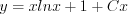
Пусть необходимо решить дифференциальное уравнение вида 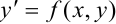
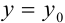
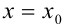
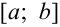
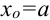
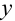
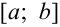
Выполним следующие действия:
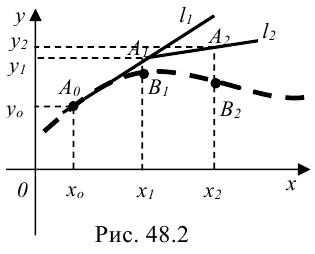
1. С помощью точек 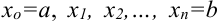
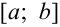
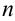
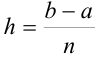
2. Попытаемся искомую интегральную кривую приближенно заменить касательными, проведенными в крайней левой точке каждого отрезка 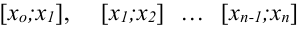
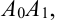
Уравнение касательной, проведенной к графику функции 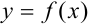
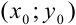
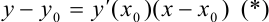
3. Рассмотрим первый отрезок 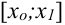
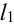
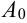
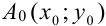
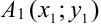
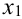
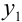
Поскольку точки 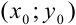
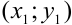
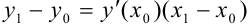
По условию исходное дифференциальное уравнение имеет вид 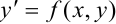
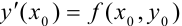
Подставим 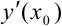
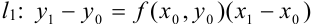
Длина отрезка 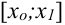
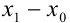
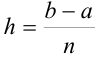
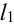
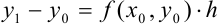
Выразим из этого уравнения неизвестную переменную 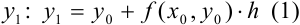
С помощью формулы (1) мы нашли ординату точки 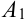
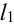
по-возможности небольшой, то ордината точки 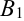
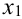
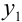
4. Рассмотрим отрезок 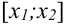
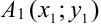
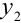
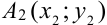
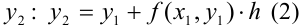
Полученное число 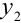
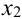
Формулу (2) в общем виде можно записать следующим образом: 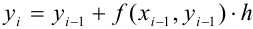
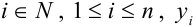
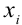
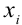
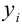
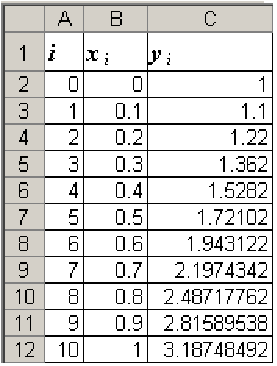
Пример №48.1.
Дано дифференциальное уравнение 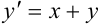
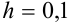
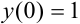
Решение:
Заданное дифференциальное уравнение 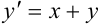
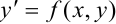
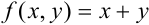
Для удобства вычислений все расчеты будем выполнять в электронных таблицах Microsoft Excel. В качестве шапки таблицы можно предложить следующий вариант:
В столбце 
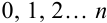
В столбце 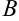
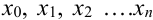
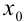
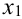
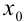
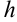
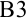
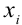
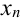
В столбце 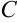
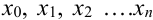
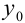
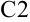
получить значение 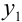
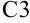
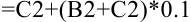
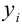
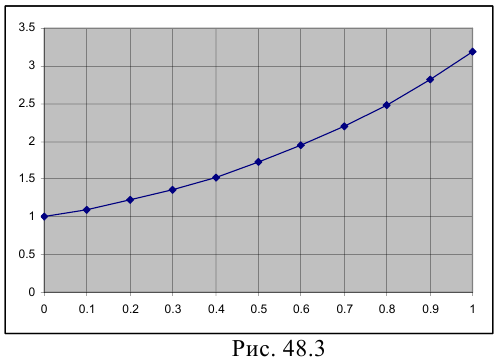
Данная таблица как раз и представляет собой численное решение задачи Коши методом Эйлера. Пользуясь этой таблицей можно построить на отрезке [0;1] искомую интегральную кривую, проходящую через точку (0; 1) (рис 48.3).
Подведем итог. Метод Эйлера задает простой алгоритм вычислений, но определяет табличные значения 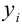
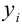
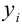
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Предмет высшая математика
Другие лекции по высшей математике, возможно вам пригодятся:
|
0 / 0 / 0 Регистрация: 24.11.2016 Сообщений: 3 |
|
|
1 |
|
Найти интегральную кривую уравнения24.11.2016, 19:26. Показов 3020. Ответов 5
Добрый вечер, помогите пожалуйста, нужно найти интегральную кривую уравне-ния: xy`=2y , проходящую через точку Mo(2;3)
0 |
|
2614 / 2228 / 684 Регистрация: 29.09.2012 Сообщений: 4,578 Записей в блоге: 13 |
|
|
24.11.2016, 19:37 |
2 |
|
найти интегральную кривую Разделите переменные и интегрируйте
1 |
|
8742 / 6335 / 3404 Регистрация: 14.01.2014 Сообщений: 14,553 |
|
|
24.11.2016, 21:22 |
3 |
|
Возможно требовалось ещё численное решение Миниатюры
1 |
|
0 / 0 / 0 Регистрация: 24.11.2016 Сообщений: 3 |
|
|
27.11.2016, 18:34 [ТС] |
4 |
|
Спасибо ребята!)
0 |
|
0 / 0 / 0 Регистрация: 24.11.2016 Сообщений: 3 |
|
|
28.11.2016, 18:42 [ТС] |
5 |
|
mathidiot,М0(2 3) — как так сделать?Пробел между цифрами если точнее.
0 |
|
8742 / 6335 / 3404 Регистрация: 14.01.2014 Сообщений: 14,553 |
|
|
28.11.2016, 20:14 |
6 |
|
Набираете сначала M.o:= дальше щелкаете мышкой на палитре «Матрица» и при этом задаете число строк, равным 1, и число столбцов, равным 2, появится шаблон с двумя местами под числа.
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
28.11.2016, 20:14 |
|
Помогаю со студенческими работами здесь Построить интегральную кривую проходящую через точку Найти решение уравнения, изоклинную и интегральную кривые, решение задачи Коши б)… Найти интегральную функцию распределения Построить кривую и написать уравнения директрис Добавлено… Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 6 |