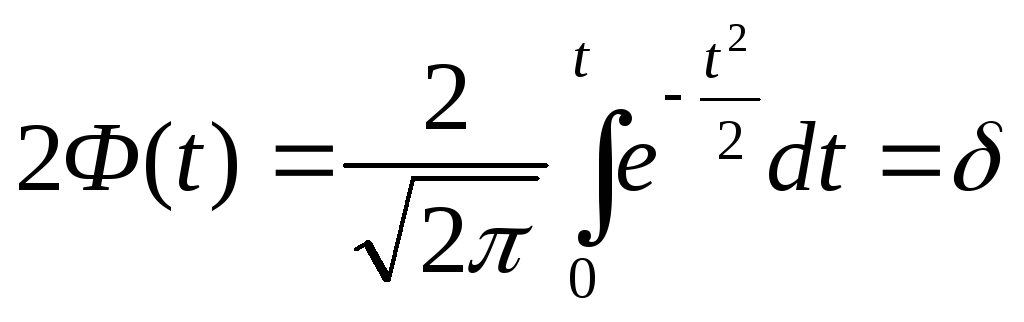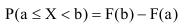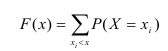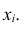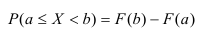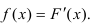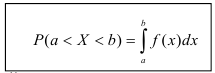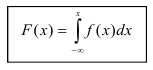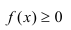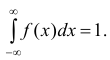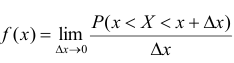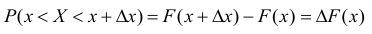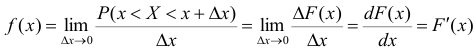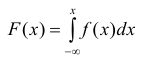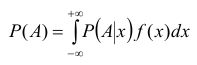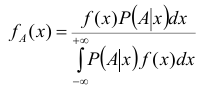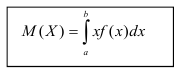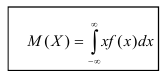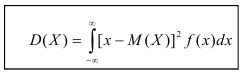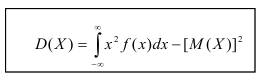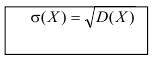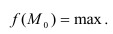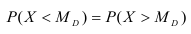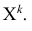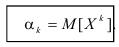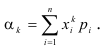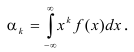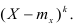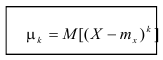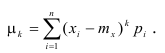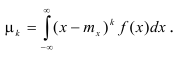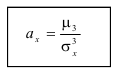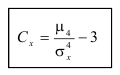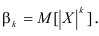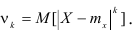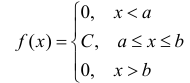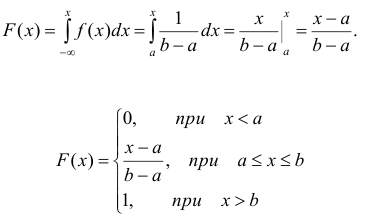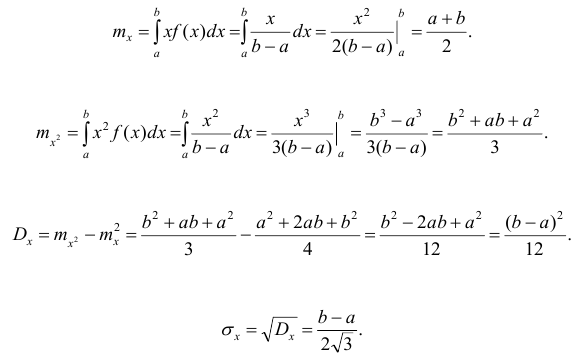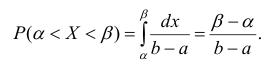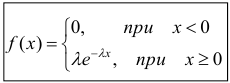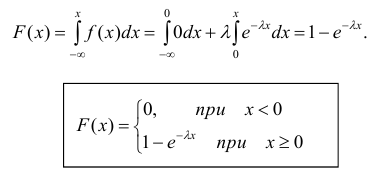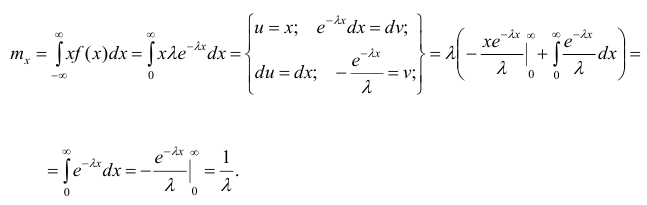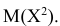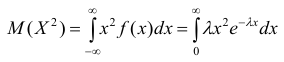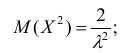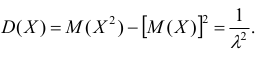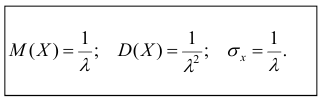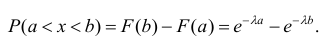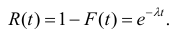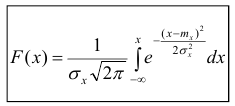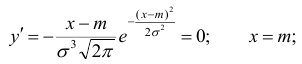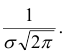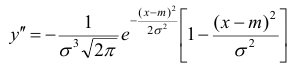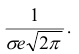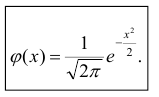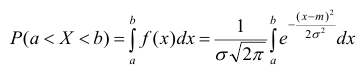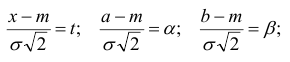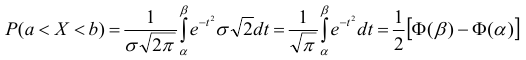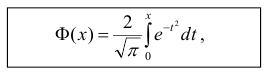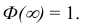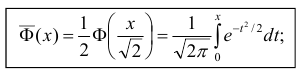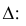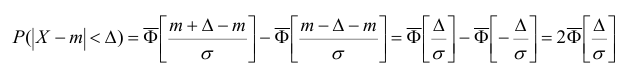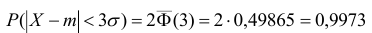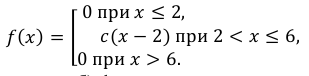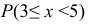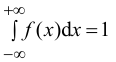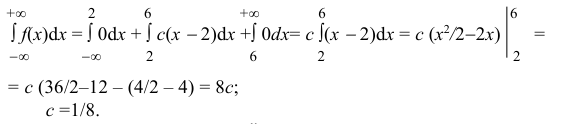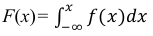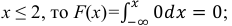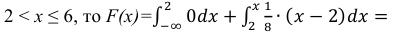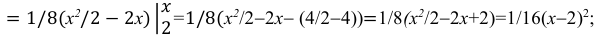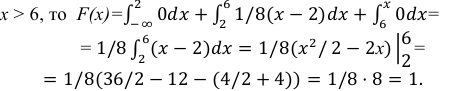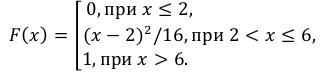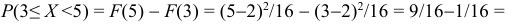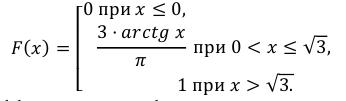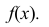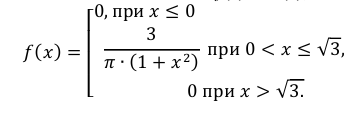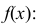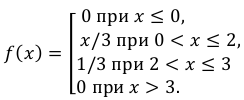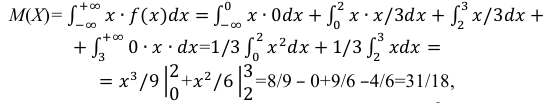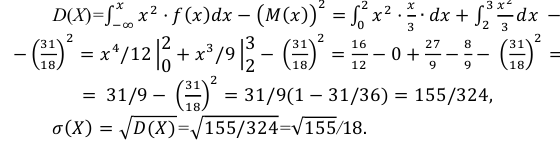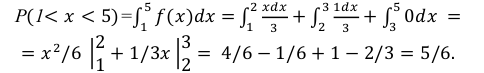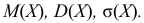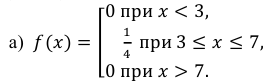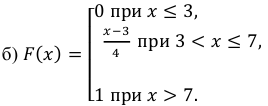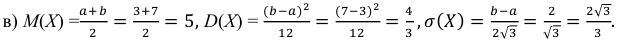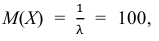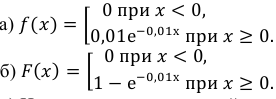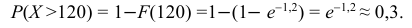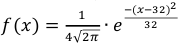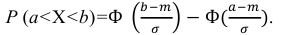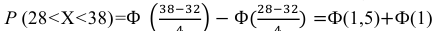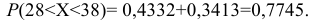Как найти интеграл вероятностей

Интеграл вероятностей

Интегральная
функция нормального распределения
результатов измерения F
(X) или ошибок F(Δx)
в новых переменных будет иметь один и
тот же вид:

(26)

Вероятность
того, что возможный результат измерения
Х окажется внутри заданного интервала
(Х₁,
Х₂)
согласно (26) может быть вычислен по
уравнению:

где

В
частности, для симметричного относительно
истинного значения Х₀
интервала ()
получим:

(27)

Здесь
учитывается, что функция
является нечетной.

Функция

(28)

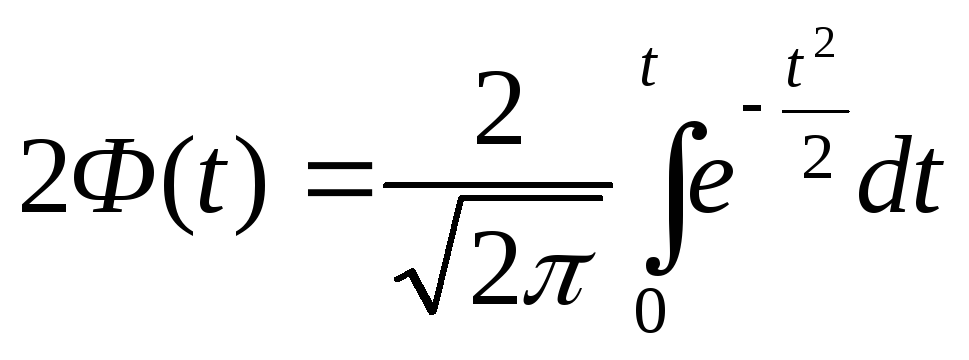
называется
функцией Лапласа или интегралом
вероятностей (табл.1).

Таблица
1

Функция
Лапласа

Интеграл
вероятностей (28) по уравнению (27) позволяет
вычислять вероятность нахождения
результата измерения Х или его ошибки
ΔХ в заданном симметричном относительно
центра распределения интервала (-σt,
σt
). Для этого нужно величинузаданного интервале ()
или ()
выразить в долях σ .т.е. найтии по табл1 определить искомую вероятность.

Решается
и обратная задача. Для заданной вероятности
δ (по табл.1) определяют t
и по известному σ находят искомый
интервал ().

Найдем
значения вероятностей δ для интервалов
()
приt=
I. 2. 3 :

Из
последнего равенства следует, что 99,73%
всех результатов измерений находятся
в пределах интервала

()
и лишь 0,27% — за его пределами.

На
рис.4 искомые вероятности δ изображены
заштрихованными площадями под кривыми
Гаусса f(t).
Вся площадь код кривой равна единице
(на рис. 4а

-t=1,
δ=0,68; 4б –t=2,
δ=0,95;
4в –t=3,
δ=0,997).

Те
результаты измерений, ошибки которых
вышли за пределы ± 3 σ , имеют очень малую
вероятность и такие измерения практически
невозможны («правило трех сигм»).
При большом числе отсчетов “правило
трех сигм” применяют для выявления
грубых ошибок — промахов.

Ошибка среднего арифметического

На
практике обычно вы-полняется некоторый
ряд из n
измерений

x₁,
x₂,
x₃,…
x_n.
(29)

Этот
ряд можно рассмат­ривать как случайную
выборку из нормальной генеральной
совокупности возможных ре-зультатов с
математическим ожиданием М(Х)=Х₀
и диспер- сией :D(х)=σ².

В
качестве приближенно­го значения Х₀
целесообразно принять среднее
арифмети-ческое из результатов изме-рений:

(30)

Основной
задачей теории ошибок является оценка
точности приближенного равенства (30).

Среднее
арифметическое
случайных величин является также
случайной величиной, имеющей нормальное
распределение с тем же центром М(Х)=Х₀,
но с дисперсией

(31)

Величину
называют средней квадратичной ошибкой
среднего арифметического. Следовательно,
средняя квадратичная ошибка среднего
арифметического изn
измерений в
раз меньше средней квадратичной ошибки
отдельного измерения.

Следует
помнить, что σ
зависит от обстоятельств измерений
изучаемого объекта, инструмента,
обстановки измерений и наблюдателя.
Поэтому когда характеризуют точность
применяемого способа измерения или же
сравнивают качество отдельных результатов
(выделение промахов), пользуются величиной
σ. Когда же оценивают точность
окончательного результата измерений
(среднего арифметического), применяют
.

Остается
выяснить, как можно вычислить
из опытных данных (29).

Согласно
определению (12) дисперсия
можно было бы вычислить следующим
образом:

однако
нам неизвестно истинное значение х₀.

Если
Х₀
заменить его приближенным значением
,
то, как показывает теория, для вычисления
дисперсии получится приближенная
формула:

(32)

Дисперсию
называют выборочной дисперсией, а
разность

(33)

остаточной
ошибкой отдельного измерения. Извлекая
квадратный корень из (32), получим

(34)

Эта
формула, определяющая среднюю квадратичную
ошибку по данным случайной выборки,
называется формулой Бесселя.

Из
выражения (31) аналогично найдем
приближенную оценку средней квадратичной
ошибки среднего арифметического

(35)

Соседние файлы в папке МЕХАНИКА

• #

  12.03.20151.05 Mб276BAZA.XLS

• #
• #
• #
• #
• #
• #
• #

§ 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

3.5. Нормальное распределение.

Говорят, что случайная величина нормально распределена или подчиняется
закону распределения Гаусса, если ее плотность распределения имеет вид

(28)

где a — любое действительное число, а >0. Смысл параметров
a и будет установлен в дальнейшем (см. §4, п. 2).
Исходя из связи между плотностью распределения и функцией распределения F(x) [см. формулу (22)], имеем

График функции симметричен относительно прямой x=a. Несложные исследования показывают,
что функция достигает максимума при x=a, а ее график имеет точки перегиба при и .
При график функции асимптотически приближается к оси Ox. Можно показать, что при увеличении кривая плотности
распределения становится более пологой. Наоборот, при уменьшении график плотности распределения сжимается к оси симметрии. При a=0 осью
симметрии является ось Oy.

На рис. 11 изображены два графика функции y=. График I соответствует значениям a=0, =1,
а график II — значениям a=0, =1/2.

Покажем, что функция удовлетворяе условию (24), т.е. при
любых a и выполняется соотношение

В самом деле, сделаем в этом интеграле замену переменной, полагая . Тогда

В силу четности подинтегральной функции имеем

Следовательно,

Но,

В результате получим

(29)

Найдем вероятность . По формуле (23) имеем

Сделаем в этом интеграле замену переменной, снова полагая . Тогда , и

(30)

Как мы знаем, интеграл не берется в элементарных функциях. Поэтому для вычисления определенного интеграла (30) вводится функция

(31)

называемая интегралом вероятностей. Для этой функции составлены таблицы ее значений для различных значений аргумента (см. табл. II Приложения). Используя формулу (31) получим

Итак,

(32)

Легко показать, что функция Ф(х) (интеграл вероятностей) обладает следующими свойствами.

1°. Ф(0)=0

2°. ; при величина практически равна 1/2 (см. табл. II).

3°. Ф(-x)=-Ф(х), т.е. интеграл вероятностей является нечетной функцией.

График функции Ф(х) изображен на рис. 12.
 

Таким образом, если случайная величина нормально распределена с параметрами a и ,
то вероятность того, что случайная величина удовлетворяет неравенствам , определяется соотношением (32).

Пусть >0. Найдем вероятность того, что нормально распределенная случайная величина
отклонится от параметра a по абсолютной величине не более, чем на , т.е. .

Так как неравенство равносильно неравенствам , то полагая в соотношении (32)
, получим

Вследствие того, что интеграл вероятностей — нечетная функция, имеем

(33)

Пример 1.
Пусть случайная величина подчиняется нормальному закону распределения вероятностей с параметрами
a=0, =2.

Определить: (Решение)

1) ;

2) ;

Пример 2.
В каких пределах должна изменяться случайная величина, подчиняющаяся нормальному закону распределения, чтобы (Решение)

Из последнего примера следует, что если случайная величина подчиняется нормальному закону распределения, то
можно утверждать с вероятностью, равной 0,9973, что случайная величина находится в интервале .
Так как данная вероятность близка к единице, то можно считать, что значения нормально распределенной случайной величины практически
не выходят за границы интервала . Этот факт называют правилом трех сигм.

Дальше…

Содержание:

Непрерывные случайные величины: функция распределения случайной величины:

Если вычислить вероятность появления непрерывной случайной величины не составляет особого труда, то решение основной задачи теории вероятностей для непрерывной случайной величины несёт большие трудности. Поэтому в материалах сегодняшней лекции мы рассмотрим методы определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.

Функция распределения непрерывной случайной величины

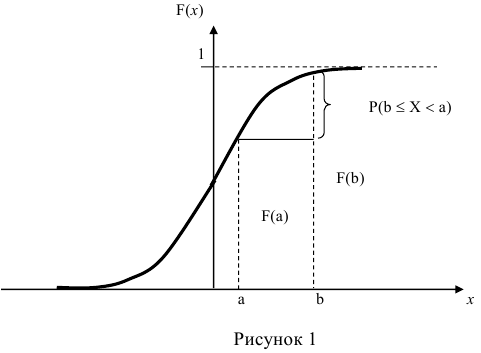
Зная функцию распределения непрерывной случайной величины, задача определения вероятности её попадания на интервал (а; b) может быть решена следующим образом.

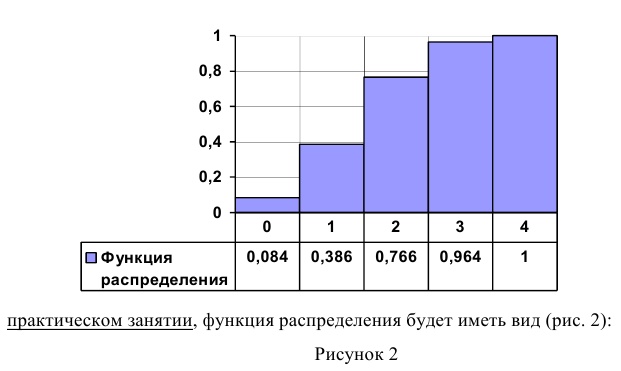
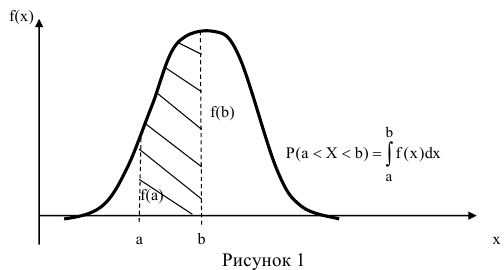
По известной функции распределения вероятность попадания непрерывной случайной величины на интервал (а; b) равна приращению функции распределения на этом участке (рис. 1).

Во всех рассмотренных выше случаях случайная величина определялась путём задания значений самой величины и вероятностей этих значений.

Однако такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, её значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.

Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов?

Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.

Пусть х — действительное число. Вероятность события, состоящего в том, что X примет значение, меньшее х, т.е. X

Определение. Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х.

F(x) = Р(Х < х)

Функцию распределения также называют интегральной функцией. Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.

Для дискретной случайной величины функция распределения имеет

Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.

Функция распределения дискретной случайной величины X разрывна и возрастает скачками при переходе через каждое значение

Так для примера, который мы будем рассматривать на следующем

Свойства функции распределения

1)    значения функции распределения принадлежат отрезку [0, 1].

2)    F(x) — неубывающая функция.

3)    Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b) , равна приращению функции распределения на этом интервале.

4)    На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.

5)    Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.

Таким образом, не имеет смысла говорить о каком — либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой — либо интервал, что соответствует большинству практических задач.

Заключение по лекции:

В лекции мы рассмотрели методы решения основной задачи теории вероятностей — определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.

Плотность вероятности. Числовые характеристики. Моменты случайных величин

Если вычислить вероятность появления непрерывной случайной величины не составляет особого труда, то решение основной задачи теории вероятностей для непрерывной случайной величины несёт большие трудности. Поэтому в материалах сегодняшней лекции мы рассмотрим методы определения вероятности попадания непрерывной случайной величины на интервал с помощью плотности
распределения.

Плотность распределения

Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.

Определение. Плотностью распределения вероятностей непрерывной случайной величины X называется функция f(x) — первая производная от функции распределения F(x).

Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.

Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина X в некоторой окрестности точки х при повторении опытов.

После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.

Определение. Случайная величина X называется непрерывной, если её функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением (может быть, конечного числа точек).

Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина X примет значение, принадлежащее заданному интервалу.

Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b.

Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения (см. лекцию тема № 10).

Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми х=а и х=b.

Геометрически вероятность Р(а < X < b) представляется в виде заштрихованной области, ограниченной кривой распределения и осью Ох на интервале(а; b) (рис 1).

Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:

Свойства плотности распределения

1) Плотность распределения — неотрицательная функция.

2) Несобственный интеграл от плотности распределения в пределах от —
равен единице.

Плотность распределения
можно представить как:

тогда
Поэтому иногда функцию плотности распределения f(x) называют также дифференциальной функцией распределения или дифференциальным законом распределения величины X, а функцию распределения F(x) -интегральной функцией распределения или интегральным законом распределения.

Следует заметить, что интеграл 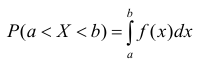возможно трактовать как сумму бесконечно большого числа несовместных элементарных событий, каждое из которых заключается в попадании случайной величины в бесконечно малый участок (х, х + dx) и имеет вероятность:

Р(х < X < х + dx) = dF(x) = f(x)dx

Величину f(x)dx называют элементом вероятности.

По своему содержанию элемент вероятности есть вероятность попадания случайной величины X на элементарный участок dx, прилежащий к точке X.

Функция распределения случайной величины X по известной плотности распределения может быть найдена, как интеграл от плотности распределения в интервале от

В схеме непрерывных случайных величин можно вывести аналогии формулы полной вероятности и формулы Бейеса, рассмотренные при изучении темы 4.

Обозначим Р(А /х) условную вероятность события А при условии Х= х. Заменяя в формуле полной вероятности вероятность гипотезы элементом вероятности f(x)dx, а сумму — интегралом, получим полную вероятность события А.

Данная формула называется интегральной формулой полной вероятности.

Соответствующий аналог в схеме непрерывных случайных величин имеет и формула Бейеса. Обозначив условную плотность распределения случайной величины X при условии, что в результате опыта появилось событие A через 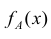, получим:

Данная формула называется интегральной формулой Бейеса.

Числовые характеристики непрерывных случайных величин

Пусть непрерывная случайная величина X задана функцией распределения f(x). Допустим, что все возможные значения случайной величины принадлежат отрезку [а,b].

Математическое ожидание

Определение. Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а,b], называется определенный интеграл

Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

При этом, конечно, предполагается, что несобственный интеграл сходится.

Дисперсия

Определение. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата её отклонения.

По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:

Среднеквадратичное отклонение

Определение. Средним квадратичным отклонением называется квадратный корень из дисперсии.

Мода

Определение. Модой 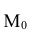дискретной случайной величины называется её наиболее вероятное значение. Для непрерывной случайной величины мода — такое значение случайной величины, при которой плотность распределения имеет максимум.

Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным.

Если распределение имеет минимум, но не имеет максимума, то оно
называется антимодальным.

Медиана

Определение. Медианой 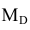случайной величины X называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.

Геометрически медиана — абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.

Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.

Начальный момент

Определение. Начальным моментом порядка k случайной величины X называется математическое ожидание величины

Для дискретной случайной величины:
Для непрерывной случайной величины:

Начальный момент первого порядка равен математическому ожиданию.

Центральный момент

Определение. Центральным моментом порядка k случайной величины X называется математическое ожидание величины

Для дискретной случайной величины:

Для непрерывной случайной величины:
Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.
 

Коэффициент асимметрии

Определение. Отношение центрального момента третьего порядка к среднеквадратическому отклонению в третьей степени называется коэффициентом асимметрии.

Эксцесс

Определение. Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом.

Кроме рассмотренных величин используются также так называемые абсолютные моменты:

Абсолютный начальный момент: 

Абсолютный центральный момент:

Абсолютный центральный момент первого порядка называется средним арифметическим отклонением.

Заключение по лекции:

В лекции мы рассмотрели методы решения основной задачи теории вероятностей — определения вероятности попадания непрерывной случайной величины на интервал с помощью плотности распределения.

Законы распределения непрерывных величин: нормальное, равномерное, показательное

В материалах сегодняшней лекции мы рассмотрим законы распределения непрерывных величин.

Равномерное распределение

Определение. Непрерывная случайная величина имеет равномерное распределение на отрезке [а,b], если на этом отрезке плотность

распределения случайной величины постоянна, а вне его равна нулю.

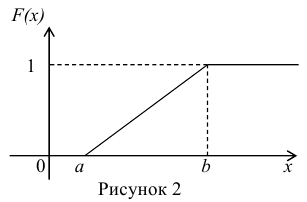
Постоянная величина С может быть определена из условия равенства единице площади, ограниченной кривой распределения, представленной на рис. 1
        

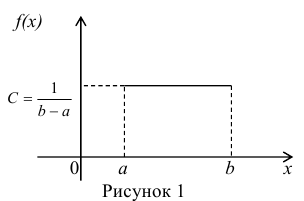
Получаем        .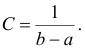

Найдём функцию распределения F(x) на отрезке [а,b] (рис. 2).

Для того, чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы её значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны.

Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения.

Вероятность попадания случайной величины в заданный интервал:

 

Показательное распределение

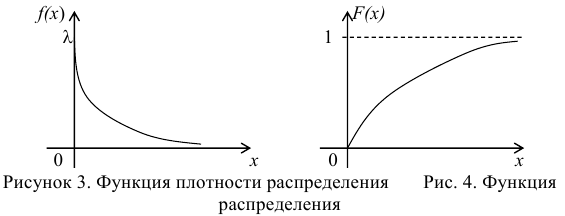
Определение. Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины X, которое описывается плотностью    

где 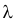— положительное число.

Найдём закон распределения.

Графики функции распределения и плотности распределения представлены на рис. 3, 4.

Найдём математическое ожидание случайной величины, подчинённой показательному распределению.

Результат получен с использованием того факта, что

Для нахождения дисперсии найдём величину

Дважды интегрируя по частям, аналогично рассмотренному случаю, получим:

Тогда
Итого:

Видно, что в случае показательного распределения математическое ожидание и среднеквадратическое отклонение равны.

Также легко определить и вероятность попадания случайной величины, подчиненной показательному закону распределения, в заданный интервал.

Показательное распределение широко используется в теории надёжности.

Допустим, некоторое устройство начинает работать в момент времени to=0, а через какое- то время t происходит отказ устройства.

Обозначим Т непрерывную случайную величину — длительность безотказной работы устройства.

Таким образом, функция распределения F(t) = P(T

Вероятность противоположного события (безотказная работа в течение времени t) равна R(t) = P(T>t) — l — F(t).

Функция надежности

Определение. Функцией надёжности R(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.

Часто на практике длительность безотказной работы подчиняется показательному закону распределению.

Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.

Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.

Функция надёжности для какого- либо устройства при показательном законе распределения равна:

Данное соотношение называют показательным законом надежности.

Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.

Таким образом, безотказная работа устройства зависит только от интенсивности отказов 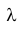и не зависит от безотказной работы устройства в
прошлом.

Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.

Нормальный закон распределения

Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

Нормальный закон распределения также называется законом Гаусса.

Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Можно легко показать, что параметры 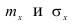входящие в плотность распределения являются соответственно математическим ожиданием и среднеквадратическим отклонением случайной величины X.

Найдём функцию распределения F(x).

График плотности нормального распределения называется нормальной кривой или кривой Гаусса.

Нормальная кривая обладает следующими свойствами:

1)    Функция определена на всей числовой оси.

2)    При всех х функция распределения принимает только положительные значения.

3)    Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента л значение функции стремится к нулю.

4)    Найдём экстремум функции.

Т.к. при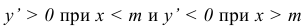 , то в точке х = m функция имеет максимум, равный

5)    Функция является симметричной относительно прямой x = а, т.к. разность

(х — а) входит в функцию плотности распределения в квадрате.

6)    Для нахождения точек перегиба графика найдем вторую производную функции плотности.

При 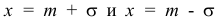вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.

В этих точках значение функции равно     
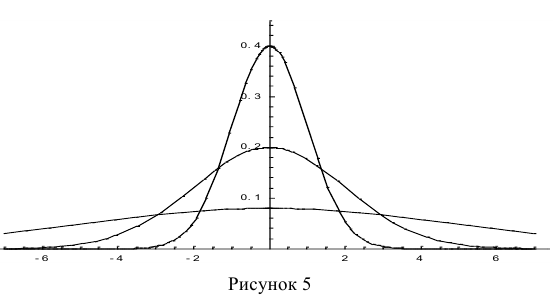
Построим график функции плотности распределения (рис. 5).

Построены графики при м =0 и трёх возможных значениях среднеквадратичного отклонения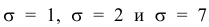. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается.

Если а > 0, то график сместится в положительном направлении, если а < 0 — в отрицательном.

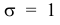
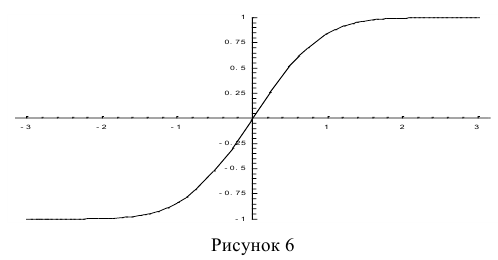
При а = 0 и кривая называется нормированной. Уравнение нормированной кривой:

Функция Лапласа

Найдём вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.

Обозначим

Тогда
Т.к. интеграл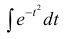 не выражается через элементарные функции, то вводится в рассмотрение функция

которая называется функцией Лапласа или интегралом вероятностей.

Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах.

На рис. 6 показан график функции Лапласа.

Функция Лапласа обладает следующими свойствами:

• 1)    Ф(0) = 0;
• 2)    Ф(-х) = — Ф(х);
• 3)  

Функцию Лапласа также называют функцией ошибок и обозначают
erf х.

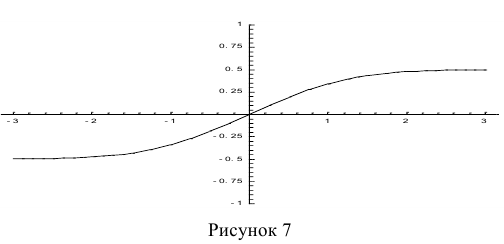
Ещё используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:

На рис. 7 показан график нормированной функции Лапласа.

Правило трёх сигм

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.

Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины

Если принять 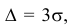, то получаем с использованием таблиц значений функции Лапласа:

Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую, чем утроенное среднее квадратичное отклонение, практически равна нулю.

Это правило называется правилом трех сигм.

Не практике считается, что если для какой-либо случайной величины выполняется правило трёх сигм, то эта случайная величина имеет нормальное распределение.

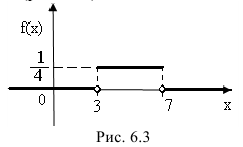
Пример:

Случайная величина Х задана плотностью распределения вероятностей:

Найти: а) значение с; б) функцию распределения F(х) и построить ее график; в)
 

Решение:

а) Значение с найдем из условия нормировки:
Следовательно,

б) Известно, что 

Поэтому, если 

если 

если 

Таким образом,

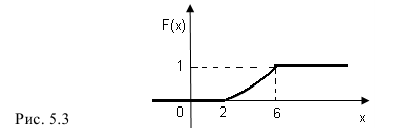
График функции F(х) изображен на рис. 5. 3.

в) 

Пример:

Случайная величина Х задана функцией распределения:

Найти дифференциальную функцию распределения  
 

Решение:  

Так как 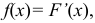 то

Пример:

Случайная величина Х задана дифференциальной функцией

Найти 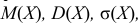 а также 

Решение:

Некоторые законы распределения непрерывной случайной величины 

Пример:

Случайная величина Х равномерно распределена на отрезке [3;7]. Найти:

а) плотность распределения вероятностей 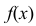 и построить ее график;

б) функцию распределения 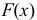 и построить ее график;

в)
Решение: Воспользовавшись формулами, рассмотренными выше, при а = 3, b = 7, находим:

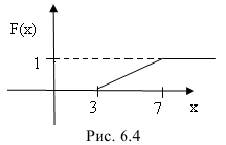
Построим ее график (рис. 6.3):

Построим ее график (рис. 6.4):

Пример:

Среднее время безотказной работы прибора равно 100 ч.
Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:

а) плотность распределения вероятностей;

б) функцию распределения;

в) вероятность того, что время безотказной работы прибора превысит 120 ч.
 

Решение.

По условию математическое ожидание
откуда 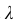 = 1/100 = 0,01.
Следовательно,

в) Искомую вероятность найдем, используя функцию распределения: 

Пример:

Случайная величина Х распределена нормально с математическим ожиданием 32 и дисперсией 16. Найти: а) плотность распределения вероятностей 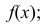 б) вероятность того, что в результате испытания Х примет значение из интервала (28;38).
 

Решение:

По условию m = 32, σ2 = 16, следовательно, σ = 4, тогда

а) 

б) Воспользуемся формулой:

Подставив a = 28, b = 38, m = 32, σ = 4, получим

По   таблице   значений   функции   Ф(х)   находим   Ф(1,5) = 0,4332, Ф(1) = 0,3413.
Итак, искомая вероятность:

Заключение по лекции:

В лекции мы рассмотрели законы распределения непрерывных величин.