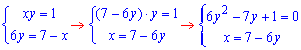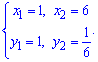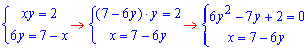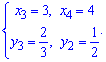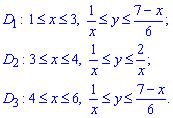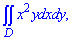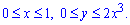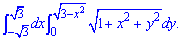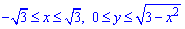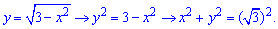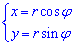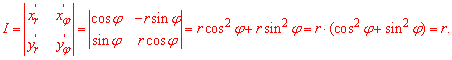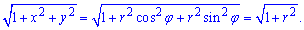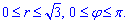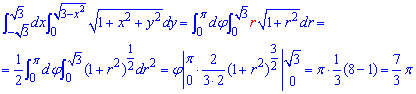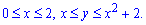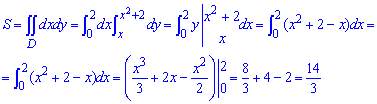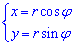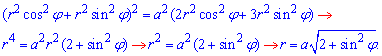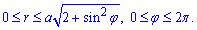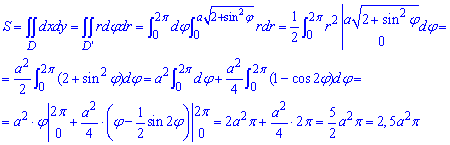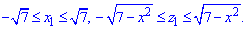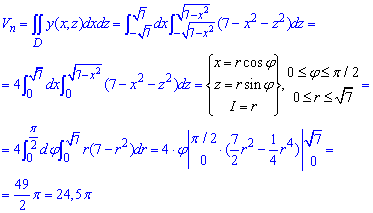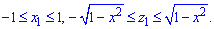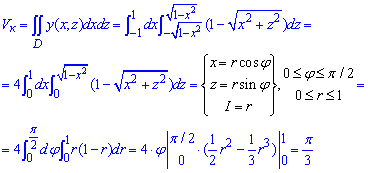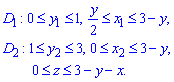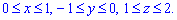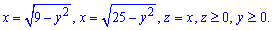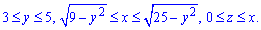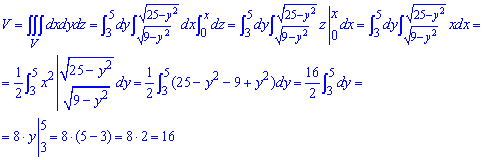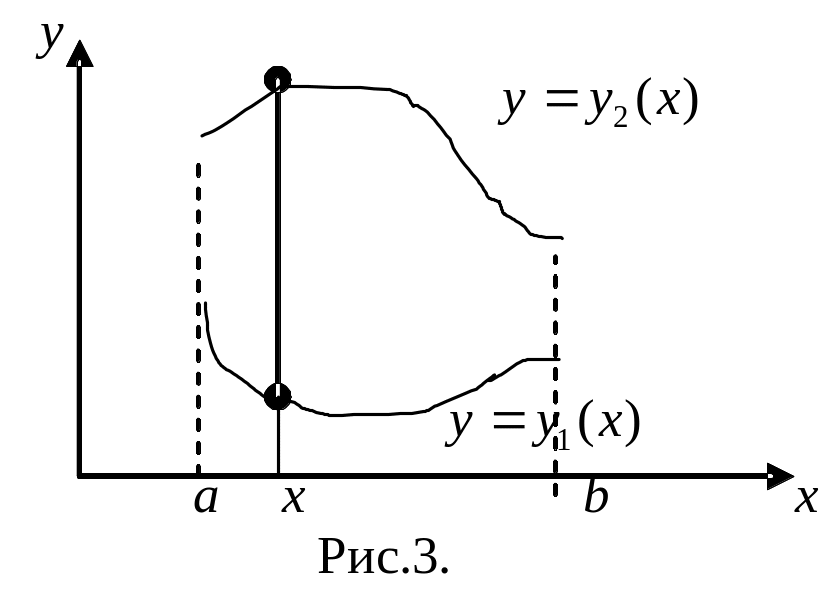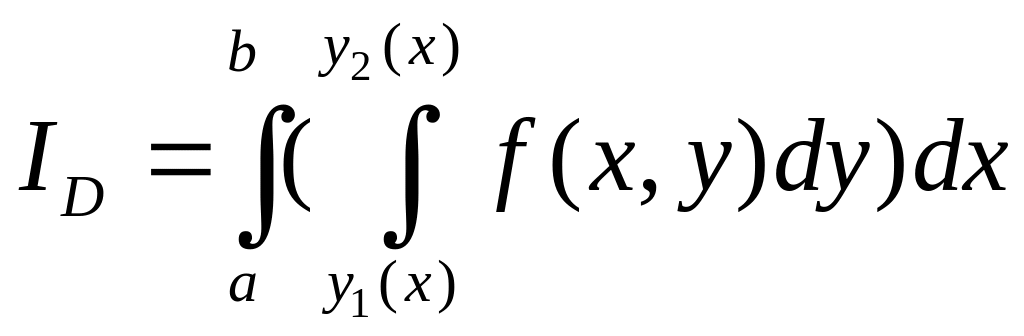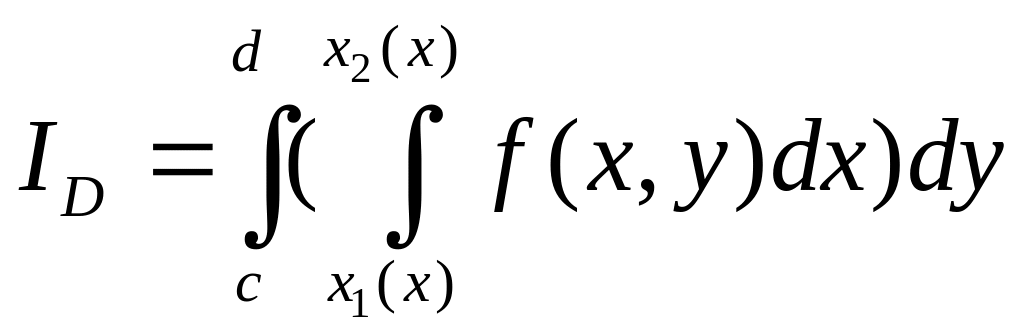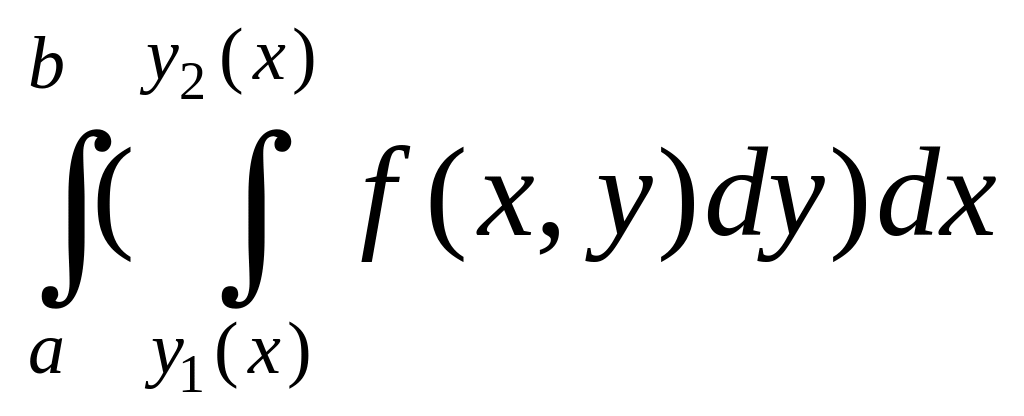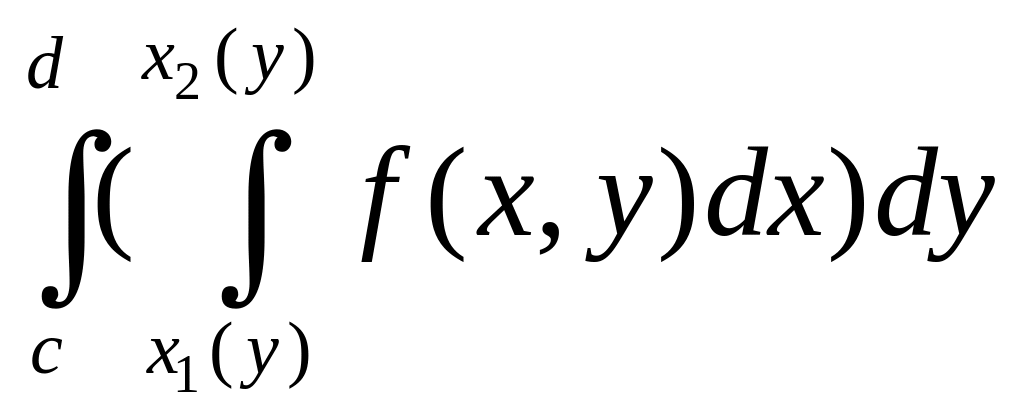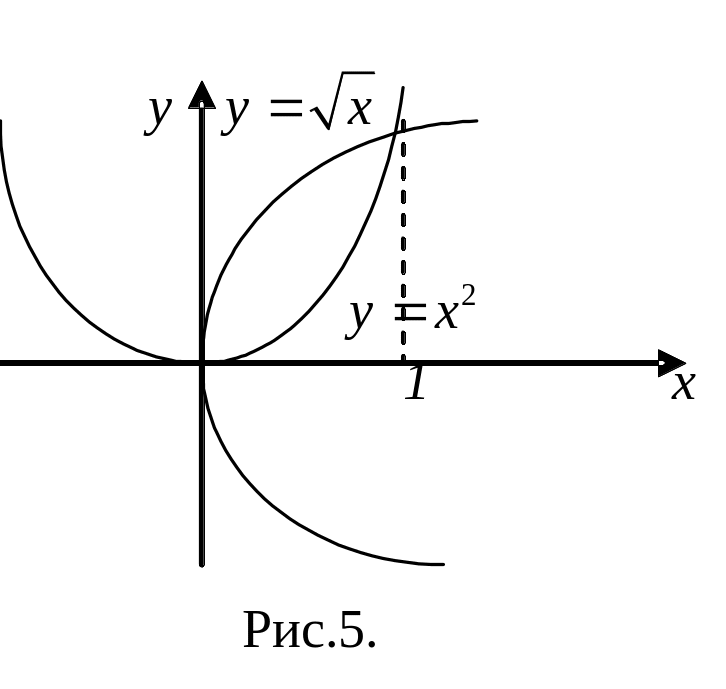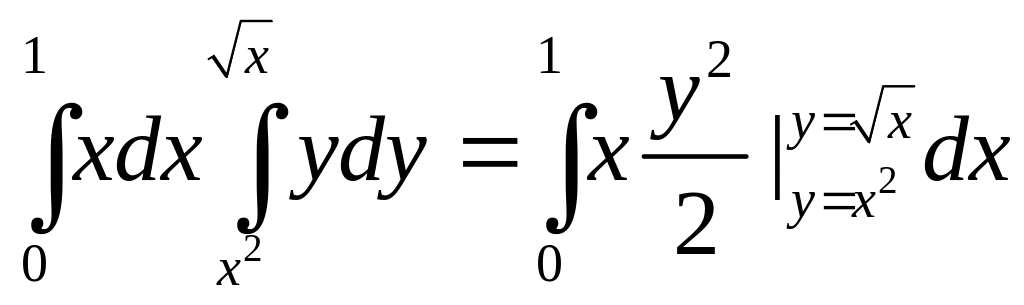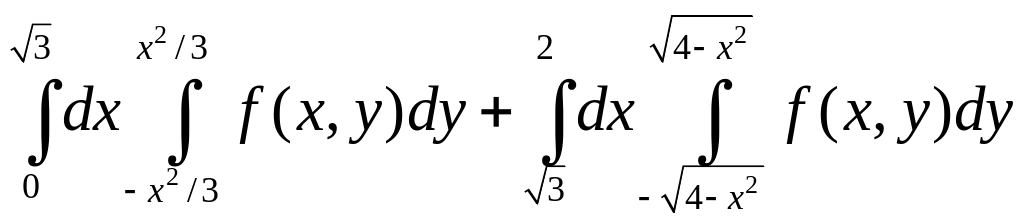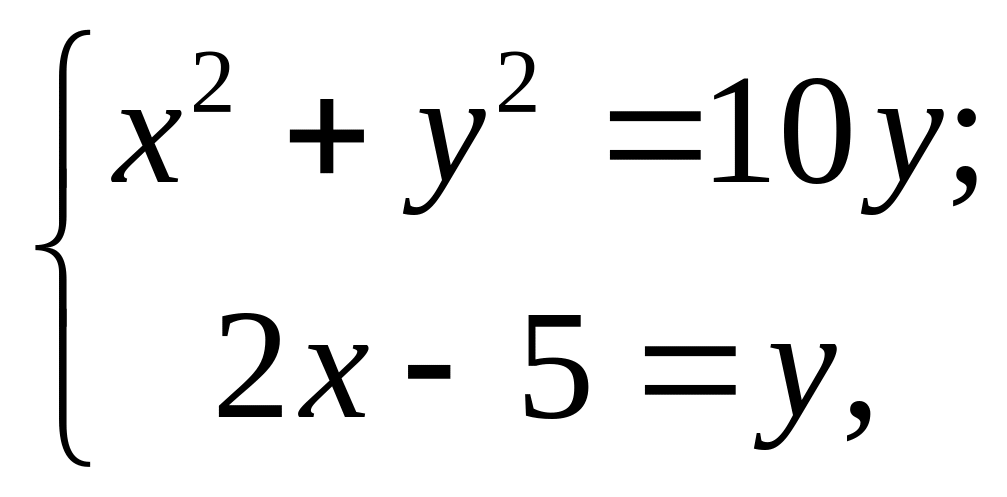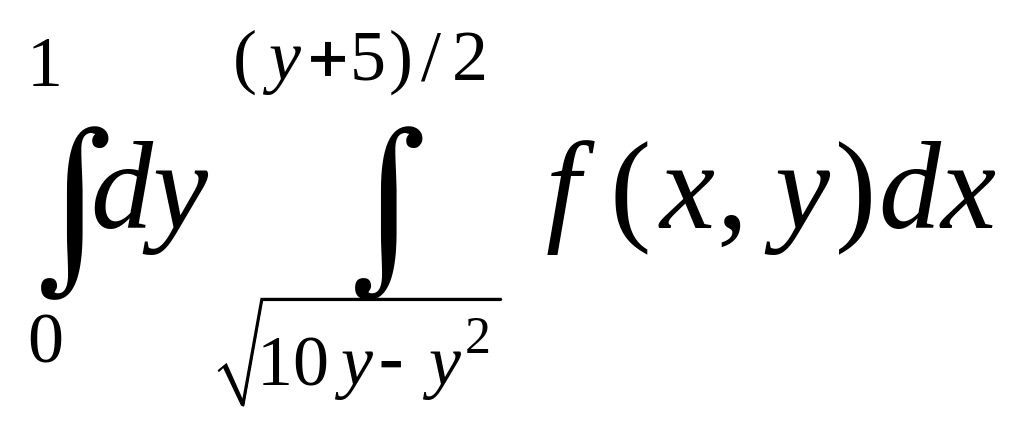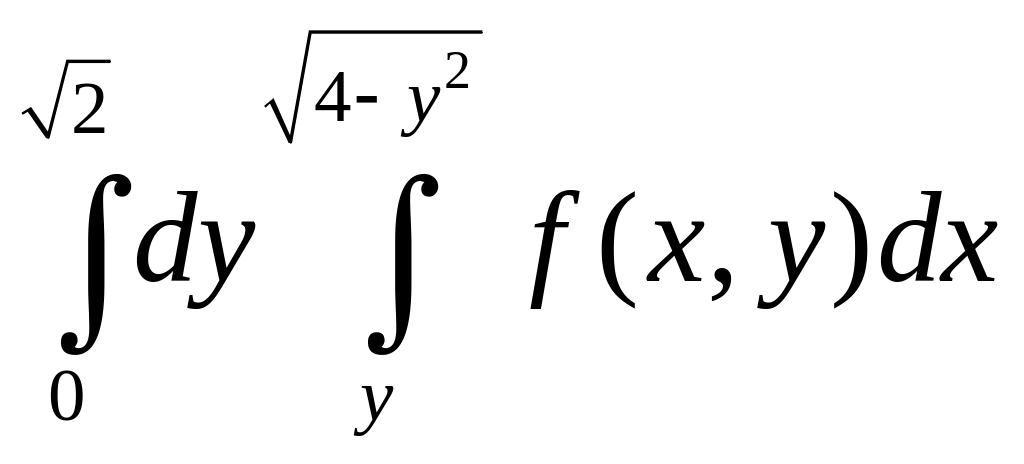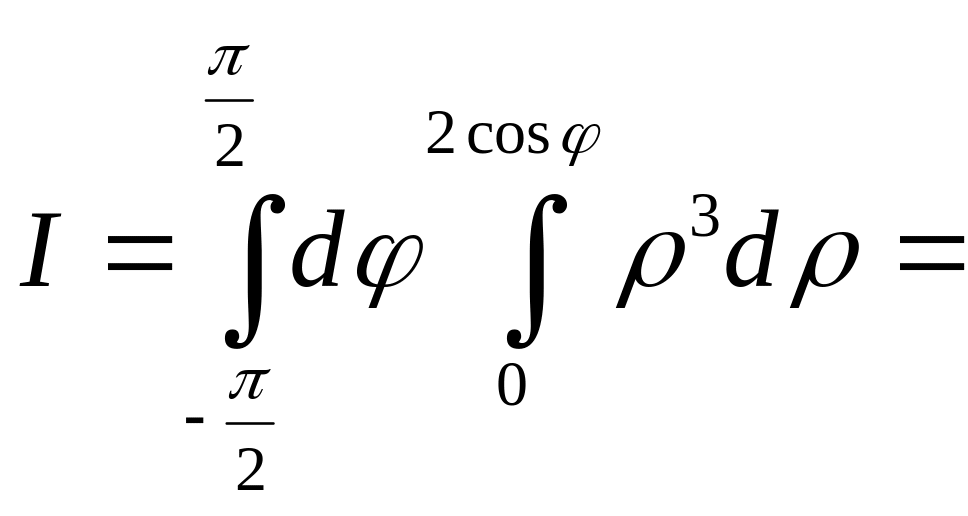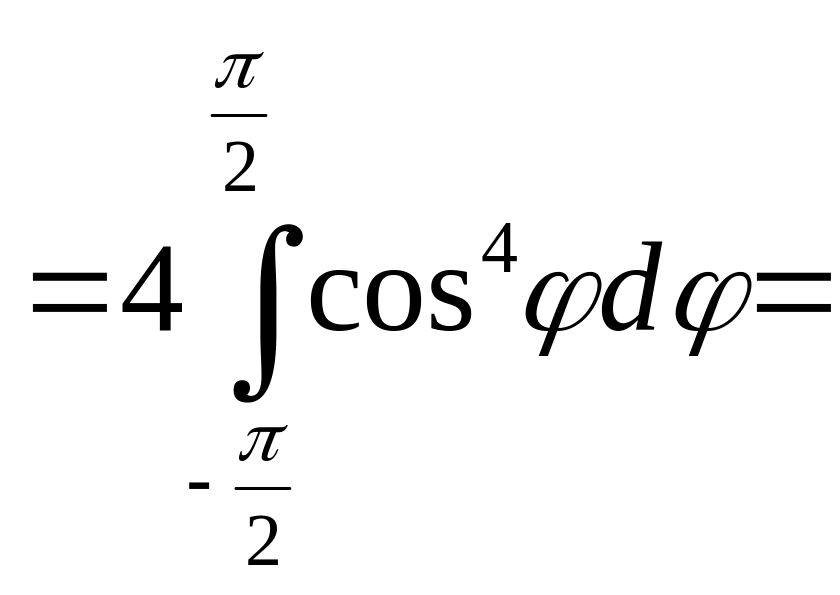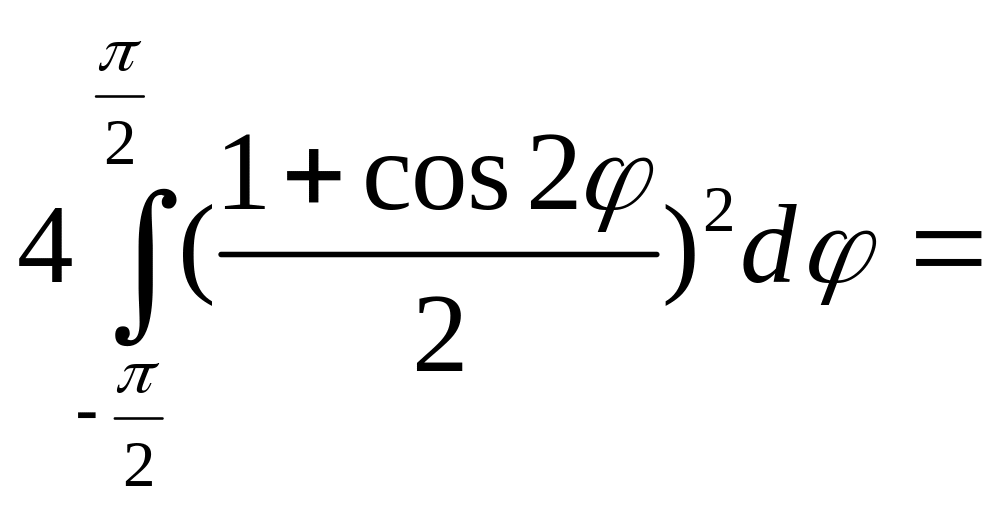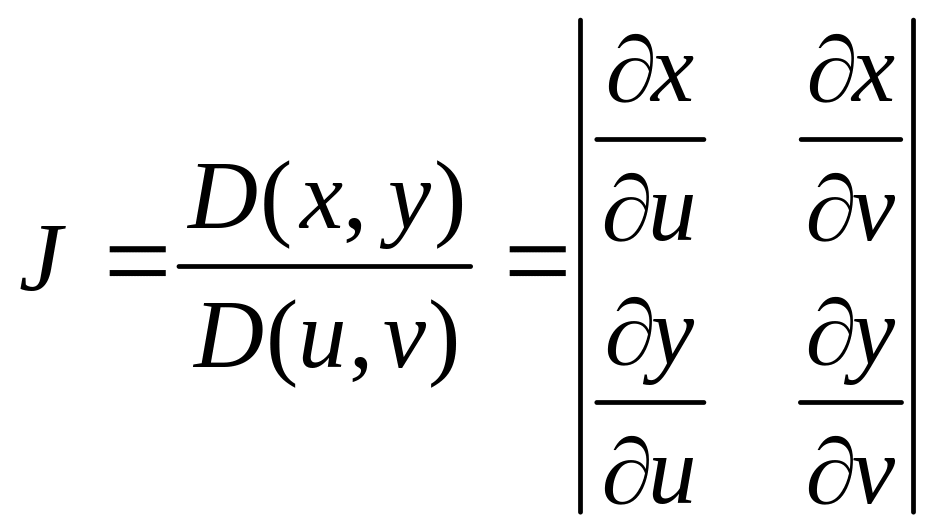Двойные и тройные интегралы даются трудно всем студентам. Одна из причин — это отсутствие возможности качественно строить области интегрирования.
Из воображения их брать удается не многим специалистам. Что касается нахождения объемов, образованных пересечением плоскостей, то здесь эта проблема становится еще большей.
Другое дело, что часто кратные интегралы начинают изучать когда студенты только что научились находить определенные интегралы.
Всем Вам помогут в учебе готовые ответы индивидуальной работы.
Приведенные ниже 10 примеров научат Вас решать задание разной сложности.
ВАРИАНТ — 19
Двойной интеграл
ЗАДАНИЕ 2.13 Найти площадь плоской фигуры, заданной следующими условиями, : xy=1, xy=2, 6y=7-x.
Решение: Сначала выполняем построение кривых, чтобы понять площадь какой фигуры ищем
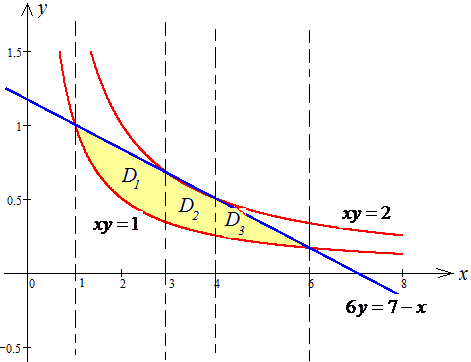
Дальше видим, что область интегрирования нужно разбивать на три части.
Есть другой вариант, более легкий с точки зрения практической реализации.
Можно найти площадь между двумя красными кривыми и от нее отнять площадь в области D2 между красной и синей кривыми. В результате получим разницу двух двойных интегралов.
Но здесь пойдем более длинным по пути, описанный попробуйте реализовать самостоятельно.
Первое, что нам нужно — это определить в каких точках графика кривые пересекают друг друга.
Найдем точки пересечения графиков 1 и 3 функций:
складываем систему из двух уравнений
и находим решение
Пересечение второй и третьей функций дают систему уравнений
для определения двух точек
Заданную область будем разбивать на три области: D=D1+D2+D3.
Расставим пределы интегрирования в каждой области:
Через двойной интеграл вычисляем площадь фигуры, ограниченной заданными кривыми:
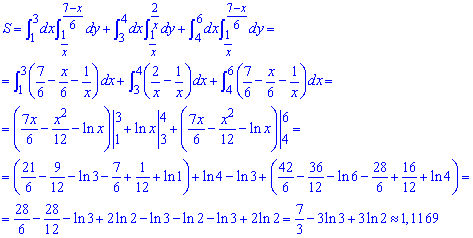
Приближенно площадь поверхности равна 1,12 единиц квадратных.
ЗАДАНИЕ 3.12 Вычислить двойной интеграл по области D, ограниченной указанными линиями:
D: y=2x3, y=0, x=1.
Решение: Найдем точки пересечения графиков заданных функций : 2x3=0, x=0.
Изобразим графически область интегрирования
Расставим пределы в заданной области D:
Вычислим двойной интеграл по области D, ограниченной указанными линиями: 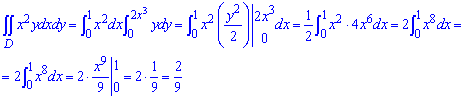
Площадь имеет место лишь в тех случаях, когда функция интегрирования равна единице.
ЗАДАНИЕ 4.11 Вычислить двойной интеграл, используя полярные координаты:
Решение: Запишем область интегрирования, которая ограничена кривыми
где
Получили круг с центром в точке O (0;0) и радиусом ровным ругаю из трех 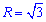
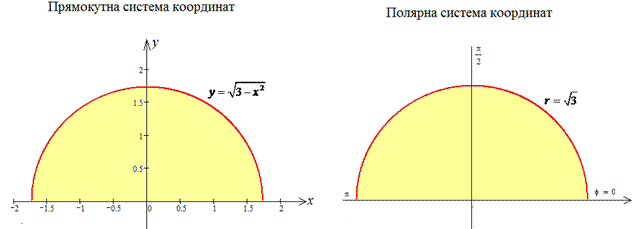
Изобразим полукруг в декартовой и полярной системе координат
Перейдем к полярной системе координат (СК), используя следующую замену переменных :
Следует помнить, что дополнительно нужно вычислить якобиан перехода от декартовой к полярной СК:
Он важен, поскольку на него нужно домножити подинтегральную функцию, выраженную в новых координатах
Найдем вид подинтегральной функции в полярной системе координат :
Запишем пределы интегрирования в полярной СК:
Осталось вычислить двойной интеграл:
Интеграл равен I=7*Pi/3.
То, что интеграл содержит число Pi лишь подтверждает правильность вычислений, ведь для круговых форм это распространено.
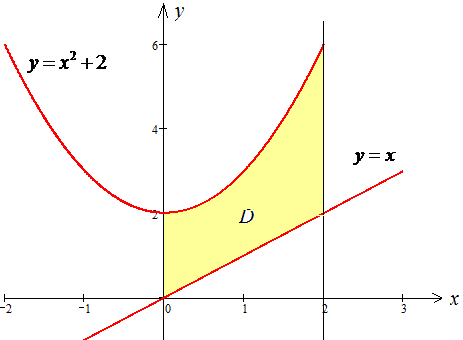
ЗАДАНИЕ 5.10 Вычислить площадь области D, ограниченной указанными линиями:
D: y=x2+2, x=2, y=x
Решение: Расставим пределы в заданной области D:
Построим кривые, чтобы представить фигуру площадь которой мы ищем.
Здесь есть два варианта: сложный — когда внутренний интеграл за переменной x предусматривает нахождение площади, через сумму двойных интегралов по 2 или 3 областям.
Мы же пойдем легким по пути и определим площадь заштрихованной фигуры с помощью одного двойного интеграла.
Вычислим площадь криволинейной трапеции, ограниченной указанными линиями:
Площадь равна S=14/3 единиц квадратных.
Как видите — выбор порядка интегрирования может существенно сэкономить время при написании контрольной работы, на экзамене или практических заданиях. Для сравнения попробуйте вычислить первым временем и сравнить масштаб выполненных работ.
ЗАДАНИЕ 6.9 Используя двойной интеграл, вычислить, перейдя к полярным координатам, площадь плоской фигуры : (x2+y2)2=a2(2x2+3y2).
Решение: Один из предыдущих примеров содержал переход к полярной системе координат :
и был найден якобиан переходу I=r.
Определим пределы интегрирования :
Пределы интегрирования:
Их легко определить в полярной СК — радиус изменяется от нуля к кривой, которая ограничивает площадь, а угол изменяется от 0 до 360 градусов.
Это Вы должны знать при вычислении подобных заданий.
Вычислим площадь плоской фигуры:
Под интегралом пришлось понижать степень синуса за известной тригонометрической формулой. На пратиці Вы такие случаи рассматривали, то же здесь мы Вам ничего нового не открываем.
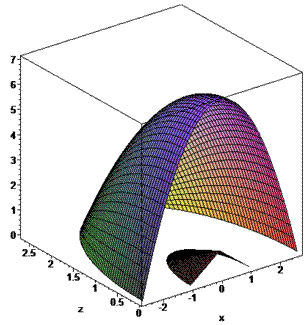
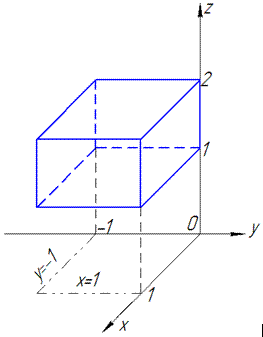
ЗАДАНИЕ 7.8 Найти объем тела, заданного поверхностями, что его ограничивают:
y=7-x2-z2, 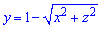
Решение: Половину 3d рисунка тела изобразим графически — это хорошая подсказка, которая развивает воображение.
Вычислим объем тела, которое ограничивает эти две поверхности (то есть рисунок разрезали пополам для наглядного отражения)+ снизу плоскостью y=0.
Чтобы упростить интегралы объем тела найдем как разницу объемов параболоида и конуса (см. рис.).
Расставим пределы в заданной области D1 (круг радиусом 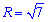
Найдем объем параболоида:
При нахождении двойного интегралу целесообразно перейти к полярной СК, поскольку обе фигуры образованы вращением кривой вокруг оси Oy.
Расставим пределы в области D2 (круг радиусом R=1):
Вычислим объем конуса:
Он равен V=Pi/3 единиц кубических.
Здесь также во время интегрирования перешли к полярной СК.
Последним шагом найдем объем тела, которое находится между параболоидом и конусом, :
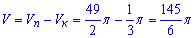
Тройной интеграл
ЗАДАНИЕ 8.7 Расставить пределы интегрирования в тройном интеграле 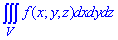
V: 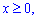
Нарисовать область интегрирования.
Решение: В плоскости Oxy уравнение прямых запишем следующим образом: y=1, x=y/2, x=3-y.
Уравнение плоскости в пространстве запишем в виде: z=3-y-x.
Построим пространственный рисунок тела и его проекцию в декартовую плоскость
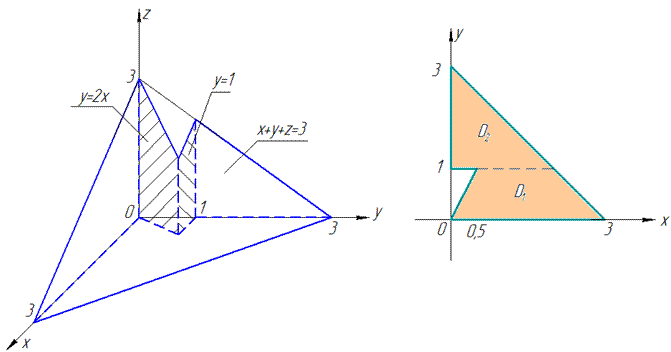
D=D1+D2, поэтому пределы интегрирования расставляем следующим образом:
На основе проведенного анализа записываем пределы в тройной интеграл
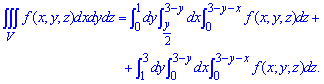
Легко убедиться, что получим сумму из трех тройных интегралов.
ЗАДАНИЕ 9.6 Вычислить тройные интегралы: 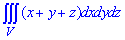
Решение: Область являет собой параллелепипед, который изображен ниже
Это значительно упрощает интегрирование
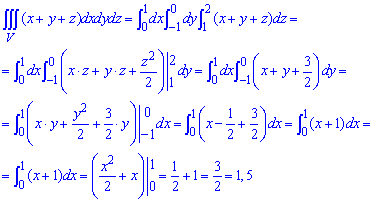
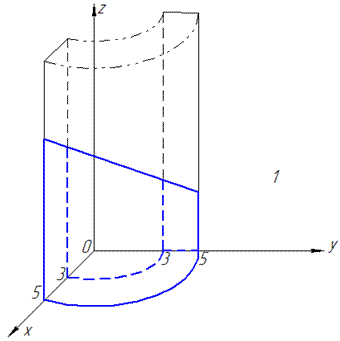
ЗАДАНИЕ 10.5 Используя тройной интеграл, вычислить объем тела, ограниченного поверхностями:
Нарисовать область интегрирования.
Решение: Прежде всего выполняем построение к условию, в крайнем случае старайтесь схематически нарисовать область интегрирования
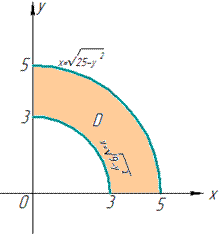
Дальше записываем пределы интегрирования, учитывая выполненный рисунок:
Через тройной интеграл находим объем тела:
Превращения не сложны и их разберите самостоятельно.
Объем ровный 16 куб. од.
На этом индивидуальная работа из повторных интегралов выполнена.
Больше примеров на двойные и тройные интегралы Вы можете найти в следующих материалах.
Вычисление двойных интегралов с помощью повторного интегрирования
Пусть
функция
определена в области
,
где
и
—
непрерывные функции на отрезке
.
Область, в которой
всякая прямая параллельная оси
,
проходящая через внутреннюю точку
области, пересекает ее границы в двух
точках, называется правильной
относительно
оси
(рис.3).
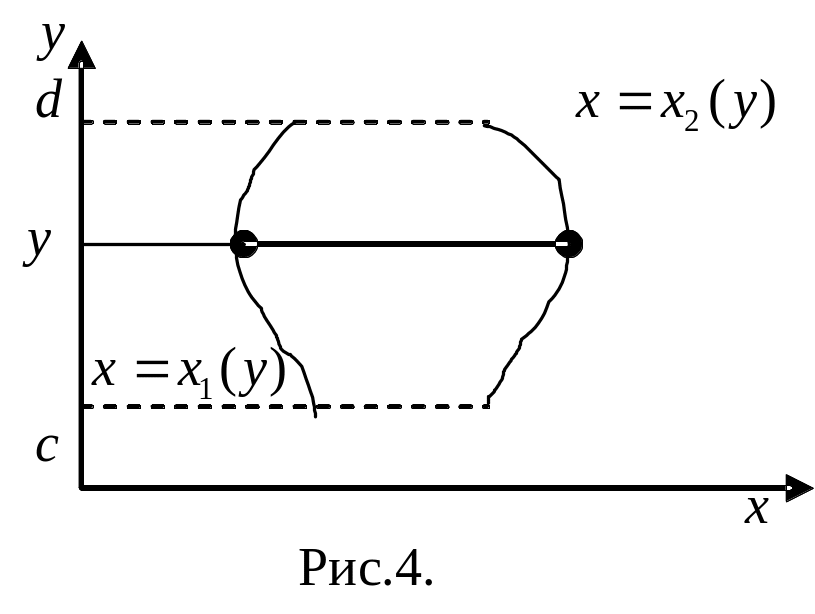
Аналогично
определяется о
бласть
правильная
относительно оси
:
где
функции
и
—
непрерывные функции на отрезке
(рис.4).
Выражения
вида
,
называются
повторными
интегралами
от функции
по
области
.
Теорема.
Двойной интеграл от непрерывной функции
по
правильной области
равен повторному интегралу от этой
функции по области
.
=
.
Если
область правильная относительно оси
,
то двойной интеграл вычисляется как
повторный вида
=
В
случае, когда область
не является правильной, ее разбивают
на части, каждая из которых является
правильной.
Частный
случай. Если
область интегрирования есть прямоугольник,
ограниченный прямыми
то
формула преобразования двойного
интеграла в повторный имеет вид
.
Если
кроме того, в подынтегральной функции
переменные разделены, то есть
,
то двойной интеграл превращается в
произведение двух определенных
интегралов:
.
Пример.
Найти
,
где
—
область, ограниченная линиями
(рис.5).
Решение.
=
=
Пример.
Найти
,
где
—
квадрат
(рис.6).
Решение.
=
=
Представление
двойного интеграла в виде повторного
=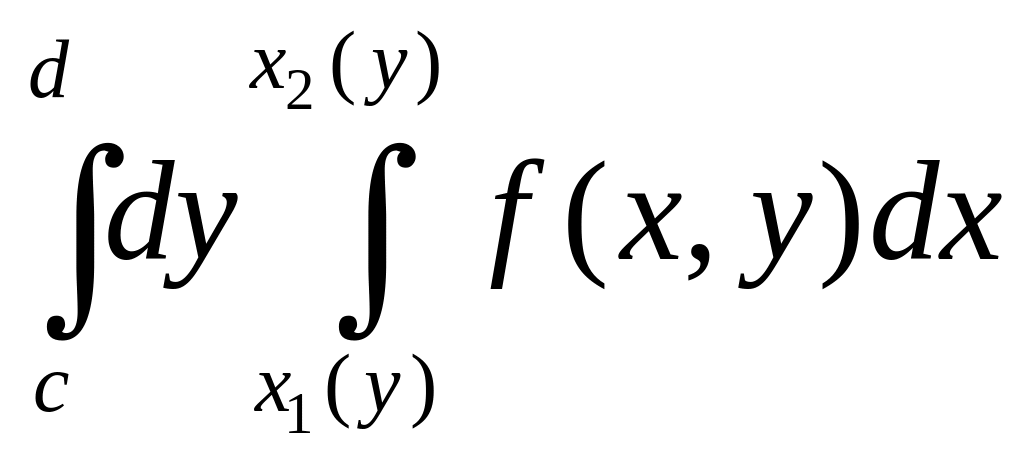
называют
расстановкой пределов интегрирования
в определенном порядке. Задача расстановки
пределов интегрирования допускает
несколько вариантов.
1.
Задан двойной интеграл по области
.
Расставить пределы интегрирования в
том и другом порядке.
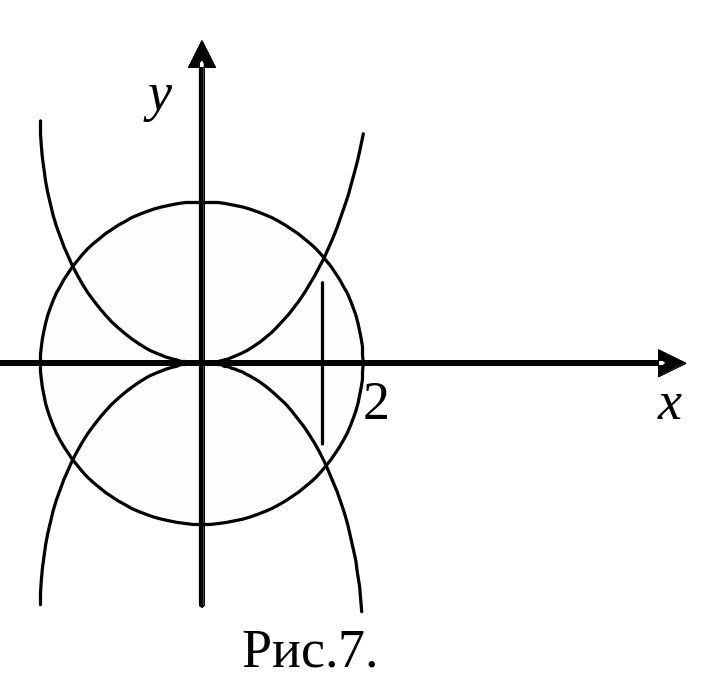
Пример. Область
лежит в правой полуплоскости (т.е.
и
ограничена
кривыми:
(рис.7). В двойном интеграле
расставить пределы интегрирования в
одном и другом порядке.
Решение.
Запишем неравенства, которым должны
удовлетворять координаты точек области
:
или
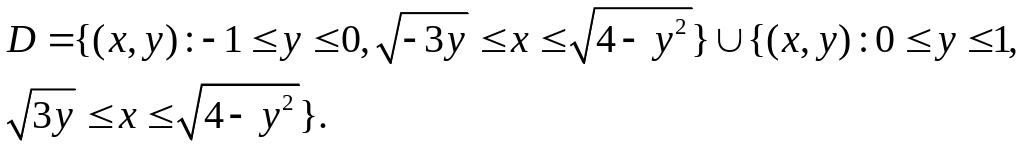
Расставим
пределы интегрирования
=
=

2.
Задан двойной интеграл по области
.
Расставить пределы интегрирования в
каком-либо порядке.
В
этом случае выбирают порядок
интегрирования, при котором интеграл
имеет наиболее простое представление.
Выбор может определяться как видом
области интегрирования, так и свойствами
подынтегральной функции. Например,
расстановка пределов в одном порядке
требует разбиения множества
на меньшее число составляющих, чем
расстановка в другом порядке.
Пример. Расставить
пределы интегрирования в интеграле
,
где
—
область ограниченная линиями:
,
,
(рис.8).
Решение.
Для расстановки пределов интегрирования
в порядке
можно не разбивать
на составляющие области, а для другого
порядка расстановки пределов такое
разбиение необходимо. Исходя из этого
выбираем порядок
.
Решая систему
получаем координаты точек пересечения:
.
Следовательно,
и
=
.
3.Задан
повторный интеграл
.
Поменять порядок интегрирования.
Для
решения такой задачи сначала делают
переход от заданного повторного интеграла
к двойному, то есть восстанавливают по
данным пределам область интегрирования
:
=
.
Условия на координаты точек (
множества
получаем исходя из заданного повторного
интеграла
.
В полученном двойном интеграле проведем
расстановку пределов интегрирования
в требуемом порядке. Таким образом,
считая область
правильной относительно обеих осей
и
,
получаем цепочку равенств
=
=
.
Пример. Изменить
порядок интегрирования в повторном
интеграле
.
Решение.
Запишем условие на координаты точек
из множества
,
по которому берется
интеграл:
(рис.9).
Область
правильная как относительно оси
,
так и относительно оси
.
Так как при интегрировании в порядке
верхняя граница области
задается двумя различными функциями,
представим множество
в виде
,
где

Итак,
=
.
Двойной
интеграл в полярной системе координат
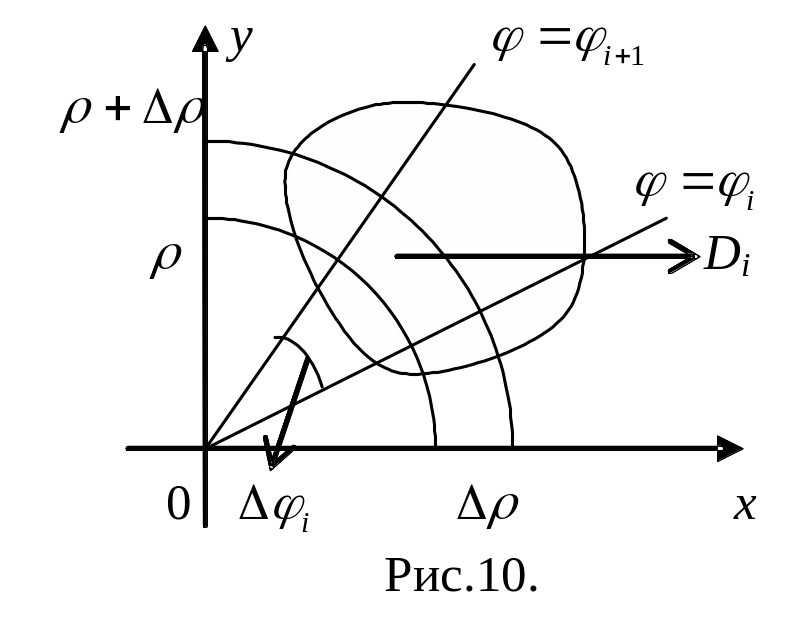
Выведем
формулу перехода от декартовых координат
к полярным в двойном интеграле.
Пусть
— непрерывная функция на ограниченной
замкнутой области
.
Так как при определении двойного
интеграла предел последовательности
интегральных сумм не зависел от способа
разбиения области
на
части
,
то разобьем область
на
концентрическими окружностями
и лучами
(рис.10). Тогда площадь
с
точностью до бесконечно малых более
высокого порядка малости чем
.
Таким образом, двумерный элемент
площади в полярных координатах
запишется в виде
.
Пусть теперь
область
правильная относительно
,
то есть любой луч, исходящий из полюса
и проходящий через внутреннюю точку
области пересекает границу области
только в двух точках. В этом случае
область
можно задать множеством
(рис.11).
Тогда повторный интеграл по области
представим в виде

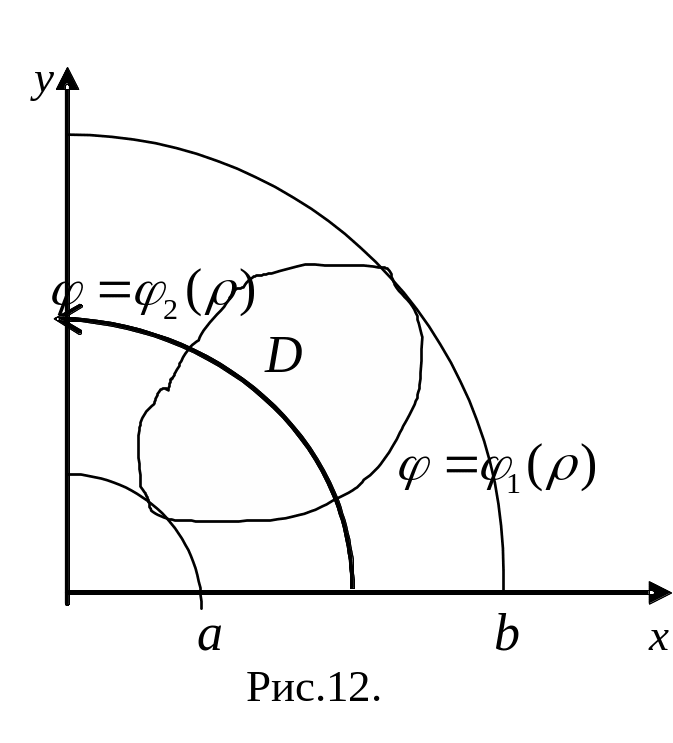
Е
сли
любая окружность с центром в начале
координат, проходящая через внутреннюю
точку области пересекает линию границы
в двух точках, то есть область
есть множество:
,
(рис.12), то повторный интеграл примет
вид
=
В
случае, когда полюс лежит внутри области
и любой луч пересекает границу не более
чем в одной точке (рис.13), для вычисления
удобно использовать формулу

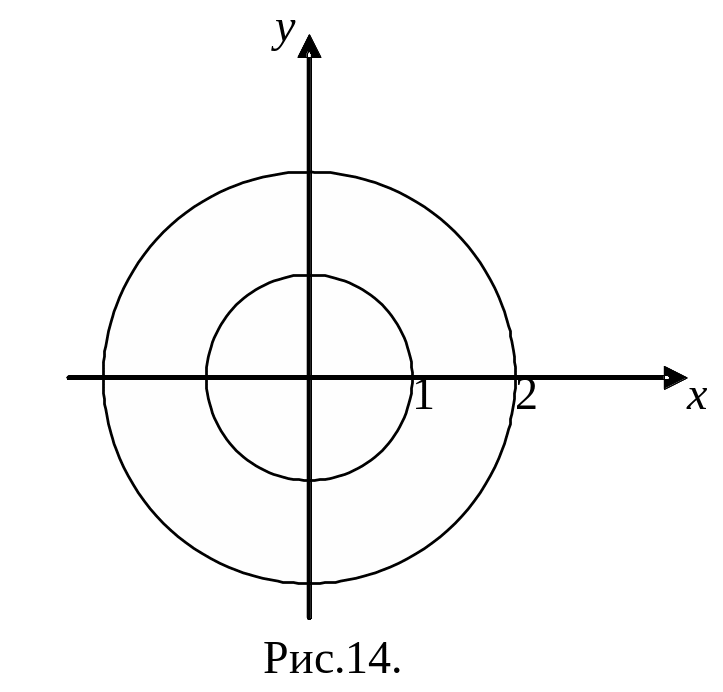
Пример.
Вычислить двойной интеграл
в
полярной
системе координат по области
,
ограниченной линиями
,
расположенной в I
квадранте (рис.14).
Решение.
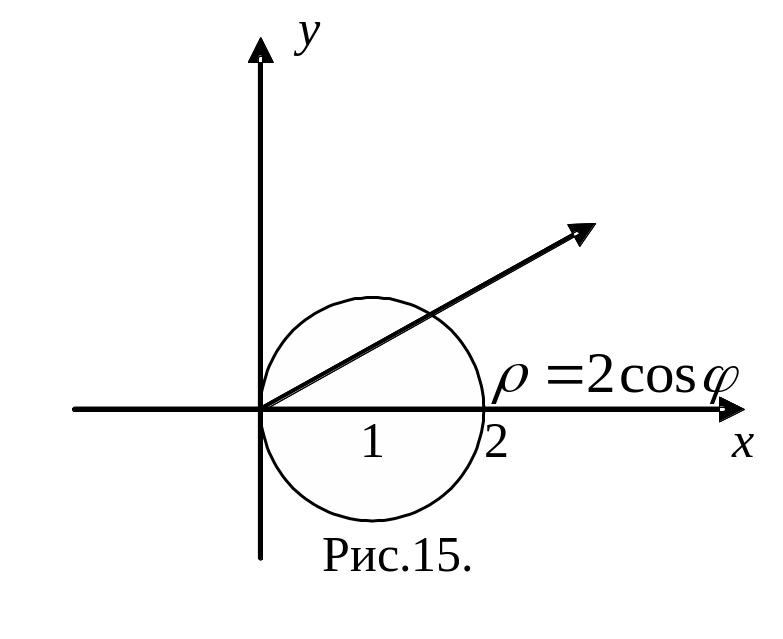
Пример. Вычислить
двойной интеграл
в полярной системе координат по области
,
ограниченной окружностью
(рис.15).
Решение.
Перейдем к полярным координатам c
полюсом в точке
:
Угол
изменяется от
до
Подставляя полярные
координаты
в уравнение окружности, получим
,
откуда
или
— уравнение окружности в полярных
координатах. Двойной интеграл по области
сводится повторному
=
Замена
переменных в двойном интеграле.
Рассмотрим
двойной интеграл вида
.
Замена переменных в двойном интеграле
состоит в переходе от
переменных
и
к новым переменным
и
по формулам
,
.
При этом каждая точка
области
соответствует некоторой точке
области
,
а каждая точка
области
переходит в некоторую точку
области
Функции
называют также отображением области
плоскости
на область
плоскости
.
Пусть отображение удовлетворяет
следующим условиям:
1.
Отображение взаимно однозначно, то есть
различным точкам
области
соответствуют различные точки
области
.
2.Функции
имеют
в области
непрерывные частные производные первого
порядка.
3.
Якобиан отображения
отличен от нуля во всех точках области
.
Тогда
справедливо равенство
=
Эта
формула называется формулой замены
переменных в
двойном
интеграле.
Замечание.
При переходе к полярной системе координат
якобиан перехода имеет вид
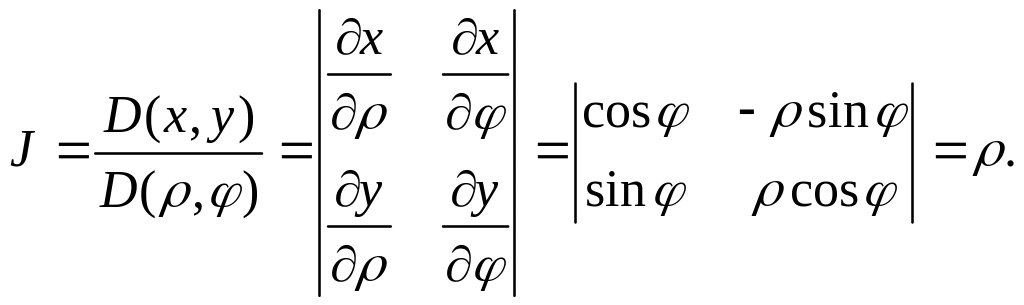
Приложения
двойных интегралов.
Двойные
интегралы применяются для вычисления
площадей плоских фигур и поверхностей,
объемов пространственных тел, механических
величин связанных с непрерывным
распределением массы в плоской области,
а также для решения многих других задач.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
(схема 40)
Для функции двух переменных имеет место обобщение определенного интеграла — двойной интеграл, относящийся к кратным интегралам.
Рассмотрим в плоскости x0y замкнутую
область D с границей L. Пусть непрерывная функция f(x,y) определена в области D. Произвольными линиями разобьем область D на конечное число n частей
– площадок: 

соответствующих площадок, но и их площади.
В каждой из ∆Si (внутри или на границе) возьмем точку Pi;
получим n точек: 

сумму произведений вида 

Эта
сумма называется интегральной суммой для функции f(x,y) в
области D. Если f ≥ 0 в области D, то каждое
слагаемое 
Рассмотрим произвольную
последовательность интегральных сумм, составленных с помощью функции f(x,y) для данной области D:

при
различных способах разбиения
области D на
части ∆Si. Очевидно, при n→∞ максимальный диаметр
площадок ∆Si стремится к нулю.
Теорема
6.1.
Если функция f(x,y) непрерывна в замкнутой области D, то
существует предел последовательности (6.2) интегральных сумм (6.1) при условии, что максимальный диаметр площадок ∆Si стремится к нулю, а n→∞. Этот предел один и тот же
для любой последовательности вида (6.2), то есть он не зависит ни от способов разбиения
области D на площадки ∆Si, ни от
выбора точек Pi внутри площадок ∆Si
Этот предел 

Область D при этом называется
областью интегрирования.
1. Вычисление двойного интеграла в декартовой система
координат
Рассмотрим область D, лежащую в плоскости x0y и являющуюся правильной в направлении оси 0y. Это означает, что всякая прямая, параллельная оси 0y и проходящая через
внутреннюю точку области, пересекает границу области в двух точках N1 и N2.
Мы
предположим, что в рассматриваемом случае область D
ограничена линиями: 

на отрезке [a;b]. Аналогично определяется
область D, правильная
в направлении оси 0x.
Если область D является правильной как в направлении оси 0x, так и в направлении оси 0y, то
она называется просто правильной областью.
Пусть функция f(x,y) непрерывна в области D. Рассмотрим
выражение

которое назовем двукратным
интегралом от функции f(x,y) по
области D. В этом
выражении сначала вычисляется внутренний интеграл, стоящий в скобках, причем
интегрирование производится по y, а x
считается постоянной величиной. В
результате интегрирования получится непрерывная функция от x:

Эту функцию мы интегрируем по x
в пределах от a
до b:

В результате получается некоторое постоянное число.
Теорема
6.2. Двойной интеграл от непрерывной функции f(x,y) по
правильной области D равен двукратному
интегралу от этой функции по области, то
есть

Пусть правильная в направлении оси 0x область D
ограничена линиями 

Очевидно, что в этом случае

Таким образом, для вычисления двойного
интеграла его надо представить в виде двукратного, в зависимости от вида
области D или
подынтегральной функции, либо с помощью формулы (6.5), либо (6.6) .
Пример
6.1. Вычислить 
определяемый неравенствами и

Решение. Применим
формулу (6.5), считая внутренний интеграл по переменной y:
Если область D является правильной в направлении обеих осей
координат, то применимы обе формулы (6.5) и (6.6), следовательно,

Таким образом, повторное интегрирование не
зависит от порядка интегрирования. Поэтому при вычислении двойного
интеграла следует пользоваться той из двух формул, которая приводит к менее трудоемким
выкладкам. Полезно для упражнения в вычислении повторного интегрирования рассматривать задачу о замене порядка
интегрирования в двойном интеграле 
последовательность действий:
1) чертят область интегрирования D, которая
находится в полосе между прямыми x=a и x=b, при этом ограничена снизу линией y=φ1(x), а сверху
– линией y=φ2(x);
2) область D проектируют на ось 0y и находят уравнения
прямых y=c и y=d, ограничивающих снизу и
сверху полосу, в которой расположена область
D;
3) находят
левую x=ψ1(y) и правую x=ψ2(y) границу области D.
Аналогичные выкладки производят при
необходимости замены порядка интегрирования в двойном интеграле :
1) чертят область интегрирования D, которая находится в полосе между прямыми y=c и y=d, при этом ограничена слева линией x=ψ1(y), а справа
– линией x=ψ2(y);
2) область D проектируют на ось 0x и находят уравнения
прямых x=a и x=b, ограничивающих слева и
справа полосу, в которой расположена область
D;
3) находят нижнюю y=φ1(x) и
верхнюю y=φ2(x) границу области D.
Примечание. В случае, когда какая-либо из этих границ состоит из
двух или большего числа линий, записанных разными уравнениями, то область D разбивается на части, а интеграл – на сумму
интегралов по этим частям
Пример 6.2. Изменить
порядок интегрирования 
Решение. Область D расположена в плоскости x0y между прямыми x=0 и x=1 (рис. 6.1). Ее нижняя граница y=x,
верхняя –

области является прямая x=0, правой на участке
участке

2. Вычисление двойного интеграла в полярной системе
координат
Пусть область D задана в полярной системе координат (рис. 6.2). Если ее полюс O совпадает с началом
координат декартовой системы, а полярная ось совпадает с осью 0x, то формулы перехода имеют
вид:

полярной системе. Тогда

Для вычисления
такого двойного интеграла применяют то же правило сведения его к двукратному
интегралу. Так, если область D имеет
вид, изображенный на рисунке 6.2 (ограничена лучами φ=α и φ=β,
где α < β, и кривыми 
луч, выходящий из полюса, пересекает ее границу L не более чем в двух точках), то правую часть формулы
(6.7) можно записать в виде:

Внутренний интеграл берется при
постоянном φ и переменной r, при
вычислении внешнего интеграла φ
становится переменной.
Если полюс O лежит внутри области D, то каждый полярный радиус
пересекает контур L в одной точке. При этом следует рассматривать 
Пример 6.3. Вычислить двойной интеграл 
полукруг с центром в точке (3;0) и с радиусом, равным 3 (рис. 6.3).
Решение. Перейдём к полярной
системе координат. Пусть полюс совпадает
с началом координат, а полярная ось совпадает с положительным направлением оси 0x. Чтобы найти
уравнение полуокружности АМО в полярной системе координат, выберем на ней
произвольную точку M(r;φ) и определим
зависимость между полярными координатами r и φ. Как видно, при любом выборе точки M угол АМО будет прямым. Следовательно, r=OA∙cos φ или r=6∙cos φ (так как AO=6). Таким образом, в
заданной области D полярный радиус r меняется от 0 до 6∙cos φ, а полярный угол φ
– от 0 до
Переходя к полярной системе координат с помощью (6.8),
получаем:
Примечание. Переход к полярным координатам полезен, когда подынтегральная
функция имеет вид 
линий, ограничивающих область D, также преобразуются к полярным координатам
Двойной интеграл по-шагам
Что умеет?
- Вычисляет двойной интеграл по области, ограниченной указанными линиями
- Вычисляет с помощью двойного интеграла площадь фигуры, ограниченной линиями
- Вычисляет повторные интегралы (с уже известными пределами)
- Записывает двойной интеграл от f(x, y) в виде повторного
Вычисление площади
Для вычисления площади фигуры, ограниченной линиями с помощью двойного интеграла подставьте в подинтгральную функцию просто 1
Примеры двойных интегралов
- С квадратом
-
8*x*y+9*x^2*y^2
- С кубом
-
x^3+x*y^2
- С синусом и квадратным корнем
-
sin(sqrt(x^2 + y^2))/sqrt(x^2 + y^2)
- Линейная функция
-
2*x + y
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
-
квадратные корни sqrt(x),
кубические корни cbrt(x) -
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
-
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x) -
натуральные логарифмы ln(x),
десятичные логарифмы log(x) -
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x) -
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) -
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x) -
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) -
знак числа:
sign(x) -
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x) -
Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
-
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- — умножение
- 3/x
- — деление
- x^2
- — возведение в квадрат
- x^3
- — возведение в куб
- x^5
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- Действительные числа
- вводить в виде 7.5, не 7,5
Постоянные
- pi
- — число Пи
- e
- — основание натурального логарифма
- i
- — комплексное число
- oo
- — символ бесконечности
Данные примеры также можно применять при вводе верхних и нижних пределов в двойном интеграле.