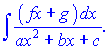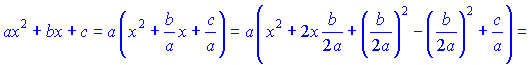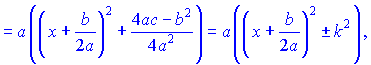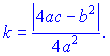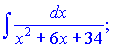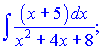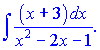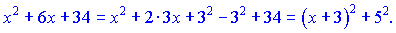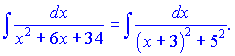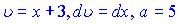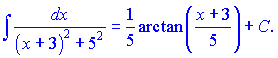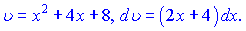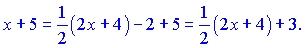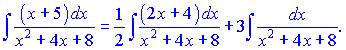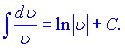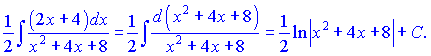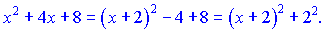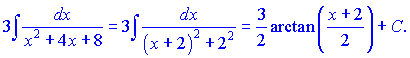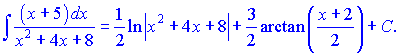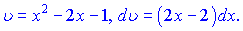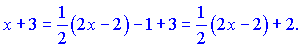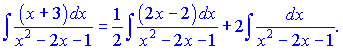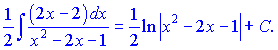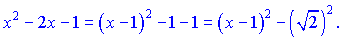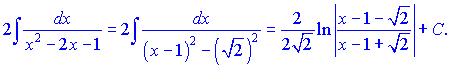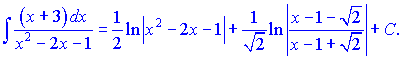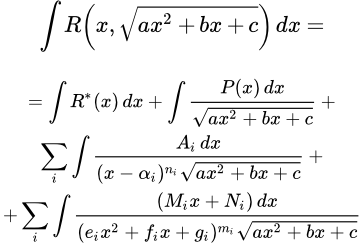Как найти интеграл квадратной функции

Рассмотрим
интегралы
или .
В знаменателе находится квадратный
трёхчлен, с отрицательным дискриминантом,
который не имеет корней и на множителе
не раскладывается.

Такие
интегралы с помощью выделения полного
квадрата приводятся к табличным интеграла
вида: ,
,
.

Пример.

Найти
интеграл .

Решение:
Найдём дискриминант знаменателя

D=9-4*2*4=-23<0
– следовательно действительных корней
нет.

Вынесем
2 за знак интеграла, получим

.

Выделим
полный квадрат

—+=

Это
табличный интеграл вида
=∙arctg

+ c

u
=
x
+ ;
du=dx

И
согласно формуле (16)

I
=(
∙ arctg

)+С.

Ответ:

arctg
+ С.

Теперь
рассмотрим интегралы вида

В
числителе появился многочлен первой
степени, который не является производной
знаменателя, а знаменатель по прежнему
имеет отрицательный дискриминант.

Вычисление
интегралов такого вида рассмотрим на
примере.

Пример.

Найти
интеграл
dx

Примем весь квадратный трёхчлен за
новую переменную

.
Найдём du=(4x+3)dx.

,
необходимо, чтобы du=(4x+3)dx.
Но в задании числитель (3x+5),
выделим из (3x+5)→
(4x+3)
следующим образом

(3x+5)=
(4x+3)
—
+5=
(4x+3)
+
, т.е. числитель получился состоящим из
суммы, которую распишем на два интеграла

I
=
dx+
=
+

Тогда
I
=
+

+c.

Задание
4

Найти
интегралы.

§5. Интегрирование рациональных функций с помощью разложения на простейшие дроби. (Метод неопределённых коэффициентов)

Перед
интегрированием рациональной дроби
нужно
сделать следующее алгебраические
преобразования:

1. Если
   дана неправильная рациональная дробь,
   то выделить из неё целую часть,
   т.е.представить в виде:

,
где М(x)
– многочлен, а
– правильная рациональная дробь.

1. Разложить
   знаменатель дроби на линейные и
   квадратичные множители (если это
   возможно).

3)
Правильную рациональную дробь разложить
на простейшие дроби с неизвестными
коэффициентами А, В, С,… это разложение
записывается в зависимости от знаменателя
дроби (если знаменатель дроби имеет
различные линейные множители):

а)
=…;

б);

в);

г).

4)
Вычислить неопределённые коэффициенты
А, В, С,… (Вычисление рассмотрим на
конкретных примерах).

В
результате интегрирование рациональной
дроби сведётся к нахождению интегралов
от многочлена и от простейших рациональных
дробей.

Пример.

Найти
интеграл

.

Решение:
Рассмотрим подынтегральную функцию.

1. Так
   как степень числителя больше степени
   знаменателя, т.е. дробь неправильная,
   то выделим из неё целую часть.

−

−

Итак
получим
;

2)
Разложим знаменатель оставшейся
правильной дроби на множители, для этого
найдём корни; в данном случае воспользуемся
методом подбора корней: Например х₁=1

=1-7+6=0

Значит
х₁=1
является одним из корней, а (х-1) один из
множителей знаменателя. Выполним деление
и получим степень знаменателя

−

−

−

0

Оставшийся
квадратный трёхчлен имеет корни х₂=2;
и х₃=-3;
т.е.
отсюда получим

.

и различны (случай (а))

Представим
теперь дробь
в виде суммы простейших дробей с
неопределёнными коэффициентами

И
рассмотрим один из способов нахождения
неопределённых коэффициентов как раз
удобный для случая, когда знаменатель
имеет неповторяющиеся множители первой
степени.

Итак
приведём правую часть к общему знаменателю

Т.к.
знаменатели левой и правой частей равны,
то приравняем числители

Далее
будем подставлять значения х в получившееся
уравнение, желательно, чтобы это были
значения, являющиеся действительными
корнями знаменателя при
х=1
(можно найти А)

15∙1+12∙1=
А(12)∙(1+3)+В∙0+С∙0;

27=А∙(1)
∙4

4∙А=27

А=

При
х
=3
(можно найти С)

15∙9+12∙(3)=А∙0+В∙0+С∙(31)
(32);

13536=(4)∙(5)∙С

99=20С

С=

При
х=2
(найдём В)

15∙4+12∙2=
А∙0+В(21)(2+3)+
С∙0

84=
5В∙1

В=.

Подставим
найденные коэффициенты и вычислим
интеграл:

+

Пример.
Найти интеграл

Решение:
Так как подынтегральная функция является
правильной рациональной дробью, то
целую часть выделять не будем.

Знаменатель
дроби на множители больше не раскладывается,
т.к. квадратный трёхчлен
— не имеет действительных корней (случай
(в)). Приступаем к разложению подынтегральной
дроби на сумму простейших дробей с
неопределёнными коэффициентами:

В
этот раз применим другой способ нахождения
неопределённых коэффициентов. Также
приведём правую часть к общему знаменателю

Т.к.
знаменатели равны, то приравняем
числители

Раскроем
скобки, получим

.

Теперь
сгруппируем в правой части члены с
одинаковыми степенями
и вынесем их за скобки, .

Будем
приравнивать коэффициенты левой и
правой частей при одинаковых степенях
х, т.е. получим систему

А+В=1,

4А+2В+С=3,

5А+2С=2.

из
первого уравнения В=1А;

из
третьего С=;

подставим
во второе уравнение 4А+22А+
найдём А

2А+

4А+2-5А=10

А=12

А=12.

Тогда
В=112=11

В=11,

С
=,

С=29.

Подставим
в подынтегральное выражение и вычислим
интегралы

+dx
= 12 ln
—
dx.

Найдём
второй интеграл

u=;

du=(2x4)dx;

11x+29=;

dx=

=

Окончательно

I
= 12 ln

Пример.

Найти
интеграл
dx.

Решение:
Дробь правильная, значит целую часть
выделять не будем.

Разложим
знаменатель на множители,

Значит
подынтегральное выражение примет вид:

(случай (б)). Представим дробь в виде
суммы простейших дробей с неопределёнными
коэффициентами

.

Здесь
можно применить комбинированный способ.
Сначала найдём А при х=2

x5=;

25=
A;

;
А
=.

При
х=2
получим

;

7=
4∙C;
C
=

Зная
А и С будем определять В следующим
образом:

х5=,

подставим
х=0

5=,

5=

4В=

4В=

В =

Найдём
интеграл:

dx
=
++

+.

Задание
5

Найти
интегралы.

Интегралы от функций, содержащих квадратный трехчлен

Для отыскания указанных интегралов от функций, содержащих квадратный трехчлен, для преобразования их к формулам интегрирования следует вначале выделить полный квадрат из квадратного трехчлена, в результате чего он преобразуется в квадратный двучлен

В дальнейшем интегралы указанных видов можно свести к формулам интегрирования посредством преобразований, применяемых в решении следующих задач.
Пример 1. Найти интегралы:
1)
2)
3)
4)
Решение. 1) Выделив из квадратного трехчлена полный квадрат , записав вместо и интегрируя, получим

по формуле 8, при
2) Выделим из квадратного трехчлена полный квадрат

и заменим переменную , полагая . Тогда получим: ,

Далее разложим полученный интеграл на два слагаемых интеграла, соответственно двум слагаемым в числителе, и находим их по формулам:

Возвращаясь к переменной , окончательно получим

3) Выделяем полный квадрат , вводим новую переменную ; тогда получим и

4) Вначале выделяем из подынтегральной неправильной дроби целую часть, деля числитель на знаменатель:

затем интегрируем каждое слагаемое отдельно:

Интеграл преобразуем к формулам 2 и 9:

Окончательно получим

Данная статья учит решать интегралы в которых в знаменателе имеем квадратное уравнение

Для нахождения таких интегралов требуется преобразование их в формулы интегрирования, для этого необходимо сначала выделить полный квадрат с квадратного уравнения.

где

Дальнейшее интегрирование сводится к отысканию табличных интегралов. Рассмотрим конкретные примеры, для закрепления данного материала.

Пример 1.

Вычислить интегралы

а)

б)

в)

Решение.

а) Выделим полный квадрат из уравнения

Искомый интеграл примет вид

Для сведения к табличному виду интеграла выполним замену переменных

и проинтегрируем

б) Данный тип интеграла сложнее предыдущего тем, что в числителе имеем функцию от 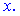Такие интегралы находят следующим образом. Сначала делаем замену переменных в интеграле

Для получения в числителе выражения порядке 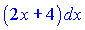умножим и разделим наш числитель на 2.

Получим

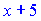
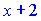
Если в числителе вместо имели , то интегрирование можно свести к отысканию одного интеграла. Однако такой вариант выбран специально, чтобы научить Вас больше. С такой заменой разбиваем интеграл на два слагаемых

Замену мы делали для того, чтобы легко было свести первое слагаемое к табличному виду

В нашем случае получим

Второе слагаемое сводится по схеме, приведенной в предыдущем примере. Для этого в знаменателе выделяем полный квадрат

Далее находим интеграл

Окончательно, искомый интеграл равен сумме двух

Схема возведения хорошо работает когда в знаменателе легко выделяется полный квадрат, в других случаях приходится иметь дело с корнями.

Также встречаются примеры когда в числителе встречаются функции 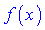высших порядков — квадратные уравнения и старше. В таких случаях их делим на знаменатель и сводим к рассматриваемому виду.

в) Делаем замену переменных

Чтобы получить в числителе выражение, содержащее 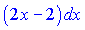умножим и разделим наш числитель на 2:

Наш интеграл запишем в виде суммы двух

Первое слагаемое даст следующий вклад

Для нахождения второго выделим в знаменателе полный квадрат

Применяя табличную формулу ко второму слагаемому, получим

Суммируя слагаемые, будем иметь

Рассмотренные три примера описывают самые распространенные интегралы данной темы. Если Вам встретятся сложные интегралы попробуйте найти решение самостоятельно, если не сможете решить обращайтесь к нам.

Практикуйте и подобные интегралы не будет у Вас препятствием в обучении.

Интегрирование рациональной функции от квадратного корня из квадратного трехчлена

Метод интегрирования

Здесь мы рассматриваем интегралы вида:
,
где R – рациональная функция.

Ранее мы рассмотрели интегралы с квадратным корнем от трехчлена трех типов.
(i) Подробнее >>>
(ii) Подробнее >>>
(iii) Подробнее >>>
Здесь P_n ( x ) – многочлен степени n от x .

Покажем, что любой интеграл от рациональной функции вида , можно выразить через интегралы (i), (ii) и (iii) и интеграл от рациональной функции .

Доказательство

Прежде всего заметим, что любая целая степень от квадратного корня является или многочленом (для четных степеней), или произведением многочлена на корень .
Действительно, имеем.
;
;
;
;
И так далее.

Любую рациональную функцию можно представить в виде дроби, в числителе и знаменателе которой стоят суммы конечного числа членов от целочисленных степеней ее аргументов.
.
Поскольку целая степень от квадратного корня является или многочленом от x , или произведением многочлена на корень, то
,
где P ( x ) , Q ( x ) , V ( x ) , W ( x ) – многочлены от x .

Умножим числитель и знаменатель на и применим формулу ( a + b )( a – b ) = a 2 – b 2 .
В знаменателе имеем.

.
Как видно, знаменатель становится многочленом, который мы обозначили через U ( x ) . В числителе по прежнему имеется сумма произведений целочисленных степеней от x и . Поэтому числитель имеет прежний вид , где P * ( x ) , Q * ( x ) — многочлены. Таким образом, имеем
,
где R ( x ) – рациональная функция, Q ** ( x ) – многочлен.

Если степень многочлена Q ** ( x ) больше, чем у многочлена U ( x ) , то выделим целую часть. Тогда
,
где P ** ( x ) – многочлен, – правильная дробь. Имеем . Правильную дробь разложим на простейшие. Это даст сумму членов вида и .

Подставляя все члены разложения в и интегрируя получаем, что интеграл выражается через интегралы вида , , и .

Что и требовалось доказать.

Пример

Умножим числитель и знаменатель на .

.

Ищем решение оставшегося интеграла в виде
.
Дифференцируем по x .

.
Умножая на , имеем
.
Сравнивая левую и правую части, находим значения коэффициентов.
2 A = 1 , A = 1/2 ;
B = 0 ;
D – A = – 1 , D = A – 1 = – 1/2 .

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 16-02-2015

Интегрирование иррациональных функций: способы и примеры решений

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Рассмотрим интегралы от иррациональных функций, то есть функций, содержащих переменную (обычно икс) под корнем или, что то же самое — в дробной степени. Интегралы от таких функций с помощью подстановок приводятся к интегралам от рациональных функций и могут быть проинтегрированы окончательно.

В подынтегральном выражении — различные дробно-рациональные функции

Разберём интегралы, где в подынтегральном выражении переменная присутствует под корнем. В формально обобщённом виде речь идёт об интегралах вида

,

В примерах мы увидим, что переменная икс, присутствующая под корнем, присутствует там без степени. В примере 3 икс присутствует также в квадрате, но при этом — не по корнем. То есть корни отдельно, степени — отдельно.

В этом случае важное значение имеет наименьшее общее кратное чисел λ , . μ (или общий знаменатель, если эти числа дробные). Обозначим это наименьшее общее кратное (общий знаменатель) через n . Рассматриваемые интегралы от иррациональных функций можно найти, используя следующую подстановку:

Тогда каждая дробная степень «икса» выразится через целую степень «тэ» и подынтегральная функция преобразуется в рациональную функцию от «тэ».

Пример 1. Найти интеграл от иррациональной функции .

Решение. Преобразуем все корни икса в степени. Выписываем степени при иксе в подынтегральном выражении — все, которые там находим:

.

Находим наименьшее общее кратное знаменателей этих чисел: 4.

Поэтому используем следующую подстановку:

Подставляем и преобразуем:

Возвращаясь к переменной икс, окончательно находим:

.

Пример 2. Найти интеграл от иррациональной функции .

Решение. Используем следующую подстановку:

Подставляем и преобразуем:

Интегрируем и получаем:

Возвращаясь к переменной икс, окончательно находим:

.

Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение

Пример 3. Найти интеграл от иррациональной функции .

Пример 4. Найти интеграл от иррациональной функции

.

Корень из квадратного трёхчлена и подстановки Эйлера

Если дан интеграл иррациональной функции вида

,

то есть в подынтегральном выражении — корень из квадратного трёхлчена, то можно воспользоваться подстановками Эйлера.

,

В зависимости от характера корней квадратного уравнения используются следующие подстановки Эйлера.

1. Если x 1 , x 2 — действительные числа (не комплексные), то используется подстановка

(первая подстановка Эйлера).

2. Если x 1 , x 2 — комплексные числа и a > 0 , то используется подстановка

(вторая подстановка Эйлера).

3. Если x 1 , x 2 — комплексные числа и c > 0 , то используется подстановка

(третья подстановка Эйлера).

Пример 5. Найти интеграл от иррациональной функции .

Решение. Разложим квадратный трёхчлен на множители:

Используем первую подстановку Эйлера:

Интегрируем и получаем:

Возвращаясь к переменной икс, сначала долго занимаемся преобразованием выражений, а затем окончательно находим:

Пример 6. Найти интеграл от иррациональной функции .

Используем вторую подстановку Эйлера:

Интегрируем и получаем:

.

Возвращаясь к переменной икс, окончательно находим:

.

Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение

Пример 7. Найти интеграл от иррациональной функции .

(использовать третью подстановку Эйлера).

Интегралы от дифференциального бинома и подстановки Чебышева

,

где m, n, p — рациональные числа (целые или дробные), называются интегралами от дифференциального бинома. В примерах мы увидим, что в подынтегральных выражениях переменная икс присутствует не только под корнем: она под корнем, но ещё и в степени. В этом главное отличие рассматриваемых интегралов от тех, которые были рассмотрены в первом параграфе.

Чтобы найти такие интегралы, используются подстановки Чебышева.

1. Если p — целое число, то используется подстановка

,

где k — наименьшее общее кратное знаменателей m и n.

2. Если — целое число, то используется подстановка

,

где s — знаменатель дроби p .

3. Если — целое число, то используется подстановка

,

где s — знаменатель дроби p .

Русский математик П.Л. Чебышев доказал, что только в перечисленных трёх случаях интеграл от дифференциальных биномов с рациональными показателями степени выражается через элементарные функции.

Пример 8. Найти интеграл от иррациональной функции .

Преобразуем корни в степени и избавимся от дроби:

Здесь p = -1 (целое число). Чтобы избавиться от степени икса в скобках, сделаем промежуточную подстановку

:

.

Теперь сделаем следующую подстановку:

Подставляем и получаем:

Возвращаемся к переменной z :

.

Возвращаясь к переменной икс, окончательно находим:

.

Пример 9. Найти интеграл от иррациональной функции .

Преобразуем корни в степени и избавимся от дроби:

.

Здесь m = 3 , n = 2 , , (целое число).

Cделаем промежуточную подстановку

:

.

Теперь, чтобы избавиться от дробной степени выражения в скобках, сделаем следующую подстановку:

.

Интегрируем и получаем:

.

Возвращаемся к переменной z :

.

Возвращаясь к переменной икс, окончательно находим:

.

Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение

Пример 10. Найти интеграл от иррациональной функции .

— целое число.

Частный случай квадратичных иррациональностей

Рассмотрим интеграл от иррациональной функции вида

, (1)

где в знаменателе — квадратный корень из квадратного трёхчлена.

Чтобы проинтегрировать любой интеграл такого вида, необходимо уметь находить интегралы и .

Формула для нахождения первого из них:

(2)

Второй интеграл находится по формуле

(3)

Формулы (2 и (3) можно условно считать табличными интегралами. Если в подкоренном выражении интеграла (1) выделить полный квадрат, то при a > 0 это выражение примет вид

После подстановки t = x – m в первом случае интеграл (1) приводится к интегралу (3), во втором – к интегралу (2).

Пример 11. Найти интеграл от иррациональной функции

Решение. Выделим в подкоренном выражении полный квадрат:

Произведя теперь подстановку

причём при интегрировании воспользовались формулой (3). Возвращаясь к старой переменной, окончательно получим

Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение

Пример 12. Найти интеграл от иррациональной функции

Интеграл от корня квадратного уравнения

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25