Как найти инертность тела

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Решение:

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Решение:

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Содержание:

Во время равномерного прямолинейного движения тело движется с постоянной по значению и направлению скоростью. Скорость неравномерного движения изменяется со временем. Рассмотрим теперь явления, вследствие которых тело изменяет собственную скорость движения или её направление.

Наблюдение. Из повседневного опыта следует: чтобы тело пришло в движение (т. е. набрало скорость), на него должно подействовать другое тело. Например, лежащий на футбольном поле мяч, придёт в движение только тогда, когда на него налетит другой мяч или по нему ударят ногой (рис. 48). Но если на мяч не действуют другие тела, то он сам по себе не изменит собственную скорость, не придёт в движение относительно Земли.

Опыт 1. На одну из двух тележек, стоящих на рельсах, положили магнит, а на другую — стальной брусок (рис. 49). Под рельсами перекинута нить, которая своими концами закреплена позади каждой из тележек и не позволяет им сблизиться. Если нить пережечь, то тележки начинают двигаться навстречу друг другу, изменяя свою скорость от нуля до некоторого значения. Причиной изменения скорости тележек является притяжение между магнитом и железным бруском, т. е. взаимодействие между ними.

Опыт 2. Толкнём шарик, лежащий на горизонтальном столе, — он начнет равномерно двигаться по прямолинейной траектории. Положим на стол магнит перед шариком на расстоянии от линии его движения. Шарик вследствие взаимодействия с магнитом начнёт увеличивать свою скорость и отклоняться в сторону магнита, т. е. он изменит направление движения (рис. 50).

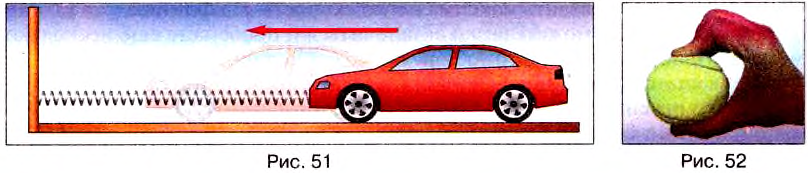
Опыт 3. Один конец пружины прикрепим к игрушечному автомобилю (рис. 51), другой — к стойке на краю стола. Потянем за автомобиль в сторону от стойки — начнётся взаимодействие руки с автомобилем и пружиной, в результате чего их скорости изменяются, а пружина растягивается. Отпустим машинку — теперь взаимодействуют пружина и автомобиль — пружина начинает сжиматься и двигаться с ним в обратном направлении. Во всех этих опытах взаимодействие тел приводит к изменению их скоростей.

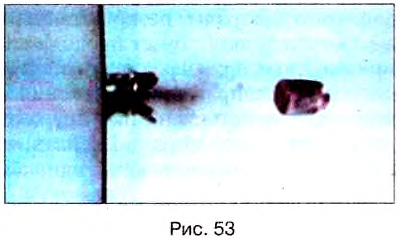
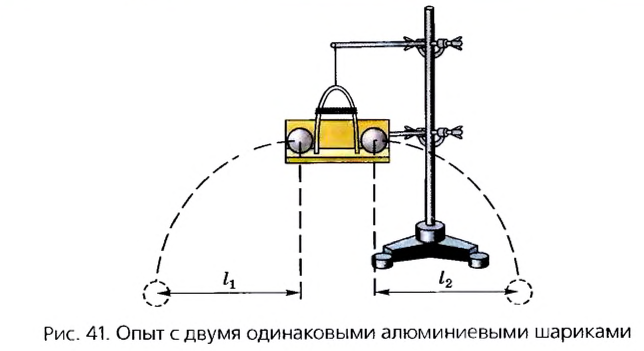
При взаимодействии тел может изменяться скорость движения не только тел в целом, но и отдельных их частей. Это происходит, например, если мы сжимаем в руке теннисный мяч (рис. 52). Вследствие неодинакового перемещения отдельных частей мяч сжимается и деформируется (изменяет свою форму). Также изменяют свою форму и пальцы руки. На фотографии (рис. 53) показано, как пуля пробивает стальной лист.

В этом случае произошло взаимодействие пули с листом, в результате чего они деформировались, а пуля ещё и изменила свою скорость движения.

Вследствие взаимодействия тел они изменяют скорость и направление своего движения, а также деформируются.

Что такое инерция

Повседневный опыт подтверждает вывод, сделанный нами из предыдущих опытов: скорость и направление движения тела могут изменяться лишь при взаимодействии его с другим телом.

Рассмотрим случаи, когда тело в начале наблюдения уже находится в движении. Увидим, что уменьшение скорости движения и остановка тела не могут происходить сами по себе, а обусловлены действием на него другого тела.

Наблюдение 1. Вы, наверное, неоднократно наблюдали, как пассажиры, едущие в транспорте, вдруг наклоняются вперёд во время торможения или прижимаются к стенке на крутом повороте.

Наблюдение 2. Когда на уроке физкультуры вы пробегаете дистанцию 60 м, то стараетесь развить максимальную скорость. На финише уже можно не бежать, но вы не можете резко остановиться и пробегаете ещё несколько метров. Подобно этому автомобиль не может остановиться мгновенно, а движется ещё определённое время при отключённом двигателе или даже во время торможения. Поэтому нельзя перебегать улицу перед приближающимся автомобилем: водитель не сможет его резко остановить.

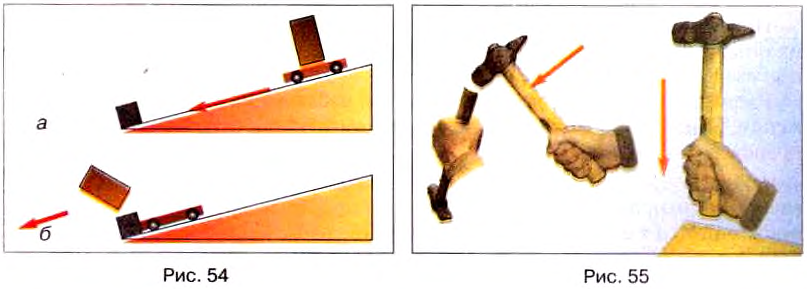
Опыт. Тележку с бруском на нём поставим на наклонную плоскость и отпустим (рис. 54, а). Она будет двигаться вниз, набирая скорость, но достигши преграды, резко остановится. Видим, что брусок, не связанный жёстко с тележкой, будет продолжать свое движение дальше (рис. 54, б). Из приведённых примеров видим, что все тела имеют свойство сохранять скорость и направление движения и не могут мгновенно их изменить в результате действия на них другого тела. Можно предположить, что при отсутствии внешнего воздействия тело будет сохранять скорость и направление движения как угодно долго.

Явление сохранения скорости движения тела при отсутствии действия на него других тел называют инерцией.

Явление инерции открыл итальянский учёный Галилео Галилей. На основе своих опытов и размышлений он утверждал: если на тело не действуют другие тела, то оно или находится в покое, или движется прямолинейно и равномерно. В этом случае говорят, что тело движется по инерции.

Инерция — это латинское слово, которое означает «недвижимость», «бездеятельность».

Явление инерции широко используют в технике и быту. Например, чтобы насадить молоток на ручку (рис. 55), нужно другим молотком ударять по торцу ручки или торцом ручки — по массивному неподвижному предмету.

Примером движения по инерции является также движение молекул газа -каждая молекула в интервале времени между двумя последовательными столкновениями с другими молекулами движется по инерции.

Инертность тел и масса

Всегда ли одинаковый результат действия силы?

Результатом действия силы на тело является изменение его скорости или формы. Однако действие одной и той же силы не всегда сопровождается одинаковым эффектом. Он будет зависеть и от свойств тела, к которому приложена сила.

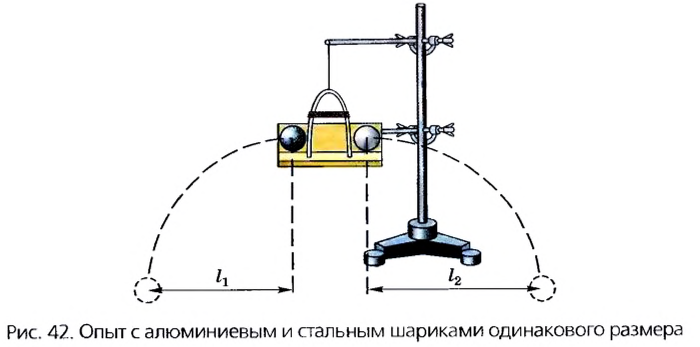
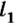
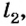
Разместим на полочке, закрепленной в штативе, два алюминиевых шарика (рис. 41). Упругую пластинку согнем, концы ее завяжем ниткой и введем между шариками. Если нитку перерезать, то пластинка распрямится и толкнет оба шарика, придав им определенные скорости. Измерив расстояния  и на которые отлетели шарики, увидим, что они равные:

Если опыт повторить, поменяв один из алюминиевых шариков на стальной такого же диаметра (рис. 42), то расстояния, на которые сместятся шарики, будут различными:

Таким образом, при действии одной и той же сжатой пружины за одинаковый интервал времени шарики приобрели различные скорости. Большее изменение скорости наблюдалось у алюминиевого шарика. Скорость же стального шарика изменялась меньше. С учетом подобных явлений одни тела называют более инертными (в нашем опыте — стальной шарик) и менее инертными (алюминиевый шарик).

Инертность — это свойство тела сохранять свое состояние движения или покоя.

• Заказать решение задач по физике

Явление инерции

Физическое явление сохранения телом состояния покоя или равномерного прямолинейного движения называют инерцией (от латин. іnertia — неподвижность, бездеятельность).

Инерция — это явление сохранения скорости движения тела при отсутствии или скомпенсированности действий на него других тел. В физике движение тела в идеальных условиях (когда на тело не действуют другие тела) называют движением по инерции. В реальности невозможно создать условия, когда действие других тел отсутствует. Поэтому в повседневной жизни движением по инерции считают случаи, когда действие на тело других тел достаточно слабо и до заметного изменения скорости своего движения тело проходит значительный путь (рис. 14.8).

Действие одного тела на другое

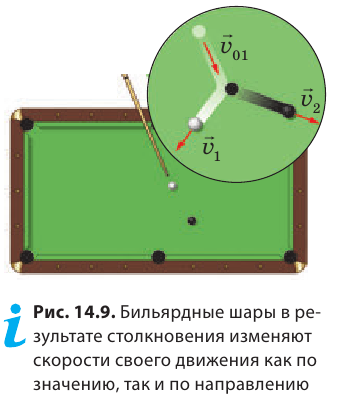
А как будет двигаться тело, на которое действуют другие тела и действия этих тел не будут скомпенсированы? Например, как будет двигаться бильярдный шар, на который налетает другой шар и его удар ничем не скомпенсирован? Как будет двигаться груз, висящий на нити, если нить перерезать и действие Земли не будет уравновешено действием нити? Что будет, если, двигаясь на велосипеде, вы прекратите вращать педали и ваше действие не будет компенсировать сопротивление движению велосипеда? В этих и многих других случаях тела изменяют скорость своего движения: бильярдные шары полетят в разные стороны с разными скоростями (рис. 14.9); груз начнет падать с увеличивающейся скоростью; велосипед станет двигаться медленнее и наконец остановится. Итак, можно сделать следующий вывод. Если действия на тело других тел не скомпенсированы, то тело изменяет скорость своего движения по значению или направлению либо одновременно по значению и направлению*.

Итоги:

Тело движется равномерно прямолинейно или находится в состоянии покоя только тогда, когда на него не действуют другие тела или действия других тел скомпенсированы.

Инерция — это явление сохранения скорости движения тела при отсутствии или скомпенсированности действий на него других тел. Если действия на тело других тел не скомпенсированы, то тело изменяет скорость своего движения по значению или направлению либо по значению и направлению одновременно.

Инертность тела и масса

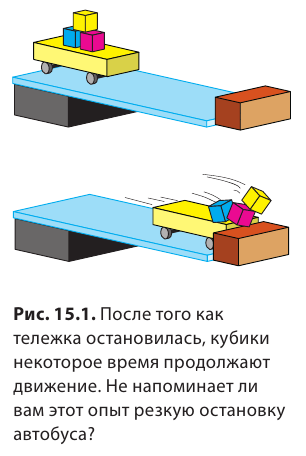
Вспомните: вы заходите в автобус, все места заняты. Двери закрываются, автобус резко начинает движение, и вы должны приложить усилия, чтобы не упасть. Следующая остановка — и вы снова вынуждены цепляться за поручни, ведь автобус остановился достаточно резко. Почему что-то «толкает» вас вперед или назад? Вы узнаете, из-за какого свойства физических тел вы отклоняетесь назад, когда транспортное средство набирает скорость, и вперед — в момент его резкой остановки (см. рис. 15.1).

Что такое инертность

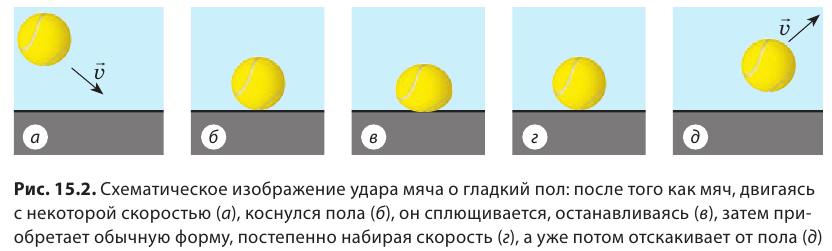
Наверняка вы все играли в «квача». Вспомните момент, когда вам нужно было резко изменить направление или скорость своего движения: остановиться, разогнаться, свернуть. Удавалось ли вам сделать это мгновенно? Конечно нет! Вам приходилось за кого-то цепляться, делать до остановки несколько лишних шагов, тратить время на разбег и т. д. Рассмотрим еще пример. Когда вы играете в спортзале с мячом, вам, кажется, что мяч, ударившись о пол, в тот же момент отскакивает от него. Но это не так! Если сфотографировать движение мяча в режиме скоростной фотосъемки, то увидим, что собственно удар мяча о пол длится некоторое время (рис. 15.2).

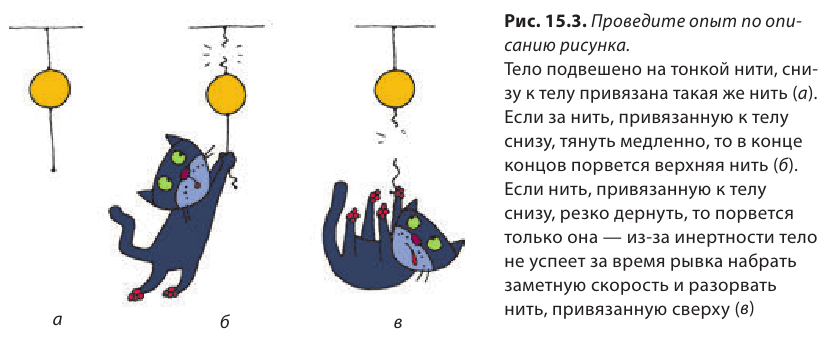
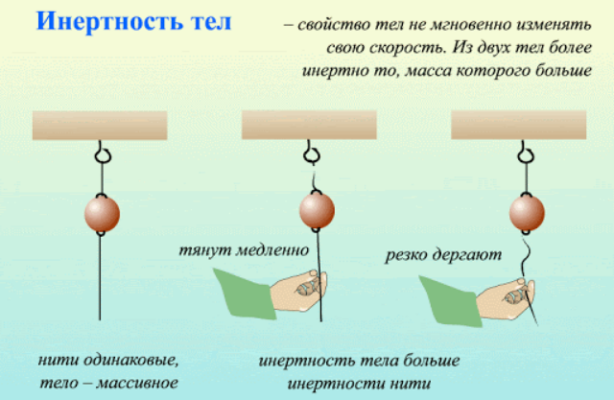
Вообще ни одно тело не может изменить скорость своего движения мгновенно. Говорят, что все тела «оказывают сопротивление» попытке измененить скорость их движения. В физике такое свойство тел называют инертностью. Инертность — свойство тела, которое заключается в том, что для изменения скорости движения тела в результате взаимодействия требуется время. Инертность тела проявляется тогда, когда мы пытаемся изменить скорость движения этого тела (см. рис. 15.1–15.3).

Определение массы тела

В результате одинакового воздействия одни тела изменяют скорость своего движения достаточно быстро, другие — намного медленнее. Например, чтобы с помощью весел придать определенную скорость легкой байдарке, нужно намного меньше времени, чем для придания такой же скорости тяжелой лодке. В таком случае говорят, что лодка более инерт­на, чем байдарка. Инертность тел характеризуется физической величиной — массой. Чем больше масса тела, тем больше времени нужно для изменения скорости его движения в результате одного и того же воздействия.

Масса тела — это физическая величина, которая является мерой инертности тела. Массу тела обозначают символом m. Единица массы в СИ — килограмм: [m]=кг. Кроме килограмма используют также другие единицы массы, например тонна (т), грамм (г), миллиграмм (мг):

Масса — это одна из основных единиц СИ, поэтому для нее существует эталон. Международный эталон килограмма был создан в 1880 г.*; его используют и сейчас. Эталон килограмма — это цилиндр, изготовленный из сплава платины и иридия (рис. 15.4). Масса цилиндра — ровно 1 килограмм.

Сначала в качестве эталона килограмма был принят 1 л чистой воды при температуре около +4 °C. Однако такой эталон был очень неудобным.

Международный эталон килограмма хранится во Франции, в Международном бюро мер и весов, расположенном в г. Севр (предместье Парижа). Эталон достают из хранилища не чаще одного раза в 15 лет. В Украине, в Национальном научном центре «Институт метрологии» (г. Харьков), хранится государственный эталон единицы массы 1 кг.

Измеряем массу тела взвешиванием:

Кроме инертности любое физическое тело имеет также свойство притягиваться к другим телам благодаря гравитационному взаимодействию *. Как вы уже, возможно, догадались, мерой гравитационного свойства тела также является масса. Именно на гравитационном свойстве тел основан самый распространенный способ измерения массы — взвешивание (рис. 15.5): чем больше масса тела, тем сильнее оно притягивается к Земле и поэтому сильнее давит на весы.

Подробнее об измерении масс тел взвешиванием вы узнаете при выполнении лабораторной работы № 6.

Еще об одном способе измерения массы:

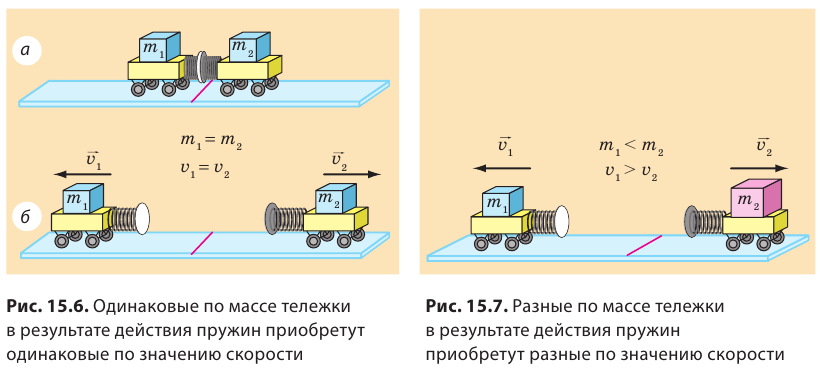
Массу тела можно также измерить, основываясь на инертности тел. Поставим две тележки со сжатыми пружинами на гладкую горизонтальную поверхность (рис. 15.6, а). Распрямляясь, пружины придадут тележкам некоторые скорости. Если тележки приобретут одинаковые скорости и, соответственно, проедут до остановки одинаковое расстояние, то это означает, что их массы равны (рис. 15.6, б). Если одна из тележек, например тележка 2, приобретет меньшую скорость и, соответственно, проедет меньшее расстояние, то она имеет большую массу (рис. 15.7). 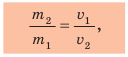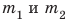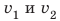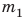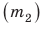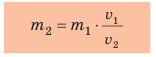При этом во сколько раз скорость движения тележки 2, будет меньше скорости движения тележки 1, во столько же раз масса тележки 2 больше массы тележки 1: где — массы тележек; — скорости движения, которые приобрели тележки в результате взаимодействия. Полученное равенство позволяет определить отношение масс взаимодействующих тел по измеренным скоростям движений, которые приобретают эти тела в результате взаимодействия. Если же при этом масса одного из тел (например, ) известна, то можно определить массу второго тела : На первый взгляд, способ измерения масс, основанный на инертности тел, неудобен, но он является единственным, если тела невозможно взвесить (например, элементарные частицы или космические тела)*.

В большинстве таких случаев в формулу подставляют не приобретенные телами скорости движения, а изменение скорости движения каждого тела в результате взаимодействия.

Итоги:

Инертность — это свойство тела, которое заключается в том, что для изменения скорости движения тела в результате взаимодействия требуется время.

Масса тела (m) — это физическая величина, которая является мерой инертного и гравитационного свойств тела.

Единица массы в СИ — килограмм.

Массу тела можно определить взвешиванием (этот способ основан на том, что масса является мерой гравитационного свойства тела), а также сравнив, как изменились скорости движения тел в результате взаимодействия (способ основан на том, что масса является мерой инертности тела).

Измерение массы и объема. Плотность вещества

1. Закон инерции
2. Инертность тела
3. Инертная и гравитационная масса
4. Измерение массы с помощью весов
5. Плотность вещества
6. Задачи
7. Лабораторная работа №5. Определение плотности жидкостей
8. Лабораторная работа №6. Определение плотности твердых тел

п.1. Закон инерции

Как свидетельствуют многочисленные эксперименты и наш повседневный опыт, чтобы неподвижное тело сдвинулось с места, на него должно подействовать другое тело. С другой стороны, чтобы остановить тело, уже находящееся в движении, или изменить его траекторию, также необходимо внешнее воздействие (обычно, причиной остановки в механике является трение; причиной изменения траектории — столкновение с другим телом и т.п.).

Возникает вопрос: а что будет с телом, если на него не действуют никакие другие тела?

Очевидно, если тело покоилось, то оно продолжит покоиться.

А если оно двигалось, что тогда произойдет?

А теперь представим себе идеальный случай: трение полностью отсутствует.

В этом случае шарик будет двигаться с постоянной скоростью бесконечно долго.

Закон инерции
Если на тело не действуют другие тела, оно либо покоится, либо движется прямолинейно и равномерно.

Закон инерции впервые был сформулирован Галилео Галилеем в его работе «Диалог о двух главнейших системах мира» (опубликована в 1632 г.). Однако Галилей ошибочно считал, что свободное равномерное движение тела возможно не только по прямой, но и по окружности.

В 1644 г. Рене Декарт уточнил формулировку Галилея, указав, что для изменения направления скорости также необходимо внешнее воздействие. Т.к. при равномерном движении по окружности направление скорости всё время меняется, оно не является свободным. Следовательно, свободное движение может быть только прямолинейным.

п.2. Инертность тела

Инертность – это свойство тела сохранять состояние покоя или прямолинейное и равномерное движение.

Благодаря инертности, тело не может мгновенно перейти из состояния покоя в движение или из состояния движения в покой. Для изменения скорости тела необходимо определенное время.

При взаимодействии инертность проявляется в том, что разные тела под одинаковым внешним воздействием получают разные ускорения (об ускорении — см. §11 данного справочника).

п.3. Инертная и гравитационная масса

Инертная масса – это количественная мера инертности, показатель того, в какой степени данное тело будет препятствовать изменению своей скорости.

Гравитационная масса – это количественная характеристика способности тела к взаимодействию по закону всемирного тяготения.

На сегодняшний день с высоким уровнем точности (относительная ошибка (sim 10^{-13}) в эксперименте 2009 г.) установлено, что значения инертной и гравитационной массы одного и того же тела равны. Поэтому инертную и гравитационную массы на практике не различают (принцип эквивалентности) и рассматривают «просто» массу тела.

Единицей массы в системе СИ является килограмм (кг).

Масса является одной из семи основных единиц системы СИ (см. §2 данного справочника).

При изучении очень больших или очень малых физических тел удобней использовать внесистемные единицы массы.

Например, в астрофизике единицей для сравнения масс небесных тел служит масса Солнца, (M_{odot}approx 1,99cdot 10^{30} text{кг}). А в физической химии при определении масс атомов и молекул используется атомная единица массы, равная 1/12 массы свободного покоящегося атома углерода, (1 text{а.е.м.}approx 1,66cdot 10^{-27} text{кг}).

п.4. Измерение массы с помощью весов

Весы – это прибор для измерения массы по весу тела на основании принципа эквивалентности инертной и гравитационной масс.

Весы равноплечие рычажные лабораторные и наборы гирек к ним

Вес тела определяется сравнением с весом эталонной массы (гири). Весы находятся в равновесии, если помещенные на их чаши тела одинаково притягиваются к Земле. Чтобы найти массу тела, его кладут на одну чашу весов, а на другую – гири известной массы, пока весы не уравновесятся. Гири граммового набора рекомендуется брать руками в медицинских перчатках, а миллиграммового – пинцетом, чтобы не изменить их массу. Уравновешивание следует начинать с гирь большей массы, а затем переходить к меньшим разновесам, т.к. иначе их может не хватить.

Метод двойного взвешивания (метод Гаусса)
Шаг 1. Поместить тело для взвешивания на левую чашку весов, а на правую чашку весов поставить гири до полного уравновешивания. Записать полученный результат (m_1).
Шаг 2. Переложить тело на правую чашку весов, а гири – на левую. Повторить уравновешивание. Записать полученный результат (m_2).
Шаг 3. Найти массу тела как среднее арифметическое $$ m=frac{m_1+m_2}{2}. $$ Абсолютная погрешность двойного взвешивания – это большая из двух величин $$ Delta m=max(|m_1-m_2|; 0,01text{%}m) $$ т.к. (delta_m=0,01text{%}) — относительная погрешность для весов класса точности III.

п.5. Плотность вещества

Плотность вещества однородного тела – это физическая величина, равная отношению массы тела к его объему: $$ rho=frac mv $$

Единицей плотности в системе СИ является килограмм на метр кубический (кг/м³).

Плотности различных веществ тщательно измерены и занесены в справочные таблицы.

Плотности в справочнике даны для химически чистых веществ (содержание основного вещества 98% и выше), при нормальных условиях (давление 760 мм рт.ст. и температура 0°С), если не указаны другие значения давления и температуры.

Плотность зависит от следующих свойств вещества:

• масса молекул (атомов) вещества. Например, масса атомов алюминия 27 а.е.м., а атомов золота 197 а.е.м. При этом плотность алюминия 2700 кг/м³, а плотность золота 19300 кг/м³, что приблизительно соответствует соотношению масс атомов. Небольшое различие можно объяснить большим расстоянием между более крупными атомами золота в кристаллической решетке (гранецентрированный куб, как для алюминия, так и для золота).
• расположение частиц вещества. Например, расстояния между слоями атомов углерода в графите в 3 раза больше, чем межатомные расстояния в самих слоях; а вот в алмазе атомы углерода упакованы очень плотно. В результате плотность графита 2160 кг/м³, а плотность алмаза 3510 кг/м³, хотя оба вещества состоят из атомов углерода.
• агрегатное состояние, в котором находится вещество. Наименьшие плотности у газов, наибольшие – у твердых веществ. Например, плотность воздуха (газ) 1,29 кг/м³, плотность воды (жидкость) 1000 кг/м³, плотность железа (твердое тело) 7900 кг/м³.

п.6. Задачи

Задача 1. Найдите плотность мела, если масса кусочка равна 7,2 г, а объем – 3,6 см³.

Дано:
(m=7,2 text{г}=7,2cdot 10^{-3} text{кг})
(V=3,6 text{см}^3=3,6cdot 10^{-6} text{м}^3)
__________________
(rho-?)

Плотность (rho=frac mv) $$ rho=frac{7,2cdot 10^{-3}}{3,6cdot 10^{-6}}=2cdot 10^3=2000 (text{кг/м}^3) $$ Ответ: (2000 text{кг/м}^3)

Задача 2. Найдите объем тела человека массой 60 кг, ели средняя плотность человеческого тела равна плотности воды. Ответ дайте в литрах.

Дано:
(m=60 text{кг})
(rho=1000 text{кг/м}^3)
__________________
(V-?)

Плотность (rho=frac mv Rightarrow) Объем (V=frac mp) $$ V=frac{60}{1000}=0,06 (text{м}^3)=60 (text{л}) $$ Ответ: 60 л.

Задача 3. Алюминиевая кастрюля имеет массу 0,5 кг. Если кастрюлю таких же размеров изготовить из стали, какая у неё будет масса?

Дано:
(m_1=0,5 text{кг})
(rho_1=2700 text{кг/м}^3)
(rho_2=7800 text{кг/м}^3)
__________________
(m_2-?)

У кастрюль одинаковых размеров одинаковый объем. Получаем: begin{gather*} V=frac{m_1}{rho_1}=frac{m_2}{rho_2}Rightarrow m_2=frac{rho_2}{rho_1}m_1\ m_2=frac{7800}{2700}cdot 0,5approx 1,4 (text{кг}) end{gather*} Ответ: ≈1,4 кг.

Задача 4*. В банку, до краев наполненную водой, опустили кусок золота массой 1 кг. В другую такую же банку опустили кусок меди массой 1 кг. Где больше вылилось воды и насколько больше? (ответ дайте в миллилитрах).

Дано:
(m=1 text{кг})
(rho_1=19320 text{кг/м}^3)
(rho_2=8940 text{кг/м}^3)
__________________
(Delta V-?)

Объем вытесненной воды равен объему погруженного тела: $$ V_1=frac{m}{rho_1}, V_2=frac{m}{rho_2} $$ Т.к. (rho_1gt rho_2, V_1lt V_2), объем воды, вытесненной медью, больше. $$ Delta V=V_2-V_1=frac{m}{rho_2}-frac{m}{rho_1}=mleft(frac{1}{rho_2}-frac{1}{rho_2}right)=mfrac{rho_1-rho_2}{rho_1rho_2} $$ Подставляем: begin{gather*} Delta V=1cdotfrac{19320-8940}{19320cdot 8940}approx 6,01cdot 10^{-5} text{м}^3\ 1 text{л}=10^{-3} text{м}^3, 1 text{мл}=1 text{cм}^3=10^{-3} text{л}=10^{-6} text{м}^3\ Delta Vapprox 60,1 text{мл} end{gather*} Ответ: ≈60,1 мл; больше вылилось во втором случае, для меди.

п.7. Лабораторная работа №5. Определение плотности жидкостей

Цель работы
Научиться измерять массу и объем жидкостей. Научиться определять жидкости по плотности, оценивать погрешность полученных результатов.

Теоретические сведения
Для определения массы тел в данной работе используется метод двойного взвешивания (см. выше в данном параграфе).

Масса тела определяется как среднее арифметическое двух взвешиваний на разных чашках весов: $$ m=frac{m_1+m_2}{2}. $$ Абсолютная погрешность двойного взвешивания – это большая из двух величин $$ Delta m=max(|m_1-m_2|; 0,01text{%}m) $$ Пусть масса стакана с жидкостью равна (M), абсолютная погрешность этого взвешивания (Delta M); масса пустого стакана (m_{text{ст}}), абсолютная погрешность (Delta m_{text{ст}}). Тогда масса жидкости $$ m=M-m_{text{ст}} $$ Абсолютная и относительная погрешности определения массы жидкости $$ Delta m=Delta M+Delta m_{text{ст}}, delta_m=frac{Delta m}{m}cdot 100text{%} $$ Мерный цилиндр проградуирован в миллилитрах. Для расчёта плотности жидкости в системе СИ необходимо помнить, что $$ 1 text{мл}=1 text{cм}^3=10^{-6} text{м}^3 $$ Абсолютная погрешность измерения объема жидкости равна половине цены деления мерного цилиндра $$ Delta V=frac d2 $$ Относительная погрешность равна $$ delta_V=frac{Delta V}{V}cdot 100text{%}. $$ Плотность жидкости равна $$ rho=frac mv. $$ Относительная погрешность результата $$ delta_{rho}=delta_m+delta_V. $$ Абсолютная погрешность результата $$ Deltarho=rhocdot delta_{rho} $$ Перевод полученных результатов в систему СИ $$ 1frac{text{г}}{text{см}^3}= frac{10^{-3} text{кг}}{10^{-6} text{м}^3}=10^3frac{text{кг}}{text{м}^3}=1000frac{text{кг}}{text{м}^3} $$

Приборы и материалы
Два стакана с неизвестными жидкостями; мерный цилиндр; весы с разновесом.

Ход работы
1. Приготовьте весы к взвешиванию.
2. Поставьте на весы первый стакан с жидкостью. Методом двойного взвешивания определите массу стакана и жидкости (M_1). Оцените абсолютную погрешность взвешивания.
3. Вылейте жидкость из первого стакан в мерный цилиндр и определите её объем (V_1). Оцените абсолютную погрешность измерения объема.
4. Методом двойного взвешивания определите массу первого стакана (m_{text{ст1}}). Оцените абсолютную погрешность взвешивания.
5. По формулам, данным в теоретической части, определите плотность жидкости, относительную и абсолютную погрешности полученного результата.
6. По таблице в справочнике определите, какая жидкость находится в первом стакане.
7.-11. Повторите шаги 2.-6. для второго стакана с жидкостью.
12. Сделайте выводы о проделанной работе.

Результаты измерений и вычислений

Цена деления мерного цилиндра (d=1 text{мл}=1 text{см}^3)
Первый стакан

Стадии двойного взвешивания	(M, text{г})	(m_{text{ст}}, text{г})
(m_1)	151,2	50,1
(m_2)	150,8	49,9
(m=frac{m_1+m_2}{2})	151,0	50,0
(|m_1-m_2|)	0,4	0,2
(0,01text{%}m)	0,015	0,005
(Delta m)	0,4	0,2

Масса первой жидкости

begin{gather*} m=151,0-50,0=101,0,\ Delta m=0,4+0,2=0,6,\ delta_m=frac{0,6}{101,0}cdot 100text{%}=0,59text{%} end{gather*}

Объем первой жидкости

begin{gather*} V=109 text{мл},\ Delta V=frac d2=0,5 text{мл},\ delta_V=frac{0,5}{109}cdot 100text{%}=0,46text{%} end{gather*}

Плотность первой жидкости

begin{gather*} rho=frac mV=frac{101,0}{109}approx 0,927frac{text{г}}{text{см}^3}=927frac{text{кг}}{text{м}^3},\ delta_{rho}=delta_m+delta_V=0,59text{%}+0,46text{%}approx 1,1text{%},\ delta rho=rhocdotdelta_{rho}=927cdot 0,011approx 10frac{text{кг}}{text{м}^3},\ rho=(927pm 10)frac{text{кг}}{text{м}^3},\ delta_{rho}=1,1text{%} end{gather*}

В первом стакане – подсолнечное масло.

Второй стакан

Стадии двойного взвешивания	(M, text{г})	(m_{text{ст}}, text{г})
(m_1)	100,4	50,0
(m_2)	100,2	49,9
(m=frac{m_1+m_2}{2})	100,3	49,95≈50,0
(|m_1-m_2|)	0,2	0,1
(0,01text{%}m)	0,01	0,005
(Delta m)	0,2	0,1

Масса второй жидкости

begin{gather*} m=100,3-50,0=50,3,\ Delta m=0,2+0,1=0,3,\ delta_m=frac{0,3}{50,3}cdot 100text{%}=0,6text{%} end{gather*}

Объем второй жидкости

begin{gather*} V=50 text{мл},\ Delta V=frac d2=0,5 text{мл},\ delta_V=frac{0,5}{50}cdot 100text{%}=1,0text{%} end{gather*}

Плотность второй жидкости

begin{gather*} rho=frac mV=frac{50,3}{50,0}= 1,006frac{text{г}}{text{см}^3}=1006frac{text{кг}}{text{м}^3},\ delta_{rho}=delta_m+delta_V=0,6text{%}+1,0text{%}= 1,6text{%},\ delta rho=rhocdotdelta_{rho}=1006cdot 0,016approx 16frac{text{кг}}{text{м}^3},\ rho=(1006pm 16)frac{text{кг}}{text{м}^3},\ delta_{rho}=1,6text{%} end{gather*}

Во втором стакане – вода.

Выводы
На основании проделанной работы можно сделать следующие выводы.

Для определения плотности жидкости в работе методом двойного взвешивания измерялась масса (стакана с жидкостью и пустого стакана) и объем жидкости в мерном цилиндре.

Результаты для двух данных жидкостей

begin{gather*} rho_1=(927pm 10)frac{text{кг}}{text{м}^3}, delta_{rho 1}=1,1text{%}\ rho_2=(1006pm 16)frac{text{кг}}{text{м}^3}, delta_{rho 2}=1,6text{%} end{gather*}

По таблицам в справочнике было определено, что в первом стакане – растительное масло, а во втором – вода. Полученные результаты также подтверждаются цветом (желтоватый – для масла, прозрачный – для воды) и запахом (характерный запах у масла и отсутствие запаха у воды).

п.8. Лабораторная работа №6. Определение плотности твердых тел

Цель работы
Научиться измерять массу и объем твердых тел неправильной формы. Научиться определять вещества твердых тел по плотности, оценивать погрешность полученных результатов.

Теоретические сведения
Для определения массы тел в данной работе используется метод двойного взвешивания (см. выше в данном параграфе).

Масса тела определяется как среднее арифметическое двух взвешиваний на разных чашках весов: $$ m=frac{m_1+m_2}{2}. $$ Абсолютная погрешность двойного взвешивания – это большая из двух величин $$ Delta m=max(|m_1-m_2|; 0,01text{%}m) $$ Относительная погрешность $$ delta_m=frac{Delta m}{m}cdot 100text{%} $$ Объем твердого тела неправильной формы определяется с помощью погружения в жидкость.
Пусть объем жидкости в мерном цилиндре до погружения тела (V_0), после погружения – (V’).
Тогда объем самого тела (V=V’-V_0).
Абсолютная погрешность измерения объема равна половине цены деления мерного цилиндра (Delta V_0=frac d2) для прямого измерения. Для разности двух прямых измерений общая абсолютная погрешность $$ Delta V=2Delta V_0=d $$ Относительная погрешность $$ delta_V=frac dVcdot 100text{%}. $$ Плотность твердого тела равна $$ rho=frac mv. $$ Относительная погрешность результата $$ delta_{rho}=delta_m+delta_V. $$ Абсолютная погрешность результата $$ Deltarho=rhocdot delta_{rho} $$ Перевод полученных результатов в систему СИ $$ 1frac{text{г}}{text{см}^3}= frac{10^{-3} text{кг}}{10^{-6} text{м}^3}=10^3frac{text{кг}}{text{м}^3}=1000frac{text{кг}}{text{м}^3} $$

Приборы и материалы
Мерный цилиндр, наполненный водой наполовину; два тела неправильной формы из металлов; весы с разновесом.

Ход работы
1. Приготовьте весы к взвешиванию.
2. Методом двойного взвешивания определите массу первого тела. Найдите абсолютную и относительную погрешность взвешивания.
3. С помощью погружения первого тела в жидкость найдите его объем. Абсолютная погрешность равна цене деления мерного цилиндра. Рассчитайте относительную погрешность.
4. По формулам, данным в теоретической части, определите плотность твердого тела, относительную и абсолютную погрешности полученного результата.
5. По таблице в справочнике определите, из какого вещества изготовлено первое тело.
6-9. Повторите шаги 2.-5. для второго твердого тела неправильной формы.
10. Сделайте выводы о проделанной работе.

Результаты измерений и вычислений

Цена деления мерного цилиндра (d=0,5 text{мл}=0,5 text{см}^3)
Первое тело

Стадии двойного взвешивания	(m, text{г})
(m_1)	22,34
(m_2)	22,38
(m=frac{m_1+m_2}{2})	22,36
(|m_1-m_2|)	0,04
(0,01text{%}m)	0,002
(Delta m)	0,04
(delta m)	0,18%

Стадии определения объема	(V, text{см}^3)
(V_0)	50,0
(V’)	58,5
(V=V’-V_0)	8,5
(Delta V=d)	0,5
(delta_V)	5,9%

Плотность первого тела

begin{gather*} rho=frac mV=frac{22,36}{8,5}approx 2,631frac{text{г}}{text{см}^3}=2631frac{text{кг}}{text{м}^3},\ delta_{rho}=delta_m+delta_V=0,18text{%}+5,9text{%}approx 6,1text{%},\ delta rho=rhocdotdelta_{rho}=2631cdot 0,061approx 160frac{text{кг}}{text{м}^3},\ rho=(2630pm 160)frac{text{кг}}{text{м}^3},\ delta_{rho}=6,1text{%} end{gather*}

Первое тело изготовлено из алюминия.

Второе тело

Стадии двойного взвешивания	(m, text{г})
(m_1)	101,21
(m_2)	101,27
(m=frac{m_1+m_2}{2})	101,25
(|m_1-m_2|)	0,06
(0,01text{%}m)	0,005
(Delta m)	0,06
(delta m)	0,06%

Стадии определения объема	(V, text{см}^3)
(V_0)	50,0
(V’)	63,0
(V=V’-V_0)	13,0
(Delta V=d)	0,5
(delta_V)	3,8%

Плотность второго тела

begin{gather*} rho=frac mV=frac{101,25}{13,0}approx 7,788frac{text{г}}{text{см}^3}=7788frac{text{кг}}{text{м}^3},\ delta_{rho}=delta_m+delta_V=0,06text{%}+3,8text{%}approx 3,9text{%},\ delta rho=rhocdotdelta_{rho}=7788cdot 0,039approx 300frac{text{кг}}{text{м}^3},\ rho=(7790pm 300)frac{text{кг}}{text{м}^3},\ delta_{rho}=3,9text{%} end{gather*}

Второе тело изготовлено из железа.

Выводы
На основании проделанной работы можно сделать следующие выводы.

Для определения плотности твердых металлических тел неправильной формы в работе методом двойного взвешивания измерялась масса тел. Объем определялся методом погружения в мерном цилиндре.

Результаты для двух данных тел

begin{gather*} rho_1=(2630pm 160)frac{text{кг}}{text{м}^3}, delta_{rho 1}=6,1text{%}\ rho_2=(7790pm 300)frac{text{кг}}{text{м}^3}, delta_{rho 2}=3,9text{%} end{gather*}

По таблицам в справочнике было определено, что первое тело изготовлено из алюминия, второе – из железа.