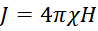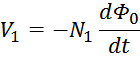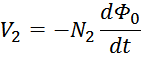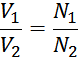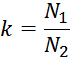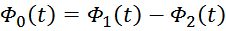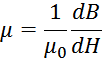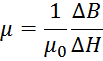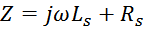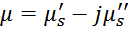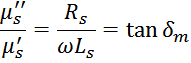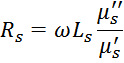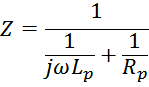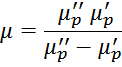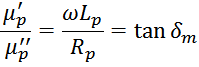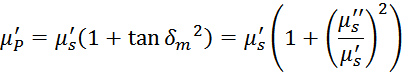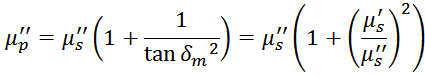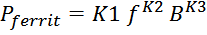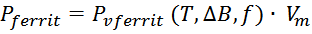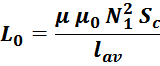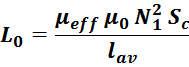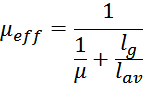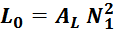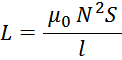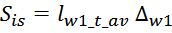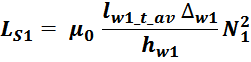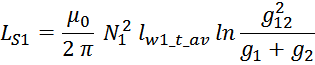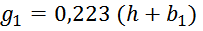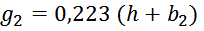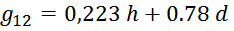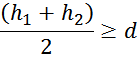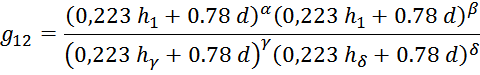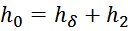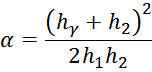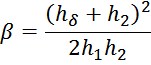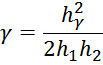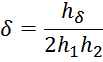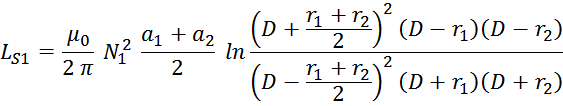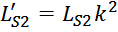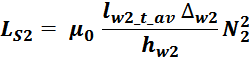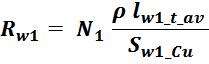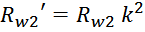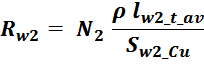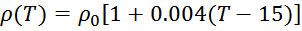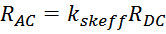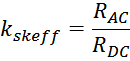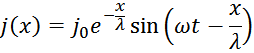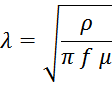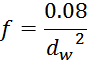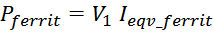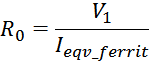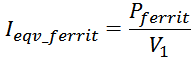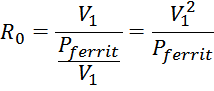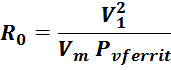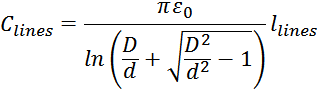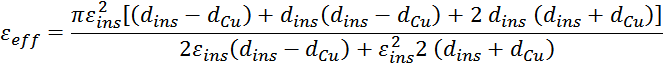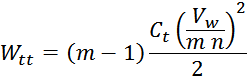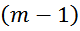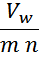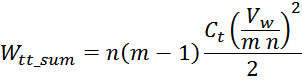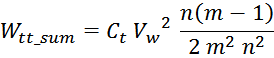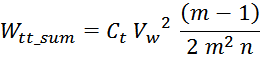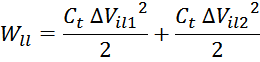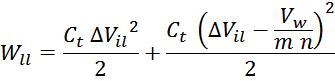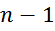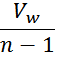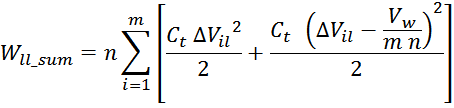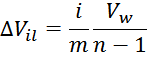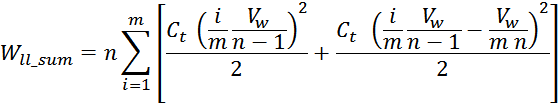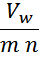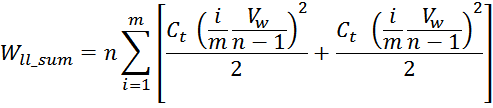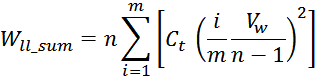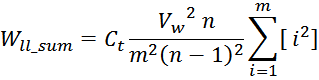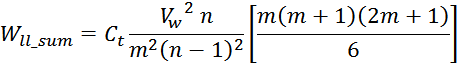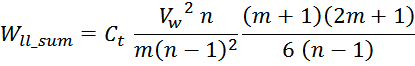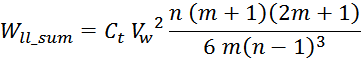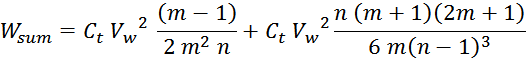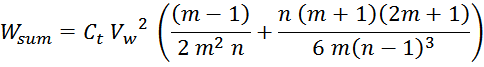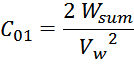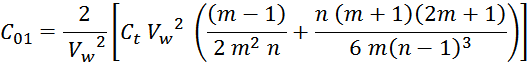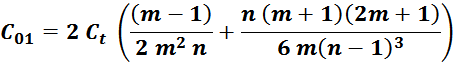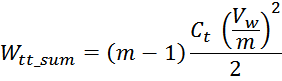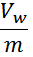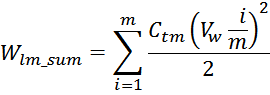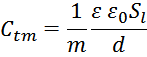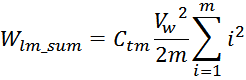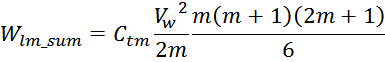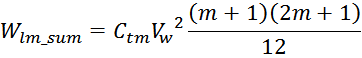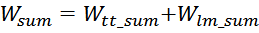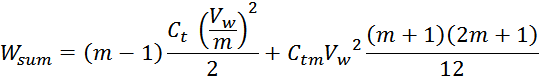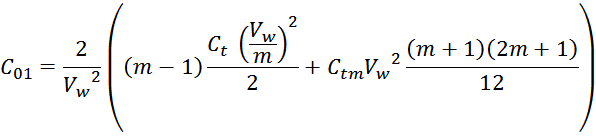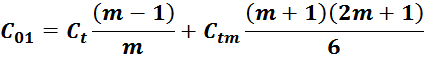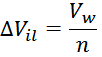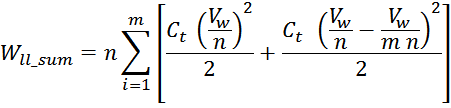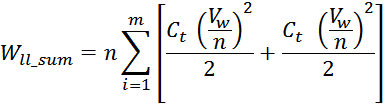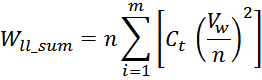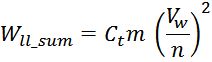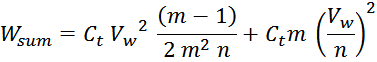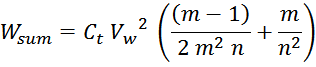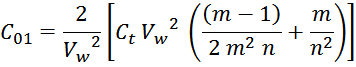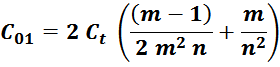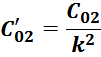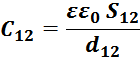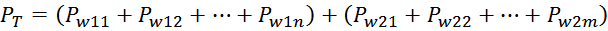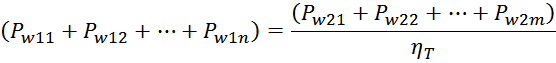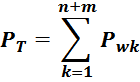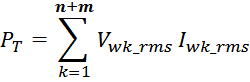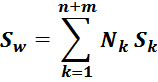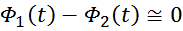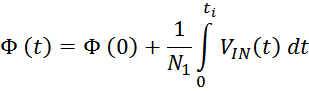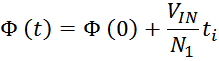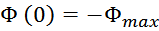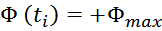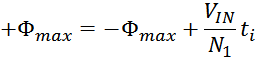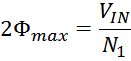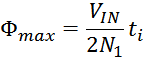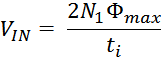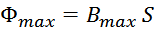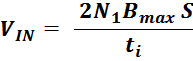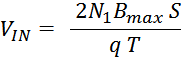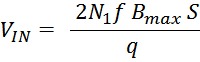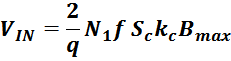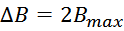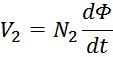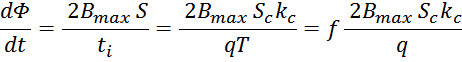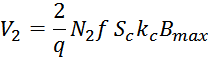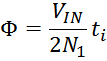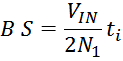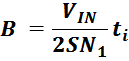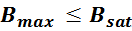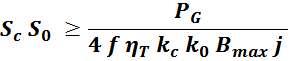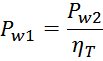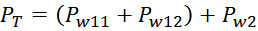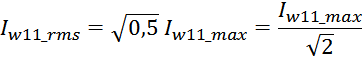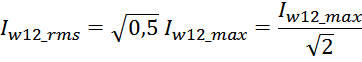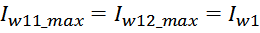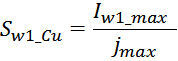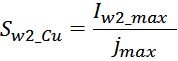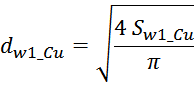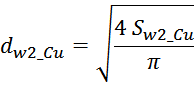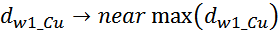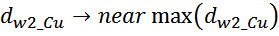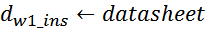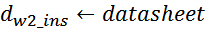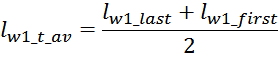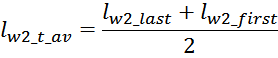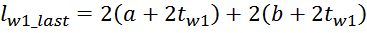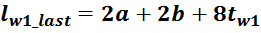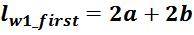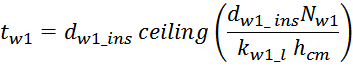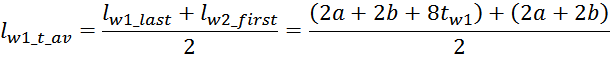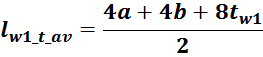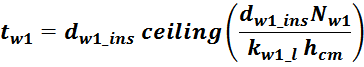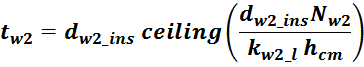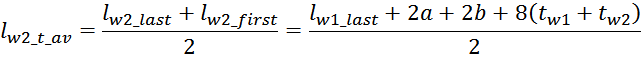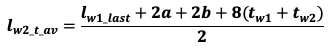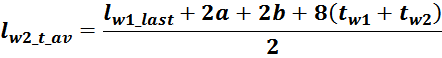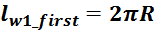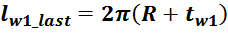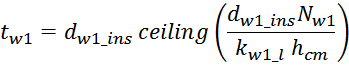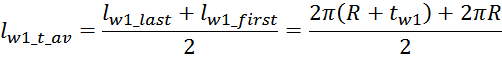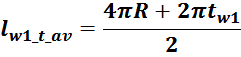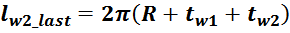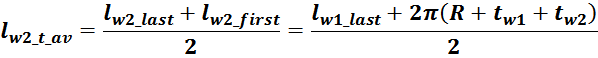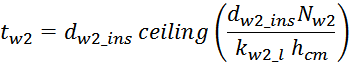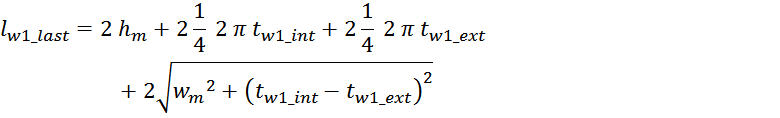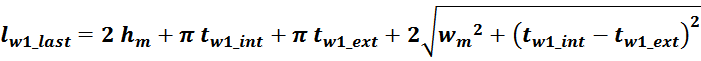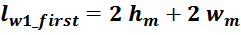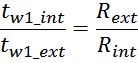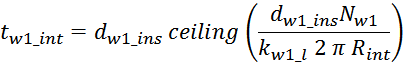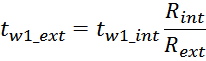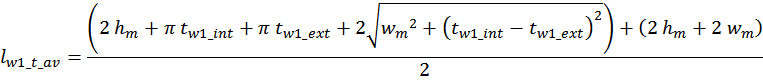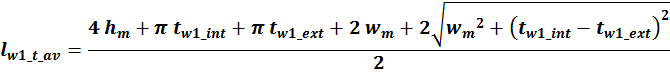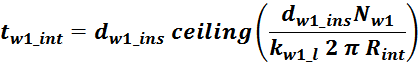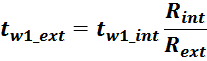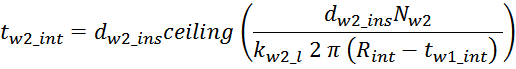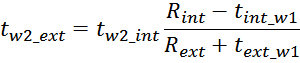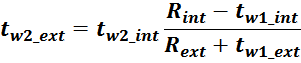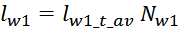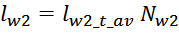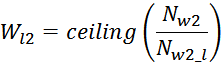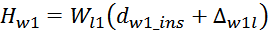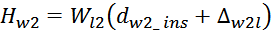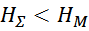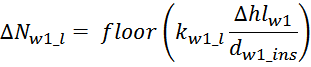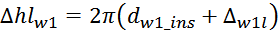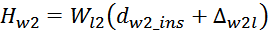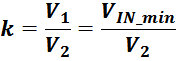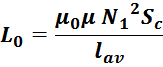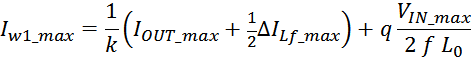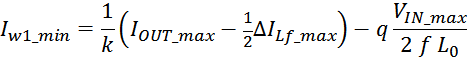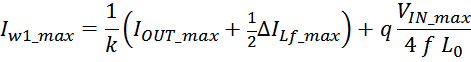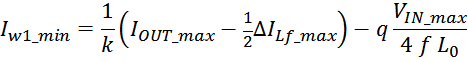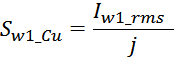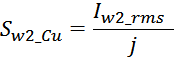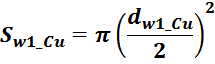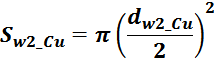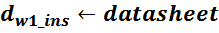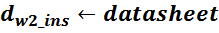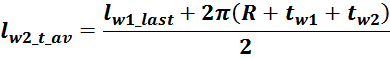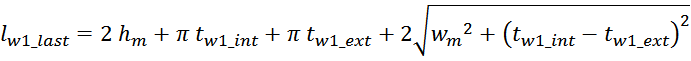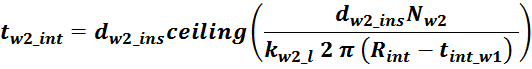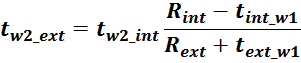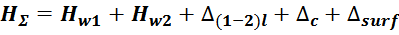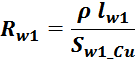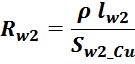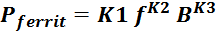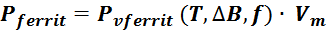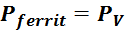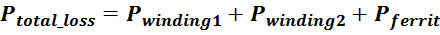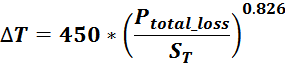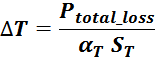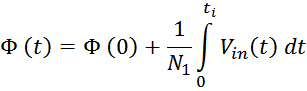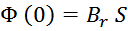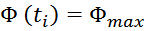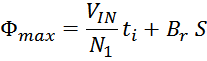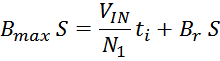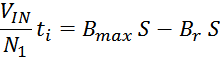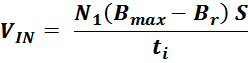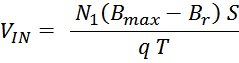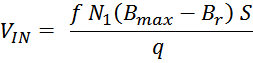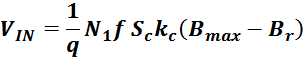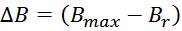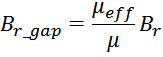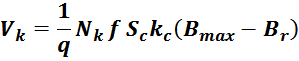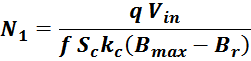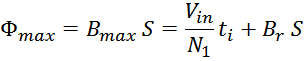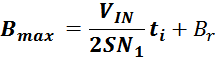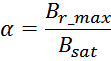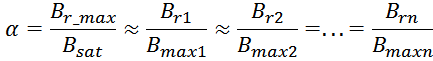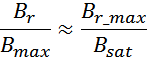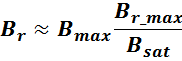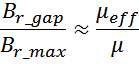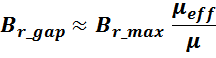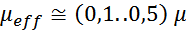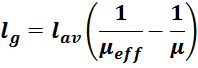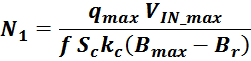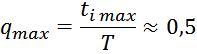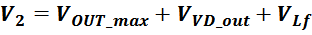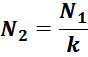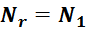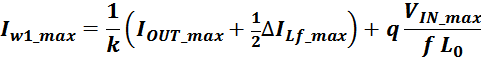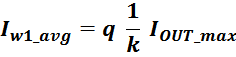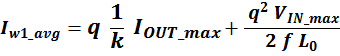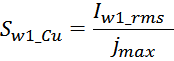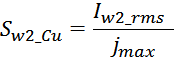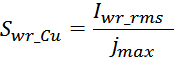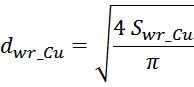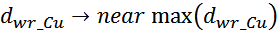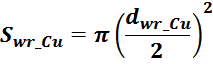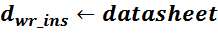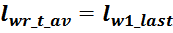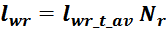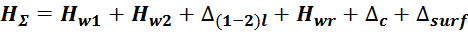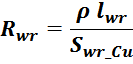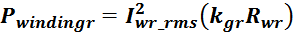Трансформатор, как элемент радиотехники и электротехники, работает на основе электромагнитной индукции. Говоря об индуктивности трансформатора, имеют в виду индуктивность обмоток и взаимоиндукцию между ними.
Каждая из обмоток представляет некоторое количество витков провода, намотанных на ферромагнитный сердечник, то есть обыкновенную катушку индуктивности.
Трудность в определении параметров катушки заключается в том, что они изменяются в зависимости от нескольких параметров и их сочетания:
- токи в обмотках;
- уровень намагниченности магнитопровода;
- магнитные характеристики сердечника;
- взаимодействие между соседними обмотками;
- наличия постоянной составляющей тока.
Содержание
- Конструкция и принцип действия силового трансформатора
- Физическое понятие индуктивности обмоток
- Формулы и измерение
- Как измерить в домашних условиях
- Пример расчета
Конструкция и принцип действия силового трансформатора
В основе конструкции любого трансформатора находятся следующие элементы:
- Сердечник из ферромагнитного материала.
- Первичная и вторичные обмотки. В случае автотрансформатора одна обмотка выполняет обе функции.
В сетях переменного тока промышленной частоты (50 или 60Гц) в качестве ферромагнитного материала используется сталь, обработанная по специальной технологии. На высоких частотах часто делаются трансформаторы без сердечника, поскольку для нормальной работы достаточно взаимосвязи межу катушками.
Принцип работы:
- в первичной обмотке, подключенной в цепь питания, создается переменное электрическое поле;
- под действием поля первичной катушки в сердечнике создается переменное магнитное поле;
- в силу электромагнитной индукции во всех обмотках наблюдается ЭДС индукции.
ЭДС индукции в первичной обмотке направлена противоположно поданному напряжению, поэтому они взаимно компенсируются. В результате, при отсутствии нагрузки через первичную обмотку протекает сравнительно небольшой ток холостого хода.
Наличие тока вторичной цепи аналогично вызывает дополнительный магнитный поток, а он – ЭДС самоиндукции в первичное катушке. В результате компенсация первичного напряжения снижается и растет ток в первичной цепи.
Физическое понятие индуктивности обмоток
Индуктивность представляет собой коэффициент пропорциональности между током, создаваемым замкнутым электрическим контуром, и магнитным потоком, который создается этим контуром.
Более понятной формулировкой будет та, которая говорит о величине ЭДС самоиндукции в замкнутом контуре, которая возникает при изменении силы тока за единицу времени. То есть, понятие индуктивности справедливо для изменяющегося тока.
При постоянном токе говорить об индуктивности бессмысленно.
В идеальном трансформаторе все электромагнитное поле, создаваемое обмотками, замкнуто в магнитном сердечнике. В реальных конструкциях существует поле рассеяния, величина которого зависит от способа выполнения катушки и конструктивных особенностей сердечника. Чем больше толщина намотки, тем большая часть электромагнитного поля замыкается вне магнитопровода.
Этому способствует также качество сборки магнитопровода. Зазоры между пластинами способствуют резкому увеличению рассеивания. В связи с этим наилучшими свойствами обладают О-образные сердечники.
Формулы и измерение
Формулы для расчета индуктивности катушек довольно сложны и имеет различный вид для различных типов исполнения обмоток:
- линейный проводник;
- одновитковая катушка;
- плоская катушка;
- соленоидальная обмотка;
- тороидальная форма.
Наибольшие сложности возникают при расчетах многовитковых многослойных катушек, то есть тех, которые составляют обмотку трансформаторов.
В подавляющем большинстве случаев точный расчет невозможен, поэтому приходится использовать примерные данные и уточнять их после проведения измерений.
Формулы для расчета индуктивности трансформатора основаны на расчетах соленоида:
L=µ0µN2S/l, где
µ0 – магнитная постоянная;
µ – магнитная проницаемость сердечника;
N – количество витков;
S – площадь одного витка;
l – длина обмотки.
Для измерения индуктивности существует несколько методик и приборов, созданных на их основе. В большинстве случаев измерение производится путем вычислений индуктивного сопротивления катушки при подаче образцового напряжения заданной частоты и измеренного значения тока через обмотку.
В специализированных приборах вычисления производятся автоматически, и пользователь только считывает показания шкалы прибора, выраженные в единицах индуктивности – Гн, мГн или мкГн.
Как измерить в домашних условиях
Приборы для непосредственного измерения индуктивности имеют высокую стоимость и редко используются в домашних условиях. С приемлемой точностью результаты можно получить, используя обычные приборы для измерения переменного тока: амперметр и вольтметр. Также необходим омметр.
Порядок действий следующий:
- При помощи омметра определяют активное сопротивление обмотки R.
- Подключают трансформатор последовательно с амперметром в сеть.
- Параллельно обмотке подключают вольтметр.
- По показаниям приборов определяют полное сопротивление трансформатора: Z=U/I
- Индуктивное сопротивление находят, вычитая из полного сопротивления активное: XL=Z-R
- Индуктивность определяется по формуле: L=XL/(2πf), где π – число пи 3.14, f – частота измерений.
Как правило, активное сопротивление намотки значительно (на несколько порядков) меньше индуктивного, поэтому можно его не учитывать. Именно поэтому, включение трансформатора в цепь постоянного напряжения вызывает короткое замыкание. Ток обмотки при этом будет ограничиваться только активным сопротивлением.
Пример расчета
К примеру, требуется рассчитать индуктивность первичной обмотки трансформатора питания. Путем измерений определено:
- Сопротивление обмотки 3 Ом.
- Напряжение сети 220 В.
- Частота питающего напряжения 50 Гц.
- Ток холостого хода 05 А.
Полное сопротивление:
Z=U/I=220/0.05=4400 Ом
Активное сопротивление меньше полного в 10000 раз и его можно не учитывать.
Определяем индуктивность:
L=XL/(2πf) =4400/ (2∙3.14∙50) =14 Гн.
Создать тему меня побудило чтение другой темы «Ламповый Усилитель От Василича, Делаем Сами». А именно, поста № 104, в котором предлагается методика измерения индуктивности первичных обмоток ТС и ТВЗ.
Поскольку тема закрыта, пришлось создать новую, чтобы устранить замеченные неточности.
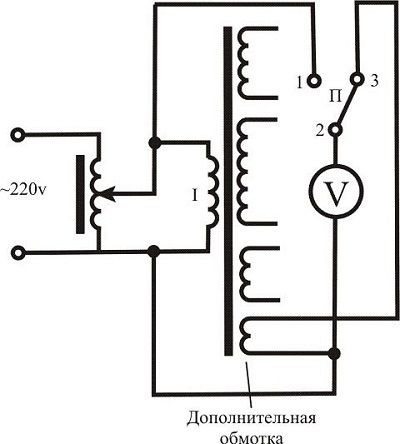
Последовательно с первичкой ТС или ТВЗ или любого дросселя,которые нужно измерить,включаем переменное сопротивление. Подаём на эту цепочку напряжение от сети или понижающего трансформатора любого,с любым напряжением. крутим резистора ось , выставляем на этом резисторе половину напряжения от входного. Отключаем схему. Измеряем номинал получившегося сопротивления резистора в ОМАХ. Делим на число 312 (для частоты 50гц) и получаем индуктивность в Генри. С достаточной для нас точностью.
В данной методике предполагается, что получив на резисторе падение в половину сетевого, мы имеем равенство величин индуктивного сопротивления обмотки и потенциометра.
Это не совсем так. Как известно, напряжения на последовательно соединённых индуктивности и сопротивлении имеют фазовый сдвиг. А именно 90 градусов в случае идеальной индуктивности. Т.е., для вычисления недостающего компонента применимы формулы треугольников. В данном случае, квадрат длины гипотенузы равен сумме квадратов длин катетов. Где гипотенуза — это сетевое напряжение, а катеты — напряжения на катушке и сопротивлении.
Примем напряжение сети за 1-цу. По методике, напряжение на резисторе равно 0,5 от сетевого. Длина недостающего катета (напряжения на катушке) может быть найдена как корень(1^2 — 0.5^2) = 0.866.
Поскольку через резистор и катушку течёт один и тот же ток, то реактивное сопротивление катушки будет в 0.866 / 0.5 = 1.732 раза больше, чем велиина сопротивления.
По методике Василичь’а (см. пример) индуктивность равна 6000 / 312 = 19,23 Гн, округлено до 19. (к стати, почему 312? 2 х pi() х 50 = 314)
На самом деле, сопротивление катушки составит 6000 х 1.732 = 10392 Ом, а индуктивность 10392 / 314 = 33,1 Гн.
Как видите, разница существенная. Утешает одно — счёт в нашу пользу! Катушка в жизни даже лучше, чем по результатам измерения.
Но, всё ли так плохо? Вовсе нет. Методика работоспособно, только коэффициент в формуле Василичь’а надо изменить на 314 / 1.732 = 181 для учёта фазовых соотношений в схеме.
Упомянутые явления легко увидеть, измеряв напряжения на катушке и резисторе тестером. Нпряжение сети в момент измерения 223 Вольта. Сопротивление резистора 2600 Ом.
Стоит учесть, что на резисторе рассеивается существенная мощность 110^2 / 6000 = 2 Ватта, поэтому он должен быть проволочным.
В моём практическом случае на потенциометре рассеивается 107.9^2 / 2600 = 4.5 Ватта!!
Тут следует внести небольшое дополнение. Видно, что сумме квадратов длин катетов (168^2 + 107.9^2 = 39866.41) не равно квадрату гипотенузы 223^2 = 49729.
С чего бы это? А с того, что катушка наша не идеальная и имеет сопротвление потерь, что приводит к отклонению фазового угла от 90 градусов. Насколько, давайте посчитаем.Воспользуемся соотношениями сторон разносторонненго треугольника
Примем a -напряжение сети, b — напряжение на резисторе, с — напряжение на катушке. Альфа — сдвиг фаз иежду последними напряжениями.
Немного преобразовав формулу, найдем косинус альфа, а из него угол. Для данного случая он составит 105,8 градусов, т.е., отклоненеи от теоретического угла составляет более 15-ти градусов.
Зная величину сопротивления (2600 Ом) и напряжения на катушке, находим полное сопротивление катушки. 2600 х 168 / 107,9 = 4048.2 Ома. Зная фазовый сдвиг, несложно найти индуктивную составляющую — 3895.5 ома и сопротивление потерь — 1101.3 Ома.
Из индуктивной составляющей находим величину индуктивности 3895.5 / 314 = 12,4 Гн
Сравним с результатом по скорретированной методике Василичь’а 2600 / 181 = 14,36 Гн.
Как видите, результат, полученный по упрощённой методике, дал завышение на 15,8%. Много это или мало? Вроде, многовато. Но, не будем забывать, что измерения по методике Василичь’а имеют оценочный характер, да и надо помнить, что манитная проницаемость железа зависит от величины магнитной индукции сердечника, иначе — от напряжения на обмотке. Поэтому, при измерениях нижней границы АЧХ усилителя, мы получим разные результаты, в зависимости от выходной мощности.
Физика работы импульсного трансформатора
Расчет трансформатора является одним из наиболее
трудных вопросов при проектировании и разработке импульсных источников питания. Для предварения практических
технических расчетов представим основные соотношения и определения, описывающие физику работы трансформатора,
используемые далее в практических расчетах.
Определение трансформатора как устройства
Трансформатор представляет собой электромагнитное устройство, предназначенное для преобразования
электрической энергии переменного тока с одними параметрами (напряжение, ток) в энергию переменного тока с
другими параметрами (напряжение, ток). Частота при этом не изменяется. Преобразование параметров переменного
напряжения осуществляется с помощью двух и более индуктивно связанных обмоток намотанных на одном
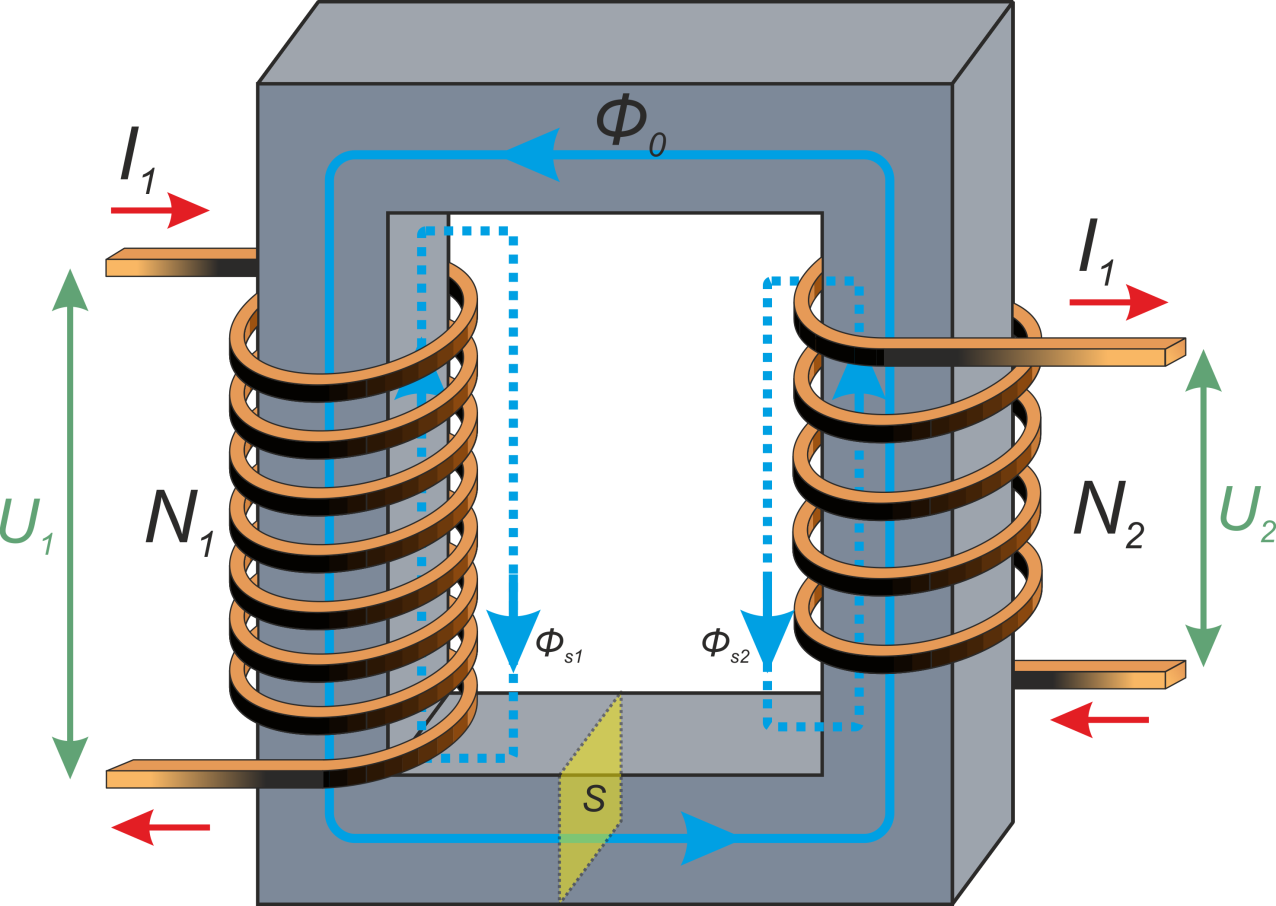
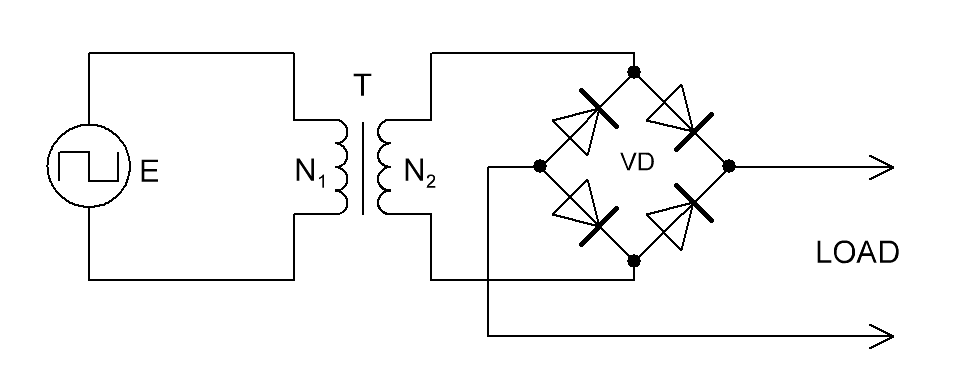
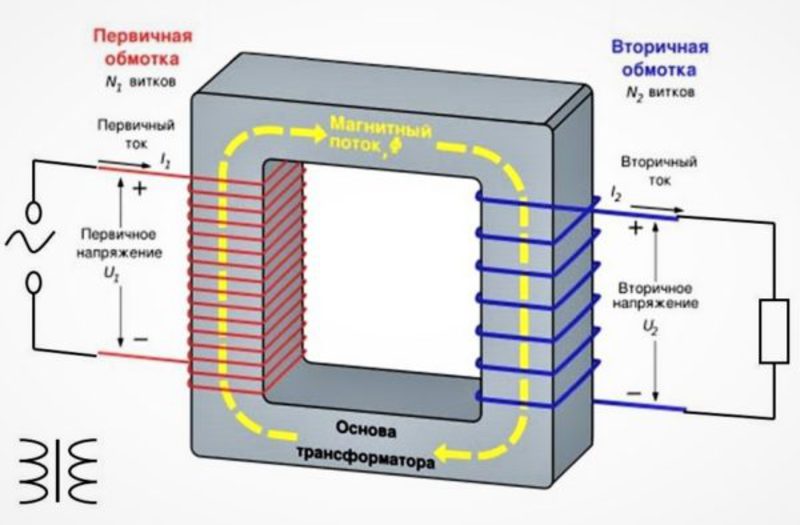
магнитопроводе. Схематично конструкция трансформатора представлена на рисунке T.1.
Рисунок T.1 – Устройство трансформатора
Трансформаторы играют двоякую роль – с одной стороны преобразуют параметры электрической энергии – повышают
или понижают напряжение и соответственно понижают или повышают ток, с другой стороны трансформатор
обеспечивает гальваническую развязку между первичной и вторичной обмотками.
Базовые характеристики магнитного поля
Поскольку трансформатор является электромагнитным устройством, то для количественного расчета трансформатора
кроме электрических параметров (напряжение, ток и т.д.) необходимо оперировать магнитными величинами.
Основной характеристикой магнитного поля является напряженность магнитного поляона количественно
описывает степень взаимодействия проводников с током. Обозначение – H. Единица измерения в системе СИ – А/м.
Магнитная индукция — векторная величина характеризующая силу магнитного поля. Обозначение – B.
Единица измерения в системе СИ – Тесла, Тл, (кг·с−2·А−1).
Интегральной характеристикой является поток вектора магнитной индукции. Обозначение – Ф. Единица
измерения в системе СИ – Вебер, Вб (кг·м²·с−2·А−1).
Мера сохранения магнитных свойств тел называется намагниченностью. Обозначение – J. Единица
измерения в системе СИ – А/м.
Намагниченность связана с напряженность внешнего магнитного поля:
где:
χ – магнитная восприимчивость материала;
H – напряженность магнитного поля.
Простейший трансформатор. Исходные параметры
Для выполнения дальнейших математических выкладок, необходимых для количественного расчета трансформатора
определим основные параметры трансформатора:
— Количество обмоток – 2;
— Количество выводов от каждой обмотки – 2
— Число витков первичной обмотки — N1 ;
— Число витков вторичной обмотки — N2 ;
— Площадь поперечного сечения магнитопровода – S (полагается неизменной по всей длине);
Таким образом, рассматриваемый в дальнейшем трансформатор имеет простейшую конфигурацию без выводов от
средней точки в первичной и вторичной обмотках. Введение дополнительных отводов вносит некоторую коррективу
в расчет, но не влияет на основные выкладки.
Закон электромагнитной индукции и коэффициент трансформации
Как и следует из определения трансформатора первичная и вторичная обмотки трансформатора связаны индуктивно
магнитным потоком магнитопровода Φ0 (единым для всех обмоток трансформатора), точнее его
изменением во времени. Так ЭДС первичной и вторичной обмотки в соответствии с законом электромагнитной
индукции равны:
Данные соотношения показывают физические процессы, происходящие при работе трансформатора:
— скорость изменения магнитного потока в магнитопроводе (сердечнике) пропорциональна напряжению на выводах
первичной обмотки и обратно пропорциональна числу витков в ней;
— напряжение на выводах вторичной обмотки пропорционально скорости изменения магнитного потока в
магнитопроводе и числу витков в ней.
В соответствии с принципом причинно-следственной закономерности скорость изменения магнитного потока является
причиной возникновения следствия — ЭДС во вторичной обмотке. Для многообмоточного трансформатора соотношения
для других обмоток, третьей, четвертой и т.д. идентичны.
Отношение напряжений на обмотках пропорционально отношению витков в обмотках:
Коэффициент трансформации k равен отношению числа витков первичной обмотки N1 к числу витков во
вторичной обмотке N2:
Магнитный поток в сердечнике трансформатора. Влияние нагрузки
При подключении к первичной обмотке источника переменного напряжения V1 по ней в ней возникнет ток
i1 и в магнитопроводе возникнет первичный магнитный поток Ф1(t). В результате действия
магнитного потока во вторичной обмотке возникает ЭДС самоиндукции V2и, при наличии нагрузки,
подключенной ко вторичной обмотке, возникает ток вторичной обмотки i2. Ток i2 в свою
очередь создает вторичный магнитный поток Ф2(t) направленный навстречу первичному потоку. В
результате в магнитопроводе устанавливается суммарный магнитный поток:
Незначительная часть потока первичной обмотки замыкается через воздух и называется потоком рассеяния
первичной обмотки ФS1(t). Аналогично существует поток рассеяния вторичной обмотки
ФS2(t).
Увеличение нагрузки и соответственно тока вторичной обмотки приводит к увеличению магнитного потока
Ф2(t) и соответственно потока Ф1(t). При этом суммарный магнитный поток Ф0(t)
практически не изменяется. Как и не изменится магнитная индукция в магнитопроводе. Это важно понимать.
Аналогичный процесс происходит при уменьшении нагрузки. Результирующий магнитный поток Ф0(t) и
вызывает перемагничивание сердечника трансформатора [Гейтенко Е.Н. Источники вторичного электропитания.
Схемотехника и расчет.Учебное пособие. — М.: СОЛОН-ПРЕСС, 2008. — 448 с.].
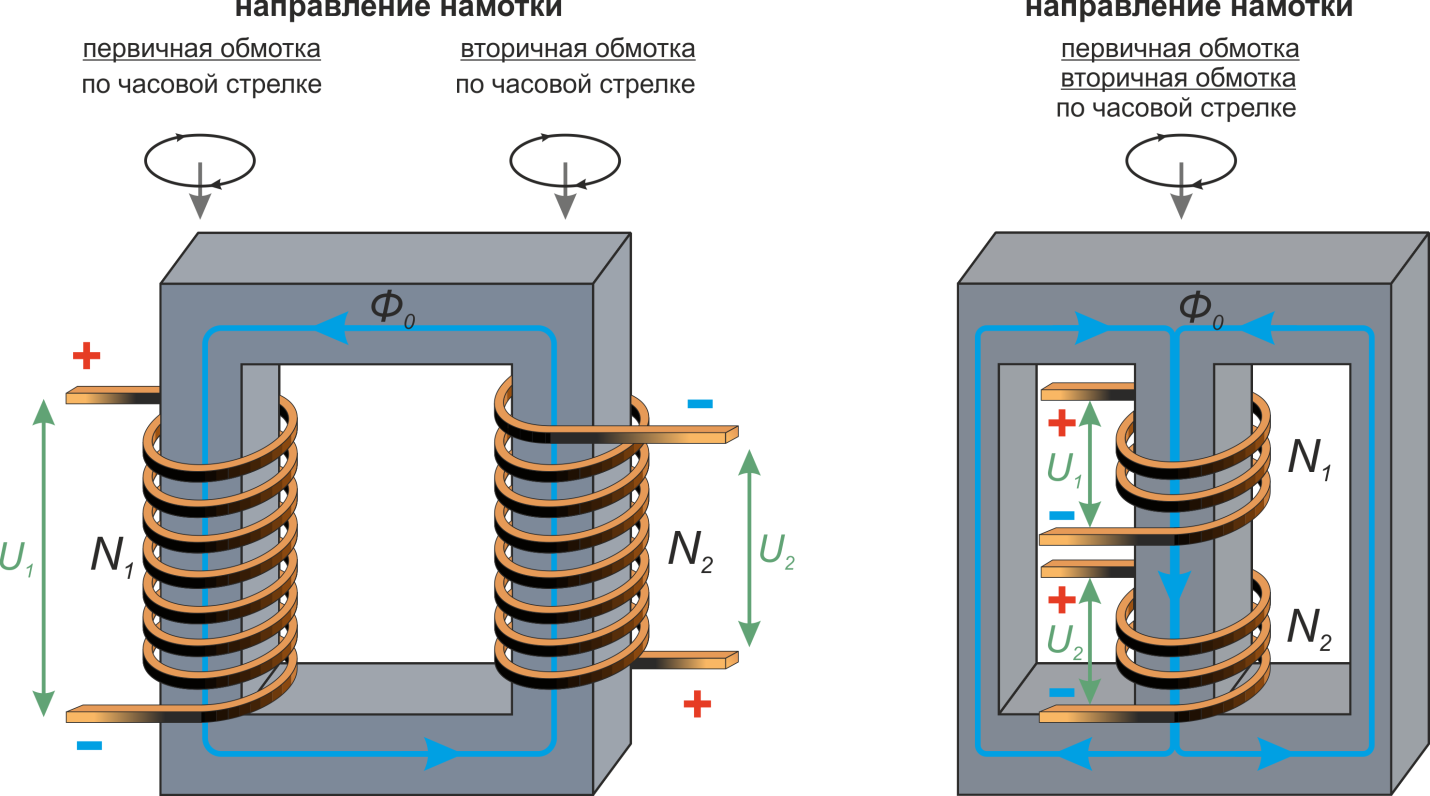
Фазировка обмоток трансформатора. Полярность. Связь геометрии намотки и полярностей входного и
выходного напряжения
При намотке и подключении трансформатора в «несимметричных» преобразователях (обратноходовой, прямоходовый)
важно соблюдать правильную фазировку обмоток трансформатора – то есть соблюдение «полярности» начала и конца
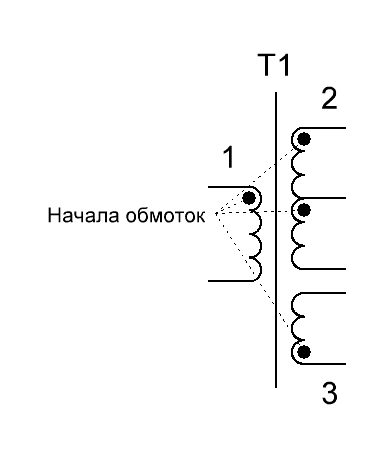
обмотки. На условном обозначении трансформатора начало обмотки отмечается точкой (рисунок T.2).
Рисунок T.2 — Начало обмотки отмечается точкой
Физически расположение начала и конца обмотки на магнитопроводе изображено на рисунке T.3.
Рисунок T.3 – К определению полярности входного и выходного напряжения трансформатора
Для наглядности можно представить, что:
— ток, проходя по кольцам обмотки, раскручивает находящиеся в ней электроны в некотором направлении создавая
вихрь. Электроны, находящиеся в другой, изолированной обмотке чувствуют этот вихрь и раскручиваются в том же
направлении, создавая ток.
Или:
— если сложить два изолированных провода вместе, затем намотать их на магнитопровод, то начала и концы
обмоток будут вместе.
Конструктивные элементы трансформатора и дросселя
Магнитопровод
Ключевым элементом любого трансформатора или дросселя является магнитопровод. Он обеспечивает сильную
магнитную связь между обмотками трансформатора. Именно благодаря наличию этой связи энергия передается от
первичной обмотки во вторичную. Магнитопровод характеризуется своей формой и ферромагнитным материалом, из
которого он был изготовлен.
Геометрия магнитопровода
Геометрические параметры магнитопровода
Основными геометрическими параметрами магнитопровода, определяемыми его формой являются:
— длина средней линии — lav;
— площадь окна — S0;
— площадь сечения Sc;
— объем — Vm;
— длина немагнитного зазора lg;
— суммарная и рабочая площадь охлаждения магнитопровода ST.
Геометрические параметры магнитопровода — длина средней линии и площади окна входят в формулу расчета
габаритной мощности.
Объем магнитопровода используется при расчете потерь в магнитопроводе и соответственно его температурного
режима.
Площадь сечения и длина немагнитного зазора входит в формулы расчета индуктивности намагничивания
трансформатора и ряда других параметров. Существуют магнитопроводы с уже выставленным немагнитным
зазором.
Все геометрические параметры магнитопровода определяются типом формы или другими словами типом геометрии
магнитопровода. Об этом – в следующем разделе.
Типы геометрии магнитопроводов
Существует большое число типов геометрий магнитопроводов. Многообразие форм продиктовано многообразием
применений, для которых важны те или иные параметры геометрии или конструктивные факторы. Так в соответствии
с принятой международной классификацией магнитопроводы разделяются на следующие типы, представленные в
таблице T.1 [Swithing Power Supply Design. Second Edition. Abraham I. Pressman. The McGraw-Hill Companies.
1998. 669 p. ; http://ferrite.rct.ru/uu-ferrite-cores.html].
Таблица T.1 — Типы и сравнительная характеристика магнитопроводов различных типов.
| Тип магнитопровода | Описание | Изображение | Особенности применения |
| EE | Ш-образный магнитопровод cпрямоугольным центральным стрежнем | 
|
— стандартные силовые трансформаторы, дроссели |
| ETD | Ш-образный магнитопровод c круглым центральным стрежнем |

|
— стандартные силовые трансформаторы, дроссели |
| EC | Ш-образный магнитопровод c круглым центральным стрежнем и пазом вблизи него |

|
— стандартные силовые трансформаторы, дроссели |
| EER | Ш-образный широкий магнитопровод c круглым центральным стрежнем |

|
— силовые трансформаторы низкопрофильных конструкций источников питания |
| PEE | Ш-образный плоский магнитопровод c прямоугольным стрежнем |

|
— планарные трансформаторы на основе печатных плат |
| PEI | Магнитопровод состоящий из Ш-образного плоского сегмента и сегмента в виде бруска |

|
— планарные трансформаторы на основе печатных плат |
| EFD | Ш-образный магнитопровод c узким прямоугольным центральным стрежнем |

|
— силовые трансформаторы низкопрофильных конструкций источников питания |
| UU | П-образный с прямоугольным стержнем |

|
— высоковольтные трансформаторы |
| CUT | Чашкообразный магнитопровод |

|
— низковольтные силовые трансформаторы и дроссели с малым уровнем помех |
| POT | Чашкообразный магнитопровод |

|
— низковольтные силовые трансформаторы и дроссели с малым уровнем помех |
| PM | Чашкообразный магнитопровод открытого типа круглой формы |

|
— низковольтные силовые трансформаторы и дроссели с малым уровнем помех |
| PQ | Чашкообразный магнитопровод открытого типа прямоугольной формы |

|
— низковольтные силовые трансформаторы и дроссели с малым уровнем помех |
| RM | Чашкообразный магнитопровод открытого типа ромбовидной формы |

|
— низковольтные силовые трансформаторы и дроссели с малым уровнем помех |
| LP | Чашкообразный ассиметричный магнитопровод открытого типа прямоугольной формы |

|
— низковольтные силовые трансформаторы и дроссели с малым уровнем помех |
| R | Кольцевой магнитопровод |

|
— силовые трансформаторы низкопрофильных конструкций источников питания, дроссели, дроссели фильтров |
Подробное описание типоразмеров магнитопроводов и параметров существующих стандартных рядов представлены
datasheet-ах производителей магнитопроводов.
Выбор типа магнитопровода осуществляется в зависимости от ряда факторов, включая назначение устройства,
планируемую стоимость, особенности корпуса конечного устройства и т.д. В таблице T.2 представлено
сравнительное описание преимуществ и недостатков различных типов геометрии магнитопроводов [Magnetic Cores
for Switching Power Supplies.Magnetics. Technical documents. General information.
https://www.mag-inc.com/Design/Technical-Documents/General-Information.aspx ps-01.pdf]:
Таблица T.2 — Применимость магнитопроводов различных геометрий
| Характеристика | Тип магнитопровода | ||||
| POT | RM | EE | EER | ETD | |

|

|

|

|

|
|
| Стоимость магнитопровода | высокая | высокая | Низкая | средняя | средняя |
| Стоимость каркаса | низкая | низкая | Низкая | средняя | средняя |
| Стоимость намотки | низкая | низкая | Низкая | низкая | низкая |
| Гибкость (технологическая простота) намотки | хорошая | хорошая | Отличная | отличная | отличная |
| Сборка | простая | простая | Простая | средняя | средняя |
| Технологичность монтажа | хорошая | хорошая | Хорошая | приемлемая | приемлемая |
| Теплорассеяние | плохое | хорошее | Отличное | хорошее | хорошее |
| Экранирование, электромагнитная совместимость | отличное | хорошее | хорошее | хорошее | хорошее |
Таблица T.2 — Применимость магнитопроводов различных геометрий. Продолжение.
| Характеристика | Тип магнитопровода | ||||
| EС | PQ | EP, LP | R | UU | |

|

|

|

|

|
|
| Стоимость магнитопровода | средняя | высокая | Средняя | очень низкая | низкая |
| Стоимость каркаса | средняя | высокая | Высокая | — | низкая |
| Стоимость намотки | низкая | низкая | Низкая | высокая | низкая |
| Гибкость (технологическая простота) намотки | отличная | хорошая | Хорошая | приемлемая | отличная |
| Сборка | средняя | простая | Простая | — | простая |
| Технологичность монтажа | приемлемая | приемлемая | Хорошая | плохая | хорошая |
| Теплорассеяние | хорошее | хорошее | Плохое | хорошее | Отличное |
| Экранирование, электромагнитная совместимость | хорошее | приемлемая | Отличное | хорошее | Хорошее |
Как правило, в справочных листках (по английскому — datasheet) компанией-производителем представлены
исчерпывающие данные о геометрических параметрах конкретного магнитопровода.
Универсальными типами магнитопроводов являются те, которые позволяют установку немагнитного зазора между
частями сердечника, что бывает необходимо при проектировании однотактных типов преобразователей. При
разработке двухтактных преобразователей (в которых наличие зазора не так важно) возможно использование
кольцевых тороидальных магнитопроводов. Преимуществами кольцевых магнитопроводов являются относительно малая
стоимость, отсутствие каркаса. Ш-образные магнитопроводы (E, EI, ER, ETD и т.д.) и особенно П-образные
магнитопроводы (UU) хорошо подходят для построения мощных и высоковольтных трансформаторов, поскольку имеют
большую ширину окна для размещения межслоевой и межобмоточной изоляции значительной толщины. С целью
увеличения эффективной площади сечения магнитопроводы можно складывать параллельно. Для этой цели особенно
шорошо подходят Ш-образные магнитопроводы типа EE, П-образные типа UU и кольцевые магнитопроводы.
Факторы, определяющие выбор типа магнитопровода
Преимущество использования того или иного типа магнитопровода (и феррита из которого он изготовлен, но об
этом — далее), зависит от ряда факторов:
— Топология преобразователя
— Рабочая частота
— Необходимость регуляции
— Стоимость
— КПД источника питания
— Выходное напряжение
— Допустимый температурный режим
— Массогабаритные требования
Для каждой топологии преобразователей существуют наиболее подходящие типы магнитопроводов, что обусловлено
физикой работы преобразователей и особенностями конструкции. Сравнительные данные о целесообразности
использования того или иного типа магнитопровода для построения различных типов преобразователей
представлены в таблице T.3 [Transformers, Inductors, and Coils. Design Guide. OEM Group. ACTOWN ELECTROCOIL,
INC]:
Таблица T.3 — Использование того или иного типа магнитопровода для построения различных типов
преобразователей
| Тип магнитопровода | Обратноходовый, дроссель импульсных стабилизаторов | Прямоходовый | Полумост, мост, пуш-пул |
| EE, EС | Хорошо | Хорошо | Приемлемо |
| ETD | Приемлемо | Хорошо | Хорошо |
| EFD | Нежелательно | Хорошо | Хорошо |
| EP | Нежелательно | Хорошо | Приемлемо |
| RM | Приемлемо | Хорошо | Приемлемо |
| POT | Приемлемо | Хорошо | Приемлемо |
| R | Нежелательно | Хорошо | Приемлемо |
Материал магнитопровода
Геометрия магнитопровода это форма, теперь перейдем к содержанию — ферромагнитному материалу из которого
изготавливаются магнитопроводы. Подавляющее большинство магнитопроводов импульсных источников питания
изготавливается из ферритов. Другие типы ферримагнитных материалов – сталь, альсиферы и т.д. используются
крайне редко. Поэтому в данной работе будут рассмотрены только ферриты.
Ферриты – основной материал магнитопроводов импульсных источников питания
Феррит – это класс материалов, из которых сделан магнитопровод практически всех импульсных источников
питания. Другие типы ферромагнитных материалов – электротехнические стали (частотный диапазон – до 3000 Гц),
альсиферы, пермаллои (чувствительность к механическим воздействиям, сложность технологии изготовления),
пресспермы, карбонильное железо используются в инверторной технике существенно реже. Ферриты представляют
собой керамические материалы, состоящие из смеси оксидов магнитных металлов с оксидом железа. Оксиды
металлов в той или иной степени являются изоляторами, что и обуславливает высокое сопротивление
ферритов.
По своему составу ферриты делятся на никель-цинковые (NiZn), марганец-цинковые (MnZn), и ферритовые
полимерные композиционные материалы (FPC) с распределенным магнитным зазором. [Ферритовые изделия фирмы
EPCOS. В. Мелёшин. Компоненты и технологии, №4, 2002]. Каждый из выпускаемых типов феррита имеет свою
область применения. NiZn-ферриты используются преимущественно для радиотехнических задач (рабочих частотах
выше 2 МГц) [Трансформаторы и дроссели для импульсных источников питания. А. Кузнецов. Схемотехника, 2000,
№1, с. 30—33, №2, с. 48, 49, 2001, №1, с. 32—34.]. Для магнитопроводов изделий силовой электроники
традиционно используются MnZn-ферриты. Марки ферритов, предназначенные для использования в импульсных
источниках питания с указанием их характеристик представлены в таблице Т.4. [Трансформаторы и дроссели для
импульсных источников питания. А. Кузнецов. Схемотехника, 2000, №1, с. 30—33, №2, с. 48, 49, 2001, №1, с.
32—34.].
Характеристики ферритов
Основными количественными параметрами ферритов являются:
— магнитная проницаемость;
— максимальное значение магнитной индукции;
— частотный диапазон (верхняя граничная частота);
— величина удельных потерь;
— коэрцитивная сила;
— точка Кюри (критическая температура, при которой ферромагнетики теряют свои магнитные свойства).
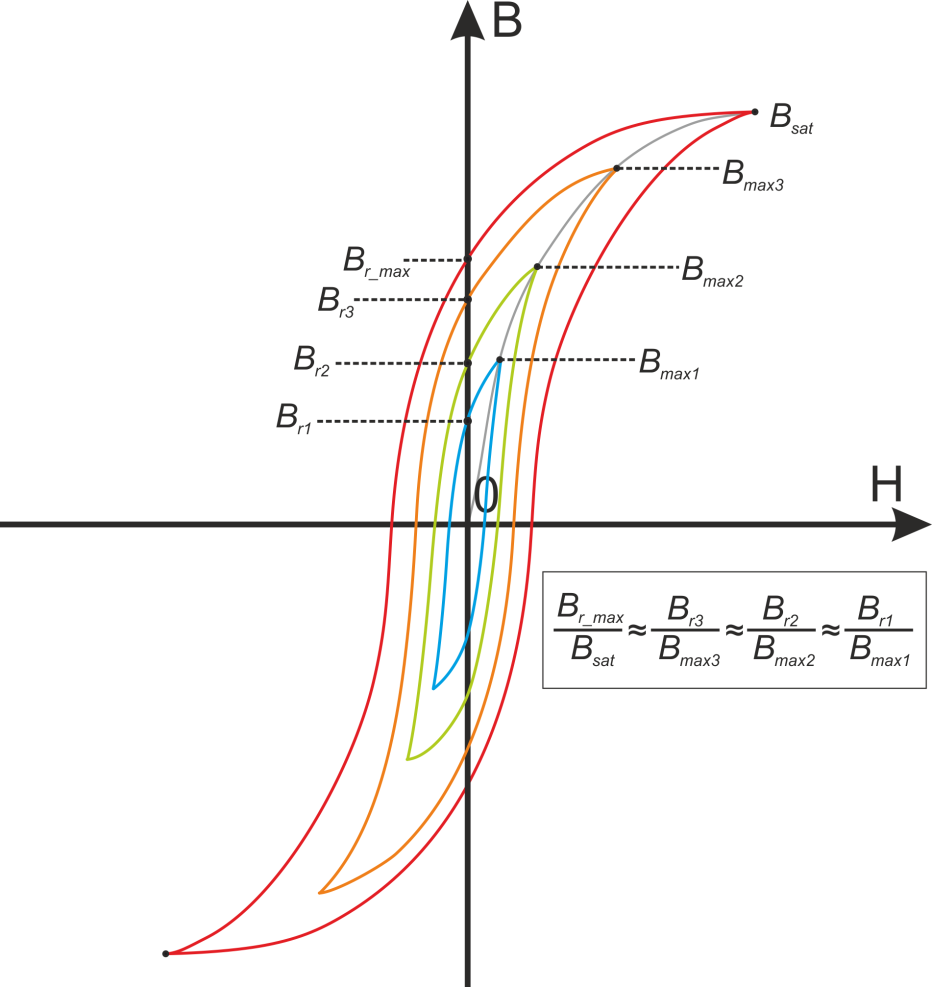
Четыре параметра одной петли: индукция насыщения, коэрцитивная сила, остаточная индукция,
напряженность магнитного поля при насыщении
Изменение напряженности магнитного поля H, создаваемой внешним током, приводит к увеличению магнитной
индукции в нем [Transformer and inductor design Handbook. Third Edition, Revised and Expanded. Colonel Wm.
T. McLyman. Marcel Dekker, Inc., 2004]. Однако это зависимость нелинейна – во первых, с ростом напряженности
H замедляется рост индукции B, во вторых при некотором значении H наступает насыщение магнитной индукции и
она более не увеличивается, в третьих зависимость B от H имеет гистерезис, то есть эффект памяти предыдущего
состояния.
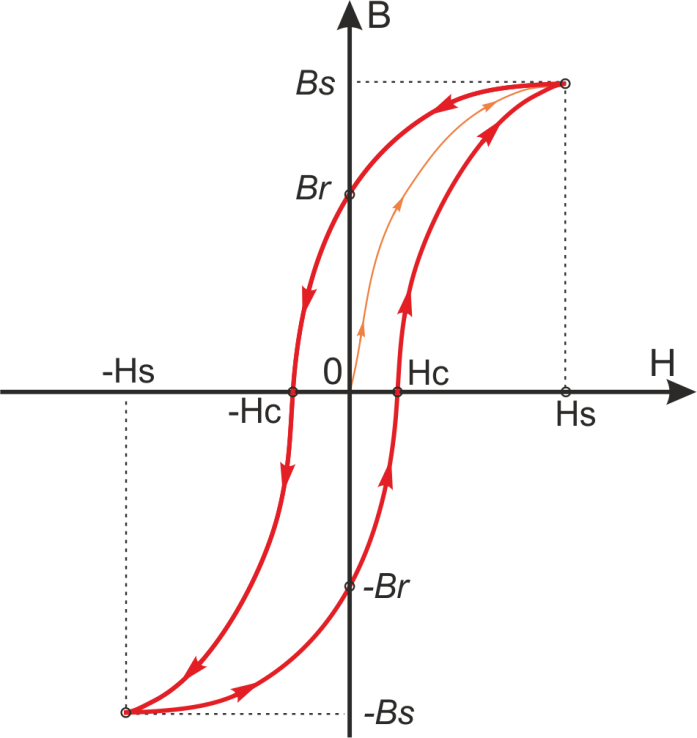
Петля гистерезиса зависимости B(H) определяет ряд базовых параметров феррита (рисунок T.4):
— Bs – индукция насыщения, не изменяющаяся при дальнейшем увеличении Н магнитного поля;
— Hs – максимальная напряженность поля, при которой достигается индукция насыщения;
— Hc – коэрцитивная сила или напряжённость магнитного поля, в котором происходит размагничивание
(B=0) феррита намагниченного до насыщения;
— Br — остаточная индукция, — величина магнитной индукции после снятия магнитного поля.
Рисунок T.4 — Общий вид петли гистерезиса для феррита
Максимальное значение индукции в магнитопроводе. Насыщение магнитопровода
Если через обмотку трансформатора или силового дросселя протекает слишком большой ток, создающий в сердечнике
величину индукции магнитного поля большую чем величина предельного значения индукции Bmax, то
материал магнитопровода входит в насыщение. При насыщении сердечника его магнитная проницаемость резко
уменьшается, что приводит к соответствующему уменьшению индуктивности и резкому росту тока. Визуально
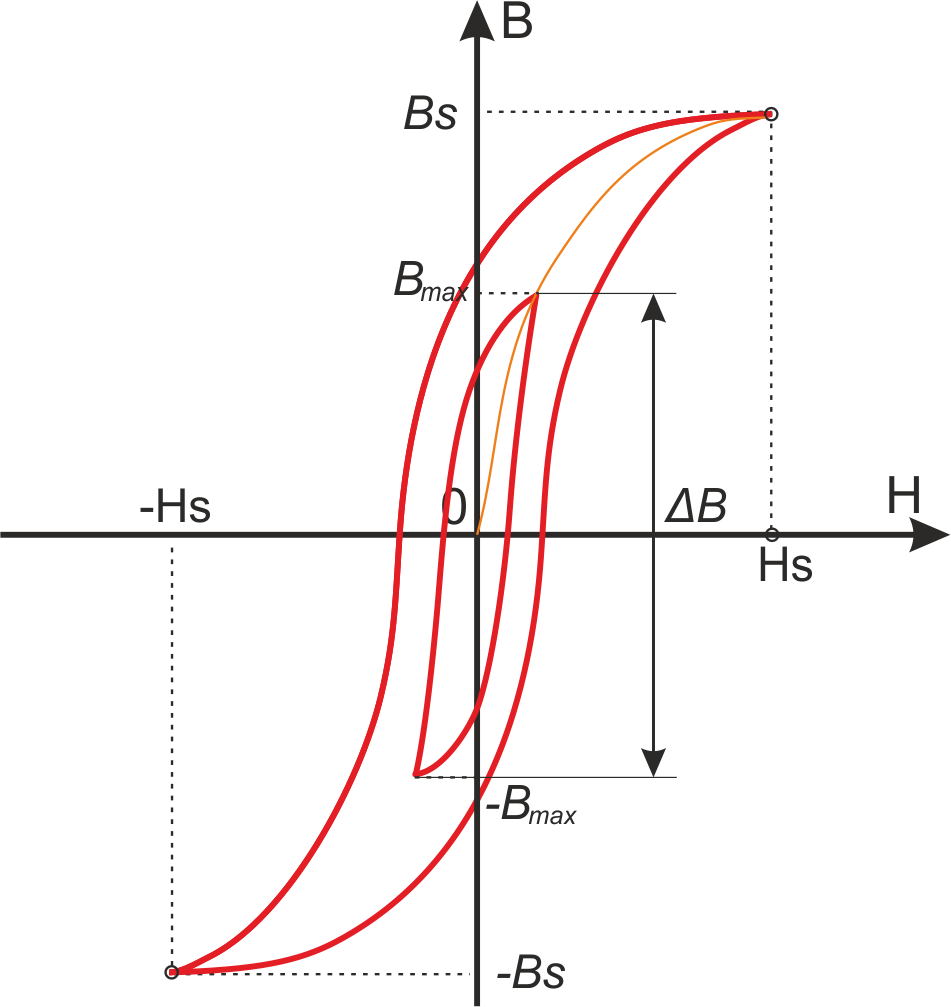
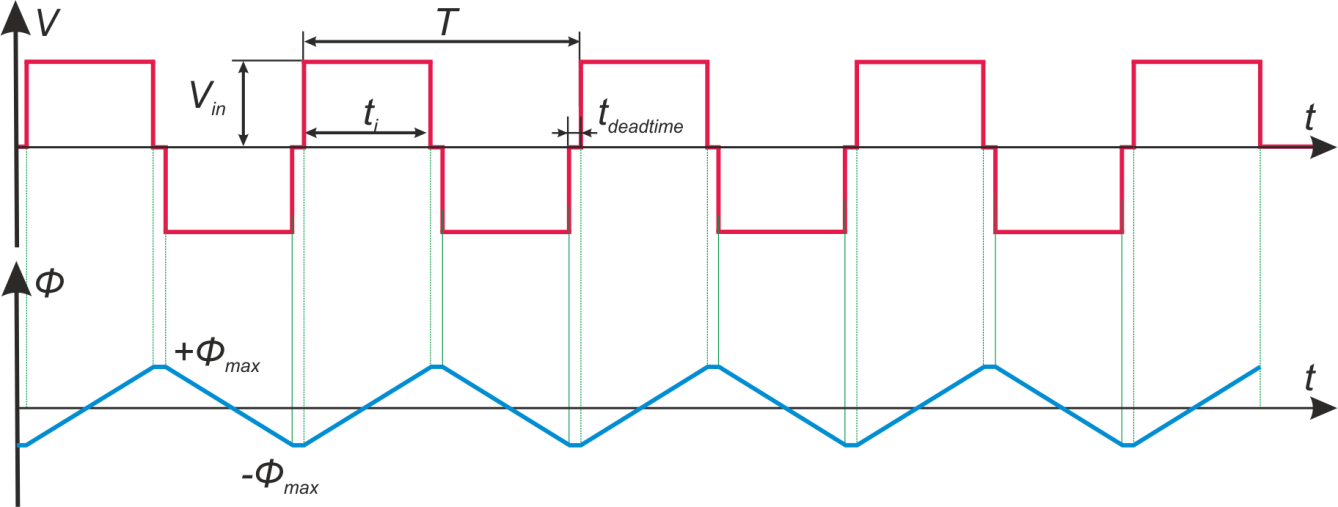
симметричный рабочий цикл магнитной индукции с заходом в область насыщения представлен на рисунке T.5
[Импульсные источники питания. Теоретические основы проектирования и руководство по практическому
применению. Раймонд Мэк. Додэка XXI. 2008. 274 с.]
Рисунок T.5 Петли гистерезиса для феррита: a – с заходом в область насыщения (основная кривая
намагничивания), б – кривая рабочего цикла перемагничивания магнитопровода без насыщения
Негативными последствиями насыщения трансформаторов и дросселей являются:
— резкий рост тока через первичную обмотку вызывает токовые перегрузки ключей, их перегрев, что может стать
причиной выхода их из строя;
— увеличение потерь в магнитопроводе;
— большие импульсные токи через обмотки могут стать причиной перегрева электролитических конденсаторов;
— рост омических потерь в обмотках (пропорциональны квадрату тока).
Двухтактные преобразователи критичны к несимметричному перемагничиванию магнитопровода в результате которого
возникает подмагничивающий ток и возможно насыщение магнитопровода. Для предотвращения этого вводят
воздушный зазор и включают конденсатор последовательно с первичной обмоткой трансформатора.
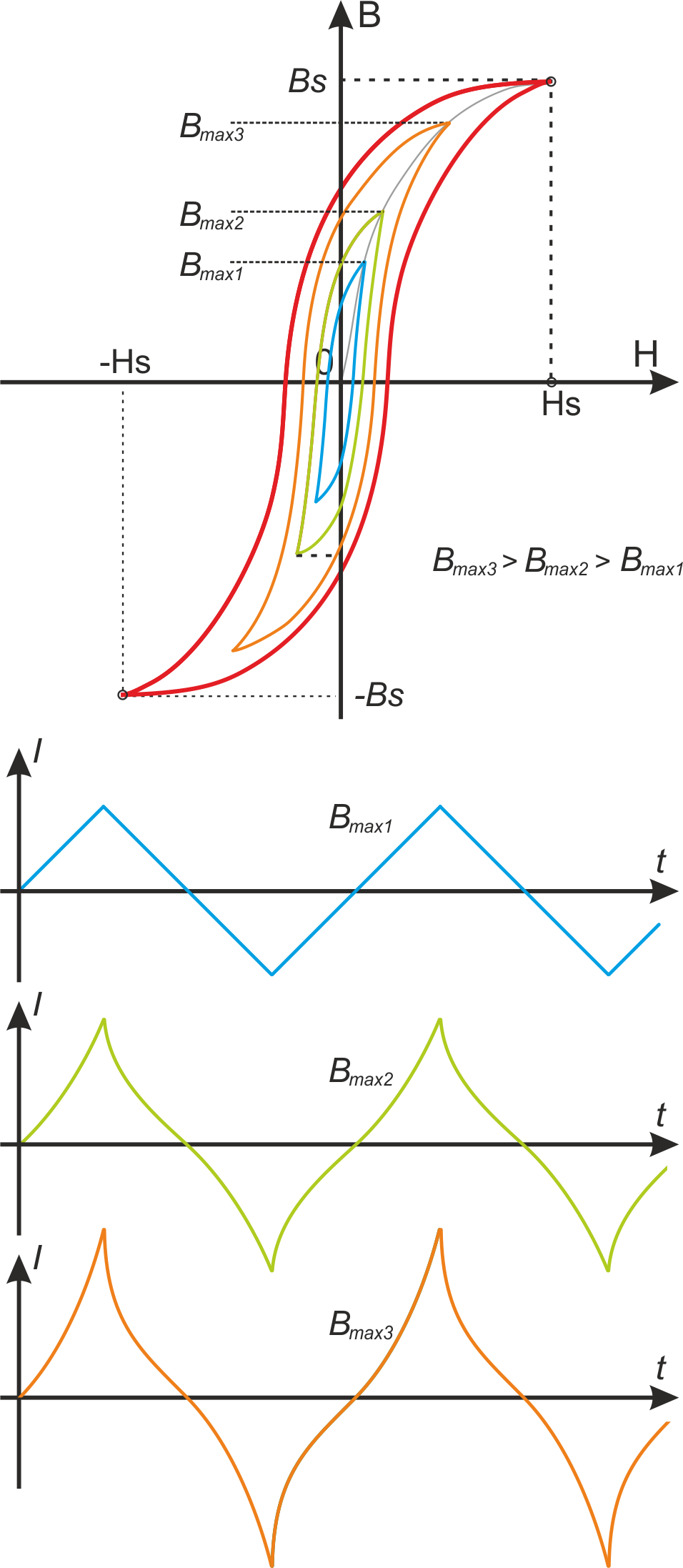
Временная диаграмма тока (треугольной составляющей) первичной обмотки трансформатора (и силового дросселя)
при вхождении в режим насыщения представлена на рисунке T.6.
Рисунок T.6 — Петли гистерезиса и соответствующая им форма тока
Магнитная проницаемость
Одной из основных характеристик ферритов является магнитная проницаемость μ. Чем выше магнитная
проницаемость, тем выше значение индуктивности первичной обмотки при прочих равных условиях. Обратной
стороной является то, что с ростом μ возрастают потери на высоких частотах. Поэтому высокочастотные марки
ферритов обладают меньшими значениями магнитной проницаемости.
Величина магнитной проницаемости не является однозначной константой. Для определения магнитной проницаемости
в каждой точки цикла гистерезиса используют понятие дифференциальной магнитной проницаемости [Вдовин С. С.
Проектирование импульсных трансформаторов. — 2-е изд., перераб. и доп. — Л.: Энергоатомиздат. Ленингр.
отд-ние, 1991. — 208 с: ил.]:
Для оценки магнитной проницаемости на конкретной кривой гистерезисного цикла:
то есть магнитная проницаемость является фактически касательной к кривой петли гистерезиса.
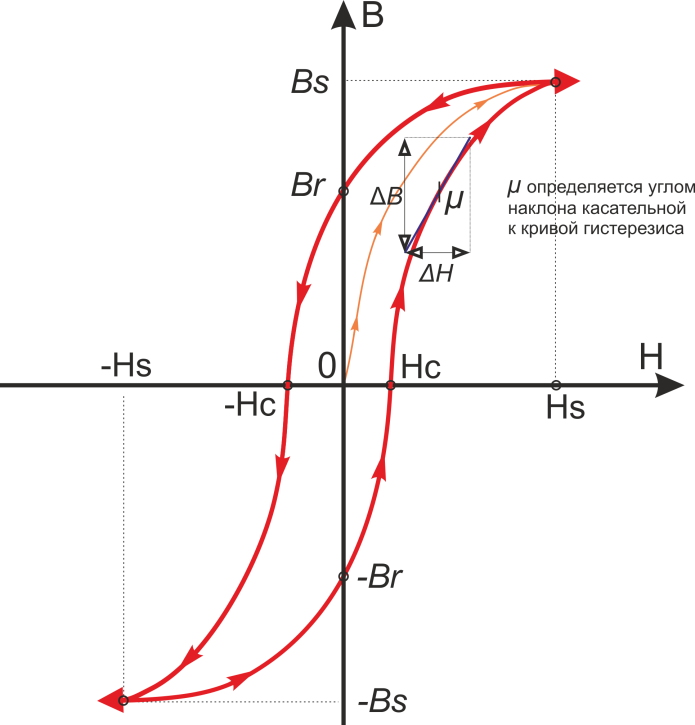
График зависимости индукции магнитного поля в ферромагнетике от напряженности магнитного поля имеет вид петли
гистерезиса. Типичный вид петли гистерезиса феррита представлен на рисунке T.7.
Рисунок T.7 — К пояснению понятия магнитной проницаемости. Магнитная проницаемость μ определяется
касательной к кривой петли гистерезиса.
Обычно в datasheet представлена так называемая начальная магнитная проницаемость μi(Initial
permeability) измеряемая в начале петли гистерезиса при малых магнитных полях – рисунок T.7.
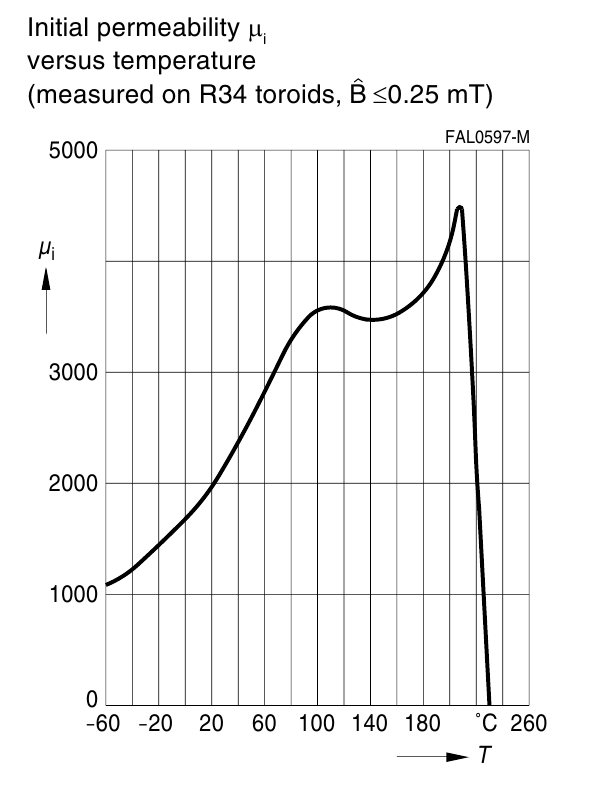
Зависимость магнитной проницаемости феррита от температуры
Зависимость магнитной проницаемости ферритов от температуры имеет сложный характер. В целом увеличение
температуры примерно от 25 °С до 200 °С приводит к росту μ, а далее достигая максимума при некоторой
температуре (температуре Ж. Кюри) ≈200 °С резко спадает (рисунок T.8).
Рисунок T.8 — Зависимость начальной магнитной проницаемости от температуры для феррита N87 [Ferrites and
accessories. SIFERRIT material N87, EPCOS AG 2006]
Зависимость магнитной проницаемости феррита от частоты
Прежде чем рассмотреть зависимость магнитной проницаемости феррита от частоты сделаем небольшое отступление,
чтобы понять глубину вопроса.
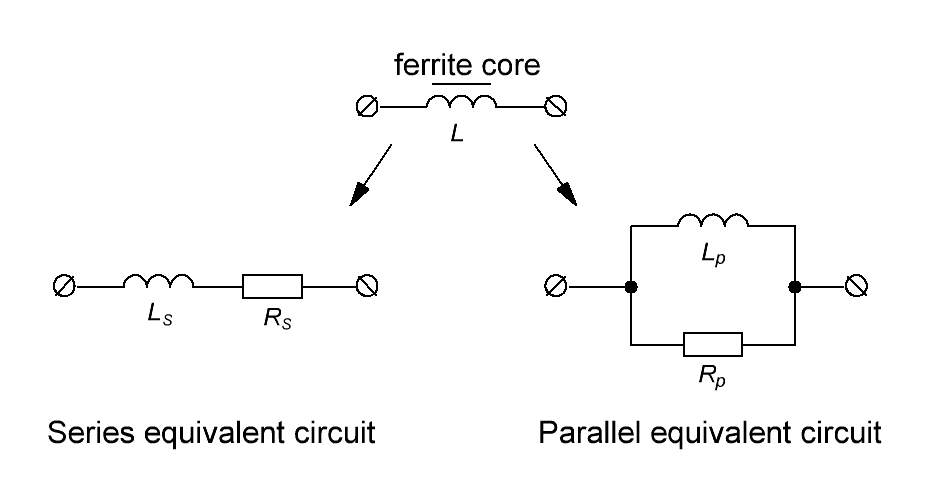
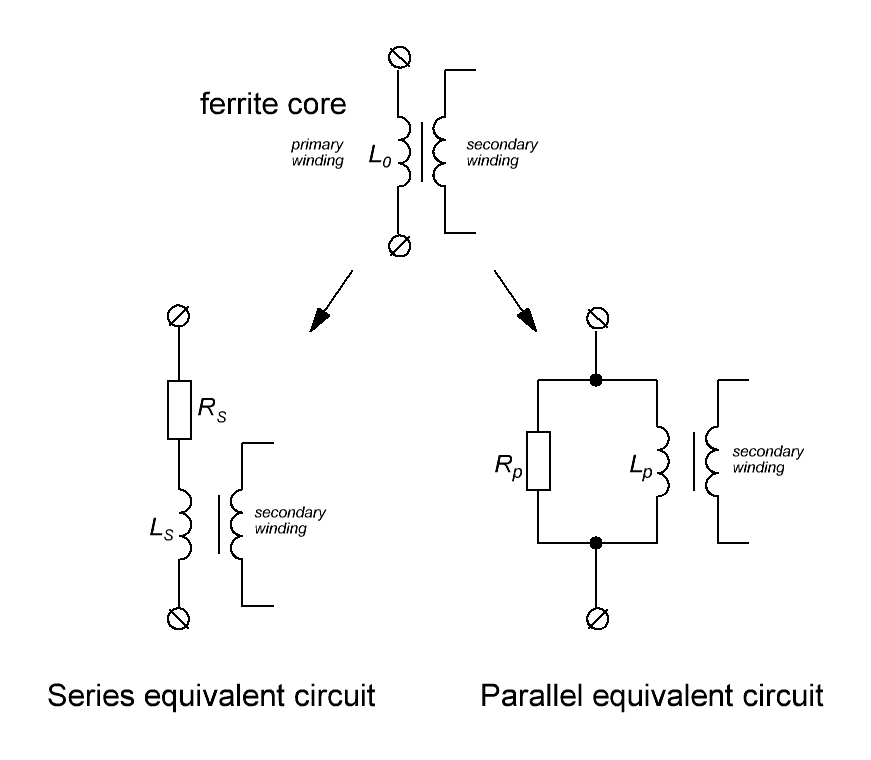
Индуктивность намагничивания L0 первичной обмотки трансформатора с сердечником из магнитомягкого
материала, например феррита (провода без сопротивления) можно представить как последовательное соединение
идеальной индуктивности Ls и некоторого сопротивления потерь Rs (последовательная
схема замещения) или как параллельное соединение идеальной индуктивности LP и некоторого
сопротивления потерь RP (параллельная схема замещения). Оба типа схемы замещения
представлены на рисунке T.9.
а
б
Рисунок T.9 — Последовательная и параллельная схемы замещения дросселя (а), и первичной обмотки
трансформатора (б) с ферритовым сердечником. Схема учитывает особенности поведения конкретного типа
феррита
с измерением частоты
Вводимые в схему замещения эквивалентные сопротивления учитывают (обобщают) потери на гистерезис, вихревые
токи и остаточную намагниченность.
Для последовательной схемы замещения суммарное активно-реактивное сопротивление Z будет определяться
выражением [Electronic components and materials textbook volume ii. Thanassis G. Giokas. ATH. STAMOULIS
PUBLICATIONS. 2004. 332 p. (CHAPTER 6 — 6.2 Attributes of ferrites)]:
Соответственно реактивная и активная составляющая этой формулы определяют действительную и мнимую
составляющую:
где:
μS’ – действительная составляющая μ, которая отвечает за собственно индуктивность LS;
μS’’ – мнимая составляющая μ, которая определяет потери – эквивалентное последовательное
сопротивление RS.
При этом отношение мнимой части к действительной равно отношению активного сопротивления к реактивному и
определяет угол сдвига фаз (тангенс угла потерь):
Отсюда можно вычислить величину активного сопротивления потерь:
Для схемы замещения с параллельным сопротивлением Rp суммарное активно-реактивное сопротивление
будет определяться выражением:
Соответственно:
Тангенс угла будет иметь значение:
В datasheet на ферриты как правило приводится только данные по схеме с последовательным сопротивлением.
Однако зная μS’ и μS’’ можно получить μP’ и μP’’. Всоотсветствии
с [Electronic components and materials textbook volume ii. Thanassis G. Giokas. ATH. STAMOULIS PUBLICATIONS.
2004. 332 p. (CHAPTER 6 — 6.2 Attributes of ferrites)] получаем:
В эквивалентной схеме трансформатора удобнее использовать параллельное сопротивление Rp, напротив
при расчете дросселей удобнее использование последовательного сопротивления потерь RS.
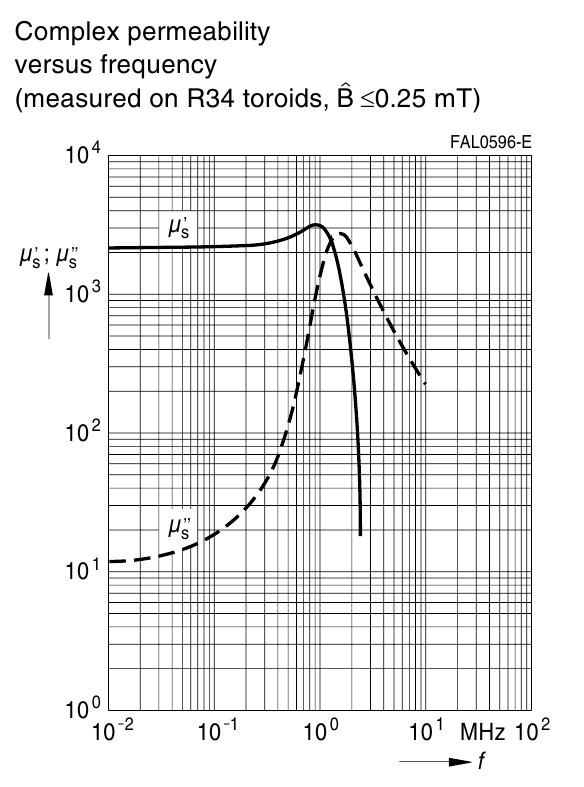
Пример частотной зависимости различных составляющих магнитной проницаемости ферритов представлен на рисунке
T.10. Видно, что μ при малых частотах «индуктивная» часть μS’ практически не изменяется, далее
немного возрастает и резко спадает, начиная с некоторой граничной частоты. А «омическая» часть μS’’
определяющая потери с ростом частоты существенно возрастает приближаясь в максимуме к μS’ . Спад
μS’’ начинается после спада μS’.
Рисунок T.10 — Зависимость различных составляющих комплексной проницаемости от частоты для феррита N87
[Ferrites and accessories. SIFERRIT material N87, EPCOS AG 2006]
Потери в магнитопроводе обусловленные свойствами феррита
Тепловая энергия, выделяемая в магнитопроводе выполненном из любого магнитного материала определяется
траекторией полета по петле гистерезиса и сколько кругов по этой петле будет намотано за единицу времени.
Выражаясь научными терминами, — размахом магнитной индукции B и рабочей частотой f. Для расчета потерь в
магнитопроводе Pferrit можно использовать следующее аппроксимирующее выражение [Optimum design of
a high-power, high-frequency transformer. R. Petkov. IEEE Transactions on Power Electronics (Volume: 11,
Issue: 1, Jan 1996)]:
где:
f – частота;
B – размах индукции;
K1, K2, K3 – аппроксимационные коэффициенты, определенные для каждого конкретного типа феррита.
В большинстве случаев справочные листки на ферриты не содержат информации об аппроксимационных коэффициентах,
и для определения потерь в магнитопроводе можно использовать соотношение:
где:
Pvferrit — мощность потерь на единицу объема, являющаяся функцией температуры, магнитной индукции
и частоты;
Vm – объем магнитопровода.
Мощность потерь на единицу объема Pvferrit определяется типом феррита и приводится в
справочных данных на конкретный тип магнитного материала. Использование удельной мощности потерь на единицу
объема является удобным способом расчета потерь в магнитопроводе.
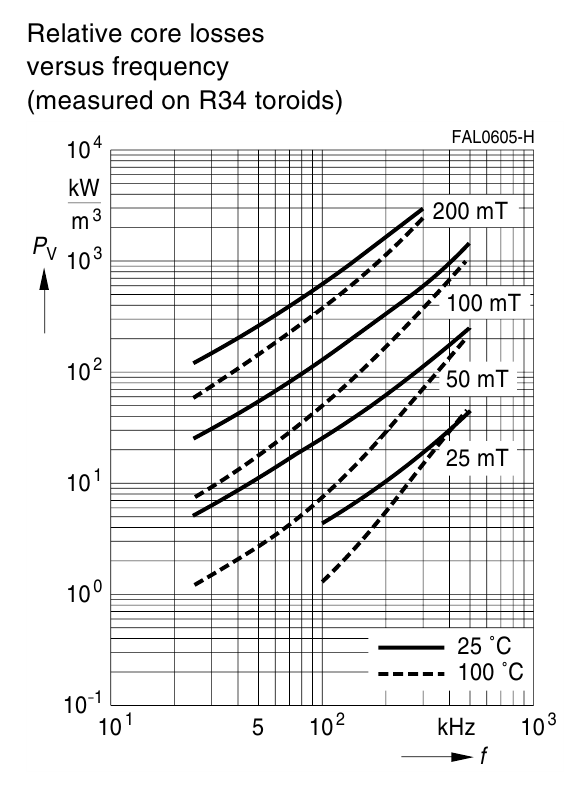
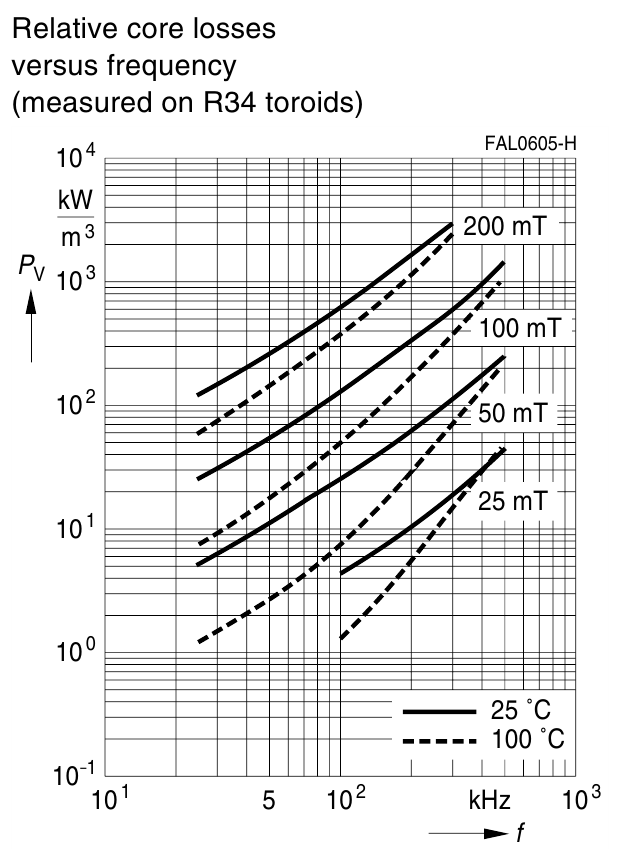
На рисунке T.11 представлена зависимость мощности потерь от частоты при различных значениях индукции
магнитного поля и температуре для феррита N87.
Рисунок T.11 — Зависимость мощности потерь от частоты при различных значениях индукции магнитного поля и
температуре для феррита N87[Ferrites and accessories. SIFERRITmaterial N87, EPCOS AG 2006]
Распространенные типы ферритов для импульсных источников питания и их характеристики
Таблица T.4 содержит данные о наиболее используемых типах силовых ферритов. Более подробно параметры всех
основных типов ферритов используемых в элементах силовой электроники представлены в соответствующих
datasheet-ах производителей магнитопроводов.
Таблица T.4 — Наиболее распространенные типы ферритов, предназначенные для использования в импульсных
источниках питания
|
Тип феррита |
Область применения, особенности |
Материал |
Оптимальный частотный диапазон, кГц |
Магнитная проницаемость μ |
Максимальная индукция Bmax, Тл |
Коэрцитивная сила, Hс, |
Производитель, ссылка |
||
| 25 ºС | 100 ºС | 25 ºС | 100 ºС | ||||||
| N27 | Трансформаторы обратноходовых преобразователей. Низкая стоимость, используется. для мощных источников |
MnZn | 25 — 150 | 2000 | 500 | 410 | 23 | 19 | EPCOS [Ferrites and accessories SIFERRIT material N27. EPCOS AG 2006] [Siemens Matsushita Components. Ferrites and Accessories] |
| N41 | Трансформаторы тока, дроссели | MnZn | 25 – 150 | 2800 | 490 | 390 | 22 | 20 | EPCOS [Ferrites and accessories SIFERRIT material N41. EPCOS AG 2006] [Siemens Matsushita Components. Ferrites and Accessories] |
| N87 | Стандартные источники питания | MnZn | 25 — 500 | 2200 | 490 | 390 | 21 | 13 | EPCOS [Ferrites and accessories SIFERRIT material N87. EPCOS AG 2006] |
| 3C90 | Трансформаторы импульсных источников питания | MnZn | До 200 кГц | 2300 | 470 | 380 | 16 | 12 | Philips — Ferroxcube [Soft Ferrites and Accessories, 2000 Apr 20] [3C90 Material specification, Ferroxcube, 2008 Sep 01] |
| 3C95 | Трансформаторы импульсных источников питания | MnZn | До 500 кГц | 3000 | 530 | 410 | 13 | 7 | Philips — Ferroxcube [3C95Material specification, Ferroxcube, 2008 Sep 01] |
| 3F3 | Трансформаторы импульсных источников питания | MnZn | 200-500 | 2000 | 440 | 370 | 15 | 11 | Philips — Ferroxcube [Soft Ferrites and Accessories, 2000 Apr 20] [3F3Material specification, Ferroxcube, 2008 Sep 01] |
| PC47 | Для силовых трансформаторов и дросселей | MnZn | До 300 кГц* | 2500 | 530 | 420 | 13 | 6 | TDK [Ferrite for Switching Power Supplies Summary. June 2012. TDK] |
| PC90 | Для силовых трансформаторов и дросселей | MnZn | До 300 кГц* | 2200 | 540 | 450 | 13 | 6.5 | TDK [Ferrite for Switching Power Supplies Summary. June 2012. TDK] |
| PC95 | Для силовых трансформаторов и дросселей | MnZn | До 300 кГц* | 3300 | 530 | 410 | 9.5 | 6.5 | TDK [Ferrite for Switching Power Supplies Summary. June 2012. TDK] |
| 2500НМС1 | Для силовых трансформаторов и дросселей | MnZn | До 100 кГц | 2500 | 290 | ОАО «Ферроприбор» [http://www.rusgates.ru] | |||
| 2500НМС2 | Для силовых трансформаторов и дросселей | MnZn | До 100 кГц | 2200 | 330 | ОАО «Ферроприбор» [http://www.rusgates.ru] | |||
| 2500НМС5 | Для силовых трансформаторов и дросселей | MnZn | До 200 кГц | 3300 | 310 | ОАО «Ферроприбор» [http://www.rusgates.ru] | |||
| 3000НМС | Для силовых трансформаторов и дросселей | MnZn | 30-50 кГц | ОАО «Ферроприбор» [http://www.rusgates.ru] |
Среди ферритов российского производства наилучшими характеристиками для целей силовой электроники обладают
ферриты марки 2500НМС [Силовая электроника. Профессиональны решения. Борис Семенов. Солон-Пресс, ДМК Пресс,
2011, 416 c.].
Необходимо отметить, что ферриты подвержены старению. В связи с этим необходимо проектирование устройств с
некоторым запасом.
Обмотки
Обмотка трансформатора или дросселя – это базовый элемент обеспечивающий формирование магнитного поля и
возбуждение ЭДС индукции (см. пункт «Физика работы импульсного трансформатора» настоящего раздела). Она
играет роль «концентрированного» проводника с током.
Как правило, обмотка выполняется из медного провода в эмалевой изоляции и выполняется на каркасе,
конструктивно комплементарном с магнитопроводом. Ниже представлены конструктивные особенности данных
элементов.
Конструктивные особенности обмоток
Обмотки трансформатора и силового дросселя должны быть хорошо изолированы как от магнитопровода, так и между
собой [Расчет трансформаторов и дросселей малой мощности. Белопольский И.И. М.: Госэнергоиздат, 1963. – 207
с.: ил.].
Для изоляции обмоток от магнитопровода используется каркас (или изоляционный слой в случае кольцевых
трансформаторов), изоляция обмоток между собой осуществляется за счет межобмоточной изоляции и наконец, для
обеспечения взаимной изоляции слоев при высоких напряжениях на обмотке используют межслоевую изоляцию.
Межслоевая изоляция
Межслоевая изоляция используется при достаточно высоких напряжениях в обмотках трансформаторов для
предотвращения межвиткового пробоя. При малых напряжениях на обмотке межслоевая изоляция может не
использоваться и её функцию выполняет изоляция провода обмотки. При выполнении одной из обмоток хорошо
изолированным проводом необходимость в межобмоточной изоляции так-же отсутствует.
Межслоевая изоляция напрямую влияет на паразитные параметры трансформатора — увеличение межслоевой изоляции
приводит с одной стороны к росту индуктивности рассеяния обмотки, а с другой стороны – к уменьшению её
паразитной емкости.
Межобмоточная изоляция
Межобмоточная изоляция необходима для изоляции обмоток друг от друга. В ряде случаев функцию межобмоточной
изоляции выполняет секционированный каркас. Толщина изоляции влияет на межобмоточную емкость.
Материалы для изоляции обмоток
Тип используемых изоляционных материалов зависит от условий эксплуатации трансформатора. Срок службы изоляции
определяется, прежде всего, температурой её эксплуатации. Используются две величины температур:
— среднее значение увеличения температуры;
— увеличение температуры в горячих пятнах, образующихся в результате неравномерности охлаждения
трансформатора;
Таблица T.5 — Взаимосвязь между допускаемым температурным режимом, способом охлаждения и рекомендуемым типом
диэлектрика для выполнения межобмоточной и межслоевой изоляции [Силовая электроника. Руководство
разработчика. Кит Сукер. Додэка XXI. 2008. 256 c. ; Источники питания. Расчет и конструирование. Мартин
Браун. МК-Пресс. 2005, 288 c.]
| Способ охлаждения | Среднее увеличение температуры, °С | Увеличение температуры в горячих пятнах, °С | Рекомендуемый диэлектрик |
| Масло или принудительная воздушное охлаждение | 55 | 10 | Крафт-бумага, ХБ-лента, ПВХ-лента и т.д. |
| Воздушное охлаждение | 80 | 30 | Майларовая пленка, эпоксидные композиции |
| Воздушное охлаждение | 115 | 30 | Изоамидная изоляция |
| Воздушное охлаждение | 150 | 30 | Изоамидная изоляция, Номекс |
Способы намотки
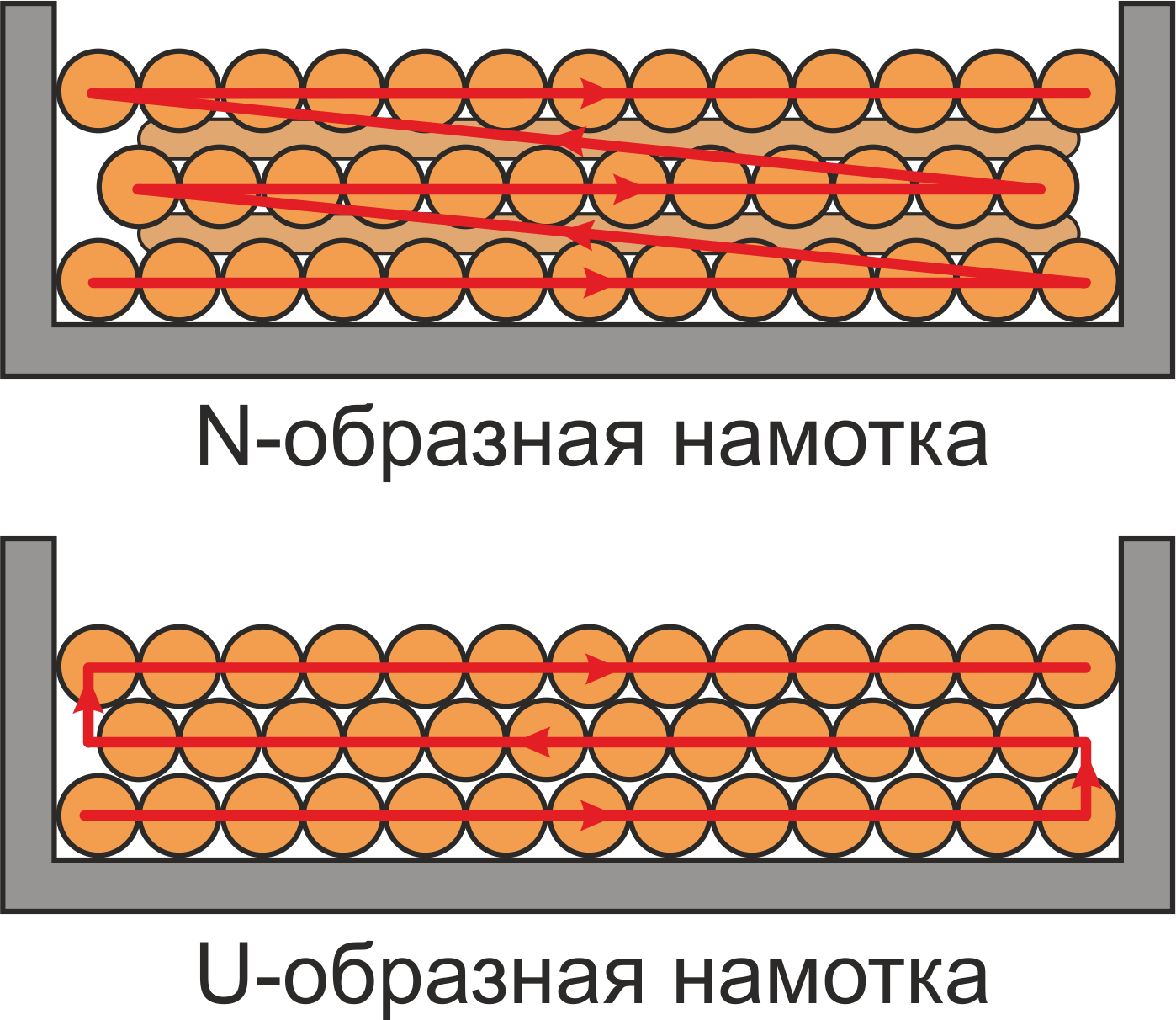
Существует несколько способов намотки – рядовая обмотка («виток к витку») имеющая две разновидности: —
N-образная намотка и U- образная намотка [Импульсные источники питания. Теоретические основы проектирования
и руководство по практическому применению. Раймонд Мэк. «Додэка-XXI», 2008. 274 с.]. Рядовой способ намотки
позволяет обеспечить максимальную равномерность и плотность обмотки.
Рисунок T.12 — Способы намотки: N-образная намотка и U-образная намотка
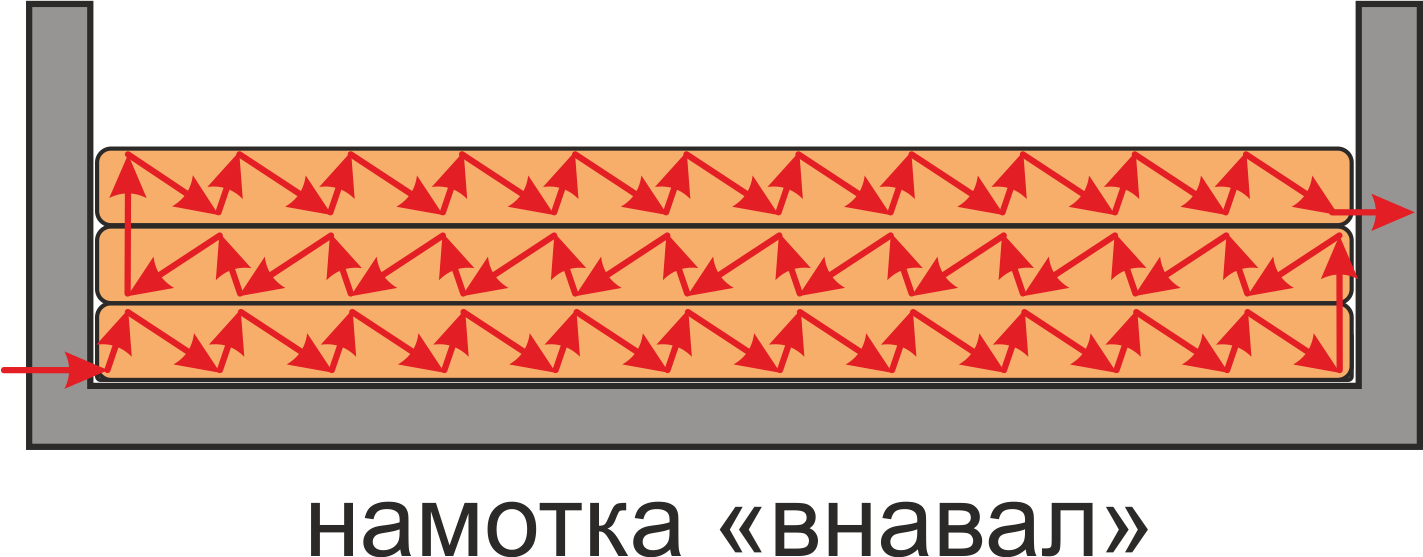
Другой способ выполнения обмотки — обмотка «внавал», с беспорядочным расположением витков в окне
магнитопровода. Такой способ намотки допустим при небольших напряжениях.
Рисунок T.13 Способ намотки «внавал»
При рядовом способе выполнения обмотки («виток к витку») чаще всего используется U-образная намотка (рисунок
T.12) в которой между концами слоев существует большая разность потенциалов и следовательно запасаемая
энергия и эквивалентная паразитная емкость обмотки. С целью уменьшения паразитной емкости обмотки используют
N-образный способ намотки, при котором каждый слой наматывается в одном и том-же направлении, а соединение
слоев осуществляется стежками прокладываемыми вдоль обмотки. При этом разность потенциалов между обмотками
будет одинакова по всей длине обмотки.
С целью снижения паразитной емкости между слоями используют прокладку слоев изолирующей ленты.
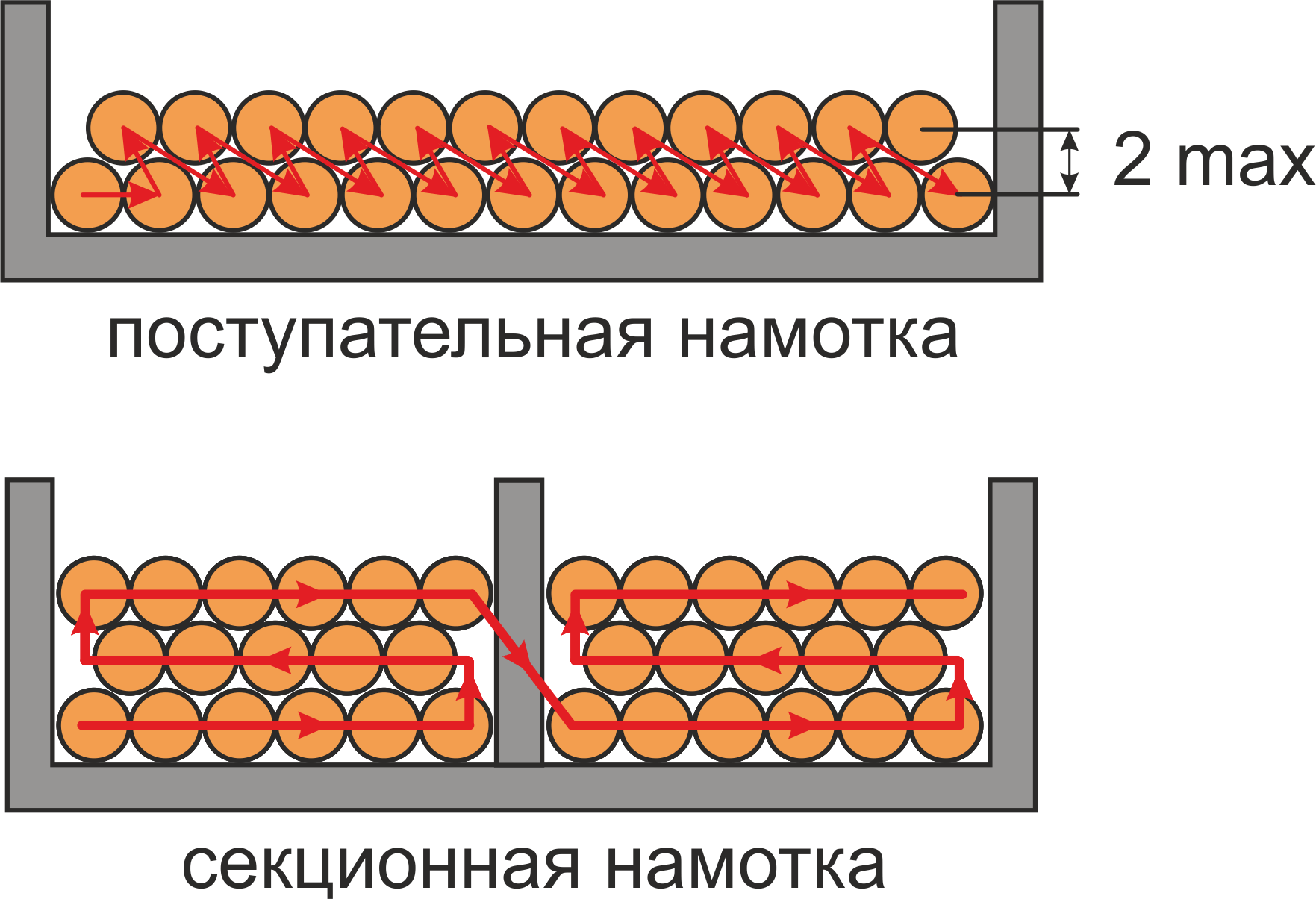
Для уменьшения паразитной емкости используют поступательную намотку (при сравнительно толстом проводе и в
случае если число слоев равно 2-м) или секционную обмотку (рисунок T.14). Кроме уменьшения емкости
использование секционной обмотки существенно увеличивает рабочее напряжение обмотки и поэтому конструктивный
прием секционирования обмоток часто используется в высоковольтных трансформаторах.
Рисунок T.14 — Способы намотки: поступательная намотка, секционная обмотка
Каркас
Для Ш- П- образных (и т.д.) магнитопроводов обмотка выполняется на каркасе, изготавливаемом из пластмассы и
играющем роль изолятора обмоток от магнитопровода. Кроме этого каркас содержит выводы для крепления выводов
обмоток. Особо следует отметить, что каркас, изготавливаемый из термопластичных пластмасс – ПВХ,
полипропилена может размягчаться под действием чрезмерного нагрева магнитопровода и обмоток.
Расположение обмоток внутри магнитопровода
С целью уменьшения длины провода обмоток ближе к сердечнику целесообразно располагать обмотку имеющую большее
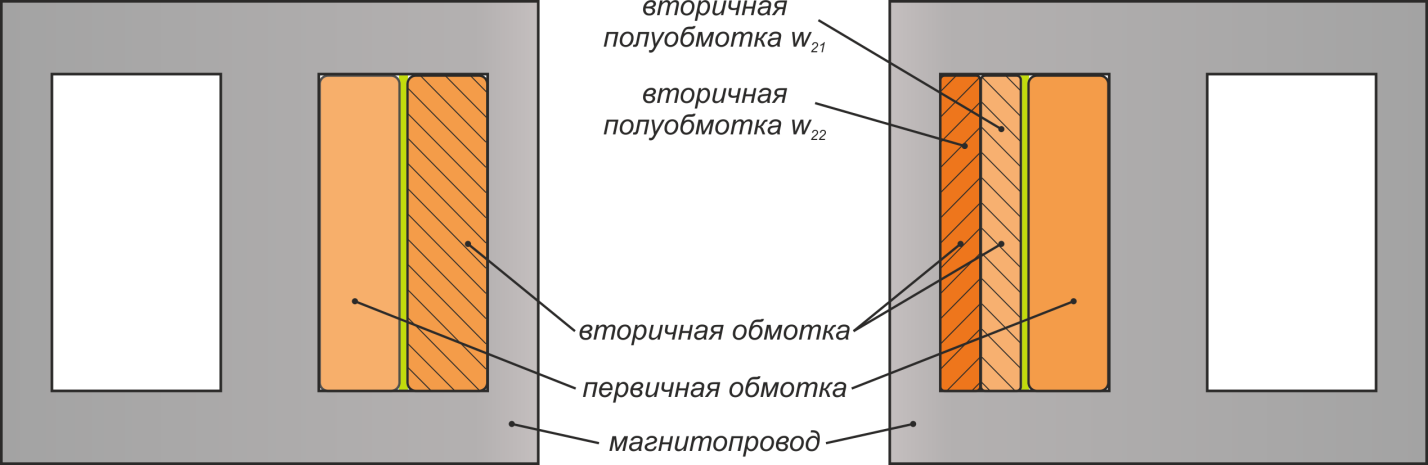
число витков. С целью увеличения магнитной связи между обмотками и уменьшения индуктивности рассеяния
используют чередование обмоток внутри магнитопровода: сначала на каркас наматывается половина
первичной обмотки, затем половина вторичной, затем вторая половина первичной затем вторая половина
вторичной. Таким образом, получается слоеный бутерброд, межобмоточная емкость возрастает, а индуктивность
рассеяния снижается. Для трансформаторов с малым числом витков и низким межобмоточным напряжением
используется намотка соединёнными вместе проводами первичной и вторичной обмоток. Этот способ часто
используется при создании трансформаторов пуш-пул преобразователей.
Электростатическая защита (экран Фарадея) между обмотками
Электростатическая защита между первичной и вторичной обмотками используется для устранения синфазных помех
из цепи первичной обмотки возникающих за счет емкостной связи между обмотками [Силовая электроника.
Руководство разработчика. Кит Сукер. Додэка XXI. 2008. 256 c.]. Электростатическая защита представляет собой
заземленный экран из медной фольги, размещаемый между первичной и вторичной обмотками. Введение экрана
Фарадея в конструкцию трансформатора снижает его технологичность и может стать причиной электрического
пробоя межу экраном и проводниками обмоток в местах их выхода для соединения с выводами каркаса
трансформатора. По этим причинам использование экрана Фарадея в трансформаторах допускается в случае крайней
необходимости. Виток экрана должен быть обязательно разомкнутым.
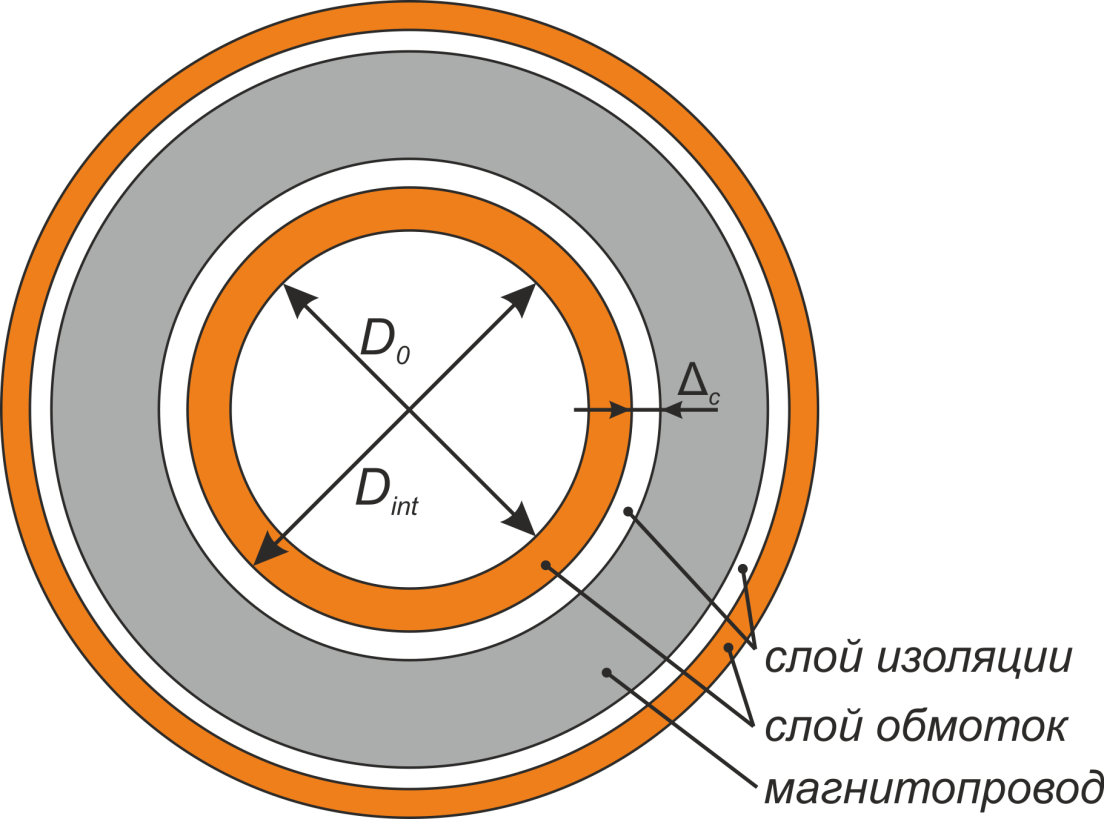
Технологические особенности намотки кольцевых и тороидальных трансформаторов
Особенностью намотки трансформаторов на кольцевых и тороидальных магнитопроводах является необходимость
равномерности распределения обмотки по всей длине магнитопровода. Несоблюдение этого условия может стать
причиной насыщения отдельных участков магнитопровода, что приведет к увеличению потерь в магнитопроводе и
возрастанию тока в цепи.
Выполнение обмоток для тороидальных трансформаторов имеет ряд конструктивных особенностей [Расчет
трансформаторов и дросселей малой мощности. Белопольский И.И. М.: Госэнергоиздат, 1963. – 207 с.: ил.].
Во-первых, для у тороидальных трансформаторов отсутствует каркас и изоляция осуществляется путем обматывания
магнитопровода изоляционным материалом. Необходимо отметить, что существуют кольцевые магнитопроводы с уже
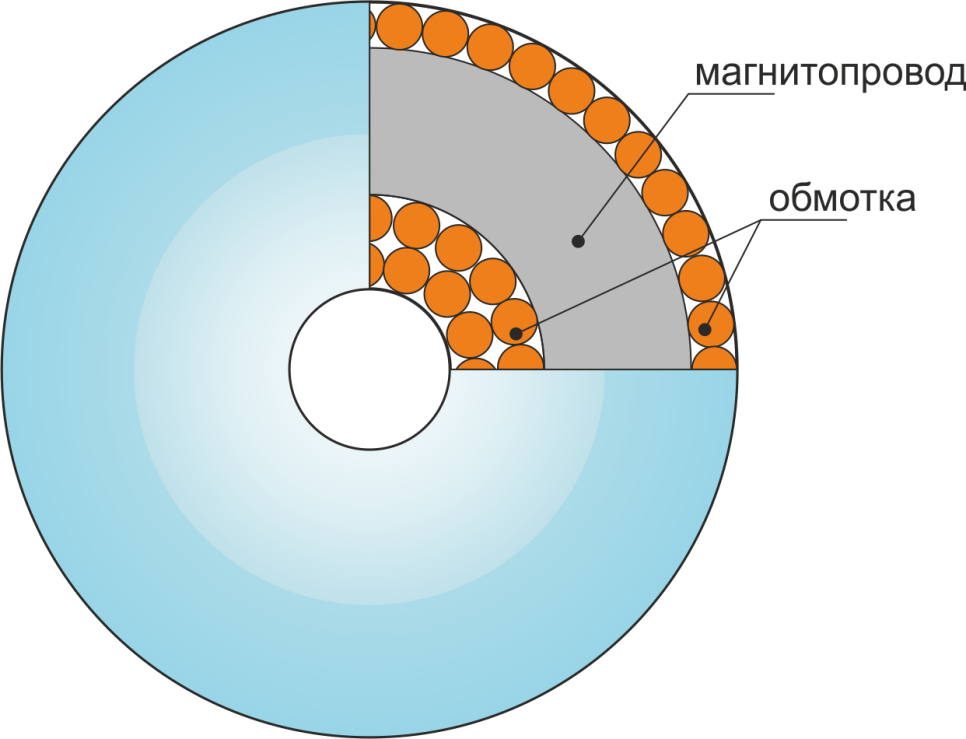
нанесенным однородным слоем полимерной изоляции. Во-вторых, обмотка располагается по всей длине
магнитопровода трансформатора (закрывает его). Третьей конструктивно особенностью является различие внешнего
и внутреннего диаметров. Следствием этого является высокая плотность обмотки по внутренней части окна и
расстояния между витками по наружной части магнитопровода (рисунок T.15). Это ограничивает возможности
применения межслоевой изоляции, и для изготовления обмоток тороидальных трансформаторов используют провода с
повышенной электрической прочностью.
Рисунок T.15 — Обмотка тороидальных трансформаторов. Видно утолщение обмотки обмотки во внутреннем кольце
тора
Эквивалентная схема трансформатора
Для расчета работы трансформатора в том или ином режиме используют эквивалентную схему замещения
трансформатора, учитывающую его реальные характеристики и паразитные параметры. В настоящее время существует
несколько типов эквивалентных схем замещения, учитывающих или не учитывающих те или иные паразитные
параметры трансформатора.
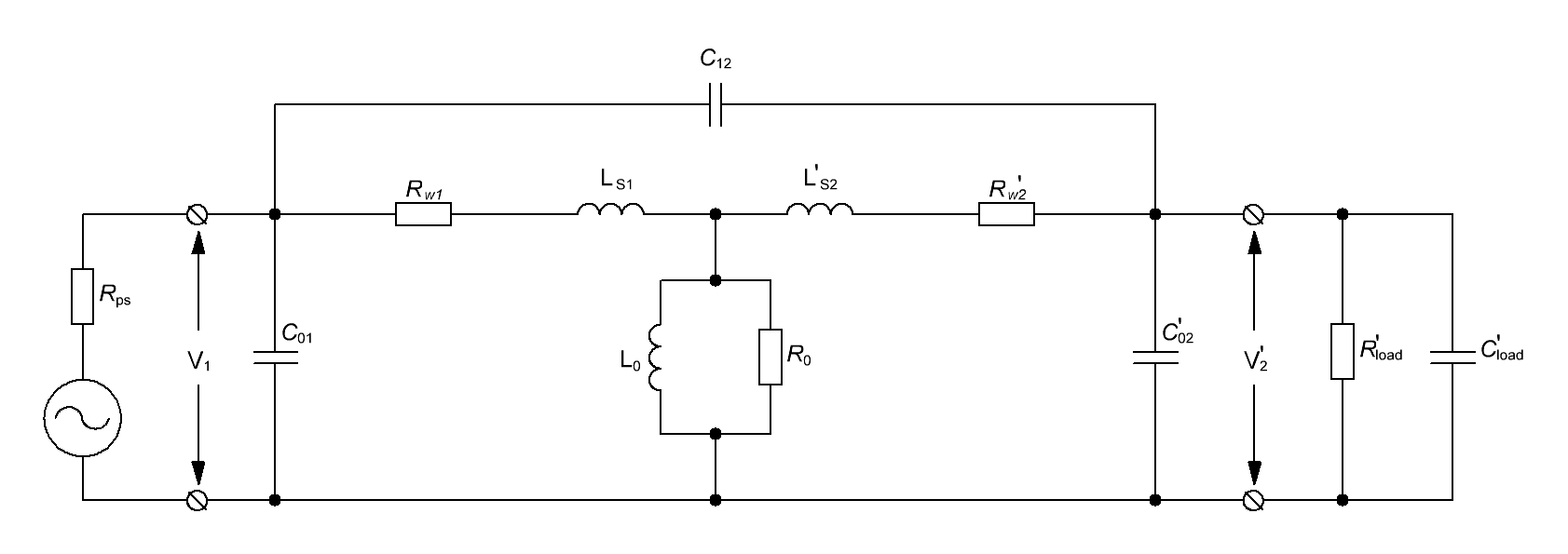
Наиболее полная эквивалентная схема двухобмоточного трансформатора, приведенная к первичной обмотке
представлена на рисунке T.16 [Силовая электроника: от простого к сложному. Борис Семенов. Солон-Пресс. 2006.
416 с. ; Теория и расчет трансформаторов малой мощности. Ю.Н. Стародубцев. РадиоСофт. 2011. 320 с.] [Вдовин
С. С. Проектирование импульсных трансформаторов. — 2-е изд., перераб. и доп. — Л.: Энергоатомиздат. Ленингр.
отд-ние, 1991. — 208 с: ил.]. В данной эквивалентной схеме в качестве внешних элементов присутствует
электрическое сопротивление, емкость нагрузки и внутреннее сопротивление источника.
При расчете паразитных элементов необходимо помнить, что трансформатор – это достаточно сложный
электромагнитный прибор с распределенными паразитными параметрами, и приведение их к дискретным параметрам
весьма условно, но, тем не менее, позволяет оценить порядки величин искажений, обусловленных паразитными
элементами.
Рисунок T.16 — Эквивалентная схема трансформатора
Эквивалентная схема трансформатора содержит следующие параметры:
— индуктивность намагничивания L0 ;
— индуктивность рассеивания первичной обмотки LS1 ;
— приведенная индуктивность рассеивания вторичной обмотки LS2’ ;
— сопротивление первичной обмотки Rw1 ;
— приведенное сопротивление вторичной обмотки Rw2’ ;
— сопротивление активных потерь в магнитопроводе R0 ;
— межвитковая емкость первичной обмотки С01 ;
— приведенная межвитковая емкость вторичной обмотки С02’;
— межобмоточная емкость С12 .
Индуктивность намагничивания L
0
Индуктивность намагничивания фактически представляет собой собственную индуктивность первичной обмотки
трансформатора. Она определяется геометрическими параметрами магнитопровода и материала, из которого он
изготовлен. Расчет индуктивности намагничивания для магнитопроводов с зазором и без него осуществляется по
формулам:
— для трансформаторов с замкнутыми магнитопроводами (например ферритовые кольца) индуктивность определяется
по формуле:
μ0 – магнитная постоянная, 1,25663 — 10-6 Гн/м;
μ – магнитная проницаемость материала сердечника;
N1 – число витков первичной обмотки;
Sc – эффективная площадь сечения магнитопровода;
lav – эффективная длина средней линии магнитопровода.
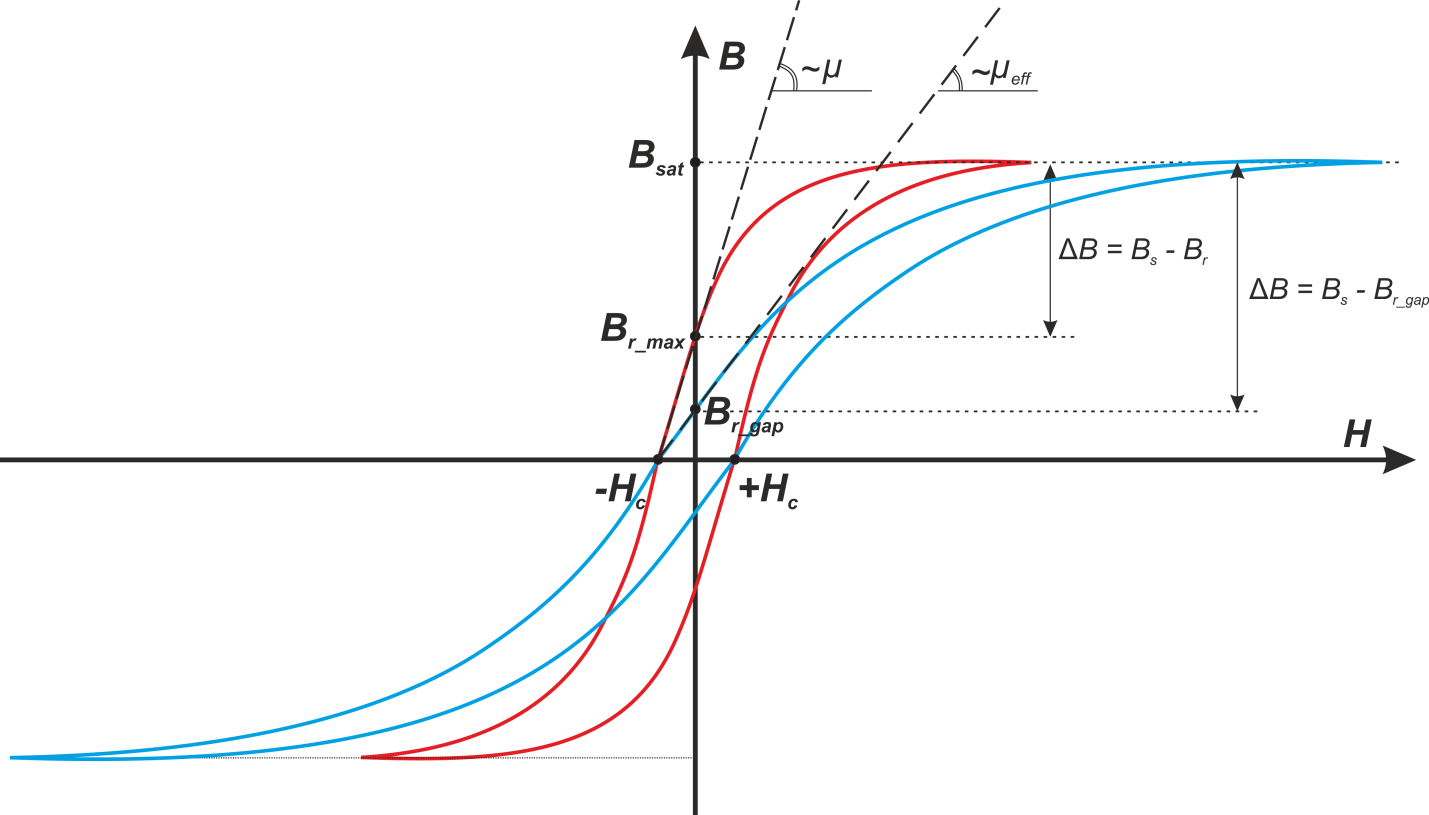
— для трансформаторов с зазором в магнитопроводе индуктивность намагничивания определяется по формуле [Теория
и расчет трансформаторов источников вторичного электропитания. А. В. Хныков. СОЛОН-Пресс. 2010. 127 с.]:
где:
μeff – магнитная проницаемость материала сердечника с зазором:
где:
μ – магнитная проницаемость материала сердечника;
lg – длина магнитного зазора.
Как правило, в справочных листках (datasheet) на конкретный магнитопровод приводится справочный параметр
сердечника AL , (nH). Этот параметр учитывает параметры и геометрию магнитопровода более точно,
по сравнению с соотношением L0 (особенно для магнитопроводов с интегрированным зазором). В этом
случае индуктивность намагничивания вычисляется по соотношению:
Индуктивность рассеивания первичной обмотки LS1
Индуктивность рассеяния рассчитывают исходя из площади охватываемой током и не являющейся частью площади
магнитопровода. Индуктивность рассеяния первичной обмотки является та часть её индуктивности, которая не
связанна с магнитопроводом и вторичной обмоткой. То есть фактически это площадь «воздушного зазора» между
обмоткой и магнитопроводом, поскольку в данном случае часть магнитного потока замыкается не через
магнитопровод, а замыкается «через воздух».
Для Ш- и П- образных сердечников индуктивность рассеяния рассчитывается по формуле для индуктивности
соленоида без магнитопровода:
в которой в качестве площади S входит эффективная площадь Sis охватываемая током, и не являющаяся
площадью магнитопровода, в качестве длины соленоида входит hw1 – высота обмотки.
Эффективная площадь Sis может быть определена по соотношению (рисунок T.17):
где:
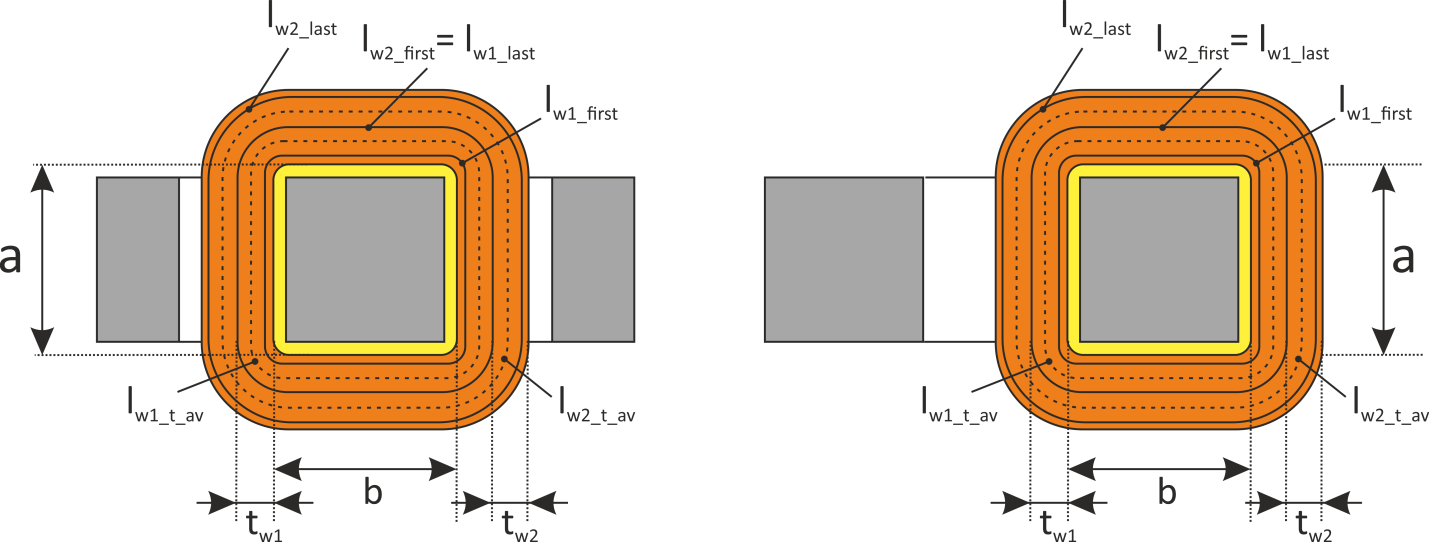
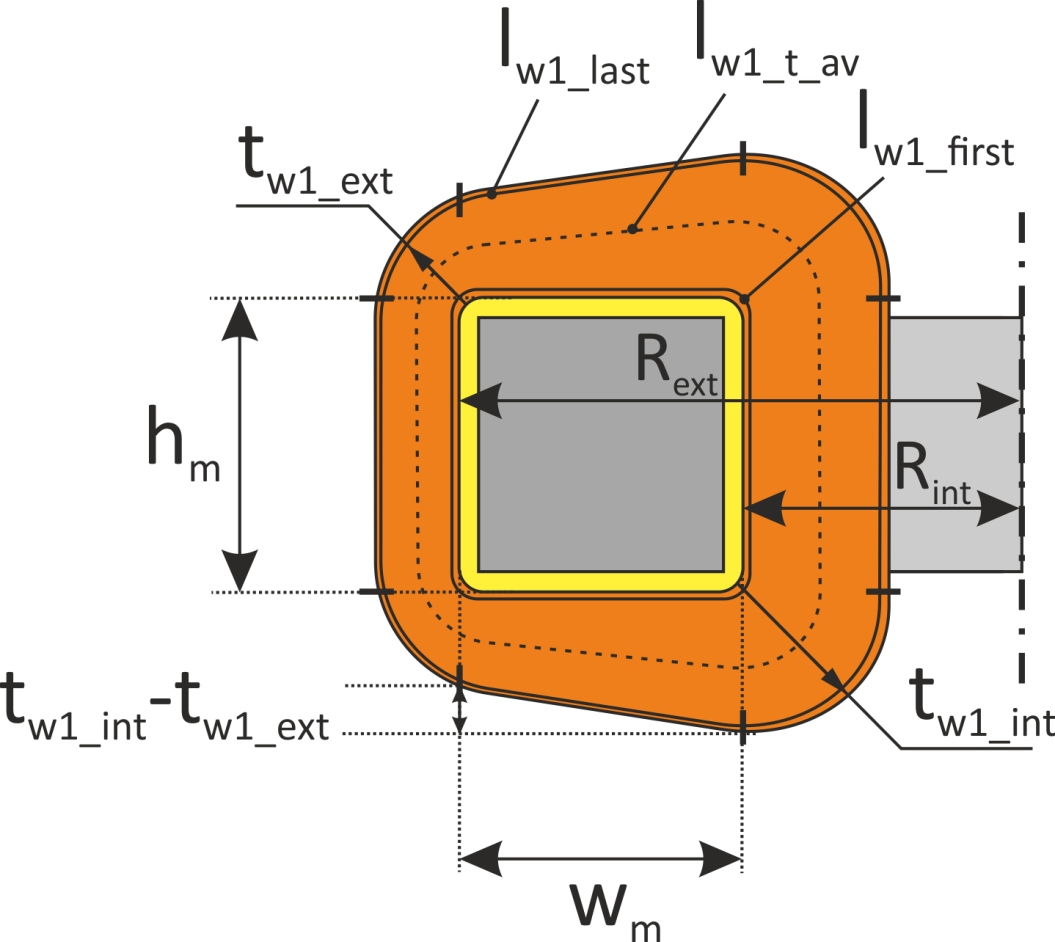
— lw1_t_av – средняя длина витка первичной обмотки;
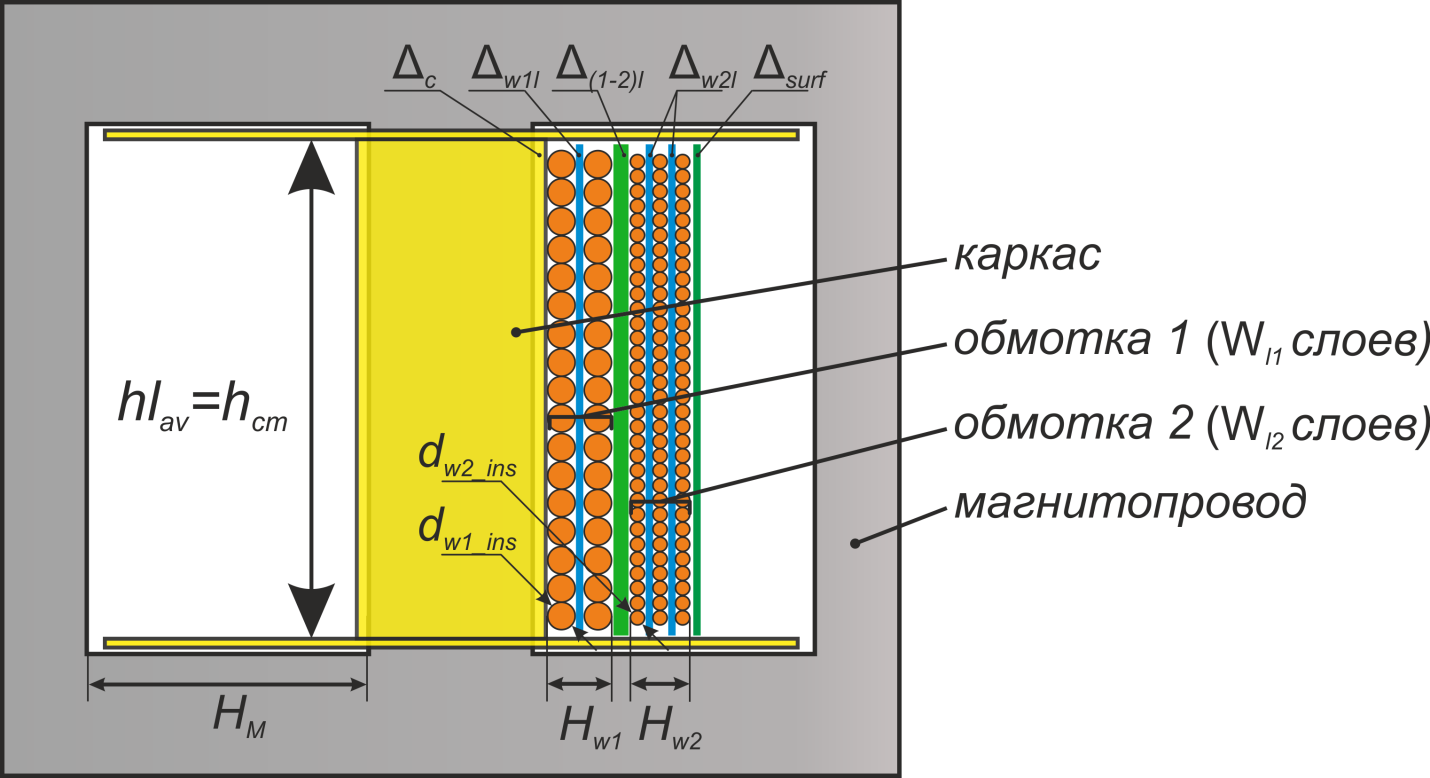
— Δw1 – расстояние от «среднего витка» первичной обмотки, расположенного посередине
толщины намотки, до магнитопровода. Или Δw1 — толщина намотки в случае соленоида.
В итоге получаем, формулу для приближенного расчета индуктивность рассеяния:
lw1_t_av – средняя длина витка первичной обмотки;
Δw1 – расстояние от «среднего витка» первичной обмотки (расположенного посередине
обмотки), до магнитопровода;
hw1 – высота первичной обмотки. В случае кольцевых магнитопроводов – длина средней
линии магнитопровода, в случае если обмотка равномерно распределена по магнитопроводу или длина сектора, в
случае частичного охвата обмоткой длины кольца магнитопровода.
Представленной формулы так же будет достаточно для получения оценочного значения индуктивности рассеяния.
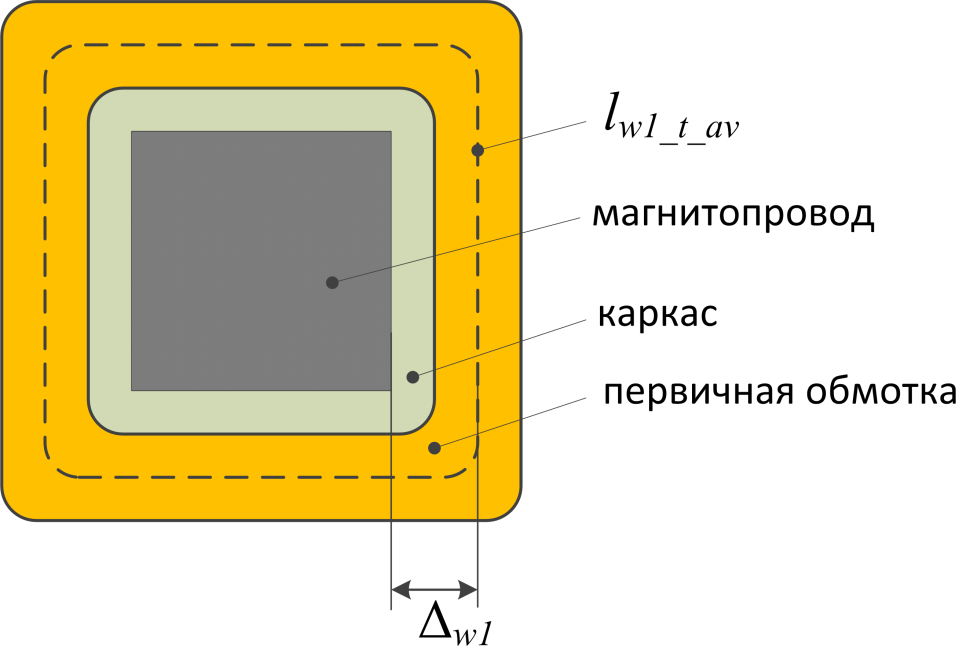
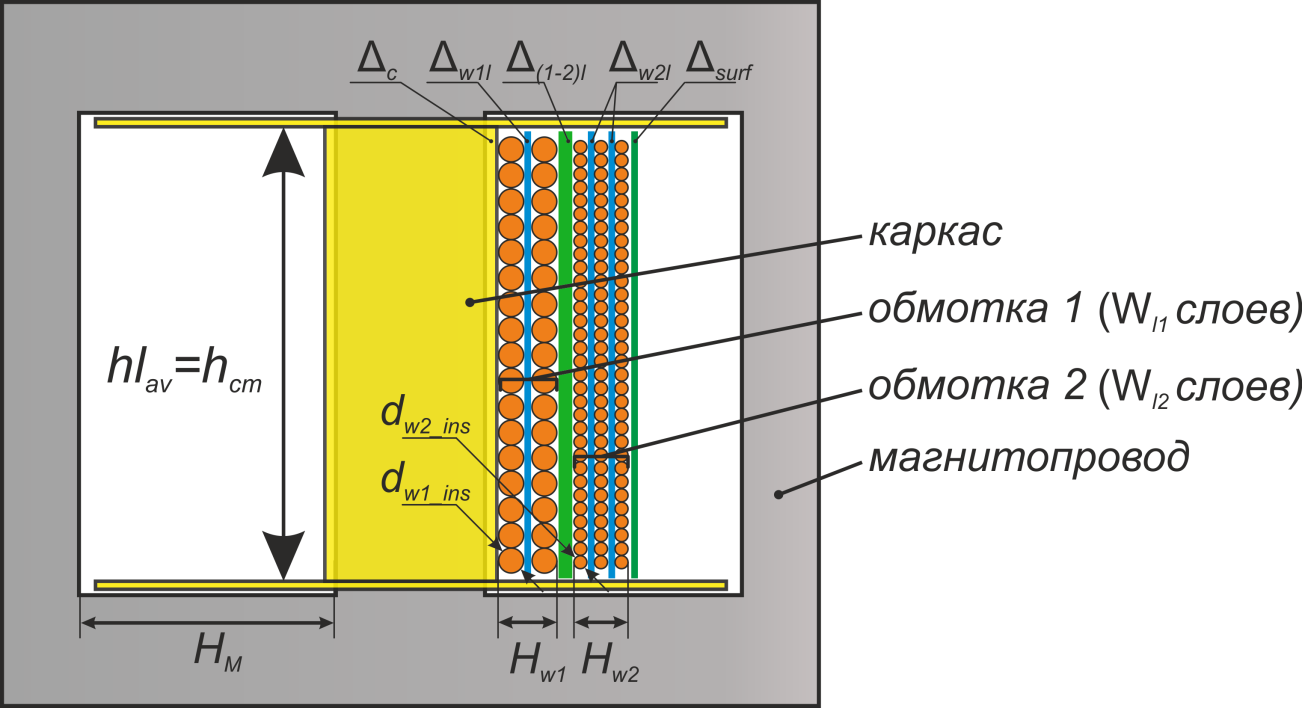
Рисунок T.17 – К оценке индуктивности рассеяния. Поперечное сечение трансформатора — сердечника, каркас,
первичная обмотка. Показана ширина обмотки и средняя линия
Для вычисления индуктивности рассеяния обмоток на магнитопроводах различных конфигураций, отличающихся от Ш-
и П- образной геометрии можно воспользоваться соотношениями приведенными ниже.
Соотношения для вычисления индуктивность рассеивания первичной обмотки LS1
для различных геометрий магнитопроводов
Коаксиальные цилиндрические обмотки
Для более точного вычисления индуктивности рассеяния коаксиальных цилиндрических обмоток можно
воспользоваться следующим соотношением [Электромагнитные элементы радиоэлектронной аппаратуры. Русин Ю.С.,
Гликман И.Я., Горский А.Н. Радио и связь. 1991. 224 с.]:
где:
lw1_t_av– средняя длина витка первичной обмотки;
μ0 – магнитная постоянная, 1,25663 — 10-6 Гн/м;
N1 – число витков первичной обмотки;
g1, g2, g12 – параметры геометрии.
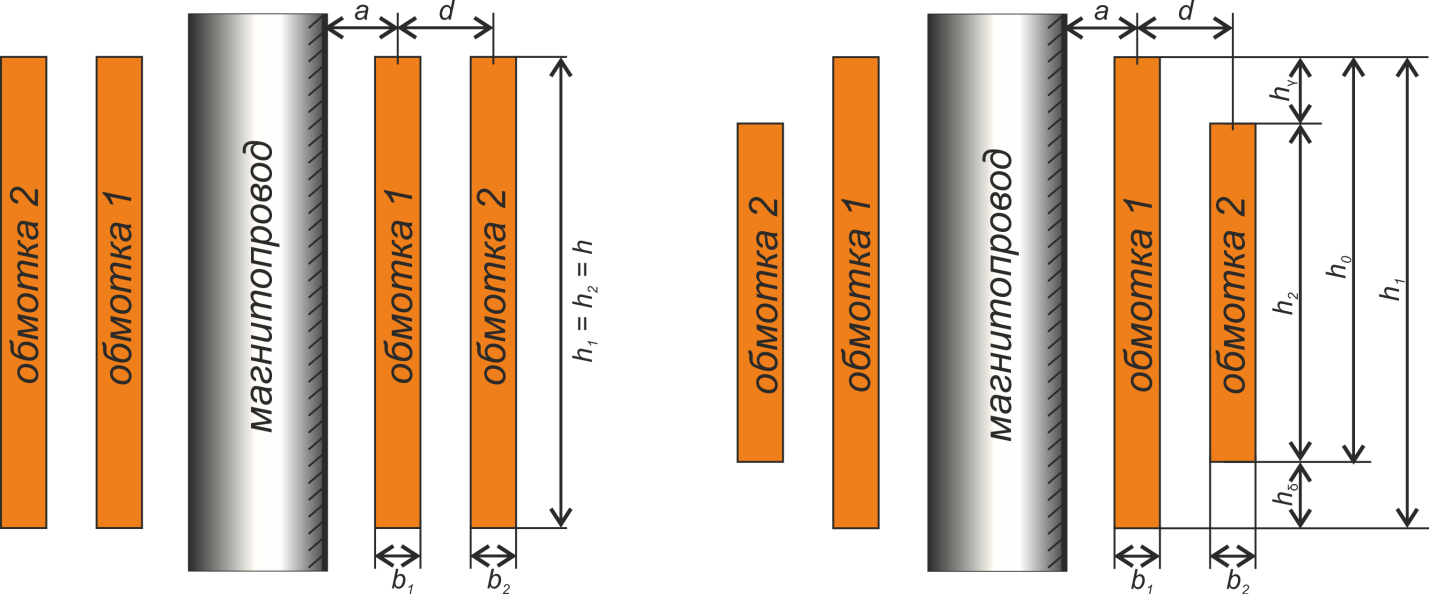
Рисунок T.18 – К расчету индуктивности рассеяния коаксиальных цилиндрических обмоток
Характерные параметры геометрии g1, g2, g12 – находятся из соотношений
(рисунок T.18):
g1 – характерный параметр для первичной обмотки вычисляется по формуле:
g2 – характерный параметр для вторичной обмотки вычисляется по формуле:
g12 — характерный параметр для межобмоточного пространства вычисляется по формуле:
— для обмоток, имеющих одинаковую высоту:
— для обмоток, имеющих разную высоту при условии, что
где:
здесь:
h1 – высота первичной обмотки;
h2 – высота вторичной обмотки;
hδ – смещение вторичной обмотки относительно первичной снизу;
hγ – смещение вторичной обмотки относительно первичной сверху;
h0 – сумма высоты вторичной обмотки и смещения вторичной обмотки относительно первичной сверху;
b1 – толщина первичной обмотки;
b2 – толщина вторичной обмотки;
a – расстояние от магнитопровода до центральной части первичной обмотки;
d – расстояние от центральной части первичной обмотки до центральной части вторичной обмотки.
В первом приближении при значительной толщине обмоток данные расчетные соотношения можно использовать для
расчета трансформаторов с квадратным сечением магнитопровода.
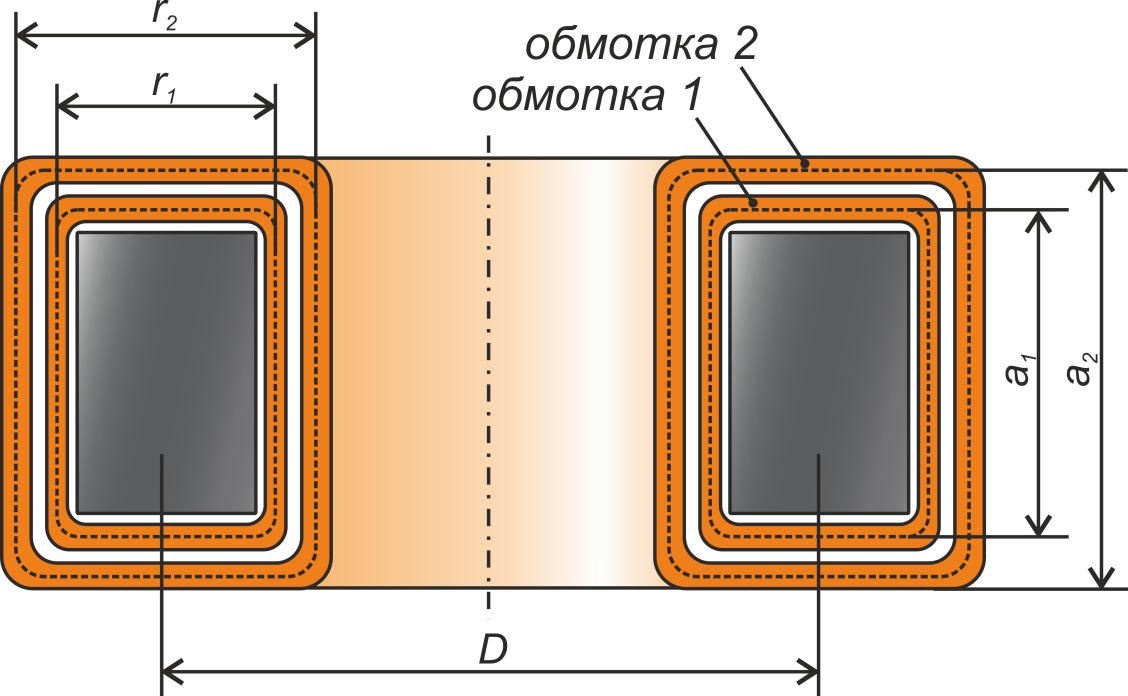
Обмотки на кольцевом сердечнике
Для обмоток на кольцевом сердечнике можно воспользоваться следующим соотношением
[Электромагнитные элементы радиоэлектронной аппаратуры. Русин Ю.С., Гликман И.Я., Горский А.Н. Радио и
связь. 1991. 224 с.]:
μ0 – магнитная постоянная, 1,25663 — 10-6 Гн/м;
N1 – число витков первичной обмотки;
D – средний диаметр кольцевого сердечника (среднее между внешним и внутренним диаметром);
a1 – высота среднего витка первичной обмотки (см. рисунок T.19);
a2 – высота среднего витка вторичной обмотки (см. рисунок T.19);
r1 – ширина среднего витка первичной обмотки (см. рисунок T.19);
r2 – ширина среднего витка вторичной обмотки (см. рисунок T.19).
Рисунок T.19 – К расчету индуктивности рассеяния коаксиальных цилиндрических обмоток
При частичном заполнении обмотками поверхности кольцевого магнитопровода индуктивность рассеяния рассчитывают
как индуктивность рассеяния цилиндрических обмоток, принимая за высоту обмотки её радиальную длину.
Способы уменьшения индуктивности рассеяния
Индуктивность рассеяния, как правило, оказывает негативное влияние на работу трансформатора (индуктивность
рассеяния влияет на динамические характеристики, снижая скорость роста тока в обмотках). Кроме этого
трансформатор с высокой индуктивностью рассеяния является источником электромагнитных помех повышенного
уровня.
Из представленных формул для нахождения индуктивностей рассеяния обмоток трансформатора следуют несколько
важных выводов:
— чем ближе обмотка к сердечнику, тем меньше индуктивность рассеяния;
— чем меньше толщина обмотки, тем меньше индуктивность рассеяния;
— в случае кольцевых магнитопроводов необходимо равномерно распределять обмотку по всему кольцу
магнитопровода с целью уменьшения индуктивность рассеяния;
— в зависимости от того, какая обмотка первичная или вторичная будет ближе к магнитопроводу у той и
индуктивность рассеяния будет меньше;
— использование магнитопровода с длинным центральным стержнем приводит к снижению индуктивности рассеяния
(так как высота первичной обмотки стоит в знаменателе выражения для расчета индуктивности рассеяния). Чем
длиннее обмотка, тем меньше индуктивность рассеяния [Источники питания. Расчет и конструирование. Мартин
Браун. МК-Пресс. 2005, 288 c.];
— значительного уменьшения индуктивности рассеяния можно добиться путем секционирования обмоток;
— уменьшение числа витков приводит к уменьшению индуктивности рассеяния и эта зависимость квадратична (так,
для случая трансформатора обратноходового преобразователя уменьшение числа витков приводит к существенному
снижению требований к демпферу и соответственно к его массогабаритным характеристикам).
Существует несколько способов снижения индуктивности рассеяния [Транзисторная преобразовательная техника.
Мелешин В.И. Техносфера. 2005. 626 с.]:
— для трансформаторов на кольцевых сердечниках целесообразно совместная намотка проводников первичной и
вторичной обмоток;
— для П- и Ш- образных сердечников необходимо располагать одну обмотку под другой, размещение обмотки в один
ряд, чередование обмоток. Или размещение вторичной обмотки между двух слоев первичной приводит к снижению
индуктивности рассеяния [Источники питания. Расчет и конструирование. Мартин Браун. МК-Пресс. 2005, 288
c.].
Индуктивность рассеяния увеличивается при:
— разнесении обмоток на магнитопроводе;
— увеличение толщин изоляции между магнитопроводом и обмотками, изоляции между обмотками;
— увеличение толщины обмотки;
— увеличение числа витков;
— уменьшение длины обмотки.
Индуктивность рассеяния трансформатора кроме этого зависит от посторонних факторов — близко расположенных к
трансформатору предметов из магнитных материалов, других магнитопроводов и т.д.
Приведенная индуктивность рассеивания вторичной обмотки LS2’
Индуктивность рассеивания вторичной обмотки LS2’, приведенная к первичной обмотке
вычисляется по соотношению:
где k – коэффициент трансформации.
Индуктивность рассеивания вторичной обмотки LS2: рассчитывается аналогично
индуктивности рассеивания первичной обмотки:
lw2_t_av – средняя длина витка вторичной обмотки;
Δw2 – расстояние от «среднего витка» вторичной обмотки (расположенного посередине
обмотки), до магнитопровода;
hw2 – высота вторичной обмотки.
Сопротивление первичной обмотки Rw1
Электрическое сопротивление первичной обмотки R1 рассчитывается по соотношению для расчета омического
сопротивления проводника:
где:
N1 – число витков первичной обмотки;
ρ – удельное сопротивление материала провода (для меди — 0,0175 Ом·мм2 м-1);
lw1_t_av – средняя длина витка первичной обмотки;
Sw1_Cu – площадь поперечного сечения провода первичной обмотки.
При высоких рабочих температурах трансформатора необходимо учитывать влияние температуры на удельное
сопротивление проводников обмоток. При высоких частотах необходимо оценить увеличение эффективного
сопротивления обмоток в результате действия скин-эффекта (см. пункт «Влияние скин-эффекта на сопротивление
обмоток при высоких частотах» настоящего раздела).
Приведенное сопротивление вторичной обмотки Rw2’
Приведенное электрическое сопротивление вторичной обмотки R2’ (значение, приведенное к первичной обмотке)
определяется по соотношению:
где омическое сопротивление вторичной обмотки:
где:
N2 – число витков вторичной обмотки;
ρ – удельное сопротивление материала провода (для меди — 0,0175 Ом·мм2 м-1 );
lw2_t_av – средняя длина витка вторичной обмотки;
Sw1_Cu – площадь поперечного сечения провода вторичной обмотки.
Рекомендации по учету влияния температуры и высокой частоты на эффективное сопротивление аналогичны
рекомендациям для первичной обмотки (см. следующий раздел).
Особенности и тонкости расчета омического сопротивления обмоток
Влияние температуры на удельное сопротивление обмоток
Рост температуры приводит к увеличению удельного сопротивления проводников. Так для меди это изменение
описывается уравнением [Вдовин С. С. Проектирование импульсных трансформаторов. — 2-е изд., перераб. и доп.
— Л.: Энергоатомиздат. Ленингр. отд-ние, 1991. — 208 с: ил.]:
здесь:
ρ0 – удельное сопротивление меди — 0,0175 Ом·мм2 м-1 при T=15 °C );
T – температура в градусах Цельсия.
Так, при повышении температуры с 15 °C до 70 °C удельное сопротивление меди возрастает на 22% и составляет
0,02135 Ом·мм2 м-1. Этот простой расчет показывает важность учета влияния температуры
при расчете трансформатора.
Увеличение сопротивления с ростом температуры приводит к положительной обратной связи – с ростом температуры
увеличивается сопротивление, рост сопротивления приводит к увеличению выделяемой мощности, а рост выделяемой
мощность приводит к увеличению температуры. Таким образом, при проектировании трансформатора или силового
дросселя следует уделять особое внимание режиму охлаждения.
Влияние скин-эффекта на сопротивление обмоток при высоких частотах
Для уменьшения омических потерь в обмотках необходимо использовать провод большего сечения. При этом
омическое сопротивление постоянному току снижается пропорционально увеличению площади сечения. Однако на
высокой частоте (более 50-100 кГц) и особенно при толстых проводах обмоток и более начинает проявляться
скин-эффект.
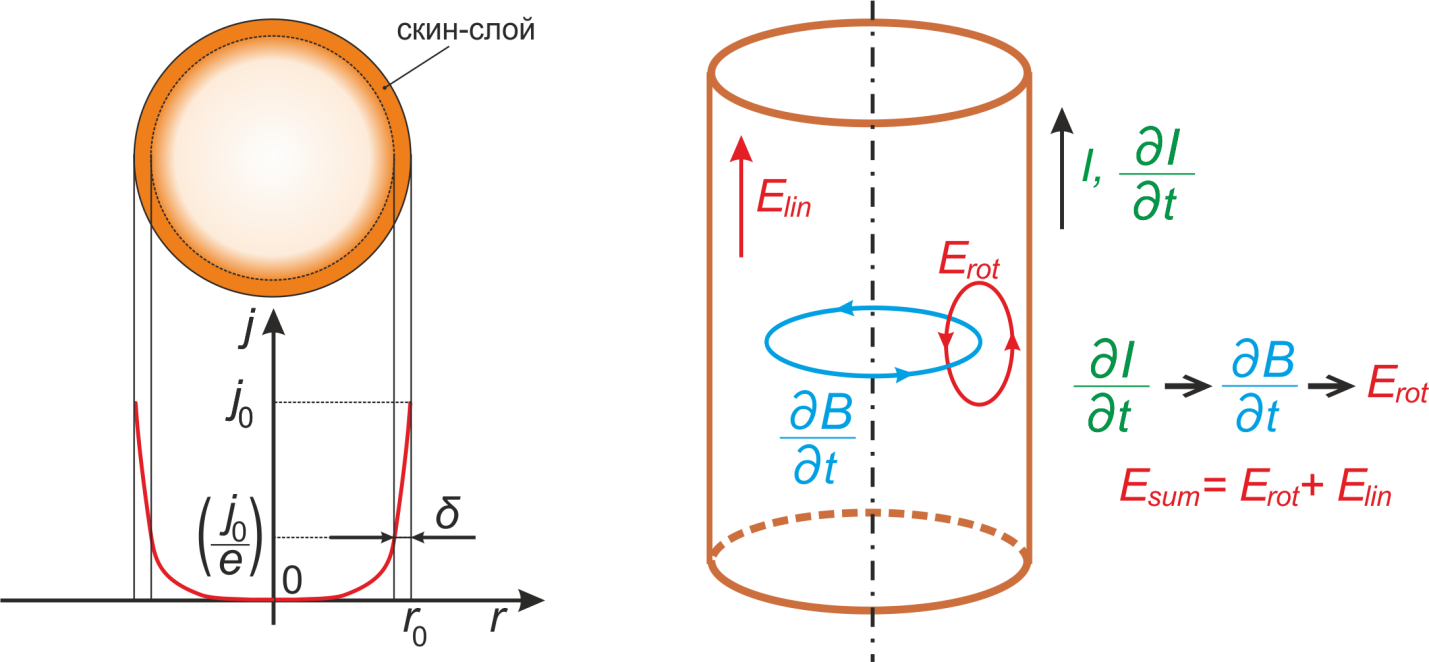
Физика скин-эффекта заключается в следующем – при высоких частотах изменение тока протекающего через
проводник, приводит к изменению магнитного поля внутри этого проводника, а изменение магнитного поля, в свою
очередь приводит к образованию вихревого электрического поля (см. рисунок T.20). Это вихревое электрическое
поле Erot накладывается на линейное поле постоянного тока Elin однородное по всему
сечению проводника. В результате близи поверхности проводника поля складываются, а внутри – вычитаются и
взаимно компенсируются. Таким образом, ток вытесняется к поверхности.
Сущность скин-эффекта заключается в вытеснении на высоких частотах тока к поверхности проводника. При этом
распределение плотности тока изменяется (рисунок T.20). Видно, что ток внутренняя часть проводника
практически не переносит тока и весь ток протекает вблизи поверхности.
Рисунок T.20 — Распределение плотности тока в цилиндрическом проводнике вдоль радиуса при высоких
частотах
(глубина скин-слоя, на которой плотность тока j уменьшается в eраз обозначена символом δ) и иллюстрация
причинно-следственной связи возникновения скин-эффекта: рост тока (∂I/∂t) приводит к изменяющемуся
магнитному полю (∂B/∂t) которое порождает вихревое электрическое поле Erot уменьшающее
напряженность поля внутри проводника и увеличивающее вблизи поверхности и соответственно
перераспределяющее
плотность тока по сечению.
Таким образом, сопротивление проводника на высоких частотах Reff определяется по формуле [Силовая
электроника: от простого к сложному. Борис Семенов. Солон-Пресс. 2006. 416 с.]:
kskeff – коэффициент добавочных потерь в результате скин-эффекта;
RDC – сопротивление проводника на постоянном токе.
RAC – сопротивление проводника на переменном токе.
kskeff – коэффициент добавочных потерь является функцией частоты, толщины провода, его геометрии и
определяется как отношение сопротивления проводника на переменном токе к его сопротивлению постоянному току:
Для определения влияния скин-эффекта на сопротивление проводника в первом приближении можно использовать
таблицу T.6 [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян. Энергоатомиздат.
Ленингр. отд-ние, 1991, 176 с.]:
Таблица T.6 — Значения коэффициента добавочных потерь kskeff для одиночных проводов
|
Частота, кГц |
Диаметр провода (мм) и соответствующий коэффициент добавочных |
||||||
| 0,8 мм | 0,7 мм | 0,6 мм | 0,5 мм | 0,4 мм | 0,3 мм | 0,2 мм | |
| 500 кГц | 2,37 | 2,12 | 1,85 | 1,59 | 1,32 | 1,13 | 1,026 |
| 400 кГц | 2,16 | 1,93 | 1,67 | 1,46 | 1,21 | 1,083 | 1,0 |
| 300 кГц | 1,9 | 1,7 | 1,48 | 1,3 | 1,14 | 1,06 | 1,0 |
| 250 кГц | 1,76 | 1,57 | 1,38 | 1,23 | 1,1 | 1,034 | 1,0 |
| 200 кГц | 1,6 | 1,43 | 1,27 | 1,2 | 1,083 | 1,03 | 1,0 |
| 150 кГц | 1,4 | 1,28 | 1,11 | 1,072 | 1,0 | 1,0 | 1,0 |
| 100 кГц | 1,3 | 1,24 | 1,08 | 1,025 | 1,0 | 1,0 | 1,0 |
| 75 кГц | 1,24 | 1,097 | 1,06 | 1,0 | 1,0 | 1,0 | 1,0 |
| 50 кГц | 1,065 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 |
| 20 кГц | 1,014 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,0 |
Для цилиндрического проводника (рисунок T.20) плотность тока на расстоянии х от поверхности проводника
определяется из выражения:
где
j0 – плотность тока у поверхности проводника;
ω – круговая частота тока (2 π f);
λ – глубина проникновения тока внутрь проводника:
где
ρ – удельное сопротивление проводника;
f – частота переменного тока;
μ – абсолютная магнитная проницаемость материала проводника.
Для практических расчетов граничной частоты, при которой проявляется скин-эффект в медном проводе круглого
сечения используют формулу [Импульсные источники питания. Теоретические основы проектирования и руководство
по практическому применению. Раймонд Мэк. «Додэка-XXI», 2008. 274 с.]:
где:
f – граничная частота в МГц;
dw – диаметр провода в мм.
Если проводники обмоток трансформатора и частота их режима работы удовлетворяют данным критериям, то влиянием
скин-эффекта можно пренебречь, если нет, то изменение сопротивление провода можно рассчитать.
Однако таблица T.6 не учитывает «эффект близости» (proximity effect), проявляющийся во взаимном влиянии
близкорасположенных проводников в обмотке друг на друга. Влияние эффекта близости особенно сильно
проявляется при значительном (большем 2-3) числе слоев в обмотке.
Рекомендации по снижению потерь в трансформаторе обусловленных скин-эффектом
При проектировании трансформатора существует баланс между сечением проводов и потерями. Для минимизации
потерь целесообразно увеличение сечения проводов до достижения условия заполнения обмоткой всей площади окна
магнитопровода.
С целью снижения потерь, возникающих вследствие скин-эффекта используют:
— обмотки, выполненные из нескольких параллельных проводов меньшего диаметра; вместо одного толстого провода
использую несколько изолированных друг от друга жил
— обмотки, выполненные из литцендрата;
— обмотки, выполненные из плоских проводников.
Сопротивление активных потерь в магнитопроводе R0
Сопротивление активных потерь в магнитопроводе – параметр, характеризующий потери в магнитопроводе. При этом
мощность потерь в магнитопроводе можно выразить через произведение напряжения прикладываемого к первичной
обмотке V1 и некоторого приведенного к первичной обмотке эквивалентного тока протекающего в
феррите Ieqv_ferrit :
Сопротивление потерь в магнитопроводе R0 определяется как:
Выражая ток Ieqv_ferrit как:
И подставляя в выражение для сопротивления получаем:
Поскольку мощность потерь в феррите можно представить как произведение мощности удельных потерь на объем
магнитопровода, то итоговое выражение для сопротивления эквивалентных потерь:
где:
Vm – объем магнитопровода (м3);
PVferrit – мощность удельных объемных потерь (Вт/м3) – индивидуальная для каждого типа
материала магнитопровода характеристика, зависящая от частоты, величины магнитной индукции и температуры
(фактически также являющаяся функцией напряжения V1);
V1 – напряжение, приложенное к первичной обмотке (В).
При этом важно понимать, что мощность удельных потерь увеличивается с ростом напряжения.
Другой способ расчета сопротивления активных потерь в магнитопроводе состоит в использовании данных о мнимой
составляющей магнитной проницаемости μ, представленной в справочных данных для ферритов. Подробно об этом –
пункт «Зависимость магнитной проницаемости феррита от частоты» настоящего раздела.
Межвитковая емкость первичной обмотки С01
Межвитковая емкость первичной обмотки представляет собой распределенную емкость первичной обмотки. В
межвитковой емкости, особенно при больших напряжениях может запасаться значительная энергия, что может
вносить существенные искажения в работу схемы.
По причине распределенного характера емкости её приведение к некому эквиваленту C01 представляет
собой достаточно сложную задачу, решение которой целесообразно с позиций расчета суммарной энергии,
запасаемой в емкостной структуре обмотке.
Емкость Clines между двумя параллельными проводниками в вакууме определяется по соотношению
[Classical Electrodynamics. Jackson, J. D. 1975. Wiley. (p. 80). ; Transmission Lines, Matching, and
Crosstalk. Kenneth L. Kaiser. CRC Press. 2005. (2-28). 448 p.]:
где:
D – расстояние между проводниками;
d – диаметр проводников;
llines – длина проводников.
Это соотношение учитывает неоднородное распределение поверхностной плотности заряда по поверхности
проводников и позволяет рассчитывать емкость при малых значениях расстояния, меньших диаметра
проводников.
Реальное значение емкости между соседними витками будет несколько больше по причине того, что изоляция
провода выполнена из материала с некоторой диэлектрической проницаемостью, например полиэфирных и
полиуретановых лаков с ε = 3 – 5.
Для приближенного учета заместим провод с диэлектрическим покрытием на провод без изоляции, но большего
диаметра, с тем, чтобы их единичные емкости в вакууме были одинаковы.
Соотношение для определения емкости между двумя соседними витками в
изоляции Ct
(turn-виток)
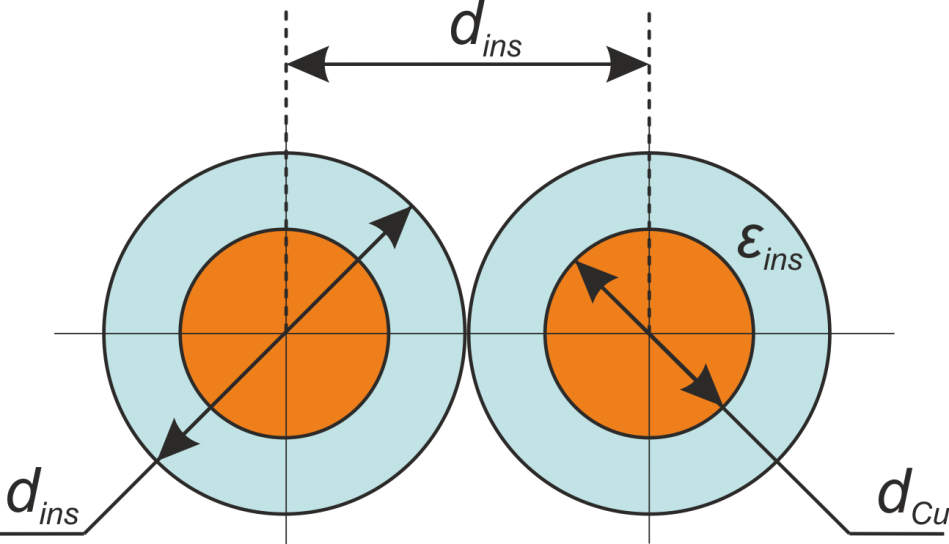
Конфигурация двухпроводной системы с цилиндрическими проводниками диаметром «по меди» dCu и
диаметром по изоляции dins и диэлектрической проницаемости изоляции εinsпредставлена
на рисунке T.21.
Рисунок T.21 — Конфигурация двухпроводной системы с цилиндрическими проводниками диаметрами «по меди»
dCu
и диаметрами по изоляции dins и диэлектрической проницаемости изоляции εins
В работе [Смородинов Д. А. Оценивание рабочей ёмкости и эквивалентной диэлектрической проницаемости изоляции
витой пары кабеля связи. Молодой ученый. — 2013. — №4. — С. 27-33.] с использованием конформных
преобразований получено соотношение для данной сложной системы, которое после
преобразованийдля случая емкости между двумя соседними витками проводников
обмотокимеет вид:
где:
dins – диаметр проводников в изоляции (равен расстоянию между проводниками);
dCu – диаметр проводников «по меди»;
lt – длина витка проводника обмотки;
εeff – эффективная диэлектрическая проницаемость системы:
где:
εins – диэлектрическая проницаемость изоляции.
Это соотношение справедливо для случая, когда цилиндрические проводники соприкасаются друг с другом (диаметр
проводников в изоляции равен расстоянию между проводниками.
Элементарная емкость между двумя соседними витками Ct в первом приближении может быть определена
по вышеприведенному соотношению в котором длина проводника равна средней длине витка.
Суммарная емкость намотки рассчитывается в зависимости от типа намотки. Об этом далее.
Расчет емкостей обмотки при различных типах намотки
Тип намотки – «виток к витку», послойно
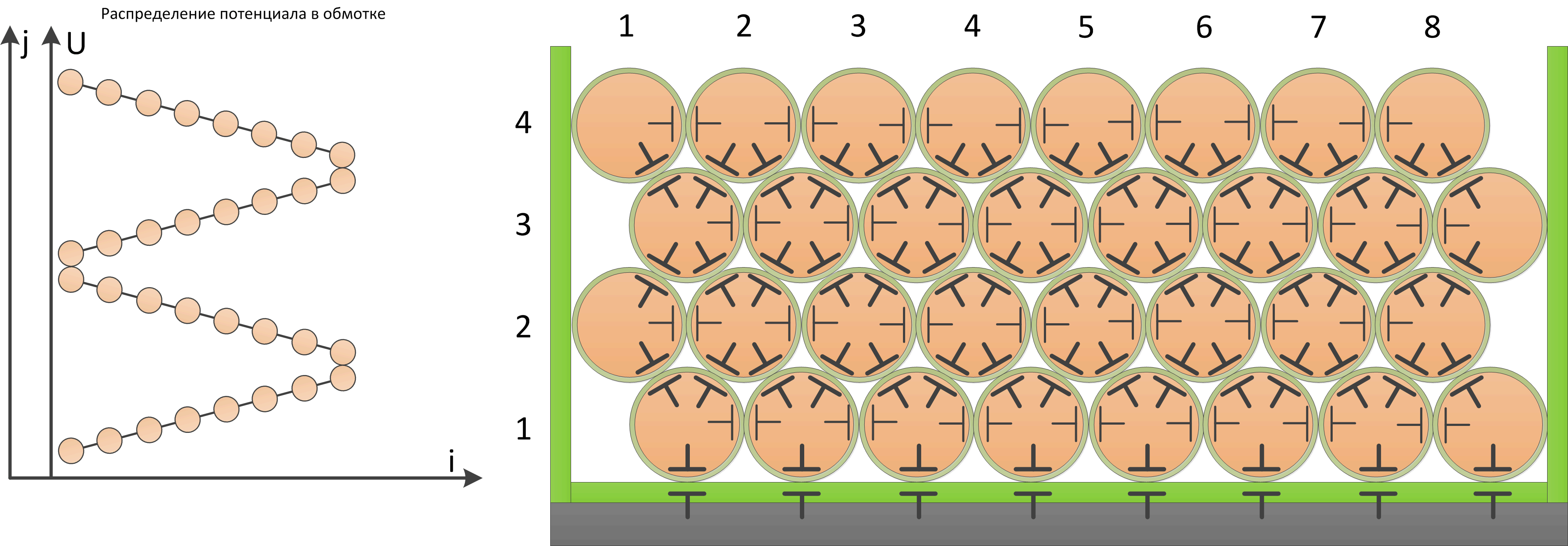
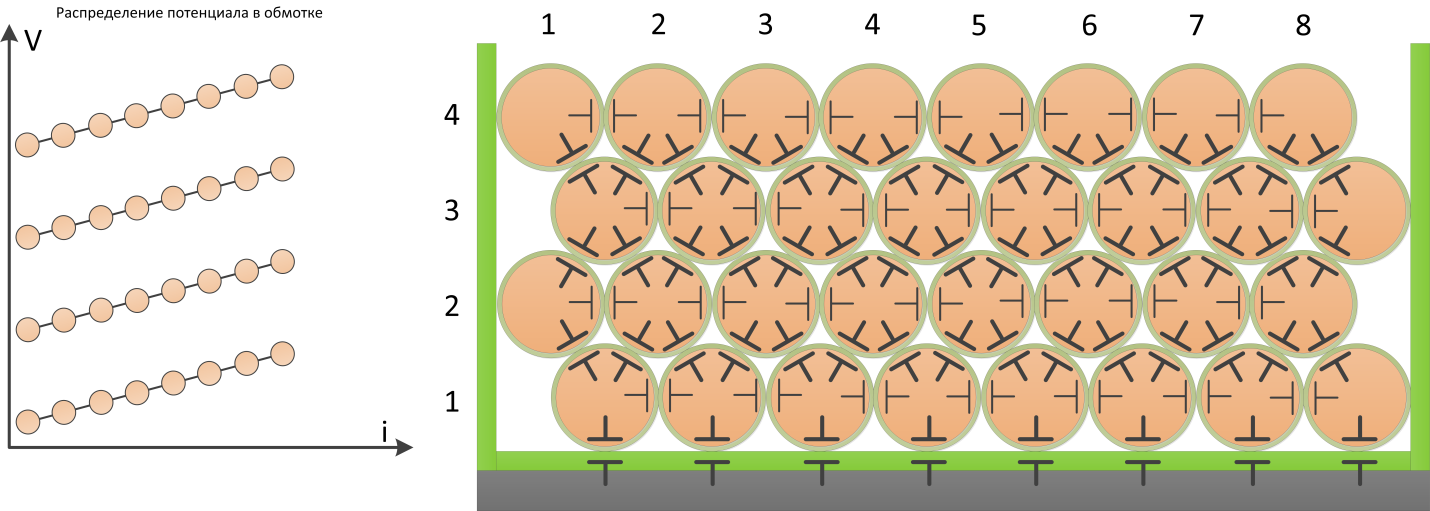
На рисунке изображена внутренняя структура межвитковой емкости обмотки, и распределение потенциала в случае
отсутствия межслойной изоляции и обмотки уложенной «виток к витку».
Для расчета данной энергии введем условные обозначения:
— емкость между двумя соседними витками равна Ct (turn-виток);
— число витков в слое обмотки – m;
— число слоев обмотки – n;
— напряжение, прикладываемое к обмотке – Vw.
Энергия запасается внутри структуры обмотки как между витками одного слоя (turn-turn) так и между витками
различных слоев (layer-layer);
Рассчитаем энергию, запасаемую в межвитковых емкостях (turn-turn) одного слоя:
здесь :
число элементарных межвитковых емкостей:
напряжение между двумя соседними витками:
Отсюда следует, что общая энергия Wtt_summ, запасаемая в межвитковых
емкостях внутри слоев равна:
Рисунок T.22 — Межвитковые емкости и распределение потенциала по обмотке для обмотки уложенной «виток к
витку»
Рассчитаем энергию, запасаемую в межслоевых емкостях (между двумя слоями) при условии, что число слоев – n ≥
2. При способе намотки виток к витку каждый виток имеет емкость по отношению к двум соседним виткам другого
слоя (рисунок T.22). Энергия, запасаемая в этих емкостях равна:
здесь:
∆Vil1, ∆Vil2 – напряжения между витком и двумя соседними виткам
другого слоя;
С учетом того, что разница напряжения между соседними витками составляет величину:
то выражение для энергии, запасаемой в межслоевых емкостях можно переписать в виде:
или:
где:
∆Vil – напряжение между соседними витками разных слоев (для упрощения ∆Vil1
было заменено на ∆Vil);
Wll — энергия, запасаемая в межвитковой емкости «виток — два соседних витка другого слоя».
При этом энергия запасается в межслоевой границе. Число межслоевых границ равно:
Максимальное падение напряжения между крайними витками соседних слоев равно (максимальное напряжение между
витками слоев у краев):
Таким образом, с учетом линейного распределения напряжения между витками в слое получим выражение для
суммарной энергии в межслоевых емкостях Wll_summ:
где:
∆Vil – напряжение между соседними витками разных слоев:
Подставляя, получаем:
В этом выражении член:
показывает разность потенциалов между соседними витками одного слоя. При достаточно большом числе витков
обмотки (а именно в этом случае и рассчитывают паразитную емкость обмотки) этой разностью можно пренебречь и
выражение упростить:
В соответствии с выражением для суммы квадратов первых натуральных чисел получаем:
Сокращая, получаем:
Таким образом, суммарная энергия, запасаемая в паразитной емкостной структуре равна сумме энергии межвитковых
емкостей внутри слоев Wtt_summ и энергии межслоевых емкостей Wll_summ:
Или, упрощая:
Эквивалентная ёмкость первичной обмотки может быть определена из выражения:
Упрощая которое (Vw сокращается) получаем итоговое выражение для емкости многослойной обмотки
трансформатора с укладкой виток к витку:
где:
Ct — емкость между двумя соседними витками равна (turn-виток);
m — число витков в слое;
n — число слоев.
Тип намотки – «один слой поверх магнитопровода»
На рисунке T.23 изображена внутренняя структура межвитковой емкости обмотки, и распределение потенциала в
обмотке, когда обмотка представляет собой один слой, уложенный поверх изоляции на магнитопроводе.
Рисунок T.23 — Межвитковые емкости и распределение потенциала в однослойной обмотке уложенной «виток к
витку»
поверх магнитопровода
Для расчета данной энергии введем условные обозначения:
— емкость между двумя соседними витками равна Ct (turn-виток);
— емкость между витком и магнитопроводом равна Ctm (core-магнитопровод);
— число витков в слое – m;
— напряжение, прикладываемое к обмотке – Vw;
Энергия, запасаемая в межвитковых емкостях слоя обмотки (layer):
здесь напряжение между двумя соседними витками равно:
Энергия, запасаемая в емкости между витками и магнитопроводом:
здесь:
Vw – максимальное напряжение между витками и магнитопроводом (у края);
– множитель, показывающий постепенное увеличение напряжения между витками и магнитопроводом (справа налево
или слева направо);
Сtm – элементарная емкость «виток-магнитопровод» (эквивалентная). Может быть упрощенно определена
по выражению:
ε – диэлектрическая проницаемость материала каркаса обмотки;
Sl – площадь внутреннего слоя обмотки;
d – расстояние между обмоткой и магнитопроводом.
Упрощая выражение под знаком суммы (с учетом выражения для суммы квадратов первых натуральных чисел)
получаем:
Таким образом, суммарная энергия, запасаемая в паразитной емкостной структуре в данном случае равна сумме
энергии межвитковых емкостей внутри слоев Wtt_summ и энергии в емкости
между витками и магнитопроводом Wlm_summ:
Эквивалентная ёмкость первичной обмотки:
Подставляя в которое выражение для энергии получаем:
Это итоговое выражение для емкости однослойной обмотки трансформатора с укладкой виток к витку:
где:
Ct — емкость между двумя соседними витками равна (turn-виток);
Сtm – элементарная емкость «виток-магнитопровод»;
m — число витков в слое обмотки.
Тип намотки – «виток к витку N-образная»
Данный тип намотки отличается от обычного W-образного типа намотки «виток к витку» тем, что выполняется
перехлест провода обмотки для уменьшения межслоевой емкости.
Рисунок T.24 — Межвитковые емкости и распределение потенциала в N-образной обмотке
На рисунке T.24 изображена внутренняя структура межвитковой емкости N-образной обмотки, и распределение
потенциала в случае отсутствия межслойной изоляции.
Расчет емкости обмотки аналогичен расчету емкости обычной W-образной обмотки. Энергия запасается внутри
структуры обмотки как между витками одного слоя (turn-turn) так и между витками различных слоев
(layer-layer).
Энергия, запасаемая в межвитковых емкостях (turn-turn) одного слоя равна:
здесь напряжение между двумя соседними витками равно:
Общая энергия, запасаемая в межвитковых емкостях внутри слоев равна (выражение выведено ранее в разделе «Тип
намотки – «виток к витку»):
Рассчитаем энергию, запасаемую в межслоевых емкостях (между двумя слоями) при условии, что число слоев – n ≥
2. При способе намотки виток к витку каждый виток имеет емкость по отношению к двум соседним виткам другого
слоя (рисунок T.24). Энергия, запасаемая в этих емкостях равна:
Здесь:
∆Vil – напряжение между соседними витками разных слоев;
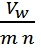
При этом энергия запасается в межслоевой границе. Число межслоевых границ равно:
Напряжение между витками соседних слоев при N-образном способе намотки одинаково по всей длине обмотки и
равно:
Таким образом, с учетом линейного распределения напряжения между витками в слое получим выражение для
суммарной энергии в межслоевых емкостях:
В этом выражении член:
показывает разность потенциалов между соседними витками одного слоя. При достаточно большом числе витков
обмотки (а именно в этом случае и рассчитывают паразитную емкость обмотки) этой разностью можно пренебречь и
выражение упростить:
Таким образом, суммарная энергия, запасаемая в паразитной емкостной структуре равна сумме энергии межвитковых
емкостей внутри слоев Wtt_summ и энергии межслоевых емкостей Wll_summ:
или, упрощая:
Эквивалентная ёмкость первичной обмотки может быть определена из выражения:
Подставляя в которое выражение для энергии получаем:
Упрощая которое (Vw сокращается) получаем итоговое выражение для емкости многослойной обмотки
трансформатора с укладкой виток к витку:
где:
Ct — емкость между двумя соседними витками равна (turn-виток);
m — число витков в слое;
n — число слоев.
Межвитковая емкость вторичной обмотки С02’
Межвитковая емкость вторичной обмотки С02’(значение, приведенное к первичной обмотке)
рассчитывается в соответствии с соотношением:
где:
C02 — емкость вторничной обмотки трансформатора (рассчитывается, в зависимости от типа обмотки, по
соотношениям, представленным ранее для емкости первичной обмотки C01);
k – коэффициент трансформации.
Межобмоточная емкость С12
Межобмоточная емкость определяется конструкцией взаимного расположения обмоток. В случае наиболее
распространенной геометрии расположения одной обмотки поверх другой емкость рассчитывается по соотношению
емкости плоского конденсатора:
где:
ε – диэлектрическая проницаемость;
ε0 – диэлектрическая постоянная;
S12 – эффективная площадь между обмотками;
d12 – толщина межобмоточной изоляции.
Эффективную площадь между обмотками можно оценить по соотношению:
где:
h – высота обмотки;
l12 – длина витка межобмоточной изоляции.
Через межобмоточную емкость осуществляется передача синфазной помехи.
В случае введения электростатической защиты (экрана Фарадея) между обмотками с целью устранения синфазной
помехи, эквивалентная схема трансформатора изменяется и появляются дополнительные емкости – между обмотками
и общим проводом (землей), расчет которых осуществляется аналогично расчету межобмоточной емкости.
Особенности влияния паразитных параметров на работу импульсных трансформаторов
Особенностью повышающего высоковольтного трансформатора является то, что на режим работы большое влияние
суммарная индуктивность рассеяния LS = LS1 + LS2’,
паразитная емкость вторичной обмотки C02 , межобмоточная емкость С12. [Динамические
характеристики умножителей напряжения высоковольтных электротехнических систем. Диссертация. Хречков Николай
Григорьевич. 2006 г.].
Потери в трансформаторе
Омические потери в проводниках обмоток
Суммарные потери на омическом сопротивлении обмоток трансформатора определяются по формуле:
Rwk – сопротивление k-й обмотки;
Iwk_rms – ток в k-й обмотки (действующее или среднеквадратичное значение);
m – число обмоток.
Среднеквадратичное или действующее значение для тока (периодическая несинусоидальная функция с периодом T)
определяется по формуле:
Таким образом, выделяемая мощность рассчитывается с учетом значения относительной длительность импульса q и
формы тока (включающих прямоугольную и треугольную составляющие) [Трансформаторы и дроссели для импульсных
источников питания. А. Кузнецов. Схемотехника, 2000, №1, с. 30—33, №2, с. 48, 49, 2001, №1, с. 32—34.].
Сопротивление обмотки не является величиной постоянной и зависит от температуры и частоты протекающего
тока.
Выбор допустимой плотности тока в обмотках
Допустимая величина плотности тока определяется типом и геометрией трансформатора и как правило выбирается в
пределах 2-5 А/мм2 в зависимости от условий охлаждения и типа магнитопровода. Так при
использовании чашеобразных магнитопроводов (POT) целесообразно использовать меньшую плотность тока (2-3 А/мм2),
поскольку условия охлаждения обмоток затруднены. При использовании стандартных, не низкопрофильных Ш- или
П-образных магнитопроводов допустимую плотность тока можно взять вблизи верхней границы этого диапазона (3-5
А/мм2). При использовании обмоток малой толщины (1-2 слоя) возможно повышение допустимой
плотности тока вплоть до 7-10 А/мм2. Оценка максимальной величины плотности тока в зависимости от
мощности преобразователя представлена в таблице Т.8 настоящего раздела.
Потери в магнитопроводе
Тепловая энергия, выделяемая в магнитопроводе определяется режимом работы, — частотой работы f и уровнем
магнитной индукции B. Для расчета потерь в магнитопроводеPferrit используют следующее
аппроксимирующее выражение [Optimum design of a high-power, high-frequency transformer. R. Petkov. IEEE
Transactions on Power Electronics (Volume: 11, Issue: 1, Jan 1996)]:
где:
f – частота;
B – индукция;
K1, K2, K3 – аппроксимационные коэффициенты, определенные для каждого конкретного типа феррита.
В случае, если справочные листы на магнитомягкие материалы не содержат информации об аппроксимационных
коэффициентах, то для определения потерь в магнитопроводе можно использовать соотношение:
где:
Pvferrit — мощность потерь на единицу объема, являющейся функцией температуры, магнитной индукции
и частоты;
Vm – объем магнитопровода.
Мощность потерь на единицу объема определяется типом феррита и приводится в справочных данных на конкретный
тип магнитного материала (пример – на рисунке T.25).
Рисунок T.25 — Зависимость мощности потерь от частоты при различных значениях индукции магнитного поля и
температуре для феррита N87
Диэлектрические потери
Примечание – в ряде случаев, особенно при высокой частоте и в высоковольтных трансформаторах возможны потери
в изоляционных слоях, выполненных из диэлектриков с высоким коэффициентом потерь. Для большинства
практических случаев эти потери пренебрежимо малы по сравнению с остальными видами потерь.
Потери в трансформаторе определяют нагрев его элементов – обмоток, магнитопровода.
Тепловой режим трансформатора
Тепловой режим трансформатора фактически является лимитирующим фактором для габаритной мощности
трансформатора, поскольку в формулу её расчета входит плотность тока, максимальная индукция и частота.
Основными источниками тепла, выделяемого трансформатором в процессе работы являются обмотки и магнитопровод.
В процессе работы трансформатора тепло передается в окружающую среду и при некоторой температуре
устанавливается тепловое равновесие. При этом мощность суммарных потерь выделяемая трансформатором Ptotal_loss
будет равна мощности рассеиваемой в окружающую среду Pdissipation. Рассеиваемая
мощностьпропорциональна площади поверхности трансформатора ST, и разности температур
трансформатора и окружающей среды ΔT:
где α – коэффициент теплоотдачи, равный мощности рассеиваемой единицей поверхности при изменении температуры
трансформатора на 1º. Коэффициент теплоотдачи определяется множеством факторов, но для практических расчетов
[Теория и расчет трансформаторов малой мощности. Ю.Н. Стародубцев. РадиоСофт. 2011. 320 с. стр. 67] можно
использовать значение α равное 12 Вт/(м2 град) представляющее среднее значение коэффициента
теплоотдачи при условии естественной конвекции и интервале температур ΔT = 20 – 50 °С.
Установившаяся температура перегрева трансформатора относительно окружающей среды ∆T (дельта перегрева) может
быть приблизительно оценена по соотношению [McLymanC. Transformer and inductor design handbook.2004]:
где:
Ptotal_loss – мощность суммарных потерь в трансформаторе;
ST – суммарная эффективная площадь охлаждения трансформатора (в см2).
Для трансформаторов больших габаритов (с рассеваемой площадью более 1000 см2) установившаяся
температуру перегрева трансформатора относительно окружающей среды ∆T (дельта перегрева) целесообразно
оценивать по соотношению [В.Е. Китаев, А.А. Бокуняев. Проектирование источников электропитания устройств
связи. Учеб. пособие.- М.: Связь,1972.- 200 с.]:
где:
Ptotal_loss – мощность суммарных потерь в трансформаторе;
αT – коэффициент теплоотдачи, зависящий от множества факторов (материал трансформатора,
конструктивное исполнение, температуры окружающей среды и т.д.) и для практических расчетов принимается
равным 11-13 Вт/м2 °С.
ST – суммарная площадь охлаждения трансформатора.
Трансформаторы импульсных источников питания
Режимы работы импульсного трансформатора
Форма переменного напряжения, прикладываемого к первичной обмотке, теоретически может быть любой. В случае,
если форма напряжения является или близка к форме прямоугольных импульсов, то трансформатор называется
импульсным. Исключение составляют лишь резонансные трансформаторы, питание которых осуществляется от
ключевых преобразователей.
Трансформатор в преобразовательной технике может работать в двух принципиально различных режимах
[Транзисторная преобразовательная техника. Мелешин В.И. Техносфера. 2005. 626 с.]:
— прямая передача энергии «из обмотки в обмотку». Энергия передается из первичной обмотки во вторичную,
синхронно во времени в соответствии с законом электромагнитной индукции (пункт «Физика работы импульсного
трансформатора» настоящего раздела). В данном случае энергия, накапливаемая в сердечнике не передается в
выходные обмотки. Это режим работы обычного трансформатора, он еще называется прямоходовым режимом;
— трансформатор является промежуточным накопителем энергии: в один интервал времени он накапливает энергию в
сердечнике, подводимую через первичную обмотку, в другой интервал времени эта энергия передается в нагрузку
через вторичную обмотку. Это трансформатор обратноходового преобразователя. По сути это уже не
трансформатор, а дроссель с двумя изолированными обмотками.
Первый, классический «трансформаторный» режим используется в двухтактных преобразователях с топологией мост,
полумост, пуш-пул, и однотактных прямоходовых преобразователях, второй «накопительный» – в
обратноходовых.
В подходах к расчету трансформаторов можно четко выделить три типа:
— прямоходовый двухтактный трансформатор;
— прямоходовый однотактный трансформатор;
— обратноходовый трансформатор.
Порядок расчета трансформаторов для различных топологий отличается, но имеет ряд общих моментов.
Понятие габаритной мощности трансформатора
Величина габаритной мощности трансформатора является одним из базовых понятий. По габаритной мощности
определяется тип и размеры сердечника трансформатора.
Согласно определению, габаритная мощность трансформатора равна сумме мощностей первичных и вторичных обмоток
[Transformer and inductor design Handbook. Third Edition, Revised and Expanded. Colonel Wm. T. McLyman.
Marcel Dekker, Inc., 2004]. Это обусловлено тем, что все обмотки и первичная и вторичная размещаются в одном
окне трансформатора. Кроме этого если обмотка имеет отвод от середины, то это два сегмента обмотки — две
полуобмотки, мощность каждой из них считается отдельно. Если имеется несколько вторичных обмоток, то также
мощность каждой из них считается отдельно. Таким образом, суммарная мощность обмотки трансформатора
складывается из мощностей всех его сегментов – обмоток или полуобмоток.
В простейшем случае для двухобмоточного трансформатора его габаритная мощность PTравна:
где:
Pw1 – мощность первичной обмотки;
Pw2 – мощность вторичной обмотки.
В общем случае, если первичная обмотка трансформатора состоит из n сегментов (обмоток или полуобмоток), а
вторичная обмотка трансформатора состоит из m сегментов, то соотношение для габаритной мощности будет иметь
вид:
где:
Pw11 , Pw12 , Pw1n – мощности
сегментов первичной обмотки;
Pw21 , Pw22 , Pw2m – мощности
сегментов вторичной обмотки.
Поскольку мощность в трансформаторе передается из первичной обмотки во вторичную обмотку то мощности
первичной и вторичной обмотки связаны между собой через КПД-трансформатора:
где:
ηT – КПД трансформатора.
Обобщенно габаритную мощность трансформатора можно записать как сумму всех сегментов обмоток трансформатора —
всех первичных и вторичных обмоток или полуобмоок:
где:
n+m – суммарное число всех обмоток трансформатора (первичных и вторичных обмоток или полуобмоок);
Pwk – мощность k-й обмотки.
Представляя мощность как произведение среднеквадратичных значений напряжения и тока получим:
где:
Vwk_rms – среднеквадратичное (действующее) значение тока в k-й обмотке;
Iwk_rms – среднеквадратичное (действующее) значение тока в k-й обмотке;
n+m – суммарное число всех обмоток или полуобмоток.
Данное соотношение является базовым для расчета габаритной мощности трансформатора преобразователя прямого
хода.
Соотношения для габаритной мощности, представленного выше, недостаточно для взаимосвязи мощности с
габаритными (геометрическими) параметрами магнитопровода. Получим еще несколько опорных формул.
Действующее значение тока в k-й обмотке равно произведению плотности тока в проводе обмотки j на площадь
поперечного сечения провода этой обмотки Sk :
Подставляя это соотношение в выражение для габаритной мощности получаем новое соотношение:
где:
j — плотность тока в проводах обмотки (среднеквадратичная);
Sk — площадь поперечного сечения провода k-й обмотки;
Vwk_rms – действующее значение тока в k-й обмотке;
n+m – суммарное число всех обмоток или полуобмоток.
В реальности не все окно магнитопровода может быть заполнено «медью обмоток», есть еще изоляция, воздушные
промежутки – зазоры, каркас, много чего. В связи с этим вводят понятие коэффициента заполнения окна.
Габаритная мощность представляет собой практически важный параметр, физически обозначающий максимальную
мощность, которую можно прокачать в данных габаритах и конструкции трансформатора.
Коэффициент заполнения окна сердечника k0 определяется
отношением:
где:
S0 – общая площадь окна сердечника;
Sw – часть площади окна сердечника заполненную проводниками обмоток (площадь, заполненная медью).
Площадь окна сердечника определяется конкретным типом магнитопровода и его значение представлено в
datasheet-ах на магнитопровод. Коэффициент заполнения окна сердечника k0 зависит от различных
факторов – плотности намотки, изоляции проводников обмоток, межслоевой изоляции, толщины каркаса и т.д.
Из определения коэффициента заполнения окна сердечника k0 следует выражение, определяющее полезную
площадь по меди Sw:
Суммарная площадь проводников обмоток Sw внутри окна магнитопровода равна сумме площадей,
занимаемых каждой из обмоток в отдельности.
где:
Nk – число витков в k-й обмотке (полуобмотке);
Sk – площадь поперечного сечения провода k-й обмотки.
Таким образом, полученная система опорных уравнений:
будет использоваться для вывода выражений габаритной мощности трансформаторов различных типов
преобразователей прямого хода.
Влияние и взаимовлияние различных параметров на габаритную мощность трансформаторов прямого
хода
Рабочая индукция В
Рабочая индукция уменьшается при увеличении числа витков, при увеличении площади поперечного сечения
магнитопровода. Уменьшение индукции приводит к снижению потерь. Но если это уменьшение было достигнуто
увеличением числа витков, то потери в меди возрастают.
Число витков N
Уменьшение числа витков приводит к уменьшению потерь в проводниках, с другой стороны это приводит к
увеличению потерь в магнитопроводе. Увеличение потерь в проводниках, приводит к росту температуры, что
увеличивает сопротивление обмоток и соответственно потери.
Площадь сечения магнитопровода S
С ростом площади сечения уменьшаются потери в магнитопроводе. С другой стороны с ростом S увеличивается длина
провода и возрастают потери в обмотках.
Частота f
С ростом частоты увеличиваются потери в магнитопроводе, но при этом, если напряжение постоянно снижается
уровень рабочей индукции. При высоких частотах начинает проявляться скин-эффект в проводниках. Повышение
частоты приводит к уменьшению габаритов трансформатора.
Трансформатор двухтактного прямоходового преобразователя
Режим работы. Основные соотношения
Прямоходовый двухтактный трансформатор – это трансформатор преобразователей с симметричным перемагничиванием
магнитопровода. Такими преобразователями являются — полумостовой, мостовой преобразователи и пуш-пул.
В качестве примера, для более наглядного рассмотрения процессов используем простой двухобмоточный
трансформатор с одной первичной и одной вторичной обмотками без выводов. В любой топологии прямоходового
двухтактного трансформатора (полумост, мост, в случае пуш-пул – то же самое, только первичная обмотка
разбивается на две полуобмотки) к первичной обмотке прикладываются импульсы напряжения различной полярности,
следующие через некоторую паузу.
Установим взаимосвязь между параметрами импульсов напряжения (амплитуда, длительность), прикладываемого к
первичной обмотке трансформатора, числом витков в ней, параметрами магнитопровода и достигаемой величины
индукции магнитного поля.
Начальные условия и соотношения:
Основные количественные параметры прямоугольных импульсов прикладываемых к первичной обмотке:
— длительность импульса напряжения, прикладываемого к первичной обмотке трансформатора — ti ;
— период импульсов напряжения, прикладываемого к первичной обмотке трансформатора T ;
— время задержки между импульсами верхнего и нижнего ключей (мертвое время) — tdeadtime ;
— амплитуда напряжения, прикладываемого к первичной обмотке трансформатора — VIN .
Форма импульсов напряжения, прикладываемых к первичной обмотке трансформатора представлена на рисунке T.26.
Форма импульсов напряжения соответствует реальной работе двухтактных преобразователей прямого хода.
Рисунок T.26 – Напряжение на первичной обмотке и магнитный поток (индукция) в сердечнике.
Как видно из рисунка T.26 период между импульсами складывается из длительностей импульсов напряжения и
длительностей времен задержки:
При отсутствии нагрузки на вторичной обмотке после приложения к первичной обмотке трансформатора импульса
напряжения в ней возникнет ток, поскольку первичная обмотка ведет себя как дроссель с индуктивностью,
называемой индуктивностью намагничивания. При этом в магнитопроводе возникает магнитный поток Ф0(t).
То есть, если вторичная обмотка ни к чему не подключена, то трансформатор ведет себя как дроссель.
Рассмотрим случай, когда к выходу вторичной обмотки трансформатора подключается нагрузка (омическая для
простоты выводов). В результате действия закона электромагнитной индукции на выводах вторичной обмотке
возникает ЭДС самоиндукции V2, которое прикладывается к нагрузке, подключенной к вторичной
обмотке. Таким образом, во вторичной обмотке возникает ток I2 который в свою очередь индуцирует в
магнитопроводе вторичный магнитный поток Ф2(t). Реакцией на это является одновременное увеличение
тока первичной обмотки I1 который создаёт дополнительный первичный магнитный поток Ф1(t)
направленный противоположно Ф2(t). Поскольку увеличение магнитного потока Ф1(t) от
тока первичной обмотки практически равно увеличению магнитного потока Ф2(t) от тока вторичной
обмотки, то результирующее изменение магнитного потока в магнитопроводе практически равно нулю:
Увеличение нагрузки и соответственно тока вторичной обмотки приводит к увеличению магнитного потока вторичной
обмотки Ф2(t) и соответственно потока Ф1(t). При этом протекающий в магнитопроводе
магнитный поток Ф0(t) практически не изменяется и определяется только индуктивностью первичной
обмотки. Аналогичный процесс происходит при уменьшении нагрузки. Магнитный поток Ф0(t) вызывает
перемагничивание сердечника трансформатора [Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника
и расчет.Учебное пособие. — М.: СОЛОН-ПРЕСС, 2008. — 448 с.]. Таким образом, магнитные потоки обмоток,
обусловленные током нагрузки в магнитопроводе взаимно компенсируют друг друга. Магнитопровод «не чувствует»
нагрузки.
Таким образом, после приложения к первичной обмотке импульса напряжения начинает возрастать ток
намагничивания через неё. При этом магнитный поток Φ(t) за время импульса tiтакже увеличивается,
что описывается соотношением:
где:
Φ(0) – начальное значение магнитного потока в магнитопроводе до приложения импульса.
Полагая, что амплитуда напряжение VIN прикладываемого к первичной обмотке трансформатора в течение
импульса не изменяется (VIN = const) — получим выражение для магнитного потока:
В процессе работы преобразователя происходит симметричное перемагничивание сердечника трансформатора по
линейному закону. Полагая, что во время задержи между импульсами tdeadtime магнитный поток
изменяется незначительно, то к моменту времени соответствующему началу импульса поток в сердечнике был равен
максимальному значению, достигнутому в ходе предыдущего импульса отрицательной полярности:
А значение магнитного потока в конце импульса равно:
Таким образом, подставляя это значение в формулу для временной зависимости магнитного потока получаем:
Откуда:
Из этого соотношения выразим амплитуду импульсов напряжения через достигаемое значение магнитного потока и
длительность импульса и число витков первичной обмотки:
Магнитный поток равен произведению индукции магнитного поля на площадь, в которой она есть:
С учетом этого предыдущее выражение для амплитуды напряжения VIN приобретает вид:
Это выражение определяетвзаимосвязь между амплитудой VIN и длительностью
импульсов напряжения ti, прикладываемого к первичной обмотке трансформатора, числом витков в ней
N1, площадью поперечного сечения магнитопровода S и достигаемой величины индукции магнитного поля
Bmax. Это практически важное выражение, часто используемое в расчетах двухтактных
преобразователей. Продолжим эволюцию данного соотношения.
При расчете элементов импульсной преобразовательной техники часто пользуются понятием относительной
длительности импульса q равным отношению длительности ti к периоду T:
С учетом этого можно получить выражение, содержащее относительную длительность импульса q :
И вспоминая, что частота, есть величина, обратная периоду получаем:
Поскольку в реальности не вся площадь контура охватываемого витками обмотки занята магнитопроводом, то
использую понятие коэффициента заполнения сердечника.
Коэффициент заполнения сердечника (ferrimagnetic core) kc находится из соотношения
площади контура, охватываемого током (витком) S и площади занимаемой собственно магнитопроводом
Sc:
Выражая отсюда площадь:
И подставляя это выражение в формулу для VIN, получаем соотношение для величины напряжения,
прикладываемого к первичной обмотке трансформатора:
где:
q — относительная длительность импульса по отношению к периоду;
N1 – чисто витков первичной обмотки;
f – частота импульсов;
kc – коэффициент заполнения сердечника магнитопроводом;
Sc – площадь магнитопровода;
Bmax – максимальное значение индукции магнитного поля.
Данное соотношение устанавливает взаимосвязь между амплитудой, длительностью импульсов напряжения
прикладываемого к первичной обмотке трансформатора, характеристиками магнитопровода, числом витков и
максимальным значением индукции магнитного поля, достигаемым в сердечнике. В соотношении подразумевается,
что размах магнитной индукции ΔB равен удвоенному значению максимальной индукции в магнитопроводе:
Для величины напряжения появляющегося на вторичной обмотке соотношение аналогично. Покажем это. В
соответствии с соотношением для ЭДС индукции вторичной обмотки напряжение V2 на ней
пропорционально числу витков и скорости изменения магнитного потока через неё:
Скорость изменения магнитного потока с учетом всех преобразований равна:
Подставляя это соотношение в предыдущее получаем выражение для напряжения на вторичной обмотке:
Если выходных обмоток много, то выражения аналогичны:
где:
Vwk_max – максимальное (амплитудное) напряжение на k-й обмотке (для любой
k-й обмотки).
Расчет числа витков первичной обмотки
Из полученного выше выражения для VIN можно определить число витков первичной обмотки. Число
витков первичной обмотки трансформатора двухтактного преобразователя определяется по соотношению:
Оно позволяет определить минимальное число витков в первичной обмотке трансформатора при заданных q,
VIN, f, Sc, kc, Bmax. Полученные выше соотношения для
VIN и N1 справедливы для двухтактных преобразователей c топологией «мост» и
«полумост», а также «пуш-пул».
При расчете числа витков здесь используется максимальное значение относительной длительности импульса по
отношению к периоду (в большинстве случаев – 0,5, если нет дополнительных мер по ограничению верхнего
значения q за счет управления временем задержки «deadtime»). Несоблюдение этого может привести к насыщению
сердечника и выходу источника из строя [Сетевые блоки питания с высокочастотными преобразователями. О.А.
Эраносян. Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]. В случае если входное напряжение изменяется в
широком диапазоне, то в формулу расчета числа витков подставляется минимальное значение напряжения и
максимальное значение относительной длительности импульса. При этом в процессе работы преобразователя
обратная связь ШИМ контроллера обеспечивает произведение qVIN неизменным:
Важно понимать, что при практических расчетах используется произведение максимальных значений q и
VIN с целью обеспечения безопасного режима работы преобразователя во всем диапазоне входных
напряжений при инерционности обратной связи, отрабатывающей изменение коэффициента q с некоторой задержкой.
Расчет максимального значения индукции в магнитопроводе трансформатора двухтактного прямоходового
преобразователя
При прямоугольной форме импульсов в двухтактном преобразователе выражение для магнитного потока Φ имеет
вид:
где:
VIN – амплитуда импульсов напряжения прикладываемых к обмотке;
ti – длительность импульсов напряжения прикладываемых к обмотке;
N1 – число витков в первичной обмотке трансформатора.
NB. Важно понимать, что «2» в знаменателе стоит только потому, что
магнитный поток в двухтактных преобразователях в установившемся режиме изменяется от «минус Φmax»
до «плюс Φmax» , то есть с размахом 2 Φmax. В начальный момент запуска
преобразователя, если к обмотке с нулевым значением магнитного потока приложить напряжение VIN то
сердечник впадет в глубокое насыщение, что станет причиной неконтролируемого роста тока и, как правило,
выход из строя силовых ключей. В связи с этим двухтактные трансформаторы «раскачивают» плавно либо
постепенно повышая рабочее напряжение, либо постепенно увеличивая длительность импульсов ti но
номинальной. Последнее встречается чаще и называется схемой плавного пуска (soft start).
Учитывая, что магнитный поток равен произведению индукции магнитного поля на площадь, то :
Отсюда следует выражение для значения индукции в магнитопроводе:
Это соотношение связывает величину индукции B достигаемой в магнитпроводе двухтактного преобразователя c
амплитудой импульсов VIN их длительностью ti площадью S и числом витков обмотки N1.
Важно понимать, что величина индукции B ограничена «сверху» индукцией насыщения Bsat:
Необходимо отметить, что в начальный момент времени после подачи импульса напряжения, когда B(0) = 0 возможен
импульс тока. Для предотвращения этого необходимо при включении источника обеспечивать постепенное
увеличение длительности импульса до номинального ti – так называемый «мягкий старт». Большинство
специализированных силовых контроллеров имеют функцию «мягкий старт» с возможностью управления времени
перехода в квазистационарный режим. [Теория и расчет трансформаторов малой мощности. Ю.Н. Стародубцев.
РадиоСофт. 2011. 320 с.].
Как видно из формулы для индукции в магнитопроводе магнитный поток в магнитопроводе зависит только от
амплитуды импульсов напряжения VIN прикладываемых к первичной обмотке, длительности импульса
ti и числа витков N1. При подключении нагрузки ко вторичной обмотке возникающий в ней
ток создает магнитный поток, направленный навстречу основному магнитному потоку. Это ведет к увеличению тока
в первичной обмотке, которое в свою очередь компенсирует ожидаемое снижение магнитного потока. Таким
образом, величина магнитного потока и соответственно магнитной индукции не изменяются при подключении
нагрузки. Это следует и из эквивалентной схемы трансформатора.
Габаритная мощность прямоходового двухтактного трансформатора
Базовое соотношение для расчета габаритной мощности прямоходового трансформатора имеет вид:
где:
Vwk_rms – среднеквадратичное (действующее) значение тока в k-й обмотке;
Iwk_rms – среднеквадратичное (действующее) значение тока в k-й обмотке;
n+m – суммарное число всех обмоток или полуобмоток.
Формулу как было показано ранее можно преобразовать к виду
где:
j — плотность тока в проводах обмотки;
Sk — площадь поперечного сечения провода k-й обмотки;
Среднеквадратичное значение напряжения и его амплитудное значение для формы импульсов характерных для
двухтактного преобразователя (рисунок T.26) связано выражением (см. раздел «Резисторы»):
где q – коэффициент заполнения.
С учетом этого соотношение для габаритной мощности будет иметь вид:
Физически выражение наглядно показывает, что при постоянных максимальных значениях напряжения и тока через
обмотки мощность «прокачиваемая» через трансформатор пропорциональна коэффициенту заполнения q и максимальна
при полном заполнении периода импульсами. В этом случае, при q=0.5 выражение для PT можно
упростить:
Выражение для амплитудного значения напряжения Vwk_max любой k-q обмотки
двухтактного прямоходового преобразователя (полученное ранее) имеет вид:
А с учетом максимального q=0.5 :
Подставляя в формулу для габаритной мощности получаем:
Выносим все постоянные из под знака суммы:
Поскольку суммарная площадь проводников обмоток внутри равна сумме площадей, занимаемых каждой из обмоток в
отдельности (соотношение в пункте «Понятие габаритной мощности трансформатора» настоящего радела):
получаем:
Подставляя выражение, связывающее общую площадь окна Sw и коэффициент его заполнения «медью»:
Получаем почти финишное выражение:
Перегруппируя множители, получаем выражение для габаритной мощности двухтактного прямоходового
преобразователя:
где:
f – рабочая частота;
kс – коэффициент заполнения сердечника;
k0 – коэффициент заполнения окна сердечника медью;
Bmax – максимальное значение индукции в магнитопроводе;
j – максимальная плотность тока в проводах обмотки (среднеквадратичное значение);
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника.
Из выражения для габаритной мощности определяют соотношение габаритного типоразмера, необходимое для выбора
параметров магнитопровода трансформатора:
Данное соотношение выведено при допущении, что КПД трансформатора равен 1. При практических расчетах,
значение КПД трансформатора ηT вносится и конечная формула будет иметь вид:
где:
ηT – КПД трансформатора;
f – рабочая частота;
k0 – коэффициент заполнения окна сердечника медью;
kС – коэффициент заполнения сердечника;
Bmax – максимальное значение индукции в магнитопроводе;
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника;
j — максимальная плотность тока в проводах обмотки (среднеквадратичное значение).
Эта формула для габаритной мощности одно из базовых соотношений, используемых при расчете трансформатора.
Из соотношения следует, что массогабаритные показатели трансформатора, характеризуемые
ScS0 снижаются с ростом частоты, увеличением максимальной индукции насыщения
материала, плотности тока в обмотке.
Важно понимать, что соотношение для расчета габаритной мощности во многом носит формальный характер. В
реальности максимальная мощность трансформатора определяется, прежде всего, конструктивными особенностями и
условиями охлаждения. Один и тот-же трансформатор может иметь различную максимальную выходную мощность в
зависимости от условий отвода тепла от него. Интересно, что при резком уменьшении сопротивления нагрузки и
последующем увеличения тока нагрузки возрастет плотность тока в обмотках j, входящая в формулу габаритной
мощности. При этом габаритная мощность формально увеличивается, но при этом возрастают тепловые потери в
обмотке, что приводит к увеличению температуры трансформатора и следовательно снижению допустимого уровня
магнитной индукции Bmax.
Взаимосвязь габаритной мощности с выходной мощностью трансформатора для различных топологий
Установим взаимосвязь между мощностью выходной (вторичной) обмотки и габаритной мощностью трансформатора.
Мощность обмотки определяется формой тока в ней. А форма тока определяется в свою очередь топологией
трансформатора и схемы преобразователя. Рассмотрим основные распространенные случаи. Полученные соотношению
имеют практическую важность при расчете трансформаторов преобразователей различных конфигураций.
Двухобмоточный трансформатор двухтактного преобразователя
Область использования: топологии полумостовой и мостовой двухтактные преобразователи. Энергетически выгодна
при сравнительно небольших выходных токах и больших значениях выходного напряжения. Вторичная обмотка
трансформатора подключена к мостовому выпрямителю.
Рисунок T.27 — Двухобмоточный трансформатор двухтактного преобразователя
Для двухобмоточного трансформатора двухтактного преобразователя (рисунок T.27) габаритная мощность
трансформатора определяется по формуле:
Поскольку мощность в трансформаторе передается из первичной обмотки во вторичную обмотку, то мощности обмоток
связаны между собой через КПД-трансформатора:
Отсюда соотношение габаритной мощность трансформатора можно представить в виде:
или:
где:
Pw2 – мощность вторичной обмотки;
ηT – КПД трансформатора.
Трансформатор двухтактного преобразователя с вторичной обмоткой, имеющей отвод средней точки
Область использования: топологии полумостовой и мостовой двухтактные преобразователи. Энергетически выгодна
при больших выходных токах и небольших значениях выходного напряжения. Вторичная обмотка трансформатора
подключена к двухполупериодному выпрямителю со средней точкой.
Рисунок T.28 — Трансформатор двухтактного преобразователя с вторичной обмоткой, имеющей отвод средней
точки
Для трансформатора двухтактного преобразователя с вторичной обмоткой, имеющей отвод средней точки (рисунок
T.28) габаритная мощность определяется по формуле:
Ток через каждую полуобмотку имеет форму прямоугольных импульсов, максимальное значение коэффициента
заполнения в двухтактных преобразователях равно 0,5. Таким образом, среднеквадратичное значение тока в
полуобмотках определяется по соотношению:
Здесь амплитудные значения токов в полуобмотках равны между собой и равны суммарному выходному току вторичной
обмотки трансформатора:
Напряжение на выходе вторичных полуобмоток равно выходному напряжению вторичной обмотки
Vw2 .
С учетом этого соотношение для габаритной мощности можно переписать в виде:
Здесь произведение выходного напряжения обмотки на выходной ток равно суммарной мощности вторичной обмотки
Pw2:
С учетом того, что мощности первичной и вторичной обмоток связаны через КПД-трансформатора, получаем:
где:
Pw2 – мощность вторичной обмотки;
ηT – КПД трансформатора.
Трансформатор двухтактного преобразователя с первичной обмоткой, имеющей отвод средней точки
Область использования: топология пуш-пулл. Энергетически выгодна при сравнительно небольших выходных токах и
больших значениях выходного напряжения. Вторичная обмотка трансформатора подключена к мостовому
выпрямителю.
Рисунок T.29 — Трансформатор двухтактного преобразователя с первичной обмоткой, имеющей отвод средней точки
Для трансформатора двухтактного преобразователя с первичной обмоткой, имеющей отвод средней точки (рисунок
T.29) габаритная мощность определяется по формуле:
Ток через каждую полуобмотку имеет форму прямоугольных импульсов, максимальное значение коэффициента
заполнения в двухтактных преобразователях равно 0,5. Таким образом, среднеквадратичное значение тока в
полуобмотках определяется по соотношению:
Здесь амплитудные значения токов в полуобмотках равны между собой и равны суммарному входному току первичной
обмотки трансформатора:
Напряжение на входе первичных полуобмоток фактически равно входному напряжению Vw1 .
С учетом этого соотношение для габаритной мощности можно переписать в виде:
Здесь произведение входного напряжения первичной обмотки на входной ток равно суммарной мощности первичной
обмотки Pw1:
С учетом того, что мощности первичной и вторичной обмоток связаны через КПД-трансформатора, получаем:
где:
Pw2 – мощность вторичной обмотки;
ηT – КПД трансформатора.
Трансформатор двухтактного преобразователя с первичной и вторичной обмотками, имеющими отвод средней
точки
Область использования: топология пуш-пулл. Энергетически выгодна при больших выходных токах и небольших
значениях выходного напряжения. Вторичная обмотка трансформатора подключена к двухполупериодному выпрямителю
со средней точкой.
Рисунок T.30 — Трансформатор двухтактного преобразователя с первичной и вторичной обмотками, имеющими
отвод
средней точки
Для трансформатора двухтактного преобразователя с первичной и вторичной обмотками, имеющими отвод средней
точки (рисунок T.30) габаритная мощность определяется по формуле:
Ток через каждую полуобмотку имеет форму прямоугольных импульсов, максимальное значение коэффициента
заполнения в двухтактных преобразователях равно 0,5. Таким образом, среднеквадратичное значение тока в
полуобмотках определяется по соотношению:
Для каждой обмотки амплитудные значения токов в полуобмотках равны между собой и равны суммарному току
соответствующей обмотки трансформатора:
С учетом этого соотношение для габаритной мощности можно переписать в виде:
Здесь произведение напряжения обмотки на ток равно суммарной мощности соответствующей обмотки:
С учетом того, что мощности первичной и вторичной обмоток связаны через КПД-трансформатора, получаем:
где:
Pw2 – мощность вторичной обмотки;
ηT – КПД трансформатора.
Пояснение уменьшения габаритной мощности трансформатора при использовании обмоток с отводом от
средней точки
На первый взгляд может показаться, что разбивка обмотки на две полуобмотки никак не влияет на габаритную
мощность трансформатора. Такое впечатление может сложиться из-за того, что ток распределяется поровну меду
обмотками.
В реальности габаритная мощность трансформатора ограничена шириной окна магнитопровода, в котором размещаются
обмотки. Площадь окна распределяется между первичной и вторичной обмотками. Для случая простой двухвыводной
обмотки в каждый момент времени через обмотку протекает ток, в прямом или в обратном направлении,
следовательно, выделенная под обмотку часть окна магнитопровода используется полностью. Если мы разбиваем
обмотку на две полуобмотки, то в каждый момент времени для прохождения тока используется только одна
половина выделенной под обмотку части окна. Это служит причиной снижения габаритной мощности
трансформатора.
На рисунке T.31 схематично изображены два случая расположения обмоток в окне магнтопровода. В первом случае
вторичная обмотка состоит из одной обмотки, во втором – из двух полуобмоток.
Рисунок T.31 — Схематичное изображение трансформатора с единой вторичной обмоткой и с разделенной
вторичной
обмоткой имеющей отвод от средней точки
Мощность, которую можно отвести из площади окна, отведенной под вторичную обмотку определятся конструктивом
трансформатора и не зависит от того разбита ли обмотка на полуобмотки или нет. Максимальная мощность
определяет максимальный ток, который можно пропустить через обмотку:
Для простой двухвыводной вторичной обмотки соотношение, связывающее максимальный ток и максимальная мощность
имеет вид:
Для вторичной обмотки, состоящей из двух полуобмоток:
Здесь сопротивление полуобмоток в два раза больше, поскольку площадь сечения проводников полуобмоток
уменьшена в два раза пропорционально уменьшению площади сечения полуобмотки по отношению к обмотке. Вынесем
общий множитель за скобки.
С учетом формы тока в полуобмотках:
Получаем:
Амплитудные значения токов в полуобмотках равны между собой и равны суммарному выходному току вторичной
обмотки трансформатора с выводом от средней точки (при прямоугольной форме импульсов для суммарного
выходного тока при q=0.5 максимальное и среднеквадратичное значения равны):
Таким образом, можно записать мощности вторичной обмотки для двух случаев:
— для простой двухвыводной обмотки:
— для вторичной обмотки состоящей из двух полуобмоток:
Приравнивая мощности:
Получаем соотношение выходных токов обычной обмотки и обмотки с отводом от средней точки при условии
одинаковой рассеваемой мощности :
где:
Iw2_rms – среднеквадратичное значение тока простой двухвыводной обмотки;
Iw2_rms* – максимальное среднеквадратичное значение тока обмотки
с отводом от средней точки.
Таким образом, можно сделать практически важный вывод о том, что ток, который можно пропустить через обмотку
разбитую на две полуобмотки уменьшиться в 1/√2 раза (≈0,707). То есть габаритная мощность трансформатора при
использовании обмоток с отводами от средней точки должна быть больше.
Зазор в магнитопроводе трансформатора двухтактного преобразователя
Введение магнитного зазора позволяет существенно увеличить ток через индуктивный элемент (обмотку
трансформатора), при этом чем больше зазор тем больший ток насыщения будет достигнут. Обратной стороной
этого является снижение индуктивности. Чтобы сохранить величину индуктивности на прежнем уровне необходимо
увеличивать число витков. Это ведет к омическими потерям… И ограничено сверху шириной окна [Трансформаторы и
дроссели для импульсных источников питания. А. Кузнецов. Схемотехника, 2000, №1, с. 30—33, №2, с. 48, 49,
2001, №1, с. 32—34.]. Так что, как правило, зазор в магнитопровод трансформатора двухтактного
преобразователя как правил не вводят. Однако, в ряде случаев, для повышения устойчивости режима работы
трансформатора по отношению к несимметричному подмагничиванию магнитопровода зазор используют.
Основные соотношения расчета конструкции трансформатора
Конструктивный расчет является важной составляющей расчета трансформатора, так как только после выполнения
расчета конструкции можно корректно рассчитать все паразитные параметры трансформатора, определить его
тепловой режим и в конечном итоге спроектировать надежный источник питания.
Расчет конструктивных особенностей трансформатора во многом определяется типом магнитопровода. Порядок
расчета значительным образом отличается для магнитопровода с цилиндрической обмоткой (Ш-, П-образный,
чашкообразный) и обмоткой тороидальной (тор, кольцо).
Параметры обмоточного провода
Площадь поперечного сечения провода первичной и вторичной обмоток Sw1_Cu , Sw2_Cuрассчитывается
по соотношению, связывающему заданную максимальную плотность тока в обмотке jmax и максимальное
значение тока Iw1_max, Iw2_max :
Более корректно было бы учитывать не максимальное, а среднеквадратичное значение, но на практике в
большинстве случаев такое упрощение не существенно влияет на результат, поскольку для двухтактных
преобразователей при максимальной выходной мощности обеспечивается максимальное значение коэффициента
заполнения и среднеквадратичное значение приближается к максимальному. Кроме этого, плотность тока в начале
расчета выбирается ориентировочно. В дальнейшем выполняется точное вычисление рассеиваемой мощности и по
необходимости вносятся коррективы в конструкцию.
В случае если первичная обмотка состоит из двух полуобмоток (пуш-пул преобразователь) то полученное значение
площади сечения Sw1_Cu делится на два. Аналогично в случае если вторичная
обмотка состоит из двух полуобмоток (вторичная обмотка трансформатора имеет вывод от средней точки) то
полученное значение площади сечения Sw2_Cu делится на два.
Исходя из вычисленных значений площади Sw1_Cu ,
Sw2_Cu рассчитывают диаметр проводов обмоток (по меди)
dw1_Cu , dw2_Cu исходя из соотношения,
связывающего площадь с диаметром:
Однако полученные значения диаметров dw1_Cu ,
dw2_Cu почти наверняка точно не совпадет с характеристиками выпускаемых
обмоточных проводов. Поэтому на основании вычисленного диаметра провода (по меди) выбирается ближайший
диаметр провода (по меди) из номенклатуры диаметров выбранного типа провода (ПЭЛ, ПЭТВ и т.д.). Округление
производится в большую сторону:
В соответствии со справочным листком определяется диаметр с изоляцией выбранного типа обмоточного провода
dw1_ins , dw2_ins :
Диаметр провода в изоляции, является одним из базовых параметров и учитывается при расчете числа витков в
одном слое, проверки условия размещения обмоток в окне магнитопровода и т.д.
Средняя длина витка обмоток трансформатора
Средняя длина витка для первичной lw1_t_av, и
вторичной обмоток lw2_t_avопределяется исходя из
геометрических соображений как среднее арифметическое между длинами первых lw1_first,
lw2_first и последних витков lw1_last ,
lw1_last обмоток:
Ниже представлены соотношения для расчета средней длины витка для различных типов магнитопроводов.
Ш- и П- образные и чашеобразные магнитопроводы
Для Ш- и П- образных магнитопроводов с прямоугольным сечением магнитопроводасредняя длина
витка оценивается исходя из конфигурации магнитопровода (рисунок T.32).
Рисунок T.32 — К определению средней длины витка для Ш- и П- образных магнитопроводов
Как правило, первичная обмотка наматывается первой (располагается ближе к магнитопроводу). Длина внешнего
витка первичной обмотки lw1_last (без учета закруглений) равна:
Или, упрощая:
Длина внутреннего витка lw1_first равна:
Здесь:
a, b – геометрические параметры характеризующие сечение каркаса магнитопровода;
tw1 – толщина первичной обмотки.
В первом приближении толщину первичной обмотки tw1 можно посчитать исходя из
соотношения, учитывающего число слоев и толщину провода (здесь не учитывается межслоевая изоляция и
плотность намотки):
где:
dw1_ins – диаметр провода первичной обмотки с изоляцией;
функция (ceiling) — округление до большего целого;
hcm – высота каркаса магнитопровода определяющая высоту обмотки;
Nw1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) первичной обмотки, зависящий от толщины
провода (таблица T.7).
Таблица T.7 — Коэффициент укладки в зависимости от диаметра провода для трансформаторов кольцевой конструкции
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.]
| Диаметр провода с изоляцией, мм | 0,08 – 0,31 | 0,31-0,5 | 0,5-2,1 |
| Коэффициент укладки | 0,8-0,75 | 0,75-0,7 | 0,65-0,6 |
Итого, объединяя, получаем для первичной обмотки:
где:
Длина внутреннего витка вторичной обмотки lw2_first принимается равной длине
внешнего витка первичной обмотки (при условии, что вторичная обмотка укладывается поверх вторичной):
Длина внешнего витка вторичной обмотки (без учета закруглений) равна:
Или, упрощая:
Здесь:
tw2 – толщина вторичной обмотки.
Толщина вторичной обмотки tw2 оценивается по соотношению:
где:
dw1=2_ins – диаметр провода вторичной обмотки с изоляцией;
функция (ceiling) — округление до большего целого;
hcm – высота каркаса магнитопровода определяющая высоту обмотки;
Nw2 – число витков в вторичной обмотке;
kw2_l – коэффициент укладки (laying) вторичной обмотки, зависящий от толщины
провода (таблица T.7).
Итого, объединяя, получаем для вторичной обмотки:
где:
Для Ш- и П- образных, чашеобразных и других магнитопроводов с круглым сечением центрального стержня
магнитопровода средняя длина витка оценивается следующим образом:
Длина внутреннего витка первичной обмотки lw1_first равна:
где:
R – радиус каркаса магнитопровода.
Длина внешнего витка первичной lw1_last равна:
где:
tw1 — толщина первичной обмотки.
В первом приближении толщину первичной обмотки tw1 можно посчитать исходя из
соотношения учитывающее число слоев и толщину провода (здесь не учитывается межслоевая изоляция и плотность
намотки):
Итого, объединяя, получаем для первичной обмотки:
где:
Длина внутреннего витка вторичной обмотки lw2_first принимается равной длине
внешнего витка первичной обмотки (при условии, что вторичная обмотка укладывается поверх вторичной):
Длина внешнего витка вторичной обмотки (без учета закруглений) равна:
где:
tw1 — толщина первичной обмотки;
tw2 — толщина вторичной обмотки.
Толщину вторичной обмотки tw2 можно оценить исходя из соотношения, учитывающего число
слоев и толщину провода (здесь не учитывается межслоевая изоляция и плотность намотки):
Итого, объединяя, получаем для вторичной обмотки:
где:
Тороидальные магнитопроводы
Для тороидальных магнитопроводов расчет среднего витка несколько сложнее. Это обусловлено тем, что толщина
внутреннего слоя обмотки будет выше плотности намотки внешнего слоя вследствие того, что длина внутреннего
кольца тора меньше длины внешнего кольца.
Внешний виток обмотки на тороидальных магнитопроводах представляет собой трапецию со скругленными углами
(рисунок T.33). Разобьём внешний виток первичной обмотки на 8 частей: четыре сектора по четверти окружности,
два из которых имеют радиус равный толщине внешнего tw1_ext, а два —
внутреннего tw1_int слоев обмотки, две высоты магнитопровода hm
и два сегмента (боковые стороны трапеции) длина которых определяется из теоремы Пифагора для прямоугольного
треугольника (из ширины магнитопровода wm, и разницы высот внутреннего tw1_ext
и внешнего tw1_int витков).
Рисунок T.33 — К определению средней длины витка тороидальных магнитопроводов (показаны обозначения
только
первичной обмотки)
Общая длина внешнего витка первичной обмотки с учетом закруглений равна:
Или:
Общая длина внутреннего витка первичной обмотки при условии прямоугольного сечения магнитопровода равна:
Плотность намотки и соответственно толщина внутреннего слоя обмотки будет выше плотности намотки внешнего
слоя. В первом приближении коэффициент пропорциональности равен отношению длин окружностей внешнего и
внутреннего радиусов тора. Можно считать, что толщины внешнего tw1_ext и
внутреннего tw1_int слоев обмотки связаны этим коэффициентом
пропорциональности. Таким образом:
Rext – внешний радиус тора (с учетом изоляции);
Rint – внутренний радиус тора (с учетом изоляции).
Аналогично случаю с Ш- и П- образными магнитопроводами можно в первом приближении найти толщину
tw1_int
внутреннего слоя первичной обмотки исходя их соотношения учитывающее число слоев и толщину провода (здесь не
учитывается межслоевая изоляция и плотность намотки). Только в качестве высоты обмотки используем длину
внутренней окружности тора:
где:
функция (ceiling) — округление до большего целого;
dw1_ins — диаметр обмоточного провода первичной обмотки с изоляцией;
Rint – внутренний радиус тора;
Nw1 – число витков в обмотке;
kw1_l – коэффициент укладки (laying) первичной обмотки, зависящий от толщины
провода (таблица T.7).
На основании оценочного значения толщины внутреннего слоя tw1_int можно
воспользовавшись пропорцией определить толщину внешнего слоя первичной обмотки:
Итого, объединяя, получаем для первичной обмотки:
где:
Длина внутреннего витка вторичной обмотки lw2_first принимается равной длине
внешнего витка первичной обмотки (при условии, что вторичная обмотка укладывается поверх вторичной):
Толщина внутреннего слоя вторичной обмотки рассчитывается аналогично:
Формула учитывает уменьшение внутреннего радиуса тора за счет размещения первичной обмотки. На основании
оценочного значения толщины внутреннего слоя tw2_intможно воспользовавшись
пропорцией определить толщину внешнего слоя:
Общая длина внешнего витка вторичной обмотки с учетом закруглений равна:
Итого, объединяя, получаем для вторичной обмотки:
где:
Определение длины обмотки
Длина обмоток определяется как произведение средней длины витка на число витков:
Полученная величина определяет, сколько провода нужно отмерить на обмотки трансформатора и используется при
расчете омического сопротивления обмоток.
Фактическая проверка возможности размещения обмоток трансформатора
Несмотря на то, что в начале проектирования дросселя задается коэффициент заполнения окна магнитопровода
k0, исходя из типа магнитопровода, по окончании расчета необходимо выполнить окончательную
проверку возможности размещения обмотки. Дело в том, что коэффициент заполнения окна магнитопровода
k0 является оценочным параметром, на основе которого определяется габаритный параметр
трансформатора. В зависимости от выбранного типа магнитопровода, типа и толщины обмоточного провода, толщины
межслоевой изоляции реальный коэффициент k0 может существенно изменяться. Поэтому после всех
расчетов необходимо проверить факт реального размещения обмотки в окне магнитопровода. Кроме этого, может
быть неоптимальное использование окна магнитопровода, если останется слишком много свободного места в окне
обмотки.
Расчет структуры трансформатора существенным образом различается для различных типов магнитопровода. Ниже
приведен расчет для наиболее распространенных геометрий магнитопровода:
Ш- и П- образные и чашеобразные магнитопроводы
Для конструктивного расчета структуры цилиндрической обмотки трансформатора определяется средняя ширина
намоточного слоя hlav. Она равна высоте каркаса магнитопровода hcm (рисунок
T.34):
Высота каркаса магнитопровода hcm определяется из справочных данных (datasheet) на магнитопровод.
В ряде случаев, например при использовании секционирования обмотки, в качестве высоты каркаса hcm
используется высота секции.
Рисунок T.34 — К расчету конструкции обмотки трансформатора преобразователя
Исходя из полученной величины hlav и известной величины диаметра проводников обмоток с изоляцией dw1_ins
и dw2_ins определяются числа витков в одном слое обмоток Nw1_l
и Nw2_l. Число витков в одном слое рассчитывается как меньшее целое (floor)
от произведения коэффициента укладки kw1_l ,
kw2_l и отношения hcm (определяет hlav) к диаметру
проводника обмотки с изоляцией:
где:
hcm — высота каркаса магнитопровода;
dw1_ins , dw2_ins — диаметры проводников
обмоток с изоляцией;
kw1_l , kw2_l – коэффициенты укладки
(laying), зависящие от толщины провода (таблица T.7).
Таблица T.7 Коэффициент укладки в зависимости от диаметра провода для трансформаторов кольцевой конструкции
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.].
| Диаметр провода с изоляцией, мм | 0,08 – 0,31 | 0,31-0,5 | 0,5-2,1 |
| Коэффициент укладки | 0,8-0,75 | 0,75-0,7 | 0,65-0,6 |
На основе числа витков в одном слое обмоток Nw1_l и
Nw2_l рассчитывается общее число слоев обмоток. Число слоев в первичной
Wl1 и вторичной Wl2 обмотках трансформатора определяется как
отношение числа витков в обмотке к числу витков в единичном слое с округлением до большего целого (ceiling):
где:
Nw1, Nw2 — число витков в первичной и вторичной обмотках,
соответственно;
Nw1_l , Nw2_l — число витков в одном слое
первичной и вторичной обмоток, соответственно.
Теперь, когда известно число слоев можно рассчитать толщины обмоток. Толщины обмоток трансформатора
Hw1 , Hw2 рассчитываются по соотношению, учитывающему толщину
межслоевой изоляции [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
для первичной обмотки:
где:
Δw1l – толщина межслоевой изоляции первичной обмотки;
Wl1 — число слоев в первичной обмотке;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
для вторичной обмотки:
где:
Δw2l – толщина межслоевой изоляции вторичной обмотки;
Wl2 — число слоев в вторичной обмотке;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
В случае если межслоевой изоляции не предусмотрено, то величины Δw1l и
Δw2lпринимаются равными нулю (в реальности, при плотной намотке за счет
укладывания витков следующего слоя в пазы слоя предыдущего толщина обмотки может быть несколько меньше).
Далее рассчитывается общая толщина обмоток. В случае намотки обмоток трансформатора одна поверх другой
(типично для импульсных преобразователей) общая толщина обмоток складывается из толщин каждой из обмоток,
толщины межобмоточной изоляции Δ(1-2)l и толщины каркаса Δc (расстояния
между поверхностью каркаса и магнитопроводом) и толщины слоя внешней изоляции обмотки Δsurf:
Складывая все составляющие, проверяется условие фактического размещения обмотки в окне магнитопровода:
где:
HΣ — суммарная толщина «пирога» намотки;
HM – ширина окна магнитопровода.
Тороидальные магнитопроводы
Особенностью использования тороидальных (кольцевых) магнитопроводов является то, что по мере выполнения
обмотки ширина намоточного слоя hl (высота обмотки) которая определяется внутренней окружностью уменьшается.
То есть число витков в последующем слое обмотке будет меньше, чем в предыдущем. Эта нелинейность вносит
существенные коррективы в расчет конструкции трансформаторов и дросселей, выполненных на тороидальных
магнитопроводах (рисунок T.35). Полученные ниже соотношения в целом аналогичны соотношениям, представленным
в разделе «Индуктивность», но вместе с тем имеется ряд особенностей.
Рисунок T.35 — К расчету конструкции обмоток тороидального трансформатора: Dint – внутренний
диаметр тора магнитопровода с учетом слоя изоляции, D0 — остаточный технологический диаметр.
В разделе «Индуктивность» были получены соотношения для расчета конструкции дросселей на тороидальном
магнитопроводе. Эти соотношения применимы и для трансформаторов.
Число слоев первичной обмотки Wl1 определяется выражением:
где:
Nw1 – число витков первичной обмотки;
Nl_1 – число витков первого слоя первичной обмотки, определяемое из выражения:
здесь:
операция (floor) – округление до меньшего целого;
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции);
Δw1l – толщина межслоевой изоляции первичной обмотки;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
kw1_l – коэффициент укладки обмотки, зависящий от толщины провода (таблица
T.7).
ΔNw1_l — уменьшение числа витков от слоя к слою определяется выражением:
где:
операция (floor) – округление до меньшего целого;
Δhlw1 — уменьшение ширины намоточного слоя от слоя к слою для первичной обмотки:
Полученное значение Wl1, как правило, будет дробным, и число слоев первичной обмотки
определяется округлением полученного числа до большего целого (ceiling):
Толщина первичной обмотки Hw1 рассчитывается по соотношению, учитывающему толщину
межслоевой изоляции [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
где:
Δw1l – толщина межслоевой изоляции первичной обмотки;
Wl1 — число слоев в первичной обмотке;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
Далее выполняют аналогичные расчеты для вторичной обмотки:
Число слоев вторичной обмотки Wl2 определяется выражением:
где:
Nw2 – число витков вторичной обмотки;
Nl_2 – число витков первого слоя вторичной обмотки, определяемое из выражения:
здесь:
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции);
Δw2l – толщина межслоевой изоляции вторичной обмотки;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
kw2_l – коэффициент укладки обмотки, зависящий от толщины провода (таблица
T.7);
Hw1 — толщина первичной обмотки.
ΔNw2_l — уменьшение числа витков от слоя к слою для вторичной обмотки
определяется выражением:
где:
операция (floor) – округление до меньшего целого;
Δhlw2 — уменьшение ширины намоточного слоя от слоя к слою для вторичной обмотки:
Полученное значение Wl2, как правило, будет дробным, и число слоев первичной обмотки
определяется округлением полученного числа до большего целого (ceiling):
Толщина вторичной обмотки Hw2 рассчитывается по соотношению, учитывающему толщину
межслоевой изоляции [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
где:
Δw2l – толщина межслоевой изоляции вторичной обмотки;
Wl2 — число слоев в вторичной обмотке;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
Далее необходима проверка условия фактического размещения обмотки в окне тороидального магнитопровода.
Суммарная толщина «пирога» намотки составляет:
Общая толщина обмоток складывается из толщин каждой из обмоток, толщины межобмоточной изоляции
Δ(1-2)l и толщины слоя внешней изоляции обмотки Δsurf:
Складывая все составляющие, проверяется условие фактического размещения обмотки в окне магнитопровода:
где:
HΣ — суммарная толщина «пирога» намотки;
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции) который фактически определяет
ширину окна магнитопровода;
D0 — остаточный диаметр внутри тороидального трансформатора (технологический).
Последовательность расчета трансформатора двухтактного преобразователя
Данный алгоритм расчета относится к расчету трансформаторов двухтактных преобразователей прямого хода:
полумостового преобразователя, мостового преобразователя, преобразователя «пуш-пул».
1. Начальное определение типа магнитопровода и феррита
Определяем типы магнитопровода и феррита на основе исходных данных проектирования. Рекомендации по выбору
типа магнитопровода и феррита представлены в пункте «Конструктивные элементы трансформатора и дросселя.
Магнитопровод» настоящего раздела. Этот шаг необходим для предварительного определения коэффициента
заполнения окна сердечника медью k0 имаксимального значения индукции в магнитопроводе
Bmax, входящих в формулу габаритной мощности.
2. Расчет габаритного параметра
трансформатора SCS0
Определяем габаритный параметр трансформатора SCS0:
где:
PT — габаритная мощность трансформатора;
ηT – КПД трансформатора;
f – рабочая частота;
k0 – коэффициент заполнения окна сердечника медью;
kС – коэффициент заполнения сердечника;
Bmax – максимальное значение индукции в магнитопроводе;
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника;
j — плотность тока в проводах обмотки.
Габаритная мощность трансформатора PT является исходным параметром
расчета. Габаритная мощность трансформатора определяется максимальной мощностью вторичной обмотки
Pw2, КПД трансформатора ηT и типом топологии трансформатора, которая в свою
очередь зависит от выбранного типа выходного выпрямителя – с отводом от средней точки или мостовой:
— для простого двухобмоточного трансформатора двухтактного преобразователя с мостовым выпрямителем:
Рисунок T.36 — Двухобмоточный трансформатор двухтактного преобразователя
габаритная мощность равна:
где:
Pw2 – мощность вторичной обмотки;
ηT – КПД трансформатора.
— для трансформатора двухтактного преобразователя с вторичной обмоткой, имеющей отвод средней точки:
Рисунок T.37 — Трансформатор двухтактного преобразователя с вторичной обмоткой, имеющей отвод средней
точки
габаритная мощность равна:
— для трансформатора двухтактного преобразователя с первичной обмоткой, имеющей отвод средней точки
(топология преобразователя – пуш-пул):
Рисунок T.38 — Трансформатор двухтактного преобразователя с первичной обмоткой, имеющей отвод средней
точки
габаритная мощность равна:
— для трансформатора двухтактного преобразователя с первичной и вторичной обмотками, имеющими отвод средней
точки (топология преобразователя – пуш-пул):
Рисунок T.39 — Трансформатор двухтактного преобразователя с первичной и вторичной обмотками, имеющими
отвод
средней точки
габаритная мощность равна:
Коэффициент полезного действия трансформатора ηT принимается в
соответствии с мощностью трансформатора. В соответствии с [Эраносян О.А. Сетевые блоки питания с
высокочастотными преобразователями.— Л.: Энергоатомиздат. Лени игр. отд-ние, 1991,— 176 с: ил. 109 стр.],
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.] на начальной стадии расчета КПД трансформатора ηT принимается в
соответствии с мощностью трансформатора (у Эраносяна – мощностью нагрузки):
— при POUT_max ≤ 10 Вт принимается ηT = 0,93;
— при 10 Вт < POUT_max ≤ 50 Вт принимается ηT = 0,95;
— при POUT_max > 50 Вт принимается ηT = 0,97.
Необходимо отметить, что не более чем начальное приближение, необходимое для выполнения предварительного
этапа расчета.
Коэффициент заполнения окна сердечника медью k0 выбирается
в зависимости от типа используемого магнитопровода:
— для Ш-образного магнитопровода [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
в ряде случаев, в особенности, когда S0 представляет собой площадь окна сердечника дросселя уже с
учетом каркаса магнитопровода, то может быть выбран k0 вплоть до 0,28-0,4 — [McLyman C.
Transformer and inductor design handbook.2004].
— для кольцевого магнитопровода [Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет.
Учебное пособие. — М.: СОЛОН-ПРЕСС, 2008. — 448 с. — 57 стр.]:
В любом случае это является первым приближением и факт размещения обмотки проверяется последующим
конструктивным расчетом.
Коэффициент заполнения сердечника kС принимается равным 1 в
случае использования магнитопровода из феррита.
Максимальное значение индукции в магнитопроводе Bmax определяется
исходя из параметров выбранного феррита и рабочей частоты. В первом приближении и в типовом случае
принимается в пределах 0,15-0,2 Тл.
Максимальное значение плотность тока в проводах обмотки j выбирается в зависимости
от выходной мощности источника в соответствии с таблицей [Эраносян О.А. Сетевые блоки питания с
высокочастотными преобразователями.— Л.: Энергоатомиздат. Лени игр. отд-ние, 1991,— 176 с: ил. 109 стр.].
Таблица T.8 – Максимально допустимая плотность тока в проводах обмотки при различной выходной мощности
источника
| POUT_max , Вт | 1 — 7 | 8 — 15 | 16 — 40 | 41 — 100 | 101 – 200 |
| j, А/мм2 | 7 — 12 | 6 — 8 | 5 — 6 | 4 — 5 | 4 — 4,5 |
Обычно плотность тока в проводнике выбирается в пределах 4-8 А/мм2. Чем больше «прокачиваемая»
мощность, тем меньше выбирается значение плотности тока. При
POUT_maxбольшей 200 Вт
плотность тока может быть выбрана в пределах 3-4 А/мм2.
Необходимо понимать, что это тоже первое приближение, необходимое для начального расчета и корректируемое
впоследствии.
Абсолютной гарантией того, что потери в обмотках не приведут к их перегреву является выбор плотности тока
равной 2 А/мм2. Однако это «советское» решение приведет к значительному увеличению габаритов и
повышению стоимости данного решения.
3. Выбор типа магнитопровода и феррита
Выбор марки магнитопровода осуществляется в соответствии с рассчитанным параметром ScS0
и конструктивными особенностями (формфактор, технологичность намотки, электромагнитная совместимость,
экономика и т.д.). Феррит выбирается исходя из компромисса «стоимость-технические характеристики».
При этом в качестве площади поперечного сечения сердечника SС должна быть использована минимально
обеспечиваемая величина площади поперечного сечения (Minimum core cross section) – Amin, а не
Ae эффективная площадь сечения магнитопровода (Effective magnetic cross section). Все эти
параметры указаны в datasheet-ах.
Определившись с конкретной маркой магнитопровода и феррита мы будем знать следующие параметры:
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника;
Bmax – максимальное значение индукции в магнитопроводе при выбранной частоте;
4. Расчет числа витков первичной обмотки
Число витков первичной обмотки рассчитывается по формуле:
где:
q – относительная длительность импульса (максимальное значение);
VIN_max – напряжение на первичной обмотке трансформатора (максимальное
значение);
f – рабочая частота;
SС – площадь поперечного сечения сердечника;
kС – коэффициент заполнения сердечника;
Bmax – максимальное значение индукции в магнитопроводе (если габаритный параметр выбранного
типоразмера магнитопровода трансформатора более чем в 1,5 раза превышает рассчитанное значение то имеет
смысл уменьшить максимальную индукцию в магнитопроводе за счет увеличения числа витков в обмотках. При этом
потери в магнитопроводе могут быть значительно уменьшены);
Относительная длительность импульса q рассчитывается как отношение максимальной
длительности импульса ti_max к периоду и для двухтактных преобразователей
может быть принята равной 0,5:
Здесь напряжение на первичной обмотке трансформатора в первом приближении принимается равным входному
напряжению преобразователя VIN_max (по максимальному значению). При расчете
преобразователей с широким диапазоном входного напряжения используется максимальное значение относительной
длительности импульса qmax и максимальное значение напряжения
Vin_max. Это обеспечит область безопасной работы трансформатора во всем
диапазоне входных напряжений и коэффициентов заполнения, что особенно важно при большой иннерции обратной
связи. В установившемся рабочем режиме преобразователя при увеличении напряжения коэффициент q будет
пропорционально уменьшаться и произведение qV останется неизменным.
5. Расчет выходного напряжения вторичной обмотки трансформатора
Выходное напряжение вторичной обмотки трансформатора V2 рассчитывается как сумма выходного
напряжения преобразователя и суммы падений напряжений на выходном выпрямителе и силовом дросселе:
где:
VOUT_max – выходное напряжение преобразователя;
ΣVVD_out – суммарное падение напряжения на диодах выходного выпрямителя;
VLf – падение напряжения на выходном силовом дросселе.
На первой итерации расчета можно использовать оценочные значения величин падений напряжения. Так в случае
использования выпрямителя с выводом от средней точки суммарное падение напряжения на выходном выпрямителе
равно падению напряжения на диоде (для Siдиодов – 1,5 В, для диодов Шоттки – 0,5 В). При использовании
мостового выпрямителя суммарное падение напряжения на выпрямителе равно удвоенному падению напряжения на
диоде. В первом приближении падение напряжения на выходном дросселе VLf можно в первом
приближении принять равным 2-5 % от выходного напряжения преобразователя.
6. Расчет коэффициента трансформации
Коэффициент трансформации k рассчитывается как отношение входного напряжения VIN_min,
прикладываемого к первичной обмотке трансформатора и выходного напряжения на вторичной обмотке V2
:
где:
V2 – напряжение на выходе вторичной обмотки;
VIN_min — минимальное значение напряжения, прикладываемого к первичной обмотке.
7. Расчет числа витков вторичной обмотки
Число витков вторичной обмотки N2 рассчитываются по соотношению:
где:
N1 – число витков первичной обмотки;
k — коэффициент трансформации.
8. Расчет индуктивности намагничивания первичной обмотки трансформатора
Индуктивность намагничивания первичной обмотки трансформатора L0 рассчитывается по соотношению:
где:
µ0 – магнитная постоянная;
µ – магнитная проницаемость материала магнитопровода;
SС – площадь сечения магнитопровода;
lav – эффективная длина средней линии магнитопровода;
N1 – число витков первичной обмотки.
9. Расчет токов первичной обмотки трансформатора
Подробный вывод выражений для расчета токов обмоток трансформатора двухтактного преобразователя прямого хода
представлен в разделах «Полумостовой преобразователь», «Мостовой преобразователь» и «Двухтактный
преобразователь push-pull».
Амплитудное значение тока первичной обмотки
Амплитудное значение тока первичной обмотки Iw1_max определяется выражением:
для мостовой схемы и пуш-пул:
для полумостовой схемы:
где:
k — коэффициент трансформации;
IOUT_max – выходной ток преобразователя (максимальное значение);
∆ILf_max – максимальная величина пульсаций тока дросселя, размах пульсаций
(входное значение для расчета трансформатора);
q – относительная длительность импульса (максимальное значение);
VIN_max — напряжение, прикладываемое к первичной обмотке (максимальное
значение);
f – рабочая частота;
L0 — индуктивность намагничивания первичной обмотки трансформатора.
Среднее значение тока первичной обмотки
Среднее значение тока первичной обмотки Iw1_avg определяется выражением:
где:
k — коэффициент трансформации;
IOUT_max – выходной ток преобразователя (используется максимальное значение
тока).
Среднеквадратичное значение тока первичной обмотки
Среднеквадратичное значение тока первичной обмотки Iw1_rms вычисляется по
формуле (см. раздел «Резисторы»):
где:
q – относительная длительность импульса (максимальное значение);
Iw1_max, Iw1_min — максимальное и
минимальное значения тока первичной обмотки вычисляются по соотношениям:
для мостовой схемы и пуш-пул:
для полумостовой схемы:
10. Расчет токов вторичной обмотки трансформатора
Амплитудное значение тока вторичной обмотки
Амплитудное значение тока вторичной обмотки Iw2_max определяется выражением:
где:
IOUT_max – выходной ток преобразователя (максимальное значение);
∆ILf_max – максимальная величина пульсаций тока дросселя (входное значение
для расчета трансформатора).
Среднее значение тока вторичной обмотки
Среднее значение тока вторичной обмотки Iw2_avg определяется выражением:
В случае наличия двух полуобмоток, итоговое выражение имеет вид:
Среднеквадратичное значение тока вторичной обмотки
В достаточно точном приближении среднеквадратичное значение тока вторичной обмотки Iw2_rms
(пусть даже состоящей из двух полуобмоток) равно среднеквадратичному значению тока выходного дросселя. Ток
выходного дросселя имеет форму треугольных импульсов с постоянной составляющей и вычисляется по выражению
(см. раздел «Резисторы»):
вычисляется по выражению:
где:
IOUT_max – выходной ток (максимальное значение);
ΔILf_max – пульсация тока дросселя (размах между максимальным и
минимальным значениями).
11. Расчет конструкции трансформатора
В результате выполненного последовательного расчета по шагам 1-10 мы получаем следующие параметры:
— конкретный тип магнитопровода c конкретными геометрическими параметрами;
— число витков первичной и вторичной обмоток N1 и N2.
Далее после получения этих базовых параметров выполняется детальный конструктивный расчет. Последовательность
расчета представлена ниже.
11.1 Расчёт параметров проводов обмоток
Минимальная площадь поперечного сечения обмоток (по меди) рассчитывается по соотношениям:
Sw1_Cu – площадь поперечного сечения проводника первичной обмотки;
Sw2_Cu – площадь поперечного сечения проводника вторичной обмотки;
Iw1_rms , Iw2_rms – среднеквадратичные
значения токов первичной и вторичной обмоток соответственно;
j – выбранное значение максимальной плотности тока в обмотках.
В случае если первичная обмотка состоит из двух полуобмоток (пуш-пул преобразователь) то полученное значение
площади сечения Sw1_Cu делится на два. Аналогично в случае если вторичная
обмотка состоит из двух полуобмоток (вторичная обмотка трансформатора имеет вывод от средней точки) то
полученное значение площади сечения Sw2_Cu делится на два.
Далее вычисляется диаметр проводов (по меди) для выполнения обмоток:
11.2 Выбор типа провода обмоток и определение диаметра и площади поперечного сечения проводников с
изоляцией
На основании вычисленного диаметра провода (по меди) выбирается ближайший диаметр провода из номенклатуры
диаметров выбранного типа провода (ПЭЛ, ПЭТВ и т.д.). Округление производится в большую сторону:
В соответствии с выбранным типом провода пересчитывается площадь поперечного сечения выбранного типа провода
по меди по формулам:
Далее в соответствии со справочным листком на выбранный тип обмоточного провода определяется его диаметр с
изоляцией для первичной и вторичной обмоток dw1_ins и
dw2_ins :
11.3 Расчёт средней длины витка обмоток трансформатора
Ш- и П- образные, чашеобразные магнитопроводы
Для Ш- и П- образных магнитопроводов с прямоугольным сечением магнитопроводасредние длины
витков рассчитываются по соотношениям:
для первичной обмотки:
где:
a, b – геометрические параметры характеризующие сечение каркаса магнитопровода (см. рисунок T.40);
tw1 – толщина обмотки, вычисляемая по соотношению:
здесь:
функция (ceiling) — округление до большего целого;
hcm – высота каркаса магнитопровода определяющая высоту обмотки;
Nw1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) первичной обмотки, зависящий от толщины
провода (таблица T.7).
Таблица T.7 — Коэффициент укладки в зависимости от диаметра провода для трансформаторов кольцевой конструкции
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.]
| Диаметр провода с изоляцией, мм | 0,08 – 0,31 | 0,31-0,5 | 0,5-2,1 |
| Коэффициент укладки | 0,8-0,75 | 0,75-0,7 | 0,65-0,6 |
Рисунок T.40 — К определению средней длины витка для Ш- и П- образных магнитопроводов
для вторичной обмотки:
где:
lw1_last — длина внешнего витка первичной обмотки, вычисляемая по
соотношению:
tw2 – толщина вторичной обмотки, вычисляемая по соотношению:
здесь:
Nw2 – число витков в вторичной обмотке;
kw2_l – коэффициент укладки (laying) вторичной обмотки, зависящий от толщины
провода (таблица T.7).
Для Ш- и П- образных, чашеобразных и других магнитопроводов с круглым сечением центрального стержня
магнитопровода средняя длина витка рассчитывается по следующим соотношениям:
для первичной обмотки:
где:
R – радиус каркаса магнитопровода;
tw1 – толщина первичной обмотки, вычисляемая по соотношению:
где:
функция (ceiling) — округление до большего целого;
hcm – высота каркаса магнитопровода определяющая высоту обмотки;
Nw1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода
(таблица T.7).
для вторичной обмотки:
где:
lw1_last — длина внешнего витка первичной обмотки, вычисляемая по
соотношению:
tw2 – толщина вторичной обмотки, вычисляемая по соотношению:
здесь:
Nw2 – число витков в вторичной обмотке;
kw2_l – коэффициент укладки (laying) вторичной обмотки, зависящий от толщины
провода (таблица T.7).
Тороидальные магнитопроводы
Для тороидальных магнитопроводов расчет среднего витка осуществляется по соотношениям:
для первичной обмотки:
где:
wm — ширина магнитопровода;
hm — высота магнитопровода;
tw1_int — толщина внутреннего слоя первичной обмотки;
tw1_ext — толщина внешнего слоя первичной обмотки.
Толщины tw1_int и tw1_ext определяются по
соотношениям:
здесь:
функция (ceiling) — округление до большего целого;
Rint – внутренний радиус тора;
Rext – внешний радиус тора;
dw1_ins — диаметр обмоточного провод первичной обмотки с изоляцией;
Nw1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода
(таблица T.7).
Рисунок T.41 — К определению средней длины витка тороидальных магнитопроводов. (показаны обозначения
только первичной обмотки)
для вторичной обмотки:
где:
lw1_last — длина внешнего витка первичной обмотки, вычисляемая по
соотношению:
tw1_int и tw1_ext определяются по
соотношениям:
здесь:
dw2_ins — диаметр обмоточного провод первичной обмотки с изоляцией;
Nw2 – число витков в первичной обмотке;
kw2_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода
(таблица T.7).
11.4 Определение длин проводников первичной и вторичной обмоток
Длина проводников обмоток определяется как произведение средней длины витка на число витков:
Полученная величина определяет, сколько провода нужно отмерить на обмотки трансформатора.
11.5 Конструктивный расчет структуры обмотки трансформатора, фактическая проверка возможности
размещения обмотки
Использование некоторой предопределенной величины коэффициента заполнения окна не дает однозначной гарантии
размещения обмотки в окне магнитопровода. Поэтому необходима проверка конструктивного условия размещения
обмотки в окне магнитопровода. Кроме этого, может быть неоптимальное использование окна магнитопровода, если
останется слишком много свободного места в окне обмотки.
Для конструктивного расчета структуры обмотки трансформатора выполняется следующая последовательность
действий:
Ш- и П- образные, чашеобразные магнитопроводы
— определяется средняя ширина намоточного слоя hlav. Она равна высоте каркаса магнитопровода
hcm (рисунок T.42):
Высота каркаса магнитопровода hcm определяется из справочных данных (datasheet) на магнитопровод.
В ряде случаев, например при использовании секционирования обмотки, в качестве высоты каркаса hcm
используется высота секции.
Рисунок T.42 — К расчету конструкции обмотки трансформатора преобразователя
— определяется число витков в одном слое для первичной и вторичной обмоток
Nw1_l и Nw2_l :
где:
операция (floor) – округление до меньшего целого;
hcm — высота каркаса магнитопровода;
dw1_ins , dw2_ins — диаметры проводников
обмоток с изоляцией;
kw1_l , kw2_l – коэффициенты укладки
(laying), зависящие от толщины провода (таблица T.7).
— рассчитывается общее число слоев для первичной и вторичной обмоток Wl1 ,
Wl2:
где:
(ceiling) — округление до большего целого;
Nw1, Nw2 — число витков в первичной и вторично обмотках,
соответственно;
Nw1_l , Nw2_l — число витков в одном слое
первичной и вторичной обмоток, соответственно.
— рассчитываются толщины обмоток трансформатора Hw1 , Hw2 :
для первичной обмотки:
где:
Δw1l – толщина межслоевой изоляции первичной обмотки;
Wl1 — число слоев в первичной обмотке;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
для вторичной обмотки:
где:
Δw2l – толщина межслоевой изоляции вторичной обмотки;
Wl2 — число слоев в вторичной обмотке;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
В случае если межслоевой изоляции не предусмотрено, то величины Δ1l и
Δ2lпринимаются равными нулю (в реальности, при плотной намотке за счет укладывания
витков следующего слоя в пазы слоя предыдущего толщина обмотки может быть несколько меньше).
— рассчитывается общая толщина «пирога» обмотки HΣ:
где:
Δ(1-2)l – толщина слоя межобмоточной изоляции;
Δc — толщина каркаса (расстояние между поверхностью каркаса и магнитопроводом);
Δsurf — толщина слоя внешней изоляции обмотки;
Hw1 , Hw2 — толщины обмоток трансформатора.
— проверяется условие фактического размещения всех конструктивных элементов «пирога» обмоток в окне
магнитопровода:
где:
HΣ — суммарная толщина «пирога» обмоток;
HM – ширина окна магнитопровода.
В случае невыполнения данного условия необходимо использовать другой магнитопровод и повторить процедуру
расчета (пункты 3 – 11).
Тороидальные магнитопроводы
В случае тороидальных магнитопроводов ширина намоточного слоя уменьшается по мере намотки. Поэтому все
сложнее.
Рисунок T.43 — К расчету конструкции обмоток тороидального трансформатора: Dint – внутренний
диаметр тора магнитопровода с учетом слоя изоляции, D0 — остаточный технологический диаметр.
— рассчитывается число слоев первичной обмотки Wl1 по выражению:
где:
Nw1 – число витков первичной обмотки;
Nl_1 – число витков первого слоя первичной обмотки, определяемое из выражения:
здесь:
операция (floor) – округление до меньшего целого;
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции);
Δw1l – толщина межслоевой изоляции первичной обмотки;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
kw1_l – коэффициент укладки обмотки, зависящий от толщины провода (таблица
T.7).
ΔNw1_l — уменьшение числа витков от слоя к слою определяется выражением:
где:
операция (floor) – округление до меньшего целого;
Δhlw1 — уменьшение ширины намоточного слоя от слоя к слою:
Полученное значение Wl1, как правило, будет дробным, и число слоев первичной обмотки
определяется округлением полученного числа до большего целого (ceiling):
— рассчитывается толщина первичной обмотки Hw1 по соотношению, учитывающему толщину
межслоевой изоляции [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
где:
Δw1l – толщина межслоевой изоляции первичной обмотки;
Wl1 — число слоев в первичной обмотке;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
— рассчитывается число слоев вторичной обмотки Wl2 по выражению:
где:
Nw2 – число витков вторичной обмотки;
Nl_2 – число витков первого слоя вторичной обмотки, определяемое из выражения:
здесь:
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции);
Δw2l – толщина межслоевой изоляции вторичной обмотки;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
kw2_l – коэффициент укладки обмотки, зависящий от толщины провода (таблица
T.7);
Hw1 — толщина первичной обмотки.
ΔNw2_l — уменьшение числа витков от слоя к слою для вторичной обмотки
определяется выражением:
где:
операция (floor) – округление до меньшего целого;
Δhlw2 — уменьшение ширины намоточного слоя от слоя к слою:
Полученное значение Wl2, как правило, будет дробным, и число слоев первичной обмотки
определяется округлением полученного числа до большего целого (ceiling):
— рассчитывается толщина вторичной обмотки Hw2 по соотношению, учитывающему толщину
межслоевой изоляции [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
где:
Δw2l – толщина межслоевой изоляции вторичной обмотки;
Wl2 — число слоев в вторичной обмотке;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
— рассчитывается суммарная толщина «пирога» намотки HΣ:
где:
Δ(1-2)l — толщины межобмоточной изоляции
Δsurf — толщина слоя внешней изоляции обмотки;
Hw1 , Hw2 — толщины обмоток трансформатора.
— проверяется условие фактического размещения обмотки в окне магнитопровода:
где:
HΣ — суммарная толщина «пирога» намотки;
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции) который фактически определяет
ширину окна магнитопровода;
D0 — остаточный диаметр внутри тороидального трансформатора (технологический).
В случае невыполнения данного условия необходимо использовать другой магнитопровод и повторить процедуру
расчета (пункты 3-11).
12. Расчет сопротивления обмоток трансформатора
Электрическое сопротивление обмоток трансформатора Rw1 и Rw2
рассчитывается по формуле для расчета омического сопротивления протяженного проводника:
где:
ρ – удельное сопротивление материала провода (для меди — 0,0175 Ом·мм2 м-1 );
lw1 , lw2 – длины проводов первичной и вторичной обмоток
соответственно;
Sw1_Cu , Sw2_Cu – площади поперечного
сечения выбранного типа провода (по меди).
13. Расчет омических потерь в обмотках
Суммарные потери на омическом сопротивлении обмоток определяются по формулам:
где:
Rw1 , Rw2 — сопротивление первичной и вторичной обмоток на
постоянном токе;
kg1 , kg2 – коэффициент добавочных потерь за счет скин-эффекта и
эффекта близости в первичной и вторичной обмотках соответственно;
Iw1_rms , Iw2_rms –
среднеквадратичное значение тока в первичной и вторичной обмотках соответственно.
NB: При высоких рабочих температурах трансформатора необходимо учитывать влияние температуры на удельное
сопротивление проводников обмоток. При высоких частотах необходимо оценить увеличение эффективного
сопротивления обмоток в результате действия скин-эффекта (см. пункт «Влияние скин-эффекта на сопротивление
обмоток при высоких частотах»).
14. Оценка уровня потерь в магнитопроводе
Существуют три способа определения потерь в магнитопроводе:
— рассчитать по формуле (при наличии аппроксимацонных коэффициентов);
— определить по графику из datasheet;
— определить экспериментально.
Расчёт по аппроксимацонным коэффициентам
Тепловая энергия, выделяемая в магнитопроводе определяется режимом работы дросселя — частотой работы f и
уровнем магнитной индукции Bmax. Для расчета потерь в магнитопроводе Pferrit
используют следующее аппроксимирующее выражение [Optimum designof a high-power, high-frequency transformer.
R. Petkov. IEEE Transactions on Power Electronics (Volume: 11, Issue: 1, Jan 1996)]:
где:
f – частота;
B – индукция;
K1, K2, K3 – аппроксимационные коэффициенты, определенные для каждого конкретного типа феррита.
Определение по графику относительных потерь из datasheet
Для определения потерь в магнитопроводе можно использовать соотношение:
где:
Pvferrit — мощность потерь на единицу объема, являющейся функцией температуры, магнитной индукции
и частоты. Графики данной зависимости представлены в справочных листах (datasheet) на каждый ферромагнитный
материал магнитопровода;
V – объем магнитопровода (приводится в справочных листах (datasheet).
Мощность потерь на единицу объема определяется типом феррита и приводится в справочных данных на конкретный
тип магнитного материала.
Рисунок T.44 — Зависимость мощности потерь от частоты при различных значениях индукции магнитного поля и
температуре для феррита N87 [Ferrites and accessories. SIFERRITmaterial N87, EPCOS AG 2006]
Определение по уровню максимальных потерь из datasheet на магнитопровод
Максимальный уровень потерь в магнитопроводе соответствует крайним режимам эксплуатации магнитопровода.
Уровень максимальных потерь часто приводится в datasheet на конкретный тип магнитопровода при различных
условиях (индукция магнитного поля, частота, температура). Уровень максимальных потерь обозначается как
PV (W/set).
В этом случае мощности потерь в магнитопроводе Pferrit приравнивается к уровню максимальных потерь
PV представленном в datasheet для наиболее близких условий эксплуатации:
Экспериментальное определение
В случае отсутствия данных для расчета остается путь экспериментального определения потерь.
15. Расчет суммарных потерь
Суммарные потери трансформатора Ptotal_loss складываются из омических потерь
обмотки и потерь магнитопровода:
где:
Pwinding1 , Pwinding2 – омические потери в первичной и вторичной
обмотке соответственно;
Pferrit – потери в магнитопроводе.
16. Расчет температурного режима трансформатора и оптимизация
Установившаяся температура перегрева трансформатора относительно окружающей среды ∆T (дельта перегрева)
приблизительно оценивается по соотношению [McLyman C. Transformer and inductor design handbook.2004]:
где:
Ptotal loss – мощность суммарных потерь в трансформаторе;
ST – суммарная эффективная площадь охлаждения трансформатора (в см2).
Если полученное с учетом рассчитанной «дельты перегрева» значение температуры нагрева трансформатора лежит в
пределах 50-80°С, то расчет трансформатора можно считать законченным. Если полученное значение превышает
80°С, то имеет смысл использовать магнитопровод большего размера.
Если в результате расчета уровень перегрева трансформатора ΔT будет значительно меньше максимально
допустимого:
то имеет смысл использовать оптимизировать конструкцию трансформатора с целью уменьшения стоимости и
массогабаритных показателей — уменьшить формфактор магнитопровода и варьировать плотность тока, размах
индукции (можно делать одновременно с повышением частоты).
Кроме того, если при допустимом уровне нагрева трансформатора получится, что мощность, выделяемая на активном
сопротивлении обмотки существенно меньше, чем в феррите магнитопровода:
то имеет смысл использовать большую плотность тока, протекающего через обмотки и повторить расчет по пунктам
1-12.
Для трансформаторов больших габаритов (с рассеваемой площадью более 1000 см2) установившаяся
температура нагрева трансформатора относительно окружающей среды ∆T (дельта перегрева) оценивается по
соотношению [В.Е. Китаев, А.А. Бокуняев. Проектирование источников электропитания устройств связи. Учеб.
пособие.- М.: Связь,1972.- 200 с.]:
где:
Ptotal_loss – мощность суммарных потерь в трансформаторе;
αT – коэффициент теплоотдачи, зависящий от множества факторов (материал трансформатора,
конструктивное исполнение, температуры окружающей среды и т.д.). Для практических расчетов принимается
равным: 11-13 Вт/м2 °С.
ST – суммарная площадь охлаждения трансформатора.
Необходимо понимать, что оптимизация расчета трансформатора проводится с учетом целевых приоритетов:
Приоритет 1 — Малые массогабаритные параметры трансформатора и, соответственно, стоимость. В этом случае
необходимо провести расчет всех параметров трансформатора с целью обеспечения (но не превышения) заданного
уровня перегрева и минимальной стоимости/массогабаритных параметров. В этом случае плотность тока, размах
индукции итерационно увеличиваются;
Приоритет 2 — Высокий КПД. В этом случае необходимо задаться максимальными массогабаритными параметрами и с
учетом этого варьируя параметры трансформатора (индукция, плотность тока и т.д.) провести расчет всех
параметров трансформатора с целью минимизации мощности потерь. В этом случае плотность тока, размах индукции
итерационно уменьшаются;
Трансформатор однотактного прямоходового преобразователя
Режим работы. Основные соотношения
Прямоходовый однотактный трансформатор – это трансформатор преобразователей с несимметричным
перемагничиванием магнитопровода, когда используется только работа в одном квадранте петли гистерезиса.
Такими преобразователями являются — прямоходовый одноключевой однотактный преобразователь, и прямоходовый
двухключевой однотактный преобразователь (он же – «косой полумост»).
В качестве примера, для более наглядного рассмотрения процессов, используем простой двухобмоточный
трансформатор с одной первичной и одной вторичной обмотками без дополнительных отводов, что типично для
преобразователя «косой полумост», где размагничивающая обмотка отсутствует. В другой топологии прямоходового
однотактного одноключевого преобразователя трансформатора присутствует размагничивающая обмотка, но в целом
режим работы трансформатора остается все тот же.
К первичной обмотке трансформатора однотактного прямоходового преобразователя прикладываются однополярные
импульсы напряжения следующие друг за другом через некоторую паузу.
Установим взаимосвязь между параметрами импульсов напряжения (амплитуда, длительность), прикладываемого к
первичной обмотке трансформатора, числом витков в ней, параметрами магнитопровода и достигаемой величины
индукции магнитного поля.
Начальные условия и соотношения :
Основные количественные параметры прямоугольных импульсов прикладываемых к первичной обмотке:
— длительность импульсов напряжения, прикладываемого к первичной обмотке трансформатора — ti ;
— период импульсов напряжения, прикладываемого к первичной обмотке трансформатора T ;
— амплитуда напряжения, прикладываемого к первичной обмотке трансформатора — VIN .
Форма импульсов напряжения, прикладываемых к первичной обмотке трансформатора представлена на рисунке T.45.
Форма импульсов напряжения соответствует реальной работе однотактных преобразователей прямого хода.
Рисунок T.45 — Временные диаграммы импульсов управления, токов через первичную и рекуперирующую обмотки,
напряжения на силовом ключе, тока через силовой дроссель фильтра и диоды. [Dokic B.L., Blanusa B. Power
Electronics: Converters and Regulators. Springer Cham Heidelberg New York Dordrecht London, 2015. XVIII,
598
p. — стр. 241]
После приложения к первичной обмотке трансформатора импульса напряжения в ней возникнет ток, и при отсутствии
нагрузки первичная обмотка ведет себя как дроссель с индуктивностью, называемой индуктивностью
намагничивания. При этом в магнитопроводе возникает магнитный поток Ф0(t).
Если к вторичной обмотке трансформатора подключается нагрузка (омическая для простоты выводов), то в во
вторичной обмотке возникает ток I2 который в свою очередь индуцирует в магнитопроводе вторичный
магнитный поток Ф2(t). Реакцией на это является одновременное увеличение тока первичной обмотки I1
который создаёт дополнительный первичный магнитный поток Ф1(t) направленный противоположно Ф2(t).
Поскольку увеличение магнитного потока Ф1(t) от тока первичной обмотки практически равно
увеличению магнитного потока Ф2(t) от тока вторичной обмотки, то результирующее изменение
магнитного потока в магнитопроводе практически равно нулю:
Увеличение нагрузки и соответственно тока вторичной обмотки приводит к увеличению магнитного потока вторичной
обмотки Ф2(t) и соответственно потока Ф1(t). При этом протекающий в магнитопроводе
магнитный поток Ф0(t) практически не изменяется и определяется только индуктивностью первичной
обмотки. Аналогичный процесс происходит при уменьшении нагрузки. Магнитный поток Ф0(t) вызывает
перемагничивание сердечника трансформатора [Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника
и расчет.Учебное пособие. — М.: СОЛОН-ПРЕСС, 2008. — 448 с.]. Таким образом, магнитные потоки обмоток,
обусловленные током нагрузки в магнитопроводе взаимно компенсируют друг друга. Магнитопровод «не чувствует»
нагрузки.
Тем не менее, магнитный поток в магнитопроводе все равно изменяется, поскольку он (магнитопровод)
намагничивается током первичной обмотки, которая ведет себя как дроссель. Первичная обмотка-дроссель имеет
индуктивность называемую индуктивностью намагничивания.
После приложения к первичной обмотке импульса напряжения начинает возрастать ток намагничивания через неё.
При этом магнитный поток Φ(t) в магнитопроводе за время импульса ti также увеличивается, что
описывается соотношением [Теория и расчет трансформаторов источников вторичного электропитания. А. В.
Хныков. СОЛОН-Пресс. 2010. 127 с.]:
где:
Φ(0) – начальное значение магнитного потока в магнитопроводе до приложения импульса.
Полагая, что амплитуда напряжение VIN прикладываемого к первичной обмотке трансформатора в течение
импульса не изменяется (VIN = const) — получим выражение для магнитного потока:
В процессе работы преобразователя происходит перемагничивание сердечника трансформатора по линейному закону.
При этом схемотехника работы такова, что за время паузы ток намагничивания в первичной обмотке спадает до
нуля, то есть к моменту времени соответствующему началу следующего импульса поток в сердечнике определяется
остаточным значением индукции магнитопровода Br (величина магнитной индукции после снятия
магнитного поля):
А значение магнитного потока в конце импульса равно:
Таким образом, подставляя это значение в формулу для временной зависимости магнитного потока получаем:
Магнитный поток равен произведению индукции магнитного поля на площадь, в которой она есть:
С учетом этого предыдущее выражение приобретает вид:
Из этого соотношения выразим амплитуду импульсов напряжения через достигаемое значение магнитного потока,
длительность импульса и число витков первичной обмотки:
Это выражение определяетвзаимосвязь между амплитудой VIN и длительностью
импульсов напряжения, прикладываемого к первичной обмотке трансформатора, числом витков в ней N1,
площадью поперечного сечения магнитопровода S и достигаемой величины индукции магнитного поля. Это
практически важное выражение, часто используемое в расчетах однотактных прямоходовых преобразователей.
Продолжим эволюцию данного соотношения.
При расчете элементов импульсной преобразовательной техники часто пользуются понятием относительной
длительности импульса q равным отношению длительности ti к периоду T:
С учетом этого можно получить выражение, содержащее относительную длительность импульса q :
И вспоминая, что частота, есть величина, обратная периоду получаем:
Поскольку в реальности не вся площадь контура охватываемого витками обмотки занята магнитопроводом, то
используют понятие коэффициента заполнения сердечника.
Коэффициент заполнения сердечника (ferrimagnetic core) kc находится из соотношения
площади контура, охватываемого током (витком) S и площади занимаемой собственно магнитопроводом
Sc:
Выражаем отсюда площадь S:
И подставляя эту формулу в выражение для VIN, получаем соотношение для величины напряжения
прикладываемого к первичной обмотке однотактного прямоходового трансформатора:
где:
q — относительная длительность импульса по отношению к периоду;
N1 – чисто витков первичной обмотки;
f – частота импульсов;
kc – коэффициент заполнения сердечника магнитопроводом;
Sc – площадь магнитопровода;
Bmax – максимальное значение индукции магнитного поля;
Br – остаточное значение индукции магнитопровода (величина магнитной индукции после снятия
магнитного поля индукцией Bmax).
Данное соотношение устанавливает взаимосвязь между амплитудой, длительностью импульсов напряжения
прикладываемого к первичной обмотке трансформатора, характеристиками магнитопровода, числом витков и
максимальным значением индукции магнитного поля, достигаемым в сердечнике. В соотношении подразумевается,
что размах магнитной индукции ΔB равен разнице между максимальной индукцией в магнитопроводе и остаточным
значением индукции для данного магнитопровода :
Таким образом, отсюда видно, что максимальный размах индукции магнитного поля определяется разницей между
максимальным значением магнитной индукции, которая ограничивается «сверху» индукцией насыщения
Bsat и «снизу» остаточной индукцией Br.
Основным способом снижения остаточной индукции Br является введение немагнитного зазора в
магнитопровод (см. раздел «Индуктивность»). При введении зазора эта величина уменьшается пропорционально
уменьшению эффективной магнитной проницаемости:
где:
где:
μ – магнитная проницаемость материала сердечника;
lg – длина магнитного зазора;
lav – эффективная длина средней линии магнитопровода.
Для напряжения на вторичной обмотке соотношение аналогично. Покажем это. В соответствии с соотношением для
ЭДС индукции вторичной обмотки напряжение на ней V2пропорционально числу витков и скорости
изменения магнитного потока через неё:
Скорость изменения магнитного потока с учетом всех преобразований равна:
Подставляя это соотношение в предыдущее получаем выражение для напряжения на вторичной обмотке:
Если выходная обмотка не одна, то это выражение можно обобщить на все обмотки:
(для любой k-й обмотки).
Расчет числа витков первичной обмотки
Из выражения для VIN полученного в предыдущем разделе можно определить число витков первичной
обмотки. Число витков первичной обмотки трансформатора однотактного прямоходового преобразователя
определяется по соотношению:
Эта формула позволяет определить минимальное число витков в первичной обмотке трансформатора при заданных q,
VIN, f, Sc, kc, Bmax, Br. Полученные выше соотношения
для VINи N1 для справедливы для однотактного одноключевого прямоходового
преобразователя с размагничивающей обмоткой и двухключевого прямоходового преобразователя (косой полумост).
При расчете числа витков здесь используется максимальное значение относительной длительности импульса q по
отношению к периоду (в большинстве случаев – 0,5, если нет дополнительных мер по увеличению q путем
интенсивного размагничивания магнитопровода. В случае если входное напряжение изменяется в широком
диапазоне, то в формулу расчета числа витков подставляется минимальное значение напряжения и максимальное
значение относительной длительности импульса. При этом в процессе работы преобразователя обратная связь ШИМ
контроллера обеспечивает произведение qVIN неизменным:
При практических расчетах используется произведение максимальных значений q и VIN с целью
обеспечения безопасного режима работы преобразователя во всем диапазоне входных напряжений, и учете
инерционности обратной связи, отрабатывающей изменение коэффициента q с некоторой задержкой.
Расчет максимального значения индукции в магнитопроводе трансформатора однотактного
прямоходового
преобразователя
При прямоугольной форме импульсов в однотактном преобразователе выражение для максимального значения
магнитного потока Φmax имеет вид:
где:
VIN – амплитуда импульсов напряжения прикладываемых к обмотке;
ti – длительность импульсов напряжения прикладываемых к обмотке;
N1 – число витков в первичной обмотке трансформатора;
S – площадь магнитопровода;
Bmax – максимальное значение индукции магнитного поля;
Br – остаточное значение индукции магнитопровода (величина магнитной индукции после снятия
магнитного поля).
Отсюда следует выражение для максимального достигаемого значения индукции в магнитопроводе:
Это соотношение связывает величину индукции B достигаемой в магнитпроводе однотактного прямоходового
преобразователя c амплитудой импульсов VIN их длительностью tiплощадью S и числом
витков обмотки N1. Важно понимать, что максимальная величина индукции B ограничена «сверху»
индукцией насыщения Bsat.
Как видно из формулы для максимального значения индукции магнитный поток в магнитопроводе зависит только от
амплитуды импульсов напряжения VIN прикладываемых к первичной обмотке, длительности импульса
ti, числа витков N1 и – остаточного значения индукции Br. При подключении
нагрузки ко вторичной обмотке возникающий в ней ток создает магнитный поток, направленный навстречу
основному магнитному потоку. Это ведет к увеличению тока в первичной обмотке, которое в свою очередь
компенсирует ожидаемое снижение магнитного потока. Таким образом, величина магнитного потока и
соответственно магнитной индукции не изменяются при подключении нагрузки. Это следует и из эквивалентной
схемы трансформатора.
Габаритная мощность прямоходового однотактного трансформатора
Базовое соотношение для расчета габаритной мощности прямоходового трансформатора имеет вид:
где:
Vwk_rms – среднеквадратичное (действующее) значение тока в k-й обмотке;
Iwk_rms – среднеквадратичное (действующее) значение тока в k-й обмотке;
n+m – суммарное число всех обмоток или полуобмоток.
Формулу, как было показано ранее, можно преобразовать к виду
где:
j — плотность тока в проводах обмотки;
Sk — площадь поперечного сечения провода k-й обмотки;
Среднеквадратичное значение напряжения и его амплитудное значение для формы импульсов характерных для
однотактного преобразователя (рисунок T.45) связаны выражениями:
где q – коэффициент заполнения.
С учетом этого соотношение для габаритной мощности будет иметь вид:
Физически выражение наглядно показывает, что при постоянных максимальных значениях напряжения и тока через
обмотки мощность «прокачиваемая» через трансформатор пропорциональна коэффициенту заполнения q и максимальна
при полном заполнении периода импульсами. Типовой случай максимального значения коэффициента заполнения qдля
однотактного прямоходового преобразователя: q=0.5. В этом случае, при q=0.5 выражение для PT
можно упростить:
Выражение для напряжения любой k-q обмотки однотактного прямоходового преобразователя (полученное ранее)
имеет вид:
здесь Vwk_max – амплитудное значение напряжения.
С учетом максимального значения коэффициента q=0.5 получаем:
Подставляя в формулу для габаритной мощности получаем:
Выносим все постоянные из под знака суммы:
Поскольку суммарная площадь проводников обмоток внутри равна сумме площадей, занимаемых каждой из обмоток в
отдельности (соотношение в пункте «Понятие габаритной мощности трансформатора» настоящего радела):
получаем:
Подставляя выражение, связывающее общую площадь окна и коэффициент его заполнения «медью»:
Получаем выражение:
Перегруппируя множители, получаем выражение для габаритной мощности однотактного прямоходового
преобразователя:
где:
f – рабочая частота;
kс – коэффициент заполнения сердечника;
k0 – коэффициент заполнения окна сердечника медью;
Bmax – максимальное значение индукции в магнитопроводе;
Br – остаточное значение индукции магнитопровода;
j – максимальная плотность тока в проводах обмотки (среднеквадратичное значение);
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника.
Из выражения для габаритной мощности определяют соотношение габаритного типоразмера, необходимое для выбора
параметров магнитопровода трансформатора:
Данное соотношение выведено при допущении, что КПД трансформатора равен 1. При практических расчетах,
значение КПД трансформатора ηT вносится и конечная формула будет иметь вид:
где:
ηT – КПД трансформатора;
f – рабочая частота;
k0 – коэффициент заполнения окна сердечника медью;
kС – коэффициент заполнения сердечника;
Bmax – максимальное значение индукции в магнитопроводе;
Br – остаточная индукция магнитопровода;
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника;
j – максимальная плотность тока в обмотках (среднеквадратичное значение).
Это соотношение для габаритной мощности одно из базовых соотношение используемых при расчете
трансформатора.
Из соотношения следует, что массогабаритные показатели трансформатора, характеризуемые
ScS0 снижаются с ростом частоты, увеличением максимальной индукции насыщения
материала, плотности тока в обмотке.
Важно понимать, что соотношение для расчета габаритной мощности во многом носит формальный характер. В
реальности максимальная мощность трансформатора определяется, прежде всего, конструктивными особенностями и
условиями охлаждения. Один и тот-же трансформатор может иметь различную максимальную выходную мощность в
зависимости от условий отвода тепла от него. Интересно, что при резком уменьшении сопротивления нагрузки и
последующем увеличения тока нагрузки возрастет плотность тока в обмотках j входящая в формулу габаритной
мощности. При этом габаритная мощность формально увеличивается, но при этом возрастают тепловые потери в
обмотке, что приводит к увеличению температуры трансформатора и следовательно снижению допустимого уровня
магнитной индукции Bmax.
NB: Сопоставляя полученное соотношение габаритной мощности трансформатора однотактного прямоходового
преобразователя с формулой для габаритной мощности трансформатора двухтактного преобразователя видно, что
при одинаковой мощности габаритный параметр однотактного трансформатора должен быть в 2√2 больше
двухтактного трансформатора. Это обусловлено двумя факторами. Во-первых, максимальный размах индукции в
магнитопроводе однотактного трансформатора в 2-а раза меньше. Это дает двукратное увеличение необходимого
габаритного параметра (по площади сечения магнитопровода). Во-вторых, за счет прямоугольной формы импульсов
тока в обмотке необходимый габаритный параметр должен быть в √2-раза больше (по площади окна
магнитопровода).
Способы уменьшения остаточной индукции, зазор в трансформаторе однотактного прямоходового
преобразователя
В соотношение габаритной мощности трансформатора однотактного прямоходового преобразователя входит
Br – остаточное значение индукции магнитопровода. Чем больше Brтем меньше габаритная
мощность. С целью снижения остаточной индукции используют немагнитный зазор.
Введение зазора увеличит габаритную мощность трансформатора за счет увеличения размаха индукции магнитного
поля. С другой стороны это приведет к снижению индуктивности намагничивания первичной обмотки трансформатора
L0, что приведет к некоторому росту амплитуды тока первичной обмотки и увеличению потерь в
обмотке. Для обоснованного ответа на этот вопрос нужен технико-экономический расчет в каждом конкретном
случае.
Поскольку параметр остаточной индукции феррита Br_max, соответствующий
предельной петле гистерезиса проходящей через точки Bsat и Hc в подавляющем
большинстве случаев практических расчетов не используется, то в datasheet-ах его численное значение
приводится редко (обозначается в datasheet просто как Br). Поэтому распространенным приближением
является расчет габаритной мощности, в котором Br принимается равным нулю и выбирается
магнитопровод обеспечивающий 30-40% запас по габаритной мощности. Однако в ряде случаев, особенно для мощных
преобразователей с топологией «косой полумост» необходим более точный расчет. Дело в том, что Br
для различных типов ферритов может оставлять 20-50% от величины Bmax. Ниже приведена методика
оценки значения остаточной индукции феррита Br и соответствующего расчета габаритной мощности
трансформатора.
Величина максимального значения остаточной индукции феррита Br_max может
быть определена следующими способами:
— поиск численного значения Br_max в datasheet-ах на выбранный тип
ферромагнитного материала (обозначается в datasheet просто как Br);
— определение Br_max из приведенных в datasheet-ах кривых гистерезиса.
Необходимо отметить, что это определение не всегда получается точным по причине большого масштаба по оси
магнитной напряженности H в результате размер петли становится сопоставим с шириной линии графика;
Полученное значение остаточной индукции Br_max сравнивается с максимальным
значением индукции насыщения Bsat и принимается решение о целесообразности или нецелесообразности
введения немагнитного зазора. В случае если остаточная индукция Br_maxсоставляет
более 25-35% от значения максимальной индукции Bsat то рекомендуется вводить в магнитопровод
немагнитный зазор. Если же значение Br составляет меньше 25-35% от Bsat то решение о
зазоре принимается исходя из технико-экономических соображений конкретного случая.
Величина остаточной индукции Br зависит от величины максимально достигаемой индукции. Отношение
остаточной индукции Br к индукции насыщения называется коэффициентом прямоугольности α [В. П.
Миловзоров. Электромагнитная техника. М., Высшая школа. 1966г., стр. 19-20]:
Исходя из приближения подобия петель гистерезиса (рисунок T.46) можно считать, что коэффициент α остается
постоянным для различных петель гистерезиса, соответствующих различным токам:
где:
Br_max , Br1 , Br2 ,
Brn – значения остаточной индукции соответствующие петлям гистерезиса с максимальным значением
индукции Bsat , Bmax1 , Bmax2 и
Bmaxn соответственно.
Отсюда следует, что для выбранного максимального значения индукции Bmax можно определить
Br :
где:
Br — величина остаточной индукции соответствующая максимальному значению индукции Bmax;
Br_max — величина остаточной индукции соответствующая индукции насыщения
Bsat.
Рисунок T.46 — Петли гистерезиса при различных значениях достигаемой индукции.
Введение в магнитопровод немагнитного зазора изменяет ход петли гистерезиса (рисунок T.47) – петля
вытягивается вдоль оси H. Участок кривой гистерезиса соединяющий точки Br и Hcхорошо
аппроксимируется линейной функцией. Угол наклона линейной функции для магнитопровода без зазора
пропорционален эффективной магнитной проницаемости µ магнитопровода, а для магнитопровода с зазором угол
наклона пропорционален эффективному значению магнитной проницаемости µeff.
Поскольку обе линейных функции имеют пересечение на оси H в точке советующей коэрцитивной силе Hc
, то можно вывести пропорцию:
Отсюда следует выражение для оценки величины остаточной индукции Br_gap в
случае введения зазора в магнитопровод:
где:
Br_max — величина остаточной индукции соответствующая индукции насыщения
Bsat;
µ — магнитная проницаемость магнитнопровода без зазора (эффективное значение относительной магнитной
проницаемости магнитопровода без зазора — Relative effective permeability, часто обозначается в datasheet
как µe);
µeff — эффективное значение магнитной проницаемости магнитнопровода с зазором.
Рисунок T.47 — Изменение хода петли гистерезиса при введении в магнитопровод немагнитного зазора.
Эффективная магнитная проницаемость сердечника с зазором μeff вычисляется по соотношению:
где:
μ – магнитная проницаемость материала сердечника;
lg – длина немагнитного зазора;
lav – длина магнитной линии магнитопровода.
Как правило, если принимается решение вводить зазор, то целевое значение эффективной проницаемости
μeff принимается в 2-10 раз меньше магнитной проницаемость материала сердечника μ :
При таком уровне уменьшения μ до μeff величина вводимого зазора незначительна и явлением
«выпучивания поля» можно пренебречь.
Длина зазора в этом случае вычисляется согласно выражению:
где:
lav – длина магнитной линии магнитопровода;
μeff – эффективная магнитная проницаемость сердечника с зазором;
μ – магнитная проницаемость материала сердечника.
Взаимосвязь габаритной мощности однотактного прямоходового трансформатора с его выходной
мощностью
Установим взаимосвязь между мощностью выходной (вторичной) обмотки и габаритной мощностью трансформатора.
Мощность обмотки определяется формой тока в ней. Форма тока в обмотках однотактного прямоходового
преобразователя в первом приближении имеет форму однополярных прямоугольных импульсов. В дальнейших расчетах
мы не будем учитывать рекуперационную обмотку, поскольку её мощность существенно меньше мощности силовых
обмоток.
Для двухобмоточного трансформатора однотактного прямоходового трансформатора габаритная мощность
трансформатора определяется по формуле:
Поскольку мощность в трансформаторе передается из первичной обмотки во вторичную обмотку то мощности обмоток
связаны между собой через КПД-трансформатора:
Отсюда соотношение габаритной мощность трансформатора можно представить в виде:
или:
где:
Pw2 – мощность вторичной обмотки;
ηT – КПД трансформатора.
Последовательность расчета трансформатора однотактного прямоходового преобразователя
Данный алгоритм расчета относится к расчету трансформаторов однотактных преобразователей прямого хода:
прямоходового одноключевого преобразователя, преобразователя «косой полумост».
1. Начальное определение типа магнитопровода и феррита
Определяем типы магнитопровода и феррита на основе исходных данных проектирования.
Рекомендации по выбору типа магнитопровода и феррита представлены в разделе «Конструктивные элементы
трансформатора и дросселя. Магнитопровод». Предварительный выбор магнитопровода и феррита необходим для
определения коэффициента заполнения окна сердечника медью k0 ,максимального значения индукции в
магнитопроводе Bmax и величины остаточной индукции Br входящих в формулу габаритной
мощности. Феррит выбирается исходя из компромисса «стоимость-технические характеристики». При этом выбранный
тип феррита менять нежелательно, поскольку это приведет к необходимости пересчета значения габаритной
мощности.
2. Расчет габаритного параметра трансформатора SCS0, оценка
целесообразности
введения немагнитного зазора и расчет его параметров
Определяем габаритный параметр трансформатора однотактного преобразователя SCS0:
где:
η – КПД трансформатора;
f – рабочая частота;
k0 – коэффициент заполнения окна сердечника медью;
kС – коэффициент заполнения сердечника;
Bmax – максимальное значение индукции в магнитопроводе;
Br – остаточная индукция магнитопровода;
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника.
j – максимальная плотность тока в обмотках (среднеквадратичное значение).
Габаритная мощность трансформатора PT является исходным параметром
расчета. В данном соотношении габаритная мощность трансформатора принимается равной максимальной входной
мощности PIN_max:
где:
Pw2 – мощность вторичной обмотки;
ηT – КПД трансформатора.
Коэффициент полезного действия трансформатора ηT принимается в
соответствии с мощностью трансформатора. В соответствии с [Эраносян О.А. Сетевые блоки питания с
высокочастотными преобразователями.— Л.: Энергоатомиздат. Лени игр. отд-ние, 1991,— 176 с: ил. 109 стр.],
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.] на начальной стадии расчета трансформатора ηT принимается в
соответствии с мощностью трансформатора (у Эраносяна – мощностью нагрузки):
— при PIN_max ≤ 10 Вт принимается ηT = 0,93;
— при 10 Вт < PIN_max ≤ 50 Вт принимается ηT = 0,95;
— при PIN_max > 50 Вт принимается ηT = 0,97.
Необходимо отметить, что это начальное приближение, необходимое для выполнения предварительного этапа
расчета.
Коэффициент заполнения окна сердечника медью k0 выбирается
в зависимости от типа используемого магнитопровода:
— для Ш-образного магнитопровода [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
в ряде случаев, в особенности, когда S0 представляет собой площадь окна сердечника дросселя уже с
учетом каркаса магнитопровода, то может быть выбран k0 вплоть до 0,28-0,4 — [McLyman C.
Transformer and inductor design handbook.2004].
— для кольцевого магнитопровода [Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет.
Учебное пособие. — М.: СОЛОН-ПРЕСС, 2008. — 448 с. — 57 стр.]:
В любом случае это является первым приближением и факт размещения обмотки проверяется последующим
конструктивным расчетом.
Коэффициент заполнения сердечника kС принимается равным 1 в
случае использования магнитопровода из феррита.
Максимальное значение индукции в магнитопроводе Bmax определяется
исходя из параметров используемого феррита и рабочей частоты. В первом приближении и в типовом случае
принимается в пределах 0,15-0,2 Тл.
Плотность тока в проводах обмотки j выбирается в зависимости от выходной мощности
источника в соответствии с таблицей T.8 [Эраносян О.А. Сетевые блоки питания с высокочастотными
преобразователями.— Л.: Энергоатомиздат. Лени игр. отд-ние, 1991,— 176 с: ил. 109 стр.].
Таблица T.8 – Максимально допустимая плотность тока в проводах обмотки при различной выходной мощности
источника
|
POUT_max , Вт |
1 — 7 | 8 — 15 | 16 — 40 | 41 — 100 | 101 – 200 |
| j, А/мм2 | 7 — 12 | 6 — 8 | 5 — 6 | 4 — 5 | 4 — 4,5 |
При POUT_max большей 200 Вт плотность тока может быть выбрана в пределах 3-4
А/мм2.
Остаточная индукция Br магнитопровода определяется исходя из
соотношения:
где:
Bmax – выбранное максимальное значение индукции в магнитопроводе;
Bsat — индукция насыщения материала магнитопровода;
Br_max — величина остаточной индукции соответствующая индукции насыщения
Bsat.
Величина максимального значения остаточной индукции феррита Br_max может
быть определена следующими способами:
— поиск численного значения Br_max в datasheet-ах на выбранный тип
ферромагнитного материала (обозначается в datasheet просто как Br);
— определение Br_max из приведенных в datasheet-ах кривых гистерезиса.
Необходимо отметить, что это определение не всегда получается точным по причине большого масштаба по оси
магнитной напряженности H в результате размер петли становится сопоставим с шириной линии графика. В
качестве примера на рисунке T.48 представлена петля гистерезиса популярного феррита N87 (согласно
datasheet). Оценочное значение Br_max для феррита N87 составляет примерно
160 мТл.
Рисунок T.48 — Петля гистерезиса феррита N87 согласно данным [datasheet EPCOS AG — Ferritesand
accessories
SIFERRIT material N87. September 2017]
Оценка целесообразности введения немагнитного зазора и расчет его параметров
Полученное значение остаточной индукции Br_max сравнивается с максимальным
значением индукции насыщения Bsat и принимается решение о целесообразности или нецелесообразности
введения немагнитного зазора. В случае если остаточная индукция Br_maxсоставляет
более 25-35% от значения максимальной индукции Bsat то для трансформаторов прямоходовых
преобразователей рекомендуется вводить в магнитопровод немагнитный зазор.В особенности это касается мощных
преобразователей с топологией «косой полумост». Если же значение Br_max
составляет меньше 25-35% от Bsat то решение о зазоре принимается исходя из технико-экономических
соображений конкретного случая.
В случае введения зазора в магнитопровод целевое значение эффективной проницаемости μeff
принимается в 2-10 раз меньше начальной магнитной проницаемости материала сердечника μ (при таком уровне
уменьшения μ до μeff величина вводимого зазора незначительна и явлением «выпучивания поля» можно
пренебречь):
где:
µ — магнитная проницаемость магнитнопровода без зазора (эффективное значение относительной магнитной
проницаемости магнитопровода без зазора — Relative effective permeability, часто обозначается в datasheet
как µe).
При введении зазора новая величина остаточной индукции Br_gap
пересчитывается по формуле:
где:
Br_max — величина остаточной индукции соответствующая индукции насыщения
Bsat;
µ — магнитная проницаемость магнитнопровода без зазора (эффективное значение относительной магнитной
проницаемости магнитопровода без зазора — Relative effective permeability, часто обозначается в datasheet
как µe);
µeff — эффективное значение магнитной проницаемости магнитнопровода с зазором.
При расчете габаритной мощности трансформатора с зазором используется новое скорректированное значение
остаточной индукции Br_gap. Далее при расчетах необходимо использовать это
значение остаточной индукции Br_gap , а также значение эффективной
магнитной проницаемости μeff .
3. Выбор конкретного типа магнитопровода и феррита
Выбор конкретной марки магнитопровода осуществляется в соответствии с рассчитанным параметром
ScS0 и конструктивными особенностями (формфактор, технологичность намотки,
электромагнитная совместимость, экономика и т.д.).
При этом в качестве площади поперечного сечения сердечника SС должна быть использована минимально
обеспечиваемая величина площани поперечного сечения (Minimum core cross section) – Amin, а не
Ae (Effective magnetic cross section). Все эти параметры указаны в datasheet-ах.
Определившись окончательно с конкретной маркой магнитопровода и феррита мы будем знать следующие
параметры:
S0 – площадь окна сердечника трансформатора;
SС – площадь поперечного сечения сердечника;
Bmax – максимальное значение индукции в магнитопроводе при выбранной частоте.
В случае введения немагнитного зазора его длина lg вычисляется согласно выражению:
где:
lav – длина магнитной линии выбранного типа магнитопровода;
μeff – эффективная магнитная проницаемость сердечника с зазором;
μ – магнитная проницаемость материала сердечника (определяется из datasheet на выбранный магнитопровод).
В случае если магнитопровод состоит из двух половинок, то мы имеем два зазора, длина каждого из них
составляет половину вычисленного значения немагнитного зазора lg.
4. Расчет числа витков первичной обмотки
Число витков первичной обмотки рассчитывается по формуле:
где:
qmax – относительная длительность импульса (максимальное значение);
VIN_max – напряжение на первичной обмотке трансформатора (максимальное
значение);
f – рабочая частота;
SС – площадь поперечного сечения сердечника;
kС – коэффициент заполнения сердечника;
Bmax – максимальное значение индукции в магнитопроводе;
Br – остаточная индукция магнитопровода (при введении в магнитопровод немагнитного зазора
используется величина Br_gap).
Относительная длительность импульса qmax рассчитывается как отношение
максимальной длительности импульса к периоду и может быть принята равной 0,5:
Напряжение на первичной обмотке трансформатора VIN принимается равным
максимальному входному напряжению преобразователя. При расчете преобразователей с широким диапазоном
входного напряжения используется максимальное значение относительной длительности импульса qmax и
максимальное значение напряжения VIN_max. Это условие обеспечивает
безопасную работу трансформатора преобразователя без выхода в область насыщения при переходных процессах или
при резком изменении напряжения. В установившемся режиме при увеличении напряжения коэффициент q будет
пропорционально уменьшаться и произведение qV останется неизменным.
5. Расчет выходного напряжения вторичной обмотки трансформатора
Выходное напряжение вторичной обмотки трансформатора V2 рассчитывается как сумма выходного
напряжения преобразователя и суммы падений напряжений на выходном выпрямителе и силовом дросселе:
где:
VOUT_max – выходное напряжение преобразователя (максимальное значение);
VVD_out – падение напряжения на диодах выходного выпрямителя;
VLf – падение напряжения на выходном силовом дросселе.
На первой итерации расчета можно использовать оценочные значения величин падений напряжения. Так в случае
использования кремниевого диода падение напряжение составляет 1,2 В, для диодов Шоттки – 0,5 В. При
использовании мостовой схемы выпрямления падение напряжения на диодах выходного выпрямителя равно удвоенному
падению напряжения на единичном диоде. В случае использования выпрямителя с отводом от средней точки падение
напряжения на диодах выходного выпрямителя равно падению напряжения на единичном диоде.
Падение напряжения на выходном силовом дросселе зависит от выходного тока и мощности преобразователя. В
качестве первого приближения может быть принята равной в пределах 2-5 % от выходного напряжения
преобразователя VOUT_max.
6. Расчет коэффициента трансформации
Коэффициент трансформации k рассчитывается как отношение выходного напряжения на вторичной обмотке
трансформатора V2 и напряжения прикладываемого к первичной обмотке, практически равному входному
напряжению VIN_min :
где:
V2 – напряжение на выходе вторичной обмотки;
VIN_min — напряжение, прикладываемое к первичной обмотке (минимальное
значение).
7. Расчет числа витков вторичной обмотки
Число витков во вторичной обмотке N2 рассчитываются по соотношению:
где:
N1 – число витков первичной обмотки;
k — коэффициент трансформации.
8. Расчет числа витков рекуперационной обмотки
Рассчитываем число витков рекуперационной обмотки Nr при её наличии в конструкции трансформатора.
Число витков рекуперационной обмотки Nr принимается равным числу витков первичной обмотки:
Рекуперационная обмотка используется в трансформаторе одноключевого однотактного преобразователя. В
однотактом двухключевом преобразователе типа «косой полумост» рекуперационная обмотка не нужна.
9. Расчет индуктивности намагничивания первичной обмотки трансформатора
Индуктивность намагничивания первичной обмотки трансформатора L0 рассчитывается по соотношению:
где:
µ0 – магнитная постоянная;
µ – магнитная проницаемость материала магнитопровода (при введении зазора используется μeff –
эффективная магнитная проницаемость сердечника с зазором);
SС – площадь сечения магнитопровода;
lav – эффективная длина средней линии магнитопровода;
N1 – число витков первичной обмотки.
10. Расчет токов первичной обмотки трансформатора
Амплитудное значение тока первичной обмотки
Амплитудное значение тока первичной обмотки определяется выражением:
где:
k — коэффициент трансформации;
IOUT_max – выходной ток преобразователя (используется максимальное значение тока);
∆ILf_max – максимальная величина пульсаций тока дросселя (входное значение
для расчета трансформатора);
q – относительная длительность импульса (максимальное значение);
VIN_max — напряжение, прикладываемое к первичной обмотке (максимальное
значение);
f – рабочая частота;
L0 — индуктивность намагничивания первичной обмотки трансформатора.
Среднее значение тока первичной обмотки
Среднее значение тока первичной обмотки определяется выражением:
где:
q – относительная длительность импульса (максимальное значение);
k — коэффициент трансформации;
IOUT_max – выходной ток преобразователя.
Для случая преобразователя типа «косой полумост» через обмотку еще дополнительно протекает рекуперационный
ток и выражение для среднего значения тока имеет вид:
Среднеквадратичное значение тока первичной обмотки
Среднеквадратичное значение тока первичной обмотки вычисляется по формуле (см. раздел «Резисторы»):
где:
q – относительная длительность импульса (максимальное значение);
Iw1_max, Iw1_min — максимальное и
минимальное значения вычисляются по соотношениям:
Подробный вывод выражений для расчета токов обмоток трансформатора двухтактного преобразователя прямого хода
представлен в разделе «Однотактный прямоходовый преобразователь».
11. Расчет токов вторичной обмотки трансформатора
Амплитудное значение тока вторичной обмотки
Амплитудное значение тока вторичной обмотки определяется выражением:
где:
IOUT_max – выходной ток преобразователя (максимальное значение);
∆ILf_max – максимальная величина пульсаций тока дросселя (входное значение
для расчета трансформатора).
Среднее значение тока вторичной обмотки
Среднее значение тока вторичной обмотки определяется выражением:
В случае наличия двух полуобмоток, итоговое выражение имеет вид:
Среднеквадратичное значение тока вторичной обмотки
sСреднеквадратичное значение тока вторичной обмотки имеющего форму прямоугольной трапеции
вычисляется аналогично первичной обмотке и определяется выражением (см. раздел «Резисторы»):
где:
q – относительная длительность импульса (максимальное значение);
Iw2_max, Iw2_min — максимальное и
минимальное значения вычисляются по соотношениям:
где:
IOUT_max – выходной ток преобразователя (максимальное значение);
ΔILf_max – пульсация тока дросселя.
12. Расчет токов рекуперационной обмотки трансформатора
Амплитудное значение тока рекуперационной обмотки
Амплитудное значение тока рекуперационной обмотки рассчитывается по выражению:
где:
L0 – индуктивность намагничивания (фактически индуктивность первичной обмотки);
VIN_max – напряжение, приложенное к первичной обмотке (максимальное
значение);
q – коэффициент заполнения.
Среднеквадратичное значение тока рекуперационной обмотки
Среднеквадратичное значение тока рекуперационной обмотки Iwr_rms
рассчитывается по выражению:
где:
Iwr_max – амплитудное значение тока рекуперационной обмотки;
q – коэффициент заполнения.
13. Расчет конструкции трансформатора
В результате выполненного последовательного расчета по шагам 1-10 мы получаем следующие параметры:
— конкретный тип магнитопровода c конкретными геометрическими параметрами;
— число витков первичной, вторичной обмоток N1 , N2. и при использовании –
рекуперационной обмотки Nr .
Далее после получения этих базовых параметров выполняется детальный конструктивный расчет. Последовательность
расчета представлена ниже.
13.1 Расчёт параметров проводов обмоток
Минимальная площадь поперечного сечения обмоток (по меди) рассчитывается по соотношениям:
Sw1_Cu – площадь поперечного сечения проводника первичной обмотки;
Sw2_Cu – площадь поперечного сечения проводника вторичной обмотки;
Swr_Cu – площадь поперечного сечения проводника рекуперационной обмотки;
jmax – выбранное максимальное значение среднеквадратичной плотности тока в обмотках.
Для однотактных трансформаторов, в отличие от двухтактных, при расчете сечения провода необходимо
использовать именно среднеквадратичное (в крайнем случае — среднее) значение тока. Упрощенный расчет с
использованием максимального значения приведет к значительной ошибке.
Далее вычисляется диаметр проводов (по меди) для выполнения обмоток:
13.2 Выбор типа провода обмотки и определение диаметра и площади поперечного сечения проводника с
изоляцией
На основании вычисленного диаметра провода (по меди) выбирается ближайший диаметр провода из номенклатуры
диаметров выбранного типа провода (ПЭЛ, ПЭТВ и т.д.). Округление производится в большую сторону.
В соответствии с выбранным типом провода пересчитывается площади поперечного сечения выбранного типа провода
по меди по формулам:
Далее в соответствии со справочным листком на выбранный тип обмоточного провода определяется его диаметр с
изоляцией для первичной и вторичной обмоток dw1_ins ,
dw2_insи, при использовании рекуперационной обмотки,
dwr_ins:
13.3 Расчёт средней длины витка обмоток трансформатора
Ш- и П- образные, чашеобразные магнитопроводы
Для Ш- и П- образных магнитопроводов с прямоугольным сечением магнитопроводасредние длины
витков рассчитываются по соотношениям:
для первичной обмотки:
где:
a, b – геометрические параметры характеризующие сечение каркаса магнитопровода (см. рисунок T.49);
tw1 – толщина обмотки, вычисляемая по соотношению:
здесь:
функция (ceiling) — округление до большего целого;
hcm – высота обмотки, определяется высотой каркаса магнитопровода;
Nw1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) первичной обмотки, зависящий от толщины
провода (таблица T.7).
Таблица T.7 — Коэффициент укладки в зависимости от диаметра провода для трансформаторов кольцевой конструкции
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.]
| Диаметр провода с изоляцией, мм | 0,08 – 0,31 | 0,31-0,5 | 0,5-2,1 |
| Коэффициент укладки | 0,8-0,75 | 0,75-0,7 | 0,65-0,6 |
Рисунок T.49 — К определению средней длины витка для Ш- и П- образных магнитопроводов
для вторичной обмотки:
где:
lw1_last — длина внешнего витка первичной обмотки, вычисляемая по
соотношению:
tw2 – толщина вторичной обмотки, вычисляемая по соотношению:
здесь:
Nw2 – число витков в вторичной обмотке;
kw2_l – коэффициент укладки (laying) вторичной обмотки, зависящий от толщины
провода (таблица T.7).
Для Ш- и П- образных, чашеобразных и других магнитопроводов с круглым сечением центрального стержня
магнитопровода средняя длина витка рассчитывается по следующим соотношениям:
для первичной обмотки:
где:
R – радиус каркаса магнитопровода;
tw1 – толщина первичной обмотки, вычисляемая по соотношению:
где:
функция (ceiling) — округление до большего целого;
hcm – высота обмотки, определяется высотой каркаса магнитопровода;
Nw1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода
(таблица T.7).
для вторичной обмотки:
где:
lw1_last — длина внешнего витка первичной обмотки, вычисляемая по
соотношению:
tw2 – толщина вторичной обмотки, вычисляемая по соотношению:
здесь:
Nw2 – число витков в вторичной обмотке;
kw2_l – коэффициент укладки (laying) вторичной обмотки, зависящий от толщины
провода (таблица T.7).
Тороидальные магнитопроводы
Для тороидальных магнитопроводов расчет среднего витка осуществляется по соотношениям:
для первичной обмотки:
где:
wm — ширина магнитопровода;
hm — высота магнитопровода;
tw1_int — толщина внутреннего слоя первичной обмотки;
tw1_ext — толщина внешнего слоя первичной обмотки.
tw1_int и tw1_ext определяются по
соотношениям:
здесь:
функция (ceiling) — округление до большего целого;
Rint – внутренний радиус тора;
Rext – внешний радиус тора;
dw1_ins — диаметр обмоточного провод первичной обмотки с изоляцией;
Nw1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода
(таблица T.7).
Рисунок T.50 — К определению средней длины витка тороидальных магнитопроводов. (показаны обозначения
только первичной обмотки)
для вторичной обмотки:
где:
lw1_last — длина внешнего витка первичной обмотки, вычисляемая по
соотношению:
tw1_int и tw1_ext определяются по
соотношениям:
здесь:
dw2_ins — диаметр обмоточного провод первичной обмотки с изоляцией;
Nw2 – число витков в первичной обмотке;
kw2_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода
(таблица T.7).
Средняя длина витка рекуперционной обмотки
Поскольку рекуперционная обмотка имеет малую толщину, располагается между первичной и вторичной обмотками и,
как правило, укладывается в один слой и, то можно считать, что средняя длина витка рекуперционной обмотки
lwr_t_av равна длине внешнего витка первичной обмотки
lw1_last:
Это применимо для трансформаторов, выполняемых на всех типах магнитопроводов.
13.4 Определение длин проводников первичной, вторичной и рекуперационной обмоток
Длина обмоток определяется как произведение средней длины витка на число витков:
Полученная величина определяет, сколько провода нужно отмерить на обмотки трансформатора.
13.5 Конструктивный расчет структуры обмотки трансформатора, фактическая проверка возможности
размещения обмотки
Использование некоторой предопределенной величины коэффициента заполнения окна не дает однозначной гарантии
размещения обмотки в окне магнитопровода. Поэтому необходима проверка конструктивного условия размещения
обмотки в окне магнитопровода. Кроме этого, может быть неоптимальное использование окна магнитопровода, если
останется слишком много свободного места в окне обмотки.
Для конструктивного расчета структуры обмотки трансформатора выполняется следующая последовательность
действий:
Ш- и П- образные и чашеобразные магнитопроводы
— определяется средняя ширина намоточного слоя hlav. Она равна высоте каркаса магнитопровода
hcm (рисунок T.51):
Высота каркаса магнитопровода hcm определяется из справочных данных (datasheet) на магнитопровод.
В ряде случаев, например при использовании секционирования обмотки, в качестве высоты каркаса hcm
используется высота секции.
Рисунок T.51 — К расчету конструкции обмотки трансформатора преобразователя
— определяется число витков в одном слое для первичной и вторичной обмоток
Nw1_l и Nw2_l :
где:
операция (floor) – округление до меньшего целого;
hcm — высота каркаса магнитопровода;
dw1_ins , dw2_ins — диаметры проводников
обмоток с изоляцией;
kw1_l , kw2_l – коэффициенты укладки
(laying), зависящие от толщины провода (таблица T.7).
— рассчитывается общее число слоев для первичной и вторичной обмоток Wl1 ,
Wl2:
где:
(ceiling) — округление до большего целого;
Nw1, Nw2 — число витков в первичной и вторично обмотках,
соответственно;
Nw1_l , Nw2_l — число витков в одном слое
первичной и вторичной обмоток, соответственно.
— рассчитываются толщины обмоток трансформатора Hw1 , Hw2 ,
Hwr:
для первичной обмотки:
где:
Δw1l – толщина межслоевой изоляции первичной обмотки;
Wl1 — число слоев в первичной обмотке;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
для вторичной обмотки:
где:
Δw2l – толщина межслоевой изоляции вторичной обмотки;
Wl2 — число слоев в вторичной обмотке;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
для рекуперационной обмотки:
Hwr – толщина слоя рекуперационной обмотки трансформатора, определется по соотношению:
здесь:
Δrl – толщина изоляции рекуперационной обмотки;
dwr_ins – диаметр провода рекуперационной обмотки с изоляцией.
В случае если межслоевой изоляции не предусмотрено, то величины Δ1l и
Δ2lпринимаются равными нулю (в реальности, при плотно намотке за счет укладывания
витков следующего слоя в пазы слоя предыдущего толщина обмотки может быть несколько меньше).
— рассчитывается общая толщина «пирога» обмотки HΣ:
где:
Δ(1-2)l — толщины межобмоточной изоляции;
Δc — толщина каркаса (расстояние между поверхностью каркаса и магнитопроводом);
Δsurf — толщина слоя внешней изоляции обмотки;
Hw1 , Hw2 , Hwr — толщины обмоток трансформатора.
— проверяется условие фактического размещения всех конструктивных элементов «пирога» обмоток в окне
магнитопровода:
где:
HΣ — суммарная толщина «пирога» обмоток;
HM – ширина окна магнитопровода.
В случае невыполнения данного условия необходимо использовать другой магнитопровод и повторить процедуру
расчета (пункты 3 — 13).
Тороидальные магнитопроводы
В случае тороидальных магнитопроводов ширина намоточного слоя hl уменьшается по мере намотки. Поэтому все
сложнее.
Рисунок T.52 — К расчету конструкции обмоток тороидального трансформатора: Dint – внутренний
диаметр тора магнитопровода с учетом слоя изоляции, D0 — остаточный технологический диаметр.
— рассчитывается число слоев первичной обмотки Wl1 по выражению:
где:
Nw1 – число витков первичной обмотки;
Nl_1 – число витков первого слоя первичной обмотки, определяемое из выражения:
здесь:
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции);
Δw1l – толщина межслоевой изоляции первичной обмотки;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
kw1_l – коэффициент укладки обмотки, зависящий от толщины провода (таблица
T.7).
ΔNw1_l — уменьшение числа витков от слоя к слою определяется выражением:
где:
операция (floor) – округление до меньшего целого;
Δhlw1 — уменьшение ширины намоточного слоя от слоя к слою:
Полученное значение Wl1, как правило, будет дробным, и число слоев первичной обмотки
определяется округлением полученного числа до большего целого (ceiling):
— рассчитывается толщина первичной обмотки Hw1 по соотношению, учитывающему толщину
межслоевой изоляции [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
где:
Δw1l – толщина межслоевой изоляции первичной обмотки;
Wl1 — число слоев в первичной обмотке;
dw1 ins – диаметр провода первичной обмотки с изоляцией.
— рассчитывается число слоев вторичной обмотки Wl2 по выражению:
где:
Nw2 – число витков вторичной обмотки;
Nl_2 – число витков первого слоя вторичной обмотки, определяемое из выражения:
здесь:
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции);
Δw2l – толщина межслоевой изоляции вторичной обмотки;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
kw2_l – коэффициент укладки обмотки, зависящий от толщины провода (таблица
T.7);
Hw1 — толщина первичной обмотки.
ΔNw2_l — уменьшение числа витков от слоя к слою для вторичной обмотки
определяется выражением:
где:
операция (floor) – округление до меньшего целого;
Δhlw2 — уменьшение ширины намоточного слоя от слоя к слою:
Полученное значение Wl2, как правило, будет дробным, и число слоев первичной обмотки
определяется округлением полученного числа до большего целого (ceiling):
— рассчитывается толщина вторичной обмотки Hw2 по соотношению, учитывающему толщину
межслоевой изоляции [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
где:
Δw2l – толщина межслоевой изоляции вторичной обмотки;
Wl2 — число слоев в вторичной обмотке;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
Расчитывается толщина слоя рекуперационной обмотки трансформатора Hwr, определяемая по
соотношению:
здесь:
Δrl – толщина изоляции рекуперационной обмотки;
dwr_ins – диаметр провода рекуперационной обмотки с изоляцией.
— рассчитывается суммарная толщина «пирога» намотки HΣ:
где:
Δ(1-2)l — толщины межобмоточной изоляции
Δsurf — толщина слоя внешней изоляции обмотки;
Hw1 , Hw2 , Hwr — толщины обмоток трансформатора.
— проверяется условие фактического размещения обмотки в окне магнитопровода:
где:
HΣ — суммарная толщина «пирога» намотки;
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции) который фактически определяет
ширину окна магнитопровода;
D0 — остаточный диаметр внутри тороидального трансформатора (технологический).
В случае невыполнения данного условия необходимо использовать другой магнитопровод и повторить процедуру
расчета (пункты 3-13).
14. Расчет сопротивления обмоток трансформатора
Электрическое сопротивление обмоток трансформатора Rw1 и Rw2
рассчитывается по формуле для расчета омического сопротивления протяженного проводника:
где:
ρ – удельное сопротивление материала провода (для меди — 0,0175 Ом·мм2 м-1 );
lw1 , lw2 , lwr – длины проводов первичной, вторичной
и рекуперационной обмоток соответственно;
Sw1_Cu , Sw2_Cu ,
Swr_Cu – площади поперечного сечения выбранного типа провода (по
меди).
15. Расчет омических потерь в обмотках
Суммарные потери на омическом сопротивлении обмоток определяются по формулам:
где:
Rw1 , Rw2 , Rwr — сопротивление первичной, вторичной и
рекуперационной обмоток на постоянном токе;
kg1 , kg2 , kgr – коэффициенты добавочных потерь за
счет скин-эффекта и эффекта близости в обмотках;
Iw1_rms ,
Iw2_rms ,Iwr_rms –
среднеквадратичные значение тока в первичной, вторичной и рекуперационной обмотках соответственно.
NB: При высоких рабочих температурах трансформатора необходимо учитывать влияние температуры на удельное
сопротивление проводников обмоток. При высоких частотах необходимо оценить увеличение эффективного
сопротивления обмоток в результате действия скин-эффекта (см. пункт «Влияние скин-эффекта на сопротивление
обмоток при высоких частотах» настоящего раздела).
16. Оценка уровня потерь в магнитопроводе
Существуют три способа определения потерь в магнитопроводе:
— рассчитать по формуле (при наличии аппроксимацонных коэффициентов);
— определить по графику из datasheet;
— определить экспериментально.
Расчёт по аппроксимацонным коэффициентам
Тепловая энергия, выделяемая в магнитопроводе определяется режимом работы дросселя — частотой работы f и
уровнем магнитной индукции Bmax. Для расчета потерь в магнитопроводе Pferrit
используют следующее аппроксимирующее выражение [Optimum designof a high-power, high-frequency transformer.
R. Petkov. IEEE Transactions on Power Electronics (Volume: 11, Issue: 1, Jan 1996)]:
где:
f – частота;
B – индукция;
K1, K2, K3 – аппроксимационные коэффициенты, определенные для каждого конкретного типа феррита.
Определение по графику относительных потерь из datasheet
Для определения потерь в магнитопроводе можно использовать соотношение:
где:
Pvferrit — мощность потерь на единицу объема, являющейся функцией температуры, магнитной индукции
и частоты. Графики данной зависимости представлены в справочных листах (datasheet) на каждый ферромагнитный
материал магнитопровода;
Vm – объем магнитопровода (приводится в справочных листах (datasheet).
Мощность потерь на единицу объема определяется типом феррита и приводится в справочных данных на конкретный
тип магнитного материала.
Рисунок T.53 — Зависимость мощности потерь от частоты при различных значениях индукции магнитного поля и
температуре для феррита N87 [Ferrites and accessories. SIFERRITmaterial N87, EPCOS AG 2006]
Экспериментальное определение
В случае отсутствия данных для расчета остается путь экспериментального определения потерь.
17. Расчет суммарных потерь
Суммарные потери трансформатора Ptotal_loss складываются из омических потерь
обмотки и потерь магнитопровода:
где:
Pwinding1 , Pwinding1 , Pwindingr – омические потери в
первичной, вторичной и рекуперационной обмотках соответственно;
Pferrit – потери в магнитопроводе.
18. Расчет температурного режима трансформатора и оптимизация
Установившаяся температура перегрева трансформатора относительно окружающей среды ∆T (дельта перегрева)
приблизительно оценивается по соотношению [McLyman C. Transformer and inductor design handbook.2004]:
где:
Ptotal loss – мощность суммарных потерь в трансформаторе;
ST – суммарная эффективная площадь охлаждения трансформатора (в см2).
Если полученное значение температуры нагрева трансформатора лежит в пределах 50-80°С, то расчет
трансформатора можно считать законченным. Если полученное значение превышает 80°С, то имеет смысл
использовать магнитопровод большего размера.
Если в результате расчета уровень перегрева трансформатора ΔT будет значительно меньше максимально
допустимого:
то имеет смысл использовать оптимизировать конструкцию трансформатора с целью уменьшения стоимости и
массогабаритных показателей — уменьшить формфактор магнитопровода и варьировать плотность тока, размах
индукции (можно делать одновременно с повышением частоты).
Кроме того, если при допустимом уровне нагрева трансформатора получится, что мощность, выделяемая на активном
сопротивлении обмоток существенной меньше, чем в феррите магнитопровода:
то имеет смысл использовать большую плотность тока, протекающего через обмотки и повторить расчет по пунктам
2-18.
Для трансформаторов больших габаритов (с рассеваемой площадью более 1000 см2) установившаяся
температура нагрева трансформатора относительно окружающей среды ∆T (дельта перегрева) оценивается по
соотношению [В.Е. Китаев, А.А. Бокуняев. Проектирование источников электропитания устройств связи. Учеб.
пособие.- М.: Связь,1972.- 200 с.]:
где:
Ptotal_loss – мощность суммарных потерь в трансформаторе;
αT – коэффициент теплоотдачи, зависящий от множества факторов (материал трансформатора,
конструктивное исполнение, температуры окружающей среды и т.д.). Для практических расчетов принимается
равным: 11-13 Вт/м2 °С.
ST – суммарная площадь охлаждения трансформатора.
Необходимо понимать, что оптимизация расчета трансформатора проводится с учетом целевых приоритетов:
Приоритет 1 — Малые массогабаритные параметры трансформатора и, соответственно, стоимость. В этом случае
необходимо провести расчет всех параметров трансформатора с целью обеспечения (но не превышения) заданного
уровня перегрева и минимальной стоимости/массогабаритных параметров. В этом случае плотность тока, размах
индукции итерационно увеличиваются;
Приоритет 2 — Высокий КПД. В этом случае необходимо задаться максимальными массогабаритными параметрами и с
учетом этого варьируя параметры трансформатора (индукция, плотность тока и т.д.) провести расчет всех
параметров трансформатора с целью минимизации мощности потерь. В этом случае плотность тока, размах индукции
итерационно уменьшаются;
Трансформатор обратноходового преобразователя
Трансформатор обратноходового преобразователя, по сути, представляет собой многообмоточный дроссель.
Индуктивность первичной обмотки играет роль накопителя энергии, которая «складируется» в магнитопрововоде
(и, забегая вперед, в немагнитном зазоре). Передача накопленной энергии осуществляется через вторичные
обмотки, которые расположены на этом же магнитопроводе. Таким образом, Flyback-трансформатор представляет
собой несколько магнитно-связанных индуктивностей, что и отличает его от обычного трансформатора. Хотя
конструктивно он выглядит практически аналогично.
Поскольку накопление энергии осуществляется через первичную обмотку, то это формулирует основное исходное
требование методики проектирования: первичная обмотка должна иметь заданную величину индуктивности
L1, которая должна работать без насыщения при заданном максимальном токе
Iw1_max. При этом должны быть обеспечены минимальные габариты и стоимость и
потери.
Трансформатор обратноходового преобразователя может работать в двух режимах:
— режим прерывистых токов;
— режим непрерывных токов.
Подробно особенности работы и сопоставление обоих режимов дано в специализированном разделе «Обратноходовый
преобразователь». Резюмируя можно сказать, что режим прерывистых токов имеет ряд преимуществ, прежде всего –
позволяет использовать меньшие размеры трансформатора.
При выборе материала трансформатора обратноходового преобразователя целесообразно учитывать ряд факторов
[Magnetics Design Handbook from TI by Lloyd H. Dixon. Section 5. Inductor and Flyback. Transformer Design.
Texas Instruments. 2001. http://www.ti.com/lit/ml/slup127/slup127.pdf]:
— при работе преобразователя в непрерывном режиме необходимо чтобы присутствовал некоторый запас по индукции
насыщения, поскольку к началу нового цикла заряда магнитопровод остается подмагниченным. Целесообразно
использовать материалы с большей индуктивностью насыщения – аморфное железо, Kool-mu, пермаллой.
При выборе формы магнитопровода трансформатора обратноходового преобразователя целесообразно использовать
магнитопровод обеспечивающий хорошее охлаждение обмоток. И в конструкции использовать минимальное число
слоев.
EC, ETD, LP, EE – типы магнитопровода являются подходящими для трансформатора flyback-преобразователя. Так же
могут быть использованы кольцевые магнитопроводы с распределенным зазором. PQ и чашкообразные сердечники не
рекомендуется использовать по причине того, что соотношение размера магнитопровода и окна магнитопровода не
является оптимальным для обратноходовых преобразователей [Magnetics Design Handbook from TI byLloyd H.
Dixon. Section 5. Inductor and Flyback. Transformer Design. Texas Instruments. 2001.
http://www.ti.com/lit/ml/slup127/slup127.pdf].
Методика проектирования трансформатора обратноходового преобразователя и соотношение для расчета габаритного
параметра даны в разделе «Индуктивность» — пункт «Трансформатор обратноходового преобразователя».
Как рассчитать индуктивность силового трансформатора, формулы и примеры
Трансформатор, как элемент радиотехники и электротехники, работает на основе электромагнитной индукции. Говоря об индуктивности трансформатора, имеют в виду индуктивность обмоток и взаимоиндукцию между ними.
Каждая из обмоток представляет некоторое количество витков провода, намотанных на ферромагнитный сердечник, то есть обыкновенную катушку индуктивности.
Трудность в определении параметров катушки заключается в том, что они изменяются в зависимости от нескольких параметров и их сочетания:
- токи в обмотках;
- уровень намагниченности магнитопровода;
- магнитные характеристики сердечника;
- взаимодействие между соседними обмотками;
- наличия постоянной составляющей тока.
Конструкция и принцип действия силового трансформатора
В основе конструкции любого трансформатора находятся следующие элементы:
- Сердечник из ферромагнитного материала.
- Первичная и вторичные обмотки. В случае автотрансформатора одна обмотка выполняет обе функции.
В сетях переменного тока промышленной частоты (50 или 60Гц) в качестве ферромагнитного материала используется сталь, обработанная по специальной технологии. На высоких частотах часто делаются трансформаторы без сердечника, поскольку для нормальной работы достаточно взаимосвязи межу катушками.
- в первичной обмотке, подключенной в цепь питания, создается переменное электрическое поле;
- под действием поля первичной катушки в сердечнике создается переменное магнитное поле;
- в силу электромагнитной индукции во всех обмотках наблюдается ЭДС индукции.
ЭДС индукции в первичной обмотке направлена противоположно поданному напряжению, поэтому они взаимно компенсируются. В результате, при отсутствии нагрузки через первичную обмотку протекает сравнительно небольшой ток холостого хода.
Наличие тока вторичной цепи аналогично вызывает дополнительный магнитный поток, а он – ЭДС самоиндукции в первичное катушке. В результате компенсация первичного напряжения снижается и растет ток в первичной цепи.
Физическое понятие индуктивности обмоток
Индуктивность представляет собой коэффициент пропорциональности между током, создаваемым замкнутым электрическим контуром, и магнитным потоком, который создается этим контуром.
Более понятной формулировкой будет та, которая говорит о величине ЭДС самоиндукции в замкнутом контуре, которая возникает при изменении силы тока за единицу времени. То есть, понятие индуктивности справедливо для изменяющегося тока.
При постоянном токе говорить об индуктивности бессмысленно.
В идеальном трансформаторе все электромагнитное поле, создаваемое обмотками, замкнуто в магнитном сердечнике. В реальных конструкциях существует поле рассеяния, величина которого зависит от способа выполнения катушки и конструктивных особенностей сердечника. Чем больше толщина намотки, тем большая часть электромагнитного поля замыкается вне магнитопровода.
Этому способствует также качество сборки магнитопровода. Зазоры между пластинами способствуют резкому увеличению рассеивания. В связи с этим наилучшими свойствами обладают О-образные сердечники.
Формулы и измерение
Формулы для расчета индуктивности катушек довольно сложны и имеет различный вид для различных типов исполнения обмоток:
- линейный проводник;
- одновитковая катушка;
- плоская катушка;
- соленоидальная обмотка;
- тороидальная форма.
Наибольшие сложности возникают при расчетах многовитковых многослойных катушек, то есть тех, которые составляют обмотку трансформаторов.
В подавляющем большинстве случаев точный расчет невозможен, поэтому приходится использовать примерные данные и уточнять их после проведения измерений.
Формулы для расчета индуктивности трансформатора основаны на расчетах соленоида:
µ – магнитная проницаемость сердечника;
Для измерения индуктивности существует несколько методик и приборов, созданных на их основе. В большинстве случаев измерение производится путем вычислений индуктивного сопротивления катушки при подаче образцового напряжения заданной частоты и измеренного значения тока через обмотку.
В специализированных приборах вычисления производятся автоматически, и пользователь только считывает показания шкалы прибора, выраженные в единицах индуктивности – Гн, мГн или мкГн.
Как измерить в домашних условиях
Приборы для непосредственного измерения индуктивности имеют высокую стоимость и редко используются в домашних условиях. С приемлемой точностью результаты можно получить, используя обычные приборы для измерения переменного тока: амперметр и вольтметр. Также необходим омметр.
Порядок действий следующий:
- При помощи омметра определяют активное сопротивление обмотки R.
- Подключают трансформатор последовательно с амперметром в сеть.
- Параллельно обмотке подключают вольтметр.
- По показаниям приборов определяют полное сопротивление трансформатора: Z=U/I
- Индуктивное сопротивление находят, вычитая из полного сопротивления активное: XL=Z-R
- Индуктивность определяется по формуле: L=XL/(2πf), где π – число пи 3.14, f – частота измерений.
Как правило, активное сопротивление намотки значительно (на несколько порядков) меньше индуктивного, поэтому можно его не учитывать. Именно поэтому, включение трансформатора в цепь постоянного напряжения вызывает короткое замыкание. Ток обмотки при этом будет ограничиваться только активным сопротивлением.
Пример расчета
К примеру, требуется рассчитать индуктивность первичной обмотки трансформатора питания. Путем измерений определено:
- Сопротивление обмотки 3 Ом.
- Напряжение сети 220 В.
- Частота питающего напряжения 50 Гц.
- Ток холостого хода 05 А.
Активное сопротивление меньше полного в 10000 раз и его можно не учитывать.
Источник
Методика и формулы для расчета трансформаторного блока питания
Как рассчитать мощность трансформатора
Особенность работы стандартного трансформатора представлена процессом преобразования электроэнергии переменного тока в показатели переменного магнитного поля и наоборот. Самостоятельный расчет трансформаторной мощности может быть выполнен в соответствии с сечением сердечника и в зависимости от уровня нагрузки.
Расчет обмотки преобразователя напряжения и его мощности
По сечению сердечника
Электромагнитный аппарат имеет сердечник с парой проводов или несколькими обмотками. Такая составляющая часть прибора, отвечает за активное индукционное повышение уровня магнитного поля. Кроме всего прочего, устройство способствует эффективной передаче энергии с первичной обмотки на вторичную, посредством магнитного поля, которое концентрируется во внутренней части сердечника.
Параметрами сердечника определяются показатели габаритной трансформаторной мощности, которая превышает электрическую.
Расчетная формула такой взаимосвязи:
- Sо — показатели площади окна сердечника;
- Sс — площадь поперечного сечения сердечника;
- Рг — габаритная мощность;
- Bс — магнитная индукция внутри сердечника;
- А — токовая плотность в проводниках на обмотках;
- F — показатели частоты переменного тока;
- Ко — коэффициент наполненности окна;
- Кс — коэффициент наполненности сердечника.
Показатели трансформаторной мощности равны уровню нагрузки на вторичной обмотке и потребляемой мощности из сети на первичной обмотке.
Самые распространенные разновидности трансформаторов производятся с применением Ш —образного и П — образного сердечников.
По нагрузке
При выборе трансформатора учитывается несколько основных параметров, представленных:
- категорией электрического снабжения;
- перегрузочной способностью;
- шкалой стандартных мощностей приборов;
- графиком нагрузочного распределения.
В настоящее время типовая мощность трансформатора стандартизирована.
Чтобы выполнить расчет присоединенной к трансформаторному прибору мощности, необходимо собрать и проанализировать данные обо всех подключаемых потребителях. Например, при наличии чисто активной нагрузки, представленной лампами накаливания или ТЭНами, достаточно применять трансформаторы с показателями мощности на уровне 250 кВА.
В системах электрического снабжения показатели трансформаторной мощности приборов должны позволить обеспечивать стабильное питание всех потребителей электроэнергии.
СДЕЛАЕМ УПРОЩЕННЫЙ РАСЧЕТ ТРАНСФОРМАТОРА 220/36 ВОЛЬТ.
Мощность во вторичной цепи: Р_2 = U_2 · I_2 = 60
ватт
Где:Р_2
– мощность на выходе трансформатора, нами задана 60 ватт
;
U
_2
— напряжение на выходе трансформатора, нами задано 36 вольт
;
I
_2
— ток во вторичной цепи, в нагрузке.
КПД трансформатора мощностью до 100 ватт
обычно равно не более η = 0,8
.КПД определяет, какая часть мощности потребляемой от сети идет в нагрузку. Оставшаяся часть идет на нагрев проводов и сердечника. Эта мощность безвозвратно теряется.
Определим мощность потребляемую трансформатором от сети с учетом потерь:
Р_1 = Р_2 / η = 60 / 0,8 = 75 ватт
.
Мощность передается из первичной обмотки во вторичную через магнитный поток в магнитопроводе.Поэтому от значения
Р_1
, мощности потребляемой от сети 220
вольт,
зависит площадь поперечного сечения магнитопровода S
.
Магнитопровод – это сердечник Ш – образной или О – образной формы, набранный из листов трансформаторной стали. На сердечнике будут располагаться первичная и вторичная обмотки провода.
Площадь поперечного сечения магнитопровода рассчитывается по формуле:
Где:S
— площадь в квадратных сантиметрах,
P
_1 — мощность первичной сети в ваттах.
S = 1,2 · √75 = 1,2 · 8,66 = 10,4 см².
По значению S
определяется число витков w
на один вольт по формуле:
В нашем случае площадь сечения сердечника равна S = 10,4 см.кв.
w = 50/10,4 = 4,8
витка на 1 вольт.
Рассчитаем число витков в первичной и вторичной обмотках.
Число витков в первичной обмотке на 220 вольт:
W1 = U_1 · w = 220 · 4.8 = 1056 витка.
Число витков во вторичной обмотке на 36 вольт:
W2 = U_2 · w = 36 · 4,8 = 172.8 витков
,
В режиме нагрузки может быть заметная потеря части напряжения на активном сопротивлении провода вторичной обмотки. Поэтому для них рекомендуется число витков брать на 5-10 % больше рассчитанного. Возьмем W2 = 180 витков.
Величина тока в первичной обмотке трансформатора:
I_1 = P_1/U_1 = 75/220 = 0,34 ампера
.
Ток во вторичной обмотке трансформатора:
I_2 = P_2/U_2 = 60/36 = 1,67 ампера.
Диаметры проводов первичной и вторичной обмоток определяются по значениям токов в них исходя из допустимой плотности тока, количества ампер на 1 квадратный миллиметр площади проводника. Для трансформаторов плотность тока,
для медного провода,
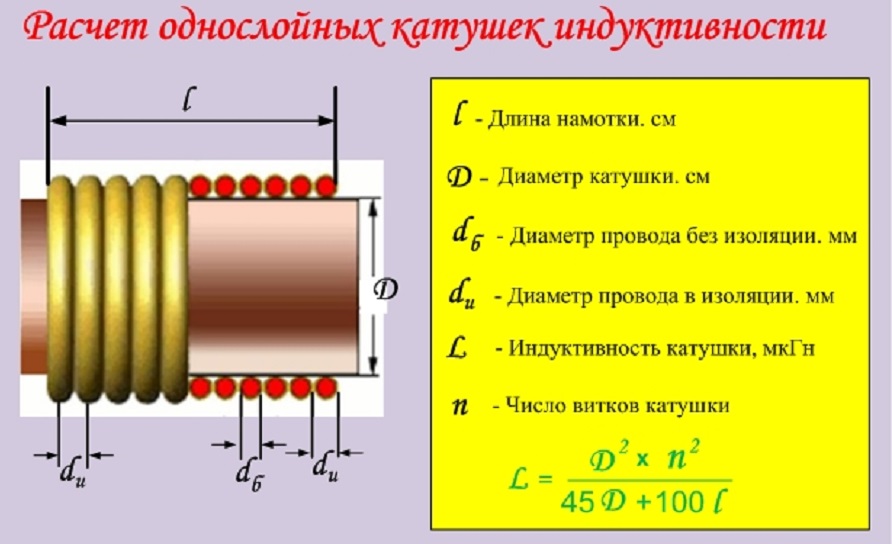

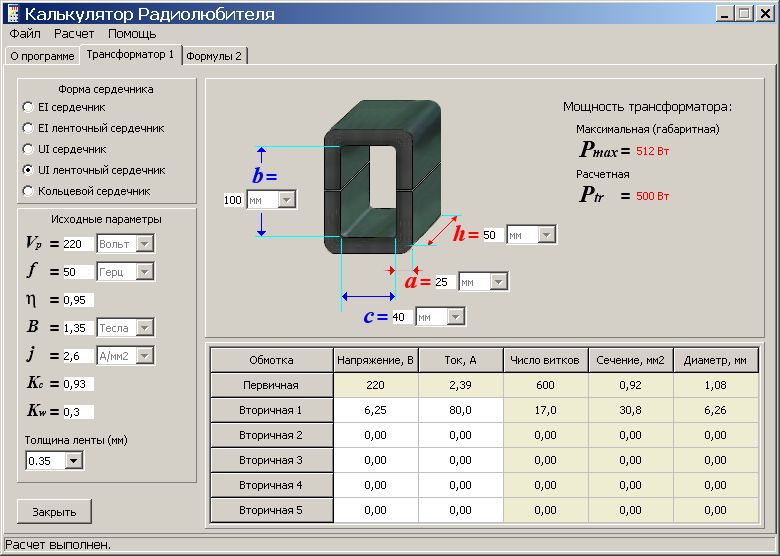
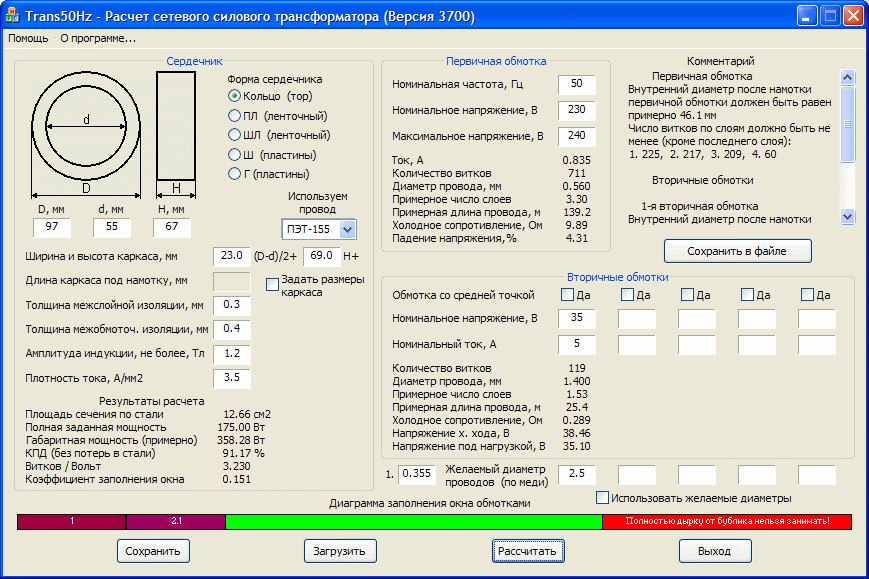
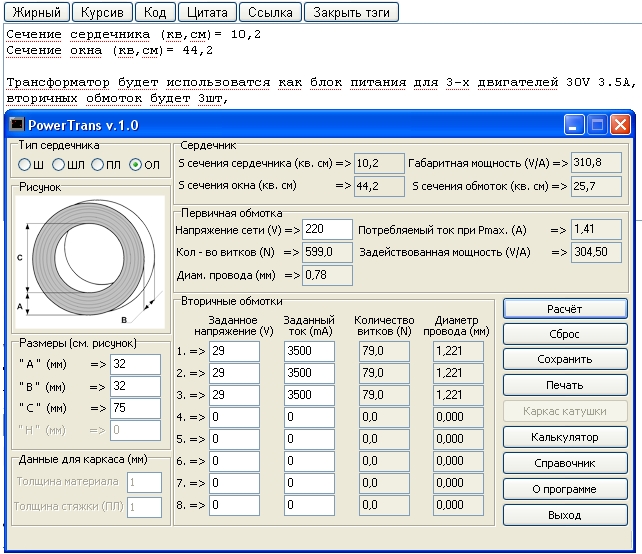
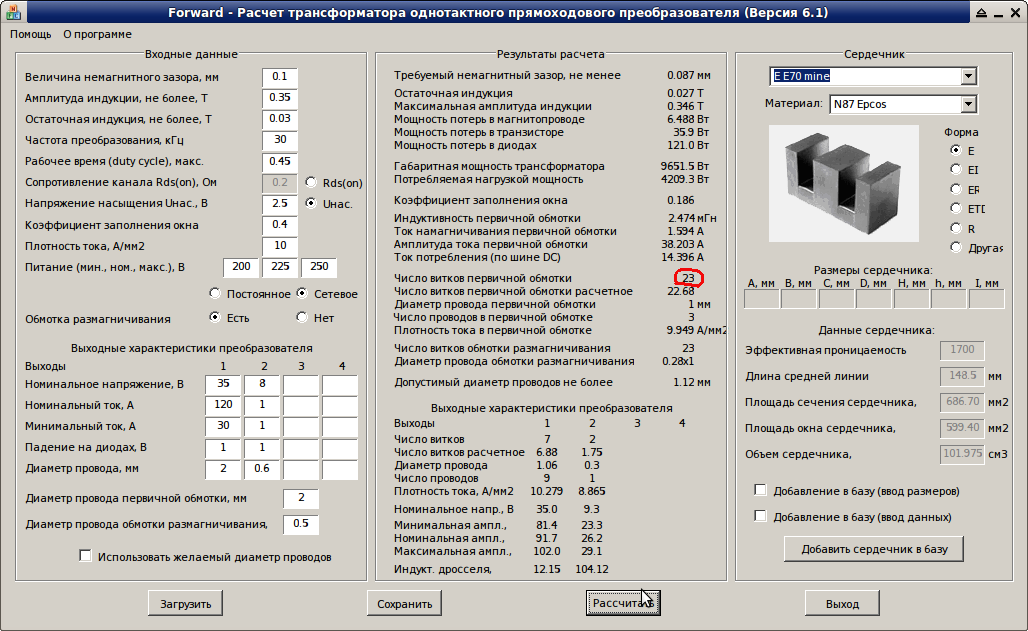
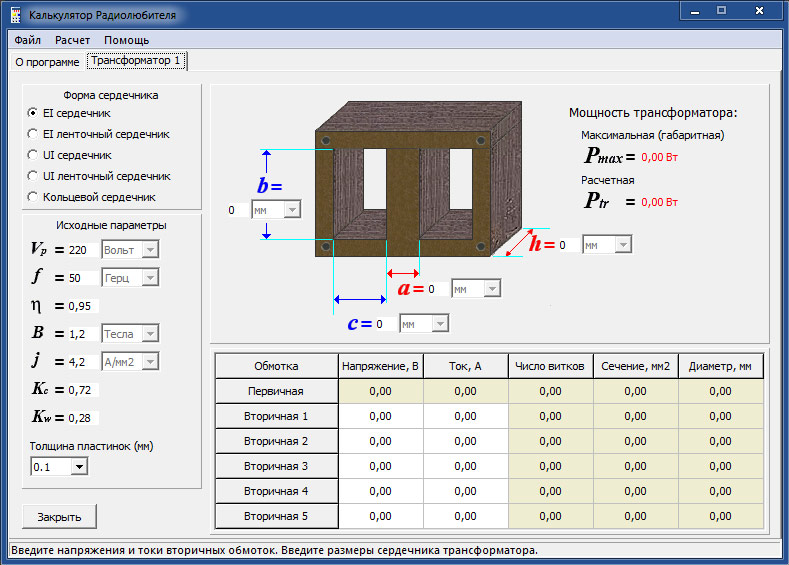

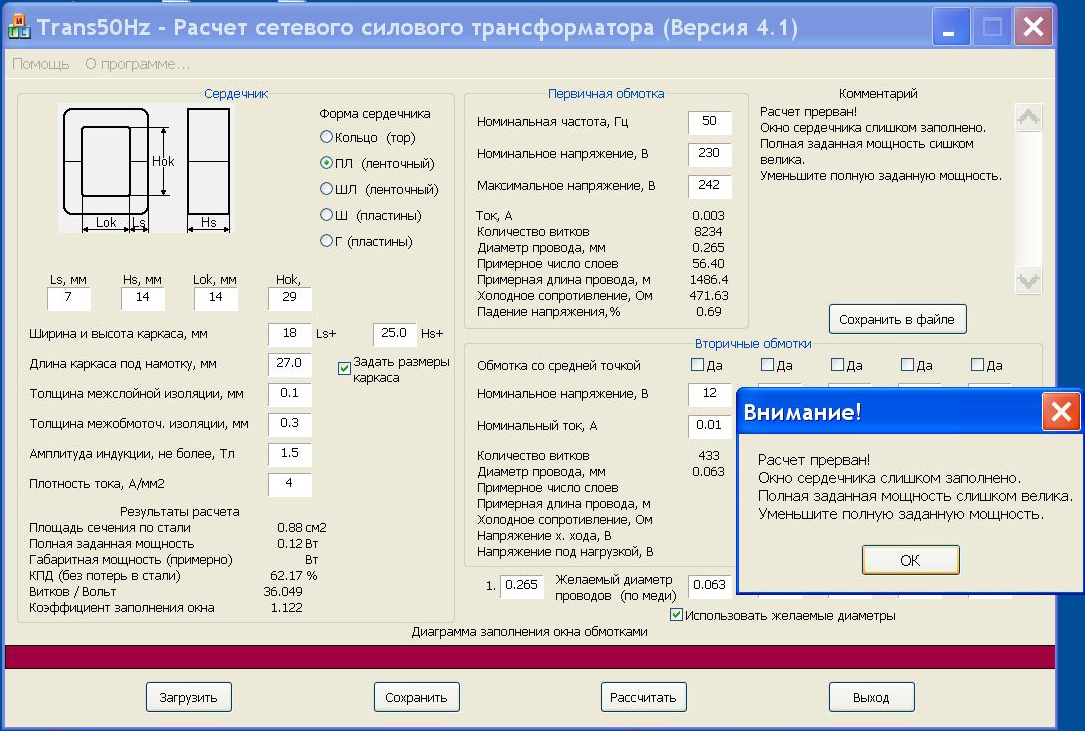
При такой плотности тока диаметр провода без изоляции в миллиметрах определяется по формуле: d = 0,8√I
.
Для первичной обмотки диаметр провода будет:
d_1 = 0,8 · √1_1 = 0,8 · √0,34 = 0,8 · 0,58 = 0,46 мм. Возьмем 0,5 мм
.
Диаметр провода для вторичной обмотки:
d_2 = 0,8 · √1_2 = 0,8 · √1,67 = 0,8 · 1,3 = 1,04 мм. Возьмем 1,1 мм.
ЕСЛИ НЕТ ПРОВОДА НУЖНОГО ДИАМЕТРА,
то можно взять несколько, соединенных параллельно, более тонких проводов. Их суммарная площадь сечения должна быть не менее той, которая соответствует рассчитанному одному проводу.
Площадь поперечного сечения провода определяется по формуле:
Например: мы не смогли найти провод для вторичной обмотки диаметром 1,1
мм.
Площадь поперечного сечения провода диаметром 1,1
мм. равна:
s = 0,8 · d² = 0,8 · 1,1² = 0,8 · 1,21 = 0,97 мм²
.
Из
таблицы
выбираем диаметры двух проводов сумма площадей сечения которых равна 1.0 мм².
Например, это два провода диаметром по 0,8 мм
. и площадью по0,5 мм²
.
Или два провода: — первый диаметром 1,0 мм
. и площадью сечения 0,79 мм²
,
— второй диаметром 0,5 мм
. и площадью сечения 0,196 мм²
.что в сумме дает: 0,79 + 0,196 = 0,986 мм².
Намотка катушки ведется двумя проводами одновременно, строго выдерживается равное количество витков обоих проводов. Начала этих проводов соединяются между собой. Концы этих проводов также соединяются.
Получается как бы один провод с суммарным поперечным сечением двух проводов.
Смотрите статьи:
— «Как намотать трансформатор на Ш-образном сердечнике».
— «Как изготовить каркас для Ш — образного сердечника».
Электрический аппарат — трансформатор используется для преобразования поступающего переменного напряжения в другое — исходящее, к примеру: 220 В в 12 В (конкретно это преобразование достигается использованием понижающего трансформатора). Прежде чем разбираться с тем, как рассчитать трансформатор, вы в первую очередь должны обладать знаниями о его структуре.
Простейший трансформатор является компоновкой магнитопровода и обмоток 2-х видов: первичной и вторичной, специально намотанных на него. Первичная обмотка воспринимает подающееся переменное напряжение от сети (н-р: 220 В), а вторичная обмотка, посредством индуктивной связи создает другое переменное напряжение. Разность витков в обмотках влияет на выходное напряжение.
Расчет
Существует несколько видов расчетов, которыми пользуются профессионалы. Для новичков все они достаточно сложные, поэтому рекомендуем так называемый упрощенный вариант. В его основе лежат четыре формулы.

Формула закона трансформации
Итак, закон трансформации определяется нижеследующей формулой:
- U1 – напряжение на первичной обмотке,
- U2 – на вторичной,
- n1 – количество витков на первичной обмотке,
- n2 – на вторичной.
Так как разбирается именно сетевой трансформатор, то напряжение на первичной обмотке у него будет 220 вольт. Напряжение же на вторичной обмотке – это необходимый для вас параметр. Для удобства расчета берем его равным 22 вольт. То есть, в данном случае коэффициент трансформации будет равен 10. Отсюда и количество витков. Если на первичной обмотке их будет 220, то на вторичной 22.
Представьте, что прибор, который будет подсоединен через трансформатор, потребляет нагрузку в 1 А. То есть, на вторичную обмотку действует именно этот параметр. Значит, на первичную будет действовать нагрузка 0,1 А, потому что напряжение и сила тока находятся в обратной пропорциональности.
А вот мощность, наоборот, в прямой зависимости. Поэтому на первичную обмотку будет действовать мощность: 220×0,1=22 Вт, на вторичную: 22×1=22 Вт. Получается, что на двух обмотках мощность одинаковая.
Что касается количества витков, то рассчитать их на один вольт не составит большого труда. В принципе, это можно сделать методом «тыка». К примеру, наматываете на первичную обмотку десять витков, проверяете на ней напряжение и полученный результат делите на десять. Если показатель совпадает с необходимым для вас напряжением на выходе, то, значит, вы попали в яблочко. Если напряжение снижено, значит, придется увеличить количество витков, и наоборот.
И еще один нюанс. Специалисты рекомендуют наматывать витки с небольшим запасом. Все дело в том, что на самих обмотках всегда присутствуют потери напряжения, которые необходимо компенсировать. К примеру, если вам нужно напряжение на выходе 12 вольт, то расчет количества витков проводится из расчета напряжения в 17-18 В. То есть, компенсируются потери.
Площадь сердечника
Как уже было сказано выше, мощность блока питания – это сумма мощностей всех его вторичных обмоток. Это основа выбора самого сердечника и его площади. Формула такая:
В этой формуле мощность устанавливается в ваттах, а площадь получается в сантиметрах квадратных. Если сам сердечник имеет Ш-образную конструкцию, то сечение берется среднего стержня.
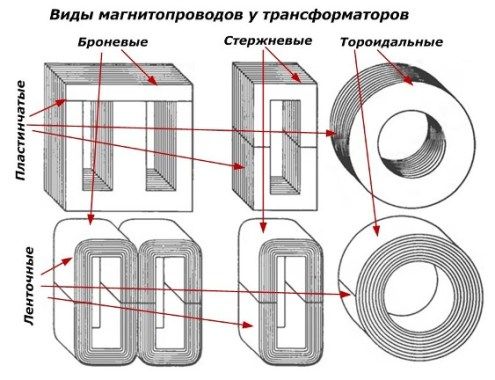
Разновидности сердечников для трансформатора.
Количество витков в первичной обмотке
Здесь используется следующая формула:
n=50*U1/S, понятно, что U1 равно 220 В.
Кстати, эмпирический коэффициент «50» может изменяться. К примеру, чтобы блок питания не входил в насыщение и тем самым не создавал лишних помех (электромагнитных), то лучше в расчете использовать коэффициент «60». Правда, это увеличит число витков обмотки, трансформатор станет немного больше в размерах, но при этом снизятся потери, а, значит, режим работы блока питания станет легче
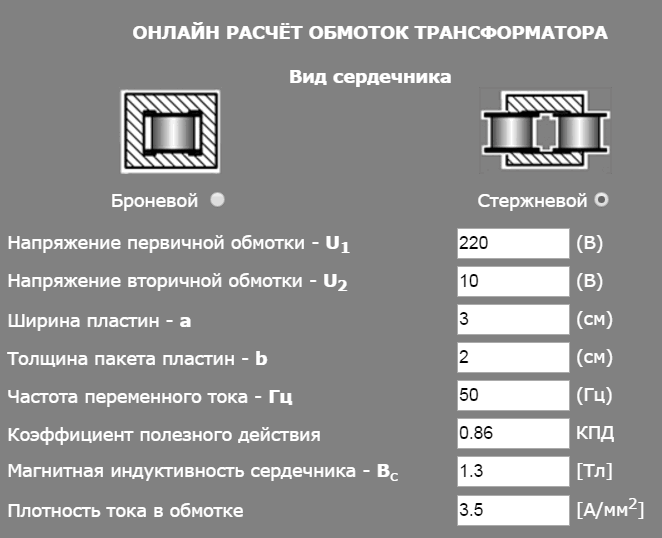
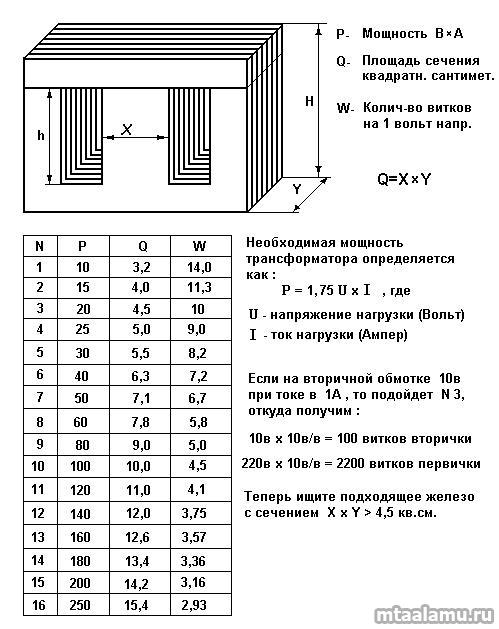
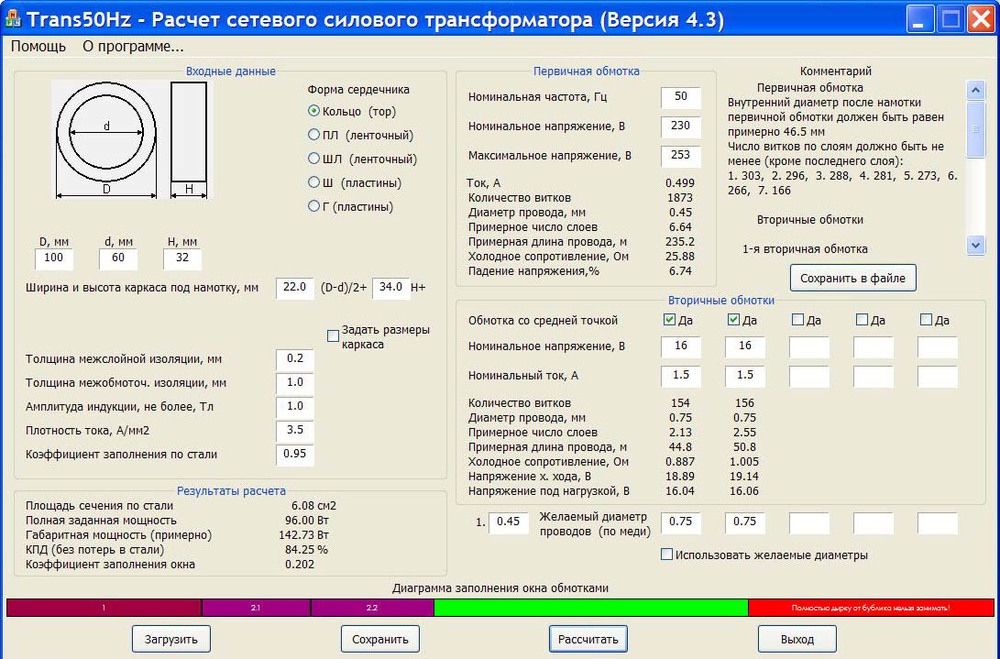
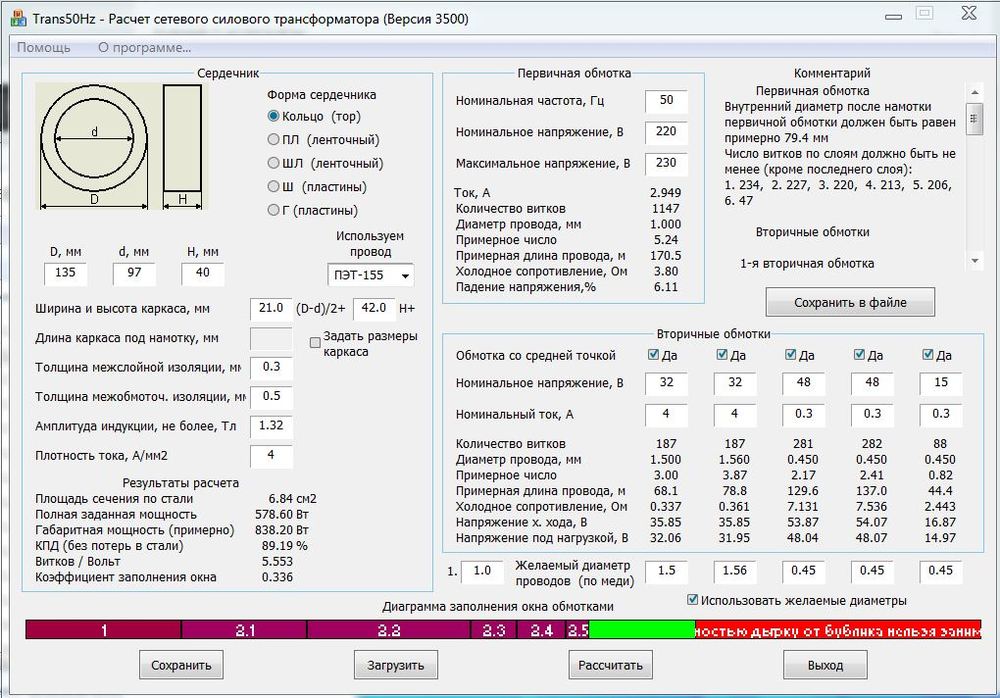
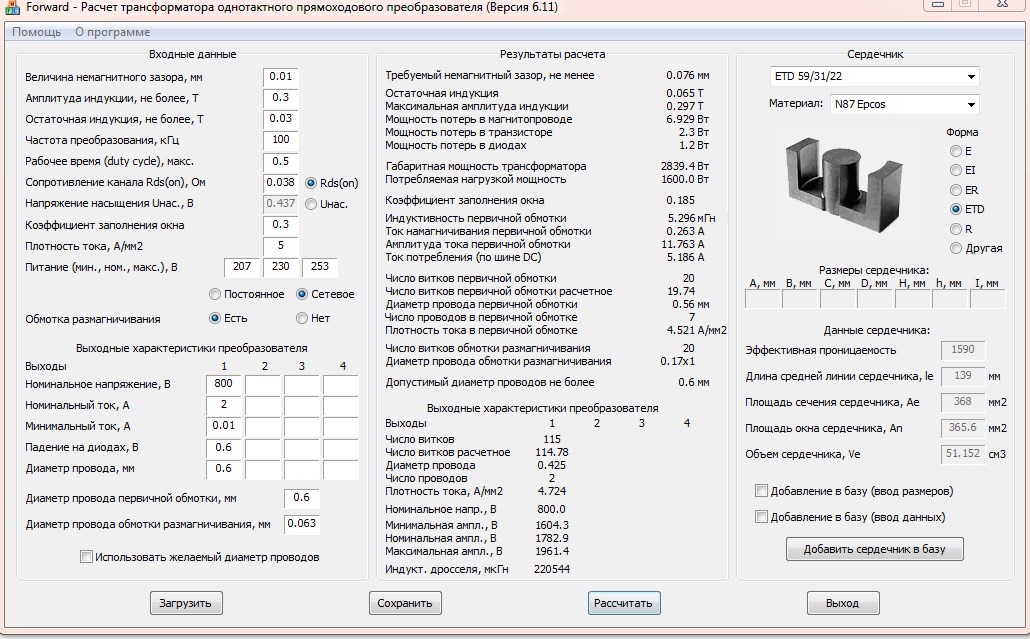
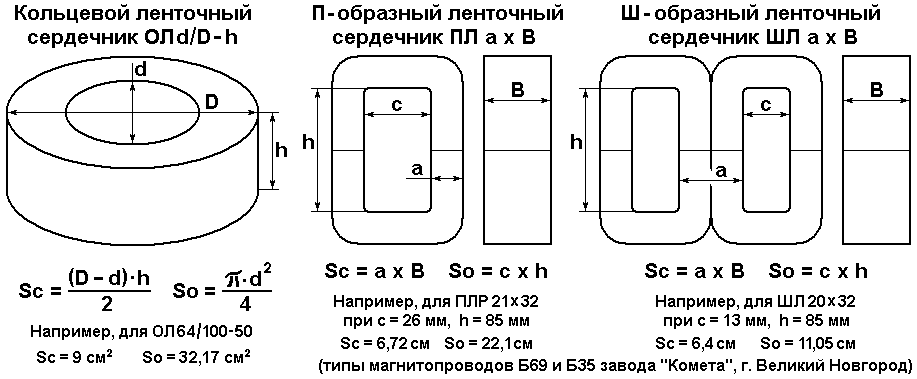
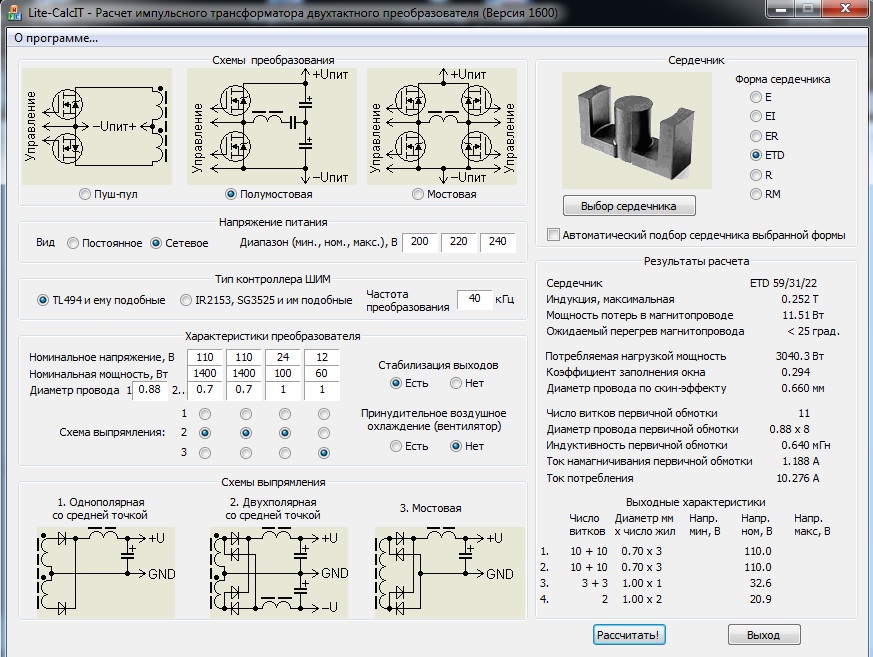
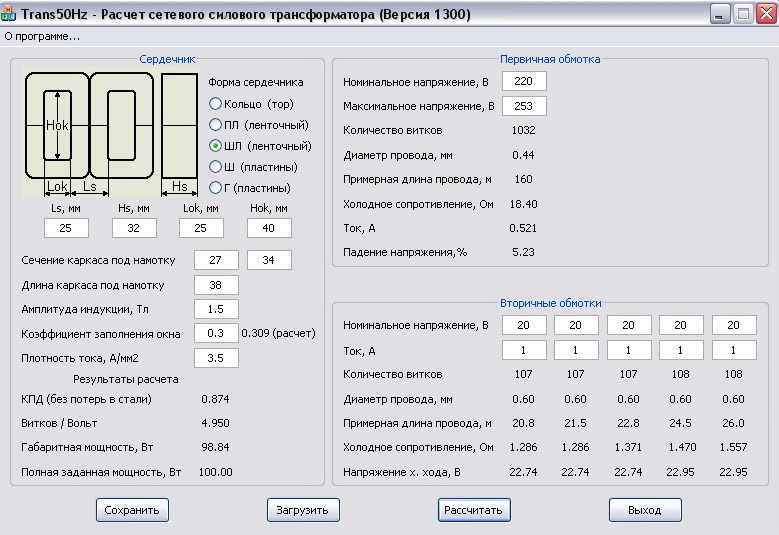
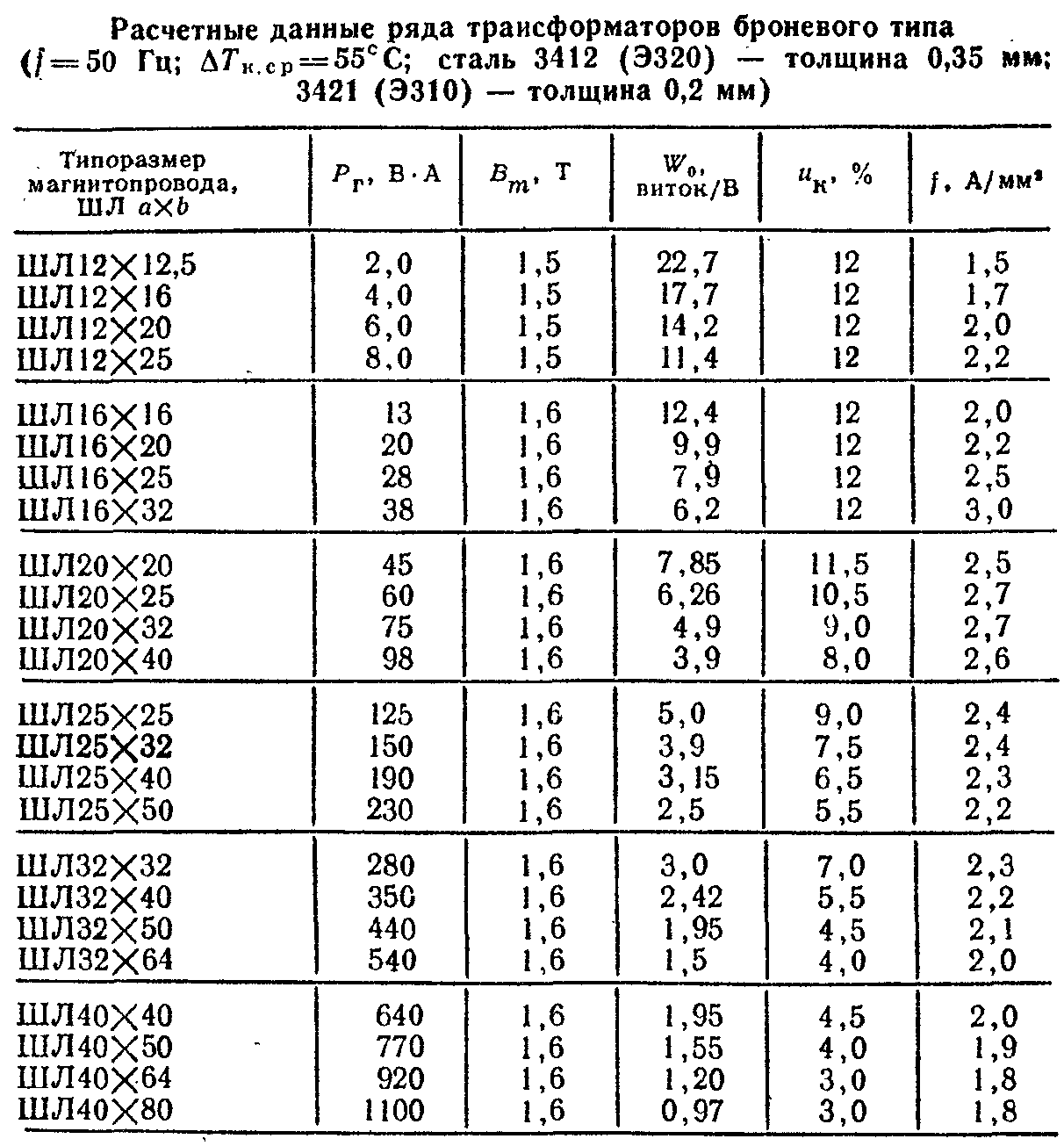
Здесь важно, чтобы количество обмоток уместилось
Сечение провода
И последняя четвертая формула касается сечения используемого медного провода в обмотках.
d=0,8*√I, где d – это диаметр провода, а «I» – сила тока в обмотке.
Расчетный диаметр необходимо также округлить до стандартной величины.
Итак, вот четыре формулы, по которым проводится подбор трансформатора тока
Здесь неважно покупаете ли вы готовый прибор или собираете его самостоятельно. Но учтите, что такой расчет подходит только для сетевого трансформатора, который будет работать от сети в 220 В и 50 Гц
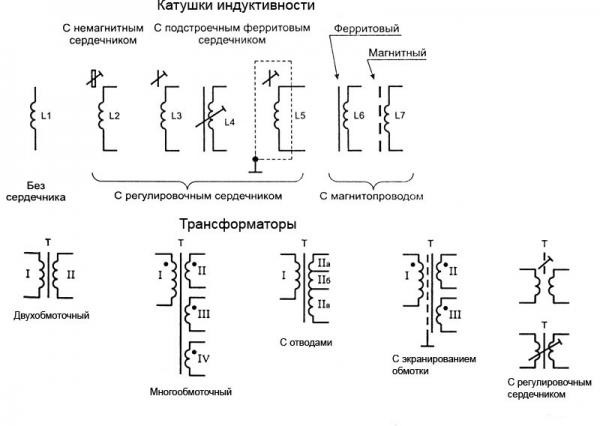
Для высокочастотных приборов используются совершенно другие формулы, где придется проводить расчет потерь трансформатора тока. Правда, формула коэффициента трансформации и у него точно такая же. Кстати, в этих устройствах устанавливается ферромагнитный сердечник.
Примеры реальных расчетов
В качестве примера рассчитаем трансформатор питания для зарядного устройства. Исходные данные:
- напряжение сети – 220В;
- выходное напряжение – 14В;
- ток вторичной обмотки – 10А;
Используя выходные параметры, определяем мощность вторичной обмотки: P=14∙10=140 Вт
Габаритная мощность: P=1.25∙ 140=175 Вт.
Площадь сечения магнитопровода сердечника составит: S=√175=13.3 см2
Наилучшими параметрами обладают конструкции, у которых сечение сердечника приближается к квадратному. Таким образом выбираем ленточный бронепровод с размерами сердечника 3.5х4 см. Его площадь равняется 14 см2.
Для данного сердечника К=50. Таким образом: W=50/14=3.6 вит/вольт
Для обмоток общее количество витков равняется:
- первичная обмотка n1=220∙3.6= 792 витка;
- вторичная обмотка n2=14∙3.6=50 витков.
Определяем диаметр обмоточных проводов: d2=0.7√10=2.2 мм.
Ближайшее стандартное значение – 2.4 мм.
Для нахождения диаметра провода первичной обмотки найдем ток через нее: I=P/U=175/220=0.8А.
Данному току соответствует диаметр: d1=0.7√0.8=0.63 мм.
Ближайшее стандартное значение имеет как раз такое значение.
Более углубленный расчет предполагает оценку коэффициента заполнения свободного окна магнитопровода. Большое значение числа вторичных обмоток может не поместиться в свободном окне, тогда необходимо будет выбрать более мощный сердечник. При слишком свободном размещении обмоток ухудшается КПД устройства, увеличивается магнитное поле рассеивания. Однако, как показывает практика, при правильном выборе сечения сердечника подобные расчеты становятся излишними.
Примеры реальных расчетов
В качестве примера можно выбрать питающую подстанцию жилого района. Нагрузка подстанции является III категории, поэтому коэффициент загрузки допустимо выбирать из большего значения – 0.9-0.95.
Характер потребления тока бытового сектора зависит от времени суток и сезона, но с учетом высокого коэффициента загрузки допустимо учитывать среднее значение потребляемой мощности. Для повышения надежности работы в период максимального потребления рекомендуется использование маслонаполненных трансформаторов, которые отличаются большой перегрузочной способностью в течение длительного периода времени (30% перегрузки в течение 2-х часов).
Расчёт параметров прибора
Иногда в руки к электрику попадает прибор без описания технических характеристик. Тогда специалист определяет мощность трансформатора по сечению магнитопровода. Площадь сечения находится перемножением ширины и толщины сердечника. Полученное число возводится в квадрат. Результат укажет на примерную мощность устройства.
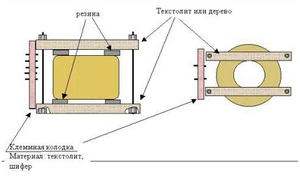
Практический расчёт силового трансформатора не займёт много времени. Например, перед домашним мастером стоит задача осветить рабочий уголок в гараже. В помещении имеется бытовая розетка на 220 В, в которую необходимо подключить светильник с лампой мощностью 40 Вт на 36 В. Требуется рассчитать технические параметры понижающего трансформатора.
Определение мощности
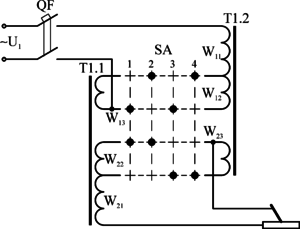
Округление осуществляется в бо́льшую сторону. Результат 50 Вт.
Вычисление сечения сердечника
От мощности трансформатора зависят размеры магнитопровода. Площадь сечения определяется следующим образом.
Расчёт количества витков
Площадь магнитопровода помогает определить количество витков провода на 1 вольт напряжения:
Разности потенциалов в один вольт будут соответствовать 5‚89 оборотам провода вокруг сердечника. Поэтому первичная обмотка с напряжением 220 В состоит из 1296 витков, а для вторичной катушки потребуется 212 витков. Во вторичной обмотке происходят потери напряжения, вызванные активным сопротивлением провода. Вследствие этого специалисты рекомендуют увеличить количество витков в выходной катушке на 5−10%. Скорректированное число витков будет равно 233.
Токи в обмотках
Следующий этап — нахождение силы тока в каждой обмотке, которое вычисляется делением мощности на напряжение. После нехитрых подсчётов получается требуемый результат.
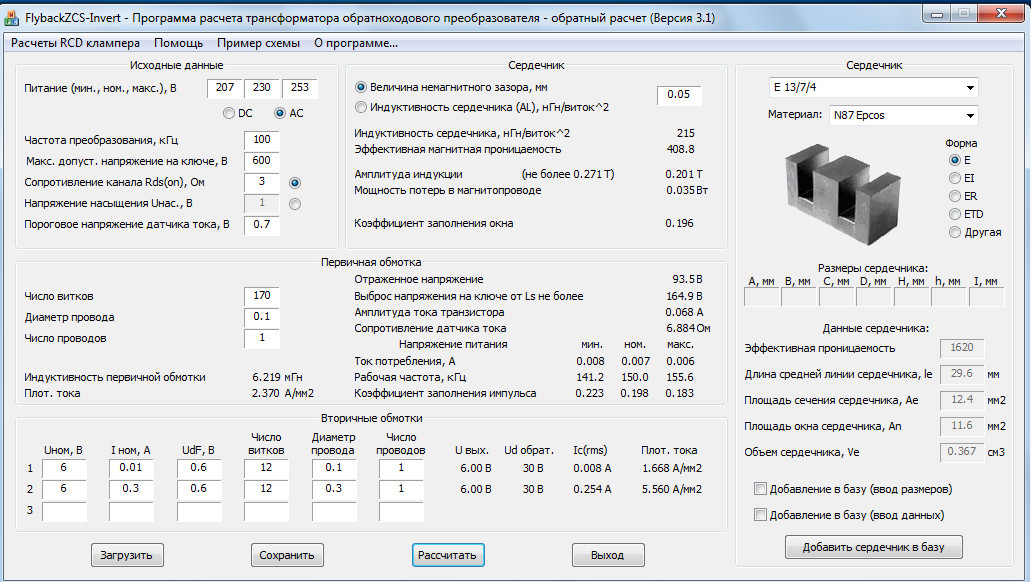
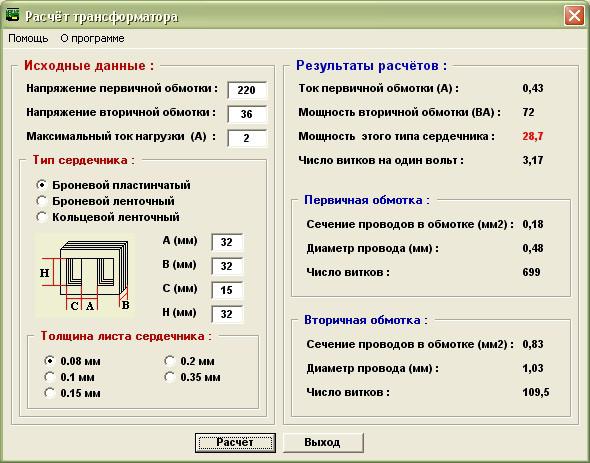
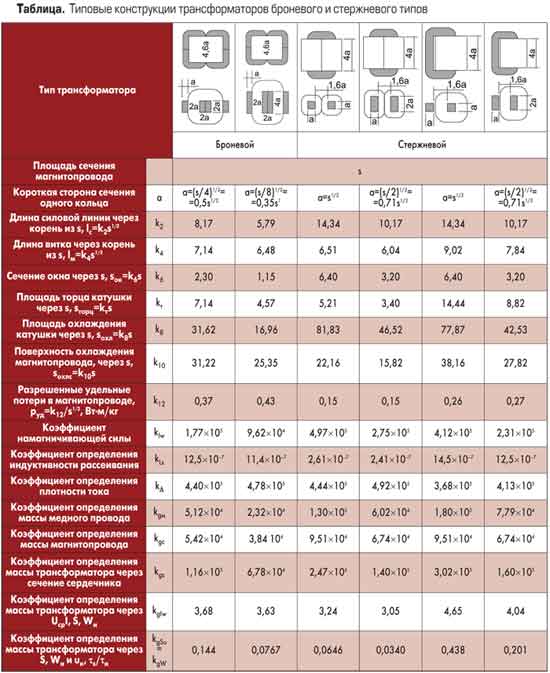

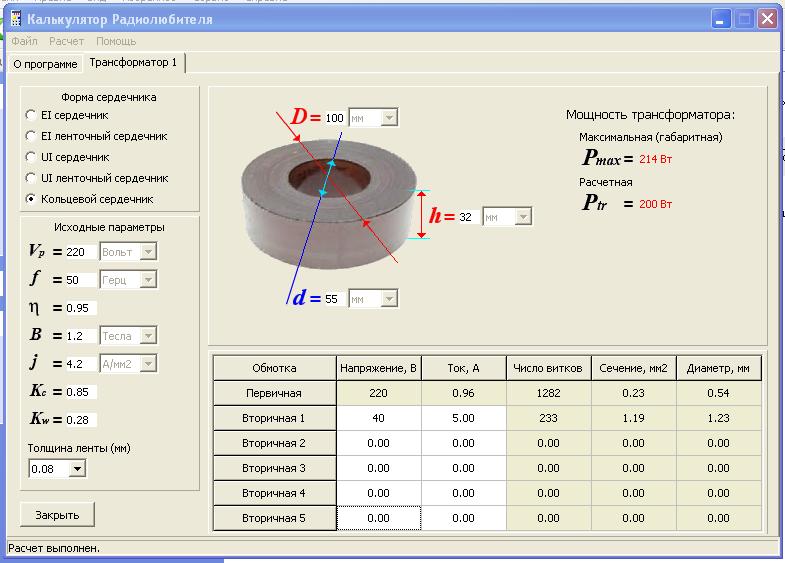
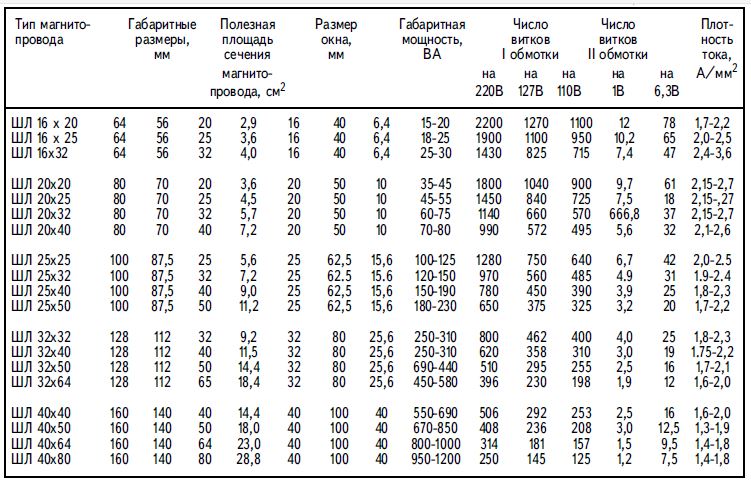
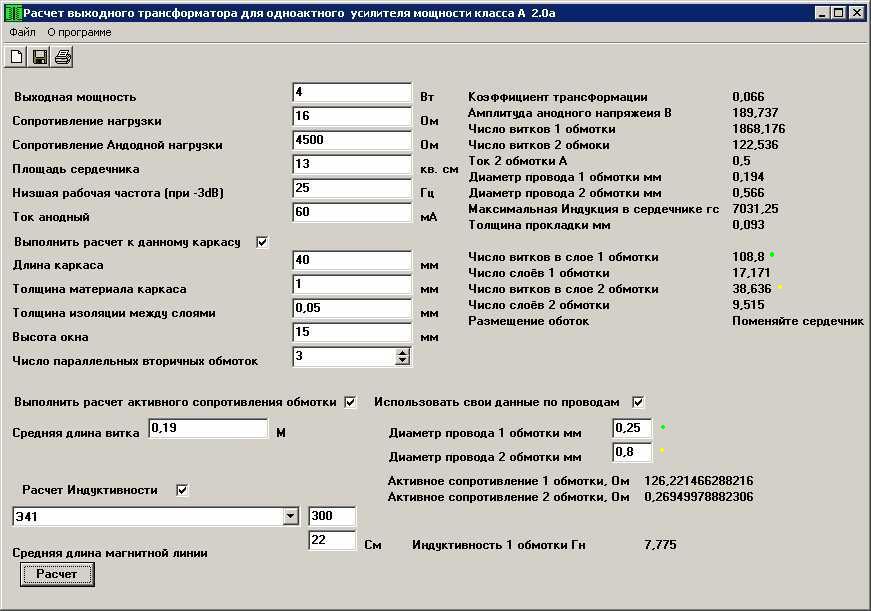
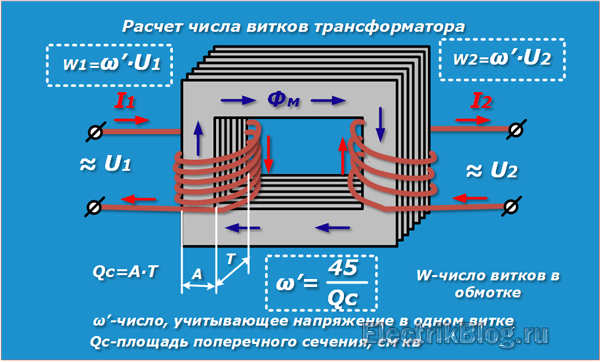
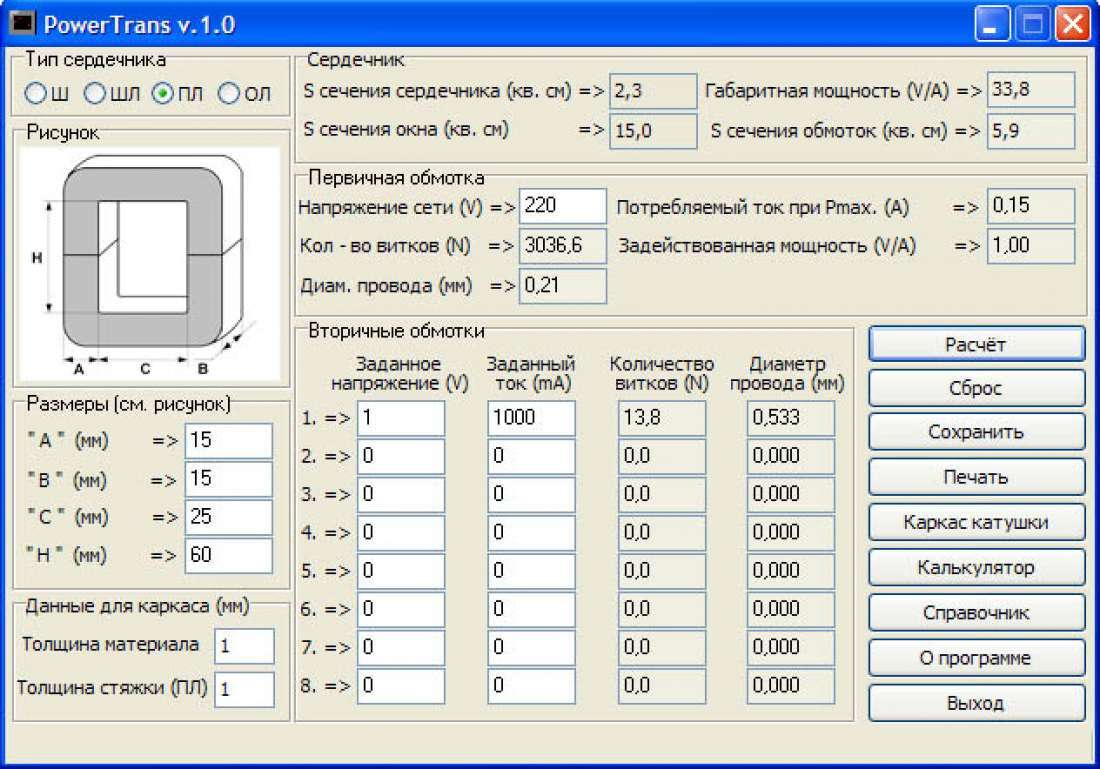
В первичной катушке I₁ = P₁ ∕ U₁ = 50 ∕ 220 = 0‚23 ампера, а во вторичной катушке I₂ = P₂ ∕ U₂ = 40 ∕ 36 = 1‚12 ампера.
Диаметр провода
Расчёт обмоток трансформатора завершается определением толщины провода, сечение которого вычисляется по формуле: d = 0‚8 √ I. Слой изоляции в расчёт не берётся. Проводник входной катушки должен иметь диаметр:
d₁ = 0‚8 √I₁ =0‚8 √0‚23 = 0‚8 ∙ 0‚48 = 0‚38.
Для намотки выходной обмотки потребуется провод с диаметром:
d₂ = 0‚8 √I₂ =0‚8 √1‚12 = 0‚8 ∙ 1‚06 = 0‚85.
Плотность тока можно выбрать по таблице
| Конструкция трансформатора | Плотность тока (а/мм2) при мощности трансформатора (Вт) | ||||
| 5-10 | 10-50 | 50-150 | 150-300 | 300-1000 | |
| Однокаркасная | 3,0-4,0 | 2,5-3,0 | 2,0-2,5 | 1,7-2,0 | 1,4-1,7 |
| Двухкаркасная | 3,5-4,0 | 2,7-3,5 | 2,4-2,7 | 2,0-2,5 | 1,7-2,3 |
| Кольцевая | 4,5-5,0 | 4,0-4,5 | 3,5-4,5 | 3,0-3,5 | 2,5-3,0 |
Ток, протекающий через катушки «III» и «IV» – 1,2 Ампера.
А плотность тока я выбрал – 2,5 А/ мм².
У меня нет провода диаметром 0,78 мм, но зато есть провод диаметром 1,0мм. Поэтому, я на всякий случай посчитаю, хватит ли мне места для этих катушек.
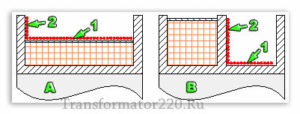
- Количество витков в одном слое.
- Количество слоёв.
Ширина моего не секционированного каркаса 40мм.
Мне нужно намотать 124 витка проводом 1,0 мм, у которого диаметр с изоляцией равен 1,08 мм. Таких обмоток требуется две.
124 * 1,08 * 1,1 : 40 ≈ 3,68 слоя
1,1 – коэффициент. На практике, при расчёте заполнения нужно прибавить 10 – 20% к полученному результату. Я буду мотать аккуратно, виток к витку, поэтому добавил 10%.
Получилось 4 слоя провода диаметром 1,08мм. Хотя, последний, четвёртый слой заполнен только на несколько процентов.
Определяем толщину обмотки:
У меня в распоряжении 9мм глубины каркаса, а значит, обмотка влезет и ещё останется свободное место.
Ток катушки «II» вряд ли будет больше чем – 100мА.
Диметр провода катушки «II» – 0,23мм.
Это малюсенькая по заполнению окна обмоточка и её можно даже не принимать в расчёт, когда остаётся так много свободного места.
Конечно, на практике у радиолюбителя выбор проводов невелик. Если нет провода подходящего сечения, то можно намотать обмотку сразу несколькими проводами меньшего диаметра. Только, чтобы не возникло перетоков, мотать нужно одновременно двумя, тремя или даже четырьмя проводами. Перетоки, возникают тогда, когда есть даже незначительные отклонения в длине обмоток соединённых параллельно. При этом, из-за разности напряжений, возникает ток, который греет обмотки и создаёт лишние потери.
Перед намоткой в несколько проводов, сначала нужно посчитать длину провода обмотки, а затем разрезать провод на требуемые куски.
Длина проводов будет равна:
p – периметр каркаса в середине намотки,
Толстый провод необходимо мотать виток к витку, а более тонкие провода можно намотать и в навал. Главное, чтобы обмотка поместилась в окно магнитопровода.
Если намотка производится аккуратно без повреждения изоляции, то никаких прокладок между слоями можно не применять, так как, при постройке УНЧ средней мощности, большие напряжения не используются. Изоляция же обмоточного провода рассчитана на напряжение в сотни вольт. Чем толще провод, тем выше пробивное напряжение изоляции провода. У тонкого провода пробивное напряжение изоляции около 400 Вольт, а у толстого может достигать 2000 Вольт.
Закрепить конец провода можно обычными нитками.
Если при удалении вторичной обмотки повредилась межобмоточная изоляция, защищающая первичную обмотку, то её нужно обязательно восстановить. Тут можно применить плотную бумагу или тонкий картон. Не рекомендуется использовать всякие синтетические материалы вроде скотча, изоленты и им подобные.
Если катушка разделена на секции для первичных и вторичных обмоток трансформатора, то тогда и вовсе можно обойтись без изоляционных прокладок.
Видео: Расчет сечения провода в силовом трансформаторе. Excel
Пример использования Excel в качестве универсального калькулятора для расчета диаметра провода в импульсном трансформаторе. Произведен расчет зависимости максимального тока от сечения проводника.
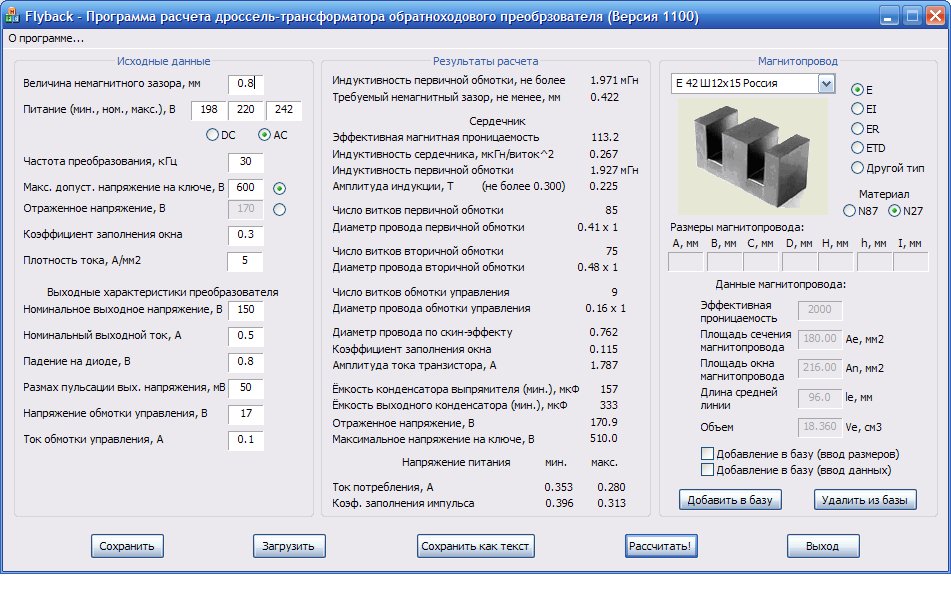


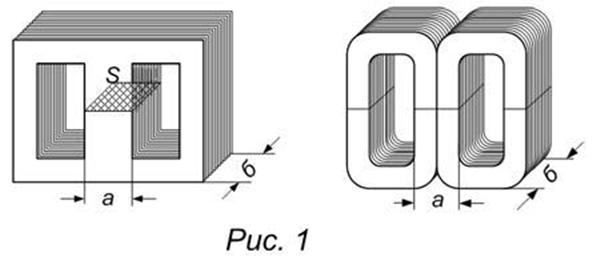
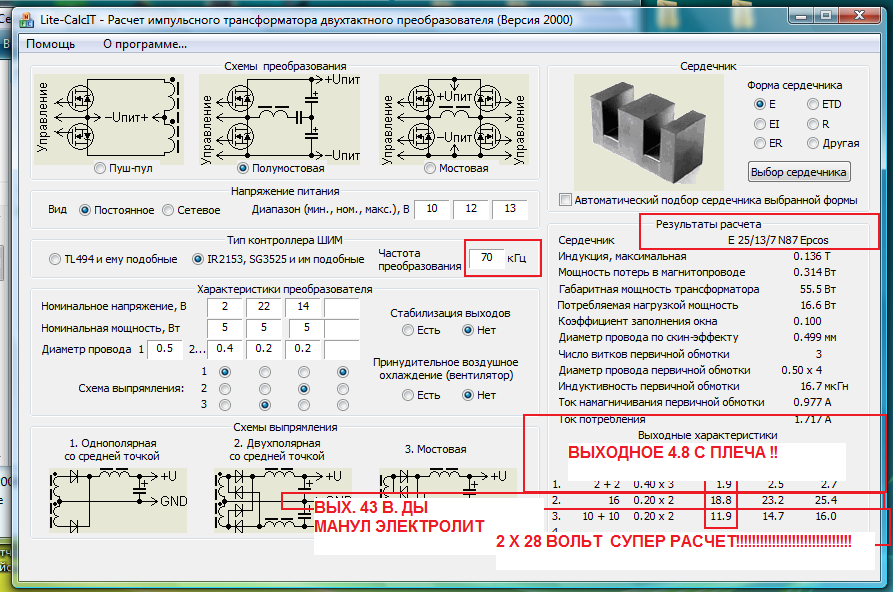
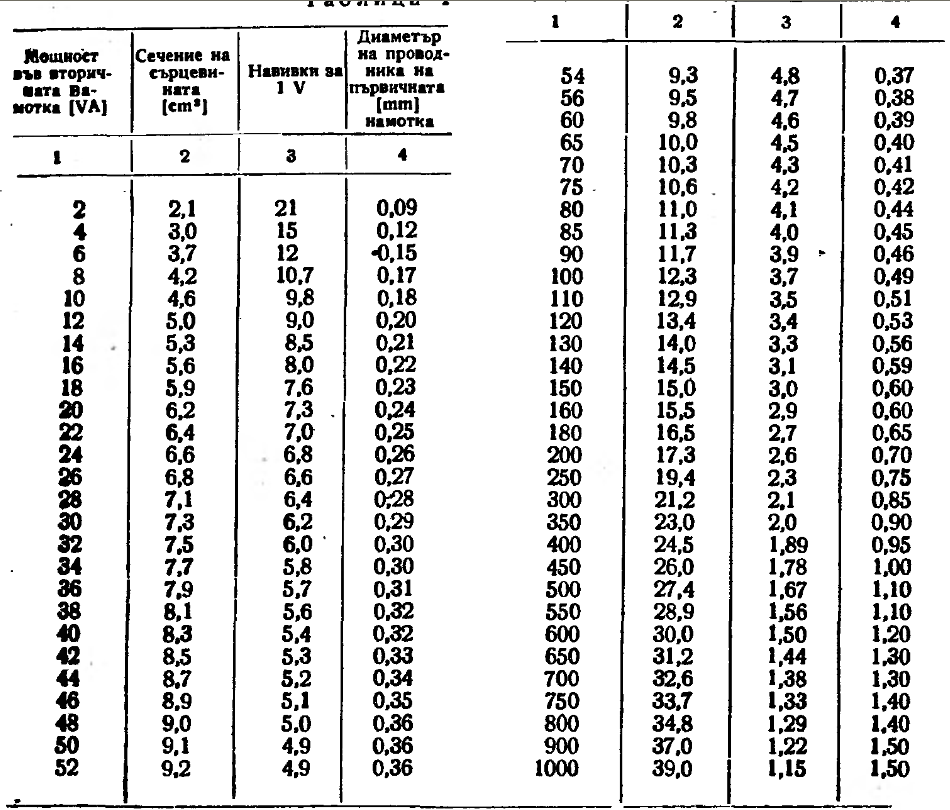
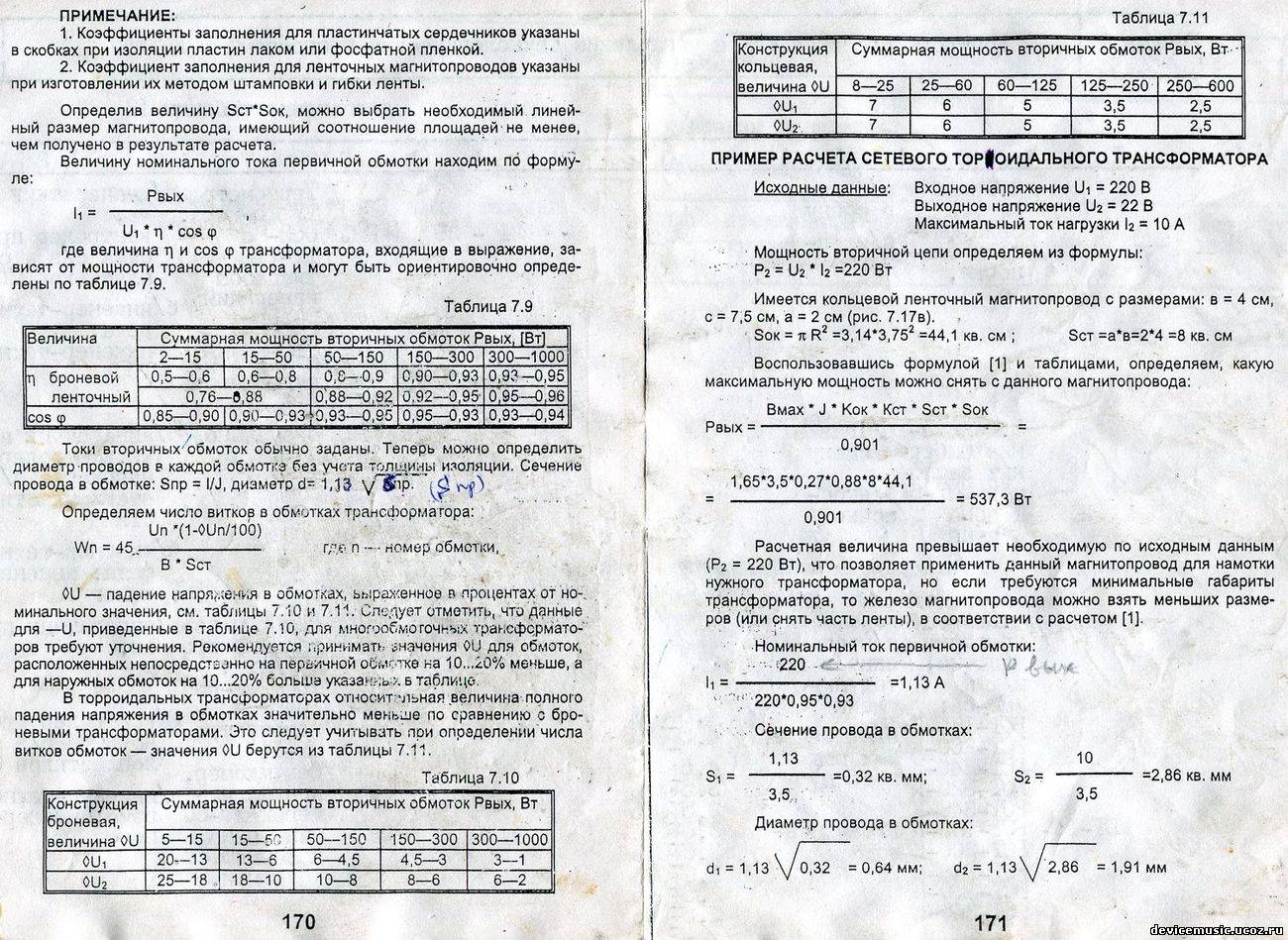

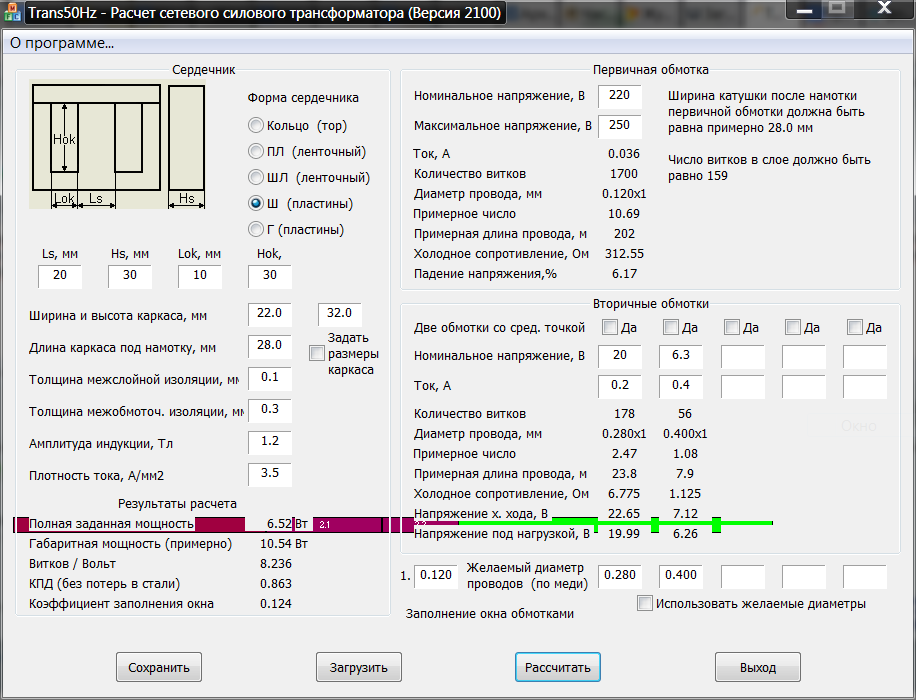
Типы магнитопроводов
Основой трансформатора переменного тока является магнитопровод, который должен обладать определенными магнитными свойствами. В трансформаторах используется сталь особого состава и со специфической обработкой (трансформаторное железо). В процессе работы трансформатора в магнитопроводе образуются вихревые токи, которые нагревают сердечник и ведут к снижению КПД трансформатора. Для снижения вихревых токов сердечник выполняют не монолитным, а собранным из тонких стальных пластин или лент, покрытых непроводящим оксидным слоем.
По типу используемого металла сердечники разделяют на:
Первый тип сердечников собирается в виде пакета из отдельных пластин соответствующей формы, а второй – наматывается из ленты. В дальнейшем ленточный сердечник может быть разрезан на отдельные сегменты для удобства намотки провода.
По типу магнитопровода различают сердечники:
Каждый из перечисленных типов может различаться формой пластин или сегментов:
Форма и тип сердечника в теории не влияют на методику расчета, но на практике это следует учитывать при определении КПД и количества витков обмоток.
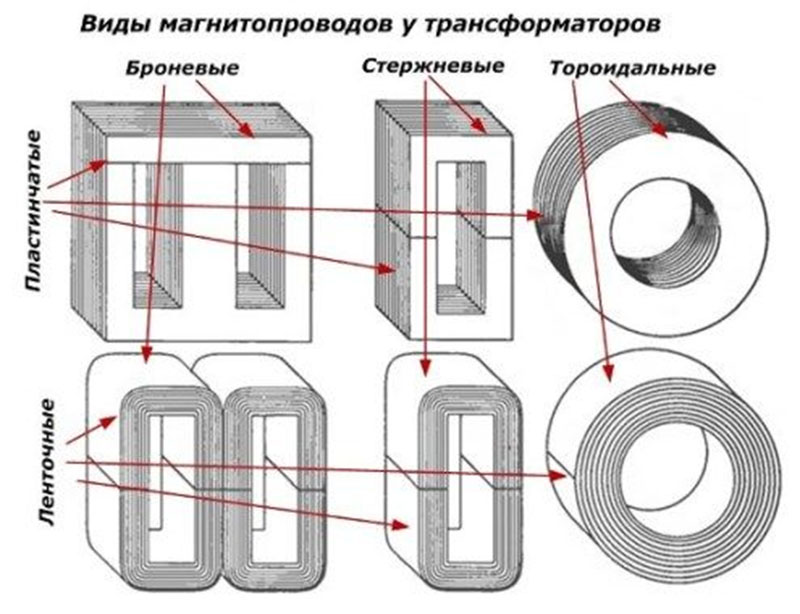
Кольцевой (тороидальный) сердечник отличается наилучшими свойствами. Трансформатор, выполненный на таком магнитопроводе, будет иметь максимальный КПД и минимальный ток холостого хода. Это оправдывает самую большую трудоемкость выполнения обмоток, поскольку в домашних условиях эта работа выполняется исключительно вручную, без использования намоточного станка.
Как определить число витков обмотки трансформатора не разматывая катушку
При отсутствии данных о конкретной модели трансформатора, количество витков в обмотках определяется при помощи одной из функций мультиметра.
Мультиметр следует перевести в режим омметра. Затем определяются выводы всех имеющихся обмоток. Если между магнитопроводом и катушкой имеется зазор, то сверху всех обмоток наматывается дополнительная обмотка из тонкого провода. От количества витков будет зависеть точность результатов измерений.
Один щуп прибора подключается к концу основной обмотки, а другой щуп – к дополнительной обмотке. По очереди выполняются измерения всех обмоток. Та из них, у которой наибольшее сопротивление, считается первичной. Полученные данные позволяют выполнить расчет трансформатора и вместе с другими параметрами выбрать наиболее оптимальную конструкцию для конкретной электрической цепи.
Сайт для радиолюбителей
Если у Вас есть некий трансформаторный сердечник, из которого нужно сделать трансформатор, то необходимо замерить сердечник (как показано на рисунке), а так же замерить толщину пластины или ленты.
Первым делом необходимо рассчитать площадь сечения сердечника — Sc (см²) и площадь поперечного сечения окна — Sо (см²).
Для тороидального трансформатора:
Для Ш и П — образного сердечника:
Определим габаритную мощность нашего сердечника на частоте 50 Гц:
- η — КПД трансформатора,
- Sc — площадь поперечного сечения сердечника, см 2 ,
- So — площадь поперечного сечения окна, см 2 ,
- f — рабочая частота трансформатора, Гц,
- B — магнитная индукция, T,
- j — плотность тока в проводе обмоток, A/мм 2 ,
- Km — коэффициент заполнения окна сердечника медью,
- Kc — коэффициент заполнения сечения сердечника сталью.
При расчете трансформатора необходимо учитывать, что габаритная мощность трансформатора должна быть больше расчетной электрической мощности вторичных обмоток.
Как измерить диаметр провода.
Если у Вас дома завалялся микрометр, то можно им замерить диаметр провода.
Провод сначала лучше прогреть на пламени спички и лишь потом скальпелем удалить ослабленную изоляцию. Если этого не сделать, то вместе с изоляцией можно удалить и часть меди, что снизит точность измерения особенно для тонкого провода.
Если микрометра нет, то можно воспользоваться обыкновенной линейкой. Нужно намотать на жало отвёртки или на другую подходящую ось 100 витков провода, сжать витки ногтем и приложить полученный набор к линейке.
Разделив полученный результат на 100, получим диаметр провода с изоляцией. Узнать диметр провода по меди можно из таблицы приведённой ниже.
Я намотал 100 витков провода и получил длину набора –39 мм.
По таблице определяю диметр провода по меди – 0,35мм.
Таблица данных обмоточных проводов.
| Диаметр без изоляции, мм | Сечение меди, мм² | Сопротив-ление 1м при 20ºС, Ом | Допустимая нагрузка при плотности тока 2А/мм² | Диаметр с изоляцией, мм |
Вес 100м с изоляцией, гр |
| 0,03 | 0,0007 | 24,704 | 0,0014 | 0,045 | 0,8 |
| 0,04 | 0,0013 | 13,92 | 0,0026 | 0,055 | 1,3 |
| 0,05 | 0,002 | 9,29 | 0,004 | 0,065 | 1,9 |
| 0,06 | 0,0028 | 6,44 | 0,0057 | 0,075 | 2,7 |
| 0,07 | 0,0039 | 4,73 | 0,0077 | 0,085 | 3,6 |
| 0,08 | 0,005 | 3,63 | 0,0101 | 0,095 | 4,7 |
| 0,09 | 0,0064 | 2,86 | 0,0127 | 0,105 | 5,9 |
| 0,1 | 0,0079 | 2,23 | 0,0157 | 0,12 | 7,3 |
| 0,11 | 0,0095 | 1,85 | 0,019 | 0,13 | 8,8 |
| 0,12 | 0,0113 | 1,55 | 0,0226 | 0,14 | 10,4 |
| 0,13 | 0,0133 | 1,32 | 0,0266 | 0,15 | 12,2 |
| 0,14 | 0,0154 | 1,14 | 0,0308 | 0,16 | 14,1 |
| 0,15 | 0,0177 | 0,99 | 0,0354 | 0,17 | 16,2 |
| 0,16 | 0,0201 | 0,873 | 0,0402 | 0,18 | 18,4 |
| 0,17 | 0,0227 | 0,773 | 0,0454 | 0,19 | 20,8 |
| 0,18 | 0,0255 | 0,688 | 0,051 | 0,2 | 23,3 |
| 0,19 | 0,0284 | 0,618 | 0,0568 | 0,21 | 25,9 |
| 0,2 | 0,0314 | 0,558 | 0,0628 | 0,225 | 28,7 |
| 0,21 | 0,0346 | 0,507 | 0,0692 | 0,235 | 31,6 |
| 0,23 | 0,0416 | 0,423 | 0,0832 | 0,255 | 37,8 |
| 0,25 | 0,0491 | 0,357 | 0,0982 | 0,275 | 44,6 |
| 0,27 | 0,0573 | 0,306 | 0,115 | 0,31 | 52,2 |
| 0,29 | 0,0661 | 0,2бб | 0,132 | 0,33 | 60,1 |
| 0,31 | 0,0755 | 0,233 | 0,151 | 0,35 | 68,9 |
| 0,33 | 0,0855 | 0,205 | 0,171 | 0,37 | 78 |
| 0,35 | 0,0962 | 0,182 | 0,192 | 0,39 | 87,6 |
| 0,38 | 0,1134 | 0,155 | 0,226 | 0,42 | 103 |
| 0,41 | 0,132 | 0,133 | 0,264 | 0,45 | 120 |
| 0,44 | 0,1521 | 0,115 | 0,304 | 0,49 | 138 |
| 0,47 | 0,1735 | 0,101 | 0,346 | 0,52 | 157 |
| 0,49 | 0,1885 | 0,0931 | 0,378 | 0,54 | 171 |
| 0,51 | 0,2043 | 0,0859 | 0,408 | 0,56 | 185 |
| 0,53 | 0,2206 | 0,0795 | 0,441 | 0,58 | 200 |
| 0,55 | 0,2376 | 0,0737 | 0,476 | 0,6 | 216 |
| 0,57 | 0,2552 | 0,0687 | 0,51 | 0,62 | 230 |
| 0,59 | 0,2734 | 0,0641 | 0,547 | 0,64 | 248 |
| 0,62 | 0,3019 | 0,058 | 0,604 | 0,67 | 273 |
| 0,64 | 0,3217 | 0,0545 | 0,644 | 0,69 | 291 |
| 0,67 | 0,3526 | 0,0497 | 0,705 | 0,72 | 319 |
| 0,69 | 0,3739 | 0,0469 | 0,748 | 0,74 | 338 |
| 0,72 | 0,4072 | 0,043 | 0,814 | 0,78 | 367 |
| 0,74 | 0,4301 | 0,0407 | 0,86 | 0,8 | 390 |
| 0,77 | 0,4657 | 0,0376 | 0,93 | 0,83 | 421 |
| 0,8 | 0,5027 | 0,0348 | 1,005 | 0,86 | 455 |
| 0,83 | 0,5411 | 0,0324 | 1,082 | 0,89 | 489 |
| 0.86 | 0,5809 | 0,0301 | 1,16 | 0,92 | 525 |
| 0,9 | 0,6362 | 0,0275 | 1,27 | 0,96 | 574 |
| 0,93 | 0,6793 | 0,0258 | 1,36 | 0,99 | 613 |
| 0,96 | 0,7238 | 0,0242 | 1,45 | 1,02 | 653 |
| 1 | 0,7854 | 0,0224 | 1,57 | 1,07 | 710 |
| 1,04 | 0,8495 | 0,0206 | 1,7 | 1,12 | 764 |
| 1,08 | 0,9161 | 0,0191 | 1,83 | 1,16 | 827 |
| 1,12 | 0,9852 | 0,0178 | 1,97 | 1,2 | 886 |
| 1,16 | 1,057 | 0,0166 | 2,114 | 1,24 | 953 |
| 1,2 | 1,131 | 0,0155 | 2,26 | 1,28 | 1020 |
| 1,25 | 1,227 | 0,0143 | 2,45 | 1,33 | 1110 |
| 1,3 | 1,327 | 0,0132 | 2,654 | 1,38 | 1190 |
| 1,35 | 1,431 | 0,0123 | 2,86 | 1,43 | 1290 |
| 1,4 | 1,539 | 0,0113 | 3,078 | 1,48 | 1390 |
| 1,45 | 1,651 | 0,0106 | 3,3 | 1,53 | 1490 |
| 1,5 | 1,767 | 0,0098 | 3,534 | 1,58 | 1590 |
| 1,56 | 1,911 | 0,0092 | 3,822 | 1,64 | 1720 |
| 1,62 | 2,061 | 0,0085 | 4,122 | 1,71 | 1850 |
| 1,68 | 2,217 | 0,0079 | 4,433 | 1,77 | 1990 |
| 1,74 | 2,378 | 0,0074 | 4,756 | 1,83 | 2140 |
| 1,81 | 2,573 | 0,0068 | 5,146 | 1,9 | 2310 |
| 1,88 | 2,777 | 0,0063 | 5,555 | 1,97 | 2490 |
| 1,95 | 2,987 | 0,0059 | 5,98 | 2,04 | 2680 |
| 2,02 | 3,205 | 0,0055 | 6,409 | 2,12 | 2890 |
| 2,1 | 3,464 | 0,0051 | 6,92 | 2,2 | 3110 |
| 2,26 | 4,012 | 0,0044 | 8,023 | 2,36 | 3620 |
| 2,44 | 4,676 | 0,0037 | 9,352 | 2,54 | 4220 |
Принцип работы устройства
Трансформатор — это электротехническое устройство, предназначенное для передачи энергии без изменения её формы и частоты. Используя в своей работе явление электромагнитной индукции, устройство применяется для преобразования переменного сигнала или создания гальванической развязки. Каждый трансформатор собирается из следующих конструктивных элементов:
- сердечника;
- обмотки;
- каркаса для расположения обмоток;
- изолятора;
- дополнительных элементов, обеспечивающих жёсткость устройства.
В устройстве трансформатора такая катушка называется первичной или сетевой. Она предназначена для создания магнитного поля. Стоит отметить, что такое поле обязательно должно всё время изменяться по направлению и величине, то есть быть переменным.
Классический трансформатор состоит из двух катушек и магнитопровода, соединяющего их. При подаче переменного сигнала на контакты первичной катушки возникающий магнитный поток через магнитопровод (сердечник) передаётся на вторую катушку. Таким образом, катушки связаны силовыми магнитными линиями. Согласно правилу электромагнитной индукции при изменении магнитного поля в катушке индуктируется переменная электродвижущая сила (ЭДС). Поэтому в первичной катушки возникает ЭДС самоиндукции, а во вторичной ЭДС взаимоиндукции.
От сечения провода, используемого в трансформаторе, зависит нагрев всего устройства. Правильно подобрать сечение возможно, воспользовавшись специальными таблицами из справочников, но проще использовать трансформаторный онлайн-калькулятор.
Правильная работа трансформатора зависит и от частоты сигнала. Чем она больше, тем меньше возникает потерь во время передачи энергии. А это означает, что от её значения зависят размеры магнитопровода: чем частота больше, тем размеры устройства меньше. На этом принципе и построены импульсные преобразователи, изготовление которых связано с трудностями разработки, поэтому часто используется калькулятор для расчёта трансформатора по сечению сердечника, помогающий избавиться от ошибок ручного расчёта.
Возможные схематические решения
Схем подключения вторичной обмотки трансформаторов, да и вообще всей электроники две:
- Звезда, которая используется для повышения мощности сети.
- Треугольник, который поддерживает постоянное напряжение в сети.
Вне зависимости от выбранной схемы, наиболее трудными считается изготовление и подключение небольших трансформаторов. Сюда относится и столь популярный в запросах поисковиков аtx. Это модель, которая устанавливается в системных блоках компьютеров, и изготовить ее самостоятельно крайне трудно.
В число трудностей при изготовлении маленьких трансформаторов стоит отнести сложность обмотки и изоляции, правильного подключения вторичной обмотки вне зависимости от выбранной схемы, а так же сложности с поиском сердечника. Короче говоря, проще и дешевле такой трансформатор купить. А вот как выбрать подходящую модель – это совсем другая история.
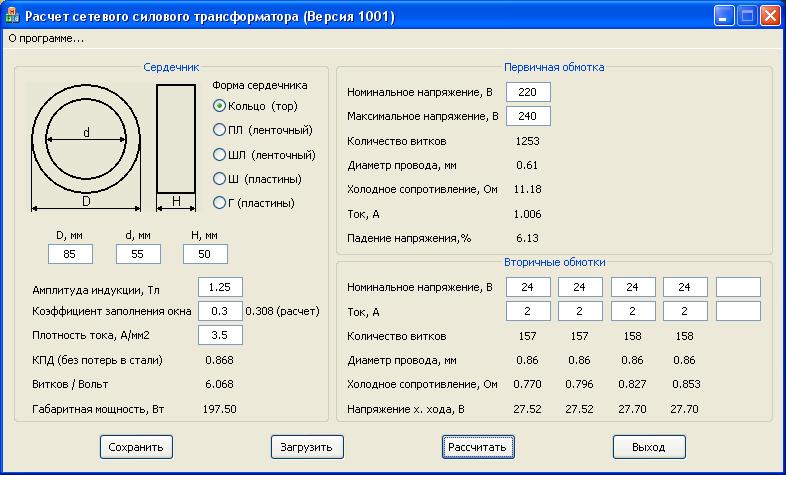
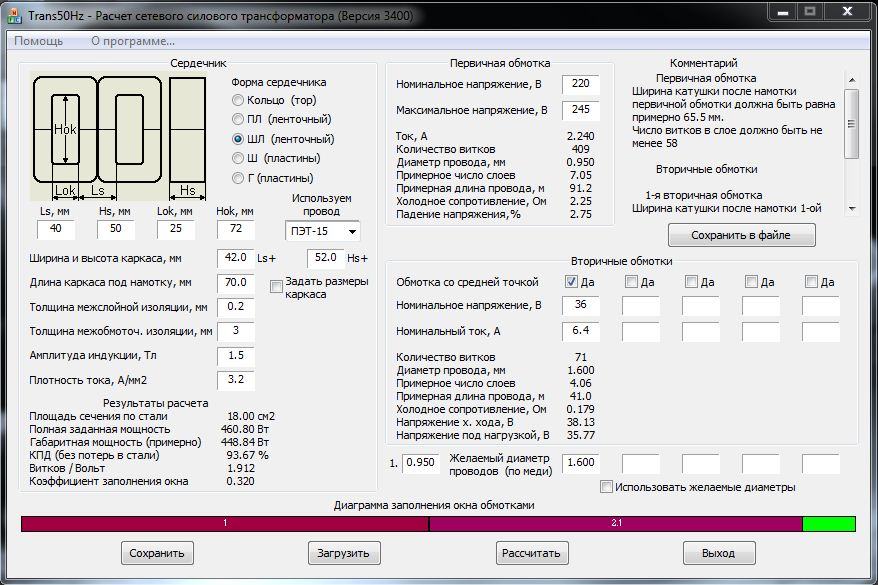
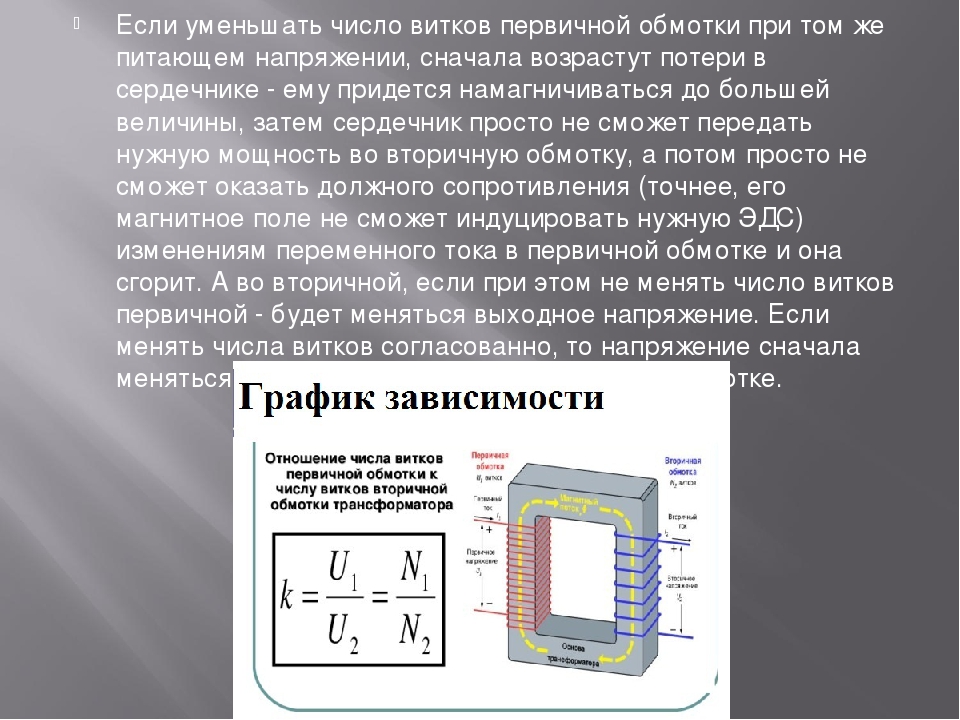
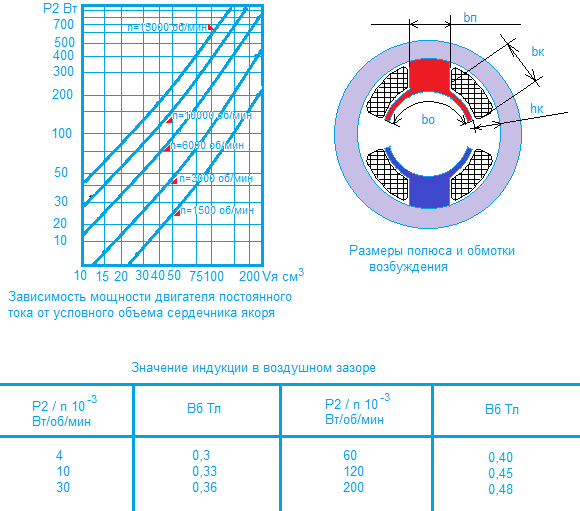
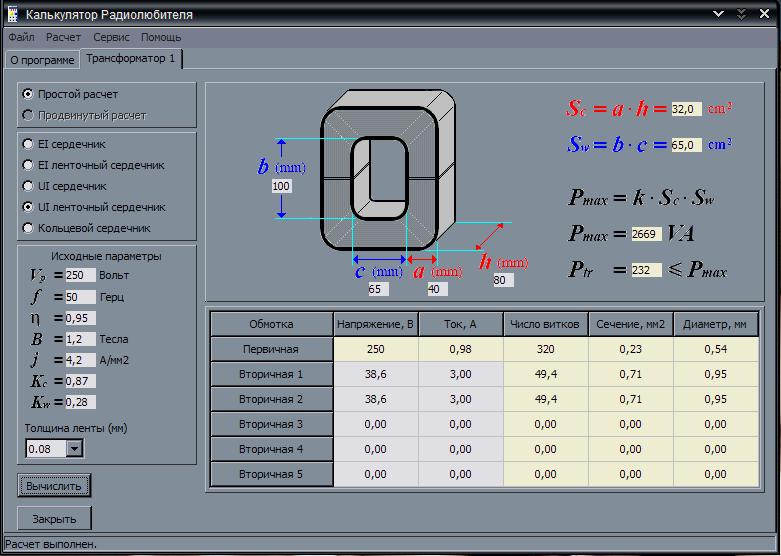
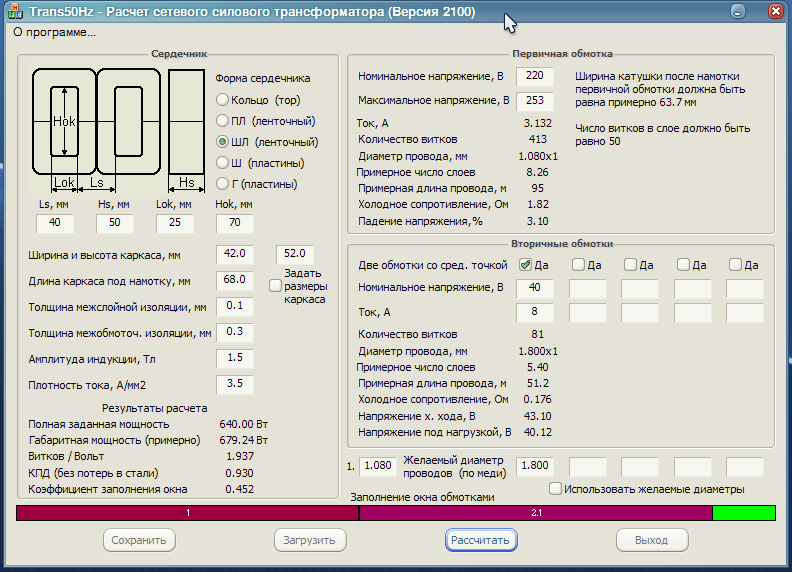
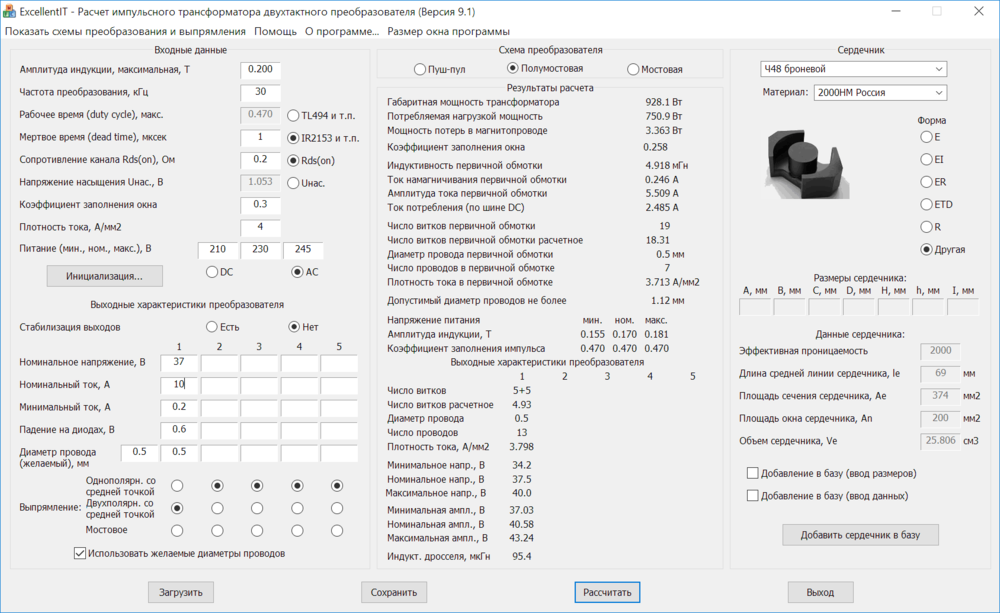
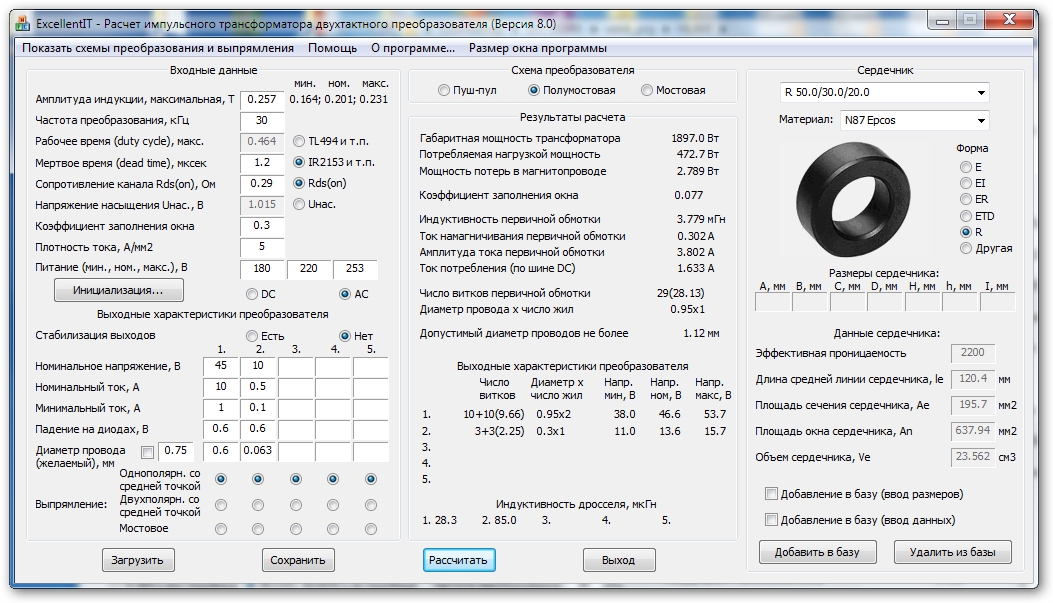
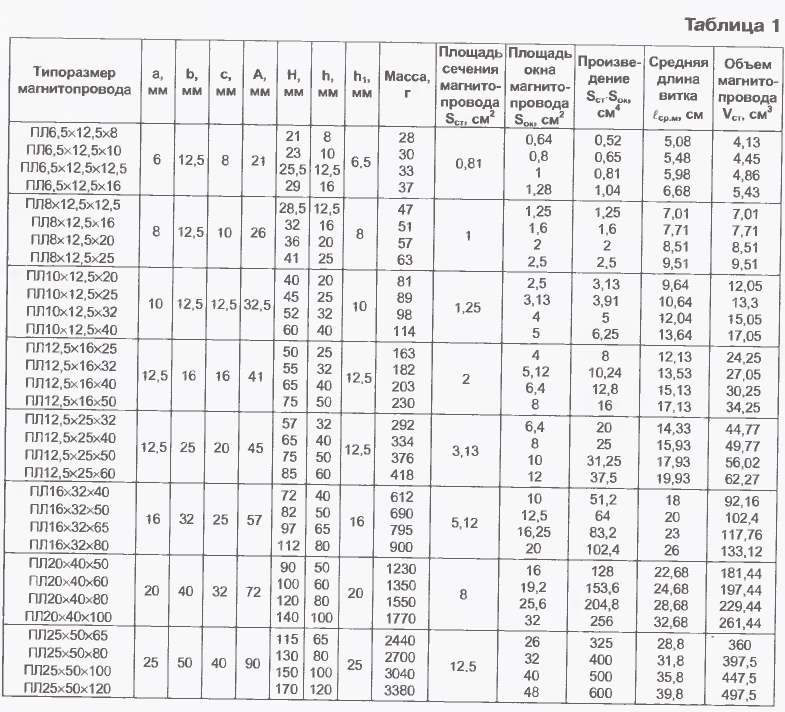
Формулы и измерение
Формулы для расчета индуктивности катушек довольно сложны и имеет различный вид для различных типов исполнения обмоток:
- линейный проводник;
- одновитковая катушка;
- плоская катушка;
- соленоидальная обмотка;
- тороидальная форма.
Наибольшие сложности возникают при расчетах многовитковых многослойных катушек, то есть тех, которые составляют обмотку трансформаторов.
Формулы для расчета индуктивности трансформатора основаны на расчетах соленоида:
µ – магнитная проницаемость сердечника;
Для измерения индуктивности существует несколько методик и приборов, созданных на их основе. В большинстве случаев измерение производится путем вычислений индуктивного сопротивления катушки при подаче образцового напряжения заданной частоты и измеренного значения тока через обмотку.
В специализированных приборах вычисления производятся автоматически, и пользователь только считывает показания шкалы прибора, выраженные в единицах индуктивности – Гн, мГн или мкГн.
Как выбрать ферритовый кольцевой сердечник?
Выбрать примерный размер ферритового кольца можно при помощи калькулятора для расчета импульсных трансформаторов и справочника по ферритовым магнитопроводам. И то и другое Вы можете найти в .
Вводим в форму калькулятора данные предполагаемого магнитопровода и данные, полученные в предыдущем параграфе, чтобы определить габаритную мощность срдечника.
Не стоит выбирать габариты кольца впритык к максимальной мощности нагрузки. Маленькие кольца мотать не так удобно, да и витков придётся мотать намного больше.
Если свободного места в корпусе будущей конструкции достаточно, то можно выбрать кольцо с заведомо бо’льшей габаритной мощностью.
В моём распоряжении оказалось кольцо М2000НМ типоразмера К28х16х9мм. Я внёс входные данные в форму калькулятора и получил габаритную мощность 87 Ватт. Этого с лихвой хватит для моего 50-ти Ваттного источника питания.
Запустите программу. Выберете «Pacчёт тpaнcфopмaтopa пoлумocтoвoго пpeoбpaзoвaтeля c зaдaющим гeнepaтopoм».
Чтобы калькулятор не «ругался», заполните нолями окошки, неиспользуемые для расчёта вторичных обмоток.
Как правильно мотать
Получив большинство технических данных, определив точное назначение и сферу использования будущего устройства, элементов обмоток катушки трансформатора, получив заводские шаблоны для выбранного вида обмотки приступают к практической реализации намоточных процессов.
Здесь большую роль будет играть опытность исполнения таких работ, наличие инструментов для такой работы, а также терпение.
Требуется использовать обязательный алгоритм действий в таком формате работ и приготовится к нескольким неудачам заблаговременно, если опыта проведения намотки витков катушки трансформатора ранее не было. В настоящее время как электронных, так и бумажных обучающих источников по всем правилам намотки обмотки трансформатора достаточно много для того, чтобы новичок через некоторое время в этих работах смог стать профессионалом.
Принцип действия аппарата
Принцип действия устройства основан на импульсной подачи энергии. Оборудование разделяется на две обширных группы: с сигмамодуляцией и импульсной модуляцией. Первые отличаются тем, что они изменяются соотношения продолжительности импульсов с их частотой. Момент выбирается, когда закончится подача энергии и включится транзистор.
Продолжительность функционирования зависит от характеристик выходного напряжения. Если говорить о вариантах с широтно-импульсной модуляцией, то тут частота идентичная и постоянная. Напряжение — характеристика стабильная, определяется оно длительностью импульса к периоду его прохождения.
Также принцип работы определяется тем непрерывный или прерывистый поток магнитного поля установлен. Нельзя сказать, что какой-то из них лучше, просто это определяет вариативность использования.
Любой одноходовый импульсный трансформатор имеет как достоинства, так и недостатки. Среди преимуществ использования выделяют:
- минимальный вес и размеры, если сравнивать с другим видом оборудования, предназначенным для работы с частотой около 50 Гц;
- не нужна защита от короткого замыкания, так как оно произойти теоретически не может;
- сокращение использования меди, в результате чего трансформатор имеет минимальную цену;
- изменение показателей в зависимости от характеристик питающей цепи;
- нет помех, передача туда и обратно исключена из-за конструктивных особенностей.
Но, как и любое другое оборудование, обратноходовый импульсный трансформатор имеет и недостатки. К их числу относятся:
- максимальный запас энергии составляет 200 Вт — показатель ограничен работой дросселя;
- нет возможности работы на холостом ходу, то есть нагрузка подключается в обязательном порядке;
- возникают электромагнитные помехи и передаются, так как они есть в нагрузке, а она нужна.
Источник
Трансформатор, как элемент радиотехники и электротехники, работает на основе электромагнитной индукции. Говоря об индуктивности трансформатора, имеют в виду индуктивность обмоток и взаимоиндукцию между ними.
Каждая из обмоток представляет некоторое количество витков провода, намотанных на ферромагнитный сердечник, то есть обыкновенную катушку индуктивности.
Трудность в определении параметров катушки заключается в том, что они изменяются в зависимости от нескольких параметров и их сочетания:
- токи в обмотках;
- уровень намагниченности магнитопровода;
- магнитные характеристики сердечника;
- взаимодействие между соседними обмотками;
- наличия постоянной составляющей тока.
Что делает трансформатор
У трансформатора много полезных и важных функций:
- Передает электричество на расстояние. Он способен повышать переменное напряжение. Это помогает передавать переменный ток на большие расстояния. Так как у проводов тоже есть сопротивление, от источника тока требуется высокое напряжение, чтобы преодолеть сопротивление проводов. Поэтому, трансформаторы незаменимы в электросетях, где они повышают напряжение до десятки тысяч вольт. Еще возле электростанций, которые вырабатывают электрический ток, стоят распределительные трансформаторы. Они повышают напряжение для передачи их потребителям. А возле потребителей стоит понижающий трансформатор, который уменьшает напряжение до 220 В 50 Гц.
- Питает электронику. Трансформатор — это часть блока питания. Он понижает входное сетевое напряжение, которое затем выпрямляется диодным мостом, фильтруется и подается на плату. По сути, он используется практически в любом блоке питания и преобразователе.
- Питает радиолампы и электронно-лучевые трубки. Для радиоламп нужен большой спектр напряжений. Это и 12 В и 300 В и др. Для этих целей и делают трансформаторы, которые понижают и повышают сетевое напряжение. Это делается за счет разных обмоток на одном сердечнике. Разновидностью ламп являются электронно-лучевые трубки (ЭЛТ). Они используются в электронных микроскопах, где с помощью пучка электронов можно получить детальные изображения микроскопических поверхностей. Для них нужны высокие напряжения, порядка нескольких десятков тысяч киловольт. Это нужно для того, чтобы в вакуумной трубке можно было разогнать пучок электронов до больших скоростей. Электрон в вакууме может повышать скорость своего передвижения за счет повышения напряжения. И снова используется импульсный трансформатор. Он повышает напряжение за счет работы ШИМ (широтно импульсной модуляции). Такие трансформаторы называются строчными (или развертки). Такое название не спроста. По сути кинескоп — это и есть электронно-лучевая трубка. Поэтому, для работы телевизоров, где используется кинескоп, нужен строчный трансформатор.
- Согласует сопротивления. В усилителях звука согласование источника и потребителя играет важную роль. Поэтому, есть согласующие трансформаторы, которые позволяют передать максимум мощности в нагрузку. Если бы не было такого трансформатора, то лаповые усилители, которые были рассчитаны на 100 Вт, выдавали бы менее 50 Вт в нагрузку. Например, выход усилителя 2 кОм, а трансформатор согласует и понижает напряжение. А на его катушке сопротивление всего несколько десятков Ом.
- Для безопасности. Трансформатор создает гальваническую развязку между сетью и блоком питания. Это последний рубеж безопасности в блоке питания, если что=то пойдет не так. Будет время для срабатывания предохранителя. Или же катушки и магнитопровод расплавятся, но потребителю не дадут сетевую нагрузку. Он физически не связан с сетью 222 В. Связь есть только с помощью магнитного поля (взаимоиндукции). И если трансформатор рассчитан на 100 Вт, то он сможет выдать только 100 Вт. Поэтому, потребитель будет защищен от опасных высоких токов. Именно из-за этого бестрансформаторные блоки питания считаются опасными.
- Деталь оружия. В электрошокерах используются высокие напряжения. И их помогает форматировать высоковольтный трансформатор. А еще он используется в некоторых схемах Гаусс пушки.
Физические особенности процесса
Оптимальная величина потока определяется особенностями устройства. Проходя путь от генератора (места выработки) до потребителя, электрическая энергия трансформируется. В генераторе показатели выше, так как проходить ток будет большие расстояния (от 1-10 метров, до 1-10 км). Нормативные показатели – 10 кВ. Потребитель по установленным правилам должен получить электроэнергию, мощность которой равна 380 или 220 В. Добиться необходимых изменений позволяет трансформатор с вращающимся магнитным полем.
Коэффициент трансформации
При определении работы установки применяется такое понятие, как коэффициент трансформации. Его формула представлена далее:
К = Е1/Е2 = W1/W2
Отсюда следует, что напряжение на вторичном контуре будет определяться соотношением количества витков. Чтобы иметь возможность регулировать выходное электричество, в конструкцию установки вмонтирован специальный прибор. Он переключает число витков на первичном контуре. Это анцапфа.
Для проведения опыта на холостом ходу регулятор ставится в среднее положение. При этом измеряется коэффициент.
Однофазные приборы
Для проведения представленного опыта, при использовании понижающего или повышающего бытового агрегата, в расчет берется представленный коэффициент. При этом используют два вольтметра. Первый прибор подключается к первичной обмотке. Соответственно второй вольтметр подсоединяется к вторичному контуру.
Входное сопротивление измерительных приборов должно соответствовать номинальным характеристикам установки. Она может работать в понижающем или повышающем режиме. Поэтому при необходимости провести ремонтные работы, на нем измеряют не только подачу низкого, но и высокого напряжения.
Трехфазные приборы
Для трехфазных агрегатов в ходе проведения опыта исследуются показатели на всех контурах. При этом потребуется применять сразу 6 вольтметров. Можно использовать один прибор, который будет подключаться поочередно ко всем точкам измерения.
Если установленное производителем значение на первичной обмотке превышает 6 кВ, на нее подают ток 380 В. При измерении в высоковольтном режиме нельзя определить показатели с требуемым классом точности. Поэтому замер производят в режиме низкого напряжения. Это безопасно.
Применение коэффициента
В процессе проведения измерения анцапфу перемещают во все установленные производителем положения. При этом замеряют коэффициент трансформации. Это позволяет определить наличие в витках замыкания.
Если показания по фазам будут иметь разброс при замерах больше, чем 2%, а также их снижение в сравнении с предыдущими данными, это говорит об отклонениях в работе агрегата. В первом случае в системе определяется короткое замыкание, а во втором – нарушение изоляции обмоток. Агрегат не может при этом работать правильно.
Такие факты требуют подтверждения. Например, это может быть измерение сопротивления. Влиять на увеличение разброса показателей коэффициента могут возрастание сопротивления между контактами анцапфы. При частом переключении возникает такая ситуация.
Как измерить в домашних условиях
Приборы для непосредственного измерения индуктивности имеют высокую стоимость и редко используются в домашних условиях. С приемлемой точностью результаты можно получить, используя обычные приборы для измерения переменного тока: амперметр и вольтметр. Также необходим омметр.
Порядок действий следующий:
- При помощи омметра определяют активное сопротивление обмотки R.
- Подключают трансформатор последовательно с амперметром в сеть.
- Параллельно обмотке подключают вольтметр.
- По показаниям приборов определяют полное сопротивление трансформатора: Z=U/I
- Индуктивное сопротивление находят, вычитая из полного сопротивления активное: XL=Z-R
- Индуктивность определяется по формуле: L=XL/(2πf), где π – число пи 3.14, f – частота измерений.
Как правило, активное сопротивление намотки значительно (на несколько порядков) меньше индуктивного, поэтому можно его не учитывать. Именно поэтому, включение трансформатора в цепь постоянного напряжения вызывает короткое замыкание. Ток обмотки при этом будет ограничиваться только активным сопротивлением.
Знакомство с информацией
На видимой стороне представленного оборудования имеются данные, нанесение которых осуществляется одним из трех нижеперечисленных способов, таких как теснение, травление или гравировка. Каждый из представленных методов гарантирует долговечность сохранения информации. Также надпись сохраняет свою четкость на протяжении длительного периода, независимо от факторов окружающей среды и каких-либо дополнительных особенностей хранения оборудования. Информация о заводе, где было произведено оборудование, указывается на щитке, который выполнен из металла. Также там расположен год производства и заводской номер, который был присвоен оборудованию в процессе производства.
Кроме информации, которая предоставляется об производителе, в любом случае будет присутствовать информация относительно самого агрегата. Поэтому на всем оборудовании представлена номер стандарта, к которому относится само оборудование. Также обязательной для нанесения является информация о показателе номинальной мощности. Важным является наличие данных о напряжении ответвлений витков катушек.
Для каждого типа обмотки имеется определенный показатель номинального тока
Важно точно привести данные о количестве фаз для установки и частоты тока. Обязательной к предоставлению является информация о конфигурации и групп соединения катушек
Исходя из данных, которые были приведены вашему вниманию немного выше, следует перейти к информации о трансформатор маркировка с параметрами напряжения. К установке имеются определенные требования, соблюдение которых является необходимым. Различают два типа установки трансформатора маркировка – наружную и внутреннюю.
Благодаря указанию в маркировке трансформаторов технических характеристик имеется возможность точно определиться с предполагаемым методом охлаждения оборудования, вес масла, который размещается в бачке, массу начинки, которая является активной. Возле привода переключателя имеется информация относительно его расположения. В том случае, когда в установке используется способ охлаждения сухого типа, представляются на оборудовании данные относительно мощности аппаратуры в случае отключенного вентилятора. Возле щитка в обязательном порядке выбивается заводской номер конструкции. Также эта информация имеется и на баке и возле сердечника.
Специальные виды трансформаторов
К этой группе относят:
Разделительные трансформаторы
Размещение двух обмоток совершенно одинаковой конструкции на общем магнитопроводе позволяет из 220 вольт 50 герц на входе получать такое же напряжение на выходе.
Напрашивается вопрос: зачем делать такое преобразование? Ответ прост: в целях обеспечения электрической безопасности.
При пробое изоляционного слоя провода первичной схемы, на корпусе прибора появляется опасный потенциал, который по случайно сформированной цепи через землю способен поразить человека электрическим током, нанести ему электротравму.
Гальваническое разделение схемы позволяет оптимально использовать питание электрооборудования и в то же время исключает получение травм при пробоях изоляции вторичной схемы на корпус.
Поэтому разделительные трансформаторы широко используются там, где проведение работ с электроинструментом требует принятия дополнительных мер безопасности. Также они широко используются в медицинском оборудовании, допускающем непосредственный контакт с телом человека.
Высокочастотные трансформаторы
Отличаются от обычных материалом магнитопровода, который способен, в отличие от обычного трансформаторного железа, хорошо, без искажений передавать высокочастотные сигналы.
Используется в электротермии, в частности при индукционном нагреве в электротермических установках для высокочастотной сварки металлов, плавки, пайки, закалки и т.д.
Согласующие трансформаторы
Основное назначение — согласование сопротивлений разных частей в электронных схемах. Согласующие трансформаторы нашли широкое применение в антенных устройствах и конструкциях усилителей на электронных лампах звуковых частот.
Сварочные трансформаторы
Первичная обмотка создается с большим число витков, позволяющих нормально обрабатывать электрическую энергию с входным напряжением 220 или 380 вольт. Во вторичной обмотке число витков значительно меньше, а ток протекающий по ним высокий. Он может достигать тысяч ампер.
Поэтому толщина провода этой цепи выбирается повышенного поперечного сечения. Для управления сварочным током существует много различных способов.
Сварочные трансформаторы массово работают в промышленных установках и пользуются популярностью у любителей изготавливать различные самоделки своими руками.
Рассмотренные виды трансформаторов являются наиболее распространёнными. В электрических схемах работают и другие подобные устройства, выполняющие специальные задачи технологических процессов.
Векторная диаграмма трансформатора
Для упрощения расчётов напряжений и токов в трансформаторе используют векторную диаграмму, которая является графическим изображением всех уравнений трансформатора на комплексной плоскости. Векторную диаграмму строят на основе эквивалентной схемы замещения и уравнений трансформатора.
Обозначения на схеме: U1, I1, R1, X1 – напряжение, ток, активное и реактивное сопротивление первичной обмотки, U/2, I/2, X/2, R/2, Z/H – приведённые напряжение, ток, активное, реактивное сопротивление и полное сопротивление нагрузки вторичной обмотки, Е – ЭДС трансформатора, I0 – намагничивающий ток трансформатора, I0r и I0a – реактивная и активная составляющая намагничивающего тока.
Построение векторной диаграммы начинается с вектора основного магнитного потока Ф, начальная фаза которого принимается равной нулю, вектор ЭДС Е = Е/2 отстаёт от вектора Ф на 90°. Вектор тока намагничивания I0 опережает вектор магнитного потока на угол α, зависящий от магнитных потерь в сердечнике и содержит две составляющие I0r и I0a.
Для определения направлений векторов I и U/2 на вторичной обмотке можно определить из углов φн и φ/1
где x/2, r/2 – приведённое реактивное и активное сопротивление вторичной обмотки,
x/Н, r/Н – приведённое реактивное и активное сопротивление нагрузки.
Данные выражения позволяют построить вектор напряжения на выходе трансформатора U/2, на активном сопротивлении обмотки I/2r/2 и реактивном сопротивлении обмотки I/2jх/2.
Для продолжения построения необходимо воспользоваться уравнениями трансформатора. Вектор I1 равен геометрической сумме векторов I0 и –I. Произведём суммирование и изобразим на диаграмме
Вектор (-I) откладывается от конца вектора I0 параллельным переносом вектора I, но в противоположном направлении. В результате вектор I1 откладывается от начала координат и до конца вектора (-I).
Вектор напряжения на первичной обмотке
Вектор (–Е) строится от начала координат в направлении противоположном вектору Е, то есть он опережает вектор Ф на 90°, вектор I1x1 откладывается от конца вектора (–Е) перпендикулярно вектору тока I1, а вектор I1r1 – параллельно.
Построенная векторная диаграмма имеет общий характер, но её можно перестроить в зависимости от режимов работы трансформатора и позволяет определить электрические параметры трансформатора в этих режимах.
Основные причины
Перегрев оценивается с точки зрения вероятности, частоты и сложности места обнаружения. Рассмотрим ситуации, которые встречаются чаще.
Короткозамкнутый виток
Механическая неисправность, проявляющаяся в следующих случаях:
- Ошибка в обмотке. В распределительных трансформаторах присутствуют две обмотки – первичная и вторичная. Высокое напряжение (и соответственно малый ток) находится на первичной обмотке. Оттуда они путём электромагнитной индукции преобразуются в пониженное напряжение и повышенный ток во вторичной обмотке. В процессе такой трансформации обмотки неоднократно подвергаются диэлектрическим, термическим и механическим нагрузкам. В результате вероятно повреждение обмоток, которое заключается в нарушении целостности или даже в частичном выгорании;
- Нарушение изоляции. Чаще встречается в местах изгиба или поворота обмотки на следующий виток. Возникает тогда, когда фактические значения тока и напряжения превышают максимально допустимые значения (этот предел указывается предприятием-изготовителем в сопроводительной документации). В случае разрушения изоляции (например, при ударе молнии) наблюдается пробой обмотки и короткое замыкание. Несмотря на кратковременность такого процесса, перегрев значителен.
Недостаточная нагрузка
При недостаточной нагрузке во вторичной цепи входное напряжение не понижается. Из-за этого возможны диэлектрические утечки, приводящие к перегреву. Причина легко обнаруживается, поскольку недонагруженный трансформатор изменяет звуковой тон работы.
Перегрузка
Материал обмоток – медный провод, характеризующийся незначительными тепловыми потерями. Однако при нерегулярном техническом обслуживании отдельные части обмоток перегреваются. Если устройство периодически работает на повышенных значениях рабочих характеристик, то с течением времени наблюдается износ и ухудшение качества поверхностного слоя изоляции. Обмотки подвергаются тепловому деформированию, что вызывает ослабление или смещение обмоток. Трансформатор теряет в производительности, а температура на поверхности обмоток (при неудовлетворительном состоянии вентиляции) резко поднимается.
Причинами перегрузки могут быть также:
- Вибрации агрегата;
- Внезапный скачок напряжения;
- Постепенно накапливающиеся коррозионные процессы.
Сердечники
Выход из строя сердечников связан с некачественной сборкой, поэтому редко становится причиной отказа. Сердечники ламинируются, чтобы избежать появления вихревых токов, способствующих перегреву. Качество ламинирующего слоя резко ухудшается, если его не контролировать. Перегрев начинается на поверхности, распространяясь вглубь, пока не достигает обмоток. Далее происходит перегрев масла, которое испаряется, и повреждает остальные узлы агрегата.
Вероятна также и механическая поломка сердечника, проявляющаяся при попадании внутрь воды (которая впоследствии интенсивно испаряется) и из-за естественного старения материала детали. Опасность перегрева устраняется заменой трансформаторного масла.
Заземляющие втулки
Конструктивно представляют собой изолирующие устройства, которые предотвращают попадание высокого напряжения на проводник при переходе к заземляющему узлу. Внутри трансформатора используются бумажные изоляторы, которые окружены маслом, обеспечивающим дополнительную изоляцию. Пробой на гильзе втулки происходит со временем, и вызывает перегрев.
Регулирующая автоматика и система охлаждения
Основная часть такой системы – тепловое реле, при помощи которого изменяются уровень и диапазон напряжения. В этом случае включаются/выключаются отдельные части обмоток, и возможный перегрев предотвращается. Первым признаком неисправности теплового реле считается несвоевременность отработки команд на изменение численных значений характеристик вторичной цепи. Немедленной замене подлежит исполнительная пружина реле, материал которой от длительного использования утратил упругость. Поэтому не происходит включения подачи масляного охладительного потока.
Проверке подлежат охлаждающие вентиляторы, масляные насосы и теплообменники с водяным охлаждением.
Это интересно: Подключение духового шкафа и варочной панели к одной розетке: изучайте с нами
Содержание Предыдущий § Следующий
Глава четырнадцатая СХЕМА ЗАМЕЩЕНИЯ ТРАНСФОРМАТОРА И ЕЕ ПАРАМЕТРЫ
§ 14-1. Индуктивности обмоток трансформатора и электромагнитное рассеяние
Индуктивности обмоток.
В трансформаторах со стальным сердечником магнитная проницаемость стали ц. во время цикла пере-магничивания непостоянна. Поэтому в течение этого цикла непостоянны также собственные
L
и взаимные
М
индуктивности обмоток трансформатора. В результате такого непостоянства
ц,
при подключении трансформатора к сети с синусоидальным напряжением в его намагничивающем токе f’o возникают высшие гармоники (см. § 13-1).
При работе трансформатора на ток i0
накладывается ток нагрузки, по отношению к которому ток j0 и, в особенности, его высшие гармоники малы. Поэтому при исследовании режимов работы трансформатора указанными гармониками можно пренебречь и учитывать только основную гармонику тока /0- Это равносильно
допущению, что во время цикла перемагничивания ц, L
и
М
постоянны. Влияние насыщения сердечника при этом можно учесть, принимая в расчет при разных режимах работы трансформатора, при разных амплитудах потока сердечника, значения (д,,
L
и
М
для данного режима работы. В соответствии с изложенным будем полагать, что
ц, L
и
М
постоянны.
Рассмотрим индуктивности и индуктивные сопротивления обмоток, обусловленные магнитным потоком сердечника Фс, все силовые линии которого полностью замыкаются по замкнутому сердечнику и поэтому сцепляются со всеми витками первичной и вторичной обмоток (рис. 14-1).
Картина магнитного поля, замыкающегося целиком по сердечнику, одинакова независимо от того, какой из обмоток это поле создается. Поэтому и магнитное сопротивление -потоку Фс одинаково для поля обеих обмоток и в равенства (14-4), (14-5) и (14-6) входит одинаковая величина /?цС. Вследствие этого также
Первые слагаемые равенств (14-9) и (14-10) значительно больше вторых, так как потоки через воздух относительно малы.
Понятие об электромагнитном рассеянии. Полнота электромагнитной связи двух индуктивно связанных цепей характеризуется коэффициентом связи этих цепей
Как известно из курса теоретических основ электротехники, в реальных условиях всегда с
< 1.
Если бы в трансформаторе отсутствовали потоки Фв1 и Фв2, замыкающиеся по воздуху, то Lu —
Lcl, L22 = Lc2,
M —
Me, и в этом случае в соответствии с равенствами (14-4), (14-5), ^14-6) и (14-11)
Таким образом, неполнота электромагнитной связи в трансформаторе, выражаемая неравенством с < 1, обусловлена наличием потоков Фв1 и Фн2 или, точнее, неодинаковым их сцеплением с обеими обмотками. Условие с
— 1 было бы достигнуто только в том случае, если бы удалось полностью совместить первичную и вторичную обмотки» что фактически невозможно.
Явление неполной электромагнитной связи называется электромагнитным рассеянием.
Наряду с соотношением (14-11) целесообразно ввести в рассмотрение коэффициент электромагнитного рассеяния
Чем меньше с
и чем больше
а,
тем больше рассеяние.
Ввиду того что явление рассеяния обусловлено неодинаковостью или неполнотой сцепления потоков Фв1 и Фв2, проходящих по воздуху, с обеими обмотками, эти потоки называют часто также потоками рассеяния, однако это название до некоторой степени условно, так как потоки Фв1 и Фв2 обусловливают также явление взаимной индукции, поскольку Мв Ф
0. Как, будет выяснено ниже, степень неполноты электромагнитной связи, или величина электромагнитного рассеяния, оказывает большое влияние на многие
технические показатели и характеристики трансформаторов и вращающихся электрических машин.
В трансформаторах с ферромагнитным сердечником потоки ФВ1 и Фв2 относительно малы.
I Поэтому электромагнитная связь в трансформаторах весьма высока, а рассеяние мало.
В силовых трансформаторах, например, с
= 0,998 -*- 0,9995 и соответственно о = 0,001 ч- 0,004.
Вследствие этого значение а,
определяемое по формуле (14-12), представляет собой разность весьма близких величин и вычисление а по этой формуле связано с весьма большими погрешностями, так как
Ln, L%%
и
М в
практических устройствах не могут быть рассчитаны или определены из опыта с досхаточ-ной степенью точности. Поэтому возникает необходимость в непосредственном определении параметров, характеризующих электромагнитное рассеяние.
§ 14-2. Уравнения напряжения трансформатора
Рабочий процесс трансформатора можно исследовать на основе уравнений напряжения его обмоток.
Емкостные токи между элементами обмоток (витки и катушки) и между обмотками и сердечником трансформатора в обычных условиях работы трансформаторов (f
< 1000 -f- 5000
гц)
весьма малы, и ими можно пренебречь. В трансформаторах без ферромагнитного сердечника
Ln,
L22 и
М
постоянны. В соответствии с изложенным в § 14-1 можно принять, что эти величины постоянны также для любого рассматриваемого режима работы трансформатора со стальным сердечником. Пренебрежем сначала магнитными потерями в сердечнике. Тогда для однофазного двухобмо-
точного трансформатора (рис. 14-2) действительны следующие уравнения напряжения в дифференциальной форме:
Рис. 14-2. Схема однофазного двухобмоточного трансформатора
Здесь иъ и.2, ilt i2
— мгновенные значения напряжения и тока первичной и вторичной обмоток;
гх, г.г, Lu,
L22 — активные сопротивления и собственные индуктивности обмоток;
М
— взаимная индуктивность обмоток.
На схеме рис. 14-2 указаны положительные направления и
и
i,
причем стрелка
и
направлена от точки с высшим потенциалом к точке с низшим потенциалом.
При составлении уравнений (14-13) первичная обмотка рассматривается как приемник, а вторичная — как источник электрической энергии, и сами эти уравнения истолковываются следующим образом.
Первичное напряжение их
является приложенным, расходуется на падение напряжения г^ и уравновешивание э. д. с. первичной обмотки
и состоит поэтому из двух составляющих: rxix
и —
ех,
что и выражается первым уравнением (14-13). Вторичное напряжение
и%
возникает вследствие индуктирования-во вторичной обмотке э. д. с.
что соответствует второму уравнению (14-13). В уравнениях (14-13) считается, что М
> 0 и положительные токи
ix
и
i2
создают в сердечнике потоки одинакового направления.
Отметим, что в правой части второго уравнения (14-13) можно было бы изменить знаки на обратные. Тогда и2 следовало бы трактовать как напряжение, приложенное к вторичной обмотке со стороны вторичной сети. Некоторые, в особенности иностранные, авторы применяют также и эту последнюю форму записи.
Обычно силовые трансформаторы, а также ряд видов специальных трансформаторов работают с синусоидально изменяющимися токами и напряжениями. В этом случае вместо дифференциальных Уравнений (14-13) удобнее пользоваться комплексными уравнениями Для действующих значений токов и напряжений. Для получения этих уравнений в уравнения (14-13) следует подставить
xn — (nLu; xn
= col22; дг12 = соМ (14-15)
представляют собой полные собственные и взаимные индуктивные сопротивления обмоток.
При симметричной нагрузке трехфазных трансформаторов электромагнитные процессы протекают во всех фазах одинаково и соответствующие электромагнитные величины в каждой фазе также-одинаковы и лишь сдвинуты по фазе на 120°. Некоторая несимметрия магнитной цепи трехстержневого трансформатора, а также появление в ряде случаев (см. § 13-1) третьих гармоник потока обычно нет оказывают заметного влияния на работу трансформатора под’ нагрузкой. К тому же эти .явления при необходимости можно учесть отдельно. По этим причинам уравнения (14-14) с большой точностью* применимы также для фазных величин трехфазного трансформатора при симметричной его нагрузке. Система уравнений (14-14)- не учи* тывает лишь потерь в стали сердечника трансформатора. Учет этиэ* потерь будет рассмотрен отдельно.
Для трехфазного трансформатора в соответствии со сказанным выше 0it U2,
/х и /2 представляют собой фазные значения напряжений и токов.
Уравнения (14-13) и (14-14) полностью определяют процессы происходящие в трансформаторе при указанных выше допущениях и позволяют решать задачи, связанные с работой трансформатора Например^если определить из первого уравнения (14-14) /хи под ставить его значение во второе уравнение (14-14), то получим зав» симость вторичного напряжения 0%
от тока нагрузки
1г:
а второй член — падение напряжения на вторичных зажимах npij нагрузке.
Из этих соотношений видно, что такие важные с эксплуатационной точки зрения величины, как падение напряжения и ток короткого замыкания, определяются небольшой долей а
полного индуктивного сопротивления дг22, обусловленной электромагнитным рассеянием. Это же можно сказать и о ряде других величий, характеризующих эксплуатационные свойства трансформаторов и вращающихся электрических машин. Поэтому определение величин, характеризующих электромагнитное рассеяние, составляет важную задачу теории электрических машин.
Кроме указанных соображений о точности результатов, расчеты на основе уравнений (14-13) и (14-14) неудобны также в связи с тем, Что ввиду неравенства чисел витков (w1 Ф
до2) параметры
rlt
г2,
Ъп,
L22,
М, хп,
х22 и
х12,
а также напряжения
иъ и2, Ult U.z
и токи i2, /1( /2 сильно различаются по величине.
В связи с изложенным теорию электрических машин в отношении рассматриваемых вопросов целесообразно развить в следующих тесно связанных друг с другом направлениях:
1. Индуктивно связанные обмотки приводятся путем-соответствующих пересчетов к одинаковому числу витков, е результате чего порядки напряжений, токов и параметров этих обмоток становятся соответственно одинаковыми.
2. Из полных собственных индуктивностей Ln,
/_22 и индуктивных сопротивлений самоиндукции
хп
и х22 выделяются составляющие — индуктивности рассеяния
Si}
S2 и индуктивные сопротивления рассеяния
хх
и
х%,
обусловленные явлением электромагнитного рассеяния, причем это выделение производится с таким расчетом, что остающиеся части полных индуктивностей (Lu —
Si,
L22 — S2) и индуктивных сопротивлений
(хц
—
хи Х22
—
хй)
соответствуют индуктивно связанным цепям с полной связью
(с =
1).
3. Разрабатываются непосредственные методы расчета малых параметров — индуктивностей и индуктивных сопротивлений рассеяния — независимо от расчета полных индуктивностей и индуктивных сопротивлений, чем достигается необходимая точность в определении этих малых параметров.
4. От электрических цепей с индуктивной связью делается переход к схемам замещения с электрической связью цепей, что приводит к упрощению расчетов и большей наглядности теории.
5. Индуктивности и индуктивные сопротивления рассеяния вводятся в явном виде в расчетные соотношения и схемы замещения, что позволяет с необходимой точностью рассчитывать величины, зависящие от электромагнитного рассеяния.
Эти вопросы применительно к трансформаторам рассматриваются ииже.
§ 14-3. Схемы замещения двухобмоточного трансформатора
Приведение вторичной обмотки к первичной.
Первичные и вторичные токи, напряжения и другие величины имеют одинаковый порядок, если у первичной и вторичной обмоток число витков одинаково. Рассмотрим поэтому вместо реального трансформатора эквивалентный ему так называемый приведенный трансформатор, первичные и вторичные обмотки которого имеют одинаковое число витков.
Представим себе, что реальная вторичная обмотка трансформатора с числом витков ш2 заменена воображаемой, или приведенной,
обмоткой с числом витков w — Wx.
При этом число витков вторичной обмотки изменится в
раз. Величина k
называется коэффициентом приведения или трансформации.
В результате такой замены, или приведения, э. д. с. Е’2
и напряжение
U2
приведенной обмотки также изменяются в
k
раз по сравнению с величинами £2 и
U2
реальной вторичной обмотки:
Чтобы мощности приведенной и реальной обмоток при всех режимах работы были равны, необходимо соблюдать равенство
где 1’%
— приведенный вторичный ток. Отсюда с учетом второго равенства (14-21) следует, что
Намагничивающие силы приведенной и реальной обмоток на основании выражений (14-20) и (14-22) равны:
/>; = /аш2. (14-23)
Для того чтобы электромагнитные процессы в реальном и приведенном трансформаторах протекали одинаково, приведенная и реальная вторичные обмотки должны создавать одинаковые магнитные поля. Для этого, кроме соблюдения условия (14-23), необходимо, чтобы приведенная вторичная обмотка имела те же геометрические размеры и конфигурацию и была расположена в окне сердечника трансформатора так же, как и реальная вторичная, обмотка (см. например, рис. 12-2, 12-26). Поэтому суммарное сечение всех витков приведенной обмотки должно быть таким же, как и у реальной обмотки, а сечение каждого витка приведенной обмотки должно уменьшиться в k
раз. Но поскольку приведенная обмотка имеет в
k
раз больше витков, то в итоге активное сопротивление приведенной обмотки в
k2
раз больше, чем реальной:
Так как при одинаковых геометрических размерах и одинаковом расположении катушек их индуктивности и индуктивные сопротивления пропорциональны квадратам чисел витков, то между индуктивными сопротивлениями приведенной обмотки х’3
и реальной лг2 существует такое же соотношение:
Таким образом, все энергетические и электромагнитные соотношения в приведенном и реальном трансформаторах одинаковы, что и позволяет производить указанное приведение.
Схема замещения без учета магнитных потерь.
В соответствии с изложенным сделаем в уравнениях напряжения трансформатора (14-14^ поястановки:
При переходе к электрической связи двух цепей в соответствующей схеме замещения должна появиться общая для обеих цепей ветвь, которая обтекается суммой токов обеих цепей /г + 1[.
Соответственно этому в уравнениях напряжений этих цепей должны появиться одинаковые члены с множителями (/х + /J). Из уравнений (14-27) видно, что для получения в них таких членов нужно прибавить к первому из этих уравнений и вычесть из него член
]кхп!г
и прибавить ко второму и вычесть из него член
]кхп{‘%.
При этом получим
Введем следующие наименования и обозначения:
1) приведенное активное сопротивление вторичной обмотки
Уравнениям (14-34), как нетрудно видеть, соответствует схема замещения рис. 14-3, а.
Действительно, мысленно обойдя левый и правый контуры схемы рис. 14-3,
а
и составив уравнения напря-жеяия для этих контуров, вновь получим уравнения (14-34). Таким образом, схема рис. 14-3, а представляет собой схему замещения трансформатора, л^ответст^ующую уравнениям (14-14) и (14-34).
Аналогичным образом можно также преобразовать уравнения напряжения в дифференциальной форме (14-13), произведя в них подстановки
При этом получается схема замещения рис. 14-3, б,
где
представляют собой индуктивности рассеяния первичной и вторичной обмоток, а
— приведенную взаимную индуктивность.
Схема замещения рис. 14-3, б
действительна при любых закономерностях изменения напряжения и токов во времени, в том
числе и в случае переходных процессов.
Уравнения (14-34) и схемы замещения рис. 14-3 можно трактовать таким образом, что сопротивления гх
и
хъ г’ъ
и
х
или индуктивности
St
и Sj включены в цепи дбмоток до и после трансформатора, а параметры обмоток трансформатора уменьшены на эти величины. В результате получается идеальный трансформатор, активные сопротивления которого равны нулю, а коэффициент электромагнитной-связи с = 1. Действительно, у такого идеального трансформатора приведенные собственные и взаимные индуктивные сопротивления одинаковы и равны
х’п
=
kxn
и поэтому в соответствии с равенствами (14-12) и (14-19) с2 = 1 и
а
= 0.
Рис. 14-3. Схемы замещения двух-
обмоточного трансформатора без
учета магнитных потерь
Отметим, что, как следует из рассмотрения приведенных преобразований, соотношения (14-26) и все последующие, а также схемы замещения рис. 14-3 справедливы и правильно отражают все процессы в трансформаторе при любом значении k.
С математической точки зрения эти преобразования означают переход от переменных /72 и /2 к новым переменным
О’2я 1’2
по формулам (14-26), что возможно при любом значении
k.
В связи с этим необходимо подчеркнуть, что индуктивные сопротивления и индуктивности рассеяния, согласно равенствам (14-30) — (14-33), (14-36), (14-37) и (14-38), определяются неоднозначно и зависят от коэффициента приведения
к.
Однако для силовых трансформаторов
k
рационально определять по формуле (14-20), как это и принято на практике и всюду в данной книге. Выбор иного значения
k
целесообразен лишь в специальных случаях, например в измерительных трансформаторах тока *.
Параметры схемы замещения.
Рассмотрим параметры схем замещения рис. 14-3 при
k
=
wjw2
[см. равенство (14-20)].
Приведенная взаимная индуктивность на основании равенств (14-6), (14-10) и (14-38)
Следовательно, сопротивление х’п
с большой точностью равно сопротивлению самоиндукции первичной обмотки от потока, замыкающегося по сердечнику.
1 А. И. Воль дек. О
схеме замещения трансформатора и ее параметрах. «Электричество», 1952,
№.
8, с. 21-25.
Ветви 1
—
2
схем замещения рис. 14-3 называются намагничивающими ветвями. Протекающий по этим ветвям намагничивающий то«
Таким образом, индуктивности рассеяния Slt
52 и Sj и индуктивные сопротивления рассеяния
Однако вторыми членами равенств (14-42) и (14-43) по сравнению с первыми пренебречь нельзя, и поэтому потоки, замыкающиеся по воздуху, можно назвать потоками рассеяния лишь условно.
Схема замещения с учетом магнитных потерь.
Потери в стали сердечника рвг при заданной частоте пропорциональны следующим величинам:
Таким образом, потери #вг пропорциональны квадрату напряжения Un
на зажима*
1
—2 намагничивающей цепи схемы замещения рис. 14-3,
а.
Если к этим зажимам параллельно
х’п
=
хс1
подключить активное сопротивление гмг, как показано на рис. 14-4,
а,
Величину рят
при заданной а. д. с.
Ех
можно считать известной из расчетных (см. § 13-2) ил.и опытных данных. Тогда можно считать известным- также гмг.
Намагничивающий ток
разделяется в двух ветвях намагничивающей цепи (рис. 14-4, а) на активную /ма и реактивную 1ЯГ
составляющие (см. § 13-2), из которых первая определяет мощность магнитных потерь, а вторая создает поток сердечника.
то потери в этом сопротивлении также будут пропорциональны (7i3. Величину сопротивления гмг можно подобрать так, чтобы потери в нем равнялись магнитным потерям:
Рис. 14-4. Намагничивающая цепь схемы замещения с учетом магнитных потерь
Схема с двумя параллельными ветвями намагничивающей цепнг хорошо согласовывается с реальными физическими явлениями. Однако расчеты на основе схемы замещения вести удобнее, если объединить две параллельные ветви схемы рис. 14-4, а
в одну общую ветвь, как показано на рис. 14-4,
б.
Тогда сопротивление этой ветви
Ф
При увеличении насыщения сердечника, т. е. при увеличении , Ei
или
Ult
сопротивление
х’п
при / = const уменьшается. Однако
при этом гмг«=! const, а значение гм уменьшается.
Схема замещения трансформатора с учетом магнитных потерь согласно рис. 14-4, б
показана нд рис. 14-5,
а.
Если использовать обозначения
то схему замещения можно изобразить более компактно, как пока’ зано на рис. 14-5,6. В_режиме холостого хода /а = 0 и Д = /н — току холостого хода трансформатора. В итоге получилась весьма простая Г-образная схема замещения трансформатора, представляющая собой пассивный четырехполюсник. Сопротивление намагничивающей цепи этой схемы ZM отражает явления в ферромагнитном сердечнике. Оно значительно больше сопротивлений Zx
и
Ъ’г,
которые включают в себя активные сопротивления и индуктивные сопротивления рассеяния обмоток. Для силовых трансформаторов в относительных единицах
Рис. 14-5. Схема замещения друх-обмоточного трансформатора с учетом магнитных потерь
Уравнения напряжений и схему замещения трансформатора можно представлять также в относительных единицах. Имея в виду, что
левые части уравнений вида (14-34) можно разделить на £/,,, а правые части — на ZH/H, в результате чего и будет совершен переход к относительным единицам. Абсолютные значения U, I, r, x
и Z в схемах замещения также можно заменить относительными. При этом расчеты режимов работы трансформатора можно вести в относительных единицах.
Нетрудно видеть, что относительные величины сопротивлений, токов и напряжений вторичной цепи будут зависеть от того, какая величина коэффициента k
была использована при приведении вторичной обмотки к первичной. Неопределенность в этом вопросе исчезает, если определять
k
всегда одинаковым образом. Например, в силовых трансформаторах всегда берут
к =
шх/а>а.
Упрощенная схема замещения.
Так как 2М >>
1Хта Z’%,
то во многих случаях можно положить 2М = оо, что означает разрыв намагничивающей цепи схемы замещения рис. 14-5. При ZM = оо будет /м = 0, т. е. такое допущение эквивалентно пренебрежению намагничивающим током или током холостого хода, что ввиду малости /м во многих случаях допустимо. При этом
1г =
—
l’t — t.
При
2М = оо и /м = 0 схема замещения принимает вид, изображенный на рис. 14-6. Параметры этой схемы
называются соответственно полным, активным и индуктивным сопротивлениями короткого замыкания (см. также § 14-5). Такие названия обусловлены тем, что замыкание вторичных зажимов трансформатора накоротко соответствует замыканию накоротко вторичных (правых) зажимов схемы замещения рис. 14-6 и при этом сопротивление трансформатора при коротком замыкании будет равным ZK.
Схема замещения рис. 14-6 чрезвычайно проста. Согласно этой схеме, трансформатор эквивалентен сопротивлению ZK. Обычно в силовых трансформаторах гк* = 0,05 -г- 0,15.
§ 14-4. Расчетное определение параметров схемы замещения трансформатора
Параметры схемы замещения могут быть определены расчетным или опытным путем.
Активные сопротивления обмоток легко рассчитываются по обмоточным данным, если известны коэффициенты вытеснения тока, учитывающие увеличение активных сопротивлений под влиянием
Рис. 14-6. Упрощенная схема замещения трансформатора
поверхностного эффекта (см. § 12-3). Обычно эти коэффициенты находятся в пределах 1,005—1,15.
Параметры намагничивающей цепи,легко определяются по данным расчета магнитной цепи (см. § 13-2). Сопротивление гмг для схемы рис. 14-4, а
уже было определено в § 14-3 [см. формулу (14-45)].
Для того чтобы найти х’и
для заданного значения э. д. с.
Ег
[см. формулу (12-3)1, надо определить поток Фс, затем н. с.
F
и, наконец, по формулам (13-3) или (13-6) ток
1Ог,
Тогда
После этого могут быть использованы формулы (14-46) и (14-47).
Метод противовключения. Наибольшую трудность вследствие сложного характера магнитных полей в воздухе представляет определение индуктивных сопротивлений рассеяния xt
и
х[.
Вместе с тем достаточно точное определение этих параметров имеет важное значение (см. § 14-1). Рассматривая схему замещения рис. 14-5, а, можно отметить, что влияние параметров
хг
и
x’t
этой схемы на эксплуатационные показатели и характеристики трансформатора гораздо больше, чем влияние параметров намагничивающей цепа.
Для вычисления л?! и х’%
используется метод так называемого противовключения, который был предложен в 1909 г^ немецким электротехником В. Роговским и заключается в следующем.
Нслн питать трансформатор с первичной и вторичной сторон такими напряжениями Ut
и
Oit
что
IB связи с изложенным можно сказать, что в режиме противо-включения существуют только магнитные поля рассеяния.
Осуществление опыта противовключения при wt ф w2
в действительности практически невозможно, так как весьма трудно достичь соблюдения условия (14-50) с большой точностью. При небольшом нарушении этого условия в сердечнике возникает заметный поток Фс, сравнимый с потоками в воздухе Фв, и равенства (14-51) и (14-53) грубо нарушаются. Поэтому осуществление этого опыта на практике возможно только при изготовлении геометрически подобного макета исследуемого трансформатора с
wx
= ш2 или при замене вторичной обмотки приведенной. В этом случае опыт можно осуществить по схеме рис. 14-7. Идея метода противовключения
Рис. 14-7. Схема опыта противовключения
лежит в основе всех расчетных методов определения индуктивных сопротивлений рассеяния.
Расчет индуктивных сопротивлений рассеяния
по отдельности для каждой из обмоток представляет значительные трудности. Поэтому обычно рассчитывается сумма этих сопротивлений исходя из картины магнитного поля в режиме противовключения, когда
кЩ + кЩ
=
(h + i*) wx
= 0.
На рис. 14-8, а
изображены сечения концентрических обмоток, расположенных в окне трансформатора, и характер создаваемого им магнитного поля в режиме противовключения. Эту картину поля можно заменить слегка идеализированной (рис. 14-8,
б),
когда все магнитные линии направлены вертикально и их эквивалентная расчетная длина между ярмами
1а
несколько больше высоты обмотки /, т. е.
/, = //**, (14-54)
где kR
= 0,93 -г 0,98 представляет собой так называемый коэффициент Роговского.
Определим закономерность распределения напряженности поля вдоль координаты х
на рис. 14-8,
б.
Применим закон полного тока
для магнитной линии в зоне / (0<: х
«£бг). Для стали можно принять |ic = оо и, следовательно,
Нс
= 0. Поэтому круговой инте-
Рис. 14-8. Картины магнитных полей трансформатора в режиме противовключения
грал равен Нх11а,
а рассматриваемая магнитная линия сцепляется с током
График изменения Нх
вдоль координаты
х
изображен на рис. 14-9.
Установить на рис. 14-8 точную границу раздела магнитных линий, сцепляющихся с разными обмотками, затруднительно. Поэтому вычисление хх
и дг^ по отдельности невозможно. Однако можно вычислить сумму
хх
и
х’%
и тогда расположение этой границы не имеет значения и можно условно принять, что она проходит посредине области // на рис. 14-8,
б.
Пренебрежем изменением диаметра вдоль координаты х
и примем в расчет средний диаметр двух обмоток
Dcp.
Тогда элементарная магнитная трубка кольцевидного сечения в зоне / с координатой
х
заключает поток
Рис. 14-9. Кривая напряженности поля рассеяния Их
= /
(х)
сцепляется с количеством витков щ.
Поэтому на основании выражений (14-55) и (14-56) потокосцепление первичной обмотки
Пусть вторичная обмотка приведена к первичной. Тогда для нее аналогичным образом получим
Величина
называется также приведенной величиной зазора между обмотками. Из {
14-58) видна зависимость сопротивлений рассеяния от геометрических соотношений. Увеличение диаметра сердечника
Dc
при
Вс =
const приводит к увеличению потока сердечника пропорционально О’нк уменьшению
wl
и /. В результате сопротивление рассеяния уменьшается. Если при проектировании трансформатора заданной мощности сечение сердечника уже выбрано, то этим определяется также величина
Ос„,
количество витков
wx
и площади сечения обмоток /бх «=« /б2. Если при этом выбирать / больше, а бх и б2 меньше, то рассеяние будет уменьшаться, и наоборот.
Расстояние между двумя обмотками б выбирается исходя из условий электрической прочности и исключения пробоя обмоток в зависимости от их номинальных напряжений. С ростом номинальных напряжений б растет и соответственно увеличивается также рассеяние.
Формулы для расчета индуктивных сопротивлений рассеяния чередующихся обмоток могут быть получены аналогичным образом.
Выше был рассмотрен расчет магнитного поля и индуктивных сопротивлений рассеяния для простейшего трансформатора с обмотками простой формы и с равномерным распределением полного тока обмотки iw
вдоль стержня. В более сложных случаях соответствующие расчеты сильно усложняются.
Глубокие исследования магнитных полей и индуктивных сопротивлений рассеяния трансформаторов в СССР выполнены Г. Н. Петровым, Е. Г. Марквардтом, Э. А. Манькиным и др.
§ 14-5. Опытное определение параметров схемы замещения трансформатора
Опыт холостого хода.
Опытное определение параметров схемы замещения трансформатора производится по данным опыта холостого хода и короткого замыкания.
Схема опытов холостого хода однофазного (т = 1) и трехфазного (т = 3) двухобмоточных трансформаторов приведены на рис. 14-10. Первичная обмотка трансформатора подключается на синусоидальное напряжение, а вторичная обмотка разомкнута. Измеряются первичные напряжения Uo
=
Uw,
ток /0 =
1г
и мощность
Ро
=
Pi,
а также вторичное напряжение
Uw.
Из данных опыта для однофазного трансформатора определяются полное, активное и индуктивное сопротивления холостого хода:
Рис. 14-10. Схемы опытов холостого
х°Да однофазного (а) и трехфазного (б)
двухобмоточных трансформаторов
Для трехфазного трансформатора по показаниям трех амперметров и вольтметров определяются средние значения линейного тока /Ол и линейного напряжения 1/Ол,
а по показаниям ваттметров — мощность холостого хода трех фаз
Ро
=
Р’
+
Р»>
Физический смысл имеют только значения сопротивлений, рассчитанные для фазы обмотки. Поэтому необходимо принять во внимание схему соединения обмотки. В случае соединения первичной обмотки в звезду
Коэффициент трансформации трехфазного трансформатора может рассчитываться по фазным напряжениям (&) или по линейным напряжениям (&л). Для теории трансформатора имеет значение первое из указанных значений коэффициента трансформации.
Целесообразно определять относительные значения перечисленных сопротивлений:
Уравнению напряжения холостого хода (14-7U) соответствует векторная диаграмма холостого хода на рис. 14-11. На этой диаграмме для ее ясности падения напряжения rjQ
и
jxjo
изображены весьма большими. В действительности они составляют доли процента от
Uo,
поэтому ими можно пренебречь и положить
Uo
= = —£1. Вследствие преобладания индуктивного сопротивления при
Uo
=
UH
коэффициент мощности cos
0 «£ 0,1.
Так как гх
<^ гм, то потери холостого хода практически представляют собой потери в стали сердечника, включая потери от вихревых токов в стенках бака в режиме холостого хода.
Опыт холостого хода производят обычно для ряда значений Uo:
от
Uo
а* 0,3
Un
до
Uo
« 1,1 (/„и по полученным данным строят характеристики холостого хода, представляющие собой зависимости /0, jP0, 2о, r0, coscp0 от
Uo
(рис. 14-12). При увеличении
Uo
насыщение сердечника увеличивается, вследствие чего /0 растет быстрее
UQ.
Поэтому
z0
и
х0
с ростом
Uo
уменьшаются. Так как
Рп г^ Е2 ^ U2,
а
Ро
растет быстрее
Щ,
то
г0
с ростом
Uо
также . уменьшается. По характеристикам холостого хода устанавливаются значения соответствующих величин для
Uo
==
UH.
Опыт короткого замыкания производится по схемам рис. 14-13. Вторичные обмотки замыкаются накоротко, а к первичным обмоткам во избежание перегрева и повреждения трансформатора подводится пониженное напряжение с таким расчетом, чтобы ток находился в пределах номинального.
Полное zK, активное гк
и реактивное
хк
сопротивления короткого замыкания рассчитываются по формулам, аналогичным для случая холостого хода.
Для однофазного трансформатора
Для трехфазного трансформатора по показаниям приборов определяются средние значения линейного напряжения £/кл, линейного тока /кл и мощности короткого замыкания трех фаз Рк. При соединении первичной обмотки в звезду параметры короткого замыкания на фазу будут следующие:
Рис. 14-12. Характеристики холостого хода трансформатора с соединением обмоток Y/Yo,
240
кв • а,
3150/380
в,
замеренные со стороны НН
Рис. 14-13. Схемы опытов короткого замыкания однофазного (а) и трехфазного (б) явухобмоточных трансформаторов
Векторная диаграмма трансформатора при коротком замыкании с /к = /н изображена в двух видах на рис. 14-15, а, б.
Треугольник на рис. 14-15,
б
называется треугольником короткого замыкания. Его катеты представляют собой активную и реактивную составляющие напряжения короткого замыкания:
ика = ик
cos фк; MKr = uKsin
K. (14-79)
В трансформаторах мощностью SB =
10
кв -а
обычно cos
K « я» 0,65, а в трансформаторах мощностью SH = 60 000 кв -а
обычно cos фк « 0,05. Таким образом, в мощных трансформаторах преобладают составляющие
uv
и
х&
по сравнению с ыка и гк. Очевидно,
что мКо* = гк*,
«кг* = *к*- Величина
ика*
приводится к температуре обмоток, равной 75е С.
Согласно изложенному, напряжение короткого замыкания характеризует величину активных сопротивлений и индуктивных сопротивлений рассеяния трансформатора и является поэтому важной характеристикой трансформатора. Величина ико/о указывается в паспортной табличке трансформатора. В силовых трансформаторах ик%
= 4,5 -5- 15. Первая цифра относится к трансформаторам с номинальным линейным напряжением {/лн=^ 10 к», авто-рая — к трансформаторам с
Un,
н = 500 /се, которые обладают большим рассеянием вследствие большого расстояния между обмотками.
Величина э. д. с. Ег
в опыте короткого замыкания при ^к — ^н в 15—40 раз меньше [/„. При этом магнитные потери в 225—1600 раз меньше, чем в случае
U = UB,
и весьма малы. Поэтому мощность короткого замыкания
Рк
с большой точностью представляет собой мощность электрических потерь в обмотках, включая добавочные потери в стенках бака и в крепежных деталях от потоков рассеяния трансформатора. Следовательно, и
гк
— гх + г«, определенное из опыта короткого замыкания, является эквивалентным сопротивлением с учетом этих потерь.
Если короткое замыкание происходит при номинальном первичном напряжении, то
Рис. 14-14. Характеристики короткого замыкания трансформатора с соединением обмоток Y/Yo, 240 кв-а,
3150/380 в, замеренные со стороны ВН
Рис. 14-15. Векторные диаграммы трансформатора при коротком замыкании с /* = /„
Содержание Предыдущий § Следующий
Измерение и расчет предельной кратности
При превышении предельного нормированного показателя прибор переходит из стабильной области работы в фазу насыщения. Точность функционала оценивается по математическим кривым, условия которых приведены в таблицах. Коэффициент устанавливается не опытным путем, а по специальным табличным данным. Кривые состоят из информации о наибольшем отношении тока вторички к среднему номинальному назначению, которое подается на первичку.
Расчет производится таким образом, чтоб полная ошибка при вычисляемых данных (то есть при включении заданной информации о вторичной нагрузке) не было больше десяти процентов. Математические кривые позволяют вычислить характеристики проводов, приборов, реле, схемы подсоединения и составить схему таким образом, чтоб не происходило пересыщение и приборы работали в оптимальном режиме.
Оборудование, дополненное дифференциальной защитой, при сквозном токе короткого замыкания должно иметь идентичную предельную кратность.
Расчетные кривые приводятся для вычислений работы по установленному режиму. Если апериодическая стремится к max, то есть режим переходный, то параметр достигает и 70-75%.
Класс точности выбирают в зависимости от назначения. Такие же требования применяются и к устройствам с неидентичными типами нагрузок.
Выпрямители
Выпрямитель со средней точкой силового трансформатора позволяет преобразовать переменный ток в постоянный. Используется полупроводниковый диод, который заставляет совокупность электронов помещаться в одну сторону и протекать не отклоняясь от маршрута.
Наиболее простой с технологической точки зрения, но отнюдь не эффективный, – это однополупериодный выпрямитель. Это устройство отличается те, что добавляет в нагрузку лишь единственный полупериод — отсюда и соответствующее название.
Используется данный вариант не часто. Дело в том, что это экономически неоправданно. Сложны для фильтрации и подачи в итоге ровного и чистого сигнала, он возникшие в форме кривой гармоники разного типа. Также нежелательны для трансформаторов силового типа поступающие токовые импульсы от источника переменного в нагрузку, учитывая только нахождение там в полупериоде. Используются приборы в основном в схемах, где требуется быстрое и эффективное снижение мощности с использованием резисторов. Например, при ослаблении яркости лампы будет нагрузка подаваться, а при получении полной мощности отключаться.
Меньше половины изначальной мощности поучит лампа (возьмем ее для примера), если включить ее в положении уменьшенной силы. То есть выпрямитель в данной ситуации не используется в линии подачи энергии. Мерцания света не заметно человеческим глазом по той причине, что пульсация тока гораздо быстрей получается, чем охлаждение и нагревание поэтапно нити накаливания. Нить нагревается постепенен больше, так как увеличиваются промежутки, но сила света ослабляется.
Пульсация токовых импульсов часто используется в промышленности. Это необходимо для того, чтоб получать энергию тепла, которая выделяется при выключении устройства. Схема простейшая, она служит лишь примером для начинающих специалистов, которым необходимо понять, как происходит питание и действует нагрузка.
Схема
Сложность заключается в том, что при выпрямлении переменного тока необходимо применять два значения полупериода. Объединить устройства не получится, необходимо использование прибора, который включал бы в себя преимущества оба. Инженеры придумали двухполупериодные выпрямители. Подключение вторичных обмоток силового трансформатора со средней точкой проводится именно по такому типу. Подразумевается, что использоваться будет средняя точка вторички и два диода дополнительно.
Принцип действия будет больше понятен, если описать принципы работы обоих полупериодов. Первый определяется, когда напряжение сверху сугубо положительное, а снизу отрицательное. Данные фиксируются на схеме. Если построить синусоиду подачи тока, то видно, что проводящим ток является только верхний диод. Он заметен по графику только первый период синусоиды, построенной ранее. А нижняя часть поступления тока убирается, она заблокирована. По сути, движение цикла наблюдается лишь в первой половине обмотки. Это видно по графику синусоиды, и необязательно рассматривать точки на силовом трансформаторе или выпрямителе.
Рассматривая второй цикл заметно, что полярность импульса вариативна. Ток идет по следующему диоду, который инженеры называют вторичным. Переменный ток распространяется по второй половине обмотки внешней плана. Другая же половина, которая была задействована ранее в приведенном алгоритме выше, сейчас бездействует, импульсов и токов ней нет. Ситуация по схеме синусоиды меняется. Нагрузка заметна только в той половине графика, которая ниже. Обратите внимание, что положительные характеристики тока такими же и остаются верху, внизу они будут соответственно отрицательными. Полярность идентичная при прохождении импульсом любой части устройства.
Минусы
Минус оборудования состоит в том, что нужный становится вариант отвода от средней точки. Речь идет о вторичной обмотке трансформатора. Используется отвод в маломощных системах и вариантах со средними показателями. Для соединения элементов мощной схемы не удаться обойтись единственным выпрямителем со средней точкой. Придется заказывать профессиональный тс, который имеют большую цену. Отдельно отметить стоит, что:
- изменить полярность выпрямителя возможно просто включив обратным образом диоды;
- установленные обратным образом детали располагаются параллельным образом.
Зачем нужно изменять ход течения тока станет понятно, если рассмотреть схемы подключения. Получается, что возможен вход двух полярный, что упрощает использование устройства в домашних и промышленных целях. Используется идентичная компоновка, что и в мостовой цепи.
Есть вариант выпрямителя, строящиеся не и двух диодов с идентичной конфигурацией, а из четырех. Носит он название моста, ток проходит только в одну сторону. Типология его движения не зависит от ходовой полярности. Инженер должен заметить, что положительный знак на нагрузке равняется отрицательному у подключаемого прибора. Отметим, что:
- выбор полярности не играет роли;
- в любом случае ток направится по параллельным образом подключенным диодам;
- уменьшение показателей линейное, оно удваивается, если использованы стандартные кремниевые пластины.
Критична эта потеря напряжения в удвоенной сумме лишь для низковольтных источников питания. Для высоковольтных подобные характеристики не действительны.
Особенности
Выпрямитель с любым типом фаз дает на выход ток, относящийся к пульсирующему типу. Для современных приборов поступление тока с пульсирующими, временными характеристикам неприемлемо. Оборудование нуждается в постоянном импульсе, чтоб поддерживать работоспособность. Схемы со средней точкой используются в случае небольшой мощности и несущественных экстремальных колебаний показателей.
Число пульсаций, которые получаются на выходе, вычисляется в зависимости от количества оборотов тока по кругу. Эту характеристику вычисляют стандартным методом, просто умножив импульс на полный цикл движения и выявив геометрическую прогрессию. То есть, если речь идет о однополупериодном варианте, то коэффициент составит единицу. То есть за цикл перехода тока наблюдался единственный импульс за все время.
Для двух выпрямителя характерно увеличение пульсации вдвое, как уже говорилось, частота пульсаций прямо пропорциональна увеличению на 2 сетевой частоте. Для двухполупериодного устройства характеристика равна двойке Для двухполупериодного оборудования коэффициент умножается на шесть (два на каждые два проводника, установленных в системе). Возможна установка многофазных систем, то в таком случае потребуется применение систем соединения треугольник-звезда, звезда-треугольник и других. Расчет для средней точки производится индивидуально.
Ремонт трансформаторов
Ремонт и перемотка электротрансформаторов производится в определенном порядке:
- Разобрать магнитопровод. Железо сложить отдельно, по пластинам.
- Размотать сгоревшую катушку, считая число витков. Замерять микрометром диаметр провода.
- Намотать новые обмотки. Между слоями намотки и катушками проложить изоляционный материал. Его толщина зависит от диаметра провода.
- Собрать аппарат. Пластины трансформаторного железа необходимо плотно прижать, а при необходимости расклинить деревянными клиньями в катушке.
Для намотки необходимо использовать специальный станок. Намотать катушку руками, особенно с большим количеством витков из тонкого провода практически невозможно.
Совет! Если сгорела только одна из вторичных обмоток, то остальные не перематываются.
Частичная перемотка трансформатора
Для перемотки одной из вторичных катушек необходимо:
- разобрать устройство – вынуть сердечник и размотать сгоревшую катушку;
- снова собрать устройство, подключить его к сети и проверить работу в режиме холостого хода;
- после проверки снова разобрать прибор, намотать недостающие обмотки и произвести окончательную сборку и проверку в работе аппарата.
От чего зависит ЭДС в обмотках трансформатора?
В прошлой статье я указал, что мгновенное значение ЭДС в обмотке трансформатора определяется числом витков ω провода в ней и скоростью изменения магнитного потока dΦ/dt
где ω – число витков обмотки трансформатора,
dФВ/dt – скорость изменения магнитного потока.
Однако в большинстве случаев нам интересно не мгновенное значение ЭДС, а действующее. Поэтому выведем выражение, определяющее действующее значение ЭДС в обмотках трансформатора. Это можно сделать аналитически проинтегрировав функцию изменения магнитного потока dΦ/dt, либо же путем нахождения среднего значения ЭДС Ecp и коэффициента формы ЭДС kф. Я буду выводить выражение вторым способом.
Магнитный поток протекая в сердечнике трансформатора изменяется в соответствии с некоторой периодичной функцией имеет два амплитудных значения максимальное +Фm и минимальное –Фm, тогда полное изменение магнитного потока за полупериод Т/2 будет иметь значение
Тогда среднее значение ЭДС Еср в обмотке трансформатора будет иметь вид
где ω – число витков обмотки трансформатора,
Т/2 – полупериод изменения функции магнитного потока,
f – частота изменения магнитного потока,
Фm – амплитуда магнитного потока.
Действующее значение ЭДС и её среднее значение связывает коэффициент формы кривой ЭДС kф, тогда действующее значение ЭДС в обмотке трансформатора будет определяться следующим выражением
где kф – коэффициент формы ЭДС,
f – частота изменения ЭДС,
ω – число витков обмотки трансформатора,
B – магнитная индукция в сердечнике,
Sc – площадь сечения сердечника трансформатора.
Приведём примеры действующего значение ЭДС для синусоидального, прямоугольного (меандр) и треугольного изменения
Из вышесказанного следует, что при условии постоянства электромагнитной индукции B, ЭДС пропорциональна конструктивным параметрам трансформатора сечению магнитопровода Sc и количеству витков ω. Правильный выбор величины электромагнитной индукции В является одной из ключевых задач при проектировании трансформатора. Кроме того, с ростом частоты f увеличивается ЭДС, поэтому для реализации одинаковой ЭДС с ростом частоты требуются меньшие размеры и вес трансформатора. Данный фактор является основным преимуществом трансформаторов высокой частоты, которые чаще всего применяются в настоящее время.
Как проверить полярность?
Для проверки синфазности включения обмоток ТТ в измерительную цепь могут применяться как простейшие способы с использованием миллиамперметра и батарейки, так и профессиональные методы, основанные на применении специальных измерительных приборов.
С помощью батарейки и миллиамперметра
В ней источником является элемент питания с заявленным напряжением от 2-х до 6 Вольт. Типовая батарейка типа 3R12 на 4,5 Вольта с подпаянными к клеммам проводами вполне сгодится для этого.
Функцию измерителя выполняет миллиамперметр, имеющий пределы от 10-ти до 100 мА.
Обратите внимание: Следует выбрать индикатор с нулем по центру шкалы, что позволит отслеживать изменения любой полярности. В начале измерений за правильную маркировку силовой обмотки принимается обозначение, указанное на рисунке (Л1 – справа, а Л2 – слева)
Подсоединив «+» батарейки к началу Л1, а минус – к ее концу Л2 и замкнув тумблер, обнаружим, что стрелка индикатора на мгновение отклонилась вправо. Это значит, что изменение токов в обеих катушках происходит синфазно и что они включены правильно
В начале измерений за правильную маркировку силовой обмотки принимается обозначение, указанное на рисунке (Л1 – справа, а Л2 – слева). Подсоединив «+» батарейки к началу Л1, а минус – к ее концу Л2 и замкнув тумблер, обнаружим, что стрелка индикатора на мгновение отклонилась вправо. Это значит, что изменение токов в обеих катушках происходит синфазно и что они включены правильно.
Если же стрелка при измерении отклонилась влево – это означает противоположность процессов. Когда в первичной обмотке ток возрастает, то одновременно во вторичной его значение уменьшается. В данной ситуации контакты И1и И2 следует поменять местами.
С помощью РЕТОМ-21
В меню прибора РЕТОМ-21 выбирается значение параметра первичной обмотки, а ток во вторичной цепи измеряется встроенным модулем РА. При этом на дисплее регистрируются его значение и фазный сдвиг. Если прибор показывает нулевую разницу фаз – катушки включены правильно (синфазно). В противном случае он будет показывать значение, близкое к 180-ти градусам.
С использованием ВАФ
Измерение этим прибором аналогично уже описанному выше способу, согласно которому в первичную обмотку поступает токовый импульс заданной величины. Вместе с тем на дисплее индицируется значение вторичного тока и его фаза по отношению к первичному. При нулевых фазных показаниях следует считать, что катушки включены правильно. В противном случае (разница фаз – 180 градусов) контакты второй обмотки придется поменять местами.
Трансформаторы 110 кВ
Трёхфазные двухобмоточные трансформаторы 110 кВ
| Тип | Sном, МВА |
Пределы регулирования |
Каталожные данные | Расчетные данные | |||||||
| Uном обмоток | Uк, % | ΔРк, кВт | Рх, кВт | Iх, % | Rт, Ом | Хт, Ом | ΔQх, квар | ||||
| ВН | НН | ||||||||||
| ТМН-2500/110 | 2,5 | +10*1,5 % −8*1,5 % | 110 | 6,6;11 | 10,5 | 22 | 5,5 | 1,5 | 42,6 | 508,2 | 37,5 |
| ТМН-6300/110 | 6,3 | ±9*1,78 % | 115 | 6,6;11 | 10,5 | 44 | 11,5 | 0,8 | 14,7 | 220,4 | 50,4 |
| ТДН-10000/110 | 10 | ±9*1,78 % | 115 | 6,6;11 | 10,5 | 60 | 14 | 0,7 | 7,95 | 139 | 70 |
| ТДН-16000/110 | 16 | ±9*1,78 % | 115 | 6,5;11 | 10,5 | 85 | 19 | 0,7 | 4,38 | 86,7 | 112 |
| ТРДН(ТРДНФ25000/110 | 25 | ±9*1,78 % | 115 | 6,3/6,5;6,3/10,5;10,5/10,5 | 10,5 | 120 | 27 | 0,7 | 2,54 | 55,9 | 175 |
| ТДНЖ-25000/110 | 25 | ±9*1,78 % | 115 | 27,5 | 10,5 | 120 | 30 | 0,7 | 2,5 | 55,5 | 175 |
| ТД-40000/110 | 40 | ±2*2,5 % | 121 | 3,15;6,3;10,5 | 10,5 | 160 | 50 | 0,65 | 1,46 | 38,4 | 260 |
| ТРДН-40000/110 | 40 | ±9*1,78 % | 115 | 6,3/6,3;6,3/10,5;10,5/10,5 | 10,5 | 172 | 36 | 0,65 | 1,4 | 34,7 | 260 |
| ТРДЦН-63000/110 | 63 | ±9*1,78 % | 115 | 6,3/6,3;6,3/10,5;10,5/10,5 | 10,5 | 260 | 59 | 0,6 | 0,87 | 22 | 410 |
| ТРДЦНК-63000/110 | 63 | ±9*1,78 % | 115 | 6,3/6,3;6,3/10,5;10,5/10,5 | 10,5 | 245 | 59 | 0,6 | 0,8 | 22 | 378 |
| ТДЦ-80000/110 | 80 | ±2*2,5 % | 121 | 6,3;10,5;13,8 | 10,5 | 310 | 70 | 0,6 | 0,71 | 19,2 | 480 |
| ТРДЦН(ТРДЦНК)-80000/110 | 80 | ±9*1,78 % | 115 | 6,3/6,3;6,3/10,5;10,5/10,5 | 10,5 | 310 | 70 | 0,6 | 0,6 | 17,4 | 480 |
| ТДЦ-125000/110 | 125 | ±2*2,5 % | 121 | 10,5;13,8 | 10,5 | 400 | 120 | 0,55 | 0,37 | 12,3 | 687,5 |
| ТРДЦН-125000/110 | 125 | ±9*1,78 % | 115 | 10,5/10,5 | 10,5 | 400 | 100 | 0,55 | 0,4 | 11,1 | 687,5 |
| ТДЦ-200000/110 | 200 | ±2*2,5 % | 121 | 13,8;15,75;18 | 10,5 | 550 | 170 | 0,5 | 0,2 | 7,7 | 1000 |
| ТДЦ-250000/110 | 250 | ±2*2,5 % | 121 | 15,75 | 10,5 | 640 | 200 | 0,5 | 0,15 | 6,1 | 1250 |
| ТДЦ-400000/110 | 400 | ±2*2,5 % | 121 | 20 | 10,5 | 900 | 320 | 0,45 | 0,08 | 3,8 | 1800 |
Примечания. 1. Регулирование напряжения осуществляется за счет РПН в нейтрали, за исключением трансформаторов типа ТМН-2500/110 с РПН на стороне НН и ТД с ПБВ на стороне ВН. 2. Трансформаторы типа ТРДН могут изготавливаться также с нерасщепленной обмоткой НН 38,5 кВ, трансформатор 25 МВА — с 27,5 кВ (для электрификации железных дорог).
Трёхфазные трехобмоточные трансформаторы 110 кВ
| Тип | Sном, МВА |
Каталожные данные | Расчетные данные | ||||||||||||||
| Uном обмоток | Uк, % | ΔРк, кВт | Рх, кВт | Iх, % | Rт, Ом | Хт, Ом | ΔQх, квар | ||||||||||
| ВН | СН | НН | ВН | СН | НН | ВН | СН | НН | ВН | СН | НН | ||||||
| ТМТН-6300/110 | 6,3 | 115 | 38,5 | 6,6;11 | 10,5 | 17 | 6 | 58 | 14 | 1,2 | 9,7 | 9,7 | 9,7 | 225,7 | 131,2 | 75,6 | |
| ТДТН-10000/110 | 10 | 115 | 38,5 | 6,6;11 | 10,5 | 17 | 6 | 76 | 17 | 1,1 | 5 | 5 | 5 | 142,2 | 82,7 | 110 | |
| ТДТН-16000/110* | 16 | 115 | 38,5 | 6,6;11 | 10,5 | 17 | 6 | 100 | 23 | 1 | 2,6 | 2,6 | 2,6 | 88,9 | 52 | 160 | |
| ТДТН-25000/110 | 25 | 115 | 11;38,5 | 6,6;11 | 10,5 | 17,5 | 6,5 | 140 | 31 | 0,7 | 1,5 | 1,5 | 1,5 | 56,9 | 35,7 | 175 | |
| ТДТНЖ-25000/110 | 25 | 115 | 38,5;27,5 | 6,6;11; 27,5 | 10,5(17) | 17(10,5) | 6 | 140 | 42 | 0,9 | 1,5 | 1,5 | 1,5 | 57 | 0(33) | 33(0) | 225 |
| ТДТН-40000/110* | 40 | 115 | 11;22;38, 5 | 6,6;11 | 10,5(17) | 17(10,5) | 6 | 200 | 43 | 0,6 | 0,8 | 0,8 | 0,8 | 35,5 | 0(22,3) | 22,3(0) | 240 |
| ТДТНЖ-40000/110 | 40 | 115 | 27,5;35,5 | 6,6;11; 27,5 | 10,5(17) | 17(10,5) | 6 | 200 | 63 | 0,8 | 0,9 | 0,9 | 0,9 | 35,5 | 0(20,7) | 20,7(0) | 320 |
| ТДТН(ТДЦНТ) −63000/110* | 63 | 115 | 38,5 | 6,6;11 | 10,5 | 17 | 6,5 | 290 | 56 | 0,7 | 0,5 | 0,5 | 0,5 | 22 | 13,6 | 441 | |
| ТДТН(ТДЦТН, ТДЦТНК) −80000/110* | 80 | 115 | 38,5 | 6,6;11 | 11(17) | 18,5(10,5) | 7(6,5) | 390 | 82 | 0,6 | 0,4 | 0,4 | 0,4 | 18,6(21,7) | 0(10,7) | 11,9(0) | 480 |
При Хт обмотки СН, равном нулю, обмотки НН изготавливаются с Uном, равным 6,3 или 10,5 кВ.
Примечание. Все трансформаторы имеют РПН ±9*1,78 % в нейтрали ВН за исключением трансформатора ТНДТЖ-40000 с РПН ±8*1,5 % на ВН.
Классификация и выбор
По конструкции и исполнению трансформаторы тока используемые в измерительных цепях делятся на:
- Встроенные. Первичная обмотка у них служит элементом для другого устройства. Они устанавливаются на вводах и имеют только вторичную обмотку. Функцию первичной обмотки выполняет другой токоведущий элемент линейного ввода. Конструктивно это магнитопровод кольцевого типа, а его обмотки имеют отпайки, соответствующие разным коэффициентам трансформации;
- Опорные. Предназначенные для монтажа и установки на опорной ровной плоскости;
- Проходной. По своей структуре это тот же встроенный, только вот находиться он может снаружи другого электрического устройства;
- Шинный. Первичной обмоткой служит одна или несколько шин включенных в одну фазу. Их изоляция рассчитывается с запасом, что бы он мог выдержать даже многократное увеличение напряжения;
- Втулочный. Это одновременно и проходной, и шинный трансформатор тока;
- Разъемный. Его магнитопровод состоит из разборных элементов;
- Переносной. Это устройство электрики называют токоизмерительные клещи. Они являются переносным и удобным измерительным трансформатором тока, у которого магнитная система размыкается и замыкается уже вокруг того провода в котором и нужно измерять значение тока.
При выборе трансформатора тока стоит знать главное, что при протекании по первичной обмотке номинального тока в его вторичной обмотке, которая замкнута на измерительный прибор, будет обязательно 5 А. То есть если нужно проводить измерение токовых цепей где его расчётная рабочая величина будет примерно равна 200 А. Значит, при установке измерительного трансформатора 200/5, прибор будет постоянно показывать верхние приделы измерения, это неудобно. Нужно чтобы рабочие пределы были примерно в середине шкалы, поэтому в этом конкретном случае нужно выбирать трансформатор тока 400/5. Это значит что при 200 А номинального тока оборудования на вторичной обмотке будет 2,5 А и прибор будет показывать эту величину с запасом в сторону увеличения или уменьшения. То есть и при изменениях в контролируемой цепи будет видно насколько данное электрооборудование вышло из нормального режима работы.
Вот основные величины, на которые стоит обратить внимание при выборе измерительных трансформаторов тока:
- Номинальное и максимальное напряжение в первичной обмотке;
- Номинальное значение первичного тока;
- Частота переменного тока;
- Класс точности, для цепей измерения и защиты он разный.
Формулы и измерение
Формулы для расчета индуктивности катушек довольно сложны и имеет различный вид для различных типов исполнения обмоток:
- линейный проводник;
- одновитковая катушка;
- плоская катушка;
- соленоидальная обмотка;
- тороидальная форма.
Наибольшие сложности возникают при расчетах многовитковых многослойных катушек, то есть тех, которые составляют обмотку трансформаторов.
В подавляющем большинстве случаев точный расчет невозможен, поэтому приходится использовать примерные данные и уточнять их после проведения измерений.
Формулы для расчета индуктивности трансформатора основаны на расчетах соленоида:
L=µ0µN2S/l, где
µ0 – магнитная постоянная;
µ – магнитная проницаемость сердечника;
N – количество витков;
S – площадь одного витка;
l – длина обмотки.
Для измерения индуктивности существует несколько методик и приборов, созданных на их основе. В большинстве случаев измерение производится путем вычислений индуктивного сопротивления катушки при подаче образцового напряжения заданной частоты и измеренного значения тока через обмотку.
В специализированных приборах вычисления производятся автоматически, и пользователь только считывает показания шкалы прибора, выраженные в единицах индуктивности – Гн, мГн или мкГн.
Понятие начала и конца обмотки, обозначения по ГОСТ 11677-85
По сфере применения преобразователи напряжения делятся на промежуточные, измерительные, защитные, лабораторные. Электрический ток создает магнитное поле, направление которого зависит от направления тока. Необходимость определять начало и конец обмотки трансформатора возникает, если требуется проверить достоверность маркировки или определить характеристики при ее отсутствии.
Сначала немного теории. Обмотка может быть правая (с витками, расположенными по часовой стрелке) или левая (с витками, расположенными против часовой стрелки). Хотя понятия «начало» и «конец» условные, в процессе эксплуатации и при необходимости в ремонте они имеют значение, так как определяют полярность. Проверки проводятся, если нет данных производителя и паспорта.
Порядок маркировки силового трансформаторного оборудования установлен ГОСТ 1167- 85. В однофазном трансформаторе начало обозначается буквой A (для высокого напряжения), a (для низкого напряжения), конец – буквой X, x. При наличии третьей катушки ее начало Am, конец Xm.
В трехфазных трансформаторах:
- высокое напряжение – А, В, С; X, Y, Z;
- среднее напряжение – Аm, Вm, Сm; Хm, Ym, Zm;
- низкое напряжение – а, b, с; х, у, z.
- При отводе нейтрали она обозначается как О, Оm и о.
Схема «в звезду» указывается как Y, в треугольник – Δ. При отводе нейтрали соединение определяется знаком Yн. Если обвивка высокого напряжения соединяются «в звезду», низкого – в треугольник, сочетание помечается как Y/Δ.
No tags for this post.