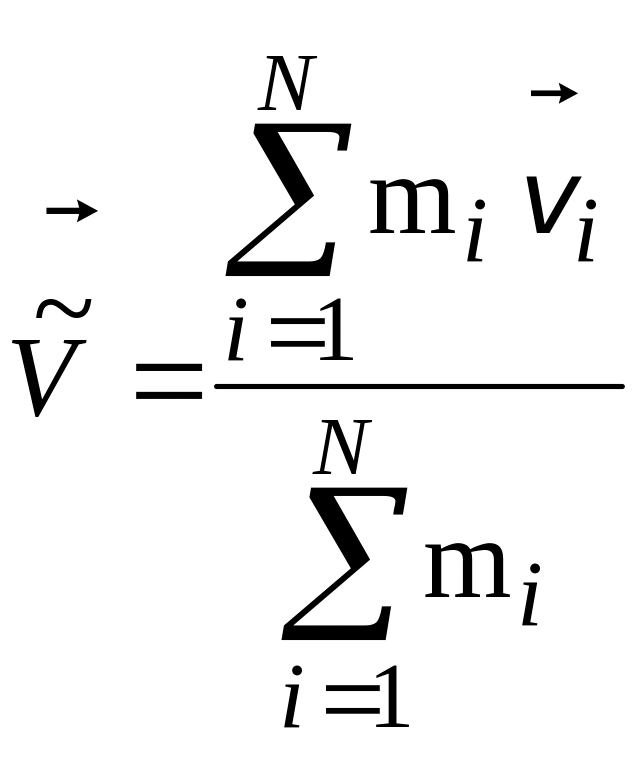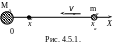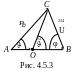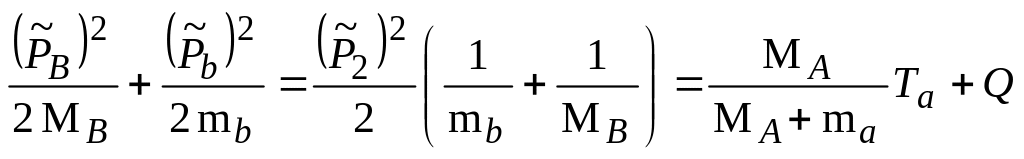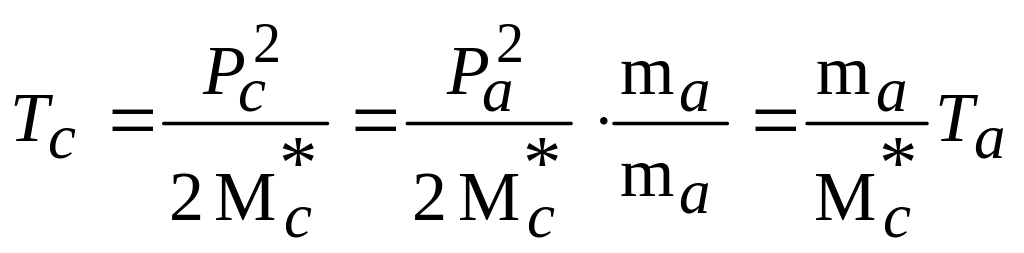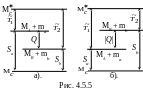Как найти импульс ядра

На странице вопроса Спортивное ядро летит со скоростью 20м / с? из категории Физика вы найдете
ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не
устраивает и нужно расшить круг поиска, используйте удобную поисковую
систему сайта. Можно также ознакомиться с похожими вопросами и ответами
других пользователей в этой же категории или создать новый вопрос. Возможно,
вам будет полезной информация, оставленная пользователями в комментариях, где
можно обсудить тему с помощью обратной связи.

Напомним, что кинематикой
называют раздел механики, посвященный
изучению геометрических свойств движения
тел без учета действующих на тела сил.
Движение любого тела в кинематике
изучают по отношению к некоторой системе
координат, позволяющей задать относительное
положение движущегося объекта в любой
момент времени. В ядерной физике обычно
используют две системы координат:
лабораторную (ЛСК), связанную с
ядром-мишенью, и систему центра инерции
(СЦИ), определение которой будет
дано ниже.

Кинематическая схема ядерной
реакции и связь между энергиями,
импульсами и углами вылета частиц в ЛСК
и СЦИ имеет наглядное графическое
представление и может быть проанализирована
с помощью импульсной диаграммы
(векторной диаграммы импульсов).
Построение импульсной диаграммы основано
на применении законов сохранения энергии
и импульса.

Рассмотрение
выполним для случая, когда скорости
движения объектов существенно меньше
скорости света, т.е. когда массы
частиц m >> T
– их кинетической энергии, и можно
использовать законы классической
механики.

Пусть
имеется произвольная инерциальная
система координат К’, которая движется
относительно ЛСК со скоростью

.
Тогда скорость

любой
из i = 1,
2, 3, . . . , N частиц в ЛСК
и скорость

в К’‑системе связаны следующим
образом (принцип относительности
Галилея):

Закон
сохранения импульса для выбранной
совокупности частиц записывается
следующим образом:

Первое слагаемое в правой части есть
суммарный импульс

частиц
в К’-системе, а второе — определяет
импульс движения К’-системы как
целого относительно ЛСК, который
носит название переносного импульса.
Соответствующим выбором вектора скорости

можно
добиться, чтобы суммарный импульс частиц
в К’-системе был равен нулю:

Система
координат, в которой суммарный импульс

частиц
равен нулю, называется системой центра
инерции (СЦИ). Условимся величины,
относящиеся к СЦИ, обозначать сверху
значком “~” (тильда). Положив в (4.5.2)

= 0,
найдем скорость движения СЦИ
относительно ЛСК:

Обратимся
к рассмотрению процесса (4.1.1). Пусть в
ЛСК
частица а
движется со скоростью

,
а ядро-мишень А
– покоится. Используя (4.5.4) найдем
скорость движения центра инерции системы
(или составного ядра, если таковое
образуется) относительно ЛСК:

Из сотношения
(4.5.2) и (4.5.5) следует, что переносной
импульс СЦИ
относительно ЛСК
равен импульсу частицы а
в ЛСК:

Поместим ядро-мишень
А в начале координат (рис. 4.5.1). Если
частица а движется параллельно оси
Х навстречу частице А, то из
(4.5.5) следует, что координата центра
инерции

на
оси Х в любой момент времени связано
следующим образом с координатой х_а
частицы а:

т
.к.
скорость движения вдоль оси Х есть
dx/dt.
На рисунке показано, что центр инерции
всегда располагается между частицами
а и А,
двигаясь вдоль оси Х со скоростью

,
относительно ядра-мишени А.

Найдем с помощью
(4.5.1) и (4.5.5) скорости движения частицы а
и ядра-мишени А в СЦИ и
соответствующие им импульсы:

Таким
образом, импульсы частиц а и А
в СЦИ равны друг другу и противоположно
направлены, как и должно быть.

Используя
(4.5.8) и (4.5.9), выразим суммарную
кинетическую энергию

частиц a и А в СЦИ
через кинетическую энергию Т_a
частицы a
в ЛСК

Кинетическая
энергия

есть энергия взаимного движения частиц
а и А и она меньше суммарной
кинетической энергии Т₁ =
Т_а
на величину

которая есть ничто иное, как кинетическая
энергия движения центра инерции системы
(или составного ядра) относительно ЛСК.
Действительно, кинетическая энергия
движения частиц а и А относительно
ЛСК равна

Очевидно,
что кинетическая энергия (4.5.12) движения
центра инерции системы не может перейти
во внутреннюю энергию частиц и не может
быть использована в ядерной реакции.

На
этом закончим рассмотрение входного
канала процесса (4.1.1) и перейдем к
рассмотрению выходного канала.

В ЛСК
сумма импульсов частиц b
и В, образовавшихся в результате
ядерной реакции, по закону сохранения
импульса равна импульсу налетающей
частицы а:

Н

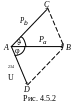
а
рис. 4.5.2 представлена схема одного из
возможных вариантов разлета продуктов
реакции, а на рис. 4.5.3 графический аналог
векторного уравнения (4.5.13). На этих
рисунках

и
φ – углы вылета частиц b
и B относительно
направления движения частицы а.
Очевидно, что отрезок СВ на рис.
4.5.3 равен импульсу

на рис. 4.5.2. Остальные величины совпадают
с рис. 4.5.2. Поэтому в дальнейшем будем
рассматривать векторный треугольник
АСВ (рис. 4.5.3).

Так
как сумма импульсов частиц b
и В относительно ЛСК согласно
(4.5.6) должна быть равна импульсу

,
т.е. (см. (4.5.6))

то отношение

и в соответствии с (4.5.15) точка О
на рис. 4.5.3 делит отрезок АВ =

на отрезки АО =

и
ОВ =

,
т.е. АО/ОВ = m_a/M_A.

Очевидно,
что ОС =
,
так как

а угол

на рис. 4.5.3 — есть угол вылета частицы b
в СЦИ.

Вектор

,
согласно свойствам СЦИ, равен вектору

по абсолютной величине:

и направлен в
противоположную сторону, т.е. частицы
b и B
в СЦИ разлетаются с равными и
противоположными импульсами.

Вычислим величину

.
Из формулы (4.4.6):

Или, учитывая
(4.5.10),

Из последнего
уравнения находим

где

— есть приведенная
масса частиц b и B.

П
олученные
результаты можно использовать для
построения векторной диаграммы импульсов,
графически связывающей импульсы в ЛСК
и СЦИ. Для этого отрезок АВ,
изображающий импульс Р_а
(рис. 4.5.4), надо разделить точкой
О в отношении

.
Затем из этой точки радиусом

(4.5.20)
следует провести окружность, которая
является геометрическим местом точек
С для любого угла

вылета частицы b.
Тогда, если известна хотя бы одна из
величин Р_b
, Р_B
,

,
φ,

,


,
то из диаграммы можно определить
графически все остальные.

В
случае упругого рассеяния (Q
= 0) состав выходного канала тождественен
составу входного канала и из (4.5.20)
следует, что

Далее построение
векторной диаграммы импульсов для
упругого рассеяния не имеет особенностей
и выполняется аналогичным образом.

Приведем
теперь несколько примеров применения
законов сохранения в ядерных реакциях.

Определим
энергетический порог для
эндоэнергетической реакции. В СЦИ
из формулы (4.4.6) имеем

и, следовательно, минимальное значение

(когда

—
продукты реакции неподвижны)
составит

Используя (4.5.10) найдем
минимальную кинетическую энергию
частицы а в лабораторной системе
координат (ЛСК):

Полученное
значение кинетической энергии
бомбардирующей частицы в ЛСК, при
котором становится возможным протекание
эндоэнергетической реакции, называется
порогом реакции.

Получим формулу
(4.2.2) для вычисления возможной энергии
W_c
возбуждения составного ядра. По
определению

где массы
основного и возбужденного состояний
составного ядра выражены в энергетических
единицах.

Пусть
ядро-мишень А покоится. Запишем
законы сохранения энергии и импульса
для первой стадии реакции

стадии образования составного ядра С*
(звездочка означает возбужденное
состояние):

Рассмотрение
проведем для нерелятивистского случая,
когда кинетическая энергия налетающей
частицы Т_а
≤ 10 МэВ << m_a.
Тогда

Подставляя
(4.5.28) в (4.5.27), получим
квадратное уравнение для нахождения

:

В
(4.5.29) последнее слагаемое составляет
ничтожную долю от первых двух, так как

.
Поэтому в качестве первого приближения
принимаем

.
Для получения второго приближения
подставляем это выражение в (4.5.29).
Получаем

Подставив
(4.5.30) в (4.5.25), получим формулу

Первый
член в этом выражении есть ни что иное,
как энергия отделения

частицы а
от составного ядра (см., например,
(1.4.17)). Второй член
— суммарная кинетическая энергия

частиц
a
и А до реакции в системе центра
инерции. Итак,

На
рис. 4.5.5а приведена энергетическая
диаграмма для экзоэнергетической
реакции (Q > 0),
а на рис. 4.5.5б — для эндоэнергетической
реакции (Q < 0).
На диаграммах изображен процесс
образования составного возбужденного
ядра

и его распад с образованием част
иц
B и b
для обоих типов реакций. S_а = M_A
+ m_a — M_c
– есть энергия связи частицы а,
а S_b = M_B
+ m_b — M_c
– частицы b
относительно составного ядра М_с
соответственно.