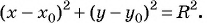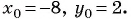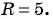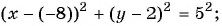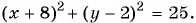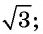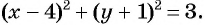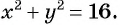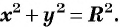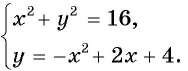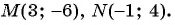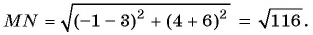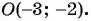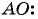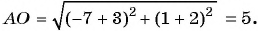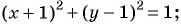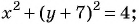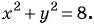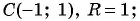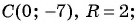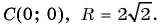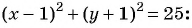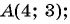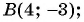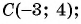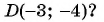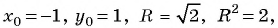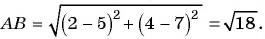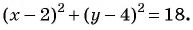Иногда линейные уравнения принимают вид, когда неизвестное оказывается в числителе одной или нескольких дробей.
Как, например, в уравнении ниже.
В таких случаях подобные уравнения можно решить двумя способами.
I способ решения
Сведение уравнения к пропорции
Запомните!
При решении уравнений способом пропорции необходимо выполнить следующие действия:
- привести все дроби к общему знаменателю и сложить их как алгебраические дроби
(в левой и правой части должно остаться только по одной дроби); - полученное уравнение решить по правилу пропорции.
Итак, вернемся к нашему уравнению. В левой части у нас и так стоит только одна дробь, поэтому в ней не нужны
никакие преобразования.
Будем работать с правой частью уравнения.
Упростим правую часть уравнения так, чтобы там осталась только одна дробь.
Для этого вспомним правила сложения числа с алгебраической дробью.
Теперь используем правило пропорции и решим уравнение до конца.
II способ решения
Сведение к линейному уравнению без дробей
Рассмотрим уравнение выше еще раз и решим его другим способом.
Мы видим, что в уравнении присутствуют две дроби
«» и
«».
Наша задача сделать так, чтобы в уравнении не осталось ни одной дроби.
Другими словами, необходимо свести уравнение к обычному
линейному уравнению без неизвестного в дроби.
Запомните!
Чтобы избавиться от дробей в уравнении нужно:
- найти число, которое без остатка будет делиться на каждый из знаменателей;
- умножить каждый член уравнения на это число.
Давайте зададим себе вопрос: «Какое число без остатка делится на каждый из знаменателей дробей, то есть и на
«5», и на «9» ?».
Таким ближайшим наименьшим числом будет число «45».
Умножим каждый член уравнения на «45».
Важно!
При умножении уравнения на число нужно каждый член уравнения
умножить на это число.
Другие примеры решения уравнений с неизвестным в дроби
Решение уравнения I способом (через пропорцию)
-
+=
+
=
+
=
=
=
(49 − 23y) · 2 = 15 · (y + 6)
98 − 46y = 15y + 90
−46y − 15y = 90 − 98
−61y = −8 | :(−61)
y =
Ответ: y =
Решение уравнения II способом
(сведение к уравнению без дробей)
-
2 − +
= 0 | ·202 · 20 − +
= 0 · 2040 − 5 ·(3x − 7) + 4 · (x + 17) = 0
40 − 15x + 35 + 4x + 68 = 0
−15x + 4x + 40 + 35 + 68 = 0
−11x + 75 + 68 = 0
−11x + 143 = 0
−11x = −143 | :(−11)
x = 13
Ответ: x = 13
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
25 августа 2016 в 13:08
Виктория Лебеденко
Профиль
Благодарили: 0
Сообщений: 1
Виктория Лебеденко
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
3 сентября 2016 в 19:36
Ответ для Виктория Лебеденко
Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
раскроем скобки x2+3x-x-3-x2-5=0(уничтожим x2 и-x2) получим 2x-8=0
2x=8
x=8 :2
x=4
0
Спасибо
Ответить
Итак, друзья, продолжаем осваивать решение основных типов алгебраических уравнений. Мы с вами уже хорошо (надеюсь) знаем, как именно надо решать линейные и квадратные уравнения. Осталось разобрать ещё одним основным типом уравнений — дробными уравнениями.
Иногда их называют более научно и солидно — дробные рациональные уравнения. Или дробно-рациональные уравнения. Это сути не меняет.)
Дробные уравнения — незаменимая вещь во многих других темах математики. Особенно — в текстовых задачах. Но для успешного их решения жизненно необходимо ориентироваться в трёх смежных темах:
1. Дроби и действия с дробями и дробными выражениями.
2. Тождественные преобразования уравнений.
3. Решение линейных и квадратных уравнений.
Без этих трёх китов браться за решение дробных уравнений слишком уж самонадеянно, я бы сказал. Почему? Да потому, что непонимание, как, скажем, работать с дробями (сокращать, приводить к общему знаменателю и т.д.) автоматически будет приводить к полному провалу и в дробных уравнениях. Намёк понятен?)
Так что тем, у кого проблемы хотя бы по одной из вышеперечисленных тем — настоятельно рекомендую освежить их в памяти, да и по ссылочкам пройтись.
Итак, вперёд!
Что такое дробное уравнение? Примеры.
Дробное уравнение, как следует непосредственно из названия, — это уравнение, в котором есть дроби. Обязательно. Причём (важно!) не просто дроби, а дроби, у которых есть икс в знаменателе. Хотя бы в одном.
Например, вот такое уравнение:
Или такое:
Или вот такое:
И так далее.) Напоминаю, что, если в знаменателях сидят только числа, то такие уравнения к дробным не относятся. Либо это линейные уравнения, либо квадратные.
Например:
Это линейное уравнение, хотя тут тоже есть дроби. Почему? Да потому, что знаменатели дробей — четвёрка и пятёрка. Т.е. просто числа. И ни один из знаменателей не содержит иксов.
Или такое уравнение:
Это обычное квадратное уравнение, несмотря на двойку в знаменателе. Опять же, по причине того, что двойка — не икс, и деления на неизвестное в дроби нету.
В общем, вы поняли.
Как решать дробные уравнения? Убираем дроби!
Как это ни странно, дробные уравнения в большинстве своём решаются довольно просто. По чётким и несложным правилам. Каким же именно образом?
Первым делом надо избавиться от дробей! Это ключевой шаг в решении любого дробного уравнения, который должен быть освоен идеально. Ибо после того, как все дроби исчезли, уравнение, чаще всего, превращается в линейное или квадратное. А дальше мы уже с вами знаем, что делать.)
Но… Как же нам избавиться от дробей?! Легко! Применяя всё те же старые добрые тождественные преобразования! В чём же суть?
Вникаем. Нам надо помножить обе части уравнения на одно и то же выражение. Но не на какое попало, а на такое, чтобы все знаменатели посокращались! Одним махом.) Ибо дальше, без знаменателей, жизнь становится гораздо проще и приятнее.)
Это только на конкретном примере показать можно. Итак, решаем первое уравнение из нашего списка:
Первое, что приходит на ум — перенести всё в одну сторону, привести всё к общему знаменателю и т.д. Забудьте, как кошмарный сон! Так делают только в одном случае — при решении дробно-рациональных неравенств методом интервалов. Это отдельная большая тема.
А в уравнениях нам надо сразу умножить обе части на такое выражение, которое нам позволит сократить все знаменатели. И какое же это выражение?
Давайте его конструировать.) Смотрим ещё раз на уравнение:
Понятно, что в левой части для ликвидации знаменателя нам необходимо умножение на (х+3), а в правой — на 3. Но математика позволяет умножать обе части уравнения только на одно и то же выражение! На разные — не катит. Ничего не поделать, так уж она устроена…)
Значит, нам надо скомбинировать такое выражение, которое одновременно делилось бы как на (х+3), так и на тройку. Причём очень важно — только с помощью умножения! И какое же это выражение? Очевидно, это 3(х+3). То есть, по сути, общий знаменатель обеих дробей.
Итак, для ликвидации всех дробей наше уравнение надо умножать на выражение 3(х+3).
Умножаем:
Это самое обычное умножение дробных выражений, но, так уж и быть, расписываю детально:
Прошу обратить внимание: скобки (х+3) я не раскрываю! Прямо так, целиком, их и пишу, как будто бы это одна буква. Ибо наша основная на данный момент задача — дроби убрать. Чего без произведения никак не сделаешь… И зачем же нам тогда париться с раскрытием скобок?!
А вот теперь мы видим, что в левой части сокращается целиком (х+3), а в правой 3. Чего мы и добивались! И теперь с чувством глубокого удовлетворения производим сокращение:
Вот и отлично. Дроби исчезли. После сокращения получилось безобидное линейное уравнение:
2∙3 = х+3
А его (надеюсь) уже решит каждый:
х = 3
Решаем следующий примерчик:
И опять избавляемся от того, что нам не нравится. В данном примере это дробь 20/х. Одна единственная. Для её ликвидации правую часть надо домножить на знаменатель. То есть, просто на х. Но тогда и левую часть тоже надо домножить на х: так уж второе тождественное преобразование требует.
Вот и домножаем! Всю левую часть и всю правую часть:
Напоминаю, что эта вертикальная чёрточка с умножением всего лишь означает, что обе части нашего уравнения мы умножаем на «х».
Вперёд!
А вот теперь — снова внимание! Очередные грабли. Заметьте, что при умножении левой части на икс, выражение (9 — х) я взял в скобки! Почему? Потому, что мы умножаем на икс всю левую часть целиком, а не отдельные её кусочки!
Дело всё в том, что частенько после умножения народ записывает левую часть вот так:
Это категорически неверно. Дальше можно уже не решать, да…)
Но у нас всё хорошо, будем дорешивать.
С чистой совестью сокращаем икс справа и получаем уравнение уже безо всяких дробей, в одну строчку.
(9 — х)∙х = 20
Вот и отлично. Все дроби исчезли напрочь, теперь можно и скобки раскрыть:
9х — х2 = 20
Переносим всё влево и приводим к стандартному виду:
Получили классическое квадратное уравнение. Но минус перед квадратом икса — нехорош. Забыть его проще простого! От него всегда можно избавиться умножением (или делением) уравнения на (-1). Проще говоря, меняем в левой части все знаки на противоположные. А справа как был ноль, так ноль же и останется:
Решаем через дискриминант (или подбираем по теореме Виета) и получаем два корня:
х1 = 4
х2 = 5
И все дела.)
Как вы видите, в первом случае уравнение после преобразований стало линейным, а здесь — квадратным.
А бывает и так, что после ликвидации дробей вообще все иксы сокращаются и остаётся чистая правда. Что-нибудь типа 3=3. Это означает, что икс может быть любым. Какой икс ни возьми — всё равно всё посокращается и останется железное равенство 3=3.
Или наоборот, может получиться какая-нибудь белиберда, типа 3=4. А это будет означать, что корней нет. Какой икс ни возьми — всё сократится и останется бред…
Надеюсь, такие сюрпризы вас уже нисколько не удивят.) Если всё же удивят, то прогуляйтесь по ссылочке: Линейные уравнения. Как решать линейные уравнения? А чуть конкретнее — особые случаи при решении линейных уравнений. Эти сюрпризы (полная пропажа иксов после преобразований) — они ко всем видам уравнений относятся. И дробные — не исключение.)
Разумеется, при попытке ликвидации дробей встречаются и неожиданности. И одну из них мы рассмотрим прямо сейчас.
Раскладываем на множители!
Решаем третье уравнение по списку:
А вот тут некоторые могут и зависнуть. На что же такое надо домножить всё уравнение, чтобы за один шаг сократились все знаменатели? Можно, конечно, взять и тупо перемножить все три знаменателя, получить
x(x2+2x)(x+2)
и домножить на эту конструкцию всё уравнение. Математика не возражает.) Но… Может быть, есть выражение попроще?
Что ж, вскрою тайну: да, всё гораздо проще! Если в совершенстве владеть таким мощным приёмом, как разложение на множители. Привет седьмому классу!)
А попробуем-ка разложить на множители каждый из знаменателей? Ну, с х и х+2 точно ничего не сделать, а вот х2+2х вполне себе раскладывается! Выносим один икс за скобку и получаем:
х2+2х = х(х+2)
Отлично. Вставим наше разложение в исходное уравнение:
Вот теперь всё и прояснилось.) Теперь уже отчётливо видно, что гораздо проще будет умножать обе части уравнения на х(х+2). Это выражение гораздо короче и прекрасно делится на каждый из знаменателей: и на x, и на (х+2), и само на себя — на х(х+2).
Вот на х(х+2) и умножаем:
И снова расписываю подробно, дабы не запутаться. В левой части я буду использовать скобки: там сумма дробей. В правой части скобки не нужны: там одна дробь. Вот и пишем:
А теперь производим умножение. В левой части большие скобки умножаем на наше выражение х(х+2). Разумеется, по правилу раскрытия скобок, сначала первую дробь, затем — вторую. Ну, а в правой части, по правилу умножения дробей, просто умножаем числитель:
Я уж не стал здесь рисовать единички в знаменателях, несолидно… И, опять же, малые скобки в числителях я не раскрываю! Они нам сейчас для сокращения понадобятся! И да… Откуда появились скобки (х — 3) в числителе первой дроби — думаю, уже не стоит объяснять?)
С удовольствием сокращаем все дроби:
(x-3)(x+2) + 3 = x
Раскрываем оставшиеся скобки, приводим подобные и собираем всё слева:
x2 + 2x — 3x — 6 + 3 — х = 0
x2 — 2x — 3 = 0
И снова получили квадратное уравнение.) Решаем и получаем два корня:
x1 = -1
x2 = 3
Вот и всё. Это и есть ответ.)
Из этого примера можно сделать важный вывод:
Если знаменатели дробей можно разложить на простые множители — обязательно делаем это! Пригодится при ликвидации дробей. Причём раскладываем всё до упора, используя все возможные способы из алгебры седьмого класса!
Как вы видите, всё просто и логично. Мы меняем исходное уравнение так, чтобы после наших преобразований из примера исчезло всё то, что нам не нравится. Или мешает. В данном случае это — дроби. И точно так же мы будем поступать и со всякими логарифмами, синусами, показателями и прочей жестью.) Мы всегда будем от всего этого избавляться.)
Ну что, порешаем?)
Решить уравнения:
Ответы (как обычно, вразброс):
x = 3
x1 = 0,5; x2 = 3
x = 2
х = 6
x = 2,6
x1 = 2; x2 = 5
Последнее задание не решается? Что ж, формулы сокращённого умножения всяко помнить надо, да…)
Всё решилось? Что ж, здорово! Значит, полпути в решении дробных уравнений мы с вами уже преодолели. Эта первая часть пути — избавление от дробей. Осталась вторая. Не менее важная!
Всё просто, но… Пришло время открыть вам горькую правду. Успешное решение дробных уравнений этого урока вовсе не гарантирует успех в решении всех остальных примеров этой темы. Даже очень простых, подобных этим. К сожалению…
Но об этом — дальше.)
- Построение графика функции $y = frac{x+1}{x-1}$ последовательными преобразованиями гиперболы $y = frac{1}{x}$
- Анализ асимптот
- Алгоритм построения графика дробно-линейной функции
- Примеры
Построение графика функции $y = frac{x+1}{x-1}$ последовательными преобразованиями гиперболы $y = frac{1}{x}$
Начнём исследование с построения графика для $y = frac{x+1}{x-1}$.
Выделим целую часть в дроби: $y = frac{x+1}{x-1} = frac{(x-1)+2}{x-1} = 1+ frac{2}{x-1}$
Согласно §47-48 данного справочника, эта функция последовательно получается из гиперболы
$$ y = frac{1}{x} xrightarrow{2f(x)} y = frac{2}{x} xrightarrow{2f(x-1)} y = frac{2}{x-1} xrightarrow{2f(x-1)+1} y = frac{2}{x-1} +1 $$
Шаг 1. 2f(x) – функция $y = frac{1}{x}$ растягивается в 2 раза по оси OY, получаем $y = frac{2}{x}$
Шаг 2. 2f(x-1) – функция $y = frac{2}{x}$ сдвигается вправо на 1 по оси OX, получаем $y = frac{2}{x-1}$
Шаг 3. 2f(x-1)+1 — функция $ y = frac{2}{x-1}$ сдвигается вверх на 1 по оси OY, получаем $y = frac{2}{x-1}+1$.
Анализ асимптот
Итоговым графиком $y = frac{x+1}{x-1}$ является гипербола.
Ветки гиперболы ограничены двумя прямыми, которые называют асимптотами.
Ветки на бесконечности стремятся к этим прямым, но никогда их не достигают.
Рассмотрим смещение асимптот при построении.
Для исходного графика $y = frac{1}{x}$ асимптотами являются оси координат, x=0,y=0
Для графика $y = frac{2}{x}$ оси координат остаются асимптотами.
Для графика $y = frac{2}{x-1}$ происходит сдвиг вправо, асимптоты x=1,y=0
Для графика $y = frac{2}{x-1}+1$ происходит сдвиг вверх, конечные асимптоты x = 1, y = 1
Асимптоты служат хорошим ориентиром для построения графика гиперболы.
В данном случае, достаточно построить гиперболу $y = frac{2}{x}$ и переместить её параллельным переносом, заданным переносом точки пересечения асимптот из (0;0) в (1;1).
Алгоритм построения графика дробно-линейной функции
На входе
$$ y = frac{ax+b}{cx+d}, c neq 0, ad-bc neq 0 $$
Шаг 1. Выделить целую часть из дроби и представить её в виде $y = frac{A}{x+B}+C$
Шаг 2. Построить график $y = frac{A}{x}$.
Шаг 3. Построить горизонтальную асимптоту x = -B.
Шаг 4. Построить вертикальную асимптоту y = C.
Шаг 5. Переместить исходный график $y = frac{A}{x}$ параллельным переносом точки пересечения асимптот из (0;0) в (-B;C).
Если необходимо, отметить дополнительные точки, соединить кривой.
Гипербола $y = frac{A}{x+B}+C$ построена.
Примеры
Пример 1. Постройте график функции $y = frac{x+1}{x-3}$
Выделяем целую часть: $y = frac{x+1}{x-3} = frac{(x-3)+4}{x-3} = frac{4}{x-3} +1$
Исходная гипербола $y = frac{4}{x}$.
Асимптоты: x = 3, y = 1.
Получаем:
Пример 2. Постройте график функции $y = frac{x}{x+2}$
Выделяем целую часть: $y = frac{x}{x+2} = frac{(x+2)-2}{x+2} = frac{2}{x+2} +1$
Исходная гипербола $y = -frac{2}{x}$.
Асимптоты: x = -2, y = 1.
Получаем:
Пример 3*. Постройте график функции $y = frac{2x^2-8x}{x^2-7x+12}$
Преобразуем дробь:
$$ y = frac{2x^2-8x}{x^2-7x+12} = frac{2x(x-4)}{(x-3)(x-4)} = {left{ begin{array}{c} frac{2x}{x-3} \ x neq 4 end{array} right.} $$
$x neq 4$ — исключенная точка.
Выделим целую часть:
$$ y = frac{2x}{x-3} = frac{2x-6+6}{x-3} = frac{2(x-3)+3}{x-3} = frac{3}{x-3} +2 $$
Исходная гипербола $y = frac{3}{x}$.
Асимптоты: x = 3, y = 2.
Учитывая исключенную точку, получаем:
Дробно-рациональная функция — это функция вида , где f(x) и g(x) — некоторые функции.
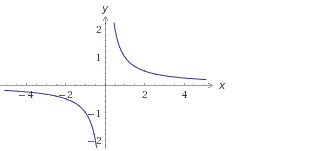
График дробно-рациональной функции представляет собой гиперболу.
Функция имеет две асимптоты — вертикальную и горизонтальную.
Определение.Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность:
x=a уравнение вертикальной асимптоты
y=b уравнение горизонтальной асимптоты
y=kx+b уравнение наклонной асимптоты
Дробно-линейная функция представляет собой частный случай дробно-рациональной функции.
Дробно-линейная функция – это такая алгебраическая дробь , у которой числитель и знаменатель представляют собой линейные функции.
Во всякой дробно-линейной функции можно выделить целую часть.
Построим график функции y=1/x:
D(y): х≠0
E(y): у≠0
y = k/x — нечетная
Построим график функции y=k/x:
При k=2 y=-2/x:
ООФ: х≠0
МЗФ: у≠0
y=k/x – нечетная
Пример1 . Построим график функции , т.е. представим ее в виде
: выделим целую часть дроби, разделив числитель на знаменатель, мы получим:
.
Итак, . Мы видим, что график этой функции может быть получен из графика функции у=5/х с помощью двух последовательных сдвигов: сдвига гиперболы у=5/х вправо на 3 единицы, а затем сдвига полученной гиперболы
вверх на 2 единицы.
При этих сдвигах асимптоты гиперболы у=5/х также переместятся: ось х на 2 единицы вверх, а ось у на 3 единицы вправо.
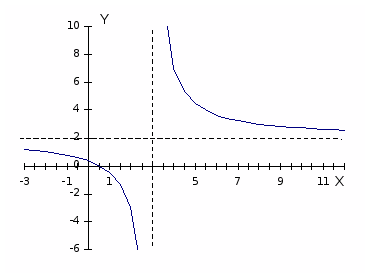
Для построения графика проведем в координатной плоскости пунктиром асимптоты: прямую у=2 и прямую х=3. Так как гипербола состоит из двух ветвей, то для построения каждой из них составим две таблицы: одну для х3 (т. е. первую слева от точки пересечения асимптот, а вторую справа от нее):
|
x |
-7 |
-2 |
-1 |
0 |
1 |
2 |
2,5 |
|
y |
1,5 |
1 |
0,75 |
0,33 |
-0,5 |
-3 |
-8 |
|
x |
3,5 |
4 |
5 |
6 |
7 |
8 |
13 |
|
y |
12 |
7 |
4,5 |
3,33 |
3,25 |
3 |
2,52 |
Отметив в координатной плоскости точки, координаты которых указаны в первой таблице, и соединив их плавной линией, получим одну ветвь гиперболы. Аналогично (используя вторую таблицу) получим вторую ветвь гиперболы. График функции изображен на рисунке 3.
Любую дробь можно записать аналогичным образом, выделив ее целую часть. Следовательно, графики всех дробно-линейных функций являются гиперболами, различным образом сдвинутыми параллельно координатным осям и растянутыми по оси Оу.
Пример 2.
Построим график функции .
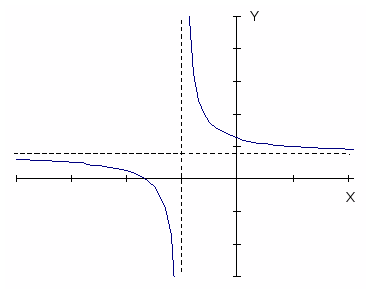
Поскольку мы знаем, что график есть гипербола, достаточно найти прямые, к которым приближаются ее ветви (асимптоты), и еще несколько точек.
Найдем сначала вертикальную асимптоту. Функция не определена там, где 2х+2=0, т.е. при х=-1. Стало быть, вертикальной асимптотой служит прямая х=-1.
Чтобы найти горизонтальную асимптоту, надо посмотреть, к чему приближаются значения функций, когда аргумент возрастает (по абсолютной величине), вторые слагаемые в числителе и знаменателе дроби относительно малы. Поэтому
.
Стало быть, горизонтальная асимптота – прямая у=3/2.
Определим точки пересечения нашей гиперболы с осями координат. При х=0 имеем у=5/2. Функция равна нулю, когда 3х+5=0, т.е. при х=-5/3.
Отметив на чертеже точки (-5/3;0) и (0;5/2) и проведя найденные горизонтальную и вертикальную асимптоты, построим график (рис.4).
Вообще, чтобы найти горизонтальную асимптоту, надо разделить числитель на знаменатель, тогда y=3/2+1/(x+1), y=3/2 – горизонтальная асимптота.
Алгоритм построения графика дробно-рациональной функции, содержащей квадратный трехчлен.
-
Найти область определения функции.
-
Разложить на множители квадратный трехчлен.
-
Сократить дробь.
-
Построить график (параболу, гиперболу, кубическую параболу).
-
Исключить из графика точки, не входящие в область определения («выколотые» точки).
-
Найти значение функции в «выколотых» точках.
-
Определить, при каких значениях b прямая y=b имеет с графиком ровно одну общую точку.
ЗАДАНИЕ
Построить график функции (D(y), на графике – выколотые точки):
Дробно-рациональные уравнения — это уравнения c одной переменной.
Содержание:
Определение дробно-рационального уравнения
Определение дробно-рационального уравнения:
Например, уравнения
являются дробно-рациональными.
Рассмотрим дробно-рациональное уравнение 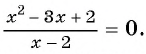
Рациональная дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю.
Таким образом, получим:
Ответ: 1.
Вернемся к уравнению 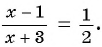
1) Перенесем все слагаемые из правой части уравнения в левую:
2) Преобразуем левую часть уравнения к рациональной дроби:
3) Применим условие равенства дроби нулю:
Ответ: 5.
Что нужно для решения дробно-рационального уравнения
Чтобы решить дробно-рациональное уравнение, нужно:
- Перенести все слагаемые из правой части уравнения в левую.
- Преобразовать левую часть уравнения к рациональной дроби.
- Применить условие равенства дроби нулю.
- Записать ответ.
Рассмотрим задачу: В дроби числитель на 2 больше знаменателя. Если числитель этой дроби уменьшить на 3, а знаменатель увеличить на 3, то новая дробь будет равна 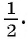
Решение:
Обозначим знаменатель первоначальной дроби через х, тогда ее числитель равен
Если числитель дроби уменьшить на 3, то получится числитель новой дроби: 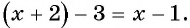
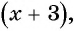
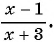
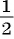
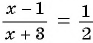
Решение многих задач приводит к уравнениям, у которых в левой или правой (или в той и другой) частях записаны дробные рациональные выражения. Такие уравнения называют дробно-рациональными уравнениями.
Пример №1
Решите уравнение
Решение:
(1)
(2)
(3)
(4) Ответ:
Пример №2
Решите уравнение
Решение:
(1)
(2)
(3)
(4) Ответ:
Пример №3
Решите уравнение
Решение:
(1)
(2)
(3)
(4) Ответ: -2; 6.
Пример №4
Решите уравнение
Решение:
Выполним замену переменной 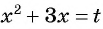
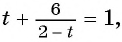
Подставим найденные значения 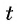
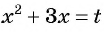
Ответ:
Дробно-рациональные уравнения используются как математические модели для решения задач, описывающих реальные ситуации.
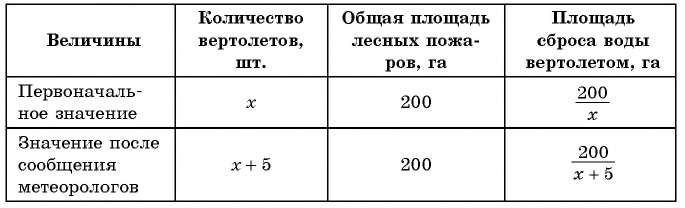
Например, рассмотрим задачу. На тушение лесных пожаров площадью 200 га отправлено несколько вертолетов с водосливными устройствами. По информации метеорологов предполагается усиление ветра, поэтому было выделено еще 5 вертолетов, в связи с чем площадь для сброса воды каждым вертолетом уменьшилась на 20 га. Сколько вертолетов участвовало в тушении пожаров первоначально?
Решение:
(1) Выясним, о каких величинах и зависимостях между ними в задаче идет речь. В задаче речь идет о площади лесных пожаров и количестве вертолетов для тушения пожаров.
(2) Выясним, какие значения, величин и зависимости между ними, известны. Известна зависимость между количеством вертолетов и площадью для сброса воды.
(3) Выясним, какие значения величин и зависимости между ними не известны. Неизвестно, сколько потребовалось вертолетов.
(4) Обозначим неизвестное значение одной величины через х, а остальные выразим через х и зависимости между величинами. Обозначим через 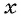
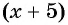
(5) Используя зависимости между известными и неизвестными значениями величин, составим уравнение (математическую модель задачи) и решим его.
По условию задачи 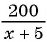
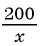
(6) Запишем ответ в соответствии со смыслом задачи. Поскольку 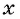
Ответ: 5 вертолетов.
Многие задачи, описывающие реальные процессы, имеют одну и ту же математическую модель. К таким относятся, например, задачи на движение, работу и т. п.
Рассмотрим две задачи:
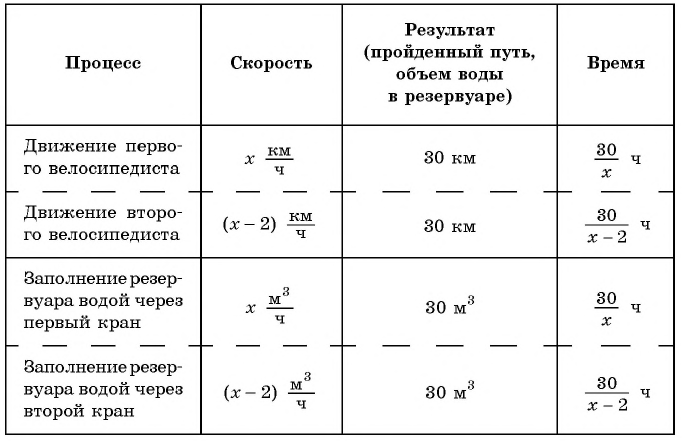
Задача 1. Два велосипедиста выехали одновременно из поселка 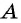
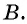
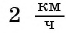
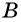
Задача 2. Для заполнения водой резервуара объемом 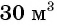
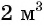
В обеих задачах речь идет о процессах: в первой — о процессе движения, во второй — о процессе заполнения резервуара водой.
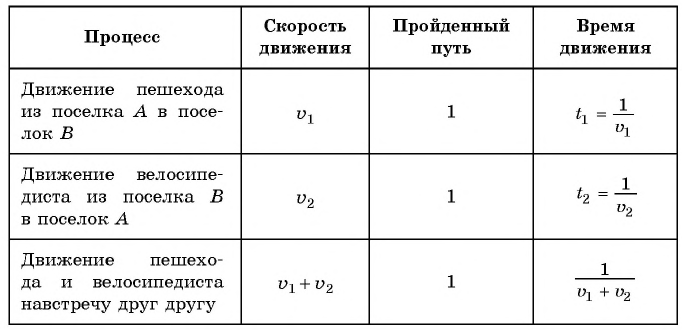
Составим таблицу зависимостей между величинами.
Поскольку первый велосипедист прибыл в поселок на 0,5 ч раньше второго, а один кран заполняет резервуар на 0,5 ч быстрее другого, то уравнение 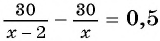
Решим полученное уравнение:
По условию каждой задачи подходит число 12.
Ответ задачи 1: скорость первого велосипедиста 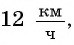
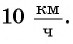
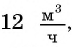
Пример №5
Является ли дробно-рациональным уравнение:
а)
б)
в)
г)
Решение:
Уравнение а) не является дробно-рациональным, так как его левая и правая части — целые рациональные выражения. Уравнения б)—г) являются дробно-рациональными, так как левые части этих уравнений — дробно-рациональные выражения.
Пример №6
Решите уравнение, используя условие равенства дроби нулю:
а)
б)
в)
г)
Решение:
а)
Ответ: 6.
б)
Ответ: -6.
в)
Ответ: 0; 6.
г)
Ответ: нет корней.
Пример №7
Какие из уравнений:
а)
б)
в)
г) 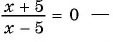
Решение:
а)
б)
в)
г)
Ответ: уравнения а), в), г) имеют один и тот же корень (уравнения равносильны).
Пример №8
Решите уравнение:
а)
б)
Решение:
а) (1)
(2)
(3)
(4) Ответ: 1; 2.
б)
Разложим на множители квадратный трехчлен в знаменателе первой дроби и получим:
Ответ: 2,5.
Пример №9
Найдите нули функции
Решение:
Так как нули функции — это значения аргумента, при которых значение функции равно нулю, то для решения задачи нужно решить уравнение
Используем условие равенства дроби нулю:
Ответ: 0; 3.
Пример №10
Найдите корни уравнения
Решение:
Выполним замену переменной в данном уравнении: 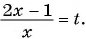
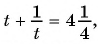
Решим его:
Выполним подстановку найденных значений переменной 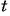
Ответ:
Моделирование реальных процессов с помощью дробно-рациональных уравнении
Задача:
Катер прошел 15 км по течению реки и 4 км по озеру, затратив на весь путь 1 ч. Чему равна скорость катера при движении по озеру, если скорость течения реки 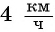
Решение:
В задаче идет речь о процессах движения катера по реке и по озеру. Составим таблицу зависимостей между величинами.
Так как по условию задачи на весь путь затрачен 1 ч, то составим уравнение: 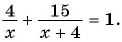
По условию подходит число 16.
Ответ: 16
Системы нелинейных уравнений для решения дробно-рациональных уравнений
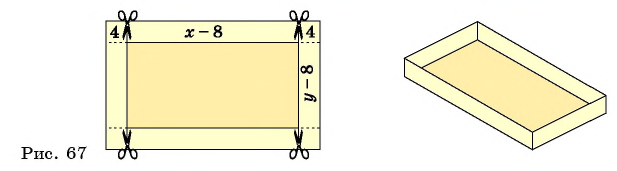
Рассмотрим задачу. Из листа картона прямоугольной формы нужно изготовить коробку без крышки, сделав надрезы в углах длиной 4 см (рис. 67). Найдите длину и ширину листа, зная, что его периметр равен 60 см, а объем коробки должен быть равен
Решение:
Обозначим длину и ширину листа соответственно 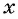
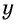
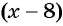

По условию задачи периметр листа прямоугольной формы равен 60 см, а объем коробки равен 160 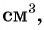
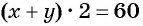
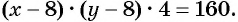
Полученная система уравнений содержит нелинейное рациональное уравнение 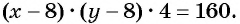
Способ подстановки
Решим полученную в задаче систему уравнений способом подстановки:
Из первого уравнения системы выразим переменную 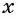
Заменим во втором уравнении переменную 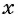
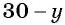
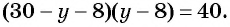
Найденные значения 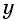
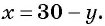
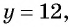
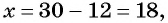
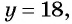
Решениями системы уравнений являются пары чисел 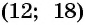
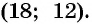
Чтобы решить систему уравнений способом подстановки, нужно:
- Из одного уравнения системы выразить одну из переменных.
- Заменить в другом уравнении эту переменную на ее выражение.
- Решить полученное уравнение.
- Найденные значения одной переменной подставить в выражение для другой переменной и найти значение другой переменной.
- В виде упорядоченных пар чисел записать ответ.
Решите систему уравнений
Решение:
(1) Из второго уравнения системы выразим переменную
(2) Заменим в первом уравнении переменную 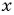
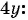
(3) Решим уравнение 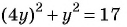
(4) Найденные значения 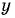
Если 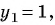
Если 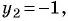
(5) Ответ: (4; 1), (-4; -1).
Способ сложения
Чтобы решить систему уравнений способом сложения, нужно:
- Одно из уравнений системы оставить без изменения, а другое заменить суммой уравнений системы.
- Из полученного уравнения (суммы) найти значения одной из переменных.
- Подставить эти значения переменной в оставленное без изменения уравнение системы и найти значения другой переменной.
- Записать ответ.
Решите систему уравнений
Решение:
(1)
(2)
(3) При 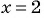
При 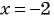
(4) Ответ: (2;1), (2;-1), (-2;1), (-2;-1).
- Заказать решение задач по высшей математике
Графический метод решения систем нелинейных уравнений
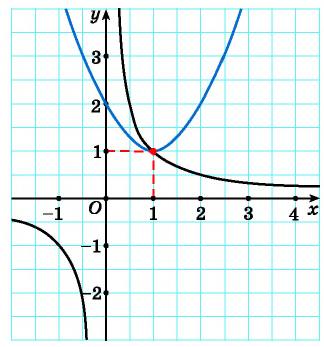
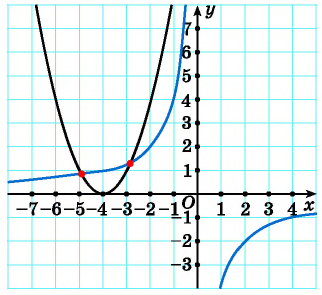
Решим систему уравнений 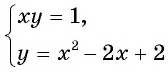
Первое уравнение системы равносильно уравнению 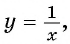
Графиком второго уравнения системы 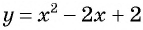
Единственная точка пересечения гиперболы 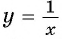
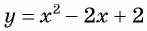
Рис. 68
Поскольку графический метод решения систем уравнений не является точным, то полученный результат необходимо проверить.
Подставим пару чисел (1; 1) в каждое из уравнений системы 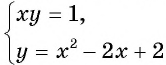
В рассмотренной системе решением оказалась пара целых чисел, которую легко было найти с помощью построенных графиков. В других случаях найти точные значения переменных по графику может оказаться затруднительно. Но, как правило, с помощью графического метода можно определить число решений системы уравнений.
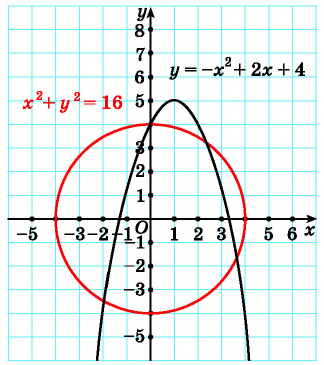
Например, определим число решений системы уравнений 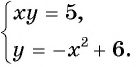
Рис. 69
Моделирование реальных процессов с помощью систем нелинейных уравнений
Системы нелинейных уравнений также являются математическими моделями при решении задач.
Задача:
Лечебными травами было решено засеять прямоугольный участок площадью 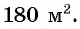
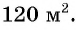
Решение:
В задаче речь идет о длине и ширине прямоугольного участка и его площади.
Если одну сторону участка обозначить через 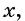
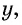
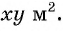
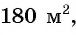
После уменьшения размеров участка площадь станет равной 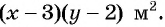
Объединим оба уравнения в систему
Получили математическую модель задачи в виде системы нелинейных уравнений. Решим ее, используя способ подстановки.
Условию задачи удовлетворяют найденные решения системы: стороны участка равны либо 15 м и 12 м, либо 18 м и 10 м.
Ответ: 15 м, 12 м или 18 м, 10 м.
Пример №11
Решите систему уравнений:
а)
б)
Решение:
а) Решим систему способом подстановки:
Ответ: (3; 0), (0; 3).
б) Применим способ сложения. Умножим первое уравнение на 2, сложим со вторым и получим:
Ответ:
Пример №12
Решите графически систему уравнений
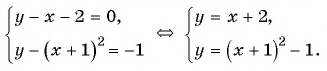
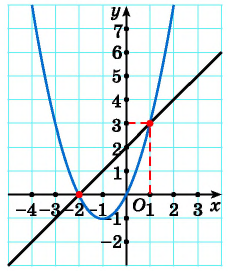
Решение:
Построим графики уравнений системы
График первого уравнения — прямая, проходящая через точки (-2; 0), (1; 3). График второго уравнения — парабола с вершиной в точке (-1; -1), пересекающая ось абсцисс в точках (-2; 0) и (0; 0), проходящая через точку (1; 3).
Прямая пересекается с параболой в точках с координатами (-2; 0), (1; 3). С помощью проверки убеждаемся, что пары чисел (-2; 0) и (1; 3) являются решениями данной системы.
Ответ: (-2; 0), (1; 3).
Пример №13
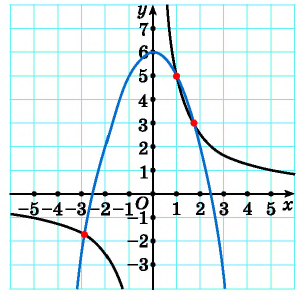
Сколько решений имеет система уравнений
Решение:
Построим в одной системе координат графики уравнений системы. Графиком первого уравнения системы является гипербола, проходящая через точки (-1; 4), (-4; 1). График второго уравнения — парабола с вершиной в точке (-4; 0), пересекающая ось ординат в точке (0; 16).
На рисунке видны только две точки пересечения графиков. Но, учитывая то, что парабола пересекает ось ординат, а гипербола не пересекает, делаем вывод, что графики пересекаются еще в одной точке. Таким образом, графики пересекаются в трех точках, а, значит, система имеет три решения.
Пример №14
Решите систему уравнений
Решение:
Решим систему методом замены переменных. Введем новые переменные: 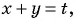
Тогда система примет вид
Решим ее способом подстановки:
Подставим 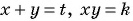
Решив каждую из двух систем совокупности способом подстановки, получим следующие решения исходной системы уравнений: (-5; 1); (1; -5); (4; 1); (1; 4).
Ответ: (-5; 1); (1; -5); (4; 1); (1; 4).
Задача:
Сумма квадратов цифр двузначного числа равна 13. Если из этого числа вычесть 9, то получится число, записанное теми же цифрами, но в обратном порядке. Найдите данное число.
Решение:
Обозначим цифру десятков данного числа через 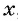
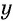
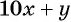
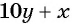
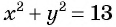
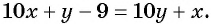
По условию задачи подходит только
Ответ: 32.
Задача:
Из поселка 
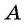
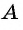
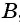
Решение:
Составим таблицу зависимостей между величинами.
По условию задачи велосипедист проделал бы тот же путь на 4 ч быстрее пешехода, поэтому получим уравнение
При движении навстречу друг другу пешеход и велосипедист встретились через 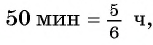
Составим и решим систему уравнений:
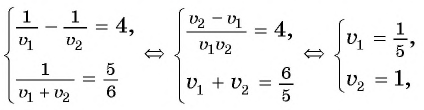
Ответ: 5 ч.
Задача:
Две бригады, работая вместе, ремонтировали дорогу в течение б дней, а затем одна вторая бригада закончила ремонт за 10 дней. За сколько дней могла бы отремонтировать дорогу одна первая бригада, если она может выполнить эту работу на б дней быстрее, чем одна вторая?
Решение:
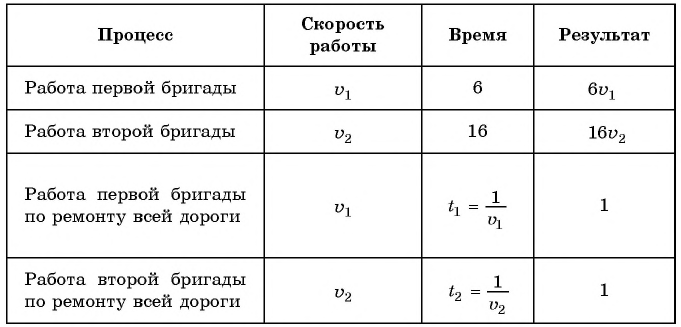
Составим таблицу зависимостей между величинами.
Обозначим объем всей работы через 1, тогда получим уравнение
Зная, что одна первая бригада может выполнить эту работу на б дней быстрее, чем одна вторая, составим уравнение
Составим и решим систему уравнений:
Ответ: 18 ч.
Формула длины отрезка с заданными координатами его концов. Уравнение окружности
Для применения графического метода решения систем необходимо знать графики различных уравнений. Многие из них вам уже знакомы. Это, например, прямая, гипербола, парабола.
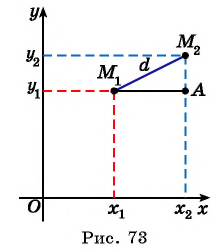
Расширим возможности использования графического метода решения систем нелинейных уравнений и выведем уравнение окружности с центром в заданной точке с заданным радиусом. Для этого сначала выведем формулу для вычисления длины отрезка с заданными координатами его концов, т. е. для вычисления расстояния между двумя точками, заданными своими координатами.
Рассмотрим точки 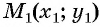
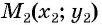
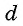
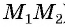
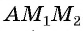
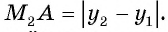
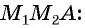
Получили формулу длины отрезка с заданными координатами его концов, или формулу расстояния между двумя точками с координатами
Пример №15
Найдите расстояние между точками А(-1; 3) и В(2; 5).
Решение:
Подставим координаты точек А(-1; 3) и В(2; 5) в формулу расстояния между двумя точками 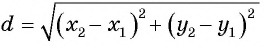
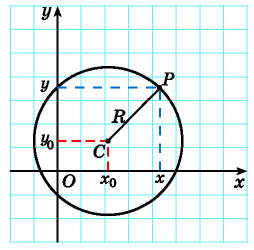
Рассмотрим окружность на координатной плоскости. Окружность — это множество точек плоскости, расстояние от каждой из которых до одной данной точки (центра окружности) является величиной постоянной, равной радиусу окружности
По формуле расстояния между двумя точками найдем расстояние от данной точки 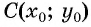
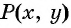
Рис. 74
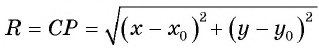
Таким образом, если точка принадлежит окружности с центром 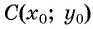
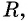
Уравнение 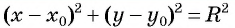
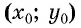
Если координаты точки удовлетворяют уравнению 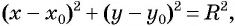
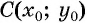
Покажем, что если точка 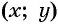
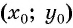
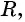
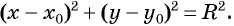
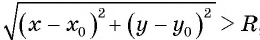
т. е.
Чтобы составить уравнение окружности, нужно:
- Определить координаты центра окружности
- Определить радиус окружности
- Подставить найденные значения
и
в уравнение окружности
Составьте уравнение окружности с центром в точке (-8; 2) и радиусом 5.
Решение:
(1)
(2)
(3)
Пример №16
Составьте уравнение окружности:
а) с центром в точке (4; -1) и радиусом
б) с центром в точке (0; 0) и радиусом 4.
Решение:
а) Подставим координаты центра окружности 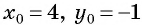
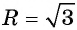
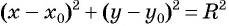
б) Координаты центра окружности: 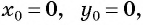
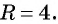
Если центром окружности радиуса 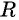
Пример №17
Определите количество решений системы уравнений
Решение:
Рис. 75
Построим графики уравнений системы. Первое уравнение — это уравнение окружности с центром в начале координат и радиусом, равным 4. Графиком второго уравнения является парабола с вершиной в точке (1; 5), пересекающая ось ординат в точке (0; 4).
Построенные графики пересекаются в четырех точках (рис. 75). Значит, данная система уравнений имеет 4 решения.
Ответ: 4 решения.
Пример №18
Найдите длину отрезка 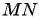
Решение:
По формуле длины отрезка 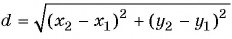
Пример №19
Найдите длину диагонали прямоугольника, если заданы его вершина 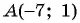
Решение:
Найдем длину отрезка
Длина отрезка 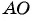
Пример №20
Определите координаты центра и радиус окружности:
а)
б)
в)
Решение:
а)
б)
в)
Пример №21
Какие из данных точек лежат на окружности
а)
б)
в)
г)
Решение:
Подставим координаты точек в уравнение окружности:
а) 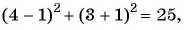
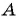
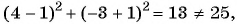
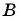
в) 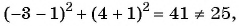
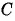
г) 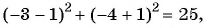
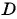
Пример №22
Запишите уравнение окружности с центром в точке (-1; 1) и радиусом
Решение:
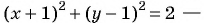
Пример №23
Запишите уравнение окружности с центром в точке 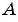
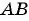
Решение:
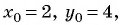
Уравнение окружности
Пример №24
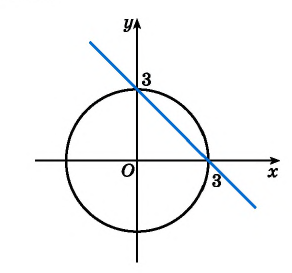
Решите систему уравнений 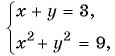
Решение:
График первого уравнения — прямая, проходящая через точки (3; 0), (0; 3). График второго уравнения — окружность с центром в начале координат и радиусом, равным 3.
Координаты точек пересечения (3; 0), (0; 3) — решения системы.
- Дробно-рациональные неравенства
- Прогрессии в математике — арифметическая, геометрическая
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла
- Рациональная дробь
- Функция в математике
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей

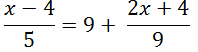
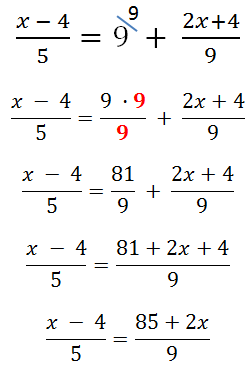
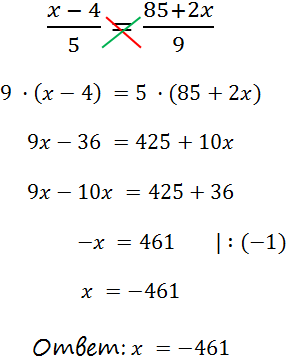
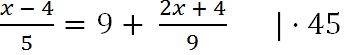

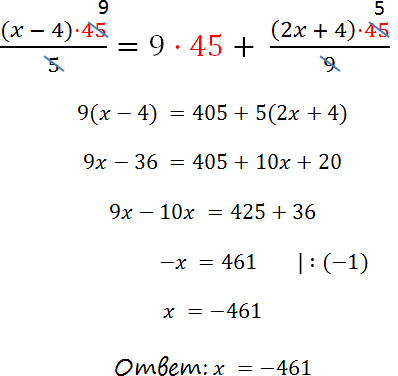



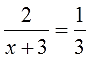
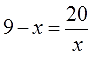
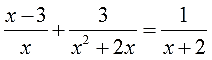
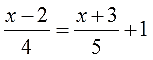
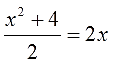
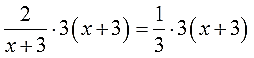
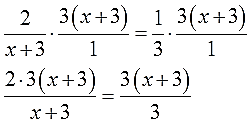
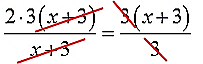
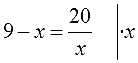
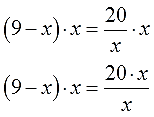
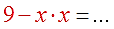
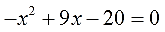
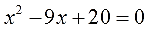
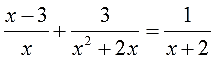
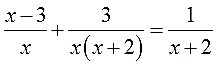
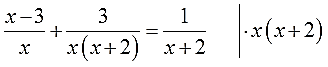
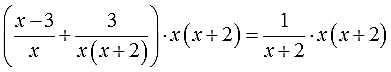
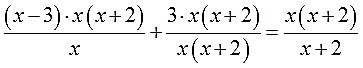
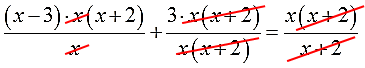
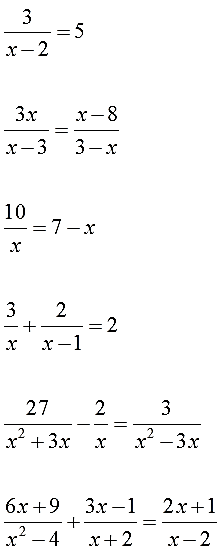







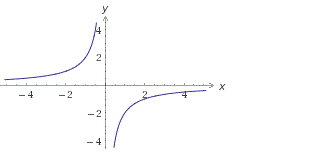
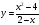
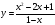
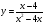
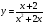
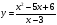
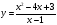
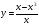
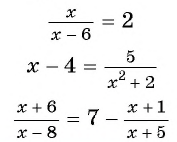
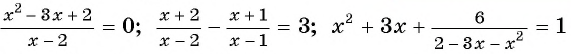
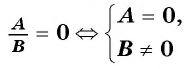
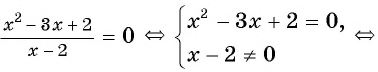
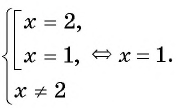
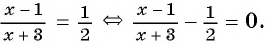
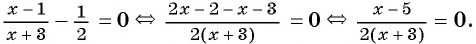
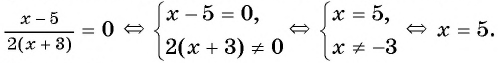
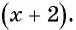
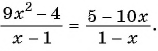
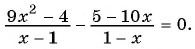
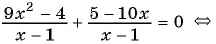
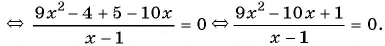
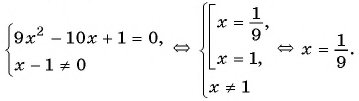
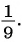
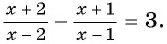
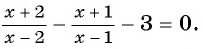
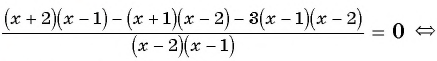
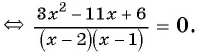
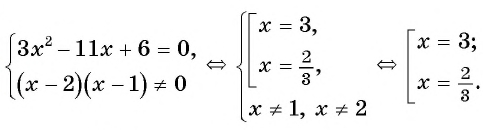
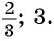
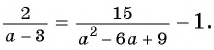
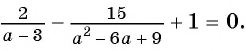
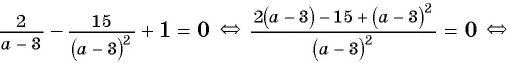
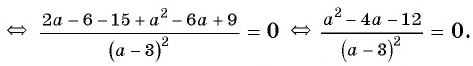
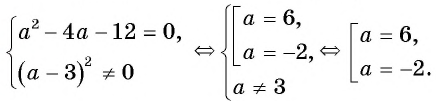
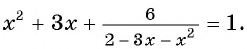
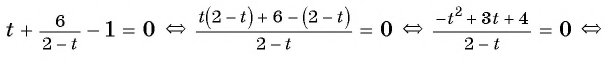
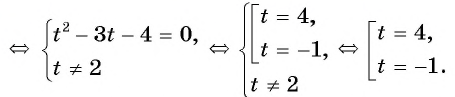
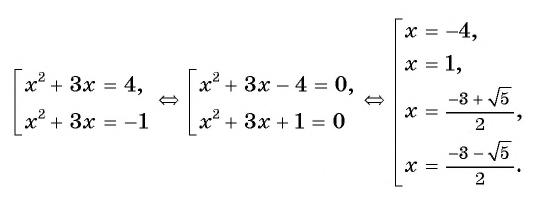

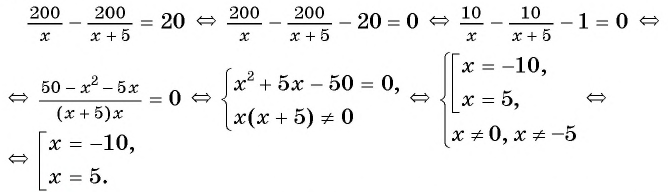
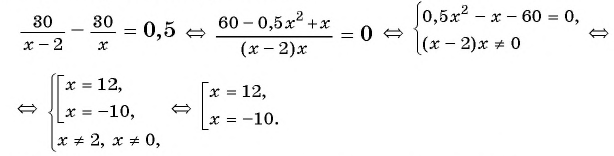
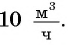
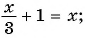
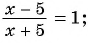
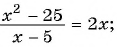
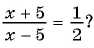
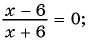
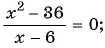
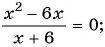
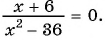
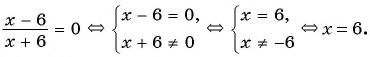
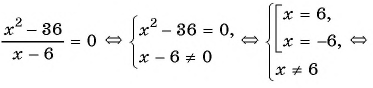
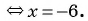
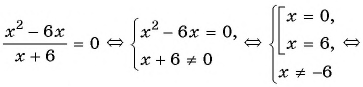
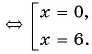
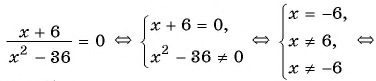
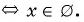
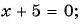
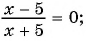
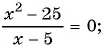
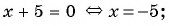
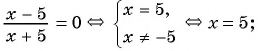
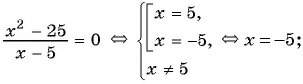
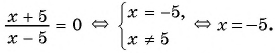
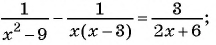
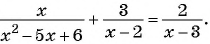
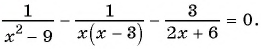
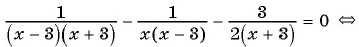
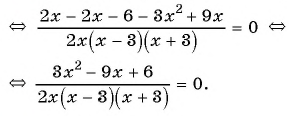
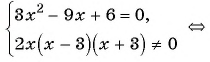
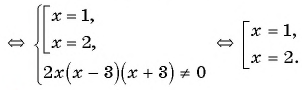
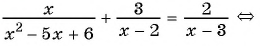
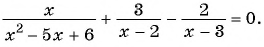
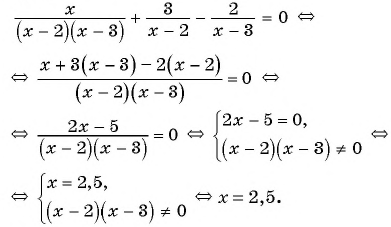
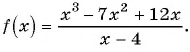
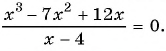
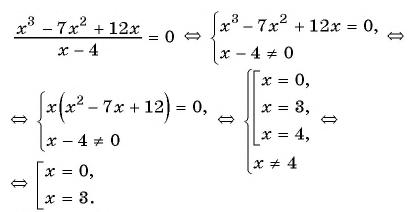
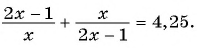
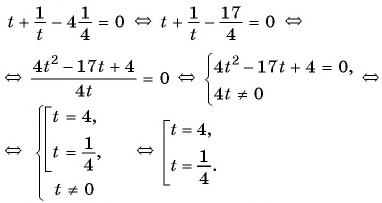
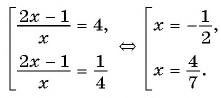
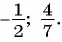

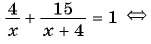
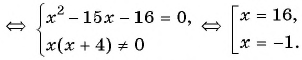
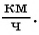
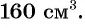
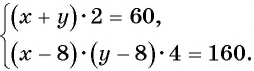
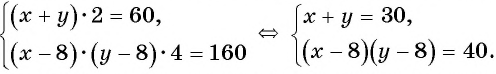
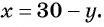
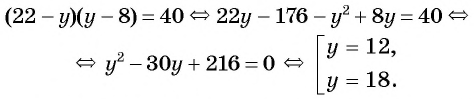
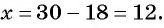
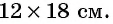
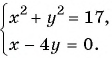
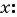
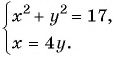
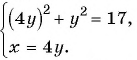
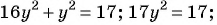
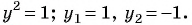
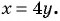
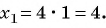
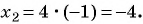
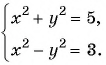
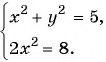
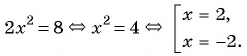
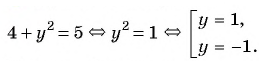
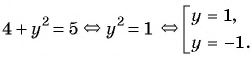
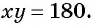
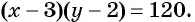
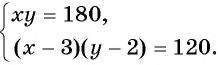
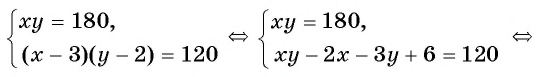
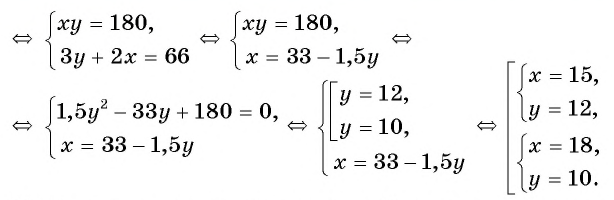
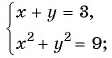
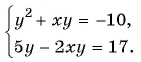
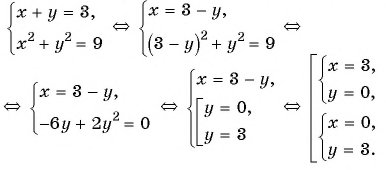
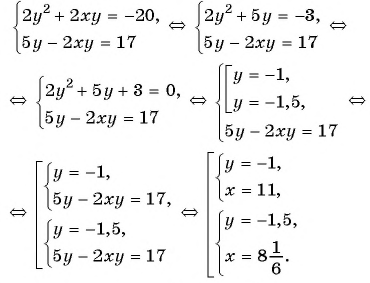
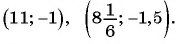
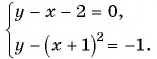
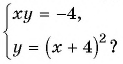
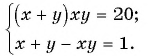
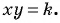
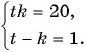
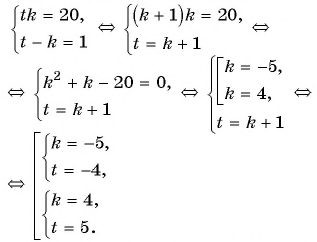
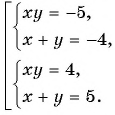
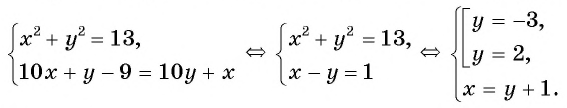
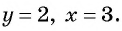
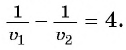
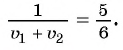
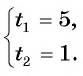
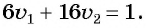
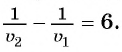
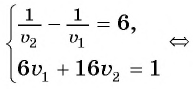
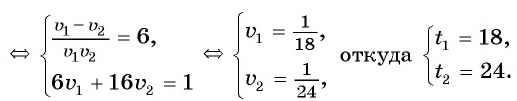
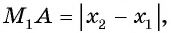
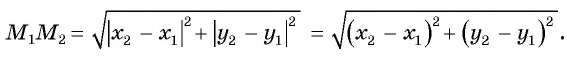
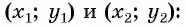
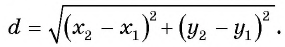
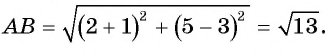
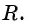
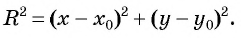
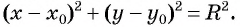
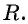
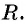
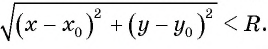
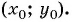
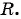
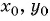 и
и 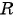 в уравнение окружности
в уравнение окружности