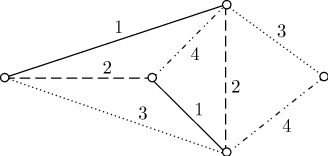
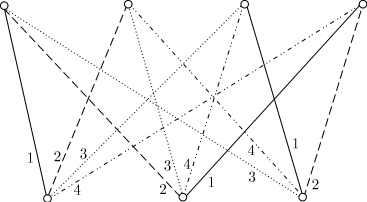
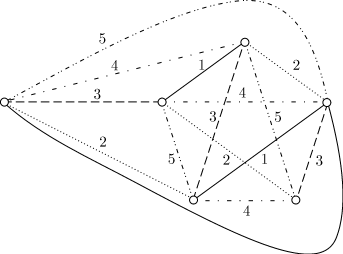
Реберная раскраска
Граф
G называется реберно к —
раскрашиваемым, если его ребра можно раскрасить к красками таким образом, что никакие два смежных
ребра не окажутся одного цвета. Если граф G реберно
к — раскрашиваем, но не является
реберно (к
— 1) -раскрашиваемым, то к называется хроматическим классом или хроматическим индексом, или реберно-хроматическим числом графа G . При этом используется запись Xe(G) = к. На
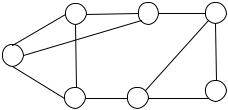
рисунке изображен граф G , для которого Xe(G) = 4.
Ясно, что если наибольшая из степеней
вершин графа G равна p , то Xe(G)≥ p
. Следующий результат, известный как теорема Визинга, дает точные оценки для
хроматического класса графа G.
Доказательство этой теоремы можно найти у Оре (Ore O. The four—color problem, Academic Press, New York,
1967).
Теорема.(Визинг, 1964) Пусть в графе G, не имеющем петель, наибольшая из степеней вершин равна p; тогда p
≤ Xe(G) ≤ p + 1.
Задача, состоящая в выяснении того,
какие графы имеют хроматический класс p, а какие p + 1,
не решена. Однако в некоторых частных случаях соответствующие результаты
находятся легко. Например, Xe(Cn)= 2 или 3 в
зависимости от того, четно n или
нечетно, а Xe(Wn)= n — 1
, при n≥ 4. Хроматические классы полных графов
и полных двудольных графов вычисляются тоже просто.
Теорема. Xe(Km,n )= p= max(m,n).
Доказательство
Без потери общности можно считать,
что m ≥ n и что граф Km,n изображен так:
n вершин
расположены на горизонтальной линии под m вершинами.
Тогда искомая реберная раскраска получается последовательным окрашиванием
ребер, инцидентных этим та вершинам, с
использованием следующих групп красок: {1,2, …, m};{2,3, …,m, 1}:…: {n, …, m, 1, …, n — 1}:при этом краски
из каждой группы располагаются по часовой стрелке, вокруг соответствующей
вершины.
Теорема. Хe(Кп) — n,
если n нечетно (n ≠1), и Хе(Кn) = n — 1, если n четно.
Доказательство
В случае нечетного п расположим вершины графа Кп в виде правильного n-угольника. Тогда его
ребра можно раскрасить следующим образом: сначала окрашиваем каждую сторону n-угольника в
свой цвет, а затем каждое из оставшихся ребер, диагонали n-угольника, окрашиваем в
тот же цвет, что и параллельная ему сторона.
То, что граф Кп
не является реберно (n— 1) -раскрашиваемым, сразу же следует из того,
что максимально возможное число ребер одного цвета равно (n — 1)/2.
В случае четного n(≥ 4) граф Кп
можно рассматривать как соединение полного (п — 1) — графа Кn-1и отдельной
вершины. Если в Кn-1 окрасить ребра описанным выше способом, то для
каждой вершины останется один неиспользованный цвет, причем все эти
неиспользованные цвета будут различными. Таким образом, чтобы получить реберную
раскраску Кп,
достаточно окрасить оставшиеся ребра в соответствующие «неиспользованные»
цвета.
Свойство 1. Любая вершина полного
графа с шестью или более вершинами и ребрами двух цветов принадлежит, по
меньшей мере, трем ребрам одного цвета.
Свойство 2. В любом полном графе с
шестью или более вершинами и ребрами двух цветов найдется, по меньшей мере,
один треугольник с одноцветными сторонами.
Свойство 3. Если в полном графе с
пятью вершинами и ребрами двух цветов не найдется треугольника с одноцветными
сторонами, то граф можно изобразить в виде «пятиугольника» с красными
сторонами и синими диагоналями.
Свойство 4. В любом полном графе с
шестью или более вершинами и ребрами одного из двух цветов всегда найдутся два
разных треугольника с одноцветными сторонами. Эти два треугольника могут иметь
общую вершину или даже общее ребро.
Если два треугольника имеют общую
вершину или ребро, то их называют сцепленными.
Свойство 5. В полном графе с
семнадцатью или более вершинами и ребрами трех цветов всегда найдется, по
меньшей мере, один треугольник с одноцветными сторонами.
Свойство 6. В полном графе с
восемью вершинами, ребра которого окрашены в два цвета, обязательно найдутся
два треугольника с одноцветными сторонами, которые не являются сцепленными.
Хроматическое число
Рассмотрим задачу: при каких
условиях вершины графа можно раскрасить так, чтобы каждое ребро было инцидентно
вершинам разного цвета? Нас больше всего интересует вопрос, какие графы можно
раскрасить с соблюдением определенных условий, чем вопрос, сколькими способами
можно выполнить это раскрашивание.
Пусть граф G не имеет петель; тогда G называется к —
раскрашиваемым, если каждой его вершине можно приписать один из к цветов таким
образом, чтобы никакие две смежные вершины не оказались одного цвета. Если граф
G является к
-раскрашиваемым, но не является (к — 1) — раскрашиваемым, назовем его к
-хроматическим, а число к назовем хроматическим числом графа G и обозначим через X(G ). На рисунке изображен 4-хроматический (и, следовательно, к
-раскрашиваемый граф при к ≥ 4) граф; цвета обозначены греческими буквами.
Для удобства будем предполагать,
что все графы не содержат петель. Однако будем допускать существование кратных
ребер, так как они не влияют на наши рассуждения.
Ясно, что Х(Кп)=n,
и, следовательно, легко построить графы со сколь угодно большим хроматическим
числом. С другой стороны, нетрудно видеть, что X(G )=1 тогда и только тогда, если G — вполне несвязный граф, и
что
X(G )=2 тогда и только тогда, если G — двудольный граф, отличный от вполне несвязного графа.
Теорема. Если наибольшая из степеней вершин графа G равна
p, то этот граф (р + 1) -раскрашиваем.
Доказательство. Проведем индукцию по числу вершин в G . Пусть G — граф с n вершинами; если
из него удалить произвольную вершину V вместе
с инцидентными ей ребрами, то в оставшемся графе будет n -1 вершин, причем степени вершин по-прежнему не превосходят p. По предположению индукции этот граф (р + 1) — раскрашиваем, отсюда получится (р + 1) -раскладка для G ,
если окрасить вершину V цветом, отличным от
тех, которыми окрашены смежные с ней вершины, а их не более чем Р.
Теорема (Брукса). Пусть G — простой связный граф, не являющийся полным; если
наибольшая из степеней его вершин равна р(р ≥ 3), то он Р -раскрашиваем.
Доказательство. Проведем индукцию по числу вершин графа G . Предположим, что G имеет
n вершин. Если при этом степень какой-нибудь его
вершины меньше Р, дальше можно рассуждать,
как в доказательстве теоремы 1, и все будет закончено. Поэтому без потери
общности можно считать граф G
регулярным степени Р.
Выберем
произвольную вершину V и удалим ее, вместе с
инцидентными ей ребрами. Останется граф с n — 1 вершинами, в котором наибольшая из степеней вершин не превосходит Р. По предположению
индукции этот граф Р-раскрашиваем. Теперь
окрасим вершину V в один из имеющихся Р цветов. Как и
раньше, считаем, что смежные с V вершины V1, …, Vp расположены вокруг V по часовой
стрелке и окрашены в различные цвета Ai,C2,..,Ср.
Определяя
подграфы Hij(i≠j, 1≤i,j ≤ р), когда Vi, Vj
лежат в разных компонентах графа Hij. Таким образом,
можно считать, что при любых данных i,j вершины Vi, Vj связаны простой цепью, целиком
лежащей в Hij
. Обозначим компоненту графа Hij, содержащую
вершины Vi, Vj, через Cij .
Ясно, что
если вершина Vi — смежная более чем с одной вершиной цвета Cj, то существует цвет, отличный от Ci, не приписанный
никакой из вершин, смежных с Vi. Тогда вершину Vi можно окрасить в этот цвет, что, в свою очередь,
позволит окрасить вершину V
в цвет Ci и
закончить на этом доказательство теоремы. Если этот случай не имеет места, то
используем аналогичное рассуждение, чтобы показать, что каждая вершина из Cij (отличная от Vi и от Vj )
должна иметь степень 2. Предположим, что W — первая вершина простой цепи из в Vj,
которая имеет степень больше 2; тогда W можно перекрасить в цвет, отличный от Ci или Cj, нарушая тем самым свойство, что Vi и Vj связаны простой цепью, целиком лежащей в Cij. Поэтому мы
можем считать, что для любых i
и j компонента
Cij состоит только из простой цепи, соединяющей вершину
Vi
с Vj .
Заметим
теперь, что две простые цепи вида Cij
и Cji , где i ≠ I
, можно считать пересекающимися только
в вершине Vj,
так как если W— другая
точка пересечения, то ее можно перекрасить в цвет, отличный от Ci или Cj, или Cl, а это противоречит факту, что Vi и
Vj связаны
простой цепью.
Для завершения доказательства выберем (если это возможно)
две несмежные вершины Vi , Vj и допустим,
что W — вершина цвета Cj, смежная с Vi. Поскольку
Сil — простая цепь (для любого I ≠ j
), можно поменять между собой цвета
вершин в этой цепи, не затрагивая раскраску остальной части графа. Но это
приводит к противоречию, потому что тогда w будет
общей вершиной простых цепей Cij
и Cji. Отсюда следует, что нельзя
выбрать две вершины Vi и Vj несмежными,
и поэтому G должен быть полным графом Kp+1.
А так как это не допускается условием теоремы, то все возможные случаи
рассмотрены.
Гипотеза
о четырех красках
Уже сто с лишним лет математики пытаются
доказать гипотезу четырех красок. В этом направлении был достигнут значительный
прогресс. В печати появилось сообщение (K.Appel, W.Haken, Every planar map is
four colorable, Bull. of Amer. Math. Soc., 82, No,5 (sept. 1976)), что
гипотезу четырех красок удалось обосновать с использованием ЭВМ.
Сформулируем без доказательства несколько
относящихся к этой проблеме результатов:
1. Если гипотеза четырех красок не верна, то любой
опровергающий ее пример будет очень сложным. Известно, например, что всякий
планарный граф, имеющий менее 52 вершин, 4-раскрашиваем.
2. Любой не содержащий треугольников планарный
граф 3-раскрашиваем (теорема Греча).
3. Если попытаться доказать гипотезу четырех
красок, то достаточно доказать ее для гамильтоновых планарных графов (довольно
неожиданный результат Уитни).
Возникновение гипотезы четырех красок
исторически связано с раскрашиванием географических карт. Если имеется карта с
изображением нескольких стран, то интересно узнать, сколько понадобится цветов
для такой раскраски этих стран, чтобы никакие две соседние страны не были
окрашены в один и тот же цвет. Возможно, самая привычная форма гипотезы четырех
красок такова: любую карту можно раскрасить с помощью четырех красок.
Чтобы сделать это утверждение точным, надо
определить, что означает слово «карта». Поскольку в рассматриваемых
нами задачах о раскраске требуется, чтобы страны, расположенные по обе стороны
ребра, были разного цвета, придется исключить карты, обладающие мостом. Таким
образом, удобно определить карту как связный плоский граф, не содержащий
мостов. Заметим, что при таком определении карты не исключаем петель или
кратных ребер.
Назовем карту k — раскрашиваемой, если ее грани можно
раскрасить k красками так, чтобы никакие две смежные
грани, то есть грани, границы которых имеют общее ребро, не были одного цвета.
Там, где можно запутаться, будем использовать термин вершинно k — раскрашиваемой , имея в виду k -раскрашиваемость в
описанном выше смысле. Например, изображенный ниже граф является
3-раскрашиваемым и вершинно 4-раскрашиваемым.
Теперь сформулируем гипотезу четырех красок для карт: всякая карта 4-раскрашиваема.
Теорема.
Карта G является 2-раскрашиваемой тогда и только тогда, если G представляет собой эйлеров граф.
Доказательство.
Любую вершину V из G должно
окружать четное число граней, так как их можно раскрасить в два цвета. Отсюда
следует, что степень каждой вершины четна, и поэтому G — эйлеров граф.
Жордановой кривой, или жордановой дугой, на
плоскости называется непрерывная кривая, не имеющая самопересечений; замкнутой
жордановой кривой называется жорданова кривая, начало и конец которой
совпадают.
Опишем метод, дающий нужную раскраску
граней графа G. Выберем
произвольную x грань F
и окрасим ее в красный цвет. Проведем жорданову кривую из точки грани F в некоторую точку любой грани, причем
так, чтобы эта кривая не проходила ни через какую вершину графа G. Если на пути от точки x до точки y
грани F‘ наша кривая пересечет четное число
ребер, окрасим грань F‘
в красный цвет; в противном случае — в синий.
Нетрудно показать, что раскрашивание
определено корректно: берем «цикл», состоящий из двух таких
жордановых кривых (то есть замкнутую жорданову кривую), и показываем, что он
пересекает четное число ребер графа G (надо использовать индукцию по числу вершин, находящихся внутри
цикла, и тот факт, что каждой вершине графа G инцидентно четное число ребер).
Из нее получаем логическое выражение (идем по строчкам):
Покрытие = (1+2+3) · (1+2+3+4+5) · (1+2+3+5+6) · (2+4+5) × × (2+3+4+5+6) · (3+5+6).
Упрощаем с учетом того, что по закону поглощения: (1+2+3) · (1+2+3+4+5) = (1+2+3), (2+4+5) · (2+3+4+5+6) = (2+4+5), (1+2+3+5+6) · (3+5+6) = (3+5+6).
Покрытие = (1+2+3) · (2+4+5) · (3+5+6).
Раскрываем скобки с учетом того, что
(2+4+5) · (3+5+6)=5+2·3+2·6+4·3+4·6. Покрытие = (1+2+3) · (5+2·3+2·6+4·3+4·6) =
=1·5+1·2·3+1·2·6+1·4·3+1·4·6+2·5+2·2·3+2·2·6+2·4·3+2·4·6+3·5+
+3·2·3+3·2·6+3·4·3+3·4·6.
Упрощаем по закону поглощения (x+x·y=x) и с учетом x·х=x.
Покрытие = 1·5+1·2·3+1·2·6+1·4·3+1·4·6+2·5+2·2·3+2·2·6+
+2·4·3+2·4·6+3·5+3·2·3+3·2·6+3·4·3+3·4·6 =
=2·6+2·3+2·3+4·3+1·5+1·4·6+2·5+3·5 = =
2·6+2·3+4·3+1·5+1·4·6+2·5+3·5.
Получили ДНФ, выбираем самое короткое слагаемое, например 2·6. Значит, искомое число внешней устойчивости равно 2, а пример внешне устойчивого множества вершин – {2,6}.
Ответ: β0.=2.
6.7.1. Хроматическое число
Пусть необходимо раскрасить вершины графа так, чтобы любые две смежные вершины были раскрашены в разные цвета, при этом число использованных цветов должно быть наименьшим.
Это число называется хроматическим числом графа, будем его обозначать h(G). Если h(G)=k, то граф называется k-
раскрашиваемым.
Заметим, что если данный граф является полным, т. е. любые две вершины являются смежными, то хроматическое число такого графа равно п, где п – число вершин.
177
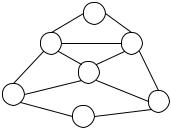
Существует несколько алгоритмов нахождения точного зна-
чения хроматического числа. Один из них основан на методе поиска наименьшего покрытия.
Поскольку при любой допустимой раскраске графа G множество вершин, окрашиваемых в один и тот же цвет, должно быть независимым множеством, то всякую допустимую раскраску можно интерпретировать как разбиение всех вершин графа G на такие независимые множества. Далее, если каждое независимое множество расширить до максимального (путем добавления к нему других вершин), то раскраска графа G может быть тогда истолкована как покрытие вершин графа G максимальными независимыми множествами вершин (пустыми подграфами). Очевидно, что в последнем случае некоторые вершины графа G могут принадлежать более чем одному максимальному независимому множеству (пустому подграфу). Это говорит о возможности существования различных допустимых раскрасок (использующих одно и то же число цветов), так как вершину, принадлежащую разным максимальным множествам, можно окрасить в любой из цветов, соответствующих тем множествам, которым она принадлежит.
Итак, пусть построены все максимальные независимые множества графа G (пусть таких множеств t) и пусть задана (n×t) матрица M = {mij}, у которой mij=1, если вершина xi принадлежит j-му максимальному независимому множеству, и mij=0 в противном случае. Если теперь каждому максимальному независимому множеству сопоставить единичную стоимость, то задача раскраски сведется просто к задаче нахождения наименьшего числа столбцов в матрице М, покрывающих все ее строки х. Каждый столбец из решения
этой задачи соответствует определен-
|
1 |
ному цвету, который может быть ис- |
|
|
2 |
3 |
пользован для окраски всех вершин |
|
максимального независимого множест- |
||
|
5 |
ва, представленного этим столбцом. |
|
|
Задача 6.10. Найти точное значение |
||
|
4 |
||
|
6 |
хроматического числа графа (рис. 6.30) |
|
|
7 |
и предложить вариант раскраски. |
|
|
Решение. В соответствии с алгорит- |
|
Рис. 6.30 |
мом найдем все пустые подграфы: |
178
{2,6}, {2,7}, {1,5}, {1,4,6}, {3,2,7}, {3,4}, {5,7}, {4,3}.
Составим матрицу покрытий:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Цвет |
|
|
{2,6} |
1 |
1 |
a |
|||||
|
{2,7} |
1 |
1 |
b |
|||||
|
{1,5} |
1 |
1 |
c |
|||||
|
{1,4,6} |
1 |
1 |
1 |
d |
||||
|
{3,2,7} |
1 |
1 |
1 |
e |
||||
|
{3,4} |
1 |
1 |
f |
|||||
|
{5,7} |
1 |
1 |
g |
Присвоим каждому пустому подграфу свой цвет. Запишем покрытие, используя логические операции (аналогично тому, как мы поступали при поиске внешне устойчивых множеств вершин). Для этого рассмотрим составленную матрицу по столбцам: 1-й столбец покрывается 3-й или 4-й строкой (это означает, что первую вершину можно окрасить в цвет с или d), 2-й столбец покрывается 1-й, 2- й или 5-й строкой (действительно, вторую вершину можно окрасить в цвет a, c или e) и т.д. Получим логическое выражение
(с+d)·(a+b+e)·(e+f)·(d+f)·(c+g)·(a+d)·(b+e+g), которое можно упро-
стить, сначала перемножив соответственно 2-ю и 7-ю, 1-ю и 5-ю, 3- ю и 4-ю скобки (b+e+a·g)·(c+d·g)·(f+e·d)·(a+d). Дальнейшее легкое упрощение невозможно и строго говоря, если бы стояла задача найти все возможные способы покрытий, необходимо было бы раскрыть все скобки и провести окончательное упрощение. В нашем случае необходимо найти одно решение с минимальной мощностью. Например, в результате умножения получится слагаемое g·d·e (из первой скобки e, из второй d·g, из третьей e·d, из четвертой d), мощность которого равна трем. Это и есть точное значение хроматического числа. Соответствующая этому решению раскраска выглядит так: в цвет g (например, красный) красим вершины {5,7}, в цвет d (синий) красим вершины {1,4,6}, в цвет e (зеленый) по идее следует покрасить вершины {3,2,7}, но вершине 7 уже присвоен красный цвет, поэтому в множество зеленых вершин еe включать не будем.
Ответ: h=3, раскраска: {5,7} – красный цвет, {1,4,6} – синий, {3,2} – зеленый.
179
Одной из наиболее полезных теорем при определении хроматического числа является следующая теорема.
Теорема 6.9. Хроматическое число графа равно 2 тогда и только тогда, когда все имеющиеся в графе циклы содержат четное число ребер.
Довольно много задач решается на основе этого правила. В остальных случаях приходится прибегать к различным способам оценки хроматического числа.
Теорема 6.10. Если наибольшая из степеней вершин графа G равна ρ, то этот граф (ρ+1)-раскрашиваем (т.е. его хроматическое число не превосходит (ρ+1)).
Оценка хроматического числа, даваемого этой теоремой, является достаточно грубой. Особенно наглядно это выглядит на примере дерева, для которого степень вершин может быть как угодно велика, а хроматическое число равно 2.
При этом хроматическое число графа равно Stm + 1 только в двух случаях: во-первых, если граф является полным (или, точнее, содержит полный подграф на Stm + 1 вершине, и, во-вторых, если Stm = 2 и при этом данный граф содержит контур нечетной длины (такой граф изображен на рис. 6.31, б, максимальная степень его вершин – 2, а хроматическое число – 3).
4
Во всех остальных случаях хроматическое число графа не превосходит максимальной степени вершин, конечно, за исключением ситуации, когда граф тривиальный (максимальная степень тогда равна 0, но первая краска все равно потребуется). На рис. 6.31, а
180
изображен граф, максимальная степень вершин которого равна 3, и, поскольку он не содержит полного подграфа на четырех вершинах, оценка хроматического числа может быть снижена до Stm.
Улучшение на единицу оценки, даваемое теоремой 6.10, позволяет сформулировать другую теорему, имеющую в ряде случае довольно явное практическое значение при решении задач.
Теорема 6.11. Если наибольшая из степеней вершин нетривиального графа G равна Stm, то этот граф Stm-раскрашиваемый (т.е. его хроматическое число не превосходит Stm) всегда, за исключением двух случаев:
1)граф содержит полный подграф на Stm + 1 вершине,
2)Stm = 2 и при этом данный граф содержит контур нечетной длины.
Иногда эта теорема формулируется еще проще, сразу исключая обе эти ситуации при помощи ограничений формулировки.
В качестве примера приведем условие задачи, которая легко решается именно с помощью этой теоремы.
Задача 6.11. Определить с достаточным обоснованием точное значение хроматического числа графа (рис. 6.32).
|
2 |
3 |
4 |
|
|
1 |
|||
|
Рис. 6.32 |
7 |
6 |
5 |
Решение. Максимальная степень вершины Stm = 3, граф связный и не является полным, значит, по теореме Брукса он 3-раскра- шиваемый, т.е. h≤3.
Граф содержит контуры нечетной длины, значит, по теореме 6.9 его хроматическое число строго больше двух: h > 2.
Так как h – натуральное число, совмещая данные ограничения получим 2 < h ≤ 3 и отсюда h = 3.
Хроматическое число графа на n вершинах может изменяться от 1 до n. Ясно, что у полного графа χe (K n ) = n , и, следовательно,
181
легко построить графы со сколь угодно большим хроматическим числом. С другой стороны, нетрудно видеть, что χ(G) =1 тогда и
только тогда, если G – вполне несвязный (пустой) граф, и что χ(G) = 2 тогда и только тогда, если G – двудольный граф, отлич-
ный от вполне несвязного графа. Не следует, впрочем, путать двудольные графы с графами, имеющими двудольное представление.
Если обратиться к привычным терминам, то можно утверждать, что хроматическое число, равное двум, имеют:
•ациклические графы, содержащие хотя бы одно ребро,
•простые циклы на четном числе вершин,
•двудольные графы,
•графы, содержащие только четные циклы.
Все указанные четыре категории графов по своей сути являются двудольными.
6.7.2. Поиск хроматического числа при операциях над графами
Операция удаление ребра. При удалении ребер из полных графов хроматическое число уменьшается, причем размер этого уменьшения зависит от того, какую конфигурацию образуют удаляемые ребра. Напомним, что у полного графа на n вершинах хроматическое число h(Kn)=n.
При удалении одного ребра у полного графа на n вершинах хроматическое число снижается на единицу, так как образуются две несмежные вершины, которые можно покрасить в единый цвет. Таким образом, h = n – 1.
При удалении двух ребер у полного графа на n вершинах хроматическое число снижается на единицу или сразу на две единицы, в зависимости от того, являются ли удаляемые ребра смежными или несмежными (рис. 6.33). В случае на рис. 6.33, б образуются две пары несмежных вершин (1,2) и (3,4), каждую пару можно покрасить в свой цвет, т.е. сэкономить удастся два цвета и h = n – 2. В случае на рис. 6.33, в образуется одна вершина (2), которая несмежна с двумя другими (1, 3), но поскольку между собой эти вер-
182
шины соединены ребром, то вершине 2 можно присвоить цвет, совпадающий, например, с цветом вершины 1 и на этом процесс экономии завершится, и в результате h = n – 1.
|
а) |
красный |
б) |
красный |
||
|
1 |
|||||
|
зеленый |
1 |
||||
|
белый |
зеленый |
||||
|
5 |
2 |
красный |
|||
|
5 |
2 |
||||
|
4 |
3 |
4 |
3 |
||
|
фиолетовый |
синий |
||||
|
синий |
синий |
||||
|
К5, |
|||||
|
К5, у которого |
|||||
|
h=5 |
|||||
|
удалены два |
|||||
|
несмежных ребра, |
|||||
|
в) |
красный |
h=5-2=3 |
|||
|
1 |
|||||
|
зеленый |
|||||
|
красный |
|||||
|
5 |
2 |
К5, у которого удалены два смежных ребра, h=5-1=4
Рис. 6.33
При удалении трех ребер у полного графа на n вершинах хроматическое число снижается на одну, две или сразу на три единицы, в зависимости от того, какую конфигурацию образуют удаляемые ребра (рис. 6.34). В случае, если все три ребра попарно несмежны (рис. 6.34, б), образуются три пары несмежных вершин (1,2) и (3,4) и (5,6), каждую пару можно покрасить в свой цвет, т.е. сэкономить удастся 3 цвета и h = n – 3.
В случае, если удаляемые ребра образуют простой цикл (рис. 6.34, в), формируется множество из трех попарно несмежных вершин (1,2,3), которое можно покрасить в единый цвет. Таким образом, для этих трех вершин ранее расходовалось три цвета, а теперь достаточно одного, т.е. экономия составляет два цвета и в резуль-
183
тате h = n – 2. Если же удаляемые ребра имеют одну общую вершину (рис. 6.34, г), то образуется одна вершина (2), которая несмежна с тремя другими (1, 3, 4), но поскольку между собой эти вершины соединены ребрами, то вершине 2 можно присвоить цвет, совпадающий, например, с цветом вершины 1 и на этом процесс экономии завершится, в результате h = n – 1.
а)
красный
желтый
фиолетовый зеленый
синий
К6, h = 6
в) красный красный 
красный
фиолетовый 
зеленый
синий
синий
б)
красный
зеленый
красный
зеленый
синий
К6, у которого удалены 3 несмежных ребра, h = 6 – 3 = 3
г) красный красный 
красный
фиолетовый зеленый
красный
|
К6, у которого удалены |
К6, у которого удалены 3 ребра, |
|
3 смежных ребра, |
имеющие одну общую вершину, |
|
h = 6 – 2 = 4 |
h = 6 – 1 = 5 |
|
Рис. 6.34 |
184
Операция дополнение. При выполнении операции дополнения хроматическое число может как возрастать, так и уменьшаться. Интерес представляют следующие часто встречающиеся ситуации.
Дополнение полного графа представляет собой пустой граф (рис. 6.35, а и 6.36, а), и его хроматическое число равно 1.
Рис. 6.35
Если из полного графа были удалены некоторые ребра и затем построено его дополнение, то в это дополнение войдут именно удаленные ребра и, значит, необходимо рассмотреть, какую конфигурацию они образуют. При удалении двух ребер в случае на рис. 6.33, б дополнение будет выглядеть так, как на рис. 6.35, б,
иh = 2. При удалении двух ребер в случае, как на рис. 6.33, в, и применения операции дополнения получим граф, как на рис. 6.35, в,
иснова h = 2. При удалении трех ребер ситуация уже может отличаться.
Для графа на рис. 6.34, в в его дополнении образуется цикл на нечетном количестве вершин (рис. 6.36, в), и хроматическое число получается равным 3. Для случаев на рис. 6.34, б и г дополнением являются ациклические графы на рис. 6.36, б и г, и их хроматические числа равны 2.
Рис. 6.36
185
Дополнение простого цикла представляет собой довольно интересную ситуацию. Например, возьмем простой цикл на семи вершинах (рис. 6.37, а), изначально, как и у любого нечетного цикла, h = 3. Построим его дополнение (рис. 6.37, б).
Начнем раскрашивать вершины. Вершины v1 и v2 несмежны, значит, их можно окрасить в один цвет, например красный. Вершину v3 в красный цвет открасить нельзя, так как она смежна с v1, значит, на нее расходуем новый цвет, например синий. Ее соседку v4 можно тоже покрасить в синий цвет ввиду отсутствия ребра (v3,v4). Далее процесс продолжается.
|
фиолетовый |
||||
|
7 |
7 |
красный |
||
|
6 |
1 |
зеленый 6 |
1 |
|
|
красный |
||||
|
2 |
2 |
|||
|
5 |
5 |
|||
|
4 |
3 |
зеленый |
3 |
|
|
4 |
||||
|
синий |
||||
|
С7 |
синий |
|||
|
б |
С7 |
|||
|
а |
||||
|
Рис. 6.37 |
Таким образом, каждые две вершины, если идти по внешнему кругу (бывшему циклу), окрашиваются в один цвет. В рассматриваемом случае вершина v7, получив фиолетовый цвет, останется единственной вершиной этого цвета, так как число вершин в графе нечетно. Всего на процесс оказывается потраченным четыре цвета. В общем случае, если G – дополнение простого цикла на n вершинах, то h(G)=[(n+1)/2], где n – количество вершин, а квадратные скобки обозначают целую часть.
Применение операции дополнения к полному двудольному графу может только увеличить хроматическое число, которое изначально у всех двудольных графов всегда равно двум. Например, дополнением полного двудольного графа K5,7 является граф, со-
186
стоящий из двух компонент: K5 и K7. Соответственно, его хроматическое число будет равно 7.
Операция объединение и пересечение графов. При объедине-
нии двух графов, не имеющих общих вершин, хроматическое число результирующего графа равно максимальному из хроматических чисел исходных графов. Итак, если G = G1 G2 , V1 ∩V2 = 0 ,
то верно
h(G)=max (h(G1), h(G2)). (6.2)
При сложении двух графов, не имеющих общих вершин, хроматическое число результирующего графа равно сумме хроматических чисел исходных графов. Итак, если G=G1+G2, V1 ∩V2 = , то
|
верно |
|
|
h(G)=h(G1) + h(G2). |
(6.3) |
Задача 6.12. Вычислить диаметр, цикломатическое и хроматическое числа графа ( G1 G2 ), где G1 – простой цикл на 20 верши-
нах, G2 – полный граф на 6 вершинах, у которого удалили три ребра, образующих цикл. При этом графы не имеют общих вершин, горизонтальная черта сверху обозначает дополнение.
Решение. Для всех задач данного типа рекомендуется заполнить таблицу (табл. 6.6), с помощью которой проще отслеживать результаты операций.
Начнем с графа G1. Простой цикл на 20 вершинах имеет 20 ребер, он связный (k=1), его цикломатическое число равно единице (m-n+k=20-20+1=1). Хроматическое число простого цикла с четным числом вершин равно 2. Диаметр такого графа равен половине длины цикла, т.е. 10.
Таблица 6.6
Форма для решения задачи 6.12
G1 G1 G2 G2 G1 G2
N
m
K
Γ
h
d
187
Дополнение графа G1 содержит столько же вершин (20), а количество его ребер равно количеству ребер в полном графе на 20 вершинах (20·19/2=190) за вычетом имеющихся 20, т.е. 170. Компонента связности по-прежнему будет одна, цикломатическое число рассчитывается по формуле m–n+k=170-20+1=151. Интерес представляет расчет хроматического числа: оно будет равно половине числа вершин с округлением вверх, т.е.]20[ = 10. Диаметр, как видно, равен 2. В итоге заполнены первые два столбца табл. 6.7.
Таблица 6.7
Решение задачи 6.7 – данные о графе G1
|
G1 |
G1 |
|||
|
n |
20 |
20 |
||
|
m |
20 |
20·19/2-20 = 170 |
||
|
k |
1 |
1 |
||
|
γ |
1 |
170-20+1=151 |
||
|
h |
2 |
]20[ = 10 |
||
|
d |
10 |
2 |
G2 – полный граф на 6 вершинах, у которого удалили три ребра, образующих цикл. Подсчитаем количество ребер: 6·5/2 – 3 = 12. Граф связный (k=1), его цикломатическое число равно m – n + k = =12-6+1=7. Интерес представляет расчет хроматического числа: по аналогии с рис. 6.34, в оно будет равно: 6 исходных цветов минус 2 цвета, которые удастся сэкономить, итого 4.
188
Судя по внешнему виду графа, диаметр будет равен 2 (рис. 6.38, а), так как между вершинами, инцидентными удаленным ребрам, расстояние равно 2. Дополнение графа G2 содержит столько же вершин (6), а количество его ребер равно количеству ребер в полном графе на 6 вершинах (6·5/2=15) за вычетом имеющихся 12, т.е. 3 (еще проще – число ребер в дополнении равно числу ребер, которые были удалены из исходного полного графа, а их было удалено именно 3).
Компонент связности, судя по внешнему виду графа будет 4 (одна компонента на трех вершинах и три изолированные вершины), цикломатическое число рассчитывается как m – n + k = = 3 – 6 + 4 = 1 (что хорошо согласуется с внешним видом графа на рис. 6.38, б).
В силу наличия цикла нечетной длины хроматическое число будет равно 3. Диаметр равен бесконечности на основании того, что граф несвязный (табл. 6.8).
Таблица 6.8
Решение задачи 6.7 – данные о графе G2
|
G2 |
G2 |
|||
|
n |
6 |
6 |
||
|
m |
6·5/2 – 3 = 12 |
6*5/2-12=15-12=3 |
||
|
k |
1 |
4 |
||
|
γ |
12-6+1=7 |
3-6+4=1 |
||
|
h |
6-(3-1)=4 |
3 |
||
|
d |
2 |
Бесконечность |
В результате объединения двух графов G1 и G2 (графы не
имеют общих вершин), получим следующие характеристики. Количество вершин складывается (20+6=26), то же верно в отношении ребер (170+3=173) и компонент (1+4=5). Цикломатическое число при объединении графов в случае отсутствия общих вершин также получается путем сложения цикломатических чисел исходных графов. Хроматическое число можно вычислить, а диаметр равен бесконечности в силу того, что граф несвязный (табл. 6.9).
189
Chromatic Index of a graph is the parameter which indicates the minimum number of colours needed to colour all the edges of graph such that no two edges sharing the common vertex have same coloured edge. In this article, we will discuss how to find the chromatic index of cyclic graphs using the Java programming language.
What is a Cyclic Graph?
Cyclic Graph is a graph which consists of at least one cycle path in that particular graph. Cyclic path is a path that starts from a specific node and ends at the same node.
What is Graph Colouring?
The process which is used to colour graph’s edges or graph’s vertices is known as “Graph Colouring”.
The chromatic index of a graph is one of the most important topic in graph theory as it has many practical applications in real-life scenarios such as the scheduling of tasks, frequency assignment in wireless communication networks, register allocation and many more. In this article, we will discuss Vizing’s theory for detecting the chromatic index of a cyclic graph and implement using Java programming language.
What is Degree of a Vertex?
The number of edges connecting a vertex is known as “Degree of a Vertex”.
Vizing’s Theorem
Vizing’s theorem states that if a simple graph ‘G’ has a maximum degree of ‘d’ then the chromatic index of graph ‘G’ can be either ‘d’ or ‘d+1’. You can go through in detail about algorithm at vizing’s theorem.
Algorithm
STEP 1 − Initialize a 2d-array with represents a graph.
STEP 2 − Initialize a variable with zero which indicates the chromatic index of the graph.
STEP 3 − Find the degrees of each vertex of the Graph ‘G’.
STEP 4 − Calculate the maxDegree of the Graph ‘G’.
STEP 5 − If the maxDegree of the Graph ‘G’ is even, then the Chromatic Index of graph is maxDegree.
STEP 6 − Else if the maxDegree of Graph ‘G’ is odd then theChromatic Index of Graph is maxDegree + 1.
Example
In this below example the Vizing’s algorithm is implemented in Java Programming Language to find the Chromatic Index of Graph.
We initialize a 2-d array which represents a Graph and the graph is passed to a function “chromaticIndexOfGraph”. This function returns the chromatic index of the graph. The function uses vizing’s theorem in calculating the chromatic index of the graph which generally calculates the degree of each vertex of the Graph. After finding the degree of each vertex it finds the maxDegree from the degree[] array. If the maxDegree is even, then the function returns the maxDegree else if maxDegree is odd it returns the value maxDegree + 1.
import java.util.*;
public class Main {
// returns the chromatic index of the graph
public static int chromaticIndexOfGraph(int[][] graph, int n) {
int maxDegree = 0;
int degree[] = new int[n];
for (int i = 0; i < graph.length; i++) {
for (int j = 0; j < graph[i].length; j++) {
if (graph[i][j] == 1) {
degree[j]++;
}
}
}
for(int i=0 ; i<degree.length; i++) {
if(degree[i] > maxDegree) {
maxDegree = degree[i];
}
}
System.out.println("Max Degree:" + maxDegree);
if (maxDegree % 2 == 0) {
return maxDegree; //if maxDegree is even then chromaticIndex is maxDegree
} else {
return maxDegree + 1; //if maxDegree is odd then chromaticIndex is maxDegree+1
}
}
public static void main(String[] args) {
int n = 4; // defines the number of vertices in Graph
int[][] graph = {
{0, 1, 1, 1},{1, 0, 1, 0},{1, 1, 0, 1},{1, 0, 1, 0}
};
int chromatic_index = chromaticIndexOfGraph(graph, n);
System.out.println("Chromatic index: " + chromatic_index);
}
}
Output
Max Degree:3 Chromatic index: 4
Time Complexity: O(N2) Auxiliary Space: O(N)
In this article, we have learned how to find the Chromatic Index of Cyclic Graph using Java Programming Language.
Аннотация: Реберная раскраска. Задачи на графы с цветными ребрами и вытекающие
из них свойства. Задача о несцепленных треугольниках с одноцветными
сторонами.
Реберная раскраска
Граф 
называется реберно 
— раскрашиваемым,
если его ребра можно раскрасить красками таким образом, что никакие
два смежных ребра не окажутся одного цвета. Если граф реберно -раскрашиваем, но не является реберно 
-раскрашиваемым, то
называется хроматическим классом или хроматическим
индексом, или реберно-хроматическим числом графа . При этом
используется запись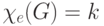 
. На рисунке изображен граф ,
для которого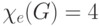 
.
Ясно, что если наибольшая из степеней вершин графа
равна 
, то 
. Следующий результат, известный как теорема
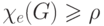
Визинга, дает точные оценки для хроматического класса графа .
Доказательство этой теоремы можно найти у Оре (Ore O. The four-color
problem, Academic Press, New York, 1967).
Теорема 7.1.(Визинг, 1964)
Пусть в графе , не имеющем петель, наибольшая из степеней вершин
равна 
тогда 
.
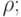
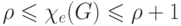
Задача, состоящая в выяснении того, какие графы имеют хроматический
класс , а какие 
, не решена. Однако в
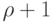
некоторых частных случаях соответствующие результаты находятся легко. Например,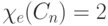 
или 3 в зависимости от того, четно 
или
нечетно, а 
, при 
. Хроматические
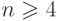
классы полных графов и полных двудольных графов вычисляются тоже просто.
Теорема 7.2.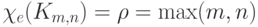 
.
Доказательство
Без потери общности можно считать, что 
и что граф 
изображен так:
вершин расположены на горизонтальной линии под 
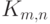
вершинами. Тогда искомая реберная раскраска получается последовательным окрашиванием ребер,
инцидентных этим вершинам, с использованием следующих групп
красок:
при этом краски из каждой группы располагаются по часовой стрелке, вокруг
соответствующей вершины.
Теорема 7.3.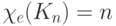 
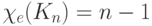
, если нечетно 
, и 
, если четно.
Доказательство
В случае нечетного расположим вершины
графа 
в виде правильного -угольника. Тогда его ребра можно раскрасить
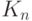
следующим образом: сначала окрашиваем каждую сторону -угольника в свой
цвет, а затем каждое из оставшихся ребер, диагонали -угольника,
окрашиваем в тот же цвет, что и параллельная ему сторона.
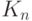
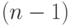
То, что граф не является реберно 
-раскрашиваемым, сразу
же следует из того, что максимально возможное число ребер одного цвета
равно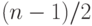 
.
В случае четного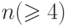 
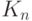
граф можно
рассматривать как соединение полного 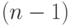— графа 
и отдельной вершины. Если в 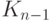окрасить ребра описанным выше способом, то для каждой
вершины останется один неиспользованный цвет, причем все эти неиспользованные
цвета будут различными. Таким образом, чтобы получить реберную
раскраску 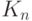, достаточно окрасить оставшиеся ребра в
соответствующие «неиспользованные» цвета.
