2021-11-23
На диагоналях трапеции как на диаметрах построены окружности.
а) Докажите, что их общая хорда перпендикулярна основаниям трапеции.
б) Найдите длину этой хорды, если известно, что основания трапеции равны 1 и 11, а диагонали — 6 и 8.
Решение:
а) Пусть $O_{1}$ и $O_{2}$ — середины диагоналей $AC$ и $BD$ трапеции $ABCD$ с основаниями $BC$ и $AD$ (рис.1). Тогда $O_{1}$ и $O_{1}$ — центры окружностей с диаметрами $AC$ и $BD$. Пусть $M$ и $N$ — точки пересечения этих окружностей. Линия центров пересекающихся окружностей перпендикулярна их линии центров, поэтому $MNperp O_{1}O_{2}$, а т.к. отрезок, соединяющий середины диагоналей трапеции, параллелен её основаниям, то $MNperp AD$ и $MNperp BC$.
б) Пусть $BC=1$, $AD=11$, $AC=6$, $BD=8$ (рис.2). Расстояние между серединами диагоналей трапеции равно полуразности оснований (см. задачу 4883), поэтому
$O_{1}O_{2}=frac{AD-BC}{2}=frac{11-1}{2}=5.$
Линия центров пересекающихся окружностей перпендикулярна общей хорде и делит её пополам, поэтому отрезок $MN$ вдвое больше высоты $MK$ треугольника $O_{1}MO_{2}$ со сторонами $O_{1}M=frac{1}{2}AC=3$, $O_{2}M=frac{1}{2}BD=4$ и $O_{1}O_{2}=5$. Этот треугольник прямоугольный с прямым углом при вершине $M$. Значит,
$MK=frac{O_{1}Mcdot O_{2}M}{O_{1}O_{2}}=frac{3cdot4}{5}=frac{12}{5}.$
Следовательно, $MN=2MK=frac{24}{5}=4{,}8$.
25
Июл 2013
Категория: Справочные материалы
Трапеция. Свойства трапеции
2013-07-25
2016-06-15
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка —
и
, то
Площадь
или
где
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
Автор: egeMax |
комментарий 431
Печать страницы
Трапеция и ее свойства
Трапеция —
четырехугольник, у которого две
стороны параллельны, а две другие —
нет.
Параллельные
стороны трапеции называются основаниями.
Другие две — боковые стороны.
Если
боковые стороны равны, трапеция называется
равнобедренной.
Площадь
трапеции равна произведению полусуммы
оснований на высоту:
Отрезок,
соединяющий середины оснований трапеции,
называется средней линией трапеции.
Средняя линия трапеции параллельна
основаниям, а длина ее равна
полусумме оснований:
Как
видим, теория очень проста. А задачи,
в которых применяются свойства
трапеции, весьма разнообразны. В этой
статье разобраны и стандартные задачи
(номер 1 и 2),
и более интересные.
1.
Найдите высоту трапеции ABCD,
опущенную из вершины B,
если стороны квадратных клеток равны
.

Высота
трапеции — это отрезок, перпендикулярный
ее основаниям. Проведем высоту
из вершины В.
Ответ:
2.
2.
Основания трапеции равны 18 и 6,
боковая сторона, равная 7,
образует с одним из оснований
трапеции угол 150.
Найдите площадь трапеции.
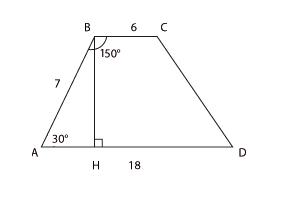
Это
стандартная задача. Углы АВН
и ВАН —
односторонние, значит, их сумма равна
180°,
и тогда угол ВАН
равен 30°.
Из треугольника АВН
найдем высоту ВН.
Катет, лежащий напротив угла в 30,
равен половине гипотенузы. Получаем,
что ВН = 3,5
и площадь трапеции равна 42.
3.
Основания трапеции равны 4 и 10.
Найдите больший из отрезков, на которые
делит среднюю линию этой трапеции одна
из ее диагоналей.
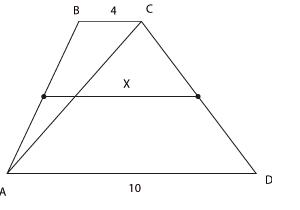
Скажите,
что вы видите на чертеже? Можно
сказать, что изображена трапеция АВСD,
и в ней проведена средняя линия.
А можно увидеть и другое — два
треугольника, АВС
и АСD,
в которых проведены средние линии.
Мы помним,
что средняя линия треугольника —
это отрезок, соединяющий середины двух
его сторон. Средняя линия треугольника
параллельна третьей его стороне и равна
половине этой стороны.
Из треугольника
АВD находим:
х
= 5.
В следующей
задаче мы тоже воспользуемся свойством
средней линии треугольника.
4.
Основания трапеции равны 3 и 2.
Найдите отрезок, соединяющий середины
диагоналей трапеции.
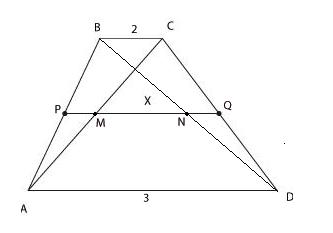
Проведем
PQ —
среднюю линию трапеции, PQ
= 2,5.
Легко доказать, что отрезок MN,
соединяющий середины диагоналей
трапеции, лежит на средней линии.
Дальше все просто. Найдем отрезки РМ
и NQ,
являющиеся средними линиями треугольников
ABC
и BCD,
а затем отрезок MN.
Он равен 0,5.
5.
Прямая, проведенная параллельно боковой
стороне трапеции через конец меньшего
основания, равного 4,
отсекает треугольник, периметр которого
равен 15.
Найдите периметр трапеции.

Периметр
треугольника равен сумме его сторон,
то есть a
+ b + c.
Периметр трапеции равен а
+ b + 4 + c + 4.
На сколько периметр трапеции
больше периметра треугольника? Чему
равен периметр трапеции?
Ответ:
23.
Окружность. Центральный и вписанный угол
Центральный
угол —
это угол, вершина которого находится
в центре окружности.
Вписанный
угол —
угол, вершина которого лежит на окружности,
а стороны пересекают ее.
На рисунке —
центральные и вписанные углы, а также
их важнейшие свойства.
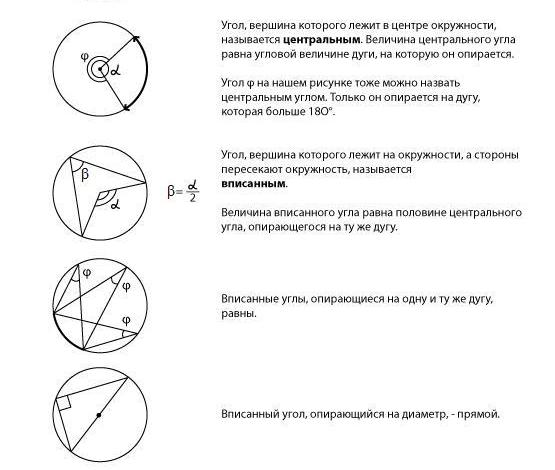
Итак,
величина
центрального угла равна угловой величине
дуги, на которую он опирается.
Значит, центральный угол величиной
в 90 градусов
будет опираться на дугу, равную 90°,
то есть
круга.
Центральный угол, равный 60°,
опирается на дугу в 60 градусов,
то есть на шестую часть круга.
Величина
вписанного угла в два раза меньше
центрального, опирающегося на ту же
дугу.
Также
для решения задач нам понадобится
понятие «хорда».

Равные
центральные углы опираются на равные
хорды.
1.
Чему равен вписанный угол, опирающийся
на диаметр окружности? Ответ дайте
в градусах.
Вписанный
угол, опирающийся на диаметр, —
прямой.
Ответ:
90.
2.
Центральный угол на 36° больше
острого вписанного угла, опирающегося
на ту же дугу окружности. Найдите
вписанный угол. Ответ дайте в градусах.
Пусть
центральный угол равен х,
а вписанный угол, опирающийся на ту же
дугу, равен у.

Мы знаем,
что х
= 2у.
Отсюда 2у
= 36 + у,
у = 36.
Ответ:
36.
3.
Радиус окружности равен 1.
Найдите величину тупого вписанного
угла, опирающегося на хорду, равную
.
Ответ дайте в градусах.

Пусть
хорда АВ равна
.
Тупой вписанный угол, опирающийся на эту
хорду, обозначим α.
В треугольнике АОВ
стороны АО
и ОВ
равны 1,
сторона АВ
равна
.
Нам уже встречались такие треугольники.
Очевидно, что треугольник АОВ —
прямоугольный и равнобедренный,
то есть угол АОВ
равен 90°.
Тогда дуга АСВ
равна 90°,
а дуга АКВ
равна 360° —
90° = 270°.
Вписанный угол α опирается
на дугу АКВ
и равен половине угловой величины
этой дуги, то есть 135°.
Ответ:
135.
4.
Хорда AB делит
окружность на две части, градусные
величины которых относятся как 5:7.
Под каким углом видна эта хорда из точки C,
принадлежащей меньшей дуге окружности?
Ответ дайте в градусах.
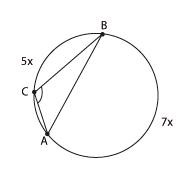
Главное
в этой задаче — правильный чертеж
и понимание условия. Как вы понимаете
вопрос: «Под каким углом хорда видна
из точки С?»
Представьте, что вы сидите в точке С
и вам необходимо видеть всё, что
происходит на хорде АВ.
Так, как будто хорда АВ —
это экран в кинотеатре 
Очевидно,
что найти нужно угол АСВ.
Сумма двух дуг, на которые хорда АВ
делит окружность, равна 360°,
то есть
5х
+ 7х = 360°
Отсюда
х
= 30°,
и тогда вписанный угол АСВ
опирается на дугу, равную 210°.
Величина вписанного угла равна
половине угловой величины дуги, на которую
он опирается, значит, угол АСВ
равен 105°.
Ответ:
105.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
30.03.201540.15 Mб22спицын мартыненко.djvu
- #
- #
- #
- #
- #
- #
- #
- #
Трапеция. Формулы, признаки и свойства трапеции
Определение.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Элементы трапеции:
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
Виды трапеций:
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
AB + CD = BC + AD
2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:
BC : AD = OC : AO = OB : DO
7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c2 + d2
Сторона трапеции
Формулы определения длин сторон трапеции:
1. Формула длины оснований трапеции через среднюю линию и другую основу:
a = 2m — b
b = 2m — a
2. Формулы длины основ через высоту и углы при нижнем основании:
a = b + h · (ctg α + ctg β)
b = a — h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a — c·cos α — d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Определение.
Средняя линия — отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
1. Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
1. Формулы диагоналей по теореме косинусов:
d1 = √a2 + d2 — 2ad·cos β
d2 = √a2 + c2 — 2ac·cos α
2. Формулы диагоналей через четыре стороны:
| d1 = | √ | d 2 + ab — | a(d 2 — c2) |
| a — b |
| d2 = | √ | c2 + ab — | a(c2 — d 2) |
| a — b |
3. Формула длины диагоналей через высоту:
d1 = √h2 + (a — h · ctg β)2 = √h2 + (b + h · ctg α)2
d2 = √h2 + (a — h · ctg α)2 = √h2 + (b + h · ctg β)2
4. Формулы длины диагонали через сумму квадратов диагоналей:
d1 = √c2 + d 2 + 2ab — d22
d2 = √c2 + d 2 + 2ab — d12
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 — | ( | (a — b)2 + c2 — d 2 | ) | 2 |
| 2 | 2(a — b) |
5. Формула Герона для трапеции
| S = | a + b | √(p — a)(p — b)(p — a — c)(p — a — d) |
| |a — b| |
где
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
P = a + b + c + d
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p — a)(p — c)(p — d1) |
где
a — большее основание
Окружность вписанная в трапецию
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
a + b = c + d
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Трапеция. Определение, формулы и свойства
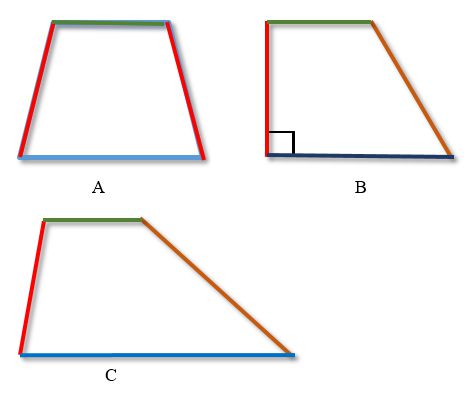
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.
Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние ;
— равнобокие;
— прямоугольные
.
Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У равнобокой трапеции боковые стороны равны, а основания параллельны.
У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей, равен половине разности оснований и лежит на средней линии. Его длина
- Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
- Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапеции бывают острые, прямые и тупые.
Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые, а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему по длине основанию, а острые – большему основанию.
Любую трапецию можно рассматривать как усеченный треугольник, у которого линия сечения параллельна основанию треугольника.
Важно. Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
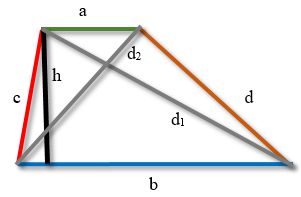
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h1h2 — диагонали
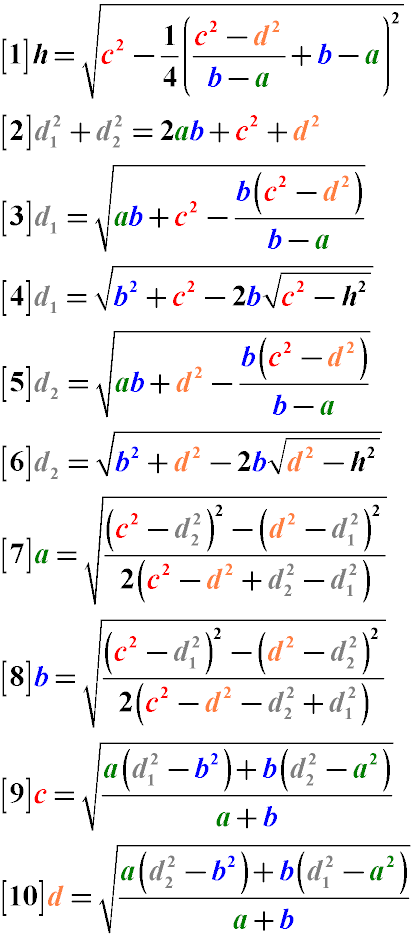
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Площадь трапеции
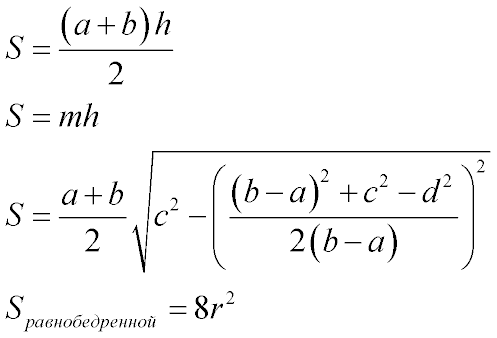
где
a и b — параллельные основания трапеции
c и d — боковые стороны трапеции
m — средняя линия трапеции
r — радиус вписанной в трапецию окружности
S — площадь трапеции
0
Ромб |
Описание курса
| Площадь трапеции