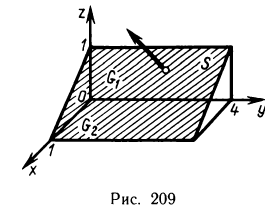
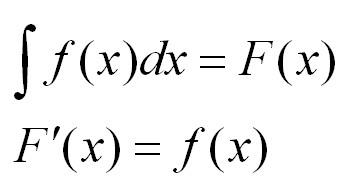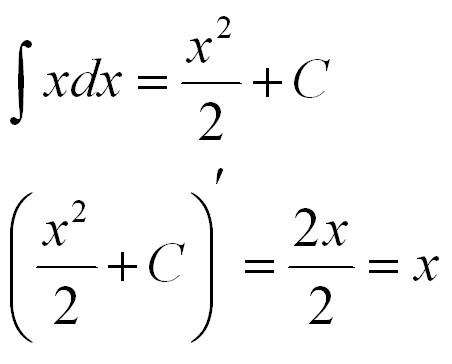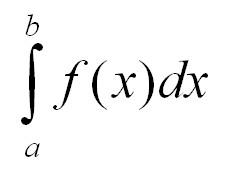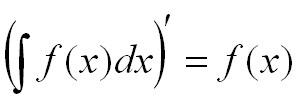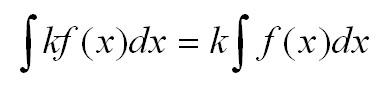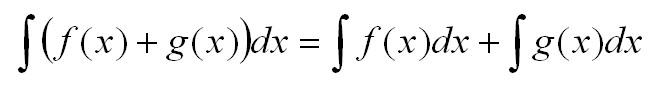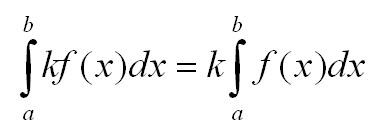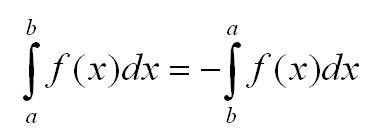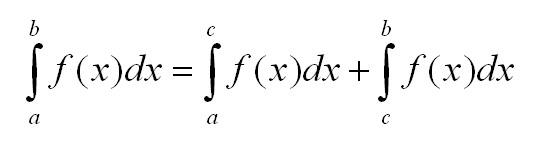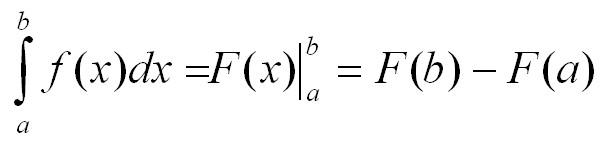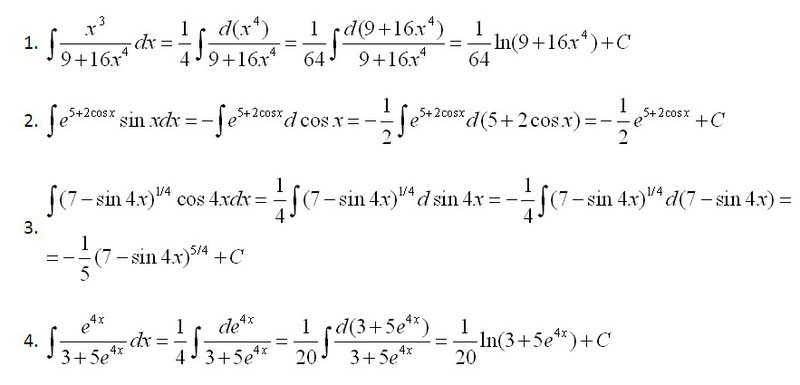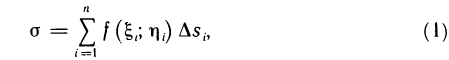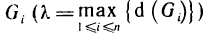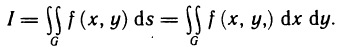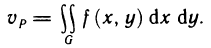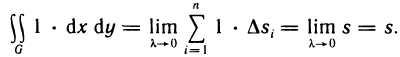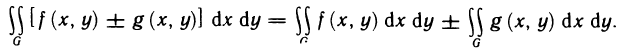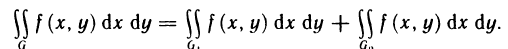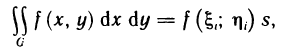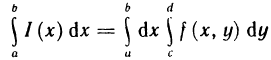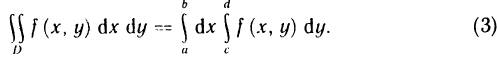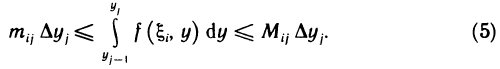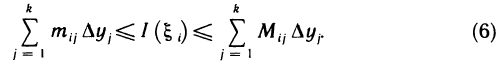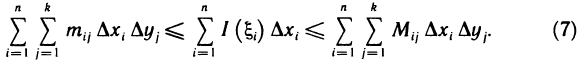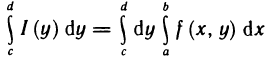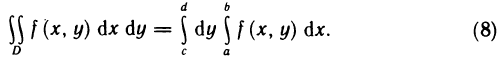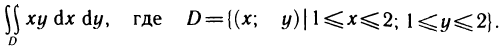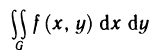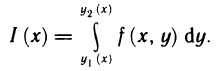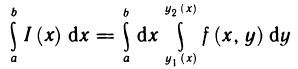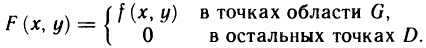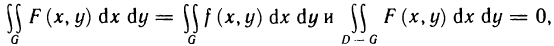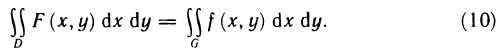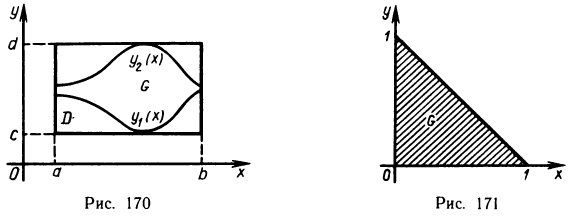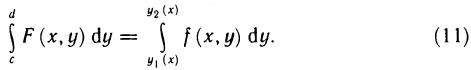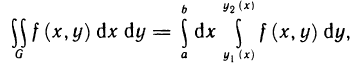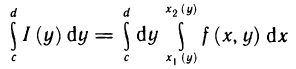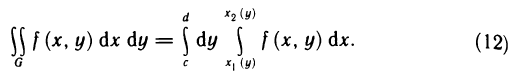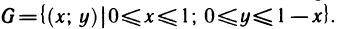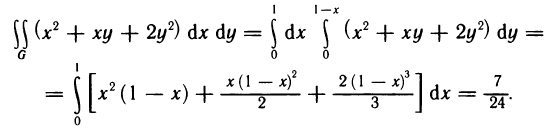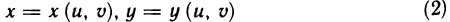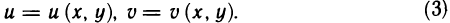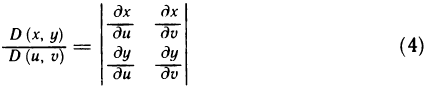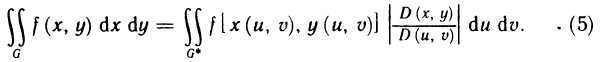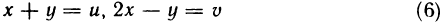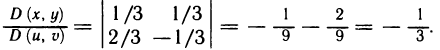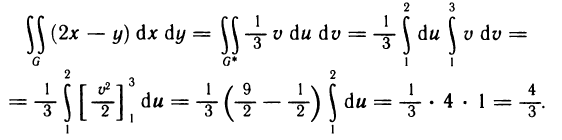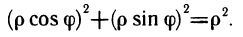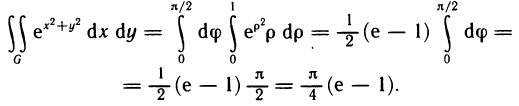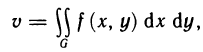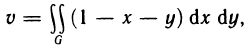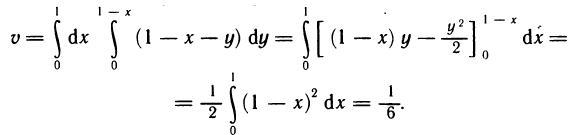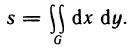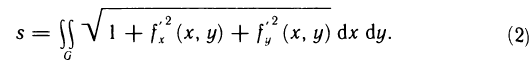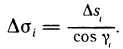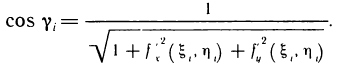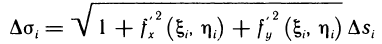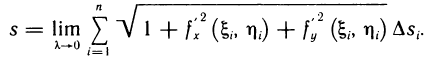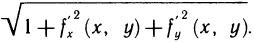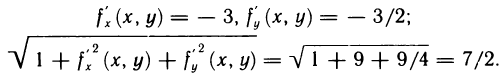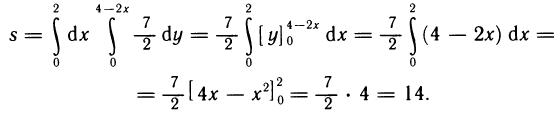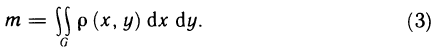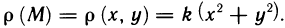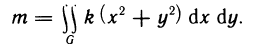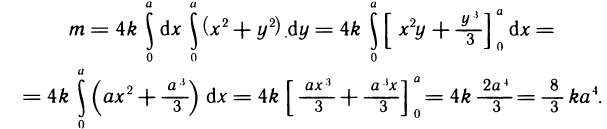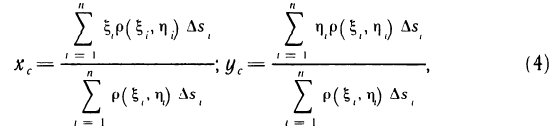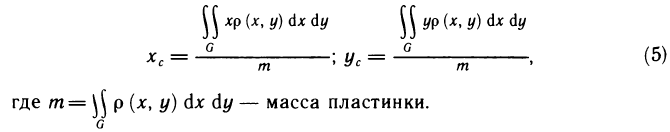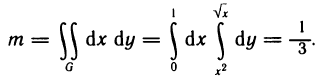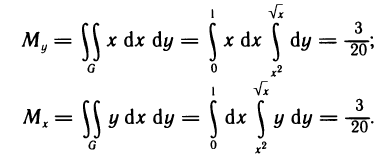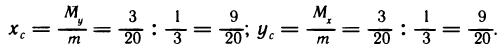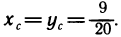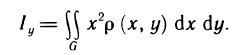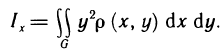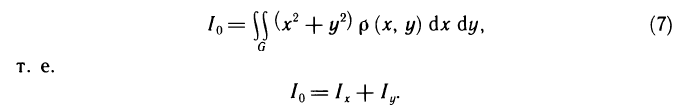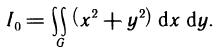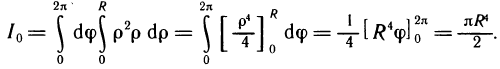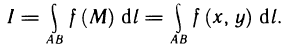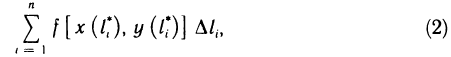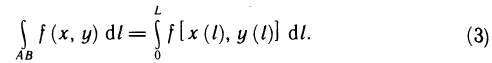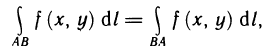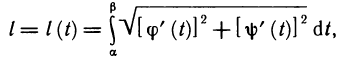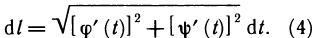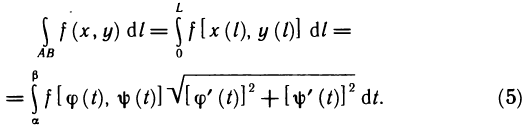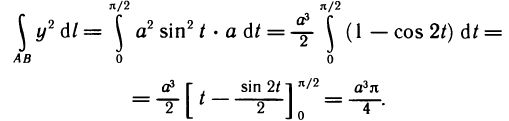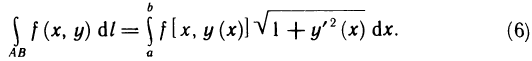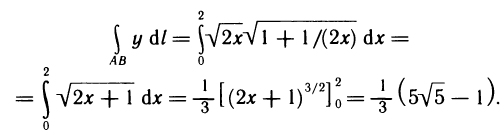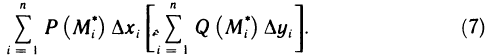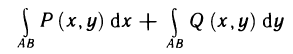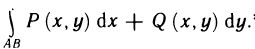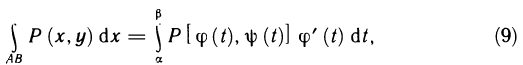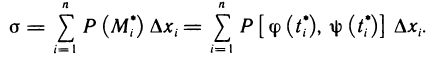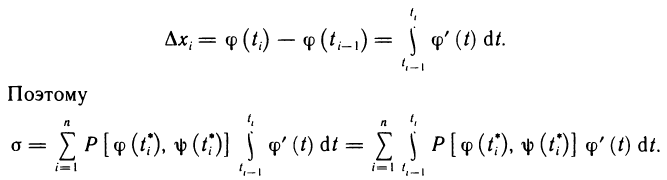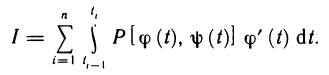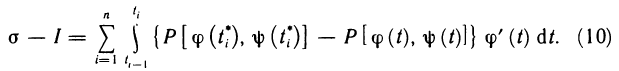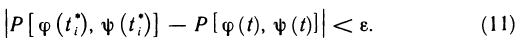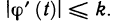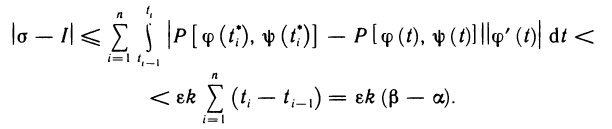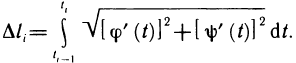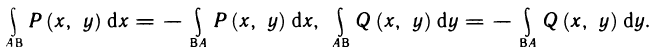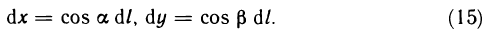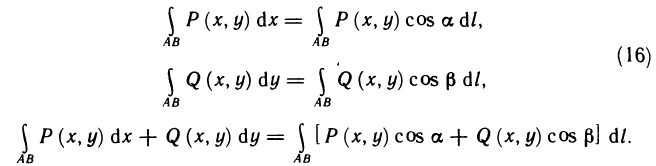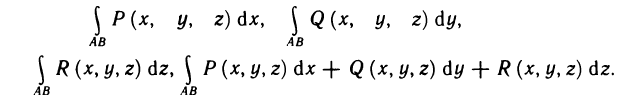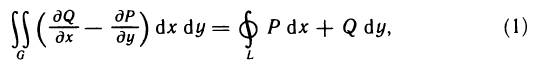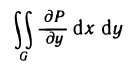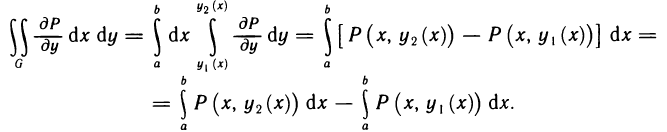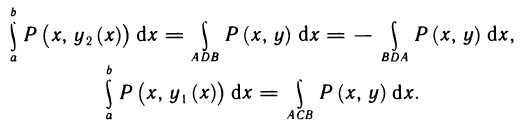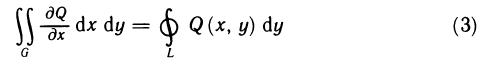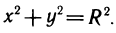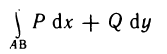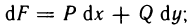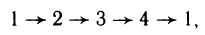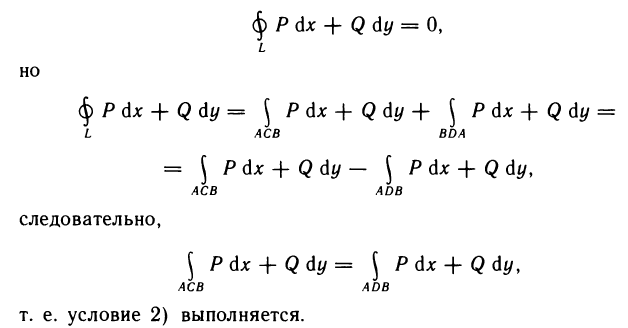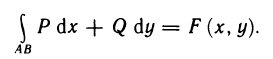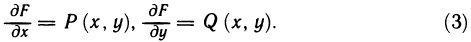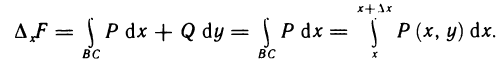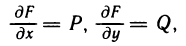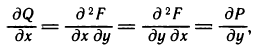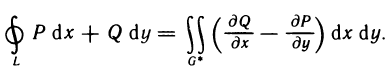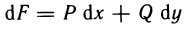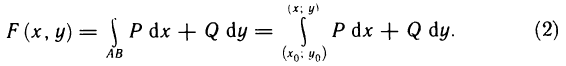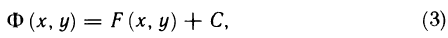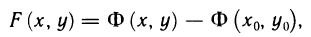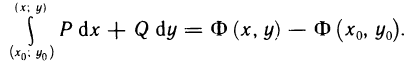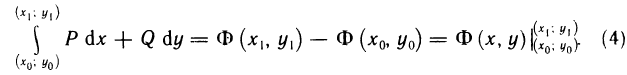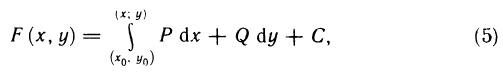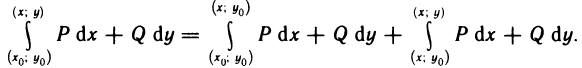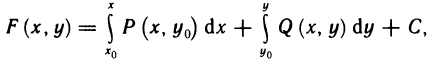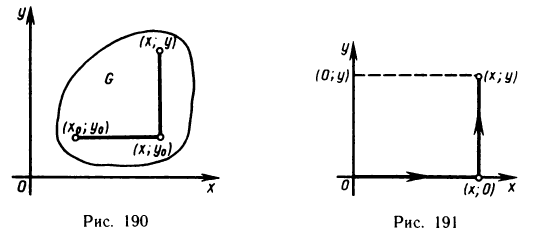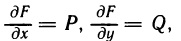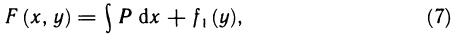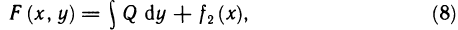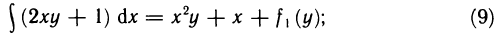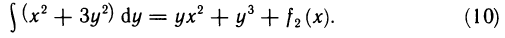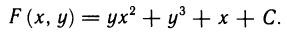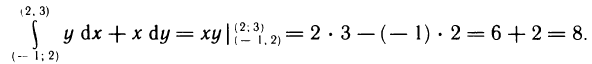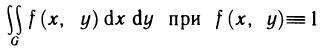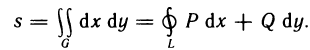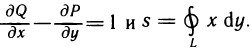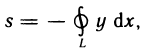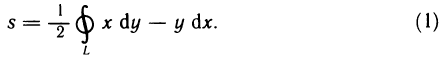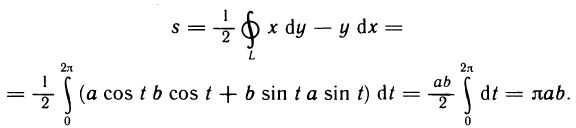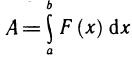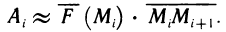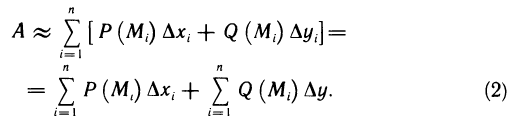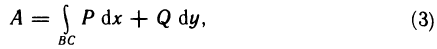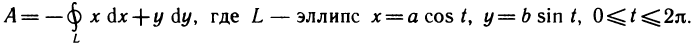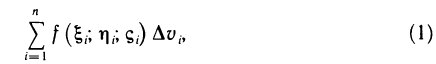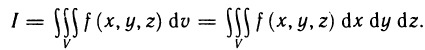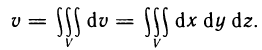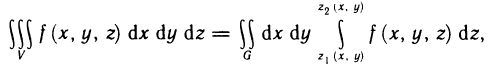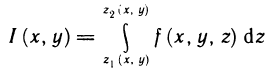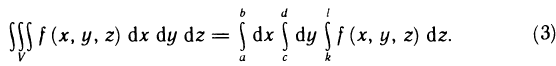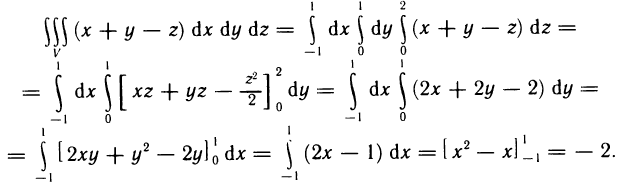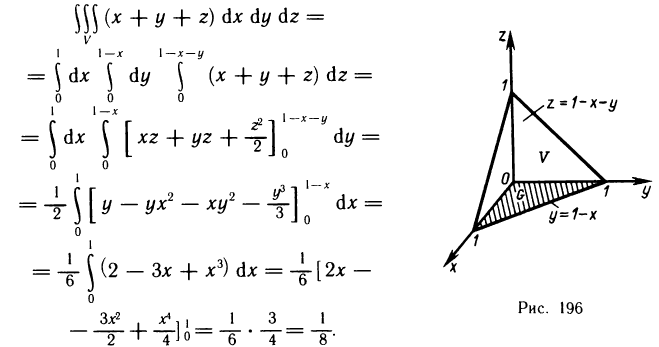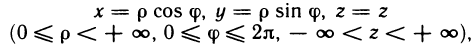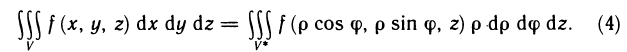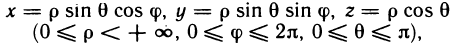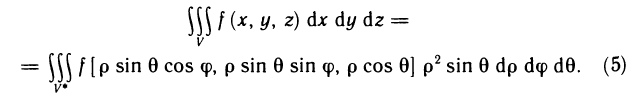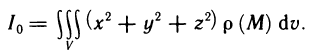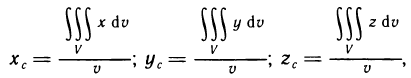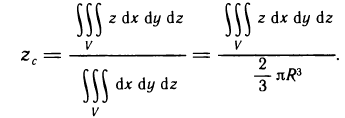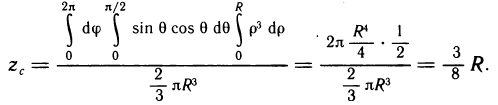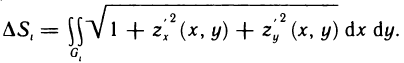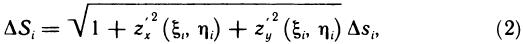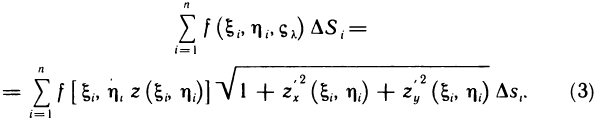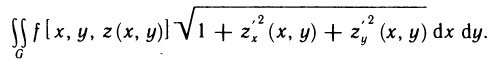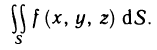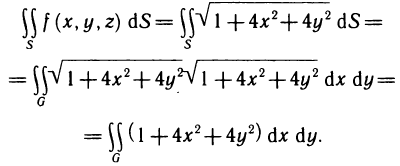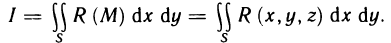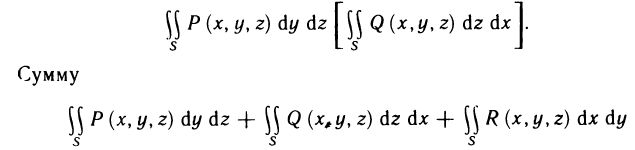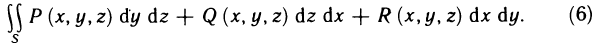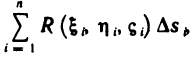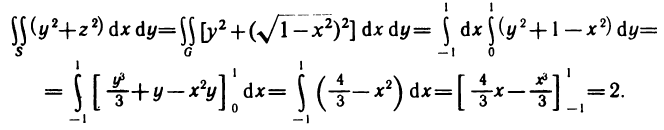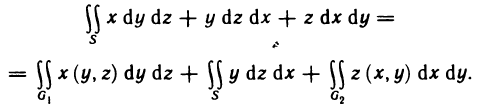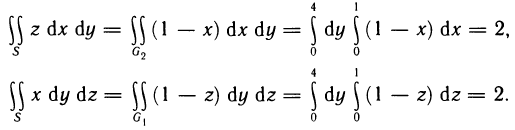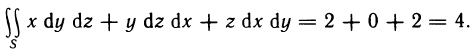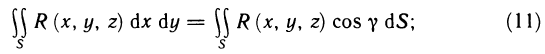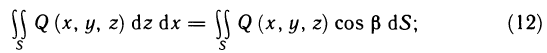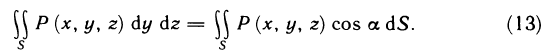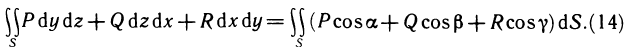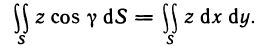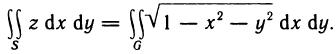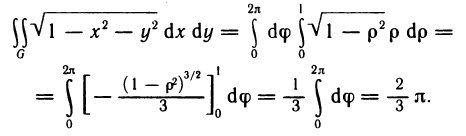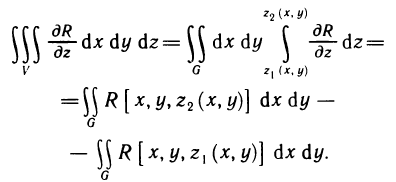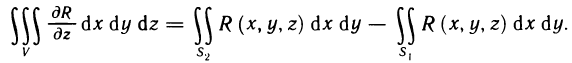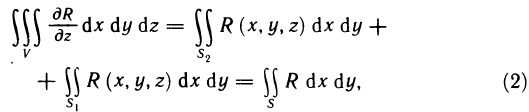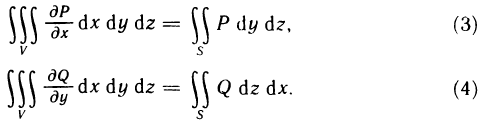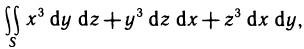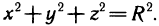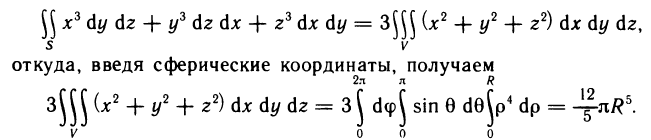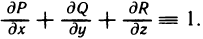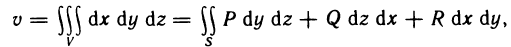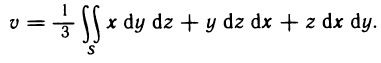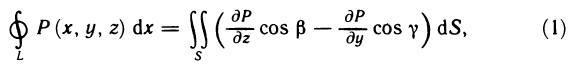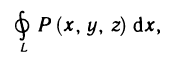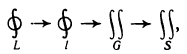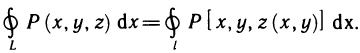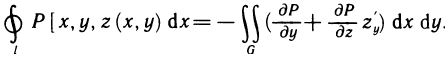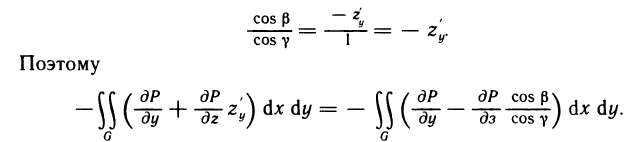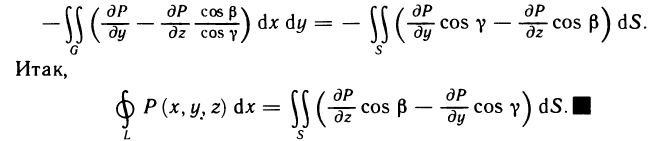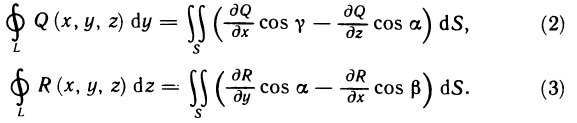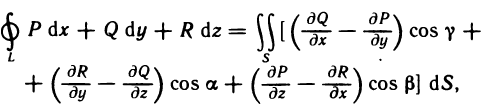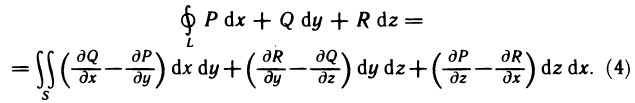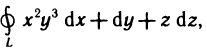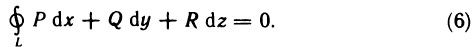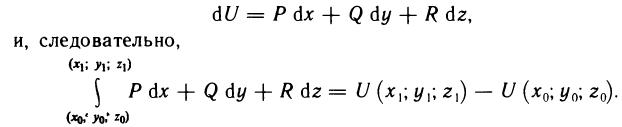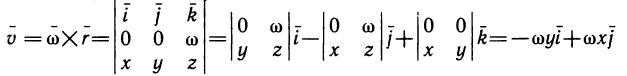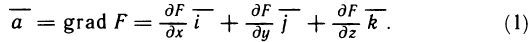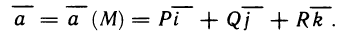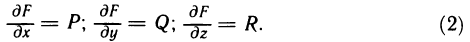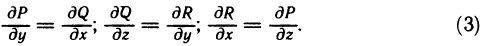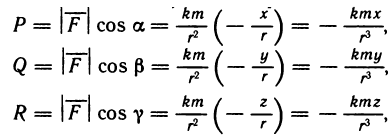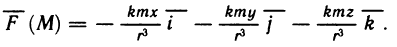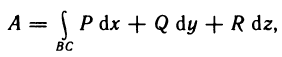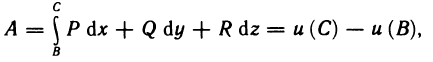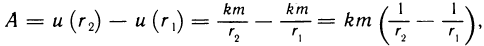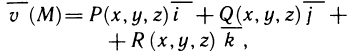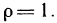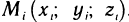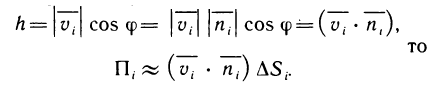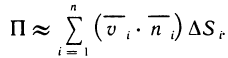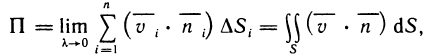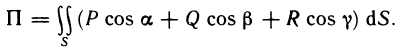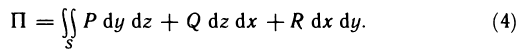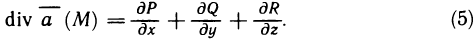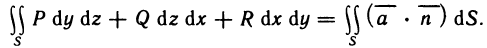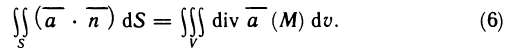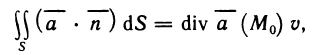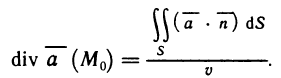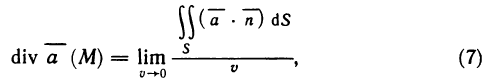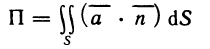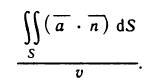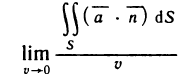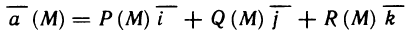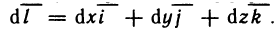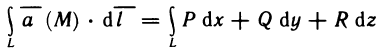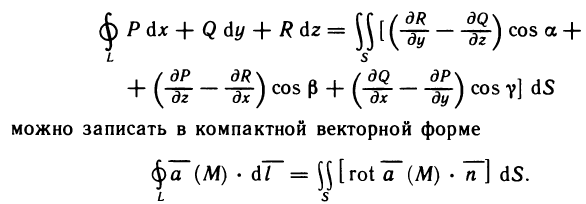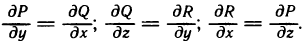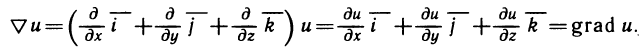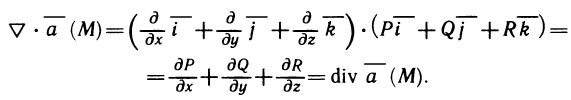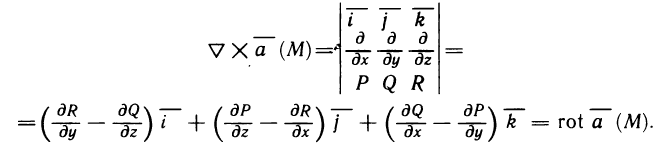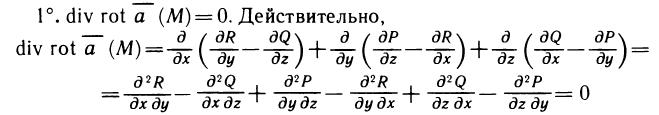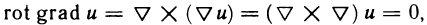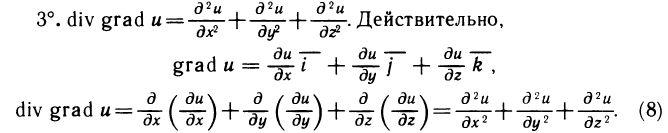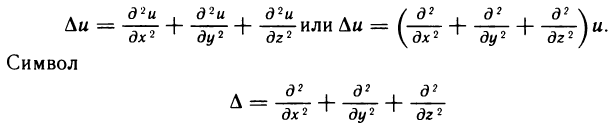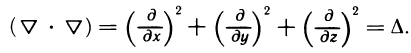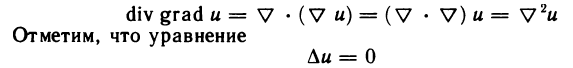Содержание:
- Определённый интеграл
- Геометрическое содержание определённого интеграла
- Основные свойства определённого интеграла
- Непосредственное вычисление определённого интеграла
- Вычисление определённого интеграла методом подстановки
- Вычисления определённого интеграла частями
- Приближённые методы вычисления определённых интегралов
- Практическое применение определённого интеграла
- Вычисление площадей плоских фигур
- Объём тела вращения
- Путь, пройденный точкой
- Сила давления жидкости
- Несобственные интегралы
- История определенного интеграла
- Определенный интеграл в математике
- Геометрический смысл интеграла
- Понятие определенного интеграла
- Задачи, приводящие к понятию определенного интеграла
- Задача о нахождении площади криволинейной трапеции
- Задача об определении пройденного пути материальной точки
- Задача о нахождении объема продукции
- Основные свойства определенного интеграла
- Связь между определенным и неопределенным интегралами
- Формула Ньютона-Лейбница
- Методы вычисления определенного интеграла
- Непосредственное определенное интегрирование
- Вычисление интеграла методом подстановки
- Интегрирования по частям в определенном интеграле
- Длина дуги плоской кривой
- Вычисление площади геометрической фигуры
- Вычисление объемов тел по известным площадям поперечных сечений
- Вычисление объема тела вращения
- Приближенное вычисление определенных интегралов
- Формула прямоугольников
- Формула трапеций
- Формула Симпсона
Определённый интеграл
Определенный интеграл – это число, а именно величина площади криволинейной трапеции. Неопределенный интеграл – это функция (точнее, семейство функций), которая является первообразной для интегрируемой функции.
Понятие определённого интеграла:
Пусть функция f(х) определена на промежутке 




где 
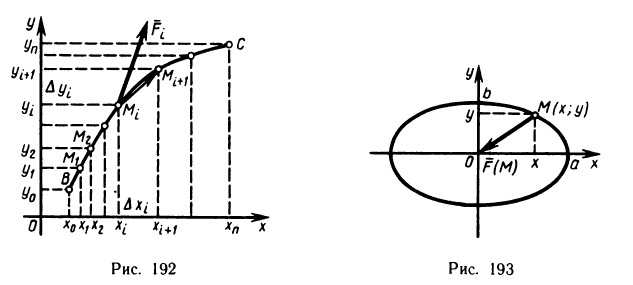
Геометрически (рис. 1) каждое слагаемое интегральной суммы равно площади прямоугольника с основанием 

Очевидно, при всех возможных разбиениях отрезка 
Будем увеличивать число точек разбиения так, чтобы длина наибольшего отрезка 

Это предел и называют определённым интегралом для функции f(х) на отрезке
Определённым интегралом для функции f(х) на отрезке 



По определению
Число 

Отметим, что любая непрерывная на промежутке 
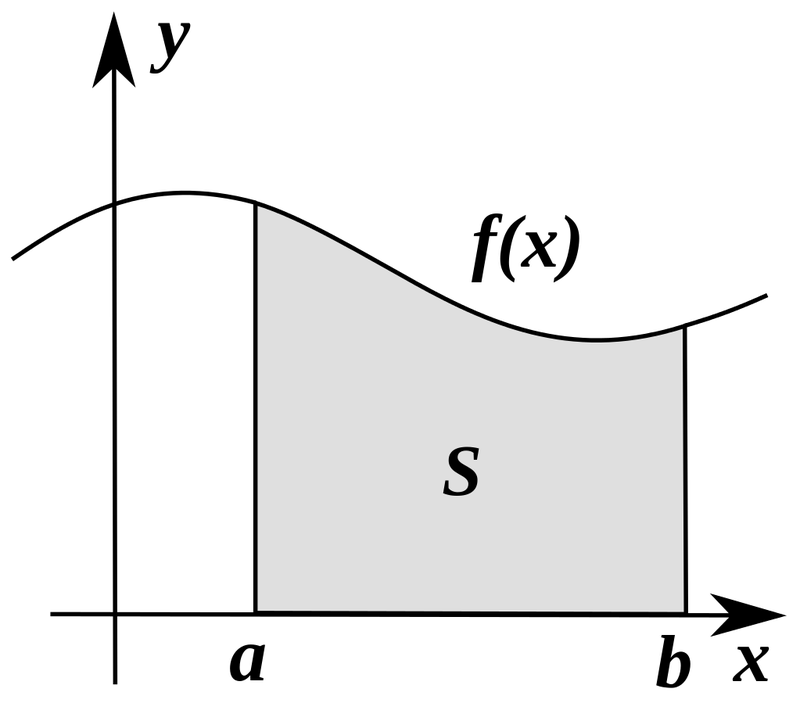
Геометрическое содержание определённого интеграла
Если интегрированная на отрезке 


Уточним, что криволинейную трапецией называют фигуру, ограниченную графиком непрерывной функции у=f(х), где 

Следовательно, геометрическое содержание определённого интеграла — это площадь криволинейной трапеции.
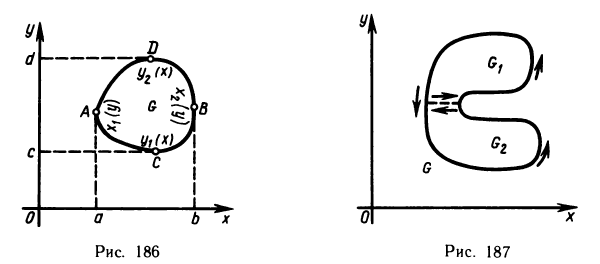
Рассмотрим криволинейную трапецию CHKD (см. рис. 2), в которой абсцисса точки С равна х, а точки 
Поскольку площадь криволинейной трапеции ОАНС зависит от х, то её можно изобразить символом S(х). Аналогично, площадь криволинейной трапеции CHKD является функцией от 


Построим два прямоугольника CHED и CMKD. Площадь первого равна 
Разделим обе части этого неравенства на 
Вспомним, что 
получим:
отсюда

то есть производная площади криволинейной трапеции равна функции, которая задаёт верхнюю границу трапеции.
Таким образом, площадь криволинейной трапеции является одной из первичных функций, которая задаёт верхнюю границу трапеции, и может быть вычислена с помощью интегрирования.
Последнее равенство верно для всех х с промежутка 




При х=b получим выражение для вычисления площади криволинейной трапеции
Полученное выражение для вычисления S является приростом первичной F(х) на 

определённым интегралом называют прирост произвольной первичной при изменении аргумента от 
Данное определение записывают в виде формулы Ньютона-Лейбница:
где F(х) — первичная для функции f(х).
Основные свойства определённого интеграла
Все ниже приведённые свойства сформулированы в предположении, что данные функции интегрированы на определённых промежутках.
1. Определённый интеграл с одинаковыми границами интегрирования равен нулю:
2. При перестановке границ интегрирования определённый интеграл меняет знак на противоположный:
3. Отрезок интегрирования можно разбивать на части:

4. Постоянный множитель можно вынести за знак определённого интеграла:
5. Определённый интеграл от алгебраической суммы конечного числа функции равен алгебраической сумме определённых интегралов от функции, сто доказываются:
Доказательство свойств базируется на формуле ньютона-Лейбница. Как пример, докажем свойство 3:
что и требовалось доказать.
Данное свойство легко иллюстрировать графически (рис. 3).
или
На рис. 3 легко увидеть справедливость утверждения теоремы о среднем.
Теорема. Если функция f(х) непрерывна на промежутке 
То есть, площадь криволинейной трапеции 

Непосредственное вычисление определённого интеграла
Для вычисления определённого интеграла при условии существования первичной пользоваться формулой Ньютона-Лейбница:
По этой формуле виден порядок вычисления определённого интеграла:
1) найти неопределённый интеграл от данной функции;
2) в полученную первичную подставить на место аргумента сначала в верхнюю, а потом нижнюю границу интеграла;
3) найти прирост первично, то есть вычислить интеграл.
Пример 1: Вычислить интеграл:
Решение: Использовав указанные правила, вычислим данный определённый интеграл:
Ответ:
Пример: Вычислить интеграл:
Решение: Используем определение степени с дробным отрицательным показателем и вычислить определённый интеграл:
Ответ:
Пример 3: Вычислить интеграл:
Решение: Интеграл от разности функций заменим разностью интегралов от каждой функции.
Ответ:
Пример 4: Вычислить интеграл:
Решение: Используем определения степени с дробным показателем, правило деления суммы на число и вычислить определённый интеграл от суммы:
Ответ:
Вычисление определённого интеграла методом подстановки
Вычисление определённого интеграла методом подстановки выполняется в такой последовательности:
1) ввести новую переменную;
2) найти дифференциал новой переменной;
3) найти новые границы определённого интеграла;
4) всё подынтегральное выражение выразить через новую переменную;
5) вычислить полученный интеграл.
Пример 5. Вычислить интеграл:
Решение: Сделаем замену 
Вычислим границы интегрирования для переменной t.
При х=0 получаем tн=8-0=8, при х=7 получим tb=8-7=1.
Выразим подынтегральное выражение через t и dt и перейдём к новым границам, получим:
Пример 6. Вычислить интеграл:
Решение: Будем считать, что х3+2=t, тогда 

Выразим подынтегральное выражение через t и dt, затем перейдём к новым пределам, получим:
Ответ:
Пример 7. Вычислить интеграл:
Решение: Пусть 
Вычислим границы интегрирования для переменной t:
Выразим подынтегральное выражение через t и dt, и перейдём к новым пределам, получим:
Ответ:
Пример 8. Вычислить интеграл:
Решение: Сначала преобразуем подынтегральное выражение:
Вычислим интеграл от разности функций, заменив его разностью определённых интегралов от каждой функции:
Ответ:
Вычисления определённого интеграла частями
Если функции 



Пример 9. Вычислить интеграл:
Решение:
Ответ:
Пример 10. Вычислить интеграл:
Решение:
Ответ:
Приближённые методы вычисления определённых интегралов
В тех случаях, когда вычислить определённый интеграл по формуле Ньютона-Лейбница невозможно или сложно, используют методы приближённого интегрирования. Все они основываются на простых геометрических построениях. Очевидно, что при достаточно малом отрезке 
Запишем следующие приближённые равенства:
Чтобы добиться большей точности при нахождении площади S, промежуток от 
Если для каждой из маленьких дуг использовать предыдущие приближения, то для всей площади S получим приближённое значение представленное в виде суммы площадей криволинейных трапеций:
Первые две формулы носят названия формул «левых» и «правых» прямоугольников соответственно, третья — формулы трапеции, а последняя — формулы Симпсона.
Пример 11. Вычислить по формулам прямоугольников и трапеций 
Решение: Разделим отрезок [0; 1] на (n=10) заданное количество частей. Тогда составим таблицу значений подынтегральной функции в точках разбиения.
По формуле «левых» прямоугольников имеем:
По формуле «правых» прямоугольников имеем:
По формуле трапеции получим:
Для достижения большей точности число разбиений отрезка необходимо увеличить, например взять n=20.
Практическое применение определённого интеграла
С помощью определённого интеграла можно решать задачи физики, механики и т. д., которые тяжело или невозможно решить методами элементарной математики. Так, понятия определённого интервала используют при решении задач на вычисление площади фигур, работы переменной силы, давления на вертикальную поверхность, пути, пройденного телом и ряда других. Рассмотрим некоторые из них.
Вычисление площадей плоских фигур
Если фигура Ф является криволинейной трапецией, то её площадь Sф согласно геометрическому содержанию определённого интеграла равна:
Если фигура Ф не является криволинейной трапецией, то вычисления её площади сводится к одному из следующих случаев:
а) кривая у=f(х)<0 на 
в этом случаи площадь можно вычислить по формуле:
б) если f(х)=
в этом случаи для нахождения площади фигуры находят точку с, как абсциссу точки перегиба графиков функций 
в) если фигура ограничена двумя кривыми у=f1(х) и у=f2(х), (
в этом случаи площадь Sф находят по формуле:
Пример 12. Вычислить площадь фигуры, ограниченную гиперболой ху=1, осью ОХ и прямыми х=1; х=е (рис. 11).
Решение: Использовав формулу вычисления площади криволинейной трапеции, получаем:
Ответ: S=1 кв. ед.
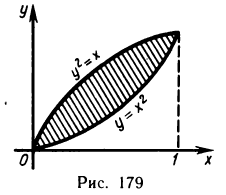
Пример 13. Вычислить площадь фигуры ограниченной линиями у=х2 и у2=х (рис. 12).
Решение: найдём пределы интегрирования, то есть абсциссы точек перегиба графиков функций у=х2 и у2=х. Для этого решим систему:
Вычисление площади фигуры сводится к случаю в) 
Ответ: Sф = 1/3 кв. ед.
Пример 14. Вычислить площадь фигуры ограниченной параболами у=4-х2; у=х2-2х (рис. 13).
Решение: Найдём границы интегрирования, то есть абсциссы точек перегиба графиков функций у=4-х2 и у=х2-2х. Для этого решим систему:
Искомую площадь вычисляем по формуле
Ответ: S=9 кв. ед.
Объём тела вращения
Объём тела, образованного вращением вокруг оси ОХ криволинейной трапеции 




Пример 15. Вычислить объём шара радиусом R (рис. 15).
Решение: Шар образован вращением вокруг оси ОХ круга, ограниченного кругом х2+у2=R2 с центром в начале координат и радиусом R.
Учитывая симметрию круга относительно оси ординат, сначала найдём половину искомого объёма:
Ответ: 
Путь, пройденный точкой
Если точка движется прямолинейно и её скорость 

Пример 16. Тело движется прямолинейно со скоростью 
Решение: Используя формулу находим:

Ответ: S = 250 (м).
Пример 17. Скорость тела, которое движется прямолинейно равна 

Решение: В момент остановки скорость тела равна нулю, то есть
Следовательно, тело остановится через 4 с.
Путь, который прошло тело за это время, вычисляем по формуле:
Ответ:
Работа силы.
Если переменная силы F=F(x) действует в направлении оси ОХ, то работа силы на отрезке 
Пример 18. Вычислить работу силы, которая необходима при сжимании пружины на 0,08 м., если для сжимания её на 1 см., необходима сила 10Н.
Решение: Согласно закона Гука, сила F, которая растягивает или сжимает пружину на х метров, равна F=kх, где k — коэффициент пропорциональности.
Следовательно, 10=k*0.01, то есть k=1000, отсюда F=kx=1000x.
Искомую работу находим по формуле:
Ответ: А= 3,2 (Дж).
Пример 19. Сила 196,2Н растягивает пружины на 18 см. Какую работу она выполняет?
Решение: Согласно закона Гука F=kx, отсюда 
Ответ: А=17,7 (Дж).
Пример 20. Для сжатия пружины на 3 см. необходимо выполнить работу в 16 Дж. На какую длину можно сжать пружину, выполнив работу в 144 Дж.?
Решение: Согласно закона Гука, F=kx; тогда
Ответ: Пружину можно сжать на 9 см.
Сила давления жидкости
Сила давления Р жидкости плотностью р на вертикальную пластину, погружённую в жидкость, вычисляется по формуле:
Где 
Пример 21. Вычислить силу давления воды на одну из стенок аквариума, длиною 30 см. и высотою 20 см.
Решение: Стенка аквариума имеет форму прямоугольника, поэтому S=0,3х, где 
Ответ: Р=58,86 (Н).
Пример 22. Вычислить силу давления бензина на стенки цилиндрического бака высотой 3 м. и радиусом 1 м.
Решение: Площадь поверхности стенки цилиндрического бака 

Ответ: Р= 2,2*105 (Н).
Пример 23. Вычислить давление воды на погружённую в неё вертикальную треугольную пластину, с основанием 6 м. и высотой 2 м., считая, что вершина треугольника лежит на поверхности воды, а основание параллельно ей (рис. 16).
Решение: Пусть NM — ширина пластины на уровне BE=х. Из схожих треугольников ABC и MBN, находим
Использовав формулу получаем:
Ответ: Р = 78480 (Н).
Несобственные интегралы
Интегралы с бесконечными границами интегрирования или от функций, которые имеют бесконечный разрыв называют несобственными.
Несобственные интегралы с бесконечными границами интегрирования определяют следующим образом:
где с — произвольное действительное число.
Несобственные интегралы от функций с бесконечными разрывами также вычисляют через предельный переход.
Если функция разрывная на одном конце отрезка интегрирования, например, в точке х=b, то
если же функция f(х) имеет безграничный разрыв в точке х=с, где 
Если приведённые выше пределы существуют для конкретного интеграла, то его называют сходящимся, если же предела не существует — расходящимся.
Поскольку вычисление пределов — трудоёмкая работа, то иногда для вычисления схожести несобственного интеграла можно воспользоваться признаком схожести:
Признак схожести: Пусть 


Геометрически, в прямоугольной системе координат, несобственный интеграл — это площадь криволинейной трапеции с бесконечной основой либо «незакрытой» сверху.
Пример 1: Вычислить интеграл
Решение: Это несобственный интеграл с верхней границей равной 
Следовательно, интеграл сходящийся.
Пример 2: Вычислить интеграл
Решение: Это несобственный интеграл, так как функция 

Вычислим 
Ответ:
История определенного интеграла
Интегральный расчет получен в результате определения площади и объема. Эмпирически обнаруженные правила измерения площади и объема некоторых простейших фигур были известны древним восточным ученым. Уже в 2000 году до нашей эры. Египтяне и вавилоняне, в частности, знали правила расчета площади круга и расчета объема усеченной пирамиды на основе квадрата. Древнегреческая наука значительно продвинула расчет площади и объема различных фигур. Особенно значительный вклад внес Архимед. Архимед обнаружил множество человеческих территорий и значительное количество объемов тела, основываясь на идее, что плоская фигура состоит из бесчисленных прямых линий, а геометрическое тело состоит из бесчисленных параллельных плоских частей.
Архимед (287-212 до н.э.) — древнегреческий математик, физик, астроном и изобретатель. Родился в Сиракуз (Сицилия) и жил во времена Первой и Второй Поенских войн. Архимед является автором многих технических изобретений. Ирригационные машины с нулевой точкой, подъемные механизмы (винты Архимеда), рычажные системы, блоки для подъема тяжелых предметов, военные метательные машины. Его метательная машина заставила римлян отказаться от попыток совершить набег на город и заставить их пойти на осаду.
Математические исследования Архимеда намного опередили свое время и были правильно оценены только в эпоху исчисления. Архимед вычислил площадь эллипса, параболы и осколков из сегментов и нашел площадь поверхности и шара, сегмент шара и сферы, а также объем различных вращающихся тел и их сегментов. Он также относится к понятию центра тяжести тела, находит положение центра тяжести различных людей и тел и дает математический вывод закона биений. Архимед, как сообщается, находит решение проблемы определения количества золота и серебра в короне жертвоприношения короля Сиракузы Иерона во время омовения и крика «Эврика!» Его величайшим достижением в астрономии было создание планетария — полой вращающейся сферы, которая могла наблюдать Солнце и пять планет, фазы Луны, а также движение Солнца и лунное затмение.
Архимед был убит римским солдатом во время захвата Сиракузы. Согласно легенде, он сталкивался со словами «Не трогай мою фотографию». На могиле Архимеда был установлен памятник с изображением шара и цилиндра вокруг него. Надпись показала, что эти объемы тела i, i называются двумя.
Систематическое развитие подобные представления получили значительно позже — лишь в 
Теорема Архимеда о том, что площадь круга равна площади треугольника с основанием, равным окружности, и высотой, равной радиусу, I. Площадь круга состоит из бесконечного числа треугольников, которые в совокупности равны одинаковой высоте, радиусу и треугольнику, основание которого равно сумме всех оснований, окружности.
Кеплер (Kepler) Йохан (1571-1630) — немецкий астроном и математик. Родился в Вайль-дер-Штадт (Вюртемберг, Германия). Обрабатывая наблюдения датского астронома Г. Врага, он установил три закона движения планет. Он изложил теорию солнечных и лунных затмений, их причины и методы прогнозирования. Изобрел самый легкий телескоп. Это до сих пор называют его именем. Он нашел 92 вращающихся тела как оригинальный метод интеграции.
Используя такие рассуждения, Кеплер нашел объем многих новых революционных тел. Закон Кеплера, известный в астрономии, также был фактически получен с использованием приближенного интегрирования.
Удивительно остроумный трюк Архимеда. Но Кеплер и другие ученые не были строгими, и, самое главное, в принципе, они обладали свойством геометрического преобразования.
Кавальер и, Торричелли, Ферма, Паскаль и другие ученые 

И. Ньютон открыл взаимность операций дифференциации и интеграции. Он отметил, что все задачи нового анализа сводятся к двум взаимно противоположным задачам, которые можно сформулировать с точки зрения механики: 1) Использование известного пути к скорости в определенный момент 2) определите путь, пройденный в конкретное время по известной скорости движения. В данном случае «время» понималось просто как общее обсуждение всех переменных. Он также вводит понятие дифференциации. И. Ньютон намечает программу построения анализа на основе учения о пределе, не давая впрочем формального определения этого понятия, получившего глубокое развитие в математике 
Г. Лейбниц использует нотацию для выражения определенных различных способов вычисления площадей и получения касательных в единую систему взаимосвязанных аналитических концепций и для бесконечного отслеживания действий определенных алгоритмов. Это может быть выполнено. Кроме того, различие в основном понималось как небольшая разница между двумя смежными значениями величины (поэтому символ 

Дальнейшее развитие методы интегрирования получили в 



Дальнейшее обобщение концепции интеграции связано с немецким ученым Б. Риманом и французским ученым А. Лебегом.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Определенный интеграл в математике
Пусть на отрезке 



1. Раздробим отрезок 


Для единообразия обозначений положим еще 




называется рангом произведенного дробления.
2. На каждом отрезке 



3. Умножим 

4. Сложим все полученные произведения, т. е. составим сумму
Эта сумма носит название интегральной суммы или суммы Римана (по имени немецкого математика 19-го века, изучавшего такие суммы).
5. Будем измельчать произведенное дробление, заставляя 


Этот предел
и называется определенным интегралом от функции 

Числа 

Так как определенный интеграл есть предел некоторой переменной величины, а вовсе не всякая переменная имеет предел, то не у всякой функции существует определенный интеграл. Однако справедлива важная
Теорема. Если функция 


существует.
Эту теорему мы примем без доказательства. В дальнейшем будут рассматриваться, главным образом, функции непрерывные, хотя справедлива и более общая
Теорема. Интеграл 

Понятие .кусочно непрерывной* функции легко разъяснить на простом примере. Пусть 










Возможно вам будут полезны данные страницы:
Геометрический смысл интеграла
Пусть 

Заметим, что дробление, т. е. набор точек деления


точки
Рассмотрим (рис. 200) фигуру, ограниченную снизу осью 




была прямой, то наша фигура представила бы собой обыкновенную трапецию. В общем же случае эта фигура называется криволинейной трапецией.
Найдем площадь 


Если через точки деления провести прямые 





непрерывности эта функция не успевает заметно измениться на 







Поскольку длина основания этого прямоугольника, очевидно, равна 


Из самого вывода ясно, что точность этого равенства тем выше, чем меньше отрезки 


Поскольку, однако, сумма (8) является суммой Римана, то по самому
определению ее пределом при
служит интеграл
Таким образом мы приходим к формуле
Читая ее справа налево, выясняем
Геометрический смысл интеграла.
Если 
непрерывна и положительна на 

Интеграция может быть использована для поиска областей, объемов, центральных точек и многих полезных вещей. Но это часто используется, чтобы найти область под графиком функции
Примеры с решением
Пример 1:
Найти
Решение:
Фигура, ограниченная линиями 

откуда
Пример 2:
Найти
Решение:
Линия 






Сейчас мы еще не научились вычислять определенные интегралы, я в этих примерах нам пришлось прибегнуть к помощи геометрии. В дальнейшем, наоборот, с помощью интегрального исчисления мы сможем вычислять площади различных криволинейных фигур *).
Два простейших свойства интеграла. Когда мы занимались неопределенными интегралами, то отмечали, что
Таким образом, в записи подынтегральной функции и в записи результата интегрирования независимая переменная обозначалась одной и той же буквой. Стало быть, обозначение этой независимой переменной, которую называют переменной интегрирования, оказывалось существенным .
Это становится ясным, если мы вспомним хотя бы, как вычисляетсяинтеграл 





I. Обозначение переменной интегрирования в определенном интеграле никакой роли не играет
Читатель сразу поймет это, если задаст себе вопрос: который из двух интегралов
Больше? Ясно, что они одинаковы! Более отчетливо мы разберемся в этом, если заметим, что для вычисления любого из интегралов мы должны разбить отрезок [3, 5] на мелкие части, в каждой части выбрать по точке и вычислить в ней значение подынтегральной функции (а она в обоих интегралах одна и та же: удвоенный куб аргумента, сложенный с самим аргументом) и т. д. Иными словами все вычисления в обоих случаях будут тождественными. Также обстоит дело и в более общем случае интегралов чем и доказано формулированное свойство 
Переходя к другому важному его свойству, заметим, что в выражении
мы предполагали 
На этот вопрос легко ответить, если вспомнить геометрический смысл интеграла. В нашем случае боковые стороны криволинейной трапеции 

т.е.
Определенный интеграл с совпадающими пределами интегрирования равен нулю.
Например,
Понятие определенного интеграла
Рассмотрим непрерывную функцию 







или криволинейной трапецией.
Если требуется вычислить площадь 

Можно вычислить площадь криволинейной трапеции и с помощью тонких прямоугольников. Лейбниц считал, что криволинейная трапеция составлена из бесконечно тонких прямоугольников (рис. 12.2). Каждый такой прямоугольник поднимается над точкой 


Малую ширину 


Напомним, Лейбниц писал 


(первой буква слова Summa). Погаже ученик Лейбница Иоган Вернул-ли предложил отличат!» «целостную сумму бесконечно малых» от обычной суммы и предложил знак именовать интегралом от латинского слова integrals (целостный). Фурье усовершенствовал обозначение Лейбница, предложив явно указывать начальное и конечное значения
Рассуждения математиков XIX века носили нестрогий характер. Термин бесконечно малая величина не был достаточно строго определен, что приводило к противоречиям. Строгое определение основано на понятии предела и интегральной суммы. Оно вобрало в себя качественный смысл определения Лейбница и устранило нечеткость формулировок.
Пусть функция 



На каждом отрезке разбиения выберем точку 
Тогда произведение 


Сумма площадей всех таких прямоугольников равна сумме вида
Эта сумма представляет площадь ступенчатой фигуры. Чем уже ступеньки, тем ближе площадь ступенчатой фигуры к площади криволинейной трапеции (рис. 12.2). Естественно ожидать, что при неограниченном возрастании числа промежутков, так что наибольшая из их длин стремится к нулю, сумма 
Введем теперь точное определение. Пусть на отрезке 




На каждом отрезке разбиения 

Сумму вида
назовем интегральной суммой для функции 






Определение. Пусть предел интегральной суммы
при стремлении 



а сама функция 

Эта запись читается: «интеграл от а до бэ эф от икс дэ икс». При этом число 





Несмотря на сходство в обозначениях и терминологии, определенный и неопределенный интегралы существенно различные понятия. Неопределенный интеграл представляет функцию (а точнее семейство функций), а определенный интеграл — это число.
Из определения следует, что величина определенного интеграла не зависит от обозначения переменной интегрирования, т. е.
Верхний предел 

В первом случае

Поэтому по определению полагают
Понятие определенного интеграла распространяют и на случай 
Это соглашение оправдано тем, что интегральная сумма стремится к нулю при сближении
Очевидно, если функция 





интегральную сумму можно сделать сколь угодно большой, а такая интегральная сумма не имеет конечного предела, что противоречит определению, согласно которому предел интегральной суммы 
Покажем на примере функции Дирихле, что обратное утверждение неверно: существует ограниченная функция, не являющаяся интегрируемой. Напомним, что функция Дирихле равна единице в рациональных точках и нулю — в иррациональных. На любом отрезке 


Если выбрать иррациональную точку 

Таким образом, с одной стороны 

Поэтому предел интегральных сумм не существует и функция Дирихле не является интегрируемой.
Отметим без доказательств, что справедливы следующие утверждения:
1. Если функция


2. Если функция 

3. Если функция 

Пример 3:
Вычислить
Решение. Запишем выражение для интегральной суммы, предполагая, что все отрезки 








Известно, что сумма квадратов чисел натурального ряда равна
Следовательно,
Анализ приведенного примера показывает, что успешное решение поставленной задачи оказалось возможным благодаря тому, что интегральную сумму удалось привести к виду, удобному для нахождения предела. Однако такая возможность существует далеко не всегда, поэтому долгое время задача интегрирования конкретных функций оставалась задачей чрезвычайно сложной.
Пример 4:
Вычислить:
Решение:
а) Произвольная первообразная для функции 


что совпадает, конечно, с результатом, полученным в примере 11.1.
б) Первообразную подынтегральной функции найдем, используя формулу (10.9). Применяя формулу Ньютона—Лейбница, получаем При нахождении интеграла из примера 11.26 было использовано свойство приращения первообразной
где-
Заметим,что введеное ранее определение (11.2) и его следствие (11.3) согласованы с формулой Ньютона-Лейбница. Действительно,
и
Таким образом, и при применении формулы Ньютона-Лейбница несущественно, какой из пределов интегрирования больше: верхний или нижний.
Пример 5:
Вычислить
Решение:
Положим 



Рассмотрим теперь, как выполняется интегрирование по частям в определенном интеграле.
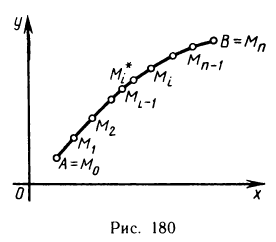
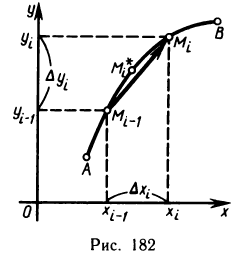
Задачи, приводящие к понятию определенного интеграла
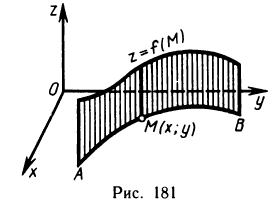
Пусть неотъемлемая функция 



Задача о нахождении площади криволинейной трапеции
Пусть плоская фигура ограничена графиком функции 





Рис. 23.1
Необходимо определить ее площадь.
Для решения задачи выполним следующее:
1) разобьем отрезок 

2) выберем на каждом из частичных отрезков 
Длину частичного отрезка 
3) вычислим значение функции 

Сумма 



4) найдем границу 


Если существует конечный предел интегральной суммы при условии, что 



Задача об определении пройденного пути материальной точки
Задача об определении пройденного пути материальной точки за промежуток времени от 



Если скорость не изменяется в течение времени, то есть 


При переменной скорости совершаем те же действия, что и в предыдущей задаче:
1) разобьем отрезок 



2) выберем на каждом из частичных отрезков времени 
3) вычислим значения скорости 









4) найдем границу интегральной суммы 

Если существует конечный предел интегральной суммы (при условии — 


Задача о нахождении объема продукции
Пусть функция 



Если производительность не меняется в течение времени, то есть 






1) разобьем отрезок 

2) выберем на каждом из отрезков 
3) вычислим производительность труда в каждой точке 







4) найдем границу 


Следует отметить, что при решении этих трех различных задач, были выполнены одни и те же действия, и мы пришли к одному и тому же итоге — возникает необходимость определить границу интегральной суммы.
Если существует конечный предел интегральной суммы 








где 





Теорема 23.1 (о существовании определенного интеграла). Если функция 

Теорема существования определенного интеграла примем без доказательства.
Соответственно, функция 

Вернемся к первой из рассмотренных задач и приведем геометрический смысл определенного интеграла: если функция 


численно равна площади криволинейной трапеции, ограниченной кривой 


Основные свойства определенного интеграла
Поскольку по определению определенный интеграл является границей интегральной суммы, то доказательства его свойств базируется на свойствах границ с привлечением, для наглядности и лучшего понимания, геометрического содержания определенного интеграла.
1 (о интеграл с равными пределами интегрирования). Для любой интегрируемой функции 
ведь криволинейная трапеция вырождается в вертикальный отрезок.
2 (об изменении знака). Если функция 

то есть, если поменять местами пределы интегрирования, то определенный интеграл изменит свой знак на противоположный.
Действительно, в интегральной сумме приросты 
3 (о стабильном множителе). Если функция 

поскольку 
4 (о определенном интеграле от суммы функций). Если функции 


Справедливость (23.11) следует из того, что интегральную сумму левой части равенства можно представить в виде алгебраической суммы двух интегральных сумм:
а по свойству границы суммы функций и получаем (23.11).
Свойство распространяется на любое конечное число слагаемых.
5 (о аддитивности). Если отрезок интегрирования разбит на две части, то определенный интеграл на 
так как по геометрическим содержанием таком разбивке соответствуют две криволинейные трапеции, сумма площадей которых равна площади выходной трапеции.
Свойство распространяется на любое конечное число частей разбиения.
6 (о переходе к определенному интегралу в неровностях). Если на отрезке интегрирования 



Действительно, при одном и том же разбиении отрезка 


7 (о границах значений определенного интеграла). Если 




Если функция 




при этом
тогда
и свойство доказано.
Если доводить это свойство по геометрическим содержанием определенного интеграла (рис. 23.2), то площадь криволинейной трапеции, которая соответствует определенному интегралу, не может быть меньше (больше) за площадь прямоугольника с основанием 


Рис. 23.2
8 (теорема о среднем). Если функция 


Таких точек на промежутке 
Отношение определенного интеграла от функции 

С геометрической точки зрения теорема о среднем (рис. 23.3) означает, что площадь под кривой 


Рис. 23.3
Связь между определенным и неопределенным интегралами
Если функция 




В этом выражении переменная интегрирования обозначена буквой 

Теорема 23.2. Если функция 



Доказательство. Для доказательства этой теоремы применим определение производной.
По условию функция 





Последний интеграл было получено с помощью свойства 5 определенного интеграла. Поскольку
то применяя на отрезке 
где
Переходя к пределу при 


Равенство 





Формула (23.19) описывает связь между определенным и неопределенным интегралами: неопределенный интеграл является суммой определенного интеграла с переменным верхним пределом и произвольной действительной постоянной.
Формула Ньютона-Лейбница
Теорема 23.3 (основная формула интегрального исчисления). Если функция 





Формула (23.20) для вычисления определенного интеграла называется формулой Ньютона-Лейбница
Доказательство основывается на соотношении (23.19), которое позволяет любую первоначальную функции 



Подставляя вместо 


Отметим, что поскольку все первоначальные отличаются друг от друга только константой, то разница 
Для обозначения прироста первоначальной на отрезке 

Заметим, что именно формула Ньютона-Лейбница отображает тесная связь между неопределенным и определенным интегралами. По этой формуле вычисления определенного интеграла сводится к двум шагов:
1) нахождение одной из первоначальных 


2) вычисление значений первоначальной в точках, соответствующих границам интегрирования и определение разницы между ее значениями на верхней и нижней границах.
Вычислим определенный интеграл:
Обычно шаги 1), 2) осуществляют одной цепочкой:
Методы вычисления определенного интеграла
При вычислении определённых интегралов используются методы непосредственного интегрирования, замены переменной (подста-. новки) и интегрирования по частям. Непосредственное интегрирование предполагает сведение данного интеграла с помощью алгебраических и арифметических преобразований к формулам таблицы основных интегралов и использование формулы Ньютона-Лейбница.
Непосредственное определенное интегрирование
Поскольку вычисления определенного интеграла по формуле Ньютона-Лейбница предполагает сначала взятия неопределенного интеграла, а затем выполнение арифметических действий, то это означает, что принципиальных различий в методах нахождения неопределенного и вычисления определенного интегралов нет, следовательно, непосредственное вычисление определенного интеграла предусматривает непосредственное неопределенное интегрирование (нахождение одной из первоначальных).
Вычислим интеграл
Вычисление интеграла методом подстановки
Напомним, что существует два типа подстановок, которые используются при интегрировании с применением новой переменной: 
Пусть для определенности при вычислении интеграла 
Теорема 23.4 (о замене переменной в определенном интеграле). если:
1) функция 

2) значение 



3) составлена функция 

то сравнивая результаты интегрирования по переменным 

Подстановка 

Отметим, что при вычислении определенного интеграла методом подстановки нет необходимости возвращаться к исходной переменной, вместо этого нужно находить пределы интегрирования по новой переменной.
Вычислим определенные интегралы:
Интегрирования по частям в определенном интеграле
Рассмотрим случай, когда при вычислении определенного интеграла нахождения первоначальной требует применения интегрирования по частям.
Теорема 23.5 (формула интегрирования по частям для определенного интеграла). Если в определенном интеграле 




Доказательство. Поскольку
то
Применяя к левой части последнего равенства формулу Ньютона-Лейбница, а также учитывая, что 

отсюда окончательно имеем:
Теорема доказана.
Соотношение (23.23) называется формулой интегрирования по частям в определенном интеграле.
Если пределы интегрирования симметричны относительно нуля, то для упрощения вычислений целесообразно учитывать четности и нечетности подынтегральной функции.
Так, если 
а если 
Это легко обосновать, опираясь на формулу Ньютона-Лейбница.
Вычислим определенные интегралы:
Подынтегральная функция является четной, то есть 
Применение определенного интеграла в некоторых геометрических и экономических задачах
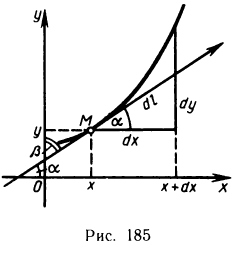
Длина дуги плоской кривой
Пусть функция 

Разобьем отрезок 


Рис. 24.1
Пусть абсциссами вершин ломаной линии имеет значение 

Отсюда
На каждом частичном отрезке 


Тогда
Длина 

Следовательно, длина дуги кривой, соответствующей графику функции 

Если кривая задана уравнениями в параметрической форме
то длина дуги такой кривой определяется формулой:
где 


Наряду с хорошо известной декартовой системой координат 

Зафиксируем на плоскости некоторую точку 


Расстояние 


Угол наклона 


Числа 



Полюс 


Полярный угол определяется неоднозначно: при заданном 





Уравнения 





где 


Связь между координатами точки в полярной 

Рис. 24.3
С 
где 
Если дуга задается уравнением в полярных координатах:
то по формулам (24.2) и (24.4) определяем:
Следовательно, длину дуги в полярных координатах находим по формуле:
где 

Вычислить длину дуги кривой
Сначала надо установить пределы интегрирования. для этого найдем область определения данной функции, решив систему неравенств:
Далее находим производную функции
следовательно,
По формуле (24.1) имеем:
Рассмотрим пример нахождения длины дуги, если кривая заданная параметрически. Система уравнений
определяет линию, которая называется астроидом (рис. 24.4). Найдем ее длину.
Рис. 24.4
Кривая симметрична относительно осей 




Находим производные от 
По формуле (24.2) получаем:
Соответственно, длина всей астроиды равна:
Найдем длину дуги, заданной в полярных координатах уравнением 
Рис. 24.5
Кардиоида симметрична относительно полярной оси, поэтому найдем половину ее длины. Итак, полярный угол 

Имеем:
По формуле (24.5) получаем:
Тогда длина всей линии равна:
Вычисление площади геометрической фигуры
Вычисление площади плоской фигуры в декартовых координатах опирается на геометрический смысл определенного интеграла.
Рассмотрим несколько случаев вычисления площадей геометрических фигур.
1. По геометрическому содержанию определенный интеграл от непрерывной функции 








То есть для 
2. Если функция 



Рис. 24.6
3. Если функция 





Следовательно, если функция 

Рис. 24.7
4. Если надо определить площадь фигуры, ограниченной кривыми 


Рис. 24.8
5. Если плоская фигура ограничена графиком непрерывной на промежутке 



Рис. 24.9
Найдем площадь фигуры, ограниченной графиком функции 


Рис. 24.10
Устанавливаем пределы интегрирования:
Поскольку функция 

Вычислим площадь фигуры, ограниченной линиями: 


Рис. 24.11
Промежутком интегрирования является отрезок
Поскольку подынтегральная функция 

Найдем площадь фигуры, ограниченной линиями: 
Рис. 24.12
Функция 


Найдем площадь фигуры, ограниченной линиями: 

Рис. 24.13
Для определения границ интегрирования находим точки пересечения линий:
Откуда получаем:
Согласно формуле (24.10) имеем:
Подчеркнем, что в формуле (24.10) в роли 
6. Пусть фигура ограничена кривой, уравнение которой задано в параметрической форме, то есть зависимость 
где 
Площадь фигуры, как и раньше, вычисляем по формуле (24.7), но в ней сделаем замену переменной: 
Следовательно,
Найдем площадь фигуры, ограниченной эллипсом (рис. 24.14), заданным параметрическими уравнениями
Рис. 24.14
Поскольку эллипс симметричен относительно осей координат, то найдем площадь 
Определим границы интегрирования. Если 

получаем, что параметр 
Осуществляем по формуле (24.12) определено интегрирование:
Отсюда площадь всей фигуры равна:
7. Площадь криволинейного сектора
Рассмотрим в полярных координатах геометрическую фигуру, которая ограничена линией 





Рис. 24.15
Выполняем те же шаги, которые осуществлялись при решении задачи нахождения площади криволинейной трапеции:
1) разобьем криволинейный сектор для 



2) выберем на каждом из частичных секторов произвольный луч под углом 
3) вычислим площадь кругового сектора радиуса 



которая является интегральной суммой для сложной функции от
4) найдем границу интегральной суммы 


Вычислим площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда 

Рис. 24.16
При чередовании 


Вычисление объемов тел по известным площадям поперечных сечений
Пусть имеем некоторое геометрическое тело, для которого известна площадь любого сечения этого тела плоскостью 



Рис. 24.17
1) разобьем тело произвольным образом на 



2) выберем на каждом частичном промежутке 




3) вычислим объем цилиндра с площадью основания 


которая является интегральной суммой для функции 
4) найдем границу интегральной суммы 


Найдем объем тела, ограниченного плоскостями 

Проведем плоскость 
Перейдем к каноническому уравнению эллипса:
где
Площадь сечения находим по известной формуле площади фигуры, ограниченной эллипсом (24.13):
Следовательно, вычислим объем тела по формуле (24.15) с переменной интегрирования
Вычисление объема тела вращения
Пусть на промежутке 




Рис. 24.19
При вращении каждая точка дуги кривой описывает круг, а поперечным сечением тела вращения является круг радиуса 



На этом основании расчетную формулу для вычисления объема тела 



Найдем объем шара радиуса 


Объем этого шара можно найти по формуле (24.16):
Если в соотношении для 




Приближенное вычисление определенных интегралов
Формула Ньютона-Лейбница как основная формула интегрального исчисления является главным средством вычисления определенного интеграла, если при нахождении первоначальной не возникает трудностей. В случае, если неопределенный интеграл «не берется», то есть первоначальную нельзя представить в виде конечного числа элементарных функции, или подынтегральная функция задана графиком или таблицей, то используют приближенные формулы. Эти формулы основаны на геометрическом смысле определенного интеграла как площади криволинейной трапеции.
Формула прямоугольников
Пусть надо вычислить определенный интеграл от непрерывной на отрезке 

Поделим отрезок 

Вычислим значение функции 

Тогда площадь криволинейной трапеции, изображенной на рис. 24.23, а вместе с тем и определенный интеграл для функции 


Рис. 24.23
Полученное выражение (24.24) называется формулой прямоугольников с высотами 
Если высоты прямоугольников взять равными значениям функции 
Поскольку для функции 





где
Относительная погрешность определяется как отношение абсолютной погрешности к точному значению интеграла и подается в процентах.
Формула трапеций
Рассмотрим еще один способ приближенного вычисления определенного интеграла.
Как и в предыдущем случае, отрезок 





Рис. 24.24
Каждая часть площади под кривой 




трапеций, ограниченных сверху отрезками этой ломаной.
Соответственно, получаем:
Это и есть формула трапеций. Формула (24.26), как и в предыдущем случае, будет тем точнее, чем больше число
Можно доказать, что если функция f



Для функций, которые имеют ограниченную вторую производную 

Формула Симпсона
Поделим отрезок 







Рис. 24.25
Аналогичные параболы строим и для всех остальных пар частичных отрезков.
Сумма площадей криволинейных трапеций, ограниченных параболами, и даст приближенное значение интеграла.
Покажем, что площадь криволинейной трапеции, ограниченной сверху параболой, проходящей через три точки 
где 

Рис. 24.26
Коэффициенты параболы 


Найдем площадь криволинейной трапеции для 
С учетом значений функции в точках с абсциссами 


Итак, 


Если сложить левые и правые части записанных равенств, то получим:
или
— формула Симпсона, или формула парабол.
Если функция 





Таким образом, формула Симпсона (при одинаковом количестве частичных отрезков разбиения промежутка интегрирования) дает наилучшее приближение к искомому интеграла по сравнению с формулами прямоугольников или трапеций.
Вычислим интеграл 
Сравним этот результат с результатами приближенного вычисления по формулам прямоугольников, трапеций, парабол при 
Для применения выведенных формул приближенного вычисления определенных интегралов разобьем отрезок 

Составим таблицу значений функции для каждой границы интервала разбиения.
Таблица 24.1
По формуле прямоугольников (24.24), если принимать высоты прямоугольника значение 
По формуле прямоугольников (24.25), если принимать высоты прямоугольника значение 
По формуле трапеций (24.26) имеем промежуточное значение по сравнению с обеими формулами прямоугольников:
По формуле парабол (24.30):
При вычислении интеграла по формуле прямоугольников (24.24) абсолютная погрешность составляет:
а относительная погрешность равна:
При вычислении интеграла по формуле прямоугольников (24.25) абсолютная и относительная погрешности составляют:

При вычислении интеграла по формуле трапеций имеем:

При вычислении интеграла по формуле парабол получаем:

Итоговая таблица (табл. 24.2) убедительно подтверждает, что формула парабол действительно дает наибольшую точность при приближенном вычислении определенных интегралов. Конечно, если подынтегральная функция отлична от многочлена второго или третьей степени, то погрешность не будут нулевыми.
Таблица 24.2
По объему вычислительной работы формула Симпсона не имеет преимуществ перед другими формулами.
Лекции:
- Замена переменной в определенном интеграле
- Формулы тригонометрии и их использование для преобразования тригонометрических выражений
- Интегральный признак Коши
- Правила дифференцирования
- Построение графика функции
- Связь между непрерывностью и дифференцируемостью функции
- Функции комплексного переменного
- Преобразование подобия
- Формулы производных
- Изометрия
Интеграл является одним из наиболее важных понятий в математическом анализе. Его применяют в алгебре для расчета площади под кривой, преодоленного пути в процессе неравномерного движения, массы, которой обладает неоднородное тело и решения других подобных задач. С помощью интеграла вычисляют функцию по известной производной.
Интегралы для чайников — базовые понятия
Понятие интеграла в теории основано на нахождении непрерывной функции. Для начала следует ознакомиться с этим термином.
Непрерывная функция F(х) представляет собой первообразную функции f(х) на понятном промежутке х при условии, что F(х)=f(х).
Процедура поиска первообразной функции f(х) представляет собой операцию интегрирования в определенном порядке.
Интеграл в кратком смысле является аналогом суммы для бесконечного числа бесконечно малых слагаемых.
Неопределенный интеграл
Неопределенным интегралом называют комплекс всех первообразных функции f(х).
В легком виде формулу для расчета неопределенного интеграла можно записать в такой форме:
(int f(x)dx=F(x)+C), где
- f(x) является подынтегральной функцией;
- F(x) представляет собой первообразную функцию функции f(x);
- dx определяется дифференциалом;
- C является численной константой интегрирования.
В неопределенный интеграл включен спектр первообразных, так как имеется постоянная интегрирования. Дифференциалом называют произвольное, бесконечно малое приращение переменной величины. Среди основных свойств неопределенного интеграла можно отметить такие пояснения:
Табличная форма неопределенных интегралов в виде (int f(x)dx=F(x)+C) имеет вид:
Определенный интеграл
Определенным интегралом называют приращение одной из первообразных функции f(х), соответствующих отрезку [a;b].
В общем виде определенный интеграл можно записать таким образом:
(int_{a}^{b}{} f(x)dx), где
- f(x) представляет собой подынтегральную функцию;
- a и b являются пределами интегрирования;
- dx соответствует дифференциалу.
Вычислить определенный интеграл можно с помощью уравнения Ньютона-Лейбница:
Свойства определенных интегралов:
- если определенный интеграл обладает одинаковыми пределами интегрирования, то его значение соответствует нулю;
- значение определенного интеграла является независимой от обозначения переменной интегрирования величиной;
- постоянный множитель допустимо выносить за знак определенного интеграла;
- определенный интеграл в случае алгебраической суммы конечного числа функций рассчитывается как алгебраическая сумма определенных интегралов;
- при разбивке отрезка интегрирования на части определенный интеграл в отношении всего отрезка соответствует сумме определенных интегралов его частей;
- перестановка пределов интегрирования не меняет абсолютную величину определенного интеграла, а изменяет его знак;
- определенный интеграл рассчитывается как произведение длины отрезка интегрирования и значения подынтегральной функции в какой-то точке х0 внутри него;
- в том случае, если верхний предел интегрирования больше, чем нижний, и подынтегральная функция соответствует неотрицательному или положительному значению, определенному интегралу будет соответствовать неотрицательная или положительная величина;
- когда верхний предел интегрирования больше, чем нижний, и функции f(х) и g(х) не прерываются, то допустимо почленно интегрировать неравенство f(x) >=g(x).
Таблица интегралов для студентов (основные формулы)
Существует несколько основных приемов решения задач с интегралами. Процесс заключается в интегрировании функции по переменной. В том случае, если интеграл обладает табличным видом, то проблем с поиском его значения не возникнет. Когда форма записи интеграла отлична от табличной, решение сводится к приведению интеграла к табличному виду.
Таблица первообразных для решения интегралов имеет следующий вид:
В первую очередь необходимо ознакомиться с основными свойствами интегралов:
С помощью данных понятий можно решать несложные интегралы. Но в большинстве случаев встречаются задачи с непростыми интегралами, для работы с которыми требуется прибегнуть к дополнительным приемам.
Правила вычисления интегралов, примеры решения
Специальные методики позволяют рассчитывать большую часть интегралов. Основными приемами для поиска решений являются:
- Замена переменной с применением навыков нахождения производных.
- Интегрирование по частям с помощью формулы: (int udv=uv-int vdu).
- Интегрирование дробно-рациональных функций:
- разложением дроби на простейшие (int F_{n}(x)/G_{m}(x)dx);
- выделением полного квадрата (int dx/(ax^{2}+bx+c));
- созданием в числителе дифференциала знаменателя (int (mx+n)dx/(ax^{2}+bx+c)).
- Интегрирование дробно-иррациональных функций:
- выделением под корнем полного квадрата (int dx/(sqrt{ax^{2}+bx+c}));
- созданием в числителе дифференциала подкоренного выражения (int (mx+n)dx/(sqrt{ax^{2}+bx+c})).
- Интегрирование тригонометрических функций:
- с помощью формул разложения для произведения (int sin alpha x*cos beta xdx);
- с помощью создания (d(cos x)) при m-нечетном, n-любом для выражений вида (int sin^{n}x*cos^{m} xdx) применимо тождество (sin^{2}+cos^{2}=1), где m, n являются четными, (sin^{2}x=(1-cos^{2}x)/2$$ и $$ cos^{2}x=(1+cos^{2}x)/2);
- Применение свойства (tan ^{2}x=1/cos ^{2}x-1) для выражения в виде (int tan^{n}xdx).
Решать интегралы целесообразно с помощью данного алгоритма:
- Вникнуть в суть интегралов, включая базовые понятия и методы решения. Интеграл представляет собой сумму элементарных частей объекта интегрирования. В том случае, когда рассматривается интегрирование функции, следует идентифицировать интеграл как площадь фигуры между графиком функции, осью х и границами интегрирования. При неопределенном интеграле, то есть неизвестных границах интегрирования, решать задачу необходимо с помощью нахождения первообразной. В случае определенного интеграла в найденную функцию подставляют значения границ.
- Научиться пользоваться таблицей первообразных и основными свойствами интегралов. Множество функций уже определены первообразными, которые отмечены в таблице. Для интегралов, которые занесены в табличную форму, уже имеется готовое решение.
- Освоение способов и приобретение навыков решения интегралов. В том случае, когда в задаче имеется интеграл, не соответствующий табличной форме, его необходимо привести к этому виду. Данная операция выполняется с помощью применения основных свойств интегралов и приемов по их решению.
На первых этапах обучения следует проверять собственные решения задач на интегралы. Для этого можно дифференцировать полученное выражение и сравнить его с исходным интегралом.
Примеры решения интегралов:
Задача 1
Требуется решить интеграл:
(int (x^{5}+frac{1}{sqrt{x}})dx)
Решение
Заметим, что по условию интеграл — неопределенный. Сначала необходимо найти первообразную. Для этого интеграл суммы можно разложить на сумму интегралов:
(int x^{5}dx+frac{1}{sqrt{x}}dx)
Таким образом, каждый из интегралов преобразован в табличный вид. Решение можно найти с помощью таблицы:
(frac{x^{6}}{6}+2sqrt{x}+С)
Выполним проверку решения с помощью поиска производной:
((frac{x^{6}}{6}+2sqrt{x})^{,}=x^{2}+frac{1}{sqrt{x}})
Ответ: (frac{x^{6}}{6}+2sqrt{x}+С)
Задача 2
Требуется решить интеграл:
(int sqrt[5]{(x+5)})
Решение
Имеется неопределенный интеграл. Для начала необходимо найти первообразную. При сравнении с таблицей выяснилось, что подобное решение отсутствует. Способ разложения, исходя из свойств интеграла, не применим в данном случае. Следует обратиться к приемам. В этом случае целесообразно воспользоваться заменой переменной. Таким образом, выполним замену выражения (х+5) на (t^{5}).
(t^{5}=x+5)
После преобразований получим (int tdx.)
Выражение dx также требуется заменить на t. В таком случае:
(x=t^{5}-5)
(dx=(t^{5}-5)^{,}=5t^{4})
Выполним подстановку значений:
(5int t^{4}*tdt=5int t^{5}dt)
Интеграл соответствует табличной форме. Его можно посчитать (frac{5t^{6}}{6}).
Далее необходимо заменить t на выражение (sqrt[5]{(x+5)}).
Таким образом:
(int sqrt[5]{(x+5)}=5/6sqrt[5]{(x+5)^{6}})
Ответ: (int sqrt[5]{(x+5)}=5/6sqrt[5]{(x+5)^{6}}.)
Задача 3
Необходимо найти решение интеграла:
(int frac{dx}{sqrt{4x^{2}+4x+5}})
Решение
В рамках данной задачи целесообразно выделить полный квадрат:
(4x^{2}+4x+5=4x^{2}+4x+1+4=(2x+1)^{2}+1)
(int frac{dx}{sqrt{4x^{2}+4x+5}}=int frac{dx}{sqrt{(2x+1)^{2}+1}}=frac{1}{2}int frac{d(2x+1}{sqrt{(2x+1)^{2}+1}})
Результат преобразований соответствует табличному виду. Можно найти первообразную:
(int frac{dx}{sqrt{x^{2}+a^{2}}}=ln left|x+sqrt{x^{2}+a^{2}} right|+C)
(int frac{dx}{sqrt{4x^{2}+4x+5}}=ln left|2x+1+sqrt{(2x+2)^{2}+1} right|+C)
((2x+1)^{2}+1=4x^{2}+4x+1)
В результате получим:
(int frac{dx}{sqrt{4x^{2}+4x+5}}=ln left|2x+1+sqrt{4x^{2}+4x+1} right|+C)
Ответ: (int frac{dx}{sqrt{4x^{2}+4x+5}}=ln left|2x+1+sqrt{4x^{2}+4x+1} right|+C)
Математический анализ — достаточно сложная дисциплина. Одной из главных тем является решение интегралов. С подобными задачами часто сталкиваются учащиеся профильных вузов. Если в процессе обучения студент испытывает какие-либо трудности, правильное решение — обратиться к сервису Феникс.Хелп.
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Изучаем понятие «интеграл»
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x).
Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов
Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:
Точки а и b называются пределами интегрирования.
«Интеграл»
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
- Производная от интеграла равна подынтегральной функции:
- Константу можно выносить из-под знака интеграла:
- Интеграл от суммы равен сумме интегралов. Верно также для разности:
Свойства определенного интеграла
- Линейность:
- Знак интеграла изменяется, если поменять местами пределы интегрирования:
- При любых точках a, b и с:
Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Рассмотрим основные вопросы интегрирования функций двух переменных. Полученные определения и результаты могут быть перенесены на функции трех и более переменных.
Двойные интегралы
Двойной интеграл представляет собой обобщение понятия определенного интеграла на случай функций двух переменных.
Определение и условия существования двойного интеграла
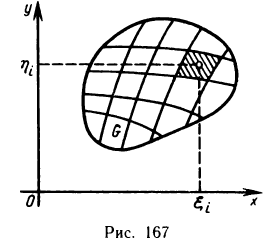
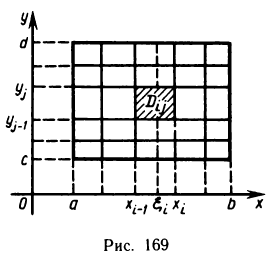
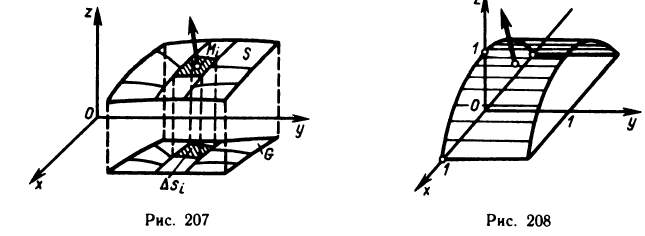
Пусть G — некоторая замкнутая ограниченная область, a z=f(x, у) — произвольная функция, определенная и ограниченная в этой области.
Предполагается, что граница области G состоит из конечного числа кривых, заданных уравнениями вида y=f(x) или 
Разобьем область G произвольно на n частей 
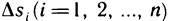
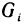
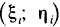
которую назовем интегральной суммой для функции f (х, у) в области G. Назовем диаметром d (G) области G наибольшее расстояние между граничными точками этой области. Обозначим через Я. наибольший из диаметров частичных областей
Определение:
Если интегральная сумма (1) при 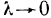
В этом случае функция f (х, у) называется интегрируемой в области G, G — областью интегрирования, х и у — переменными интегрирования, ds (или dx dу) —элементом площади.
Давая определение двойного интеграла, мы предполагаем, что функция f (х, у) ограничена. Как и для функции одной переменной, это условие является необходимым условием интегрируемости. Однако оно не является достаточным, т. е. существуют ограниченные, но не интегрируемые функции. Примером таких функций является функция, определенная на квадрате 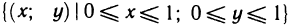
Доказательство неинтегрируемости такой функции непосредственно следует из определения двойного интеграла.
Для нахождения достаточных условий интегрируемости, как и в случае одной переменной, удобно воспользоваться теорией сумм Дарбу, которая полностью переносится на случай двойного интеграла. Аналогично доказательству соответствующей теоремы для определенного интеграла доказывается следующая теорема.
Теорема:
Функция f (x, у), непрерывная в замкнутой ограниченной области G, интегрируема в этой области. Однако не следует считать, что двойной интеграл существует только для непрерывных функций. Имеет место более общая теорема.
Теорема:
Функция f (х, у), ограниченная в замкнутой ограниченной области G и непрерывная в ней всюду, кроме точек, лежащих на конечном числе кривых, являющихся графиками непрерывных функций вида у=f (х) или 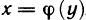
Геометрический смысл двойного интеграла
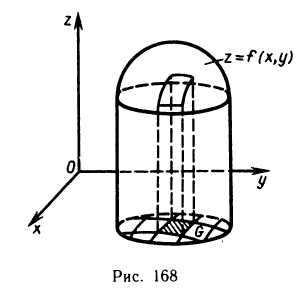
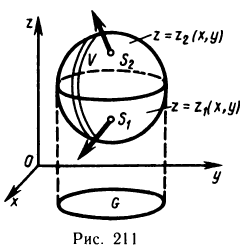
Пусть в пространстве дано тело Р (рис. 168), ограниченное сверху графиком непрерывной и неотрицательной функции z=f (х, у), которая определена в области G, с боков — цилиндрической поверхностью, направляющей которой служит граница области G, а образующие параллельны оси Oz, и снизу областью G, лежащей в плоскости Оху. Тело такого вида называют криволинейным цилиндром.
Аналогично тому как задача о вычислении площади криволинейной трапеции приводит к установлению геометрического смысла определенного интеграла, так и задача о вычислении объема тела Р приводит к геометрическому толкованию двойного интеграла.
Действительно, в данном случае интегральная сумма (1) представляет собой сумму объемов прямых цилиндров с площадями оснований 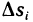
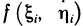
Это приближенное равенство тем точнее, чем мельче разбиение области G на части. При переходе к пределу при 
Так как функция f (x, у) интегрируема, то предел интегральной суммы существует и равен двойному интегралу от этой функции по области G. Следовательно,
Отсюда следует геометрический смысл двойного интеграла: двойной интеграл от непрерывной, неотрицательной функции равен объему криволинейного цилиндра.
Замечание:
Если положить 
Свойства двойного интеграла
Основные свойства двойного интеграла аналогичны соответствующим свойствам определенного интеграла. Поэтому ограничимся формулировкой этих свойств, не останавливаясь на доказательствах.
1°. Если k — произвольное число и функция f (x, у) интегрируема в области G, то функция kf (х, у) тоже интегрируема в G и 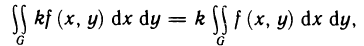
2°. Если функции f (х, у) и g (х, у) интегрируемы в области G, то их алгебраическая сумма также интегрируема в этой области и
3°. Если область G является объединением областей 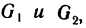
4°. Теорема о среднем. Если функция f(x, у) непрерывна в области G, то в этой области найдется такая точка 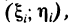
где s — площадь фигуры G.
Итак, рассмотрены определение и основные свойства двойного интеграла, условия существования, выяснен его геометрический смысл. Теперь рассмотрим способы вычисления двойных интегралов.
Сведение двойного интеграла к повторному
Случай прямоугольной области
Сначала рассмотрим двойной интеграл по некоторому прямоугольнику D со сторонами, параллельными осям координат.
Теорема:
Пусть для функции f (х, у) в прямоугольнике 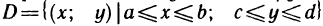
Пусть, далее, для каждого х из отрезка [а, b] существует определенный интеграл
Тогда существует интеграл
(он называется повторным) и справедливо равенство
Доказательство:
Разобьем прямоугольник D с помощью точек 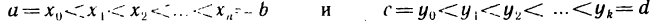
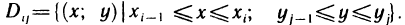
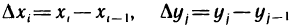
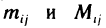
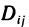
Положим в этом неравенстве 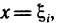
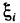
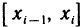
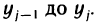
Суммируя (5) по всем j от 1 до k и используя обозначение (2) имеем
Далее, умножая (6) на 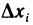
Пусть наибольший диаметр частичных прямоугольников 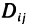

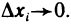
Тем самым доказано существование повторного интеграла и равенство (3). ■
Замечание:
Если в теореме 13.3 поменять х и у ролями, то будет доказано существование повторного интеграла
и справедливость равенства
С помощью формул (3) и (8) двойной интеграл приводится к повторному. Например, в формуле (8) интегрирование сначала производится по х при постоянном у, а затем полученный результат интегрируется по у, т. е. последовательно вычисляются два определенных интеграла.
Пример:
Вычислить
Решение:
Имеем
Случай криволинейной области
Теорема:
Пусть функция z=f(x, у) определена в области 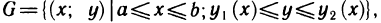
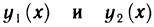
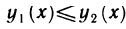
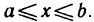
и для каждого х из отрезка [а, b] существует определенный интеграл
Тогда существует повторный интеграл
и справедливо равенство 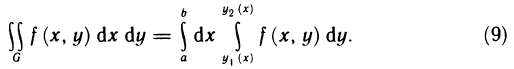
Положим 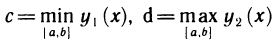
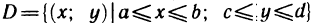
Эта функция удовлетворяет условиям предыдущей теоремы. Действительно, она интегрируема в области G, так как совпадает в ней с f (x, у), и интегрируема в остальной части D — G прямоугольника D, где она равна нулю. Следовательно, согласно свойству 3°
§ 1, она интегрируема и по всему прямоугольнику D. При этом
откуда
Далее, для каждого х из [а, b] существует интеграл 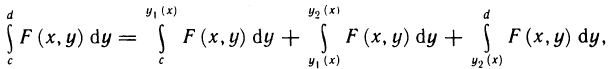
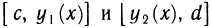
равны нулю, а второй интеграл существует по условию, так как 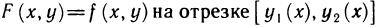
Таким образом, для функции F (х, у) выполнены все условия теоремы 13.3 и, следовательно, двойной интеграл от этой функции по прямоугольнику D может быть сведен к повторному
Отсюда и из равенств (10) и (11) получаем
т. е. формулу (9). ■
Замечание:
Если в теореме 13.4 поменять ролями х и у, то теорема будет утверждать существование повторного интеграла
и равенства
Пример:
Вычислить интеграл 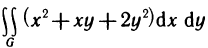
Решение:
Область G представляет собой треугольник, ограниченный осями координат и прямой 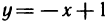
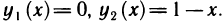
Данный интеграл можно вычислить и по формуле (12), если в G поменять х и у ролями. Тогда треугольник определяется неравенствами 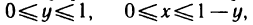
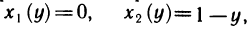
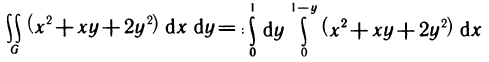
Замечание:
Если область G не удовлетворяет условиям теоремы 13.4 (например, прямые (вертикальные или горизонтальные) пересекают ее границу более чем в двух точках), то необходимо область G разбить на части, каждая из которых удовлетворяла бы условиям теоремы 13.4, и сводить к повторному каждый из соответствующих двойных интегралов отдельно.
Замена переменных в двойном интеграле
Пусть функция f (х, у) непрерывна в некоторой замкнутой ограниченной области G. Тогда для функции f (х, у) существует двойной интеграл
Предположим, далее, что с помощью формул
мы переходим к новым переменным 
С помощью формул (3) каждой точке М (х; у) из области G ставится в соответствие некоторая точка 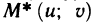
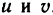
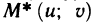
При сделанных предположениях можно доказать, что если функции (2) имеют в области G* непрерывные частные производные первого порядка и если определитель
отличен в G от нуля, то для интеграла (1) справедлива формула замены переменных
Определитель (4) называется функциональным определителем или якобианом (по имени немецкого математика Якоби) функций 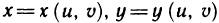
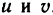
Коротко изложенное можно сформулировать в виде следующей теоремы.
Теорема:
Если преобразование (2) переводит замкнутую ограниченную область G в замкнутую ограниченную область G* и является взаимно однозначным и если функции (2) имеют в области G* непрерывные частные производные первого порядка и отличный от нуля якобиан (4), а функция f (х, у) непрерывна в области G, то справедлива формула замены переменных (5).
Доказательство теоремы достаточно сложное и здесь не приводится.
Как в двойном, так и в определенном интеграле замена переменных — важнейший способ приведения интеграла к виду, более удобному для вычисления.
Пример:
Вычислить интеграл 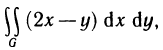
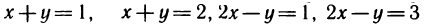
Решение:
Непосредственное вычисление этого интеграла достаточно громоздкое, так как для сведения его к повторному (сначала по у, а затем по х) необходимо область G разбить на три области (штриховые линии на рис. 172) и затем вычислить соответственно три интеграла. Однако простая замена переменных
позволяет значительно упростить решение. Прямые 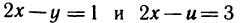
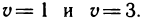
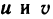
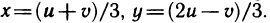
Следовательно,
По формуле (5) окончательно получаем
Замечание:
Если подынтегральная функция или уравнение границы области интегрирования содержат сумму 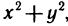
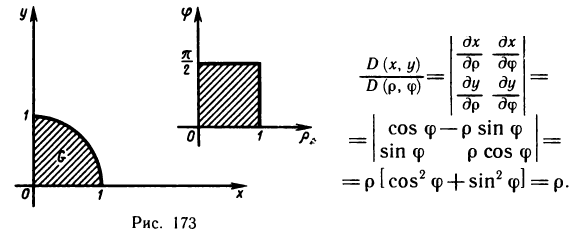
Пример:
Вычислить интеграл 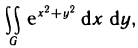
Решение:
Преобразуем интеграл к полярным координатам по формулам 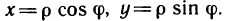
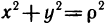
Наглядно видно, что в области G р изменяется в пределах от 0 до 1, а 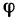
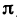
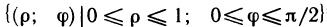
Таким образом, по формуле (5) получаем
На практике при замене переменных нет необходимости детально строить область G*. Обычно выясняют пределы изменения новых координат, используя вид области G на плоскости Оху, что и сделано вначале в данном примере.
Некоторые геометрические и физические приложения двойных интегралов
Вычисление объема
Как известно, объем v криволинейного цилиндра, ограниченного сверху поверхностью z=f(x, у)>0, снизу плоскостью z=0 и с боковых сторон цилиндрической поверхностью, у которой образующие параллельны оси Oz, а направляющей служит контур области G, вычисляется по формуле
т. е. с помощью двойных интегралов можно вычислять объемы тел.
Пример:
Вычислить объем тела, ограниченного поверхностями 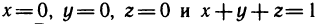
Решение:
Имеем
где G — треугольная область интегрирования, ограниченная прямыми 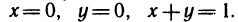
Вычисление площади
Как было установлено, площадь s области G может быть вычислена с помощью двойного интеграла по формуле
Эта формула более универсальна, чем соответствующая формула выражающая площадь криволинейной трапеции с помощью определенного интеграла, так как данная формула применима не только к криволинейным трапециям, но и к фигурам, расположенным произвольно по отношению к координатным осям.
Пример:
Вычислить площадь области G, ограниченной линиями 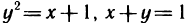
Решение:
Область G представляет собой фигуру, ограниченную слева параболой 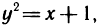
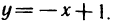
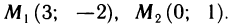
При вычислении двойных интегралов с помощью повторного интегрирования одним из главных моментов является расстановка пределов интегрирования. Если в данном примере выбрать другой порядок повторного интегрирования (сначала по у, а затем по х),
то область G предварительно пришлось бы разбить на две части (осью Оу), так как она ограничена сверху линией, заданной на отрезках 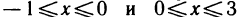
Поэтому полезно запомнить следующее правило: если все прямые, параллельные оси Оу, входят в область интегрирования G на линии, заданной одним уравнением, и выходят из области на линии, заданной одним уравнением, то внутренний интеграл целесообразно брать по переменной у, а внешний — по х аналогично, если все прямые, параллельные оси Ох, входят в область интегрирования на линии, заданной одним уравнением (в данном случае на параболе), и выходят на линии, заданной одним уравнением (в данном случае на прямой), то внутренний интеграл следует брать по переменной х, а внешний — по у: в этом случае область интегрирования не нужно разбивать на части.
Вычисление площади поверхности
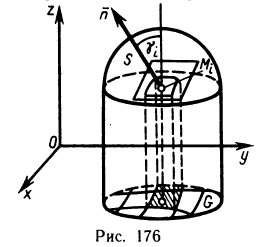
С помощью двойных интегралов можно вычислять площади не только плоских фигур, но и кривых поверхностей.
Пусть поверхность S задана уравнением z=f (x, у), проекцией S на плоскость Оху является область G (рис. 176) и в этой области функция f (x, у) непрерывна и имеет непрерывные частные производные
Для определения площади поверхности S разобьем область G произвольно на n частей G, без общих внутренних точек с площадями 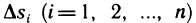
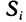
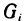
В каждой части 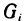
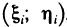
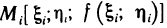
здесь х, у, z — координаты произвольной точки на плоскости; 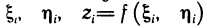
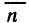
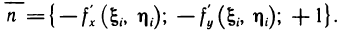
Рассмотрим на касательной плоскости ту ее часть, проекцией которой на плоскость Оху является область 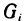
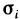
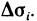
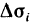
приближенным значением площади всей поверхности S.
За точное значение площади поверхности S примем по определению предел такой суммы
где 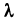
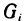
Обозначим через 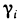
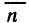
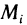
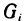
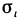
Действительно, данная формула, как известно, справедлива для треугольников. Она, очевидно, справедлива и для плоских многоугольников, так как плоский многоугольник можно разбить на несколько треугольников. Она также справедлива и для любой плоской фигуры площади 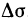
С другой стороны, как известно из аналитической геометрии,
Следовательно,
Подставляя значение 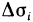
Стоящая под знаком предела сумма представляет собой интегральную сумму для функции
Так как эта функция по условию непрерывна в области G, то предел этой суммы при 
Соотношение (2) представляет собой формулу, с помощью которой вычисляется площадь поверхностей, заданных уравнением z=f(x, у).
Пример:
Вычислить площадь той части плоскости 
Решение:
Так как функция 
Областью G является треугольник, ограниченный осями Ох, Оу и прямой 
Вычисление массы пластинки
Рассмотрим на плоскости Оху материальную пластинку, т. е. некоторую область G, по которой распределена масса m с плотностью р (х, у). Вычислим по заданной плотности р (х, у) массу т этой пластинки, считая, что р (х, у)— непрерывная функция. Разобьем G произвольно на n частей 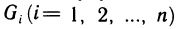
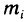
В каждой части произвольно возьмем точку 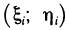
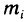
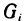
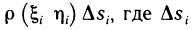
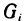
которая является интегральной суммой для непрерывной функции
р (х, у) в области G. В пределе при 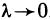
Пример:
Определить массу квадратной пластинки со стороной 2а, если плотность р (x, у) в каждой точке М (х; у) пропорциональна квадрату расстояния от точки М до точки пересечения диагоналей, и коэффициент пропорциональности равен k.
Решение:
Выберем систему координат так, как показано на рис. 178. После этого можно найти функцию р (х, у) исходя из условия задачи. Пусть М (х; у) — произвольная точка квадратной пластинки. Тогда квадрат расстояния от точки М до точки пересечения диагоналей равен 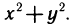
По формуле (3) имеем
Учитывая, что подынтегральная функция четна относительно х и у, а область интегрирования симметрична относительно осей координат, можно ограничиться вычислением интеграла по той части области G, которая расположена в I четверти, т. е.
Вычисление координат центра масс пластинки
Найдем координаты центра масс пластинки, занимающей в плоскости Оху некоторую область G. Пусть р (х; у) — плотность этой пластинки в точке М (х; у), причем р (х; у)—непрерывная функция. Разбив область G на части 
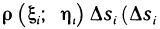
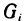
Если считать, что каждая из этих масс сосредоточена в одной точке, а именно в точке 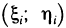
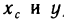
которые представляют собой приближенные значения координат центра масс пластинки. Чтобы получить точные значения этих координат, необходимо в (4) перейти к пределу при 
Если пластинка однородна, т. е. 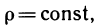
Величины 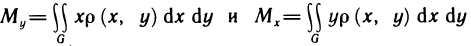
Таким образом, вычисление координат центра масс пластинки сводится к вычислению трех двойных интегралов.
Пример:
Найти координаты центра масс однородной пластинки, ограниченной двумя параболами 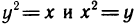
Решение:
Координаты центра масс данной пластинки найдем по формулам (6). Сначала вычислим массу пластинки
Далее вычислим статические моменты ее относительно осей координат:
Затем по формулам (6) найдем
Итак,
Вычисление момента инерции пластинки
Как известно, момент инерции материальной точки относительно некоторой оси равен произведению массы точки на квадрат ее расстояния до этой оси, а момент инерции системы материальных точек равен сумме моментов инерции этих точек.
Пусть область G плоскости Оху занята пластинкой, имеющей непрерывную плотность р (х, у). Разбив область G на части 
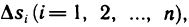
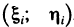
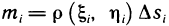
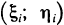
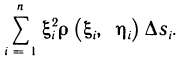
Примем это выражение за приближенное значение момента инерции пластинки. Но оно же представляет собой интегральную сумму для непрерывной функции 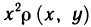
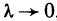
Аналогично, момент инерции пластинки относительно оси Ох равен
Найдем момент инерции 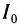
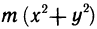
Пример:
Найти момент инерции круга радиуса R с постоянной плотностью р (x, у)=1 относительно начала координат.
Решение:
По формуле (7) имеем
Перейдем к полярным координатам. Уравнение окружности (границы круга) в полярных координатах имеет вид 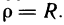
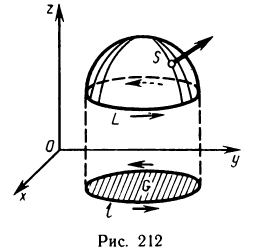
Криволинейные интегралы
Обобщим понятие определенного интеграла на случай, когда областью интегрирования является отрезок некоторой кривой, лежащей в плоскости.
Интегралы такого рода называются криволинейными. Они имеют широкое применение в различных разделах математики.
Различают два типа криволинейных интегралов: криволинейные интегралы первого и второго рода.
Определение криволинейного интеграла первого рода
Рассмотрим на плоскости Оху некоторую кривую АВ, гладкую или кусочно-гладкую, и предположим, что функция z=f(x, у) определена и ограничена на кривой АВ.
Разобьем кривую АВ произвольно на п частей точками 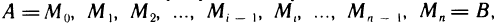
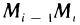
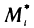
где 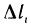
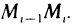
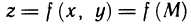
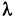
Определение:
Если интегральная сумма (1) при 
В этом случае функция f (x, у) называется интегрируемой вдоль кривой АВ, сама кривая АВ — контуром интегрирования, А — начальной, а В — конечной точками интегрирования.
Криволинейный интеграл первого рода легко сводится к определенному интегралу. Действительно, приняв на кривой АВ за параметр длину дуги 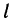
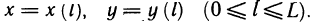
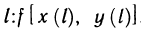
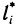
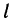
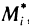
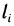
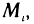
где 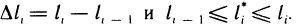
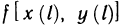
Заметим, что формула (3) не только выражает криволинейный интеграл через определенный, но и доказывает существование криволинейного интеграла от функции f (х, у), непрерывной вдоль рассматриваемой кривой АВ.
Как было показано, криволинейный интеграл первого рода непосредственно сводится к определенному, однако между этими понятиями имеется следующее различие. В интегральной сумме (1) величины 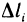
в то время как определенный интеграл 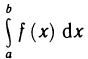
Криволинейный интеграл первого рода, так же как и определенный, имеет геометрический смысл. Если определенный интеграл 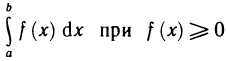
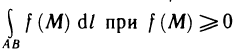
В частности, если АВ — не кривая, а отрезок прямой [а, b], расположенный на оси Ох, то 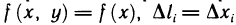
Наконец, если положить 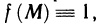
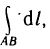
Таким образом, с помощью криволинейного интеграла первого рода можно вычислять площадь цилиндрических поверхностей и длины дуг. Кроме этого, криволинейный интеграл первого рода имеет широкое применение в физике. С его помощью можно, как это делали в случае двойных интегралов, находить массу материальной кривой по ее плотности, моменты инерции относительно координатных осей, координаты центра масс такой кривой и т. д.
Вычисление криволинейных интегралов первого рода
Вычисление криволинейных интегралов первого рода сводится к вычислению определенных интегралов.
Пусть кривая АВ задана параметрически уравнениями 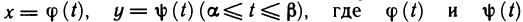
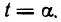
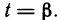
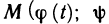
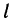
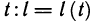
откуда, согласно правилу дифференцирования интеграла по верхнему пределу,
Заменяя переменную 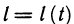
Пример:
Вычислить криволинейный интеграл 
где АВ — часть окружности
Решение:
Так как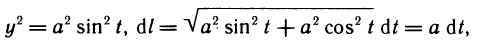
то по формуле (5) получаем
В частности, если кривая АВ задана уравнением у=у(х), 
Пример:
Вычислить криволинейный интеграл
где АВ — дуга параболы 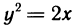
Имеем 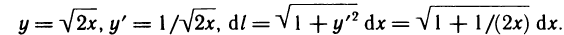
Замечание:
Формула (4) представляет самостоятельный интерес. Возводя в квадрат, получаем: 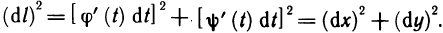
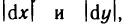
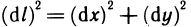
Определение криволинейного интеграла второго рода
Пусть на кривой АВ определены две ограниченные функции 
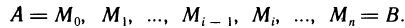
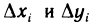
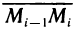
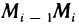
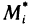
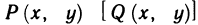
Определение:
Если интегральная сумма (7) при 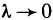
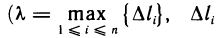
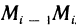
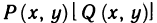
Сумму
называют общим криволинейным интегралом второго рода и обозначают символом
Криволинейные интегралы второго рода, как и интегралы первого рода, легко сводятся к определенным интегралам.
Действительно, пусть кривая АВ задана параметрически уравнениями 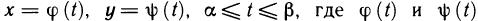
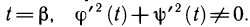
Р (х, у) и Q (х, у) непрерывны вдоль кривой АВ. Тогда справедливы следующие формулы: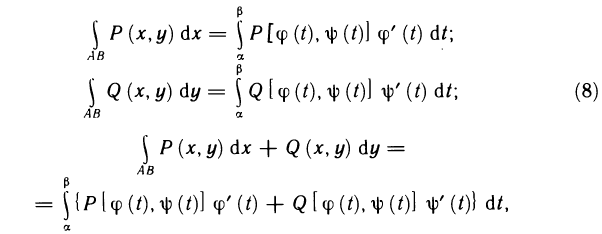
Докажем первую из формул (8):
вторая формула доказывается аналогично, а третья получается в результате сложения первой и второй.
Пусть точкам 
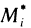
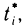
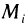
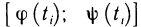
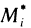
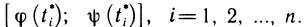
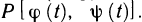
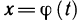
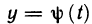
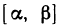
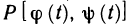
Составим интегральную сумму (7) для функции Р (х, у):
Так как 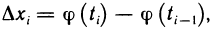
С другой стороны, так как функция 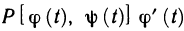
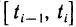
Рассмотрим и оценим разность
Из непрерывности функции 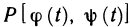
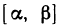
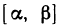
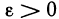
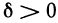
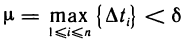
Из непрерывности функции 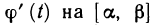
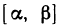
Используя (11) и (12), получаем для разности (10) следующую оценку:
Отсюда, в силу произвольности 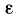
Но при 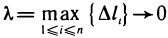
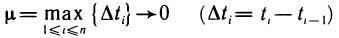
Из непрерывности функций 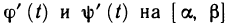
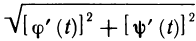
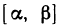
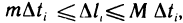
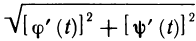
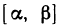
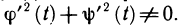




т. е. существует криволинейный интеграл 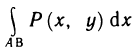
Криволинейный интеграл второго рода обладает свойствами, аналогичными свойствам определенного интеграла, что непосредственно вытекает из формул (8).
В отличие от криволинейного интеграла первого рода криволинейный интеграл второго рода зависит от того, в каком направлении (от А к В или от В к А) проходится кривая АВ, и меняет знак при изменении направления обхода кривой, т. е.
Действительно, изменив направление обхода кривой, мы соответственно изменим знаки проекций 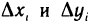
Таким образом, при вычислении криволинейных интегралов второго рода необходимо учитывать направление интегрирования.
В случае, когда L замкнутая кривая, т. е. когда точка В совпадает с точкой А, из двух возможных направлений обхода замкнутого контура L условимся называть положительным то направление, при котором область, лежащая внутри этого контура, остается слева по отношению к точке, совершающей обход. Противоположное направление обхода контура L условимся называть отрицательным.
Криволинейный интеграл по замкнутому контуру L, пробегаемому в положительном направлении, часто обозначают символом
Вычисление криволинейных интегралов второго рода
Криволинейные интегралы второго рода вычисляют сведением их к определенным интегралам по формулам (8).
В частности, если кривая АВ задана уравнением вида 
Аналогичные формулы имеют место, если кривая АВ задана уравнением вида х=х(у).
Пример:
Вычислить интеграл 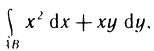
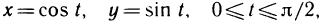
Решение:
Имеем 
Пример:
Вычислить интеграл 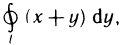
Решение:
На рис. 183 положительное направление обхода контура L обозначено стрелками. Разбивая весь контур интегрирования на части, запишем:
Легко заметить, что интегралы вдоль участков АВ и CD равны нулю, так как на них у является постоянным и, следовательно, dу=0. Поэтому остается вычислить интегралы по участкам ВС и DA. По формуле, аналогичной первой из формул (14) [заменяя 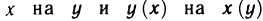
Таким образом, окончательно имеем
Пример:
Вычислить интеграл 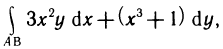

По третьей формуле (14) имеем:
Заметим, что взяв три различных пути, соединяющих одни и те же точки, мы получили три одинаковых результата. Это обстоятельство не является случайным. Причина его будет раскрыта в § 7.
Связь между криволинейными интегралами первого и второго рода
Обозначим через 
Заменяя в криволинейных интегралах второго рода dх и dу их выражениями (15), преобразуем эти интегралы в криволинейные интегралы первого рода:
Таким образом, формулы (16) выражают криволинейные интегралы второго рода через криволинейные интегралы первого рода и устанавливают связь между ними. При изменении направления движения точки по кривой на противоположное 
В заключение заметим, что были рассмотрены криволинейные интегралы для плоских кривых. Однако их определение и свойства нетрудно перенести и на пространственные кривые.
Пусть АВ — пространственная кривая и на этой кривой определены функции 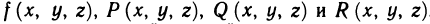
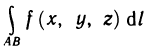
Техника вычисления таких интегралов не отличается по существу от техники вычисления интегралов по плоской кривой.
Формула Грина
Формула Грина устанавливает связь между криволинейными и двойными интегралами. Она имеет широкое применение как в самом анализе, так и в его приложениях.
Докажем эту формулу для замкнутой области, граница которой пересекается с прямыми, параллельными осям координат, не более чем в двух точках. Для краткости будем называть такие области простыми: Предполагается, что контур, ограничивающий область, гладкий или кусочно-гладкий.
Теорема:
Пусть G — некоторая простая замкнутая область, ограниченная контуром L, и пусть функции Р (х, у) и Q (х, у) непрерывны вместе со своими частными производными 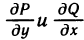
называемая формулой Грина.
Доказательство:
Пусть контур L, ограничивающий область G, может быть задан как уравнениями 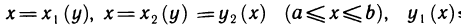
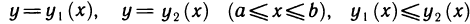
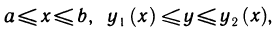
в криволинейный. Для этого сведем его к повторному интегралу и по формуле Ньютона—Лейбница выполним интегрирование по у. Получим
Каждый из этих двух определенных интегралов равен криволинейному интегралу второго рода, взятому по соответствующей кривой (см. формулы (14), § 5), а именно:
Таким образом, 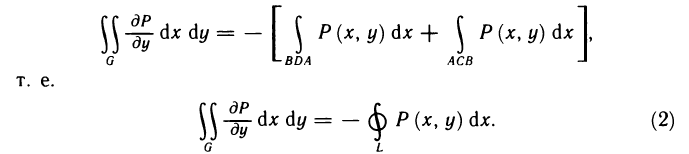
при этом область G задается неравенствами
Вычитая из равенства (3) почленно равенство (2), получаем искомую формулу (1).
Замечание. Формула Грина остается справедливой для всякой замкнутой области G, которую можно разбить проведением дополнительных линий на конечное число простых замкнутых областей. Действительно, пусть область G с границей L имеет вид, изображенный на рис. 187. Разобьем ее на две простые области 
Пример:
С помощью формулы Грина вычислить криволинейный интеграл 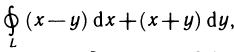
Решение:
Функции 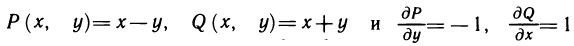
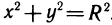
Следовательно, по теореме 13.6 формула Грина применима к данному интегралу. Имеем 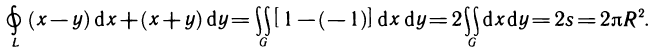
Условия независимости криволинейного интеграла от пути интегрирования
Как уже отмечалось при решении примера 5 (см. § 5, п. 4), в некоторых случаях величина криволинейного интеграла 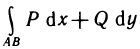
Определение:
Плоская область G называется односвязной, если каков бы ни был замкнутый контур L, лежащий внутри этой области, ограниченная этим контуром часть плоскости целиком принадлежит области G.
Образно говоря, односвязность области означает, что область не имеет «дыр». Например, односвязными областями являются внутренность круга, эллипса, многоугольника и т. п. Простейшим примером неодносвязной области служит область, заключенная между окружностями 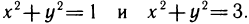
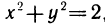
Теорема:
Пусть функции Р (х, у) и Q (х, у) определены и непрерывны вместе со своими частными производными 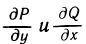
1) для любой замкнутой кусочно-гладкой кривой L, расположенной в G,
2) для любых двух точек А и В области G значение интеграла
не зависит от выбора пути интегрирования, целиком лежащего в G;
3) выражение 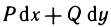
4) в области G всюду
Доказательство:
Доказательство теоремы проведем по схеме
т. е. покажем, что из первого условия следует второе, из второго — третье, из третьего — четвертое, а из четвертого — снова первое. Тем самым будет доказана эквивалентность всех условий.
Первый этап: 
Второй этап: 
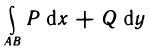
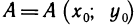
то этот интеграл будет некоторой функцией координат х и у точки В=В(х; у):
Покажем, что функция F (х, у) дифференцируема и что
Для этого достаточно доказать, что в каждой точке В области существуют частные производные 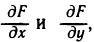
Так как Р (х, у) и Q (х, у) непрерывны в G, то из (3) следует дифференцируемость функции F (х, у) и равенство (2).
Для доказательства существования частной производной функции F (х, у) по х и первого из равенства (3) составим частное приращение по х функции F(х, у) в точке В (х; у): 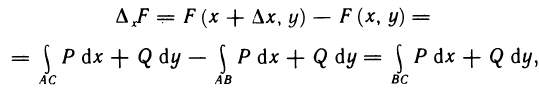
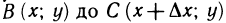
Применяя к последнему интегралу теорему о среднем, получаем 
Третий этап: 
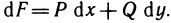
и по теореме о равенстве смешанных производных
т. е. получено требуемое равенство (1).
Четвертый этап: 
В силу условия 4) интеграл справа равен нулю. Следовательно,
для всякого замкнутого контура L, лежащего в области G.
Замечание:
Из эквивалентности условий 1) — 4) теоремы 13.7, в частности, следует, что условие 3) представляет собой необходимое и достаточное условие, при котором криволинейный интеграл не зависит от выбора пути интегрирования. Однако для приложений более удобным, необходимым и достаточным условием является условие 4).
Теорема 13.7 позволяет легко решать вопрос о том, зависит или не зависит криволинейный интеграл от выбора пути интегрирования. Так, например, 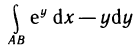
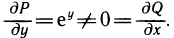
где L — окружность радиуса R с центром в начале координат. Имеем:
Видим, что условие независимости интеграла от выбора пути формально выполнено, но, однако, интеграл по окружности L нулю не равен. Действительно, задав окружность уравнениями 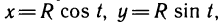
На самом деле никакого противоречия с теоремой здесь нет. Просто не выполнено одно из условий теоремы: функции Р и Q и их частные производные 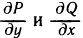
Интегрирование полных дифференциалов
Из рассмотрения условий независимости криволинейного интеграла 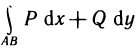
Было доказано, что если функции Р (х, у) и Q (x, у) и их частные производные 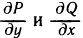
является полным дифференциалом некоторой функции в этой области в том и только в том случае, когда 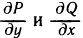
Далее мы показали, что если это равенство выполнено, то условию
удовлетворяет функция
Пусть теперь выражение (1) является полным дифференциалом некоторой функции Ф (х, у). Тогда 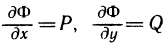
где С — некоторая постоянная. Полагая 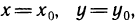
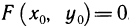
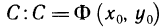
а равенство (2) — в виде
Если, наконец, положить 
Формула (4) аналогична формуле Ньютона—Лейбница, несправедлива только при условии независимости криволинейного интеграла от выбора пути интегрирования.
Используя полученные результаты, теперь можно указать способ восстановления функции F (х, у), полный дифференциал которой есть заданное выражение (1).
Формула
где 
Для отыскания F (x, у) по формуле (5) достаточно, выбрав любую точку 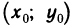
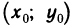
Так как 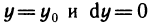
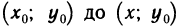
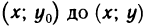
где первый определенный интеграл вычисляется при постоянном у, равном 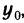
Пример:
Проверить, является ли выражение 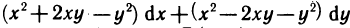
Решение. В данном выражении функции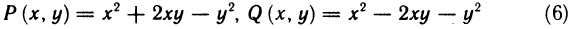
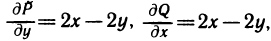
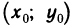
В данном случае за точку А 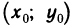
Учитывая, что криволинейный интеграл 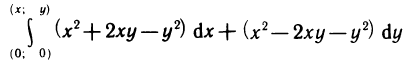
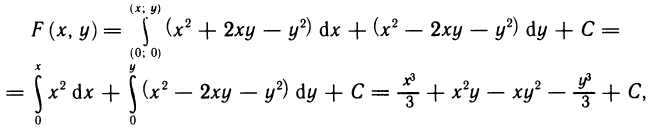
Практически при отыскании функции по ее полному дифференциалу удобно поступать следующим образом. Если
то, интегрируя первое из этих равенств по х, получаем
а интегрируя второе равенство по у, имеем
где 
Так, например, пусть 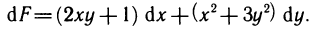
интегрируя коэффициент при dy по у, имеем
Правые части равенств (9) и (10) совпадают, если положить 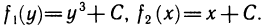
Пример:
Вычислить криволинейный интеграл
Решение:
В данном случае функции
непрерывны и частные производные равны между собой. Значит, выражение уdх+хdу является полным дифференциалом dF (х, у) и данный интеграл не зависит от пути интегрирования. По формулам (7) и (8) находим F (х, у)=ху, и по формуле (4) получаем
Заметим, что данный интеграл можно вычислить и непосредственно, если, например, взять в качестве пути интегрирования ломаную, соединяющую точки (— 1; 2), (2; 2) и (2; 3), звенья которой параллельны осям координат (проделайте самостоятельно).
Некоторые приложения криволинейных интегралов второго рода
Криволинейные интегралы второго рода, так же как и первого рода, имеют широкое применение в геометрии, физике и технике. Ограничимся рассмотрением двух задач: вычислением площадей плоских фигур и определением работы силы.
Вычисление площади с помощью формулы Грина
Пусть G — некоторая область с границей L и s — площадь этой области. Известно, что двойной интеграл
выражает площадь области G. Поэтому если в формуле Грина подобрать функции Р(х,у) и Q(x,y) таким образом, чтобы 
Положим 
Полагая 
а при 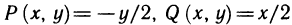
Таким образом, получены три формулы для вычисления площадей плоских фигур, ограниченных контуром L.
Пример:
Найти площадь фигуры, ограниченной эллипсом. Решение. Вычислим, например, площадь по формуле (1). Используя параметрические уравнения эллипса 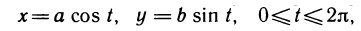
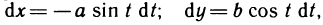
Работа силы
Известно, что работа, совершаемая переменной силой F (х), направленной вдоль оси Ох, по перемещению материальной точки вдоль оси Ох из точки х=а в точку 
(гл. 6, § 8, п. 6). Рассмотрим более общую задачу.
Пусть материальная точка под действием силы 
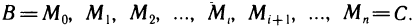
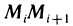
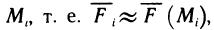
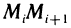
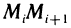
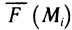
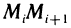
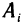
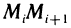
Правая часть этого приближенного равенства представляет собой скалярное произведение двух векторов 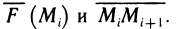
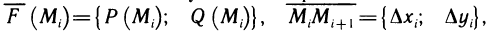
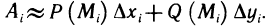
За точное значение работы А принимается предел, к которому стремится ее приближенное значение при стремлении к нулю наибольшей из длин дуг 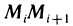
Р (х, у) и Q (х, у), заданных на кривой ВС. По определению пределом этой суммы является криволинейный интеграл второго рода.
Следовательно, работа силы определяется по формуле
где Р и Q — координаты (или проекции на оси координат) силы 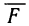
Если рассмотреть данную задачу не на плоскости, а в пространстве, то решение ее сводится к вычислению криволинейного интеграла второго рода по пространственной кривой по формуле
Пример:
Вычислить работу силы 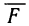
Решение:
По условию, 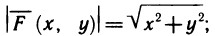
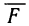
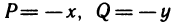
Следовательно,
Заметим, что из того, что интеграл оказался равным нулю, следует, что подынтегральное выражение является полным дифференциалом некоторой функции (найдите эту функцию самостоятельно).
Тройные интегралы
В начале главы было введено понятие двойного интеграла от функции двух переменных. Определим интеграл от функции трех переменных — так называемый тройной интеграл. Тройные интегралы, как и двойные, имеют широкое применение в различных физических и геометрических задачах.
Определение тройного интеграла
Тройной интеграл является аналогом двойного интеграла и вводится для функции трех переменных.
Пусть в некоторой замкнутой ограниченной области V трехмерного пространства задана ограниченная функция 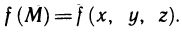
В каждой области возьмем произвольную точку 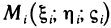
которая называется интегральной суммой для функции f (x, у, z) по области V. Обозначим через 
Определение:
Если интегральная сумма (1) при 
В этом случае функция f (x, у, z) называется интегрируемой в области V; V — областью интегрирования; х, у и z — переменными интегрирования; 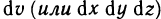
В дальнейшем, поскольку результаты, полученные для двойных интегралов, вместе с их доказательствами могут быть перенесены на тройные интегралы, ограничимся только формулировками утверждений и краткими пояснениями.
Тройные интегралы являются непосредственным обобщением двойных интегралов на случай трехмерного пространства. Они обладают аналогичными двойным интегралам необходимыми и достаточными условиями существования и свойствами. Если положить всюду в области 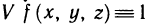
Вычисление тройных интегралов
Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов меньшей кратности.
Рассмотрим область V, ограниченную снизу и сверху поверхностями 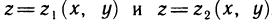
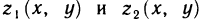
позволяющая свести вычисление тройного интеграла к последовательному вычислению внутреннего определенного интеграла по переменной z (при постоянных х и у) и внешнего двойного интеграла по области G.
Выражение
представляет собой функцию двух переменных. Если для этой функции и области G, по которой она интегрируется, выполнены условия теоремы 13.4, то, переходя от двойного интеграла
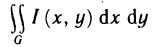
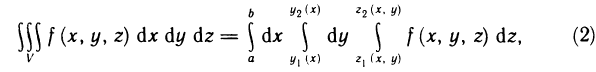
В частности, если V— параллелепипед с гранями 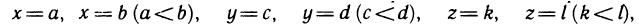
В этом случае интегрирование можно производить в любом порядке.
Пример:
Вычислить интеграл 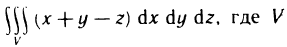
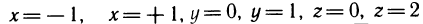
Решение. По формуле (3) имеем
Пример:
Вычислить интеграл 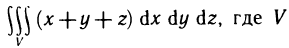
Решение. Область V проектируется на плоскость Оху в треугольник G, ограниченный прямыми х=0 у=0, у=1-х. По формуле (2) имеем
Замена переменных в тройном интеграле
Как для двойных интегралов, так и для тройных имеют место формулы перехода от прямоугольных координат к новым системам координат, наиболее употребительными из которых являются цилиндрические и сферические координаты.
Замену переменных в тройном интеграле производят по следующему правилу.
Если ограниченная замкнутая область V пространства (х, у, z) взаимно однозначно отображается на область V* пространства 
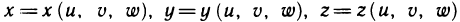
В частности, при переходе от прямоугольных координат х, у, z к цилиндрическим координатам 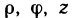
якобиан преобразования J=р, поэтому
Название цилиндрические координаты связано с тем, что координатная поверхность p=const (т. е. поверхность, все точки которой имеют одну и ту же координату р) является цилиндром, прямолинейные образующие которого параллельны оси Oz.
При переходе от прямоугольных координат х, у, z к сферическим координатам 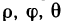
якобиан преобразования 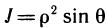
Название «сферические координаты» связано с тем, что координатная поверхность р=const (т. е. поверхность, все точки которой имеют одну и ту же координату р) является сферой. Сферические координаты иначе.- называют полярными координатами в пространстве.
При вычислении тройного интеграла путем перехода к цилиндрическим или сферическим координатам область V* обычно не изображают, а пределы интегрирования расставляют непосредственно по виду области V, используя геометрический смысл новых координат.
Пример:
Вычислить интеграл 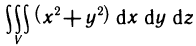
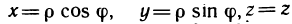
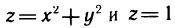
Решение:
Так как область V на плоскость Оху проектируется в круг 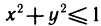
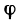
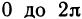
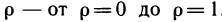
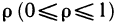
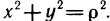
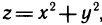
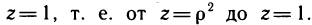
Трудно дать какую-либо общую рекомендацию, когда следует применять ту или иную систему координат. Это зависит и от области интегрирования, и от вида подынтегральной функции. Однако, например, формулой (5) удобнее пользоваться, когда f (х, у, г.z) имеет вид 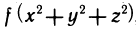
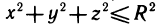
Пример:
Вычислить интеграл 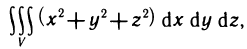
Решение:
В данном случае удобно перейти к сферическим координатам: 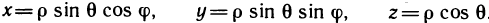
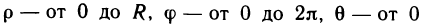
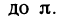
Некоторые приложения тройных интегралов
Кратко рассмотрим типичные задачи применения тройных интегралов, ограничившись приведением необходимых формул, так как их вывод аналогичен выводу соответствующих формул в случае двойных интегралов.
Если дано некоторое тело V с плотностью p(M)=p(x, у, z), представляющей собой непрерывную функцию, то тройной интеграл
представляет собой массу m данного тела.
Моменты инерции тела V с плотностью р(М)=р(x, у, z) относительно осей координат определяются следующими формулами:
Момент инерции относительно начала координат
Координаты центра масс определяются следующими формулами: 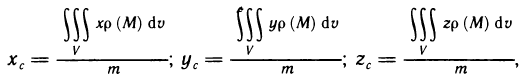
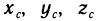
р (х, у, z)=const, то выражения для координат центра масс упрощаются и принимают вид
где 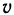
Как уже было отмечено, тройной интеграл 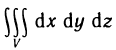
Тройные интегралы в некоторых случаях более удобны для вычисления объемов, чем двойные, так как с их помощью можно вычислить объем не только криволинейного цилиндра, но и других тел.
Пример:
Определить координаты центра масс верхней половины однородного шара V радиуса R с центром в начале координат.
Решение:
Данный полушар ограничен поверхностями 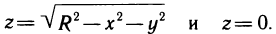
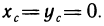
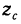
Переходя к сферическим координатам, получаем
Поверхностные интегралы
В этом параграфе рассмотрены интегралы от функций, заданных на поверхности, так называемые поверхностные интегралы.
Теория поверхностных интегралов во многом аналогична теории криволинейных интегралов. Различают поверхностные интегралы первого и второго рода.
Определение поверхностного интеграла первого рода
Пусть в точках некоторой поверхности S гладкой или кусочно-гладкой определена ограниченная функция 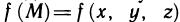
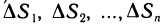
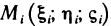
Сумма (1) называется интегральной суммой для функции f (M) по поверхности S. Обозначим через 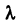
Определение:
Если интегральная сумма (1) при 
В этом случае функция f (х, у, z) называется интегрируемой по поверхности S, S — областью интегрирования.
Данное определение по сути аналогично определению двойного интеграла. Поэтому свойства двойных интегралов и условия их существования без особых изменений переносятся на поверхностные интегралы.
В частности, если 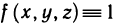
где s — площадь поверхности S, т. е. с помощью поверхностного интеграла первого рода можно вычислять площади поверхностей.
Кроме того, с их помощь!о можно определять массы, статические моменты, моменты инерции, координаты центра масс и подобные величины для материальных поверхностей с известной поверхностной плотностью распределения масс. Эти задачи решаются аналогично соответствующим задачам для случая материальной кривой, материальной плоской и пространственной области.
Вычисление поверхностных интегралов первого рода
Вычисление поверхностного интеграла первого рода производится сведением поверхностного интеграла к двойному.
Пусть поверхность S задана уравнением z=z(x, у), где функция z(x, у) вместе с производными 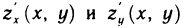
Разобьем поверхность S произвольно на n частей и спроектируем это разбиение на плоскость Оху. Получим соответственно разбиение области G на части 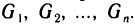
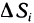
Применяя к двойному интегралу теорему о среднем, получаем
где 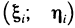
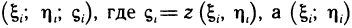
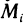
В правой части равенства находится интегральная сумма для двойного интеграла от непрерывной в области G функции 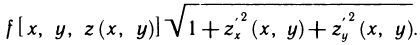

Так как функция f (x, у, z) интегрируема по поверхности S, то предел левой части (3) при 
Следовательно, переходя к пределу в (3) при 
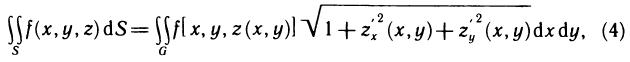
Аналогично получаются формулы, выражающие интеграл по поверхности S через двойные по ее проекциям на плоскости Оуz и Oxz.
Пример:
Вычислить интеграл 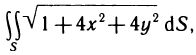
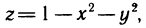
Решение. Поверхность S, заданная уравнением 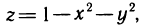
Следовательно, областью G является круг 
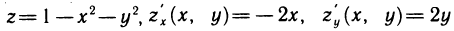
Переходя в полученном двойном интеграле к полярным координатам 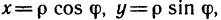
Определение поверхностного интеграла второго рода
Введем предварительно понятие стороны поверхности.
Возьмем на гладкой поверхности S произвольную точку М и проведем через нее нормаль к поверхности (вектор 
Если обход по любому замкнутому контуру, лежащему на поверхности S и не пересекающему ее границы, при возвращении в исходную точку не меняет направления нормали к поверхности, то поверхность называется двусторонней.
Примерами двусторонних поверхностей служат плоскость, сфера, любая поверхность, заданная уравнением z=f (x, у), где 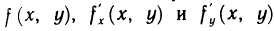
Если же на поверхности S существует замкнутый контур, при обходе которого направление нормали меняется после возвращения в исходную точку на противоположное, то поверхность называется односторонней.
Простейшим примером односторонней поверхности служит лист Мёбиуса, изображенный на рис. 205. Его можно получить, взяв полоску бумаги ABCD и склеив ее так, чтобы точка А совпала с точкой С, а точка В — с точкой D, т. е. повернув перед склеиванием один из ее краев на 180°. При обходе листа Мёбиуса по его средней линии и возвращении в исходную точку направление нормали меняется на противоположное.
В дальнейшем рассматриваются только двусторонние поверхности. Для двусторонней поверхности совокупность всех ее точек с выбранным в них направлением нормали, изменяющимся непрерывно при переходе от точки к точке, называется стороной поверхности, а выбор определенной ее стороны — ориентацией поверхности. Двустороннюю поверхность называют также ориентируемой, а одностороннюю — неориентируемой.
С понятием стороны поверхности тесно связано понятие ориентации ее границы.
Пусть S — ориентированная (сторона уже выбрана) поверхность, ограниченная контуром L, не имеющим точек самопересечения. Будем считать положительным направлением обхода контура L то, при движении по которому наблюдатель, расположенный так, что направление нормали совпадает с направлением от ног к голове, оставляет поверхность слева от себя (рис. 206). Противоположное направление обхода называется отрицательным. Если изменить ориентацию поверхности, т. е. изменить направление нормали на противоположное, то положительное и отрицательное направления обхода контура L поменяются ролями.
Перейдем теперь к определению поверхностного интеграла второго рода.
Пусть S — гладкая поверхность, заданная уравнением 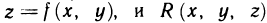
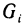
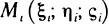
где 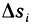
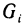
Определение:
Если интегральная сумма (5) при 
В этом случае функция R (х, у, z) называется интегрируемой по поверхности S по переменным х и у.
Аналогично определяется поверхностный интеграл второго рода по выбранной стороне поверхности S по переменным у и z [z и x] от функции 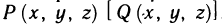
называют общим поверхностным интегралом второго рода и обозначают символом
Поверхностный интеграл второго рода обладает такими же свойствами, как и поверхностный интеграл первого рода, но в отличие от последнего при изменении стороны поверхности (переориентации) он меняет знак.
К понятию поверхностного интеграла второго рода приводит, например, задача о потоке векторного поля, которая будет рассмотрена в $ 14.
Для односторонней поверхности понятие поверхностного интеграла второго рода не вводится.
Вычисление поверхностных интегралов второго рода
Поверхностные интегралы второго рода вычисляют сведением их к двойным интегралам.
Пусть ориентированная (выберем верхнюю сторону) гладкая поверхность S задана уравнением z=f( x, у), где функция f (x, у) определена в замкнутой области G — проекции поверхности S на плоскость Оху, a R (х, у, z) — непрерывная функция на поверхности S.
Разобьем поверхность S произвольно на п частей и спроектируем это разбиение на плоскость Оху (рис. 207). Область G разобьется соответственно на части 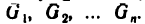
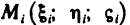
где 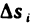
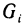
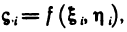
В правой части равенства находится интегральная сумма для двойного интеграла от непрерывной в области G функции
R [x, у, f(x, у)]. Переходя к пределу в (7) при 
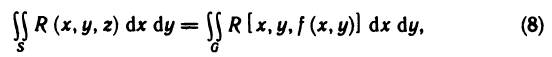
Аналогично устанавливается справедливость следующих формул:
где поверхность S задана соответственно уравнением x=f(y, z) и
y=f(x, z), a 
Для вычисления интеграла общего вида (6) используют те же формулы (8) — (10), если поверхность S однозначно проектируется на все три координатные плоскости. В более сложных случаях поверхность S разбивают на части, обладающие указанными свойствами, а интеграл (6) — на сумму интегралов по этим частям.
Пример:
Вычислить интеграл 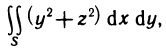
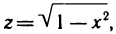
Решение:
Проекцией G данной поверхности на плоскость Оху является прямоугольник, определяемый неравенствами 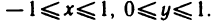
Пример:
Вычислить интеграл 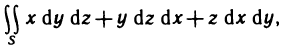
у=0, у=4 и лежащая в первом октанте (рис. 209).
Решение:
По определению,
Здесь 
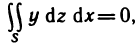
так как плоскость S параллельна оси Оу. По формулам (8) и (9) соответственно находим
Следовательно,
Связь между поверхностными интегралами первого и второго рода
Поверхностные интегралы второго рода можно ввести и другим способом, а именно как поверхностные интегралы первого рода, в которых под знаком интеграла стоят некоторые специальные выражения. Обозначим через 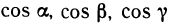
1. поверхностный интеграл второго рода для плоскости Оху от функции R(x, у, z) выражается через поверхностный интеграл первого рода с помощью следующей формулы:
2. поверхностный интеграл второго рода для плоскости Oxz от функции Q (х, у, z) выражается через поверхностный интеграл первого рода с помощью следующей формулы:
3. поверхностный интеграл второго рода для плоскости Oyz от функции Р(х, у, z) выражается через поверхностный интеграл первого рода с помощью следующей формулы:
Суммируя формулы (11) — (13), получаем формулу, выражающую поверхностный интеграл второго рода общего вида по выбранной стороне поверхности через поверхностный интеграл первого рода:
Если выбрать другую сторону поверхности, то направляющие косинусы нормали 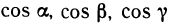
Пример:
Вычислить интеграл 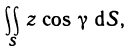
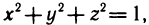
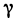
Решение:
По формуле (11), связывающей поверхностные интегралы обоих типов, имеем
Проекцией G данной поверхности S на плоскость Оху является круг 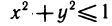
Переходя в двойном интеграле к полярным координатам, находим
Формула Остроградского
Формула Остроградского устанавливает связь между поверхностным интегралом по замкнутой поверхности и тройным интегралом по пространственной области, ограниченной этой поверхностью. Эта формула является аналогом формулы Грина, которая, как известно, связывает криволинейный интеграл по замкнутой кривой с двойным интегралом по плоской области, ограниченной этой кривой. Формула Остроградского имеет широкое применение как в самом анализе, так и в его приложениях.
Выведем эту формулу для замкнутой пространственной области, граница которой пересекается с любой прямой, параллельной осям координат, не более чем в двух точках. Назовем для краткости такие области простыми. При этом будем рассматривать внешнюю сторону поверхности, ограничивающей эту область. Предполагается, что поверхность гладкая или кусочно-гладкая.
Теорема:
Пусть V — простая замкнутая область, ограниченная поверхностью S и пусть функции Р (х, у, z), Q (х, у, z) и R (х, у, z) непрерывны вместе со своими частными производными первого порядка в данной области. Тогда имеет место следующая формула: 
Доказательство:
Пусть область G — проекция поверхности S (и области V) на плоскость Оху (рис. 211), a 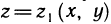
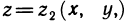
Преобразуем тройной интеграл
в поверхностный. Для этого сведем его к повторному интегралу и по формуле Ньютона—Лейбница выполним интегрирование по z. Получим
Так как область G является проекцией на плоскость Оху и поверхности 
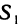
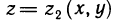
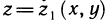
Меняя в интеграле по 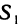
где S — внешняя сторона поверхности, ограничивающей область V.
Аналогично доказываются формулы
Складывая почленно равенства (2), (3), (4), приходим к формуле (1). ■
Замечание:
Формула Остроградского верна для любой замкнутой пространственной области V, которую можно разбить на конечное число простых областей. В самом деле, применяя формулу (1) к каждой из областей разбиения и складывая результаты, получаем в левой части равенства тройной интеграл по всей области V, а в правой — поверхностный интеграл по поверхности S, ограничивающей область V, так как поверхностные интегралы по вспомогательным поверхностям берутся дважды по противоположным сторонам и при суммировании взаимно уничтожаются.
С помощью формулы Остроградского удобно вычислять поверхностные интегралы по замкнутым поверхностям.
Пример:
Вычислить интеграл
где S — внешняя сторона пирамиды, ограниченной плоскостями 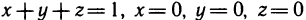
Решение:
Используя формулу Остроградского, получаем
Пример:
Вычислить интеграл
где S — внешняя сторона сферы
Решение:
Применяя формулу Остроградского, имеем
Как было отмечено (§ 9, п. 1), формула Грина выражает площадь области через криволинейный интеграл по ее границе. Точно также из формулы Остроградского легко получить выражение для объема области в виде поверхностного интеграла по замкнутой поверхности S — границе этой области. Действительно, подберем функции Р, Q и R так, чтобы
Тогда получим
где 
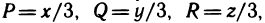
Формула Стокса
Формула Стокса устанавливает связь между поверхностным и криволинейным интегралами. Подобно формулам Грина и Остроградского, формулу Стокса широко применяют как в самом анализе, так и в его приложениях.
Пусть S — поверхность, заданная уравнением z=z(х, у), где функции 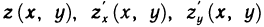
Теорема:
Если функция Р (х, у, z) непрерывна вместе со своими частными производными первого порядка на поверхности S, то имеет место следующая формула:
где 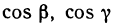
Доказательство:
Преобразуем криволинейный интеграл
взятый по контуру L, в интеграл по поверхности S. Это преобразование проведем по следующей схеме:
т. е. криволинейный интеграл по пространственному контуру L преобразуем сначала в криволинейный интеграл по плоскому контуру l, затем переведем его в двойной интеграл по области G и, наконец, этот последний интеграл преобразуем в интеграл по поверхности S.
Так как контур L лежит на поверхности S, то координаты его точек удовлетворяют уравнению z=z(x, у) и поэтому значения функции Р (х, y, z) в точках контура L равны значениям функции Р [х, у, z(x, у)] в соответствующих точках контура l, являющегося проекцией L. Проекции же соответствующих участков разбиения контуров L и l на ось Ох совпадают. Поэтому совпадают также интегральные суммы для криволинейных интегралов второго рода от функции Р по контурам L и l, а значит, равны и интегралы:
Далее, применяя формулу Грина, перейдем к двойному интегралу по области G. Получаем
Здесь подынтегральная функция равна частной производной по у от сложной функции, получающейся из Р (х, у, z) после подстановки
z (x, у) вместо z.
Поскольку s — верхняя сторона поверхности, т. е. 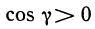
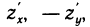
Теперь, воспользовавшись формулами (8) и (11) из § 11, можно этот двойной интеграл преобразовать в поверхностный. Получаем
Аналогично доказывается при соответствующих условиях справедливость следующих двух формул:
Складывая почленно равенства (1), (2), (3), получаем формулу
которая называется формулой Стокса.
С помощью формулы, связывающей поверхностные интегралы, (14) из § 11 формулу Стокса можно переписать в следующем виде:
Формулу Стокса легко запомнить, заметив, что первое слагаемое в правой ее части это то же самое выражение, которое стоит под знаком двойного интеграла в формуле Грина, а второе и третье получаются из него циклической перестановкой координат х, у, z и функций Р, Q, R.
В частности, если поверхность S — область плоскости Оху, ограниченная контуром L, то интегралы по dzdx и dydz обращаются в нуль и формула Стокса переходит в формулу Грина.
Формула Стокса позволяет вычислять криволинейные интегралы по замкнутым контурам с помощью поверхностных интегралов.
Пример:
Вычислить с помощью формулы Стокса интеграл
где L — окружность, заданная уравнениями 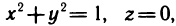
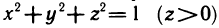
Решение:
Так как 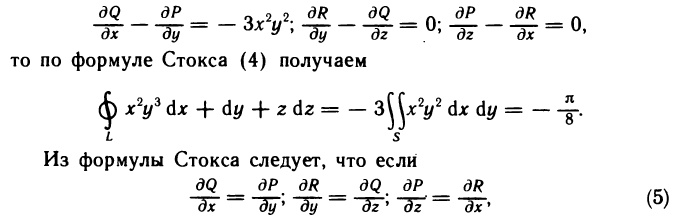
А это значит, что в данном случае криволинейный интеграл не зависит от выбора пути интегрирования.
Как и в случае плоской кривой, условия (5) являются необходимыми и достаточными для выполнения равенства (6).
При выполнении условий (5) или (6) подынтегральное выражение 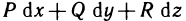
Справедливость этого равенства устанавливается так же, как соответствующая формула (4) из § 8 для функции двух переменных.
Скалярное и векторное поля
Понятие поля лежит в основе многих представлений современной физики. Изучение теории поля выходит за рамки данного курса, поэтому ограничимся только краткими сведениями.
В общем случае говорят, что в пространстве задано поле некоторой величины u, если в каждой точке пространства (или некоторой его части) определено значение этой величины. Так, например, при изучении потока газа приходится исследовать несколько полей: температурное поле (в каждой точке температура имеет определенное значение), поле давлений, поле скоростей и т. д.
Поле величины u называется стационарным (или установившимся), если и не зависит от времени t. В противном случае поле называется нестационарным (или неустановившимся). Таким образом, величина u есть функция точки М и времени t.
В физических задачах чаще всего приходится иметь дело со скалярными и векторными величинами. В соответствии с этим различают два вида полей: скалярные и векторные. Для простоты будем считать их стационарными.
Скалярное поле
Пусть G — некоторая область на плоскости или в пространстве. Если в каждой точке М из G определена скалярная величина u, то говорят, что в области G задано скалярное поле. Понятия скалярного поля и функции, определенной в области G, совпадают. Обычно используют следующую терминологию: скалярное поле задается с помощью функции u=F(M), которая называется скалярной функцией. Если в пространстве ввести систему координат Oxyz, то каждая точка М будет иметь определенные координаты х, у, z и скалярная величина и является функцией этих координат: u=F(М)= F(х, у, z).
Примером скалярного поля может служить поле температур воздуха в некотором помещении, если температуру рассматривать как функцию точки. В точках, расположенных ближе к источнику теплоты, температура выше, дальше от источника теплоты — ниже.
Если окажется, что температура везде одинаковая, то в этом случае скалярное поле постоянно.
Векторное поле
Аналогично с понятием скалярного поля вводится понятие векторного поля: если в каждой точке М из G определен вектор 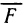
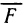
Примером векторного поля может служить поле сил любой природы. Каждой точке области соответствует определенный вектор, имеющий числовую величину и направление силы в этой точке.
Пример:
Найти векторное поле скоростей 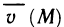
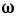
Решение:
Скорость 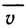
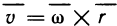
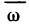
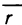
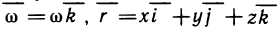
— искомое векторное поле.
Потенциальное поле
Введем понятие потенциального поля. Рассмотрим некоторое скалярное поле F(М). Если в каждой точке М из G определен вектор grad F, то поле этого вектора называется потенциальным полем. Само скалярное поле называется при этом потенциалом векторного поля, а вектор, определяющий потенциальное поле, часто называют потенциальным вектором, т. е. вектор 
Возникает вопрос, при каких условиях данное векторное поле 
В силу соотношения (1) векторное поле 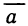
В теореме 13.7 было показано, что выражение 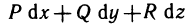
Но если 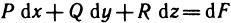
т. е. условие (3) как раз и означает, что данное векторное поле потенциальное. Функция F (х, у, z) в этом случае называется потенциальной функцией поля.
Примером потенциального поля служит поле сил тяготения. Если в начале координат помещена масса т, то эта масса создает поле сил тяготения; в каждой точке М пространства на помещенную в эту точку единичную массу по закону Ньютона действует сила 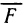
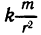
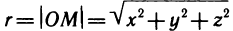
Пусть х, у, z — координаты точки М. Тогда проекции Р, Q и R силы 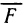
где 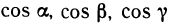
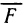
Можно проверить, что данное векторное поле потенциальное и его потенциальная функция
В заключение найдем работу силы 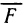
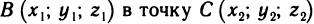
Как известно, работа А выражается криволинейным интегралом
где Р, Q и R — проекции силы 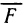
т. е. работа силы 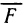
где 
Заметим, что областью, в которой определено поле сил тяготения, является все пространство, за исключением начала координат.
Задача о потоке векторного поля
Пусть в пространстве задано векторное поле 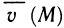
где Р, Q и R — проекции скорости на оси координат. Пусть Р, Q и R — непрерывные функции координат. Вычислим количество П жидкости, протекающей за единицу времени через некоторую ориентированную поверхность S, ограниченную пространственной кривой L, считая плотность жидкости
Пусть 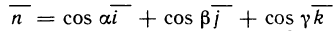
Разобьем поверхность S произвольно на n частей с площадями 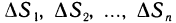
Найдем количество П, жидкости, протекающей за единицу времени через i-ю часть поверхности (рис. 213). Обозначим через 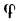
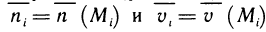
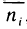
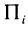
Приближенно можно считать, что при достаточно мелком разбиении поверхности S скорость 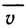
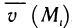
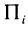
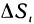
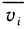
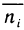
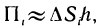
Суммируя по i от l до n, получаем приближенное значение количества П жидкости, протекающей через ориентированную поверхность S за единицу времени:
Сумма справа является интегральной суммой для функции 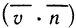
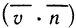
или, выражая скалярное произведение через координаты векторов,
Воспользовавшись формулой (14) из § 11, связывающей поверхностные интегралы первого и второго рода, окончательно имеем
Таким образом, количество П жидкости, протекающей за единицу времени через ориентированную поверхность S, представляет собой поверхностный интеграл второго рода по выбранной стороне поверхности.
Для произвольного векторного поля 
Дивергенция
Пусть в некоторой области V, ограниченной поверхностью S, задано векторное поле 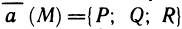
Определение:
Дивергенцией векторного поля 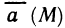
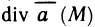
Используя выражение для дивергенции и понятие потока вектора через поверхность, формулу Остроградского (см. формулу (1), § 12) можно записать в более компактной векторной форме. Поверхностный интеграл в формуле Остроградского представляет собой поток вектора 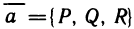
Используя это выражение и формулу (5), запишем формулу Остроградского в виде
Таким образом, поток вектора 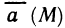
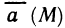
Покажем, что дивергенция не зависит от выбора системы координат, хотя ее определение и было с ней связано. Для этого возьмем произвольную точку Л1, заключим ее в область V, ограниченную поверхностью S, и применим к области V формулу Остроградскаго. Далее, используя теорему о среднем для тройного интеграла, получаем
где 
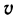
Будем теперь стягивать область V в точку М. При этом 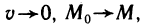
т. е. дивергенция векторного поля 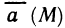
Выясним теперь с помощью формулы (7) физический смысл дивергенции. Для этого будем рассматривать векторное поле 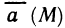
вектора 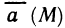
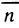
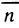
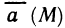
Оно представляет собой среднюю плотность источников (или стоков), т. е. количество жидкости, возникающей (или исчезающей) за единицу времени в единице объема области V, а предел
при условии, что область V стягивается в точку М, можно назвать плотностью источников (или стоков) в точке М. Но этот предел равен 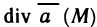
Если 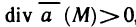
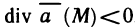
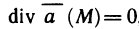
Для произвольного векторного поля 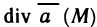
Векторное поле 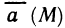
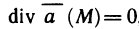
Пример:
Вычислить дивергенцию поля скоростей 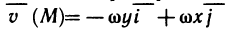
Решение. Здесь 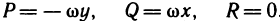
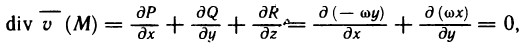
Циркуляция. Ротор
Пусть снова в некоторой области задано векторное поле
и L — гладкая или кусочно-гладкая кривая, расположенная в этой области. Выберем на кривой L одно из двух направлений движения и обозначим через 
Тогда криволинейный интеграл от скалярного произведения векторов 
называется циркуляцией векторного поля 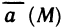
Определение:
Ротором векторного поля 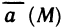
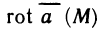
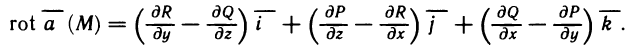
Таким образом, циркуляция векторного поля 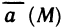
Так же как и для дивергенции, можно показать, что 
Пример:
Вычислить ротор поля скоростей 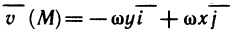
Решение:
Используя определение ротора, получаем
т. е. ротор данного векторного поля направлен по оси вращения Oz, а по модулю равен удвоенной угловой скорости.
Понятие ротора непосредственно связано с понятием потенциального поля. Было показано, что векторное поле 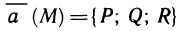
Но это означает, равенство нулю всех трех координат ротора поля 
Оператор Гамильтона
Основные понятия теории поля: градиент, дивергенция, ротор и операции над ними удобно представлять с помощью оператора Гамильтона, или оператора «набла»:
Оператор 
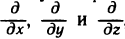
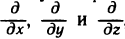
Основные понятия теории поля: градиент, дивергенция, ротор и операции над ними удобно представлять с помощью оператора Гамильтона, или оператора «набла»:
Оператор 
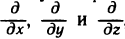
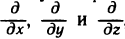
Примеры:
1. Пусть u (x, у, z) — скалярная функция. Тогда произведение оператора 
2. Пусть 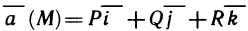

3. Векторное произведение оператора 
В приложениях часто встречаются так называемые операции второго порядка, т. е. попарные комбинации трех указанных выше операций. Рассмотрим наиболее важные из них.
в силу равенства смешанных производных второго порядка. Этот же результат легко получить с помощью оператора 
так как здесь имеем смешанное произведение трех «векторов»: 
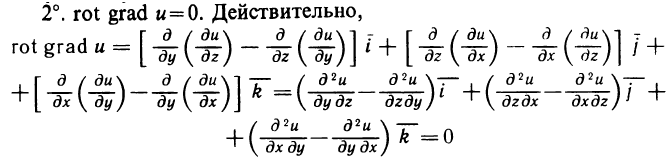

так как векторное произведение одинаковых «векторов» равно нулю.
Правая часть равенства (8) символически обозначается так:
называется оператором Лапласа*. Оператор Лапласа 

Поэтому равенство (8) с помощью оператора 
называется уравнением Лапласа. С его помощью описываются стационарные процессы различной физической природы, например: стационарное распределение теплоты, электростатическое поле точечных зарядов, установившееся движение несжимаемой жидкости внутри некоторой области и т. д. Скалярное поле u (х, у, z), удовлетворяющее условию 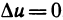
Дополнение к интегрированию
Смотрите также:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат