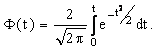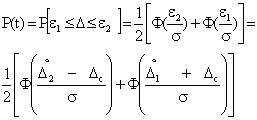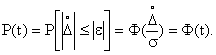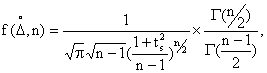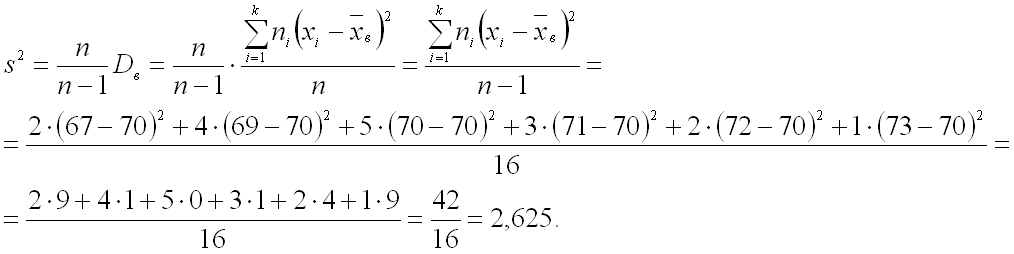Абсолютная
погрешность.
Начнем
с простого примера.
Пусть
диаметр болта, измереный штангенциркулем,
оказался равным 14 мм. Можно ли быть
уверенным, что он пройдет в
“идеальное”отверстие того же диаметра?
Если бы этот вопрос был поставлен в
чисто ”математическом“ виде, то ответ
был бы утвердительным: пройдет “в
притирочку”. На практике может получится
иначе. Диаметр равный 14 мм был получен
с помощью реального прибора у которого
есть погрешности. Так что было бы
правильней говорить, что мы получили
приближенное значение диаметра — . Каково
же его истинное значение? На этот вопрос
ни один человек не сможет дать ответ.
Максимально что можно сделать в этой
ситуации, это указать границы около
приближенного результата, внутри которых
находится истинное значение диаметра.
Эта граница называется границей
абсолютной погрешности и обозначается
(е¸ так же часто называют просто абсолютной
погрешностью). Так что в нашем примере
болт может как пройти в отверстие, так
и не пройти в него: все зависит от того,
в каком месте интервала находится
истинное значение диаметра. На рисунке
1 показан случай, когда болт в отверстие
не пройдет.
¨ще
раз подчеркнем: абсолютная погрешность
показывает, насколько неизвестное
экспериментатору истинное значение
измеряемой величины может отличаться
от измеренного значения. Результат
измерения записывают так:
Относительная
погрешность.
Граница
абсолютной погрешности не в полной мере
характеризует результат измерения.
Пусть, например, в результате измерений
установлено, что длина стола равна см,
а толщина его крышки см. Хотя граница
абсолютной погрешности измерений в
этих двух случаях одинакова ясно, что
качество измерений в первом случае
выше.
Качество
измерений характеризуется относительной
погрешностью , равной отношению абсолютной
погрешности к значению величины ,
получаемой в результате измерения: .
Так
как погрешности возникают при любых
измерениях, то сначала их систематизируем.
При проведении практических работ
выделяют следующие виды погрешностей:
а)
погрешности прямых измерений;
б)
погрешности косвенных измерений;
в)
случайные погрешности;
г)
систематические погрешности.
Начнем
с ними разбираться по порядку.
2.
Погрешности прямых измерений
Прямое
измерение.
Это
такое измерение, в котором результат
находится непосредственно в процессе
считывания со шкалы (или показаний
цифрового прибора). В нашем первом
примере речь шла как раз о таком измерении.
Если
вы умеете правильно пользоваться
измерительным прибором, то погрешность
прямого измерения (обозначается значком
) зависит только от его качества и
складывается из инструментальной
погрешности прибора — и погрешности
отсчета -. Таким образом =+
Инструментальная
погрешность определяется на
заводе-изготовителе. Например, динамометр
для лабораторных работ имеет погрешность
= 0,05 H, амперметр и вольтметр для
лабораторных работ — =0,05 А и = 0,15 В
соответственно.
Инструментальные
погрешности электроизмерительных
приборов.
Если
во время выполнения работы приходится
пользоваться электроизмерительными
приборами, не указанными в таблице 1, то
инструментальную погрешность прибора
можно определить следующим способом.
Каждый
электроизмерительный прибор в зависимости
от качества изготовления имеет
определенный класс точности. Значение
класса точности наносится на его шкалу
(изображается числом в кружке), который
позволяет определить погрешность этого
прибора. Пусть, класс точности
миллиамперметра 4, а предел измерения
этим прибором равен 250 мА; тогда абсолютная
инструментальная погрешность прибора
составляет 4% от 250 мА, т.е. =10 мА.
4.
СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
Часто
при проведении повторных измерений
какой-либо величины получаются несколько
различные результаты, отличающиеся
друг от друга больше, чем сумма погрешностей
прибора и отсчета. Это вызвано действием
случайных факторов, которые невозможно
устранить в процессе эксперимента.
Пусть
мы определяем дальность полета шарика,
пущенного из баллистического пистолета
в горизонтальном направлении.
Даже
при неизменных условиях эксперимента
шарик не будет попадать в одну и ту же
точку поверхности стола.( Это связано
с тем, что шарик имеет не совсем правильную
форму, на боек ударного механизма при
движении в канале пистолета действует
сила трения, изменяющаяся по величине,
положение пистолета в пространстве не
совсем жестко зафиксировано и т.д.)
Такой
разброс результатов происходит
практически всегда при выполнении серии
экспериментов.
В
этом случае за приближенное значение
измеряемой величины берут среднее
арифметическое.
Причем,
чем больше будет проведено экспериментов,
тем ближе будет среднее арифметическое
к истинному значению измеряемой величины.
Но
и среднее арифметическое, вообще говоря,
не совпадает с истинным значением
измеряемой величины. Как же найти границу
интервала, в котором находится истинное
значение? Эта граница называется границей
случайной погрешности — . В теории расчета
погрешностей показывается, что , где
— значения физической величины в 1, 2,…n
опыте
Погрешность
среднего арифметического.
Когда
мы находим среднее арифметическое
значение величины по результатам серии
опытов, то естественно считать, что оно
имеет меньшее отклонение от истинного
значения, чем каждый опыт серии. Другими
словами, погрешность среднего меньше,
чем погрешность каждого опыта серии. В
теории погрешностей доказывается, что
граница погрешности среднего значения
равна:
.
Окончательно имеем:
.
Из
формулы следует, что граница случайной
погрешности среднего значения стремится
к нулю при увеличении числа опытов в
серии. Это не значит, однако, что можно
проводить абсолютно точные измерения
ведь приборы, с помощью которых мы
получили результаты, также имеют
погрешности. Поэтому погрешность
среднего при бесконечном увеличении
числа опытов стремится к погрешности
прибора.
Очевидно,
что число опытов имеет смысл выбрать
таким, чтобы случайная погрешность
среднего сравнялась с погрешностью
прибора либо стала меньше ее. Дальнейшее
увеличение числа измерений теряет
смысл, так как не увеличит точность
получаемого результата: , где — граница
погрешности измерительного прибора.
Если
нет возможности по каким-либо причинам
провести достаточное количество опытов
(т.е. не удалось сделать погрешность
среднего равной погрешности приборов),
то результат должен быть взят в виде: ,
где — граница случайной погрешности
среднего.
Соседние файлы в папке измерения
- #
- #
- #
- #
Доверительный интервал и доверительная вероятность
Наряду с точечными широко применяют интервальные оценки числовых характеристик случайных величин, выражающеся границами интервала, внутри которого с определенной вероятностью заключено истинное значение результата измерения. Вероятность того, что погрешность не выйдет за границы некоторого интервала, определяется по площади, ограниченной кривой распределения и границами этого интервала, отложенными по оси абсцисс (квантилями), что показано на рис. 1.10.
Рис.1.10.
Таким образом, интервал , за границы которого погрешность не выйдет с некоторой вероятностью, называется доверительным интервалом, а характеризующая его вероятность — доверительной вероятностью. Границы этого интервала называются доверительными значениями погрешности. При измерениях можно задаваться доверительным интервалом и по нему определять доверительную вероятность, либо, наоборот, по доверительной вероятности подсчитывать доверительный интервал. Чем больше доверительная вероятность, тем шире доверительный интервал; поэтому на практике обычно выбирают доверительную вероятность 0,95 и даже 0,90.
Доверительный интервал обычно выражают через относительную величину в долях среднего квадратического отклонения (“кратность”)
. Для нормального закона доверительную вероятность
определяют по значениям интеграла вероятности (функции Лапласа), который в математической справочной литературе обозначается
и определяется
Зная доверительные границы и
можно определить доверительную вероятность
Если значения доверительных границ и
симметричны, т.е.
, то
и
.
Тогда
Для наиболее часто встречающихся значений доверительной вероятности в табл. 1.3 указаны соответствующие значения кратности. Таблица 1.3
|
P(t) |
0,90 |
0,95 |
0,99 |
0,999 |
|
t |
1,645 |
1,960 |
2,576 |
3,291 |
При нормальном законе распределения доверительный интервал имеет доверительную вероятность
=0,9973, что означает, что из 370 случайных погрешностей только одна по абсолютному значению будет больше
. На основании этого основан один из критериев грубых погрешностей, когда остаточная погрешность какого-либо результата измерения превышает значение
, то этот результат считается промахом и исключается из ряда измерений.
Пример. Для известного числа измерений получены значения
и
. Определить вероятность того, что имеет место неравенство 1,26
1,28.
Так как , то
0,01/0,025=0,4. Используя таблицу интеграла вероятности, находим
. Следовательно, около 30% общего числа измерений будут иметь случайную погрешность
, не превышающую ±0,01.
Распределение Стьюдента
При малом числе повторных измерений 20 используется распределение случайных погрешностей, предложенное Стьюдентом. Плотность вероятности по этому закону зависит от значения случайной погрешности
и от числа измерений:
где (
,
)-плотность вероятности случайной погрешности при заданном числе измерений
;
-гамма-функция;
s=
/
— коэффициент Стьюдента (“кратность” случайной погрешности).
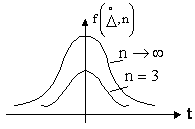
На рис.1.11 показаны графики кривых распределения случайных погрешностей по закону Стьюдента для двух значений . При
→∞ распределение Стьюдента совпадает с нормальным, а при
20 всё более и более от него отличается.
Доверительный интервал и доверительная вероятность
s также зависят от числа измерений. Соответствующие значения
s при заданном значении
и
приводятся в таблицах.
Рис.1.11
Коэффициент Стьюдента s определяется из соотношения
s=
=
,где
-СКО ряда измерений,
-доверительный интервал.
Пример. Для числа измерений =6 среднее арифметическое значения
=35,4, а СКО ряда наблюдений.
Определить доверительную вероятность
s , если
отличается от истинного значения
на величину доверительного интервала
т.е. 35,2
≤35,6.
Определим коэффициент Стьюдента s=
=
.По таблицам распределения Стьюдента находим
= 0,9. Следовательно, случайная погрешность
результата измерения в 90% случаев не выйдет за пределы доверительного интервала.
Доверительный интервал
Что такое доверительный интервал:
Это оценка диапазона, используемого в статистике, который содержит параметр совокупности. Этот неизвестный параметр популяции находится в выборочной модели, рассчитанной на основе собранных данных .
Пример: среднее значение выборки x̅ может соответствовать или не соответствовать истинному среднему значению для населения µ. Для этого можно рассмотреть диапазон выборочных средств, в которых может содержаться это среднее значение. Чем длиннее этот интервал, тем больше вероятность этого.
Доверительный интервал выражается в процентах, обозначенных уровнем достоверности, причем 90%, 95% и 99% являются наиболее указанными. Например, на изображении ниже мы имеем 90% доверительный интервал между его верхним и нижним пределами (a и -a ).

Доверительный интервал является одним из наиболее важных понятий в рамках проверки гипотез в статистике, поскольку он используется в качестве меры неопределенности. Термин был введен польским математиком и статистиком Ежи Нейманом в 1937 году.
Какова актуальность доверительного интервала?
Доверительный интервал важен для указания границы неопределенности (или неточности) в сравнении с выполненными расчетами. Этот расчет использует выборку исследования для оценки фактического размера результата в исходной популяции.
Расчет доверительного интервала — это стратегия, которая учитывает выборку ошибок. Размер результата вашего исследования и ваш доверительный интервал характеризуют предполагаемые значения для исходной популяции.
Чем уже доверительный интервал, тем больше вероятность того, что процент исследуемой совокупности представляет реальное число исходной совокупности, что дает большую уверенность в отношении результата исследуемого объекта.
Как интерпретировать доверительный интервал?
Правильная интерпретация доверительного интервала, вероятно, является наиболее сложным аспектом этой статистической концепции. Примером наиболее распространенной интерпретации концепции является следующее:
Существует 95% вероятность того, что в будущем истинное значение параметра совокупности (например, среднее значение) попадет в диапазон X (нижний предел) и Y (верхний предел).
Таким образом, доверительный интервал интерпретируется следующим образом: он на 95% уверен, что интервал между X (нижняя граница) и Y (верхняя граница) содержит истинное значение параметра совокупности.
Было бы совершенно неверно утверждать, что: существует 95% вероятность того, что интервал между X (нижняя граница) и Y (верхняя граница) содержит реальное значение параметра совокупности.
Вышеприведенное утверждение является наиболее распространенным заблуждением о доверительном интервале. После расчета статистического диапазона он может содержать только параметр совокупности или нет.
Тем не менее, интервалы могут варьироваться между выборками, в то время как истинный параметр популяции одинаков независимо от выборки.
Следовательно, доверительный интервал доверительного интервала может быть сделан только в случае, когда доверительные интервалы пересчитываются для количества выборок.
Этапы расчета доверительного интервала
Диапазон рассчитывается с использованием следующих шагов:
- Соберите пример данных: n ;
- Рассчитать среднее значение выборки x̅;
- Определить, является ли стандартное отклонение популяции ( σ ) известным или неизвестным;
- Если стандартное отклонение популяции известно, z- точка может использоваться для соответствующего уровня достоверности;
- Если стандартное отклонение популяции неизвестно, мы можем использовать статистику t для соответствующего уровня достоверности;
- Таким образом, нижний и верхний пределы доверительного интервала находятся по следующим формулам:
а) Стандартное отклонение известной популяции :
Формула для расчета стандартного отклонения известной совокупности.
б) стандартное отклонение неизвестной популяции :
Формула для расчета стандартного отклонения неизвестной популяции.
Практический пример доверительного интервала
Клиническое исследование оценило связь между наличием астмы и риском развития обструктивного апноэ сна у взрослых.
Некоторые взрослые были случайным образом набраны из списка государственных служащих, за которыми следили в течение четырех лет.
Участники с астмой, по сравнению с теми, у кого нет, имели более высокий риск развития апноэ через четыре года.
При проведении клинических исследований, подобных этому примеру, подмножество интересующей группы населения обычно привлекается для повышения эффективности исследования (меньше затрат и меньше времени).
Эта подгруппа лиц, изучаемая популяция, состоит из тех, кто соответствует критериям включения и согласен участвовать в исследовании, как показано на рисунке ниже.

Затем исследование завершается и рассчитывается величина эффекта (например, средняя разница или относительный риск ), чтобы ответить на вопрос исследования.
Этот процесс, называемый выводом, включает использование данных, собранных у исследуемой совокупности, для оценки величины фактического воздействия на представляющую интерес совокупность, то есть совокупность происхождения.
В приведенном примере исследователи набрали случайную выборку государственных служащих (исходная популяция), которые имели право и согласились участвовать в исследовании (исследуемая популяция), и сообщили, что астма увеличивает риск развития апноэ в исследуемой популяции.
Чтобы учесть ошибку выборки из-за набора только подгруппы представляющего интерес населения, они также рассчитали 95% доверительный интервал (около оценки) от 1, 06 до 1, 82, что указывает на вероятность 95 %, что истинный относительный риск в исходной популяции будет между 1, 06 и 1, 82 .
Доверительный интервал для среднего
Когда у человека есть информация о стандартном отклонении населения, он может рассчитать доверительный интервал для среднего или среднего значения этого населения.
Когда измеряемая статистическая характеристика (например, доход, IQ, цена, рост, количество или вес) является числовой, в большинстве случаев оценивается, что найдено среднее значение для населения.
Таким образом, мы пытаемся найти среднее значение популяции ( μ ), используя среднее значение выборки ( x̅ ), с пределом погрешности. Результат этого расчета называется доверительным интервалом для среднего населения .
Когда стандартное отклонение популяции известно, формула для доверительного интервала (CI) для среднего значения популяции:
где:
- х̅ — среднее значение по выборке;
- σ — стандартное отклонение населения;
- n — размер выборки;
- Ζ * представляет подходящее значение стандартного нормального распределения для желаемого уровня достоверности.
Ниже приведены значения для различных уровней достоверности ( Ζ * ):
| Уровень доверия | Значение Z * — |
|---|---|
| 80% | 1:28 |
| 90% | 1.645 (обычный) |
| 95% | 1, 96 |
| 98% | 2:33 |
| 99% | 2:58 |
В таблице выше приведены значения z * для предоставленных уровней достоверности. Обратите внимание, что эти значения получены из стандартного нормального распределения (Z-).
Область между каждым значением z * и отрицательным значением этого значения является (приблизительным) процентом достоверности. Например, область между z * = 1, 28 и z = -1, 28 составляет приблизительно 0, 80. Следовательно, эта таблица также может быть расширена до других доверительных процентов. В таблице указаны только наиболее часто используемые проценты доверия.
Смотрите также значение гипотезы.
Тема
«Оценка истинного
значения измеряемой величины«
Примеры
решения задач
Пример 1.
После проведения независимых равноточных измерений физической величины получена
следующая совокупность данных:
|
|
67 |
69 |
70 |
71 |
72 |
73 |
|
|
2 |
4 |
5 |
3 |
2 |
1 |
Необходимо оценить истинное
значение измеряемой величины с надежностью .
Решение.
Будем рассматривать результаты
отдельных измерений как нормально распределенные случайные величины, имеющие
одно и то же математическое ожидание
(истинное значение измеряемой величины) и одинаковые средние квадратические
отклонения ,
причем последнее значение ( )
считаем неизвестным.
Следовательно, для оценки истинного значения измеряемой величины при неизвестном
необходимо найти доверительный интервал, покрывающий неизвестный параметр
с заданной надежностью :

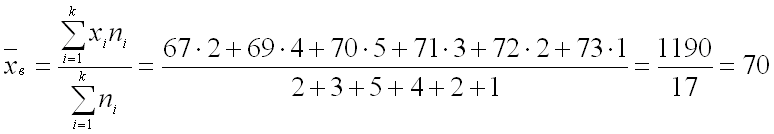
По известным
на основе таблицы найдем .
Найдем границы доверительного интервала:
Ответ:
с надежностью
истинное значение измеряемой величины заключено в интервале .
Функция ДОВЕРИТ в Excel предназначена для определения доверительного интервала для среднего значения, найденного для генеральной совокупности, которая имеет нормальное распределение.
Другими словами, рассматриваемая функция позволяет определить допустимые отклонения для найденного среднего значения с учетом известных уровня значимости (заданная вероятность того, что некоторое значение находится в доверительном интервале) и стандартного отклонения (меры степени разброса значений относительно среднего значения для генеральной совокупности).
Как построить доверительный интервал нормального распределения в Excel
Поскольку интервал значений, в котором находится некоторая неизвестная величина, совпадает с областью, в которой могут изменяться значения этой величины, то вероятность правильности оценки данной величины стремится к нулю. Поэтому, принято устанавливать определенное значение вероятности для нахождения границ изменения некоторой величины. Значения, находящиеся между этими границами, называют доверительным интервалом.
Примечание:
Рассматриваемая функция была заменена функцией ДОВЕРИТ.НОРМ с версии Excel 2010. Функция ДОВЕРИТ была оставлена для обеспечения совместимости с документами, созданными в более ранних версиях табличного редактора.
Пример расчета доверительного интервала в Excel
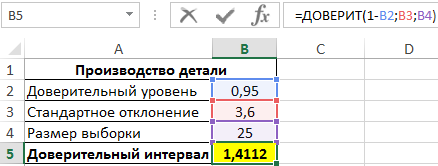
Пример 1. В заводском цехе производят деталь, длина которой должна составлять 200 мм. Стандартное отклонение от длины – 3,6 мм. Для контроля качества деталей из партии (генеральная совокупность) делают выборку из 25 деталей. Определить интервал с доверительный уровнем 95%.
Вид таблицы данных:
Для определения доверительного интервала используем функцию:
=ДОВЕРИТ(1-B2;B3;B4)
Описание параметров:
- 1-B2 – уровень значимости (рассчитан с учетом зависимости от доверительного уровня);
- B3 – значение стандартного отклонения;
- B4 – количество деталей в выборке.
Полученный результат:
То есть, границы доверительного интервала соответствуют: (Xср-1,4112;Xср+1,4112). Допустим, было определено среднее значение выборки – 199,5 мм. Тогда доверительный интервал примерно определяется как (198,1;200,9), при этом номинальная длина детали (200 мм) находится в доверительном диапазоне, то есть производственный процесс не нарушен.
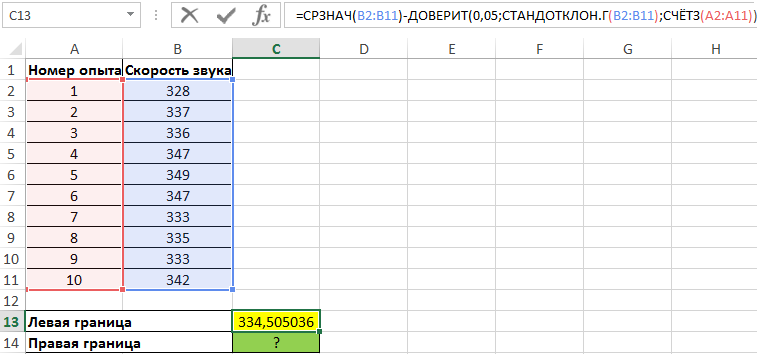
Как найти границы доверительного интервала в Excel
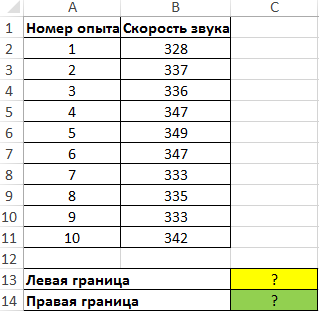
Пример 2. Были проведены опыты по определению скорости распространения звуковой волны в воздухе. Результаты 10 опытов записаны в таблицу. Определить левую и правую границы доверительного интервала для среднего значения.
Вид таблицы данных:
Для нахождения левой границы используем формулу:
В данном случае выборка и генеральная совокупность приняты как имеющиеся данные для 10 проведенных опытов. Среднее выборочное значение рассчитано с помощью функции СРЗНАЧ. Для получения левой границы доверительного интервала из данного значения вычитаем число, полученное в результате выполнения функции ДОВЕРИТ, в которой значение второго аргумента определено с помощью функции СТАНДОТКЛОН.Г, а число опытов – подсчетом количества ячеек функцией СЧЁТЗ.
Поскольку уровень значимости не задан, используем стандартное значение – 0,05.
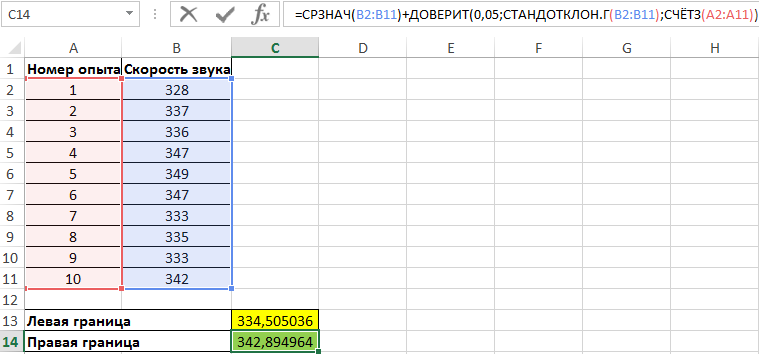
Правая граница определяется аналогично с разницей в том, что к среднему значению выборки прибавляется результат расчета функции ДОВЕРИТ:
Полученные значения:
Как посчитать доверительный интервал по функции ДОВЕРИТ в Excel
Функция имеет следующую синтаксическую запись:
=ДОВЕРИТ(альфа;стандартное_откл;размер)
Описание аргументов:
- альфа – обязательный, принимает числовое значение, характеризующее уровень значимости – вероятность отклонения нулевой (неверной) гипотезы в том случае, когда она на самом деле верна. Определяется как 1-, где — уровень доверия (вероятность нахождения истинного значения некоторой оцениваемой величины в определенном интервале, называемом доверительным).
- стандартное_откл – обязательный, принимает значение стандартного отклонения величины для генеральной совокупности значений (в Excel предусмотрена функция для определения этой величины — СТАНДОТКЛОН.Г).
- размер – обязательный, принимает числовое значение, характеризующее количество точек данных в анализируемой выборке (ее размер).
Примечания:
- Все аргументы функции должны указываться в виде числовых значений или данных, которые могут быть преобразованы в числа (например, текстовые строки с числами, логические ИСТИНА, ЛОЖЬ). В противном случае результатом выполнения функции ДОВЕРИТ будет код ошибки #ЧИСЛО!
- Аргумент альфа должен быть указан числовым значением из диапазона от 0 до 1 (оба включительно). Иначе функция ДОВЕРИТ вернет код ошибки #ЧИСЛО! Аналогичная ошибка возникает в случаях, когда аргумент стандартное_откл задан числом, взятым из диапазона отрицательных значений или нулем.
- Диапазон допустимых значений для аргумента размер – от 1 до бесконечности со знаком плюс.