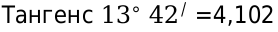Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Тригонометрия в прямоугольном треугольнике
- Тригонометрический круг
- Основное тригонометрическое тождество
- Таблица значений тригонометрических функций
- Градусы и радианы
- Формулы приведения
- Теорема синусов
- Расширенная теорема синусов
- Теорема косинусов
- Тригонометрические уравнения (10-11 класс)
- Примеры решений заданий из ОГЭ
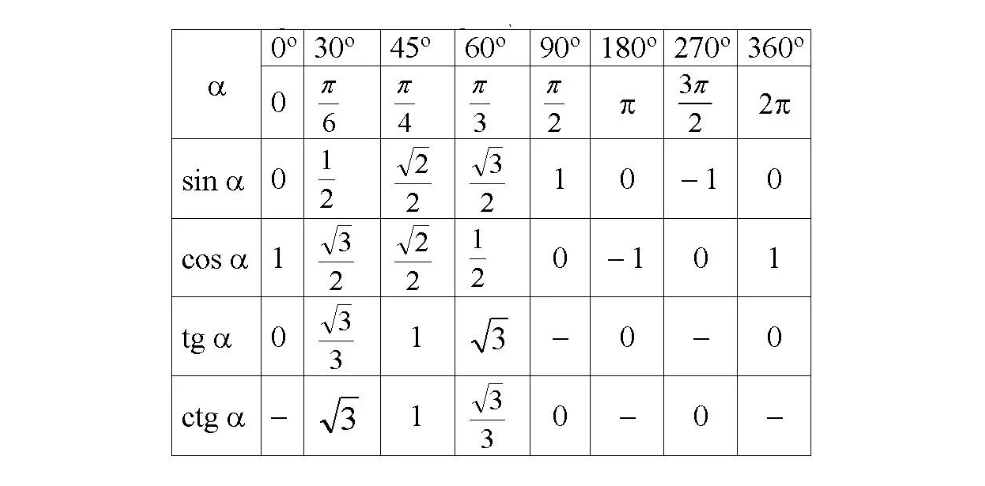
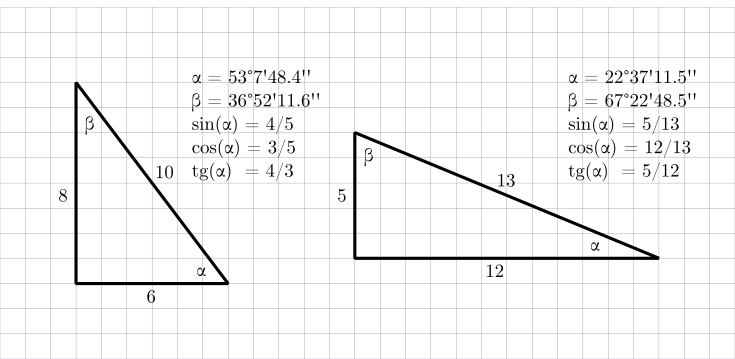
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник ABC, угол C равен 90°:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x, ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x, против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A. Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B) и на ось игрек (точка C).
Отрезок OB является проекцией отрезка OA на ось x, отрезок OC является проекцией отрезка OA на ось y.
Рассмотрим прямоугольный треугольник AOB:
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y. Точка B в этом случае будет иметь отрицательную координату по оси x. Косинус тупого угла отрицательный.
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x. (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y.
Координата по оси x – косинус угла, координата по оси y – синус угла.
Пример:
cos 150 ° = − 3 2
sin 150 ° = 1 2
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный.
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
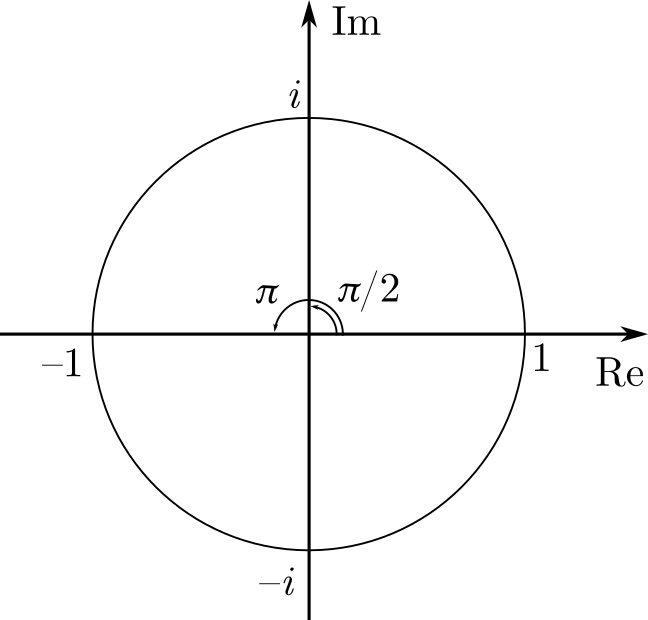
Тригонометрия: Таблица значений тригонометрических функций
| 0° | 30° | 45° | 60° | 90° | |
| sinα | 0 | 12 | 22 | 32 | 1 |
| cosα | 1 | 32 | 22 | 12 | 0 |
| tgα | 0 | 33 | 1 | 3 | нет |
| ctgα | нет | 3 | 1 | 33 | 0 |
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β:
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Скачать домашнее задание к уроку 1.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Тригонометрия простыми словами
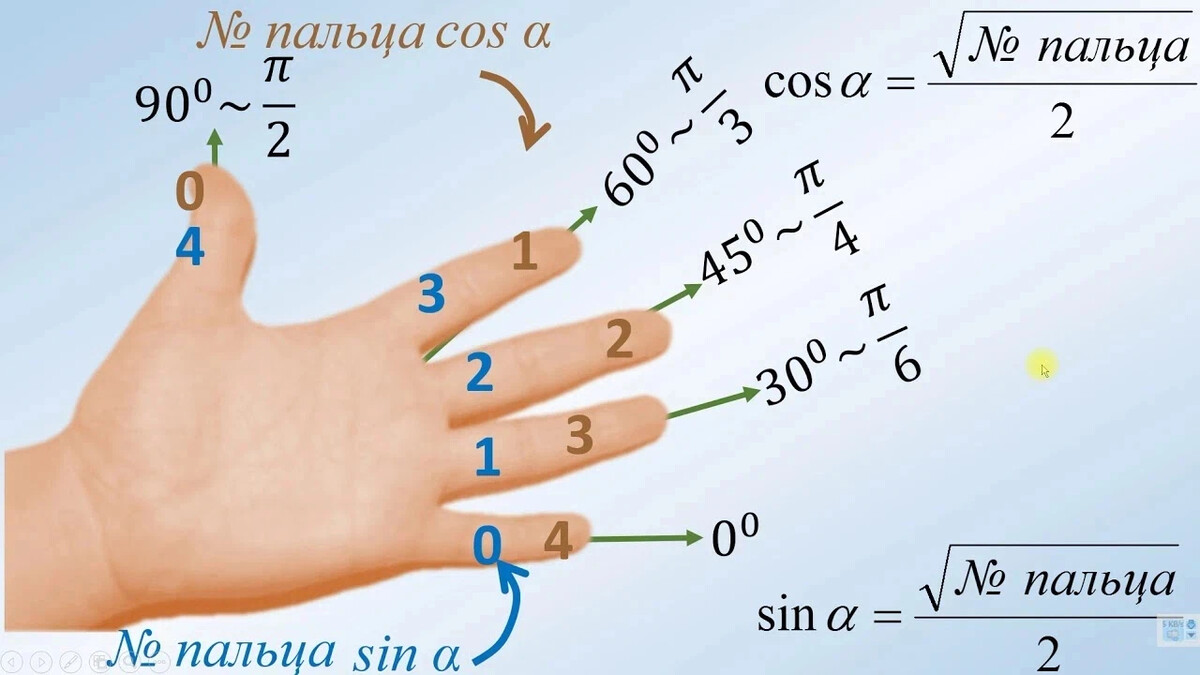
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
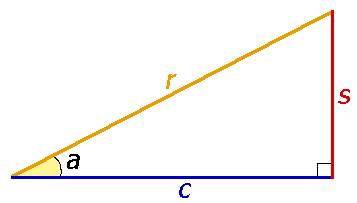
Или в виде формул:
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| sin | 0 |
|
|
|
1 |
| cos | 1 |
|
|
|
0 |
| tg | 0 |
|
1 | √3 | – |
| ctg | – | √3 | 1 |
|
0 |
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.
В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.
Например, значения тригонометрических функций для углов 270° и -90° равны.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.
Тригонометрический круг
Углы в радианах
Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2πr. Следовательно 360° в радианах равно 2π, а 180° равно π радиан.
Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π.
Например, для угла 90° будет
- 90°
- 180°
· π =
- 1
- 2
π
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
 |
Онлайн тренажер
|
Простые тригонометрические тождества
Используя вышеописанные формулы:
тангенс угла выражается через отношение синуса к косинусу:
tg(a) =
- s
- c
=
- sin(a) · r
- cos(a) · r
=
- sin(a)
- cos(a)
;
Соответственно котангенс выражается аналогично:
ctg(a) =
- c
- s
=
- cos(a) · r
- sin(a) · r
=
- cos(a)
- sin(a)
;
Также можно заметить, что произведение тангенса на котангес равно единице:
tg(a) · ctg(a) =
- sin(a)
- cos(a)
·
- cos(a)
- sin(a)
=
- sin(a) · cos(a)
- cos(a) · sin(a)
= 1
Иными словами, тангенс угла обратно пропорционален котангенсу угла и наоборот:
tg(a) · ctg(a) = 1
;
tg(a) =
- 1
- ctg(a)
;
сtg(a) =
- 1
- tg(a)
Используя теорему Пифагора в треугольнике, что сумма квадратов катетов равно квадрату гипотенузы
r2 = s2 + c2 = (sin(a) · r)2 + (cos(a) · r)2;
r2 · (sin(a)2 + cos(a)2) = r2
Сократим обе части на r2, получим:
sin2a + cos2a = 1
Разделив обе части на квадрат синуса или квадрат косинуса, получим еще два основных тригонометрических тождества:
1 + tg2a =
- 1
- cos2a
;
1 + ctg2a =
- 1
- sin2a
Построение тригонометрической окружности
А теперь сделай вот что: возьми-ка в руки циркуль и нарисуй любую (самую любую, но лучше достаточно немаленькую) окружность.
Получилось?
Ну да ладно, задачка не самая сложная. Так, ты не потерял ту точку, в которой у тебя был центр (куда ты прикладывал острую ножку циркуля)? Я вот у себя потерял, растяпа! Ну ладно, найду!
А что пока делать тебе?
А вот что: проведи через эту точку две линии, которые пересекаются «прямым крестиком», то есть под прямым углом. И пусть их точка пересечения – это центр (который ты не потерял!) окружности.
Нарисовал? У меня получилось что-то вроде вот этого.
Правда я чуть-чуть поторопился и сразу «обозвал» эти прямые ( displaystyle x) и ( displaystyle y) и точку пересечения через ( displaystyle O).
А что такое в таком случае ( displaystyle R)?
Это радиус нашей окружности.
Как называлась наша тема? Единичная окружность.
Тогда будем считать ( но не будем так рисовать!), что ( displaystyle R=1 ).
А рисовать мы так не будем, потому что на такой крошечной картинке ты ничего не разберешь! Ты же понимаешь, что когда инженеры проектируют самолеты, скажем, они не рисуют его в натуральную величину?
Так и мы не будем рисовать единичную окружность в самом деле единичной. Это нам нужно исключительно для удобства.
Теперь отмечаем: ( displaystyle OR=1). Что же мы с тобой на самом деле сделали? А вот что:
Мы поместили нашу окружность в систему координат ( displaystyle mathbf{X0Y}), сделав центр окружности началом координат!
Это позволит изучать свойства такой окружности уже не с геометрической, а с математической точки зрения. Этот подход был придуман хитрым математиком и философом Рене Декартом еще в 17 веке!
Перегнать фигуру в цифры, каково, а?
Но допустим, мы поместили нашу окружность в координаты. В скольких точках она пересекается с осями системы координат?
В четырех. Вот они:
Эти точки ( displaystyle left( A; B; C; D right)) имеют координаты:
( displaystyle Aleft( 1,0 right)); ( displaystyle Bleft( 0,1 right)); ( displaystyle Cleft( -1;0 right)); ( displaystyle Dleft( 0;-1 right)).
Теперь вспомни, как называются области, на которые этот «координатный крестик» делит всю плоскость?
Они называются координатные четверти.
Тогда посмотри на рисунок. Наша окружность тоже оказалась разрезанной на 4 равные дольки. Давай пронумеруем каждую из этих долек против часовой стрелки:
Ты уже можешь догадаться, как называются эти самые дольки:
1 четверть, 2 четверть, 3 четверть, 4 четверть
(Прямо как четверти в школе!)
Углы на тригонометрической окружности
Теперь давай сделаем еще вот что. Снова посмотрим на предыдущую картинку.
Чему на ней равен ( displaystyle angle AOB)?
Он равен ( displaystyle 90{}^circ ).
Также, как и ( displaystyle angle BOC), как и угол ( displaystyle angle COD), и угол ( displaystyle angle DOA).
( displaystyle angle text{AOB}=angle text{BOC}=angle text{COD}=angle text{DOA}=90{}^circ )
Тогда чему равна их сумма?
Она равна ( displaystyle 360{}^circ ).
Вместе же эти 4 угла составляют всю окружность целиком!
Градусная мера окружности равна ( displaystyle 360{}^circ )!
( displaystyle angle Atext{OC}=angle text{AOB}+angle text{BOC}=180{}^circ )
Что еще можно вытянуть? А вот что:
( displaystyle angle Atext{OD}=angle text{AOB}+angle text{BOC}+angle text{COD}=270{}^circ )
Отметим эти значения также на нашей окружности:
Однако, ты нередко можешь увидеть и вот такую картинку:
где вместо привычных нам градусов появляются некие буковки «пи» ( displaystyle pi ) с цифрами.
В чем же тут дело, кто прав и кто виноват?
Ну так вот, кто прав, кто виноват, решать, увы, не нам. Но чтобы «воз не был поныне там», нам нужно уделить этому моменту пару минут времени.
В самом деле, есть два способа измерять углы:
- Через градусы
- Через радианы
Как измерять углы через градусы мы все знаем. Это нам привычно. Однако в некоторых случаях их измеряют по-другому (как в градуснике есть несколько шкал: цельсий, кельвин, фаренгейт и т. д.), а именно: через радианы.
Для того, чтобы перейти от одной формы записи к другой, используется вот такое основное соотношение:
( displaystyle 180{}^circ =pi ~рад.)
И все, больше знать ничего не надо!
По пропорции ты легко получишь, что для того, чтобы пересчитать угол из градусов в радианы, нужно применить вот такую незамысловатую формулу:
( displaystyle P~рад.=frac{alpha {}^circ cdot pi }{180})
И наоборот: от радиан к градусам:
( displaystyle alpha {}^circ =frac{P~рад.cdot 180}{pi })
Ты должен уметь ориентироваться и в той, и в другой форме записи.
Потренируйся на следующих примерах:
- Перевести угол в ( displaystyle 30) градусов в радианы;
- Перевести угол ( displaystyle frac{pi }{4}) радиан в градусы;
- Перевести угол в ( displaystyle 60) градусов в радианы;
- Перевести угол в ( displaystyle frac{pi }{2}) радиан в градусы;
- Перевести угол в ( displaystyle 120) градусов в радианы;
- Перевести угол в ( displaystyle frac{3pi }{4}) радиан в градусы;
- Перевести угол в ( displaystyle 150) градусов в радианы.
Я сделаю только первые два, а остальные реши сам!
- ( P~рад.=frac{30cdot pi }{180}=frac{pi }{6}), тогда угол в ( displaystyle 30) градусов равен углу в ( displaystyle frac{pi }{6}) радиан;
- ( alpha {}^circ =frac{frac{pi }{4}cdot 180}{pi }=frac{45pi }{pi }=45{}^circ ), тогда угол в ( displaystyle frac{pi }{4}) радиан равен углу в ( displaystyle 45) градусов.
Все очень просто, не так ли? Остальные значения ты можешь найти в следующей таблице:
| ( displaystyle 0{}^circ ) | ( displaystyle 30{}^circ ) | ( displaystyle 45{}^circ ) | ( displaystyle 60{}^circ ) | ( displaystyle 90{}^circ ) | ( displaystyle 120{}^circ ) | ( displaystyle 135{}^circ ) | ( displaystyle 150{}^circ ) | ( displaystyle 180{}^circ ) |
| ( displaystyle 0) | ( displaystyle frac{pi }{6}) | ( displaystyle frac{pi }{4}) | ( displaystyle frac{pi }{3}) | ( displaystyle frac{pi }{2}) | ( displaystyle frac{2pi }{3}) | ( displaystyle frac{3pi }{4}) | ( displaystyle frac{5pi }{6}) | ( displaystyle pi ) |
| ( displaystyle 210{}^circ ) | ( displaystyle 225{}^circ ) | ( displaystyle 240{}^circ ) | ( displaystyle 270{}^circ ) | ( displaystyle 300{}^circ ) | ( displaystyle 315{}^circ ) | ( displaystyle 330{}^circ ) | ( displaystyle 360{}^circ ) |
| ( displaystyle frac{7pi }{6}) | ( displaystyle frac{5pi }{4}) | ( displaystyle frac{4pi }{3}) | ( displaystyle frac{3pi }{2}) | ( displaystyle frac{5pi }{3}) | ( displaystyle frac{7pi }{4}) | ( displaystyle frac{11pi }{6}) | ( displaystyle 2pi ) |
Так что впредь не удивляйся, когда ты увидишь вместо привычных градусов углы в радианах. Теперь ты знаешь, что это такое, и с чем его едят!
Синус, косинус, тангенс и котангенс на тригонометрической окружности
Но мы с тобой и так слишком увлеклись. Ты давно уже, наверное, заждался обещанных синусов и косинусов на тригонометрической окружности. Не смею более отвлекаться!
Давай сделаем вот что: совместим два знакомых нам объекта: тригонометрическую окружность (пока в том виде, в котором она у нас есть) и прямоугольный треугольник.
Что нам нужно, чтобы наш треугольник «целиком влез» в окружность?
Его гипотенуза должна быть не более единицы. Пусть же она у нас в точности будет равна единице.
Совместим мы их вот так:
Я нарисовал прямоугольный треугольник с центром в начале координат и гипотенузой равной ( 1). Это так потому, что окружность-то у меня единичная!
Тогда по определению синуса и косинуса:
- ( sin alpha =frac{AB}{OB}=frac{AB}{1}=AB)
- ( cos alpha =frac{OA}{OB}=frac{OA}{1}=OA)
А что же такое отрезки ( OA) и ( OB)? Чему равны их длины?
Смотри, сейчас будет самое главное: мы взяли угол ( alpha ) и провели луч, соединяющий этот угол с точкой на окружности.
Обозначим эту точку через ( B). Пусть ( B) имеет координаты ( Bleft( x,y right)).
Тогда длина отрезка ( OA) равна ( x), а длина отрезка ( AB)–равна ( y).
Но мы с тобой помним, что ( sin alpha =AB), ( cos alpha =OA), тогда:
- ( y=sin alpha )
- ( x=cos alpha )
Ух ты! Это надо еще раз обдумать, что же мы такое получили.
Давай проговорим еще раз: мы выбрали некоторый угол ( alpha ) и хотим найти его синус и косинус.
Что мы делаем?
- Проводим единичную окружность с центром, совпадающим с вершиной угла;
- Ищем точку пересечения нашего угла с окружностью;
- Её «иксовая» координата – это косинус нашего угла;
- Её «игрековая» координата – это синус нашего угла.
Вот и все! Теперь синус и косинус искать стало намного проще! Допустим, мы хотим найти синус, косинус ( 30) градусов.
Отмечаем ( 30) градусов на окружности и «достраиваем» этот угол до треугольника (как показано на рисунке выше).
Как найти ( x) и ( y)?
Да очень просто: в прямоугольном треугольнике катет, лежащий против угла в ( 30) градусов равен половине гипотенузы (это известный факт из геометрии 7 класса).
Так как гипотенуза равна ( 1), то противолежащий ей катет равен ( 0,5), откуда:
( sin 30{}^circ =0,5)
Что касается косинуса: для этого нам потребуется заметить, что выполняется тривиальное утверждение (основное тригонометрическое тождество):
( si{{n}^{2}}alpha +co{{s}^{2}}alpha =1)
Как ты думаешь, откуда оно берется? Да это же пресловутая теорема Пифагора!
Наши катеты в треугольничке равны ( x) и ( y), которые в свою очередь совпадают с ( cos alpha ) и ( sin alpha ). Гипотенуза в треугольнике равна ( 1).
Тогда:
( {{x}^{2}}+{{y}^{2}}=1) или, что то же самое,
( si{{n}^{2}}alpha +co{{s}^{2}}alpha =1)
Эта формула позволит по известному синусу вычислить неизвестный косинус и наоборот.
В частности, если:
( si{{n}^{2}}30{}^circ +co{{s}^{2}}30{}^circ =1) и ( sin 30{}^circ =0,5), то
( frac{1}{4}+co{{s}^{2}}30{}^circ =1)
( displaystyle co{{s}^{2}}30{}^circ =frac{3}{4})
( displaystyle cos 30{}^circ =pm sqrt{frac{3}{4}}=pm frac{sqrt{3}}{2})
Определение знака синуса, косинуса, тангенса и котангенса
Вообще, этот вопрос заслуживает особого внимания, но здесь все просто: у угла ( displaystyle 30) градусов и синус и косинус положительны (смотри рисунок), тогда берем знак «плюс».
( displaystyle cos 30{}^circ =frac{sqrt{3}}{2})
Теперь попробуй на основе вышеизложенного найти синус и косинус углов: ( displaystyle 60{}^circ ) и ( displaystyle 45{}^circ )
Можно схитрить: в частности для угла в ( displaystyle 60{}^circ ) градусов. Так как если один угол прямоугольного треугольника равен ( displaystyle 60{}^circ ) градусам, то второй – ( displaystyle 30{}^circ ) градусам. Теперь вступают в силу знакомые тебе формулы:
( displaystyle sin 30{}^circ =cos 60{}^circ )
( displaystyle sin 60{}^circ =cos 30{}^circ )
Тогда так как ( displaystyle sin 30{}^circ =0,5), то и ( displaystyle cos 60{}^circ =0,5). Так как ( displaystyle cos 30{}^circ =frac{sqrt{3}}{2}), то и ( displaystyle sin 60{}^circ =frac{sqrt{3}}{2}).
C ( displaystyle 45) градусами все еще проще: так если один из углов прямоугольного треугольника равен ( displaystyle 45) градусам, то и другой тоже равен ( displaystyle 45) градусам, а значит такой треугольник равнобедренный.
Значит, его катеты равны. А значит равны его синус и косинус.
Тогда:
( displaystyle si{{n}^{2}}45{}^circ +co{{s}^{2}}45{}^circ =2si{{n}^{2}}45{}^circ =1)
( displaystyle si{{n}^{2}}45{}^circ =co{{s}^{2}}45{}^circ =1/2)
Откуда: ( displaystyle sin 45{}^circ =cos 45{}^circ =sqrt{1/2}=frac{sqrt{2}}{2})
Теперь найди сам по новому определению (через икс и игрек!) синус и косинус углов в ( displaystyle 0) градусов и ( displaystyle 90) градусов. Здесь уже никакие треугольники нарисовать не получится! Уж слишком они будут плоские!
У тебя должно было получиться:
( displaystyle sin 0{}^circ =0), ( displaystyle cos 0{}^circ =1), ( displaystyle sin 90{}^circ =1), ( displaystyle cos 90{}^circ =0).
Тангенс и котангенс ты можешь отыскать самостоятельно по формулам:
( displaystyle text{t}g alpha =frac{sin alpha }{cos alpha }), ( displaystyle ctg alpha =frac{cos alpha }{sin alpha })
Обрати внимание, что на ноль делить нельзя!!
Теперь все полученные числа можно свести в таблицу:
Здесь приведены значения синуса, косинуса, тангенса и котангенса углов I четверти.
Для удобства углы приведены как в градусах, так и в радианах (но ты-то теперь знаешь связь между ними!). Обрати внимание на 2 прочерка в таблице: а именно у котангенса нуля и тангенса ( displaystyle 90) градусов. Это неспроста!
В частности:
( displaystyle ctg 0=frac{cos 0}{sin 0}=frac{1}{0}=?????)
Поэтому мы с тобой будем считать, что тангенс ( displaystyle 90) градусов и котангенс нуля просто-напросто не определены!
Теперь давай обобщим понятие синус и косинус на совсем произвольный угол. Я рассмотрю здесь два случая:
- Угол лежит в пределах от ( displaystyle 0) до ( displaystyle 360) градусов;
- Угол больше ( displaystyle 360) градусов.
Честно говоря, я скривил немного душой, говоря про «совсем все» углы. Они бывают также и отрицательными! Но этот случай мы с тобой рассмотрим чуть позже. Вначале остановимся на первом случае.
Если угол лежит в 1 четверти – то тут все понятно, мы этот случай уже рассмотрели и даже таблицы нарисовали.
Теперь же пусть наш угол больше ( displaystyle 90) градусов и не больше чем ( displaystyle 360).
Это значит, что он расположен либо во 2, либо в 3 или же в 4 четверти.
Как мы поступаем? Да точно так же!
Давай рассмотрим вместо вот такого случая…
…вот такой:
То есть рассмотрим угол ( displaystyle alpha ), лежащий во второй четверти. Что мы можем сказать про него?
У точки ( displaystyle {{M}_{1}}), которая является точкой пересечения луча и окружности по-прежнему имеет 2 координаты (ничего сверхъестественного, правда?). Это координаты ( displaystyle {{x}_{1}}) и ( displaystyle {{y}_{1}}).
Причем первая координата отрицательная, а вторая – положительная! Это значит, что у углов второй четверти косинус отрицателен, а синус – положителен!
Удивительно, правда? До этого мы еще ни разу не сталкивались с отрицательным косинусом.
Да и в принципе этого не могло быть, когда мы рассматривали тригонометрические функции как отношения сторон треугольника.
Кстати, подумай, у каких углов косинус равен ( displaystyle -1)? А у каких ( displaystyle -1) равен синус?
Аналогично можно рассмотреть углы во всех остальных четвертях. Я лишь напомню, что угол отсчитывается против часовой стрелки! (так, как это показано на последнем рисунке!).
Конечно, можно и отсчитывать в другую сторону, но вот подход к таким углам будет уже несколько другой.
Исходя из приведенных выше рассуждений, можно расставить знаки у синуса, косинуса, тангенса (как синус деленный на косинус) и котангенса (как косинус деленный на синус) для всех четырех четвертей.
Но еще раз повторюсь, нет смысла запоминать этот рисунок. Все, что тебе нужно знать:
Синус – это игрек. Косинус – это икс. Тангенс – это синус деленный на косинус. Котангенс – это косинус деленный на синус.
Углы больше 360 градусов
А как быть с углами, большими чем ( displaystyle 360) градусов?
Возьму я, скажем, угол в ( displaystyle 30) градусов (( displaystyle frac{pi }{6}) радиан) и пойду от него против часовой стрелки…
На рисунке я нарисовал спираль, но ты-то понимаешь, что на самом деле у нас нет никакой спирали: у нас есть только окружность.
Так куда же мы попадем, если стартуем от определенного угла и пройдем полностью весь круг (( displaystyle 360) градусов или ( displaystyle 2pi ) радиан)?
Куда мы придем? А придем мы в тот же самый угол!
Это же, конечно, справедливо и для любого другого угла:
Взяв произвольный угол ( displaystyle alpha ) и пройдя полностью всю окружность, мы вернемся в тот же самый угол ( displaystyle alpha ).
Что же нам это даст? А вот что: если ( displaystyle sin alpha =y,~cos alpha =x), то
( displaystyle sin left( alpha +2pi k right)=y), ( displaystyle cos left( alpha +2pi k right)=x), откуда окончательно получим:
( displaystyle sin left( alpha +2pi k right)=sinalpha )
( displaystyle cos left( alpha +2pi k right)=cosalpha )
Для любого целого ( displaystyle k). Это значит, что синус и косинус являются периодическими функциями с периодом ( displaystyle 2pi ).
Таким образом, нет никакой проблемы в том, чтобы найти знак теперь уже произвольного угла: нам достаточно отбросить все «целые круги», которые умещаются в нашем угле и выяснить, в какой четверти лежит оставшийся угол.
Например, найти знак:
- ( displaystyle text{sin}1000{}^circ ),
- ( displaystyle text{cos} 605{}^circ ),
- ( displaystyle text{cos}frac{16pi }{7}),
- ( displaystyle text{sin}frac{19pi }{4}).
Проверяем:
Отрицательные углы
Отрицательные углы в тригонометрии откладываются на тригонометрическом круге вниз от начала, по направлению движения часовой стрелки:
Давай вспомним, как мы до этого откладывали углы на тригонометрической окружности.
Мы шли от положительного направления оси ( displaystyle Ox) против часовой стрелки:
Тогда на нашем рисунке построен угол, равный ( displaystyle 180+45=225{}^circ ). Аналогичным образом мы строили все углы.
Однако ничего нам не запрещает идти от положительного направления оси ( displaystyle Ox) по часовой стрелке.
Мы будем тоже получать различные углы, но они будут уже отрицательными:
А следующей картинке изображено два угла, равные по абсолютной величине (если не знаешь, что это такое, читай здесь про «Модуль числа»), но противоположные по знаку:
В целом правило можно сформулировать вот так:
- Идем против часовой стрелки – получаем положительные углы
- Идем по часовой стрелке – получаем отрицательные углы
Схематично правило изображено вот на этом рисунке:
Ты мог бы задать мне вполне резонный вопрос: ну углы нам нужны для того, чтобы измерять у них значения синуса, косинуса, тангенса и котангенса.
Так есть ли разница, когда у нас угол положительный, а когда – отрицательный? Я отвечу тебе: как правило есть.
Однако ты всегда можешь свести вычисление тригонометрической функции от отрицательного угла к вычислению функции в угле положительном.
Посмотри на следующую картинку:
Я построил два угла, они равны по абсолютному значению, но имеют противоположный знак. Отметим для каждого из углов его синус и косинус на осях.
Что мы с тобой видим? А вот что:
Синусы у углов ( displaystyle alpha ) и ( displaystyle -alpha ) противоположны по знаку!
Тогда если ( displaystyle text{sin} text{ }!!alpha!!text{ }=text{y}),
то ( displaystyle sin left( -text{ }!!alpha!!text{ } right)=-text{y})
( displaystyle sin left( -text{ }!!alpha!!text{ } right)=-text{sin} text{ }!!alpha!!text{ }).
Косинусы у углов ( displaystyle alpha ) и ( displaystyle -alpha ) совпадают!
Тогда если ( displaystyle text{cos} text{ }!!alpha!!text{ }=text{x}),
то и ( displaystyle cos left( -text{ }!!alpha!!text{ } right)=text{x})
( displaystyle cos left( -text{ }!!alpha!!text{ } right)=text{cos} text{ }!!alpha!!text{ })
Так как ( displaystyle text{tg}left( -text{ }!!alpha!!text{ } right)=frac{text{sin}left( -text{ }!!alpha!!text{ } right)}{text{cos}left( -text{ }!!alpha!!text{ } right)}=frac{-text{sin}left( text{ }!!alpha!!text{ } right)}{text{cos}left( text{ }!!alpha!!text{ } right)}), то:
( displaystyle text{tg}left( -text{ }!!alpha!!text{ } right)=-text{tg }!!alpha!!text{ })
Так как ( displaystyle text{ctg}left( -text{ }!!alpha!!text{ } right)=frac{text{cos}left( -text{ }!!alpha!!text{ } right)}{text{sin}left( -text{ }!!alpha!!text{ } right)}=frac{text{cos}left( text{ }!!alpha!!text{ } right)}{-text{sin}left( text{ }!!alpha!!text{ } right)}), то:
( displaystyle text{ctg}left( -text{ }!!alpha!!text{ } right)=-text{ctg} text{ }!!alpha!!text{ })
Таким образом, мы всегда можем избавиться от отрицательного знака внутри любой тригонометрической функции: либо просто уничтожив его, как у косинуса, либо поставив его перед функцией, как у синуса, тангенса и котангенса.
Кстати, вспомни-ка, как называется функция ( displaystyle f(x)), у которой для любого допустимого ( displaystyle x) выполняется:( displaystyle f(-x)=-f(x))?
Такая функция называется нечетной.
А если же для любого допустимого ( displaystyle x) выполняется: ( displaystyle f(-x)=f(x))? То в таком случае функция называется четной.
Таким образом, мы с тобой только что показали, что:
Синус, тангенс и котангенс – нечетные функции, а косинус – четная.
Таким образом, как ты понимаешь, нет никакой разницы, ищем ли мы синус от положительного угла или отрицательного: справиться с минусом очень просто. Так что нам не нужны таблицы отдельно для отрицательных углов.
С другой стороны, согласись, было бы очень удобно зная только тригонометрические функции углов первой четверти, уметь вычислять аналогичные функции и для остальных четвертей.
Можно ли это сделать? Конечно, можно!
У тебя есть по крайней мере 2 пути: первый – строить треугольник и применять теорему Пифагора (так мы с тобой и отыскали значения тригонометрических функций для основных углов первой четверти)
Второй – запомнив значения функций для углов в первой четверти и некое несложное правило, уметь вычислять тригонометрические функции для всех остальных четвертей.
Второй способ избавит тебя от долгой возни с треугольниками и с Пифагором, поэтому мне он видится более перспективным:
Итак, данный способ (или правило) называется формулами приведения.
Формулы приведения
Грубо говоря, эти формулы помогут тебе не запоминать вот такую таблицу (она между прочим содержит 98 чисел!):
…если ты помнишь вот эту (всего на 20 чисел):
То есть ты сможешь не забивать себе голову совершенно ненужными 78 числами! Пусть, например, нам нужно вычислить ( displaystyle text{sin} 855{}^circ ). Ясно, что в маленькой таблице такого нет. Что же нам делать? А вот что:
Во-первых, нам понадобятся следующие знания:
Синус и косинус имеют период ( displaystyle 2pi ) (( displaystyle 360) градусов)
То есть
( displaystyle sinleft( 2pi k+x right)=sin x)
( displaystyle cosleft( 2pi k+x right)=cos x)
Тангенс (котангенс) имеют период ( displaystyle pi ) (( displaystyle 180) градусов)
( displaystyle tgleft( pi k+x right)=tg x)
( displaystyle ctgleft( pi k+x right)=ctg x)
( displaystyle k) – любое целое число
Синус и тангенс – функции нечетные, а косинус – четная:
( displaystyle sinleft( -x right)=-sin x)
( displaystyle tgleft( -x right)=-tgleft( x right))
( displaystyle cosleft( -x right)=cosleft( x right))
Первое утверждение мы уже доказали с тобой, а справедливость второго установили совсем недавно.
Непосредственно правило приведения выглядит вот так:
Если мы вычисляем значение тригонометрической функции от отрицательного угла – делаем его положительным при помощи группы формул о четности.
Например:
( displaystyle sinleft( -855{}^circ right)=-sin855{}^circ),
( displaystyle cosleft( -855{}^circ right)=cos855{}^circ).
Отбрасываем для синуса и косинуса его периоды: ( displaystyle 2pi k) (по ( displaystyle 360) градусов), а для тангенса – ( displaystyle pi k) (( displaystyle 180) градусов).
Например:
( displaystyle sin 855{}^circ =sinleft( 2cdot 360{}^circ +135{}^circ right)=sin 135{}^circ )( displaystyle tg 225{}^circ =tgleft( 180{}^circ +45{}^circ right)=tg 45{}^circ )
Если оставшийся «уголок» меньше ( displaystyle 90) градусов, то задача решена: ищем его в «малой таблице».
Иначе ищем, в какой четверти лежит наш угол ( displaystyle alpha ): это будет 2, 3 или 4 четверть. Смотрим, какой знак имеет искомая функция в четверти. Запомнили этот знак!!!
Представляем угол ( displaystyle alpha )в одной из следующих форм:
- ( displaystyle alpha =90+beta ) (если во второй четверти)
- ( displaystyle alpha =180-beta ) (если во второй четверти)
- ( displaystyle alpha =180+beta ) (если в третьей четверти)
- ( displaystyle alpha =270-beta ) (если в третьей четверти)
- ( displaystyle alpha =270+beta ) (если в четвертой четверти)
- ( displaystyle alpha =360-beta ) (если в четвертой четверти)
…так, чтобы оставшийся угол ( displaystyle beta ) был больше нуля и меньше ( displaystyle 90) градусов.
Например:
( displaystyle 135{}^circ =180{}^circ -45{}^circ )
( displaystyle 135{}^circ =90{}^circ +45{}^circ )
( displaystyle 315{}^circ =270{}^circ+45{}^circ )
( displaystyle 240{}^circ =180{}^circ +60{}^circ )
( displaystyle 240{}^circ =270{}^circ -30{}^circ )…
В принципе не важно, в какой из двух альтернативных форм для каждой четверти ты представишь угол. На конечном результате это не скажется.
Теперь смотрим, что у нас получилось: если ты выбрал запись через ( displaystyle 180) или ( displaystyle 360) градусов плюс минус что-либо, то знак функции меняться не будет: ты просто убираешь ( displaystyle 180) или ( displaystyle 360) и записываешь синус, косинус или тангенс оставшегося угла.
Если же ты выбрал запись через ( displaystyle 90) или ( displaystyle 270) градусов, то синус меняем на косинус, косинус на синус, тангенс на котангенс, котангенс – на тангенс.
Ставим перед получившимся выражением знак, который мы запомнили.
Определение значения синуса, косинуса, тангенса и котангенса
Определение
Тригонометрия — это техническая часть математики, в которой представлены особенности взаимосвязи между сторонами и углами треугольников.
Тригонометрические функции, является очень важной составляющей не только математики, но других технических наук.
Применяя основные формулы и законы тригонометрии при вычислении задач. Огромное значение имеют таблицы значений данных функций. Они существенно упрощают решение задач различной сложности.
Процесс работы и расчета функций данного вида, очень непростой. Решение задач и уравнение, очень часто вызывают сложности. Поэтому, со временем, были созданы и разработаны несколько видов решений, чтобы облегчить жизнь математика и всем представителям технических наук. Преобразовывая тригонометрические формулы, необходимо руководствоваться следующими правилами:
- Нельзя продумывать весь процесс решения от начала до самого конца сразу. Нужно определиться с основными задачами и данными.
- Весь пример, подвергать упрощению или преобразования постепенно;
- Разрешается применять все преобразования и действия, связанные с алгеброй, а именно: вынести значение за пределы скобок. сократить значение и многое другое:
[ sin x=frac{a}{c} ; cos x=frac{b}{c} ; operatorname{tg} x=frac{sin x}{cos x} ; operatorname{ctg}=frac{1}{operatorname{tg} x}=frac{sin x}{cos x} ]
Зная основные определения тригонометрических функций, можно определить их угловые значения. Для углов от нуля до трехсот шестидесяти градусов, вычислим данные и запишем их в виде таблицы.
Значения вышеупомянутых математических функций, в частности в разделе геометрия, вычисляются как соотношения длин прямоугольного треугольника.
Углы геометрической фигуры имеют соответствующие значения в градусах. Используя основные определения математики, а именно тригонометрии можно определить нужные нам данные.
Определим основные значения
1.синуса (sin):
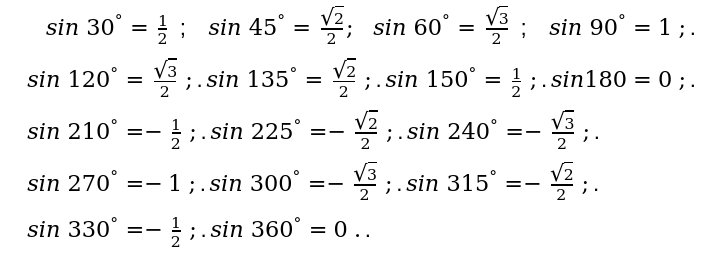
2. косинуса (cos):
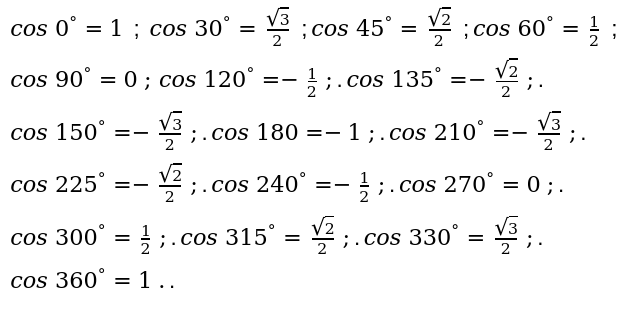
3. тангенса(tg):
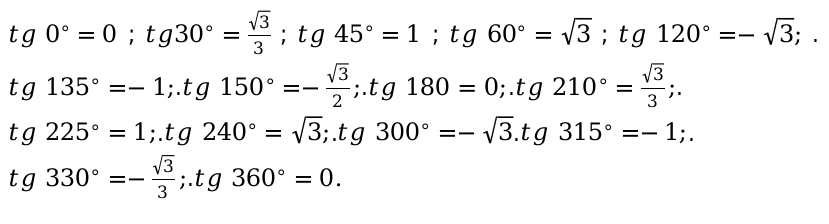
[ operatorname{tg} 90^{circ}, 270^{circ} ]
Данные выше угловые значения, не определяются, согласно основным законам геометрии и математики.
4. котангенса (ctg)
[ operatorname{ctg} 0^{circ}, 180^{circ}, 360^{circ} ]
Для перечисленных выше угловых значений по законам математики и всех технических наук в целом, значения не определяются
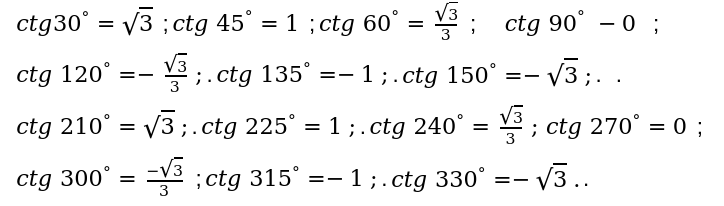
Мы произвели основные расчеты. Определили результаты угловых значений.
Мы определились с основными угловыми значениями функций. Следующим шагом будет их сведение в таблицу.
Таблица1. Основные значения функций косинус, синус, тангенс и котангенс, для угловых значений и радиан
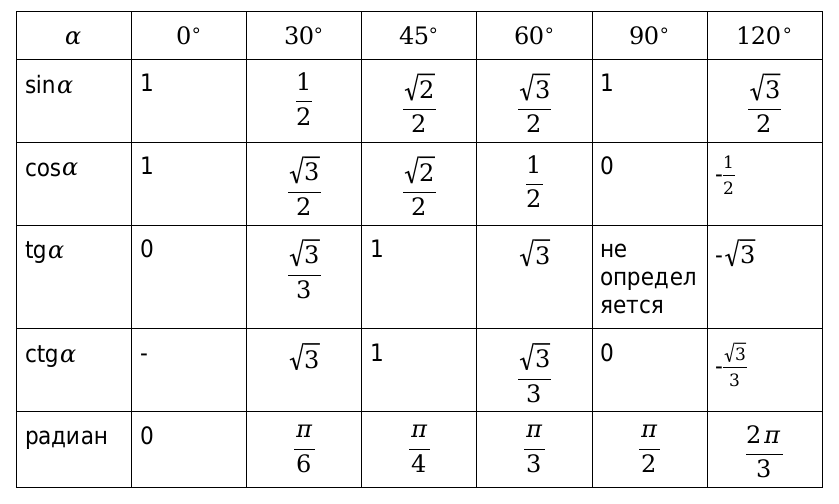
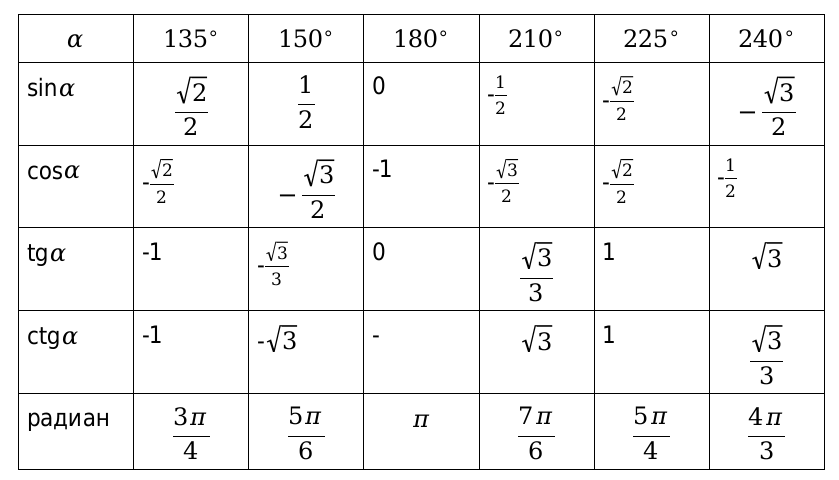
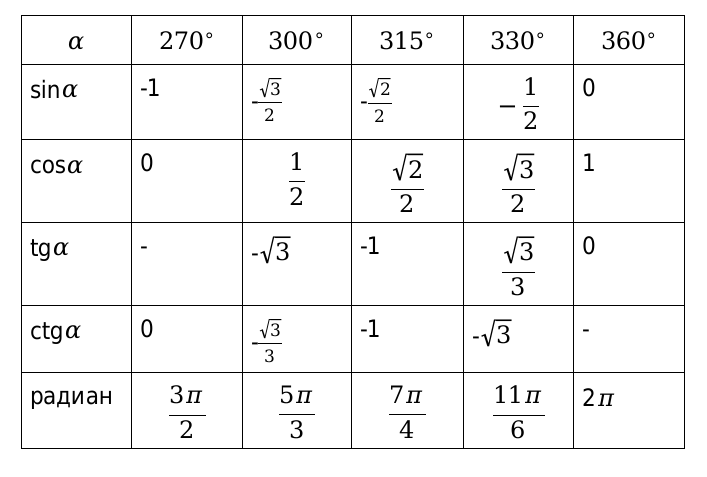
Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более лучшего восприятия. Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.
Таблица 2. Нестандартные углы функций косинус, синус, тангенс и котангенс в тригонометрии

В данной таблице приведены значения углов, которые считаются нестандартными, также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.
Например:
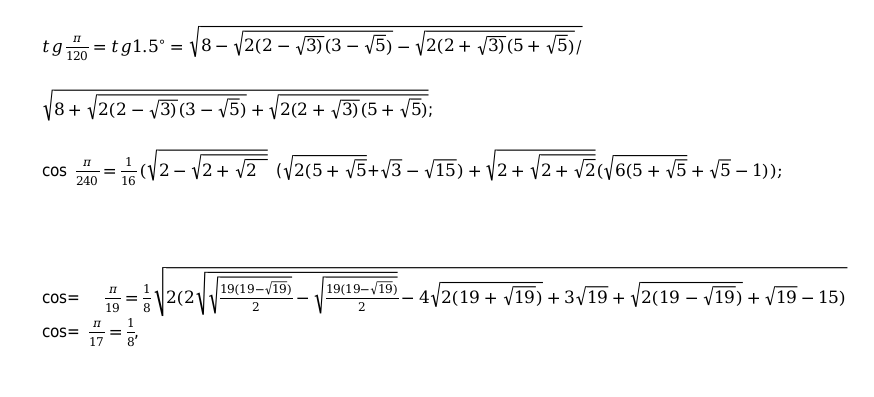
Значение заданной функции берется из таблицы. Оно равняется данному, которое попадает на пересечение столбца и строки.
Пример №1. Необходимо определить чему равен [operatorname{tg} 300]
Берем левый столбец с наименованием функции, находим в верхней строке нужный градус, и на пересечении определяем нужный ответ.
Следовательно:[operatorname{tg} 300^{circ}=-sqrt{3}].
Пример №2. Необходимо определить чему равен [cos frac{5 pi}{3}].
Берем левый столбец с наименованием функции, находим в нижней строке значение радиан, поднимается на верх таблицы и определяем градусы.
[text { Следовательно: } operatorname{tg} 300^{circ}=frac{1}{2} .]
Пример №3. Необходимо определить чему равен [cos frac{11 pi}{6}].
Проводим аналогичные действия, как в предыдущих двух примерах и определяем угловое значение.
[text { Следовательно } cos =frac{sqrt{3}}{2}=330^{circ}.]
Таблица Брадиса для решения основных задач по тригонометрии
Первое упоминание о таблице, датируется 20-ми годами прошлого века. Основоположником, является советский ученый математик, и талантливый педагог Владимир Брадис. Созданная Брадисом таблица, позволяет определить значения тригонометрических функций, с большой точностью, а именно до четырех знаков. На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух. Произвести простых четыре перемножения. Дважды разделить, умножить и отнять.
Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме. В таблице представлены следующие данные:
- число в квадратной и кубической степени;
- числа квадратных корней;
- логарифмические функции и значение;
- функции тригонометрии, представленный в градусах и радианах;
- обратные функции.
Можно определить точность углового значения до минуты. Существуют также таблицы, где есть семизначные значения.
Для того чтобы составить таблицы следует пользовался методом разложения функций (либо метод разложения на степень в ряд)
Примеры решения задач
Пример 1:
Необходимо определить синус угла 18 ° 44 ‘.
По таблице значений определяем данные синуса 18 ° 42 ‘. Далее используем поправку, равную две минуты. Плюсуем ее и заданные минуты: 18 ° 44 ‘ − 18 ° 42 ‘ = 2 ‘
Нужное значение равняется — 0,0006.
Узнав все необходимые значения, находим окончательное решение:
sin 18 ° 44 ‘ = 0. 3208 + 0. 0006 = 0. 3214
Пример 2:
Условие задачи, заключается в необходимости вычислить угол функции синус 76 ° 12. В таблице находим столбец с название угол и ищем 76 градусов и строку со значением 12. Далее, исходя из найденных ячеек, находим значение угла — 0,2284.
Ответ: синус 76 ° 12 =0,2284.
Пример 3:
Нужно найти значение синус 16 градусов 32 минут. Для того чтобы посчитать значение 16 ° 32 минуты. В таблице находим значение нужного угла, которое ближе всего по значению подходит к заданному. Это sin16 30 =0.2840. Так как 16 32=16 30+2, то в столбце, выбираем нужную поправку, которая находится на пересечении со строкой, со значением 16 градусов стоит 0,0006, то есть
sin 16 ° 32 ‘ = 0. 3208 + 0. 0006 = 0. 3214
Пример 4:
Нужно найти значение синус 22 градусов 10 минут. Чтобы посчитать значение 22 ° 12, в таблице найдем значение необходимого угла, наиболее подходящее заданному. Это sin16 30 =0.3778. Так как 22 ° 10= 22 ° 12+2, то тогда выбираем поправку равную двум и видим, что нужный нам градус равный 22 ° имеет значение 0,0005. Далее записываем:
sin 22 ° 10 ‘ = (22 12-2) =0. 3778 + 0. 0005 = 0. 3773
Пример 5:
Нужно найти значение косинус 50 градусов 33 минут. Для того, чтобы посчитать значение 53 31 в таблице найдем значение нужного угла, наиболее близкого к искомому со знаком минус. Это косинус 50 33 =0.6361 Так как 50 33=50 30+3, то в нужном столбце выбираем значение 3. Далее находим значение 0,0007, и записываем следующее уравнение:
косинус 50 ° 33 ‘ = (50 30-3) =0. 6361 +(- 0. 0007) = 0. 6454
Пример 6:
Нужно найти tg 35 градусов 6 минут. В таблице значений функции, в столбце найдем значение 35 градусов, а в строке 6 минут. Определяем нужное значение по таблице равное 0,7028.
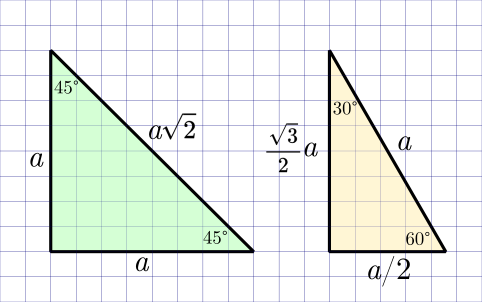
Пример 7:
Нужно найти значение котангенс 13 градусов 42 минут. Снова применим таблицу значения функций и найдем значение 13 градусов, а в строке 40 минут и поправку равную 2. Находим искомое значение 4,102.
Пример 8:
Нужно найти значение косинус для 49° 33 минут.
Для того чтобы вычислить значение 49° 31. В таблице найдем значение угла, наиболее близкого по значению к заданному, но только с отрицательным знаком минус. Это косинус 49° 31/ =0.6361 Так как 49° 31/=50 30+3, из этого следует, что поправка равняется трем. Значение 49 градусов равно 0,0007, поэтому: косинус 49° 33 ‘ = ( 49° 31-3) =0 . 6361 +(- 0 . 0007) = 0,6454
Нет времени решать самому?
Наши эксперты помогут!
Основные способы, которые помогут заполнить таблицу функций
1 Действие: Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.
В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.
Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции. Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс (sec).
2. Действие: Заполняем пустые ячейки со значение синус. Берем выражение [frac{sqrt{x}}{2}] и подставляем числовые значения, то есть величины углов. они записаны в первом столбике. Далее применяя [frac{sqrt{x}}{2}] можно вычислить данные для углов, которые нам необходимы. Вычисленные значения, записываются в таблицу.
Для наглядности все прописанные действия, можно разобрать на конкретном примере.
Например, мы заполняем ячейку sin 0 градусов. На месте неизвестного значения в выражении [frac{sqrt{x}}{2}] записываем значение угла.
Получаем следующую запись: [frac{sqrt{x}}{2}=frac{0}{2}=0]. Затем, проводим те же операции для заполнения оставшихся пустых строк.
[ frac{sqrt{1}}{2}=frac{1}{2} ; frac{sqrt{2}}{2}=frac{(sqrt{2 cdot 2})}{(2 cdot sqrt{2})}=frac{2}{2 cdot sqrt{2}}=frac{1}{sqrt{2}} ; frac{sqrt{3}}{2} frac{sqrt{4}}{2}=frac{2}{2}=1 ]
Необходимо первым делом заполнять неизвестные ячейки, для функции синус. Это значительно в будущем облегчит заполнение всей таблицы. Так как именно за данной функции и ее данных и завязана вся работы таблицы.
3. Действие: Продолжаем считать таблицу. для этого значения синуса, которые подсчитаны были ранее, переписываем для функции косинус. Только делаем это в порядке обратном значению синусу. Данная теория действительна, потому что sin x° = cos (90-x). Если в самой крайней ячейке синус, имеется 1(sin90°=1). То в первую строку значения косинус, перепишется это числовое значение, cos 0° = 1. Таким образом заканчиваем заполнение до конца.
4. Действие: Для определения тангенса. Необходимо произвести деление данных синуса на косинус. Так как тангенс равен данной функции. [operatorname{tg}=frac{sin }{cos }]. Выходим что искомое значение равно данному выражению. Если [operatorname{tg} 45^{circ}=frac{sin }{cos }=frac{sqrt{1}}{2} / frac{sqrt{3}}{2}=frac{1}{sqrt{3}} .]
Аналогично поступаем и далее.
5. Действие: Для заполнения граф косеканс и секанс нужно 1/sin и 1/cos.
[text { Так как, } operatorname{cosec}=frac{1}{sin } . text { Например, } sin 40^{circ}=frac{1}{2}, text { поэтому } operatorname{cosec} 40^{circ}=frac{1}{frac{1}{2}}=2]
Действие 6: Оставшиеся функции тангенс и котангенс. также записываются обратно значениям. Если tg90 равняется ctg0, значение tg60 будет соответственно равен значению ctg 30 градусов.
[text { Таким же методом заполняются оставшиеся строки таблицы. Так } text { как } operatorname{ctg}=frac{1}{t g}, text { в свою очередь } operatorname{ctg}=frac{cos }{sin }]
Вычисление данных при помощи фигуры — прямоугольный треугольник
Для этого строится нужный треугольник заданным углом, который необходимо определить. Строится угол, точка и луч, которые выходят из данной точки под определенным углом. Соединяем лучи, прямой линией перпендикулярной, одному из лучей. В конечном итоге получаем фигуру, угол которой равняется заданному в задаче углу. В процессе вычисления, также задаются длины сторон. Поэтому трудней с построением не должно возникнуть.
Вычисление при помощи длин сторон треугольника происходит следующим образом:
- обозначается катет;
- сторона возле угла;
- сторона напротив угла с прямым значением.
Функции могут выражаться по-разному в отношении сторон. Например, нам нужно определим значение sin 45°. Поделим имеющуюся длину значения противолежащего катета на значение длины гипотенузы. Если заданные значения длины равны 4 и 6 соответственно. Тогда, составим следующее выражение и получим sin[45^{circ}=frac{4}{6}=0,67]
Для определения значений основных функций в математике, необходимо заучить наизусть определение основных понятий, связанный с данной темой.
В процессе решения задачи, это придется применять постоянно.
Значения косеканса и секанса определяются в обратном порядке. Для этого необходимо знать какие стороны нужно делить для определения вышеперечисленных функций.
Косеканс находится [operatorname{cosec}=frac{1}{sin }] следовательно, нужно разделить гипотенузу на противолежащий катет. Секанс, наоборот к прилежащему катету [mathrm{sec}=frac{1}{cos }].
Например, для определения cosec 40°, если катет равен 5, а гипотенуза соответственно равна 8. Нужно разделить 5/8 и получим ответ cosec 40° = 0,63.
При вычислениях всегда рекомендуется исключать значение под корнем в знаменателе, это наиболее облегчает процесс расчета.
Рассмотренная тема преобразования и расчета функций, является довольно громоздкой, на первый взгляд. Применяя для решения огромные формулы и функции можно растеряться и не сразу сообразить, как производить их расчет. Однако досконально рассмотрев и изучив каждый раздел, становится понятно, что все достаточно просто и громоздкие таблицы освоить можно быстро и легко.
Вычисление значений углов по окружности
Самый простой и понятный способ для вычисления углов и радиан.
Для этого вычерчиваем окружность с радиусом R. Он в свою очередь, равен единичному значению. Центр окружности равен центру системы координат. От положительной оси считаем углы, по часовой стрелке, выполняющей движении против хода. Точка, имеющая координаты 1;0 равняется угловому значению ноль. если координаты -1;0, тогда угол равен 90 градусов. Точка, находящаяся на окружности, соответствует углу от нуля до 360 градусов. Так как окружность является единичной, значения углов для синуса и косинуса находятся в пределах от -1 до 1:
Определяются знаки функций, также по окружности. если угловое значение более 360 градусов, делается два оборота по часовой стрелке и плюсуется еще дополнительно 12 минут.
[ cos (alpha+360 cdot n)=sin alpha ;] [ sin (alpha+360 cdot n)=sin alpha / ]
Значения тангенсов и котангенсов, можно вычислить аналогично, по окружности. Однако легче посчитать по формулам, уже известных данных.
[ operatorname{tg} alpha=frac{sin alpha}{cos alpha} ; operatorname{ctg} alpha=frac{cos alpha}{sin alpha} ]
Математическая продлёнка. Про углы и тригонометрию
Уровень сложности
Средний
Время на прочтение
17 мин
Количество просмотров 13K
Продолжаю знакомить вас с наработками к занятиям математического кружка. В этой статье собраны два сюжета, связанные друг с другом одной темой: математика углов и тригонометрия. Каким образом обосновываются угловые меры? Какие из них для чего более пригодны? Почему значения тригонометрических функций от рациональных долей окружности почти все иррациональны и, наоборот, почему в рациональной тригонометрии только восемь рациональных углов и те, по большей части тривиальны? Материал рассчитан на школьников, но он приоткрывает двери в большую математику, поэтому здесь появятся элементы теории чисел, теории алгебраических полей и полиномы Чебышёва.
В чём лучше измерять углы?
— А вам зачем? Определить направление в море, или, может быть, узнать уклон дороги? Хотите найти расстояние на сфере, либо угловое расстояние между звёздами? Или вам для геометрических нужд, треугольничек построить или звезду пятиконечную? Может, вас тригонометрия интересует, синус вычислить, координату какую отыскать, или фигуру Лиссажу нарисовать даме к 8 марта? Или вы больше по физике: вращения, колебания, гармонические функции, спектры, дифференциальные уравнения. А топологию окружности или группу поворотов изучить не желаете?
Для разных задач годятся разные меры, и какую попало выбирать не стоит. Во-первых, надо, что бы углы выражались числами (желательно, удобными — целыми или рациональными) и были пригодны для бытового использования. Во-вторых, они должны быть удобны для геометрических построений, имели внятные значения для часто встречающихся геометрических фигур. И, в-третьих, помогали нам дружить с тригонометрией и алгеброй — не одними же только циркулем и линейкой вычислять!
Обороты
Для длины абсолютной единицы не существует, выбирай, хоть аршин, хоть астрономическую единицу, хоть планковскую. А вот с оборотами не так. Полный оборот — сам себе единица. Вещь в себе, так сказать. Раз такое дело, самым естественным решением будет измерять углы оборотами и его долями. Нормальный способ, именно его мы используем для измерения частоты вращения, когда пишем об/минуту или когда просим кого нибудь повернуться на четверть-оборота для фотографии.
Однако, для геометрических нужд имеет смысл оборот представить, не как единицу, а как двойку, точнее, как два развернутых угла. Преимущества этого способа могут быть заметны при измерении углов правильных многоугольников, все они будут выражаться понятными говорящими дробями. Сумма углов в треугольнике тогда будет равна 1, в правильном многоугольнике с вершинами —
Углы в квадрате: 1/4, в равностороннем треугольнике — 1/3, в пятиугольной звезде — 1/10, в пятиугольнике — 3/5. Удобно.
Грады и градусы
Но правильные дроби нравятся не всем. Так вышло, что законодателями мод в измерении углов были моряки и астрономы, и именно им принадлежат основные практичные угловые меры.
Мореходы и землемеры, в своё время, решили, что разделить угол между Севером и Востоком на 100 частей будет в самый раз! Так получились грады. Прямой угол — 100 град, развёрнутый — 200 град, полный оборот — 400. Кстати, при таком способе 1 град это 1% от прямого угла, можно было бы записывать углы в процентах.
Есть у град один конструктивный недостаток: у числа 400 сравнительно немного делителей: 2, 4, 5, 8, 10, 16, 20, 25, 40, 50, 80, 100, 200 и среди них нет чисел, кратных трём. Так что у равностороннего треугольника получится угол в 133⅓ града, которые в десятичной дроби представляются лишь периодичной дробью. Давайте поищем что-нибудь получше. Взглянем на то, как растёт количество делителей у чисел в первой тысяче:
Как видите, есть такие числа, которые имеют наибольшее число делителей, среди всех предыдущих. Среди них значится знакомое число 360. Так что, если вам хочется рисовать правильные многоугольники, у которых 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 24, 30, 36, 40, 45, 60, 72, 90, 120 и 180 вершин, имеющие целые значения углов, или заниматься астрономией, в которой угловые размеры Солнца и Луны составляют половину деления, то 360° — ваш выбор!
Ну, а если вам до зарезу нужны семиугольники, то вместо 360 делений выбирайте, например, 420. Делителей у этого числа столько же, что и у трёхсот шестидесяти, но среди них есть кратные 7. Если полный оборот принять за 420 единиц, то прямой угол будет равен 105, углы в правильном треугольнике — 70, в пятиугольнике — 127, в шестиугольнике — 140, семиугольнике — 150. Красота!
Часы
А ещё мне по душе штурманский способ измерять угол в часах и минутах. Разделив оборот на 24 часа, а час — на 60 минут, мы получим привычное бытовое деление суточного периода. К тому же, число 24 относится к числам с наибольшим числом делителей в своей весовой категории. Более того, 24×60 = 1440 имеет целых 34 делителя!
Так что углы во всех привычных правильных многоугольниках будут иметь вполне аккуратное выражение: треугольник — 4ʰ, квадрат — 6ʰ, пятиугольная звезда — 2ʰ24ᵐ, а пятиугольник — 7ʰ12ᵐ. Это менее привычно, чем десятичная запись, но легко ложится на визуальный образ циферблата. Вместо 24 делений можно использовать и 12 часов, но тогда половина прямого угла будет выражаться как 1ʰ 30ᵐ. Зато транспортир превратится в хорошо знакомый и привычный для нас часовой циферблат.
Но особенно мне нравится, как выглядит таблица тригонометрических функций, в которой аргумент выражен в часах:
Кроме привычных значений, в этой таблице можно разместить две дополнительные величины в 1 час и в 5 часов, соответствующие 15° и 75°. Значения синусов и косинусов для них громоздковаты, конечно, но во второй части статьи мы с вами убедимся в том, что это хорошие величины: они имеют алгебраическую степень равную четырём, но при этом выражаются в виде внятного сочетания корней. Таким образом, все целые часы имеют относительно неплохие значения тригонометрических функций.
Румбы
Углы это не только части оборота, это ещё и способ обозначать направления. В отличие от оборотов, направления образуют модулярную арифметику, то есть, не бывает направления соответствующего 25 часам. Так что 25ʰ = 1ʰ и 20ʰ + 6ʰ = 2ʰ. Ещё более явно эту особенность алгебры направлений демонстрируют румбы и азимуты.
К любому углу можно подобраться с помощью дихотомии или методом деления пополам. Сначала выясняем в какой полуплоскости лежит нужное нам направление, потом — в какой четверти, потом — в какой из половинок четвертей и так далее. Так с незапамятных времён делили горизонт моряки, измеряя углы в румбах, разделив окружность на 2⁵ = 32 части, и дав им звучные имена, типа вест-зюйд-вест, норд-ост-тень-ост или даже стрик встока к обеднику, которые очень прикольно выкрикивать хриплым голосом, стоя на мостике.
Наконец, углы можно измерять даже в пальцах, как это делают бывалые морские и речные волки, идя «на два пальца левее Алголя«.
Однако, степени двойки, не могут похвастаться большим числом делителей, у числа 32 их всего 5 и все… степени двойки. Так что, поскольку 1/6 выражается только в виде бесконечной двоичной дроби:
используя номенклатуру румбов, угол в равностороннем треугольнике придётся выражать бесконечным символом. И о тригонометрии на языке румбов говорить будет нелегко, поскольку косинусы углов, являющихся степенями двойки, кроме четверти и восьмой части оборота, вычисляются не особо изящно:
Ну, а для других румбов тригонометрические дела обстоят и того хуже!
Радианы
Все описанные выше способы деления окружности, более или менее, подходят для базовой тригонометрии и бытового использования. Но если вы решите вычислить производную от какого-нибудь синуса, то она не будет равна косинусу, покуда аргумент будет измеряться в оборотах, градах, часах или румбах. Однако, при равномерном вращении, скорости изменения прямоугольных координат точки выражаются именно так:
Если в качестве угловой меры взять расстояние, на которое прокатится колесо единичного радиуса, при известном повороте, то угол поворота будет измеряться в радианах, то есть, в отношениях длины дуги, стягиваемой углом, к её радиусу. При этом появится иррациональное число , но этот значок не хуже значка ° или, например, ₽. Если вместо «пи» произносить «развёрнутый угол», то смысл угла, выраженного в радианах станет яснее. Например, угол в правильном треугольнике равен π/3, то есть трети развёрнутого угла, а у квадрата — π/2, сиречь половина развёрнутого угла. А формула Эйлера
гласит, что число −1, если рассматривать его, как комплексное
, имеет аргумент, равный развёрнутому углу.
Несомненные выгоды от использования радиан начинаются при занятиях серьёзной тригонометрией и матанализом. В радианах синусы и косинусы решают дифференциальное уравнение: их можно раскладывать в ряды, и использовать методы приближённых вычислений, типа
для малых углов. С аргументом, выраженным в радианах, тригонометрия позволяет решать задачи на движение, строить теорию функций комплексного переменного и методы разложения в ряды Фурье для решения задач матфизики. Начиная с первого курса физфака или мехмата, про градусы можно забыть.
Уклоны
Наконец, можно отказаться от равномерных делений и сразу измерять углы в тангенсах. Именно этот способ используется на дорожных знаках, где уклон дороги, то есть тангенс угла, образуемого дорогой к горизонту, выражен в процентах. Этот подход полезен в геодезии и в дорожном строительстве. И даже позволяет кое-где упростить тригонометрию.
Например, если величина угла выражается через его тангенс рациональной дробью, то нетрудно точно посчитать его синус и косинус, не используя калькулятор:
Но есть и существенные проблемы. Уклон в равностороннем треугольнике будет равен 1/√3 ≈57.73%, а вот угол квадрата, простите, будет неопределён, ибо тангенс для прямого угла терпит разрыв. Но самое главное: углы, измеряемые таким образом, перестают быть аддитивными. Это значит, что сумма двух уклонов или, скажем, удвоение уклона будут вычисляться весьма нетривиально, особенно, с учётом разрывов.
От геометрии к алгебре
Эти ограничения можно обойти, если использовать не дробь для выражения тангенса, а пару чисел: (числитель, знаменатель). Тогда прямой угол примет безопасное «значение» (1,0), а его половина может быть выражена, как (1,1) или (√2,√2) — это одно и тоже. Последовательно развивая такое представление, можно прийти к теоретикогрупповому представлению об угле, как о повороте, то есть, действии на множестве точек пространства или элементов поля.
Если разглядеть в упомянутых выше парах чисел комплексные числа, то алгебру углов можно определить, как мультипликативную группу комплексных чисел, факторизованную по норме (модулю). Тогда аддитивная абелева группа поворотов становится изоморфна мультипликативной группе комплексных чисел. Сложению углов (композиции поворотов) соответствует умножение соответствующих комплексных чисел, а вычитанию — умножение на сопряжённое число.
Ограничившись только такими парами чисел , что
, получим полноценную алгебру, в которой повороты можно складывать таким образом:
. Если все числа в парах будут рациональными, то результаты тоже окажутся парами рациональных чисел. Так можно построить группу рациональных точек окружности и рациональную тригонометрию, в которой нет корней, зато полно дробей с пугающими числами.
Наконец, окончательно абстрагировавшись от угловых мер, градусов, румбов и даже радиан, можно рассматривать углы, как топологическое пространство и унитарную группу первого порядка
изоморфную группе вращений двумерного вещественного пространства SO(2). Впрочем, этот подход, необходимый для определения базовых понятий в геометрии, для решения прикладных геометрических и инженерных задач, всё-таки, не очень удобен. Даже тот фундаментальный для евклидовой геометрии факт, что сумма углов в треугольнике равна развёрнутому углу, будет непросто выразить и доказать, оперируя комплексными числами или рациональными точками на окружности. Но в следующей части статьи именно такой взгляд на углы станет нашим основным инструментом.
Эй, тригонометрия, ты почему такая иррациональная?!
Вернёмся к таблице тригонометрических функций, заучиваемой в школе. Почему в школьной таблице синусов и косинусов так мало чисел, которые легко запомнить? Почему тангенсы, синусы и косинусы от «хороших» углов имеют «нехорошие» значения?
Взгляните ещё раз на привычную таблицу тригонометрических функций:
Вся эта красота врывается в жизнь восьмиклассника и способна здорово отравить её неинтуитивными иррациональными значениями, содержащими корни не то из 2 не то из 3, которые как-то надо запоминать. Рациональные значения представлены в этой таблице только четырьмя числами: 0,1/2 и ±1, все же остальные содержат квадратные корни. Наконец, в таблице кроме нулевого и прямого, нет таких углов, для которых все тригонометрические функции принимали бы рациональные значения одновременно.
Из-за этой сплошной иррациональности полностью решить прямоугольный треугольник, то есть узнать все точные значения углов, сторон и их отношений, возможно лишь в двух особых случаях: в треугольнике с углами (45°, 45°, 90°) и с углами (30°, 60°, 90°). Этим треугольникам в школьной программе можно смело ставить памятник!
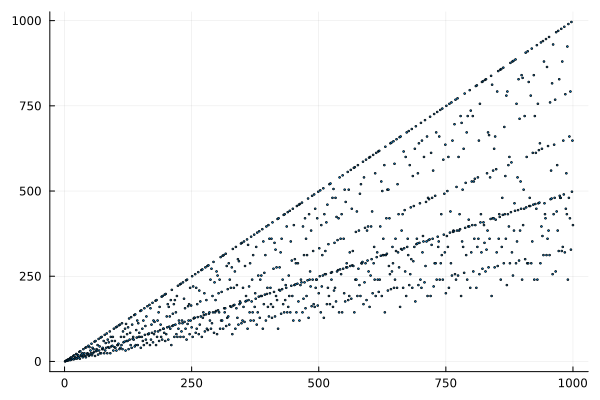
Что же делает перечисленные углы «хорошими», и почему именно их мы заучиваем в школе? Они выражаются целыми числами в угловой мере, то есть, являются делителями 360°, или полного оборота. Может быть, мы не те углы выбрали для таблицы? Давайте взглянем на некоторые другие рациональные доли полного оборота:
Жуть! Ещё хуже стало. Получается, что в школьную таблицу попали те углы, для которых тригонометрия ещё терпимо иррациональна. У других шансов получить звание «хороших» очень невелики.
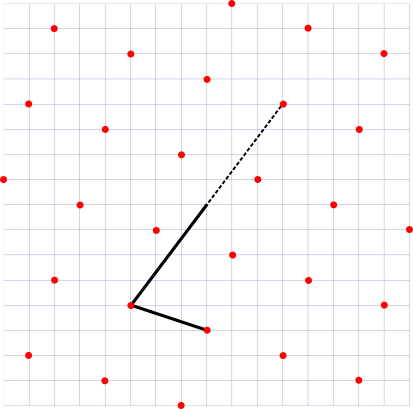
В то же самое время, все тригонометрические функции, это ведь просто отношения длин сторон в прямоугольном треугольнике. В обыкновенной тетрадке в клеточку мы можем нарисовать сколько угодно прямоугольных треугольников с целочисленными сторонами, для которых все тригонометрические функции будут принимать внятные рациональные значения:
Почему же эти значения не оказываются в таблицах тригонометрических функций? Дело в том, что для этих чудесных треугольников невозможно точно вычислить углы: они не будут рациональными долями 360° или полного оборота.
Получается, что либо углы рациональны, но тогда тригонометрия превращается в нагромождение корней, либо тригонометрия рациональна, а углы — нет. Одновременно всё становится рациональным только в самых примитивных случаях для 0°, 90°, 180° и 270°. Это значит, что углы и тригонометрические функции почти всегда несоизмеримы друг с другом. И дело тут не в выборе конкретной угловой меры, а в более фундаментальном свойстве евклидова пространства, в котором мы работаем.
А почему не вместе?
Все прямоугольные треугольники с рациональной тригонометрией имеют стороны, образующие, так называемые, пифагоровы тройки: целые числа и
, такие что
. И все они могут быть построены на регулярной прямоугольной решётке. Но увы, кажется, на этой же решётке невозможно построить никакой угол, выражающийся через рациональную долю полного оборота, кроме тех, что кратны 45°.
Для того, чтобы убедиться в этом, нужно представить точки на регулярной квадратной решётке, как комплексные числа с целыми вещественной и мнимой частями. Они называются гауссовыми числами. Они образуют алгебраическое кольцо и для этих чисел действует основная теорема арифметики и любое гауссово число раскладывается на простые множители не единственным, но вполне определённым способом. Эти разложения имеют некоторые особенности, существенно отличающие их от разложения вещественных целых чисел и из этих особенностей можно вывести следующее утверждение:
Если гауссово число
при возведении в степень
становится вещественным, то либо
, либо
, либо
.
Схема доказательства
Пусть и
. Обозначим как
один из простых делителей
, тогда и сопряжённое ему число
, должно быть делителем числа
, поскольку
, по нашему предположению, вещественное. Отсюда следует, что
делит
, а значит, и
. Таким образом, мы можем заключить, что если
это простой делитель гауссова числа
, то вещественное целое
тоже является делителем
.
Поскольку число
раскладывается на простые множители, каждый из которых должен быть ассоциирован со своим сопряжённым. Для числа
ассоциированными являются три числа:
. Сопряжённое число может быть ассоциированным только если
, или
, или
. Первые два случая соответствуют вещественным множителям. Из третьего случая следует, что
для любого простого делителя
, а это значит, что
должно быть ассоциированным числу
для какого-то целого числа
.
Из этого свойства вытекает следующее:
Углы, которые опираются на узлы регулярной квадратной решётки либо кратны 45°, либо несоизмеримы с 360°.
Доказательство
Доказать это утверждение можно, если вспомнить, что любое комплексное число можно представить в форме
. В такой форме удобно перемножать комплексные числа и возводить в степень. Так, в частности,
.
Рассмотрим гауссово число , образующее с горизонталью (вещественной осью) угол
, где
— натуральное число, а
— целое. Тогда число
будет вещественным. Это для гауссовых чисел означает, что либо
и
, либо
и
, либо
и
. Во всех же остальных случаях многократное умножение на
, эквивалентное повороту вектора
на угол
и одновременному увеличению его длины в
раз, никогда не приведёт к вещественному значению, а значит, этот угол несоизмерим с 360°.
Осталось показать, что это свойство относится не только к углам, отсчитываемым от горизонтальной оси, но справедливо для любого угла, опирающегося на узлы решётки. Это легко продемонстрировать на рисунке, который показывает, что переходя к регулярным подрешёткам, легко можно свести любой угол к доказанному случаю.
Таким образом, школьные задачи, подразумевающие внятный ответ, в которых нужно найти углы, опирающиеся на узлы квадратной сетки, скорее всего, имеют решение 45°, 90° или 135°. Либо задача формулируется на поиск тангенса угла.
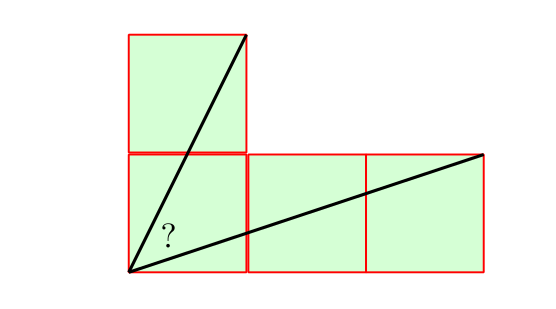
В этой популярной задаче нужно найти точное значение угла, а значит, это может быть только 45°. Её можно решить разными способами, с привлечением геометрии, векторов, вычисляя арктангенсы, но если вас спрашивают про угол, то единственный возможный точный ответ, в принципе, вы уже знаете.
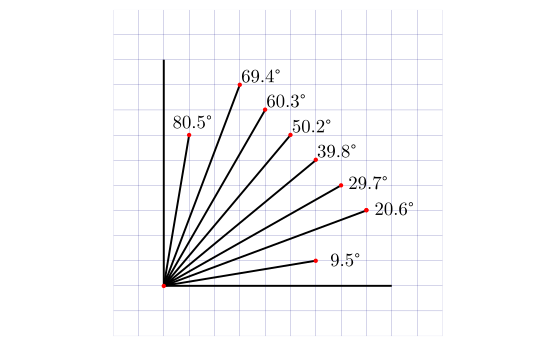
В сети легко найти множество рекомендаций по построению приближений к углам, кратным 10° или даже 5°. Однако, очень мало где говорится, то это только приближения, причём, удобно работающие только для построения углов, отсчитываемых от горизонтали. Впрочем, для быстрых построений они, действительно, могут быть полезны.
Копаемся в тригонометрическом лайфхаке
На многих ресурсах, созданных для облегчения жизни школьникам, то и дело появляются разнообразные лайфхаки: приёмы, существенно облегчающие запоминание чего-либо или упрощающие вычисления. Отношение у педагогов к таким приёмам неоднозначное. Одни с удовольствием их пропагандируют, продвигая мысль, что «Математика — это просто!». Другие возражают: «Ученик — не попка, заученное, но не понятое бесполезно», и считают лайфхаки, шпаргалки и линейки с формулами вредными.
Мне не нравится считать математику простой. Она сложна, но невероятно интересна, а главное, она познаваема! Это же относится и к жизни. Не уверен, что хочу прожить «простую» жизнь, в которой «всё понятно», потому что есть «правильные ответы», найденные кем-то для меня и выученные мною до автоматизмов. Это не вопрос «свободы выбора» или «права на самовыражение». Это про удовольствие, про красоту, про интерес, про мастерство, как в математике, так и в жизни. Так что, мне кажется очень полезным и интересным рассмотреть ответы, найденные другими, и самостоятельно постараться понять, что они означают и откуда взялись.
Выходит, я отношусь тем, кто любит лайфхаки, и с удовольствием о них рассказывает, но использует их, как повод заглянуть «под капот», и разобраться с тем почему, как и при каких условиях они работают. Многие «простые приёмы» имеют под собой интереснейшие и глубокие основания, открывающие двери в разделы серьёзной математики.
Уверен, многие из вас встречали этот симпатичный способ запомнить табличные значения тригометрических функций, синуса и косинуса, в первой четверти, который столь же часто рекомендуют, сколько поругивают:
Польза от этого способа есть, он позволяет не только запомнить значения синуса и косинуса, но и усвоить кто из них растёт, а кто убывает в первой четверти. Но есть в нём кое-что любопытное. Аргумент меняется неравномерно, а под корнями при этом наблюдаются линейные зависимости. Но мы же прекрасно понимаем, что тригонометрия не ограничивается квадратными корнями. О чём говорит нам эта линейная зависимость? Почему значений именно пять, а не больше? И почему под корнями равномерно перебираются четверти?
Откуда взялась линейность
Давайте сначала посмотрим на то, как этот способ выглядит графически. Нанесём значения синуса и косинуса из таблицы, как точки на координатной плоскости.
Ожидаемо получим пять точек, лежащих на окружности с единичным радиусом. Точки, соответствующие подкоренным выражениям (зелёные), при этом выстраиваются в аккуратную линию. В этом тоже нет ничего неожиданного, если вспомнить, что , а значит, квадраты синуса и косинуса, действительно, связаны линейным соотношением.
Почему значений только пять?
В теории полей, есть такой термин степень алгебраического числа. Им обозначается минимальная степень многочлена, корнем которого может быть число.
Например, целые и рациональные числа имеют алгебраическую степень, равную единице, потому что они могут быть решением уравнения для целых коэффициентов
и
. Числа
,
или золотое сечение имеют степень равную двум, потому что являются корнями квадратных уравнений, так же как и гауссовы числа, не являющиеся вещественными. А вот кубический корень, решая квадратное уравнение с рациональными коэффициентами получить не выйдет, тут требуется уравнение третьей степени. Так что
имеет алгебраическую степень, равную трём.
Методами теории полей можно показать, что алгебраическая степень значений тригонометрических функций от угла вида зависит от числа
:
В приведённой выше формуле используется функция Эйлера , которая играет очень важную роль в теории чисел. Она определена на множестве натуральных чисел и равна количеству чисел, не превышающих n и взаимно с ним простых.
Взгляните на первые двенадцать значений функции Эйлера, а также на соответствующие доли круга и алгебраические степени косинуса и синуса для этих долей:
Эту таблицу можно продолжить и дальше, но чем больше оказывается число n, тем больше можно отыскать чисел с ним взаимно простых. Вот как растёт функция Эйлера:
Более или менее удобоваримыми можно считать числа с алгебраической степенью 1 и 2. Но становится больше 2, для всех
, а если
, то
уже не опустится ниже четырёх. Это значит, что в табличке мы перечислили все возможные рациональные доли окружности, в которых косинус и синус имеют шанс попасть на страницы школьного учебника. Таких углов в первой четверти оказывается всего пять, и это ровно те углы, что оказались в таблице, с которой начался наш разговор.
Вот как выглядит распределение по углам максимального значения алгебраических степеней для тригонометрических функций.
Табличные значения углов попадают внутрь радиуса, ограничивающего алгебраические степени меньше 3.
А причём тут четвёрки?
Итак, почему чисел в таблице всего пять, мы разобрались. Понятно также почему они образуют линейную зависимость под корнем. Но каким образом они оказались расположены на одинаковом расстоянии друг от друга, и отчего во всех подкоренных выражениях в знаменателях четвёрки?
Пора нам взглянуть на те самые алгебраические уравнения, о решениях которых мы говорили, когда рассуждали об алгебраических степенях.
В школьном курсе значения тригонометрических функций от примечательных углов выводятся геометрически. Однако эти вычисления можно свести к решению чисто алгебраических задач.
Из формул косинуса суммы несложно получить полезное соотношение:
Подставляя натуральные числа , можно вывести следующие равенства:
Если теперь заменить на формальную переменную
и ввести обозначение
то мы получим последовательность многочленов:
для которых выполняется общее правило:
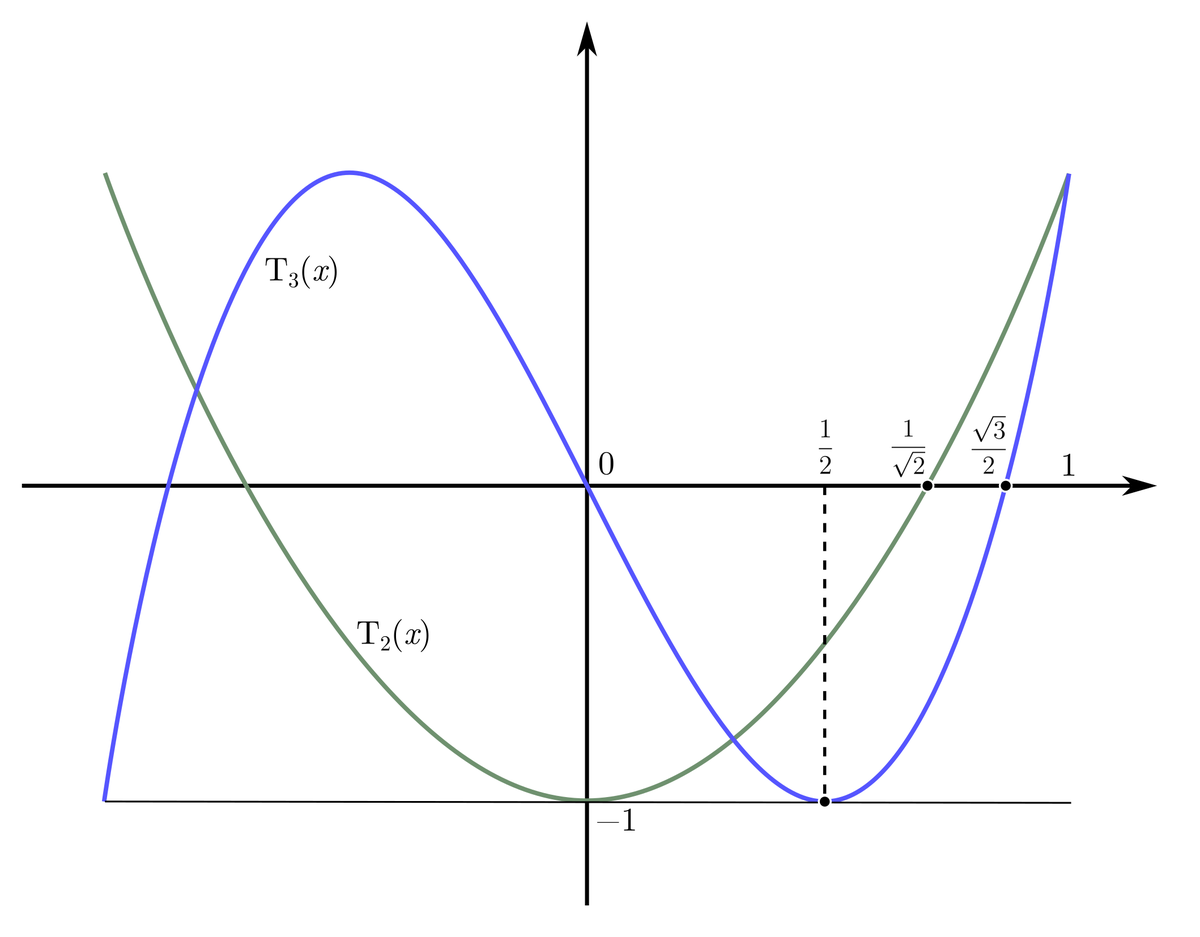
Мы получили семейство многочленов Чебышёва (первого рода), которые используются в широком ряде задач от приближённых вычислений и численного интегрирования, до теории сигналов и радиосвязи.
Приравнивая многочлен к значениям косинуса какого-нибудь угла, можно вычислить косинус от
-ной доли этого угла. Например, решив уравнение
, мы найдём
.
Так можно найти все значения из обсуждаемой нами волшебной таблицы. Например, для мы получаем:
вы можете найти сами алгебраические значения и
, и чтобы почувствовать себя крутым математиком, косинусы румбов NNE и NbE.
Имея общий вид для многочленов Чебышёва, можно увидеть откуда берутся четвёрки в таблице-лайфхаке. Обратите внимание на то, что все многочлены имеют коэффициент при старшей степени вида
, который появляется из-за двойки в рекуррентном определении многочленов. В то же время, все пять значений из мнемонической таблицы получаются из уравнений, вытекающих из
и
. А в них старшие коэффициенты равны 2 или 4. В результате, все квадраты значений с алгебраической степенью не превышающей 2, можно записать так, чтобы старший коэффициент был равен 4. Для других долей окружности порядки уравнений становятся выше, и либо их решения будут выражаться через нагромождение корней и дробей, либо не решаются в конечной форме вовсе.
Подведём итог нашей вылазки. Мы выяснили, что среди углов, являющихся рациональной долей полного круга, есть только пять, для которых значения синуса и косинуса имеют алгебраическую степень 1 или 2. Для всех этих углов уравнения, выводимые из многочленов Чебышёва имеют старший коэффициент 2 или 4, таким образом, все эти значения будут квадратными корнями из рациональных чисел со знаменателем 4. Так как все они должны оказаться в интервале [0, 1], то в нашем распоряжении оказывается ровно пять таких рациональных чисел: 0/4, 1/4, 2/4, 3/4 и 4/4. Иные значения возможны, но будут иметь более сложную структуру и более высокую алгебраическую степень.
Используя теорию чисел, можно составить исчерпывающий список значений уклонов, имеющих алгебраическую степень 2, соответствующих углам, соизмеримым с 2π. И убедиться в том, что все они выражаются целыми значениями, если измерять углы в часах.
По-моему, теория чисел и теория полей — это круто! Здорово иметь возможность не просто вычислять какие-то значения, а ещё до начала вычислений знать, в какой мере эти значения вычислимы. Именно благодаря таким рассуждениям удалось дать исчерпывающий ответ на давний вопрос: какие задачи можно решить с помощью циркуля и линейки, а какие нельзя.
Благодарю за храбрость тех, кто пробрался вместе со мной сквозь дебри теории! Вместе не так страшно. А тех, кому интересно, приглашаю на Дзен-канал Онлайн-кружок математики, в котором занимательно-математические статьи появляются в облегчённом варианте.
Предыдущие статьи в серии Математическая продлëнка:
Квадратные уравнения во всей красе
Теория чисел на пальцах