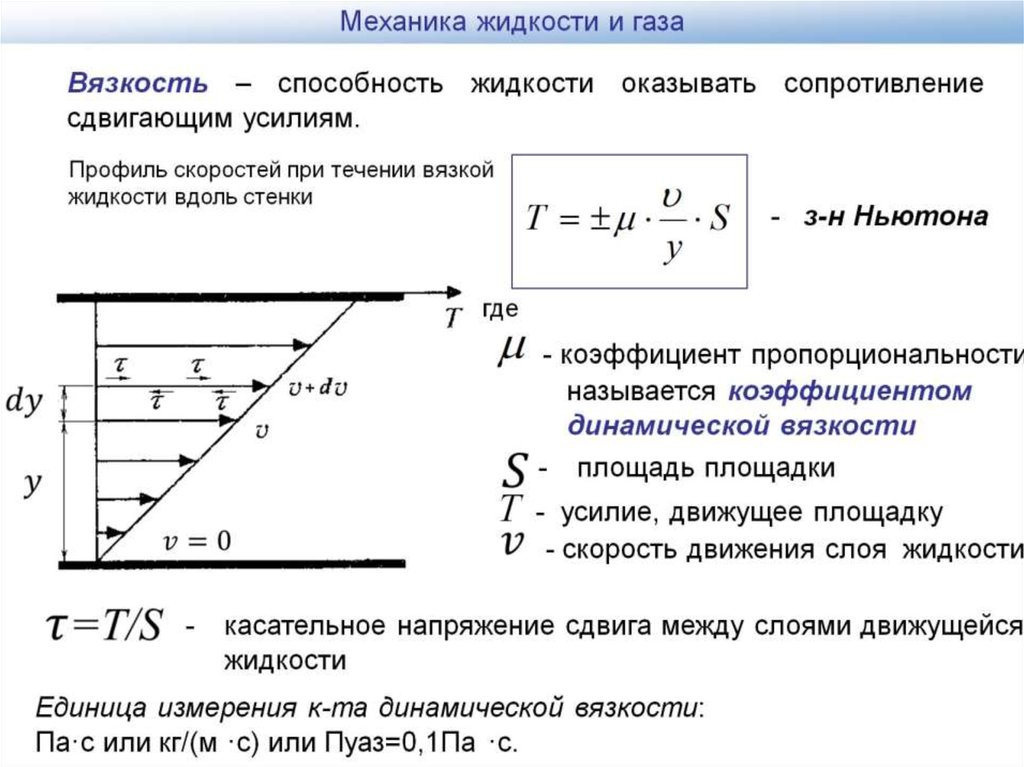
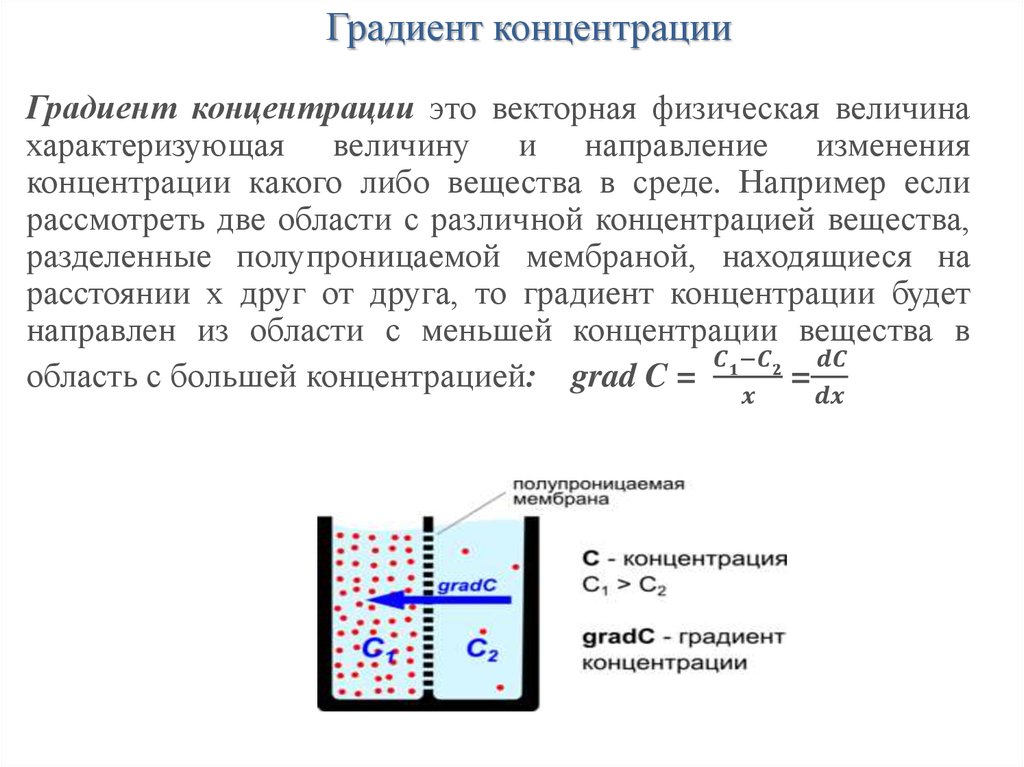
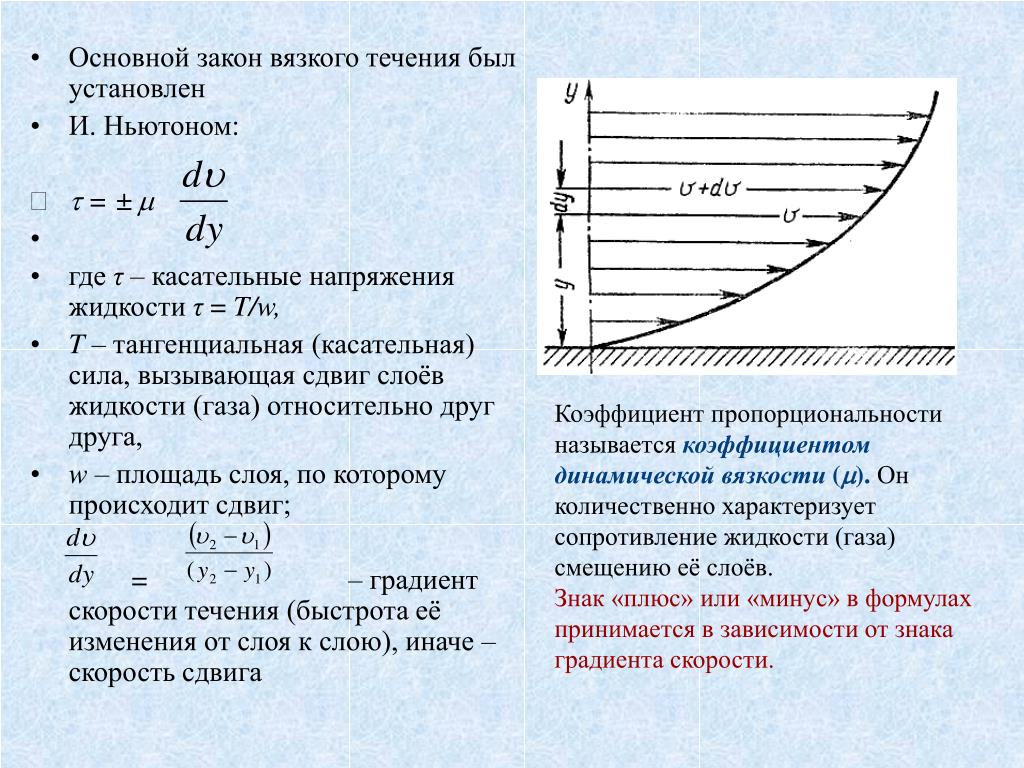
Физический смысл градиента скорости:
Градиентом
любой физической величины называется
изменение этой величины, отнесённое
к расстоянию, вдоль которого это изменение
происходит.
3.
Силы внутреннего трения зависят от
природы жидкости, так как молекулы
различных жидкостей находятся на
различных расстояниях
и имеют различную скорость, а следовательно
и кинетическую энергию. Эта зависимость
учитывается коэффициентом вязкости
— η.
Таким
образом, силы внутреннего трения зависят
от природы жидкости, прямо пропорциональны
градиенту скорости и площади
соприкасающихся слоев.
Fη
= η
(dυ/dx)S
Эта
формула получила название формулы
Ньютона. Если площадь соприкасающихся
слоев S
= 1 и градиент скорости dυ/dx
= 1, то Fтр
=
η
Коэффициентом
вязкости или
вязкостью жидкости называется
величина численно равная силе трения,
возникающей между двумя слоями жидкости,
соприкасающимися на площади равной
единице и при градиенте скорости между
ними равным единице.
Коэффициент
вязкости измеряется в системе СИ: η
=Fηdx/Sdυ;
Н м / м2
(м/с) = Н с / м2
= Па с
В
системе СГС: Пуаз (Пз) = дн с / см2;
Н с / м2
= 105
дн с / 104
см2
= 10 Пз. В медицине принято измерять
вязкость в Пуазах.
Коэффициент
вязкости зависит не только от природы
жидкости, но и от температуры. С
повышением температуры коэффициент
вязкости уменьшается. Это объясняется
тем, что с повышением температуры
расстояния между молекулами увеличиваются,
а силы взаимодействия ослабляются.
Ввиду
больших трудностей, возникающих при
непосредственном измерении вязкости
её определяют косвенным путём. Наибольшее
применение имеют методы: падающего
шарика и капиллярного визкозиметра.
Метод
падающего шарика основан на законе
Стокса. Стокс установил, что на
небольшое тело шаровидной формы,
перемещающееся в жидкости, действует
сила трения, прямо пропорциональная
радиусу этого тела, его скорости и
коэффициенту вязкости жидкости.
Fтр
= 6πηrυ
Если
бросить в жидкость металлический шарик
диаметром 0,2—0,3 мм, то он будет двигаться
в жидкости равномерно. На движущийся
шарик будут действовать три силы
1.
Сила тяжести Р = mg,
направленная вертикально вниз.
2.
Выталкивающая сила FB,
направленная вертикально вверх.
3.
Сила трения FTp,
направленная также вертикально
вверх.
По
первому закону Ньютона тело двигается
равномерно, если равнодействующая всех
сил, действующих на него, равна 0.
По
закону Стокса Fтр
= 6πηrυ,
P
= mg;
m
= pTV;
P=pTVTg
=4/3 πr3pTg
Радиус
шарика можно измерить с помощью микроскопа
с окулярным микрометром, скорость
движения шарика можно определить по
формуле V
= s
/t,
измерив линейкой s,
а секундомером — t.
Метод довольно точен, используется в
санитарии. В медицинской практике для
определения коэффициента вязкости
крови, спиномозговой жидкости и других
биологических жидкостей пользуются
методом капиллярного вискозиметра,
основанный на законе Гагена-Пуазейля.
Они установили, что объём
жидкости, протекающей через поперечное
сечение капилляра (R<1мм
) в единицу времени прямо пропорционален
R4,
dP/dl
и обратно пропорционален η, коэффициент
пропорциональности в системе СИ
равен π/8.
Q=(πR4dP)/(8ηdl)
где
dP/dl
— градиент давления, dP
— разность давлений в начале и в конце
капилляра, dl
— длина капилляра. При пропускании
жидкостей через капилляры с одинаковым
радиусом при одинаковом градиенте
давления, получим:
V1/t
= πR4/8η1dl
объём 1 жидкости
V2/t
= πR4/8η2dl
объем 2 жидкости
Найдём
относительную вязкость, поделив 1
выражение на 2.
η2/η1
= V1/V2
— формула Гагена-Пуазейля.
Вискозиметр
состоит из двух пипеток — капилляров,
укреплённых на общей подставке. Один
капилляр имеет кран. Сначала втягивая
воздух заполняют капилляр (б) стандартной
жидкостью, как правило водой, до нулевого
деления, закрывают кран и затем
заполняют капилляр (а) исследуемой
жидкостью до нулевого деления. Открыв
кран, втягивают обе жидкости одновременно
так, чтобы исследуемая жидкость дошла
до деления.
Тогда
число делений трубки (б) укажет
относительную вякость. Зная η1,
определим η2
по
формуле:
η2
= η1V1
Преимущество
и недостатки этого метода:
1.
Позволяет измерять вязкость небольшого
количества .жидкости;
2.
Быстрота измерения (особенно для крови
— быстро свёртывается);
3.
Измерение вязкости непрозрачных
жидкостей.
Недостаток
— малая точность ввиду отсутствия
стандарта. Течение жидкости называется
ламинарным
или
слоистым, если поток жидкости представляет
собой совокупность слоев, перемещающихся
относительно друг друга без перемешивания.
При некоторой высокой скорости
течение становится турбулентным
(вихревым),
когда
происходит перемешивание слоев жидкости.
При
турбулентном течении жидкости возрастают
силы трения, а следовательно и работа
по преодолению сил трения. Это течение
жидкости сопровождается звуковым
феноменом.
Скорость,
при которой ламинарное течение переходит
в турбулентное называется критической
(υ кр.)
Величина
этой скорости зависит от вязкости
жидкости, радиуса трубки, плотности
жидкости и состояния внутренней
поверхности. Критическая скорость
вычисляется по формуле:
υкр
= (Rсеη)/pD
где
η — вязкость жидкости, р — плотность, D
—
диаметр трубки. Безразмерная величина
Rсе
называется числом Рейнольдса. Для
гладких трубок Rсе
= 2300, для трубок с шероховатыми
поверхностями эта величина меньше.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Градиенты скорости Калькулятор
| Search | ||
| Дом | Инженерное дело ↺ | |
| Инженерное дело | Гражданская ↺ | |
| Гражданская | Гидравлика и гидротехнические сооружения ↺ | |
| Гидравлика и гидротехнические сооружения | Ламинарный поток ↺ | |
| Ламинарный поток | Измерение вязкости — вискозиметры ↺ | |
| Измерение вязкости — вискозиметры | Вискозиметры с коаксиальным цилиндром ↺ |
|
✖Радиус 2 — это радиальная линия от фокуса до любой точки кривой для 2-го радиуса.ⓘ Радиус 2 [r2] |
+10% -10% |
||
|
✖Угловая скорость определяется как скорость изменения углового смещения.ⓘ Угловая скорость [Ω] |
+10% -10% |
||
|
✖Радиус 1 — это радиальная линия от фокуса до любой точки кривой для 1-го радиуса.ⓘ Радиус 1 [r1] |
+10% -10% |
|
✖Градиент скорости – это разница скоростей между соседними слоями жидкости.ⓘ Градиенты скорости [VG] |
⎘ копия |
Градиенты скорости Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Радиус 2: 13 метр —> 13 метр Конверсия не требуется
Угловая скорость: 5 оборотов в секунду —> 31.4159265342981 Радиан в секунду (Проверьте преобразование здесь)
Радиус 1: 12 метр —> 12 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
42.7682857358759 метр в секунду —> Конверсия не требуется
22 Вискозиметры с коаксиальным цилиндром Калькуляторы
Градиенты скорости формула
Градиент скорости = pi*Радиус 2*Угловая скорость/(30*(Радиус 2—Радиус 1))
VG = pi*r2*Ω/(30*(r2—r1))
Что такое градиент скорости?
Разница в скорости между соседними слоями жидкости известна как градиент скорости и определяется выражением v / x, где v — разность скоростей, а x — расстояние между слоями.
Что такое градиент скорости физика?
Что такое градиент скорости физика?
Градиент скорости — В вязкой жидкости существует перепад скоростей ее движущихся слоев вдоль оси Z, перпендикулярной направлению движения жидкости. Количественно величина различий в скорости движения слоев жидкости характеризуется градиентом скорости dv/dx,… … Википедия градиент скорости — — [А.
Что если градиент равен нулю?
Мы можем смело сказать , что если градиент равен нулю в одной декартовой системе координат, то он равен нулю в каждой подобной системе координат. А если градиент не равен нулю то его независимость от выбора декартовой системы координат следует из его геометрического смысла .
Что такое градиент скалярного поля?
Если в каждой точке пространственной области определено значение некоторой величины, то говорят, что в данной области задано поле этой величины. Таким образом, в направлении градиента скалярная функция изменяется быстрее, чем в других направления. …
Что представляет собой градиент скорости?
В вязкой жидкости существует перепад скоростей ее движущихся слоев вдоль оси Z, перпендикулярной направлению движения жидкости. Количественно величина различий в скорости движения слоев жидкости характеризуется градиентом скорости dv/dx, называемым также скоростью сдвига.
Как определить скорость роста функции?
Скорость изменения функции — это первая производная. Если она больше нуля, то функция растёт, если равна нулю — то функция в окрестности данной точки не изменяется, если же она меньше нуля, то функция убывает. Чем производная по модулю больше, тем быстрее функция изменяется.
Что растет быстрее экспонента или степенная функция?
Показательная функция растет быстрее степенной, а степенная – быстрее логарифмической.
Что растет быстрее Факториал или экспонента?
Известно что экспонента растет быстрее любого конечного полинома.
Экспонента за единицу времени увеличивается в константу раз, а факториал — во все возрастающее число раз. следовательно факториал растет быстрее любого конечного полинома.
Что такое производная на графике?
Производная — это скорость изменения функции. На рисунке — графики трех функций.
Что такое производная функции простым языком?
Понятие производной Производная функции — это отношение приращения функции к приращению аргумента при бесконечно малом приращение аргумента. Приращением в математике называют изменение.
Что такое дифференциал в математике простым языком?
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции. Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Что такое производная простыми словами?
Производная по определению это предел отношения прироста значения функции к приросту аргументы при стремлении прироста аргумента к нулю.
Что является производной в механическом смысле?
Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017. Давайте вспомним механический смысл производной: Производная y'(x) функции y=f(x) – это мгновенная скорость изменения этой функции.
Как называется действие нахождения производной?
Определение. Производной функции называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует): . … Процесс нахождения производной функции называется дифференцированием этой функции.
Что такое производная?
Произво́дная — функция, являющаяся результатом применения той или иной операции дифференцирования к исходной функции. Физический смысл производной — скорость изменения величины или процесса.
Чему равна производная функции?
Произво́дная функции — понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке.
Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует.
Чему равна производная?
Производная от числа всегда равна 0. Так как скорость изменения значения функции в данном случае равна 0 при любом изменении аргумента.
Что показывает первая производная функции?
(first derivative) Темп прироста значения функции при приросте ее аргумента в какой-либо точке, если сама функция в этой точке определена. На графике первая производная функции показывает угол ее наклона.
Что такое производная от числа?
Пояснение: Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях — скорость его изменения всегда равна нулю.
Зачем дифференцировать функцию?
Дифференцируют непрерывные функции, потому что для них нельзя просто взять какие то два значения и рассчитать скорость изменения функции — это будет средняя скорость на этом участке, а не моментальная.
Поэтому придумали дифференциальное исчисление.
Для чего нужна производная функции?
Производная функции в точке является основным понятием дифференциального исчисления. Она характеризует скорость изменения функции в указанной точке. Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости различного рода процессов.
Что такое производная функции для чайников?
Определение производной: Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю. … Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Чему равна производная линейной функции?
Формула Производная линейной функции равна константе, стоящей возле переменной x.
В чем заключается геометрический смысл производной функции?
Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. … В этом и состоит геометрический смысл производной.
Что значит касательная?
Прямая, имеющая одну общую точку с окружностью и лежащая с ней в одной плоскости, называется касательной к окружности.
В чем заключается геометрический и механический смысл производной?
Геометрический и механический смысл производной Производная. … Производной функции в точке называется предел, к которому стремится отношение приращение функции к приращению аргумента, когда приращение аргумента стремится к нулю (формула 1).
Какую прямую называют касательной к графику функции?
Касательная к графику функции Если точку P двигать по графику, приближая ее к точке M, то прямая MP начнет поворачиваться вокруг точки M. … Это предельное положение представляет собой прямую, которая и называется касательной к графику функции y = f (x) в точке x = a.
Градиент скорости Калькулятор | Вычислить Градиент скорости
|
✖Изменение скорости — это разница между скоростями соседних слоев жидкости.ⓘ Изменение скорости [dv] |
Сантиметр в часСантиметр в минутуСантиметр в секундуКосмическая скорость прежде всегоКосмическая скорость СекундаКосмическая скорость третьяСкорость ЗемлиФут в часФут в минутуФут в секундуКилометры / часКилометр в минутуКилометры / секМорской узелУзел (Великобритания)маакМаха (стандарт СИ)Метр в часМетр в минутуметр в секундумили / часмили / минутумили / секМиллиметр / часМиллиметр в минутуМиллиметр / секМорская миля в деньМорская миля в часСкорость звука в чистой водеСкорость звука в морской воде (20 ° C и 10 метров глубиной)Двор / часДвор / минутуДвор / сек |
+10% -10% |
|
|
✖Изменение расстояния — это разница между последовательными точками между соседними слоями жидкости.ⓘ Изменение расстояния [dy] |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
+10% -10% |
|
✖Градиент скорости — это разница скоростей между соседними слоями жидкости. |
АттогерцУдары / минутаСантигерцЦикл / секДекагерцдецигерцExahertzFemtohertzфрамес 3a второйГигагерцгектогерцГерцКилогерцмегагерцмикрогерцмиллигерцнаногерцпетагерцPicohertzРеволюция в деньоборотов в часоборотов в минутуоборотов в секундуТерагерцЙоттахерцЗеттахерц |
⎘ копия |
ⓘ Градиент скорости [dv/dy]
👎
Формула
сбросить
👍
Градиент скорости Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
Преобразование входов в базовый блок
Изменение скорости: 10 метр в секунду —> 10 метр в секунду Конверсия не требуется
Изменение расстояния: 1000 Миллиметр —> 1 метр (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
10 Герц —>10 Цикл / сек (Проверьте преобразование здесь)
<
10+ Свойства жидкости Калькуляторы
Градиент скорости формула
Градиент скорости = Изменение скорости/Изменение расстояния
dv/dy = dv/dy
Что такое градиент скорости?
Разница в скорости между соседними слоями жидкости известна как градиент скорости и выражается как v / x, где v — разность скоростей, а x — расстояние между слоями.
Share
Copied!
Важность градиента скорости и крутящего момента при расчете двигателя постоянного тока
Градиент скорости / крутящего момента является показателем производительности двигателя.
Чем меньше значение, тем мощнее двигатель и, следовательно, меньше скорость двигателя изменяется при изменении нагрузки. Он основан на соотношении идеальной скорости холостого хода и идеального крутящего момента.
Важность градиента скорости-крутящего момента при определении размера двигателя постоянного тока
Уоррен Осак | Серво2Го
23.04.20, 05:28
| Промышленная робототехника, автоматизация производства
| Servo2Go.com Ltd.
| мотор, отдел запчастей
Часто при расчете двигателей постоянного тока упускается из виду градиент скорости-крутящего момента.
Градиент скорости-крутящего момента определяется как Δn / ΔM [об/мин/мНм].
Градиент скорости/крутящего момента – это показатель производительности двигателя.
Чем меньше значение, тем мощнее двигатель и, следовательно, меньше скорость двигателя изменяется при изменении нагрузки. Он основан на соотношении идеальной скорости холостого хода и идеального крутящего момента.
Градиент крутящего момента скорости можно рассматривать как меру мощности двигателя, которая определяется типом и размером двигателя, а не выбранной обмоткой. По сути, это то, насколько падает скорость двигателя на каждый 1 мНм крутящего момента.
На рисунке выше увеличение момента нагрузки приводит к линейному уменьшению скорости. Таким образом, становится ясно, что означает Δn/ΔM: это градиент линии скорость-момент.
Содержание и мнения в этой статье принадлежат автору и не обязательно отражают точку зрения RoboticsTomorrow
Servo2Go.com Ltd.
Servo2Go.com является онлайн-дистрибьютором систем и компонентов автоматизации и управления движением. в том числе: серводвигатели и приводы, шаговые двигатели и приводы, контроллеры автоматизации и движения, системы позиционирования и приводы, коробки передач, муфты, тормоза, энкодеры, тахометры, датчики линейного перемещения, HMI, ПЛК и встроенные контроллеры.
Servo2Go.com является ISO9001:2008 Зарегистрированная компания.
Другие статьи
Понимание постоянной двигателя при расчете двигателя постоянного тока
Одним из наиболее часто упускаемых из виду параметров двигателей постоянного тока (как щеточных, так и бесщеточных) является Км или постоянная двигателя. Постоянная двигателя (выраженная в км) определяет способность двигателя преобразовывать электрическую энергию в механическую.
Понимание пульсаций крутящего момента в серводвигателях
Пульсации крутящего момента должны определяться как функция выходной нагрузки и скорости. Для спецификации нагрузки наиболее подходящей номинальной точкой является номинальный тепловой крутящий момент для непрерывного режима работы серводвигателя.
Подробнее о Servo2Go.com Ltd.
23.
04.20, 05:28
| Промышленная робототехника, автоматизация производства
| Servo2Go.com Ltd.
| мотор, отдел запчастей
Другие статьи по автоматизации производства | Истории | Новости
Эта запись не имеет комментариев. Будьте первым, кто оставит комментарий ниже.
Опубликовать комментарий
Прежде чем оставлять комментарии, вы должны войти в систему. Войти сейчас.
Рекомендуемый продукт
Harmonic Drive представляет новые облегченные версии отдельных редукторов.
Компания Harmonic Drive LLC, лидер в области высокоточного управления движением, представляет новые облегченные версии некоторых редукторов. Новые редукторы идеально подходят для конструкций, в которых вес является критическим фактором.
Основываясь на успехе нынешних редукторов Harmonic Drive LLC, новые облегченные версии стали следующей логической эволюцией продуктовых линеек CS/SH. Благодаря снижению веса на 20-30 % без снижения номинального крутящего момента легкие (LW) редукторы обеспечивают исключительную плотность крутящего момента.
Счет, математика и статистика — Набор академических навыков
Графики скорость-время и расстояние-время (механика)
Главное меню ContentsToggle 1 Графики скорость-время 2 Рабочий пример: Графики скорость-время и графики ускорение-время 3 Проверьте себя
Графики скорость-время
На графике скорость-время скорость всегда откладывается по вертикальной оси, а время всегда откладывается по горизонтальной. Это представляет собой движение частицы, ускоряющейся от скорости в момент времени $0$, $u$, до скорости $v$ в момент времени $t$.
Градиент линии графика скорость-время есть ускорение частицы (для прямых ускорение постоянно).
begin{align} text{Градиент линии} & = frac{text{изменение скорости} }{text{время}}, \ & = frac{v — u}{t}, \ &= а. end{align} Площадь под графиком скорость-время — это расстояние, которое проходит частица. begin{align} text{Заштрихованная область} & = left( frac{u + v}{2} right)t, \ & = s. end{выравнивание}
Графики «расстояние-время» и Графики «ускорение-время» также могут быть построены для движения частицы, где время всегда откладывается по горизонтальной оси.
Прямая линия на графике расстояние-время показывает, что частица имеет постоянную скорость
. Кривизна предполагает, что частица ускоряется или замедляется .
Рабочий пример: графики скорость-время и ускорение-время
Пример с автомобилем на прямой дороге 9{-1} }$ за $2T mathrm{seconds}$. Затем он движется с постоянной скоростью в течение $1 mathrm{минуты}$. Затем автомобиль равномерно замедляется до состояния покоя еще за $8T mathrm{seconds}$.
Градиент скорости
- Градиент скорости
-
Градиент скорости
В вязкой жидкости существует перепад скоростей ее движущихся слоев вдоль оси Z, перпендикулярной направлению движения жидкости.
Количественно величина различий в скорости движения слоев жидкости характеризуется градиентом скорости dv/dx, называемым также скоростью сдвига.
Значение градиента скорости жидкости, текущей по трубе, так же как и величина скорости, изменяется от стенок к центру. Однако,если скорость минимальна у стенок и максимальна в центре, то значение градиента, наоборот, максимально у стенок и минимально вблизи центра.
Wikimedia Foundation.
2010.
The velocity gradient is defined by L=∂v∂x=(∇v)T=(gradv)T or Lij=∂vi∂xj, which is additively decomposed into the symmetric and skew-symmetric parts as(2.3.2)L=12(L+LT)+12(L−LT)=D+WorLij=12(Lij+Lji)+12(Lij−Lji),respectively.
From: Dislocation Mechanism-Based Crystal Plasticity, 2019
Nonlocal continuum plasticity
George Z. Voyiadjis, Mohammadreza Yaghoobi, in Size Effects in Plasticity, 2019
2.4.1.9 Spin tensor
The velocity gradient tensor lij can be additively decomposed to the symmetric and unsymmetric tensors as follows:
(2.336)lij=dij+ωij
where dij is the symmetric part of the velocity gradient tensor lij [Eq. (2.332)], while ωij, which is commonly termed as the spin tensor, is its asymmetric part, i.e., ωij = −ωji. The spin tensor ωij can be obtained by rewriting Eqs. (2.332), (2.336) as follows:
(2.337)ωij=lij−dij=12lij−lji
It can be proved that the spin tensor ωij can be related to the rotation tensor Rij by substituting Eqs. (2.327), (2.292a) as follows (see Bonet and Wood, 2008):
(2.338)ωij=ṘiKRjK
One can see that the spin tensor ωij is solely related to the rotation tensor Rij. In other words, while the rate of deformation tensor dij is the representative of the contribution of stretching to the velocity gradient tensor lij, the spin tensor ωij is the contribution of rotary deformation.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128122365000025
Kinematics
Stephen E. Bechtel, Robert L. Lowe, in Fundamentals of Continuum Mechanics, 2015
3.4 Velocity gradient, rate of deformation tensor, vorticity tensor
The velocity gradient L is defined as the gradient of the spatial description of the velocity v, i.e.,
(3.56)L=gradv=∂∂xv~(x,t).
Following (2.17), the velocity gradient may be expressed as the sum of a symmetric tensor D and a skew tensor W, i.e.,
(3.57)L=D+W,
where
(3.58)D=12(L+LT),W=12(L−LT).
D and W are called the rate of deformation tensor and the vorticity tensor, respectively. Note that (3.57) is an additive (or parallel) decomposition of the velocity gradient L; contrast this with the multiplicative (or serial) decomposition of the deformation gradient F presented in Section 3.3.3.
Recall that there is a one-to-one correspondence between vectors and skew tensors (refer to (2.65)). Thus, given the skew vorticity tensor W in (3.58), there exists a unique vector w such that
Ws=w×s
for any vector s. The vector w is the axial vector of the vorticity tensor W, and may be expressed as
(3.59)w=12curlv=12ω.
In (3.59), ω is called the vorticity vector, and the velocity v is regarded as a function of x and t (spatial description).
It can be shown (refer to Problems 3.10–3.12) that the material derivatives of F, C, E, and J are
Problem 3.10
In direct notation, prove that F.=LF.
Solution
F.=∂∂tF^(X,t)(description(3.13))=∂∂t(∂χ(X,t)∂X)(definition(3.27))=∂∂X(∂χ(X,t)∂t)(continuity ofχ(X,t))=∂v^(X,t)∂X(definition(3.14)1)=∂v^(x,t)∂x∂χ(X,t)∂X(switch to Eulerian description ofv)=LF(definitions(3.27)and(3.56)).
Problem 3.11
Prove in direct notation that C.=2E.=2FTDF.
Solution
To begin, we have
C.=FTF¯·=FTF¯·+FTF.=(F.)TF+FTF.,
where results (3.22)5 and (3.23)2 have been used. Then,
(F.)TF+FTF.=(LF)TF+FTLF=FTLTF+FTLF=2FT[12(LT+L)]F=2FTDF,
so
C.=2FTDF.
Also,
E.=12(C−I)¯·=12C.=FTDF.
Problem 3.12
In direct notation, show that J.=Jdivv.
Solution
We have
J.=detF¯·=ddF(detF)·F.,
which follows from use of the chain rule (2.95)1. Recall from Problem 2.48 that
ddA(detA)·S=(detA)tr(SA−1)
for any tensor S; it follows from this result (by setting A = F and S=F.) that
ddF(detF)·F.=(detF)tr(F.F−1)=Jtr(LFF−1)=Jtr(LI)=JtrL.
Thus,
J.=JtrL=Jtr(gradv)=Jdivv.
(3.60)F.=LF,C.=2E.=2FTDF,J.=detF¯·=Jdivv.
We can also verify that
(3.61)F.=Gradv,F−1¯·=−F−1L,divv=trD.
Recall from Section 3.3.2 that λ is the stretch of the line element dx in the current configuration (whose direction is along unit normal n), which was formerly line element dX in the reference configuration (whose direction was along unit normal N). It can be shown (refer to Problem 3.13) that
Problem 3.13
Prove in direct notation that λ./λ=D·(n⊗n).
Solution
To begin, we take the material derivative of (3.33), which leads to
2λλ.=C.·(N⊗N),
where we have used result (3.22)6; note that N⊗N¯·=0. Now, working with the right-hand side, we have
C.·(N⊗N)=2FTDF·(N⊗N)=2N·(FTDF)N,
where we have used results (2.43) and (3.60)2. Definition (2.13) and results (2.43) and (3.32) then imply that
2N·FT(DFN)=2(FN)·D(FN)=2(λn)·D(λn)=2λ2(n·Dn)=2λ2D·(n⊗n).
Thus,
2λλ.=2λ2D·(n⊗n),
or, equivalently,
λ.λ=D·(n⊗n).
(3.62)λ.λ=lnλ¯·=n·Dn=D·(n⊗n).
Result (3.62) indicates the physical significance of D as a measure of the rate of stretching and rate of shearing of line elements: diagonal components of D give the logarithmic rates of stretching of line elements instantaneously aligned with the basis directions; off-diagonal components of D give the rate of shearing of line elements instantaneously aligned with perpendicular basis directions.
If n* is an eigenvector of D, then it can be shown (refer to Problem 3.14) that
Problem 3.14
If n* is an eigenvector of D, prove in direct notation that
- (a)
-
Dn*=(λ.*/λ*)n*, so the associated eigenvalue is λ.*/λ*, and
- (b)
-
n.*=Wn*=w×n*.
Solution
- (a)
-
Recall from (3.62) that
n·Dn=λ.λ,
where λ is the stretch associated with the line element oriented along direction n in the present configuration. Since n is a unit vector, n · n = 1, and we have
n·Dn=λ.λ(n·n).
Properties (2.6) of the inner product then allow us to write
(Dn−λ.λn)·n=0,
from which the eigenvalue problem for D follows:
Dn=λ.λn.
If n = n* is an eigenvector of D, then it satisfies the above equation, i.e.,
Dn*−λ.*λ*n*,
and the associated eigenvalue is λ.*/λ*.
- (b)
-
Recall from (3.32) that
λn=FN.
Taking the material derivative of both sides, i.e.,
λn¯·=FN¯·,
leads to
λ.n+λn.=F.N+FN.,
where we have used (3.22). Noting that N.=0, we find from (3.32) and (3.60)1 that
n.=Ln−λ.λn.
If n = n* is an eigenvector of D, with associated eigenvalue λ.*/λ*, then
n.*=Ln*−λ.*λ*n*=Ln*−Dn*=[L−12(L+LT)]n*=12(L−LT)n*=Wn*.
The vorticity tensor W is a skew tensor, and for every skew tensor there exists a unique axial vector w such that Ws = w × s for any vector s. Thus,
n.*=Wn*=w×n*.
(3.63)Dn*=λ.*λ*n*,
so the associated eigenvalue of D is λ.*/λ*. Also, we can verify (refer to Problem 3.14) that
(3.64)n.*=Wn*=w×n*.
It is seen from (3.64) that the axial vector w is the angular velocity of the line element that is along an eigenvector of D, so W has the physical significance of being the rate of rotation of the small neighborhood. Motions for which W (or w) are zero are called irrotational motions.
Note that the velocity gradient L, the rate of deformation tensor D, and the vorticity tensor W depend only on the present configuration, and have no connection to any reference or previous configuration. This is in contrast to the deformation measures F, F−1, C, B, c, E, and e of Section 3.3, which all describe some feature of the present configuration relative to a reference configuration.
Loosely, the response of a “solid” depends on the deformation of the continuum away from some reference (usually stress-free) configuration, whereas the response of a “fluid” depends only on the flow configuration at that instant. Therefore, as we shall see, the response functions (e.g., the relations between stress and strain) for a “solid” involve deformation measures like F, and the response functions for a “fluid” involve deformation measures like L. The response functions of rate-dependent materials (e.g., viscoelastic materials) involve both F and L (through F.=LF; such materials have both “solid-like” and “liquid-like” characteristics).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123946003000034
Single-Phase Liquid Flow in Minichannels and Microchannels
Satish G. Kandlikar, in Heat Transfer and Fluid Flow in Minichannels and Microchannels (Second Edition), 2014
3.2.2 Fully developed laminar flow
The velocity gradient at the channel wall can be readily calculated from the well-known Hagen–Poiseuille parabolic velocity profile for the fully developed laminar flow in a circular pipe. Using this velocity profile, τw and f are obtained from Eqs. (3.3) and (3.4). The result for friction factor f is presented in the following form:
(3.8)f=PoRe
where Po is the Poiseuille number, (Po=f Re), which depends on the flow-channel geometry. Table 3.1 gives the f Re product and the constant Nusselt number (Nu) in the fully developed laminar flow region for different duct shapes, as derived from Kakac et al. (1987).
Table 3.1. Fanning Friction Factor and Nusselt Number for Fully Developed Laminar Flow in Ducts, Derived from Kakac et al. (1987)
| Duct Shape | NuH | NuT | Po=f Re | ||
|---|---|---|---|---|---|
| Circular | 4.36 | 3.66 | 16 | ||
| Flat channel | 8.24 | 7.54 | 24 | ||
| Rectangular, aspect ratio, b/a = | 1 | 3.61 | 2.98 | 14.23 | |
| 2 | 4.13 | 3.39 | 15.55 | ||
| 3 | 4.79 | 3.96 | 17.09 | ||
| 4 | 5.33 | 4.44 | 18.23 | ||
| 6 | 6.05 | 5.14 | 19.70 | ||
| 8 | 6.49 | 5.60 | 20.58 | ||
| ∞ | 8.24 | 7.54 | 24.00 | ||
| Hexagon | 4.00 | 3.34 | 15.05 | ||
| Isosceles triangle, apex angle θ = | 10° | 2.45 | 1.61 | 12.47 | |
| 30° | 2.91 | 2.26 | 13.07 | ||
| 60° | 3.11 | 2.47 | 13.33 | ||
| 90° | 2.98 | 2.34 | 13.15 | ||
| 120° | 2.68 | 2.00 | 12.74 | ||
| Ellipse, major/minor axis a/b= | 1 | 4.36 | 3.66 | 16.00 | |
| 2 | 4.56 | 3.74 | 16.82 | ||
| 4 | 4.88 | 3.79 | 18.24 | ||
| 8 | 5.09 | 3.72 | 19.15 | ||
| 16 | 5.18 | 3.65 | 19.54 |
Nu=hDh/k, Re=ρumDh/μ
NuH—Nu under a constant heat flux boundary condition, constant axial heat flux, and uniform circumferential temperature.
NuT—Nu under a constant wall temperature boundary condition.
f—friction factor.
It can be seen that for a circular pipe,
(3.9)Po=fRe=16
Shah and London (1978) provided the following equation for a rectangular channel with short side a and long side b, and a channel aspect ratio defined as αc=a/b.
(3.10)fRe=24(1–1.3553αc+1.9467αc2–1.7012αc3+0.9564αc4–0.2537αc5)
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978008098346200003X
Principal coordinate system based on velocity gradient tensor
Chaoqun Liu, … Yisheng Gao, in Liutex and its Applications in Turbulence Research, 2021
2.1 Matrix representation of velocity gradient tensor and Cauchy–Stokes decomposition
A velocity gradient tensor in three-dimensional case can be represented by a 3×3 matrix:
(2.1)∇v→=[∂u∂x∂u∂y∂u∂z∂v∂x∂v∂y∂v∂z∂w∂x∂w∂y∂w∂z],
where u, v, w represent the components of the velocity vector v→ respectively and x, y, z the axes of the original Cartesian coordinate respectively.
The Cauchy–Stokes decomposition decomposes ∇v→ into a symmetric part and an antisymmetric part, analogous to the Helmholtz velocity decomposition, which decomposes a smooth, rapidly decaying vector field into an irrotational (curl-free) vector field and a solenoidal (divergence-free) vector field:
(2.2)∇v→=[∂u∂x∂u∂y∂u∂z∂v∂x∂v∂y∂v∂z∂w∂x∂w∂y∂w∂z]=A+B
A=12(∇v→+∇v→T)=[∂u∂x12(∂u∂y+∂v∂x)12(∂u∂z+∂w∂x)12(∂v∂x+∂u∂y)∂v∂y12(∂v∂z+∂w∂y)12(∂w∂x+∂u∂z)12(∂w∂y+∂v∂z)∂w∂z]
B=12∇v→−∇v→T=012∂u∂y−∂v∂x12∂u∂z−∂w∂x−12∂u∂y−∂v∂x012∂v∂z−∂w∂y−12∂u∂z−∂w∂x−12∂v∂z−∂w∂y0
and
(2.3)∇v→·dl→=A·dl→+B·dl→=A·dl→+12∇×v→×dl→.
The right-hand side of Eq. (2.3) uses a property of 3×3 antisymmetric matrix, which can represent cross-products as matrix multiplications. The symmetric part A, called strain rate tensor, is considered as the average deformation. The antisymmetric part B, called angular rotation rate tensor, spin tensor, or vorticity tensor, is considered as the average rotation. But as will be shown in the following chapters, the antisymmetric part, namely vorticity tensor, cannot represent fluid rotation and must be decomposed to a rigid rotation part and an antisymmetric shear part.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128190234000161
Pneumatic Measurements for Pressure, Velocity, and Flow-direction
K. Kim, in Application of Thermo-Fluidic Measurement Techniques, 2016
3.3.5 Velocity Gradient Effect
The transverse velocity gradient, which is the difference in velocity between adjacent boundary layers, will result in a measurement error of the stagnation pressure measurements (Schlichting, 1979). There are two measurement errors that can result.
The first measurement error results when the pressure probes are exposed to a high stagnation pressure gradient field, which is seen when measuring inside the boundary layer or near solid boundaries. This results in the streamlines deflecting to a region of lower velocities. This deflection will cause the pressure probes to show a higher than normal stagnation pressure. A solution to minimize this measurement error is to use a flattened tip probe (called a “Boundary Layer probe” in Fig. 3.12b) to measure the stagnation pressure provided the flow direction is known.
The second error results due to the stagnation pressure being proportional to the square of the velocity. Integrating the velocity gradient at the pressure probe’s nose will result in a higher stagnation pressure value than the stagnation pressure calculated from the square of the average velocity. This error can be minimized by using a “Boundary Layer probe” to reduce the distance between the center of the tube and the solid boundary surface.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128097311000034
Dense Matter Physics
Y.C.Leung George, in Encyclopedia of Physical Science and Technology (Third Edition), 2003
V.C Shear Viscosity
When a velocity gradient exists in a fluid, a shearing stress is developed between two layers of fluid with differential velocities. The shear viscosity is given by the ratio of the shearing stress to the transverse velocity gradient. Elementary kinetic theory suggests that the shear viscosity of a dilute gas is given by:
(52)η=13nmυ―2τ
where n is the molecular density, m the mass of each molecule, υ― the average thermal velocity of the molecules, and τ the relaxation time. Viscosity is expressed in units of g/cm/sec, which is also called poise. In appearance it is similar to the expression for thermal conductivity with the exception that the specific heat per particle in the thermal conductivity is being replaced by the particle mass. Consequently, we may suspect that the electron component of the viscosity should behave similarly to the thermal conductivity. This, however, is not true due to the fact that the relaxation time involved relates to different aspects of the scattering mechanism. Also, there is an additional component to the viscosity. The solid lattice can make a great contribution to the total viscosity. Unfortunately, the determination of the lattice viscosity is very difficult, and no adequate work has been performed to determine its properties at the present time. The following discussion relates only to the electron viscosity.
The electron relaxation time is determined by electron scatterings by phonons, impurities, electrons, and nuclei. Shearing stress is developed when electrons belonging to fluid layers of different velocities are exchanged. Thus, viscosity is related to mass transfer or the transfer of electrons. This is similar to electric conduction where the transfer of electrons gives rise to charge transfer and is different from heat conduction which involves the adjustment of electron energy distributions. The evaluation of the relaxation times for the viscosity due to different scattering mechanisms is similar to that for the electrical conductivity.
The viscosity of dense matter at 108 K due to different scattering mechanisms is shown in the Fig. 10. The temperature dependence of the viscosity due to electron–phonon scattering is approximately T−1, as in the case of the electrical conductivity. This is also true of the viscosity due to electron-impurities scattering, which is independent of temperature as in the case of the electrical conductivity. While electron–electron scatterings do not contribute to the electrical conductivity, they play a role in viscosity giving rise to a temperature dependence of T−2.
FIGURE 10. The viscosity of dense matter at a temperature of T = 108 K. For densities below 2 × 1012 g/cm3, the viscosity due to electron–phonon scattering is drawn as a solid line. If the lattice is melted, the viscosity is due to electron–ion scattering, which is drawn as a dotted line. The viscosity due to electron–electron scattering is drawn as a dot-dashed line, and the viscosity due to electron-impurities scattering is drawn as a dashed line, where the impurity concentration factor is taken to be Ximp = 0.01. For densities above 2 × 1012 g/cm3, the viscosity receives contributions from neutrons, electrons, and protons, and they are shown as thin dashed lines and labeled n, e, and p, respectively. The total viscosity from these three components is drawn as a solid line and labeled “total.” [From Elliott, F., and Itoh, N., Astrophys. J. 206, 218, 1976; 230, 847, 1979. Reprinted with permission of The Astrophysical Journal, published by the University of Chicago Press; © 1976 and 1979 The American Astronomical Society.]
In the neutron matter region, 1014−1015 g/cm3, all three types of particles—neutrons, protons, and electrons—contribute to the viscosity. The contributions from neutrons, protons, and electrons to the viscosity are shown separately in Fig. 10 in this density range by dashed lines. The total viscosity is drawn as a solid line. They all have a temperature dependence of T−2.
When the temperature drops below the critical temperature Tc, superfluid proton and/or neutron components appear. The behavior of the viscosity in the superfluid state is very similar to the thermal conductivity. If the protons turn superfluid, the viscosity is basically unaltered from the normal viscosity, because the proton contribution is small. If the neutrons turn superfluid, the superfluid component of the neutrons has vanishing viscosity. The viscosity is dominated by the electron contribution which is determined by the electron–electron scattering and electron-proton scattering mechanisms. When both protons and neutrons turn superfluid, then the viscosity is determined entirely by electron–electron scattering, and the general result is indicated by the extension of the electron–electron curve for densities below 1014 g/cm3.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B0122274105001666
Multiplicative decomposition of deformation gradient tensor
Koichi Hashiguchi, in Nonlinear Continuum Mechanics for Finite Elasticity-Plasticity, 2020
8.2.2.2 Strain rate and spin tensors in intermediate configuration
The following velocity gradient tensor based on the contravariant−covariant pull-back of the velocity gradient tensor l by Fe to the intermediate configuration is additively decomposed into the purely elastic and plastic parts, noting Eq. (8.22) with Eq. (8.23).
(8.29)L¯=L¯e+L¯p
where
(8.30){L¯≡Fe−1lFe(=l←G¯·G¯e)=(gi⋅g·j)G¯i⊗G¯jL¯e≡Fe−1leFe(=l←eeG¯·G¯)=Fe−1F·e=(gi⋅g·j)G¯i⊗G¯j−G¯·i⊗G¯iL¯p≡Fe−1lpFe(=l←peG¯·G¯)=F·pFp−1=G¯·i⊗G¯i
noting Eq. (3.14) and
Fe−1lFe=G¯i⊗gi(g·r⊗gr)gj⊗G¯j=(gi⋅g·j)G¯i⊗G¯jFe−1leFe=G¯i⊗gi{g·r⊗gr−(G¯r⋅G¯·s)gr⊗gs}gj⊗G¯j=(gi⋅g·r)G¯i⊗G¯j−(G¯r⋅G¯·s)G¯i⊗G¯j=(gi⋅g·j)G¯i⊗G¯j−(G¯i⋅G¯·j)G¯i⊗G¯j=(gi⋅g·j)G¯i⊗G¯j−G¯·i⊗G¯i
Therefore L¯ and L¯e,L¯p can be pertinently adopted in the formulation of elastoplastic constitutive equation. Let them be decomposed additively into the symmetric and the antisymmetric parts, that is,
(8.31){L¯=D¯+W¯L¯e=D¯e+W¯e,L¯p=D¯p+W¯p
with
(8.32)D¯=D¯e+D¯p,W=W¯e+W¯p
where
(8.33){D¯≡sym[L¯],D¯e≡sym[L¯e],D¯p≡sym[L¯p]W¯≡ant[L¯],W¯e≡ant[L¯e],W¯p≡ant[L¯p]
Noting Eq. (2.31), it follows from Eq. (8.30) that
(8.34){D¯=sym[(gi⋅g·j)G¯i⊗G¯j]=12[(gi⋅g·j)G¯i⊗G¯j+(gi⋅g·j)G¯j⊗G¯i]=12[(gr⋅g·j)G¯ir+(gr⋅g·I)G¯jr]G¯i⊗G¯jD¯e=D¯−D¯p=12[(gi⋅g·j)G¯i⊗G¯j+(gi⋅g·j)G¯j⊗G¯i−(G¯i⋅G¯j)⋅G¯i⊗G¯j]=12[(gr⋅g·j)G¯ir+(gr⋅g·i)G¯jr−G¯·ij]G¯i⊗G¯jD¯p=sym[G¯·i⊗G¯i]=12(G¯i⋅G¯j)⋅G¯i⊗G¯j=12G¯·ijG¯i⊗G¯j
because of
2sym[(gi⋅g·j)G¯i⊗G¯j]=(gi⋅g·j)G¯i⊗G¯j+(gi⋅g·j)G¯j⊗G¯i=(gi⋅g·j)(G¯i⋅G¯r)G¯r⊗G¯j+(gi⋅g·j)G¯j⊗(G¯i⋅G¯r)G¯r=(gr⋅g·j)(G¯r⋅G¯i)G¯i⊗G¯j+(gr⋅g·i)G¯i⊗(G¯r⋅G¯j)G¯j
2sym[G¯·i⊗G¯i]=G¯·i⊗G¯i+G¯j⊗G¯·i=(G¯·i⋅G¯r)G¯r⊗G¯i+G¯i⊗(G¯·i⋅G¯r)G¯r=(G¯·j⋅G¯i)G¯i⊗G¯j+G¯i⊗(G¯·i⋅G¯j)G¯j=(G¯i⋅G¯j)⋅G¯i⊗G¯j
Incidentally, it follows from Eqs. (2.32) and (8.30)3 that
(8.35)W¯p=ant[G¯·i⊗G¯i]=12(G¯i⋅G¯·j−G¯·i⋅G¯j)G¯i⊗G¯j
The plastic strain rate D¯p is related to the rate of plastic right Cauchy–Green deformation tensor as follows:
(8.36)C·p=2FpTD¯pFp=2D¯←pGGp
noting
(FpTFp)⋅=F·pTFp+FpTF·p=FpT(Fp−TF·pT+F·pFp−1)Fp
The rate of C¯e is given from Eqs. (8.16) and (8.29) with Eq. (8.30)2 as
(8.37)C¯·e=2sym[C¯eL¯e]=2sym[C¯e(L¯−L¯p)]
noting
C¯·e=(FeTFe)⋅=FeTF·e+F·eTFe=FeTFe(Fe−1F·e)+(F·eTFe−T)FeTFe=C¯eL¯e+L¯eTC¯e
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128194287000080
Liutex methods for science and engineering applications
Chaoqun Liu, … Yisheng Gao, in Liutex and its Applications in Turbulence Research, 2021
12.2.1 Short review
The study of the velocity gradient tensor has great significance in understanding of flow complex motion. It contains geometric information about the orientation of vorticity and strain-rate eigenvectors, so it can identify the areas of the flow in which either strain rate or vorticity prevails (Martins and Meneveau, 2010). The local statistics and geometric structure of three-dimensional turbulence can be described by the properties of velocity gradient tensor (Chevillard and Meneveau, 2006), and many studies on turbulent flows have been based on the velocity gradient tensor. Chong et al. (1990) classified the local structure of velocity fields in terms of the three invariants of the velocity gradient tensor. Contours of joint distributions of these invariants obtained from turbulent flows have a tear-drop shape. In homogeneous, isotropic, and incompressible turbulent flow, Ooi et al. (1999) observed that successive positions of a fluid particle occupy different parts of this tear drop, representing flow in sheet-like regions followed by stretching, then compression, in a repetitive cycle. These studies mainly focus on the evolution of the velocity gradient tensor and the full tensor for incompressible flow. Studies of the velocity gradient tensor in compressible flows have received far less attention, but essential features from a homogeneous, isotropic, decaying turbulence field were presented by Lee et al. (2009). Suman and Girimaji (2009, 2010) closed the equations for velocity gradient tensor evolution assuming a polytropic process to obtain the Homogenized Euler Equation (HEE) model, which reproduced the deformation caused by compressibility as observed in attenuated turbulence data. Mathew et al. (2016) studied the relationship between the flow structure and compressibility at the turbulent and nonturbulent interface of temporal plane mixing layers by analyzing the invariants of the velocity gradient tensor. Processes in turbulent flows may be understood from the view of the dynamics of coherent structures and their influence on surrounding flow. By analyzing the velocity gradient tensor, the local flow topologies can be revealed, which is helpful to understand the flow mechanism. The analysis based on the velocity gradient tensor of fluid element has made the complex motion of fluid element understood to a certain extent (Li et al., 2014; Gao et al., 2019a).
It is a great challenge to understand how and where energy is dissipated in turbulent flow, which is of great significance in many fields such as fundamental research, aeronautics, industry, and so on. In the classical three-dimensional turbulence phenomenology, energy is injected at large scales by the forcing mechanism, transferred downscale at a constant rate following a self-similar cascade, and then dissipated into heat at the Kolmogorov length scale, where viscous effects become dominant. On the basis of the properties of the velocity gradient tensor, the feature of the fine-scale motion can be studied properly (Atkinson et al., 2012). Wu et al. (2015) studied the evolution of the dynamics and the geometry of the planar jets along with the flow transition based on the characteristics of the invariants of the velocity gradient tensor. Their results show that the flow transition is accompanied by a severe rotation and straining of the flow elements, where the vortex structure evolves faster than the fluid element deformation, as well as the initial flow near the jet exit is strongly predominated by the dissipation over the entropy. Kuzzay et al. (2015) investigate the relations between global and local energy transfers in a turbulent von Kármán flow by using particle image velocimetry (PIV) measurements and a new method based on the work of Duchon and Robert (2000). The results evidence a stationary energy cycle within the flow where energy is injected at the top and the bottom impellers and dissipated within the shear layer. However, there are few studies on the proportion of shear in deformation and the effect of shear on energy dissipation with quantitative analyses.
Based on the principal coordinate, the principal decomposition of the velocity gradient tensor is conducted. The physical meaning of each tensor term is discussed and the effects on energy dissipation are analyzed. A separated boundary layer flow with pressure gradient is taken as an example for the analysis.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128190234000112
Liutex-based velocity gradient tensor decomposition and vorticity R-S decomposition
Chaoqun Liu, … Yisheng Gao, in Liutex and its Applications in Turbulence Research, 2021
5.5.1 Velocity gradient tensor decomposition in the principal coordinate
A general 2D velocity gradient tensor can be decomposed to be a rigid rotation part R and a nonrotation part NR in the principal coordinate as
(5.57)∇V→=λcr∂U∂Y∂V∂Xλcr=λcr−R/2R/2+ελcr=0−R/2R/20+λcr0ελcr=R+NR
where R/2=−∂U∂Y>0, and ∂V∂X=R/2+ε (assume ∂V∂X>0 and | ∂V∂X|>| ∂U∂Y|). Eq. (5.57) is called 2D UTA R-NR decomposition. The first part on the right side represents the rigid rotation, while the second part has two real eigenvalues and therefore has no fluid rotation itself.
The nonrotation part NR in Eq. (5.57) can be further decomposed to a diagonal matrix CS, which represents the compression or stretching and a lower triangular matrix SS represents the shearing as
(5.58)NR=λcr0ελcr=λcr00λcr+00ε0=CS+SS
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128190234000021
Velocity and mass flow by pressure measurements
Giuseppe P. Russo, in Aerodynamic Measurements, 2011
2.4.3 Effect of shear rate and proximity of a wall
The presence of a velocity gradient in a boundary layer does not involve a gradient of static pressure but the gradient of stagnation pressure produces a deviation of streamlines towards the lowest speed and then induces variations in the pressure read by the probe. A similar phenomenon occurs for the downwash on the support of the probe. The proximity of a wall increases the speed and decreases the pressure on one side of the probe; errors less than 1% in detecting the static pressure are made only if the probe is kept at a distance of at least 5 diameters from the wall.
Both phenomena actually discourage the use of static probes for measurements in the boundary layer: since static pressure is constant in the layer, it can be measured in a hole in the wall.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9781845699925500024