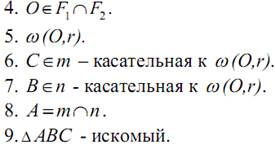Как найти гмт треугольника

Геометрические места точек

Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком.

Другими словами, все точки из рассматриваемого геометрического места точек, и только они, удовлетворяют заданному условию.

Примеры геометрических мест точек (сокращённо ГМТ ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом .

Примеры решения задач, решаемых методом ГМТ

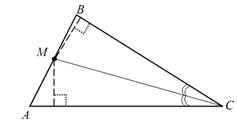
Задача 1. На стороне треугольника найти точку, равноотстоящую от двух

других сторон треугольника.

Анализ. Пусть задача решена и точка М на стороне АВ находится на

одинаковом расстоянии от сторон АС и ВС, образующих угол С.

Так как все точки, равноудаленные от сторон угла С лежат на биссектрисе этого угла (гмт 5), то точка М удовлетворяет двум независимым условиям:

Доказательство. Легко видеть, что точка М удовлетворяет требованиям

Задача 2. Построить треугольник по основанию а, углу при вершине А

Анализ. Допустим, что задача решена и искомый треугольник ΔАВС

построен так, что BC = a, AM = m_а – медиана и ∟ВАС = α.

Отрезок ВС, равный данному, всегда может быть построен. Тогда задача сводится к построению точки А, удовлетворяющей двум независимым условиям:

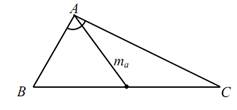
1 0 . Точка А находится на расстоянии m_а от середины М стороны ВС, т.е.

2 0 . Так как ∟ВАС = α, то точка А принадлежит ГМТ F1, из которых отрезок ВС виден под углом α, т.е.

Таким образом,

Заданные по условию задачи элементы могут быть выбраны перед построением или анализом.

Доказательство: BC = a, AM = m_а по построению, и ∟СВО = 90 0 – α, следовательно, ∟ВОМ = α, следовательно, ∟ВОС=2α, а ∟ВАС =0,5*∟ВОС= α

и, следовательно ΔАВС, удовлетворяет всем условиям задачи и потому искомый.

Исследование: Задача имеет столько решений, сколько точек содержит

пересечение двух окружностей. Если пересечение в двух точках, то два

решения; в одной (окружности касаются) – одно решение, не пересекаются –нет решений.

Задача 3. Построить окружность данного радиуса r, проходящую через данную точку М и высекающую на данной прямой l отрезок длины d, равный данному.

Анализ: Пусть искомая окружность построена. Пусть О – ее центр, r – данный радиус, М – данная точка, АВ – хорда длины d, построенной окружности, лежащей на данной прямой l. Опустим перпендикуляр ОC на прямую l. В прямоугольном треугольнике ОВС известна гипотенуза (данный радиус r) и катет ВС, равный половине данного отрезка. Кроме того, ОМ = r.

Значит, искомый центр О принадлежит, во-первых ГМТ F1, удаленных от данной прямой l на расстояние, равное ОС(ГМТ 3); во-вторых ГМТ F2, удаленных от данной точки М на расстояние, равное данному радиусу r (гмт2).

Окружность ω может быть построена, ГМТ F1 может быть построено, если мы найдем расстояние OC = h.

Для этого построим вспомогательный треугольник О₁В₁С₁ по гипотенузе О₁В₁ = r и катету В₁С₁ = d/2. Тогда h = O₁C₁ будет найден.

Построение:

Доказательство: Убеждаемся в том, что построенная окружность удовлетворяет всем требованиям задачи. OM = r по построению. Докажем, что AB = d.

Действительно, ΔАОВ — равнобедренный (ОС –

медиана и высота), отсюда АВ = 2ВС = 2*d/2 = d.

Исследование: Построение 1 возможно, если d 0 ) точки О можно отметить сразу – она находится на расстоянии r от стороны ВС, то есть центр О вписанной окружности принадлежит ГМТ, находящихся на расстоянии r от прямой ВС (ГМТ 3). (Как правило, мы строим только в одной из двух полуплоскостей, определяемых заданной прямой). Второе свойство, которым обладает точка О, видно не сразу. Но, исходя из свойств вписанной окружности, это свойство мы можем найти: центр вписанной окружности находится на пересечении биссектрис треугольника и потому ОВ и ОС – биссектрисы углов В и С.

Тогда: ∟ВОС = 180 0 – 0,5(∟В + ∟С) = 180 0 – 0,5 (180 0 — ∟А) = 90 0 + 0,5∟А

Так как ∟ВОС =90 0 +∟A/2, то точка О принадлежит ГМТ F2, из которых

данный отрезок ВС виден под данным углом α = 90 0 + ∟А/2 (ГМТ 6). ГМТ F1 и F2 может быть построено, а потому и точка может быть построена и мы можем перейти к построению искомой фигуры.

Доказательство: Убеждаемся в том, что построенный треугольник

удовлетворяет всем требованиям задачи. ВС = а, окружность ω(O,r) вписана в

треугольник по построению. Остается доказать, что ∟ВАС равен данному углу

А. Действительно, по построению ∟О₁ ВК = ∟А/2. Тогда

Теперь находим:

Значит, ΔАВС удовлетворяет всем условиям задачи, а потому – искомый.

Исследование. Построения 1-3 выполняются и притом однозначно при

любых a, r и ∟ A 0 . Построение 4 возможно лишь тогда, когда прямая F1

пересекает окружность F2, то есть при условии или при: (*). При этом прямая F1 пересекает окружность F2 в

двух или одной точке соответственно. Построения 6 и 7 всегда выполнимы, так

как из любой точки вне окружности можно провести к ней две касательные

(одна из них в данном случае прямая ВС). А вот построение 8 возможно не всегда: прямые m и n могут быть параллельными или могут пересекаться в полуплоскости, не содержащей точку О. В этих случаях в нужной нам полуплоскости точка А не строится. Вывод: при выполнении условий ∟A 0 и (*) задача может иметь одно, два или ни одного решения.

4. Построение Штейнера и построение с помощью
двусторонней линейки, прямого или острого угла [2], [5]

Якоб Штейнер (18.05 1795г. – 01.04.1863г.) сын простых поселян из Уцисдорфа Германии. Как он сам писал: «Только на девятнадцатом году стремление к образованию стало для меня потребностью…. и с осени 1822г. Вынужден с величайшим трудом добывать средства к существованию частными уроками. Почти бессознательно я пришел таким образом к собственно геометрическому способу рассмотренья, как оно должно быть присуще геметрии древности, но я находился в случае, противоположном им. Мне было дано множество разрешимых задач и предложений, и мне приходилось заняться не фиксацией отдельных предложений, а установлением того свойства общих законов систематического построения, что из них вытекают все открытия подобного рода, и их соответственным образом исчерпать».

«Геометрия в более тесном смысле для своих построений нуждается только в двух инструментах, циркуле и линейке. …. все построения могут быть выполнены только при помощи линейки, если где-либо в дан будет вспомогательный неподвижный круг»

Рассмотрим решение задач проведением только одних прямых линий, причём на чертеже иногда уже имеется начерченной какая-нибудь одна вспомогательная фигура. Из всех таких способов наиболее сильными являются решения с помощью:

1. Двусторонней линейки, другие инструменты при этом не допускаются

2. Прямого или острого угла, сделанного из дерева или металла — другие инструменты не допускаются.

3. Односторонней линейки, причём на чертеже уже имеется начерченной окружность с известным центром.

Далее, всякая не вспомогательная окружность считается данной, если известно положение ее центра и длина радиуса, заданная где-нибудь начерченным отрезком. Однако ни одна точка такой окружности точку какого-нибудь свойства, то должны ограничиться проведением только прямых линий.

Мы знаем, что решение квадратной задачи сводится к известным четырём основным построениям.

Из этих основных задач первая и третья решаются способами 1, 2 и 3

непосредственно — одной линейкой. Моя цель показать, что две другие основные задачи решаются теми же тремя способами, которые решают теми же способами всякую квадратную задачу.

Решим несколько задач проведением одних прямых линий (односторонней линейкой).

Найти геометрическое место центров окружностей, проходящих через две данные точки.

Пусть окружность с центром O проходит через данные точки A и B. Поскольку OA = OB (как радиусы одной окружности), точка O лежит на серединном перпендикуляре к отрезку AB. Обратно, каждая точка O, лежащая на серединном перпендикуляре к AB, равноудалена от точек A и B. Значит, точка O — центр окружности, проходящей через точки A и B.

Проведем диаметры АА1, ВВ1, затем хорды АВ1, ВА1, эти последние перпендикулярны АВ и потому параллельны между собой. Поэтому для решения задачи нужно провести через точку О прямую, параллельную эти хордам. Она будет серединным перпендикуляром к АВ, т.е. искомым ГМТ [5, стр.21]

Дан прямоугольник ABCD. Найдите ГМТ X, для которых AX + BX = CX + DX.

Пусть l — прямая, проходящая через середины сторон BC и AD.

Предположим, что точка X не лежит на прямой l, например, что точки A и X лежат по одну сторону от прямой l. Тогда AX

Геометрическое место точек

Геометрическое место точек (ГМТ) — это фигура, состоящая из всех точек плоскости, удовлетворяющих определённому условию.

Чтобы выяснить, что собой представляет некоторая фигура F — геометрическое место точек, удовлетворяющих заданному условию P, нужно доказать:

1) если определённая точка принадлежит фигуре F, то она удовлетворяет заданному условию P;

2) если определённая точка удовлетворяет заданному условию P, то она принадлежит фигуре F.

(то есть требуется доказать прямую теорему — свойство P точек, принадлежащих фигуре F, и обратную теорему — признак фигуры F: если точка удовлетворяет условию P, то она принадлежит F).

Геометрическое место точек, равноудалённых от данной точки — окружность.

Это следует непосредственно из определения окружности.

Некоторые теоремы о ГМТ

1) Геометрическим местом точек, равноудалённых от двух данных точек, является серединный перпендикуляр к отрезку, соединяющему эти точки.

2) Геометрическим местом точек, равноудалённых от сторон неразвёрнутого угла, является биссектриса этого угла.

3) Геометрическим местом точек, удалённых от данной прямой на расстояние h, состоит из двух прямых, параллельных данной прямой и отстоящих от неё на h.

4) Геометрическим местом точек, равноудалённых от двух параллельных прямых, является прямая, параллельная этим прямым и проходящая через середину их общего перпендикуляра.

Понятие ГМТ часто используют при решении задач на построение.

Четыре замечательные точки треугольника

Определение

Окружность называется вписанной в многоугольник, если она касается
всех его сторон. Многоугольник в таком случае называется описанным.

Определение

Окружность называется описанной около многоугольника, если она
проходит через все его вершины. Многоугольник в таком случае
называется вписанным в данную окружность.

Определение

Точка пересечения медиан треугольника называется центроидом или
центром масс.

Замечение

Медианы треугольника пересекаются в одной точке по теореме.

Теорема о биссектрисе, как ГМТ

Доказательство

Теорема

Доказательство

Первый способ.

Второй способ.

Следствие

Доказательство

Следствие

Если все биссектрисы выпуклого многоугольника пересекаются в одной
точке, то в него можно вписать окружность, центром которой будет
точка пересечения биссектрис.

Доказательство

Если все биссектрисы пересекаются в одной точке, то эта точка будет
равноудалена от всех её сторон, то есть перпендикуляры к сторонам
многоугольника будут равны, а окружность с центром в этой точке и с
радиусом, равным расстоянию от точки пересечения биссектрис до
стороны, будет касаться всех сторон.

Теорема о серединном перпендикуляре, как ГМТ

Доказательство

Следствие

Доказательство

Следствие

Доказательство

Следствие

Если все серединные перпендикуляры к сторонам выпуклого
многоугольника пересекаются в одной точке, то около него можно
описать окружность, центром которой будет точка пересечения
серединных перпендикуляров.

Доказательство

Если все серединные перпендикуляры к сторонам выпуклого
многоугольника пересекаются в одной точке, то эта точка равноудалена
от всех его вершин, и, следовательно, окружность с центром в этой
точке и с радиусом, равным расстоянию от этой точки до какой-либо из
его вершин, будет описанной около этого многоугольника.

Теорема

Доказательство

Следствие

Если через вершины треугольника провести прямые, параллельные
противоположным сторонам, то пересекаясь, они образуют треугольник
подобный исходному с коэффициентом $2$. При этом вершины исходного
треугольника являются серединами сторон образовавшегося
треугольника.

Следствие

Серединные перпендикуляры треугольника являются высотами серединного
треугольника. Следовательно, ортоцентр серединного треугольника
является центром окружности, описанной около исходного треугольника.

Доказательство

Утверждение полностью следует из доказательства теоремы.

Определение

Точка пересечения высот треугольника называется ортоцентром
треугольника.

Геометрическое место точек. Метод геометрических мест

Определение: Геометрическим местом точек называется геометрическая фигура на плоскости, каждая точка которой обладает одним и тем же определенным свойством.

Метод геометрических мест применяется чаще всего при построениях. Например, серединный перпендикуляр к отрезку можно определить как геометрическое место точек, равноудаленных от точек концов отрезков; окружность можно определить как геометрическое место точек, равноудаленных от данной точки.

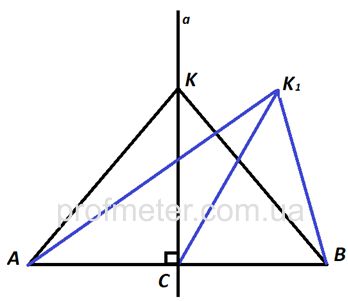
Теорема (о геометрическом месте точек). Геометрическое место точек, равноудаленных от двух данных точек, есть прямая, перпендикулярная отрезку, соединяющему эти точки, и проходящая через его середину.

Доказательство. Пусть даны точки А и В, а точка С
– середина отрезка АВ. Нужно найти геометрическое место точек, равноудаленных от точек А и В.

Доказательство основано на свойстве серединного перпендикуляра к отрезку.

Серединный перпендикуляр СК, принадлежащий прямой а, как и любая точка этой прямой, — есть геометрическое место точек, равноудаленных от А и В, так как СКꓕАВ.

Допустим, что есть еще точка К₁, расстояние до которой от А и В одинаково.

Рассмотрим ∆АК₁В, он разбит отрезком К₁С
на два треугольника: ∆АК₁С и ∆К₁СВ. Если эти треугольники равны, то точка К₁
тоже удалена на одинаковое расстояние от А и В.

Через точку С проходят две прямые СК
и СК₁. На основании теоремы 16 (о единственности перпендикуляра из точки к прямой), если СКꓕАВ
по построению, то СК₁ не может быть перпендикулярна АВ.

Так как из двух смежных углов (∟К₁СА и ∟К₁СВ) один должен быть острый, а второй – тупой, то ∆К₁СА≠∆К₁СВ, следовательно, К₁А≠К₁В (есть две равные стороны, АС=ВС
и К₁С
– общая, но нет равных углов между ними), значит, К₁С – наклонная к АВ и АК₁≠ВК₁.

Метод геометрических мест

Определение: Сущность метода геометрических мест в том, что при наличии не одного, а нескольких условий для построения геометрической фигуры, нужно построить несколько геометрических фигур, которые по очереди будут удовлетворять каждому из условий, а потом найти такое геометрическое место точек, которое при пересечении или совмещении этих фигур будет удовлетворять всем условиям построения.

Например: Даны три точки: А, В, С.

Построить точку Х, равноудаленную от А и В и находящуюся на расстоянии h от точки С.

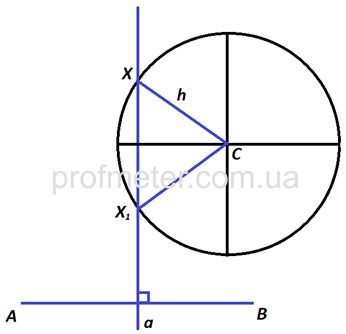
Порядок построения:

1.Построим геометрическое место точек, удовлетворяющее первому условию: это будет серединный перпендикуляр к отрезку АВ. Прямая а, которая содержит серединный перпендикуляр к отрезку АВ, удовлетворяет полностью первому условию.

2.На перпендикуляре (прямая а) должна находится точка Х, которая удовлетворяла бы второму условию (расстояние от нее до С должно составлять h).

Если из точки С
радиусом h провести окружность, то все точки окружности будут расположены от С на одинаковом расстоянии h (построили второе геометрическое место точек, равноудаленных от С).

3.Пересечение первого геометрического места точек (прямая а) и второго (окружности с центром в точке С) будет удовлетворять обоим условиям задачи. Точки пересечения окружности и прямой (Х₁
и Х) и будут теми искомыми точками, которые равноудалены от точек А
и В
и находятся от С на расстоянии h.

0
 

 Точки, отрезки и прямые |

Описание курса

| Отрезки в координатной плоскости 

§ 23. Метод геометрических мест точек в задачах на построение

Известно, что если смешать синий и жёлтый цвета, то получим зелёный.

Пусть на плоскости надо найти точки, обладающие какими-то двумя свойствами одновременно. Если синим цветом покрасить точки, обладающие первым свойством, а жёлтым — обладающие вторым свойством, то понятно, что зелёные точки будут обладать сразу двумя свойствами. В этом и состоит идея метода ГМТ, которую проиллюстрируем следующими задачами.

Задача 1. Постройте треугольник по трём данным его сторонам.

Решение. Пусть даны три отрезка, длины которых равны a, b, c (рис. 327). Надо построить треугольник ABC, в котором AB = c, AC = b, BC = a.

Проведём произвольную прямую. С помощью циркуля отложим на ней отрезок CB, равный a (рис. 328). Понятно, что задача свелась к построению третьей вершины треугольника, точки A.

Воспользуемся тем, что точка A обладает сразу двумя свойствами:

1)принадлежит геометрическому месту точек, удалённых от точки B на расстояние c, т. е. окружности с центром в точке B радиуса с (см. рис. 328);

2)принадлежит геометрическому месту точек, равноудалённых от точки C на расстояние b, т. е. окружности с центром в точке С радиуса b (см. рис. 328).

В качестве точки A можно выбрать любую из двух образовавшихся зелёных точек.

Полученный треугольник ABC является искомым, так как в нём AB = c, AC = b, BC = a.

Из описанного построения следует, что если каждый из трёх данных отрезков меньше суммы двух других, то эти отрезки могут служить сторонами треугольника.

Задача 2. Постройте фигуру, все точки которой принадлежат данному углу, равноудалены от его сторон и находятся на заданном расстоянии a от его вершины.

Решение. Искомые точки принадлежат сразу двум геометрическим местам точек: биссектрисе данного угла и окружности с центром в его вершине и радиусом, равным a.

Построим биссектрису угла и указанную окружность (рис. 329). Их пересечением является искомая точка X.

Задача 3. Постройте центр окружности радиуса R, проходящей через данную точку M и касающуюся данной прямой a.

Решение. Поскольку окружность касается прямой a, то её центр находится на расстоянии R от этой прямой. Геометрическим местом точек, удалённых от данной прямой на данное расстояние, являются две параллельные прямые (см. упражнение 498). Следовательно, центр окружности находится на прямой b или на прямой с (рис. 330).

Геометрическое место точек, являющихся центрами окружностей радиуса R, проходящих через точку M, — это окружность данного радиуса с центром в точке M. Поэтому в качестве центра искомой окружности можно выбрать любую из точек пересечения окружности с одной из прямых b или с (рис. 331).

Построение для случая, когда данная точка принадлежит данной прямой, рассмотрите самостоятельно.

Задача 4. Постройте треугольник по стороне, медиане, проведённой к этой стороне, и радиусу описанной окружности.

Решение. Построим окружность данного радиуса и проведём хорду AB, равную стороне искомого треугольника. Тогда концы хорды являются двумя вершинами искомого треугольника. Понятно, что третья вершина принадлежит одновременно построенной окружности и окружности с центром в точке O, являющейся серединой хорды AB, и радиусом, равным данной медиане. Каждый из треугольников ABС1 и ABС2 (рис. 332) является искомым. Поскольку эти треугольники равны, то задача имеет единственное решение.

Упражнения

622.Даны прямая m и точки A и B вне её (рис. 333). Постройте на прямой m точку, равноудалённую от точек A и B.

623.Точки A и B принадлежат прямой m. Постройте точку, удалённую от прямой m на расстояние a и равноудалённую от точек A и B. Сколько решений имеет задача?

624.Точки B и C принадлежат разным сторонам угла A, причём АВ ≠ АС. Постройте точку M, принадлежащую углу, равноудалённую от его сторон и такую, что MB = MC.

625.Точки B и C принадлежат разным сторонам угла A. Постройте точку D, принадлежащую углу, равноудалённую от его сторон и такую, что DC = BC. Сколько решений может иметь задача?

626.Постройте равнобедренный треугольник по основанию и боковой стороне.

627.Для данной окружности постройте точку, являющуюся её центром.

628.Постройте окружность данного радиуса, проходящую через данную точку, центр которой принадлежит данной прямой.

629.Постройте окружность данного радиуса, проходящую через две данные точки.

630.Найдите все точки, принадлежащие данной окружности и равноудалённые от концов данного отрезка. Сколько решений может иметь задача?

631.Даны две пересекающиеся прямые m и n и отрезок AB. Постройте на прямой m точку, удалённую от прямой n на расстояние AB. Сколько решений имеет задача?

632.В треугольнике ABC известно, что ∠C = 90°. На катете AC постройте точку D, удалённую от прямой AB на расстояние CD.

633.Постройте равнобедренный треугольник по основанию и радиусу описанной окружности. Сколько решений может иметь задача?

634.Постройте треугольник по двум сторонам и медиане, проведённой к одной из данных сторон.

635.Постройте равнобедренный треугольник по боковой стороне и медиане, проведённой к боковой стороне.

636.На данной окружности постройте точку, находящуюся на данном расстоянии от данной прямой. Сколько решений может иметь задача?

637.На данной окружности постройте точку, равноудалённую от двух данных пересекающихся прямых. Сколько решений может иметь задача?

638.Между двумя параллельными прямыми дана точка. Постройте окружность, проходящую через эту точку и касающуюся данных прямых. Сколько решений имеет задача?

639.Постройте окружность, проходящую через данную точку A и касающуюся данной прямой m в данной точке B.

640.Даны две параллельные прямые и секущая. Постройте окружность, касающуюся этих трёх прямых.

641.Постройте треугольник по двум сторонам и радиусу описанной окружности. Сколько решений может иметь задача?

642.Постройте треугольник по стороне, высоте, проведённой к этой стороне, и радиусу описанной окружности. Сколько решений может иметь задача?

643.Постройте равносторонний треугольник по радиусу описанной окружности.

644.Три прямые попарно пересекаются и не проходят через одну точку. Постройте точку, равноудалённую от всех трёх прямых. Сколько решений имеет задача?

645.Постройте прямоугольный треугольник по катету и сумме гипотенузы и другого катета.

646.Постройте прямоугольный треугольник по гипотенузе и сумме катетов.

647.Постройте прямоугольный треугольник по гипотенузе и разности катетов.

648.Постройте прямоугольный треугольник по катету и разности гипотенузы и другого катета.

649.Постройте равнобедренный треугольник по основанию и разности боковой стороны и высоты, опущенной на основание.

650.Постройте треугольник по стороне, прилежащему к ней углу и сумме двух других сторон.

651.Постройте треугольник по стороне, прилежащему к ней углу и разности двух других сторон.

652.Постройте треугольник по стороне, противолежащему ей углу и разности двух других сторон.

653.Постройте треугольник по стороне, противолежащему ей углу и сумме двух других сторон.

654.Постройте треугольник по стороне, разности углов, прилежащих к этой стороне, и сумме двух других сторон.

655.Постройте треугольник по периметру и двум углам.

656.Постройте остроугольный треугольник по периметру, одному из углов и высоте, проведённой из вершины другого угла.

657.Постройте треугольник по высоте и медиане, проведённым из одной вершины, и радиусу описанной окружности.

658.Постройте треугольник по двум сторонам и медиане, проведённой к третьей стороне.

659.Постройте треугольник по стороне, высоте, проведённой к этой стороне, и медиане, проведённой к одной из двух других сторон.

Упражнения для повторения

660.На рисунке 334 ∠A = 46°, ∠ACB = 68°, ∠DEC = 120°. Найдите углы треугольников EFC и DBE.

661.Через середину O стороны MK треугольника MKN провели прямую, перпендикулярную стороне MK и пересекающую сторону MN в точке C. Известно, что MC = KN, ∠N = 50°. Найдите угол MCO.

662.В треугольнике ABC из вершины прямого угла C провели высоту CH и биссектрису CM. Длина отрезка HM в 2 раза меньше длины отрезка CM. Найдите острые углы треугольника ABC.

663.На рисунке 335 BD = DC, DN ⊥ BC, ∠BDM = ∠MDA. Найдите сумму углов MBN и BMD.

Наблюдайте, рисуйте, конструируйте, фантазируйте

664.Разрежьте фигуру, изображённую на рисунке 336, на три части, не являющиеся квадратами, так, чтобы из этих частей можно было сложить квадрат.

Когда сделаны уроки

Из истории геометрических построений

Умение достигать результат, используя минимальные средства, всегда считалось признаком высокого мастерства. Видимо, поэтому в Древней Греции в значительной степени было развито искусство выполнять геометрические построения с помощью только двух инструментов: дощечки с ровным краем (линейки) и двух заострённых палочек, связанных на одном конце (циркуля). Такое ограничение в выборе инструментов историки связывают с древнегреческой традицией, считавшей прямую и окружность самыми гармоничными фигурами. Так, в своей книге «Начала» великий учёный Евклид описывал построения геометрических фигур, при которых использовались лишь циркуль и линейка.

Существует много задач на построение. С некоторыми из них вы уже успели познакомиться. Однако есть три задачи на построение, которые сыграли в развитии математики особую роль. Эти задачи стали знаменитыми.

Задача о квадратуре круга. Построить квадрат, площадь которого равна площади данного круга.

Задача о трисекции угла (от латинских tria — «три» и section — «разрезание»). Разделить угол на три равные части.

Задача об удвоении куба. Построить куб, объём которого в 2 раза больше объёма данного куба.

Эти задачи занимали умы людей на протяжении тысячелетий. Их пытались решить и такие выдающиеся учёные древности, как Гиппократ Хиосский, Евдокс Книдский, Евклид, Эратосфен, Аполлоний Пергский, Герон, Папп, Платон, Архимед, и гении Нового времени Рене Декарт, Франсуа Виет, Исаак Ньютон. И лишь в середине XIX века была доказана их неразрешимость, т. е. невозможность выполнить указанные построения с использованием лишь циркуля и линейки. Этот результат был получен средствами не геометрии, а алгебры, благодаря переводу этих задач на язык уравнений.

Когда вы решали задачи на построение, особенно те, которые отмечены знаком  , вы, по-видимому, испытали сложности, связанные с ограниченностью набора инструментов. Поэтому предложение ещё больше сузить возможности применяемых приборов может показаться вам по меньшей мере неожиданным. Однако ещё в Х веке персидский математик Мохаммед Абу-ль-Вефа описал решение целого ряда задач на построение с помощью линейки и циркуля, раствор которого нельзя было менять. Совсем удивительной является теорема, опубликованная в 1797 году итальянским математиком Лоренцо Маскерони (1750–1800): всякое построение, выполнимое циркулем и линейкой, можно проделать одним циркулем. При этом Маскерони обусловливал следующее: поскольку одним циркулем провести прямую нельзя, то прямая считается построенной, если построены какие-нибудь две её точки.

В ХХ веке была обнаружена книга датского учёного Георга Мора (1640–1697), в которой он также описал построения одним циркулем. Поэтому сформулированную выше теорему называют теоремой Мора — Маскерони.