Газовая постоянная, справочная таблица
| Азот газовая постоянная азота |
297 (Джоуль / (Килограмм · Кельвин)) |
| Аммиак газовая постоянная аммиака |
488 (Джоуль / (Килограмм · Кельвин)) |
| Аргон газовая постоянная аргона |
208 (Джоуль / (Килограмм · Кельвин)) |
| Ацетилен газовая постоянная ацетилена |
320 (Джоуль / (Килограмм · Кельвин)) |
| Бутан газовая постоянная бутана |
143 (Джоуль / (Килограмм · Кельвин)) |
| Водород газовая постоянная водорода |
4125 (Джоуль / (Килограмм · Кельвин)) |
| Водяной пар (100°C) газовая постоянная водяного пара |
461 (Джоуль / (Килограмм · Кельвин)) |
| Воздух газовая постоянная воздуха |
287 (Джоуль / (Килограмм · Кельвин)) |
| Гелий газовая постоянная гелия |
2078 (Джоуль / (Килограмм · Кельвин)) |
| Двуокись углерода газовая постоянная углекислого газа |
189 (Джоуль / (Килограмм · Кельвин)) |
| Кислород газовая постоянная кислорода |
260 (Джоуль / (Килограмм · Кельвин)) |
| Метан газовая постоянная метана |
519 (Джоуль / (Килограмм · Кельвин)) |
| Неон газовая постоянная неона |
412 (Джоуль / (Килограмм · Кельвин)) |
| Окись углерода газовая постоянная угарного газа |
297 (Джоуль / (Килограмм · Кельвин)) |
| Пропан газовая постоянная пропана |
189 (Джоуль / (Килограмм · Кельвин)) |
| Пропилен газовая постоянная пропилена |
198 (Джоуль / (Килограмм · Кельвин)) |
| Фреон газовая постоянная фреона |
68.7 (Джоуль / (Килограмм · Кельвин)) |
| Этан газовая постоянная этана |
277 (Джоуль / (Килограмм · Кельвин)) |
| Этилен газовая постоянная этилена |
297 (Джоуль / (Килограмм · Кельвин)) |
Газовая постоянная — справочная таблица |
стр. 862 |
|---|
Пример 4.1
Найти газовую постоянную смеси, состоящей из азота с приведенным объемом 0,4 м3 и кислорода с приведенным объемом 0,2 м3.
Решение
Общий объем смеси:
= 0,4 + 0,2 = 0,6 м3.
Объемные (или молярные) доли компонентов:
= 0,2/0,6 = 0,333;
= 0,4/0,6 = 0,667.
Молярная масса смеси:
= 0,333 · 32·10-3 + 0,667 · 28,01·10-3 = 29,34·10-3 кг/моль
Газовая постоянная смеси:
= 8,314 / 29,34·10-3 = 283 Дж/(кг·К)
Пример 4.2
Найти парциальное давление азота и кислорода газовой смеси, состоящей из азота с приведенным объемом 0,4 м3 и кислорода с приведенным объемом 0,2 м3. Давление смеси равно 0,1 МПа.
Решение
Парциальное давление компонентов равно:
= 0,333·0,1 = 33,3 кПа,
= 0,667·0,1 = 66,7 кПа.
Пример 4.3.
Продукты сгорания топлива массой 1 кг имеют следующий молярный состав: пары воды = 60,3; углекислый газ
= 73,9; азот
= 849,5; кислород
= 132,2. Найти массу и молярную массу смеси.
Решение
Число молей продуктов сгорания:
= 60,3 + 73,9 + 123,3 + 849,5 = 1106,9 моль.
Молярные доли компонентов:
= 60,3 / 1106,9 = 0,0544;
= 73,9 / 1106,9 = 0,0667;
= 123,2 / 1106,9 = 0,1113;
= 849,5 / 1106,9 = 0,7676.
Молярная масса смеси:
;
М = 0,0554 · 18,02·10-3 + 0,0667 · 44,01·10-3 + 0,1113 · 32·10-3 + 0,7676 · 28,04·10-3 =
= 28,04·10-3 кг/моль
Масса смеси:
= 28,04·10-3 · 1106,9 = 31,04 кг

α = 2731 К−1
Закон Гей-Люссака Жоржа
Открыт в 1802 году pi = po (1 +αt)
α = 2731 К−1
Закон Клапейрона Бенуа Поля Эмиля
(1799-1864)
Открыт в 1834 году
|
pV = BT , где |
B = m , |
|
|
μ |
||
|
m − |
масса |
газа; |
μ −молекулярная
масса
Закон Менделеева Дмитрия Ивановича
(1834-1907)
Открыт в 1874 году pv = RT .
Рис.4. Развитие уравнения состояния идеального газа
|
Решение. |
Дж |
Дж |
|||||||||||||||||
|
R |
= 8314 |
= 8314 =189 |
; R |
Н |
= 8314 |
= 8314 |
= 4157 |
; |
|||||||||||
|
CO |
μ |
44 |
кг К |
2 |
μ |
2 |
кг К |
||||||||||||
|
2 |
CO2 |
Н2 |
|||||||||||||||||
|
Дж |
|||||||||||||||||||
|
R |
= |
8314 |
= 8314 |
=520 |
|||||||||||||||
|
кг К |
|||||||||||||||||||
|
CН4 |
μ |
CН4 |
16 |
||||||||||||||||
Задача. Определить газовую постоянную смеси газов, состоящую из 78 % азота и 22 % кислорода.
Решение.
34

На основании уравнения Клапейрона для i-го компонента идеальногазовой смеси, занимающей объём Vсм можно написать:
Записав эти уравнения для всех компонентов смеси и просуммировав их левые и правые части, получим:
|
n |
||||||||||||||||
|
В |
соответствии |
с |
законом |
Дальтона |
∑ pi = рсм |
получаем: |
||||||||||
|
i=1 |
||||||||||||||||
|
pсмVсм = mсмRсс Tсм, где Rсм −газовая постоянная смеси. |
||||||||||||||||
|
Таким |
образом |
можно |
получить |
соотношение: |
||||||||||||
|
n |
||||||||||||||||
|
∑mi Ri |
n |
n |
ci |
=8314 (0.78 |
+ 0.22) = 288.76 |
Дж |
||||||||||
|
R |
= |
i=1 |
= |
∑c R |
=8314 ∑ |
|||||||||||
|
m |
кг К |
|||||||||||||||
|
см |
i i |
i=1 |
μ |
i |
28 |
32 |
||||||||||
|
см |
i=1 |
Уравнение состояния идеального газа написанное выше представляется в интегральной форме. Если продифференцировать уравнение состояния
|
то получим pdv + vdp = RdT , которое |
представляет |
собой процесс, |
|
показанный на рис.5 (на экране). Здесь произведение |
dlv = pdv назвают |
|
|
ДЕФОРМАЦИОННОЙ РАБОТОЙ, а |
произведение dl p = vdp — |
ТЕХНИЧЕСКОЙ РАБОТОЙ.
В первом случае работа связана с изменением объёма (например, в цилиндре поршневого двигателя), а во втором случае – с изменением давления (например, в компрессоре или турбине газотурбинного двигателя).
Уравнение состояния для реального газа было составлено
Ван-дер-Ваальсом Йоханнес Дидериком (1837-1923), нидерландским физиком (Лауреатом Нобелевской премии в 1910 г.) в 1873 году, которое учитывает размеры молекул и межмолекулярные силы притяжения; для одного моля представляется так:
( р + а )(v −b) = RT , . где b −учитывает конечность объёма молекул; v2
a −учитывает межмолекулярное давление.
35
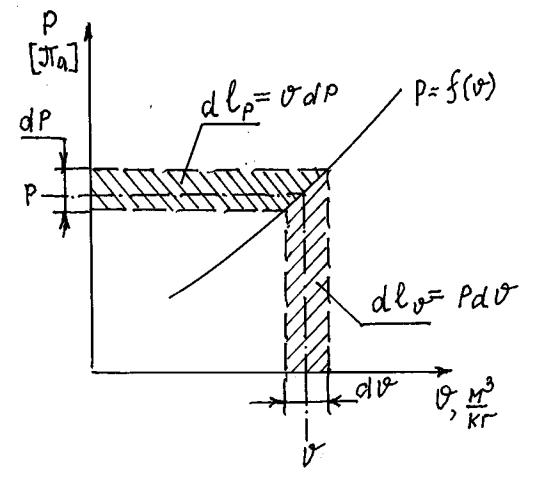
Рис.5. Уравнение состояния идеального газа в дифференциальной форме
Примеры
36

билетов к зачету по дисциплине «Термодинамика и теплопередача» для студентов 3 курса Механического факультета по спец. 160901
Московский государственный технический Университет гражданской авиации
Кафедра «Двигатели летательных аппаратов»
Зав.кафедрой
____________Никонов В.В. «___»_______2007 г.
Учебная дисциплина «Термодинамика и теплопередача»
Билет № 1
1.Поясните содержание понятий «Рабочее тело тепловых машин» и внешняя среда».
Задача. Определить газовую постоянную для следующих газов: СО 2, Н2, СН4.
2.Изобразите и поясните цикл С.Карно в p,v и T , S координатах. Укажите на
графиках площади фигур, соответствующих: работе сжатия и расширения в цикле: количество теплоты, подведенное и отведенное от рабочего тела в цикле. Задача. Определить термический КПД цикла С.Карно, если известны:
Т1 = 288К, Т2 =1500К.
3. Напишите и поясните уравнение неразрывности.
Задача. Как изменитеся расход воздуха через двигатель, если на вход его поступают: — посторонние предметы; — горячие газы от других двигателей.
Московский государственный технический Университет гражданской авиации
Кафедра «Двигатели летательных аппаратов»
Зав.кафедрой
____________Никонов В.В.. «___»_______2007 г.
Учебная дисциплина «Термодинамика и теплопередача»
Билет № 2
1.Поясните содержание понятия «Параметры состояния рабочего тела». Укажите, какие параметры состояния измеряются в эксплуатации авиационных двигателей термометрами сопротивления, термопарами и трубками Пито.
Задача. Определить газовую постоянную смеси газов, состоящую из 78 % азота
и
22% кислорода.
2.Приведите и поясните алгоритм расчета параметров состояния в контрольных точках цикла С.Карно.
Задача. Определить удельную работу сжатия Lv в адиабатном процессе, если известны параметры состояния в начале процесса (T1, p1,v1) и в конце процесса
(T2, p2,v2 ).
3. Напищите и поясните уравнение сохранения энергии в общем виде с учетом трения.
Задача. Определить число Маха воздушного судна в полете со скоростью 2000 км/ч, на высоте 18 км (Тн = 295К ).
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
37
УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ
Кафедра «Двигатели летательных аппаратов»
В.Т. Шулекин, В.В. Медведев, Н.Д. Тихонов, В.В. Дворниченко
ЛАБОРАТОРНЫЙ ПРАКТИКУМ
по дисциплине
«ТЕРМОДИНАМИКА И ТЕПЛОПЕРЕДАЧА»
для студентов специальности 160901 дневной и заочной форм обучения
Москва – 2007
38
Настоящий лабораторный практикум издается в соответствии с учебным планом для студентов специальности 160901 всех форм обучения. Практикум содержит описание семи лабораторных работ по дисциплине «Термодинамика и теплопередача».
Рассмотрено и одобрено на заседаниях кафедры от 27.03.2007г. , протокол № 6 и методического совета специальности от 27.03.2007 г.
Рецензент, профессор, д.т.н. Коняев Е.А.
39
|
Содержание |
Стр. |
||
|
Введение………… |
…………………………… |
4 |
|
|
1. |
Определение теплоемкости воздуха…………………… |
6 |
|
|
2. |
Исследование газовых процессов в элементах ТРД..… |
14 |
|
|
3. |
Исследование циклов тепловых двигателей………..…. |
20 |
|
|
4. |
Новые циклы авиадвигателей |
. . . . . . . . . . . . . . . . . . . . . |
31 |
|
5. |
Исследование сопла трения и подогрева…………….… |
40 |
|
|
6. |
Определение коэффициента тепловодности |
||
|
латунного стержня…………………………………….… |
48 |
||
|
7. |
Определение коэффициента теплоотдачи в условиях |
||
|
естественной конвекции………………………………… |
55 |
||
|
Список использованных источников . . . . . . . . . . . . . . . . . . . |
63 |
40
4
Введение
Учебная дисциплина «Термодинамика и теплопередача» является общей профессиональной дисциплиной учебного плана подготовки студентов по специальности 160901 «Техническая эксплуатация летательных аппаратов и двигателей».
Настоящий лабораторный практикум имеет целью привить студентам практические навыки и умения по экспериментальному и расчетному исследованию типовых задач термодинамики и теплопередачи.
Авиационный газотурбинный двигатель (ГТД) является тепловой машиной, в которой подводимое за счет химических реакций окисления топлива выделяемое количество теплоты преобразуется в полезную работу либо в виде приращения кинетической энергии струи рабочего тела (воздуха), проходящего через двигатель, либо в виде избыточного крутящего момента, который с помощью вала передается на воздушный винт.
Основными элементами ГТД являются входное устройство,
компрессор, камера сгорания, турбина и выходное устройство. Сумму механической работы, отводимой от двигателя, и кинетической энергии на его выходе называют свободной или полезной работой ГТД.
Предметом технической термодинамики является изучение процессов, происходящих в ГТД как тепловой машине, определение условий, при которых эффективность этой машины является максимальной, исследование основных закономерностей преобразования теплоты в работу.
Предметом теплопередачи является изучение процессов теплообмена, которые играют определяющую роль в теплотехнике при создании конкретных элементов ГТД (турбинных лопаток, корпусов, дисков, теплоизоляционных покрытий и т.д.). К основным видам теплообмена относятся теплопроводность, конвекция и тепловое излучение.
Теплопроводностью называют молекулярный перенос теплоты в сплошной среде. Этот процесс возникает при неравномерном распределении температур в среде. В этом случае теплота передается путем непосредственного соприкосновения частиц, имеющих различную скорость, что приводит к обмену энергией между молекулами, атомами или свободными электронами.
Конвекцией называют движение теплоносителя (жидкости или газа) и перенос теплоты при этом в пространстве. Теплообмен между жидкостью или газом с поверхностью твердого тела называют конвективным теплообменом. Процесс теплообмена между двумя
теплоносителями, разделенными твердой стенкой, называют
теплопередачей.
41
5
Конвективный теплообмен — весьма сложное явление, которое описывается системой дифференциальных уравнений, состоящей в общем случае из уравнений теплообмена, энергии, движения, неразрывности, диффузии и состояния. Дифференциальные уравнения отражают лишь самые общие черты явления, в них отсутствуют индивидуальные признаки конкретного единичного случая. Выделение конкретного случая из общего класса явлений конвективного теплообмена осуществляется дополнением системы уравнений условиями однозначности.
Ввиду чрезвычайной сложности системы дифференциальных уравнений конвективного теплообмена и условий однозначности, содержащих большое количество переменных, аналитическое решение ее не может быть получено в общем случае. Эти уравнения могут быть решены в отдельных случаях при существенных упрощающих предположениях.
Теория подобия устанавливает условия подобия физических явлений и на этой основе дает возможность существенно сократить число переменных. Она также дает правила рационального объединения физических величин в безразмерные комплексы — критерии, число которых существенно меньше числа величин, из которых они состоят. В результате использования этих критериев расчет конвективного теплообмена сводится к решению критериальных уравнений, и определению, в конечном итоге, коэффициента теплоотдачи α.
Тепловое излучение — процесс распространения теплоты электромагнитными волнами. Этот вид теплоты обусловлен превращением внутренней энергии вещества в энергию излучения и его поглощением веществом.
42

6
ЛР-1 ОПРЕДЕЛЕНИЕ ТЕПЛОЕМКОСТИ ВОЗДУХА (4 часа)
Цель работы: 1. Экспериментальное определение средней массовой теплоемкости воздуха при постоянном давлении срт.
2.Ознакомление с методикой измерений и обработки опытных данных.
Задание на работу
1.В рабочей тетради изобразить схему лабораторной установки для определения теплоемкости воздуха и указать ее основные элементы.
2.Ознакомиться с принципом действия установки. Подготовить установку для проведения эксперимента.
3.Ознакомиться с основными сведениями и с методикой обработки опытных данных.
4.Произвести измерения:
— температуры to и давления po наружного воздуха в лаборатории;
—температуры воздуха на выходе из термостата t1;
—напряжения uв и силы тока Iв в цепи нагревателя;
—перепада давлений на мерной диафрагме hв.
5.Выполнить обработку экспериментальных данных.
6.Оформить отчет по лабораторной работе.
Основные сведения
Отношение количества теплоты δQ , полученного рабочим телом при
бесконечно малом изменении его состояния, к связанному с этим измене-
нием температуры dT называют теплоемкостью рабочего тела [1,2,3]:
Обозначение δQ вместо dQ показывает на их различие в зависимости
от процесса подвода теплоты. Индекс «х» используется для обозначения того или иного процесса. Например, обозначая х→ р получаем
выражение для теплоемкости в изобарном процессе ( p = const) :
При x →T получаем выражение для теплоёмкости в изотермическом процессе (T = const) cT →∞; при x → k получаем ck = 0 (теплообмен
43
7
между внешней средой и рабочим телом в адиабатном процессе
pvk = const отсутствует); при x →v получаем cv в изохорном процессе
( v = const ).
Обычно теплоемкость относят к единице количества вещества и в зависимости от выбранной единицы различают:
—удельную массовую теплоемкость ст, кгДжК ;
—удельную объемную теплоемкость cv, мДж3 К ;
—удельную мольную теплоемкость μс, мольДжК .
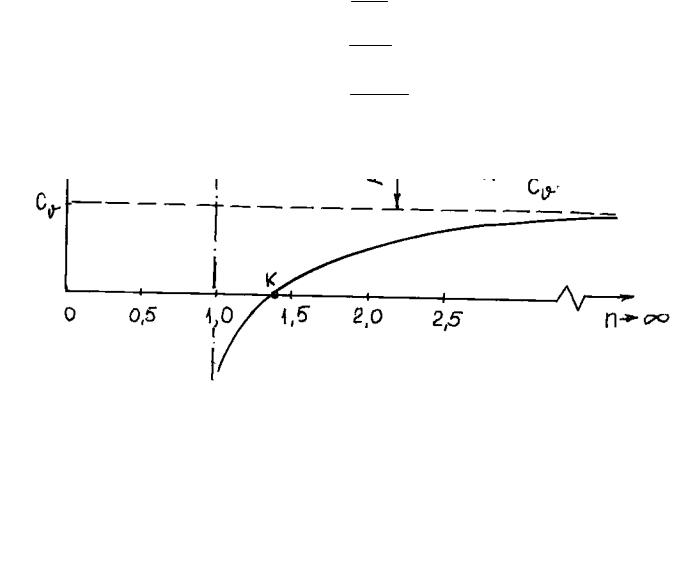
Зависимость теплоемкости от характера процесса может быть представлена графически (рис.1.1). Здесь произвольный процесс представляется политропным
Рис.1.1. Зависимость удельной массовой теплоемкости от показателя политропы п
( pvn = const ), где п – показатель политропы, может принимать значения
|
− ∞ < n < +∞. Теплоёмкость |
политропного процесса |
находится по |
||
|
формуле: |
n−k |
|||
|
c |
x |
= c |
(1.3) |
|
|
v n−1 |
44

8
Для идеального газа, молекулы которого имеют массу, бесконечно малые размеры и не взаимодействуют друг с другом (кроме столкновений), существует связь между теплоёмкостями сp и cv , полученная впервые
Юлиусом Робертом Майером (1814 – 1878) – немецким естествоиспытателем и врачом, в 1847 году:
где R — газовая постоянная идеального газа представляет собой работу совершаемую 1 кг газа в процессе постоянного давления при изменении
температуры на один градус, кгДжК . Численное значение R определяется из соотношения:
Здесь Rμ =8314 мольДжК — универсальная газовая постоянная (для всех газов); μ, молькг — масса одного моля газа. Например, для сухого воздуха
|
μ = 28.966 |
кг |
, |
R = |
8314 |
= 287 |
Дж |
, |
для |
водяного |
пара |
|||
|
моль |
28.966 |
кг К |
|||||||||||
|
Н2О μ =18 |
кг |
, R = 8314 = 462 |
Дж |
. |
|||||||||
|
моль |
|||||||||||||
|
18 |
кг К |
||||||||||||
|
Чем больше |
R , тем больше требуется работы, например, для сжатия |
||||||||||||
|
газа в компрессоре газотурбинного двигателя. |
|||||||||||||
|
В изохорном процессе |
( v = const ) |
теплота, |
сообщаемая газу, |
идёт |
|||||||||
|
только на изменение его внутренней энергии (впервые установлено в |
1843 |
году английским физиком Деймсом Прескотт Джоулем (1818 – 1889)).
Это видно из уравнения первого закона термодинамики:
|
δq |
= cvdT + pdv , |
(1.6) |
|
где pdv = 0, тогда как в |
изобарном процессе |
( p = const ) теплота |
расходуется на изменение внутренней энергии и на совершение работы против внешних сил ( pdv > 0 ). Поэтому c p больше cv на величину этой
работы.
|
В адиабатном |
процессе ( pvk = const ), |
протекающем без теплообмена |
|||
|
между рабочим |
телом и внешней |
средой ( q = 0), |
отношение |
||
|
теплоёмкостей k = |
c p |
называют показателем адиабаты. |
Для воздуха |
||
|
cv |
|||||
как идеального газа (доля кислорода в сухом воздухе составляет 20.9476 % [4], доля азота — 78.064 %), теплоёмкость которого не зависит от температуры к =1.4, для продуктов сгорания авиационного керосина k =1.33.
45

9
Величина теплоёмкостей сp и cv с учётом показателя адиабаты находится из решения системы уравнений:
c p − cv = R
k = ccpv
Отсюда
|
c |
p |
= |
kR |
; c |
= |
R |
. |
(1.7) |
||
|
k −1 |
k −1 |
|||||||||
|
v |
Для реальных газов сp − cv > R , поскольку при их расширении в
изобарном процессе совершается работа не только против внешних сил, но и против сил притяжения, действующих между молекулами, что вызывает дополнительный расход теплоты. При увеличении температуры у многоатомных молекул происходит возбуждение внутренних степеней свободы за счет возникновения колебательного движения атомов молекулы (молекула становится осциллятором). Это приводит к увеличению внутренней энергии, а следовательно, и теплоемкости с ростом температуры.
Поскольку теплоемкость реального газа зависит от температуры, в технической термодинамике различают истинную (найденную по формуле (1.1)) и среднюю теплоемкости.
Средняя теплоемкость процесса находится по формуле:
|
t2 |
t2 |
t1 |
|||||||||||
|
t2 |
q |
ccp ∫ |
−ccp ∫ t1 |
||||||||||
|
t2 |
t1 |
0 |
|||||||||||
|
ccp ∫ |
= |
или ccp ∫ = |
(1.8) |
||||||||||
|
t2 −t1 |
t2 −t1 |
||||||||||||
|
t1 |
t1 |
||||||||||||
|
В теплотехнических |
расчетах |
теплоемкости |
c p или cv находят по |
||||||||||
|
формуле: |
+ a T + a T 2 |
+ a T 3 |
|||||||||||
|
c = a |
o |
+…. |
(1.9) |
||||||||||
|
1 |
2 |
3 |
Например, для расчета теплоемкости сухого воздуха рекомендуется следующая формула:
|
c pm = 0.9952 + 0.9349 10 |
−4 |
t |
кДж |
(1.10) |
|
кг К |
||||
Описание лабораторной установки
Установка (рис.1.2) состоит из электромотора 1, частота вращения которого регулируется реостатом 2; вентилятора 3; мерной диафрагмы 4; электрического нагревателя 5, мощность которого регулируется реостатом 6; термостата 7; амперметра 8; вольтметра 9, с помощью которых
46

10
определяется мощность нагревателя на каждом режиме, термометра 10, с помощью которого измеряется температура нагретого воздуха в термостате; микроманометра 11, с помощью которого измеряется перепад статического давления на мерной диафрагме 4.
Рис.1.2. Принципиальная схема лабораторной установки для определения теплоемкости воздуха:
1 — электромотор; 2,6 — реостаты; 3 — вентилятор; 4 — мерная диафрагма; 5 — нагревательный элемент; 7 — термостат; 8 — амперметр;
9— вольтметр; 10 – термометр; 11 – микроманометр;
α— угол наклона микроманометра к горизонтали
Принцип действия установки состоит в следующем. Воздух из лаборатории с температурой to и давлением po засасывается
вентилятором 3 и подаётся по трубопроводу 10 к электронагревателю 5 открытого типа. Для полного исключения потерь тепла в окружающую среду нагреватель помещён в термостат.
Расход воздуха через трубопровод регулируется частотой вращения вентилятора.
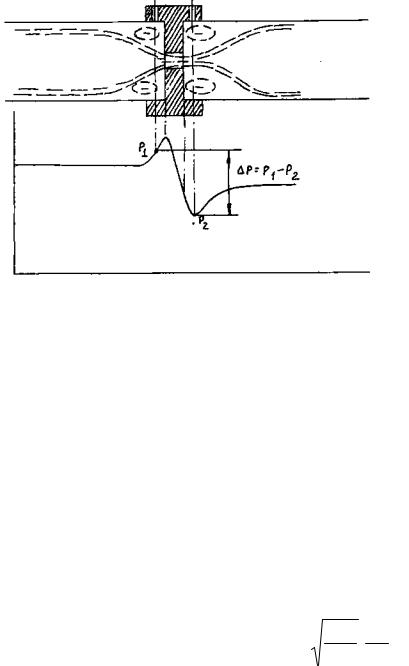
Для определения расхода в трубопроводе 10 установлена мерная диафрагма (рис.1.3), представляющая собой диск с отверстием круглого сечения, центр которого лежит на оси трубопровода. Сужение воздушного потока начинается на некотором расстоянии от диафрагмы и на некотором расстоянии за диафрагмой поток достигает минимального сечения [5]. Далее поток постепенно расширяется до полного мечения трубопровода.
Как видно из рис.1.3, давление за диафрагмой полностью не восстанавливается (перед диафрагмой происходит дросселирование струи
– ускорение потока, а непосредственно за диафрагмой давление не может сразу восстановиться, поэтому появляется разность давлений
47
11
р = р2 − р1). Разность давлений на диафрагме зависит от скорости потока
в отверстии, или, что то же самое, от объёмного расхода воздуха V = Fотвсотв, где Fотв — площадь отверстия, сотв — скорость воздуха в отверстии, а также от интенсивности вихрей, образующихся до и после диафрагмы («мертвая» зона на рис.1.3).
Рис.1.3. Характер потока и распределение статического давления при установке в трубопроводе диафрагмы
Таким образом, в лабораторной установке реализуется изобарный подвод теплоты к потоку воздуха. Уравнение теплового баланса для установки представляется так:
|
Gвc pт(T1 −To ) = IвVв, |
(1.11) |
|||
|
где Gв =Vρв — массовый расход воздуха в трубопроводе, кг/с; |
||||
|
ρв |
— плотность воздуха, |
кг |
; Т1 – температура |
воздуха на выходе из |
|
м3 |
термостата; срт — средняя массовая теплоёмкость воздуха при постоянном давлении; Iв,Vв — сила тока и напряжение в цепи нагревателя.
Для определения объёмного расхода воздуха, проходящего через диафрагму, рекомендуют следующую формулу [5]:
|
V =μεk |
F |
2 p , м3 |
, |
||||||||
|
где μ = 0.82 |
t |
отв |
ρв с |
||||||||
|
— коэффициент |
расхода |
мерной диафрагмы; |
ε =1.0 — |
||||||||
|
коэффициент, |
учитывающий |
сужение |
струи; |
kt =1.0 — |
температурный |
||||||
|
поправочный коэффициент; |
F |
= |
πdотв2 |
= 7.85 10−5м2 ; |
d |
отв |
= 0.01 м — |
||||
|
отв |
4 |
||||||||||
диаметр отверстия в диафрагме;
48

|
Н |
; α =30о |
12 |
||
|
р = h sinα — перепад давления в диафрагме, |
— угол наклона |
|||
|
в |
м2 |
|||
микроманометра к горизонту.
Подставляя значения коэффициентов в формулу, с учётом масштаба измерительной части микроманометра и его показаний в мм водяного столба, получаем расчётную формулу:
|
V = 6.45 |
10−3 hв |
, м3 |
(1.12) |
|
ρв |
с |
Порядок проведения экспериментов и методика обработки опытных данных
Перед началом проведения экспериментов необходимо подготовить таблицы 1.1 и 1.2.
Порядок обработки опытных данных следующий:
1. Определяются параметры состояния окружающего воздуха в лаборатории:
|
Т |
о |
=t |
o |
+ 273, K; p |
o |
= B |
133.2 |
Н |
, |
||||||||||||||
|
o |
м2 |
||||||||||||||||||||||
|
где Во — барометрическое давление, мм рт.ст. |
|||||||||||||||||||||||
|
Таблица 1.1 |
|||||||||||||||||||||||
|
Номер |
Перепад |
Температура |
Сила |
тока |
в |
Напряжение на |
|||||||||||||||||
|
Опыта |
давления |
на |
воздуха |
на |
цепи |
клеммах |
|||||||||||||||||
|
мерной |
выходе |
из |
нагревателя, |
спирали |
|||||||||||||||||||
|
диафрагме, |
нагревателя, |
Iв, А |
нагревателя, |
||||||||||||||||||||
|
hв, мм вод. ст. |
t1,o C |
Uв, В |
|||||||||||||||||||||
|
1 |
|||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||
|
3 |
|||||||||||||||||||||||
|
Повышение |
Таблица 1.2 |
||||||||||||||||||||||
|
Номер |
Объёмны |
Массовы |
Количество |
Средняя |
|||||||||||||||||||
|
Опыта |
й |
расход |
й |
расход |
теплоты, |
температур |
массовая |
||||||||||||||||
|
воздуха, |
воздуха, |
подведенно |
ы |
воздуха в |
теплоемкост |
||||||||||||||||||
|
м3 |
кг |
е к воздуху, |
нагревателе, |
ь воздуха, |
|||||||||||||||||||
|
V , |
с |
Gв, с |
Qв,Вт |
Тв,К |
срт, |
Дж |
|||||||||||||||||
|
кг К |
|||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||
|
3 |
49
13
2. Рассчитывается плотность воздуха из уравнения состояния
(выведено Клапейроном Бенуа Полем Эмилем (1799 – 1864)
французским физиком и инженером в 1834 году и дополнено Дмитрием Ивановичем Менделеевым (1834 – 1907), российским химиком, для одного моля идеального газа в 1874 году):
|
ρв = |
ро |
, |
кг |
, где R = 287 |
Дж |
— газовая постоянная сухого воздуха. |
|
|
RTo |
м3 |
кг К |
|||||
3.Определяется объёмный расход воздуха в трубопроводе по формуле (1.12).
4.Рассчитывается массовый расход воздуха:
Gв =ρвV , кгс
5. Количество теплоты, подведенное к воздуху в нагревателе: Qв = IвUв, Джс или Вт
6.Повышение температуры в нагревателе:
Тв =Т1 −То, где Т1 =t1 + 273, K
7.Удельная средняя массовая теплоемкость воздуха в процессе при
постоянном давлении:
|
c pm = |
Qв |
, |
Дж |
|
|
Gв Tв |
кг К |
|||
Отчетность по лабораторной работе
Включает:
1.Принципиальную схему лабораторной установки с указанием ее основных элементов.
2.Результаты измерений параметров установки при проведении опытов
иих обработки (табл.1.1-1.2).
3.Алгоритм обработки экспериментальных данных.
Ответы на контрольные вопросы:
1.Что называют теплоемкостью рабочего тела?
2.Напишите и поясните уравнение первого закона термодинамики в дифференциальной форме.
3.Напишите и поясните уравнение состояния идеального газа.
4.Напишите и поясните уравнение Ю.Майера.
5.Напишите и поясните уравнение теплового баланса для лабораторной установки.
6. Приведите примеры использования теплоёмкостей ср и cv в авиационной технике.
7.Принцип действия лабораторной установки.
8.Чем объяснить увеличение теплоемкости с ростом температуры?
50

14
ЛР-2 ИССЛЕДОВАНИЕ ГАЗОВЫХ ПРОЦЕССОВ В ЭЛЕМЕНТАХ ТРД (4 часа)
Цель работы: 1. Практическое освоение схемы и принципа действия турбореактивного двигателя.
2.Приобретение навыков по расчету параметров состояния в контрольных сечениях проточной части ТРД.
3.Сделать выводы, ответить на контрольные вопросы и оформить отчет по лабораторной работе.
Задание на работу
1. Для заданного значения степени повышения давления в
компрессоре π*к = 20 и степени подогрева воздуха в двигателе
|
Тг* |
* |
и |
||||
|
= |
= 6.5 (величины πк |
называются параметрами рабочего про- |
||||
|
Тн |
||||||
цесса (цикла) двигателя) определить:
—параметры состояния (действительные и заторможенные) воздуха или газа в контрольных сечениях проточной части (газовоздушного тракта) турбореактивного двигателя;
—энергетические показатели процессов в элементах ТРД:
а) количество теплоты, участвующее в процессе; б) работу сжатия и расширения; в) полезную работу цикла двигателя; Исходные данные:
— рабочее тело — воздух (показатель адиабаты к = 1.4, газовая постоянная Rв = 287 кгДжК , для газа кг=1.33, Rг = 287.5 кгДжК );
—давление и температура в начальной точке «н»:
рн = 760 мм рт.ст., Тн = 288 К;
—скорость полета V=0.
2.Оформить отчет по лабораторной работе.
Основные сведения
Газотурбинным двигателем (ГТД) согласно ГОСТ 23851-79 [1]
называют тепловую машину, в которой энергия сгорания топлива преобразуется в кинетическую энергию струи и в механическую работу на валу; основными элементами ГТД являются компрессор, камера сгорания и газовая турбина.
51
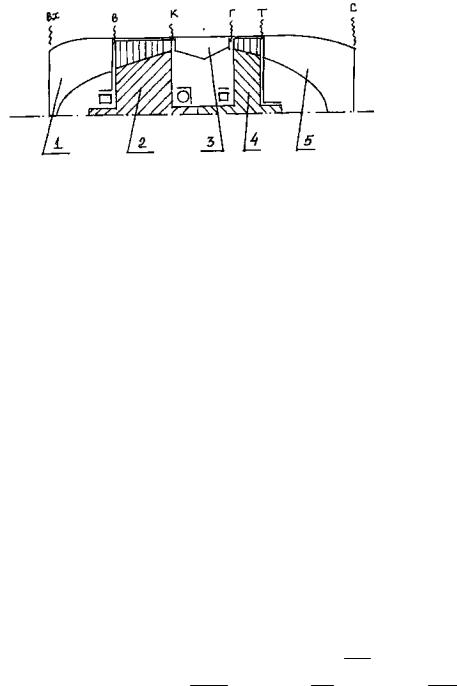
15
Турбореактивным двигателем (ТРД) или двигателем прямой реакции называют ГТД, в котором преобладающая часть энергии топлива преобразуется в кинетическую энергию струи. То есть основой ТРД является ГТД со следующими элементами: входное устройство,
компрессор, камера сгорания, турбина и выходное устройство
(рис.2.1).
Рис.2.1. Принципиальная схема турбореактивного двигателя с осевым компрессором:
1 — входное устройство; 2 — компрессор; 3 — камера сгорания; 4 -турбина; 5 — выходное устройство; вх, в, к, г, т, с -обозначения контрольных сечений проточной части двигателя
Рассмотрим принцип действия ТРД при работе на стенде (Н=0, V =0). 1. Воздух из атмосферы поступает во входное устройство (в воздухозаборник), где происходит его ускорение до скорости cв=180…220 м/с . То есть воздухозаборник на старте воздушного судна
работает в режиме расширения.
Если принять течение воздушного потока в воздухозаборнике энергоизолированным и без трения, то течение воздуха адиабатное. Параметры состояния воздуха на выходе из воздухозаборника (сечение «В-В») находятся по формулам:
а) давление и температура заторможенного потока воздуха
Тв* =Тн* =Тн (при V = 0); рв* = рн* = рн;
б) действительная температура (из выражения для полной энергии потока в сечении) и статическое давление (из уравнения адиабатного
процесса торможения от рв до рв*) в потоке
Тв =Тв* − 2ссв2рв ; рв =
в) плотность и удельный объем
к
рв* Тв* к−1; срв = кк−1 R;Тв
воздуха (из уравнения состояния)
52

16
ρв = RTрвв ; vв = ρ1в .
В этих формулах:
срв — средняя теплоемкость воздуха в изобарном процессе; Rв— газовая
постоянная для воздуха.
2. Из воздухозаборника воздух поступает в компрессор, в котором происходит сжатие (плотность увеличивается). При отсутствии теплообмена рабочего тела — воздушного потока с окружающего средой (лопатками, корпусом и т.п.) и трения процесс сжатия в компрессоре адиабатный (температура и давление в процессе сжатия также возрастают). Параметры состояния воздуха на выходе из компрессора (сечение «К-К») находятся по формулам:
|
к−1 |
ск2 |
|||||||||||||||||
|
* |
* * * |
* * |
к |
* |
||||||||||||||
|
рк |
= рв |
πк; Тк |
=Тв |
πк |
; Тк = |
Тк |
− |
; |
||||||||||
|
2срв |
||||||||||||||||||
|
к |
||||||||||||||||||
|
= р* |
Тк |
к−1 |
рк |
1 |
||||||||||||||
|
р |
к |
; ρ |
к |
= |
; v |
к |
= |
|||||||||||
|
к |
* |
RTк |
ρк |
|||||||||||||||
|
Тк |
Скорость воздушного потока на выходе из компрессора принимается равной ск=100…120 м/с.
3. Из компрессора воздух направляется в камеру сгорания, где к нему подводится теплота при сгорании топлива, впрыскиваемого топливными форсунками в камеру. Принимая процесс подвода теплоты изобарным, определяем параметры состояния газа на выходе из камеры сгорания (сечение «Г-Г»):
|
2 |
кг |
|||||||||||||||||||||||||
|
* |
* * |
* |
к |
г |
−1 |
|||||||||||||||||||||
|
сг |
* |
Тг |
||||||||||||||||||||||||
|
рг |
= |
рк; |
Тг |
=Тн ; Тг =Тг |
− |
; рг = рг |
; |
|||||||||||||||||||
|
2срг |
* |
|||||||||||||||||||||||||
|
Тг |
||||||||||||||||||||||||||
|
ρ |
г |
= |
рг |
;v |
г |
= |
1 |
; с |
рг |
= |
кг |
R . |
||||||||||||||
|
к |
||||||||||||||||||||||||||
|
R T |
ρ |
г |
г |
−1 |
г |
|||||||||||||||||||||
|
г |
г |
Скорость потока газа на выходе из камеры сгорания принимается равной сг =150…160 м/с.
4. Из камеры сгорания поток газа направляется в турбину (сечение «Г-Г»), где происходит расширение газа (плотность уменьшается). Пренебрегая теплообменом между газом и лопатками и корпусом турбины, а также трением, процесс расширения газа принимается адиабатным (при расширении газа температура и давление также уменьшаются). Параметры состояния газа на выходе из турбины (сечение «Т-Т») находятся следующим образом:
53

17
а) из условия баланса мощностей турбины и компрессора в ТРД (или баланса удельных эффективных работ):
срг(Тг* −Тт*) = срв(Тк* −Тв*)
определяется температура заторможенного потока газа за турбиной Тт* .
б) задается приведенная скорость газа на выходе из турбины
λт = 0.5…0.6 .
Действительная температура и статическое давление в потоке газа в данном сечении проточной части двигателя:
|
* |
кг −1 |
2 |
Тт |
кг |
рт |
1 |
||||||||||||||
|
кг −1 |
||||||||||||||||||||
|
Тт =Тт 1 |
− |
λт |
; рт = рг |
; ρт = |
; vт = |
; |
||||||||||||||
|
к |
г |
+1 |
Т |
R Т |
г |
ρ |
т |
|||||||||||||
|
г |
г |
в) давление заторможенного потока газа (полное давление) за турбиной
|
* |
рт |
||||||||||
|
рт |
= |
||||||||||
|
кг −1 |
2 |
кг |
|||||||||
|
к |
г |
−1 |
|||||||||
|
1− |
λ |
т |
|||||||||
|
кг +1 |
|||||||||||
5. Из турбины (сечение «Т-Т») газы направляются в выходное устройство ( в реактивное сопло) двигателя, где происходит ускорение потока (температура, давление и плотность уменьшаются, а скорость увеличивается). Если принять, что течение в реактивном сопле энергоизолированное и трение отсутствует, то процесс расширения газа можно считать адиабатическим. Параметры состояния газа на выходе из сопла (сечение «С-С») при расширении до атмосферного давления рн
находятся по формулам:
|
кг |
−1 |
2 |
||||||||||||||||||||
|
рн |
к |
г |
||||||||||||||||||||
|
р |
с |
= р |
н |
; с = |
2с |
рг |
Т |
* 1 |
− |
; Т |
* =Т |
*; Т |
с |
=Т |
* − сс |
; |
||||||
|
с |
т |
* |
с |
т |
с |
2срг |
||||||||||||||||
|
рт |
||||||||||||||||||||||
ρс = RгрТсс ; vс = ρ1с
2.Энергетические показатели процессов в элементах ТРД:
|
а) входное устройство |
ивх = сvв(Тв −Тн) , |
энтальпии |
||
|
Изменение внутренней |
энергии |
|||
|
(теплосодержания) |
iвх = срв(Тв −Тн) |
и |
энтропии sвх = 0 |
(так как |
|
теплообмен между |
потоком |
воздуха |
и |
внешней средой отсутствует, |
qвх = 0 ). Работа против сил давления lрвх(техническая работа) во
54
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
На практике часто встречаются такие изменения состояния газа, когда одновременно изменяются все три параметра – объем VV, давление pp и температура TT. В таких случаях зависимость между параметрами определяется уравнением состояния газа.
Уравнение Клапейрона
Рассмотрим процесс, в результате которого газ перешел из нормального состояния с параметрами V0V_0, p0p_0, T0T_0 в состояние с другими параметрами V1V_1, p1p_1, T1T_1.
Такой переход от начального к конечному состоянию газа можно осуществить с помощью двух известных процессов (например, сначала изобарического, а затем изотермического) по схеме:
I.V0,p0,T0;V′,p0,T;V′=V0TT0I.{{V}_{0}},{{p}_{0}},{{T}_{0}};{V}’,{{p}_{0}},T;{V}’={{V}_{0}}frac{T}{{{T}_{0}}}
II.V′,p0,T;V,p,T;p0V′=pVII.{V}’,{{p}_{0}},T;V,p,T;{{p}_{0}}{V}’=pV
Исключив из двух полученных уравнений объем V′V’ для промежуточного состояния газа, получим
pVT=p0V0T0frac{pV}{T}=frac{{{p}_{0}}{{V}_{0}}}{{{T}_{0}}}
то есть получим уравнение:
pV=ВТpV = ВТ.
Это уравнение вывел французский ученый Б. П. Э. Клапейрон в 1834 году. Постоянная BB в нем – постоянная зависимости от природы газа и его количества. Эту постоянную, рассчитанную для единицы массы газа, называют удельной газовой постоянной B0B_0.
В качестве примера вычислим удельный газовую постоянную для воздуха. Объем 1 кг воздуха – удельный объем воздуха в нормальных условиях (давление 1,013 · 105 Па и температура 273,15 К)
V0=1ρ0=11,293(м3кг){{V}_{0}}=frac{1}{{{rho }_{0}}}=frac{1}{1,293}(frac{{{м}^{3}}}{кг})
Отсюда:
B0=p0V0T0=p0V0273=1,013⋅1051,293⋅273=287,1(Джкг⋅К){{B}_{0}}=frac{{{p}_{0}}{{V}_{0}}}{{{T}_{0}}}=frac{{{p}_{0}}{{V}_{0}}}{273}=frac{1,013cdot {{10}^{5}}}{1,293cdot 273}=287,1(frac{Дж}{кгcdot К})
Аналогично вычислено, что удельная газовая постоянная для водорода равна 4125, для кислорода – 295,7; для азота – 296,7 Дж / (кг · К) и т. д.
Преобразования Менделеева
В 1874 г. русский химик Д. И. Менделеев, воспользовавшись законом Авогадро, предоставил уравнение Клапейрона в более удобном для использования виде. При этом оказалось целесообразным рассчитывать постоянную для газов, взятых в количестве 1 моль или 1 кмоль:
Rm=p0V0mT0=1,013⋅105⋅0,0224273=8,31(Джмоль⋅K){{R}_{m}}=frac{{{p}_{0}}{{V}_{0m}}}{{{T}_{0}}}=frac{1,013cdot {{10}^{5}}cdot 0,0224}{273}=8,31(frac{Дж}{мольcdot K})
Постоянную RmR_m (или просто RR) называют универсальной газовой постоянной. Уравнение состояния в расчете на 1 моль идеального газа имеет вид, аналогичный уравнению Клапейрона:
pV=RmTpV={{R}_{m}}T
В таком виде уравнения состояния идеального газа называют уравнением Клапейрона-Менделеева.
Кроме единицы количества вещества – моль – разрешается применять кратные и дольные от ее величины. В пересчете на кмоль RR составит:
R=1,013⋅105⋅22,4273=8,31⋅103(Джкмоль⋅K)R=frac{1,013cdot {{10}^{5}}cdot 22,4}{273}=8,31cdot {{10}^{3}}(frac{Дж}{кмольcdot K})
В расчете на 1 кмоль идеального газа уравнение записывают так:
pV=RTpV = RT,
а для любой массы mm – так:
pV=mμRTpV=frac{m}{mu }RT
где μμ – масса, которую имеет кмоль газа.
Для удобства расчетов преимущественно пользуются именно этой формой уравнения.
По данному уравнению легко находим зависимость плотности газа от давления и температуры, а именно:
mV=μpRTfrac{m}{V}=frac{mu p}{RT},
ρ=μpRTrho =frac{mu p}{RT}
Таковы в общем виде эмпирические закономерности в свойствах идеального газа.
Физическая суть постоянной
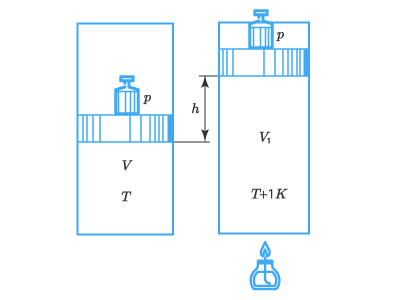
Для выяснения физической сути постоянной RR представим 1 кмоль газа под поршнем в некоем цилиндре:
При этом давление в нем составляет рр, температура – ТТ, а площадь поршня SS.
Повысим температуру газа внутри цилиндра от ТТ до (Т+1КТ + 1 К). Газ расширяется и выполняет работу, поднимая поршень на высоту hh. Эта работа составит:
А=pShА = pSh,
но Sh=ΔVSh = ΔV – прирост объема газа при расширении;
поэтому А=pΔVА = pΔV.
Данное выражение определяет работу газа в изобарическом процессе.
Применив уравнение Клапейрона-Менделеева к начальному и конечному состояниям газа, получим:
pV=RT;pV1=R(T+1K)pV=RT;p{{V}_{1}}=R(T+1K)
Отняв от второго уравнения первое, получим:
p(V1−V)=R;R=pΔVp({{V}_{1}}-V)=R;R=pDelta V
Сопоставим данное равенство с уравнением работы по подъему и найдем, что R=АR = А, то есть универсальная газовая постоянная численно равна работе расширения одного кмоль газа при изобарическом нагревании на 1К1 К.
Тест по теме: “Уравнение Клапейрона-Менделеева”
From Wikipedia, the free encyclopedia
| Value of R[1] | Unit |
|---|---|
| SI units | |
| 8.31446261815324 | J⋅K−1⋅mol−1 |
| 8.31446261815324 | m3⋅Pa⋅K−1⋅mol−1 |
| 8.31446261815324 | kg⋅m2⋅s−2⋅K−1⋅mol−1 |
| Other common units | |
| 8314.46261815324 | L⋅Pa⋅K−1⋅mol−1 |
| 8.31446261815324 | L⋅kPa⋅K−1⋅mol−1 |
| 0.0831446261815324 | L⋅bar⋅K−1⋅mol−1 |
| 8.31446261815324×107 | erg⋅K−1⋅mol−1 |
| 0.730240507295273 | atm⋅ft3⋅lbmol−1⋅°R−1 |
| 10.731577089016 | psi⋅ft3⋅lbmol−1⋅°R−1 |
| 1.985875279009 | BTU⋅lbmol−1⋅°R−1 |
| 297.031214 | inH2O⋅ft3⋅lbmol−1⋅°R−1 |
| 554.984319180 | torr⋅ft3⋅lbmol−1⋅°R−1 |
| 0.082057366080960 | L⋅atm⋅K−1⋅mol−1 |
| 62.363598221529 | L⋅Torr⋅K−1⋅mol−1 |
| 1.98720425864083… | cal⋅K−1⋅mol−1 |
| 8.20573660809596…×10−5 | m3⋅atm⋅K−1⋅mol−1 |
The molar gas constant (also known as the gas constant, universal gas constant, or ideal gas constant) is denoted by the symbol R or R. It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment per amount of substance, i.e. the pressure–volume product, rather than energy per temperature increment per particle. The constant is also a combination of the constants from Boyle’s law, Charles’s law, Avogadro’s law, and Gay-Lussac’s law. It is a physical constant that is featured in many fundamental equations in the physical sciences, such as the ideal gas law, the Arrhenius equation, and the Nernst equation.
The gas constant is the constant of proportionality that relates the energy scale in physics to the temperature scale and the scale used for amount of substance. Thus, the value of the gas constant ultimately derives from historical decisions and accidents in the setting of units of energy, temperature and amount of substance. The Boltzmann constant and the Avogadro constant were similarly determined, which separately relate energy to temperature and particle count to amount of substance.
The gas constant R is defined as the Avogadro constant NA multiplied by the Boltzmann constant k (or kB):
Since the 2019 redefinition of SI base units, both NA and k are defined with exact numerical values when expressed in SI units.[2] As a consequence, the SI value of the molar gas constant is exactly 8.31446261815324 J⋅K−1⋅mol−1.
Some have suggested that it might be appropriate to name the symbol R the Regnault constant in honour of the French chemist Henri Victor Regnault, whose accurate experimental data were used to calculate the early value of the constant. However, the origin of the letter R to represent the constant is elusive. The universal gas constant was apparently introduced independently by Clausius’ student, A.F. Horstmann (1873)[3][4]
and Dmitri Mendeleev who reported it first on Sep. 12, 1874.[5]
Using his extensive measurements of the properties of gases,[6][7]
Mendeleev also calculated it with high precision, within 0.3% of its modern value.[8]
The gas constant occurs in the ideal gas law:
where P is the absolute pressure, V is the volume of gas, n is the amount of substance, m is the mass, and T is the thermodynamic temperature. Rspecific is the mass-specific gas constant. The gas constant is expressed in the same unit as are molar entropy and molar heat.
Dimensions[edit]
From the ideal gas law PV = nRT we get:
where P is pressure, V is volume, n is number of moles of a given substance, and T is temperature.
As pressure is defined as force per area of measurement, the gas equation can also be written as:
Area and volume are (length)2 and (length)3 respectively. Therefore:
Since force × length = work:
The physical significance of R is work per degree per mole. It may be expressed in any set of units representing work or energy (such as joules), units representing degrees of temperature on an absolute scale (such as kelvin or rankine), and any system of units designating a mole or a similar pure number that allows an equation of macroscopic mass and fundamental particle numbers in a system, such as an ideal gas (see Avogadro constant).
Instead of a mole the constant can be expressed by considering the normal cubic meter.
Otherwise, we can also say that:
Therefore, we can write R as:
And so, in terms of SI base units:
- R = 8.314462618… kg⋅m2⋅s−2⋅K−1⋅mol−1.
Relationship with the Boltzmann constant[edit]
The Boltzmann constant kB (alternatively k) may be used in place of the molar gas constant by working in pure particle count, N, rather than amount of substance, n, since
where NA is the Avogadro constant.
For example, the ideal gas law in terms of the Boltzmann constant is
where N is the number of particles (molecules in this case), or to generalize to an inhomogeneous system the local form holds:
where ρN = N/V is the number density.
Measurement and replacement with defined value[edit]
As of 2006, the most precise measurement of R had been obtained by measuring the speed of sound ca(P, T) in argon at the temperature T of the triple point of water at different pressures P, and extrapolating to the zero-pressure limit ca(0, T). The value of R is then obtained from the relation
where:
- γ0 is the heat capacity ratio (5/3 for monatomic gases such as argon);
- T is the temperature, TTPW = 273.16 K by the definition of the kelvin at that time;
- Ar(Ar) is the relative atomic mass of argon and Mu = 10−3 kg⋅mol−1 as defined at the time.
However, following the 2019 redefinition of the SI base units, R now has an exact value defined in terms of other exactly defined physical constants.
Specific gas constant[edit]
| Rspecific for dry air |
Unit |
|---|---|
| 287.052874 | J⋅kg−1⋅K−1 |
| 53.3523 | ft⋅lbf⋅lb−1⋅°R−1 |
| 1,716.46 | ft⋅lbf⋅slug−1⋅°R−1 |
| Based on a mean molar mass for dry air of 28.964917 g/mol. |
The specific gas constant of a gas or a mixture of gases (Rspecific) is given by the molar gas constant divided by the molar mass (M) of the gas or mixture.
Just as the molar gas constant can be related to the Boltzmann constant, so can the specific gas constant by dividing the Boltzmann constant by the molecular mass of the gas.
Another important relationship comes from thermodynamics. Mayer’s relation relates the specific gas constant to the specific heat capacities for a calorically perfect gas and a thermally perfect gas.
where cp is the specific heat capacity for a constant pressure and cv is the specific heat capacity for a constant volume.[9]
It is common, especially in engineering applications, to represent the specific gas constant by the symbol R. In such cases, the universal gas constant is usually given a different symbol such as R to distinguish it. In any case, the context and/or unit of the gas constant should make it clear as to whether the universal or specific gas constant is being referred to. [10]
In case of air, using the perfect gas law and the standard sea-level conditions (SSL) (air density ρ0 = 1.225 kg/m3, temperature T0 = 288.15 K and pressure p0 = 101325 Pa), we have that Rair = P0/(ρ0T0) = 287.052874247 J·kg−1·K−1. Then the molar mass of air is computed by M0 = R/Rair = 28.964917 g/mol.[11]
U.S. Standard Atmosphere[edit]
The U.S. Standard Atmosphere, 1976 (USSA1976) defines the gas constant R∗ as:[12][13]
- R∗ = 8.31432×103 N⋅m⋅kmol−1⋅K−1 = 8.31432 J⋅K−1⋅mol−1.
Note the use of kilomoles, with the resulting factor of 1000 in the constant. The USSA1976 acknowledges that this value is not consistent with the cited values for the Avogadro constant and the Boltzmann constant.[13] This disparity is not a significant departure from accuracy, and USSA1976 uses this value of R∗ for all the calculations of the standard atmosphere. When using the ISO value of R, the calculated pressure increases by only 0.62 pascal at 11 kilometers (the equivalent of a difference of only 17.4 centimeters or 6.8 inches) and 0.292 Pa at 20 km (the equivalent of a difference of only 33.8 cm or 13.2 in).
Also note that this was well before the 2019 SI redefinition, through which the constant was given an exact value.
References[edit]
- ^ «2018 CODATA Value: molar gas constant». The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ «Proceedings of the 106th meeting» (PDF). 16–20 October 2017.
- ^ Jensen, William B. (July 2003). «The Universal Gas Constant R«. J. Chem. Educ. 80 (7): 731. Bibcode:2003JChEd..80..731J. doi:10.1021/ed080p731.
- ^ «Ask the Historian: The Universal Gas Constant — Why is it represented by the letter R?» (PDF).
- ^ Mendeleev, Dmitri I. (September 12, 1874). «An exert from the Proceedings of the Chemical Society’s Meeting on Sept. 12, 1874». Journal of Russian Chemical-Physical Society, Chemical Part. VI (7): 208–209.
- ^ Mendeleev, Dmitri I. (1875). On the elasticity of gases [Объ упругости газовъ]. A.M. Kotomin, St.-Petersburg.
- ^ D. Mendeleev. On the elasticity of gases. 1875 (in Russian)
- ^ Mendeleev, Dmitri I. (March 22, 1877). «Mendeleef’s researches on Mariotte’s law 1». Nature. 15 (388): 498–500. Bibcode:1877Natur..15..498D. doi:10.1038/015498a0.
- ^ Anderson, Hypersonic and High-Temperature Gas Dynamics, AIAA Education Series, 2nd Ed, 2006
- ^ Moran and Shapiro, Fundamentals of Engineering Thermodynamics, Wiley, 4th Ed, 2000
- ^ Manual of the US Standard Atmosphere (PDF) (3 ed.). National Aeronautics and Space Administration. 1962. pp. 7–11.
- ^ «Standard Atmospheres». Retrieved 2007-01-07.
- ^ a b NOAA, NASA, USAF (1976). U.S. Standard Atmosphere, 1976 (PDF). U.S. Government Printing Office, Washington, D.C. NOAA-S/T 76-1562.
{{cite book}}: CS1 maint: multiple names: authors list (link) Part 1, p. 3, (Linked file is 17 Meg)
External links[edit]
- Ideal gas calculator Archived 2012-07-15 at the Wayback Machine – Ideal gas calculator provides the correct information for the moles of gas involved.
- Individual Gas Constants and the Universal Gas Constant – Engineering Toolbox