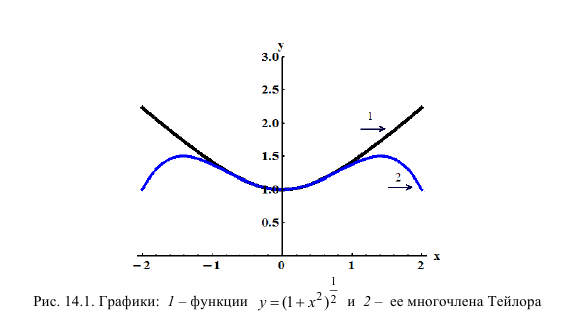
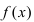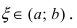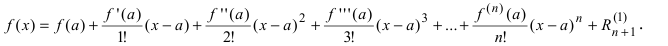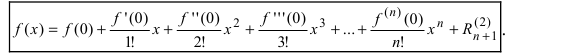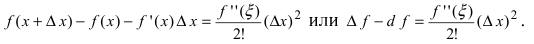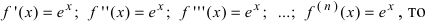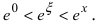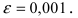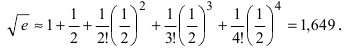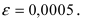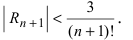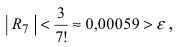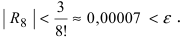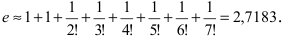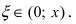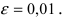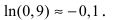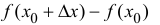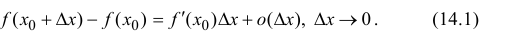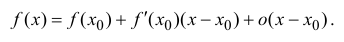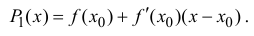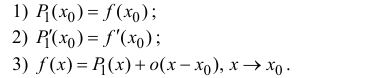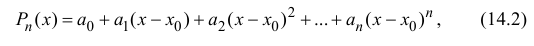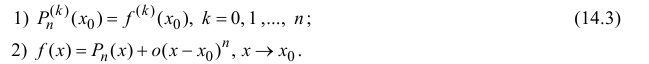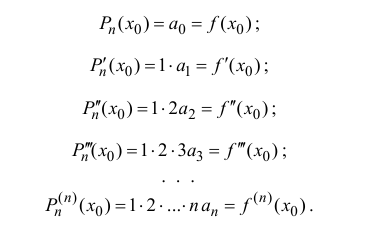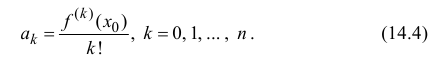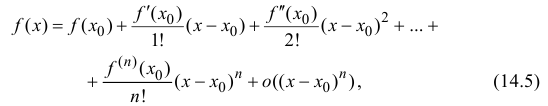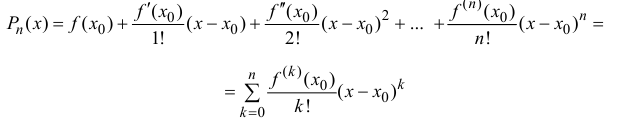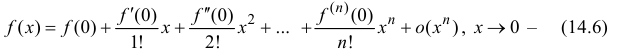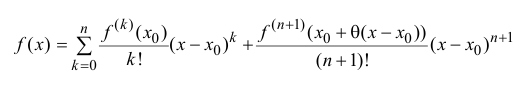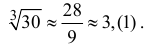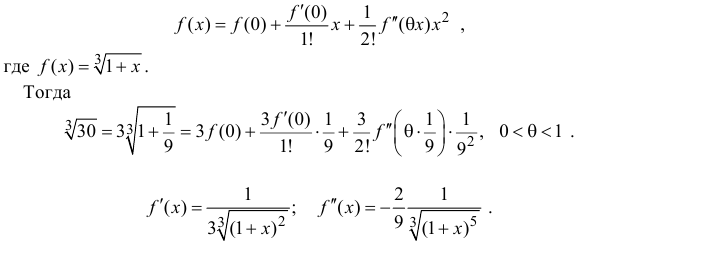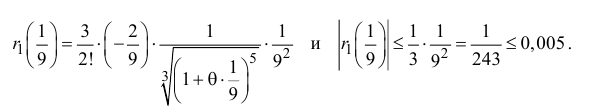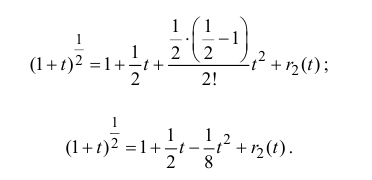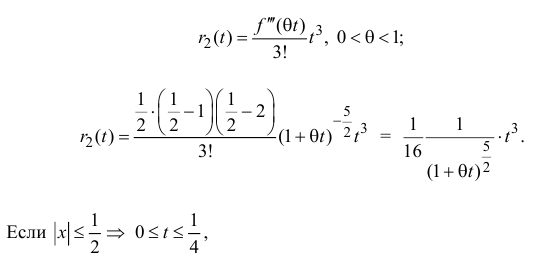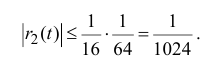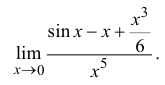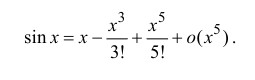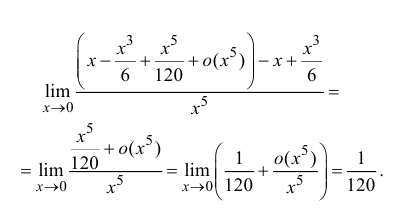Степенные ряды в форме рядов Тейлора и Маклорена
Степенные ряды и, в частности, ряды Тейлора являются одним из видов функциональных рядов.
Степенной ряд в общем виде записывается как:
a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n+…=∑k=0∞ak(x−x0)ka_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n+ldots=sumlimits_{k=0}^{infty} a_k(x-x_0)^k
где a0,a1,…,an,…a_0, a_1, ldots, a_n, ldots — постоянные, коэффициенты ряда,
x0x_0 – центр интервала сходимости ряда ∣x−x0∣<R|x-x_0|<R,
RR – радиус сходимости, когда для частичных сумм Sn(x)S_n(x) существует предел, сумма ряда S(x)S(x):
Sn(x)=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n,limn→∞Sn(x)=S(x)S_n(x)= a_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n, quad limlimits_{n to infty } S_n (x) = S (x)
Возьмем функцию действительной переменной f(x)f(x), которая является бесконечно дифференцируемой в точке x0x_0. Такую функцию можно разложить в степенной ряд следующего вида:
f(x)=f(x0)+f′(x0)1!(x−x0)+f′′(x0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=∑k=0∞f(k)(x0)k!(x−x0)kf(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +dfrac{f{»}(x_0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
Этот ряд по степеням двучлена (x−x0)(x-x_0) называют рядом Тейлора.
В случае x0=0x_0=0 полученный степенной ряд:
f(x)=f(0)+f′(0)1!x+f′′(0)2!(x−x0)2+…+f(n)(x0)n!(x−x0)n+…=∑k=0∞f(k)(x0)k!(x−x0)kf(x)=f(0)+dfrac{f{‘}( 0)}{1!} x +dfrac{f{»}(0)}{2!}(x-x_0)^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k
называют рядом Маклорена.
Ряд Тейлора можно записать в другом виде. Полагая:
x−x0=t,f(x)=f(x0+t)=g(t)x-x_0=t, quad f(x)=f(x_0+t)=g(t)
ряд Тейлора
f(x)=f(x0+t)=f(0)+f′(x0)1!t+f′′(x0)2!t2+…+f(n)(x0)n!tn+…=∑k=0∞f(k)(x0)k!tkf(x)=f(x_0+t)=f(0)+dfrac{f{‘}(x_ 0)}{1!} t +dfrac{f{»}(x_0)}{2!}t^2 +ldots+dfrac{f^{(n)}(x_0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{f^{(k)}(x_0)}{k!}t^k
сводится к ряду Маклорена:
g(t)=g(0)+g′(0)1!t+…+g(n)(0)n!tn+…=∑k=0∞g(k)(0)k!tkg(t)=g(0)+dfrac{g{‘}( 0)}{1!}t +ldots+dfrac{g^{(n)}(0)}{n!}t^n +ldots =sumlimits_{k=0}^{infty} dfrac{g^{(k)}(0)}{k!}t^k
Как и в случае произвольного степенного ряда, ряды Тейлора и Маклорена имеют интервал сходимости.
Пример
Разложим в ряд Тейлора функцию:
f(x)=1xf(x)=dfrac{1}{x}
в окрестности точки x0=1x_0=1.
С помощью замены:
x−x0=x−1=tx-x_0=x-1=t
функция сводится к виду:
f(x)=f(t+1)=11+tf(x)=f(t+1)=dfrac {1}{1+t}
Полученное выражение при ∣t∣<1|t|<1 является суммой бесконечно убывающей геометрической прогрессии знаменателем (−t)(-t), и ряд записывается в виде:
11+t=1−t+t2−t3+…+(−1)ntn+…=∑k=0∞(−1)ktkdfrac {1}{1+t}=1-t+t^2-t^3+ldots+(-1)^{n}t^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}t^{k}
Возвращаясь к переменной xx, получаем разложение по степеням двучлена (x−1)(x-1):
1x=1−(x−1)+(x−1)2−(x−1)3+…+(−1)n(x−1)n+…=∑k=0∞(−1)k(x−1)k,∣x−1∣<1dfrac {1}{x}=1-(x-1)+ (x-1)^2-(x-1)^3+ldots+(-1)^{n}(x-1)^{n}+ldots =sumlimits_{k=0}^{infty} (-1)^{k}(x-1)^{k}, quad |x-1|<1
Формула Тейлора
Следствием разложения функции в степенной ряд является соответствующая формула Тейлора. Если функция f(x)f(x) имеет в точке x0x_0 производные до nn –го порядка включительно, то функцию f(x)f(x) можно представить с помощью формулы Тейлора:
f(x)=f(x0)+f′(x0)1!(x−x0)+…+f(n)(x0)n!(x−x0)n+Rn(x)f(x)=f(x_0)+dfrac{f{‘}(x_0)}{1!}(x-x_0) +ldots+dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n +R_n (x)
или
f(x)=∑k=0nf(k)(x0)k!(x−x0)k+Rn(x)f(x)= sumlimits_{k=0}^{n} dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k +R_n (x),
где функция Rn(x)R_n (x) называется остаточным членом.
Формы остаточного члена
Существует несколько форм для остаточного члена. В частности, если f(x)f(x) дифференцируема (n+1)(n+1) раз в окрестности x0x_0, то Rn(x)R_n (x) может быть представлена в форме Лагранжа:
Rn(x)=f(n+1)(ξ)(n+1)!xn+1,x<ξ<x0R_n (x)=dfrac {f^{(n+1)}(xi)}{(n+1)!} x^{n+1}, quad x<xi<x_0 или x<ξ<x0x<xi<x_0.
Если функция f(x)f(x) дифференцируема (n−1)(n-1) раз в окрестности x0=0x_0=0, то Rn(x)R_n(x) может быть представлена в форме Пеано:
Rn(x)=o((x−x0)n)R_n(x)=o((x-x_0)^n).
Учитывая, что ряд Тейлора можно свести к ряду Маклорена, запишем формулу Тейлора для основных элементарных функций в окрестности x0=0x_0=0 и укажем соответствующие интервалы сходимости.
Показательная функция:
ex=1+x1!+x22!+x33!+…+xnn!+o(xn),∣x∣<∞e^x=1+dfrac{x}{1!} +dfrac{x^2}{2!} +dfrac{x^3}{3!}+ldots+dfrac{x^n}{n!}+o(x^n),quad |x|<infty
Тригонометрические функции:
sinx=x1!−x33!+x55!−x77!+…+(−1)n+1x2n−1(2n−1)!+o(x2n),∣x∣<∞sin x=dfrac{x}{1!} -dfrac{x^3}{3!} +dfrac{x^5}{5!} -dfrac{x^7}{7!} +ldots+dfrac{(-1)^{n+1}x^{2n-1}}{(2n-1)!}+ o(x^{2n}),quad |x|<infty
cosx=1−x22!+x44!−x66!+…+(−1)n+1x2n(2n)!+o(x2n+1),∣x∣<∞cos x=1 -dfrac{x^2}{2!} +dfrac{x^4}{4!} -dfrac{x^6}{6!} +ldots+dfrac{(-1)^{n+1}x^{2n}}{(2n)!}+ o(x^{2n+1}),quad |x|<infty
arctgx=x−x33+x55−x77+…+(−1)nx2n+12n+1+o(x2n+2),∣x∣≤1arctg x=x-dfrac{x^3}{3} +dfrac{x^5}{5} -dfrac{x^7}{7} +ldots+dfrac{(-1)^{n}x^{2n+1}}{2n+1}+ o(x^{2n+2}),quad |x|le{1}
Логарифмическая функция:
ln(1+x)=x1!−x22!+x33!−…+(−1)n+1xnn!+o(xn),x∈(−1;1]ln (1+x)=dfrac{x}{1!} -dfrac{x^2}{2!} +dfrac{x^3}{3!} -ldots+dfrac{(-1)^{n+1}x^{n}}{n!}+ o(x^n),quad xin (-1;1]
Степенная функция:
(1+x)α=1+α1!x+α(α−1)2!x2+α(α−1)(α−2)3!x3+…+α(α−1)…(α−n+1)n!xn+o(xn)(1+x)^alpha=1+dfrac{alpha }{1!}x+dfrac{alpha (alpha -1)}{2!}x^2 +dfrac{alpha (alpha -1)( alpha -2)}{3!} x^3 +ldots+dfrac{alpha (alpha -1) ldots ( alpha-n+1)} {n!} {x^n}+ o(x^n)
Пример 1
Разложим, используя формулу Тейлора, функцию
f(x)=(x+1)ln(x2+2x+2)f(x)=(x+1)ln (x^2+2x+2)
в окрестности точки x0=−1x_0=-1 с точностью до o((x+1)7)o((x+1)^7).
Выполнив замену переменной
x−x0=x+1=tx-x_0=x+1=t
получаем:
g(t)=tln(1+t2)g(t)=tln(1+t^2)
Используя разложение логарифмической функции, получаем:
g(t)=t(t21!−(t2)22!+(t2)33!+o((t2)3))=t3−t52+t76+o(t7)g(t)=t left( dfrac{t^2}{1!}-dfrac{(t^2)^2}{2!}+dfrac{(t^2)^3}{3!}+o((t^2)^3) right)=t^3-dfrac{t^5}{2}+dfrac{t^7}{6}+o(t^7)
Выполняем далее обратную замену переменной:
f(x)=(x+1)3−(x+1)52+(x+1)76+o((x+1)7)f(x)= (x+1)^3-dfrac{(x+1)^5}{2}+dfrac{(x+1)^7}{6}+o((x+1)^7)
Пример 2
Разложим, используя формулу Тейлора, функцию
f(x)=(x2−4x)cos(2x−4)f(x)=(x^2-4x)cos{(2x-4)}
в окрестности точки x0=2x_0=2 с точностью до o((x−5)5)o((x-5)^5).
Выполнив замену переменной:
x−x0=x−2=t,x=t+2x-x_0=x-2=t, quad x=t+2
получаем:
g(t)=(t2−4)cos2tg(t)=(t^2-4)cos{2t}
Используя разложение тригонометрической функции, получаем:
g(t)=(t2−4)(1−(2t)22!−(2t)44!+o(t5))=(t2−4)(1−2t2+2t43+o(t5))g(t) =(t^2-4) left( 1-dfrac{(2t)^2}{2!}-dfrac{(2t)^4}{4!}+o(t^5) right) =(t^2-4) left( 1-2t^2+dfrac{2t^4}{3}+o(t^5) right)
Раскрываем скобки, ограничиваясь слагаемыми со степенью t не выше пяти:
g(t)=(t2−2t4)−(4−8t2+8t43+o(t5))=−4+9t2−143t4+o(t5)g(t) =(t^2-2t^4)- left( 4-8t^2+dfrac{8t^4}{3}+o(t^5) right) =-4+9t^2-dfrac{14}{3} t^4+o(t^5)
Выполняя обратную замену переменной, получаем:
f(x)=−4+9(x−2)2−143(x−2)4+o((x−2)5)f(x)=-4+9(x-2)^2-dfrac{14}{3}(x-2)^4+o((x-2)^5)
Применение формулы Тейлора при x, стремящемся к бесконечности
При необходимости представить функцию с помощью формулы Тейлора при x→∞x to infty с точностью до o(1xn)oleft( dfrac {1} {x^n}right), последовательно:
- выполняем замену переменной t=1xt=dfrac{1}{x};
- полученную функцию g(t)g(t) представляем с помощью формулы Тейлора с необходимой точностью;
- с помощью обратной замены переменных находим искомое выражение для f(x)f(x).
Пример
Разложим, используя формулу Тейлора, функцию
f(x)=2x−x2−1f(x)=2x-sqrt{x^2-1}
с точностью до o(1×3)oleft( dfrac {1} {x^3}right) при x→+∞x to +infty.
Выполнив замену переменной
t=1x,x=1tt=dfrac{1}{x}, quad x=dfrac{1}{t}
получаем:
g(t)=2t−1t2−1=2−(1−t2)1/2tg(t)=dfrac {2}{t}-sqrt {dfrac{1}{t^2}-1}=dfrac{2-(1-t^2)^{1/2}}{t}
Учитывая требуемую точность o(t3)o(t^3), используем разложение степенной функции в ряд Тейлора с точностью до o(t4)o(t^4):
g(t)=2−(1−t22−t48)+o(t4)t=1t+t2−t38+o(t3)g(t)=dfrac {2-left( 1-dfrac{t^2}{2}-dfrac{t^4}{8}right)+o(t^4)}{t}=dfrac{1}{t}+dfrac{t}{2}-dfrac{t^3}{8}+o(t^3)
Выполняя обратную замену переменной, находим:
f(x)=x+12x−18×3+o(1×3),x→+∞f(x)=x+dfrac{1}{2x}- dfrac {1}{8x^3}+ oleft( dfrac {1} {x^3}right), quad x to +infty
Применение формула Тейлора при вычислении пределов
С помощью разложения функции с использованием формулы Тейлора при вычислении пределов можно избавиться от неопределённостями различного вида. Проиллюстрируем использование формулы Тейлора на примере вычисления предела функции с неопределенностью вида (00)left( dfrac {0} {0}right).
Пример 1
Вычислим, используя формулу Тейлора, предел:
limx→1ex−ecos(x−1)sin(x−1)limlimits_{x to 1 } dfrac {e^{x}-e cos{(x-1)}}{sin {(x-1)}}
Заменим ex{e^{x}} и тригонометрические функции их разложениями в степенные ряды в окрестности x0=1x_0=1, находим:
limx→1ex−ecos(x−1)sin(x−1)=limx→1(e+e(x−1)+e(x−1)22!+e(x−1)33!+…)−e(1−(x−1)22!+…)(x−1)−(x−1)33!+…=elimx→1(x−1)+(x−1)2+(x−1)36+…(x−1)−(x−1)36+…=elimx→11+(x−1)+(x−1)26+…1−(x−1)26+…=elimlimits_{x to 1 } dfrac {e^{x}-e cos{(x-1)}}{sin {(x-1)}}=limlimits_{x to 1} dfrac {left(e+e(x-1)+dfrac{e(x-1)^2}{2!}+dfrac{e(x-1)^3}{3!} +ldots right)-eleft( 1-dfrac{(x-1)^2}{2!}+ ldots right)} {(x-1)-dfrac{(x-1)^3}{3!}+ ldots}= elimlimits_{x to 1 } dfrac {(x-1)+(x-1)^2+ dfrac{(x-1)^3}{6}+ldots} {(x-1)- dfrac{(x-1)^3}{6}+ldots} =e limlimits_{x to 1 } dfrac {1+(x-1) +dfrac{(x-1)^2}{6}+ldots} {1- dfrac{(x-1)^2}{6}+ldots} =e
Тест по теме «Формула и ряд Тейлора»
Содержание:
Формула Тейлора и ее применение
Формула Тейлора
Теорема: Если функция
Эта формула была получена в 1715 г. Бруком Тейлором, который был учеником Исаака Ньютона, и носит его имя. Последнее слагаемое в формуле Тейлора 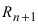
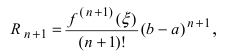
В этой формуле неизвестной является только величина 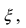
При a = 0 формула Тейлора переходит в формулу Маклoрена:
Пример:
Представить по формуле Маклорена функцию 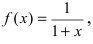
Решение:
Вычислим три первых производных заданной функции:
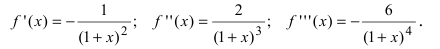
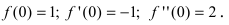
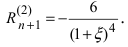
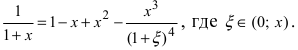
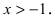
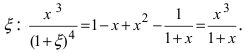
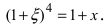
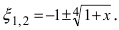
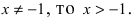
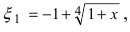
Замечание: При n = 0 формула Тейлора дает формулу конечных приращений:
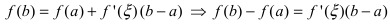
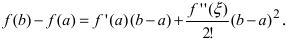
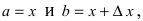
Применение формулы Тейлора
Если известны величины то формула Тейлора позволяет вычислить значение функции в некоторой точке х. В зависимости от требуемой степени точности вычислений достаточно бывает вычислить два, три или несколько первых слагаемых в формуле Тейлора. Для оценки погрешности вычислений необходимо помнить, что величина 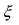
Пример:
Представить функцию 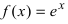
Решение:
Так как 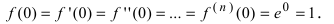
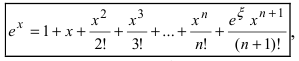
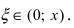
Пример:
Вычислить 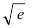
Решение:
Так как основание 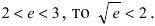
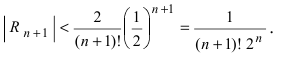
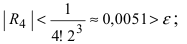
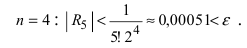
Пример:
Вычислить число е с точностью
Решение:
Согласно результатам, полученным в предыдущем примере, для достижения требуемой точности, подсчитаем остаточный член формулы Маклорена в форме Лагранжа
При n = 6 имеем
при n = 7 получаем
Итак,
Если вычислять значение числа е с точностью 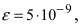
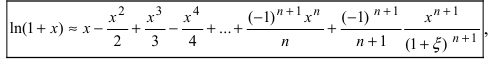
Пример:
Вычислить 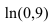
Решение:
В данном примере х = -0,1. Так как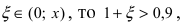
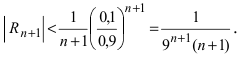
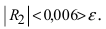
Формула тейлора
Пусть функция y=f(x) дифференцируема в точке 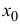
Пусть 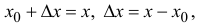
Рассмотрим многочлен
Многочлен 
Пусть функция y=f(x) n раз дифференцируема в точке 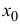
обладающий аналогичными свойствами:
Из (14.2), (14.3) следует, что
Поэтому коэффициенты 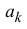
Далее
Таким образом свойства (14.3) выполняются (при этом коэффициенты
многочлена 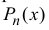
Теорема 14.1. Пусть функция y=f(x) n раз дифференцируема в точке 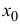
где 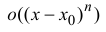
малости, чем
Формула (14.5) называется формулой Тейлора, многочлен
в правой части формулы (14.5) называется многочленом Тейлора, а представление разности 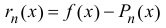
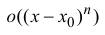
Если функция 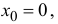
формула Маклорена.
Если функция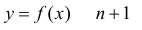
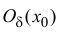
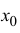
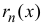
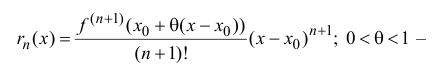
называется формулой Тейлора порядка n с остаточным членом в форме
Лагранжа.
Пример 14.1
В условиях примера 9.4 оценим погрешность вычисления значений
Решение
Запишем формулу Маклорена первого порядка с остаточным членом в форме Лагранжа:
Поэтому
Таким образом, вычисленное значение 3,(1) отличается от истинного с точностью до 0,01.
- Заказать решение задач по высшей математике
Пример 14.3
Разложить 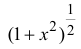
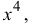
Решение
Пусть 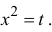
Остаточный член запишем в форме Лагранжа:
поэтому
Таким образом, 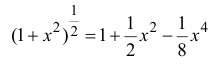
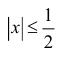
Пример 14.4
Найти
Решение
Воспользуемся разложением (14.7):
Тогда
- Интегрирование рациональных дробей
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений
- Интегрирование иррациональных функций
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
Содержание
- 1 Введение
- 2 Теорема Пеано
- 3 Теорема Лагранжа
- 4 Исследование функции на экстремум
- 5 Разложение ряда элементарных функций по формуле Тейлора
- 5.1 y = e^x
- 5.2 y = ln(x + 1)
- 5.3 y = (x + 1)^α
- 5.4 y = sin x
- 5.5 y = cos x
Введение
Пафос mode on
Формула Тейлора для функций является венцом развития классического анализа.
После её открытия анализ стал развиваться по-другому. Так-то!
Пафос mode off
Пусть функция раз дифференцируема в точке
| Определение: |
| — полином Тейлора функции |
Таким же способом, каким была найдена формула для , легко проверить основное свойство
полинома Тейлора:
. Однако, в общем случае, при ,
| Определение: |
| , где — остаток формулы Тейлора. |
Сейчас мы получим ряд свойств этого остатка при .
Если , то, по теореме Тейлора, ,
Теорема Пеано
| Теорема (Пеано): |
|
Пусть раз дифференцируема в точке . Тогда . где — такая величина, что . , где . Иначе говоря, порядок малости величины слева больше . |
| Доказательство: |
|
Нужно доказать, что — неопределённость . Раскроем по правилу Лопиталя: . Это отношение приращения функции к приращению аргумента — по определению проиизводная. |
Теорема Лагранжа
Если потребовать чего-то большего, чем существование , то остаток можно уточнить.
В этом нам поможет теорема Лагранжа.
| Теорема (Лагранж): |
|
Пусть раз дифференцируема в окрестности точки . Тогда — формула Тейлора с остатком по Лагранжу. |
| Доказательство: |
|
Введём вспомогательную функцию , причём находится Заметим, что — остаток в формуле Тейлора. Найдём : (суммы сокращаются)
, Обозначим за . Тогда . При , . Рассмотрим дробь Но, с другой стороны, Тогда получим , что и требовалось. |
Исследование функции на экстремум
Покажем, как использовать формулу Тейлора для исследования функции на экстремум.
. Нужно определить, является ли точка точкой эктремума.
Будем считать, что функция дифференцируема любое нужное нам число раз.
. Пусть .
— первое такое число, что производная такого порядка в этой точке не равна 0.
По формуле Тейлора с остатком по Пеано,
. При .
Заметим, что , а — изменяется.
Тогда возможны два случая:
- — чётное:
Тогда
Если больше , то в минимум, если меньше — то максимум.
- — нечётное:
в зависимости от того, с какой стороны находится от на числовой оси. Значит, экстремума в точке нет.
Разложение ряда элементарных функций по формуле Тейлора
Разложим ряд элементарных функций в точке по формуле Тейлора:
y = e^x
y = ln(x + 1)
y = (x + 1)^α
y = sin x
y = cos x
-
Формула Тейлора.
Теорема
6 (теорема
Тейлора).
Пусть функция
имеет в точке а и в некоторой ее
окрестности производные порядка n+1.
Пусть х – любое значение аргумента из
указанной окрестности,
.
Тогда между точками а и х найдётся
точка
такая,
что справедлива следующая формула:
(4.3)
Формула
(4.3) называется формулой
Тейлора, а
выражение
остаточным
членом в форме Лагранжа.
Его можно переписать в другом виде. Так
как точка (а,
х),
то найдётся такое число
из интервала
, что
= а+q
(х
а), и остаточный
член принимает вид
Или,
если функция
ограничена в окрестности точки а,
то
при
В этом случае говорят, что остаточный
член записан
в форме Пеано.
2.
Формула Маклорена.
Формулой Маклорена называют формулу
Тейлора (4.3) при
:
Остаточный член
имеет вид:
1)
в форме Лагранжа
2)
в форме Пеано
3. Разложение некоторых элементарных функций по формуле Маклорена.
1)
Так
как
то
формула Маклорена имеет вид
(4.4)
2)
Так
как
то
формула Маклорена имеет вид
(4.5)
3)
Так
как
то
формула Маклорена имеет вид
(4.6)
В
формуле (4.5) остаточный член записан в
виде
а не в виде
так как следующий за последним член
равен нулю (то же самое относится к
формуле (4.6)).
4)
,
где
вещественное число. Так как
то формула Маклорена
имеет вид
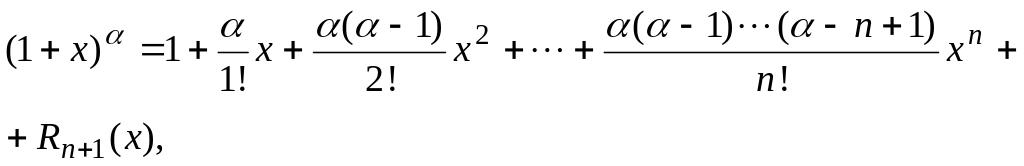
где остаточный
член в форме Лагранжа равен
В
частном случае, когда
натуральное число,
следовательно,
и мы получаем известную из элементарной
математики формулу
бинома Ньютона
(4.7)
Приведенные
выше разложения показывают, что с помощью
формулы Маклорена функции можно с
определённой степенью точности заменять
многочленами, являющимися наиболее
простыми элементарными функциями. Над
многочленами удобно выполнять
арифметические действия, нетрудно
вычислить значение многочлена в любой
точке и т.д.
Формулы Тейлора
и Маклорена позволяют приближённо
заменять многочленами и более сложные
функции. Кроме того, эти формулы имеют
широкий круг приложений.
4.
Использование формулы Маклорена для
вычисления пределов.
Формула Тейлора является эффективным
средством для вычисления пределов
функций, с которыми часто приходится
иметь дело при исследовании функций.
Пример
1. Найти
Решение.
По формуле (4.5)
при
имеем

Пример
2. Найти
Решение.
По формулам (4.4), (4.5) и (4.6)
имеем
.
(здесь
символом
обозначена
величина
являющаяся бесконечно малой при
).
4.4. Исследование поведения функций и построение графиков
1. Признак монотонности функции.
Теорема
1. Если
функция
дифференцируема на интервале
и
(
)
на
,
то функция
не убывает (не
возрастает)
на
.
Если
(
)
на
,
то функция
возрастает (убывает)
на
.
2. Отыскание точек локального экстремума функции.
Определение.
Точка
называется точкой строгого локального
максимума (минимума)
функции
,
если для всех x из некоторой —
окрестности точки
выполняется неравенство
(
)
при
(рис. 19).
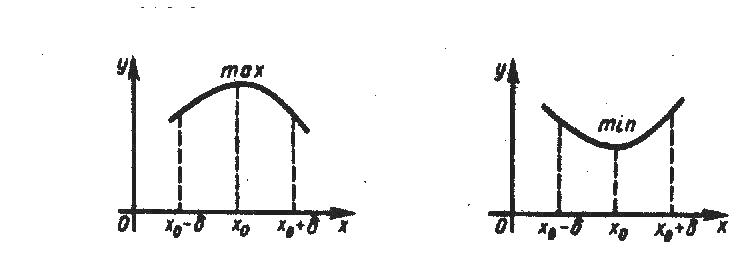
Рис.
19
Локальный
максимум (max) и локальный минимум (min)
объединяются общим названием локальный
экстремум.
Из
определения следует, что понятие
экстремума носит локальный характер в
том смысле, что неравенство
(
)
может и не выполняться для всех значений
х
в области определения функции, а должно
выполняться лишь в некоторой окрестности
точки
.
Очевидно, функция может иметь несколько
локальных максимумов и несколько
локальных минимумов, причем может так
случится, что иной локальный максимум
окажется меньше какого-то локального
минимума.
Теорема
2 (необходимое
условие локального экстремума).
Если функция
имеет в точке
локальный экстремум и дифференцируема
в этой точке, то
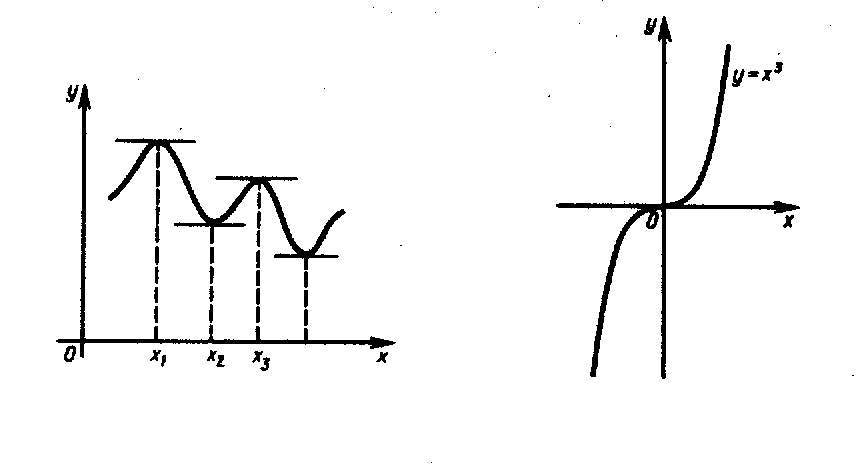
Рис.
20
Рис. 21
Теорема
2 имеет следующий геометрический смысл.
Если
точки локального экстремума и в
соответствующих точках графика существуют
касательные, то эти касательные
параллельны оси
Ох (рис. 20).
Иногда
такие точки называют стационарными; мы
будем называть их точками
возможного экстремума.
Если точка
точка возможного экстремума, т.е.
то она может и не быть точкой локального
максимума или минимума. Например, если
то
при
,
но, тем не менее, в точке
нет локального экстремума (рис. 21).
Установим
достаточное условие существования
локального экстремума. Этому посвящается
следующая теорема.
Теорема
3
(достаточное
условие локального экстремума).
Пусть
функция
дифференцируема в некоторой -окрестности
точки
.
Тогда,
если
(
)
для всех х
из
а
(
)
для всех х
из
то в точке
функция
имеет локальный максимум (минимум);
если же
во всей -окрестности
точки
имеет один и тот же знак,
то в точке
локального экстремума нет.
Другими
словами, если
при переходе через точку
меняет знак с «»
на «»,
то
точка локального максимума; если
в точке
меняет знак с «»
на «»,
то
точка локального минимума; если же
в точке
знака не меняет, то в точке
экстремума не существует.
З
а м е ч а н и е. Теорема 3 остаётся
справедливой, если функция
в самой точке
не дифференцируема, а только непрерывна.
Так, например, функция
в точке
непрерывна, но не дифференцируема.
В
качестве примера рассмотрим вопрос об
отыскании точек локального экстремума
функции
.
Находим производную
.
Решая
уравнение
,
получаем две точки возможного экстремума:
и
.
Дальнейшее исследование удобно вести,
нарисовав вспомогательный чертеж (рис.
22).
Отметим на нем точки
и
и
Р
ис.
22
определив
знак
в окрестности этих точек, получаем:
в точке
имеет локальный максимум, а в точке
локальный
минимум. Далее находим:
,
На
рис. 22 видны и интервалы монотонности
:
(,1),
(1,
1) и (1,),
причем в первом и третьем из них функция
возрастает, а во втором – убывает.
3.
Направление выпуклости и точки перегиба
графика функции. Пусть
функция
дифференцируема на интервале
.
Тогда существует касательная к
графику функции
в любой
точке
этого графика (
),
причем касательная не параллельна оси
Оу,
поскольку ее угловой коэффициент, равный
,
конечен.
Рис. 11
Рис.
11
Рис.
23
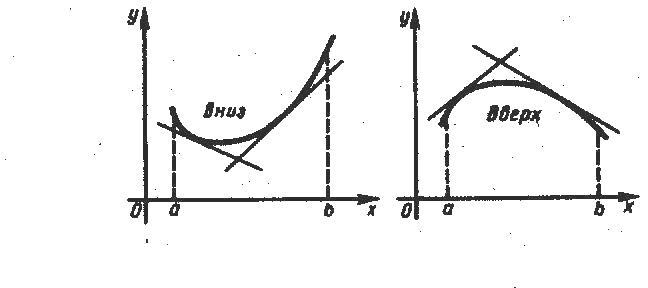
Определение
1. Будем
говорить, что график функции
имеет
на
выпуклость,
направленную вниз (вверх),
если он расположен не ниже (не
выше)
любой касательной к графику функции на
(рис. 23).
Теорема
4.
Если функция
имеет на интервале
вторую
производную и
во всех точках
,
то график функции
имеет на
выпуклость, направленную вниз (вверх).
Определение
2. Точка
М(
)
называется точкой перегиба графика
функции
,
если в точке М график имеет касательную,
и существует такая окрестность точки
,
в пределах которой график функции
слева и справа от точки
имеет разные направления выпуклости.
Рис. 24
Очевидно,
что в точке перегиба касательная
пересекает график функции, так как с
одной стороны от этой точки график лежит
под касательной, а с другой – над нею,
т.е. в окрестности точки перегиба график
функции геометрически переходит с одной
стороны касательной на другую и
«перегибается» через неё. Отсюда
произошло название «точка перегиба»
(рис. 24).
Теорема
5
(необходимое
условие точки перегиба).
Пусть график
функции
имеет перегиб в точке М(
)
и пусть функция
имеет в точке
непрерывную вторую производную.
Тогда
в точке
обращается в нуль,
т.е.
.
Следует
заметить, что не всякая точка М(
),
для которой
,
является
точкой перегиба.
Н
апример,
график функции
не имеет перегиба в точке (0; 0), хотя
при
(рис. 25).
Поэтому
равенство нулю второй производной
является лишь необходимым условием
перегиба.
Точки
М(
)
графика, для которых
,
будем называть критическими.
Необходимо
дополнительно исследовать вопрос о
наличии перегиба в каждой критической
точке, для чего следует установить
достаточное условие перегиба.
Теорема
6
(достаточное
условие точки перегиба).
Пусть функция
имеет вторую производную в некоторой
окрестности точки
.
Тогда, если в пределах указанной
окрестности
имеет разные знаки слева и справа от
точки
,
то график
имеет перегиб в точке М(
).
З
а м е ч а н и е. Теорема остаётся верной,
если
имеет вторую
производную в некоторой окрестности
точки
,
за исключением самой точки
,
и существует касательная к графику
функции в точке М.
Тогда, если в пределах указанной
окрестности
имеет разные знаки слева и справа от
точки
,
то график функции
имеет перегиб
в точке М(
).
Рассмотрим
пример:
.
Эта функция в точке
имеет
бесконечную производную, а касательная
к графику функции в точке О(0;
0) совпадает с осью Оу.
Вторая производная в точке
не существует. Однако график функции
имеет перегиб в точке
,
так как вторая производная
имеет слева и справа от точки
разные знаки (рис. 26).
Итак,
вопрос о направленности выпуклости и
точках перегиба графика функции
исследуется с помощью второй производной.
В
качестве примера возьмем функцию
которую начали рассматривать в п. 2. Знак
второй производной будем отмечать
на вспомогательном чертеже, изображенном
на рис. 22. Находим вторую производную:
Из уравнения 6х
= 0 получаем
одну критическую
т
очку:
.
Отметив точку
на вспомогательном чертеже (рис. 27) и
определив знак
в ее окрестности, получаем: слева от
точки
<0
(выпуклость графика направлена вверх),
а справа
>0
(выпуклость графика направлена вниз),
т.е. точка
является точкой перегиба графика
рассматриваемой функции. Этот график
схематически изображен на рис. 28.
4.
Асимптоты графика функции. При
исследовании поведения функции на
бесконечности, т. е. при х
и при х
или вблизи точек разрыва второго рода,
часто оказывается, что график функции
сколь угодно близко приближается к той
или иной прямой. Такие прямые называют
асимптотами.
Существуют три вида асимптот: вертикальные,
горизонтальные и наклонные.
Определение
1. Прямая
называется
вертикальной асимптотой графика функции
,
если хотя бы одно из предельных значений
или
равно
или .
В
этом случае расстояние от точки
до прямой
равно
и,
следовательно, d
0
при х
.
Например,
график функции
(рис. 29) имеет
вертикальную асимптоту
,
так как
при х
0
и
при х
0 .
Определение
2.
Прямая
называется горизонтальной асимптотой
графика функции
при
(
),
если
.
Рис.
28
Рис. 29
В
этом случае расстояние от точки
до прямой
равно
и,
следовательно,
при
,
так как,
.
Например,
график рассмотренной выше функции
имеет горизонтальную асимптоту
при
и при
,
так как
0
при
и при
.
Определение
3. Прямая
(
)
называется наклонной асимптотой графика
функции
при
(
),
если функцию
можно представить в виде
(4.8)
где
при
(
).
Рассмотрим
геометрический смысл наклонной асимптоты.
Для определенности разберем случай,
когда
.
(Случай
рассматривается аналогично).
Пусть
– точка
графика функции
и пусть прямая
является наклонной асимптотой графика
функции при
.
Текущую ординату точки на асимптоте
обозначим через
,
точку на асимптоте – через
(рис.30).Тогда
при
.
Опустим из точки М
перпендикуляр
МР на
асимптоту. Расстояние d
от точки М
до асимптоты равно
где
угол между асимптотой и осью Ох,
и, следовательно,
.
Таким
образом, расстояние от точки
графика функции до асимптоты стремится
к нулю при х+,
т.е. график функции неограниченно
приближается к асимптоте при х+.
Рассмотрим
способ отыскания наклонной асимптоты,
т.е. способ определения чисел k
и
b в уравнении
асимптоты. Разделив равенство (4.8) на х
и перейдя к пределу при х+,
получим
Итак,
(4.9)
Далее,
из соотношения (4.8) получаем:
Таким образом,
(4.10)
Доказано,
что если прямая
наклонная асимптота, то числа k
и b
находятся по формулам (4.9) и (4.10). Обратно,
если оба предела (4.9) и (4.10) существуют,
причём
,
то прямая
является наклонной асимптотой графика
функции
при х+.
В
самом деле, полагая
и используя равенство (4.10), получаем что
.
Следовательно, справедливо равенство
(4.8):
,
где
,
т.е. прямая
является наклонной асимптотой графика
функции при
.
Практически
целесообразно искать асимптоты в
следующем порядке: 1) вертикальные
асимптоты; 2) горизонтальные асимптоты;
3) наклонные асимптоты.
Пример
1. Найти
асимптоты графика функции
.
Решение.
1) Находим вертикальные асимптоты. Точка
— точка разрыва 2-го рода данной функции,
причем
при
,
при
.
Следовательно, ось ординат (
)
вертикальная асимптота.
2) Находим
горизонтальные асимптоты
,
следовательно,
горизонтальных асимптот нет.
3) Находим наклонные
асимптоты
,
.
Следовательно,
прямая
является наклонной асимптотой графика
данной функции как при
,
так и при
.
График
функции схематически изображён на рис.
31.
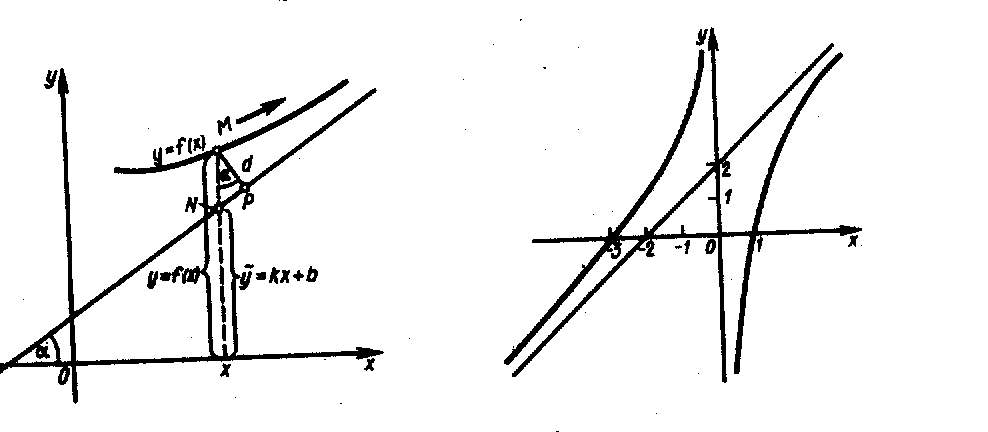
Рис. 30
Рис. 31
Пример
2. Доказать,
что гипербола
имеет своими наклонными асимптотами
прямые
.
Решение.
Так как
,
то

Следовательно,
прямые
являются наклонными асимптотами данной
гиперболы как при
,
так и при
.
5.
Схема исследования графика функции.
Рассмотрим примерную схему, по которой
целесообразно исследовать поведение
функции и строить ее график.
1. Найти область
определения функции.
2. Найти точки
пересечения графика функции с осями
координат.
3. Найти асимптоты.
4. Найти точки
возможного экстремума.
5. Найти критические
точки.
6.
С помощью вспомогательного чертежа
исследовать знак первой и второй
производных. Определить участки
возрастания и убывания функции. Найти
направление выпуклости графика, точки
экстремума и точки перегиба.
7.
Построить график, учитывая исследование,
проведенное в п. 1
6.
При
этом в начале исследования полезно
проверить, является данная функция
четной или нечетной, чтобы при построении
использовать симметрию графика
относительно оси ординат или начала
координат.
В
качестве примера построим по изложенной
выше схеме график функции
.
1.
Областью определения функции является
множество всех действительных чисел,
кроме
,
при котором обращается в нуль знаменатель.
2.
Так как уравнение
не имеет действительных корней, то
график функции не имеет точек пересечения
с осью Ox,
но пересекает ось Oy
в точке
.
3.
Выясним вопрос о существовании асимптот.
Исследуем поведение функции вблизи
точки разрыва
.
Так как
при
,
при
,
то прямая
является вертикальной асимптотой
графика функции. Если
(
),
то
(
),
следовательно, горизонтальной асимптоты
у графика нет. Далее, из существования
пределов
вытекает,
что при
и при
график функции имеет наклонную асимптоту
.
4.
Для нахождения точек экстремума вычислим
первую производную:
Решая
уравнение
,
получаем две точки возможного экстремума:
и
.
-
Для
нахождения критических точек вычислим
вторую производную:
Так
как
в нуль не обращается, то критических
точек нет.
Нарисуем
вспомогательный чертеж и исследуем
знак первой и второй производных (рис.
32). Получаем, что функция на (
)
возрастает, на (
)
убывает, а на (
)
снова возрастает.
Точки экстремума:
1)
максимум при
,
причём
;
2) минимум при
,
причём
.
На (
)
направление выпуклости графика вверх,
а на (
)
— вниз.
Рис.
32
Точки экстремума:
1)
максимум при
,
причём
;
2) минимум при
,
причём
.
На (
)
направление выпуклости графика вверх,
а на (
)
— вниз.
6
.
Используя полученные данные, строим
эскиз графика (рис. 33)
Формула Тейлора
5 разделов
от теории до практики
12 примеров
Примеры решения задач
видео
Примеры решения задач
-
Формула Тейлора с остаточным членом в форме Лагранжа.
Начать изучение
-
Формула Тейлора с остаточным членом в форме Пеано.
Начать изучение
-
Разложение основных элементарных функций по формуле Тейлора.
Начать изучение
-
Показательная функция.
Начать изучение
-
Гиперболические функции.
Начать изучение
-
Тригонометрические функции.
Начать изучение
-
Степенная функция.
Начать изучение
-
Логарифмическая функция.
Начать изучение
-
Примеры разложения функций по формулам Тейлора и Маклорена.
Начать изучение
-
Вычисление пределов с помощью формулы Тейлора.
Начать изучение
Формула Тейлора с остаточным членом в форме Лагранжа.
Лемма 1.
Если функция f(x) имеет в точке x_{0} производную n-го порядка, то существует многочлен P_{n}(x) степени не выше n такой, что tag{1} P_n(x_0)=f(x_{0}), P_{n}^{(k)}(x_{0})=f^{(k)}(x_{0}), k=overline{1,n}.
Этот многочлен представляется в виде tag{2}P_n(x)=f(x_{0})+frac{f'(x_{0})}{1!}(x-x_0)+frac{f″(x)}{2!}(x-x_0)^2+ldots+frac{f^{(n)}(x_0)}{n!}(x-x_0)^n.
Доказательство.
circ Пусть varphi(x)=(x-x_0)^m, где minmathbb{N}. Тогда varphi(x_0)=0,
tag{3}varphi^{(k)}(x_{0})=left{begin{array}{ll} 0, & если kneq m,\ k!, & если k=m.end{array}right. Из (3) следует, что многочлен P_n(x), заданный формулой (2), удовлетворяет условиям (1). Этот многочлен называют многочленом Тейлора n-го порядка для функции f(x) в точке x_{0}. bullet
Лемма 2.
Пусть функции f(x) и psi(x) определены в delta-окрестности точки x_0 и удовлетворяют следующим условиям:
- для каждого xin U_{delta}(x_0) существуют varphi^{(n+1)}(x) и psi^{(n+1)};
- tag{4}begin{array}{cc}varphi(x_0)=varphi'(x_0)=ldots=varphi^{(n)}(x_0)=0,\ psi(x_0)=psi'(x_0)=ldots=psi^{(n)}(x_0)=0;end{array}
- psi(x)neq 0, psi^{(k)}(x)neq 0 для xindot{U}_{delta}(x_{0}) и для k=overline{1,n+1}.
Тогда для каждого xindot{U}_{delta}(x_{0}) существует точка xi, принадлежащая интервалу с концами x_0 и x такая, что tag{5}frac{varphi(x)}{psi(x)}=frac{varphi^{(n+1)}(xi)}{psi^{(n+1)}(xi)}.
Доказательство.
circ Пусть, например, xin(x_0,x_0+delta). Тогда, применяя к функциям varphi и psi на отрезке [x_0,x] теорему Коши и учитывая, что varphi(x_0)=psi(x_0)=0 в силу условий (4), получаем tag{6}frac{varphi(x)}{psi(x)}=frac{varphi(x)-varphi(x_0)}{psi(x)-psi(x_0)}=frac{varphi'(xi_1)}{psi'(xi_1)}quad x_0 < xi_1 < x.
Аналогично, применяя к функциям varphi’ и psi’ на отрезке [x_{0},xi_{1}] теорему Коши, находим tag{7}frac{varphi'(xi_1)}{psi'(xi_1)}=frac{varphi'(xi_1)-varphi'(x_0)}{psi'(xi_1)-psi'(x_0)}=frac{varphi″(xi_2)}{psi'(xi_2)}quad x_0 < xi_1 < xi_2.
Из равенств (6) и (7) следует, что
frac{varphi(x)}{psi(x)}=frac{varphi'(xi_1)}{psi'(xi_1)}=frac{varphi″(xi_2)}{psi″(xi_2)},quad x_0 < xi_2 < xi_1 < x < x_0+delta.
Применяя теорему Коши последовательно к функциям varphi″ и psi″, varphi^{(3)} и psi^{(3)},ldots,varphi^{(n)} и psi^{(n)} на соответствующих отрезках, получаем
frac{varphi(x)}{psi(x)}=frac{varphi'(xi_1)}{psi'(xi_1)}=ldots=frac{varphi^{(n)}(xi_n)}{psi^{(n)}(xi_n)}=frac{varphi^{(n+1)}(xi)}{psi^{(n+1)}(xi)},
где x_0 < xi < xi_{n} < ldots < xi_{1} < x < x_0+delta.
Равенство (5) доказано для случая, когда xin(x_0,x_0+delta). Аналогично рассматривается случай, когда xin(x_0-delta,x_0). bullet
Теорема 1.
Пусть существует delta >0 такое, что функция f(x) имеет в delta-окрестности точки x_0 производные до (n+1)-го порядка включительно.
Тогда для любого xindot{U}_delta(x_0) найдется точка xi, принадлежащая интервалу Delta с концами x_{0} и x, такая, что
tag{8}f(x)=f(x_0)+frac{f'(x_{0})}{1!}(x-x_0)+ldots+frac{f^{(n)}(x_{0})}{n!}(x-x_0)^n+frac{f^{(n+1)}(xi)}{(n+1)!}(x-x_{0})^{n+1}.
Доказательство.
circ Пусть xindot{U}_delta(x_0), P_n(x)=displaystylesum_{k=0}^{n}frac{f^{(k)}(x_{0})}{k!}(x-x_0)^k — многочлен Тейлора для функции f(x). Обозначим
tag{9}r_{n}(x)=f(x)-P_n(x).
Так как многочлен P_{n}(x) удовлетворяет в силу леммы 1 условиям (1), то из равенства (9) следует, что
tag{10}r_n(x_0)=r_n'(x_0)=ldots=r_{n}^{(n)}(x_{0})=0.
Рассмотрим функции varphi(x)=r_n(x), psi(x)=(x-x_0)^{n+1}. Эти функции удовлетворяют условиям леммы 2, и поэтому для них выполняется равенство (5), то есть
tag{11}frac{varphi(x)}{psi(x)}=frac{r_n(x)}{(x-x_0)^{n+1}}=frac{r_n^{(n+1)}(xi)}{(n+1)!}=frac{f^{(n+1)}(xi)}{(n+1)!},quadxiinDelta,
так как P_n^{(n+1)}(x)equiv 0, psi^{(n+1)}(x)=(n+1)! Из равенств (11) и (9) следует формула (8). bullet
Замечание 1.
Функцию r_n(x)=displaystyle frac{f^{(n+1)}(xi)}{(n+1)!}(x-x_0)^{n+1} называют остаточным членом формулы Тейлора в форме Лагранжа. Формула (8) справедлива и при x=x_{0}.
Следствие.
Если функции varphi и psi дифференцируемы n раз при xgeq x_{0} и удовлетворяют условиям varphi^{(k)}(x_{0})=psi^{(k)}(x_{0}), k=overline{0,n-1}, varphi^{(n)}(x)>psi^{(n)}(x) при x > x_0, то varphi(x) > psi(x) при x > x_{0}.
circ Для n=1 утверждение доказано ранее (следствие 4 из теоремы Лагранжа). Обозначим f(x)=varphi(x)-psi(x). Тогда f^{(k)}(x_{0})=0 при k=overline{0,n-1}0, и по формуле (8) получаем f(x)=frac{1}{n!}(x-x_{0})^{n}f^{(n)}(xi).
Если x> x_{0}, то xi > x_0, f^{(n)}(xi)=varphi^{(n)}(xi)-psi^{(n)}(xi) > 0, и поэтому f(x) > 0, то есть varphi(x) > psi(x) при x > x_{0}. bullet
Пример 1.
Доказать, что:
- |sin t-t|leqdisplaystylefrac{t^2}{2} для tinmathbb{R};
- tag{12}x-frac{x^{3}}{3!} < sin x < x-frac{x^{3}}{3!}+frac{x^5}{5!} при x > 0.
Решение.
- triangle Применяя формулу (8) при n=2 и x_0=0 к функции f(t)=sin t, получаем sin t=t-displaystylefrac{sin{xi}}{2!}t^2, откуда следует, что |displaystyle sin t-t|leqfrac{t^{2}}{2},;tinmathbb{R}.
- Если f(x)=sin x, то f(0)=f^{(2)}(0)=f^{(4)}(0)=0, f'(0)=1, f^{(3)}(0)=-1, f^{(n)}(x)=(sin x)^{(n)}=displaystylesinleft(x+nfrac{pi}{2}right). Применяя формулу (8) при n=5, x_0=0, получаем sin x=x-frac{x^{3}}{3!}+frac{x^{5}}{5!}sin(xi+5frac{pi}{2}),откуда следует правое неравенство (12), так как, очевидно, left|displaystylefrac{x^{5}}{5!}sinleft(xi+5frac{pi}{2}right)right|leqdisplaystylefrac{x^{5}}{5!} при x >0. Используя формулу (8) для f(x)=sin x при n=3, x_0=0, докажем левое неравенство (12). blacktriangle
Формула Тейлора с остаточным членом в форме Пеано.
Теорема 2.
Если существует f^{(n)}(x_0), то tag{13}f(x)=sum_{k=0}^{n}frac{f^{(k)}(x_{0})}{k!}(x-x_{0})^{k}+o((x-x_{0})^{n}),qquad xrightarrow x_{0}.
Доказательство.
Из существования f^{(n)}(x_0) следует, что функция f(x) определена и имеет производные до (n-1)-го порядка включительно в delta-окрестности точки x_0. Обозначим varphi(x)=r_n(x), psi(x)=(x-x_0)^n, где функция r_n(x) определяется формулой (9). Функции varphi(x) и psi(x) удовлетворяют условиям леммы 2, если заменить номер n+1 на номер n-1 (см. равенства (10)). Используя лемму 2 и учитывая, что r_n^{(n-1)}(x_0)=0, получаем tag{14}frac{r_n(x)}{(x-x_0)^n}=frac{r_n^{(n-1)}(xi)-r_n^{n-1}(x_0)}{n!(xi-x_{0})}, где xi=xi(x) и tag{15}x_0 < xi < x < x_0+delta quad или quad x_0-delta < x < xi < x_0.
Пусть xrightarrow x_0, тогда из неравенств (15) следует, что xirightarrow
x_0, и в силу существования f^{(n)}(x_0) существует displaystylelim_{xrightarrow x_{0}}frac{r_n^{(n-1)}(x)-r_n^{(n-1)}(x_0)}{x-x_0}=displaystyle lim_{xrightarrow x_{0}}frac{r_n^{(n-1)}(xi)-r_n^{(n-1)}(x_0)}{xi-x_0}=r_n^{(n)}(x_0)=0, так как выполняются равенства (10). Таким образом, правая часть формулы (14) имеет при xrightarrow x_0 предел, равный нулю, а поэтому существует предел левой части этой формулы, также равный нулю. Это означает, что r_n(x)=o((x-x_0)^n), xrightarrow x_0, или f(x)-P_n(x)=o((x-x_0)^n), откуда следует равенство (13). bullet
Замечание 2.
Формулу (13) часто называют формулой Тейлора с остаточным членом в форме Пеано или
локальной формулой Тейлора.
Разложить функцию f(x) по формуле Тейлора в окрестности точки x_0 до o((x-x_0)^n) — значит представить ее в виде (13).
Теорема 3.
Если существует f^{(n)}(x_0) и если при xrightarrow x_0 tag{16}f(x)=a_0+a_1(x-x_0)+ldots+a_n(x-x_0)^n+o((x-x_0)^n), то tag{17}a_{k}=frac{f^{(k)}(x_0)}{k!},;k=overline{0,n}.
Доказательство.
circ По теореме 2 справедлива формула (13), и так как по условию выполняется равенство (16), то
tag{18}a_0+a_1(x-x_0)+ldots+a_n(x-x_0)^n+o((x-x_0)^n)=\=f(x_{0})+f'(x_{0})(x-x_0)+ldots+f^{(n)}(x_{0})frac{(x-x_{0})^{n}}{n!}+o((x-x_0)^n).
Переходя к пределу при xrightarrow x_{0} в равенстве (18), получаем a_{0}=f(x_{0}). Отбросив в левой и правой частях этого равенства одинаковые слагаемые a_{0} и f(x_{0}) и разделив обе части полученного равенства на x-x_0, имеем a_1+a_2(x-x_0)+ldots+a_n(x-x_0)^{n-1}+o((x-x_0)^{n-1})=\=f'(x_0)+frac{f″(x_{0})}{2!}(x-x_0)+ldots+frac{f^{(n)}(x_{0})}{n!}(x-x_0)^{n-1}+o((x-x_0)^{n-1}).
Переходя в этом равенстве к пределу при xrightarrow x_0, находим f'(x_{0})=a_{1}. Продолжая эти рассуждения, получаем равенства (17).bullet
Замечание 3.
Теорема 3 означает, что представление в виде (16) функции, имеющей в точке x_{0} производную n-го порядка, единственно: коэффициенты разложения (16) выражаются по формулам (17).
Пример 2.
Разложить функцию displaystyle frac{1}{1-x} по формуле Тейлора в окрестности точки x_{0}=0 до o(x^{n}).
Решение.
triangle Воспользуемся равенством (1+x+ldots+x^{n})(1-x)=1-x^{n+1}, откуда displaystyle frac{1}{1-x}=1+x+ldots+x^n+r_n(x), где r_n(x)=displaystylefrac{x^{n+1}}{1-x}=o(x^{n}) при xrightarrow 0. Таким образом,
tag{19}frac{1}{1-x}=1+x+ldots+x^n+o(x^n).
Так как функция displaystyle frac{1}{1-x} бесконечно дифференцируема при xneq 1 (имеет производные любого порядка), то по теореме 3 формула (19) дает искомое разложение. blacktriangle
Разложение основных элементарных функций по формуле Тейлора.
Если x_{0}=0 и существует f^{(n)}(0), то равенство (13) принимает вид
tag{20}f(x)=sum_{k=0}^{n}frac{f^{(k)}}{k!}x^k+o(x^n), xrightarrow 0.
Формулу (20) называют формулой Маклорена.
Замечание 4.
Пусть, функция f(x) бесконечно дифференцируема на интервале (-l,l). Если эта функция является четной, то ее производная — нечетная функция, и, наоборот, производная нечетной функции — четная функция (мы уже разбирали этот пример). Отсюда следует, что для нечетной функции f выполняются условия f^{(2k)}(0)=0, kinmathbb{N}, а для четной функции f — условия f^{(2k-1)}(0)=0, kinmathbb{N}, так как любая непрерывная нечетная функция принимает при x=0 значение нуль.
Поэтому формулу (20) для бесконечно дифференцируемой четной функции можно записать в виде tag{21}f(x)=sum_{k=0}^{n}frac{f^{(2k)}(0)}{(2k)!}x^{2k}+o(x^{2n+2}),quad xrightarrow 0, а для нечетной функции — в виде tag{22}f(x)=sum_{k=0}^{n}frac{f^{(2k+1)}(0)}{(2k+1)!}x^{2k+1}+o(x^{2n+2}),quad xrightarrow 0.
В формуле (21) остаточный член записан в виде o(x^{(2n+1)}), а не в виде o(x^{2n}), так как для четной функции f выполняется условие f^{(2n+1)}(0)=0, и поэтому член многочлена Тейлора, который следует за слагаемым displaystylefrac{f^{(2n)}(0)}{(2n)!}x^{2n} равен нулю. Аналогично рассматривается вопрос о записи остаточного члена формулы (22).
Показательная функция.
Если f(x)=e^x, то f(0)=1 и f^{(n)}(0)=1 при любом n. Поэтому формула (20) для функции e^{x} записывается в виде
tag{23}e^{x}=1+x+frac{x^{2}}{2!}+frac{x^{3}}{3!}+ldots+frac{x^{n}}{n!}+o(x^{n}), xrightarrow 0, или e^{x}=sum_{k=0}^{n}frac{x^{k}}{k!}+o(x^{n}), xrightarrow 0.
Гиперболические функции.
Так как f(x)=sh x — нечетная функция, f^{(2k+1)}(x)=ch x, f^{(2k+1)}(0)=1 при k=0,1,2,ldots, то по формуле (22) получаем
tag{24}sh x=x+frac{x^{3}}{3!}+frac{x^5}{5!}+ldots+frac{x^{2n+1}}{(2n+1)!}+o(x^{2n+2}), xrightarrow 0, или sh x=sum_{k=0}^{n}frac{x^{2k+1}}{(2k+1)!}+o(x^{2n+2}), xrightarrow 0.
Аналогично по формуле (21) находим tag{25}ch x=1+frac{x^{2}}{2!}+frac{x^{4}}{4!}+ldots+frac{x^{2n}}{(2n)!}+o(x^{2n+1}), xrightarrow 0,
или ch x=sum_{k=0}^{n}frac{x^{2k}}{(2k)!}+o(x^{2n+1}), xrightarrow 0.
Замечание 5.
Так как sh x=displaystyle frac{e^{x}-e^{-x}}{2}, ch x=displaystyle frac{e^{x}+e^{-x}}{2}, то формулы (24) и (25) можно получить, используя равенство (23) и равенство e^{-x}=displaystylesum_{k=0}^{n}frac{(-1)^{k}x^{k}}{k!}+o(x^{n}), xrightarrow 0.
Тригонометрические функции.
Функция f(x)=sin x является нечетной, f^{(2n+1)}(x)=sin left(x+displaystyle frac{pi}{2}(2n+1)right), откуда f^{(2n+1)}(0)=sinleft(frac{pi}{2}+pi nright)=cospi n= (-1)^n.
Поэтому по формуле (22) находим tag{26} sin x=x-frac{x^{3}}{3!}+frac{x^{5}}{5!}+ldots+(-1)^nfrac{x^{2n+1}}{(2n+1)!}+o(x^{2n+2}), xrightarrow 0,
или
sin x=sum_{k=0}^{n}(-1)^{k}frac{x^{2k+1}}{(2k+1)!}+o(x^{2n+2}),;xrightarrow 0.
Аналогично, f(x)=cos x — четная функция, f^{(2n)}(0)=displaystylecosleft(frac{pi}{2}2nright)=(-1)^{n}, и по формуле (21) получаем tag{27}cos x=1-frac{x^{2}}{2!}+frac{x^{4}}{4!}+ldots+(-1)^nfrac{x^{2n}}{(2n)!}+o(x^{2n+1}),;xrightarrow 0, или cos x=sum_{k=0}^{n}(-1)^{k}frac{x^{2k}}{(2k)!}+o(x^{2n+1}), xrightarrow 0.
Степенная функция.
Пусть f(x)=(1+x)^{alpha}, где alphainmathbb{R}. Тогда f^{(k)}(x)=alpha(alpha-1)ldots(alpha-(k-1))(1+x)^{alpha-k}, откуда получаем f^{(k)}(0)=alpha(alpha-1)ldots(alpha-(k-1)). Обозначим tag{28} C_{alpha}^0=1, C_{alpha}^k=frac{alpha(alpha-1)ldots(alpha-(k-1))}{k!}, kinmathbb{N}
Тогда по формуле (20) получим tag{29}(1+x)^{alpha}=sum_{k=0}^{n}C_{alpha}^{k}x^k+o(x^n), xrightarrow 0.
Отметим важные частные случаи формулы (29).
tag{30}frac{1}{1-x}=1+x+x^2+ldots+x^n+o(x^n), xrightarrow 0,
или frac{1}{1-x}=sum_{k=0}^{n}x^k+o(x^n), xrightarrow 0.
Напомним, что формула (30) была получена другим способом (пример 2).
tag{31}frac{1}{1+x}=1-x+x^{2}+ldots+(-1)^{n}x^n+o(x^n), xrightarrow 0,
или frac{1}{1+x}=sum_{k=0}^{n}(-1)^{k}x^k+o(x^n), xrightarrow 0.
Логарифмическая функция.
Если f(x)=ln (1+x), то f(0)=0,
f^{(k)}(x)=frac{(-1)^{k-1}(k-1)!}{(1+x)^{k}}, f^{(k)}(0)=(-1)^{k-1}(k-1)!,
и по формуле (20) находим tag{32}ln (1+x)=x-frac{x^{2}}{2}+frac{x^{3}}{3}+ldots+frac{(-1)^{n-1}}{n}x^{n}+o(x^{n}), xrightarrow 0,
или ln(1+x)=sum_{k=1}^nfrac{(-1)^{k-1}x^{k}}{k}+o(x^n), xrightarrow 0.
Заменяя в формуле (32) x на -x получаем tag{33}ln (1-x)=-x-frac{x^{2}}{2}-frac{x^{3}}{3}-ldots-frac{x^{n}}{n}+o(x^n), xrightarrow 0,
или ln (1-x)=-sum_{k=1}^nfrac{x^{k}}{k}+o(x^n), xrightarrow 0.
Примеры разложения функций по формулам Тейлора и Маклорена.
Пример 3.
Разложить по формуле Тейлора в окрестности точки x_0=0 до o(x^n) функцию f(x), если:
- f(x)=displaystyle frac{1}{sqrt{1+x}};
- f(x)=displaystyle frac{1}{3x+2};
- f(x)=displaystyle lnfrac{x-5}{x-4};
- f(x)=(x+3)e^{-2x}.
Решение.
- triangle Применяя формулу (29) при alpha=-displaystylefrac{1}{2}, получаем frac{1}{sqrt{1+x}}=sum_{k=0}^{n}C_{-1/2}^{k}x^k+o(x^n), xrightarrow 0,
где C_{-1/2}^{k}=frac{displaystyleleft(-frac{1}{2}right)left(-frac{1}{2}-1right)ldotsleft(-frac{1}{2}-(k-1)right)}{k!}=frac{(-1)^{k}1cdot 3ldots(2k-1)}{2^{k}k!}.Обозначим (2k-1)!!=1cdot 3ldots(2k-1), тогда tag{34}frac{1}{sqrt{1+x}}=1+sum_{k=1}^{n}frac{(-1)^{k}(2k-1)!!}{2^{k}k!}x^k+o(x^n), xrightarrow 0.
Из формулы (34) при n=3 находим tag{35}frac{1}{sqrt{1+x}}=1-frac{1}{2}x+frac{3}{8}x^2-frac{5}{16}x^3+o(x^3), xrightarrow 0. - Так как displaystylefrac{1}{3x+2}=frac{1}{2left(1+displaystylefrac{3}{2}xright)}, то, применяя формулу (31), получаем frac{1}{3x+2}=sum_{k=0}^{n}(-1)^{k}frac{3^{k}}{2^{k+1}}x^{k}+o(x^{n}), xrightarrow 0.
- Используя равенство displaystyleoperatorname{ln}frac{x-5}{x-4}=displaystyleoperatorname{ln}frac{5}{4}+operatorname{ln}frac{1-displaystylefrac{x}{5}}{1-displaystylefrac{x}{4}} и формулу (33), находим ln frac{x-5}{x-4}=lnfrac{5}{4}+sum_{k=1}^{n}frac{x^{k}}{k}left(frac{1}{4^{k}}-frac{1}{5^{k}}right)+o(x^{n}),;xrightarrow 0.
- Так как f(x)=xe^{-2x}+3e^{-2x}, то, применяя формулу (23), получаем f(x)=xleft(displaystylesum_{k=0}^{n-1}frac{(-1)^{k}2^{k}}{k!}x^{k}+o(x^{n-1})right)+3sum_{k=0}^{n}frac{(-1)^{k}2^{k}}{k!}x^{k}+o(x^{n}), x rightarrow 0,
или
f(x)=3+sum_{k=1}^{n}frac{(-1)^{k-1}2^{k-1}}{(k-1)!}x^k+sum_{k=1}^{n}frac{3(-1)^{k}2^{k}}{k!}x^k+o(x^n), xrightarrow 0,
то есть
f(x)=3+sum_{k=1}^{n}frac{(-1)^{k-1}2^{k-1}}{k!}(k-6)x^{k}+o(x^{n}), xrightarrow 0.quadblacktriangle
Пример 4.
Разложить по формуле Маклорена до o(x^{2n+1}) функцию f(x)=cos^{4}x.
Решение.
triangle Используя равенство cos^{2}x=displaystyle frac{1+cos 2x}{2}, получаем cos^{4}x=frac{1}{4}left(1+2cos{2x}+displaystyle frac{1+cos 4x}{2}right)=frac{3}{8}+frac{1}{2}cos{2x}+ displaystylefrac{1}{8}cos4x, откуда по формуле (27) находим
cos^{4}x=1+sum_{k=1}^{n}frac{(-1)^{k}2^{2k-1}}{(2k)!}(1+2^{2k-2})x^{2k}+o(x^{2n+1}), xrightarrow 0. blacktriangle
Замечание 6.
Если существует f^{(n+1)})(0) и известно разложение функции f'(x)=sum_{k=0}^{n}b_kx^k+o(x^n),
где b_k=displaystylefrac{f^{(k+1)(0)}}{k!}, то f(x)=f(0)+sum_{k=1}^{n+1}frac{f^{(k)}(0)}{k!}x^k+o(x^{n+1})=f(0)+sum_{k=0}^{n}frac{f^{(k+1)}(0)}{(k+1)k!}x^{k+1}+o(x^{n+1}), xrightarrow 0, то есть f(x)=f(0)+sum_{k=0}^{n}frac{b_{k}}{k+1}x^{k+1}+o(x^{n+1}), xrightarrow 0.
Пример 5.
Разложить по формуле Маклорена до o(x^{2n+1}) функции:
- operatorname{arctg}x;
- operatorname{arcsin}x;
- ln (1+sqrt{1+x^2}).
Решение.
- triangle Так как (operatorname{arctg}x)’=frac{1}{1+x^2}, то, используя формулу (31) и замечание 6, получаем frac{1}{1+x^{2}}=sum_{k=0}^{n}(-1)^k{x^{2k}}+o(x^{2n+1}), xrightarrow 0,
откуда
tag{36}operatorname{arctg}x=sum_{k=0}^{n}(-1)^{k}frac{x^{2k+1}}{2k+1}+o(x^{2n+2}), xrightarrow 0.
Из формулы (36) при n=2 находим
tag{37}operatorname{arctg}x=x-frac{x^3}{3}+frac{x^5}{5}+o(x^6).;xrightarrow 0. - Используя замечание 6, равенство (34) и формулу (operatorname{arcsin}x)’=displaystyle frac{1}{sqrt{1-x^{2}}}, получаем frac{1}{sqrt{1-x^{2}}}=1+sum_{k=1}^{n}displaystylefrac{(2k-1)!!}{2^{k}k!}x^{2k}+o(x^{2n+1}), xrightarrow 0,
откуда tag{38}operatorname{arcsin}x=x+sum_{k=1}^{n}displaystylefrac{(2k-1)!!}{2^{k}k!(2k+1)}x^{2k+1}+o(x^{2n+2}), xrightarrow 0.
Из формулы (38) при n=2 находим
tag{39}operatorname{arcsin}x=x+frac{1}{6}x^{3}+frac{3}{40}x^5+o(x^6), xrightarrow 0. - Так как (ln (1+sqrt{1+x^2}))’=frac{1}{sqrt{1+x^{2}}}, то, используя замечание 6 и разложение (34), получаем frac{1}{sqrt{1+x^{2}}}=1+sum_{k=1}^{n}frac{(-1)^{k}(2k-1)!!}{2^{k}k!}x^{2k}+o(x^{2n+1}), xrightarrow 0,
откуда tag{40}ln (1+sqrt{1+x^2})=x+sum_{k=1}^{n}frac{(-1)^{k}(2k-1)!!}{2^{k}k!(2k+1)}x^{2k+1}+o(x^{2n+2}), xrightarrow 0.Из формулы (40) при n=2 находим
tag{41}ln (1+sqrt{1+x^2})=x-frac{x^{3}}{6}+frac{3}{40}x^5+o(x^6), xrightarrow 0. blacktriangle
Пример 6.
Разложить по формуле Маклорена до o(x^6) функции:
- operatorname{tg}x;
- operatorname{th}x.
Решение.
- triangle Функция operatorname{tg}x является нечетной, и поэтому operatorname{tg}x=a_1x+a_3x^3+a_5x^5+o(x^6), xrightarrow 0, где a_1=1, так как operatorname{tg}xsim x при xrightarrow 0. Используя равенство sin x=cos xoperatorname{tg}x и разложения (26), (27), получаем
x-frac{x^3}{3!}+frac{x^5}{5!}+o(x^6)=(x+a_3x^3+a_5x^5+o(x^6))left(1-displaystylefrac{x^{2}}{2!}+frac{x^{4}}{4!}+o(x^5)right).
Приравнивая коэффициенты при x^3 и x^5, находим -displaystylefrac{1}{6}=-frac{1}{2}+a_{3}, displaystylefrac{1}{5!}=frac{1}{4!}-frac{a_{3}}{2!}+a_{5}, откуда a_3=displaystylefrac{1}{3}, a_{5}=displaystyle frac{2}{15}, и поэтому tag{42}operatorname{tg}x=x+displaystyle frac{x^{3}}{3}+displaystyle frac{2}{15}x^5+o(x^6), xrightarrow 0. - Так как operatorname{th}x — нечетная функция, то operatorname{th}x=a_1x+a_3x^3+a_5x^5+o(x^6), где a_{1}=1 (operatorname{th}xsim x при xrightarrow x). Применяя формулу sh x=ch xth x и используя разложения (24), (25), получаем x+frac{x^{3}}{3!}+frac{x^5}{5!}+o(x^{6})=(x+a_{3}x^{3}+a_{5}x^{5}+o(x^{6}))left(1+frac{x^{2}}{2!}+frac{x^{4}}{4!}+o(x^{5})right),
откуда, сравнивая коэффициенты при x^3 и x^5, находим a_{3}=-displaystyle frac{1}{3},;a_{5}=displaystyle frac{2}{15}. Следовательно,
tag{43}operatorname{th}x=x-frac{x^{3}}{3}+frac{2}{15}x^{5}+o(x^{6}). blacktriangle
Замечание 7.
Прием, использованный для нахождения разложений (42) и (43), называют методом неопределенных коэффициентов.
Замечание 8.
Разложение функции f(x) по формуле Тейлора (16) заменой x-x_{0}=t обычно сводится к разложению функции g(t)=f(x_0+t) по формуле Маклорена (20).
Пример 7.
Разложить по формуле Тейлора в окрестности точки x_0=-2 до o((x+2)^{n}) функцию f(x)=displaystyle frac{1}{x^{2}+5x}.
Решение.
triangle Так как f(x)=displaystylefrac{1}{5}left(frac{1}{x}-frac{1}{x+5}right), то, полагая x=t-2, получаем f(x)=g(t)=displaystylefrac{1}{5}left(frac{1}{t-2}-frac{1}{t+3}right)=frac{1}{5}left(-frac{1}{2left(1-frac{t}{2}right)}-frac{1}{3left(1+frac{t}{3}right)}right).
Применяя формулы (30) и (31), находим
g(t)=sum_{k=0}^{n}left(frac{(-1)^{k+1}}{5cdot 3^{k+1}}-frac{1}{5cdot 2^{k+1}}right)t^{k}+o(t^{n}), trightarrow 0, откуда f(x)=sum_{k=0}^{n}left(frac{(-1)^{k+1}}{5cdot 3^{k+1}}-frac{1}{5cdot 2^{k+1}}right)(x+2)^{k}+o((x+2)^n), xrightarrow-2.quadblacktriangle
Вычисление пределов с помощью формулы Тейлора.
Рассмотрим предел при xrightarrow 0 отношения displaystyle frac{f(x)}{g(x)}, где katex]f(0)=g(0)=0[/katex], то есть предел типа frac{0}{0}.
Будем предполагать, что f(0)=f'(0)=ldots=f^{(n-1)}(0)=0, f^{(n)}(0)neq 0.
Тогда разложение функции f по формуле Маклорена (20) имеет вид tag{44}f(x)=ax^n+o(x^n), xrightarrow 0, где aneq 0.
Аналогично, предполагая, что
g(0)=g'(0)=ldots=g^{(m-1)}(0)=0, g^{(m)}(0)neq 0.
по формуле (20) находим
tag{45}g(x)=bx^m+o(x^m), xrightarrow 0, где bneq 0.
Из равенств (44) и (45) следует, что
frac{f(x)}{g(x)}=frac{ax^n+o(x^n)}{bx^m+o(x^m)}, xrightarrow 0.
Если m=n, то displaystylelim_{xrightarrow 0}frac{f(x)}{g(x)}=displaystylefrac{a}{b}. В случае, когда n > m, получаем displaystylelim_{xrightarrow 0}frac{f(x)}{g(x)}=0; если же n < m, то displaystylelim_{xrightarrow 0}frac{f(x)}{g(x)}=infty.
Пример 8.
Найти displaystyle lim_{xrightarrow 0}frac{operatorname{tg}x-displaystylefrac{x}{1+x^2}}{sin x-sh x}.
Решение.
triangle Используя формулы (24), (26), (31) и (42),
получаем operatorname{tg}x-frac{x}{1+x^{2}}=x+frac{x^{3}}{3}-x(1-x^2)+o(x^3)=frac{4}{3}x^3+o(x^3),
sin x-operatorname{sh}x=x-frac{x^{3}}{6}-left(x+frac{x^{3}}{6}right)+o(x^{3})=-frac{x^{3}}{3}+o(x^{3}).
Следовательно, искомый предел равен -4. blacktriangle
Пример 9.
Найти displaystyle lim_{xrightarrow 0}frac{e(1+x)^{-1/x}-1}{x}.
Решение.
triangle Воспользуемся равенством (1+x)^{-1}/{x}=e^{-(1/x)operatorname{ln}(1+x)}. По формуле (32) получаем -displaystyle frac{1}{x}operatorname{ln}(1+x)=-1+displaystyle frac{x}{2}+o(x). Используя формулу (23), находим e(1+x)^{-1/x}-1=ecdot e^{-1+x/2+o(x)}-1=е^{x/2+o(x)}-1=frac{x}{2}+o(x).
Поэтому искомый предел равен displaystyle frac{1}{2}. blacktriangle
Пример 10.
Найти
lim_{xrightarrow 0}frac{ln(x+sqrt{1+x^{2}})+displaystylefrac{1}{sqrt{1+2x}}-ch(sqrt{3}x)}{th x-xcos x}.
Решение.
triangle Пусть f(x) и g(x) — соответственно числитель и знаменатель дроби. Тогда, используя формулы (43) и (27), получаем
g(x)=x-frac{x^{3}}{3}+o(x^4)-xleft(1-frac{x^{2}}{2}+o(x^3)right)=frac{x^{3}}{6}+o(x^4).
Поэтому числитель f(x) следует разложить до o(x^3). Применяя формулы (41), (35) и (25), находим
f(x)=x-frac{x^{3}}{6}+o(x^3)+left(1-x+frac{3}{2}x^2-frac{5}{2}x^3+o(x^3)right)-\-left(1+frac{3}{2}x^2+o(x^3)right)=-frac{16}{6}x^3+o(x^3).
Следовательно, искомый предел равен -16. blacktriangle
Локальная формула Тейлора часто используется при вычислении предела при xrightarrow x_0 функции (1+f(x))^{g(x)}, где f(x)rightarrow 0 и g(x)rightarrow infty при xrightarrow x_0. Если x_0=0 и разложение функции f по формуле Маклорена имеет вид (44), а функция g(x) представляется при xrightarrow 0 в виде g(x)=frac{1}{bx^n+o(x^n)},;где;bneq 0, ninmathbb{N},
то, используя формулу 16 (см.здесь), получаем
tag{46}lim_{xrightarrow 0}(1+f(x))^{g(x)}=lim_{xrightarrow 0}left(1+ax^n+o(x^n)right)^{1/(bx^n+o(x^n))}=e^{a/b}.
Пример 11.
Найти displaystyle lim_{xrightarrow 0}(e^{operatorname{tg}x}+operatorname{ln}(1-x))^{1/(arcsin{operatorname{sh}x}-x)}.
Решение.
triangle Используя формулы (39) и (24), получаем
arcsinoperatorname{sh}x-x=arcsinleft(x+frac{x^{3}}{6}+o(x^{4})right)-x=\=x+frac{x^{3}}{6}+frac{x^{3}}{6}+o(x^3)-x=frac{x^{3}}{3}+o(x^3).
Аналогично, разложив функции e^x,;operatorname{tg}x,operatorname{ln}(1-x) по формуле Маклорена до o(x^3), находим
e^{operatorname{tg}x}+operatorname{ln}(1-x)=e^{x+x^{3}/3+o(x^4)}-x-frac{x^{2}}{2}-frac{x^{3}}{3}+o(x^3)=\=1+x+frac{x^{3}}{3}+frac{x^{2}}{2}+frac{x^{3}}{6}+o(x^{3})-x-frac{x^{2}}{2}-frac{x^{3}}{3}+o(x^{3})=1+frac{x^{3}}{6}+o(x^3).
По формуле (46) находим, что искомый предел равен e^{1/2}. blacktriangle
При вычислении предела с помощью формулы Тейлора в конечной точке x_0neq 0 можем положить t=x-x_0 и свести задачу к вычислению предела при t=0.
Неопределенности видов displaystylefrac{infty}{infty}, 0cdotinfty, infty-infty обычно приводят к пределу типа displaystyle frac{0}{0}.
Пример 12.
Найти displaystyle lim_{xrightarrow +infty}x(sqrt{x^2+2x}-2sqrt{x^2+x}+x).
Решение.
triangle Обозначим f(x)=x(sqrt{x^{2}+2x}-2sqrt{x^{2}+x}+x), тогда f(x)=x^2left(displaystylesqrt{1+frac{2}{x}}-2sqrt{1+frac{1}{x}}+1right). Полагая displaystyle frac{1}{x}=t, получаем f(x)=g(t)=displaystylefrac{1}{t^{2}}(sqrt{1+2t}-2sqrt{1+t}+1). Используя формулу (29) при alpha=displaystyle frac{1}{2}, n=2, получаем
sqrt{1+t}=1+frac{1}{2}t-frac{1}{8}t^2+o(t^2),quad trightarrow 0.
Следовательно,
g(t)=frac{1}{t^{2}}left(1+t-frac{1}{2}t^{2}-2left(1+frac{1}{2}t-frac{1}{8}t^{2}right)+o(t^{2})+1right)=\=frac{1}{t^{2}}left(-frac{1}{4}t^{2}+o(t^{2})right),;trightarrow 0,
откуда находим, что искомый предел равен -displaystyle frac{1}{4}. blacktriangle