Home » 8 класс » Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?
Урок: как построить параболу или квадратичную функцию?
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Парабола — это график функции описанный формулой ax2+bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:
1 ) Формула параболы y=ax2+bx+c,
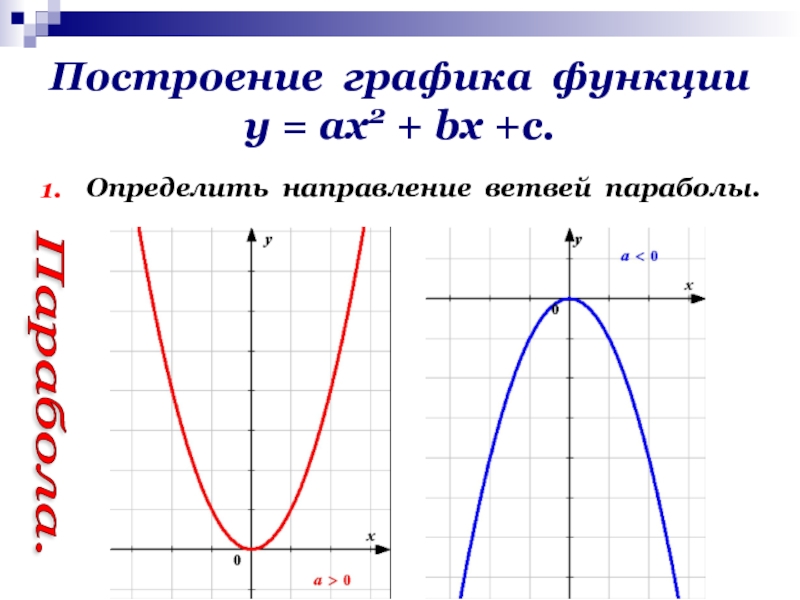
если а>0 то ветви параболы направленны вверх,
а<0 то ветви параболы направлены вниз.
Свободный член c эта точке пересекается параболы с осью OY;
2 ) Вершина параболы, ее находят по формуле x=(-b)/2a, найденный x подставляем в уравнение параболы и находим y;
3) Нули функции или по другому точки пересечения параболы с осью OX они еще называются корнями уравнения. Чтобы найти корни мы уравнение приравниваем к 0 ax2+bx+c=0;
Виды уравнений:
a) Полное квадратное уравнение имеет вид ax2+bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax2+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax2+bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax2+c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);
Как решать квадратные уравнения посмотреть тут.
4) Найти несколько дополнительных точек для построения функции.
ПРАКТИЧЕСКАЯ ЧАСТЬ
И так теперь на примере разберем все по действиям:
Пример №1:
y=x2+4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2)2+4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x2+4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b2-4ac=16-12=4
x=(-b±√(D))/2a
x1=(-4+2)/2=-1
x2=(-4-2)/2=-3
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2
х -4 -3 -1 0
у 3 0 0 3
Подставляем вместо х в уравнение y=x2+4x+3 значения
y=(-4)2+4*(-4)+3=16-16+3=3
y=(-3)2+4*(-3)+3=9-12+3=0
y=(-1)2+4*(-1)+3=1-4+3=0
y=(0)2+4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2
Пример №2:
y=-x2+4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1<0.
a=-1 b=4 c=0 x=(-b)/2a=(-4)/(2*(-1))=2 y=-(2)2+4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x2+4x=0
Неполное квадратное уравнение вида ax2+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x2+4x значения
y=02+4*0=0
y=-(1)2+4*1=-1+4=3
y=-(3)2+4*3=-9+13=3
y=-(4)2+4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2
Пример №3
y=x2-4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0)2-4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x2-4=0
Неполное квадратное уравнение вида ax2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x2=4
x1=2
x2=-2
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x2-4 значения
y=(-2)2-4=4-4=0
y=(-1)2-4=1-4=-3
y=12-4=1-4=-3
y=22-4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0
Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.
|
19 / 18 / 7 Регистрация: 16.05.2017 Сообщений: 447 |
|
|
1 |
|
Составить уравнение параболы по двум точкам18.12.2017, 15:41. Показов 23501. Ответов 12
Что я уже на час подзавис. Коэффициент c нашел, а что дальше делать не знаю. Вообще нужно решить криволинейный интеграл первого порядка, но не дана функция, а только написано, что часть параболы от точек (0;0) и (2;4). Понятно, что с=0 и что один из корней тоже равен 0. Т.е. y = x(ax + b), но как найти a и b? Нужна помощь. С интегралом и сам справлюсь. Сасибо
0 |
|
Диссидент 27472 / 17160 / 3783 Регистрация: 24.12.2010 Сообщений: 38,662 |
|
|
18.12.2017, 15:58 |
2 |
|
Вообще-то через 2 точки можно построить много парабол вида y = ax2+bx…Может быть (0,0) — вершина? Тогда и b=0 Добавлено через 1 минуту
0 |
|
6354 / 4062 / 1510 Регистрация: 09.10.2009 Сообщений: 7,550 Записей в блоге: 4 |
|
|
18.12.2017, 16:03 |
3 |
|
Байт, так первого же рода, не второго. ТС не договаривает что-то.
0 |
|
19 / 18 / 7 Регистрация: 16.05.2017 Сообщений: 447 |
|
|
18.12.2017, 18:10 [ТС] |
4 |
|
Вот задание: Но возможно, ваш интеграл не зависит от пути интегрирования… Ну я не сильно силен, учусь, но как я понял что не зависит. Добавлено через 1 минуту Добавлено через 20 минут Добавлено через 1 час 20 минут
0 |
|
3944 / 2858 / 665 Регистрация: 08.06.2007 Сообщений: 9,668 Записей в блоге: 4 |
|
|
18.12.2017, 18:52 |
5 |
|
Наверняка имеется в виду парабола
0 |
|
19 / 18 / 7 Регистрация: 16.05.2017 Сообщений: 447 |
|
|
18.12.2017, 18:54 [ТС] |
6 |
|
Да я тоже в этом уверен, но имеется в виду без доказательства вряд ли прокатит)
0 |
|
Диссидент 27472 / 17160 / 3783 Регистрация: 24.12.2010 Сообщений: 38,662 |
|
|
18.12.2017, 22:19 |
7 |
|
никто не может помочь. А как тут помочь? Данных явно мало. Придумать дополнительные данные за тебя?
0 |
|
19 / 18 / 7 Регистрация: 16.05.2017 Сообщений: 447 |
|
|
18.12.2017, 22:40 [ТС] |
8 |
|
А как тут помочь? Данных явно мало. Придумать дополнительные данные за тебя? Ну во первых мы с вами не так близко знакомы, чтобы переходить на ты. А во вторых, я полное условие написал выше, только там нет под интегралом обозначения кривой L, так как я не знаю как ее туда поместить. Я конечно тоже склоняюсь, что должно быть простое уравнение параболы y=x2, но повторюсь, что это надо как то обосновать, а не мне кажется.
0 |
|
19 / 18 / 7 Регистрация: 16.05.2017 Сообщений: 447 |
|
|
18.12.2017, 22:44 [ТС] |
9 |
|
Ну вот скрин задания, если поможет. Но оо ничем не отличается от того что я выше написал Миниатюры
0 |
|
6354 / 4062 / 1510 Регистрация: 09.10.2009 Сообщений: 7,550 Записей в блоге: 4 |
|
|
18.12.2017, 22:45 |
10 |
|
BaredJJ, а может быть ветвь параболы, положенной на бок:
0 |
|
Диссидент 27472 / 17160 / 3783 Регистрация: 24.12.2010 Сообщений: 38,662 |
|
|
18.12.2017, 22:49 |
11 |
|
чтобы переходить на ты. Простите, ради Бога, за мой шальной язык. Тут как-то не принято так жестко следить за этикетом. Но если Вас это коробит, то я, во избежании повторения таких ошибок, постараюсь избегать общения с Вами.
0 |
|
6354 / 4062 / 1510 Регистрация: 09.10.2009 Сообщений: 7,550 Записей в блоге: 4 |
|
|
18.12.2017, 22:55 |
12 |
|
Вот общий вид парабол, проходящих через указанные две точки ( (0;0) — не вершина):
1 |
|
19 / 18 / 7 Регистрация: 16.05.2017 Сообщений: 447 |
|
|
19.12.2017, 13:52 [ТС] |
13 |
|
Простите, ради Бога, за мой шальной язык. Тут как-то не принято так жестко следить за этикетом. Но если Вас это коробит, то я, во избежании повторения таких ошибок, постараюсь избегать общения с Вами. Ну вы же взрослый человек, сами меня тыкнули, а теперь из меня виноватого делаете. Будьте благоразумны и умейте спокойно относится к замечаниям и в свой адрес. Тем более, что я вам ничего плохого не сделал и не сказал, а только обратил внимание на то, что мне не очень приятно. Добавлено через 28 минут
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
19.12.2017, 13:52 |
|
13 |
С квадратными уравнениями мы уже встречались в курсе алгебры (7)-го класса.
Квадратное уравнение — это уравнение второй степени. Общий вид квадратного уравнения
ax2+bx+c=0
, где (а, b, с) могут быть любыми числами и
a≠0
,
Применяя знания о функциях и их графиках, которые нам известны, мы можем решать некоторые квадратные уравнения. Рассмотрим (5) графических способов решения квадратного уравнения
x2−2x−8=0
.
Первый способ
Построим график функции
x2−2x−8=0
.
1. Имеем: (a = 1), (b = -2),
x0=−b2a=1,y0=f(1)=12−2−8=−9
. Значит, вершиной параболы служит точка ((1; -9)), а осью параболы является прямая (x = 1).
2. Возьмём на оси (x) две точки, симметричные относительно оси параболы, например, точки (x = -2) и (x = 4). Имеем (f(-2) = f(4) = 0). Построим на координатной плоскости точки ((-2; 0)) и ((4; 0)).
3. Построим параболу по точкам ((-2; 0)), ((1; -9)), ((4; 0)).
Корни уравнения
x2−2x−8=0
— это первые координаты точек, в которых функция равна нулю (то есть в которых график пересекает ось (х)); поэтому имеем решение:
x1=−2;x2=4
.
Второй способ
Запишем уравнение в другом виде
x2=2x+8
. Рассмотрим функции в левой и правой частях уравнения
y=x2;y=2x+8
. В одной системе координат построим их графики и найдём точки пересечения графиков:
Получили две точки:: (C(- 2; 4)) и (D(4; 16)). Решением уравнения будут первые координаты точек (C) и (D), имеем:
x1=−2;x2=4
.
Преобразуем уравнение к виду
x2−8=2x
. Построим в одной системе координат графики функций:
y=x2−8;y=2x
и определим точки их пересечения:
Получили две точки: (C(-2; — 4)) и (D(4; 8)). Решением уравнения будут первые координаты точек (C) и (D), то есть
x1=−2;x2=4
.
Четвёртый способ
Преобразуем уравнение к виду
x2−2x+1−9=0
и далее
x2−2x+1=9→x−12=9
.
Построим в одной системе координат параболу
y=x−12
, прямую (y = 9) и определим точки их пересечения:
Получили две точки: (C(-2; 9)) и (D(4; 9)). Решением уравнения будут первые координаты точек (C) и (D), поэтому
x1=−2;x2=4
.
Пятый способ
Так как (x=0) не является корнем уравнения, то разделим левую и правую части на (x):
x−2−8x=0;x−2=8x.
Рассмотрим функции в левой и правой частях уравнения
y=8x
, (y = x — 2) и определим точки их пересечения:
Получили две точки: (A (-2; -4)) и (B(4; 2)). Решением уравнения будут первые координаты точек (A) и (B), следовательно,
x1=−2;x2=4
.
Квадратичная функция (парабола)
Все знают, как выглядит парабола y = x2. В седьмом классе мы рисовали таблицу:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
После этого по точкам строили график:
Параболу y = ax2 + bx + c мы не станем строить каждый раз «по точкам» — для выпускника школы это просто несолидно. Ведь нам надо знать закономерности поведения данной функции. А эти закономерности таковы.
1. Знак коэффициента a отвечает за направление ветвей. При a > 0 ветви направлены вверх, при a < 0 — вниз.
На рисунке приведены две параболы y = ax2 с равными по модулю, но противоположными по знаку значениями a.
2. Абсолютная величина коэффициента a отвечает за «раскрыв» параболы. Чем больше |a|, тем у́же парабола (больше прижата к оси Y ). Наоборот, чем меньше |a|, тем шире парабола (больше прижата к оси X).
На рисунке приведены две параболы y = a1x2 и y = a2x2, у которых a2 > a1 > 0.
3. Абсцисса вершины параболы y = ax2 + bx + c находится по формуле:
Для нахождения ординаты вершины y0 удобнее всего подставить x0 в уравнение параболы. Но вообще, полезно помнить, что
где D = b2 − 4ac — дискриминант.
4. Точки пересечения параболы y = ax2 + bx + c с осью X находятся с помощью решения квадратного уравнения
ax2 + bx + c = 0. Если дискриминант равен нулю, то парабола касается оси X. Если дискриминант меньше нуля, то парабола не пересекает ось X.
5. Точка пересечения с осью Y находится легко: мы просто подставляем x = 0 в уравнение параболы. Получается точка (0, c).
А теперь покажем, как с помощью графика функции y = ax2 + bx + c решать квадратные неравенства.
1. Часто на тестировании мы предлагаем решить неравенство
x2 < 400.
Справляются далеко не все. Очень часто, не задумываясь, выдают «ответ»: x < ± 20.
Однако сама эта запись — абсурдна! Представьте, что вы слышите прогноз погоды: «Температура будет меньше плюс-минус двадцати градусов». Что, спрашивается, надеть — рубашку или шубу? 
Давайте решим это неравенство с помощью графика. Изобразим схематично график функции y = x2 и отметим все значения x, для которых y < 400.
Теперь мы видим правильный ответ: x ∈ (−20; 20).
2. Решим неравенство: x2 − 3x − 10 ≥ 0.
Графиком функции y = x2 − 3x − 10 служит парабола, ветви которой направлены вверх. Решая квадратное уравнение x2 − 3x − 10 = 0, находим x1 = −2 и x2 = 5 — в этих точках парабола пересекает ось X. Нарисуем схематично нашу параболу:
Мы видим, что при x ∈ (−2; 5) значения функции отрицательны (график проходит ниже оси X). В точках −2 и 5 функция обращается в нуль, а при x < −2 и x > 5 значения функции положительны. Следовательно, наше неравенство выполняется при .
Обратите внимание, что для решения неравенства нам достаточно было схематично изобразить параболу. Ось Y вообще не понадобилась!
3. Ещё одно неравенство: x2 + 2x + 4 > 0.
Ветви параболы y = x2 + 2x + 4 направлены вверх. Дискриминант отрицателен, т. е. уравнение x2 + 2x + 4 = 0 не имеет корней. Стало быть, нет и точек пересечения параболы с осью X.
Раз ветви параболы направлены вверх и она не пересекает ось X — значит, парабола расположена над осью X.
Получается, что значения функции положительны при всех возможных x. Иными словами, решения нашего неравенства — это все действительные числа.
Ответ: .
Квадратные неравенства являются неотъемлемой частью ЕГЭ. Разберём типичные примеры из банка заданий ЕГЭ.
4. Завиcимоcть объeма cпроcа q (тыc. руб.) на продукцию предприятия-монополиcта от цены p (тыc. руб.) задаeтcя формулой q = 100 − 10p. Выручка предприятия за меcяц r (в тыc. руб.) вычиcляетcя по формуле r(p) = q · p. Определите наибольшую цену p, при которой меcячная выручка r(p) cоcтавит не менее 240 тыc. руб. Ответ приведите в тыc. руб.
Подставим выражение для q в формулу выручки:
r(p) = qp = (100 − 10p)p = 100p − 10p2.
Выручка должна быть не менее (то есть больше или равна) 240 тысяч рублей. Поскольку цена p уже выражена в тысячах рублей, мы можем записать это условие в виде неравенства:
100p − 10p2 ≥ 240.
Переносим всё вправо и делим на 10:
p2 − 10p + 24 ≤ 0.
Для схематичного построения параболы находим корни уравнения p2 − 10p + 24 = 0. Они равны 4 и 6. Остаётся сделать рисунок.
Решением нашего неравенства служит отрезок [4; 6]. Нас просили найти наибольшее p. Оно равно 6.
Ответ: 6.
5. Выcота над землёй подброшенного вверх мяча меняетcя по закону h(t) = 1,6 + 8t − 5t2, где h — выcота в метрах, t — время в cекундах, прошедшее c момента броcка. Cколько cекунд мяч будет находитьcя на выcоте не менее трёх метров?
Итак, требуется, чтобы выполнялось неравенство h(t) ≥ 3. Подставляем сюда выражение для h:
1,6 + 8t − 5t2 ≥ 3.
Собираем всё справа:
5t2 − 8t + 1,4 ≤ 0.
Корни соответствующего уравнения 5t2 −8t+1,4 = 0 равны t1 = 0,2 и t2 = 1,4. Как дальше действовать — мы знаем.
Таким образом, через t1 = 0,2 секунды после начала полёта мяч оказался на высоте 3 метра. Мяч продолжал лететь вверх, высота увеличивалась; затем началось снижение, высота уменьшалась, и в момент времени t = 1,4 секунды снова стала равна трём метрам над землей.
Получается, что мяч находился на высоте не менее трёх метров в течение t2 − t1 = 1,2 секунд. В бланк ответов вписываем десятичную дробь 1,2.
6. Завиcимоcть температуры (в градуcах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экcпериментально и на иccледуемом интервале температур определяетcя выражением T(t) = T0 + bt + at2, где t — время в минутах, T0 = 1400 К, a = −10 К/мин, b = 200 К/мин. Извеcтно, что при температуре нагревателя cвыше 1760 К прибор может иcпортитьcя, поэтому его нужно отключать. Определите, через какое наибольшее время поcле начала работы нужно отключать прибор. Ответ выразите в минутах.
Согласно условию, зависимость температуры нагревательного элемента от времени определяется формулой:
T(t) = 1400 + 200t − 10t2.
В нормальном режиме работы прибора должно выполняться неравенство T ≤ 1760, или
1400 + 200t − 10t2 ≤ 1760.
Переносим всё вправо и делим на 10:
t2 − 20t + 36 ≥ 0.
Находим t1 = 2, t2 = 18 и делаем рисунок:
Получаем решения нашего неравенства:
Остаётся понять: в какой же момент отключать прибор? Для этого надо представить физическую картину процесса.
Мы включаем прибор в момент времени t = 0. Температура нагревателя повышается и при t = 2 мин достигает 1760 К. Затем повышение температуры продолжается, в результате чего прибор может испортиться. Поэтому ясно, что отключать его надо при t = 2.
А что же решения t ≥ 18? Они не имеют физического смысла. Войдя в зону температур T > 1760, прибор испортится, и формула T(t) = 1400+200t−10t2, справедливая для исправного прибора, перестанет адекватно отражать реальность.
Поэтому в бланк ответов вписываем число 2.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Квадратичная функция (парабола)» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.05.2023
 3 + k).
3 + k).
- Если (k > 0), то график сдвигается на (k) единиц вверх; если (k < 0), то график сдвигается на (k) единиц вниз.
- Если (h > 0),то график сдвигается на (h) единиц вправо; если (h < 0), то график смещается на (h) единиц влево.
- Если (a < 0), график переворачивается.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявку
Репетитор по математике
Пермский государственный гуманитарно-педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов.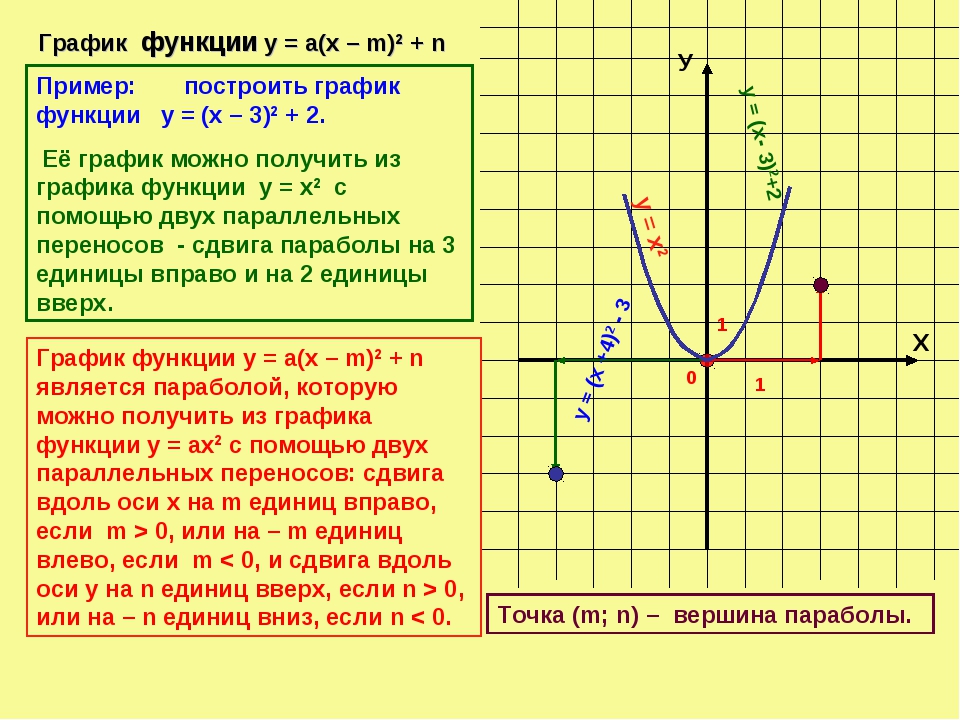
Оставить заявку
Репетитор по математике
Запорожский национальный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов.
Считаю, что при изучении математики нельзя изучать новый материал, пока дети не усвоили предыдущий. Я люблю математику за то, что она развивает логическое и алгоритмическое мышление, пространственное воображение.
Оставить заявку
Репетитор по математике
Новосибирский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов.
Убежден, что математику может понять каждый человек.
Со мной вы получите заряд уверенности в себе, поймете, что математика — это не скучно, а безумно интересно!
С нетерпением жду всех на занятиях!
Векторы
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Построение графика квадратичной функции
Построение графика квадратичной функции, заданной формулой
Предмет: алгебра
Класс: 8 «Б»
Тема: Построение графика квадратичной функции, заданной формулой
Тип: комбинированный урок.
Форма организации учебной деятельности: индивидуально-групповая.
Цели
Обучающие
· проверить знания, умения и навыки построения графика квадратичной функции, заданной формулой
· внедрить алгоритм построения графика квадратичной функции, заданной формулой
· отработать алгоритм при построении графиков квадратичной функции.
Развивающая
· продолжить работу по развитию умения работать с книгой, сравнивать; развивать коммуникативные связи, информационную грамотность, логику.
Воспитательная
· стимулировать учащихся к самооценке образовательной деятельности, вызывая чувство самопознания, самоопределения и самореализации.
Оборудование
· Доска, компьютеры, экран с проектором, карточки с алгоритмами.
Ход урока
1) Организационный момент (2 мин)
· Учитель формулирует тему и цели урока, сообщает план работы, который проецируется на экран и по мере выполнения стираются пункты плана.
Работа по плану
1) Работая устно, вспоминаем решение уравнений.
2) Учащиеся проверяют свои знания по построению графика квадратичной функции способом перемещения.
3) Знакомство с алгоритмом.
4) Отработка алгоритма при построении графиков функции, заданной формулой
2) Актуализация знаний учащихся (13 мин).
1) Фронтальная устная работа.
1. Что является графиком функции у = аx2. (парабола)
2. Как зависит график функции у = аx2 от коэффициента а.
а) Сформулируйте правило переноса графика функции вдоль оси абсцисс.
б) Сформулируйте правило переноса графика функции вдоль оси ординат.
(если а>0, то происходит растяжение графика функции от оси Ох вдоль оси Оу, ели 0<a<1, то происходит сжатие графика функции к оси Ох вдоль оси Оу)
3. Вспомни алгоритм построения графиков функций , если известен график функции у = аx2.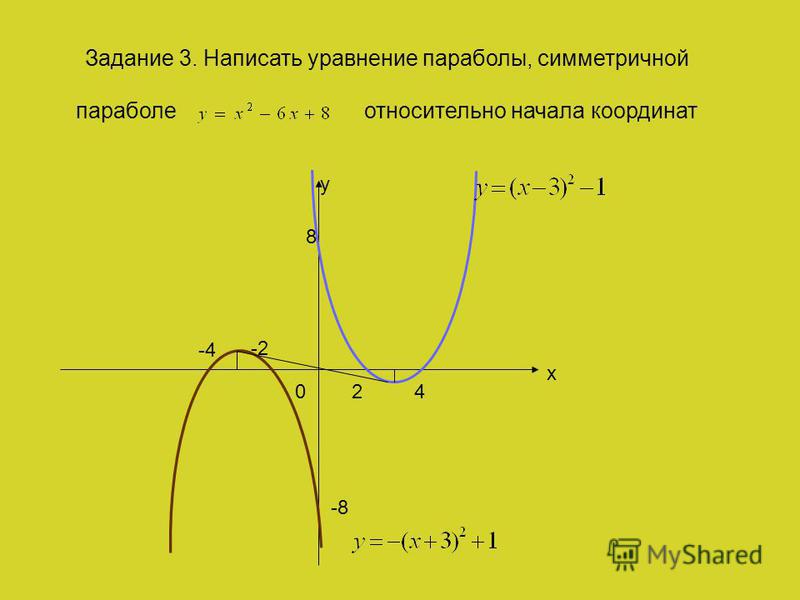
(График функции является парабола, получаема сдвигом параболы у = аx2:
вдоль оси абсцисс вправо на х0, если х0>0, влево на , если х0<0;
вдоль оси ординат вверх на у0, если у0>0, вниз на , если у0<0).
4. Как определить координаты вершины параболы?
5. Как определить точку, через которую проходит ось симметрии параболы?
6. Как определить направление «ветвей» параболы?
· Заполни пропуски (работа с интерактивной доской): все записывают в тетради. Взаимопроверка.
1. Функция у = aх2 + bx + c, где а, b, c – заданные действительные числа, а ¹ 0,
х – действительная переменная, называется … функцией. (квадратичной)
2. График функции у = ах2 при любом а ¹ 0 называют … .(параболой)
3. Функция у = х2 является … (возрастающей, убывающей) на промежутке
х £ 0. (убывающей)
4. Значения х, при которых квадратичная функция равна нулю, называют … функции (нулями функции)
5.
6. При а >0 ветви параболы у = ах2 направлены … . (вверх)
7. Если а< о и х ¹ 0, то функция у = ах2 принимает … (отрицательные)
(положительные, отрицательные) значения.
Работа у доски (индивидуальны карточки у доски)
1. Найдите координаты вершины параболы у=х2-4х+4 Ответ: (2;0)
2.Найдите нули квадратичной функции у=х2+х-2 Ответ: -2; 1
3. Выдели полный квадрат x2 — 4х + 5. И постройте график полученной функции.
Ответ: х2 — 4х + 5 = (х2 — 4х + 4) + 1 = (х — 2)2 + 1
Фронтальная работа с классом. (Презентация)
3.Учитель поясняет задание. Для каждой из функций, графики которых изображены, выберите соответствующее условие и отметьте знаком «+». Ученики выполняют работу на распечатанных листочках, осуществляя самопроверку. Листочки заранее раздать ученикам.
После того, как учащиеся закончили решение теста, выполняем самопроверку: учащиеся по очереди комментируют свои ответы, один ученик выполняет задание на интерактивной доске, на экране с помощью анимации появляются правильные ответы.
После проверки учащиеся оценивают работу соседа по следующему критерию:
- «5» — нет ошибок;
- «4» — 1 ошибка;
- «3» — 2 ошибки;
- «2» — 3 и более ошибки.
Проверка работ учащихся у доски
4.
Ответ:
(Находим нули функции: =0 х1=0; х2=-5, ветви параболы направлены вверх а>0).
Ответ: (3,0) ;
2) Индивидуальное задание
· Индивидуальная работа на компьютерах. Первая группа, проверяет свои знания по построению графиков функции – в течение 4 минут выполняет теств Excel. (11 человек). Ученикам раздаются по окончанию работы образцы для проверки.
Образец для проверки
· Фронтальная устная работа (проверка работы, анализ и комментирование). Учащиеся второй группы выполняют тест с помощью системы голосования Verdict. На экране появляется изображение соответствующего графика с указанной функцией. (15 человек).
Тест
«Квадратичная функция»
В системе Verdict
10. Функция задана формулой . Найдите .
1) 24 2) 0 3) 8 4) -8
1. График какой функции изображен на рисунке?
1) 2)
3) 4)
4. Найдите нули функции .
1) 2 и 3 2) -6 и -1 3) 1 и 6 4) -3 и -2
2. На каком рисунке изображен график функции ?
1) 2) 3) 4)
0
1
1
х
у
SHAPE * MERGEFORMAT
0
1
1
у
х
SHAPE * MERGEFORMAT
0
1
1
у
х
SHAPE * MERGEFORMAT
0
1
1
у
х
0
1
1
у
х
3.
1) 2)
3) 4)
0
1
1
у
х
8. На каком промежутке функция, изображенная на рисунке убывает?
1) 2) 3) 4)
5. График какой функции изображен на рисунке?
1) 2)
3) 4)
6. На каком рисунке изображен график функции ?
1) 2) 3) 4)
0
1
1
х
у
SHAPE * MERGEFORMAT
0
1
1
у
х
SHAPE * MERGEFORMAT
0
1
1
у
х
SHAPE * MERGEFORMAT
0
1
1
у
х
0
1
1
у
х
7.
1) 2)
3) 4)
0
1
Формула вершины параболы
☰
Обычно формулу координаты x вершины параболы используют, когда имеют дело с квадратичной функцией.
Квадратичная функция имеет вид: y = ax2 + bx + c.
Ее график — это парабола с вершиной, координаты которой определяются по формулам:
Однако формулу координаты y знать и использовать не обязательно. Обычно проще подставить найденное значение x в саму квадратичную функцию и найти оттуда y.
Например, если дана функция y = 2x2 – 4x + 5, то координата x ее вершины будет равна:
x = –(–4 / (2 × 2)) = 1
Координату же y вычислим, подставив найденный x в саму функцию:
y = 2 × 12 – 4 × 1 + 5 = 3
Таким образом, вершина графика функции y = 2x2 – 4x + 5 находится в точке с координатами (1; 3).
В остальном парабола квадратичной функции вида y = ax2 + bx + c такая же как функции вида y = ax2. Отличие лишь в сдвиге вершины по сравнению с функцией y = ax2. Так в приведенном выше примере (y = 2x2 – 4x + 5) парабола будет по форме и направлению ветвей такой же, как для функции y = 2x2. Разница лишь в координатах вершин парабол.
Формулы вершины параболы получаются при преобразовании квадратичной функции к виду y = f(x + l) + m. Делается это методом выделения полного квадрата. Как известно функции вида y = f(x + l) + m отличаются от функций y = f(x) сдвигом из графиков по оси x на –l и по оси y на m. Именно l в преобразованной квадратичной функции оказывается равным –b/2a, а m = (4ac – b2) / 4a. То есть l и m — это координаты x0 и y0 соответственно.
Доказывается это применением метода выделения полного квадрата к квадратному трехчлену общего вида ax2 + bx + c.
- Объединим первые два члена многочлена: y = (ax2 + bx) + c
-
Вынесем коэффициент a за скобку, при этом b разделится на a:
-
Представим, что у нас есть квадрат суммы, в котором x одно из слагаемых, а из выражения в скобках надо получить его полный квадрат суммы. Одночлен (b/a)x умножим на 2 и разделим на 2 одновременно. Также прибавим и вычтем квадрат второго слагаемого квадрата суммы. Получим:
-
Выделим квадрат суммы:
-
Умножим на a:
-
Приведем к общему знаменателю свободные члены:
-
Поменяем знак:
Таким образом, мы привели функцию y = ax2 + bx + c к виду y = a(x + l)2 + m, что соответствует функции y = f(x + l) + m, где f(x) = ax2. А как строить графики последней известно.
Схематично рисуем параболу по исходному выражению. Построение графика квадратичной функции. Визуальный гид (2019)
Наступает первое сентября, и
счастливые родители ведут свое чадо первый раз в
первый класс. А дальше дорога для большинства
учащихся длиною в 11 лет. Математика с ними на всем
пути, но не у всех детей прирожденная склонность
к ней.
Перед учителем встает ряд нелегких
проблем. Выделим три из них:
1. Искать те крупицы воздействия на
учащихся, которые способствовали бы стремлению
приобретать знания, расширять их, а значит
помогать начинать мыслить, включаться в урок.
2. Сделать урок таким, чтобы осталась пища для
размышлений.
3. Предвидеть, что есть учащиеся с тягой к
гуманитарным наукам, и стремиться помочь
пробудить в них желание погрузиться в
математический мир, но одновременно не забывать
увлеченных математикой и давать пищу жаждущему
ее уму.
Мы обратим внимание на материал статьи
“Рисуем графиками функций” . Автор, А. Я. Цукарь
из Новосибирска предлагает выполнить 6 рисунков
в качестве упражнений для домашних заданий,
заметив, что они будут полезны школьникам с
гуманитарной направленностью. Там же приведен
список изображаемых объектов (зонтик, очки, кит,
шахматный король, лягушка, бабочка
) и перечень
функций, графики которых участвуют в этом
изображении. Заметим, что продолжение, в смысле
новых рисунков, напечатано в газете
“Математика” .
О том, как этот материал можно
использовать с целью попытки решения тех
проблем, которые выделили выше, дальше пойдет
речь.
Наш век – век компьютеров, значит, они
должны работать и на уроках математики, а не
только на уроках информатики. Мы предлагаем
воспользоваться программой, по которой возможно
выполнить эти 6 рисунков. Программа выполнена в
формате интернет-страниц.
Все графики вычерчиваются исходя из
математических формул. На экране отображается
координатная сетка и оси.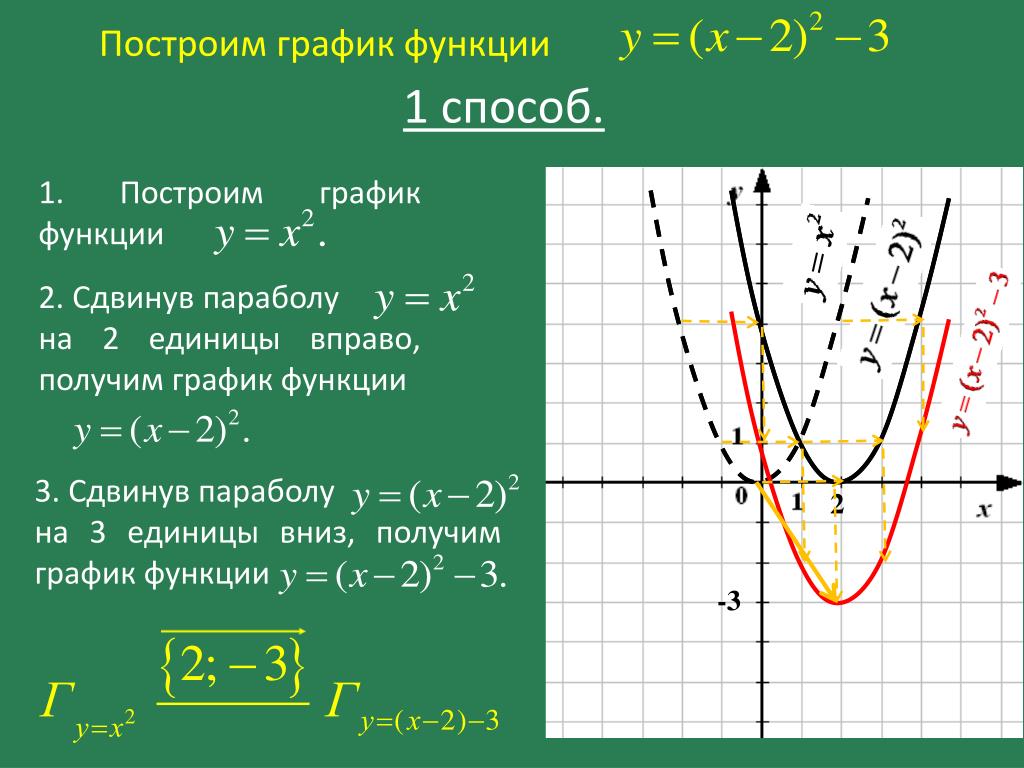
изображение уравнения происходит вычерчивание
графика, причем это построение можно повторить
несколько раз. Размер чертежа можно увеличить
или уменьшить, что позволяет уточнить координаты
той или иной точки. Программу, выполняющую данные
построения, можно найти в Интернете по адресу http://kgpu.real.kamchatka.ru
Приводим наши предложения о том, что
можно добавить к материалу при изучении
квадратичных функций и как это сделать.
Начнем с фрагмента начала урока перед
рассмотрением построения графика квадратичной
функции «y=ax 2 «.
На экране телевизора или компьютера
медленно вырисовываются в разных цветах части
парабол, которые в итоге дают изображение
лягушки.
Учитель замечает, что детали для
рисунка предоставила нам очень интересная
функция, называемая квадратичной
, построение
графиков которой – цель нашего урока. После
освоения материала (на него уйдет не один урок)
каждый сможет сам рисовать, а проверять свои
художества можно, используя компьютер.
примерно так вводит учащихся в новую тему.
Какая задумка была у учителя в самом
начале урока? Вызвать эмоциональные переживания
через удивление. На это работает необычность
приводимого факта, красота обозреваемого
объекта, скорость получения результата…
В этом случае внутренние переживания
ученика подключаются к таким процессам, как
запоминание, внимание, осмысливание. Они будут
протекать более интенсивно и способствовать
достижению решаемых задач в обучении.
В конце урока в качестве итога учитель
обращает внимание на материал стенда, который до
этого был закрыт “Изучаем на уроке”.
На нем привлекает внимание лягушонок
,
который запомнился учащимся и держит их в
ожидании нового урока. Этого нам очень хотелось
бы достичь. Потому приведены все функции,
принимавшие участие в выполнении рисунка. Они
отличаются от тех, с которыми учащиеся имели дело
на прошедшем уроке, что особо подмечал учитель.
Там же запечатлена хроника начала
урока с конкретизацией ряда моментов в шутливой
стихотворной форме и подчеркнута возможность
ученика, усвоившего изучаемый материал, в
дальнейшем так же, как компьютер, рисовать
графиками функции.
Творчески работающий учитель найдет,
где и как использовать при изучении программного
материала нижеследующие задания. Они будоражат
фантазию, развивают эстетические наклонности,
приобщают к поиску, пониманию математических
истин, увлекают в загадочный мир знаний.
Задание 1.
1) Построить график функции
и сделать трафарет.
2) С помощью трафарета дорисовать построенную
параболу до того, на чем остановится Ваша
фантазия. При этом трафарет можно
переворачивать, перемещать влево или вправо,
вверх или вниз, использовать любую его часть и
оси координат.
3) Записать формулы парабол, прямых, которые
определили Ваш рисунок.
Приводим пример выполнения задания 1. Парабола
построена .
После несложных размышлений принято
решение рисовать тюльпан
. Из параболы
получается цветок, если ее прервать, проведя
вверху изящную волнистую линию. Ось игреков от
точки О
вниз – это стебелек, справа и слева от
него можно сделать по листочку.
Наши действия: трафарет
переворачиваем (т.е. ветви направляем вниз) и
перемещаем по параболе…
Находятся такие точки С,
D, Е
, которые после совмещения (трижды) с точкой О
(на трафарете) дадут нужную линию.
Запишем формулы трех парабол,
позволившие это сделать. Работает формула
, где точка (m; n) — вершина параболы. У
нас первая точка С (-4; 19) – вершина одной из
парабол, а именно . Мы обводим только
участок параболы при . Аналогичным
будет подход в описании всех остальных случаев.
В итоге тюльпан
рисовали семь квадратичных функций и одна
линейная:
1.
2.
3.
4.
5.
6.
7.
8.
Задание 2.
Графиками функций сделать рисунок,
дать ему название.
Например. Даны функции:
1.
2.
Инструкция
Для начала, начертите на листе координатные оси: ось абсцисс и ось ординат. Подпишите их. После этого, поработайте над данной квадратичной функцией.
После нанесения точек на координатную плоскость, соедините их плавной линией, придавая ей округлые . Не заканчивайте график в верхних точках, а продлите его, так как парабола бесконечна. Не забудьте подписать график на , а также напишите необходимые координаты на осях, в противном случае, это вам могут за ошибку и снять определенное количество баллов.
Источники:
- как нарисовать параболу
В элементарной и высшей математике встречается такой термин, как гипербола. Так называют график функции, который не проходит через начало координат и представляет собой две параллельные друг другу кривые. Существует несколько способов построения гиперболы.
Инструкция
Гипербола так же, как и другие кривые может быть двумя способами. Первый из них заключается в построении по прямоугольнику, а второй — функции f(x)=k/x.
Начинать строить гиперболу следует с построения прямоугольника по оси x, именуемыми A1 и A2, и с противоположными концами по оси y, именуемыми B1 и B2.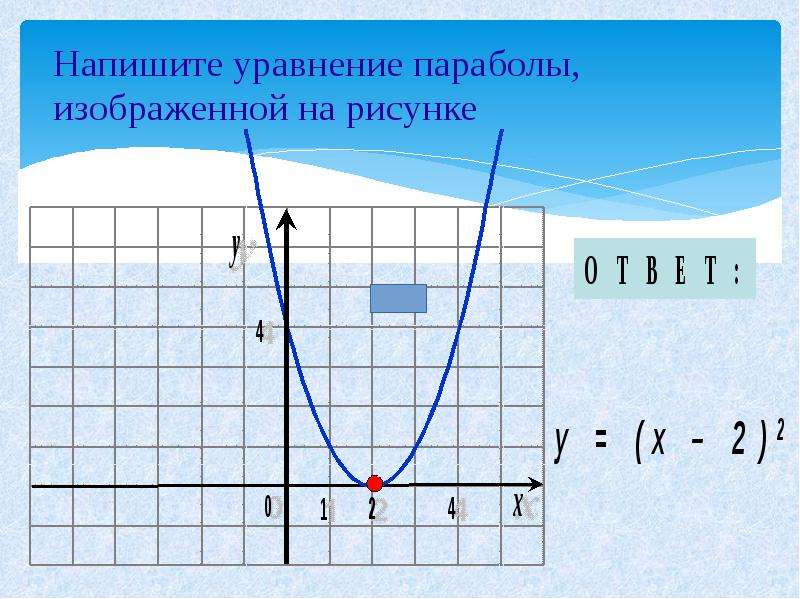
У равнобочной гиперболы асимптоты перпендикулярны друг другу. Кроме того, между y и x имеется пропорциональная , заключающаяся в том, что если x уменьшить в заданное число раз, то y увеличится во столько же раз, и наоборот. Поэтому, по-другому уравнение гиперболы записывается в виде:
y=k/x
Если в условии дана функция f(x)=k/x, то целесообразнее строить гиперболу . Учитывая, что k — величина постоянная, а знаменатель x≠0, можно придти к выводу, что график функции не проходит через начало координат. Соответственно, интервалы функции равны (-∞;0) и (0;∞), так как при обращении x в ноль функция теряет . При увеличении x функция f(x) убывает, а при уменьшении возрастает. При приближении x к нулю соблюдается условие y→∞. График функции показан на основном рисунке.
Для построения гиперболы методом расчета удобно использовать . Если он способен работать по программе или хотя бы запоминать , можно заставить его осуществить расчет несколько раз (по числу точек), не набирая выражение каждый раз заново.
Источники:
- что такое график и как его построить
Чтобы речь была более яркой и выразительной, люди используют образные средства языка и стилистические приемы: метафору, сравнение, инверсию и другие. В системе способов художественной выразительности стоит и гипербола, или преувеличение — стилистический прием, который очень часто используется как в живой разговорной речи, так и в языке художественной литературы.
Гипербола (в переводе с греческого — преувеличение) — это стилистическая фигура, или художественный прием, который заключается в намеренном преувеличении некоторых свойств изображаемого предмета или явления для создания большей выразительности и, соответственно, усиления эмоционального воздействия от них. Гипербола может проявлять себя в количественном преувеличении (например, «мы не виделись сто лет») и воплощаться в образном выражении (например, « мой»).
Гиперболу можно считать одним из основных способов создания художественного образа : живописи и литературе. Благодаря тому, что ее главной функцией является воздействие на эмоции, она широко используется авторами в качестве средства выразительности для усиления впечатления на читателя. Этот стилистический прием характерен для риторического и романтического стилей и является важнейшим способом формирования сюжета и обрисовки характеров в литературных произведениях. Гипербола как художественный прием широко распространена в фольклоре: в былинах, сказках, песнях (например, в «У страха глаза велики», былине «Илья Муромец и Соловей-разбойник»), в русской литературе как средство передачи авторской мысли. В русской литературной традиции гипербола свойственна и поэтической речи (М.
В разговорной речи гипербола реализуется с помощью различных языковых средств: лексических (например, с помошью слов «совсем», «совершенно», «все» и так далее), фразеологических (например, «это и ежу понятно»), морфологических (употребление множественного числа вместо единственного, например, «некогда чаи распивать»), синтаксических (количественнных конструкциий, например, «миллион дел»). В художественной гипербола часто употребляется непосредственно с другими тропами и стилистическими фигурами, прежде всего с метафорой и сравнением, и сближается с ними, образуя гиперболические фигуры (например, гиперболическая метафора «Весь мир — театр, и люди в нем »). Этот стилистический прием также играет большую роль не только в литературном творчестве, но и в риторике, так как способствует повышению эмоционального воздействия на слушателя.
Видео по теме
Источники:
Гипербола – график обратной пропорциональности y=k/x, где k — коэффициент обратной пропорциональности не равен нулю.
Вам понадобится
- — карандаш;
- — линейка.
Инструкция
Начертите оси координат. Нанесите все необходимые обозначения. Если y=k/x, коэффициент k — больший нуля, то ветви будут размещаться в первой и третьей четвертях. В этом случае на всей области определения, которая состоит из двух промежутков: (-∞; 0) и (0; +∞).
Постройте сначала ветвь гиперболы на промежутке (0; +∞). Найдите координаты точек, необходимые для построения кривой. Для этого задайте переменной x несколько произвольных значений и вычислите значения переменной y. Например, для функции y=15/x при x=45 получим y=1/3; при x=15, y=1; при x=5, y=3; при x=3, y=5; при x=1, y=15; при x=1/3, y=45. Чем больше точек вы определите, тем точнее графическое изображение .
Нанесите полученные точки на координатную плоскость и соедините их плавной линией.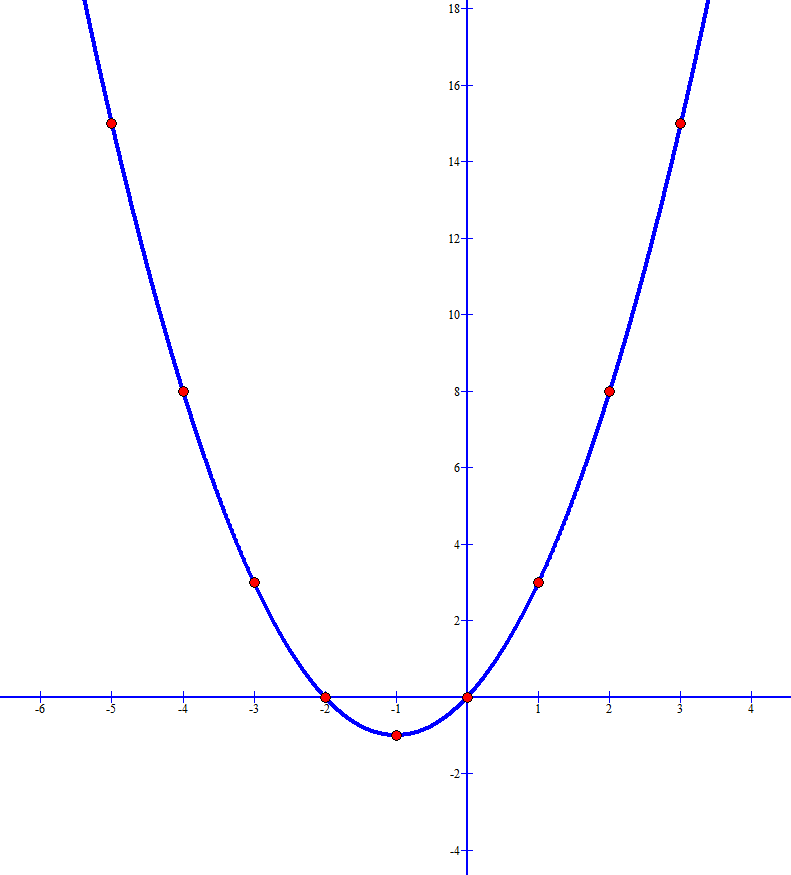
Постройте вторую кривую гиперболы на промежутке (-∞; 0). Для этого задайте переменной x несколько произвольных значений из данного числового промежутка. Вычислите значения переменной y. Так, для функции y=-15/x при x=-45 получим y=-1/3; при x=-15, y=-1; при x=-5, y=-3; при x=-3, y=-5; при x=-1, y=-15; при x=-1/3, y=-45.
Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое квадратичная функция, и с чем ее едят. Если ты считаешь себя профи по части квадратичных функций, добро пожаловать. Но если нет, тебе стоит прочитать тему .
Начнем с небольшой проверки
:
- Как выглядит квадратичная функция в общем виде (формула)?
- Как называется график квадратичной функции?
- Как влияет старший коэффициент на график квадратичной функции?
Если ты сходу смог ответить на эти вопросы, продолжай читать.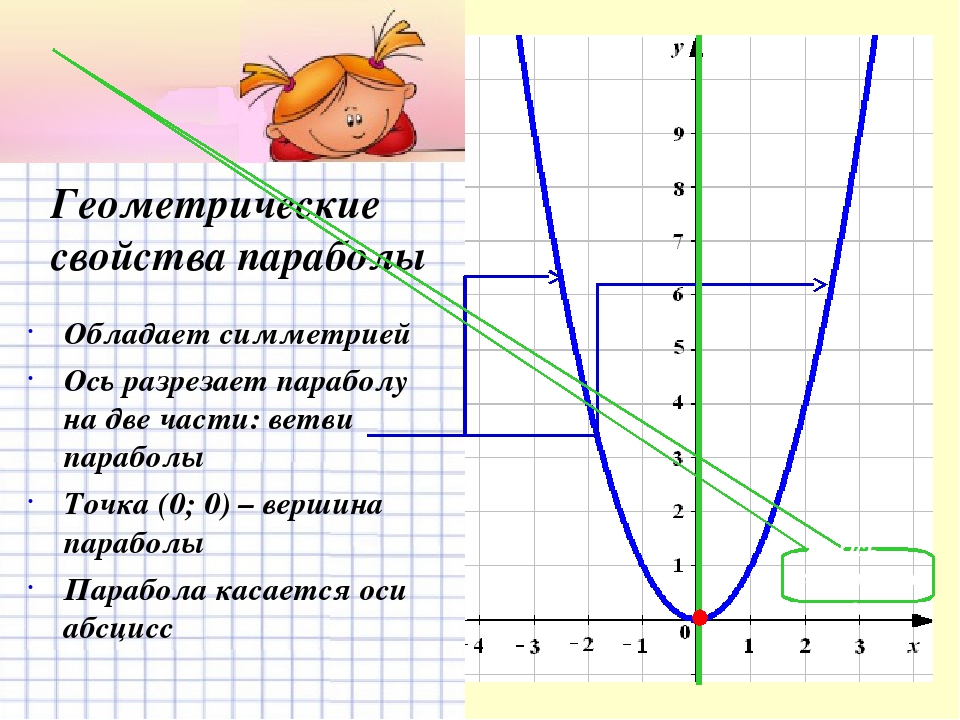
Итак, ты уже умеешь обращаться с квадратичной функцией, анализировать ее график и строить график по точкам.
Ну что же, вот она: .
Давай вкратце вспомним, что делают коэффициенты
.
- Старший коэффициент отвечает за «крутизну» параболы, или, по-другому, за ее ширину: чем больше, тем парабола у́же (круче), а чем меньше, тем парабола шире (более пологая).
- Свободный член — это координата пересечения параболы с осью ординат.
- А коэффициент каким-то образом отвечает за смещение параболы от центра координат. Вот об этом сейчас подробнее.
С чего мы всегда начинаем строить параболу? Какая у нее есть отличительная точка?
Это вершина
. А как найти координаты вершины, помнишь?
Абсцисса ищется по такой формуле:
Вот так: чем больше
, тем левее
смещается вершина параболы.
Ординату вершины можно найти, подставив в функцию:
Подставь сам и посчитай.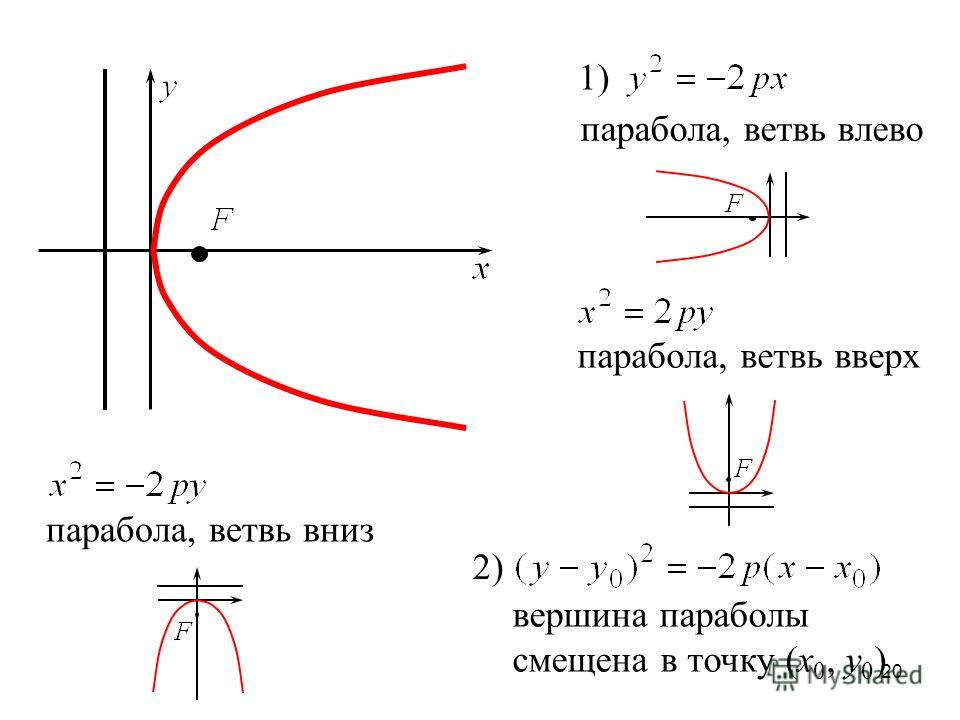
Если сделать все правильно и максимально упростить полученное выражение, получится:
Получается, что чем больше по модулю
, тем выше
будет вершина
параболы.
Перейдем, наконец, к построению графика.
Самый простой способ — строить параболу, начиная с вершины.
Пример:
Построить график функции.
Решение:
Для начала определим коэффициенты: .
Теперь вычислим координаты вершины:
А теперь вспоминаем: все параболы с одинаковым старшим коэффициентом выглядят одинаково. Значит, если мы построим параболу и переместим ее вершиной в точку, получится нужный нам график:
Просто, правда?
Остается только один вопрос: как быстро рисовать параболу? Даже если мы рисуем параболу с вершиной в начале координат, все равно приходится строить ее по точкам, а это долго и неудобно. А ведь все параболы выглядят одинаково, может, есть способ ускорить их рисование?
Когда я учился в школе, учительница математики сказала всем вырезать из картона трафарет в форме параболы, чтобы быстро ее чертить.
Рассмотрим простейшую параболу. Построим ее по точкам:
Закономерность здесь такая. Если из вершины сместиться вправо (вдоль оси) на, и вверх (вдоль оси) на, то попадем в точку параболы. Дальше: если из этой точки сместиться вправо на и вверх на, снова попадем в точку параболы. Дальше: вправо на и вверх на. Дальше что? Вправо на и вверх на. И так далее: смещаемся на вправо, и на следующее нечетное число вверх. То же самое потом проделываем с левой веткой (ведь парабола симметрична, то есть ее ветви выглядят одинаково):
Отлично, это поможет построить из вершины любую параболу со старшим коэффициентом, равным. Например, нам стало известно, что вершина параболы находится в точке. Построй (самостоятельно, на бумаге) эту параболу.
Построил?
Должно получиться так:
Теперь соединяем полученные точки:
Вот и все.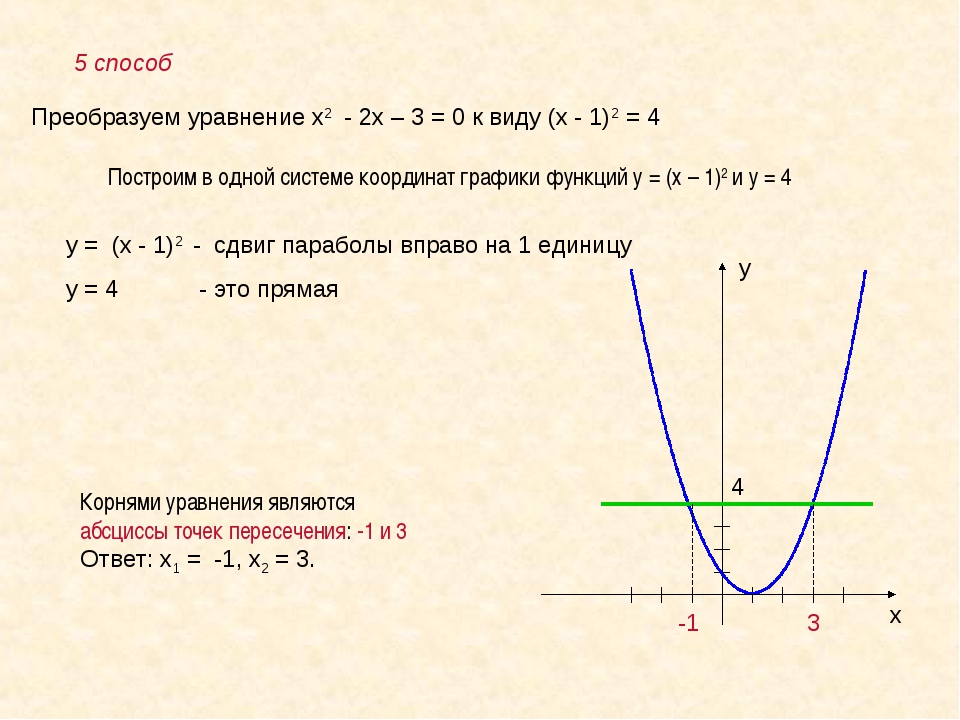
ОК, ну что же, теперь строить только параболы с?
Конечно, нет. Сейчас разберемся, что с ними делать, если.
Рассмотрим несколько типичных случаев.
Отлично, параболу рисовать научились, давай теперь потренируемся на настоящих функциях.
Итак, нарисуй графики таких функций:
Ответы:
3. Вершина: .
Помнишь, что делать, если старший коэффициент меньше?
Смотрим на знаменатель дроби: он равен. Значит, будем двигаться так:
- вправо — вверх
- вправо — вверх
- вправо — вверх
и так же влево:
4. Вершина: .
Ой, а что с этим делать? Как отмерять клетки, если вершина где-то между линиями?..
А мы схитрим. Нарисуем сперва параболу, а уже потом переместим ее вершиной в точку. Даже нет, поступим еще хитрее: Нарисуем параболу, а потом переместим оси:
— на вниз
, а — на вправо
:
Этот прием очень удобен в случае любой параболы, запомни его.
Напомню, что мы можем представить функцию в таком виде:
Например: .
Что это нам дает?
Дело в том, что число, которое вычитается из в скобках () — это абсцисса вершины параболы, а слагаемое за скобками () — ордината вершины.
Это значит, что, построив параболу, нужно будет просто сместить ось на влево и ось на вниз.
Пример: построим график функции.
Выделим полный квадрат:
Какое число вычитается
из в скобках? Это (а не, как можно решить не подумав).
Итак, строим параболу:
Теперь смещаем ось на вниз, то есть на вверх:
А теперь — на влево, то есть на вправо:
Вот и все. Это то же самое, как переместить параболу вершиной из начала координат в точку, только прямые ось двигать намного легче, чем кривую параболу.
Теперь, как обычно, сам:
И не забывай стирать ластиком старые оси!
Я в качестве ответов
для проверки напишу тебе ординаты вершин этих парабол:
Все сошлось?
Если да, то ты молодец! Уметь обращаться с параболой — очень важно и полезно, и здесь мы выяснили, что это совсем не трудно.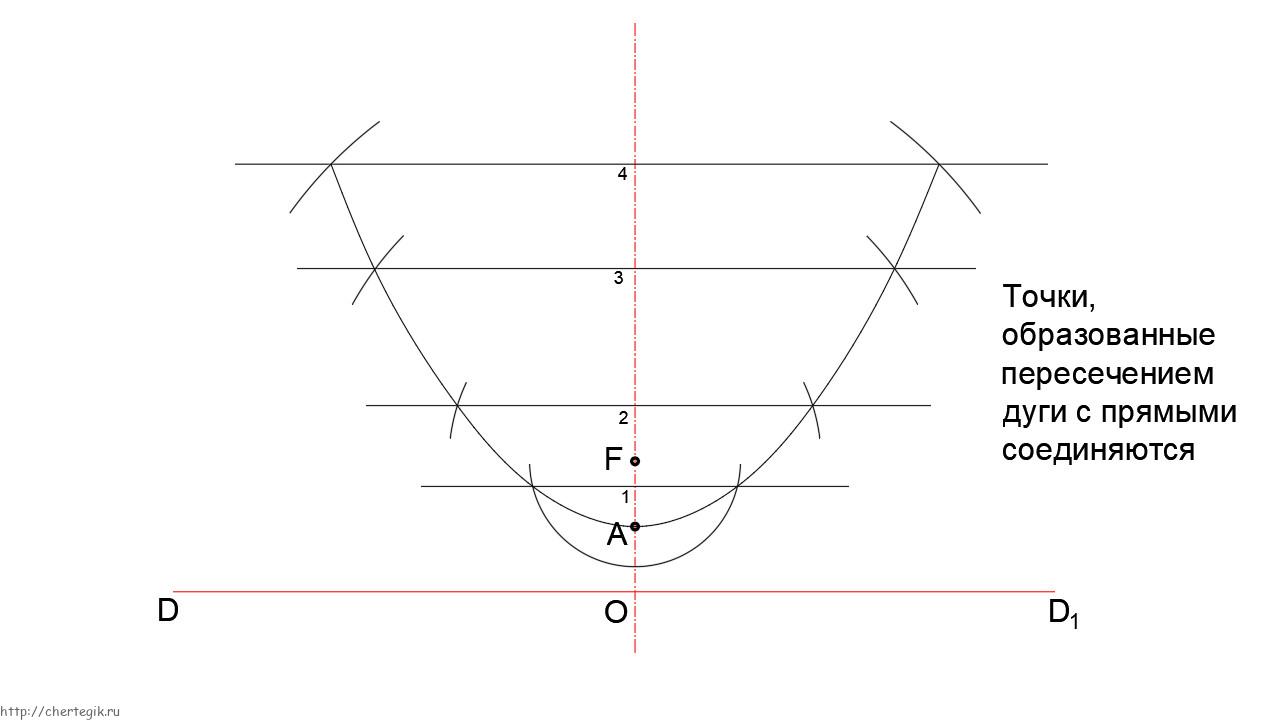
ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ. КОРОТКО О ГЛАВНОМ
Квадратичная функция
— функция вида, где, и — любые числа (коэффициенты), — свободный член.
График квадратичной функции — парабола
.
Вершина параболы:
, т.е. чем больше displaystyle b
, тем левее смещается вершина параболы.
Подставляем в функцию, и получаем:
, т.е. чем displaystyle b
больше по модулю
, тем выше будет вершина параболы
Свободный член
— это координата пересечения параболы с осью ординат.
Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ЕГЭ, для поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это — не главное.
Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но, думай сам…
Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?
НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время
.
И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.
Это как в спорте — нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором
и решай, решай, решай!
Можно воспользоваться нашими задачами (не обязательно) и мы их, конечно, рекомендуем.
Для того, чтобы набить руку с помощью наших задач нужно помочь продлить жизнь учебнику YouClever, который ты сейчас читаешь.
Как? Есть два варианта:
- Открой доступ ко всем скрытым задачам в этой статье —
- Открой доступ ко всем скрытым задачам во всех 99-ти статьях учебника — Купить учебник — 899 руб
Да, у нас в учебнике 99 таких статей и доступ для всех задач и всех скрытых текстов в них можно открыть сразу.
Доступ ко всем скрытым задачам предоставляется на ВСЕ время существования сайта.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” — это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
Пример.
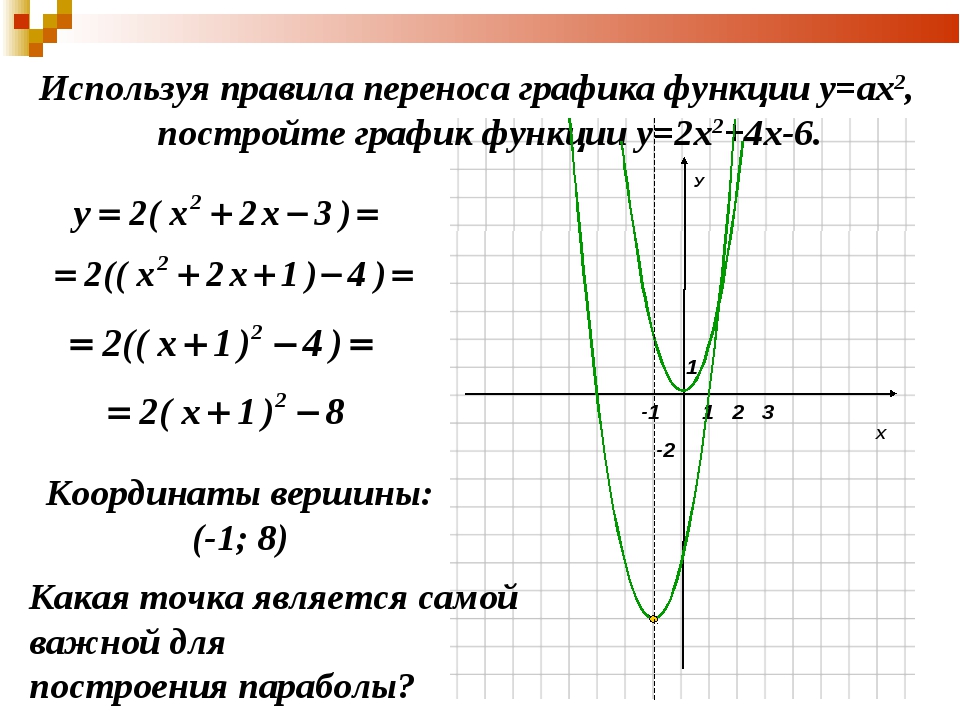
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т.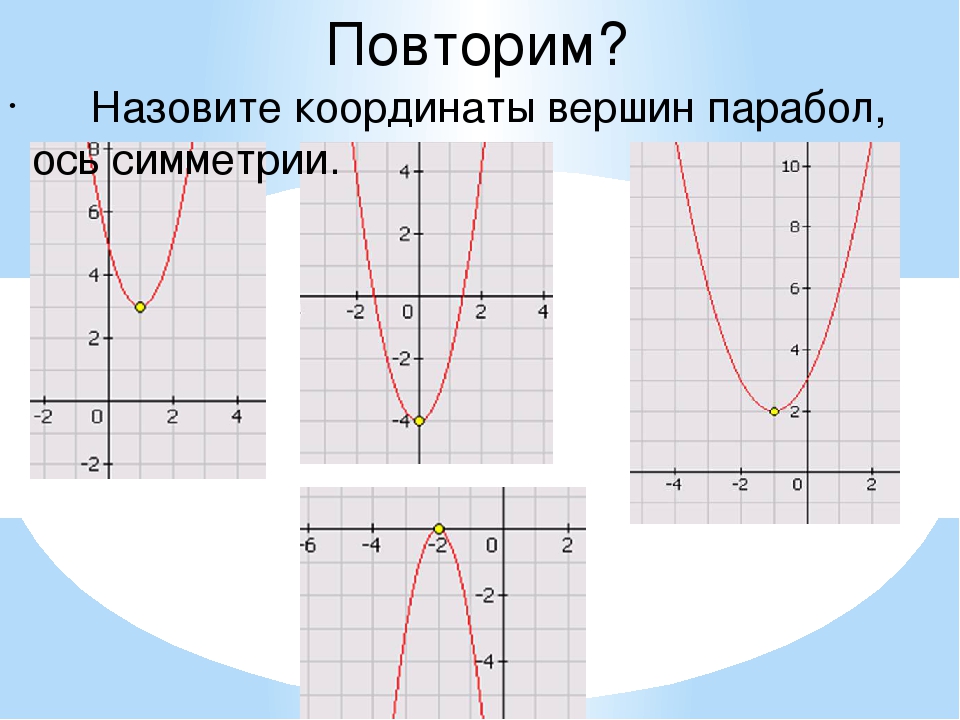
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем . В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.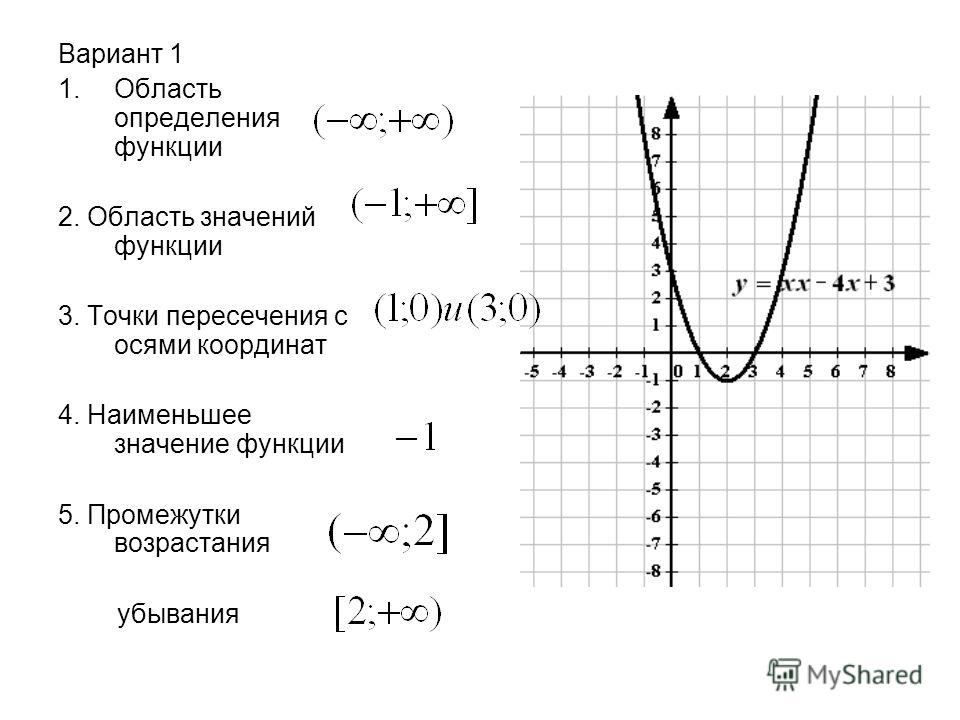
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Рубрика:
|
Парабола
|
Когда вы пинаете футбольный мяч (или стреляете стрелой, запускаете ракету или бросаете камень), он поднимается вверх по дуге и снова падает … … по пути параболы! (Кроме того, как воздух влияет на него.) |
Попробуй ударить по мячу:
images / parabola-ball.
Определение
Парабола — это кривая, в которой любая точка находится на равном расстоянии от:
- фиксированная точка (
фокус
) и - фиксированная прямая (
директрикс
)
Возьмите лист бумаги, нарисуйте на нем прямую линию, затем сделайте большую точку для фокуса (не на линии!).
Теперь поэкспериментируйте с некоторыми измерениями, пока не получите еще одну точку, которая находится на таком же расстоянии от фокуса и прямой линии.
Продолжайте, пока у вас не будет много маленьких точек, затем соедините маленькие точки, и у вас будет парабола!
Имена
Вот важные имена:
- г.
директрикс
и focus (объяснено выше) - ось симметрии (проходит через фокус, перпендикулярно директрисе)
- г.
вершина
(где парабола делает самый резкий поворот) находится на полпути между фокусом и директрисой.
Отражатель
А парабола обладает удивительным свойством:
Любой луч, параллельный оси симметрии, отражается от поверхности по прямой к фокусу .
И это объясняет, почему эта точка называется фокусом …
… потому что там фокусируются все лучи!
Таким образом, параболу можно использовать для:
- спутниковые антенны,
- антенна радарная,
- концентрирует солнечные лучи, чтобы создать горячую точку,
- отражатель на точечные светильники и фонари,
- и т. Д.
|
Мы также получаем параболу, когда разрезаем конус (разрез должен быть параллелен стороне конуса). Итак, парабола — это коническое сечение (сечение конуса). |
Уравнения
Простейшее уравнение параболы: y = x 2
В перевернутом виде получается y 2 = x
(или y = √x только для верхней половины)
Немного шире:
y 2 = 4ax
, где a — это расстояние от исходной точки до фокуса (а также от исходной точки до директрисы)
Пример:
Найдите фокус для уравнения y
2 = 5x
Преобразуя y 2 = 5x в y 2 = 4ax , мы получаем y 2 = 4 (5/4) x ,
, поэтому a = 5/4 , а фокус y 2 = 5x равен:
Уравнения парабол в разной ориентации следующие:
y 2 = 4ax
y 2 = −4ax
x 2 = 4 дня
x 2 = −4 дня
Измерения параболической тарелки
Если вы хотите построить параболическую тарелку с фокусом на 200 мм над поверхностью, какие измерения вам нужны?
Чтобы упростить сборку, давайте сделаем так, чтобы он был направлен вверх, и поэтому мы выберем уравнение x 2 = 4ay.
И мы хотим, чтобы «a» было 200, поэтому уравнение принимает следующий вид:
x 2 = 4ay = 4 × 200 × y = 800y
Переставляем так, чтобы можно было вычислить высоту:
y = x 2 /800
А вот измерения высоты, пока вы бежите:
| Расстояние вдоль («x») | Высота («y») | |
| 0 мм | 0.0 мм | |
| 100 мм | 12,5 мм | |
| 200 мм | 50,0 мм | |
| 300 мм | 112,5 мм | |
| 400 мм | 200.0 мм | |
| 500 мм | 312,5 мм | |
| 600 мм | 450.0 мм | |
Попробуйте построить его сами, это может быть весело! Только будьте осторожны, отражающая поверхность может сконцентрировать много тепла в фокусе.
567 568 833 834, 2088, 2089, 2086, 2087, 3334, 3335
предварительное вычисление алгебры — Построение параболы по двум точкам и оси симметрии
Георг и футуролог однозначно ответили на мой вопрос, и я публикую здесь еще один ответ, который я получил из намеков Георга, просто чтобы добавить немного разнообразия.
Думаю, я заметил эту конструкцию, потому что у меня было более поверхностное понимание теоремы Паскаля, ха: P
Прежде чем описывать конструкцию, сделаю несколько замечаний с двумя фигурами.
Шестиугольник в теореме Паскаля можно образовать, соединив точки в любом порядке, а чуть ниже — более простое расположение на эллипсе.
На этом рисунке выше точки в нижней половине $ ~ P_1 ‘~ $ и $ ~ P_2’ ~ $ являются зеркальными отображениями $ ~ P_1 ~ $ и $ ~ P_2 ~ $, поэтому при симметрии линия Паскаля перпендикулярна к оси симметрии $ L $, здесь также оси $ x $.
Теперь мы доводим самую правую вершину $ P _ { infty} $ до бесконечности и получаем параболу с неизменной симметрией и ортогональностью, как показано на рисунке ниже:
Здесь синяя линия $ overline {P _ { infty} P_2} $ (а также зеленая зеркальная линия $ overline {P _ { infty} P_2 ‘} $) становится параллельной оси $ L $, как ключевой момент в решении Георга и футуролога.
Здесь начинается строительство (см. Рисунок ниже):
- Постройте $ overrightarrow {P_2P_1} $ так, чтобы они пересекались с осью симметрии $ L $ в точке $ Q_0 $
- Постройте прямую через $ Q_0 $, которая перпендикулярна $ L $ и пересекает $ overline {P _ { infty} P_2} $ в точке $ Q_1 $. (Здесь синий $ overline {P _ { infty} P_2} $ построен как линия, проходящая через $ P_2 $ и параллельная $ L $; аналогично для зеленого $ overline {P _ { infty} P_2 ‘} $ )
- Постройте $ overleftrightarrow {Q_1P_1 ‘} $ так, чтобы они пересекались с $ L $ в точке $ P_0 ~ $.Этот $ P_0 $ будет вершиной. (пока что до этого шага это в основном другая версия той же конструкции, что и у Георга и футуролога)
- Постройте из точки $ P_0 $ прямую, перпендикулярную зеленому цвету $ overline {P _ { infty} P_2 ‘} $ и пересекающую ее в точке $ Q_2 $
- Средняя точка $ overline {P_0Q_2} $ будет обозначена как $ M $, так что $ overline {P_0M} = overline {Q_2M} $
- Соедините отрезок линии $ overline {P_2’M} $ так, чтобы получился прямоугольный треугольник $ треугольник Q_2MP_2 ‘$, где $ angle MQ_2P_2’ = pi / 2 $ — прямой угол.
- Найдите точку $ N $ на другой стороне $ Q_2 $ (противоположную $ P_2 ‘$), чтобы получился такой же прямоугольный треугольник, $ angle NMP_2’ = angle MQ_2P_2 ‘= pi / 2 ~ $ и $ angle MNQ_2 = angle Q_2MP_2 ‘$
- Длина $ overline {NQ_2} $ дает фокусное расстояние. Директива $ Gamma $ и фокус можно сделать легко. Смотрите рисунок.
Эта конструкция сама по себе показывает, почему она работает: есть равнобедренный треугольник, показывающий $ ~ overline {NP_2 ‘} = d ( Gamma, , P_2’) = d (F, , P_2 ‘) ~ $, где точка $ F $ — это фокус (оранжевая точка справа; для ясности не обозначена).
Обратите внимание, что шаги с 4 по 8 основаны на $ P_2 ‘$, но можно сделать то же самое для любой из точек $ ~ P_1, , P_1’, , P_2 $.
Я алгебраически проверил правильность этой конструкции. Интересно, есть ли способ НЕ использовать теорему Паскаля в аргументации этой конструкции. По сути, мне нужно было бы доказать, что пара директриса-фокус, построенная на основе $ P_2 ‘$ через эту особую точку $ P_0 $ (которая, как мы знаем, является вершиной параболы), является той же парой директриса-фокус, основанной на $ P_1’ $ .
% PDF-1.6
%
1 0 obj>
эндобдж
2 0 obj>
эндобдж
3 0 obj>
эндобдж
5 0 obj> / Font> / ProcSet [/ PDF / Text] / Properties> / MC1 >>> / ExtGState >>> / Type / Page >>
эндобдж
6 0 obj>
эндобдж
7 0 obj>
эндобдж
8 0 obj> поток
application / pdfAdobe Illustrator CS22007-03-16T15: 08: 49-04: 002007-03-23T18: 48: 07-04: 002007-03-23T18: 48: 07-04: 00
В этой статье Норман Вильдбергер объясняет, как определить квадратичную функцию, проходящую через три точки.2 + bx + c} ) задается тремя числами, разумно предположить, что мы могли бы подогнать параболу к трем точкам на плоскости. Это действительно так, и это полезная идея.
На этом шаге мы увидим, как алгебраически подогнать параболу к трем точкам на декартовой плоскости. Это включает в себя вспоминание или обучение тому, как решить три уравнения с тремя неизвестными. Это полезный навык сам по себе.
Спутниковая тарелка предназначена для сбора сигнала со спутника и
сфокусируйте его на приемнике.Чтобы определить оптимальную форму блюда, вы
необходимо найти поверхность, которая будет отражать входящий сигнал на приемник
из каждой точки на поверхности блюда.
Из физики мы знаем, что луч, падающий на плоскую поверхность, отражает так, что
угол отражения равен углу падения. Если поверхность
изогнутый, то верен тот же физический закон, где плоскость отражения является
плоскость, касающаяся поверхности в точке контакта. Чтобы показать это
параболическая форма оптимальна для спутниковой антенны, это необходимо знать
физический факт, определение параболы, некоторая элементарная геометрия и один
факт из исчисления.
Парабола — это геометрическое место точек, которые равноудалены от фиксированной точки,
фокус и фиксированная линия — директриса. Чтобы найти уравнение такой
кривой построить систему координат на плоскости так, чтобы фокус был точкой
(0, p), а директрисой является горизонтальная линия y = -p. Таким образом, точка (x, y)
на кривой тогда и только тогда, когда расстояние от (x, y) до (0, p) равно
расстояние от (x, y) до линии y = -p. Приравнивая квадраты этих
расстояния (чтобы вам не приходилось иметь дело с квадратными корнями), это требование
является
как уравнение параболы.
Предположим, что спутник находится прямо над головой, и поэтому парабола
построенный направлен на спутник. Спутник находится достаточно далеко, чтобы
можно предположить, что сигнал приближается к тарелке вертикально. Предположим, что
конкретный сигнал попадает на тарелку в точке P с координатой X a, тогда
точка P — (a, a 2 / (4p)).Продлите вертикальную линию через P до
направляющая в Q, которая тогда имеет координаты (a, -p). У фокуса есть координаты
(0, p) и, следовательно, средняя точка S отрезка FQ имеет координаты (a / 2,0) и
поэтому находится на оси X.
Из исчисления требуется тот факт, что касательная к параболе в точке
точка P имеет наклон 2 a / 4 p , и, следовательно, уравнение касательной
линия на этом
точка
Найти точку
где эта касательная линия пересекает ось X, заданную y = 0, и упростить
чтобы найти, что x = a / 2 .Но это
S, середина отрезка FQ. Поскольку | FP | = | PQ | (определение
параболы) треугольники FPS и QPS совпадают и, следовательно,
углы FPS и QPS равны. Но угол QPS равен углу падения
и, таким образом, сигнал будет отражаться вдоль линии PF и проходить через
фокус.
Размещение приемника в фокусе параболы, таким образом, приведет к
а
тарелка, которая будет отражать все сигналы со спутника на приемник.
Решение проблемы на
параболические зеркала, отправленные в Quandaries and Queries, подразумевают, что каждое
сигнал от спутника, который попадает в тарелку и, таким образом, отражается на
фокус перемещается на одно и то же расстояние независимо от того, где он встряхивает тарелку. 2 + 3.2 — 20x + 23
после объединения одинаковых терминов.