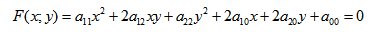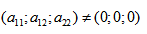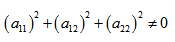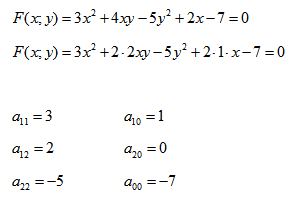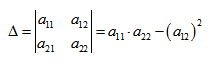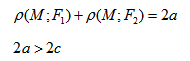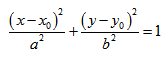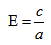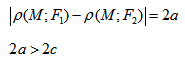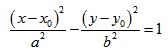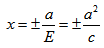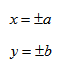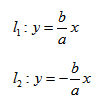Кривые второго порядка — определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Эллипс
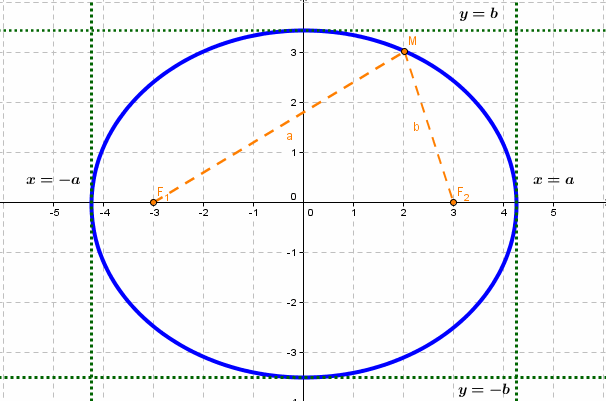
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 

Точки 
Если а =Ь, то уравнение (7.3) можно переписать в виде:

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 

Число 


Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 







Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 

Точки 



Тогда 




Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
Легко показать, что уравнение 

и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 

Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию




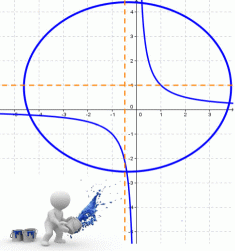
Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

Число а называют большей полуосью эллипса, число 
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 

Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:


Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 

В новой системе координат координаты 
Переходя к старым координатам, получим:
Построим график эллипса.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Аппроксимация функции одной переменной
Калькулятор использует методы регрессии для аппроксимации функции одной переменной.
Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.
Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.
Аппроксимация функции одной переменной
Линейная регрессия
Коэффициент линейной парной корреляции:
Средняя ошибка аппроксимации:
Квадратичная регрессия
Система уравнений для нахождения коэффициентов a, b и c:
Коэффициент корреляции:
,
где
Средняя ошибка аппроксимации:
Кубическая регрессия
Система уравнений для нахождения коэффициентов a, b, c и d:
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Степенная регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Показательная регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Гиперболическая регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Логарифмическая регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Экспоненциальная регрессия
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Вывод формул
Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.
Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.
Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.
Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:
Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.
Используя формулу производной сложной функции, получим следующую систему уравнений:
Для функции вида частные производные равны:
,
Подставив производные, получим:
Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.
Как сделать линейную калибровочную кривую в Excel
В Excel есть встроенные функции, которые вы можете использовать для отображения ваших данных калибровки и расчета линии наилучшего соответствия. Это может быть полезно, когда вы пишете отчет химической лаборатории или программируете поправочный коэффициент на единицу оборудования.
В этой статье мы рассмотрим, как использовать Excel для создания диаграммы, построить линейную калибровочную кривую, отобразить формулу калибровочной кривой, а затем настроить простые формулы с помощью функций НАКЛОН и ПЕРЕКЛЮЧИТЬ, чтобы использовать уравнение калибровки в Excel.
Что такое калибровочная кривая и как Excel полезен при ее создании?
Чтобы выполнить калибровку, вы сравниваете показания устройства (например, температуру, отображаемую термометром) с известными значениями, называемыми стандартами (например, точки замерзания и кипения воды). Это позволяет вам создать серию пар данных, которые вы затем будете использовать для построения калибровочной кривой.
Двухточечная калибровка термометра с использованием точек замерзания и кипения воды будет иметь две пары данных: одну с момента, когда термометр помещают в ледяную воду (32 ° F или 0 ° C), и одну в кипящую воду (212 ° F). или 100 ° С). Когда вы построите эти две пары данных в виде точек и проведете линию между ними (калибровочную кривую), а затем, предполагая, что реакция термометра является линейной, вы можете выбрать любую точку на линии, которая соответствует значению, которое отображает термометр, и вы мог найти соответствующую «истинную» температуру.
Таким образом, линия, по сути, заполняет информацию между двумя известными для вас точками, так что вы можете быть достаточно уверенными при оценке фактической температуры, когда термометр показывает 57,2 градуса, но когда вы никогда не измеряли «стандарт», который соответствует это чтение.
В Excel есть функции, которые позволяют графически отображать пары данных на графике, добавлять линию тренда (калибровочную кривую) и отображать уравнение калибровочной кривой на графике. Это полезно для визуального отображения, но вы также можете рассчитать формулу линии, используя функции Excel SLOPE и INTERCEPT. Когда вы введете эти значения в простые формулы, вы сможете автоматически рассчитать «истинное» значение на основе любого измерения.
Давайте посмотрим на пример
Для этого примера мы разработаем калибровочную кривую из серии из десяти пар данных, каждая из которых состоит из значения X и значения Y. Значения Х будут нашими «стандартами», и они могут представлять что угодно, от концентрации химического раствора, который мы измеряем с помощью научного прибора, до входной переменной программы, которая управляет пусковой машиной для мрамора.
Значения Y будут «откликами», и они будут представлять собой показания прибора, полученные при измерении каждого химического раствора, или измеренное расстояние, на котором расстояние от пусковой установки, на которую упал мрамор, используя каждое входное значение.
После того, как мы графически изобразим калибровочную кривую, мы будем использовать функции SLOPE и INTERCEPT, чтобы вычислить формулу калибровочной линии и определить концентрацию «неизвестного» химического раствора на основании показаний прибора или решить, какой ввод мы должны дать программе, чтобы мрамор приземляется на определенном расстоянии от пусковой установки.
Шаг первый: создайте свою диаграмму
Наш простой пример электронной таблицы состоит из двух столбцов: X-Value и Y-Value.
Начнем с выбора данных для построения графика.
Сначала выберите ячейки столбца «X-значение».
Теперь нажмите клавишу Ctrl и затем щелкните ячейки столбца Y-значения.
Перейдите на вкладку «Вставить».
Перейдите в меню «Графики» и выберите первый вариант в раскрывающемся меню «Разброс».
разброс» width=»314″ height=»250″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20314%20250’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/xExcel-Calibration-Curve-05.png.pagespeed.gp+jp+jw+pj+ws+js+rj+rp+rw+ri+cp+md.ic.zXPKQgYC7-.png»/>
Появится диаграмма, содержащая точки данных из двух столбцов.
Выберите серию, нажав на одну из синих точек. После выбора Excel обрисовывает в общих чертах точки.
Щелкните правой кнопкой мыши одну из точек и выберите опцию «Добавить линию тренда».
На графике появится прямая линия.
В правой части экрана появится меню «Format Trendline». Установите флажки рядом с «Показать уравнение на графике» и «Показать значение R-квадрат на графике». Значение R-квадрат является статистикой, которая говорит вам, насколько точно линия соответствует данным. Наилучшее значение R-квадрата равно 1.000, что означает, что каждая точка данных касается линии. По мере роста различий между точками данных и линией значение r-квадрата уменьшается, причем 0,000 является наименьшим возможным значением.
Уравнение и R-квадрат статистики трендовой линии появятся на графике. Обратите внимание, что в нашем примере корреляция данных очень хорошая, значение R-квадрата равно 0,988.
Уравнение имеет вид «Y = Mx + B», где M — наклон, а B — пересечение оси y прямой.
Теперь, когда калибровка завершена, давайте поработаем над настройкой диаграммы, отредактировав заголовок и добавив заголовки осей.
Чтобы изменить заголовок диаграммы, щелкните по нему, чтобы выделить текст.
Теперь введите новый заголовок, который описывает диаграмму.
Чтобы добавить заголовки к осям X и Y, сначала перейдите к «Инструменты диаграммы»> «Дизайн».
дизайн» width=»650″ height=»225″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20225’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/Excel-Calibration-Curve-14.png»/>
Нажмите «Добавить элемент диаграммы».
Теперь перейдите к Названия осей> Первичная горизонтальная.
первичная горизонтальная» width=»650″ height=»500″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20500’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/Excel-Calibration-Curve-16.png»/>
Появится название оси.
Чтобы переименовать заголовок оси, сначала выделите текст, а затем введите новый заголовок.
Теперь перейдите к Названию осей> Первичная вертикаль.
Появится название оси.
Переименуйте этот заголовок, выделив текст и введя новый заголовок.
Ваша диаграмма теперь завершена.
Шаг второй: Рассчитать линейное уравнение и R-квадрат
Теперь давайте вычислим линейное уравнение и R-квадрат, используя встроенные в Excel функции SLOPE, INTERCEPT и CORREL.
К нашему листу (в строке 14) мы добавили заголовки для этих трех функций. Мы выполним фактические вычисления в ячейках под этими заголовками.
Сначала рассчитаем НАКЛОН. Выберите ячейку A15.
Перейдите к формулам> Дополнительные функции> Статистические> НАКЛОН.
Дополнительные функции> Статистические> НАКЛОН» width=»650″ height=»435″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20435’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/Excel-Calibration-Curve-24.png»/>
Откроется окно «Аргументы функции». В поле «Known_ys» выберите или введите ячейки столбца Y-значения.
В поле «Known_xs» выберите или введите ячейки столбца X-Value. Порядок полей ‘Known_ys’ и ‘Known_xs’ имеет значение в функции SLOPE.
Нажмите «ОК». Окончательная формула в строке формул должна выглядеть следующим образом:
Обратите внимание, что значение, возвращаемое функцией SLOPE в ячейке A15, соответствует значению, отображенному на графике.
Затем выберите ячейку B15 и перейдите к «Формулы»> «Дополнительные функции»> «Статистические данные»> «ПЕРЕКРЫТЬ».
Дополнительные функции> Статистические> INTERCEPT» width=»650″ height=»435″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20435’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/xExcel-Calibration-Curve-28.png.pagespeed.gp+jp+jw+pj+ws+js+rj+rp+rw+ri+cp+md.ic.6UWCgXDsRt.png»/>
Откроется окно «Аргументы функции». Выберите или введите в ячейки столбца Y-значение для поля «Known_ys».
Выберите или введите в ячейки столбца X-Value поле «Known_xs». Порядок полей «Known_ys» и «Known_xs» также имеет значение в функции INTERCEPT.
Нажмите «ОК». Окончательная формула в строке формул должна выглядеть следующим образом:
Обратите внимание, что значение, возвращаемое функцией INTERCEPT, соответствует точке пересечения y, отображаемой на диаграмме.
Затем выберите ячейку C15 и перейдите к «Формулы»> «Дополнительные функции»> «Статистические данные»> «CORREL».
дополнительные функции> статистические> CORREL» width=»650″ height=»435″ svg+xml,%3Csvg%20xmlns=’http://www.w3.org/2000/svg’%20viewBox=’0%200%20650%20435’%3E%3C/svg%3E» data-lazy-src=»https://gadgetshelp.com/wp-content/uploads/images/htg/content/uploads/2018/12/xExcel-Calibration-Curve-32.png.pagespeed.gp+jp+jw+pj+ws+js+rj+rp+rw+ri+cp+md.ic.n7KBBl00Uj.png»/>
Откроется окно «Аргументы функции». Выберите или введите любой из двух диапазонов ячеек для поля «Массив1». В отличие от SLOPE и INTERCEPT, порядок не влияет на результат функции CORREL.
Выберите или введите другой из двух диапазонов ячеек для поля «Array2».
Нажмите «ОК». Формула должна выглядеть следующим образом на панели формул:
Обратите внимание, что значение, возвращаемое функцией CORREL, не соответствует значению «r-квадрат» на графике. Функция CORREL возвращает «R», поэтому мы должны возвести ее в квадрат, чтобы вычислить «R-квадрат».
Щелкните внутри панели функций и добавьте «^ 2» в конец формулы, чтобы возвести в квадрат значение, возвращаемое функцией CORREL. Заполненная формула теперь должна выглядеть так:
После изменения формулы значение «R-квадрат» теперь соответствует значению, отображенному на графике.
Шаг третий: настройка формул для быстрого расчета значений
Теперь мы можем использовать эти значения в простых формулах, чтобы определить концентрацию этого «неизвестного» раствора или то, что мы должны ввести в код, чтобы шарик пролетел определенное расстояние.
Эти шаги настроят формулы, необходимые для того, чтобы вы могли ввести значение X или значение Y и получить соответствующее значение на основе калибровочной кривой.
Уравнение линии наилучшего соответствия имеет вид «Y-значение = НАКЛОН * X-значение + INTERCEPT», поэтому решение для «Y-значения» выполняется путем умножения значения X и SLOPE, а затем добавив ИНТЕРЦЕПТ.
В качестве примера мы вводим ноль в качестве значения X. Возвращаемое значение Y должно быть равно ПЕРЕКЛЮЧЕНИЮ линии наилучшего соответствия. Это соответствует, поэтому мы знаем, что формула работает правильно.
Решение для значения X на основе значения Y выполняется путем вычитания INTERCEPT из значения Y и деления результата на НАКЛОН:
В качестве примера мы использовали INTERCEPT в качестве значения Y. Возвращаемое значение Х должно быть равно нулю, но возвращаемое значение равно 3.14934E-06. Возвращаемое значение не равно нулю, потому что мы непреднамеренно обрезали результат INTERCEPT при вводе значения. Однако формула работает правильно, потому что результат формулы равен 0,00000314934, что по существу равно нулю.
Вы можете ввести любое значение X в первую ячейку с толстыми границами, и Excel автоматически вычислит соответствующее значение Y.
Ввод любого значения Y во вторую ячейку с толстой рамкой даст соответствующее значение X. Эта формула используется для расчета концентрации этого раствора или того, что необходимо для запуска мрамора на определенном расстоянии.
В этом случае прибор показывает «5», поэтому при калибровке будет предложена концентрация 4,94, или мы хотим, чтобы шарик прошел пять единиц расстояния, поэтому при калибровке предлагается ввести 4,94 в качестве входной переменной для программы, управляющей пусковой установкой мрамора. Мы можем быть достаточно уверены в этих результатах из-за высокого значения R-квадрата в этом примере.
http://planetcalc.ru/5992/
http://gadgetshelp.com/how-to/kak-sdelat-lineinuiu-kalibrovochnuiu-krivuiu-v-excel/
Кривые второго порядка — определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 

Точки 
Если а =Ь, то уравнение (7.3) можно переписать в виде:

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 

Число 


Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 







Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 

Точки 



Тогда 




Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
Легко показать, что уравнение 

и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 

Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию




Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

Число а называют большей полуосью эллипса, число 
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 

Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:


Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 

В новой системе координат координаты 
Переходя к старым координатам, получим:
Построим график эллипса.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Кривые второго порядка
Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.
или можно встретить следующую форму записи:
К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.
Покажем на примере определение значений коэффициентов.
Рассмотрим кривую второго порядка:
Вычислим определитель из коэффициентов:
Если Δ = 0, кривая второго порядка параболического типа,
если Δ > 0, кривая второго порядка эллиптического типа,
если Δ F1 и F2 — фокусы.
с — фокальное расстояние,
Каноническое уравнение эллипса с центром симметрии в начале координат:
2а — большая ось эллипса, 2b — малая ось эллипса.
а — большая полуось эллипса, b — малая полуось эллипса.
Если a = b, то имеем окружность с радиусов R = a = b:
Если центр эллипса находится не в начале координат, а в некоторой точке C(x0;y0), оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид:
Эксцентриситет — число, равное отношению фокального расстояния к большей полуоси:
Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.
Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
с — фокальное расстояние,
Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
Каноническое уравнение гиперболы с центром симметрии в начале координат:
x — действительная ось, y — мнимая ось.
а — действительная полуось, b — мнимая полуось.
Если центр гиперболы находится в некоторой точке C(x0;y0), оси симметрии параллельны осям координат, то каноническое уравнение имеет вид:
Эксцентриситет гиперболы — число, равное отношению фокусного расстояния к действительной полуоси.
Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.
Директриса гиперболы — прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.
f1 — правая директриса, f2 — левая директриса.
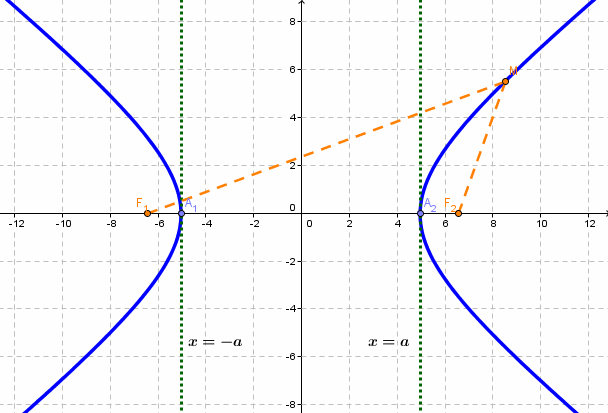
Порядок построения гиперболы :
1. Строим прямоугольник со сторонами 2a и 2b.
2. Провести асимптоты гиперболы — диагонали построенного прямоугольника.
3. Строим гиперболу с вершинами в точках А 1 (-а;0), А 2 (а;0).
Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
F — фокус параболы, f — директриса параболы.
Уравнение касательной к графику функции
п.1. Уравнение касательной
Рассмотрим кривую (y=f(x)).
Выберем на ней точку A с координатами ((x_0,y_0)), проведем касательную AB в этой точке.
Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке (x_0): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: ((y_B-y_A)=k(x_B-x_A)).
Для (A(x_0,y_0), B(x,y)) получаем: begin (y-y_0)=k(x-x_0)\ y=k(x-x_0)+y_0\ y=f'(x_0)(x-x_0)+f(x_0) end
Чтобы записать уравнение касательной с угловым коэффициентом в виде (y=kx+b), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=underbrace_<=k>x+underbrace_ <=b>$$
п.2. Алгоритм построения касательной
На входе: уравнение кривой (y=f(x)), абсцисса точки касания (x_0).
Шаг 1. Найти значение функции в точке касания (f(x_0))
Шаг 2. Найти общее уравнение производной (f’ (x))
Шаг 3. Найти значение производной в точке касания (f'(x_0 ))
Шаг 4. Записать уравнение касательной (y=f’ (x_0)(x-x_0)+f(x_0)), привести его к виду (y=kx+b)
На выходе: уравнение касательной в виде (y=kx+b)
 |
Пусть (f(x)=x^2+3). Найдем касательную к этой параболе в точке (x_0=1). |
(f(x_0)=1^2+3=4 )
(f'(x)=2x )
(f'(x_0)=2cdot 1=2)
Уравнение касательной: $$ y=2(x-1)+4=2x-2+4=2x+2 $$ Ответ: (y=2x+2)
п.3. Вертикальная касательная
Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода (x_0notin D), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку (x_0in D), входящую в область определения. График функции и касательная имеют одну общую точку ((x_0,y_0)).
Вертикальные касательные характерны для радикалов вида (y=sqrt[n]).
 |
Пусть (f(x)=sqrt[5]+1). Найдем касательную к этой кривой в точке (x_0=1). |
(f(x_0)=sqrt[5]<1-1>+1=1)
(f'(x)=frac15(x-1)^<frac15-1>+0=frac15(x-1)^<-frac45>=frac<1><5(x-1)^<frac45>> )
(f'(x_0)=frac<1><5(1-1)^<frac45>>=frac10=+infty)
В точке (x_0) проходит вертикальная касательная.
Её уравнение: (x=1)
Ответ: (y=2x+2)
п.4. Примеры
Пример 1. Для функции (f(x)=2x^2+4x)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.
 |
Находим точки пересечения, решаем уравнение: $$ 2x^2+4x=0Rightarrow 2x(x+2)=0Rightarrow left[ begin x=0\ x=-2 end right. $$ Две точки на оси: (0;0) и (-2;0). Касательная в точке (x_0=0): begin f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot 0+4=4\ y=4(x-0)+0=4x end Касательная в точке (x_0=-2): begin f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot (-2)+4=-4\ y=-4(x+2)+0=-4x-8 end |
б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.
 |
Общее уравнение касательной: (f'(x)=4x+4) По условию (f'(x_0)=tgalpha=tg45^circ=1) Решаем уравнение: $$ 4x_0+4=1Rightarrow 4x_0=-3Rightarrow x_0=-frac34 $$ Точка касания (x_0=-frac34) begin f(x_0)=2cdotleft(-frac34right)^2+4cdotleft(-frac34right)=frac98-3=-frac<15> <8>end Уравнение касательной: begin y=1cdotleft(x+frac34right)-frac<15><8>=x-frac98 end |
в) найдите, в какой точке касательная будет параллельна прямой (2x+y-6=0). Напишите уравнение этой касательной.
 |
Найдем угловой коэффициент заданной прямой: (y=-2x+6Rightarrow k=-2). Касательная должна быть параллельной, значит, её угловой коэффициент тоже (k=-2). Получаем уравнение: begin f'(x_0)=-2\ 4x_0+4=-2Rightarrow 4x_0=-6Rightarrow x_0=-frac32 end Точка касания (x_0=-frac32) begin f(x_0)=2cdotleft(-frac32right)^2+4cdotleft(-frac32right)=\ =frac92-6=-frac32 end Уравнение касательной: begin y=-2cdotleft(x+frac32right)-frac32=-2x-frac92 end Или, в каноническом виде: begin 2x+y+frac92=0 end |
г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.
 |
У горизонтальной прямой (k=0). Получаем уравнение: (f'(x_0)=0). begin 4x_0+4=0Rightarrow 4x_0=-4Rightarrow x_0=-1 end Точка касания (x_0=-1) begin f(x_0)=2cdot(-1)^2+4cdot(-1)=-2 end Уравнение касательной: begin y=0cdot(x+1)-2=-2 end |
Ответ: а) (y=4x) и (y=-4x-8); б) (y=x-frac98); в) (2x+y+frac92=0); г) (y=-2)
Пример 3*. Найдите точку, в которой касательная к графику функции (f(x)=frac-x) перпендикулярна прямой (y=11x+3). Напишите уравнение этой касательной.
Угловой коэффициент данной прямой (k_1=11).
Угловой коэффициент перпендикулярной прямой (k_2=-frac<1>=-frac<1><11>) begin f'(x)=left(fracright)’-x’=frac<2x(x+3)-(x^2+2)cdot 1><(x+3)^2>-1=frac<2x^2+6x-x^2-2-(x+3)^2><(x+3)^2>=\ =frac<(x+3)^2>=- frac<11> <(x+3)^2>end В точке касания: begin f'(x_0)=k_2Rightarrow=-frac<11><(x+3)^2>=-frac<1><11>Rightarrow (x+3)^2=121Rightarrow (x+3)^2-11^2=0Rightarrow\ Rightarrow (x+14)(x+8)=0Rightarrow left[ begin x=-14\ x=8 end right. end
Уравнение касательной при (x_0=-14) begin f(x_0)=frac<(-14)^2+2><-14+3>+14=frac<198><-11>+14=-18+14=-4\ y=-frac<1><11>(x+14)-4=-frac <11>end Уравнение касательной при (x_0=8) begin f(x_0)=frac<8^2+2><8+3>-8=frac<66><11>-8=-2\ y=-frac<1><11>(x-8)-2=-frac <11>end
Ответ: точка касания (-14;-4), уравнение (y=-frac<11>)
и точка касания (8;-2), уравнение (-frac<11>)
Пример 4*. Найдите уравнения общих касательных к параболам (y=x^2-5x+6) и (y=x^2+x+1). Укажите точки касания.
Найдем производные функций: begin f_1′(x)=2x-5, f_2′(x)=2x+1 end Пусть a – абсцисса точки касания для первой параболы, b — для второй.
Запишем уравнения касательных (g_1(x)) и (g_2(x)) через эти переменные. begin g_1(x)=f_1′(a)(x-a)+f_1(a)=(2a-5)(x-a)+a^2-5a+6=\ =(2a-5)x-2a^2+5a+a^2-5a+6=(2a-5)x+(6-a^2)\ \ g_2(x)=f_2′(b)(x-b)+f_2(b)=(2b+1)(x-b)+b^2+b+1=\ =(2b+1)x-2b^2-b+b^2+b+1=(2b+1)x+(1-b^2) end Для общей касательной должны быть равны угловые коэффициенты и свободные члены. Получаем систему уравнений: begin begin 2a-5=2b+1\ 6-a^2=1-b^2 end Rightarrow begin 2(a-b)=6\ a^2-b^2=5 end Rightarrow begin a-b=3\ (a-b)(a+b)=5 end Rightarrow begin a-b=3\ a+b=frac53 end Rightarrow \ Rightarrow begin 2a=3+frac53\ 2b=frac53-3 end Rightarrow begin a=frac73\ b=-frac23 end end Находим угловой коэффициент и свободный член из любого из двух уравнений касательных: $$ k=2a-5=2cdotfrac73-5=-frac13, b=6-a^2=6-frac<49><9>=frac59 $$ Уравнение общей касательной: $$ y=-frac x3+frac59 $$
Точки касания: begin a=frac73, f_1(a)=left(frac73right)^2-5cdotfrac73+6=frac<49><9>-frac<35><3>+6=frac<49-105+54><9>=-frac29\ b=-frac23, f_2(b)=left(-frac23right)^2-frac23+1=frac49-frac23+1frac<4-6+9><9>=frac79 end
Ответ: касательная (y=-frac x3+frac59); точки касания (left(frac73;-frac29right)) и (left(-frac23;frac79right))
Пример 5*. Докажите, что кривая (y=x^4+3x^2+2x) не пересекается с прямой (y=2x-1), и найдите расстояние между их ближайшими точками.
Решим уравнение: (x^4+3x^2+2x=2x-1) begin x^4+3x^2+1=0Rightarrow D=3^2-4=5Rightarrow x^2=frac<-3pmsqrt<5>> <2>end Оба корня отрицательные, а квадрат не может быть отрицательным числом.
Значит, (xinvarnothing) — решений нет, кривая и прямая не пересекаются.
Что и требовалось доказать.
Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом (k=2), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой (y=2x-1).
Строим уравнение касательной. По условию: (f'(x)=4x^3+6x+2=2) begin 4x^3+6x=0Rightarrow 2x(2x^2+3)=0Rightarrow left[ begin x=0\ 2x^2+3=0 end right. Rightarrow left[ begin x=0\ x^2=-frac32 end right. Rightarrow left[ begin x=0\ xinvarnothing end right. Rightarrow x=0 end Точка касания (x_0=0, y_0=0^4+3cdot 0^2+2cdot 0=0).
Уравнение касательной: (y=2(x-0)+0=2x)
 |
Ищем расстояние между двумя параллельными прямыми: (y=2x) и (y=2x-1). Перпендикуляр из точки (0;0) на прямую (y=2x-1) имеет угловой коэффициент (k=-frac12), его уравнение: (y=-frac12 x+b). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и (b=0). |
Уравнение перпендикуляра: (y=-frac x2).
Находим точку пересечения прямой (y=2x-1) и перпендикуляра (y=-frac x2): begin 2x-1=-frac x2Rightarrow 2,5x=1Rightarrow x=0,4; y=-frac<0,4><2>=-0,2 end Точка пересечения A(0,4;-0,2).
Находим расстояние (OA=sqrt<0,4^2+(-0,2)^2>=0,2sqrt<2^2+1^2>=frac<sqrt<5>><5>)
Ответ: (frac<sqrt<5>><5>)
источники:
http://matecos.ru/mat/matematika/krivye-vtorogo-poryadka.html
http://reshator.com/sprav/algebra/10-11-klass/uravnenie-kasatelnoj-k-grafiku-funkcii/
Все зависит от того что это может быть за функция. Если это абсолютно произвольная кривая, то есть вероятность того, что получить функцию в чистом виде будет очень сложно. Например цепная кривая. Есть цепь закрепленная концами так, что цепь провисает. Несмотря на всю простоту кривой, функция имеет сложный вид.
В случае если график кривой напоминает какую либо математическую функцию, то восстановить функцию можно используя характерные точки для кривых второго порядка или две точки для прямой линии.
Содержание
- Простейший график изменений
- График с двумя и более кривыми
- Добавление второй оси
- Строим график функций в Excel
- Наложение и комбинирование графиков
- Графики зависимости
Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.
Простейший график изменений
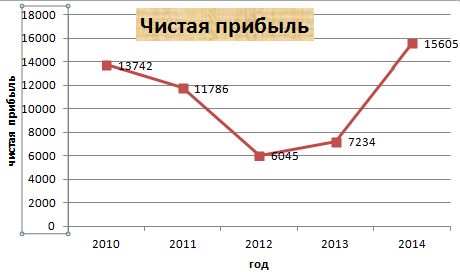
График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.
Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
* Цифры условные, для учебных целей.
Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:
Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.
Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:
Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.
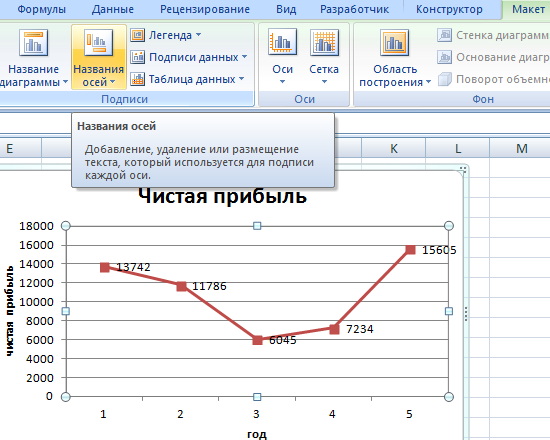
Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:
Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».
Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:
Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).
График с двумя и более кривыми
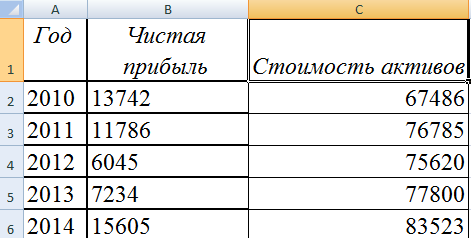
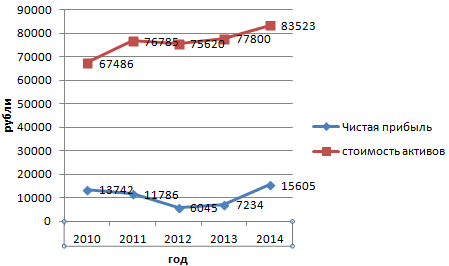
Допустим, нам нужно показать не только чистую прибыль, но и стоимость активов. Данных стало больше:
Но принцип построения остался прежним. Только теперь есть смысл оставить легенду. Так как у нас 2 кривые.
Добавление второй оси
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
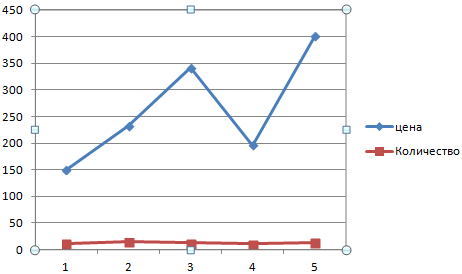
Сначала строим график так, будто у нас одинаковые единицы измерения.
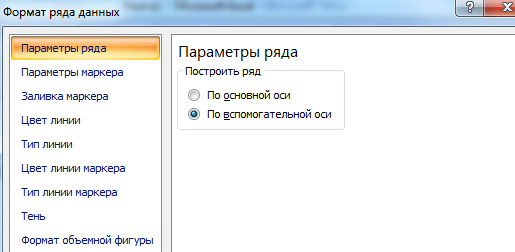
Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».
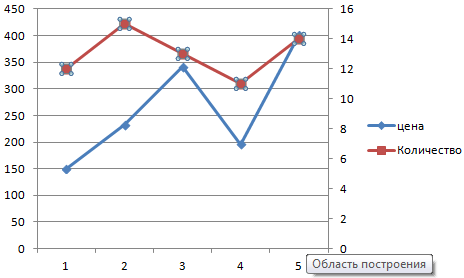
Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.
Это один из способов. Есть и другой – изменение типа диаграммы.
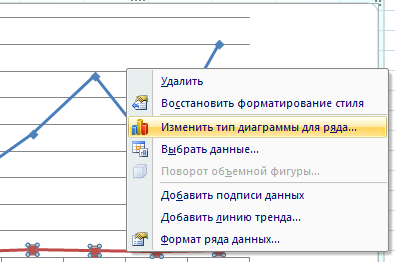
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Строим график функций в Excel
Вся работа состоит из двух этапов:
- Создание таблицы с данными.
- Построение графика.
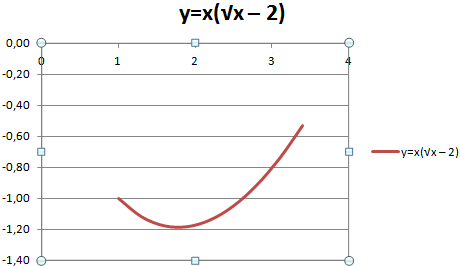
Пример: y=x(√x – 2). Шаг – 0,3.
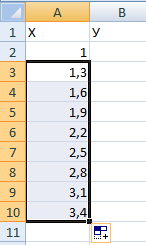
Составляем таблицу. Первый столбец – значения Х. Используем формулы. Значение первой ячейки – 1. Второй: = (имя первой ячейки) + 0,3. Выделяем правый нижний угол ячейки с формулой – тянем вниз столько, сколько нужно.
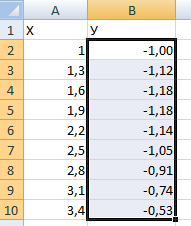
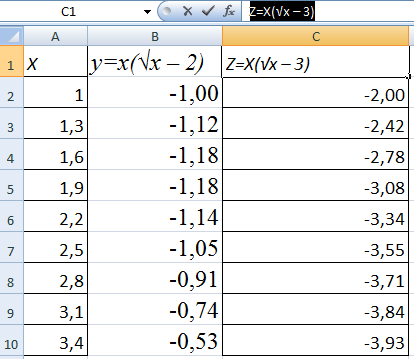
В столбце У прописываем формулу для расчета функции. В нашем примере: =A2*(КОРЕНЬ(A2)-2). Нажимаем «Ввод». Excel посчитал значение. «Размножаем» формулу по всему столбцу (потянув за правый нижний угол ячейки). Таблица с данными готова.
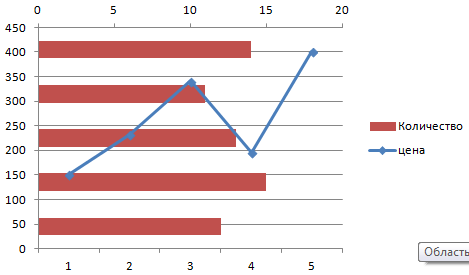
Переходим на новый лист (можно остаться и на этом – поставить курсор в свободную ячейку). «Вставка» — «Диаграмма» — «Точечная». Выбираем понравившийся тип. Щелкаем по области диаграммы правой кнопкой мыши – «Выбрать данные».
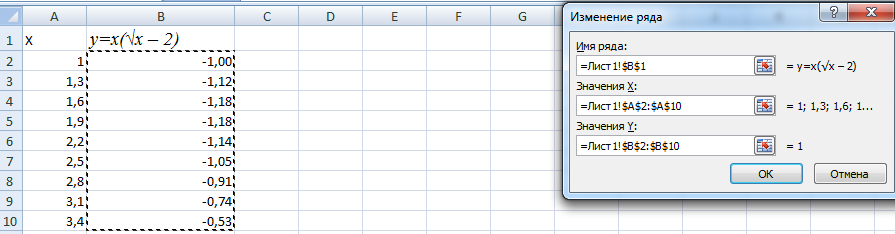
Выделяем значения Х (первый столбец). И нажимаем «Добавить». Открывается окно «Изменение ряда». Задаем имя ряда – функция. Значения Х – первый столбец таблицы с данными. Значения У – второй.
Жмем ОК и любуемся результатом.
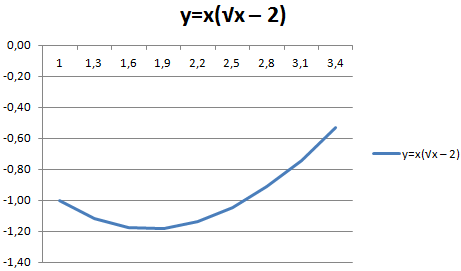
С осью У все в порядке. На оси Х нет значений. Проставлены только номера точек. Это нужно исправить. Необходимо подписать оси графика в excel. Правая кнопка мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». И выделяем диапазон с нужными значениями (в таблице с данными). График становится таким, каким должен быть.
Наложение и комбинирование графиков
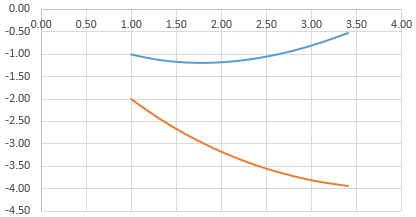
Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:
Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».
А вот наши 2 графика функций в одном поле.
Графики зависимости
Данные одного столбца (строки) зависят от данных другого столбца (строки).
Построить график зависимости одного столбца от другого в Excel можно так:
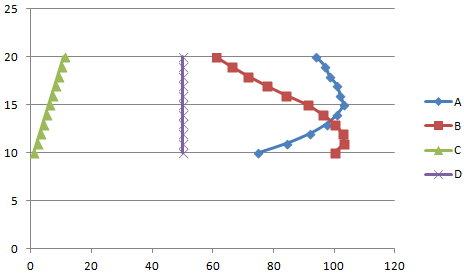
Условия: А = f (E); В = f (E); С = f (E); D = f (E).
Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.
Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.
Готовые примеры графиков и диаграмм в Excel скачать:
Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.
Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке [-3;3]. Называем столбец «х» , пишем первое значение «-3» , второе – «-2,5» . Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.
Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у» , для удобства можно вписать всю формулу. Выделяем ячейку В2 , ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6» . Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х» , в другом – рассчитаны значения для заданной функции.
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у» , переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная» . Выберите одну из предложенных видов.
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси» .
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений» , поставьте маркер в пункте «фиксированное» и впишите значение «0,5» .
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор» , «Макет» , «Формат» .
Построить график функции в Эксель можно и с помощью «Графика» . О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х» .
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные» .
В поле «Элементы легенды» кликаем на кнопочку «Добавить» .
Появится окно «Изменение ряда» . Поставьте курсор в поле «Имя ряда» и выделите ячейку С1 . Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК» .
Чтобы для первого графика в Легенде не было написано «Ряд 1» , выделите его и нажмите на кнопку «Изменить» .
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК» .
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1 , подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1» .
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Для рассмотренных выше задач удавалось построить уравнение или систему уравнений. Но во многих случаях при решении практических задач имеются лишь экспериментальные (результаты измерений, статистические, справочные, опытные) данные. По ним с определенной мерой близости пытаются восстановить эмпирическую формулу (уравнение), которая может быть использована для поиска решения, моделирования, оценки решений, прогнозов.
Процесс подбора эмпирической формулы P(x) для опытной зависимости F(x) называется аппроксимацией (сглаживанием). Для зависимостей с одним неизвестным в Excel используются графики, а для зависимостей со многими неизвестными – пары функций из группы Статистические ЛИНЕЙН и ТЕНДЕНЦИЯ, ЛГРФПРИБЛ и РОСТ .
В настоящем разделе рассматривается аппроксимация экспериментальных данных с помощью графиков Excel: на основе данных стоится график, к нему подбирается линия тренда, т.е. аппроксимирующая функция, которая с максимальной степенью близости приближается к опытной зависимости.
Степень близости подбираемой функции оценивается коэффициентом детерминации R 2 . Если нет других теоретических соображений, то выбирают функцию с коэффициентом R 2 , стремящимся к 1. Отметим, что подбор формул с использованием линии тренда позволяет установить как вид эмпирической формулы, так и определить численные значения неизвестных параметров.

1. Линейная – y=cx+b. Это простейшая функция, отражающая рост и убывание данных с постоянной скоростью.
2. Полиномиальная – y=c+c1x+c2x 2 +…+c6x 6 . Функция описывает попеременно возрастающие и убывающие данные. Полином 2-ой степени может иметь один экстремум (min или max), 3-ей степени – до 2-х экстремумов, 4-ой степени – до 3-х и т.д.
3. Логарифмическая – y=clnx+b. Эта функция описывает быстро возрастающие (убывающие) данные, которые затем стабилизируются.
4. Степенная – y=cx b , (х>0и y>0). Функция отражает данные с постоянно увеличивающейся (убывающей) скоростью роста.
5. Экспоненциальная – y=ce bx , (e – основание натурального логарифма). Функция описывает быстро растущие (убывающие) данные, которые затем стабилизируются.
Для всех 5-ти видов функций используется аппроксимация данных по методу наименьших квадратов (см. справку по F1 «линия тренда»).
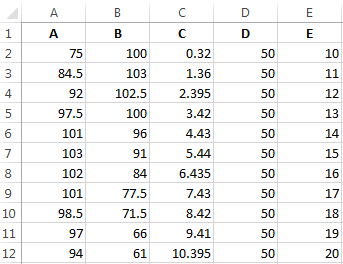
В качестве примера рассмотрим зависимость продаж от рекламы, заданную следующими статистическими данными по некоторой фирме:
| Реклама (тыс. руб.) | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 |
| Продажи (тыс. руб.) |
Необходимо построить функцию, наилучшим образом отражающую эту зависимость. Кроме того, необходимо оценить продажи для рекламных вложений в 6 тыс. руб.
Приступим к решению. В первую очередь введите эти данные в Excel и постройте график, как на рис. 38. Как видно, график построен на основании диапазона B2:J2. Далее, щелкнув правой кнопкой мыши по графику, добавьте линию тренда, как показано на рис. 38.

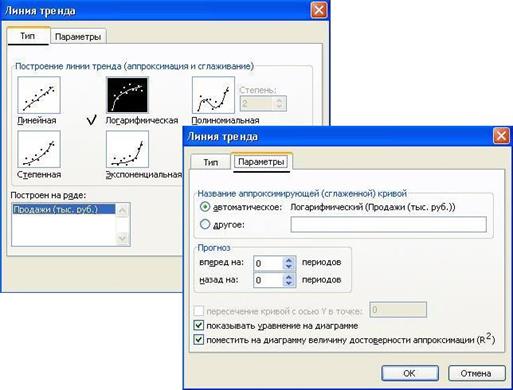
В открывшемся окне настройки (рис. 39), на закладке Тип выберите для аппроксимации логарифмическую линию тренда (по виду графика). На закладке Параметры установите флажки, отображающие на графике уравнение и коэффициент детерминации.
После нажатия ОК Вы получите результат, как на рис. 40. Коэффициент детерминации R 2 =0.9846, что является неплохой степенью близости. Для подтверждения правильности выбранной функции (поскольку других теоретических соображений нет) спрогнозируйте развитие продаж на 10 периодов вперед. Для этого щелкните правой кнопкой по линии тренда – измените формат – после этого в поле Прогноз: вперед на: установите 10 (рис. 41).
После установки прогноза Вы увидите изменение кривой графика на 10 периодов наблюдения вперед, как на рис. 42. Он с большой долей вероятности отражает дальнейшее увеличение продаж с увеличением рекламных вложений.
Вычисление по полученной формуле =237,96*LN(6)+5,9606 в Excel дает значение 432 тыс. руб.

Часть11. Контрольные задания
Последнее изменение этой страницы: 2016-08-26; Нарушение авторского права страницы
Как найти функцию по ее графику
Еще в школе мы подробно изучаем функции и строим их графики. Однако читать график функции и находить ее вид по готовому чертежу, нас, к сожалению, практически не учат. На самом деле, это совсем не сложно, если помнить несколько основных видов функций.Задача описания свойств функции по ее графику часто возникает при экспериментальных исследованиях. По графику можно определить промежутки возрастания и убывания функции, разрывы и экстремумы, а также можно видеть асимптоты.

Инструкция
Если графиком является прямая линия, проходящая через начало координат и образующая с осью ОX угол α (угол наклона прямой к положительной полуоси ОХ). Функция, описывающая эту прямую, будет иметь вид y = kx. Коэффициент пропорциональности k равен tg α. Если прямая проходит через 2-ю и 4-ю координатные четверти, то k < 0, и функция является убывающей, если через 1-ю и 3-ю, то k > 0 и функция возрастает.Пусть график представляет собой прямую линию, располагающуюся различным образом относительно осей координат. Это линейная функция, и она имеет вид y = kx + b, где переменные x и y стоят в первой степени, а k и b могут принимать как положительные, так и отрицательные значения или равны нулю. Прямая параллельна прямой y = kx и отсекает на оси ординат |b| единиц. Если прямая параллельна оси абсцисс, то k = 0, если оси ординат, то уравнение имеет вид x = const.
Кривая, состоящая из двух ветвей, располагающихся в разных четвертях и симметричных относительно начала координат, называется гиперболой. Этот график выражает обратную зависимость переменной y от x и описывается уравнением y = k/x. Здесь k ≠ 0 — коэффициент обратной пропорциональности. При этом если k > 0, функция убывает; если же k < 0 — функция возрастает. Таким образом, областью определения функции является вся числовая прямая, кроме x = 0. Ветви гиперболы приближаются к осям координат как к своим асимптотам. С уменьшением |k| ветки гиперболы все больше «вдавливаются» в координатные углы.
Квадратичная функция имеет вид y = ax2 + bx + с, где a, b и c – величины постоянные и a 0. При выполнении условия b = с = 0, уравнение функции выглядит, как y = ax2 (простейший случай квадратичной функции), а ее график является параболой, проходящей через начало координат. График функции y = ax2 + bx + с имеет ту же форму, что и простейший случай функции, однако ее вершина (точка пересечения параболы с осью OY) лежит не в начале координат.
Параболой является также график степенной функции, выраженной уравнением y = xⁿ, если n – любое четное число. Если n — любое нечетное число, график такой степенной функции будет иметь вид кубической параболы.
В случае, если n – любое отрицательное число, уравнение функции приобретает вид. Графиком функции при нечетном n будет гипербола, а при четном n их ветви будут симметричны относительно оси ОУ.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.