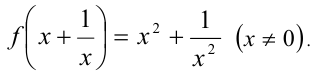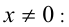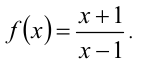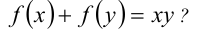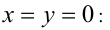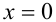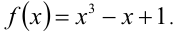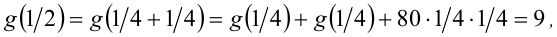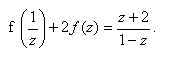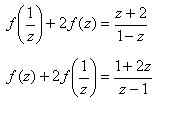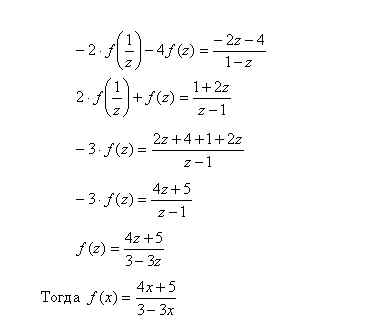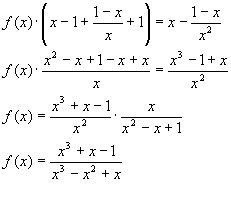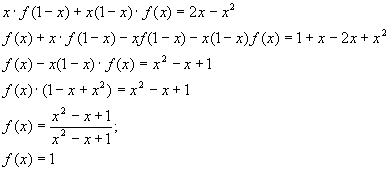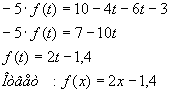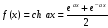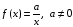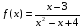Функциональные уравнения
Функциональным уравнением называется уравнение, в котором в роли неизвестного выступает функция (или функции). В этом случае решением уравнения является любая функция, при подстановке которой в уравнение оно превращается в тождество. Решить функциональное уравнение значит найти множество всех его решений. Например, дифференциальные уравнения являются частными случаями функциональных уравнений.
Один из основных методов решения функциональных уравнений — метод замены переменной (метод подстановки) [7].
Пример №396.
Решить уравнение
Решение:
Положив 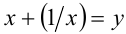
После перехода к новой переменной функциональное уравнение примет вид 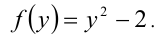
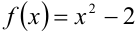
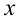
Однако необходимо сделать проверку найденного решения. Проверка нужна, в частности, по следующей причине: функция 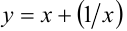
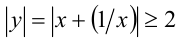
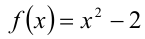
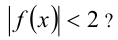
Полученное равенство, очевидно, выполняется при всех действительных 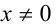
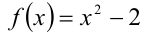
Пример №397.
Найти функцию 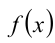
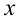
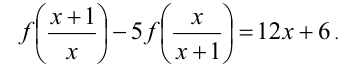
Решение:
ОДЗ: 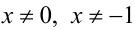
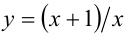
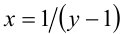
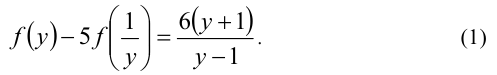
Если бы сделали замену 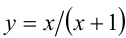
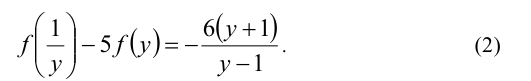
При этом оба равенства (1) и (2), согласно условию, выполняются при всех допустимых значениях 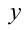
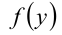
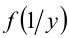
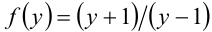
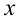
При решении функциональных уравнений нередко используется метод «от частного к общему». Рассмотрим примеры.
Пример №398.
Существует ли функция 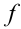
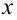
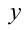
Решение:
Пользуясь тем, что 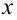
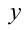
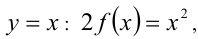
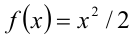
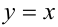
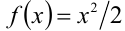
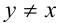
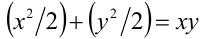
Пример №399.
Существуют ли функции 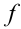
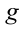
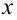
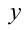
Решение:
Допустим, что такие функции 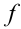
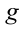
Теперь положим в нём 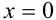
Наконец, положим в исходном равенстве 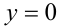
Перемножим два последних равенства:
Но в этом равенстве 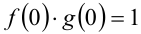
Сделаем проверку, подставив в исходное равенство:
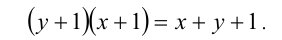
Очевидно, последнее равенство выполняется не при всех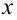
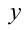
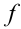
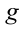
Пример №400.
Найти все функции 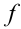
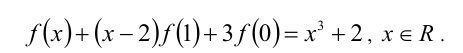
Решение:
Подставим в уравнение 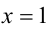
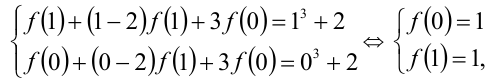
откуда получаем
Проверкой убеждаемся, что найденная функция удовлетворяет уравнению. Ответ:
В следующем примере требуется найти не саму функцию, удовлетворяющую заданному функциональному уравнению, а лишь её значение в некоторой точке. При решении необходимое значение последовательно выражается через другие (которые можно найти) значения этой функции.
Пример №401.
Числовая функция для всех действительных 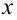
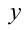
Найти 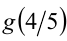
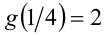
Решение:
откуда
Пусть 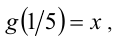
отсюда
Записывая цепочку соотношений
находим 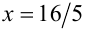
Общепризнано, что решение задач является
важнейшим средством формирования у школьников
системы основных математических знаний, умений и
навыков, ведущей формой учебной деятельности
учащихся в процессе учения математики, является
одним из основных средств их математического
развития.
Ориентируя школьников на поиски красивых,
изящных решений математических задач, учитель
тем самым способствует эстетическому воспитанию
учащихся и повышению их математической культуры.
И всё же главная цель задач — развить творческое и
математическое мышление учащихся,
заинтересовать их математикой, привести к
“открытию” математических фактов.
Достичь этой цели с помощью одних стандартных
задач невозможно. Необходимы задачи,
направленные на воспитание у учащихся
устойчивого интереса к изучению математики,
творческого отношения к учебной деятельности
математического характера. Необходимы
специальные упражнения для обучения школьников
способам самостоятельной деятельности, для
овладения ими методами научного познания
реальной действительности и приемами умственной
деятельности, которыми пользуются
ученые-математики, решая ту или иную задачу.
В данной статье речь идет о функциональных
уравнениях, о методах их решения. Функциональным
уравнением называется соотношение, выражающее
определённое свойство, которым обладает
некоторый класс функций (некоторая функция).
Простейшими примерами функциональных
уравнений могут служить : f(x) =f(- x) – уравнение
чётности, f(x+Т) = f(x) – уравнение периодичности и
др.
Функция f(x) называется решением данного
функционального уравнения, если она
удовлетворяет ему при всех значениях аргумента в
области её определения.
Например, функции f(x) = ax2,f(x)=sin2x, где aR, являются
частными решениями приведённых соответственно
выше уравнений, в чём убедимся подстановкой ах2=
а (-х)2.
Решить функциональное уравнение – значит
установить, имеет ли оно решения, и найти их, если
они имеются.
Приведем примеры решения функциональных
уравнений методом подстановки. Этот метод
заключается в том, что, применяя вместо х (или у)
различные подстановки и комбинируя полученные
уравнения с исходным, получаем (обычно путём
исключения) алгебраическое уравнение
относительно искомой функции.
Пример 1.
1) Пусть
2) Подставим в исходное уравнение, получим
3)Заменим z на
получим 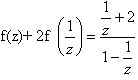
после преобразований в правой части уравнения:
4)Итак, получили два уравнения:
5)Умножим обе части 1-го уравнения на (-2) и сложим
со 2-ым уравнением, получим:
Пример 2. 2
1)Заменим в уравнении на
,
получим 2 .
2) Умножим обе части исходного уравнения 2 на (-2) и
сложим с уравнением 2 ,
получим:
.
Пример 3.
- Пусть
тогда
уравнение принимает вид:.
- Заменим в уравнении
на
,
получим.
- Умножим уравнение
на (-2) и сложим с уравнением
, получим
Таким образом,
Пример 4.
1) Заменим в уравнение на
,
.
2)Умножим уравнение на
и
вычтем из уравнения ,получим —
, где
Пример 5. 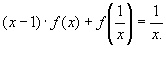
1)Заменим в уравнении на
получим .
2)Выразим из исходного уравнения , получим
или
.
3)Подставим в
уравнение ,
получим .
Выполним преобразования
Пример 6. .
- Заменим
на
, получим
- Умножим обе части уравнения
на
и вычтем из
уравнения
получим
Пример 7.
1)Пусть , тогда
уравнение принимает вид:
2)Пусть тогда
исходноеуравнение принимает вид:
3)Умножим обе части уравнения из п.1 на 2, а обе
части уравнения из п.2 на (-3) и почленно сложим
получившиеся уравнения:
Пример 8.
1) Заменим на
, получим
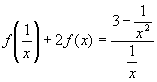
.
2)Умножим обе части уравнения из п.1 на (-2) и
сложим с исходным уравнением:
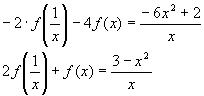
получаем :
Литература
- Кострикина Н.П. “Задачи повышенной трудности в
курсе алгебры 7-9 классов” — М: “Просвещение”,
1991г. - Смышляев В.К.. Практикум по решению задач
школьной математики. – М: “Просвещение”, 1978г.
Министерство образования и молодежной политики
Чувашской Республики
БОУ ДПО (ПК) С «Чувашский республиканский институт
образования»
Минобразования Чувашии
Кафедра математики и информационных технологий
Курсовая работа на тему:
« Функциональные уравнения. Методы их решения»
Выполнил (а): учитель математики МБОУ «СОШ № 60»
г. Чебоксары
Флегентова А.А.
Чебоксары, 2014
Содержание
Введение……………………………………………………….……………..……3
Глава 1. Понятие функционального уравнения …………………………………5
Глава 2. Практическая часть. Методы решения
функционального уравнения.9
Заключение……………………………………………………………………….24
Список литературы………………………………………………………………25
Приложения………………………………………………………………………26
Введение
Одно из важнейших
математических умений, которым должны овладеть учащиеся школы, — умение решать
уравнения. Корень уравнения находят в одно или более действий, многие текстовые
задачи решаются алгебраическим способом, в уравнении могут участвовать целые,
рациональные и другие числа, то есть уравнения одновременно сами по себе
являются задачами и способами решения задач, умение, решать, которые необходимы
всем учащимся школы. Но во время решения тренировочных заданий мне попалось
уравнение, которое я решить не смогла. Как я узнала позже от учителя, это было
функциональное уравнение.
Что же такое
функциональные уравнения? И какие способы их решения существуют? Эти вопросы
заинтересовали меня, и я решила провести исследование. функциональный
уравнение коши
Функциональными
уравнениями занимаются с очень давних пор, этому курсу так и не нашлось
достойного места в математических программах. А жаль. Ведь решение отдельных
функциональных уравнений требует достаточно глубокого понимания предмета и
прививает любовь к самостоятельной творческой работе. Так как эта тема в
школьном курсе не изучается в виду её сложности, при поступлении в престижные
ВУЗы, на олимпиадах, в части С ЕГЭ такие задачи встречаются.
В настоящее время
практически нет никаких пособий, обучающих решению функциональных уравнений.
Поэтому ощущается
потребность в пособии, которое на простых и конкретных примерах способно
показать читателю со скромной математической подготовкой весь арсенал
современных методов решения функциональных уравнений.
Цель работы —
выяснить, что является функциональным уравнением их системами, найти способы
решения и составить сборник задач для использования математическими классами.
Задачи
исследования:
1. изучение и
анализ литературы;
2. поиск способов
решения функциональных уравнений и их систем;
3. решение
функциональных уравнений
4. составление
сборника
Объект
исследования: функциональные уравнения
Предмет
исследования: изучение свойств и способов решения функциональных уравнений.
Структура:
введение, понятие функционального уравнения, сборник задач, заключение.
Глава 1. Понятие
функционального уравнения
Функциональное
уравнение – это уравнение, которое содержит одну или несколько неизвестных
функций (с заданными областями определения и значений). Решить функциональное
уравнение – это, значит, найти все функции, которые тождественно ему
удовлетворяют. Функциональные уравнения возникают в самых различных областях
математики, обычно в тех случаях, когда требуется описать все функции,
обладающие заданными свойствами. Термин функциональное уравнение обычно
используется для уравнений, несводимых простыми способами к алгебраическим
уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами
неизвестной функции в уравнении являются не сами независимые переменные, а
некоторые данные функции от них. Часто встречаются на различных математических
соревнованиях.
Некоторые
функциональные уравнения знакомы нам еще из школьного курса это
f(x) = f(-x), f(-x) =
— f(x), f(x+T) = f(x),
которые задают
такие свойства функций, как чётность, нечётность, периодичность.
Задача решения
функциональных уравнений является одной из самых старых в математическом
анализе. Они появились почти одновременно с зачатками теории функций. Первый
настоящий расцвет этой дисциплины связан с проблемой параллелограмма сил. Ещё в
1769 году Даламбер свёл обоснование закона сложения сил к решению
функционального уравнения
(1)
То же уравнение и
с той же целью было рассмотрено Пуассоном в 1804 году при некотором
предположении аналитичности, между тем как в 1821 году Коши (1789 – 1857) нашёл
общие решения
этого уравнения,
предполагая только непрерывность f(x).
Даже известная
формула неевклидовой геометрии для угла параллельности
была получена Н.
И. Лобачевским (1792 – 1856) из функционального уравнения
, (2)
которое он решил
методом, аналогичным методу Коши. Это уравнение можно привести к уравнению

Ряд
геометрических задач, приводящих к функциональным уравнениям, рассматривал
английский математик Ч. Баббедж (1792—1871). Он изучал, например, периодические
кривые второго порядка, определяемые следующим свойством для любой пары точек
кривой: если абсцисса второй точки равна ординате первой, то ордината второй
точки равна абсциссе первой. Пусть такая кривая является графиком функции у
= f(х); (х, f(х)) — произвольная ее точка. Тогда, согласно условию,
точка с абсциссой f(х) имеет ординату х. Следовательно,
(3)
Функциональному
уравнению (3) удовлетворяют, в частности, функции:
,
Одними из
простейших функциональных уравнений являются уравнения Коши
f(x+y) = f(x)+f(y), (4)
f(x+y) = f(x)·f(y), (5)
f(xy) = f(x)+f(y), (6)
f(xy) = f(x)·f(y), (7)
Эти уравнения
Коши подробно изучил в своём (Курсе Анализа), изданном в 1821 году. Непрерывные
решения этих четырёх основных уравнений имеют соответственно вид
,
,
,
В классе
разрывных функций могут быть и другие решения. Уравнение (4) ранее
рассматривалось Лежандром и Гауссом при выводе основной теоремы проективной
геометрии и при исследовании гауссовского закона распределения вероятностей.
Функциональное
уравнение (4) было опять применено Г. Дарбу к проблеме параллелограмма сил и к
основной теореме проективной геометрии; его главное достижение — значительное
ослабление предположений. Мы знаем, что функциональное уравнение Коши (4)
характеризует в классе непрерывных функций линейную однородную функцию f(x)
= ax. Дарбу же показал, что всякое решение, непрерывное хотя бы в одной
точке или же ограниченное сверху (или снизу) в произвольно малом интервале,
также должно иметь вид f(x) = ax. Дальнейшие результаты по ослаблению
предположений следовали быстро один за другим (интегрируемость, измеримость на
множестве положительной меры и даже мажорируемость измеримой функцией).
Возникает вопрос: существует ли хоть одна какая-нибудь аддитивная функция (т.
е. удовлетворяющая (4)), отличная от линейной однородной. Найти такую функцию
действительно нелегко! В ходе работы мы покажем, что при рациональных x
значения любой аддитивной функции должны совпадать со значениями некоторой
линейной однородной функции, т. е. f(x) = ax для x Q. Казалось бы, что тогда f(x)
= ax для всех действительных x. Если f(x) — непрерывна, то это
действительно так, если же данное предположение отбросить — то нет. Первый
пример отличного от f(x) = ax разрывного решения функционального
уравнения (4) построил в 1905 году немецкий математик Г. Гамель с помощью
введённого им базиса действительных чисел.
Многие
функциональные уравнения не определяют конкретную функцию, а задают широкий
класс функций, т. е. выражают свойство, характеризующее тот или иной класс
функций. Например, функциональное уравнение f(x+1) = f(x) характеризует
класс функций, имеющих период 1, а уравнение f(1+x) = f(1-x) — класс
функций, симметричных относительно прямой x = 1, и т. д.
Глава 2. Практическая часть. Методы решения
функционального уравнения
Простейшие
функциональные уравнения
1. Пусть функция
у =f(х) возрастает на R. Решите:
а) уравнение f(3х
+ 2) = f(4х2 + х);
б) неравенство
f(3х – 48) ≤ f(-х2 + х).
Решение:
а) f(3х + 2) =
f(4х2 + х)
Есть такая
теорема: если функция возрастает на промежутке Х, то каждое своё значение она
принимает, а единственной точке. Поэтому,
3х+2 = 4х2
+ х;
4х2 -2х-2=0;
2х2 –x-1=0;
х1=1 и
х2= -0,5
Ответ: х1=1
и х2= -0,5.
б) f(3х – 48) ≤
f(-х2 + х);
3х-48 ≤ -х2
+ х;
х2 +
2х – 48 ≤ 0;
х1=6 и
х2= -8:
Ответ: [-8;6].
2. Пусть функция
у =f(х) убывает на R. Решите неравенство f(2x-3)>f(х+2)
Решение:
Решаем также как
и в предыдущем задании, только меняем знак у неравенства, так как функция
убывает на R.
2х-3<x+2;
x<5
Ответ: (-∞; 5).
Решение
функциональных уравнений методом подстановки
Заменяя
некоторые переменные функционального уравнения либо конкретными значениями,
либо какими-либо другими выражениями пытаемся либо упростить это уравнение,
либо привести его к такому виду, что дальнейшее решение станет очевидным.
Особенность применяемого метода как раз и состоит в том, что в ряде случаев он
позволяет отыскать решения в классе всевозможных функций.
1. Найдите все функции,
определённые на множестве , удовлетворяющие соотношению
Решение
Придадим x значение
. Получим
Отсюда
.
Получим систему

Из уравнения (1)
выразим и
подставим в уравнение (2).
;
;
Отсюда
;
;
.
Проверим,
действительно ли функция f(x) удовлетворяет уравнению
.
x=x — верно.
Ответ: .
Решение:
1) Пусть
2) Подставим в
исходное уравнение, получим
3)Заменим z на получим или
после преобразований в правой части уравнения:
4)Итак, получили
два уравнения:
5)Умножим обе
части 1-го уравнения на (-2) и сложим со 2-ым уравнением, получим:
3.Пусть — некоторое действительное число. Найти
функцию f(x), определённую для всех x ≠ 1 и удовлетворяющую уравнению

где g
– заданная функция, определённая при x ≠ 1.
Решение:
При замене
получаем
систему

решением
которой при a2 ≠ 1 является функция
Ответ:
4. Найти решение системы функциональных уравнений относительно
неизвестных функций f(x) и g(x):
Решение:
В первом уравнении сделаем подстановку 2x = 1/z.
При
этом
и
первое уравнение принимает вид:
Или
В
результате получаем систему уравнений:
решение
которой g(x) = 1/x, f(x) = x+1.
Ответ:
g(x) = 1/x, f(x) = x+1.
5. Найдите все
функции f: R à R, которые при всех х, у € R удовлетворяют уравнению
f(х+у)=х+уf(х)+(1-х)у.
(1)
Решение: Пусть f-
функция удовлетворяющая (1). Поскольку (1) выполняется при всех значениях
переменных х и у, то оно будет выполнятся и при конкретных значениях этих
переменных. Подставив, например, у равное 0 в исходное уравнение, мы получим f(х)=х.
Это равенство должно выполнятся при любом действительном х. Таким образом, (1)
=> f(х)≡х является решением функционального уравнения (1). Непосредственная
проверка показывает, что найденная функция действительно удовлетворяет
уравнению при всех х,у € R.
6. Найдите все
функции f: R à R, которые при всех х, у € R удовлетворяют уравнению
f(х+у)=х+уf(х)+(1-sin
х)у (1)
Решение: точно
также как и в предыдущей задаче, устанавливаем, что для функции f, которая
удовлетворяет (2), должно выполнятся тождество f(х)≡х. Однако, подставив
функцию f(х)=х в (1), мы тождества не получим. Поскольку никакие другие функции
также не могут быть решениями (1), то данное уравнение решений не имеет.
7. Найдите все
функции f: R à R, которые при всех х, у € R удовлетворяют уравнению
f(х+у2+2у+1)
= у4+4у3+2ху2+5у2+4ху+2у+х2+х+1
(1)
Решение:
поскольку мы хотим получить значение f(х), попробуем избавится от слагаемого у2+2у+1
под знаком функции. Уравнение у2+2у+1=0 имеет одно решение у=-1.
Подставляя у= -1 в (1) получаем f(х)= х2-х+1 .
Ответ: f(х)= х2-х+1
8. Найдите все
функции f: R à R, которые при всех х, у € R удовлетворяют уравнению
f((х2+6х+6)у)=у2х4+12у2х3+48у2х2-4ух2+72у2х-24ух+36у2-24
(1)
Решение: Как и в
прошлой задаче, мы хотим получить под знаком функции свободную переменную (х
или у). В данном случае, очевидно, проще получить у. Решив уравнение х2+6х+6)у=0
относительно х получаем х1= -1, х2= -5. Подстановка любого
из этих значений в (1) дает нам f(у)=у2-4у.
Решение функциональных
уравнений методом Коши
1. Найдите
функцию ,
определённую на множестве натуральных чисел, удовлетворяющую условию
, где d — некоторое
действительное число.
Решение:
Будем решать это
уравнение по схеме, которая в математике называется методом Коши.
1. Найдём
выражения для Получим
,
,
.
2. Этот
“эксперимент” подсказывает, что , где
.
3. Проверим,
действительно ли выполняется равенство
,
где . Применим
для доказательства метод математической индукции.
1. Проверим,
выполняется ли равенство при x=1 : — верно.
2. Предположим,
что равенство верно при , где
, т.е.
— верно.
3. Докажем, что
из этого следует равенство для x=n. Т.к. , то при x=n получим
или
;
.
Значит, равенство
верно для любого натурального n . Таким образом, решением заданного
функционального уравнения будет функция , где f(1)- произвольное число.
2. Найдите все
непрерывные функции, удовлетворяющие условию
.
Решение:
Будем находить
решение функционального уравнения постепенно, т.е. сначала найдём его решение,
если является натуральным числом, затем – целым, потом рациональным и, наконец,
— действительным.
1. Пусть y=x.
Тогда .
2. При , получим
,
, …
3. Докажем
методом математической индукции, что при натуральных значениях (докажите это
самостоятельно) . (1)
4. При x=1 получим
.
— постоянное
число. Обозначим его через . Значит, для
, имеем
.
5. Положим в
равенстве
(1) , где
, получим
. Отсюда
или
.
Обозначив
через , получим
.
Значит, при
положительном и рациональном x мы получим
.
Предполагая, что
функция —
непрерывна, получим
,
При
,
.
6. Возьмём в
равенстве .
Получим
.
Отсюда .
1. Возьмём в этом равенстве
.
Получим
или
. Т.к.
, то
,
т.е. .
Итак, для любого
действительного решением уравнения будет функция
.
Ответ:
— уравнение называется
уравнением Коши.
3. Найдите
непрерывные функции , удовлетворяющие условию
. (1)
Решение:
Попробуем свести
это уравнение к функциональному уравнению Коши
с непрерывным
решением
.
Пусть у=0 , тогда
.
Так как — постоянное
число, обозначим его через и получим
.
Придадим теперь х
значение .
Получим
.
Из уравнения (1)
получим
или
(2).
Решением
уравнения (1) является функция
.
Значит, решением
уравнения (2) будет функция
.
Ответ:
4. Найдите все непрерывные решения уравнений Коши:
a) f
(хy) = f(x) + f(y) (x, y € R {0});
б) f(x + y) = f(xy)
(x, y€ R);
в) f(x + y) = f(x)f(y)
(x, y€. R).
Решение:
a)
Пусть
вначале x > 0. Положим
g(x) = f(eх).
Тогда
g(x + y) =
f(eх+у) = f(eхeу) = f(eх) + f(eу)
=g(x) + g(y), т. е. g(x)
удовлетворяет аддитивному уравнению Коши. Так как eх и f(x)
непрерывны, то и g(x) непрерывна и имеет вид cx, где c- константа. Тогда f(x)
имеет вид c ln x.
В частности,
f(1) = 0.
Положив
x = y = —1,
получаем
f(1) = 2f(—1),
откуда
f(—1) = 0.
Для произвольного x < 0 получаем
f(x) = f(—x) + f(—1) = f(—x).
Отсюда
f(x) = c ln
|x|
для произвольного
x ≠ 0.
б) Положив
y = 0,
получаем
f(x) = f(0),
т.е. f(x) ≡ const.
Очевидно, что любая константа подходит.
в) Если
f(x) = 0
для некоторого x,
то
f(z) = f(x)f(z—x) = 0
для любого z. В противном случае функция, будучи непрерывной, всюду имеет
один и тот же знак. Так как
f(2x) = (f(x))2,
то этот знак положителен и можно рассмотреть непрерывную
функцию
g(x) := lnf(x).
Имеем g(x+y) = ln(f(x)f(y)) = ln f(x)+ln f(y) = g(x)+g(y),
т.е. выполнено аддитивное уравнение Коши. Отсюда g(x) = cx для некоторого
c, и
f(x) = eсх.
Таким образом, либо
f(x)≡ 0, либо f(x) ≡есх.
Использование значений
функции в некоторых точках
Иногда бывает
невозможно найти подстановку, которая бы значительно упрощала бы вид уравнения.
Однако, если зафиксировать одну из свободных переменных, некоторые члены
уравнения могут также оказаться фиксированными. Для них можно ввести удобные
обозначения и использовать при решении как обычные константы. Если эти
константы войдут в ответ, проверка покажет, какие их значения являются
допустимыми.
1. Решить уравнение
f(x+f(y))=xy
Решение:
подстановка
у=0
даёт
f(x+f(0))=0.
На первый взгляд
пользы мало, так как мы не знаем, чему равно f(0). Обозначим f(0)=с, тогда
получаем f(х+с)=0. сделав замену переменной t=x+c (подстановка х=t-c), получаем
f(е)=0, но такая функция, очевидно, не удовлетворяет исходному уравнению,
поэтому решений нет.
2. Решить уравнение
f(x+f(y))=x+у
Решение: Снова
сделаем подстановку у=0 и обозначим с=f(0), получим f(х+с)=х. Замена t=х+с дает
f(t)=t-c. Несмотря, на то, что точное значение с нам известно, мы уже знаем,
что лишь функция вида f(х)=х-с, где c=const, могут удовлетворять уравнению при
всех х,у. чтобы найти с, подставим найденную функцию в исходное
уравнение(заодно таким образом сделаем проверку):
f(x+f(y))=f(x+(y-c))=(x+(y-c))-c=
x+y-2c.
Отсюда видим, что
равенство
f(x+f(y))=x+у
для всех х,у при
с равном 0 и только при нем. Поэтому ответ f(x)=x.
Ответ: f(x)=x.
Уравнение
относительно
Найти все f: R à R такие, что (f(x))2 = 1
Решение: Рассматривая это как уравнение относительно неизвестного f(х),
получаем
f(x) =
1;
f(x) =
-1
Может показаться, что ответом будут две функции,
f(х)=1, f(х)=-1.
Однако, это не так. Рассмотрим, например функцию
-1 х<0
1, х≥0
Несложно видеть, что данная функция удовлетворяет уравнению. Какой же
смысл придать совокупности? Поскольку исходное равенство должно выполнятся для
всех х€ R, то есть для каждого х имеет место одно из равенств. Однако, неверным
будет предположение, что одно из равенств выполняется сразу для всех х. Как мы
увидели на примере, для одних х может выполнятся одно из равенств, а для других
– другое. Попробуем охарактеризовать множество функций, задаваемое уравнением.
Пусть А – множество тех х, для которых выполнено первое равенство. Тогда для
всех остальных х должно быть выполнено второе. Мы видим, что множество А однозначно
задает функцию f:
Ответ:
E(f) =
{+-1}, где Е(f)
обозначает множество значений f.
Графическое
решение функционального уравнения. При каких а и b для функции
f(х)=a|x-b|
+3a|x-b |
выполнено условие
при всех действительных
х : f(х)=f(f(х))
?
Решение:
1.
При а=0
функция f(х)=0, и уравнение, очевидно, удовлетворяется.
пусть а>0,
тогда при больших х>0 функция
f(х)=а(х-b)+3a(x-b
)=4ax-a(b+3b )>0
По рис.1
определяем, что возможно только равенство f(х)=х, если значения х достаточно
велики и х>0. Конкретно, х>max{b;b }.
Следовательно,
возможные значения для параметров a и b определяются из системы:
Которая имеет два
решения:

При а=1/4, b=-1/3
получаем функцию
Ее график (рис.2)
является графическим решением уравнения
f(х)=f(f(х))
2.
Теперь
предположим, что а<0, тогда при больших по абсолютной величине и х<0.
Конкретно, х<b.
Следовательно,
возможные значения для параметров а и b определяются из системы
Которая имеет два
решения

Если
a=-1/4, b=0,
то функция
f(х)=-|х|
удовлетворяет
уравнению
f(х)=f(f(х))
Если a=-1/4,
b=-1/3, тогда получаем функцию
А вот ее график (рис.
3) не является графическим решением уравнения f(х)=f(f(х)).
Ответ: 


Заключение
В
данной работе были рассмотрены функциональные уравнения и некоторые способы их
решения. В ходе работы мы убедились, что функциональные уравнения – это общий
класс уравнений, в которых искомой является некоторая функция. К функциональным
уравнениям по существу относятся дифференциальные уравнения, интегральные
уравнения, уравнения в конечных разностях. Под функциональным уравнением в
узком смысле слова понимают уравнения, в которых искомые функции связаны с
известными функциями одного или нескольких переменных при помощи операции
образования сложной функции. Функциональное уравнение можно также рассматривать
как выражение свойства, характеризующего тот или иной класс функций.
Список
литературы
1.
Андреев А.А., Кузьмин Ю.Н.., Савин А.Н., Саушкин И.Н.
Функциональные уравнения. – Самара: В мире науки, 1999
2.
Бродский
Я. С., Слипенко А. К. Функциональные уравнения. – К.: Вища школа. Головное
издательство, 1983. – 96 с
3.
Ильин
В.А. Методы решения функциональных уравнений // Соросовский образовательный
журнал, 2001, № 2, с. 116 – 120
4.
Лихтарников
Л.М. Элементарное введение в функциональные уравнения.– СПб.: Лань, 1997. – 160
с
5.
Фихтенгольц
Г.М. Курс дифференциального и интегрального исчисления. В 3-х томах: том 1. –
М.: Наука, 1968, c. 157 – 162
6.
Сабитов
К.Б. Функциональные, дифференциальные и интегральные уравнения.М.:’’Высшая
школа’’,2005,с.190199
Размещено
на Allbest.ru
ПРИЛОЖЕНИЯ
Рис.1
Рис.2
Рис.3
Размещено на Allbest.ru
Содержание
Введение…………………………………………………………………………………………………….3
1.Функциональные уравнения. Их свойства и методы решения……………………5
1.1 Определение и примеры функциональных уравнений…………………………….5
1.2 Методы решения функциональных уравнений……………………………………….8
2. Решение функциональных уравнений Коши на множестве Q рациональных чисел………………………………………………………………………………………………………..13
2.1 Решение уравнения вида f(x+y)=f(x)+f(y) на Q……………………………………..13
2.2 Решение уравнения вида f(x+y)=f(x)∙f(y) на Q………………………………………15
2.3 Решение уравнения вида f(x∙y)=f(x)+f(y) на Q………………………………………17
2.4 Решение уравнения вида f(x∙y)=f(x)∙f(y) на Q………………………………………..19
3. Решение функциональных уравнений Коши на R…………………………………..22
3.1 Решение уравнения вида f(x+y)=f(x)+f(y) на оси R……………………………….22
3.2 Решение уравнения вида f(x+y)=f(x)∙f(y) на оси R…………………………………23
4. Решение функциональных уравнений Коши в измеримых функциях………25
5. Класс уравнений типа Коши………………………………………………………………….27
Заключение……………………………………………………………………………………………….29
Список использованных источников………………………………………………………….30
Введение
Курсовая работа посвящена изучению функциональных уравнений, весьма общему классу уравнений, в которых искомой является некоторая функция.
К функциональным уравнениям по существу относятся дифференциальные уравнения, интегральные уравнения, уравнения в конечных разностях; следует, однако, отметить, что название функциональные уравнения обычно не относят к уравнениям этих типов. Под функциональными уравнениями в узком смысле слова понимают уравнения, в которых искомые функции связаны с известными функциями одного или нескольких переменных при помощи операции образования сложной функции. Функциональные уравнения можно также рассматривать как выражение свойства, характеризующего тот или иной класс функций.
Функциональное уравнение — это уравнение, в котором неизвестными являются функции (одна или несколько). Например,
f(x)+xf(x+1) = 1
Некоторые функциональные уравнения знакомы нам еще из школьного курса это f(x) = f(-x), f(-x) = — f(x), f(x+T) = f(x), которые задают такие свойства функций, как чётность, нечётность, периодичность.
Задача решения функциональных уравнений является одной из самых старых в математическом анализе. Они появились почти одновременно с зачатками теории функций. Первый настоящий расцвет этой дисциплины связан с проблемой параллелограмма сил. Ещё в 1769 году Даламбер свёл обоснование закона сложения сил к решению функционального уравнения
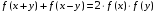
То же уравнение и с той же целью было рассмотрено Пуассоном в 1804 году при некотором предположении аналитичности, между тем как в 1821 году Коши (1789 – 1857) нашёл общие решения
Ряд геометрических задач, приводящих к функциональным уравнениям, рассматривал английский математик Ч. Баббедж (1792—1871). Он изучал, например, периодические кривые второго порядка, определяемые следующим свойством для любой пары точек кривой: если абсцисса второй точки равна ординате первой, то ордината второй точки равна абсциссе первой. Пусть такая кривая является графиком функции у = f(х); (х, f(х)) — произвольная ее точка. Тогда, согласно условию, точка с абсциссой f(х) имеет ординату х. Следовательно,
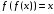
Функциональному уравнению (2) удовлетворяют, в частности, функции: 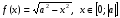
1. Функциональные уравнения. Их свойства и методы решения
1.1 Определение и примеры функциональных уравнений
Функциональные уравнения — весьма общий класс уравнений, в которых искомой является некоторая функция. К функциональным уравнениям, по существу, относятся дифференциальные уравнения, интегральные уравнения, уравнения в конечных разностях. Следует, однако, отметить, что название «функциональные уравнения» обычно не относят к уравнениям этих типов. Под функциональными уравнениями в узком смысле слова понимают уравнения, в которых искомые функции связаны с известными функциями одного или нескольких переменных при помощи операции образования сложной функции. Функциональные уравнения можно также рассматривать как выражение свойства, характеризующего тот или иной класс функций.
Например, функциональное уравнение f (x) = f (-x) характеризует класс чётных функций, функциональное уравнение f(-x) = -f(x) – класс нечетных; функциональное уравнение f (x + 1) = f (x) — класс функций, имеющих период 1, и т.д.
Одним из простейших функциональных уравнений является уравнение
f (x + у) = f (x) + f (y).
Непрерывные решения этого функционального уравнения имеют вид:
f (x) = Cx.
Однако в классе разрывных функций это функциональное уравнение имеет и иные решения. С рассмотренным функциональным уравнением связаны
f (x + у) = f (x) f (y),
f (xy) = f (x) + f (y),
f (xy) = f (x) f (y),
непрерывные решения которых имеют соответственно вид eCx, C∙lnx, xa (x 0).
Т.о., эти функциональные уравнения могут служить для определения показательной, логарифмической и степенной функций. В теории аналитических функций функциональные уравнения часто применяются для введения новых классов функций.
Например, двоякопериодические функции характеризуются функциональными уравнениями:
f (z + а) = f (z) и f (z + b) = f (z),
автоморфные функции — функциональными уравнениями:
f (saz) = f (z),
где {sa} — некоторая группа дробно-линейных преобразований.
Если функция известна в некоторой области, то знание для неё функционального уравнения позволяет расширить область определения этой функции. Например, функциональное уравнение f (x + 1) = f (x) для периодических функций позволяет определить их значение в любой точке по значениям на отрезке [0, 1]. Этим часто пользуются для аналитического продолжения функций комплексного переменного. Например, пользуясь функциональным уравнением Г (z + 1) = z∙Г (z) и зная значения гамма-функции Г(z) в полосе 0 Re z
Условия симметрии, имеющиеся в какой-либо физической задаче, обусловливают определённые законы преобразования решений этой задачи при тех или иных преобразованиях координат. Этим определяются функциональные уравнения, которым должно удовлетворять решение данной задачи. Значение соответствующих функциональных уравнений во многих случаях облегчает нахождение решений.
Решения функциональных уравнений могут быть как конкретными функциями, так и классами функций, зависящими от произвольных параметров или произвольных функций.
Для некоторых функциональных уравнений общее решение может быть найдено, если известны одно или несколько его частных решений. Например, общее решение функционального уравнения
f (x) = f (ax)
имеет вид
j(w(x)),
где j(x) — произвольная функция, а w(x) — частное решение этого функционального уравнения
Для решения функциональных уравнений их во многих случаях сводят к дифференциальным уравнениям. Этот метод даёт лишь решения, принадлежащие классу дифференцируемых функций.
Другим методом решения функциональных уравнений является метод итераций. Этот метод даёт, например, решение уравнения Абеля:
f [a(x)] = f (x) + 1,
где a(x) — заданная функция и связанного с ним уравнения Шрёдера:
f [a(x)] = c f (x).
А. Н. Коркин доказал, что если a(х) — аналитическая функция, то уравнение Абеля имеет аналитическое решение. Эти результаты, нашедшие применение в теории групп Ли, привели в дальнейшем к созданию теории итераций аналитических функций. В некоторых случаях уравнение Абеля решается в конечном виде [1].
1.2 Методы решения функциональных уравнений
Методы решения – методы нахождения точных или приближенных решений функциональных конкретных или абстрактных уравнений, т.е. уравнения вида
P(x)=y, (1.1)
где P(x) – некоторый, вообще говоря нелинейный оператор, переводящий элементы пространства X типа В (или другого типа) в элементы пространства Y того же типа. Точные решения в виде аналитических выражений получаются лишь для немногих типов функциональных уравнений, поэтому особое значение имеют приближенные методы решения.
Для нахождения решений общих функциональных уравнений развит ряд методов, например, метод бесконечных степенных рядов, метод последовательных приближений, метод Галеркина (метод моментов), метод касательных гипербол, метод Чебышева (касательных парабол), метод Ньютона–Канторовича и его модификации, метод наискорейшего спуска и др., а также методы вариации параметра (прямые, итерационные и комбинированные) определенных типов и их различные модификации, в том числе и с последовательной аппроксимацией обратного оператора. Общие методы применяются к решению различных конкретных функциональных уравнений математического анализа.
Кроме того, существуют специальные методы решения конкретных функциональных уравнений, в том числе и численные методы, например, метод сеток и др. Метод вариации параметра, метод Ньютона-Канторовича и некоторые другие из указанных методов имеют также и теоретическое значение, так как с их помощью можно делать заключение о существовании, единственности и области расположения решения функционального уравнения, не находя самого решения, что подчас не менее важно, чем фактическое значение решения. Ниже рассмотрим несколько методов решения.
-
Метод подстановок:
Пусть, например, имеется функциональное уравнение:
f (x + y) + f (x – y)=2∙f (x)∙cos y (1.2)
Применяя последовательно подстановки
x=0, y=t; x=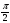
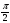
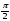
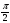
из (1.2) получают соответственно уравнения
f(t) + f(-t) = 2a cos t, f(π + t) + f(t )= 0
и
f(π + t) + f(-t)= 2b cos(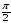
где обозначено f(0) = a, f(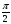
H [ f(x + y), f(x – y), f(x), x, y ] = 0
при некоторых предположениях относительно функции Н. К уравнениям других типов применяются различные другие подстановки.
Метод подстановок применяется и для сведения одних функциональных уравнений к другим уравнениям того же типа, в частности к функциональным уравнениям с известными решениями. Например, функциональное уравнение
f((x + y)/2) = f(x)/2 + f(y)/2 (1.3)
может быть приведено к функциональному уравнению Коши
f (x + y) = f(x) + f(y) (1.4)
с непрерывным решением f(x)=Cx. С этой целью в (1.3) подставляют x+y вместо х и 0 вместо у:
f((x + y)/2) = f(x +у)/2 + а/2 , где a=f(0)
Сравнивая это с исходным функциональным уравнением (1.3) получают функциональное уравнение вида f (x + y) = f(x) + f(y) – а, откуда φ(x+y)= φ(x)+ φ(y), φ(x)=f(x)-a и φ(x) = Сх. Решением является функция f(x) = Cx+a.
Для сведения к другим функциональным уравнениям того же типа применяют также логарифмирование и другие приемы. Например, решение функционального уравнения
f (x + y) = f (x) ∙ f (y) (1.5)
путем логарифмирования можно свести к решению уравнения (1.4).
b) Метод замены переменной:
Для того чтобы проиллюстрировать этот метод рассмотрим уравнение:

Предположим, что существует функция f(x), удовлетворяющая данному уравнению. Заменив x на 1-x, получим
Из (1.6) находим 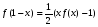
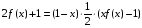
В рассмотренном уравнении под знаком уравнении под знаком неизвестной функции стоят функции f1=x и f2=1-x. Замена x на 1-x переводит функции f1 и f2 друг в друга. В результате замены переменной получено еще одно уравнение, содержащие f(x) и f(1-x). Решение функционального уравнения сводится к решению системы двух линейных уравнений с двумя неизвестными.
Рассмотрим еще одно уравнение:
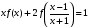
Выполним замену х→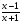
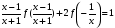
появилось новое «неизвестное» выражение 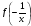

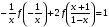
Кроме 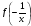

. И получаем уравнение
(1.10)
построена система линейных уравнений (1.7)-(1.10) с четырьмя неизвестными . Последовательно исключая переменные, получим
.
c) Метод решения функциональных уравнений с помощью понятия группы
Пусть в функциональном уравнении
a1f(g1)+a2f(g2)+…+anf(gn)=b (1.11)
выражения, стоящие под знаком неизвестной функции f(x) являются элементами группы G, состоящей из n функций: g1(x)=x, g2(x),…gn(x), причем коэффициенты уравнения (1.11) a1, a2, …an, b – некоторые функции от x. Предположим, что уравнение (1.11) имеет решение. Заменим x→g2(x). В результате последовательность функций g1(x), g2(x),…gn(x), перейдет в последовательность g1º g2, g2º g2,…gnº g2, состоящую из всех элементов группы.
Поэтому «неизвестные» f(g1), f(g2),… f(gn), переставятся и мы получим новое линейное уравнение того же вида, что и (1.11), далее заменим x→g3(x),… x→gn(x), после чего получим систему из n линейных уравнений, которую следует решить. Если решения есть, то проверкой нужно убедиться в том, что они удовлетворяют уравнению.
Группой называется множество G функций, обладающее следующими свойствами:
-
Для любых двух функций
и
их композиция
также принадлежит G.
-
Функция e(x)=x принадлежит G.
-
Для всякой функции
существует обратная функция f-1, которая также принадлежит G.
Из важных методов решения функциональных и функционально-дифференциальных уравнений следует отметить также метод дифференцирования, метод приведения к билинейному функциональному уравнению, метод «исключения» аргумента.
2. Решение функциональных уравнений коши на множестве q рациональных чисел
В нижеследующей главе будут рассмотрены функциональные уравнения
f (x + у) = f (x) + f (y), f (x + у) = f (x) f (y),
f (xy) = f (x) + f (y), f (xy) = f (x) f (y),
для функций, заданных на множестве рациональных чисел Q.
Впервые эти уравнения были рассмотрены Огюстеном Луи Коши, который и дал их решения в непрерывных функциях. Далее сформулируем и докажем четыре теоремы.
2.1 Решение уравнений вида f(x+y)=f(x)+f(y) на Q
Теорема 2.1. Если функция f(t), заданная для всех значений t Q удовлетворяет уравнению
f (x + у) = f (x) + f (y), (2.1)
тождественно относительно х и у, то она имеет вид f(t) = Ct. Где C — постоянное число.
Доказательство:
►Прежде всего, с помощью метода математической индукции легко обобщить соотношение (2.1) на случай любого числа (=n) слагаемых :
(2.2)
Действительно, если допустить его верность для какого-либо числа (n ≥ 2) слагаемых , то оно окажется верным и для n + 1 слагаемых:
Полагая в (2.2) x=y=…=z, найдем:
f(nx)=n∙f(x) (2.3)
Заменив здесь n на , получим
(2.4)
а затем, если подставить mx (m-натуральное) вместо х и использовать предыдущее равенство, придем к соотношению
(2.5)
Положим теперь в основном уравнении (2.1) x=y=0; получим
f(0)=2f(0), так что f(0)=0. (2.6)
Если же взять y=-x, то, с учетом (3.7), найдем:
f(-x) = — f(x)
так что функция f(x) меняет знак при изменении знака x. А тогда из (2.3) и (2.5) легко вывести:
f(-nx)=-f(nx)= -n∙f(x) (2.7)
и, аналогично, вообще
(2.8)
Полученные соотношения (2.3) – (2.8) могут быть объединены в равенстве f(rx)=r∙f(x) справедливом для любого вещественного значения x, каково бы ни было рациональное число r.
Если здесь взять х=1, и обозначить f(1)=C, то получим
f®=Cr. (2.9)
Теорема доказана. ▲ [4]
Таким образом, мы установили вид функции f , принадлежащей классу функций, заданных на Q (). При этом мы использовали только тот факт, что функция удовлетворяет условию (2.1).
2.2 Решение уравнений вида f(x+y)=f(x) ∙ f(y) на Q
Следующей задачей будет нахождение всех заданных на Q функций f(x), удовлетворяющих условию:
f(x+y)=f(x)∙f(y), (2.10)
каковы бы ни были значения х и у. Уравнение (2.10) выражает общеизвестное правило умножения степеней:
Теорема 2.2. Если функция f(t), заданная для всех значений t Q удовлетворяет уравнению
f (x + у) = f (x)∙f (y),
тождественно относительно х и у, то она имеет вид f(t) = аt, где а — неотрицательная постоянная. Доказательство:
►C помощью метода математической индукции легко обобщить соотношение (2.10) на случай любого числа (=n) слагаемых :
(2.11)
Действительно, если допустить его верность для какого-либо числа (n ≥ 2) слагаемых, то оно окажется верным и для n + 1 слагаемых
Полагая в (2.2) x=y=…=z, найдем:
f(nx)= f(x)n (2.12)
Заменив здесь n на , получим
(2.13)
а затем, если подставить mx (m-натуральное) вместо х и использовать предыдущее равенство, придем к соотношению
(2.14)
Положим теперь в основном уравнении (2.1) x=x, y=0; получим
f(x+0)= f(x)∙f(0),
так что
f(0)=1. (2.15)
Если же взять y=-x, то, с учетом (2.15), найдем:
1= f(0) = f(x—x)=f(x) ∙f(-x) ,
откуда
(2.16)
А тогда из (2.14) и (2.16) легко вывести:
(2.17)
и, аналогично, вообще
(2.18)
Полученные соотношения (2.14) — (2.18) могут быть объединены в равенстве
f(rx)= f(x)r
справедливом для любого рационального значения x, каково бы ни было рациональное число r.
Если здесь взять х=1, и обозначить f(1)=a, то получим
f(r)=ar. (2.19)
Теорема доказана.▲
Таким образом, мы установили вид функции f, принадлежащей классу функций, заданных на Q (). При этом мы использовали только тот факт, что функция удовлетворяет условию (2.10).
2.3 Решение уравнений вида f(x∙y)=f(x)+ f(y) на Q
Функциональное уравнение
f(xy) = f(x)+f(y). (2.20)
Есть запись логарифмирования произведения:
Теорема 2.3. Если функция f(t), заданная для всех положительных значений tQ, притом не сводящаяся к нулю, удовлетворяет уравнению (2.20) тождественно относительно всех положительных значений х и у, то она имеет вид f(t)=logat, где а — положительная постоянная.
Доказательство:
►Как и в двух предыдущих случаях, воспользуемся методом математической индукции. Обобщим соотношение (2.20) на случай любого числа (=n) переменных :
(2.21)
Действительно, если допустить его верность для какого-либо числа (n ≥ 2) сомножителей , то оно окажется верным и для n + 1 сомножителей :
Полагая в (2.21) x=y=…=z, найдем:
f(xn)= n∙f(x) (2.22)
Заменив здесь n на , получим
(2.23)
а затем, если подставить mx (m-натуральное) вместо х и использовать предыдущее равенство, придем к соотношению
(2.24)
Положим теперь в основном уравнении (2.20) x=x, y=1; получим
f(x∙1)= f(x)+f(1),
так что f(1)=0. (2.25)
Если же взять y=, то, с учетом (2.25), найдем:
0= f(1) = f(x)=f(x)+f(
) ,
откуда (2.26)
А тогда из (2.24) и (2.26) легко вывести:
(2.27)
и, аналогично, вообще
(2.28)
Полученные соотношения (2.23) — (2.28) могут быть объединены в равенстве
f(xr)=r∙f(x) (2.29)
справедливом для любого положительного рационального значения x, каково бы ни было рациональное число r.
Рассмотрим равенство (2.29) при натуральных значениях r и положительных рациональных значениях x:
Не нарушая общности, можно записать x в виде , где a0, a≠1 тогда для целого r можно записать:
и переписать равенство (2.29) в виде:
f()=r∙f(
) (2.30)
введем функцию φ(t)=f(at) на всей области определения функции f(x), тогда (2.30) примет вид:
φ(t+t+…+t)=φ(r∙t)=r∙φ(t) (2.31)
функция φ(t) очевидно удовлетворяет уравнению (2.3), а значит и 2.1. то есть
φ(t) = Сt.
φ(log a t) = С log a t, тогда
f(a log a t) = С log a t и окончательно:
f(t)= С log a t (2.32)
Теорема доказана. ▲
Таким образом, мы установили вид функции f , принадлежащей классу функций, заданных на Q () и удовлетворяющей (2.20)
2.4 Решение уравнений вида f(x∙y)=f(x) ∙ f(y) на Q
Наконец, рассмотрим функциональное уравнение
f(x∙y) = f(x) ∙ f(y). (2.33)
(при рациональных положительных x и y), это ничто иное, как правило возведения в степень произведения двух чисел:
,
Теорема 2.4. Если функция f(t), заданная для всех положительных значений tQ , притом не сводящаяся к нулю, удовлетворяет уравнению (2.33) тождественно относительно всех положительных значений х и у, то она имеет вид f(t)=tμ, где μ — постоянное число.
Доказательство:
►Воспользуемся методом математической индукции. Обобщить соотношение (2.33) на случай любого числа (=n) переменных :
(2.34)
Действительно, если допустить его верность для какого-либо числа (n ≥ 2) сомножителей , то оно окажется верным и для n + 1 сомножителей :
Полагая в (2.21) x=y=…=z, найдем:
f(xn)= f(x)n (2.35)
Заменив здесь n на , получим
(2.36)
а затем, если подставить mx (m-натуральное) вместо х и использовать предыдущее равенство, придем к соотношению
(2.37)
Положим теперь в основном уравнении (2.33) x=x, y=1; получим f(x∙1)= f(x)∙f(1), так что f(1)=1. (2.38)
Если же взять y=, то, с учетом (2.38), найдем:
1= f(1) = f(x)=f(x)∙f(
), откуда
(2.39)
А тогда из (2.37) и (2.39) легко вывести:
(2.40)
и, аналогично, вообще
(2.41)
Полученные соотношения (2.36) – (2.41) могут быть объединены в равенстве
f(xr)=f(x)r (2.42)
В самом деле, если дана определенная положительных для хQ функция f(x), удовлетворяющая условию (2.33), то прибегнув к той же подстановке,
, где a0, a≠1 тогда для целого r можно записать:
и переписать равенство (2.29) в виде:
f()=
(2.43)
введем функцию φ(t)=f(at) на всей области определения функции f(x), тогда (2.30) примет вид:
φ(t+t+…+t)=φ(r∙t)= φ(t)r (2.44)
функция φ(t) очевидно удовлетворяет уравнению (2.12), а значит и 2.10. то есть
φ(t) = ct.
φ(log a t) = c log a t, тогда
f(a log a t) = c=
и окончательно:
f(t)= =tμ (2.45)
(если положить μ=loga c), что и требовалось доказать. ▲[2][3]
Таким образом, мы установили вид функции f , принадлежащей классу функций, заданных на Q () и удовлетворяющей (2.33)
3. Решение функциональных уравнений коши на R
Полученные в предыдущей главе результаты, могут быть продолжены для функций, непрерывных на всей числовой оси R.
Если в дополнение к функциональным уравнениям (2.1), (2.10), потребовать еще и непрерывности, то формулировки и доказательства теорем (2.1-2.2) несколько изменятся (даже упростятся), результат же (то есть сами решения уравнений) останется тем же.
Покажем это, решив уравнения.
3.1 Решение уравнений вида f(x+y)=f(x)+f(y) на оси R
Найти все непрерывные в промежутке (-∞, +∞) функции f(x), удовлетворяющие условию:
f(x+y)=f(x)+f(y), (3.1)
каковы бы ни были значения х и у.
Легко видеть, что линейные однородные функции вида
f(x)=c∙x (c=const) (3.2)
удовлетворяют этому уравнению:
с(x+y)=cx+cy,
Для того чтобы установить, что это единственные непрерывные функции, удовлетворяющие (3.1), предположим, что некоторая непрерывная функция f(x) удовлетворяет (3.1), покажем, что она непременно имеет вид (3.2).
Теорема 3.1. Если функция f(t), заданная и непрерывная для всех значений t (— ∞; + ∞). Удовлетворяет уравнению (3.1) тождественно относительно х и у, то она имеет вид f(t) = Ct. Где C — постоянное число.
Доказательство:
►По Теореме 2.1 функция f , принадлежащей классу разрывных функций () и удовлетворяющая условию (3.1), имеет вид f®=cr ,
Пусть теперь s будет любое иррациональное значение аргумента. Легко построить стремящуюся к нему последовательность рациональных чисел.
R1, r2, …, rn, …
(можно, например, взять отрезки соответствующей бесконечной десятичной дроби).
F(rn)=crn (n=1,2,3…)
Перейдем к пределу при n→+∞; справа получим cs, слева же, именно ввиду предположенной непрерывности функции f, получится
lim f(rn)=f(s),
так что окончательно,
f(s)=cs.▲
Таким образом, действительно, наша функция при всех вещественных значениях аргумента выражается формулой (3.2). Эта формула дает решение уравнения (3.1) в классе непрерывных функций.
3.2 Решение уравнений вида f(x+y)=f(x) ∙f(y) на оси R
Найти все непрерывные в промежутке (-∞, +∞) функции f(x), удовлетворяющие условию:
f(x+y)=f(x)∙f(y), (3.3)
каковы бы ни были значения х и у.
Оказывается, что функциональным свойством (3.3), вместе со свойством непрерывности, вполне определяется показательная функция
f(x)=а x (a 0) (3.4)
Точнее говоря, единственной функцией, определенной и непрерывной во всем промежутке (-∞, +∞) и удовлетворяющей в нем условию (3.3), является показательная функция (если не считать функции тождественно равной 0).
Иными словами, формула (3.4) – за указанным исключением – дает самое общее решение функционального уравнения (3.3) в непрерывных функциях.
Теорема 3.2. Если функция f(t), заданная и непрерывная для всех значений t (— ∞; + ∞). удовлетворяет уравнению (3.3) тождественно относительно х и у, то она имеет вид f(t) = аt, где а — неотрицательная постоянная.
Доказательство:
►Для доказательства этого рассмотрим произвольную функцию f(x), Определенную и непрерывную при всех х, удовлетворяющую условию (3.3). Исключается тривиальный случай, когда f(x)≡0.
Итак, при некотором значении x=x0 эта функция отлична от 0. Полагая в (3.3) y=x0-x, получим
f(x)∙f(x0—x) = f(x0) ≠ 0;
отсюда ясно, что f(x) отлично от нуля при всяком x. Более того, заменяя в (3.3) x и y через , найдем:
,
так что f(x) всегда строго положительна.
Пользуясь этим, прологарифмируем равенство (3.3), например, по натуральному основанию е:
ln f(x+y) = ln f(x)+ln f(y).
Если положить
φ(x) = ln f(x),
то φ(x) есть непрерывная функция (как результат суперпозиции непрерывных) и удовлетворяющая условию:
φ (x+y) = φ (x)+ φ (y),
аналогичному (3.1). В таком случае, как мы установили, необходимо
φ(x) = ln f(x) = cx (c=const)
откуда, наконец,
f(x)=ecx=ax
(если положить a=ec), что и требовалось доказать. ▲
Таким образом, мы показали, что уравнения f(x+y)=f(x)+f(y) и f(x+y)=f(x)∙f(y), имеют одинаковые решения среди функций, определенных на множестве рациональных чисел и на множестве всех действительных чисел. Эти решения имеют вид: f(x)=C∙x и f(x)=ax соответственно.
4. Решение функциональных уравнений Коши в измеримых функциях
Для того чтобы рассматривать решения уравнений коши на множестве измеримых функций, дадим несколько необходимых определений:
Определение 1: Пусть X – множество, на котором задана σ-аддитивная мера μ, определенная на σ-алгебре Gμ. Действительная функция f(x) на X называется μ-измеримой, если для всякого борелевского множества А числовой прямой
f-1(A).
Иначе: функцию f(x) называют измеримой, если все множества {x:f(x)c} измеримы при любом действительном с.
Важнейшие свойства измеримых функций:
-
Измеримая функция от измеримой функции есть измеримая функция.
-
Сумма, разность, произведение двух измеримых функций измеримы.
-
Частное двух измеримых функций, при условии, что знаменатель не обращается в нуль, тоже измеримо.
-
Предел сходящейся при каждом
последовательности измеримых функций измерим
-
Функция f(x), определенная на некотором измеримом множестве Е и эквивалентная на нем некоторой измеримой функции g(x), тоже измерима (функции называют эквивалентными, если μ{x:f(x)≠g(x)}=0).
Определение измеримой функции, данное в начале главы, относится к функциям на произвольных множествах и в общем случае никак не связано с понятием непрерывной функции. Однако, если речь идет о функциях на отрезке, то имеет место следующая важная теорема, установленная в 1913 г. Н.Н. Лузиным.
Теорема 5.1. (Теорема Лузина). Для того, чтобы функция f(x), заданная на отрезке [a, b], была измерима, необходимо и достаточно, чтобы для любого ε 0, существовала такая непрерывная на [a, b] функция φ(x), что
μ{x : f(x) ≠ φ (x)} ε.
С помощью свойств измеримых функций и воспользовавшись теоремой Лузина, будем искать решения функциональных уравнений Коши в классе измеримых функций.
5. Класс уравнений типа Коши
Сделаем далее еще одно обобщение. Классические функциональные уравнения Коши f(x+y)=f(x)+f(y), f(x+y)=f(x)∙f(y), f(x∙y)=f(x)+f(y), f(x∙y)=f(x)∙f(y), имеющие непрерывные решения соответственно с∙x, , с∙lnx, xс, связывают основные смежные (в смысле распределительного закона) арифметические операции сложения + и умножения ∙ .
Указаны примыкающие к ним: «снизу» — операция xy = ln(ex+ey), «сверху» — операция x
y=e(lnx∙lny). Все эти операции являются звеньями «естественной цепи арифметических операций»
, в которой +=
0, ∙ =
+1, так что
+1=
+2 (и вообще
). Их связывает класс функциональных уравнений типа Коши (название указывает на связь различных арифметических операций)
где m,n – целые числа. Решения некоторых уравнений (с малыми индексами) таковы:
|
m |
n |
Решение |
m |
n |
Решение |
|
-1 |
-2 |
|
+1 |
-2 |
|
|
-1 |
-1 |
|
+1 |
-1 |
|
|
-1 |
0 |
|
+1 |
0 |
|
|
-1 |
+1 |
|
+1 |
+1 |
|
|
-1 |
+2 |
|
+1 |
+2 |
|
|
0 |
-2 |
|
+2 |
-2 |
|
|
0 |
-1 |
|
+2 |
-1 |
|
|
0 |
0 |
|
+2 |
0 |
|
|
0 |
+1 |
|
+2 |
+1 |
|
|
0 |
+2 |
|
+2 |
+2 |
|
Наблюдающиеся здесь закономерности справедливы в общем случае.
Заключение
В данной работе, посвященной решению некоторых функциональных уравнений, был рассмотрен важнейший класс уравнений – класс уравнений Коши.
Были приведены некоторые методы решения функциональных уравнений, с помощью которых впоследствии были решены важнейшие функциональные уравнения элементарной математики,
f(x+у) = f (x) + f (y),
f (x + у) = f (x) f (y),
f (xy) = f (x) + (y),
f (xy) = f (x) f (y),
показано, что найденные решения могут служить для определения функции f(x)=Cx, а также показательной, логарифмической, степенной функций.
Утверждения были сформулированы в виде теорем для функций, определенных на Q, функций непрерывных на R, а также для любых измеримых функций. Все теоремы были доказаны и сделан вывод о том что решения имеют один и тот же вид для функций, определенных на Q, функций непрерывных на R, а также для любых измеримых функций.
Было приведено также важное обобщение свойств уравнений типа Коши.
Список использованных источников
1. Лихтарников Л.М. Элементарное введение в функциональные уравнения СПб. :Лань1997. —160 с.
2. Функциональные уравнения. Квант, 1985.— № 7.
3. Фихтенгольц, Г. М., Курс дифференциального и интегрального исчисления. Т.1. М. : Наука, 1970.—616 с.
4. Колмогоров, А. Н., Фомин, С. В. Элементы теории функций и функционального анализа. М.: Физматлит, 2006. – 572 с.
5. Блюмин, С. Л. Класс уравнений типа Коши / Научный журнал «Фундаментальные исследования»// Российская Академия Естествознания [Электронный ресурс]. – Электрон. журн. – 2008. – №2 – Режим доступа: http://www.rae.ru
14
Эта трилогия статьей будет посвящена функциональным уравнениям. В данной статье попытаемся понять что такое функциональное уравнение и с чем его едят. В следующих статьях рассмотрим конкретные методы решения более сложных функциональных уравнений(метод подстановок, и подобное).
Функциональное уравнение — уравнение, связующее значение функции в одной точке с её значениями в других точках.
Другими словами, в функциональных уравнениях место неизвестного занимает функция. Для примера, рассмотрим такое функциональное уравнение:
$$display$$2f(x)=2$$display$$ Тут интуитивно хочется разделить обе части уравнения на 2, что сработает и мы узнаем ответ: $$display$$2f(x)=2 Rightarrow f(x)=1$$display$$ Значит ответом на функциональное уравнение может быть только значение f(x), или похожее (это обычно указывают в условии задачи).
Рассмотрим некое функциональное уравнение, где с обоих сторон будут стоят функции. $$display$$4f(x)=2f(x)+2x Rightarrow 2f(x)=f(x)+x Rightarrow f(x)=x$$display$$ Стоит отметить что функция всегда имеет под собой число ($inline$f(x)=x+2, f(1)=3, f(5)=7$inline$, а значит можно производить над ними арифметические операции. Давайте рассмотрим функциональное уравнение из двумя переменными. Задание: найти все функции $inline$f: mathbb{R} rightarrow mathbb{R}$inline$ для каких $inline$4f(x+y)=f(x)+f(y)+2$inline$. В случаях из двумя переменными необходимо припустить что $inline$x=y=0$inline$, из этого мы узнаем значение $inline$f(0)$inline$.
$inline$x=y=0$inline$
$inline$4f(0)=2f(0)+2$inline$
$inline$2f(0)=2 Rightarrow f(0)=1$inline$
Узнав значение $inline$f(0)$inline$, приравниваем $inline$y$inline$ к нулю. Таким образом узнаем значение $inline$f(x)$inline$
$inline$y=0$inline$
$inline$4f(x)=f(x)+f(0)+2$inline$
$inline$3f(x) = 3 Rightarrow f($inline$f(x)=kx$inline$x)=1 $inline$
Ответ: $inline$ f(x)=1 $inline$
При такого вида уравнениях обязательно необходимо предполагать что $inline$x=y=0$inline$, но не всегда $inline$x=0vee y=0$inline$. Существуют такие аналоги как: $inline$x=y, x=f(y), …$inline$. К примеру, $inline$4f(x-y)=f(x)+f(y)+2$inline$. Подставляем $inline$x=y=0$inline$, получаем $inline$4f(0)=2f(0)+2 Rightarrow f(0)=1$inline$, тогда $inline$x=y$inline$ значит $inline$4f(0)=2f(x)+2$inline$, разделим обе части уравнения на 2 получим что $inline$2f(0)=f(x)+1 Rightarrow f(x)=1+2f(0) Rightarrow f(x)=3$inline$, произведем проверку, которая показывает что $inline$f(x)=3$inline$ есть решением данного функционального уравнения.
Теорема 1. Функциональное уравнение Коши $inline$f(x+y)=f(x)+f(y)$inline$ удовлетворяют все линейные функции вида $inline$f(x)=kx$inline$ (1)
Теорема 2. Функциональное уравнение $inline$f(x+y)=f(x)f(y)$inline$ удовлетворяют все показательные функции вида $inline$f(x)=k^{x}$inline$ (2)
Теорема 3. Функциональное уравнение $inline$f(xy)=f(x)+f(y)$inline$ удовлетворяют все логарифмические функции вида $inline$f(x)=log_k (x)$inline$ (3)
Теорема 4. Функциональное уравнение $inline$f(xy)=f(x)f(y)$inline$ удовлетворяют все степенные функции вида $inline$f(x)=x^{k}$inline$ (4)
Доведем их.
$$display$$(1) f(x+y)=a(x+y), f(x)+f(y) = ax+ay Rightarrow f(x+y)=f(x)+f(y)$$display$$
$$display$$(2) f(x+y)=a^{x+y}, f(x)f(y) = a^{x}a^{y} Rightarrow f(x+y)=f(x)f(y)$$display$$
$$display$$(3) f(xy)=log_a (xy), f(x)+f(y)=log_a(x)+log_a(y) Rightarrow f(xy)=f(x)+f(y)$$display$$
$$display$$(4) f(xy)=(xy)^{a}, f(x)f(y) = x^{a}y^{a} Rightarrow f(xy)=f(x)f(y)$$display$$
Теорема 5. Уравнения Йенсена $inline$f(frac{x+y}{2})=frac{f(x)+f(y)}{2}, f(x)=kx+b$inline$, доводиться аналогично предыдущим.
Рассмотрим такую задачу: Найдите все линейные функции вида $inline$f(x)=ax, $inline$$inline$f: mathbb{R} rightarrow mathbb{R}$inline$ для которых правильно $inline$4(f(x-y)+f(x+y)+1)=2f(x)+f(y-1)$inline$.
Решение
Воспользуемся теоремой 1.
$inline$4(f(x-y)+f(x+y)+1) = 4(f(x)-f(y)+f(x)-f(y)+1) = 4$inline$
$inline$4=2f(x)+f(y-1)$inline$
Тут ключевой момент. Нельзя подставлять $inline$x=y=0$inline$, так как ничего не получиться. Необходимо подставить $inline$x=0, y=x+1$inline$, тогда мы сможем узнать $inline$f(0)$inline$.
$$display$$4=2f(0)+f(0) Rightarrow 4=3f(0) Rightarrow f(0)=frac{4}{3}$$display$$. Тогда подставляем $inline$x=y-1$inline$, и получаем $inline$4=2f(x)+f(x) Rightarrow 4=3f(x) Rightarrow f(x)=frac{4}{3}$inline$
Ответ: $inline$f(x)=frac{4}{3}$inline$