Как найти формулу по алгебры

Оглавление:

• Формулы сокращенного умножения
• Квадратное уравнение и формула разложения квадратного трехчлена на множители
• Свойства степеней и корней
• Формулы с логарифмами
• Арифметическая прогрессия
• Геометрическая прогрессия
• Тригонометрия
• Тригонометрические уравнения
• Геометрия на плоскости (планиметрия)
• Геометрия в пространстве (стереометрия)
• Координаты
• Таблица умножения
• Таблица квадратов двухзначных чисел
• Расширенная PDF версия документа «Все главные формулы по школьной математике»

Формулы сокращенного умножения

К оглавлению…

Квадрат суммы:

Квадрат разности:

Разность квадратов:

Разность кубов:

Сумма кубов:

Куб суммы:

Куб разности:

Последние две формулы также часто удобно использовать в виде:

Квадратное уравнение и формула разложения квадратного трехчлена на множители

К оглавлению…

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

Парабола

График параболы задается квадратичной функцией:

При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:

Игрек вершины параболы:

Свойства степеней и корней

К оглавлению…

Основные свойства степеней:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.

Основные свойства математических корней:

Для арифметических корней:

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:

Для корня четной степени имеется следующее свойство:

Формулы с логарифмами

К оглавлению…

Определение логарифма:

Определение логарифма можно записать и другим способом:

Свойства логарифмов:

Логарифм произведения:

Логарифм дроби:

Вынесение степени за знак логарифма:

Другие полезные свойства логарифмов:

Арифметическая прогрессия

К оглавлению…

Формулы n-го члена арифметической прогрессии:

Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:

Геометрическая прогрессия

К оглавлению…

Формулы n-го члена геометрической прогрессии:

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

Тригонометрия

К оглавлению…

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Формулы двойного угла

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Тригонометрические формулы преобразования произведения в сумму

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формулы половинного угла

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

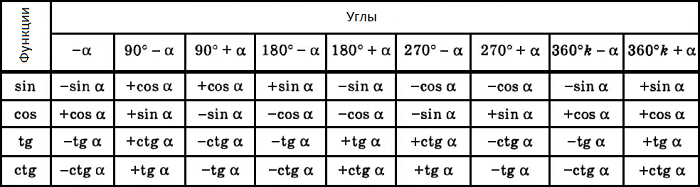
Тригонометрические формулы приведения

Формулы приведения задаются в виде таблицы:

Тригонометрическая окружность

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

Тригонометрические уравнения

К оглавлению…

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:

Для остальных тригонометрических функций запись однозначна. Для косинуса:

Для тангенса:

Для котангенса:

Решение тригонометрических уравнений в некоторых частных случаях:

Геометрия на плоскости (планиметрия)

К оглавлению…

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Формула медианы:

Свойство биссектрисы:

Формулы биссектрисы:

Основное свойство высот треугольника:

Формула высоты:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Длина средней линии трапеции:

Площадь трапеции:

Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Площадь прямоугольника через две смежные стороны:

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):

Свойство касательных:

Свойство хорды:

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

Геометрия в пространстве (стереометрия)

К оглавлению…

Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара:

Площадь поверхности шара (или, другими словами, площадь сферы):

Координаты

К оглавлению…

Длина отрезка на координатной оси:

Длина отрезка на координатной плоскости:

Длина отрезка в трёхмерной системе координат:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):

Таблица умножения

К оглавлению…

Таблица квадратов двухзначных чисел

К оглавлению…

Расширенная PDF версия документа «Все главные формулы по школьной математике»:

К оглавлению…

Algebra Formulas are the basic formulas that are used to simplify algebraic expressions. Algebraic Formulas form the basis to solve various complex problems. Algebraic Formulas are helpful in solving algebraic equations, quadratic equations, polynomials, trigonometry equations, probability questions, and others.

Algebra Formulas – Identities

An identity is an equation that is true in every sense for any values assigned to the variables. Algebraic Identities are used to solve various equations. For Algebraic Identities, L.H.S is always equal to R.H.S.

Algebraic Identities

Some important algebraic identities are

(a + b)2	a2 + b2 + 2ab
(a – b)2	a2 + b2 – 2ab
(a + b)(a – b)	a2 – b2
(x + a)(x + b)	x2 + 2(a + b) + ab

What are Algebra Formulas?

Algebraic formulas are equations that require algebraic expression on both sides of “equal to” i.e. both on LHS and RHS. Algebraic formulas are generally true for all the values. Algebraic Formula simplifies algebraic equations and is required to solve various problems in mathematics. Algebraic formulas for various classes are discussed below in this article.

Algebra Formulas for Class 8

Algebra formulas for class 8 are discussed below in this article. For three variables a, b, and c the various algebraic formulas are:

• (a + b)² = a² + 2ab + b²
• (a – b)² = a² – 2ab + b²
• (a + b)(a – b) = a² – b²
• (a + b)³ = a³ + 3a²b + 3ab² + b³
• (a – b)³ = a³ – 3a²b + 3ab² – b³
• a³ + b³ = (a + b)(a² – ab + b²)
• a³ – b³ = (a – b)(a² + ab + b²)
• (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca

Algebra Formulas for Class 9

For class 9 Logarithms formulas are very useful. They are helpful for the computation of highly complex problems of multiplication and division. The exponential form of 3² = 9 can easily be transformed into logarithmic form as log₃ 9 = 2. Also, complex multiplication and division can easily be converted to addition and subtraction by following the logarithmic formulas. 

Important log algebraic formulas that are most commonly used are discussed below:

• log_a (xy) = log_a x + log_a y
• log_a (x/y) = log_a x – log_a y
• log_a x^m = m log_a x
• log_a a = 1
• log_a 1 = 0

Law of Exponent

Exponents are ways to represent higher power. Laws of exponent are used to solve problems with the higher power. Some of the common laws of exponents with the same bases having different powers, and different bases having the same power, are useful to solve complex exponential terms. The higher exponential values can be easily solved without any expansion of the exponential terms. These exponential laws are further useful to derive some of the logarithmic laws.

• a^m× aⁿ = a^{m + n}
• a^m/aⁿ = a^{m – n}
• (a^m)ⁿ = a^mn
• (ab)^m = a^m× b^m
• a⁰ = 1
• a^-m = 1/a^m

Algebra Formulas for Class 10

“Quadratic Formula” is an important algebraic formula that is introduced to students in class 10. It is used for solving general quadratic equations. The general form of any quadratic equation is ax² + bx + c = 0, where x is variable a, b is coefficient and c is constant. There are two ways of solving this quadratic equation. 

• Solution using Algebraic Method
• Using Quadratic Formula

Other important formulas used in class 10 are

Formulas for Arithmetic Sequence

For any given arithmetic sequence {a, a + d, a + 2d, …}

• nth term, a_n = a + (n – 1) d
• Sum of the first n terms, S_n = n/2 [2a + (n – 1) d]

Formulas for Geometric Sequence

For any given geometric sequence {a, ar, ar², …}

• nth term, a_n = a rⁿ – 1
• Sum of the first n terms, S_n = a (1 – rⁿ) / (1 – r)
• Sum of infinite terms when r<1, S = a / (1 – r)

Algebra Formulas for Class 11

Algebra Formulas for Class 11 which are mostly used are formulas of permutations and combinations. If different arrangements of r things from the n available things are required then permutation formulas are used, whereas combinations formulas are used for finding the different groups of r things from n available things. 

The important permutation and combination formulas are,

Factorial Formula: 

n! = n × (n – 1) × (n – 2) × … × 3 × 2 × 1

Permutation Formulas:

ⁿP_r = n! / (n – r)!

Combination Formula:

ⁿC_r = n!/[r!(n−r)!]

Binomial Theorem is another formula that is of the utmost importance for students in class 11.

Algebra Formulas for Class 12

The important formulas for students in class 12 include vector algebra formulas. These formulas are discussed below,

Take any three vectors, a, b and c then,

• For vector a = x i+y j+z k, then magnitude of |a| =√(x²+y²+z²).
• Unit vector along a is a / |a|
• Dot product of two vectors a and b is defined as a ⋅ b = |a| |b| cos θ
  where θ is the angle between the vectors a and b.
• Cross product of vectors a and b is defined as a × b = |a| |b| sin θ
  where θ is the angle between the vectors a and b.
• Scalar Triple Product of three vectors a, b, and c are given by [a b c ] = a ⋅ (b × c) = (a × b) ⋅ c.

Also, Check

• Algebraic Identities of Polynomials
• Vector Algebra
• Percentage Formula

Solved Examples on Algebra Formulas

Example 1: Find out the value of the term, (2x + 3)² using algebraic formulae.

Solution:

Using the algebraic formula,

(a + b)² = a² + b² + 2ab

(2x + 3)² = (2x)² + 3² + 2 × 2x × 3

(2x + 3)² = 4x² + 9 + 12x

Example 2: Find out the value of the term, (5x – 3y)² using algebraic formulae.

Solution:

Using the algebraic formula,

(a – b)² = a² + b² – 2ab

(5x – 3y)² = (5x)² + (3y)² – 2 × 5x × 3y

(5 – 3)² = 25x² + 9y² – 30xy

Example 3: Find out the value of, 105×95 using algebraic formulae.

Solution:

Using the algebraic formula,

(a + b)(a – b) = a² – b²

105×95 = (100+5)(100-5)
             = 100² – 5²
             = 10000 – 25
             = 9975

Example 4: Find the roots of the quadratic equation x²+6x+8=0 using algebra formulas for quadratic equations.

Solution:

Given quadratic equation is x² + 6x + 8 = 0

Comparing above equation with ax²+bx+c=0, a=1, b=6, c=8 

Substituting the values in the quadratic formula we get,

x = [−b ± √(b² − 4ac)] / 2a
   = [−6 ± √(6² − 4(1)(8))] / 2(1)
   = [−6 ± √(36 − 4(1)(8))] / 2
   = [−6 ± √(36 − 32)] / 2
   = [−6 ± √4] / 2
   = (-6 + 2) / 2 and (-6 – 2) / 2
   = -4/2 and -8/2
   = -2 and -4

Thus, the values of x are -2 and -4

FAQs on Algebra Formulas

Question 1: What is the formula for a² – b² in Algebra?

Answer:

The formula for a²– b² defined in algebra is 

a²– b² = (a+b)(a-b)

This formula is also called the difference of squares formula.

Question 2: What are Algebraic Expressions?

Answer:

Algebraic expressions are combinations of variables and constants using arithmetic operations such as Addition, Subtraction, Multiplication, and Division. 

Example: 11 x³ + 5x is an algebraic expression. This expression has two terms 11 x³ and 5x.

Question 3: What are the three basic Algebra Formulas?

Answer:

The three basic formulas of Algebra are:

• (a + b)² = a² + b² + 2ab
• (a – b)² = a² + b² – 2ab
• (a + b)(a – b) = a² – b²

Question 4: Write the simplified form of (a+b)².

Answer:

(a+b)² can be written in simplified form as  (a²+ 2ab + b²)

Все главные формулы в математике

Формулы сокращенного умножения

Квадрат суммы:

Квадрат разности:

Разность квадратов:

Разность кубов:

Сумма кубов:

Куб суммы:

Куб разности:

Последние две формулы также часто
удобно использовать в виде:

Квадратное
уравнение и формула разложения
квадратного трехчлена на множители

Пусть квадратное уравнение имеет
вид:

Тогда дискриминант находят
по формуле:

Если D >
0, то квадратное
уравнение имеет два корня, которые
находят по формуле:

Если D =
0, то квадратное
уравнение имеет один корень (его
кратность: 2), который
ищется по формуле:

Если D <
0, то квадратное уравнение не имеет
корней. В случае когда квадратное
уравнение имеет два корня,
соответствующий квадратный
трехчлен может быть разложен на
множители по следующей формуле:

Если
квадратное уравнение имеет один корень,
то разложение
соответствующего квадратного трехчлена
на множители задается следующей формулой:

Только в
случае если квадратное уравнение имеет
два корня (т.е. дискриминант строго
больше ноля) выполняется Теорема
Виета.
Согласно Теореме
Виета,
сумма корней квадратного уравнения
равна:

Произведение корней квадратного
уравнения может быть вычислено по
формуле:

Парабола

График параболы задается
квадратичной функцией:

При этом
координаты вершины параболы могут быть
вычислены по следующим формулам. Икс
вершины:

Игрек вершины параболы:

Свойства
степеней и корней

Основные свойства степеней:

Последнее
свойство выполняется только при n >
0. Ноль можно возводить только в
положительную степень.

Основные свойства математических
корней:

Для арифметических корней:

Последнее
справедливо: если n –
нечетное, то для любого a;
если же n –
четное, то только при a больше
либо равном нолю. Для корня нечетной
степени выполняется также следующее
равенство:

Для корня четной степени имеется
следующее свойство:

Формулы с
логарифмами

Определение логарифма:

Определение логарифма можно записать
и другим способом:

Свойства логарифмов:

Логарифм произведения:

Логарифм дроби:

Вынесение степени за знак логарифма:

Другие полезные свойства логарифмов:

Арифметическая прогрессия

Формулы n-го
члена арифметической прогрессии:

Соотношение между тремя соседними
членами арифметической прогрессии:

Формула суммы арифметической
прогрессии:

Свойство арифметической прогрессии:

Геометрическая прогрессия

Формулы n-го
члена геометрической прогрессии:

Соотношение между тремя соседними
членами геометрической прогрессии:

Формула суммы геометрической
прогрессии:

Формула суммы бесконечно убывающей
геометрической прогрессии:

Свойство геометрической прогрессии:

Тригонометрия

Пусть имеется прямоугольный
треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное
тригонометрическое тождество:

Простейшие следствия из основного
тригонометрического тождества:

Формулы двойного угла

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы
преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Тригонометрические формулы
преобразования произведения в сумму

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для
синуса:

Формула понижения степени для
косинуса:

Формула понижения степени для
тангенса:

Формула понижения степени для
котангенса:

Формулы половинного угла

Формула половинного угла для
тангенса:

Формула половинного угла для
котангенса:

Тригонометрические формулы
приведения

Формулы
приведения задаются
в виде таблицы:

Тригонометрическая окружность

По тригонометрической
окружности легко
определять табличные значения
тригонометрических функций:

Тригонометрические уравнения

Формулы решений простейших
тригонометрических уравнений. Для синуса
существует две равнозначные формы записи
решения:

Для остальных тригонометрических
функций запись однозначна. Для косинуса:

Для тангенса:

Для котангенса:

Решение тригонометрических уравнений
в некоторых частных случаях:

Геометрия
на плоскости (планиметрия)

Пусть имеется произвольный
треугольник:

Тогда, сумма
углов треугольника:

Площадь треугольника через две
стороны и угол между ними:

Площадь треугольника через сторону и
высоту опущенную на неё:

Полупериметр треугольника находится
по следующей формуле:

Формула Герона для
площади треугольника:

Площадь треугольника через радиус
описанной окружности:

Формула медианы:

Свойство биссектрисы:

Формулы биссектрисы:

Основное свойство высот
треугольника:

Формула высоты:

Еще одно полезное свойство высот
треугольника:

Теорема
косинусов:

Теорема
синусов:

Радиус окружности, вписанной в
правильный треугольник:

Радиус окружности, описанной около
правильного треугольника:

Площадь правильного треугольника:

Теорема
Пифагора для
прямоугольного треугольника (c —
гипотенуза, a и b — катеты):

Радиус окружности, вписанной в
прямоугольный треугольник:

Радиус окружности, описанной вокруг
прямоугольного треугольника:

Площадь
прямоугольного треугольника (h —
высота опущенная на гипотенузу):

Свойства высоты, опущенной на
гипотенузу прямоугольного треугольника:

Длина средней линии трапеции:

Площадь трапеции:

Площадь параллелограмма через
сторону и высоту опущенную на неё:

Площадь параллелограмма через две
стороны и угол между ними:

Площадь квадрата через длину его
стороны:

Площадь квадрата через длину его
диагонали:

Площадь ромба (первая формула —
через две диагонали, вторая — через
длину стороны и угол между сторонами):

Площадь прямоугольника через две
смежные стороны:

Площадь
произвольного выпуклого четырёхугольника через
две диагонали и угол между ними:

Связь площади
произвольной фигуры, её полупериметра и
радиуса вписанной окружности (очевидно,
что формула выполняется только для фигур
в которые можно вписать окружность, т.е.
в том числе для любых
треугольников):

Свойство касательных:

Свойство хорды:

Теорема о пропорциональных отрезках
хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о
центральном и вписанном углах (величина
центрального угла в два раза больше
величины вписанного угла, если они
опираются на общую дугу):

Свойство вписанных углов (все
вписанные углы опирающиеся на общую дугу
равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и
секущих:

Условие, при выполнении которого
возможно вписать окружность в
четырёхугольник:

Условие, при выполнении которого
возможно описать окружность вокруг
четырёхугольника:

Сумма углов n-угольника:

Центральный
угол правильного n-угольника:

Площадь
правильного n-угольника:

Длина
окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

Геометрия
в пространстве (стереометрия)

Главная диагональ куба:

Объем куба:

Объём прямоугольного
параллелепипеда:

Главная диагональ прямоугольного
параллелепипеда (эту формулу также можно
назвать: «трёхмерная Теорема Пифагора»):

Объём призмы:

Площадь
боковой поверхности прямой призмы (P –
периметр основания, l –
боковое ребро, в данном случае равное
высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого
кругового цилиндра:

Объём пирамиды:

Площадь
боковой поверхности правильной пирамиды
(P –
периметр основания, l –
апофема, т.е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого
кругового конуса:

Длина образующей прямого кругового
конуса:

Объём шара:

Площадь поверхности шара (или,
другими словами, площадь сферы):

Координаты

Длина отрезка на координатной оси:

Длина отрезка на координатной
плоскости:

Длина отрезка в трёхмерной системе
координат:

Координаты середины отрезка (для
координатной оси используется только
первая формула, для координатной
плоскости — первые две формулы, для
трехмерной системы координат — все три
формулы):

Таблица
умножения

Таблица
квадратов двухзначных чисел