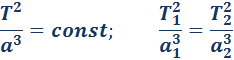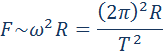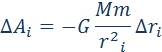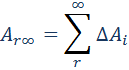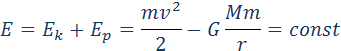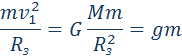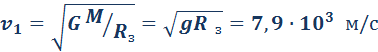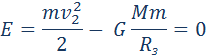Иоганн Кеплер и планеты Солнечной системы
Астрономия конца XVI века отмечает столкновение двух моделей нашей Солнечной системы: геоцентрическая система Птолемея – где центром вращения всех объектов является Земля, и гелиоцентрическая система Коперника – где Солнце является центральным телом.
Модель Солнечной системы Клавдия Птолемея
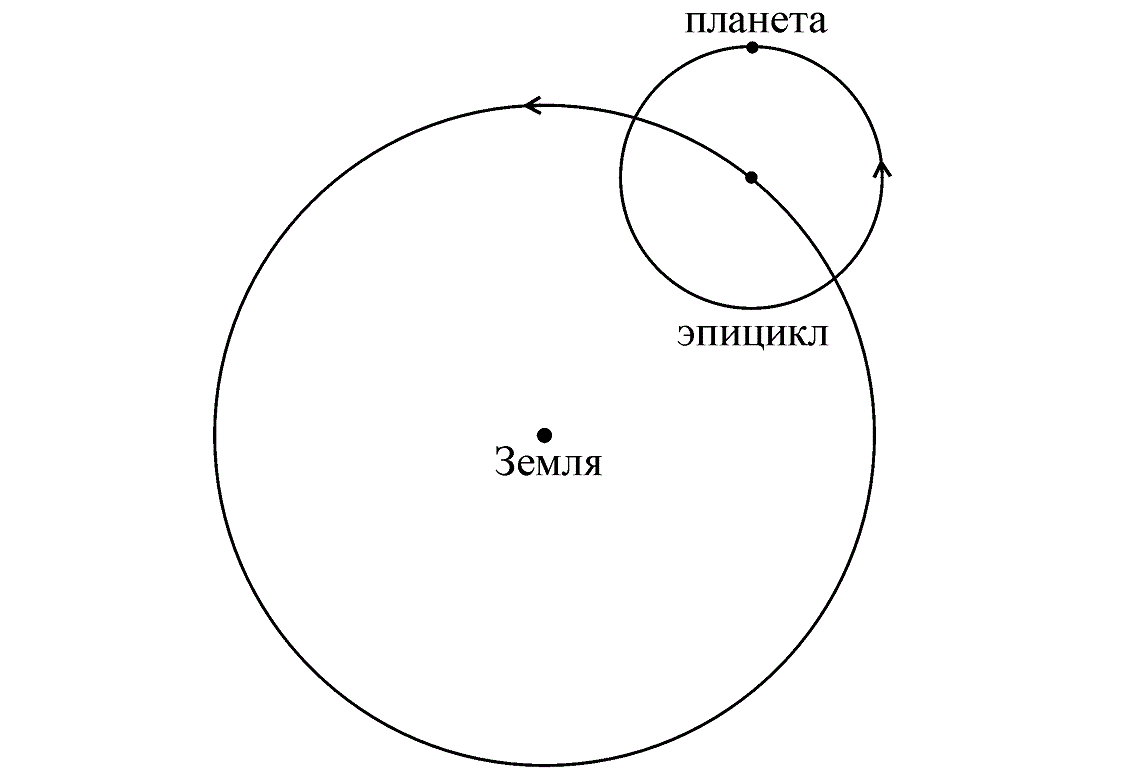
И хотя Коперник был ближе к истинной природе Солнечной системы, его работа имела недостатки. Основным из этих недостатков являлось утверждение, что планеты вращаются вокруг Солнца по круговым орбитам. С учетом этого, модель Коперника практически настолько же не согласовывалась с наблюдениями, как и система Птолемея. Польский астроном стремился исправить данное расхождение при помощи дополнительного движения планеты по кругу, центр которого уже двигался вокруг Солнца — эпицикл. Однако, расхождения в большей своей части не были устранены.
В начале XVII века немецкий астроном Иоганн Кеплер, изучая систему Николая Коперника, а также анализируя результаты астрономических наблюдений датчанина Тихо Браге, вывел основные законы относительно движения планет. Они были названы как Три закона Кеплера.
Эпицикл планеты
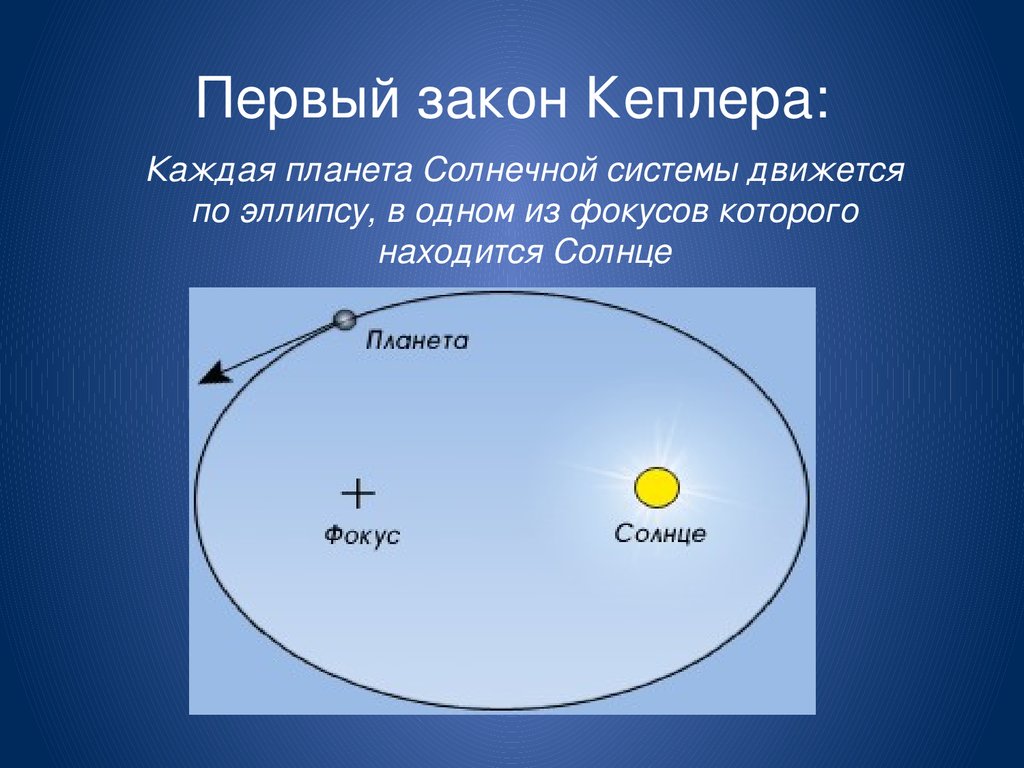
Первый закон Кеплера
Немецкий астроном пытался различными способами сохранить круговую орбиту движения планет, однако это не позволяло исправить расхождение с результатами наблюдений. Потому Кеплер прибегнул к эллиптическим орбитам. У каждой такой орбиты есть два так называемых фокуса. Фокусы – это две заданные точки, такие, что сумма расстояний от этих двух точек до любой точки эллипса является постоянной.
Иоганн Кеплер отметил, что планета движется по эллиптической орбите вокруг Солнца таким образом, что Солнце располагается в одном из двух фокусов эллипса, что и стало первым законом движения планет.
Первый закон Кеплера
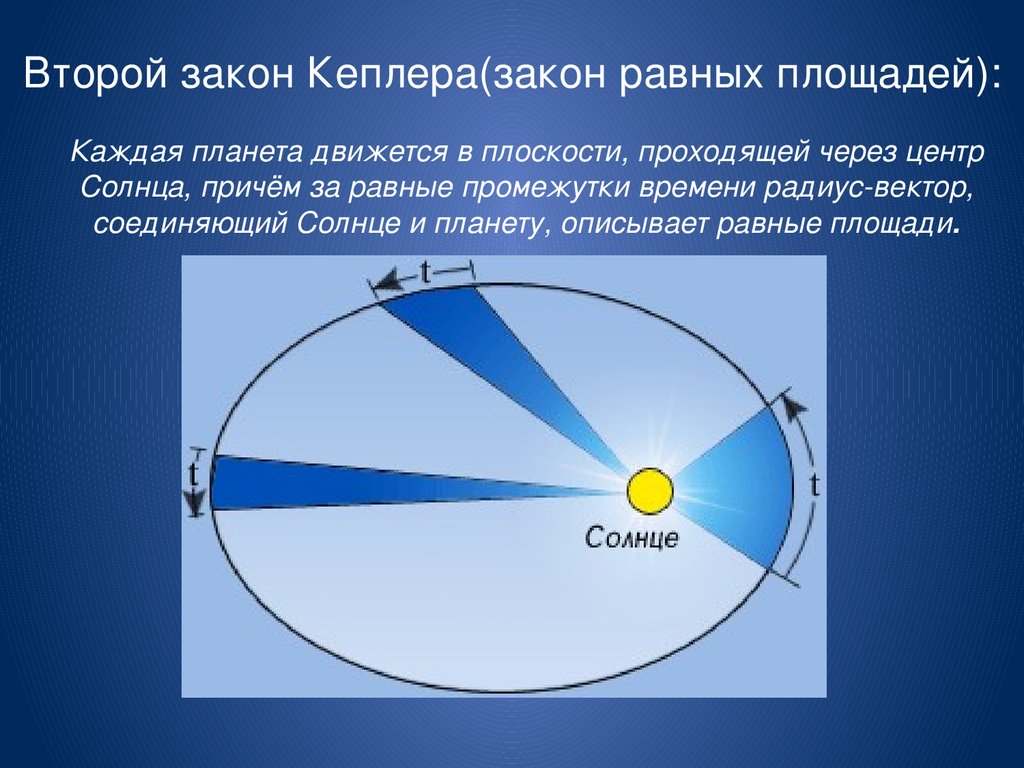
Второй закон Кеплера
Проведем радиус-вектор от Солнца, которое располагается в одном из фокусов эллипсоидной орбиты планеты, к самой планете. Тогда за равные промежутки времени данный радиус-вектор описывает равные площади на плоскости, в которой движется планета вокруг Солнца. Данное утверждение является вторым законом.
Второй закон Кеплера
Третий закон Кеплера
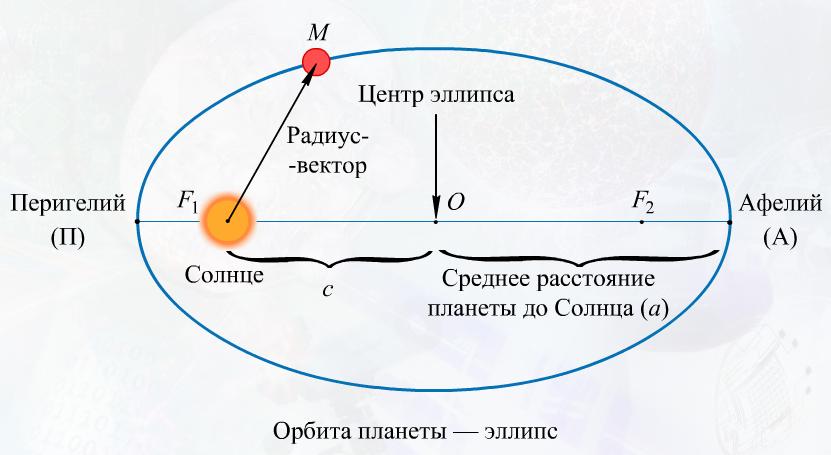
Каждая орбита планеты имеет точку, ближайшую к Солнцу, которое называется перигелием. Точка орбиты, наиболее удаленная от Солнца, называется афелием. Отрезок, соединяющий эти две точки называется большой осью орбиты. Если разделить этот отрезок пополам, то получим большую полуось, которую чаще используют в астрономии.
Основные элементы эллипса
Третий закон движения планет Кеплера звучит следующим образом:
Отношение квадрата периода обращения планеты вокруг Солнца к большой полуоси орбиты этой планеты является постоянным, и также равняется отношению квадрата периода обращения другой планеты вокруг Солнца к большой полуоси этой планеты.
Также иногда записывают другое отношение:
Одна из записей третьего закона
Дальнейшее развитие
И хотя законы Кеплера имели относительно невысокую погрешность (не более 1%), все же они были получены эмпирическим способом. Теоретическое же обоснование отсутствовало. Данная проблема позже была решена Исааком Ньютоном, который в 1682-м году открыл закон всемирного тяготения. Благодаря этому закону удалось описать подобное поведение планет. Законы Кеплера стали важнейшим этапом в понимании и описании движения планет.
Figure 1: Illustration of Kepler’s three laws with two planetary orbits.
- The orbits are ellipses, with focal points F1 and F2 for the first planet and F1 and F3 for the second planet. The Sun is placed at focal point F1.
- The two shaded sectors A1 and A2 have the same surface area and the time for planet 1 to cover segment A1 is equal to the time to cover segment A2.
- The total orbit times for planet 1 and planet 2 have a ratio
.
In astronomy, Kepler’s laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that:[1][2]
- The orbit of a planet is an ellipse with the Sun at one of the two foci.
- A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
- The square of a planet’s orbital period is proportional to the cube of the length of the semi-major axis of its orbit.
The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits. The second law helps to establish that when a planet is closer to the Sun, it travels faster. The third law expresses that the farther a planet is from the Sun, the slower its orbital speed, and vice versa.
Isaac Newton showed in 1687 that relationships like Kepler’s would apply in the Solar System as a consequence of his own laws of motion and law of universal gravitation.
Comparison to Copernicus[edit]
Johannes Kepler’s laws improved the model of Copernicus. According to Copernicus:[3][4]
- The planetary orbit is a circle with epicycles.
- The Sun is approximately at the center of the orbit.
- The speed of the planet in the main orbit is constant.
Despite being correct in saying that the planets revolved around the Sun, Copernicus was incorrect in defining their orbits. It was Kepler who correctly defined the orbit of planets as follows:[1][2][5]
- The planetary orbit is not a circle with epicycles, but an ellipse.
- The Sun is not at the center but at a focal point of the elliptical orbit.
- Neither the linear speed nor the angular speed of the planet in the orbit is constant, but the area speed (closely linked historically with the concept of angular momentum) is constant.
The eccentricity of the orbit of the Earth makes the time from the March equinox to the September equinox, around 186 days, unequal to the time from the September equinox to the March equinox, around 179 days. A diameter would cut the orbit into equal parts, but the plane through the Sun parallel to the equator of the Earth cuts the orbit into two parts with areas in a 186 to 179 ratio, so the eccentricity of the orbit of the Earth is approximately
which is close to the correct value (0.016710218). The accuracy of this calculation requires that the two dates chosen be along the elliptical orbit’s minor axis and that the midpoints of each half be along the major axis. As the two dates chosen here are equinoxes, this will be correct when perihelion, the date the Earth is closest to the Sun, falls on a solstice. The current perihelion, near January 4, is fairly close to the solstice of December 21 or 22.
Nomenclature[edit]
It took nearly two centuries for current formulation of Kepler’s work to take on its settled form. Voltaire’s Eléments de la philosophie de Newton (Elements of Newton’s Philosophy) of 1738 was the first publication to use the terminology of «laws».[6][7] The Biographical Encyclopedia of Astronomers in its article on Kepler (p. 620) states that the terminology of scientific laws for these discoveries was current at least from the time of Joseph de Lalande.[8] It was the exposition of Robert Small, in An account of the astronomical discoveries of Kepler (1814) that made up the set of three laws, by adding in the third.[9] Small also claimed, against the history, that these were empirical laws, based on inductive reasoning.[7][10]
Further, the current usage of «Kepler’s Second Law» is something of a misnomer. Kepler had two versions, related in a qualitative sense: the «distance law» and the «area law». The «area law» is what became the Second Law in the set of three; but Kepler did himself not privilege it in that way.[11]
History[edit]
Kepler published his first two laws about planetary motion in 1609,[12] having found them by analyzing the astronomical observations of Tycho Brahe.[13][14][15] Kepler’s third law was published in 1619.[16][14] Kepler had believed in the Copernican model of the Solar System, which called for circular orbits, but he could not reconcile Brahe’s highly precise observations with a circular fit to Mars’ orbit – Mars coincidentally having the highest eccentricity of all planets except Mercury.[17] His first law reflected this discovery.
In 1621, Kepler noted that his third law applies to the four brightest moons of Jupiter.[Nb 1] Godefroy Wendelin also made this observation in 1643.[Nb 2] The second law, in the «area law» form, was contested by Nicolaus Mercator in a book from 1664, but by 1670 his Philosophical Transactions were in its favour.[18][19] As the century proceeded it became more widely accepted.[20] The reception in Germany changed noticeably between 1688, the year in which Newton’s Principia was published and was taken to be basically Copernican, and 1690, by which time work of Gottfried Leibniz on Kepler had been published.[21]
Newton was credited with understanding that the second law is not special to the inverse square law of gravitation, being a consequence just of the radial nature of that law, whereas the other laws do depend on the inverse square form of the attraction. Carl Runge and Wilhelm Lenz much later identified a symmetry principle in the phase space of planetary motion (the orthogonal group O(4) acting) which accounts for the first and third laws in the case of Newtonian gravitation, as conservation of angular momentum does via rotational symmetry for the second law.[22]
Formulary[edit]
The mathematical model of the kinematics of a planet subject to the laws allows a large range of further calculations.
First law[edit]
The orbit of every planet is an ellipse with the Sun at one of the two foci.
Figure 2: Kepler’s first law placing the Sun at the focus of an elliptical orbit
Figure 3: Heliocentric coordinate system (r, θ) for ellipse. Also shown are: semi-major axis a, semi-minor axis b and semi-latus rectum p; center of ellipse and its two foci marked by large dots. For θ = 0°, r = rmin and for θ = 180°, r = rmax.
Mathematically, an ellipse can be represented by the formula:
where 
For an ellipse 0 < ε < 1 ; in the limiting case ε = 0, the orbit is a circle with the Sun at the centre (i.e. where there is zero eccentricity).
At θ = 0°, perihelion, the distance is minimum
At θ = 90° and at θ = 270° the distance is equal to 
At θ = 180°, aphelion, the distance is maximum (by definition, aphelion is – invariably – perihelion plus 180°)
The semi-major axis a is the arithmetic mean between rmin and rmax:
The semi-minor axis b is the geometric mean between rmin and rmax:
The semi-latus rectum p is the harmonic mean between rmin and rmax:
The eccentricity ε is the coefficient of variation between rmin and rmax:
The area of the ellipse is
The special case of a circle is ε = 0, resulting in r = p = rmin = rmax = a = b and A = πr2.
Second law[edit]
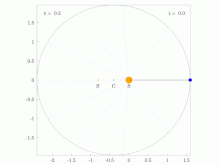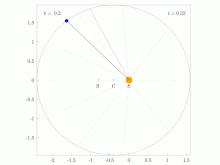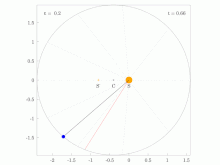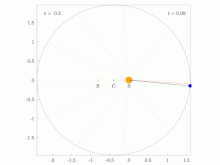
A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.[23]
The same (blue) area is swept out in a fixed time period. The green arrow is velocity. The purple arrow directed towards the Sun is the acceleration. The other two purple arrows are acceleration components parallel and perpendicular to the velocity.
The orbital radius and angular velocity of the planet in the elliptical orbit will vary. This is shown in the animation: the planet travels faster when closer to the Sun, then slower when farther from the Sun. Kepler’s second law states that the blue sector has constant area.
In a small time 



The area enclosed by the elliptical orbit is 

and the mean motion of the planet around the Sun
satisfies
And so,
| Low | High |
|---|---|
|
Planet orbiting the Sun in a circular orbit (e=0.0) |
Planet orbiting the Sun in an orbit with e=0.5 |
|
Planet orbiting the Sun in an orbit with e=0.2 |
Planet orbiting the Sun in an orbit with e=0.8 |
Third law[edit]
The ratio of the square of an object’s orbital period with the cube of the semi-major axis of its orbit is the same for all objects orbiting the same primary.
This captures the relationship between the distance of planets from the Sun, and their orbital periods.
Kepler enunciated in 1619[16] this third law in a laborious attempt to determine what he viewed as the «music of the spheres» according to precise laws, and express it in terms of musical notation.[24] It was therefore known as the harmonic law.[25]
Using Newton’s law of gravitation (published 1687), this relation can be found in the case of a circular orbit by setting the centripetal force equal to the gravitational force:
Then, expressing the angular velocity ω in terms of the orbital period 
A more detailed derivation can be done with general elliptical orbits, instead of circles, as well as orbiting the center of mass, instead of just the large mass. This results in replacing a circular radius, 



where 





Table[edit]
The following table shows the data used by Kepler to empirically derive his law:
| Planet | Mean distance to sun (AU) |
Period (days) |
 (10-6 AU3/day2) (10-6 AU3/day2)
|
|---|---|---|---|
| Mercury | 0.389 | 87.77 | 7.64 |
| Venus | 0.724 | 224.70 | 7.52 |
| Earth | 1 | 365.25 | 7.50 |
| Mars | 1.524 | 686.95 | 7.50 |
| Jupiter | 5.20 | 4332.62 | 7.49 |
| Saturn | 9.510 | 10759.2 | 7.43 |
Upon finding this pattern Kepler wrote:[26]
I first believed I was dreaming… But it is absolutely certain and exact that the ratio which exists between the period times of any two planets is precisely the ratio of the 3/2th power of the mean distance.
— translated from Harmonies of the World by Kepler (1619)
Log-log plot of period T vs semi-major axis a (average of aphelion and perihelion) of some Solar System orbits (crosses denoting Kepler’s values) showing that a³/T² is constant (green line)
For comparison, here are modern estimates:
| Planet | Semi-major axis (AU) | Period (days) |  (10-6 AU3/day2) (10-6 AU3/day2)
|
|---|---|---|---|
| Mercury | 0.38710 | 87.9693 | 7.496 |
| Venus | 0.72333 | 224.7008 | 7.496 |
| Earth | 1 | 365.2564 | 7.496 |
| Mars | 1.52366 | 686.9796 | 7.495 |
| Jupiter | 5.20336 | 4332.8201 | 7.504 |
| Saturn | 9.53707 | 10775.599 | 7.498 |
| Uranus | 19.1913 | 30687.153 | 7.506 |
| Neptune | 30.0690 | 60190.03 | 7.504 |
Planetary acceleration[edit]
Isaac Newton computed in his Philosophiæ Naturalis Principia Mathematica the acceleration of a planet moving according to Kepler’s first and second laws.
- The direction of the acceleration is towards the Sun.
- The magnitude of the acceleration is inversely proportional to the square of the planet’s distance from the Sun (the inverse square law).
This implies that the Sun may be the physical cause of the acceleration of planets. However, Newton states in his Principia that he considers forces from a mathematical point of view, not a physical, thereby taking an instrumentalist view.[27] Moreover, he does not assign a cause to gravity.[28]
Newton defined the force acting on a planet to be the product of its mass and the acceleration (see Newton’s laws of motion). So:
- Every planet is attracted towards the Sun.
- The force acting on a planet is directly proportional to the mass of the planet and is inversely proportional to the square of its distance from the Sun.
The Sun plays an unsymmetrical part, which is unjustified. So he assumed, in Newton’s law of universal gravitation:
- All bodies in the Solar System attract one another.
- The force between two bodies is in direct proportion to the product of their masses and in inverse proportion to the square of the distance between them.
As the planets have small masses compared to that of the Sun, the orbits conform approximately to Kepler’s laws. Newton’s model improves upon Kepler’s model, and fits actual observations more accurately. (See two-body problem.)
Below comes the detailed calculation of the acceleration of a planet moving according to Kepler’s first and second laws.
Acceleration vector[edit]
From the heliocentric point of view consider the vector to the planet 


where 


Differentiate the position vector twice to obtain the velocity vector and the acceleration vector:
So
where the radial acceleration is
and the transversal acceleration is
Inverse square law[edit]
Kepler’s second law says that
is constant.
The transversal acceleration 
So the acceleration of a planet obeying Kepler’s second law is directed towards the Sun.
The radial acceleration 
Kepler’s first law states that the orbit is described by the equation:
Differentiating with respect to time
or
Differentiating once more
The radial acceleration 
Substituting the equation of the ellipse gives
The relation 
This means that the acceleration vector 
where
is a constant, and 

Since mean motion 


The inverse square law is a differential equation. The solutions to this differential equation include the Keplerian motions, as shown, but they also include motions where the orbit is a hyperbola or parabola or a straight line. (See Kepler orbit.)
Newton’s law of gravitation[edit]
By Newton’s second law, the gravitational force that acts on the planet is:
where 


where 
The acceleration of solar system body number i is, according to Newton’s laws:
where 


In the special case where there are only two bodies in the Solar System, Earth and Sun, the acceleration becomes
which is the acceleration of the Kepler motion. So this Earth moves around the Sun according to Kepler’s laws.
If the two bodies in the Solar System are Moon and Earth the acceleration of the Moon becomes
So in this approximation, the Moon moves around the Earth according to Kepler’s laws.
In the three-body case the accelerations are
These accelerations are not those of Kepler orbits, and the three-body problem is complicated. But Keplerian approximation is the basis for perturbation calculations. (See Lunar theory.)
Position as a function of time[edit]
Kepler used his two first laws to compute the position of a planet as a function of time. His method involves the solution of a transcendental equation called Kepler’s equation.
The procedure for calculating the heliocentric polar coordinates (r,θ) of a planet as a function of the time t since perihelion, is the following five steps:
- Compute the mean motion n = (2π rad)/P, where P is the period.
- Compute the mean anomaly M = nt, where t is the time since perihelion.
- Compute the eccentric anomaly E by solving Kepler’s equation:
where
is the eccentricity.
- Compute the true anomaly θ by solving the equation:
- Compute the heliocentric distance r:
where
is the semimajor axis.
The Cartesian velocity vector can then be calculated as 

The important special case of circular orbit, ε = 0, gives θ = E = M. Because the uniform circular motion was considered to be normal, a deviation from this motion was considered an anomaly.
The proof of this procedure is shown below.
Mean anomaly, M[edit]
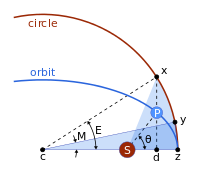
Figure 5: Geometric construction for Kepler’s calculation of θ. The Sun (located at the focus) is labeled S and the planet P. The auxiliary circle is an aid to calculation. Line xd is perpendicular to the base and through the planet P. The shaded sectors are arranged to have equal areas by positioning of point y.
The Keplerian problem assumes an elliptical orbit and the four points:
- s the Sun (at one focus of ellipse);
- z the perihelion
- c the center of the ellipse
- p the planet
and
The problem is to compute the polar coordinates (r,θ) of the planet from the time since perihelion, t.
It is solved in steps. Kepler considered the circle with the major axis as a diameter, and
The sector areas are related by 
The circular sector area 
The area swept since perihelion,
is by Kepler’s second law proportional to time since perihelion. So the mean anomaly, M, is proportional to time since perihelion, t.
where n is the mean motion.
Eccentric anomaly, E[edit]
When the mean anomaly M is computed, the goal is to compute the true anomaly θ. The function θ = f(M) is, however, not elementary.[30] Kepler’s solution is to use
x as seen from the centre, the eccentric anomaly
as an intermediate variable, and first compute E as a function of M by solving Kepler’s equation below, and then compute the true anomaly θ from the eccentric anomaly E. Here are the details.
Division by a2/2 gives Kepler’s equation
This equation gives M as a function of E. Determining E for a given M is the inverse problem. Iterative numerical algorithms are commonly used.
Having computed the eccentric anomaly E, the next step is to calculate the true anomaly θ.
But note: Cartesian position coordinates with reference to the center of ellipse are (a cos E, b sin E)
With reference to the Sun (with coordinates (c,0) = (ae,0) ), r = (a cos E – ae, b sin E)
True anomaly would be arctan(ry/rx), magnitude of r would be √r · r.
True anomaly, θ[edit]
Note from the figure that
so that
Dividing by 
to get
The result is a usable relationship between the eccentric anomaly E and the true anomaly θ.
A computationally more convenient form follows by substituting into the trigonometric identity:
Get
Multiplying by 1 + ε gives the result
This is the third step in the connection between time and position in the orbit.
Distance, r[edit]
The fourth step is to compute the heliocentric distance r from the true anomaly θ by Kepler’s first law:
Using the relation above between θ and E the final equation for the distance r is:
See also[edit]
- Circular motion
- Free-fall time
- Gravity
- Kepler orbit
- Kepler problem
- Kepler’s equation
- Laplace–Runge–Lenz vector
- Specific relative angular momentum, relatively easy derivation of Kepler’s laws starting with conservation of angular momentum
Explanatory notes[edit]
- ^ In 1621, Johannes Kepler noted that Jupiter’s moons obey (approximately) his third law in his Epitome Astronomiae Copernicanae [Epitome of Copernican Astronomy] (Linz («Lentiis ad Danubium»), (Austria): Johann Planck, 1622), book 4, part 2, pages 554–555. From pp. 554–555: » … plane ut est cum sex planet circa Solem, … prodit Marius in suo mundo Ioviali ista 3.5.8.13 (vel 14. Galilæo) … Periodica vero tempora prodit idem Marius … sunt maiora simplis, minora vero duplis.» (… just as it is clearly [true] among the six planets around the Sun, so also it is among the four [moons] of Jupiter, because around the body of Jupiter any [satellite] that can go farther from it, orbits slower, and even that [orbit’s period] is not in the same proportion, but greater [than the distance from Jupiter]; that is, 3/2 (sescupla) of the proportion of each of the distances from Jupiter, which is clearly the very [proportion] as is used for the six planets above. In his [book] The World of Jupiter [Mundus Jovialis, 1614], [Simon Mayr or] «Marius» [1573–1624] presents these distances, from Jupiter, of the four [moons] of Jupiter: 3, 5, 8, 13 (or 14 [according to] Galileo) [Note: The distances of Jupiter’s moons from Jupiter are expressed as multiples of Jupiter’s diameter.] … Mayr presents their time periods: 1 day 18 1/2 hours, 3 days 13 1/3 hours, 7 days 2 hours, 16 days 18 hours: for all [of these data] the proportion is greater than double, thus greater than [the proportion] of the distances 3, 5, 8, 13 or 14, although less than [the proportion] of the squares, which double the proportions of the distances, namely 9, 25, 64, 169 or 196, just as [a power of] 3/2 is also greater than 1 but less than 2.)
- ^ Godefroy Wendelin wrote a letter to Giovanni Battista Riccioli about the relationship between the distances of the Jovian moons from Jupiter and the periods of their orbits, showing that the periods and distances conformed to Kepler’s third law. See: Joanne Baptista Riccioli, Almagestum novum … (Bologna (Bononia), (Italy): Victor Benati, 1651), volume 1, page 492 Scholia III. In the margin beside the relevant paragraph is printed: Vendelini ingeniosa speculatio circa motus & intervalla satellitum Jovis. (Wendelin’s clever speculation about the movement and distances of Jupiter’s satellites.) From p. 492: «III. Non minus Kepleriana ingeniosa est Vendelini … & D. 7. 164/1000. pro penextimo, & D. 16. 756/1000. pro extimo.» (No less clever [than] Kepler’s is the most keen astronomer Wendelin’s investigation of the proportion of the periods and distances of Jupiter’s satellites, which he had communicated to me with great generosity [in] a very long and very learned letter. So, just as in [the case of] the larger planets, the planets’ mean distances from the Sun are respectively in the 3/2 ratio of their periods ; so the distances of these minor planets of Jupiter from Jupiter (which are 3, 5, 8, and 14) are respectively in the 3/2 ratio of [their] periods (which are 1.769 days for the innermost [Io], 3.554 days for the next to the innermost [Europa], 7.164 days for the next to the outermost [Ganymede], and 16.756 days for the outermost [Callisto]).)
Citations[edit]
- ^ a b «Kepler’s Laws». hyperphysics.phy-astr.gsu.edu. Retrieved 2022-12-13.
- ^ a b «Orbits and Kepler’s Laws». NASA Solar System Exploration. Retrieved 2022-12-13.
- ^ «Planetary Motion: The History of an Idea That Launched the Scientific Revolution». earthobservatory.nasa.gov. 2009-07-07. Retrieved 2022-12-13.
- ^ «Nicolaus Copernicus». HISTORY. Retrieved 2022-12-13.
- ^ Hurley, Steve (2018-01-20). «Johannes Kepler». Explaining Science. Retrieved 2022-12-13.
- ^ Voltaire, Eléments de la philosophie de Newton [Elements of Newton’s Philosophy] (London, England: 1738). See, for example:
- From p. 162: «Par une des grandes loix de Kepler, toute Planete décrit des aires égales en temp égaux : par une autre loi non-moins sûre, chaque Planete fait sa révolution autour du Soleil en telle sort, que si, sa moyenne distance au Soleil est 10. prenez le cube de ce nombre, ce qui sera 1000., & le tems de la révolution de cette Planete autour du Soleil sera proportionné à la racine quarrée de ce nombre 1000.» (By one of the great laws of Kepler, each planet describes equal areas in equal times ; by another law no less certain, each planet makes its revolution around the sun in such a way that if its mean distance from the sun is 10, take the cube of that number, which will be 1000, and the time of the revolution of that planet around the sun will be proportional to the square root of that number 1000.)
- From p. 205: «Il est donc prouvé par la loi de Kepler & par celle de Neuton, que chaque Planete gravite vers le Soleil, … « (It is thus proved by the law of Kepler and by that of Newton, that each planet revolves around the sun … )
- ^ a b Wilson, Curtis (May 1994). «Kepler’s Laws, So-Called» (PDF). HAD News (31): 1–2. Retrieved December 27, 2016.
- ^ De la Lande, Astronomie, vol. 1 (Paris, France: Desaint & Saillant, 1764). See, for example:
- From page 390: » … mais suivant la fameuse loi de Kepler, qui sera expliquée dans le Livre suivant (892), le rapport des temps périodiques est toujours plus grand que celui des distances, une planete cinq fois plus éloignée du soleil, emploie à faire sa révolution douze fois plus de temps ou environ; … « ( … but according to the famous law of Kepler, which will be explained in the following book [i.e., chapter] (paragraph 892), the ratio of the periods is always greater than that of the distances [so that, for example,] a planet five times farther from the sun, requires about twelve times or so more time to make its revolution [around the sun] … )
- From page 429: «Les Quarrés des Temps périodiques sont comme les Cubes des Distances. 892. La plus fameuse loi du mouvement des planetes découverte par Kepler, est celle du repport qu’il y a entre les grandeurs de leurs orbites, & le temps qu’elles emploient à les parcourir; … « (The squares of the periods are as the cubes of the distances. 892. The most famous law of the movement of the planets discovered by Kepler is that of the relation between the sizes of their orbits and the times that the [planets] require to traverse them; … )
- From page 430: «Les Aires sont proportionnelles au Temps. 895. Cette loi générale du mouvement des planetes devenue si importante dans l’Astronomie, sçavior, que les aires sont proportionnelles au temps, est encore une des découvertes de Kepler; … « (Areas are proportional to times. 895. This general law of the movement of the planets [which has] become so important in astronomy, namely, that areas are proportional to times, is one of Kepler’s discoveries; … )
- From page 435: «On a appellé cette loi des aires proportionnelles aux temps, Loi de Kepler, aussi bien que celle de l’article 892, du nome de ce célebre Inventeur; … « (One called this law of areas proportional to times (the law of Kepler) as well as that of paragraph 892, by the name of that celebrated inventor; … )
- ^ Robert Small, An account of the astronomical discoveries of Kepler (London, England: J Mawman, 1804), pp. 298–299.
- ^ Robert Small, An account of the astronomical discoveries of Kepler (London, England: J. Mawman, 1804).
- ^ Bruce Stephenson (1994). Kepler’s Physical Astronomy. Princeton University Press. p. 170. ISBN 978-0-691-03652-6.
- ^ Astronomia nova Aitiologitis, seu Physica Coelestis tradita Commentariis de Motibus stellae Martis ex observationibus G.V. Tychnonis.Prague 1609; Engl. tr. W.H. Donahue, Cambridge 1992.
- ^ In his Astronomia nova, Kepler presented only a proof that Mars’ orbit is elliptical. Evidence that the other known planets’ orbits are elliptical was presented only in 1621.
See: Johannes Kepler, Astronomia nova … (1609), p. 285. After having rejected circular and oval orbits, Kepler concluded that Mars’ orbit must be elliptical. From the top of page 285: «Ergo ellipsis est Planetæ iter; … « (Thus, an ellipse is the planet’s [i.e., Mars’] path; … ) Later on the same page: » … ut sequenti capite patescet: ubi simul etiam demonstrabitur, nullam Planetæ relinqui figuram Orbitæ, præterquam perfecte ellipticam; … « ( … as will be revealed in the next chapter: where it will also then be proved that any figure of the planet’s orbit must be relinquished, except a perfect ellipse; … ) And then: «Caput LIX. Demonstratio, quod orbita Martis, … , fiat perfecta ellipsis: … « (Chapter 59. Proof that Mars’ orbit, … is a perfect ellipse: … ) The geometric proof that Mars’ orbit is an ellipse appears as Protheorema XI on pages 289–290.
Kepler stated that every planet travels in elliptical orbits having the Sun at one focus in: Johannes Kepler, Epitome Astronomiae Copernicanae [Summary of Copernican Astronomy] (Linz («Lentiis ad Danubium»), (Austria): Johann Planck, 1622), book 5, part 1, III. De Figura Orbitæ (III. On the figure [i.e., shape] of orbits), pages 658–665. From p. 658: «Ellipsin fieri orbitam planetæ … « (Of an ellipse is made a planet’s orbit … ). From p. 659: » … Sole (Foco altero huius ellipsis) … « ( … the Sun (the other focus of this ellipse) … ). - ^ a b Holton, Gerald James; Brush, Stephen G. (2001). Physics, the Human Adventure: From Copernicus to Einstein and Beyond (3rd paperback ed.). Piscataway, NJ: Rutgers University Press. pp. 40–41. ISBN 978-0-8135-2908-0. Retrieved December 27, 2009.
- ^ In his Astronomia nova … (1609), Kepler did not present his second law in its modern form. He did that only in his Epitome of 1621. Furthermore, in 1609, he presented his second law in two different forms, which scholars call the «distance law» and the «area law».
- His «distance law» is presented in: «Caput XXXII. Virtutem quam Planetam movet in circulum attenuari cum discessu a fonte.» (Chapter 32. The force that moves a planet circularly weakens with distance from the source.) See: Johannes Kepler, Astronomia nova … (1609), pp. 165–167. On page 167, Kepler states: » … , quanto longior est αδ quam αε, tanto diutius moratur Planeta in certo aliquo arcui excentrici apud δ, quam in æquali arcu excentrici apud ε.» ( … , as αδ is longer than αε, so much longer will a planet remain on a certain arc of the eccentric near δ than on an equal arc of the eccentric near ε.) That is, the farther a planet is from the Sun (at the point α), the slower it moves along its orbit, so a radius from the Sun to a planet passes through equal areas in equal times. However, as Kepler presented it, his argument is accurate only for circles, not ellipses.
- His «area law» is presented in: «Caput LIX. Demonstratio, quod orbita Martis, … , fiat perfecta ellipsis: … « (Chapter 59. Proof that Mars’ orbit, … , is a perfect ellipse: … ), Protheorema XIV and XV, pp. 291–295. On the top p. 294, it reads: «Arcum ellipseos, cujus moras metitur area AKN, debere terminari in LK, ut sit AM.» (The arc of the ellipse, of which the duration is delimited [i.e., measured] by the area AKM, should be terminated in LK, so that it [i.e., the arc] is AM.) In other words, the time that Mars requires to move along an arc AM of its elliptical orbit is measured by the area of the segment AMN of the ellipse (where N is the position of the Sun), which in turn is proportional to the section AKN of the circle that encircles the ellipse and that is tangent to it. Therefore, the area that is swept out by a radius from the Sun to Mars as Mars moves along an arc of its elliptical orbit is proportional to the time that Mars requires to move along that arc. Thus, a radius from the Sun to Mars sweeps out equal areas in equal times.
In 1621, Kepler restated his second law for any planet: Johannes Kepler, Epitome Astronomiae Copernicanae [Summary of Copernican Astronomy] (Linz («Lentiis ad Danubium»), (Austria): Johann Planck, 1622), book 5, page 668. From page 668: «Dictum quidem est in superioribus, divisa orbita in particulas minutissimas æquales: accrescete iis moras planetæ per eas, in proportione intervallorum inter eas & Solem.» (It has been said above that, if the orbit of the planet is divided into the smallest equal parts, the times of the planet in them increase in the ratio of the distances between them and the sun.) That is, a planet’s speed along its orbit is inversely proportional to its distance from the Sun. (The remainder of the paragraph makes clear that Kepler was referring to what is now called angular velocity.)
- ^ a b Johannes Kepler, Harmonices Mundi [The Harmony of the World] (Linz, (Austria): Johann Planck, 1619), book 5, chapter 3, p. 189. From the bottom of p. 189: «Sed res est certissima exactissimaque quod proportio qua est inter binorum quorumcunque Planetarum tempora periodica, sit præcise sesquialtera proportionis mediarum distantiarum, … « (But it is absolutely certain and exact that the proportion between the periodic times of any two planets is precisely the sesquialternate proportion [i.e., the ratio of 3:2] of their mean distances, … «)
An English translation of Kepler’s Harmonices Mundi is available as: Johannes Kepler with E. J. Aiton, A. M. Duncan, and J. V. Field, trans., The Harmony of the World (Philadelphia, Pennsylvania: American Philosophical Society, 1997); see especially p. 411. - ^ National Earth Science Teachers Association (9 October 2008). «Data Table for Planets and Dwarf Planets». Windows to the Universe. Retrieved 2 August 2018.
- ^ Mercator, Nicolaus (1664). Nicolai Mercatoris Hypothesis astronomica nova, et consensus eius cum observationibus [Nicolaus Mercator’s new astronomical hypothesis, and its agreement with observations] (in Latin). London, England: Leybourn.
- ^ Mercator, Nic. (25 March 1670). «Some considerations of Mr. Nic. Mercator, concerning the geometrick and direct method of signior Cassini for finding the apogees, excentricities, and anomalies of the planets; …» Philosophical Transactions of the Royal Society of London (in Latin). 5 (57): 1168–1175. doi:10.1098/rstl.1670.0018. Mercator criticized Cassini’s method of finding, from three observations, an orbit’s line of apsides. Cassini had assumed (wrongly) that planets move uniformly along their elliptical orbits. From p. 1174: «Sed cum id Observationibus nequaquam congruere animadverteret, mutavit sententiam, & lineam veri motus Planetæ æqualibus temporibus æquales areas Ellipticas verrere professus est: … « (But when he noticed that it didn’t agree at all with observations, he changed his thinking, and he declared that a line [from the Sun to a planet, denoting] a planet’s true motion, sweeps out equal areas of an ellipse in equal periods of time: … [which is the «area» form of Kepler’s second law])
- ^ Wilbur Applebaum (2000). Encyclopedia of the Scientific Revolution: From Copernicus to Newton. Routledge. p. 603. Bibcode:2000esrc.book…..A. ISBN 978-1-135-58255-5.
- ^ Roy Porter (1992). The Scientific Revolution in National Context. Cambridge University Press. p. 102. ISBN 978-0-521-39699-8.
- ^ Victor Guillemin; Shlomo Sternberg (2006). Variations on a Theme by Kepler. American Mathematical Soc. p. 5. ISBN 978-0-8218-4184-6.
- ^ Bryant, Jeff; Pavlyk, Oleksandr. «Kepler’s Second Law», Wolfram Demonstrations Project. Retrieved December 27, 2009.
- ^ Burtt, Edwin. The Metaphysical Foundations of Modern Physical Science. p. 52.
- ^ Gerald James Holton, Stephen G. Brush (2001). Physics, the Human Adventure. Rutgers University Press. p. 45. ISBN 978-0-8135-2908-0.
- ^ Caspar, Max (1993). Kepler. New York: Dover. ISBN 9780486676050.
- ^ I. Newton, Principia, p. 408 in the translation of I.B. Cohen and A. Whitman
- ^ I. Newton, Principia, p. 943 in the translation of I.B. Cohen and A. Whitman
- ^ Schwarz, René. «Memorandum № 1: Keplerian Orbit Elements → Cartesian State Vectors» (PDF). Retrieved 4 May 2018.
- ^ Müller, M (1995). «Equation of Time – Problem in Astronomy». Acta Physica Polonica A. Retrieved 23 February 2013.
General bibliography[edit]
- Kepler’s life is summarized on pages 523–627 and Book Five of his magnum opus, Harmonice Mundi (harmonies of the world), is reprinted on pages 635–732 of On the Shoulders of Giants: The Great Works of Physics and Astronomy (works by Copernicus, Kepler, Galileo, Newton, and Einstein). Stephen Hawking, ed. 2002 ISBN 0-7624-1348-4
- A derivation of Kepler’s third law of planetary motion is a standard topic in engineering mechanics classes. See, for example, pages 161–164 of Meriam, J.L. (1971) [1966]. Dynamics, 2nd ed. New York: John Wiley. ISBN 978-0-471-59601-1..
- Murray and Dermott, Solar System Dynamics, Cambridge University Press 1999, ISBN 0-521-57597-4
- V. I. Arnold, Mathematical Methods of Classical Mechanics, Chapter 2. Springer 1989, ISBN 0-387-96890-3
External links[edit]
- B.Surendranath Reddy; animation of Kepler’s laws: applet
- «Derivation of Kepler’s Laws» (from Newton’s laws) at Physics Stack Exchange.
- Crowell, Benjamin, Light and Matter, an online book that gives a proof of the first law without the use of calculus (see section 15.7)
- David McNamara and Gianfranco Vidali, Kepler’s Second Law – Java Interactive Tutorial, https://web.archive.org/web/20060910225253/http://www.phy.syr.edu/courses/java/mc_html/kepler.html, an interactive Java applet that aids in the understanding of Kepler’s Second Law.
- Audio – Cain/Gay (2010) Astronomy Cast Johannes Kepler and His Laws of Planetary Motion
- University of Tennessee’s Dept. Physics & Astronomy: Astronomy 161 page on Johannes Kepler: The Laws of Planetary Motion [1]
- Equant compared to Kepler: interactive model [2] Archived 2008-12-26 at the Wayback Machine
- Kepler’s Third Law:interactive model [3] Archived 2008-12-26 at the Wayback Machine
- Solar System Simulator (Interactive Applet)
- Kepler and His Laws, educational web pages by David P. Stern
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
В мире атомов и элементарных частиц гравитационные силы пренебрежимо малы по сравнению с другими видами силового взаимодействия между частицами. Очень непросто наблюдать гравитационное взаимодействие и между различными окружающими нас телами, даже если их массы составляют многие тысячи килограмм. Однако именно гравитация определяет поведение «больших» объектов, таких, как планеты, кометы и звезды, именно гравитация удерживает всех нас на Земле.
Гравитация управляет движением планет Солнечной системы. Без нее планеты, составляющие Солнечную систему, разбежались бы в разные стороны и потерялись в безбрежных просторах мирового пространства.
Закономерности движения планет с давних пор привлекали внимание людей. Изучение движения планет и строения Солнечной системы и привело к созданию теории гравитации – открытию закона всемирного тяготения.
С точки зрения земного наблюдателя планеты движутся по весьма сложным траекториям (рис. 1.24.1). Первая попытка создания модели Вселенной была предпринята Птолемеем (~ 140 г.). В центре мироздания Птолемей поместил Землю, вокруг которой по большим и малым кругам, как в хороводе, двигались планеты и звезды.
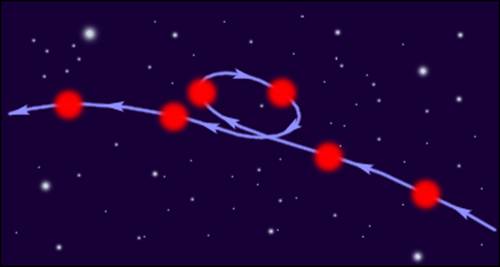 |
| Рисунок 1.24.1. Условное изображение наблюдаемого движения Марса на фоне неподвижных звезд |
Геоцентрическая система Птолемея продержалась более 14 столетий и только в середине XVI века была заменена гелиоцентрической системой Коперника. В системе Коперника траектории планет оказались более простыми. Немецкий астроном Иоганн Кеплер в начале XVII века на основе системы Коперника сформулировал три эмпирических закона движения планет Солнечной системы. Кеплер использовал результаты наблюдений за движением планет датского астронома Тихо Браге.
Первый закон Кеплера (1609 г.):
Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.
На рис. 1.24.2 показана эллиптическая орбита планеты, масса которой много меньше массы Солнца. Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка P траектории называется перигелием, точка A, наиболее удаленная от Солнца – афелием. Расстояние между афелием и перигелием – большая ось эллипса.
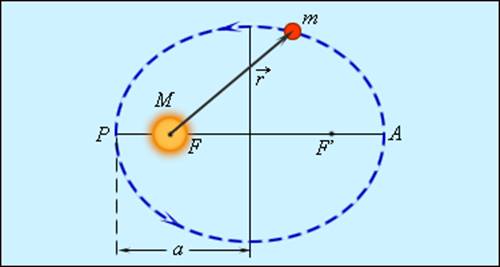 |
| Рисунок 1.24.2. Эллиптическая орбита планеты массой m << M. a – длина большой полуоси, F и F’ – фокусы орбиты |
Почти все планеты Солнечной системы (кроме Плутона) движутся по орбитам, близким к круговым.
Второй закон Кеплера (1609 г.):
Радиус-вектор планеты описывает в равные промежутки времени равные площади.
Рис. 1.24.3 иллюстрирует 2-й закон Кеплера.
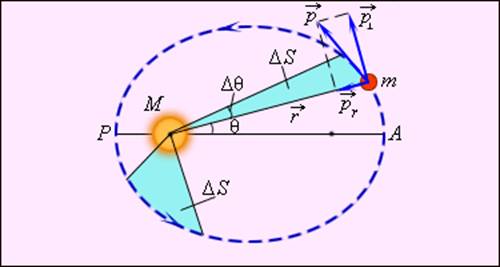 |
| Рисунок 1.24.3. Закон площадей – второй закон Кеплера |
Второй закон Кеплера эквивалентен закону сохранения момента импульса. На рис. 1.24.3 изображен вектор импульса тела и его составляющие
и
Площадь, описываемая радиус-вектором за малое время Δt, приближенно равна площади треугольника с основанием rΔθ и высотой r:
Здесь – угловая скорость.
Момент импульса L по абсолютной величине равен произведению модулей векторов и
:
Из этих отношений следует:
Поэтому, если по второму закону Кеплера , то и момент импульса L при движении остается неизменным.
В частности, поскольку скорости планеты в перигелии и афелии
направлены перпендикулярно радиус-векторам
и
из закона сохранения момента импульса следует:
Третий закон Кеплера (1619 г.):
Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит:
Третий закон Кеплера выполняется для всех планет Солнечной системы с точностью выше 1 %.
На рис. 1.24.4 изображены две орбиты, одна из которых – круговая с радиусом R, а другая – эллиптическая с большой полуосью a. Третий закон утверждает, что если R = a, то периоды обращения тел по этим орбитам одинаковы.
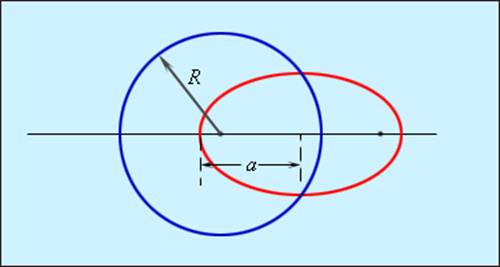 |
| Рисунок 1.24.4. Круговая и эллиптическая орбиты. При R = a периоды обращения тел по этим орбитам одинаковы |
 |
|
Модель. Законы Кеплера |
Несмотря на то, что законы Кеплера явились важнейшим этапом в понимании движения планет, они все же оставались только эмпирическими правилами, полученными из астрономических наблюдений. Законы Кеплера нуждались в теоретическом обосновании. Решающий шаг в этом направлении был сделан Исааком Ньютоном, открывшим в 1682 году закон всемирного тяготения:
где M и m – массы Солнца и планеты, R – расстояние между ними, G = 6,67·10–11 Н·м2/кг2 – гравитационная постоянная. Ньютон первый высказал мысль о том, что гравитационные силы определяют не только движение планет Солнечной системы; они действуют между любыми телами Вселенной. В частности, уже говорилось, что сила тяжести, действующая на тела вблизи поверхности Земли, имеет гравитационную природу.
Для круговых орбит первый и второй закон Кеплера выполняются автоматически, а третий закон утверждает, что T2 ~ R3, где Т – период обращения, R – радиус орбиты. Отсюда можно получить зависимость гравитационной силы от расстояния. При движении планеты по круговой траектории на нее действует сила, которая возникает за счет гравитационного взаимодействия планеты и Солнца:
Если T2 ~ R3, то
Свойство консервативности гравитационных сил позволяет ввести понятие потенциальной энергии. Для сил всемирного тяготения удобно потенциальную энергию отсчитывать от бесконечно удаленной точки.
Потенциальная энергия тела массы m, находящегося на расстоянии r от неподвижного тела массы M, равна работе гравитационных сил при перемещении массы m из данной точки в бесконечность.
Математическая процедура вычисления потенциальной энергии тела в гравитационном поле состоит в суммировании работ на малых перемещениях (рис. 1.24.5).
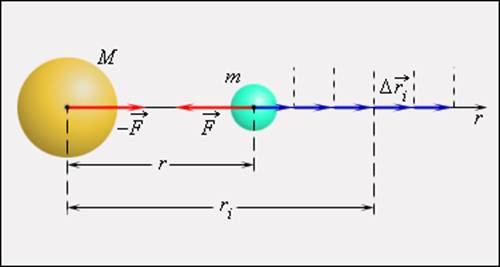 |
| Рисунок 1.24.5. Вычисление потенциальной энергии тела в гравитационном поле |
Закон всемирного тяготения применим не только к точеным массам, но и к сферически симметричным телам. Работа гравитационной силы
на малом перемещении
есть:
Полная работа при перемещении тела массой m из начального положения в бесконечность находится суммированием работ ΔAi на малых перемещениях:
В пределе при Δri → 0 эта сумма переходит в интеграл. В результате вычислений для потенциальной энергии получается выражение
Знак «минус» указывает на то, что гравитационные силы являются силами притяжения.
Если тело находится в гравитационном поле на некотором расстоянии r от центра тяготения и имеет некоторую скорость υ, его полная механическая энергия равна
В соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной.
Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела (рис. 1.24.6).
При E = E1 < 0 тело не может удалиться от центра притяжения на расстояние r > rmax. В этом случае небесное тело движется по эллиптической орбите (планеты Солнечной системы, кометы).
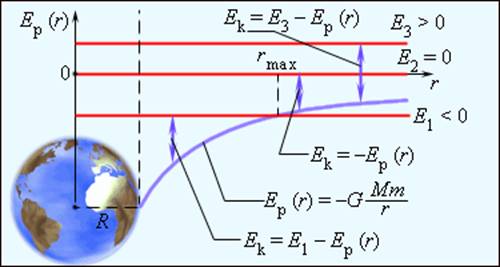 |
| Рисунок 1.24.6. Диаграмма энергий тела массой m в гравитационном поле, создаваемом сферически симметричным телом массой M и радиусом R |
При E = E2 = 0 тело может удалиться на бесконечность. Скорость тела на бесконечности будет равна нулю. Тело движется по параболической траектории.
При E = E3 > 0 движение происходит по гиперболической траектории. Тело удаляется на бесконечность, имея запас кинетической энергии.
Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля.
Первой космической скоростью называется скорость движения спутника по круговой орбите вблизи поверхности Земли.
Эту скорость необходимо набрать, чтобы преодолеть притяжение Земли и вывести тело (например, спутник) на орбиту Земли.
Второй космической скоростью называется минимальная скорость, которую нужно сообщить космическому кораблю у поверхности Земли, чтобы он, преодолев земное притяжение, превратился в искусственный спутник Солнца (искусственная планета). При этом корабль будет удаляться от Земли по параболической траектории.
Рис. 1.24.7 иллюстрирует космические скорости. Если скорость космического корабля равна υ1 = 7.9·103 м/с и направлена параллельно поверхности Земли, то корабль будет двигаться по круговой орбите на небольшой высоте над Землей. При начальных скоростях, превышающих υ1, но меньших υ2 = 11,2·103 м/с, орбита корабля будет эллиптической. При начальной скорости υ2 корабль будет двигаться по параболе, а при еще большей начальной скорости – по гиперболе.
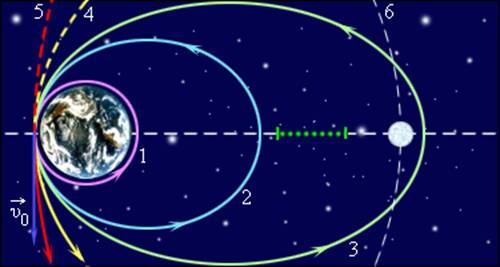 |
| Рисунок 1.24.7. Космические скорости. Указаны скорости вблизи поверхности Земли. 1: υ = υ1 – круговая траектория; 2: υ1 < υ < υ2 – эллиптическая траектория; 3: υ = 11,1·103 м/с – сильно вытянутый эллипс; 4: υ = υ2 – параболическая траектория; 5: υ > υ2 – гиперболическая траектория; 6: траектория Луны
Третья космическая скорость равна примерно 16,6·103 м/сек (при запуске на высоте 200 км над земной поверхностью) и необходима для преодоления гравитации сначала Земли, а затем и Солнца и выхода за пределы Солнечной системы. Сейчас два искусственных спутника развили такую скорость Пионер-10 и Пионер-11, запущенные 2 марта 1972 и 6 апреля 1973 года соответственно. В данный момент аппараты покинули пределы Солнечной системы. |
Цель урока: формирование понятия о
космическом явлении – движении космических тел.
Задачи обучения:
Общеобразовательные:
формирование понятий:
– о законах движения космических тел в
центральном поле тяготения (законах Кеплера);
– о траекториях движения (орбитах) космических
тел и их основных характеристиках;
– об астрономической единице измерения
межпланетных расстояний.
Воспитательные:
– формирование научного
мировоззрения в ходе знакомства с историей
человеческого познания и объяснения причин
небесных явлений, обусловленных движением
космических тел.
Развивающие:
– формирование умений решать задачи на
применение законов движения космических тел.
Ученики должны знать:
– законы движения космических тел в
центральных полях тяготения Кеплера;
– о связи между формой орбиты и скоростью
движения космических тел;
– значение астрономической единицы расстояний.
Ученики должны уметь: решать задачи на
применение законов движения космических тел.
Наглядные пособия и демонстрации:
презентация, для экономии времени каждый ученик
заполнит рабочий лист (приложение).
План урока
|
Этапы урока |
Содержание |
Методы изложения |
Время, мин |
| Проверка домашнего задания | Устные ответы учащихся | 7 | |
| Актуализация темы занятия | Фронтальный опрос, беседа | 2 | |
| Формирование понятий о движении космических тел и законах Кеплера |
Лекция | 20 | |
| Решение задач | Работа у доски, самостоятельное решение задач в тетради |
10 | |
| Астрономический диктант | Самостоятельная работа. Взаимопроверка работ. |
3 | |
| Обобщение пройденного материала, подведение итогов урока, домашнее задание |
3 |
Организационный момент (слайд 1)
Проверка домашнего задания
Устные ответы учащихся по теме “Конфигурации и
условия видимости планет”, используя для
ответов слайды 2,3.
Объяснение нового материала
Формирование понятий о движении космических
тел и законах Кеплера (слайд 4). Учащиеся
делают записи на листах опорного конспекта.
До Кеплера (слайд 5) считалось, что
движение небесных тел может происходить только
по “совершенной кривой” – окружности. Иоганн
Кеплер впервые разрушил этот предрассудок.
Используя многолетние наблюдения положения
Марса, выполненные датским астроном Тихо Браге,
Кеплер установил три закона движения планет
относительно Солнца.
I закон Кеплера (слайд 6)
Каждая планета движется по эллипсу, в
одном из фокусов которого находится Солнце.
Следовательно, орбиты всех планет
имеют общий фокус, расположенный в центре Солнца.
Эллипс – геометрическое место точек,
сумма расстояний которых от двух заданных,
называемых фокусами, есть величина постоянная и
равная 2а, где а – большая полуось эллипса.
Внимание вопрос на “5” (слайд 7): Кто
предложил остроумный и гениально простой способ
вычерчивания эллипса с помощью двух иголок и
связанной в кольцо нити? Способ был доложен на
заседании Эдинбургского Королевского общества,
но не автором, потому что ему было тогда только 15
лет”.
Ответ: Джеймс Клерк Максвелл
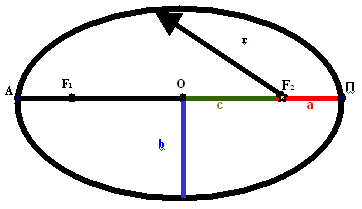
Рассмотрим важнейшие точки и линии
эллипса (слайд 8,9).
а – большая полуось,
b – малая полуось,
F1, F2 – фокусы,
r – радиус вектор,
А – афелий,
П – перигелий.
Перигелий – ближайшая к Солнцу точка
орбиты, а афелий – самая удаленная от Солнца
точка орбиты. Обе эти точки лежат на большой оси
орбиты по разные стороны от Солнца. Степень
вытянутости эллипса характеризуется
эксцентриситетом е (слайд 10).
с – расстояние от центра до фокуса, а
– большая полуось.
При совпадении фокусов с центром
(слайд 11) (е = 0) эллипс превращается в
окружность, при е = 1 становится параболой, при
е > 1 – гиперболой.
Орбиты планет – эллипсы (слайд 12), мало
отличаются от окружностей, так как их
эксцентриситеты малы. Например, еЗемли=0,017,
еМарса= 0,091.
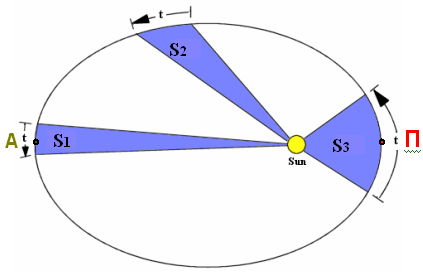
II закон Кеплера (закон равных площадей)
(слайд 13).
Радиус-вектора планеты за равные
промежутки времени описывает равновеликие
площади.
Радиус-вектор планеты – это
расстояние от Солнца до планеты.
Площади S1 и S2 равны (слайд
14), если дуги описаны заодно и тоже время. Дуги,
ограничивающие площади различны, следовательно,
линейные скорости движения планет будут разными.
Чем ближе планета к Солнцу, тем ее скорость
больше. В перигелии скорость планеты
максимальна, а в афелии – минимальна.
Таким образом, второй закон Кеплера
количественно определяет изменение скорости
движения планеты по эллипсу.
Первый и второй закон Кеплера были
опубликованы в 1608-1609 годах. Оба закона решают
задачу движения каждой планеты в отдельности.
Совершенно естественно у Кеплера возникла мысль
о существовании закономерности, связывающей все
планеты в единую стройную планетную систему.
Только в 1618 году Кеплер нашел и опубликовал в
книге “Гармония мира” эту закономерность,
известную под названием третьего закона Кеплера.
III закон Кеплера (слайд 15).
Квадраты периодов обращений планет
вокруг Солнца пропорциональны кубам больших
полуосей их эллиптических орбит.
Т1, а1 – звездный период
обращения и большая полуось одной планеты, а Т2,
а2 – другой планеты (слайд 16,17).
Большая полуось земной орбиты (слайд 18)
принята за астрономическую единицу
расстояний: 1 а. е. = 149000000000 м. Звездный период
Земли 1 год = 365 суток.
Этот закон имеет огромное значение для
определения относительных расстояний от Солнца,
так как звездный период нетрудно вычислить по
известному синодическому периоду.
Кеплер лишь описал, как движутся
планеты, но не объяснил причин движения. Это
удалось сделать лишь во второй половине 17 века
Ньютону.
Решение задач
Работа у доски, самостоятельное
решение задач в тетради.
Задача №1. (слайд 19) Противостояния
некоторой планеты повторяются через 2 года. Чему
равна большая ось ее орбиты? Ответ: 1,59а.е.
Задача №2. (слайд 20) Какова
продолжительность сидерического периода
вращения Юпитера вокруг Солнца, если он в 5 раз
дальше от Солнца, нежели Земля?
Дидактическая игра “Веришь – не
веришь” (слайд 21)
Учитель читает утверждение, если
ученик с ним согласен, то записывает в тетради
“5”, если не согласен – “0”.
- Орбиты всех планет Солнечной системы имеют
общий фокус. - Законы Кеплера применимы к искусственным
спутникам планет. - При движении планеты от перигелия к афелию
скорость планеты возрастает. - Потенциальная энергия планеты максимальна в
афелии. - Отношение кубов больших полуосей орбит двух
планет равно 16. Следовательно, период обращения
одной планеты больше периода другой в 4 раза.
Правильные ответы: 55055. (слайд 22)
Домашнее задание
1) Изучить материала учебника Е.П. Левитана § 9 (2)
2) Разгадать чайнворд “Законы Кеплера” (слайд 23)
- Мера сплюснутости эллипса.
- Имя датского ученого эпохи Возрождения. Он
первым в Европе начал проводить систематические
и высокоточные астрономические наблюдения. - Путь небесного тела в гравитационном поле
другого тела. - Малая планета Солнечной системы.
- Спутник Марса. Предположение об его
существовании высказал Иоганн Кеплер в 1610 году,
т. е. приблизительно за 270 лет до его
действительного открытия! Кеплер основывался на
логике, что если у Земли есть один спутник, а у
Юпитера — 4, то количество спутников возрастает в
геометрической прогрессии. По этой логике, у
Марса должно быть 2 спутника. - Центральное тело Солнечной системы, вокруг
которого обращаются другие объекты этой системы. - Спутник Юпитера, наименьший из четырёх
спутников, открытых Галилеем. Большая полуось –
671 тыс. км. Эксцентриситет – 0,0094. - Наиболее удаленная от центра точка орбиты.
- Точка небесной сферы, кажущаяся источником
метеоров, которые наблюдаются при встрече Земли
с роем метеорных тел, движущихся вокруг Солнца по
общей орбите. - Оптический прибор, предназначенный для
наблюдения неба. - Распространённая в астрономии внесистемная
единица измерения расстояния. - Немецкий математик, астроном, оптик и астролог.
Ответы:
ЭксцентриситеТихОрбитАстероиДеймоСолнцЕвропАпоцентРадианТелескоПарсеКеплер
Литература:
Единая коллекция цифровых образовательных
ресурсов – (http://school-collection.edu.ru/catalog/)
Приложение

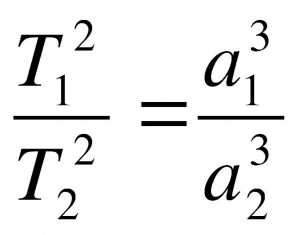








![{displaystyle {begin{aligned}a&={frac {r_{max }+r_{min }}{2}}\[3pt]a&={frac {p}{1-varepsilon ^{2}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82847fc5b12e705011877c295e4ed5b439a1ed30)
![{displaystyle {begin{aligned}b&={sqrt {r_{max }r_{min }}}\[3pt]b&={frac {p}{sqrt {1-varepsilon ^{2}}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03d3ca95934b7178477b3e16f3364de18f5fe6a9)





















































![{displaystyle {begin{aligned}tan ^{2}{frac {E}{2}}&={frac {1-cos E}{1+cos E}}={frac {1-{frac {varepsilon +cos theta }{1+varepsilon cos theta }}}{1+{frac {varepsilon +cos theta }{1+varepsilon cos theta }}}}\[8pt]&={frac {(1+varepsilon cos theta )-(varepsilon +cos theta )}{(1+varepsilon cos theta )+(varepsilon +cos theta )}}={frac {1-varepsilon }{1+varepsilon }}cdot {frac {1-cos theta }{1+cos theta }}={frac {1-varepsilon }{1+varepsilon }}tan ^{2}{frac {theta }{2}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bc0a064e24ecffca17176902230ccd78625ad9a)