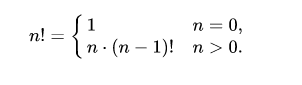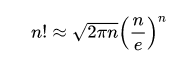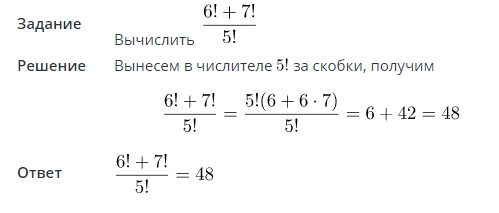Факториалы могут быть просты в вычислении и имеют множество практических применений в реальном мире. Например, некоторые компании используют факториал для анализа перестановок и комбинаций в деловых целях, например, для определения количества грузовиков, необходимых для снабжения магазинов в каждом районе. Вы можете использовать математические задачи с факториалами, если вы работаете в сфере логистики или в такой отрасли, как финансы или программное обеспечение.
В этой статье мы обсудим, что такое факториал, как вычислить факториал, приведем примеры факториалов и ответим на часто задаваемые вопросы о факториалах.
Что такое факториал?
Факториал — это функция в математике с символом (!), который умножает число (n) на каждое предшествующее ему число. Проще говоря, функция факториала означает умножение всех целых чисел от выбранного числа до единицы. В более математических терминах факториал числа (n!) равен n(n-1). Например, если вы хотите вычислить факториал для четырех, вы напишете:
4! = 4 x 3 x 2 x 1 = 24.
С помощью факториалов можно найти количество способов расположения (n) предметов. Когда порядок каждого элемента имеет значение, например, когда вы обсуждаете пароль к банковскому ящику, это перестановка. Если порядок не имеет значения, то это комбинация. Например, если вы хотите узнать, сколько комбинаций можно составить с трехзначным числом 725, вы найдете факториал 3!, которое
3! = 3 x 2 x 1 = 6.
Это означает, что существует шесть комбинаций, которые можно составить с числом 725: 725, 752, 572, 527, 275 и 257.
Формула факториала имеет вид:
n! = n*(n -1)!
Как вычислить факториал
Вы можете выполнить следующие шаги для решения факториала:
1. Определите число
Определите число, факториал которого вы хотите найти. Факториал имеет целое положительное число и восклицательный знак. Например, если вы хотите найти факториал для числа 8, математически это будет выглядеть следующим образом:
8!
2. Запишите последовательность
Используя формулу факториала, вы можете выписать последовательность чисел, которые вы будете умножать. Сюда входит число, для которого вы находите факториал, в данном примере это число 8, а также все числа, последовательно убывающие от него до единицы. Математически это будет выглядеть так:
n! = n(n-1) =
8(8 ? 1)(8 ? 2)(8 ? 3)(8 ? 4)(8 ? 5)(8 ? 6)(8 ? 7)
3. Умножьте числа
После того, как вы записали последовательность чисел, вы можете перемножить их вместе. Если вы перемножите все числа в этом примере, 8 ? 7 ? 6 ? 5 ? 4 ? 3 ? 2 ? 1, вы получите окончательный ответ 40 320. Математически это выглядит следующим образом:
n! = n(n-1) =
8(8 ? 1)(8 ? 2)(8 ? 3)(8 ? 4)(8 ? 5)(8 ? 6)(8 ? 7) =
8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40 320
Вы также можете вычислить факториал с помощью научного калькулятора. На калькуляторе должна быть кнопка с надписью x! знак. Введите число, для которого вы хотите найти факториал, в данном случае число восемь, а затем нажмите кнопку x! кнопка. Калькулятор должен выдать тот же ответ — 40 320.
Примеры
Вот несколько примеров задач, в которых используются факториалы:
Пример 1
Задача: Сколькими способами можно расположить буквы в слове компания не повторяя их?
Для решения этой задачи подсчитайте количество букв в слове компания чтобы найти шесть букв. Затем найдите факториал числа шесть вручную или с помощью научного калькулятора. Если вы решите задачу вручную, она должна выглядеть следующим образом:
n! = n(n-1) =
6(6 ? 1)(6 ? 2)(6 ? 3)(6 ? 4)(6 ? 5) =
6 x 5 x 4 x 3 x 2 x 1 = 720
Теперь вы знаете, что максимальное количество способов, которыми можно расположить буквы в слове компания без повторений — 720.
Пример 2
Задача: Какие комбинации можно составить из красного, синего и зеленого цветов??
Для этой задачи найдите факториал для числа три, поскольку существует три цвета, а затем перечислите различные комбинации. Если вы решите эту задачу вручную, она должна выглядеть следующим образом:
n! = n(n-1) =
3(3 ? 1)(3 ? 2) =
3 x 2 x 1 = 6
Шесть комбинаций:
красный, синий, зеленый
красный, зеленый, синий
зеленый, синий, красный
зеленый, красный, синий
синий, красный, зеленый
синий, зеленый, красный
Пример 3
Задача: Найти факториал числа 15.
Хотя эту задачу можно решить вручную, это может занять много времени, потому что 15 — большое число. Проще использовать научный калькулятор. Чтобы решить эту задачу с помощью калькулятора, необходимо:
-
Введите в калькулятор число 15.
-
Нажмите кнопку x! кнопка на калькуляторе.
-
Ответ 1,307,674,368,000 должен появиться на калькуляторе.
Часто задаваемые вопросы о факториалах
Вот некоторые ответы на распространенные вопросы о факториалах:
Можете ли вы найти факториал для числа ноль?
Да, вы можете найти факториал для числа ноль. Математики согласны с тем, что факториал числа ноль равен единице, или 0! =1. Может показаться странным, что 0! =1, но это легко понять, если следовать схеме обратных факториалов. Посмотрите на эту схему, начинающуюся с 4!:
4! = 24
3! = 6
2! = 2
1! = 1
0! = 1
Вы можете заметить, что каждый ответ делится последовательно, и по мере того, как вы следуете шаблону, он предсказывает следующий ответ и показывает, что 0! =1. Последовательные кратные номера выделены жирным шрифтом:
4! = 24, (24 ? 4 = 6)
3! = 6, (6 ? 3 = 2)
2! = 2, (2 ? 2 = 1)
1! = 1, (1 ? 1 = 1)
0! = 1
Можете ли вы найти факториал для отрицательного числа?
Нет, вы не можете найти факториал для отрицательного числа. Чтобы найти факториал отрицательного целого числа, нужно разделить его на ноль. Однако деление на ноль не определено. Таким образом, отрицательные целочисленные факториалы являются неопределенными.
Можете ли вы найти факториал десятичной дроби?
Да, вы можете найти факториал десятичной дроби. Если вы хотите узнать, как найти факториал десятичной дроби, вы можете познакомиться с гамма-функцией, которую также иногда называют гамма-функцией половинные факториалы. Эти задачи быстро усложняются. Например, факториал для одной половины, или .5 — половина квадратного корня из числа пи, или (-12)! = v?.
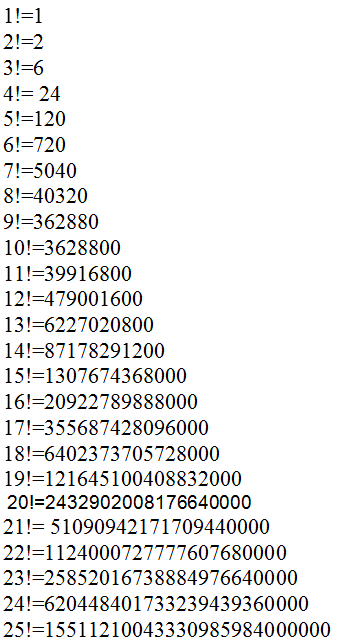
Что такое первые 15 факториалов?
Как видно из этой диаграммы, факториалы растут очень быстро. Для решения факториальных задач может быть полезно использовать научный калькулятор, особенно при работе с большими числами.
nn!
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5,040 |
| 8 | 40,320 |
| 9 | 362,880 |
| 10 | 3,628,800 |
| 11 | 39,916,800 |
| 12 | 479,001,600 |
| 13 | 6,227,020,800 |
| 14 | 87,178,291,200 |
| 15 | 1,307,674,368,000 |
In math, a Factor is a number or algebraic expression that is an exact divisor with no remainder. An integer that has the factors one and itself is known as prime factors. The integer that has more than two factors is known as composite factors. Let us learn more about the factors from this article. Go through the below section to know how to find the factors of the numbers from here.
Do refer:
- Worksheet on Factors and Multiples
- Methods of Prime Factorization
- Examples on Multiples
Factor – Definition
A factor is derived from the Latin word which means “a maker” or “a doer” or “a performer”. A factor is a whole number that can be multiplied by another whole number to produce a whole number.
Factor × Factor = Multiple
Types of Factors
There are two types of factors. They are
1. Prime factors
2. Composite Factors
Prime Factors
Prime factors of a number are the set of prime numbers which when multiplied by together give the actual number. The prime numbers are 2, 3, 5, 7, 11, 13, 17,….
Example:
Write the prime factors for 6.
Solution:
1 × 6 = 6
2 × 3 = 6
3 × 2 = 6
6 × 1 = 6
2 and 3 are the prime numbers.
Hence, 2 and 3 are the prime factors of 6.
Composite Factors
Composite factors of a number are the factors that are not prime. That means the numbers which have more than two factors are known as the composite factors.
Example:
Write the composite factors of 12.
Solution:
1 × 12 = 12
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
12 × 1 = 12
Thus the factors of 12 are 1, 2, 3, 4, 6, 12.
How to Find Factors of a Number?
We can find the factors of a number by using both the division method and the multiplication method. First, we will see how to find the factors of a number by division.
Factors by Division
1. Find the numbers less than or equal to the given number.
2. Now divide the given number by each of the numbers.
3. The remainder should be 0.
For example, let us divide 6 and 3
6 ÷ 3 = 2
Thus the factors of 6 are 2 and 3 as the remainder leaves zero.
Factors by Multiplication
Follow the below steps to find the factors using the multiplication method.
1. First write the given numbers as the product of two numbers in possible ways.
2. All the numbers involved in all these products are the factors of the given number.
3. With this we can find whether the given number is a prime factor or composite factor.
For example, write the factors of 12.
1 × 12 = 12
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
12 × 1 = 12
Thus the factors of 12 are 1, 2, 3, 4, 6 and 12.
Solved Problems on Finding Factors
Example 1.
Find the factors of 16.
Solution:
The factors of 16 are as follows
1 × 16
2 × 8
4 × 4
8 × 2
16 × 1
Therefore the factors of 16 are 1, 2, 4, 8, 16.
Example 2.
Write the prime factors for 15.
Solution:
Prime factors of a number are the set of prime numbers which when multiplied by together give the actual number.
We have to multiply directly with the prime number to find the factors of 15.
15 = 3 × 5
Thus the prime factors of 15 are 3, 5.
Example 3.
Find the Missing Factors of the following
i. 2 × _ = 10
ii. _ × 7 = 21
iii. 7 × _ = 49
iv. 9 × _ = 54
v. 10 × _ = 30
Solution:
i. 2 × _ = 10
Let the missing factor be x.
2 × x = 10
x = 10 ÷ 2
x = 5
Thus the missing factor is 5.
ii. _ × 7 = 21
Let the missing factor be a.
a × 7 = 21
a = 21 ÷ 7
a = 3
Thus the missing factor is 3.
iii. 7 × _ = 49
Let the missing factor be b.
7 × b = 49
b = 49 ÷ 7
b = 7
Thus the missing factor is 7.
iv. 9 × _ = 54
Let the missing factor be c.
9 × c = 54
c = 54 ÷ 9
c = 6
Thus the missing factor is 6.
v. 10 × _ = 30
Let the missing factor be y.
10 × y = 30
y = 30 ÷ 10
y = 3
Thus the missing factor is 3.
Example 4.
What are the factors of 72?
Solution:
The factors of 72 are
1 × 72
2 × 36
3 × 24
4 × 18
6 × 12
8 × 9
9 × 8
12 × 6
18 × 4
24 × 3
36 × 2
72 × 1
Therefore the factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 and 72
Example 5.
What are the factors of 120?
Solution:
The factors of 120 are
1 × 120
2 × 60
3 × 40
4 × 30
5 × 24
6 × 20
8 × 15
10 × 12
12 × 10
15 × 8
20 × 6
24 × 5
30 × 4
40 × 3
60 × 2
120 × 1
Therefore the factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 24, 30, 40, 60 and 120
Example 6.
Write the common factors of 21.
Solution:
Multiples of 3 – 3, 6, 9, 12, 15, 18, 21, 24.
Multiples of 7 – 7, 14, 21, 28.
Thus the common factors of 21 are 3 and 7.
FAQs on Factors
1. Define Factor
Factors are the numbers you multiply together to get another number. The factor may be both positive integer and negative integer.
2. What are the factors of 18?
The factors of 18 are
1 × 18
2 × 9
3 × 6
6 × 3
9 × 2
18 × 1
Thus the factor of 18 is 1, 2, 3, 6, 9, 18.
3. What are the types of factors?
There are three types of factors. They are
1. Direct
2. Distributed
3. Augmentative
Если вы знаете основы умножения и деления, вы уже знаете все навыки, которые вам необходимо учитывать. Числовые коэффициенты — это просто любые числа, которые можно умножить для создания этого числа. Вы также можете разложить число, разделив его на несколько раз. В то время как факторинг больших чисел поначалу может показаться сложным, есть несколько простых приемов, которые вы можете узнать, чтобы быстро найти факторы числа.
Факторы числа
Вы можете найти факторы числа, найдя все термины, которые умножаются вместе, чтобы создать это число. Например, факторы 14 равны 1, 2, 7 и 14, так как,
14 = 1 х 14 14 = 2 х 7
Чтобы полностью вычислить число, уменьшите его до его простых чисел. Они упоминаются как «главные факторы числа». Например, 6 и 8 являются коэффициентами 48, так как, 6 х 8 = 48.
Но 6 и 8 не являются простыми числами, потому что они имеют факторы, отличные от 1 и самих себя. Чтобы полностью уменьшить 48 до его основных факторов, нужно также учитывать 6 и 8.
2 х 3 = 6 2 х 2 х 2 = 8
Итак, главные факторы 48, 3 х 2 х 2 х 2 х 2 = 48
Факторинг Деревья
Вы можете использовать дерево факторинга, чтобы легко визуализировать разбиение большого числа на его основные факторы. Поместите число, которое вы хотите вычислить в верхней части выражения, и разделите его на шаги по коэффициентам. Каждый раз, когда вы делите число, поместите два фактора числа ниже. Продолжайте деление, пока все числа не будут уменьшены до их основных факторов. Например, вы можете разложить 156 с помощью дерева факторов следующим образом:
2 78 / 2 39 / 3 13
Теперь вы можете легко увидеть основные факторы 156:
2 х 2 х 3 х 13 = 156
Вы также можете разделить на составные (или не простые) факторы, чтобы создать дерево факторов. Когда вы делите на составной фактор, вы делите составной фактор на его основные факторы. Например, вы можете вычислить фактор 192, используя составные или простые факторы следующим образом:
4 2 2 12 3 32 / / / 2 2 3 4 2 16 / / 2 4 2 8 / 2 4 / 2 2
Итак, главные факторы 192
2 х 2 х 2 х 2 х 2 х 3 = 192
Факторинг с переменными
Переменные выражения — да, те, в которых есть буквы — также имеют свои факторы. Если переменная умножается на константу (определенное число), переменная является одним из факторов выражения. Например,
4y = 2 x 2 xy
Вы можете найти факторы для выражений, которые включают как переменные, так и константы. Например, вы можете разложить выражение 6y — 21 на 3, так как 6 и 21 делятся на три. Это оставляет вас с
6y — 21 = 3 (2y — 7)
Величайшие общие факторы
После того, как вы освоили основы факторинга, у вас может возникнуть проблема, которая требует от вас найти наибольший общий множитель из двух чисел или выражений. Вы можете найти наибольший общий фактор, создав список факторов обоих чисел. Наибольшим общим фактором является просто наибольшее число, которое появляется в обоих списках.
Например, Коэффициенты 48: 1, 2, 3, 4, 6, 8, 12, 16, 24 и 48 Коэффициенты 56: 1, 2, 4, 7, 8, 14, 28 и 56
Если вы сравните два набора факторов, наибольшее число в обоих наборах равно 8. Таким образом, наибольший общий коэффициент равен 8.
Вы также можете использовать списки факторов, чтобы найти наибольший общий множитель двух выражений переменных. Допустим, вам дали следующие выражения:
8й 14й ^ 2 — 6й
Сначала найдите все факторы каждого выражения. Помните, что вы можете включать переменные в факторы выражения.
Коэффициенты для 8y: 1, y, 2, 2y, 4, 4y, 8 и 8y. Коэффициенты для 14y ^ 2 — 6y: 1, y, 2, 2y, 7y — 3, 7y ^ 2 — 3y, 14y — 6, а 14й ^ 2 — 6й
Таким образом, наибольшим общим фактором обоих выражений является 2y. Обратите внимание, что 2 не является наибольшим общим фактором, так как выражения, разделенные на 2 (4y и 7y ^ 2 — 3y), оба могут быть разделены на y.
Инструкции:
Используйте эту простую факторизацию для вычисления факторов и простого разложения заданного числа, которое вы укажете в поле ниже.
Как использовать этот калькулятор факторизации простых чисел
Данный калькулятор предоставит вам факторы и соответствующее простое разложение заданного числа. Итак, вам необходимо указать действительное целое положительное число.
После этого необходимо нажать кнопку «Рассчитать», чтобы отобразились все этапы расчета.
Как вычислить простое разложение
Все, что вам нужно сделать, это найти факторы соответствующего числа. Затем эти факторы группируются, и каждому из них соответствует экспонента (отражающая количество раз, которое соответствующее простое число встречается в факторизации).
Каковы этапы факторизации простых чисел
- Шаг 1: Определите число, которое вы хотите разделить на множители. Оно должно быть целым положительным числом, иначе вы не сможете продолжить
- Шаг 2: Найдите ВСЕ коэффициенты числа
- Шаг 3: Подсчитайте, сколько раз каждый фактор встречается в разложении
Зачем нужно иметь дело с простыми числами?
Хотя они не рассматриваются в базовой алгебре, простые числа играют важнейшую роль в математике, а не только в алгебре. Кажется, что простые числа обладают какой-то магической силой и обладают невероятными свойствами.
На базовом уровне, давайте рассмотрим тот факт, что каждое положительное целое число допускает одно и только одно простое разложение, как достаточно важное свойство.
Пример: вычисление простого разложения
Вычислите простую факторизацию числа 3468.
Решение:
Сначала нужно найти все возможные простые делители числа (n = 3468). В данном случае установлено, что
[3468 = 2cdot2cdot3cdot17cdot17]
Теперь, группируя найденные выше делители, получаем следующее простое разложение в экспоненциальной форме:
[3468 = 2^2cdot3cdot17^2]
Это завершает процесс вычисления разложения простого числа, поскольку никакие факторы не могут быть разложены дальше.
Пример: другое простое число
Найдите коэффициенты числа 16.
Отвечать:
< Сначала нужно найти все возможные простые делители (n = 16). В данном случае установлено, что
[16 = 2cdot2cdot2cdot2]
Теперь, группируя найденные выше делители, получаем следующее простое разложение в экспоненциальной форме:
[16 = 2^4]
Это завершает процесс вычисления разложения простого числа, поскольку никакие факторы не могут быть разложены дальше.
Пример: другое простое число
Найдите коэффициенты числа 137.
Отвечать:
Необходимо найти все возможные простые делители числа (n = 137). В этом случае выясняется, что число (n = 137) не имеет факторов, а значит, оно простое, следовательно, простым разложением (n = 137) является оно само.
Это завершает процесс вычисления разложения простого числа, поскольку никакие факторы не могут быть разложены дальше.
Пример: прайм-разложения и праймы
Является ли 341 простым числом?
Отвечать:
Сначала нужно найти все возможные простые делители числа (n = 341). В данном случае установлено, что
[341 = 11cdot31]
Поскольку существует коэффициент (11), который не является ни 1, ни 341, мы заключаем, что 341 является простым.
Больше калькуляторов по алгебре
Алгебра — очень важная отрасль математики, возможно, самая важная, поскольку она обеспечивает базовые основы для большинства других математических областей.
Что касается калькуляторов по алгебре, вас могут заинтересовать
вычисление общих алгебраических выражений
или также с точки зрения вычисления
наименьшее общее кратное
между двумя числами, и это лишь некоторые из них.
Математическая формула представлена восклицательным знаком «!». Термин был введен в 1800 году, а обозначение появилось только в 1808. В формуле нужно умножить все целые числа от 1 до значения самого числа, стоящего под знаком факториала.
Это очень просто, вот пример:
7! = 1 * … * 7 = 5040.
Факторизация — разложение функции на множители.
Таблица факториалов
Свойства факториалов
Рекуррентная формула
Комбинаторная интерпретация
Функция n может интерпретироваться как количество перестановок. К примеру, для 3-х элементов есть 3! = 6 перестановки.
Формула Стирлинга
Позволяет не перемножать большие числа. Обычно необходим только главный член:
Можно ли вычислить 0,5 или -3,217? Нет, нельзя. Но можно использовать нечто под названием «Гамма-функция», что намного сложнее.
Расчет по предыдущему значению
Функцию легко вычислить из предыдущего значения:
-
3! = 3 × 2! = 6;
-
41160 = 5! +8! + 6!
А как вычислить факториал нуля? Если вернуться к определению, то видно, что применять его в случае «0» нет смысла. Положительных чисел до 0 нет, поэтому 0 x 0 = 0.
Однако было решено, что в случае 0 результат будет равен 1.
Некоторые очень большие значения
Онлайн калькулятор поможет сделать вычисление – всего лишь надо найти знак, похожий на «x!» или «n!». Нужно обратить внимание, что браузеры могут испытывать затруднения при попытке отобразить более крупные числа и может произойти сбой.
Некоторые браузеры могут не позволять копировать, поэтому необходимо будет загрузить большие результаты в виде текстового файла.
Примеры вычисления факториалов больших чисел:
-
70! приблизительно 1 19785716669969869891796072783721 x 10100, что немного больше, чем «гуголь» (1 и 100 нулей);
-
100! это примерно 9 33262154444944152681699238856 x 101576 x 10157;
-
200! это примерно 7 88657867867364479050355236321393 x 103743.
Как найти функцию в Паскаль? Вычисление легко реализуется на разных языках программирования. Можно выбрать два метода: итеративный, то есть он создает цикл, в котором временная переменная умножается на каждое натуральное число от 1 до n, или рекурсивный, в котором функция вызывает себя до достижения базового варианта 0! = 1.
Программа на языке Паскаль:
На языке Си вычисления делаются с помощью рекурсивной функции. Следует заметить, что если начать вычислять факториал отрицательного числа в неаккуратно написанной функции, то это приведет к зацикливанию.
Факториал дроби (½) — это половина квадратного корня pi = (½)√π.
Примеры задач с решениями
Задание 1
Задание 2
Использование факториалов
Математика и многие ее области используют функцию. В комбинаторике функция была введена именно для расчета перестановки. Также понятие тесно связано с биномом ньютона (формула бинома Ньютона необходима для разложения степени (x + y) n в многочлен).