Как найти факторгруппу группы

Значение
нормального делителя в теории групп
основано на том, что из смежных классов
по нормальному делителю может быть
построена новая
группа. Для
построения такой группы определим
операцию умножения на множестве смежных
классов. Пусть
,
тогда

(2.64)

Действительно,
для

Пусть
H
– нормальный делитель группы G.
В этом случае произведение двух смежных
классов G
по H
будет смежным классом по H.
Действительно,
имеем:

(2.65)

Таким
образом, в множестве всех смежных классов
по нормальному делителю определена
операция умножения.
Это означает, что фактор-множество

. (2.66)

является
замкнутым относительно операции
умножения смежных классов, а операция
умножения смежных классов является
алгебраической. Равенство (2.65) показывает,
что для нахождения произведения двух
данных смежных классов группы G
по нормальному делителю H
надо в каждом из этих классов выбрать
по одному представителю и потом взять
тот смежный класс, к которому принадлежит
произведение выбранных представителей.

В
случае если
– абелева группа бинарная операция на
фактор-множествевводится соотношением.
Фактор-группучасто называют группойпо модулю.

Теорема. Фактор-множество
смежных классов группыG
по нормальному делителю H
с определенной в нем операцией умножения
является группой. Эта группа называется
фактор-группой группы G
по нормальному делителю H
и обозначается символом
.

Доказательство. Для
доказательства покажем, что в
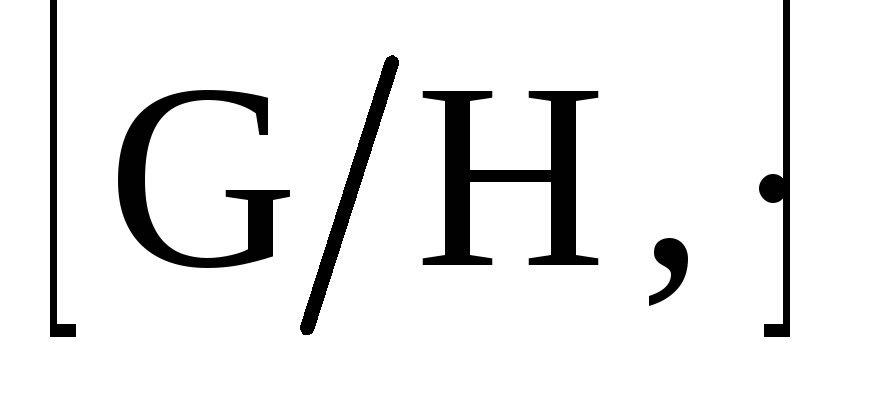
будут выполнены все аксиомы группы:

ассоциативность
умножения смежных классов следует из
ассоциативности умножения подмножеств
группы;
роль
единицы играет сама подгруппа
– нормальный делитель:
для
смежного класса
обратным является классдействительно:

Выводы. Со
всякой группой G
связан целый набор новых групп – ее
фактор-групп [G/H,
]
по различным нормальным делителям.

Примеры. 1. Пусть
– аддитивная группа целых чисел , а– подгруппа целых чисел, делящихся наm
без остатка. Подгруппа
– нормальный делитель так как– подгруппа аддитивной группы.

Фактор-группа
состоит из смежных классов– классов вычетов по модулю:

Класс
вычетов

Пусть
,
тогда таблица Кэли для фактор-группыимеет вид:

+	[0]₅	[1]₅	[2]₅	[3]₅	[4]₅
[0]₅	[0]₅	[1]₅	[2]₅	[3]₅	[4]₅
[1]₅	[1]₅	[2]₅	[3]₅	[4]₅	[0]₅
[2]₅	[2]₅	[3]₅	[4]₅	[0]₅	[1]₅
[3]₅	[3]₅	[4]₅	[0]₅	[1]₅	[2]₅
[4]₅	[4]₅	[0]₅	[1]₅	[2]₅	[4]₅

Выводы: 1. Фактор-группа
коммутативна – таблица Кэли симметрична
относительно главной диагонали.

2. Фактор-группа
циклическая группа.
Система образующих состоит из одного
элемента – смежного класса,
а все остальные смежные классы совпадают
с его степенями.

2. Пусть
– мультипликативная группа невырожденных
матриц-го
порядка с вещественными коэффициентами,
а– нормальный делитель этой группы,
который состоит из матриц, детерминант
каждой из которых равен единице.
Фактор-группасостоит из смежных классов, каждый из
которых содержит все матрицы, детерминант
которых равен данному числу.

Соседние файлы в папке ЛЕКЦИИ АиГ

Источник

Материал из Викиконспекты

Перейти к: навигация, поиск

Факторгруппа

Рассмотрим группу и ее нормальную подгруппу . Пусть — множество смежных классов по . Определим в групповую операцию по следующему правилу.

Определение:

Произведением смежностных классов и назовем смежностный класс .

Утверждение:

Определение произведения смежных классов корректно. То есть произведение смежных классов не зависит от выбранных представителей и .

Пусть . Докажем, что . Достаточно показать, что .

В самом деле, . Элемент лежит в по свойству нормальности . Следовательно, .

Определение:

Таким образом, множество смежных классов с введенной на нем операцией произведения образует группу, которая называется факторгруппой по . Нейтральным элементом является , обратным к — .

Примеры

Рассмотрим и её нормальную подгруппу , тогда (группы вычетов по модулю ) будет являться факторгруппой G по H.
Рассмотрим группу невырожденных матриц . Отображение является гомоморфизмом . Ядро — группа матриц с единичным определителем . Поэтому является нормальной подгруппой в и факторгруппа .

Утверждение:

В группе перестановок из трех элементов и ее не нормальной подгруппе перестановок из двух элементов не затрагивающих третий элемент, не будет являться группой.

Рассмотрим группу (перестановки трех элементов) и ее не нормальную подгруппу (перестановки не затрагивающие третий элемент). Рассмотрим множество перестановок :

класс и ,

класс и .

Это смежные классы для . Теперь рассмотрим произведения:

Противоречие. То есть согласованного с группой умножения нет. не является группой.

Источник

Пусть — группа, и — её нормальная подгруппа , то есть для любого элемента его правый и левый классы смежности совпадают:

Тогда на классах смежности в можно ввести умножение:

Легко проверить что это умножение не зависит от выбора элементов в классах смежности, то есть если и то .
Оно определяет структуру группы на множестве классов смежности, а полученная группа называется факторгруппой по .

Факторгруппа обозначается .

Свойства

Гомоморфный образ группы
(До победы коммунизма)
Изоморфен факторгруппе
По ядру гомоморфизма

Теорема о гомоморфизме: Для любого гомоморфизма

{displaystyle G/{rm {Ker}}phi cong phi (G)}

т.е. фактор группы

по ядру

изоморфен её образу

Примеры

Пусть = , = 2, тогда изоморфна ${displaystyle mathbb {Z} _{2}}$ .

Пусть G = UT_n (группа невырожденных верхних треугольних матриц), H = SUT_n (группа верхних унитреугольных матриц), тогда G/H изоморфна группе диагональных матриц.

См. также

Для других алгебраических структур, а также множеств, также определены понятия факторов: фактормножество, факторкольцо, факторалгебра, факторполе.

cs:Faktorová grupa
he:חבורת מנה
nl:Factorgroep
pl:Grupa ilorazowa

Источник

Фактор-группой группы С по нормальному делителю Я называется группа всех смежных классов этой группы С по подгруппе Я.

Таким образом, с группой О можно связать некоторый набор новых групп — ее фактор-групп по различным нормальным делителям.

Отметим, что фактор-группа абелевой группы является абелевой; факторгруппа циклической группы — циклической группой.

Примеры фактор-групп.

1. Пусть С — аддитивная группа целых чисел, Я — подгруппа чисел, делящихся на 3. Найдем фактор группу С/Я. Групповой операцией в данном случае является сложение. Число смежных классов равно трем (см. пример в п. 12.7): множество чисел, делящихся на 3, два множества чисел, дающих при делении на 3 соответственно остатки 1 и 2. Обозначим эти смежные классы [0], [1], [2]. В этом множестве введем операцию сложения следующим образом: сложив соответствующие числа в квадратных скобках, определим, какой остаток при делении на 3 дает их сумма, и будем считать суммой смежных классов тот, которому принадлежит полученный остаток. Таблица умножения для фактор-группы имеет вид [0]+[0] = [1]+[2] = [2]+[1] = [0], [0]+[1] = [1]+[0] = [2]+[2] = [1], [0]+[2] = [2]+[0] = [1]+[1 ]= [2]. Отсюда видно, что фактор-группа абелева. Кроме того, все смежные классы порождаются классом [1], они совпадают со степенями этого класса: [1], Р]+П]=[2], [1]+[1]+[1] = [0]. Поскольку фактор-группа порождена одним элементом, то она циклическая.

2. Пусть— аддитивная группа целых чисел,— подгруппа целых чисел, кратных натуральному числуФактор-группойЯвляется конечная

Группа порядкаСостоящая из классовЭта фактор

Группа циклическая, как и сама группа

3. Пусть— мультипликативная группа всех невырожденных матриц порядка— подгруппа матриц с определителем, равным единице. Фактор-группаИзоморфна мультипликативной группе отличных от нуля действительных чисел.

< Предыдущая		Следующая >

Источник

A quotient group or factor group is a mathematical group obtained by aggregating similar elements of a larger group using an equivalence relation that preserves some of the group structure (the rest of the structure is «factored» out). For example, the cyclic group of addition modulo n can be obtained from the group of integers under addition by identifying elements that differ by a multiple of and defining a group structure that operates on each such class (known as a congruence class) as a single entity. It is part of the mathematical field known as group theory.

For a congruence relation on a group, the equivalence class of the identity element is always a normal subgroup of the original group, and the other equivalence classes are precisely the cosets of that normal subgroup. The resulting quotient is written , where is the original group and is the normal subgroup. (This is pronounced , where is short for modulo.)

Much of the importance of quotient groups is derived from their relation to homomorphisms. The first isomorphism theorem states that the image of any group G under a homomorphism is always isomorphic to a quotient of . Specifically, the image of under a homomorphism is isomorphic to where denotes the kernel of varphi .

The dual notion of a quotient group is a subgroup, these being the two primary ways of forming a smaller group from a larger one. Any normal subgroup has a corresponding quotient group, formed from the larger group by eliminating the distinction between elements of the subgroup. In category theory, quotient groups are examples of quotient objects, which are dual to subobjects.

Definition and illustration[edit]

Given a group and a subgroup , and an element , one can consider the corresponding left coset: . Cosets are a natural class of subsets of a group; for example consider the abelian group G of integers, with operation defined by the usual addition, and the subgroup of even integers. Then there are exactly two cosets: , which are the even integers, and , which are the odd integers (here we are using additive notation for the binary operation instead of multiplicative notation).

For a general subgroup , it is desirable to define a compatible group operation on the set of all possible cosets, . This is possible exactly when is a normal subgroup, see below. A subgroup of a group is normal if and only if the coset equality holds for all . A normal subgroup of is denoted .

Definition[edit]

Let be a normal subgroup of a group . Define the set to be the set of all left cosets of in . That is, . Since the identity element , . Define a binary operation on the set of cosets, , as follows. For each and in , the product of and , , is . This works only because does not depend on the choice of the representatives, and , of each left coset, and . To prove this, suppose and for some . Then

{textstyle (ab)N=a(bN)=a(yN)=a(Ny)=(aN)y=(xN)y=x(Ny)=x(yN)=(xy)N}

This depends on the fact that N is a normal subgroup. It still remains to be shown that this condition is not only sufficient but necessary to define the operation on G/N.

To show that it is necessary, consider that for a subgroup of , we have been given that the operation is well defined. That is, for all and , for .

Let nin N and gin G . Since , we have .

Now, ${displaystyle gN=(ng)NLeftrightarrow N=(g^{-1}ng)NLeftrightarrow g^{-1}ngin N,;forall ,nin N}$ and gin G .

Hence is a normal subgroup of .

It can also be checked that this operation on is always associative, has identity element , and the inverse of element can always be represented by ${displaystyle a^{-1}N}$ . Therefore, the set together with the operation defined by forms a group, the quotient group of by .

Due to the normality of , the left cosets and right cosets of in are the same, and so, could have been defined to be the set of right cosets of in .

Example: Addition modulo 6[edit]

For example, consider the group with addition modulo 6: . Consider the subgroup , which is normal because is abelian. Then the set of (left) cosets is of size three:

{displaystyle G,/,N=left{a+N:ain Gright}=left{left{0,3right},left{1,4right},left{2,5right}right}=left{0+N,1+N,2+Nright}}

The binary operation defined above makes this set into a group, known as the quotient group, which in this case is isomorphic to the cyclic group of order 3.

Motivation for the name «quotient»[edit]

The reason is called a quotient group comes from division of integers. When dividing 12 by 3 one obtains the answer 4 because one can regroup 12 objects into 4 subcollections of 3 objects. The quotient group is the same idea, although we end up with a group for a final answer instead of a number because groups have more structure than an arbitrary collection of objects.

To elaborate, when looking at with a normal subgroup of , the group structure is used to form a natural «regrouping». These are the cosets of in . Because we started with a group and normal subgroup, the final quotient contains more information than just the number of cosets (which is what regular division yields), but instead has a group structure itself.

Examples[edit]

Even and odd integers[edit]

Consider the group of integers (under addition) and the subgroup consisting of all even integers. This is a normal subgroup, because is abelian. There are only two cosets: the set of even integers and the set of odd integers, and therefore the quotient group is the cyclic group with two elements. This quotient group is isomorphic with the set with addition modulo 2; informally, it is sometimes said that equals the set with addition modulo 2.

Example further explained…

Let

be the remainders of

when dividing by

. Then,

when

is even and

when

is odd.

By definition of gamma

, the kernel of gamma

{displaystyle ={min mathbb {Z} :gamma (m)=0}}

, is the set of all even integers.

Let

. Then,

is a subgroup, because the identity in

, which is

, is in

, the sum of two even integers is even and hence if

and

are in

is in

(closure) and if

is even,

is also even and so

contains its inverses.

Define

/ H ${displaystyle to mathbb {Z} _{2}}$

for

and

/ H is the quotient group of left cosets;

/ H

Note that we have defined

is odd and

is even.

Thus,

is an isomorphism from

/ H to ${displaystyle mathbb {Z} _{2}}$

Remainders of integer division[edit]

A slight generalization of the last example. Once again consider the group of integers under addition. Let n be any positive integer. We will consider the subgroup of consisting of all multiples of . Once again is normal in because is abelian. The cosets are the collection . An integer belongs to the coset , where is the remainder when dividing by . The quotient can be thought of as the group of «remainders» modulo . This is a cyclic group of order .

Complex integer roots of 1[edit]

The cosets of the fourth roots of unity N in the twelfth roots of unity G.

The twelfth roots of unity, which are points on the complex unit circle, form a multiplicative abelian group , shown on the picture on the right as colored balls with the number at each point giving its complex argument. Consider its subgroup made of the fourth roots of unity, shown as red balls. This normal subgroup splits the group into three cosets, shown in red, green and blue. One can check that the cosets form a group of three elements (the product of a red element with a blue element is blue, the inverse of a blue element is green, etc.). Thus, the quotient group is the group of three colors, which turns out to be the cyclic group with three elements.

The real numbers modulo the integers[edit]

Consider the group of real numbers under addition, and the subgroup of integers. Each coset of in is a set of the form , where is a real number. Since ${displaystyle a_{1}+mathbb {Z} }$ and ${displaystyle a_{2}+mathbb {Z} }$ are identical sets when the non-integer parts of $a_{1}$ and $a_{2}$ are equal, one may impose the restriction without change of meaning. Adding such cosets is done by adding the corresponding real numbers, and subtracting 1 if the result is greater than or equal to 1. The quotient group is isomorphic to the circle group, the group of complex numbers of absolute value 1 under multiplication, or correspondingly, the group of rotations in 2D about the origin, that is, the special orthogonal group . An isomorphism is given by (see Euler’s identity).

Matrices of real numbers[edit]

If is the group of invertible real matrices, and is the subgroup of real matrices with determinant 1, then is normal in (since it is the kernel of the determinant homomorphism). The cosets of are the sets of matrices with a given determinant, and hence is isomorphic to the multiplicative group of non-zero real numbers. The group is known as the special linear group .

Integer modular arithmetic[edit]

Consider the abelian group ${displaystyle mathbb {Z} _{4}=mathbb {Z} ,/,4mathbb {Z} }$ (that is, the set with addition modulo 4), and its subgroup . The quotient group ${displaystyle mathbb {Z} _{4},/,left{0,2right}}$ is . This is a group with identity element , and group operations such as . Both the subgroup and the quotient group are isomorphic with $mathbb{Z } _{2}$ .

Integer multiplication[edit]

Consider the multiplicative group ${displaystyle G=(mathbb {Z} _{n^{2}})^{times }}$ . The set of th residues is a multiplicative subgroup isomorphic to ${displaystyle (mathbb {Z} _{n})^{times }}$ . Then is normal in and the factor group has the cosets . The Paillier cryptosystem is based on the conjecture that it is difficult to determine the coset of a random element of without knowing the factorization of .

Properties[edit]

The quotient group is isomorphic to the trivial group (the group with one element), and is isomorphic to .

The order of , by definition the number of elements, is equal to , the index of in . If is finite, the index is also equal to the order of divided by the order of . The set may be finite, although both and are infinite (for example, ).

There is a «natural» surjective group homomorphism , sending each element of to the coset of to which belongs, that is: . The mapping is sometimes called the canonical projection of onto . Its kernel is .

There is a bijective correspondence between the subgroups of that contain and the subgroups of ; if is a subgroup of containing , then the corresponding subgroup of is . This correspondence holds for normal subgroups of and as well, and is formalized in the lattice theorem.

Several important properties of quotient groups are recorded in the fundamental theorem on homomorphisms and the isomorphism theorems.

If is abelian, nilpotent, solvable, cyclic or finitely generated, then so is .

If is a subgroup in a finite group , and the order of is one half of the order of , then is guaranteed to be a normal subgroup, so exists and is isomorphic to $C_{2}$ . This result can also be stated as «any subgroup of index 2 is normal», and in this form it applies also to infinite groups. Furthermore, if is the smallest prime number dividing the order of a finite group, , then if has order , must be a normal subgroup of .^[1]

Given and a normal subgroup , then is a group extension of by . One could ask whether this extension is trivial or split; in other words, one could ask whether is a direct product or semidirect product of and . This is a special case of the extension problem. An example where the extension is not split is as follows: Let ${displaystyle G=mathbb {Z} _{4}=left{0,1,2,3right}}$ , and , which is isomorphic to $mathbb{Z } _{2}$ . Then is also isomorphic to $mathbb{Z } _{2}$ . But $mathbb{Z } _{2}$ has only the trivial automorphism, so the only semi-direct product of and is the direct product. Since ${displaystyle mathbb {Z} _{4}}$ is different from ${displaystyle mathbb {Z} _{2}times mathbb {Z} _{2}}$ , we conclude that is not a semi-direct product of and .

Quotients of Lie groups[edit]

If is a Lie group and is a normal and closed (in the topological rather than the algebraic sense of the word) Lie subgroup of , the quotient / is also a Lie group. In this case, the original group has the structure of a fiber bundle (specifically, a principal -bundle), with base space / and fiber . The dimension of / equals .^[2]

Note that the condition that is closed is necessary. Indeed, if is not closed then the quotient space is not a T1-space (since there is a coset in the quotient which cannot be separated from the identity by an open set), and thus not a Hausdorff space.

For a non-normal Lie subgroup , the space of left cosets is not a group, but simply a differentiable manifold on which acts. The result is known as a homogeneous space.

Notes[edit]

^ Dummit & Foote (2003, p. 120)
^ John M. Lee, Introduction to Smooth Manifolds, Second Edition, theorem 21.17

References[edit]

Dummit, David S.; Foote, Richard M. (2003), Abstract Algebra (3rd ed.), New York: Wiley, ISBN 978-0-471-43334-7
Herstein, I. N. (1975), Topics in Algebra (2nd ed.), New York: Wiley, ISBN 0-471-02371-X

Источник

Факторгруппа

Примеры

Свойства

Примеры

См. также

Definition and illustration[edit]

Definition[edit]

Example: Addition modulo 6[edit]

Motivation for the name «quotient»[edit]

Examples[edit]

Even and odd integers[edit]

Remainders of integer division[edit]

Complex integer roots of 1[edit]

The real numbers modulo the integers[edit]

Matrices of real numbers[edit]

Integer modular arithmetic[edit]

Integer multiplication[edit]

Properties[edit]

Quotients of Lie groups[edit]

See also[edit]

Notes[edit]

References[edit]

Не пропустите также: