Материал из Викиконспекты
Перейти к: навигация, поиск
Факторгруппа
Рассмотрим группу и ее нормальную подгруппу . Пусть — множество смежных классов по . Определим в групповую операцию по следующему правилу.
| Определение: |
| Произведением смежностных классов и назовем смежностный класс . |
| Утверждение: |
|
Определение произведения смежных классов корректно. То есть произведение смежных классов не зависит от выбранных представителей и . |
|
Пусть . Докажем, что . Достаточно показать, что . В самом деле, . Элемент лежит в по свойству нормальности . Следовательно, . |
| Определение: |
| Таким образом, множество смежных классов с введенной на нем операцией произведения образует группу, которая называется факторгруппой по . Нейтральным элементом является , обратным к — . |
Примеры
- Рассмотрим и её нормальную подгруппу , тогда (группы вычетов по модулю ) будет являться факторгруппой G по H.
- Рассмотрим группу невырожденных матриц . Отображение является гомоморфизмом . Ядро — группа матриц с единичным определителем . Поэтому является нормальной подгруппой в и факторгруппа .
| Утверждение: |
|
В группе перестановок из трех элементов и ее не нормальной подгруппе перестановок из двух элементов не затрагивающих третий элемент, не будет являться группой. |
|
Рассмотрим группу (перестановки трех элементов) и ее не нормальную подгруппу (перестановки не затрагивающие третий элемент). Рассмотрим множество перестановок : класс и , класс и , класс и . Это смежные классы для . Теперь рассмотрим произведения: . Противоречие. То есть согласованного с группой умножения нет. не является группой. |
Значение
нормального делителя в теории групп
основано на том, что из смежных классов
по нормальному делителю может быть
построена новая
группа. Для
построения такой группы определим
операцию умножения на множестве смежных
классов. Пусть
,
тогда
(2.64)
Действительно,
для
Пусть
H
– нормальный делитель группы G.
В этом случае произведение двух смежных
классов G
по H
будет смежным классом по H.
Действительно,
имеем:
(2.65)
Таким
образом, в множестве всех смежных классов
по нормальному делителю определена
операция умножения.
Это означает, что фактор-множество
. (2.66)
является
замкнутым относительно операции
умножения смежных классов, а операция
умножения смежных классов является
алгебраической. Равенство (2.65) показывает,
что для нахождения произведения двух
данных смежных классов группы G
по нормальному делителю H
надо в каждом из этих классов выбрать
по одному представителю и потом взять
тот смежный класс, к которому принадлежит
произведение выбранных представителей.
В
случае если
– абелева группа бинарная операция на
фактор-множестве
вводится соотношением
.
Фактор-группу
часто называют группой
по модулю
.
Теорема. Фактор-множество
смежных классов группыG
по нормальному делителю H
с определенной в нем операцией умножения
является группой. Эта группа называется
фактор-группой группы G
по нормальному делителю H
и обозначается символом
.
Доказательство. Для
доказательства покажем, что в
будут выполнены все аксиомы группы:
-
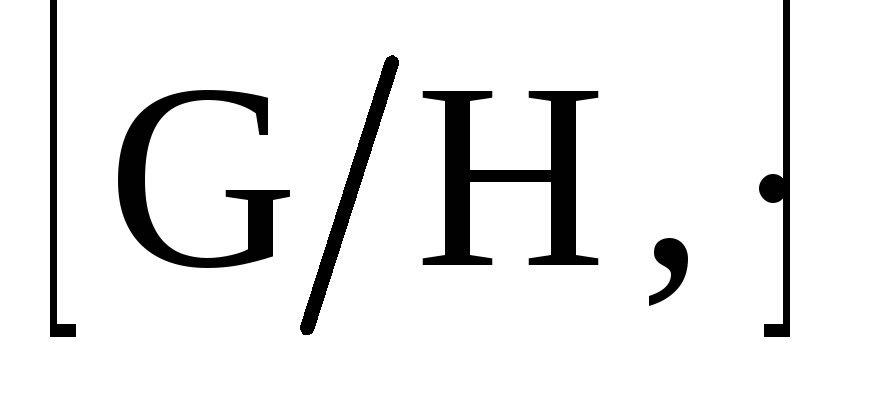
ассоциативность
умножения смежных классов следует из
ассоциативности умножения подмножеств
группы; -
роль
единицы играет сама подгруппа
– нормальный делитель:
-
для
смежного класса
обратным является класс
действительно:
– нормальный делитель:
обратным является класс
действительно:
Выводы. Со
всякой группой G
связан целый набор новых групп – ее
фактор-групп [G/H,
]
по различным нормальным делителям.
Примеры. 1. Пусть
– аддитивная группа целых чисел , а
– подгруппа целых чисел, делящихся наm
без остатка. Подгруппа
– нормальный делитель так как
– подгруппа аддитивной группы.
Фактор-группа
состоит из смежных классов
– классов вычетов по модулю
:
Класс
вычетов
Пусть
,
тогда таблица Кэли для фактор-группы
имеет вид:
-
+
[0]5
[1]5
[2]5
[3]5
[4]5
[0]5
[0]5
[1]5
[2]5
[3]5
[4]5
[1]5
[1]5
[2]5
[3]5
[4]5
[0]5
[2]5
[2]5
[3]5
[4]5
[0]5
[1]5
[3]5
[3]5
[4]5
[0]5
[1]5
[2]5
[4]5
[4]5
[0]5
[1]5
[2]5
[4]5
Выводы: 1. Фактор-группа
коммутативна – таблица Кэли симметрична
относительно главной диагонали.
2. Фактор-группа
циклическая группа
.
Система образующих состоит из одного
элемента – смежного класса
,
а все остальные смежные классы совпадают
с его степенями.
2. Пусть
– мультипликативная группа невырожденных
матриц
-го
порядка с вещественными коэффициентами,
а
– нормальный делитель этой группы,
который состоит из матриц, детерминант
каждой из которых равен единице.
Фактор-группа
состоит из смежных классов, каждый из
которых содержит все матрицы, детерминант
которых равен данному числу
.
Соседние файлы в папке ЛЕКЦИИ АиГ
- #
- #
- #
- #
- #
- #
- #
Пусть 
— группа, и 
— её нормальная подгруппа , то есть для любого элемента 
его правый и левый классы смежности совпадают:
Тогда на классах смежности в можно ввести умножение:
Легко проверить что это умножение не зависит от выбора элементов в классах смежности, то есть если 
и 
то 
.
Оно определяет структуру группы на множестве классов смежности, а полученная группа называется факторгруппой по .
Факторгруппа обозначается 
.
Свойства
Гомоморфный образ группы
(До победы коммунизма)
Изоморфен факторгруппе
По ядру гомоморфизма
- Теорема о гомоморфизме: Для любого гомоморфизма
-
- ,
- т.е. фактор группы по ядру изоморфен её образу в .
Примеры
Пусть = 
, = 2, тогда изоморфна 
.
Пусть G = UTn (группа невырожденных верхних треугольних матриц), H = SUTn (группа верхних унитреугольных матриц), тогда G/H изоморфна группе диагональных матриц.
См. также
Для других алгебраических структур, а также множеств, также определены понятия факторов: фактормножество, факторкольцо, факторалгебра, факторполе.
cs:Faktorová grupa
he:חבורת מנה
nl:Factorgroep
pl:Grupa ilorazowa