Содержание:
- Механический смысл второй производной
- Вычисления производной любого порядка, формула Лейбница
Если функция $y=f(x)$ имеет производную в каждой точке
$x$ своей области определения, то ее производная
$f^{prime}(x)$ есть функция от
$x$. Функция
$y=f^{prime}(x)$, в свою очередь, может иметь производную, которую
называют производной второго порядка функции $y=f(x)$ (или второй
производной) и обозначают символом $f^{prime prime}(x)$. Таким образом
$f^{prime prime}(x)=frac{mathrm{d}^{2} y}{mathrm{d} x^{2}}=lim _{x rightarrow x_{0}} frac{f^{prime}(x)-f^{prime}left(x_{0}right)}{x-x_{0}}=left(f^{prime}(x)right)^{prime}$
Пример
Задание. Найти вторую производную функции $y(x)=x ln (2 x+3)$
Решение. Для начала найдем первую производную:
$y^{prime}(x)=(x ln (2 x+3))^{prime}=(x)^{prime} cdot ln (2 x+3)+x cdot(ln (2 x+3))^{prime}=$
$=1 cdot ln (2 x+3)+x cdot frac{1}{2 x+3} cdot(2 x+3)^{prime}=ln (2 x+3)+$
$+frac{x}{2 x+3} cdotleft[(2 x)^{prime}+(3)^{prime}right]=ln (2 x+3)+frac{x}{2 x+3} cdotleft[2 cdot(x)^{prime}+0right]=$
$=ln (2 x+3)+frac{x}{2 x+3} cdot 2 cdot 1=ln (2 x+3)+frac{2 x}{2 x+3}$
Для нахождения второй производной продифференцируем выражение для первой производной еще раз:
$y^{prime prime}(x)=left(y^{prime}(x)right)^{prime}=left(ln (2 x+3)+frac{2 x}{2 x+3}right)^{prime}=$
$=(ln (2 x+3))^{prime}+left(frac{2 x}{2 x+3}right)^{prime}=$
$=frac{1}{2 x+3} cdot(2 x+3)^{prime}+frac{(2 x)^{prime} cdot(2 x+3)-2 x cdot(2 x+3)^{prime}}{(2 x+3)^{2}}=$
$=frac{1}{2 x+3}left[(2 x)^{prime}+(3)^{prime}right]+frac{2(x)^{prime} cdot(2 x+3)-2 x cdotleft[(2 x)^{prime}+(3)^{prime}right]}{(2 x+3)^{2}}=$
$=frac{1}{2 x+3}left[2 cdot(x)^{prime}+0right]+frac{2 cdot 1 cdot(2 x+3)-2 x cdotleft[2 cdot(x)^{prime}+0right]}{(2 x+3)^{2}}=$
$=frac{1}{2 x+3} cdot 2 cdot 1+frac{2(2 x+3)-2 x cdot 2 cdot 1}{(2 x+3)^{2}}=$
$=frac{2}{2 x+3}+frac{4 x+6-4 x}{(2 x+3)^{2}}=frac{2}{2 x+3}+frac{6}{(2 x+3)^{2}}=$
$=frac{2(2 x+3)+6}{(2 x+3)^{2}}=frac{4 x+6+6}{(2 x+3)^{2}}=frac{4 x+12}{(2 x+3)^{2}}=frac{4(x+3)}{(2 x+3)^{2}}$
Ответ. $y^{prime prime}(x)=frac{4(x+3)}{(2 x+3)^{2}}$
Производные более высоких порядков определяются аналогично. То есть производная
$n$-го порядка функции
$f(x)$ есть первая производная от производной
$(n-1)$-го порядка этой функции:
$f^{(n)}(x)=frac{mathrm{d}^{n} y}{mathrm{d} x^{n}}=left(f^{(n-1)}(x)right)^{prime}$
Замечание
Число $n$, указывающее порядок производной, заключается в скобки.
Механический смысл второй производной
Теорема
(Механический смысл второй производной)
Если точка движется прямолинейно и задан закон ее движения $s=f(t)$,
то ускорение точки равно второй производной от пути по времени:
$a(t)=s^{prime prime}(t)$
Замечание
Ускорение материального тела равно первой производной от скорости, то есть:
$a(t)=v^{prime}(t)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Материальная точка движется по закону
$s(t)=2 t^{3}+3 t$, где
$s$ измеряется в метрах, а
$t$ — в секундах. Найти значение
$t$, при котором ускорение точки равно 12.
Решение. Найдем ускорение материальной точки:
$a(t)=s^{prime prime}(t)=left(2 t^{3}+3 tright)^{prime prime}=left(left(2 t^{3}+3 tright)^{prime}right)^{prime}=left(left(2 t^{3}right)^{prime}+(3 t)^{prime}right)^{prime}=$
$=left(2 cdot 3 t^{2}+3 cdot 1right)^{prime}=left(6 t^{2}+3right)^{prime}=left(6 t^{2}right)^{prime}+(3)^{prime}=$
$=6 cdotleft(t^{2}right)^{prime}+0=6 cdot 2 t=12 t$
Искомое время $t$ найдем из уравнения:
$a(t)=12 Rightarrow 12 t=12 Rightarrow t=1 mathrm{c}$
Ответ. $t=1 c$
Вычисления производной любого порядка, формула Лейбница
Для вычисления производной любого порядка от произведения двух функций, минуя последовательное применение
формулы вычисления производной от произведения двух функций, применяется формула Лейбница:
$(u v)^{(n)}=u^{(n)} v+C_{n}^{1} u^{(n-1)} v^{prime}+C_{n}^{2} u^{(n-2)} v^{prime prime}+ldots+C_{n}^{n-1} u^{prime} v^{(n-1)}+u v^{(n)}$
где $C_{n}^{k}=frac{n !}{k !(n-k) !}$,
$n !=1 cdot 2 cdot ldots cdot n$ — факториал
натурального числа
$n$.
Пример
Задание. Найти $y^{(4)}(x)$, если
$y(x)=e^{4 x} sin 3 x$
Решение. Так как заданная функция представляет собой произведение двух функций
$u(x)=e^{4 x}$,
$v(x)=sin 3 x$, то для нахождения производной четвертого
порядка целесообразно будет применить формулу Лейбница:
$y^{(4)}(x)=left(e^{4 x}right)^{(4)} cdot sin 3 x+C_{4}^{1}left(e^{4 x}right)^{(3)} cdot(sin 3 x)^{prime}+$
$+C_{4}^{2}left(e^{4 x}right)^{prime prime} cdot(sin 3 x)^{prime prime}+C_{4}^{3}left(e^{4 x}right)^{prime} cdot(sin 3 x)^{(3)}+e^{4 x}(sin 3 x)^{(4)}$
Найдем все производные и посчитаем коэффициенты при слагаемых.
1) Посчитаем коэффициенты при слагаемых:
$C_{4}^{1}=frac{4 !}{1 ! cdot(4-1) !}=frac{4 !}{3 !}=frac{3 ! cdot 4}{3 !}=4$
$C_{4}^{2}=frac{4 !}{2 ! cdot(4-2) !}=frac{4 !}{2 ! cdot 2 !}=frac{2 ! cdot 3 cdot 4}{2 ! cdot 2 !}=frac{3 cdot 4}{2}=6$
$C_{4}^{3}=frac{4 !}{3 ! cdot(4-3) !}=frac{4 !}{3 !}=frac{3 ! cdot 4}{3 !}=4$
2) Найдем производные от функции $u(x)$:
$u(x)=e^{4 x}, u^{prime}(x)=left(e^{4 x}right)^{prime}=e^{4 x} cdot(4 x)^{prime}=e^{4 x} cdot 4 cdot(x)^{prime}=4 e^{4 x}$
$u^{prime prime}(x)=left(u^{prime}(x)right)^{prime}=left(4 e^{4 x}right)^{prime}=4 cdotleft(e^{4 x}right)^{prime}=16 e^{4 x}$
$u^{prime prime prime}(x)=left(u^{prime prime}(x)right)^{prime}=left(16 e^{4 x}right)^{prime}=64 e^{4 x}$
$u^{(4)}(x)=left(u^{prime prime prime}(x)right)^{prime}=left(64 e^{4 x}right)^{prime}=256 e^{4 x}$
3) Найдем производные от функции $v(x)$:
$v(x)=sin 3 x, v^{prime}(x)=(sin 3 x)^{prime}=cos 3 x cdot(3 x)^{prime}=3 cos 3 x$
$v^{prime prime}(x)=left(v^{prime}(x)right)^{prime}=(3 cos 3 x)^{prime}=3 cdot(cos 3 x)^{prime}=$
$=3 cdot(-sin 3 x) cdot(3 x)^{prime}=-9 sin 3 x$
$v^{prime prime prime}(x)=left(v^{prime prime}(x)right)^{prime}=-27 cos 3 x, v^{(4)}(x)=left(v^{prime prime prime}(x)right)^{prime}=81 sin 3 x$
Тогда
$y^{(4)}(x)=256 e^{4 x} cdot sin 3 x+4 cdot 64 e^{4 x} cdot 3 cos 3 x+$
$+6 cdot 16 e^{4 x} cdot(-9 sin 3 x)+4 cdot 4 e^{4 x} cdot(-27 cos 3 x)+e^{4 x} 81 sin 3 x=$
$=e^{4 x}(336 cos 3 x-527 sin 3 x)$
Ответ. $y^{(4)}(x)=e^{4 x}(336 cos 3 x-527 sin 3 x)$
Читать дальше: таблица производных высших порядков.

Производные высших порядков
На данном уроке мы научимся находить производные высших порядков, а также записывать общую формулу «энной» производной.
Кроме того, будет рассмотрена формула Лейбница 
производной и по многочисленным просьбам – производные высших порядков от неявно заданной функции. Предлагаю сразу же пройти мини-тест:
Вот функция: 
В том случае, если у вас возникли какие-либо трудности/недопонимание по поводу этого примера, пожалуйста, начните с двух базовых статей моего курса: Как найти производную? и Производная сложной функции. После освоения элементарных производных рекомендую ознакомиться с уроком
Простейшие задачи с производной, на котором мы разобрались, в частности со второй производной.
Нетрудно даже догадаться, что вторая производная – это производная от 1-й производной:
В принципе, вторую производную уже считают производной высшего порядка.
Аналогично: третья производная – это производная от 2-й производной:
Четвёртная производная – есть производная от 3-й производной:

Пятая производная: 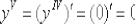
Помимо римской нумерации на практике часто используют следующие обозначения:


Иногда встречается такая запись: 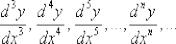
Вперёд без страха и сомнений: Пример 1 Дана функция 

Решение: что тут попишешь… – вперёд за четвёртой производной 
Четыре штриха ставить уже не принято, поэтому переходим на числовые индексы:
Ответ:
Хорошо, а теперь задумаемся над таким вопросом: что делать, если по условию требуется найти не 4-ю, а например, 20-ю производную? Если для производной 3-4-5-го (максимум, 6-7-го) порядка решение оформляется достаточно быстро, то до производных более высоких порядков мы «доберёмся» ой как не скоро. Не записывать же, в самом деле, 20 строк! В подобной ситуации нужно проанализировать
несколько найдённых производных, увидеть закономерность и составить формулу «энной» производной. Так, в Примере №1 легко понять, что при каждом следующем дифференцировании перед экспонентой будет «выскакивать» дополнительная «тройка», причём на любом шаге степень «тройки» равна номеру производной, следовательно:


И действительно, если 

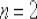


Разогреваемся самостоятельно:
Пример 2
Найти 


После бодрящей разминки рассмотрим более сложные примеры, в которых отработаем вышеприведённый алгоритм решения. Тем, кто успел ознакомиться с уроком Предел последовательности, будет чуть легче:
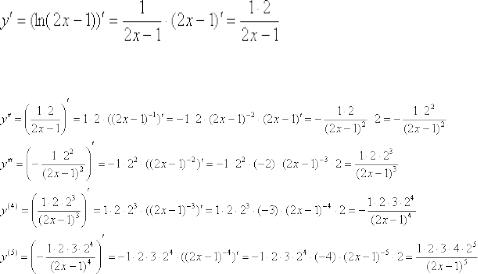
Пример 3
Найти 

Решение: чтобы прояснить ситуацию найдём несколько производных:
Полученные числа перемножать не спешим! 
Пожалуй, хватит. …Даже немного переборщил.
На следующем шаге лучше всего составить формулу «энной» производной (коль скоро, условие этого не требует, то можно обойтись черновиком). Для этого смотрим на полученные результаты и выявляем закономерности, с которыми получается каждая следующая производная.
Во-первых, они знакочередуются. Знакочередование обеспечивает «мигалка», и поскольку 1-я производная положительна, то в общую
формулу войдёт следующий множитель: 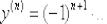

Во-вторых, в числителе «накручивается» факториал, причём он «отстаёт» от номера производной на одну единицу:

И в-третьих, в числителе растёт степень «двойки», которая равна номеру производной. То же самое можно сказать о степени знаменателя. Окончательно:
В целях проверки подставим парочку значений «эн», например, 

Замечательно, теперь допустить ошибку – просто грех:
Ответ: 
Пример 4
Найти 

Пример 5
Найти 


Ещё раз повторим порядок действий:
1)Сначала находим несколько производных. Чтобы уловить закономерности обычно хватает трёх-четырёх.
2)Затем настоятельно рекомендую составить (хотя бы на черновике) «энную» производную – она гарантированно убережёт от ошибок. Но
можно обойтись и без 
3) На заключительном этапе выполняем проверку «энной» производной – берём пару значений «эн» (лучше соседних) и выполняем подстановку. А ещё надёжнее – проверить все найдённые
ранее производные. После чего подставляем в 


Краткое решение 4 и 5-го примеров в конце урока.
В некоторых задачах во избежание проблем над функцией нужно немного поколдовать:
Пример 6
Записать формулу производной 
Решение: дифференцировать предложенную функцию совсем не хочется, поскольку получится «плохая» дробь, которая сильно затруднит нахождение последующих производных.
В этой связи целесообразно выполнить предварительные преобразования: используем формулу разности квадратов и свойство логарифма 

Совсем другое дело:
И старые подруги:
Думаю, всё просматривается. Обратите внимание, что 2-я дробь знакочередуется, а 1-я – нет. Конструируем производную 
Контроль:
Ну и для красоты вынесем факториал за скобки:
Ответ: 

Пример 7 Записать формулу производной 
Краткое решение и ответ в конце урока.
А сейчас о незыблемой круговой поруке, которой позавидует даже итальянская мафия:
Пример 8
Дана функция 
Восемнадцатая производная в точке 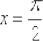
Решение: сначала, очевидно, нужно найти 
С синуса начинали, к синусу и пришли. Понятно, что при дальнейшем дифференцировании этот цикл будет продолжаться до бесконечности, и возникает следующий вопрос: как лучше «добраться» до восемнадцатой производной?
Способ «любительский»: быстренько записываем справа в столбик номера последующих производных:

Таким образом:
Но это работает, если порядок производной не слишком велик. Если же надо найти, скажем, сотую производную, то следует воспользоваться делимостью на 4. Сто делится на 4 без остатка, и легко видеть, что таковые числа располагаются в нижней строке,
поэтому: 
Кстати, 18-ю производную тоже можно определить из аналогичных соображений:
во второй строке находятся числа, которые делятся на 4 с остатком 2.
Другой, более академичный метод основан на периодичности синуса и формулах приведения. Пользуемся готовой формулой «энной»
производной синуса 
(формула приведения

(формула приведения
)
В нашем случае:

(1)Поскольку синус – это периодическая функция с периодом 

(2)Пользуемся формулой приведения 
С сотней, к слову, вообще всё элементарно – 25 «оборотов» прочь:
Заключительная, более лёгкая часть задания – это нахождение восемнадцатой производной в точке:
Ответ: 
Пример 9
Дана функция 

Кроме того, ориентируясь по таблице формул приведения, постарайтесь самостоятельно получить общую формулу «энной» производной косинуса.
На практике при аргументе синуса либо косинуса часто встречается числовой множитель, например: 
(периодичность, формулу приведения), но при каждом дифференцировании перед функцией будет дополнительно
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Производные высших порядков
- Производные высших порядков с примерами
- Производные высших порядков сложных функций, обратных функций и функций, заданных параметрически
Производные высших порядков
Производная функции у = f (x) является также функцией: у’= f’ (x).
Эта функция также может иметь производную. Эта новая производная называется второй производной функции у = f (x) или производной функции f (x) второго порядка и обозначается 

Производная второй производной, то есть функции



Пример 1. Найти производную четвертого порядка функции 
Решение. Имеем: 


Пример 2. Найти производные n-го порядка от функций
а) y = ex, б) y = sin x, в) y = cos x.
Решение.
а)
б)
и по индукции
в) аналогично находим
Производные высших порядков с примерами
Пусть функция 








Аналогично определяются и производные 
где для удобства считается, что
Примеры:
1. Если 



2. Если 

Вообще,
Аналогично,
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Теорема 1. Если функции 






Все производные в формулах (11.5) и (11.6) берутся в точке 

Символическая запись 
только вместо степеней 

Докажем формулы (11.5) и (11.6) методом математической индукции. В п. 10.5 формула (11.5) была доказана для
Пусть справедлива формула (11.5); покажем, что тогда будет справедлива и аналогичная формула для производной порядка
Формула (11.5) доказана; докажем формулу (11.6).
Возможно вам будут полезны данные страницы:
Пусть справедлива формула (11.6) для производной порядка 
Вспомнив, что (см. п. 2.4)
получим
Производные высших порядков сложных функций, обратных функций и функций, заданных параметрически
С помощью формулы производной сложной функции (см. п. 10.7) можно вычислять и производные высших порядков сложной функции. Пусть функция 






Аналогично вычисляются и производные более высоких порядков. С помощью формул производных обратной функции (см. п. 10.6) и сложной функции (см. п. 10.7) можно вычислять производные высших порядков обратных функций. Вычислим, например, вторую производную. Пусть функция 



Рассмотрим теперь параметрическое задание функций. Пусть на некотором множестве 
причем одна из них, например, 
для которой 
Тогда функция
называется параметрически заданной функцией (уравнениями (11.9)). Она определена на множестве значений функции
Если функции 






ибо
Аналогично вычисляются и производные высших порядков. Например, если функции (11.9) дважды дифференцируемы в точке 

Выведенные здесь формулы не предназначены для запоминания. Достаточно усвоить метод их получения.
Лекции:
- Логарифмы: примеры и решения
- Производная и дифференциал
- Правило Лопиталя: пример решения
- Ряд тейлора примеры решения
- Каноническое уравнение эллипса
- Рациональные числа
- Предел числовой последовательности
- Пересекающиеся прямые
- Найти оптимум функции
- Метод неопределенных коэффициентов. Первая производная
Производные высших порядков
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Дифференцируя производную первого порядка $f'(x)$, мы получим производную от производной — производную второго порядка. Производная от производной второго порядка называется производной третьего порядка, а производная $n$-го порядка называется производной от производной $n-1$-го порядка.
Производная второго порядка обозначается $y»$ или $f»(x)$. Таким образом, дифференцируя функцию $n$-раз, мы получим производную вида $f n(x)$.
Формула дифференцирования второго порядка имеет вид:
Производная n-го порядка равна нулю, если степень меньше порядка производной. Например, пятая производная функции $y = 5x^2$ равна нулю.
Пример 1
Найти вторую производную функции:
[y=xln (2x+1)]
Решение.
- Найдем производную первого порядка сложной функции по формуле произведения:
- Найдем производную второго порядка для выражения
- Упростим выражение
[left[f(x)cdot g(x)right]{{‘} } =f(x)’cdot g(x)+f(x)cdot g(x)’]
[y’=left[xcdot ln (2x+1)right]{{‘} } =x’cdot ln (2x+1)+xcdot left(ln (2x+1)right){{‘} } =1cdot ln (2x+1)+xcdot left(ln (2x+1)right){{‘} } =]
[y’=ln (2x+1)+xcdot left(ln (2x+1)right){{‘} } =ln (2x+1)+xcdot frac{1}{2x+1} cdot (2x+1)’=]
[=ln (2x+1)+2xcdot frac{1}{2x+1} =ln (2x+1)+frac{2x}{2x+1} ]
[y»=left(ln (2x+1)+frac{2x}{2x+1} right){{‘} } =ln (2x+1)’+left(frac{2x}{2x+1} right){{‘} } =frac{1}{2x+1} cdot (2x+1)’+frac{2x’cdot (2x+1)-2xcdot (2x+1)’}{left(2x+1right)^{2} } =]
[y»=frac{2}{2x+1} +frac{2(2x+1)-2xcdot 2}{left(2x+1right)^{2} } =frac{2}{2x+1} +frac{2((2x+1)-2x)}{left(2x+1right)^{2} } =frac{2}{2x+1} +frac{2}{left(2x+1right)^{2} } =]
[y»=frac{2left(2x+1right)}{left(2x+1right)^{2} } +frac{2}{left(2x+1right)^{2} } =frac{2left(2x+1right)+2}{left(2x+1right)^{2} } =frac{4x+4}{left(2x+1right)^{2} } ]
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пример 2
Найти производную четвертого порядка
[y=x^{5} -x^{4} +3x^{3} ]
Решение.
- Найдем производную первого порядка
- Найдем производную второго порядка
- Найдем производную третьего порядка
- Найдем производную четвертого порядка
[y’=left(x^{5} -x^{4} +3x^{3} right){{‘} } =5x^{4} -4x^{3} +3cdot 3x^{2} =5x^{4} -4x^{3} +9x^{2} ]
[y»=left(5x^{4} -4x^{3} +9x^{2} right){{‘} } =20x^{3} -12x^{2} +18x]
[y»’=left(20x^{3} -12x^{2} +18xright){{‘} } =60x^{2} -24x+18]
[y»»=left(60x^{2} -24x+18right){{‘} } =120x-24]
Пример 3
Найти производную четвертого порядка функции
[y=frac{x^{2} +5x^{3} }{18} ]
Решение: Самая большая степень составного неизвестного равна 3, что меньше степени производной, а значит, производная четвертого порядка равна 0.
Пример 4
Найти производную 13-го порядка функции
[y=sin x]
Решение.
- Найдем производную первого порядка
- Найдем производную второго порядка
- Найдем производную третьего порядка
- Найдем производную четвертого порядка
- Найдем производную 13-го порядка:
[y’=sin’x=cos x=sin (x+frac{pi }{2} )]
[y»=cos’x=-sin x=sin (x+2frac{pi }{2} )]
[y»’=-sin’x=-cos x=sin (x+3frac{pi }{2} )]
[y^{(4)} =-cos x’=sin x=sin (x+4frac{pi }{2} )]
Таким образом:
[y^{(n)} =sin (x+frac{ncdot pi }{2} ),nin N]
[y^{(13)} =sin (x+frac{13cdot pi }{2} )=cos x]
«Производные высших порядков» 👇
Пример 5
Найти производную n-порядка функции
[y=frac{x}{1-x} ]
Решение.
- Найдем производную первого порядка
- Найдем производную второго порядка
- Найдем производную 3 порядка
[y’=left(frac{x}{1-x} right){{‘} } =frac{x'(1-x)-x(1-x)’}{(1-x)^{2} } =frac{1-x+x}{(1-x)^{2} } =frac{1}{(1-x)^{2} } =frac{1!}{(1-x)^{1+1} } ]
[y»=left(frac{1}{(1-x)^{2} } right){{‘} } =left((1-x)^{-2} right){{‘} } =-2(1-x)^{-3} (1-x)’=-2(1-x)^{-3} cdot (-1)=frac{2}{(1-x)^{3} } =frac{2!}{(1-x)^{2+1} } ]
[y»’=left(frac{2}{(1-x)^{3} } right){{‘} } =2left((1-x)^{-3} right){{‘} } =2cdot left(-3right)(1-x)^{-4} (1-x)’=-6cdot (1-x)^{-4} cdot (-1)=frac{1cdot 2cdot 3}{(1-x)^{4} } =frac{3!}{(1-x)^{3+1} } ]
Выведем формулу производной $n$-порядка
[y^{(n)} =frac{n!}{(1-x)^{n+1} } ]
Пример 6
Найти значение второй производной в точке 1
[y=e^{2x-1} ]
Решение.
- Найдем производную первого порядка
- Найдем производную второго порядка
- Найдем производную в точке 1
[y’=left(e^{2x-1} right){{‘} } =e^{2x-1} cdot 2]
[y»=left(2cdot e^{2x-1} right){{‘} } =2cdot e^{2x-1} cdot 2=4e^{2x-1} ]
[y»=4e^{2x-1} =4e^{2cdot 1-1} =4e]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 11.12.2022
Производная функции
f(x)
,
f′(x)
, сама является функцией. Значит, можно найти её производную.
Назовём
f′(x)
производной функции
f(x)
первого порядка.
Производная от производной функции
f(x)
называется производной второго порядка (или второй производной).
Производная от второй производной называется производной третьего порядка (или третьей производной) и т. д.
Производные, начиная со второй, называются производными высших порядков и обозначаются
y′′(иногдаy2),y′′′(иногдаy3),y4,y5…yn…
Иногда используются обозначения
dydx,d2ydx2,d3ydx3…dnydxn…
Ускорение есть вторая производная координаты по времени. В этом состоит механический смысл второй производной.
Производная (n)-го порядка является производной ((n-1)) порядка: yn=yn−1′.
(Сама функция иногда считается производной (0)-го порядка.)
Пример:
y=x5;y′=x5′=5×4;y′′=(y′)′=5×4′=20×3;y3=(y′′)′=(5⋅4×3)′=60×2;y4=(y3)′=(60×2)′=120x;y5=(y4)′=(120x)′=120;y6=y7=y8=…=0.




































 называется параметрически заданной функцией (уравнениями (11.9)). Она определена на множестве значений функции
называется параметрически заданной функцией (уравнениями (11.9)). Она определена на множестве значений функции 





