Как найти энергию катушки конденсатора

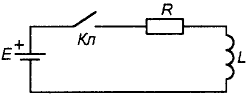
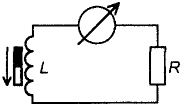   Итак, для начала немного о конденсаторах. Самый простой из них-две металлические пластины, расположенныена некотором расстоянии друг от друга (рис. 1).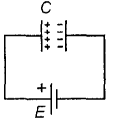 Если к такому элементу подсоединить батарейку, то он через некотороевремя зарядится до того же напряжения, что и батарейка.При этом на пластинах конденсатора будут сосредоточеныэлектрические заряды разного знака (рис. 1). Чем большеенапряжение будет приложено между обкладками, тем больше будет величина электрического заряда пластин. Посколькумежду пластинами находится воздух, а на практике чаще всего какой-либо диэлектрик (непроводящий материал), постоянный ток в цепи на рис. 1 протекать не может. В качестведиэлектрика обычно используются такие материалы, как бумага, слюда, керамика, различные органические пленки и некоторые другие. От типа диэлектрика зависят свойства конденсаторов (в первую очередь частотные), о чем мы дополнительно поговорим в рекомендациях по их выбору. Конечно, на практике через заряженный конденсатор все-таки протекает небольшой ток утечки, вызванный неидеальностью диэлектрика.

            Рис. 1

   Собственно электроемкость есть физическая величина, характеризующая способность конденсатора накапливать (запасать) электрическую энергию. Сухим физико-математическим языком многих учебников говорится, что электроемкость С=q/Uc — это коэффициент пропорциональности между зарядом конденсатора q и напряжением на нем Uc=E, где Е- напряжение источника. Это утверждение, как и многие аналогичные, строго с математической точки зрения, однако, к сожалению, не отражает физической природы явления.

   Емкость, как известно, измеряется в долях фарада (единица названа в честь выдающегося физика Майкла Фарадея). При емкости конденсатора в один фарад, электрический заряд на любой из его пластин составил бы один кулон, при напряжении между обкладками в один вольт. На практике емкости, как правило, измеряют в микрофарадах, нанофарадах и пикофарадах.

   Емкость конденсатора зависит от формы и геометрических размеров пластин, а также расстояния между ними и параметров диэлектрика. Так, емкость плоского конденсатора, изображенного на рис. 1, определяется как С=ε₀εS/d, где ε₀ — электрическая постоянная, равная 8,85·1О¹² Кл²/(Нм²); ε-диэлектрическая проницаемость диэлектрика; d ~ расстояние между обкладками; S — площадь обкладок. Физический смысл этой формулы вполне очевиден — чем больше площадь пластин и чем ближе друг к другу они расположены, тем больше емкость конденсатора. Отсюда можно сделать важный вывод — при параллельном соединении конденсаторов их емкости складываются, поскольку общая площадь пластин при этом увеличивается. А емкость последовательно соединенных конденсаторов определяется также как сопротивление параллельно включенных резисторов, т.е. итоговая емкость окажется меньше, нежели емкости каждого из последовательно включенных конденсаторов. При этом напряжение распределяется между конденсаторами пропорционально их емкости.

Рис. 2

Рис. 3

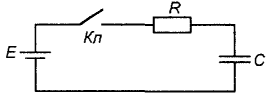
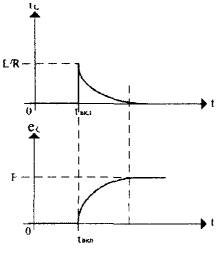
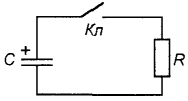
   В заряженном конденсаторе запасена электрическая энергия W_эл = CU²_c/2. Однако, накопление электрического заряда и, соответственно, энергии происходит не мгновенно. В электрической цепи, показанной на рис. 2, в момент замыкания ключа начинает протекать ток заряда, ограниченный сопротивлением R, во много раз превосходящем по величине внутренне сопротивление источника, которым в этом случае можно пренебречь. Тогда ток заряда определяется из закона Ома: I_з=E/R. Напряжение на емкости при этом отсутствует Uc=0 (конденсатор до замыкания ключа, естественно, был не заряжен). В процессе заряда конденсатора ток в цепи уменьшается, а напряжение на конденсаторе возрастает и стремится к Uc=Е. Это проиллюстрировано на графиках (рис. 3) Аналогичным образом происходит разряд конденсатора в цепи на рис. 4.

Рис. 4

Рис. 5

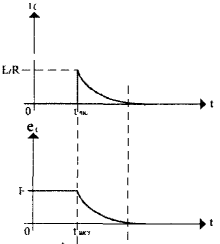
   Здесь ток разряда в момент замыкания ключа скачком возрастает от нуля до величины фаз i_раз=E/R, а затем снова плавно падает до нуля. Напряжение на конденсаторе при этом плавно падает от Uc=Е до Uc=0 (рис. 5.). При разряде конденсатора вся энергия, запасенная в нем, переходит в тепловую энергию, рассеиваемую на резисторе. Разряд и соответственно расход энергии, также как и заряд, не происходят мгновенно, а занимают определенное время. Это правило называют законом коммутации, который применительно к цепям с емкостью обычно формулируют так: напряжение на емкости мгновенно измениться не может. Действительно, при разряде конденсатора на резистор, напряжение на нем изменяется плавно:
Uc = E·EXP(-t/RC). Здесь функция ЕХР(х) — показательная функция е^x (число Эйлера е=2,718), чаще называемая экспонентой; а величину RC обычно называют постоянной времени и обозначают греческой буквой τ (тау). Действительно, от этой величины зависит длительность разряда. Процессы заряда и разряда конденсатора являются частными случаями переходных процессов.

   Теперь переидем к индуктивности. Катушка индуктивности или дроссель также являются накопителями энергии, только здесь, в отличие от конденсатора, энергия электрического тока преобразуется в энергию магнитного поля. Как известно из физики, вокруг проводника с током образуется магнитное поле, т.е. электрическое поле порождает магнитное. Если проводник свернуть в катушку, то магнитное поле возрастет. Это поле пропорционально количеству витков в катушке.

Интенсивность магнитного поля характеризуется величиной магнитного потока Ф и протекающим через катушку током I_L. Способность катушки (или проводника с током) накапливать энергию магнитного поля и характеризует величина индуктивности L, которая опять-таки математически строгим языком является коэффициентом пропорциональности между магнитным потоком и протекающим через катушку электрическим током, его порождающим L = Ф/I_L Эта величина зависит только от параметров катушки и измеряется в генри (Гн).

   Катушка индуктивностью в один генри при протекании через нее тока в один ампер создает магнитный поток величиной в один веббер (единица измерения магнитного потока). На практике индуктивность катушек обычно намного меньше величины 1 Гн и измеряется в милигенри, микрогенри и наногенри. В цепях постоянного тока сопротивление катушки определяется резистивными потерями в образующем ее проводнике и на ней не падает почти никакого напряжения. При этом, запасенная в катушке энергия магнитного поля может быть вычислена следующим образом: W_L=L·I_L²/2. Индуктивность (в микрогенри) однослойной катушки (рис. 6) можно рассчитать по следующей известной формуле: L(мкГн)=N²·r²/(9r+10l),где N — число витков, r — радиус витка (каркаса), l — длина намотки Для многослойных катушек существуют свои расчетные формулы. Часто с целью увеличения индуктивности в катушки вводят специальные сердечники из магнито-электриков -феррита, пермалоя, альсифера и т.п.

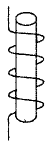
     Рис. 6

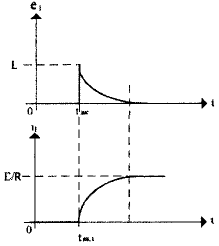
   Таким образом, катушка, как и конденсатор, является накопителем энергии. В этом случае на цепи с индуктивностями также должен распространяться закон коммутации, который на сей раз будет звучать так: ток в катушке индуктивности мгновенно изменяться не может. Действительно, при замыкании ключа в цепи на рис. 7 напряжение на катушке изменится скачком до величины E (а затем будет плавно падать до нуля), а ток будет медленно нарастать по тому же закону экспоненты (рис. 8.) от нуля до величины I_L= E/R.

Рис. 7

Рис. 8

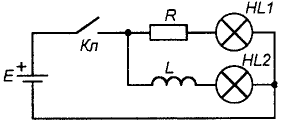
Так, в цепи на рис. 9 при замыкании ключа сначала загорится лампочка, включенная в ветвь с резистором, а затем, плавно увеличивая яркость, лампочка в индуктивной цепи. Это явление вызвано тем, что аналогично тому как электрическое поле порождает магнитное, так и магнитное, в свою очередь, порождает электрическое. Это утверждение справедливо только для переменного магнитного поля. Это наглядно иллюстрирует известный опыт (рис. 10), когда при перемещении постоянного магнита вдоль катушки в ее внешней цепи протекает ток. Так происходит и в нашем случае: при замыкании ключа через катушку начинает протекать небольшой ток, вызывающий появление около ее витков магнитного потока, изменяющегося пропорционально нарастанию тока. В свою очередь, этот изменяющийся магнитный поток приводит к появлению на катушке электродвижущей силы самоиндукции, включенной согласно закону Ленца встречно силе, вызвавшей ток. Тогда катушка будет оказывать сопротивление нарастанию тока, ровно как и его спаду. Из физики можно привести массу примеров того, когда система противодействует изменению своего стационарного состояния, и сопротивление катушки изменению тока — один из них. В процессе нарастания тока в катушке запасается энергия, а при его спаде, соответственно, тратится. В случае, если резко разомкнуть цепь на рис. 7, через ключ проскочит сильная искра, вызванная ни чем иным, как электродвижущей силой самоиндукции.

Рис. 9

Рис. 10

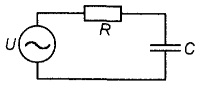
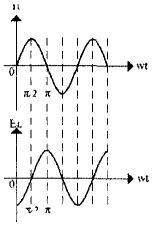
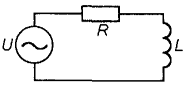
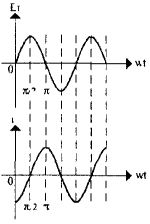
   Рассмотрим, как ведут себя емкость и индуктивность в цепях переменного (синусоидального) тока. Пусть в цепь переменного тока включена емкость (рис. 11). Каждый раз при смене полярности напряжения конденсатор будет перезаряжаться, т.е. знак заряда каждой из его обкладок будет изменяться два раза период переменного напряжения. Если длительность процессов заряда и разряда значительно превосходит период изменения напряжения, ток в цепи также будет изменяться по синусоидальному закону, однако напряжение на конденсаторе отстает по фазе от тока на 90° (рис. 12), что и не удивительно, поскольку конденсатор препятствует резкому изменению напряжения. При этом в процессе каждого заряда-разряда конденсатор будет то накапливать электрическую энергию, то отдавать некоторую ее часть во внешнюю цепь. В большинстве случаев в конденсаторе, включенном в цепь переменного тока, постоянно накоплена определенная электрическая энергия. В цепи с индуктивностью (рис. 13), наоборот, ток отстает по фазе от напряжения на 90° (рис. 14). Это тоже соответствует вышеизложенным рассуждениям -катушка оказывает сопротивление любым изменениям тока. При протекании через катушку переменного тока в ней будет запасаться энергия переменного магнитного поля, приводящая к появлению переменной электродвижущей силы самоиндукции, препятствующей протеканию переменного тока.

Рис. 11

Рис. 12

   Итак, катушка в цепи переменного тока оказывает ему сопротивление в результате наведенной переменнои электродвижущей силы самоиндукции. В то же время и конденсатор, запасая в себе электрическую энергию, оказывает сопротивление переменному току. Оба этих сопротивления называют реактивными и обозначают буквой X. В отличие от резистивного (активного) сопротивления, на реактивном не рассеивается никакой тепловой энергии, а лишь запасается энергия в виде электрического или магнитного поля.

Рис. 13

Рис. 14

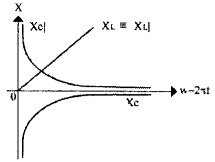
   Реактивные сопротивления катушки X_L = j·2πf·L и конденсатора Х_C = -j/2πf·C зависят от частоты f протекающего переменного тока. Мнимая единица j учитывает фазовый сдвиг 90° между током и напряжением, а знак «-» показывает, что напряжения на последовательно включенных емкости и индуктивности противофазны. Действительно, при расчете полного комплексного сопротивления цепи, содержащей индуктивности и емкости, индуктивные сопротивления необходимо складывать со знаком «+», а емкостные, наоборот, со знаком «-«. На рис. 15 показана зависимость реактивных сопротивлений индуктивности и емкости, а также их модулей от частоты. На постоянном токе, как известно, индуктивность не оказывает никакого сопротивления, а сопротивление конденсатора, наоборот, стремиться к бесконечно большому. С ростом частоты картина резко меняется — сопротивление катушки индуктивности возрастает по линейному закону, а сопротивление конденсатора падает согласно кривой, называемой гиперболой.

Рис. 15

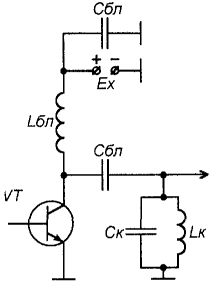
   Вышеупомянутые свойства легко пояснить на примере. На рис. 16 приведена принципиальная схема выходной цепи простейшего радиочастотного усилителя. Здесь в цепь питания коллектора транзистора включен блокировочный дроссель L6n, который на рабочей частоте усилителя имеет очень большое сопротивление. Задача этого дросселя не пропустить переменный ток коллекторной цепи транзистора в источник питания, имеющий очень ма ленькое сопротивление. Этот переменный ток должен протекать в нагрузку через разделительный конденсатор Ср, предотвращающий замыкание источника питания на нагрузку (следующий каскад). Этот конденсатор должен выбираться таким образом, чтобы на рабочей частоте усилителя не оказывать практически никакого сопротивления переменному току, т.е. его реактивное сопротивление должно быть по крайней мере на порядок (в 10 раз) меньше сопротивления нагрузки. Для того, чтобы практически весь переменный ток протекал в нагрузку, нужно, чтобы реактивное сопротивление дросселя, наоборот, по крайней мере на порядок превышало сопротивление нагрузки. Однако, поскольку реактивное сопротивление дросселя не является бесконечно большим, незначительная часть переменного тока все же пройдет через него. Во избежание попадания этого тока в источник питания включен блокировочный конденсатор Сбл, обладающий на рабочей частоте очень маленьким реактивным сопротивлением.

Рис. 16

   Катушки, дроссели и конденсаторы находят и много других различных применений в радиоэлектронных устройствах. В частности, на них строятся селективные и иные колебательные цепи, о простейших из которых пойдет речь в следующий раз.

   В завершении же сегодняшнего рассказа хотелось отметить еще один важный параметр катушек и конденсаторов. Как мы уже говорили, в катушках и конденсаторах имеются потери. В катушке это конечное сопротивление проводника r_L, а в конденсаторе — сопротивление утечки диэлектрика r_ут. Наличие этих потерь приводит к частичному преобразованию запасаемой в катушке и конденсаторе магнитной и электрической энергии в тепловую. Величина этих потерь характеризуется параметром добротность Q=Х/r, который определяется как отношение запасенной энергии к энергии потерь.

   Перейдем к более практическим вещам — как выбрать конденсаторы, дроссели, катушки для своей аппаратуры? Для начала о конденсаторах. Здесь важно знать по крайней мере три параметра — электроемкость, рабочее напряжение (а в ряде случаев и предельную реактивную мощность) и частоту (с точностью до: постоянный ток, звуковые частоты, радиочастоты). Независимо от частоты любые конденсаторы следует выбирать на рабочее напряжение (указывается на корпусе), превосходящее ориентировочно в 1,2 раза максимальное значение напряжения, прикладываемое к этому конденсатору в схеме. Не смотря на то, что напряжение пробоя диэлектрика обычно примерно в 1,5 раза превосходит указанное рабочее, такой запас делать все равно необходимо. Что же касается типа диэлектрика, то на сегодняшний день во все радиочастотные цепи в качестве блокировочных и разделительных конденсаторов, а также емкостей фильтров, необходимо устанавливать керамические конденсаторы, диапазон номиналов которых простирается от единиц пикофорад до десятков нанофарад. Следует особо оговорить, что в качество контурных конденсаторов, а также для других частотоизбирательных цепей (фильтров, цепей согласования и т.п.) следует применять конденсаторы с высокой степенью точности величины их емкости (не хуже ±5%), а вот в качестве блокировочных и разделительных элементов применяют более дешевые детали с меньшей точностью. Подстроечные конденсаторы так же, как правило, керамические, а переменные — с воздушным или твердым синтетическим диэлектриком. Большие значения емкостей, как правило, требуются в низкочастотных цепях, где вполне хорошо работают бумажные конденсаторы — герметизированные и т.п. Разброс значений таких конденсаторов составляет от десятков нанофарад да сотен микрофарад. На смену бумажным конденсаторам (с емкостями, не превышающими единиц микрофарад) все чаще приходят танталовые полупроводниковые. Что же касательно слюдяных, то большинство из них в настоящее время сняты с производства из-за своей нетехнологичности. Эти конденсаторы выпускались с величинами емкостей в пределах от сотен пикофарад до десятков нанофарад. Бумажные конденсаторы устанавливают и в цепи токов промышленной частоты (в качестве сетевых фильтров, пусковых конденсаторов двигателей и неоновых ламп и т.п.). Несколько особняком стоят конденсаторы с диэлектриком на основе различных органических пленок. Их можно применять как в низкочастотной, так и в радиочастотной аппаратуре, однако при частотах, не превышающих примерно 50, в редких случаях 100 МГц. Наконец, в цепях постоянного тока (в фильтрах выпрямителей и т.п.) наиболее предпочтительны электролитические конденсаторы, разброс емкостей которых составляет от единиц микрофарад до десятков милифарад (иногда и более). Эти конденсаторы полярны и в цепях переменного тока очень быстро выходят из строя. В виде исключения, их можно устанавливать в цепи усилителей звуковой частоты в качестве разделительных, а также в цепи смещения маломощных каскадов.

   Что касается катушек индуктивности и дросселей, то их при изготовлении любительской аппаратуры, как правило, приходится делать самому. Исключение составляют высокочастотные дроссели, которые выпускаются промышленностью на индуктивности порядка десятков — сотен микро-генри. Эти дроссели низкодобротные и ни в коем случае не могут использоваться в качестве контурных катушек и индуктивностей фильтров. Основное их назначение — блокировочные дроссели каскадов усиления радиочастоты малой и иногда средней мощности (при токах в цепях, не превышающих одного-двух ампер). В мощных каскадах передатчиков и другой генераторной аппаратуры устанавливаются самодельные дроссели, которые наматываются толстым медным проводом, способным выдерживать протекающие в этих цепях токи. Это касается и контурных катушек мощных каскадов. Их следует наматывать на теплостойких каркасах без сердечников, поскольку последние сильно разогреваются вихревыми токами высокой частоты и заметно снижают КПД каскада. А вот при намотке контурных катушек и индуктивносетй фильтров маломощных каскадов передатчиков и приемников обычно используют каркасы с сердечниками — чаще всего ферритовыми. Также иногда применяют альсиферовые и латунные (на УКВ) сердечники. В диапазонах KB и УКВ применяют однослойную намотку, а на более низких частотах — многослойную, причем при многослойной намотке желательно применять метод «универсаль» с перекрещиванием витков (как на бобине с нитками или шпагатом), что позволяет уменьшить собственную емкость катушки. Что же касается низкочастотных дросселей (фильтров выпрямителя и т.п.), то их чаще всего наматывают на сердечниках из трансформаторной стали или используют готовые от промышленной аппаратуры.

   В заключение расскажем, как при помощи старенького авометра (стрелочного тестера) определить исправность катушек и конденсаторов. Для испытаний конденсаторов тестер следует перевести на максимальный предел измерения сопротивления. Итак, исправный конденсатор емкостью менее 0,1 микрофарад не должен вызывать никакого отклонения стрелки, — в противном случае конденсатор пробит. При испытании конденсатора емкостью 0,1… 10 микрофарад стрелка должна дернуться вправо и быстро вернуться в область бесконечно большого сопротивления. Наконец, при испытании конденсаторов большой емкости (электролитических и т.п.) стрелка тестера должна резко отклониться вправо (почти до нуля сопротивлений), а затем медленно возвратиться обратно. Слабый бросок свидетельствует о потере емкости. К сожалению, при помощи цифровых мультиметров подобное испытание практически невозможно ввиду отсутствия стрелочного индикатора, однако многие из них «умеют» измерять емкость, что существенно упрощает задачу. Для проверки катушек индуктивности и дросселей тестер необходимо перевести на нижний предел измерения сопротивлений. Контурные катушки и высокочастотные дроссели имеют омическое сопротивление, близкое к нулю, а при испытании низкочастотных дросселей (а также обмоток низкочастотных и силовых трансформаторов) тестер покажет сопротивление порядка десятков — сотен Ом. При испытании низкочастотных индуктивных элементов следует избегать касания проводников незащищенными руками, поскольку в момент подсоединения дросселя или трансформатора к тестеру, на зажимах появляется ЭДС самоиндукции значительной величины.

Мощность переменного тока

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.

Пусть и — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины и можно считать постоянными в течение интервала .

Пусть за время через наш участок прошёл заряд (в соответствии с правилом выбора знака для силы тока заряд считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу

Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:

(1)

Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.

Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.

1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).

2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.

Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).

Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.

к оглавлению ▴

Мощность тока через резистор

Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током:

Поэтому для мгновенной мощности получаем:

(2)

График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор

Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:

На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между и . Где же именно?

Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?

Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:

среднее значение квадрата синуса (или косинуса) за период равно .

Этот факт иллюстрируется рисунком 2.

Рис. 2. Среднее значение квадрата синуса равно

Итак, для среднего значения мощности тока на резисторе имеем:

(3)

В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):

(4)

Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:

Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко.

Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.

к оглавлению ▴

Мощность тока через конденсатор

Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :

Для мгновенной мощности получаем:

График зависимости мгновенной мощности от времени представлен на рис. 3.

Рис. 3. Мощность переменного тока через конденсатор

Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.

Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).

Рис. 4. Напряжение на конденсаторе и сила тока через него

Рассмотрим последовательно все четыре четверти периода.

1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.

2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.

Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).

3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.

Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.

4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.

Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.

к оглавлению ▴

Мощность тока через катушку

Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на :

Для мгновенной мощности получаем:

Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).

Рис. 5. Напряжение на катушке и сила тока через неё

Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.

В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.

Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.

к оглавлению ▴

Мощность тока на произвольном участке

Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .

Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:

Тогда для мгновенной мощности имеем:

(5)

Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:

В результате получим:

(6)

Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:

(7)

Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:

Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки , и средняя мощность равна нулю.

Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.

С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.

Колебательный контур

• Электромагнитные колебания – это периодические изменения со временем электрических и магнитных величин в электрической цепи.

• Свободными называются такие колебания, которые возникают в замкнутой системе вследствие отклонения этой системы от состояния устойчивого равновесия.

При колебаниях происходит непрерывный процесс превращения энергии системы из одной формы в другую. В случае колебаний электромагнитного поля обмен может идти только между электрической и магнитной составляющей этого поля. Простейшей системой, где может происходить этот процесс, является колебательный контур.

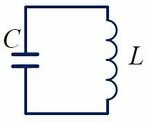
• Идеальный колебательный контур (LC-контур) — электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C.

В отличие от реального колебательного контура, который обладает электрическим сопротивлением R, электрическое сопротивление идеального контура всегда равна нулю. Следовательно, идеальный колебательный контур является упрощенной моделью реального контура.

На рисунке 1 изображена схема идеального колебательного контура.

Энергии контура

Полная энергия колебательного контура

(W=W_{e} + W_{m}, ; ; ; W_{e} =dfrac{Ccdot u^{2} }{2} = dfrac{q^{2} }{2C}, ; ; ; W_{m} =dfrac{Lcdot i^{2}}{2},)

где W_e — энергия электрического поля колебательного контура в данный момент времени, С — электроемкость конденсатора, u — значение напряжения на конденсаторе в данный момент времени, q — значение заряда конденсатора в данный момент времени, W_m — энергия магнитного поля колебательного контура в данный момент времени, L — индуктивность катушки, i —значение силы тока в катушке в данный момент времени.

Процессы в колебательном контуре

Рассмотрим процессы, которые возникают в колебательном контуре.

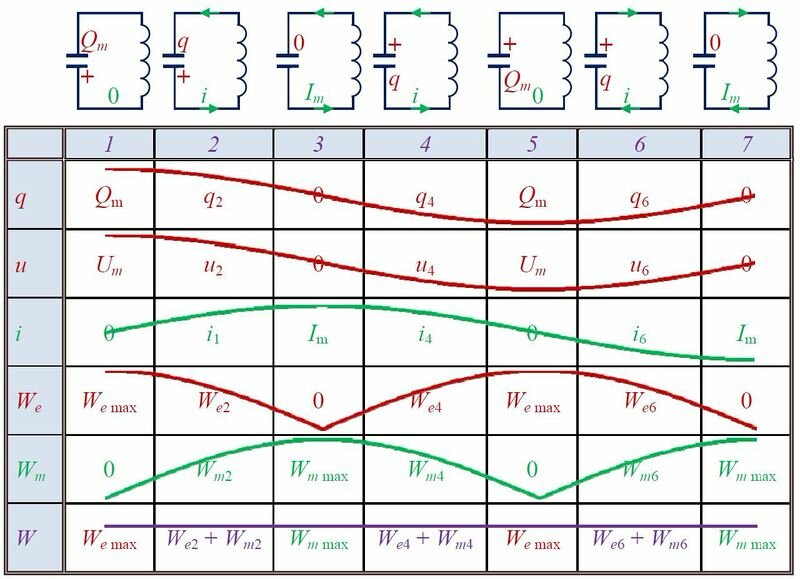
Для выведения контура из положения равновесия зарядим конденсатор так, что на его обкладках будет заряд Q_m (рис. 2, положение 1). С учетом уравнения (U_{m}=dfrac{Q_{m}}{C}) находим значение напряжения на конденсаторе. Тока в цепи в этом момент времени нет, т.е. i = 0.

После замыкания ключа под действием электрического поля конденсатора в цепи появится электрический ток, сила тока i которого будет увеличиваться с течением времени. Конденсатор в это время начнет разряжаться, т.к. электроны, создающие ток, (Напоминаю, что за направление тока принято направление движения положительных зарядов) уходят с отрицательной обкладки конденсатора и приходят на положительную (см. рис. 2, положение 2). Вместе с зарядом q будет уменьшаться и напряжение u (left(u = dfrac{q}{C} right).) При увеличении силы тока через катушку возникнет ЭДС самоиндукции, препятствующая изменению силы тока. Вследствие этого, сила тока в колебательном контуре будет возрастать от нуля до некоторого максимального значения не мгновенно, а в течение некоторого промежутка времени, определяемого индуктивностью катушки.

Заряд конденсатора q уменьшается и в некоторый момент времени становится равным нулю (q = 0, u = 0), сила тока в катушке достигнет некоторого значения I_m (см. рис. 2, положение 3).

Без электрического поля конденсатора (и сопротивления) электроны, создающие ток, продолжают свое движение по инерции. При этом электроны, приходящие на нейтральную обкладку конденсатора, сообщают ей отрицательный заряд, электроны, уходящие с нейтральной обкладки, сообщают ей положительный заряд. На конденсаторе начинает появляться заряд q (и напряжение u), но противоположного знака, т.е. конденсатор перезаряжается. Теперь новое электрическое поле конденсатора препятствует движению электронов, поэтому сила тока i начинает убывать (см. рис. 2, положение 4). Опять же это происходит не мгновенно, поскольку теперь ЭДС самоиндукции стремится скомпенсировать уменьшение тока и «поддерживает» его. А значение силы тока I_m (в положении 3) оказывается максимальным значением силы тока в контуре.

Далее сила тока становится равной нулю, а заряд конденсатора достигнет максимального значения Q_m (U_m) (см. рис. 2, положение 5).

И снова под действием электрического поля конденсатора в цепи появится электрический ток, но направленный в противоположную сторону, сила тока i которого будет увеличиваться с течением времени. А конденсатор в это время будет разряжаться (см. рис. 2, положение 6)до нуля (см. рис. 2, положение 7). И так далее.

Так как заряд на конденсаторе q (и напряжение u) определяет его энергию электрического поля W_e (left(W_{e}=dfrac{q^{2}}{2C}=dfrac{C cdot u^{2}}{2} right),) а сила тока в катушке i — энергию магнитного поля Wm (left(W_{m}=dfrac{L cdot i^{2}}{2} right),) то вместе с изменениями заряда, напряжения и силы тока, будут изменяться и энергии.

Обозначения в таблице:

Полная энергия идеального колебательного контура сохраняется с течением времени, поскольку в нем потерь энергии (нет сопротивления). Тогда

(W=W_{e, max } = W_{m, max } = W_{e2} + W_{m2} = W_{e4} +W_{m4} = …)

Свободные электромагнитные колебания

Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока i, заряда q и напряжения u, причем полная энергия контура при этом будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.

• Свободные электромагнитные колебания в контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.

Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением ЭДС самоиндукции в катушке, которая «обеспечивает» эту перезарядку. Заметим, что заряд конденсатора q и сила тока в катушке i достигают своих максимальных значений Q_m и I_m в различные моменты времени.

Свободные электромагнитные колебания в контуре происходят по гармоническому закону:

(q=Q_{m} cdot cos left(omega cdot t+varphi _{1} right), ; ; ; u=U_{m} cdot cos left(omega cdot t+varphi _{1} right), ; ; ; i=I_{m} cdot cos left(omega cdot t+varphi _{2} right).)

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.

Период свободных электромагнитных колебаний в LC-контуре определяется по формуле Томсона:

(T=2pi cdot sqrt{Lcdot C}, ;;; omega =dfrac{1}{sqrt{Lcdot C}}.)

Сточки зрения механической аналогии, идеальному колебательному контурусоответствует пружинный маятник без трения, а реальному — с трением. Вследствиедействия сил трения колебания пружинного маятника затухают с течением времени.

*Вывод формулы Томсона

Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство

(W=dfrac{Q_{m}^{2} }{2C} =dfrac{Lcdot I_{m}^{2} }{2} =dfrac{q^{2} }{2C} +dfrac{Lcdot i^{2} }{2} ={rm const}.)

Получим уравнение колебаний в LC-контуре, используя закон сохранения энергии. Продифференцировав выражение для его полной энергии по времени, с учетом того, что

(W’=0, ;;; q’=i, ;;; i’=q»,)

получаем уравнение, описывающее свободные колебания в идеальном контуре:

Переписав его в виде:

(q»+omega ^{2} cdot q=0,)

замечаем, что это — уравнение гармонических колебаний с циклической частотой

(omega =dfrac{1}{sqrt{Lcdot C} }.)

Соответственно период рассматриваемых колебаний

(T=dfrac{2pi }{omega } =2pi cdot sqrt{Lcdot C}.)

Литература

1. Жилко, В.В. Физика: учеб. пособие для 11 класса общеобразоват. шк. с рус. яз. обучения / В.В. Жилко, Л.Г. Маркович. — Минск: Нар. Асвета, 2009. — С. 39-43.

Колебательный контур – электрическая цепь, состоящая из последовательно соединённых конденсатора с ёмкостью, катушки с индуктивностью и электрического сопротивления .

Идеальный колебательный контур — цепь, состоящая только из катушки индуктивности (не имеющей собственного сопротивления) и конденсатора (-контур). Тогда в такой системе поддерживаются незатухающие электромагнитные колебания силы тока в цепи, напряжения на конденсаторе и заряда конденсатора. Давайте разберём контур и подумаем, откуда возникают колебания. Пусть изначально заряженный конденсатор помещён в описываемую нами цепь.

В начальный момент времени весь заряд сосредоточен на конденсаторе, на катушке тока нет (рис. 1.1). Т.к. на обкладках конденсатора внешнего поля тоже нет, то электроны с обкладок начинают «уходить» в цепь (заряд на конденсаторе начинает уменьшаться). При этом (за счёт освобождённых электронов) возрастает ток в цепи. Направление тока, в данном случае, от плюса к минусу (впрочем, как и всегда), и конденсатор представляет собой источник переменного тока для данной системы. Однако при росте тока на катушке, вследствие явления электромагнитной индукции, возникает обратный индукционный ток (). Направление индукционного тока, согласно правилу Ленца, должно нивелировать (уменьшать) рост основного тока. Когда заряд конденсатора станет равным нулю (весь заряд стечёт), сила индукционного тока в катушке станет максимальной (рис. 1.2).

Однако текущий заряд в цепи пропасть не может (закон сохранения заряда), тогда этот заряд, ушедший с одной обкладки через цепь, оказался на другой обкладке. Таким образом, происходит перезарядка конденсатора в обратную сторону (рис. 1.3). Индукционный ток на катушке уменьшается до нуля, т.к. изменение магнитного потока также стремится к нулю.

При полной зарядке конденсатора электроны начинают двигаться в обратную сторону, т.е. происходит разрядка конденсатора в обратную сторону и возникает ток, доходящий до своего максимума при полной разрядке конденсатора (рис. 1.4).

Дальнейшая обратная зарядка конденсатора приводит в систему в положение на рисунке 1.1. Такое поведение системы повторяется сколь угодно долго. Таким образом, мы получаем колебание различных параметров системы: тока в катушке, заряд на конденсаторе, напряжение на конденсаторе. В случае идеальности контура и проводов (отсутствие собственного сопротивления), эти колебания — гармонические.

Для математического описания этих параметров этой системы (в первую очередь, периода электромагнитных колебаний) вводится рассчитанная до нас формула Томсона:

(1)

• где

Неидеальным контуром является всё тот же идеальный контур, который мы рассмотрели, с одним небольшим включением: с наличием сопротивления (-контур). Данное сопротивление может быть как сопротивлением катушки (она не идеальна), так и сопротивлением проводящих проводов. Общая логика возникновения колебаний в неидеальном контуре аналогична той, что и в идеальном. Отличие только в самих колебаниях. В случае наличия сопротивления, часть энергии будет рассеиваться в окружающую среду — сопротивление будет нагреваться, тогда энергия колебательного контура будет уменьшаться и сами колебания станут затухающими.

Для работы с контурами в школе используется только общая энергетическая логика. В данном случае, считаем, что полная энергия системы в начале сосредоточена на конденсаторе и/или катушке, и описывается:

  (2)

• где

(3)

• где

Для идеального контура полная энергия системы остаётся постоянной:

(4)

• где
  • — полная энергия колебательной системы.

Для неидеального контура часть начальной энергии переходит в тепло, что можно описать законом Джоуля-Ленца. Тогда энергетические превращения в таком контуре можно описать:

(5)

• где

Вывод: работа с контурами достаточно сложна. Чаще всего это работа со схемами, в которых присутствуют ключи. Энергетически рассмотреть переход из начального состояния в конечное практически невозможно, тогда стоит работать с начальным и конечным положением системы. Определяем вид контура (идеальный/неидеальный) и рассмотреть энергию системы в обоих случаях. Далее, используя (4) или (5), получаем уравнение, которое можно решать.