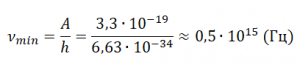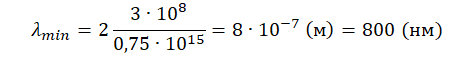Фотоны
-
Темы кодификатора ЕГЭ: фотоны, энергия фотона, импульс фотона.
-
Энергия фотона
-
Импульс фотона
-
Давление света
-
Двойственная природа света
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: фотоны, энергия фотона, импульс фотона.
В результате исследования явлений, связанных с взаимодействием света и вещества (тепловое излучение и фотоэффект), физики пришли к выводу, что свет состоит из отдельных порций энергии — фотонов. Излучение света, его распространение и поглощение происходит строго этими порциями.
Фотоны обладают энергией и импульсом и могут обмениваться ими с частицами вещества (скажем, с электронами или атомами). При этом мы говорим о столкновении фотона и частицы. При упругом столкновении фотон меняет направление движения — свет рассеивается. При неупругом столкновении фотон поглощается отдельной частицей или совокупностью частиц вещества — так происходит поглощение света.
Словом, фотон ведёт себя как частица и поэтому — наряду с электроном, протоном, нейтроном и некоторыми другими частицами — причислен к разряду элементарных частиц.
к оглавлению ▴
Энергия фотона
Выражение для энергии фотона с частотой мы уже знаем:
(1)
Часто бывает удобно работать не с обычной частотой , а с циклической частотой
.
Тогда вводят другую постоянную Планка «аш с чертой»:
Дж · с.
Выражение (1) для энергии фотона примет вид:
Фотон движется в вакууме со скоростью света и потому является релятивистской частицей: описывая фотон, мы должны привлекать формулы теории относительности. А там имеется такая формула для энергии тела массы
, движущегося со скоростью
:
(2)
Если предположить, что , то формула (2) приводит к бессмысленному заключению: энергия фотона должна быть бесконечной. Чтобы избежать этого противоречия, остаётся признать, что масса фотона равна нулю. Формула (2) позволяет сделать и более общий вывод: только безмассовая частица может двигаться со скоростью света.
к оглавлению ▴
Импульс фотона
Обладая энергией, фотон должен обладать и импульсом. Действительно, важнейшая формула теории относительности даёт связь энергии и импульса частицы:
(3)
Для фотона, имеющего нулевую массу, эта формула сводится к простому соотношению:
Отсюда для импульса фотона получаем:
(4)
Направление импульса фотона совпадает с направлением светового луча.
Учитывая, что отношение есть длина волны
, формулу (4) можно переписать так:
(5)
В видимом диапазоне наименьшими значениями энергии и импульса обладают фотоны красного света — у них самая маленькая частота (и самая большая длина волны). При движении в сторону фиолетового участка спектра энергия и импульс фотона линейно возрастают с частотой.
к оглавлению ▴
Давление света
Свет оказывает давление на освещаемую поверхность. Такой вывод был сделан Максвеллом из теоретических соображений и получил экспериментальное подтверждение в знаменитых опытах П.Н. Лебедева. Если понимать
свет как поток фотонов, обладающих импульсом , то можно легко объяснить давление света и вывести формулу Максвелла.
Предположим, что на некоторое тело падает свет частоты . Лучи направлены перпендикулярно поверхности тела; площадь освещаемой поверхности равна
(рис. 1).
Рич. 1. Давление света
Пусть — концентрация фотонов падающего света, то есть число фотонов в единице объёма.
За время на нашу поверхность попадают фотоны, находящиеся внутри цилиндра высотой
.
Их число равно:
При падении света на поверхность тела часть световой энергии отражается, а часть — поглощается. Пусть — коэффициент отражения света; величина
показывает, какая часть световой энергии отражается от поверхности. Соответственно, величина
— это доля падающей энергии, поглощаемая телом.
Как мы теперь знаем, энергия света пропорциональна числу фотонов. Поэтому можно написать, какое количество фотонов (из общего числа ) отразится от поверхности, а какое — поглотится ею:
Импульс каждого падающего фотона равен . Поглощённый фотон испытывает неупругое столкновение с телом и передаёт ему импульс
. Отражённый фотон после упругого столкновения меняет направление своего импульса на противоположное, и поэтому импульс, переданный телу отражённым фотоном, равен
.
Таким образом, от каждого фотона, входящего в световой поток, тело получает некоторый импульс. Вот простая и очевидная причина того, что свет оказывает давление на освещаемую поверхность.
Суммарный импульс, полученный телом от падающих фотонов, равен:
На нашу поверхность действует сила
, равная импульсу, полученному телом в единицу времени:
Давление света есть отношение этой силы к площади освещаемой поверхности:
(6)
Выражение имеет простой физический смысл: будучи произведением энергии фотона на число фотонов в единице объёма, оно равно энергии света в единице объёма, то есть объёмной плотности энергии
. Тогда соотношение (6) приобретает вид:
Это и есть формула для давления света, теоретически выведенная Максвеллом (в рамках классической электродинамики) и экспериментально проверенная в опытах Лебедева.
к оглавлению ▴
Двойственная природа света
В результате рассмотрения всей совокупности оптических явлений возникает естественный вопрос: что же такое свет? Непрерывно распределённая в пространстве электромагнитная волна или поток отдельных частиц — фотонов? Теория и эксперименты приводят к заключению, что оба ответа должны быть утвердительными.
1. Явления интерференции и дифракции света, характерные для любых волновых процессов, не оставляют сомнений в том, что свет есть форма волнового движения материи.
Таким образом, мы должны признать: да, свет имеет волновую природу, свет — это электромагнитная волна.
2. Однако явления взаимодействия света и вещества (например, фотоэффект) указывают на то, что свет ведёт себя как поток отдельных частиц. Эти частицы — фотоны — ведут, так сказать, самостоятельный образ жизни, обладают энергией и импульсом, участвуют во взаимодействиях с атомами и электронами. Излучение света — это рождение фотонов.
Распространение света — это движение фотонов в пространстве. Отражение и поглощение света — это соответственно упругие и неупругие столковения фотонов с частицами вещества.
Все попытки истолковать указанные явления излучения и поглощения света в рамках волновых представлений классической физики окончились неудачей. Оставалось лишь согласиться с тем, что свет имеет корпускулярную природу (от латинского слова corpusculum — маленькое тельце, частица), свет — это совокупность фотонов, мчащихся в пространстве.
Таким образом, свет имеет двойственную, корпускулярно-волновую природу — он может проявлять себя то так, то эдак. В одних явлениях (интерференция, дифракция) на передний план выходит волновая природа, и свет ведёт себя в точности как волна. Но в других явлениях (фотоэффект) доминирует корпускулярная природа, и свет ведёт себя подобно потоку частиц.
Странно всё это, не правда ли? Но что поделать — так устроена природа. Мы, люди, живём среди макроскопических тел, и наше воображение оказалось не способным полноценно представить себе явления микромира.
Природа, однако, неизмеримо шире и богаче того, что может вместить в себя человеческое воображение. Признав это и руководствуясь не столько собственным воображением, сколько наблюдениями, результатами экспериментов и весьма изощрённой математикой, люди начали успешно создавать квантовую теорию микроскопических явлений и процессов.
О некоторых парадоксальных на первый взгляд — но тем не менее подтверждённых экспериментально! — выводах квантовой теории мы поговорим в следующем листке.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Фотоны» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
07.05.2023
В сегодняшней статье нашей традиционной рубрики «физика» разбираем задачи на фотоэффект.
Подпишитесь на наш телеграм и не пропускайте важные новости. А на втором канале ищите скидки и приятные бонусы для клиентов.
Нужна помощь?
Доверь свою работу кандидату наук!
Задачи на фотоэффект с решениями
Прежде чем приступать к решению задач, напоминаем про памятку и формулы. Эти материалы пригодятся при решении задач по любой теме.
Задача на фотоны и фотоэффект №1
Условие
Найти энергию фотона ε (в Дж) для электромагнитного излучения с частотой ϑ=100·1014Гц.
Решение
Это типичная задача на энергию фотона. Применим формулу:
ε=hcλ=hϑ
Здесь h — постоянная Планка. Произведем расчет:
ε=6,63·10-34·10·1014=6,63·10-18Дж
Ответ: ε=6,63·10-18 Дж.
Задача на фотоны и фотоэффект №2
Условие
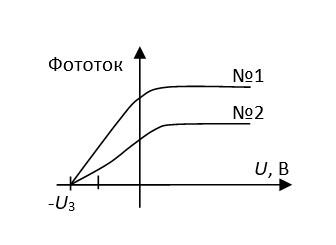
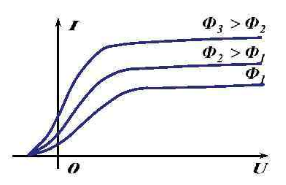
При фиксированной частоте падающего света в опытах №1 и №2 получены вольтамперные характеристики фотоэффекта (см. рис.). Величины фототоков насыщения равны I1 и I2, соответственно. Найти отношение числа фотоэлектронов N1 к N2 в этих двух опытах.
I1=13,5 мкАI2=10,6 мкА
Решение
Вольтамперная характеристика фотоэффекта показывает зависимость тока от напряжения между электродами. При выходе тока на насыщение все фотоэлектроны, выбитые из фотокатода, попадают на анод. Таким образом, величина тока насыщения пропорциональна числу фотоэлектронов. Тогда:
N1N2=I1I2=13,510,6=1,27
Ответ: 1,27.
Задача на фотоны и фотоэффект №3
Условие
На поверхность металла падают монохроматические лучи с длиной волны 0,1 мкм. Красная граница фотоэффекта 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?
Решение
Энергия падающего фотона равна:
ε=hcλ
Далее для решения задачи примененим уравнение Эйнштейна для фотоэффекта, которое можно записать в виде:
hcλ=hcλ0+Eк
Отсюда найдем кинетическую энергию:
Eк=hcλ-hcλ0=hcλ0-λλλ0
Чтобы найти искомую долю, разделим кинетическую энергию на энергию фотона:
W=Eкε=hcλ0-λλhc·λλ0=λ0-λλ0=3·10-7-10-73·10-7=0,667
Ответ: W=0,667.
Задача на фотоны и фотоэффект №4
Условие
Максимальная энергия фотоэлектронов, вылетающих из металла при его освещении лучами с длиной волны 325 нм, равна Tтax=2,3·10-19Дж. Определите работу выхода и красную границу фотоэффекта.
Решение
Формула Эйнштейна для фотоэффекта имеет вид:
hϑ=hcλ=A+Tmax
Отсюда работа выхода A равна:
A=hcλ-Tmax
Красная граница фотоэффекта определяется условием Tmax=0, поэтому получаем:
A=hcλ0λ0=hcA
Найдем:
A=6,63·10-34·3·1083,25·10-7-2,3·10-9=3,81·10-19 Дж
λ0=6,63·10-34·3·1083,81·10-19=520 нм
Ответ: A=3,81·10-19Дж; λ0=520 нм.
Задача на фотоны и фотоэффект №5
Условие
Наибольшая длина волны света λ0, при которой еще может наблюдаться фотоэффект на сурьме, равна 310 нм. Найдите скорость электронов, выбитых из калия светом с длиной волны 140 нм.
Решение
Красная граница фотоэффекта определяется условием Tmax=0, поэтому для работы выхода получаем:
A=hcλ0
Формула Эйнштейна для фотоэффекта имеет вид:
hcλ=A+Tmax
Учитывая, что Tmax=mv2max2, определим максимальную скорость электронов при фотоэффекте:
vmax=2hcm1λ-1λ0
Произведем вычисления:
vmax=2·6,63·10-349,1·10-3111,4·10-7-13,1·10-7=1,3·106 мс
Ответ: 1,3·106 мс.
Вопросы с ответами на тему «Фотоны и фотоэффект»
Вопрос 1. В чем суть фотоэффекта?
Ответ. Фотоэффект — это явление «выбивания» электронов из вещества под действием света (электромагнитного излучения).
Вопрос 2. Что такое ток насыщения?
Ответ. Ток насыщения при фотоэффекте — максимальное значение фототока.
Вопрос 3. Что такое красная граница фотоэффекта?
Ответ. Это минимальная частота или максимальная длина волны света излучения, при которой еще возможен внешний фотоэффект.
Вопрос 4. Что такое работа выхода?
Ответ. Это минимальная энергия, которую надо сообщить электрону, чтобы выбить его из металла.
Вопрос 5. Что такое квант?
Ответ. Неделимая порция какой-либо величины в физике.
Посмотри примеры работ и убедись, что мы поможем на совесть!
Нужна помощь в решении задач и выполнении других типов заданий? Обращайтесь в профессиональный сервис для учащихся по любому вопросу.
Фотон
– элементарная частица, квант
электромагнитного излучения.
Энергия
фотона:
ε
= hv,
где h
= 6,626 · 10-34
Дж·с – постоянная Планка.
Масса
фотона: m = h·v/c2.
Эта формула получается из формул
ε
= hv
и ε
= m·c2.
Масса,
определяемая формулой
m = h·v/c2,
является массой движущегося фотона.
Фотон не имеет массы покоя (m0 = 0),
так как он не может существовать в
состоянии покоя.
Импульс
фотона: Все фотоны движутся со скоростью
с = 3·108
м/с.
Очевидно импульс фотона P = m·c,
откуда следует, что
P = h·v/c = h/λ.
4. Внешний фотоэффект. Вольтамперная характеристика фотоэффекта. Законы Столетова. Уравнение Эйнштейна
В
фотоэффектом называется явление
испускания электронов веществом под
действием света.
Зависимость
тока от напряжения в цепи называется
вольтамперной характеристикой
фотоэлемента.
1)
Количество фотоэлектронов N’e,
вырываемых из катода за единицу времени,
пропорционально интенсивности света,
падающего на катод (закон Столетова).
Или иначе: ток насыщения пропорционален
мощности падающего на катод излучения:
Ńф
= P/εф
.
2)
Максимальная
скорость Vmax,
которую имеет электрон на выходе из
катода, зависит только от частоты света
ν и не зависит от его интенсивности.
3)
Для каждого вещества существует граничная
частота света ν0,
ниже которой фотоэффект не наблюдается:
v0
= Aвых/h.
Уравнение Эйнштейна: ε = Aвых
+
mv2max/2,
где ε = hv
– энергия поглощенного фотона, Aвых
– работа выхода электрона из вещества,
mv2max/2
– максимальная кинетическая энергия
вылетевшего электрона.
Уравнение
Эйнштейна, по сути, представляет собой
одну из форм записи закона сохранения
энергии. Ток в фотоэлементе прекратится,
если все вылетающие фотоэлектроны
затормозятся, не долетев до анода. Для
этого к фотоэлементу необходимо приложить
обратное (задерживающее) напряжение u,
величина которого также находится из
закона сохранения энергии:
|e|uз
= mv2max/2.
5. Давление света
Давление
света
— давление,
которое оказывает свет,
падающий на поверхность
тела.
Если
рассматривать свет как поток фотонов,
то, согласно принципам классической
механики,
частицы при ударе о тело должны передавать
импульс,
другими словами — оказывать давление.
Такое давление иногда называют
радиационным
давлением.
Для вычисления давления света можно
воспользоваться следующей формулой:
p
=
W/c
(1+p),
где
W
— количество
лучистой
энергии,
падающей нормально на 1 м2
поверхности за 1 с;
c—
скорость
света,
p
— коэффициент
отражения.
Если
свет падает под углом к нормали, то
давление можно выразить формулой:
6. Комптон – эффект и его объяснение
Эффект
Комптона
(Комптон-эффект) — явление изменения
длины
волны
электромагнитного
излучения
вследствие рассеивания
его электронами.
Для
рассеяния на покоящемся электроне
частота
рассеянного фотона:
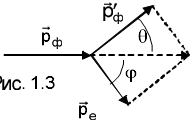
где
—
угол рассеяния (угол между направлениями
распространения фотона до и после
рассеяния).
Комптоновская
длина волны — параметр размерности
длины, характерный для релятивистских
квантовых процессов.
λС
= h/m0ec
= 2,4∙10-12м
– комптоновская длина волны электрона.
Объяснение
эффекта Комптона невозможно в рамках
классической электродинамики. С точки
зрения классической физики электромагнитная
волна является непрерывным объектом и
в результате рассеяния на свободных
электронах изменять свою длину волны
не должна. Эффект Комптона является
прямым доказательством квантования
электромагнитной волны, другими словами
подтверждает существование фотона.
Эффект Комптона является ещё одним
доказательством справедливости
корпускулярно-волнового
дуализма
микрочастиц.
Изучая
опыты Александра Григорьевича Столетова, мы с вами смогли сформулировать три
основных закона внешнего фотоэффекта. Однако все попытки экспериментально объяснить
наблюдаемые зависимости на основе законов электродинамики Максвелла, согласно
которым свет — это электромагнитная волна, непрерывно распределённая в
пространстве, оказались безрезультатными. Было абсолютно не ясно, почему
энергия фотоэлектронов определяется только частотой света и почему лишь при
достаточно малой длине волны свет вырывает электроны.
Для
того, чтобы убрать возникшие противоречия, немецкий учёный Макс Планк выдвинул
гипотезу, согласно которой атомы испускают электромагнитную энергию не
непрерывно, а отдельными порциями — квантами. При этом энергия каждой порции
прямо пропорциональна частоте излучения:
Е = hν.
Фундаментальная
постоянная, входящая в это уравнение, была названа постоянной Планка, хотя сам
Планк называл её «таинственным послом из реального мира»:
Из
гипотезы Планка следовало, что отдельный осциллятор может обладать не любой
энергией, а лишь энергией, кратной hν. Таким образом, впервые
появилась идея о квантовании энергии.
Развивая
идеи Макса Планка, Альберт Эйнштейн в 1905 году для объяснения
экспериментальных законов внешнего фотоэффекта выдвинул гипотезу о дискретности
самого электромагнитного излучения: свет излучается, поглощается и
распространяется в виде отдельных порций (квантов).
По
гипотезе Эйнштейна, монохроматическое электромагнитное излучение частотой v
обладает не только волновыми свойствами, но и свойствами, характерными для
потока частиц. Каждая такая частица движется со скоростью света и несёт квант
энергии. В 1928 году американский физик Артур Комптон предложил называть эти
частицы фотонами, что в переводе с древнегреческого означало «свет».
Энергию
фотона можно выразить и через длину волны, используя соответствующее
соотношение:
Так
же энергию фотона часто выражают и через циклическую частоту. При этом в
формуле для энергии фотона в качестве коэффициента пропорциональности вместо постоянной
Планка используют величину
Читается
она как «Аш с чертой», и называется постоянной Дира́ка:
На
одном из прошлых уроков мы с вами показали, что частица, движущаяся со
скоростью, близкой к скорости света, обладает релятивистским импульсом, который
связан с энергией частицы выражением, представленным на экране:
Если
учесть, что фотон распространяется со скоростью света, то его импульс можно
определить по одному из следующих уравнений:
Отсюда
получаем, что энергию фотона можно определить, как произведение его импульса и
скорости света:
Теперь
вспомним, как связаны между собой энергия и импульс релятивистской частицы:
При
подстановке в эту формулу энергии фотона находим, что масса фотона (а точнее,
масса покоя фотона) равна нулю.
Оказывается,
что фотон — это удивительная частица, которая обладает энергией, импульсом, но
вследствие того, что скорость его движения всегда равна скорости
распространения света, его масса покоя равна нулю. Напомним, что такие частицы
называют безмассовыми.
Следовательно,
фотон существует лишь пока он движется. Но несмотря на это, фотон является самой
распространённой по численности частицей во Вселенной. На один нуклон (то есть
на одно атомное ядро) приходится не менее 20 миллиардов фотонов.
Обобщив
выше сказанное мы можем выделить следующие свойства фотона:
·
существует
только в движении;
·
является
безмассовой частицей;
·
электрически
нейтрален;
·
модуль
его скорости движения равен модулю скорости распространения света в вакууме во
всех ИСО;
·
его
энергия пропорциональна частоте соответствующего электромагнитного излучения;
·
модуль
импульса фотона равен отношению его энергии к модулю скорости.
Таким
образом, при освещении электрода электромагнитным излучением происходит
взаимодействие фотонов с электронами вещества. Если энергия фотона достаточно
велика, то какой-либо из электронов после поглощения фотона может получить
энергию, достаточную для того, чтобы покинуть облучаемое тело. Электроны,
покинувшие образец, имеют некоторую скорость, поэтому даже при отсутствии
напряжения между электродами сила фототока не равна нулю.
Для
того чтобы покинуть вещество, электрон должен совершить работу против сил связи
электрона с атомами вещества. Она называется работой выхода. Для
металлов эта работа связана с преодолением сил взаимодействия электронов с
положительно заряженными ионами кристаллической решётки, которые удерживают
электрон в веществе. Работа выхода для металлов обычно составляет несколько
электронвольт.
Электронвольт
— это энергия, которую приобретёт частица с зарядом, равным элементарному, при
перемещении между двумя точками с ускоряющей разностью потенциалов 1 В:
1 эВ =1,6 ∙ 10–19
Дж.
Оставшаяся
часть энергии поглощённого кванта составляет кинетическую энергию
освободившегося электрона. Наибольшей кинетической энергией будут обладать те
электроны, которые поглотят кванты света вблизи поверхности металла и вылетят
из него, не успев потерять энергию при столкновениях с другими частицами в
металле.
На
основе закона сохранения энергии можно записать следующее уравнение для
фотоэлектрона:
Это
соотношение называют уравнением Эйнштейна для внешнего фотоэффекта.
Теперь,
познакомившись с фотоном и уравнением Эйнштейна, можно приступить к объяснению
экспериментальных законов фотоэффекта.
Итак,
первый закон фотоэффекта утверждает, что сила фототока насыщения
пропорциональна общему числу фотоэлектронов, покидающих поверхность металла за
единицу времени. Число же таких фотоэлектронов пропорционально числу
фотонов, падающих на поверхность за это же время. Обратите внимание, что именно
пропорционально, а не равно, так как часть квантов света поглощается
кристаллической решёткой, и их энергия переходит во внутреннюю энергию металла
(он нагревается). Поэтому логично, что при увеличении интенсивности падающего
света бо́льшее количество фотонов будут взаимодействовать с веществом. А
это приводит к росту числа фотоэлектронов, покидающих поверхность металла.
Второй
закон фотоэффекта говорит нам о том, что максимальная кинетическая энергия
фотоэлектронов прямо пропорциональна частоте падающего на катод излучения и не
зависит от интенсивности этого излучения.
И
действительно, фотоэлектрон вырывается из катода за счёт действия одного
кванта падающего излучения (одного фотона). Поэтому кинетическая энергия
фотоэлектрона зависит не от полной энергии волны, а от энергии одного кванта, которая,
как мы помним, линейно зависит от частоты излучения. При увеличении частоты
падающего света максимальная кинетическая энергия фотоэлектронов возрастает
линейно, как следует из уравнения Эйнштейна для фотоэффекта:
И,
наконец, третий закон фотоэффекта: для каждого вещества существует
минимальная частота света, называемая красной границей фотоэффекта, ниже
которой фотоэффект невозможен.
Действительно,
если частота падающего излучения меньше граничной частоты, при которой энергия
кванта света равна работе выхода (hvmin
= Aвых),
то испускания электронов не происходит.
Из
этого соотношения легко найти красную границу фотоэффекта:
Так
как h — это постоянная
величина, то из формулы следует, что красная граница фотоэффекта зависит только
от работы выхода электронов (иными словами, определяется только строением
металла и состоянием его поверхности).
Используя
соотношение между длиной волны и её частотой, можно получить формулу для
определения длины волны излучения, соответствующей красной границе фотоэффекта:
Для
закрепления нового материала решим с вами такую задачу. Определите
задерживающее напряжение между электродами фотоэлемента при освещении его
светом с длиной волны 200 нм, если работа выхода электронов из металла равна 4
эВ.
В
заключение отметим, что явление фотоэффекта нашло широкое применение не только
в технике, но и в нашей с вами повседневной жизни. Приборы, принцип действия
которых основан на явлении фотоэффекта, называют фотоэлементами.
Фотоэлементами
оборудуются многие автоматические станки на производстве, для прерывания их
работы в чрезвычайных ситуациях (например, при попадании руки человека в
рабочую зонe пресса). Фотоэлементы
применяются для выдвигания преграды в турникете метро, автоматического
включение освещения на улицах, включения воды в кране и сушилки для рук. Их
используют и в военном деле в самонаводящихся снарядах, для сигнализации и
локации невидимыми лучами. С помощью фотоэлементов осуществляется
воспроизведение звука, записанного на киноплёнке. Фотоэлементы нашли применение
и в сортировке массовых изделий по размерам и окраске. Их широко применяют при
производстве солнечных батарей, устанавливаемых на космических спутниках.
Как
видим, явление фотоэффекта, открытое более 120 лет назад Генрихом Герцем,
широко вошло в нашу повседневную жизнь и подарило множество замечательных
приборов и открытий.
Начало теории электромагнитной природы света заложил Максвелл, который заметил сходство в скоростях распространения электромагнитных и световых волн. Но согласно электродинамической теории Максвелла любое тело, излучающее электромагнитные волны, должно в итоге остынуть до абсолютного нуля. В действительности этого не происходит. Противоречия между теорией и опытными наблюдениями были разрешены в начале XX века, вскоре после того, как был открыт фотоэффект.
Что такое фотоэффект
Фотоэффект — испускание электронов из вещества под действием падающего на него света.
Александр Столетов
Явление фотоэффекта было открыто в 1887 году Генрихом Герцем. Фотоэффект также был подробно изучен русским физиком Александром Столетовым в период с 1888 до 1890 годы. Этому явлению он посвятил 6 научных работ.
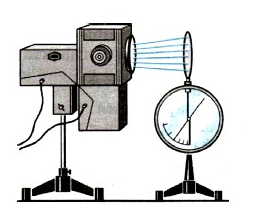
Для наблюдения фотоэффекта нужно провести опыт. Для этого понадобится электрометр и подсоединенная к нему пластинка из цинка (см. рисунок ниже). Если дать пластинке положительный заряд, то при ее освещении электрической дугой скорость разрядки электрометра не изменится. Но если цинковую пластинку зарядить отрицательно, то свет от дуги заставить электрометр разрядиться очень быстро.
Наблюдаемое во время этого эксперимента явление имеет простое объяснение. Свет вырывает электроны с поверхности цинковой пластинки. Если она имеет отрицательный заряд, электроны отталкиваются от нее, что приводит к полному разряжению электрометра. Причем при повышении интенсивности освещения скорость разрядки увеличивается, ровно, как и наоборот: при уменьшении интенсивности освещения электрометр разряжается медленно. Если же зарядить пластинку положительно, то электроны, которые вырываются светом, притягиваются к ней. Поэтому они оседают на ней, не изменяя заряд электрометра.
Если между световым пучком и отрицательно заряженной пластиной поставить лист стекла, пластинка перестанет терять электроны независимо от интенсивности излучения. Это связано с тем, что стекло задерживает ультрафиолетовое излучение. Отсюда можно сделать следующий вывод:
Явление фотоэффекта может вызвать только ультрафиолетовый участок спектра.
Волновая теория света не может объяснить, почему электроны могут вырываться только под действием ультрафиолета. Ведь даже при большой амплитуде и силе волн электроны остаются на месте, когда, казалось бы, они должны непременно быть вырванными.
Законы фотоэффекта
Чтобы получить более полное представление о фотоэффекте, выясним, от чего зависит количество электронов, вырванных светом с поверхности вещества, а также, от чего зависит их скорость, или кинетическая энергия. Выяснить все это нам помогут эксперименты.
Первый закон фотоэффекта
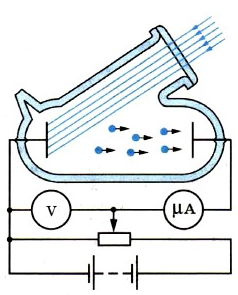
Возьмем стеклянный баллон и выкачаем из него воздух (смотрите рисунок выше). Затем поместим в него два электрода. На электроды подадим напряжение и будем регулировать его с помощью потенциометра и измерять при помощи вольтметра.
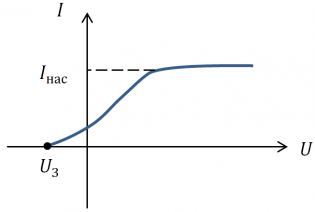
В верхней части нашего баллона есть небольшое кварцевое окошко, которое пропускает весь свет, в том числе ультрафиолетовый. Через него падает свет на один из электродов (в нашем случае на левый электрод, к которому присоединен отрицательный полюс батареи). Мы увидим, что под действием света этот электрод начнет испускать электроны, которые при движении в электрическом поле будут создавать электрический ток. Вырванные электроны будут направляться ко второму электроду. Но если напряжение небольшое, второго электрода достигнут не все электроны. Если интенсивность излучения сохранить, но увеличить между электродами разность потенциалов, то сила тока будет увеличиваться. Но как только она достигнет некоторого максимального значения, рост силы тока при дальнейшем увеличении напряжения прекратится. Максимальное значение силы тока будем называть током насыщения.
Ток насыщения — максимальное значение силы тока, также называемое предельным значением силы фототока.
Ток насыщения обозначается как Iн. Единица измерения — А (Кл/с). Численно величина равна отношению суммарному заряду вырванных электронов в единицу времени:
Iн=qt
Если же мы начнем изменять интенсивность излучения, то сможем заметить, что фототок насыщения также начинается меняться. Если интенсивность излучения ослабить, максимальное значение силы тока уменьшится. Если интенсивность светового потока увеличить, ток насыщения примет большее значение. Отсюда можно сделать вывод, который называют первым законом фотоэффекта.
Первый закон фотоэффекта:
Число электронов, вырываемых светом с поверхности металла за 1 с, прямо пропорционально поглощаемой за это время энергии световой волны. Иными словами, фототок насыщения прямо пропорционален падающему световому потоку Ф.
Второй закон фотоэффекта
Теперь произведем измерения кинетической энергии, то есть, скорости вырывания электронов. Взгляните на график, представленный ниже. Видно, что сила фототока выше нуля даже при нулевом напряжении. Это говорит о том, что даже при нулевой разности потенциалов часть электронов достигает второго электрода.
Если мы поменяем полярность батареи, то будем наблюдать уменьшение силы тока. Если подать на электроды некоторое значение напряжения, равное Uз, сила тока станет равно нулю. Это значит, что электрическое поле тормозит вырванные электроны, останавливает их, а затем возвращает на тот же электрод.
Напряжение, равное Uз, называют задерживающим напряжением. Оно зависит зависит от максимальной кинетической энергии электронов, которые вырываются под действием света. Измеряя задерживающее напряжение и применяя теорему о кинетической, можно найти максимальное значение кинетической энергии электронов. Оно будет равно:
mv22=eUз
Опыт показывает, что при изменении интенсивности света (плотности потока излучения) задерживающее напряжение не меняется. Значит, не меняется кинетическая энергия электронов. С точки зрения волновой теории света этот факт непонятен. Ведь чем больше интенсивность света, тем большие силы действуют на электроны со стороны электромагнитного поля световой волны и тем большая энергия, казалось бы, должна передаваться электронам. Но экспериментальным путем мы обнаруживаем, что кинетическая энергия вырываемых светом электронов зависит только от частоты света. Отсюда мы можем сделать вывод, являющийся вторым законом фотоэффекта.
Второй закон фотоэффекта:
Максимальная кинетическая энергия фотоэлектронов линейно растет с частотой света и не зависит от его интенсивности.
Причем, если частота света меньше определенной для данного вещества минимальной частоты νmin, фотоэффект наблюдаться не будет.
Теория фотоэффекта
Все попытки объяснить явление фотоэффекта электродинамической теорией Максвелла, согласно которой свет — это электромагнитная волна, непрерывно распределенная в пространстве, оказались тщетными. Нельзя было понять, почему энергия фотоэлектронов определяется только частотой света и почему свет способен вырывать электроны лишь при достаточно малой длине волны.
В попытках объяснить это явление физик Макс Планк предложил, что атомы испускают электромагнитную энергию отдельными порциями — квантами, или фотонами. И энергия каждой порции прямо пропорциональна частоте излучения:
E=hν
h — коэффициент пропорциональности, который получил название постоянной Планка. Она равна 6,63∙10–34 Дж∙с.
Пример №1. Определите энергию фотона, соответствующую длине волны λ = 5∙10–7 м.
Энергия фотона равна:
E=hν
Выразим частоту фотона через скорость света:
ν=cλ
Следовательно:
Идею Планка продолжил развивать Эйнштейн, которому удалось дать объяснение фотоэффекту в 1905 году. В экспериментальных законах фотоэффекта Эйнштейн увидел убедительное доказательство того, что свет имеет прерывистую структуру и поглощается отдельными порциями. Причем энергия Е каждой порции излучения, по его расчетам, полностью соответствовала гипотезе Планка.
Из того, что свет излучается порциями, еще не вытекает вывода о прерывистости структуры самого света. Ведь и воду продают в бутылках, но отсюда не следует, что вода состоит из неделимых частиц. Лишь фотоэффект позволил доказать прерывистую структуру света: излученная порция световой энергии Е = hν сохраняет свою индивидуальность и в дальнейшем. Поглотиться может только вся порция целиком.
Кинетическую энергию фотоэлектрона можно найти, используя закон сохранения энергии. Энергия порции света hν идет на совершение работы выхода А и на сообщение электрону кинетической энергии. Отсюда:
hν=A+mv22
Работа выхода — минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Полученное выражение объясняет основные факты, касающиеся фотоэффекта. Интенсивность света, по Эйнштейну, пропорциональна числу квантов (порций) энергии hν в пучке света и поэтому определяет количество вырванных электронов. Скорость же электронов согласно зависит только от частоты света и работы выхода, которая определяется типом металла и состоянием его поверхности. От интенсивности освещения кинетическая энергия фотоэлектронов не зависит.
Для каждого вещества фотоэффект наблюдается лишь при освещении его светом с минимальной частотой волны νmin. Это объясняется тем, что для вырывания электрона без сообщения ему скорости нужно выполнять как минимум работу выхода. Поэтому энергия кванта должна быть больше этой работы:
hν>A
Предельную частоту νmin называют красной границей фотоэффекта. При этой частоте фотоэффект уже наблюдается.
Красная граница фотоэффекта равна:
νmin=Ah
Минимальной частоте, при которой возможен фотоэффект для данного вещества, соответствует максимальная длина волны, которая также носит название красной границы фотоэффекта. Это такая длина волны, при которой фотоэффект еще наблюдается. Обозначается она как λmах или λкр.
Максимальная длина волны, при которой еще наблюдается фотоэффект, равна:
λmax=hcA
Работа выхода А определяется родом вещества. Поэтому и предельная частота vmin фотоэффекта (красная граница) для разных веществ различна. Отсюда вытекает еще один закон фотоэффекта.
Третий закон фотоэффекта:
Для каждого вещества существует максимальная длина волны, при которой фотоэффект еще наблюдается. При больших длинах волн фотоэффекта нет.
Вспомните опыт, который мы описали в самом начале. Когда между цинковой пластинкой и световым пучком мы поставили зеркало, фотоэффект был прекращен. Это связано с тем, что красная граница для цинка определяется величиной λmах = 3,7 ∙ 10-7 м. Эта длина волны соответствует ультрафиолетовому излучению, которое не пропускало стекло.
Пример №2. Чему равна красная граница фотоэффекта νmin, если работа выхода электрона из металла равна A = 3,3∙10–19 Дж?
Применим формулу для вычисления красной границы фотоэффекта:
Задание EF15717
При увеличении в 2 раза частоты света, падающего на поверхность металла, задерживающее напряжение для фотоэлектронов увеличилось в 3 раза. Первоначальная частота падающего света была равна 0,75 ⋅1015 Гц. Какова длина волны, соответствующая «красной границе» фотоэффекта для этого металла? Ответ записать в нм.
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу закона сохранения энергии применительно к фотоэффекту.
3.Переписать формулу закона сохранения энергии применительно к опытам 1 и 2.
4.Используя формула, связывающую задерживающее напряжение и кинетическую энергию фотона, определить работу выхода.
5.Записать формулу для красной границы фотоэффекта.
6.Выполнить решение в общем виде.
7.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Частота света в опыте 1: ν1 = ν = 0,75∙1015 Гц.
• Частота света в опыте 2: ν2 = 2ν1 = 2ν Гц.
• Задерживающее напряжение в опыте 1: U1 = U В.
• Задерживающее напряжение в опыте 2: U2 = 3U1 = 3U В.
Запишем формулу закона сохранения энергии:
hν=A+mv22
Применим ее к 1 и 2 опыту, составив систему из двух уравнений:
⎧⎪⎨⎪⎩hν1=A+mv212hν2=A+mv222
Преобразуем:
⎧⎪⎨⎪⎩hν=A+mv2122hν=A+mv222
Формула, связывающая задерживающее напряжение и кинетическую энергию фотона:
mv22=eUз
Известно, что при увеличении частоты в 2 раза задерживающее напряжение увеличилось в 3 раза. Так как задерживающее напряжение прямо пропорционально кинетической энергии фотона, то она (кинетическая энергия), также увеличивается в 3 раза. Следовательно:
mv222=3mv212
Тогда:
⎧⎪⎨⎪⎩hν=A+mv2122hν=A+3mv212
Умножим первое уравнение системы на «–3» и сложим оба уравнения:
⎧⎪⎨⎪⎩−3hν=−3A−3mv2122hν=A+3mv212
−hν=−2A
Отсюда работа выхода равна:
A=hν2
Формула для нахождения красной границы фотоэффекта:
νmin=Ah
Формула длины волны:
λ=cν
Следовательно, длина волны для красной границы фотоэффекта:
λmin=cνmin=chA=2chhν=2cν
Ответ: 800
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17645
При исследовании зависимости кинетической энергии фотоэлектронов от частоты падающего света фотоэлемент освещался через светофильтры. В первой серии опытов использовался красный светофильтр, а во второй – жёлтый. В каждом опыте измеряли напряжение запирания.
Как изменяются длина световой волны, напряжение запирания и кинетическая энергия фотоэлектронов? Для каждой величины определите соответствующий характер её изменения:
| 1) | увеличится |
| 2) | уменьшится |
| 3) | не изменится |
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
Алгоритм решения
1.Определить, от чего зависит и как меняется длина световой волны.
2.Записать закон сохранения энергии, формулу зависимости кинетической энергии от напряжения запирания.
3.Используя формулы, становить, как меняется напряжение запирания и кинетическая энергия.
Решение
Длина световой волны определяется ее цветом. Красный свет имеет большую длину волны. Следовательно, во втором опыте длина световой волны уменьшится.
Закон сохранения энергии для фотоэффекта:
hν=A+mv22
Формула зависимости кинетической энергии от напряжения запирания:
mv22=eUз
Следовательно:
hν=A+eUз
Работы выхода — величина постоянная для данного вещества. Следовательно, напряжение запирания зависит только от частоты световой волны. Частота — величина обратная длине волны. Так как длина волны уменьшилась, частота увеличилась. Следовательно, увеличилось и напряжение запирания.
Поскольку напряжение запирания прямо пропорционально кинетической энергии фотонов, то эта энергия также увеличивается.
Ответ: 211
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17973
На металлическую пластинку падает монохроматическая электромагнитная волна, выбивающая электроны из пластинки. Максимальная кинетическая энергия фотоэлектронов, вылетевших из пластинки в результате фотоэффекта, составляет 3 эВ, а работа выхода из металла в 2 раза больше этой энергии. Чему равна энергия фотонов в падающей волне?
Ответ:
а) 9 эВ
б) 2 эВ
в) 3 эВ
г) 6 эВ
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу закона сохранения энергии применительно к фотоэффекту.
3.Выполнить решение в общем виде.
4.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Максимальная кинетическая энергия выбитых электронов: Emax = 3 эВ.
• Работа выхода из металла: A = 2 Emax.
Закона сохранения энергии для фотоэффекта:
hν=A+mv22
Или:
E=A+Emax=2Emax+Emax=3Emax=3·3=9 (эВ)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.4k