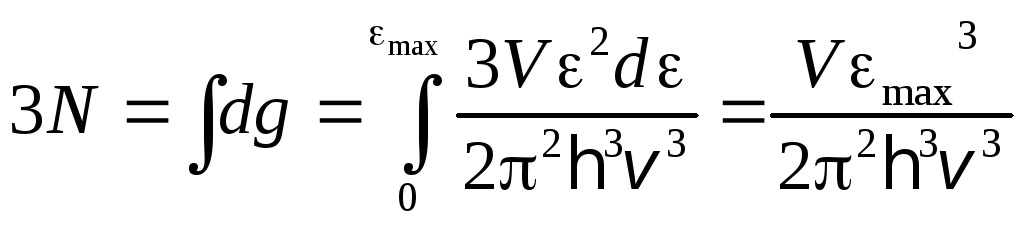Как найти энергию фонона

Фононы. Статистические свойства фононного газа

Если
кристаллическое тело рассматривать
как систему N
связанных частиц, то смещение одного
из атомов из положения равновесия влечет
за собой смещение других соседних с ним
атомов. В результате этого в кристалле
возникает упругая волна. Дойдя до границы
кристалла, волна отражается. При наложении
прямой и отраженной волн образуется
стоячая волна.

В соответствии с
гипотезой Де Бройля с каждой бегущей
монохроматической волной связаны
энергия и импульс, определяемые
соотношениями

,
(2)

введенными
по аналогии с теорией фотонов. Волна,
несущая энергию и импульс, определяемые
формулами (2), в каком-то отношении ведет
себя как частица. Частица, уподобляемая
звуковой волне в вышеуказанном смысле,
называется фононом.

Фонон во многих
отношениях ведет себя так, как если бы
он был частицей с энергией и импульсом
(2). Однако в отличие от обычных частиц
(электронов, протонов, фотонов) фонон
не может возникнуть в вакууме – для
своего возникновения и существования
фонон нуждается в некоторой среде.
Подобного рода частицы называются
квазичастицами.

Фононы
хорошо приспособлены для описания
слабых коллективных возбуждений атомов
в кристалле. Между последовательными
столкновениями фонон движется свободно,
и если «длина свободного пробега» его
достаточно велика по сравнению с
постоянной кристаллической решетки,
то возбужденное состояние кристалла
можно в известном отношении рассматривать
как фононный
газ, подобно
тому, как электромагнитное излучение
можно представить как фотонный газ,
заполняющий полость. Формально оба
представления весьма схожи – и фотоны,
и фононы подчиняются одной и той же
статистике Бозе-Эйнштейна. Однако между
фотонами и фононами имеется существенное
различие: в то время как фотоны являются
истинными частицами, фононы являются
квазичастицами.

Так как волны,
длина которых меньше удвоенного
межатомного расстояния, не имеют
физического смысла, то существует
минимальная длина волны упругих волн
в кристалле:

где
d
– расстояние между соседними атомами
в кристаллической решетке. Минимальной
длине волны соответствует максимальная
частота колебаний:

где

–
скорость упругих волн в кристалле.

Согласно
этому энергетический спектр фононов в
кристалле ограничен сверху максимальной
энергией фононов (рис. 2)

.
(3)

Для
вычисления энергии фононного газа в
кристалле воспользуемся статистическим
методом. Для этого в энергетическом
спектре фононов выделим узкую полосу
спектра с энергиями в интервале от ε до
ε+ dε , гдеdε
– ширина полосы спектра энергии фононов.

Тогда
энергия фононов в полосе спектра dε
равна:

,
(4)

Рис.
2

деdn – число
фононов в полосе спектраdε.

Это
число фононов dn
определяется функцией распределения
фононов по состояниямf
(ε) и числом состоянийdg
в полосе спектраdε
:

,
(5)

Поскольку
фононы подчиняются статистике
Бозе-Эйнштейна, то:

,
(6)

Число
состояний dg в
полосе спектраdε
нам предстоит вычислить. Для этого
рассмотрим фазовое пространство,
характеризуемое шестью координатами
(x ,y,z ,p_x,p_y,p_z).
Чтобы подсчитать число квантовых
состояний в элементе объема данного
фазового пространства, надо этот элемент
объема разделить на объем элементарной
ячейки равный.
Тогда, если мы хотим подсчитать число
состоянийdg в
интервале импульсов отрдор+dp,
надо объем, заключенный между двумя
сферами с радиусамирир+dp, умножить наVи
разделить на

,
(7)

где
V– объем кристалла.
Учитывая связь между импульсом и энергией
фонона, получим :

.
(8)

Формула
(8) не учитывает возможных видов поляризации
волны. В твердой среде вдоль некоторого
направления могут распространяться
три разные волны с одним и тем же значением
частоты ω, отличающиеся направлением
поляризации: одна продольная и две
поперечные со взаимно перпендикулярными
направлениями колебаний. В соответствии
с этим формулу (8) нужно видоизменить
следующим образом:

где
–
фазовая скорость продольных , а –поперечных
упругих волн.

Положим
для простоты ,
тогда

.
(9)

Максимальную
энергию фононов ε_maxв кристалле
можно найти, приравнивая полное число
всех квантовых состояний числу степеней
свободы, равному 3N

Отсюда

,
(10)

Исключив
из равенств (9) и (10) скорость ,
получим для числа квантовых состояний
dg
в полосе
спектра энергии dε
следующее
выражение:

.
(11)

Тогда
энергия фононов в полосе спектра dε
равна

.
(12)

Соседние файлы в папке Физика. Лекции

Источник

From Wikipedia, the free encyclopedia

Photon energy is the energy carried by a single photon. The amount of energy is directly proportional to the photon’s electromagnetic frequency and thus, equivalently, is inversely proportional to the wavelength. The higher the photon’s frequency, the higher its energy. Equivalently, the longer the photon’s wavelength, the lower its energy.

Photon energy can be expressed using any unit of energy. Among the units commonly used to denote photon energy are the electronvolt (eV) and the joule (as well as its multiples, such as the microjoule). As one joule equals 6.24 × 10¹⁸ eV, the larger units may be more useful in denoting the energy of photons with higher frequency and higher energy, such as gamma rays, as opposed to lower energy photons as in the optical and radio frequency regions of the electromagnetic spectrum.

Formulas[edit]

Physics[edit]

Photon energy is directly proportional to frequency.^[1]

where

This equation is known as the Planck–Einstein relation.

Additionally,

${displaystyle E={frac {hc}{lambda }}}$

where

E is photon energy
λ is the photon’s wavelength
c is the speed of light in vacuum
h is the Planck constant

The photon energy at 1 Hz is equal to 6.62607015 × 10⁻³⁴ J

That is equal to 4.135667697 × 10⁻¹⁵ eV

Electronvolt[edit]

Energy is often measured in electronvolts.

To find the photon energy in electronvolts using the wavelength in micrometres, the equation is approximately

${displaystyle E{text{ (eV)}}={frac {1.2398}{lambda {text{ (μm)}}}}}$

This equation only holds if the wavelength is measured in micrometers.

The photon energy of near infrared radiation at 1 μm wavelength is approximately 1.2398 eV.

Examples[edit]

An FM radio station transmitting at 100 MHz emits photons with an energy of about 4.1357 × 10⁻⁷ eV. This minuscule amount of energy is approximately 8 × 10⁻¹³ times the electron’s mass (via mass-energy equivalence).

Very-high-energy gamma rays have photon energies of 100 GeV to over 1 PeV (10¹¹ to 10¹⁵ electronvolts) or 16 nanojoules to 160 microjoules.^[2] This corresponds to frequencies of 2.42 × 10²⁵ to 2.42 × 10²⁹ Hz.

During photosynthesis, specific chlorophyll molecules absorb red-light photons at a wavelength of 700 nm in the photosystem I, corresponding to an energy of each photon of ≈ 2 eV ≈ 3 × 10⁻¹⁹ J ≈ 75 k_BT, where k_BT denotes the thermal energy. A minimum of 48 photons is needed for the synthesis of a single glucose molecule from CO₂ and water (chemical potential difference 5 × 10⁻¹⁸ J) with a maximal energy conversion efficiency of 35%.

References[edit]

^ «Energy of Photon». Photovoltaic Education Network, pveducation.org.
^ Sciences, Chinese Academy of. «Observatory discovers a dozen PeVatrons and photons exceeding 1 PeV, launches ultra-high-energy gamma astronomy era». phys.org. Retrieved 2021-11-25.

Источник

Фотоны

Темы кодификатора ЕГЭ: фотоны, энергия фотона, импульс фотона.
Энергия фотона
Импульс фотона
Давление света
Двойственная природа света

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: фотоны, энергия фотона, импульс фотона.

В результате исследования явлений, связанных с взаимодействием света и вещества (тепловое излучение и фотоэффект), физики пришли к выводу, что свет состоит из отдельных порций энергии — фотонов. Излучение света, его распространение и поглощение происходит строго этими порциями.

Фотоны обладают энергией и импульсом и могут обмениваться ими с частицами вещества (скажем, с электронами или атомами). При этом мы говорим о столкновении фотона и частицы. При упругом столкновении фотон меняет направление движения — свет рассеивается. При неупругом столкновении фотон поглощается отдельной частицей или совокупностью частиц вещества — так происходит поглощение света.

Словом, фотон ведёт себя как частица и поэтому — наряду с электроном, протоном, нейтроном и некоторыми другими частицами — причислен к разряду элементарных частиц.

к оглавлению ▴

Энергия фотона

Выражение для энергии фотона с частотой мы уже знаем:

(1)

Часто бывает удобно работать не с обычной частотой , а с циклической частотой .

Тогда вводят другую постоянную Планка «аш с чертой»:

$h^{mkern -14mu -} = frac{displaystyle h}{displaystyle 2 pi vphantom{1^a}} = 1,05 cdot 10^{-34}$ Дж · с.

Выражение (1) для энергии фотона примет вид:

$E = h^{mkern -14mu -} omega.$

Фотон движется в вакууме со скоростью света и потому является релятивистской частицей: описывая фотон, мы должны привлекать формулы теории относительности. А там имеется такая формула для энергии тела массы , движущегося со скоростью :

$E = frac{displaystyle mc^2}{displaystyle sqrt{1 - frac{displaystyle v^2}{displaystyle c^2vphantom{1^a}}} vphantom{1^a}}.$ (2)

Если предположить, что m neq 0 , то формула (2) приводит к бессмысленному заключению: энергия фотона должна быть бесконечной. Чтобы избежать этого противоречия, остаётся признать, что масса фотона равна нулю. Формула (2) позволяет сделать и более общий вывод: только безмассовая частица может двигаться со скоростью света.

к оглавлению ▴

Импульс фотона

Обладая энергией, фотон должен обладать и импульсом. Действительно, важнейшая формула теории относительности даёт связь энергии и импульса частицы:

(3)

Для фотона, имеющего нулевую массу, эта формула сводится к простому соотношению:

E = pc.

Отсюда для импульса фотона получаем:

$p = frac{displaystyle E}{displaystyle cvphantom{1^a}} = frac{displaystyle h nu}{displaystyle cvphantom{1^a}}.$ (4)

Направление импульса фотона совпадает с направлением светового луча.

Учитывая, что отношение c/ nu есть длина волны lambda , формулу (4) можно переписать так:

$p =frac{displaystyle h}{displaystyle lambda vphantom{1^a}}.$ (5)

В видимом диапазоне наименьшими значениями энергии и импульса обладают фотоны красного света — у них самая маленькая частота (и самая большая длина волны). При движении в сторону фиолетового участка спектра энергия и импульс фотона линейно возрастают с частотой.

к оглавлению ▴

Давление света

Свет оказывает давление на освещаемую поверхность. Такой вывод был сделан Максвеллом из теоретических соображений и получил экспериментальное подтверждение в знаменитых опытах П.Н. Лебедева. Если понимать
свет как поток фотонов, обладающих импульсом , то можно легко объяснить давление света и вывести формулу Максвелла.

Предположим, что на некоторое тело падает свет частоты . Лучи направлены перпендикулярно поверхности тела; площадь освещаемой поверхности равна (рис. 1).

Рич. 1. Давление света

Пусть — концентрация фотонов падающего света, то есть число фотонов в единице объёма.

За время на нашу поверхность попадают фотоны, находящиеся внутри цилиндра высотой .

Их число равно:

При падении света на поверхность тела часть световой энергии отражается, а часть — поглощается. Пусть — коэффициент отражения света; величина r < 1 показывает, какая часть световой энергии отражается от поверхности. Соответственно, величина 1 - r — это доля падающей энергии, поглощаемая телом.

Как мы теперь знаем, энергия света пропорциональна числу фотонов. Поэтому можно написать, какое количество фотонов (из общего числа ) отразится от поверхности, а какое — поглотится ею:

$N_{o} = rN, N_{n} = (1 - r)N.$

Импульс каждого падающего фотона равен . Поглощённый фотон испытывает неупругое столкновение с телом и передаёт ему импульс . Отражённый фотон после упругого столкновения меняет направление своего импульса на противоположное, и поэтому импульс, переданный телу отражённым фотоном, равен .

Таким образом, от каждого фотона, входящего в световой поток, тело получает некоторый импульс. Вот простая и очевидная причина того, что свет оказывает давление на освещаемую поверхность.

Суммарный импульс, полученный телом от падающих фотонов, равен:

На нашу поверхность действует сила , равная импульсу, полученному телом в единицу времени:

$F = frac{displaystyle P}{displaystyle t vphantom{1^a}} = (1 + r)p frac{displaystyle N}{displaystyle tvphantom{1^a}} = (1 + r) frac{displaystyle h nu}{displaystyle cvphantom{1^a}} frac{displaystyle nSct}{displaystyle tvphantom{1^a}} = (1 + r)h nu nS.$

Давление света есть отношение этой силы к площади освещаемой поверхности:

$p_{CB} = frac{displaystyle F}{displaystyle Svphantom{1^a}} = (1 + r)h nu n.$ (6)

Выражение h nu n имеет простой физический смысл: будучи произведением энергии фотона на число фотонов в единице объёма, оно равно энергии света в единице объёма, то есть объёмной плотности энергии . Тогда соотношение (6) приобретает вид:

$p_{CB} = (1 + r)w.$

Это и есть формула для давления света, теоретически выведенная Максвеллом (в рамках классической электродинамики) и экспериментально проверенная в опытах Лебедева.

к оглавлению ▴

Двойственная природа света

В результате рассмотрения всей совокупности оптических явлений возникает естественный вопрос: что же такое свет? Непрерывно распределённая в пространстве электромагнитная волна или поток отдельных частиц — фотонов? Теория и эксперименты приводят к заключению, что оба ответа должны быть утвердительными.

1. Явления интерференции и дифракции света, характерные для любых волновых процессов, не оставляют сомнений в том, что свет есть форма волнового движения материи.

Таким образом, мы должны признать: да, свет имеет волновую природу, свет — это электромагнитная волна.

2. Однако явления взаимодействия света и вещества (например, фотоэффект) указывают на то, что свет ведёт себя как поток отдельных частиц. Эти частицы — фотоны — ведут, так сказать, самостоятельный образ жизни, обладают энергией и импульсом, участвуют во взаимодействиях с атомами и электронами. Излучение света — это рождение фотонов.

Распространение света — это движение фотонов в пространстве. Отражение и поглощение света — это соответственно упругие и неупругие столковения фотонов с частицами вещества.

Все попытки истолковать указанные явления излучения и поглощения света в рамках волновых представлений классической физики окончились неудачей. Оставалось лишь согласиться с тем, что свет имеет корпускулярную природу (от латинского слова corpusculum — маленькое тельце, частица), свет — это совокупность фотонов, мчащихся в пространстве.

Таким образом, свет имеет двойственную, корпускулярно-волновую природу — он может проявлять себя то так, то эдак. В одних явлениях (интерференция, дифракция) на передний план выходит волновая природа, и свет ведёт себя в точности как волна. Но в других явлениях (фотоэффект) доминирует корпускулярная природа, и свет ведёт себя подобно потоку частиц.

Странно всё это, не правда ли? Но что поделать — так устроена природа. Мы, люди, живём среди макроскопических тел, и наше воображение оказалось не способным полноценно представить себе явления микромира.
Природа, однако, неизмеримо шире и богаче того, что может вместить в себя человеческое воображение. Признав это и руководствуясь не столько собственным воображением, сколько наблюдениями, результатами экспериментов и весьма изощрённой математикой, люди начали успешно создавать квантовую теорию микроскопических явлений и процессов.

О некоторых парадоксальных на первый взгляд — но тем не менее подтверждённых экспериментально! — выводах квантовой теории мы поговорим в следующем листке.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Фотоны» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Фотон

Фотон — это частица света или квант света; частица с которой можно делать расчёты.

Фотоны всегда находятся в движении и в вакууме движутся с постоянной скоростью 2,998 x 10^8 м/с (это называется скоростью света и обозначается буквой c).

В марте 1905 года Эйнштейн создал квантовую теорию света, это была идея о том, что свет существует в виде крошечных частиц, которые он назвал фотонами.

Позже в том же году была расширена специальная теория относительности, в которой Эйнштейн доказал, что энергия (E) и материя (масса – m) связаны, и это соотношение стало самым знаменитым в физике: E=mc²; (напомним: c — скорость света).

Формулы фотона

Эти формулы являются наиболее важными.

Формула энергии кванта/фотона (формула Планка или Энергия кванта)

Энергия — это постоянная Планка, умноженная на частоту колебаний

E = h×v

Где:

E — энергия фотона/кванта (в Дж – джоуль),
h = 6,6.10^(–34) (постоянная Планка, в Дж.с – джоуль в секунду),
ν — частота колебаний света (в Гц – герц).

Масса фотона

m = hv/c² = h/cλ

Где:

m — масса фотона (в кг),
h = 6,6.10^(–34) (постоянная Планка, в Дж.с – джоуль в секунду),
ν — частота колебаний света (в Гц – герц),
c = 3.10^8 (это скорость света в м/с),
λ — длина световой волны (в метрах).

Примечание:

Фотоны всегда движутся со скоростью света. В состоянии покоя фотоны не существуют (т.е. можно сказать, что масса покоя равна нулю).

Формула массы фотона (m = h/cλ) была выведена из формулы эквивалентности массы и энергии (E = mc²), при этом было использовано также равенство с энергией Кванта (E = h×v).

Импульс фотона

p = hv/c = h/λ

Где:

p — импульс фотона (в Н•с – ньютон-секунда),
h = 6,6.10^(–34) (постоянная Планка, в Дж.с – джоуль в секунду),
ν — частота колебаний света (в Гц – герц),
c = 3.10^8 (это скорость света в м/с),
λ — длина световой волны (в метрах).

Длина волны света, период и частота

Это ещё одно соотношение, которое может быть полезным в расчётах.

λ = cT = c/v

Где:

λ — длина световой волны (в метрах),
c = 3.10^8 (это скорость света в м/с),
T — период световых колебаний (в секундах),
ν — частота колебаний света (в Гц – герц).

Пример решения задачи с данными формулами

Определите энергию фотонов красного (λк = 0,76 мкм) света.

Известно:

λк = 0,76 мкм = 0,76 × 10^(–6) м

Решение:

Формула энергии фотонов: E = h×v

Где:

h — постоянная Планка,

v — частота света; из равенства λ = c/v выходит, что v = с/λ.

Таким образом, составляем равенство:

E = h × (с/λ) = hc / λ

Вспоминаем другие данные:

c = 3.10^8 (это скорость света в м/с)

h = 6,6.10^(–34) (постоянная Планка, в Дж.с – джоуль в секунду)

E = hc / λ = ((6,6.10^(–34) Дж.с) × (3.10^8 м/с)) / (0,76 × 10^(–6) м) = 2,6 × 10^(–19) Дж

Фотон является волной?

Фотон является одновременно частицей и волной. Согласно квантовой теории света Эйнштейна, энергия фотонов (E) равняется их частоте колебаний (v), умноженной на постоянную Планка (h); т.е. эта формула выглядит так: E = h×v.

Так он доказал, что:

свет — это поток фотонов,
энергия этих фотонов — это высота их частоты колебаний,
интенсивность света соответствует количеству фотонов.

Таким образом, учёный объяснил, что поток фотонов действует и как волна, и как частица.

Узнайте также про:

Нейтрино
Теорию относительности
Магнитную индукцию
Полимер
Теорию струн

Источник

Энергия фотона — это энергия элементарной частицы (фотона), квант электромагнитного излучения (в узком смысле — света). Это безмассовая частица, способная существовать только двигаясь со скоростью света.

$LARGE E=hnu = hfrac{c}{lambda }$

Распространение света следует рассматривать не как непрерывный волновой процесс, а как поток локализованных в пространстве дискретных частиц, движущихся со скоростью равную скорости света в вакууме. В 1926 году эти частицы получили название фотонов. Фотоны обладают всеми свойствами частицы (корпускулы).

Таким образом энергия фотона увеличивается с ростом частоты (или с уменьшением длины волны), например, фотон фиолетового света (0.38 мкм) имеет большую энергию, чем фотон красного света (0.77 мкм).

Так же фотон имеет:

Массу фотона: $LARGE m=frac{hnu }{c^2}=frac{h}{clambda }=frac{homega }{2pi c^2}$