Сообщения без ответов | Активные темы | Избранное
|
|
Найти энергию шара
|
|
21/07/17 |
Вычислить электростатическую энергию для шара, заряд которого равномерно распределен по его объему. Попытка решения: где
|
|
|
|
|
DimaM |
Re: Найти энергию шара
|
||
28/12/12 |
Энергия электростатического поля поля определяется по формуле: Надо бы еще на Из теоремы Гаусса следует, что напряженность электрического поля шара равно: Это у вас для точечного заряда, помещенного в центр шара. А в условии задачи заряд распределен по-другому. И опять же с коэффициентами бы разобраться. Подставив все в первую формулу получим: После интегрирования нужно подставлять не только верхний предел, но и нижний. Когда получите правильную формулу, имейте это в виду.
|
||
|
|
|||
|
svv |
Re: Найти энергию шара
|
||
23/07/08 |
|||
|
|
|||
|
pbm |
Re: Найти энергию шара
|
|
21/07/17 |
Цитата: Это у вас для точечного заряда, помещенного в центр шара. А в условии задачи заряд распределен по-другому. И опять же с коэффициентами бы разобраться. Я понял. В теорему Гаусса нужно подставить Цитата: Интегрирование производится по всему пространству. Ответ не совпадает. Наверное, проблема в пределах интегрирования…
|
|
|
|
|
svv |
Re: Найти энергию шара
|
||
23/07/08 |
У Вас должно быть две разных формулы для поля внутри и снаружи шара.
|
||
|
|
|||
|
DimaM |
Re: Найти энергию шара
|
||
28/12/12 |
|
||
|
|
|||
|
pbm |
Re: Найти энергию шара
|
|
21/07/17 |
Цитата: У Вас должно быть две разных формулы для поля внутри и снаружи шара. Понятно. Энергия внутри шара равна (в СГС):
И еще один вопрос. Почему в данной задачи возможно использование формулы:
|
|
|
|
|
fred1996 |
Re: Найти энергию шара
|
|
09/10/15 |
|
|
|
|
|
DimaM |
Re: Найти энергию шара
|
||
28/12/12 |
Данное выражение находит энергию поля, а не энергию шара. Так энергия хранится как раз в поле.
|
||
|
|
|||
|
pbm |
Re: Найти энергию шара
|
|
21/07/17 |
Цитата: Так энергия хранится как раз в поле. Как доказать данное утверждение.
|
|
|
|
|
DimaM |
Re: Найти энергию шара
|
||
28/12/12 |
Как доказать данное утверждение. Ну, «доказать» в математическом смысле вряд ли возможно. Можно проиллюстрировать. Например, электромагнитные волны в вакууме (в которых только поле и есть) вполне себе переносят энергию. Впрочем, можете использовать формулу для энергии через потенциал и плотность заряда (только там интегрировать придется дважды), при правильной нормировке (нулевой потенциал на бесконечности) в электростатике она дает правильный результат.
|
||
|
|
|||
|
pbm |
Re: Найти энергию шара
|
|
21/07/17 |
Цитата: Впрочем, можете использовать формулу для энергии через потенциал и плотность заряда Можно попробовать решить данную задачу через потенциал.
|
|
|
|
|
DimaM |
Re: Найти энергию шара
|
||
28/12/12 |
Для этого нужно найти потенциал снаружи и внутри шара? Снаружи не нужно — там плотность заряда нулевая. Потенциал искать по этой формуле? Нижний предел другой: нужно, чтобы на бесконечности был нуль потенциала.
|
||
|
|
|||
|
pbm |
Re: Найти энергию шара
|
|
21/07/17 |
Цитата: Нижний предел другой: нужно, чтобы на бесконечности был нуль потенциала. В данном случае нужно использовать формулу
|
|
|
|
|
DimaM |
Re: Найти энергию шара
|
||
28/12/12 |
В данном случае нужно использовать формулу Это внутри, снаружи по-другому. Кстати, эту формулу удобнее записать в виде
|
||
|
|
|||
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
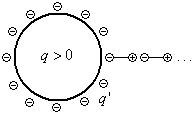
Электрическая энергия системы зарядов.
Рассмотрим систему из двух точечных
зарядов (см. рисунок) согласно принципу
суперпозиции в любой точке пространства:

Плотность энергии электрического поля

Первое и третье слагаемые связаны с
электрическими полями зарядов


отражает электрическую энергию, связанную
со взаимодействием зарядов:

Собственная энергия зарядов величина
положительная

а энергия взаимодействия может быть
как положительной, так и отрицательной
В отличие от вектора

не аддитивная. Энергию взаимодействия
можно представить более простым
соотношением. Для двух точечных зарядов
энергия взаимодействия равна:

которую
можно представить как сумму:

где
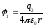


а
потенциал поля заряда

Обобщая
полученный результат на систему из
произвольного числа зарядов, получим:

где




системы.
Если заряды распределены непрерывно с
объемной плотностью

сумму следует заменить объёмным
интегралом:

где

потенциал, создаваемый всеми зарядами
системы в элементе объемом
Полученное выражение соответствуетполной электрической энергиисистемы.
Примеры.
-
Заряженный металлический шар в
однородном диэлектрике.
На этом примере мы выясним почему
электрические силы в диэлектрике меньше
чем в вакууме и рассчитаем электрическую
энергию такого шара.
Напряжённость поля в диэлектрике меньше
напряжённости в вакууме в


Это
связано с поляризацией диэлектрика и
возникновением у поверхности проводника
связанного заряда



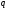
уменьшая его всюду. Напряжённость
электрического поля в диэлектрике,
равна сумме
где

Учитывая, что
находим:

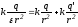
→ 


Поделив на площадь поверхности проводника,
находим связь между поверхностной
плотностью связанных зарядов

зарядов

Полученное соотношение пригодно для
проводника любой конфигурации в
однородном диэлектрике.
Найдём энергию электрического поля
шара в диэлектрике:
Здесь учтено, что

а элементарный объём с учётом сферической
симметрии поля выбран в форме шарового
слоя.
-
Свободный заряд
равномерно распределен по объему шара
радиусомиз однородного диэлектрика с проницаемостью
.
Определить энергию электрического
поля шара.
Так как зависимость напряжённости
электрического поля внутри и вне шара
от расстояния до центра шара rописывается различными функциями:
вычисление
энергии сводится к сумме двух интегралов:

Отметим, что на поверхности и в объёме
диэлектрического шара возникают
связанные заряды:


где

в шаре.
Доказательство проведите самостоятельно,
используя связи

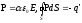

-
Система состоит из двух концентрических
металлических оболочек радиусами
и
с соответствующими зарядами
и
.Определить полную электрическую энергию
системы.
Собственная энергия каждой оболочки
равны соответственно (см. пример 1.):

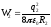
а
энергия взаимодействия оболочек:

Полная энергия системы равна:

Если оболочки заряжены одинаковыми по
величине зарядами противоположного
знака

будет равна:
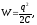
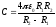
-
Плоский конденсатор заполнен двумя
слоями диэлектриков толщиной
с проницаемостью
и
.
Определить ёмкость такого конденсатора.
Напряжение,
приложенное к конденсатору равно:
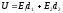
где

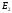
слоях.
Электрическая
индукция в слоях:

зарядов на пластинах конденсатора.
Учитывая
связь
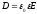

Полученная формула легко обобщается
на случай многослойного диэлектрика:

Лекция 9.
Соседние файлы в папке Физика2
- #
- #
- #
- #
- #
- #
- #
|
0 / 0 / 0 Регистрация: 03.10.2020 Сообщений: 42 |
|
|
1 |
|
Найти величину энергии электрического поля внутри шара04.11.2020, 21:44. Показов 4971. Ответов 1
Шар равномерно заряжен по объему. Энергия электрического поля в пространстве вне шара W. Найти величину энергии электрического поля внутри шара. Диэлектрическую проницаемость ε принять равной 1.
0 |
|
633 / 437 / 220 Регистрация: 10.06.2016 Сообщений: 2,022 |
|
|
05.11.2020, 11:15 |
2 |
|
Решение Поле вне шара:
1 |


 ,
,  напряженность электрического поля,
напряженность электрического поля, 
 диэлектрическая проницаемость. Из теоремы Гаусса следует, что напряженность электрического поля шара равно:
диэлектрическая проницаемость. Из теоремы Гаусса следует, что напряженность электрического поля шара равно:


 поделить, раз уж вы в СГС ответ приводите.
поделить, раз уж вы в СГС ответ приводите. . После преобразований получу:
. После преобразований получу:
![$$W=int_{0}^{V}(varepsilon E^2)dV=left[varepsilon=1right]=int_{0}^{R}frac{64}{9}pi^3 rho^2 r^4 dr=frac{4pi Q^2}{5R}$$ $$W=int_{0}^{V}(varepsilon E^2)dV=left[varepsilon=1right]=int_{0}^{R}frac{64}{9}pi^3 rho^2 r^4 dr=frac{4pi Q^2}{5R}$$](https://dxdy-04.korotkov.co.uk/f/7/0/b/70bd79b5cd0eb2af16d01bd7c23f8f9c82.png)

 . Тогда:
. Тогда:



 , если потенциал задан с нулем на бесконечности (
, если потенциал задан с нулем на бесконечности ( — плотность заряда). Идеологически так менее правильно (энергия все же хранится в поле), но зато больше похоже на именно «энергию шара».
— плотность заряда). Идеологически так менее правильно (энергия все же хранится в поле), но зато больше похоже на именно «энергию шара».
 , верно? Если ее поставить в
, верно? Если ее поставить в  получаем, что потенциал равен нулю когда
получаем, что потенциал равен нулю когда  , а на бесконечности, когда
, а на бесконечности, когда  ,
,  . Не понимаю, где я неправильно мыслю?
. Не понимаю, где я неправильно мыслю?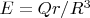 .
.
 — радиус шара.
— радиус шара.



 равномерно распределен по объему шара
равномерно распределен по объему шара из однородного диэлектрика с проницаемостью
из однородного диэлектрика с проницаемостью .
.
 и
и с соответствующими зарядами
с соответствующими зарядами и
и .Определить полную электрическую энергию
.Определить полную электрическую энергию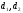 с проницаемостью
с проницаемостью и
и .
.

 Сообщение было отмечено DiFFerk как решение
Сообщение было отмечено DiFFerk как решение