1 Энергия системы точечных зарядов
Формулу
можно рассматривать как взаимную
потенциальную энергию зарядови
,
находящихся на расстоянии(рис.1).
Рис.1
Если мы теперь в поле двух зарядов
и
внесем
третий заряд,
то благодаря свойству аддитивности
энергии взаимодействий, получим:
.
Преобразуем эту сумму следующим образом.
Представим каждое слагаемое
в симметричном виде:
,
поскольку.
Тогда
.
Сгруппируем члены с одинаковыми первыми
индексами:
Каждая сумма в круглых скобках – это
энергия
взаимодействия
-го
заряда с остальными зарядами.
Поэтому можно последнее выражение
переписать так:
Обобщим это выражение на систему,
состоящую из
точечных зарядов
.
Итак, энергия взаимодействия системы
точечных зарядов
(3.1)
Имея в виду, что
,
где-i-ый заряд системы,
— потенциал, создаваемый всеми зарядами,
кроме,
в той точке, где находится заряд,
получим окончательное выражение:
(3.2)
Если заряды распределены непрерывно,
то, разлагая систему зарядов на
совокупность элементарных зарядов
и переходя от суммирования в (3.2) к
интегрированию, получаем
,
(3.3)
где
— потенциал, создаваемый всеми зарядами
системы в элементе объемом.
2 Энергия заряженных проводника и конденсатора
Энергия уединенного проводника.
Пусть проводник имеет заряди потенциал
.
Посколькуна поверхности проводника, получим
Учитывая, что
(3.4)
Любое из этих выражений определяет
энергию заряженного проводника.
Энергия заряженного конденсатора.
Предположим, что (+)
и— заряд и потенциал положительно
заряженной обкладки конденсатора, (-)
и— отрицательно заряженной обкладки
(рис. 2).
Рис. 2
Согласно формуле (3.3) интеграл можно
разбить на две части – для одной и другой
обкладок. Тогда
.
Приняв во внимание, что
,
получим для энергии заряженного
конденсатора три выражения:
(3.5)
3 Энергия и плотность энергии электрического поля
Выразим энергию заряженного плоского
конденсатора через напряженность
электрического поля. Подставим в формулу
выражение
,
получим
.
Поскольку
и
(объем между обкладками конденсатора),
то
.
Как будет показано в следующей главе,
вспомогательной характеристикой поля
в веществе является вектор электрического
смещения
,
который связан с вектором напряженности
электрического полясоотношением
.
С учетом этого соотношения полученную
формулу можно представить в виде:

Эти формулы справедливы для однородного
поля, заполняющего объем
.
Энергия распределена по объему
конденсатора равномерно. Следовательно,
в единице объема поля содержится энергия
(3.7)
Выражения (3.7) определяют плотность
энергии электрического поля.
Формулы (3.7) справедливы для любого
электрического поля. Если поле неоднородно,
то плотность энергии в некоторой точке
определяется по формулам (3.7) подстановкой
значений
(или
)
ив этой точке.
Зная плотность энергии в каждой точке,
можно найти энергию поля, заключенную
в любом объеме
.
Для этого нужно вычислить интеграл
(3.8)
Примеры решения задач
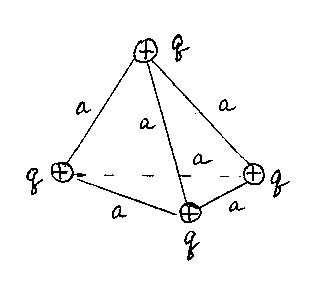
Задача 1Четыре одинаковых точечных
заряданаходятся
в вершинах тетраэдра с ребром.
Найти энергию взаимодействия зарядов
этой системы.
Решение:
-
способ. Энергия взаимодействия каждой
пары зарядов здесь одинакова и равна
.
Как видно из рисунка, всего таких
взаимодействующих пар шесть, поэтому
энергия взаимодействия всех точечных
зарядов данной системы
.
2. способ.
,
где потенциалв месте нахождения одного из зарядов,
равен.
Поэтому
.
Задача 2(С.3.114)Точечный заряд= 1 мкКл помещается в центре шарового
слоя из однородного и изотропного
диэлектрика с= 3. Внутренний радиус слоя
= 100 мм, внешний
= 200 мм. Найти энергию
,
заключенную в пределах диэлектрика.
Решение:
Напряженность поля в диэлектрике
.
Разобьем диэлектрик на шаровые слои
радиуса
и толщины
.
Объем слоя.
Плотность энергии в слое
Энергия, заключенная в слое
:
Проинтегрировав это выражение по
в пределах от
до
,
найдем энергию, заключенную в диэлектрике:
Дж.
Задача 3Найдем работу, которую надо
совершить против электрических сил,
чтобы удалить диэлектрическую пластинку
из плоского заряженного конденсатора.
Предполагается, что зарядконденсатора
остается постоянным. Емкость конденсатора
без диэлектрика равна.
Решение:
Работа против электростатических сил
в этой системе пойдет на приращение ее
электрической энергии:
,
где
— энергия поля между обкладками
конденсатора при наличии диэлектрика,— при отсутствии диэлектрика. Отсюда
.
Задача 4(С 3.111)Зарядраспределен равномерно по объему шара
радиусом.
Полагая=1, найти электрическую энергию шара
,
а также отношение энергии,
локализованной внутри шара, к энергиив окружающем пространстве.
Решение:
Прежде всего найдем с помощью теоремы
Гаусса поле внутри и вне шара:
(
);
(
).
Теперь вычислим электрическую энергию
шара:

Отсюда следует:
;
.
Тесты
1.
Емкость плоского конденсатора
пропорциональна:
1.
расстоянию между его пластинами. 2.
отношению площади его пластин к расстоянию
между ними. 3. произведению площади его
пластин на расстояние между ними. 4.
заряду пластин. 5. потенциалу пластин.
2.
Напряженность электрического поля
внутри проводника:
1.
определяется объемной плотностью заряда
в проводнике. 2. равняется нулю. 3.
определяется зарядом на поверхности
проводника. 4. определяется потенциалом
проводника. 5. зависит от напряженности
электрического поля в пространстве,
окружающем проводник.
3.
Три конденсатора одинаковой емкости
соединены параллельно. Результирующая
емкость получается
1.
равной емкости каждого из конденсаторов.
2. в три раза меньше емкости каждого из
конденсаторов. 3. в три раза больше
емкости каждого из конденсаторов.
4. Электроемкость проводника зависит
от:
1. формы и размеров, 2. площади
поверхности, 3. массы и рода вещества,
4. заряда и напряжения, 5. свойств
окружающей среды.
1.1., 2., 3. 2. 3., 4., 5. 3. 1., 2., 5.
4. 2., 3., 5.
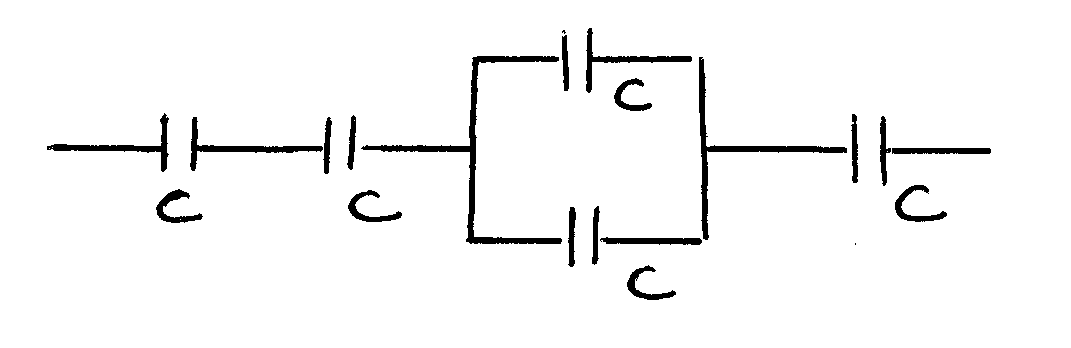
5. Емкость батареи состоящей из пяти
одинаковых конденсаторов емкостью 1
мкФ, изображенной на рисунке равна:
1. 3,5 мкФ 2. 0,286 мкФ 3. 5 мкФ
4. 0,2 мкФ
6. Взаимной электроемкостью тел называют:
-
2.
3.
.
7. Плоский воздушный конденсатор
подключили к источнику тока, а затем не
отключая от источника, погрузили в
керосин с диэлектрической проницаемостью,
равной 2. Найти отношение заряда,
первоначально находившегося на обкладках
конденсатора, к конечному заряду.
1. 0,5 2. 1 3. 2 4. 4.
8. Разность
потенциалов между обкладками конденсаторов
емкостьюмкФ
изменилась на 175 В. Определите изменение
заряда конденсатора.
1. Кл
2.Кл
3. Кл
4.0.
9. Указать неправильнуюформулу для
электроемкости плоского конденсатора
.
1.
2.
3.
4.
;
10. Конденсатор имеет емкость
пФ.
Какой заряд находится на каждой из его
обкладок, если разность потенциалов
между нимиВ?
1. Кл 2.
Кл
3. Кл
4.эВ.
11. Потенциал φ, заряд qи
емкость
уединенного проводника связаны
соотношением:
1.2.
3.
4.
.
12. Изменится ли
заряд конденсатора, подключенного к
источнику напряжения, если раздвинуть
его пластины?
1. заряд конденсатора
увеличится 2. заряд конденсатора не
изменится 3. заряд конденсатора
уменьшится 4. заряд конденсатора
не зависит от его емкости 5. заряд
конденсатора не зависит от
расстояния между пластинами.
13. Вектор напряженности электростатического
поля:
1. ортогонален эквипотенциальной
поверхности 2. направлен по касательной
к эквипотенциальной поверхности 3.
направлен под углом π./4 к эквипотенциальной
поверхности, 4. может иметь любое
направление.
14. Внутри полой проводящей сферы помещен
электрический заряд. Электрическое
поле будет существовать:
1. и вне и внутри сферы 2. только
вне сферы 3. только внутри сферы
4. ни там, ни там.
15. Электроемкость С уединенной сферы
радиуcаRв
среде равна:
1.
2.
3.
4.
16. Между обкладками конденсатора, на
концах которого поддерживается постоянная
разность потенциалов, поместили слой
диэлектрика с диэлектрической
проницаемостью ε. Напряженность поля
в диэлектрике по отношению к напряженности
поля вне его:
1.увеличилась в ε раз 2. уменьшилась
в ε раз 3.обратилась в нуль 4. не
изменилась.
17. Для проводника,
помещенного в электростатическое поле,
характерно:
1. отсутствие поля
внутри проводника 2. усиление поля
внутри проводника 3. ослабление поля
вблизи острия проводника 4. силовые
линии поля направлены по касательной
к поверхности проводника 5. потенциал
проводника максимален на его поверхности.
18. Изменится ли энергия заряженного
воздушного конденсатора, если, при
отключенном источнике, раздвинуть его
пластины?
1. Изменится за счет энергии внешних
сил, совершающих работу по раздвижению
пластин. 2.Не изменится, так как заряд
на конденсаторе не изменяется
3.Нельзя дать однозначный ответ, так как
не известны численные значения исходных
данных 4.Энергия уменьшится.
19. Потенциальная энергия взаимодействия
пластин заряженного плоского конденсатора
(указать неверныйответ):
1.
2.
3.
4.
,
где
и
– заряд и потенциал первой пластины,
и
– заряд и потенциал второй пластины;
5. все перечисленные варианты правильные.
20. Как изменится
энергия заряженного конденсатора, не
отключенного от источника, если уменьшить
расстояние между обкладками в два раза?
.
1. уменьшится в 2
раза 2. увеличится в 2 раза 3. не
изменится 4. увеличится в 4 раза
5. уменьшится в 4 раза.
21. Плотность энергии wэлектростатического поля с напряженностьюEв среде с диэлектрической
проницаемостью ε равна:
1.
2.
3.
4.
.
22. Какую из формул нельзя использовать
для расчета энергии заряженного
конденсатора?
1.
2.
3.
4.
15
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сообщения без ответов | Активные темы | Избранное
|
|
Найти энергию шара
|
|
21/07/17 |
Вычислить электростатическую энергию для шара, заряд которого равномерно распределен по его объему. Попытка решения: где
|
|
|
|
|
DimaM |
Re: Найти энергию шара
|
||
28/12/12 |
Энергия электростатического поля поля определяется по формуле: Надо бы еще на Из теоремы Гаусса следует, что напряженность электрического поля шара равно: Это у вас для точечного заряда, помещенного в центр шара. А в условии задачи заряд распределен по-другому. И опять же с коэффициентами бы разобраться. Подставив все в первую формулу получим: После интегрирования нужно подставлять не только верхний предел, но и нижний. Когда получите правильную формулу, имейте это в виду.
|
||
|
|
|||
|
svv |
Re: Найти энергию шара
|
||
23/07/08 |
|||
|
|
|||
|
pbm |
Re: Найти энергию шара
|
|
21/07/17 |
Цитата: Это у вас для точечного заряда, помещенного в центр шара. А в условии задачи заряд распределен по-другому. И опять же с коэффициентами бы разобраться. Я понял. В теорему Гаусса нужно подставить Цитата: Интегрирование производится по всему пространству. Ответ не совпадает. Наверное, проблема в пределах интегрирования…
|
|
|
|
|
svv |
Re: Найти энергию шара
|
||
23/07/08 |
У Вас должно быть две разных формулы для поля внутри и снаружи шара.
|
||
|
|
|||
|
DimaM |
Re: Найти энергию шара
|
||
28/12/12 |
|
||
|
|
|||
|
pbm |
Re: Найти энергию шара
|
|
21/07/17 |
Цитата: У Вас должно быть две разных формулы для поля внутри и снаружи шара. Понятно. Энергия внутри шара равна (в СГС):
И еще один вопрос. Почему в данной задачи возможно использование формулы:
|
|
|
|
|
fred1996 |
Re: Найти энергию шара
|
|
09/10/15 |
|
|
|
|
|
DimaM |
Re: Найти энергию шара
|
||
28/12/12 |
Данное выражение находит энергию поля, а не энергию шара. Так энергия хранится как раз в поле.
|
||
|
|
|||
|
pbm |
Re: Найти энергию шара
|
|
21/07/17 |
Цитата: Так энергия хранится как раз в поле. Как доказать данное утверждение.
|
|
|
|
|
DimaM |
Re: Найти энергию шара
|
||
28/12/12 |
Как доказать данное утверждение. Ну, «доказать» в математическом смысле вряд ли возможно. Можно проиллюстрировать. Например, электромагнитные волны в вакууме (в которых только поле и есть) вполне себе переносят энергию. Впрочем, можете использовать формулу для энергии через потенциал и плотность заряда (только там интегрировать придется дважды), при правильной нормировке (нулевой потенциал на бесконечности) в электростатике она дает правильный результат.
|
||
|
|
|||
|
pbm |
Re: Найти энергию шара
|
|
21/07/17 |
Цитата: Впрочем, можете использовать формулу для энергии через потенциал и плотность заряда Можно попробовать решить данную задачу через потенциал.
|
|
|
|
|
DimaM |
Re: Найти энергию шара
|
||
28/12/12 |
Для этого нужно найти потенциал снаружи и внутри шара? Снаружи не нужно — там плотность заряда нулевая. Потенциал искать по этой формуле? Нижний предел другой: нужно, чтобы на бесконечности был нуль потенциала.
|
||
|
|
|||
|
pbm |
Re: Найти энергию шара
|
|
21/07/17 |
Цитата: Нижний предел другой: нужно, чтобы на бесконечности был нуль потенциала. В данном случае нужно использовать формулу
|
|
|
|
|
DimaM |
Re: Найти энергию шара
|
||
28/12/12 |
В данном случае нужно использовать формулу Это внутри, снаружи по-другому. Кстати, эту формулу удобнее записать в виде
|
||
|
|
|||
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Содержание книги
Предыдующая страница
§9. Электрическое поле и его свойства
9.13 Энергия электрического поля. Плотность энергии.
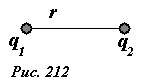
Вернемся к обсуждению вопроса об энергии взаимодействия электрических зарядов. Ранее мы показали, что потенциальная энергия электростатического взаимодействия двух точечных зарядов q1 и q2, находящихся на расстоянии r друг от друга (рис. 212), рассчитывается по формуле
(~U(r) = frac{1}{4 pi varepsilon_0} frac{q_1 q_2}{r}) . (1)
Придадим этой формуле несколько иной вид
(~U(r) = frac{1}{4 pi varepsilon_0} frac{q_1 q_2}{r} = q_1 frac{1}{4 pi varepsilon_0} frac{q_2}{r} = q_1 varphi_1) ,
здесь (~varphi_1 = frac{1}{4 pi varepsilon_0} frac{q_2}{r}) — потенциал поля, создаваемого вторым зарядом, в точке, где находится первый заряд. Аналогично можно записать
(~U(r) = frac{1}{4 pi varepsilon_0} frac{q_1 q_2}{r} = q_2 frac{1}{4 pi varepsilon_0} frac{q_1}{r} = q_2 varphi_2) ,
где (~varphi_2 = frac{1}{4 pi varepsilon_0} frac{q_1}{r}) — потенциал поля, создаваемого первым зарядом, в точке, где находится второй заряд. Теперь, перепишем выражение (1), в симметричной форме, легко допускающей обобщение
(~U(r) = frac{1}{2} (q_1 varphi_1 + q_2 varphi_2)) . (2)
В этой формуле мы выписали два равных слагаемых, каждое из которых можно трактовать как энергию взаимодействия одного из зарядов с другим, но мы подчеркивали, что энергия взаимодействия, не «принадлежит» ни одному из зарядов, поэтому нельзя учитывать эту энергию дважды – из-за этого и появляется в формуле множитель 1/2.
Если система состоит из нескольких зарядов q1, q2, …, qN , то полная энергия их взаимодействия есть сумма энергий взаимодействий всех пар зарядов. Используя симметричное выражение (2), суммирование по парам зарядов (двойную сумму), можно заменить на суммирование по самим зарядам, то есть записать
(~U = sum_{pairs} {frac{1}{4 pi varepsilon_0} frac{q_i q_k}{r_{ik}}} = frac{1}{2} (q_1 varphi_1 + q_2 varphi_2 + ldots + q_N varphi_N) = frac{1}{2} sum_{charges} {q_k varphi_k}) . (3)
В этой формуле φk — потенциал поля в точке, где находится заряд qk, причем поля, создаваемого всеми зарядами, кроме самого заряда qk (как говорят, исключая самовоздействие заряда на самого себя).
Использование понятия энергии взаимодействия требует чрезвычайной точности и внимательности. Произвол в выборе нулевого уровня энергии, с одной стороны, предоставляет определенную свободу, а, с другой, требует четкого понимания о какой именно энергии идет речь. Так, если в формуле (3) потенциалы отсчитываются относительно точек, бесконечно удаленных от зарядов, то эта формула определяет работу, которую совершит электрическое поле при удалении всех зарядов на бесконечно большие расстояния друг от друга. Если же требуется рассчитать работу поля при изменении положения зарядов, то выбор нулевого уровня не принципиален – эта работа не зависит от нулевого уровня потенциала.
Для того чтобы разобраться в некоторых нюансах применения формулы (3), рассмотрим примеры расчета энергии электростатического взаимодействия.
Три точечных заряда.
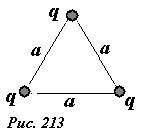
Пусть три одинаковых точечных заряда, величины которых равны между собой q1 = q2 = q3 = q, расположены в вершинах правильного треугольника со стороной a (рис.213). Для расчета энергии взаимодействия этих зарядов заметим, что все заряды равноправны, находятся в одинаковых условиях. В месте расположения одного из зарядов потенциал поля, создаваемого двумя другими зарядами равен
(~varphi_1 = varphi_2 = varphi_3 = 2 frac{q}{4 pi varepsilon_0 a}) .
В соответствии с формулой (3) энергия взаимодействия зарядов равна
(~U_0 = frac{1}{2} (q_1 varphi_1 + q_2 varphi_2 + q_3 varphi_3) = 3 frac{q^2}{4 pi varepsilon_0 a}) . (4)
Такую работу совершит электрическое поле, при удалении всех зарядов на бесконечное расстояние друг от друга.
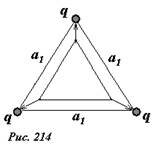
Если заряды сместятся, так что окажутся в вершинах правильного треугольника со стороной a1 , то их энергия окажется равной
(~U_1 = 3 frac{q^2}{4 pi varepsilon_0 a_1}) .
При таком смещении работа электрического поля будет равна уменьшению энергии системы
(~A = U_0 — U_1 = 3 frac{q^2}{4 pi varepsilon_0} left ( frac{1}{a} — frac{1}{a_1} right)) .
Обратите внимание, при (~a_1 to infty) эта работа становится в точности равной начальной энергии U0.
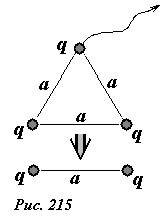
Если из первоначальной системы мы удалим один заряд при неподвижных оставшихся (рис. 215), то энергия системы станет равной
(~U_1 = frac{q^2}{4 pi varepsilon_0 a}) .
При этом поле совершит работу
(~A = U_0 — U_1 = 3 frac{q^2}{4 pi varepsilon_0 a} — frac{q^2}{4 pi varepsilon_0 a} = 2 frac{q^2}{4 pi varepsilon_0 a}) .
Если теперь удалить еще один заряд, то энергия системы станет равной нулю, при этом поле совершит работу A2 = U1. В итоге начальная энергия полностью расходуется на совершение полной работы U0 = A1 + A2 .
Задание для самостоятельной работы.
- Проанализируйте изменение энергии и совершенные работы в рассмотренной системе, если один из зарядов отрицательный.
Энергия взаимодействия двух равномерно заряженных параллельных пластин.
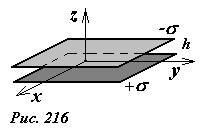
Найдем энергию взаимодействия двух равных по модулю зарядов противоположного знака, равномерно распределенными по двум параллельным пластинам. Обозначим поверхностную плотность заряда на одной пластине +σ, а на другой —σ. Расстояние между пластинами h будем считать значительно меньшим размеров пластин, площадь каждой пластины обозначим S. Краевыми эффектами пренебрежем.
Для расчета энергии взаимодействия воспользуемся формулой U = qφ’, где φ’ — потенциал поля создаваемого всеми зарядами, кроме заряда q.
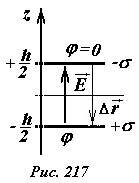
Напряженность поля между пластинами была вычислена нами ранее, она равна
(~E = frac{sigma}{varepsilon_0}) . (5)
Для «упрощения» расчетов положим потенциал отрицательно заряженной пластины равным нулю, тогда потенциал другой пластины будет равен
(~varphi = -vec E cdot Delta vec r = Eh = frac{sigma h}{varepsilon_0}) . (6)
Здесь (~Delta vec r) — вектор перемещения от отрицательной пластины к положительной. Данная формула определяет потенциал поля, создаваемого зарядами на обеих пластинах.
Теперь необходимо найти потенциал поля φ’, создаваемого только одной пластиной. Напряженность поля E’, создаваемого одной пластиной в два раза меньше напряженности поля между пластинами (~E’ = frac{E}{2} = frac{sigma}{2 varepsilon_0}) , поэтому искомый потенциал будет равен (~varphi’ = E’h = frac{sigma h}{2 varepsilon_0}) . Таким образом, энергия взаимодействия зарядов оказывается равной
(~U = q varphi’ = (sigma S) frac{sigma h}{2 varepsilon_0} = frac{sigma^2}{2 varepsilon_0} Sh) , (7)
здесь σS — заряд положительно заряженной пластины.
Не смотря на то, что противоположно заряженные пластины притягиваются, их энергия оказалась положительной – в этом нет ничего удивительного: мы положили потенциал одной из пластин равным нулю. Это значит, что нулевой энергии соответствует положение, когда положительно заряженная пластина совпадает с отрицательно заряженной, то есть когда пластины совпадают, а электрическое поле отсутствует. Если пластины находятся на некотором расстоянии h друг от друга, то при их сближении поле совершит положительную работу. Наоборот, чтобы разнести пластины, внешние силы должны совершить работу, увеличивая энергию системы.
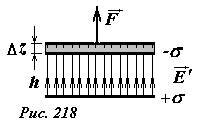
Энергию рассматриваемой системы можно найти, рассчитывая работу внешних сил, по разнесению пластин. На одну из пластин со стороны другой действует сила электрического притяжения (~F = q E’ = (sigma S) frac{sigma}{2 varepsilon_0} = frac{sigma^2}{2 varepsilon_0} S) , причем эта сила не зависит от расстояния между пластинами. Для того, чтобы раздвинуть пластины на расстояние h, необходимо приложить внешнюю силу, равную по модулю силе электрического притяжения (рис. 218). При этом эта сила совершит работу (равную увеличению энергии системы)
(~A = U = Fh = frac{sigma^2}{2 varepsilon_0} Sh) . (7′)
Таким образом, мы получаем ту же формулу для энергии систему зарядов. Используя соотношение между напряженностью поля между пластинами и поверхностной плотностью заряда σ = ε0E, выразим энергию взаимодействия через напряженность поля
(~U = frac{varepsilon_0^2 E}{2} Sh) . (8)
В процессе разнесения пластин создается электрическое поле во все большем объеме между пластинами, поэтому можно утверждать, что совершенная работа увеличивает энергию электрического поля, или работа расходуется на создание поля. Так при смещении пластины на расстояние Δz, объем занятый полем увеличивается на SΔz, если расстояние между пластинами увеличилось от нуля до некоторого значения h, то поле создается в объеме Sh. Таким образом, найденная энергия взаимодействия зарядов (7) есть энергия электрического поля — энергия «размазанная» по той области пространства, где создано поле. Косвенным подтверждением сделанного заключения, является тот факт, что энергия взаимодействия пропорциональна объему части пространства V = Sh, занятого полем и выражается через характеристику поля (его напряженность) – в формуле (8) нет характеристик зарядов. Электрическое поле, уже благодаря своему существованию обладает энергией. В качестве энергетической характеристики поля следует рассматривать энергию, содержащуюся в единице объема, то есть объемную плотность энергии[~w = frac{W}{V}] . Из выражения (8) следует, что объемная плотность энергии электрического поля определяется формулой
(~w = frac{varepsilon_0 E^2}{2}) . (9)
Как обычно, в неоднородном поле корректное определение плотности энергии «в данной точке» требует предельного перехода: плотностью энергии электрического поля называется отношение энергии поля, заключенной в малом объеме к величине этого объема, при стремлении последнего к нулю
(~w = frac{Delta U}{Delta V}) , при ΔV → 0 .
Энергия поля равномерно заряженной сферы.
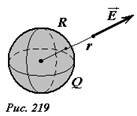
Пусть электрический заряд Q равномерно распределен по поверхности сферы радиуса R. Вне сферы электрическое поле, создаваемое зарядами на сфере, эквивалентно полю точечного заряда, помещенного в центре сфере (рис. 219). Внутри сферы поле отсутствует. Так напряженность поля в точке, находящейся на расстоянии r от центра сферы равна
(~E(r) = frac{Q}{4 pi varepsilon_0 r^2}) , (10)
в частности непосредственно у поверхности сферы напряженность поля равна
(~E_0 = frac{Q}{4 pi varepsilon_0 R^2}) . (11)
Обратим внимание, что произведение (~S = 4 pi R^2) есть площадь сферы, поэтому отношение (~frac{Q}{4 pi varepsilon_0} = sigma) является поверхностной плотностью заряда на сфере, поэтому напряженность поля у поверхности сферы выражается той же формулой, что и напряженность поля между пластинами, рассмотренными в предыдущем разделе (~E_0 = frac{sigma}{varepsilon_0}). Потенциал поверхности сферы также был вычислен нами ранее
(~varphi_0 = frac{Q}{4 pi varepsilon_0 R}) . (12)
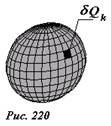
Рассчитаем теперь энергию поля, создаваемого зарядами на сфере. Мысленно разделим заряд сферы на N равных малых частей (рис.220), величины которых равны (~delta Q_k = frac{Q}{N}) (k = 1,2…N). Рассмотрим один из этих малых зарядов. В точке его расположения потенциал поля, создаваемого всеми остальными (N-1) зарядами равен (~varphi_k = frac{(N-1) delta Q}{4 pi varepsilon_0 R}). С использованием симметричной формулы (~U = frac{1}{2} sum_{k} {q_k varphi_k}) , выражение для энергии взаимодействия приобретает вид
(~U = frac{1}{2} sum_{k} {q_k varphi_k} = frac{1}{2} sum_{k=1}^{N} {delta Q_k frac{(N-1) delta Q}{4 pi varepsilon_0 R}}) ,
данная сумма содержит N одинаковых слагаемых, поэтому равна
(~U = frac{1}{2} sum_{k=1}^{N} {delta Q_k frac{(N-1) delta Q}{4 pi varepsilon_0 R}} = frac{1}{2} N delta Q frac{(N-1) delta Q}{4 pi varepsilon_0 R} = frac{1}{2} N (N-1) frac{(delta Q)^2}{4 pi varepsilon_0 R} = frac{Q^2}{8 pi varepsilon_0 R} left ( 1 — frac{1}{N} right)) . (13)
Так как число частей N, на которые разбивается сфера, может быть сделано сколь угодно большим, поэтому в пределе (~N to infty) слагаемое (~frac{1}{N}) исчезает, поэтому окончательное выражение для энергии взаимодействия зарядов сферы имеет вид
(~U = frac{Q^2}{8 pi varepsilon_0 R}) . (14)
Заметим, что полученное выражение имеет вид (~U = frac{1}{2} Q varphi_0). Если сразу заявить, что уменьшение заряда на малую величину (~delta Q) пренебрежимо мало изменяет потенциал сферы, то результат (4) получается прямым применением формулы для энергии взаимодействия зарядов. Однако обращение с малыми величинами требует известной строгости, поэтому мы и привели несколько «удлиненный» вывод.
Приведем еще один вывод этой же формулы. Для этого энергию системы рассчитаем как работу, которую необходимо совершить, чтобы зарядить сферу. Мысленно будем заряжать сферу малыми равными порциями заряда (~delta Q_k = frac{Q}{N}) (k = 1,2…N), которые будем переносить на сферу из «бесконечности». Если сфера не заряжена, то перенесение первой «порции» заряда не требует совершения никакой работы. После того как сфера приобрела некоторый электрический заряд, перенесение следующей порции заряда требует совершения работы по преодолению сил отталкивания со стороны зарядов сферы. Если на сферу перенесено (k-1) порций заряда, то ее потенциал равен (~varphi_{(k-1)} = frac{(k-1) delta Q}{4 pi varepsilon_0 R}) . Поэтому для того, что бы перенести на сферу следующую порцию заряда необходимо совершить работу
(~A_k = delta Q varphi_{(k-1)} = (k-1) frac{(delta Q)^2}{4 pi varepsilon_0 R}) .
Заметьте, что для перенесения каждой следующей порции заряда надо совершать большую работу.
Полная работа по зарядке сферы (равная энергии электрического поля сферы) выражается суммой геометрической прогрессии
(~U = A = frac{1}{2} sum_{k=1}^{N} {A} = frac{(delta Q)^2}{4 pi varepsilon_0 R} sum_{k=1}^{N} {(k-1)} = frac{(delta Q)^2}{4 pi varepsilon_0 R} frac{N (N-1)}{2} = frac{Q^2}{8 pi varepsilon_0 R} left ( 1 — frac{1}{N} right)) . (15)
Как и следовало ожидать, мы получили выражение, полностью совпадающее с (13), при бесконечном уменьшении порций переносимых зарядов ((~N to infty)) мы опять приходим к формуле (14).
В этом нет ничего удивительного, так как в первом случае мы подсчитали энергию, которая выделится при разбегании зарядов со сферы, а во втором – энергию, которую необходимо затратить, чтобы собрать их обратно.
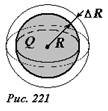
Покажем, что энергию взаимодействия зарядов и в этом случае можно истолковать как энергию электрического поля, «размазанную» по всему пространству, где существует поле. Представим, что радиус сферы увеличился на малую величину ΔR, а ее заряд при этом не изменился. Согласно формуле (14) энергия взаимодействия зарядов при этом уменьшится. В пространстве вне сферы увеличенного радиуса электрическое поле не изменилось, а в тонком сферическом слое между начальной и расширенной сферами – исчезло (рис. 221). Поэтому следует считать, что уменьшение энергии взаимодействия зарядов при увеличении радиуса сферы равно энергии, которая заключена в этом тонком сферическом слое. При малой толщине слоя его объем можно вычислить как произведение площади сферы на толщину слоя (~Delta V = 4 pi R^2 Delta R) . Пренебрегая изменением напряженности поля в пределах тонкого слоя, энергию, заключенную в нем запишем в виде
(~Delta U = w Delta V = 4 pi R^2 Delta R w) , (16)
где w — плотность энергии поля. С другой стороны эта энергия равна изменению энергии взаимодействия зарядов при увеличении радиуса сферы
(~Delta U = frac{Q^2}{8 pi varepsilon_0 R} — frac{Q^2}{8 pi varepsilon_0 (R + Delta R)} = frac{Q^2}{8 pi varepsilon_0} frac{Delta R}{R (R + Delta R)} approx frac{Q^2}{8 pi varepsilon_0} frac{Delta R}{R^2}) .
На последнем шаге, мы пренебрегли малым изменением радиуса ΔR. Наконец, выразим заряд шара через напряженность электрического поля у его поверхности (~Q = 4 pi varepsilon_0 R^2 E) :
(~Delta U = frac{Q^2}{8 pi varepsilon_0} frac{Delta R}{R^2} = frac{varepsilon_0 E^2}{2} 4 pi R^2 Delta R) .
Из сравнения с формулой (16) следует, что и в рассматриваемом случае плотность энергии электрического поля выражается формулой (~w = frac{varepsilon_0 E^2}{2}).
Следующая страница
Enter the total energy and the total volume of a system into the calculator to determine the energy density.
- All Density Calculators
- Change in Internal Energy Calculator
- Joule Calculator
- Flux Density Calculator
Energy Density Formula
The following formula is used to calculate the energy density of a volume.
- Where Ed is the energy density (J/m^3)
- E is the total energy (J)
- V is the total volume (m^3)
To calculate energy density, divide the total energy by the total volume.
Energy Density Definition
An energy density is defined as the total energy per unit of volume or area of a system.
Energy Density Example
How to calculate energy density?
- First, measure the total energy of the system.
For this example, we will say we calculated the total energy to be 1,000 Joules.
- Next, determine the total volume.
Measuring the total volume we find our system is 40 m^3.
- Finally, calculate the energy density.
Using the formula we find the energy density to be 1,000/40 = 25 J/m^3.
FAQ
What is energy density?
Energy density is a measure of the total energy per unit volume of a system. It can also be the energy per unit area when looking at a surface area.


Расчёт полной энергии сигналов
Показатели энергии и мощности сигналов одни из важнейших характеристик, определяющих коэффициент полезного действия передатчика, качество работы приемника системы связи.
Поскольку существуют временное и спектральное представления сигналов, то данные показатели могут быть вычислены двумя способами.
Энергия одиночного сигнала вычисляется через временную функцию сигнала по формуле
Бесконечные пределы в интеграле записаны для общего случая и будут уточнены для конкретного сигнала.
Спектральное представление сигнала позволило определить эти же энергетические характеристики по спектрам сигналов. Для этого существуют равенства Парсеваля. Для непериодического сигнала, при условии, что сигнал начинается в начале координат:
Если сигнал симметричен относительно начала координат, то формула (1.12) будет выглядеть следующим образом:
Рассчитаем энергию сигнала 1 по формуле (1.11). Так как сигнал конечен, то бесконечные пределы заменяем конечными.
Найдём энергию второго сигнала по формуле (1.11). Для определения пределов интегрирования, оценим скорость убывания функции. Подставим в качестве пределов интегрирования ориентировочные значения t. После расчёта числового значения интеграла увеличим принятые пределы в два раза и снова посчитаем интеграл. Если полученный результат совпадает с предыдущим с точностью до двух значащих цифр, то можно оставить принятые в первом случае пределы в качестве окончательных. После подбора примем, что верхний предел интегрирования tв = — 0.0016 с, а нижний соответственно tн= 0.0016 с.
Подставив их в (1.11), получим:
Энергию сигнала 3 определим аналогично, подставив вместо пределов интегрирования верхнюю и нижнюю границы сигнала.
Расчёт неполной энергии сигналов
По заданному проценту определим неполную энергию сигналов. Для первого сигнала:
Для второго сигнала
Для третьего сигнала
Методом итераций рассчитаем граничные частоты спектров сигналов по рассчитанной выше неполной мощности. Для расчёта граничных частот используем формулы (1.12) и (1.13). Граничные частоты: 1 = 109000 рад/с; 2 = 139500 рад/с; 3 = 259000 рад/с.
Построим графики полной энергии сигналов и отметим на них процент от полной энергии. Графики сигналов 1 3 изображены соответственно на рисунках 1.8 1.10.
Энергия сигнала
На практике часто используются такие характеристики, как энергия и мощность сигнала. Если к резистору с сопротивлением R приложено постоянное напряжение U, то выделяющаяся в резисторе мощность будет
За время Т в этом резисторе выделится тепловая энергия
Если к тому же резистору приложить не постоянное напряжение, а напряжение, описываемое сигналом S(t), то рассеивающаяся в резисторе мощность также будет зависеть от времени. Тогда мгновенную мощность можно описать выражением
Чтобы вычислить выделяющуюся за время Тэнергию, мгновенную мощность необходимо интегрировать в пределах интервала Т.
Можно ввести также понятие средней мощности за заданный промежуток времени, разделив энергию на длительность временного интервала:
Во все формулы входит сопротивление нагрузки R. Однако если энергия и мощность интересуют нас не как физические величины, а как средство сравнения различных сигналов, то этот параметр можно из формул исключить, приняв R = 1 Ом. Тогда можем определить энергию, мгновенную мощность и среднюю мощность сигнала, принятые в теории сигналов:
Фактически сигнал не производит работы и физически энергии нет, так как сигнал — это абстрактное понятие. Однако формально, взяв квадрат от сигнала, мы говорим о мощности или об энергии сигнала, применяя эти характеристики к сигналу.
В теории передачи информации практическое значение имеет равенство Парсеваля, формально описывающее закон сохранения энергии применительно к сигналам при переходе от временного представления сигнала S(t) к частотному спектру Ф(/ю). Для получения равенства Парсеваля выполним следующие действия.
1. Запишем выражение для определения энергии сигнала S(t) в виде
2. Выразим энергию через спектральную плотность амплитуд, т.е. используем обратное преобразование Фурье (3.17):
Поскольку S (/) не зависит от со, то внесем S (t) во второй интеграл:
В результате получим равенство Парсеваля:
в котором проявляется закон сохранения энергии сигнала: энергия сигнала во временной области равна энергии спектра сигнала в частотной области.
Энергия сигнала может быть конечной или бесконечной. Например, любой сигнал конечной длительности будет иметь конечную энергию (если он не содержит 6-функций или ветвей, уходящих в бесконечность). А периодический сигнал имеет бесконечную энергию, так как формально он бесконечен во времени. Если энергия сигнала бесконечна, то можно определить его среднюю мощность на всей временной оси. В результате выполнения предельного перехода интервал усреднения стремится к бесконечности:
2
Если взять квадратный корень из средней мощности, то это даст среднеквадратичное (действующее) значение или эффективное значение сигнала:
Энергетические характеристики сигналов. Спектральная плотность энергии
Пусть дан некоторый сигнал , который характеризует изменение напряжения или силы тока во времени. Тогда будет определять мгновенную мощность, выделяемую на сопротивлении 1 Ом.
Таким образом, периодические сигналы, повторяющиеся на всей оси времени мы можем характеризовать конечной средней мощностью , поскольку их энергия бесконечна. Непериодические сигналы характеризуются конечной энергией , потому что их средняя мощность на всей оси времени равна нулю.
Выражения (1)–(3) справедливы и для комплексного сигнала . В этом случае, мгновенную мощность можно определить как .
Пусть даны два сигнала и , в общем случае комплексные. Скалярным произведением сигналов называется величина равная:
Заметим, что скалярное произведение сигнала с самим собой возвращает энергию данного сигнала:
Подставим в (4) вместо обратное преобразование Фурье его спектральной плотности . Тогда:
связывающее среднюю мощность периодического сигнала. Для непериодических сигналов мы можем получить аналогичное равенство энергии сигнала во времени и в частотной области. Для этого в обобщенную формулу Рэлея подставим и получим:
Если в выражениях (7)–(9) использовать частоту , выраженную в герц, вместо циклической частоты , измеряемой в единицах рад/c, то и множитель сокращается:
было введено понятие спектральной плотности сигнала и была приведена аналогия поясняющая понятие спектральной плотности, и ее отличие от спектра периодического сигнала.
Из равенства (9) следует, что энергия сигнала может быть представлена как интеграл по всей оси частот:
Сделаем важное замечание. Спектральная плотность энергии игнорирует ФЧХ сигнала. Тогда можно заключить, что одной и той же спектральной плотности энергии могут соответствовать множество различных сигналов, имеющих одинаковую АЧХ и различные ФЧХ.
и на практике анализ поведения убывающей спектральной плотности с ростом частоты имеет важное значение. Однако графический анализ бывает затруднителен ввиду высокой скорости убывания спектральной плотности по частоте, а в случае спектральной плотности энергии затруднителен вдвойне, поскольку возведение АЧХ в квадрат только ускоряет убывание. Поэтому широкое распространение получило представление спектральной плотности энергии в логарифмическом масштабе, выраженной в единицах децибел (дБ):
В качестве примера на рисунке 1 приведены спектральные плотности энергии прямоугольного, треугольного, двустороннего экспоненциального и гауссова импульсов в линейном и логарифмическом масштабе.
Как видно из рисунка 1а, спектральные плотности энергии импульсов в линейном масштабе практически сливаются и очень сложно различимы.
Логарифмическая шкала представления спектральной плотности энергии оказывается удобной при сравнении характеристик сигналов. Если энергии двух сигналов отличаются в 100 раз, то в логарифмической шкале отношение их энергий составляет 20 дБ. Если же энергии отличаются в 1000000 раз, то в логарифмической шкале это соответствует 60 дБ. Удвоение энергии сигнала, в логарифмической шкале соответствует прибавлению 3 дБ.
В данном разделе мы рассмотрели энергетические характеристики периодических и непериодических сигналов. Мы показали, что периодические сигналы имеют бесконечную энергию, но конечную среднюю мощность. Средняя мощность непериодических сигналов стремится к нулю, а их энергия конечна.
Было введено понятие скалярного произведения сигналов и получена обобщенная формула Релея,связывающая скалярное произведение во временной и частотной областях.
Установлено равенство Парсеваля для непериодических сигналов, как частный случай формулы Релея.
Введено понятие спектральной плотности энергии как квадрата модуля спектральной плотности сигнала. Также рассмотрено представление спектральной плотности энергии в линейном и логарифмическом масштабе для различных сигналов.



 .
.
 ,
,  напряженность электрического поля,
напряженность электрического поля, 
 диэлектрическая проницаемость. Из теоремы Гаусса следует, что напряженность электрического поля шара равно:
диэлектрическая проницаемость. Из теоремы Гаусса следует, что напряженность электрического поля шара равно:


 поделить, раз уж вы в СГС ответ приводите.
поделить, раз уж вы в СГС ответ приводите. . После преобразований получу:
. После преобразований получу:
![$$W=int_{0}^{V}(varepsilon E^2)dV=left[varepsilon=1right]=int_{0}^{R}frac{64}{9}pi^3 rho^2 r^4 dr=frac{4pi Q^2}{5R}$$ $$W=int_{0}^{V}(varepsilon E^2)dV=left[varepsilon=1right]=int_{0}^{R}frac{64}{9}pi^3 rho^2 r^4 dr=frac{4pi Q^2}{5R}$$](https://dxdy-04.korotkov.co.uk/f/7/0/b/70bd79b5cd0eb2af16d01bd7c23f8f9c82.png)

 . Тогда:
. Тогда:



 , если потенциал задан с нулем на бесконечности (
, если потенциал задан с нулем на бесконечности ( — плотность заряда). Идеологически так менее правильно (энергия все же хранится в поле), но зато больше похоже на именно «энергию шара».
— плотность заряда). Идеологически так менее правильно (энергия все же хранится в поле), но зато больше похоже на именно «энергию шара».
 , верно? Если ее поставить в
, верно? Если ее поставить в  получаем, что потенциал равен нулю когда
получаем, что потенциал равен нулю когда  , а на бесконечности, когда
, а на бесконечности, когда  ,
,  . Не понимаю, где я неправильно мыслю?
. Не понимаю, где я неправильно мыслю?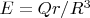 .
.
 — радиус шара.
— радиус шара.


















