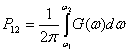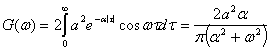При наблюдении за течением случайного процесса мы можем определить лишь текущий спектр данной реализации x(t), т. е.
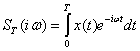
Эта функция является случайной. Поэтому удобно ввести понятие энергетического спектра, которое приводит к неслучайной функции частоты.
Энергетический спектр стационарного случайного процесса определяется как спектр его функции корреляции.
(2.81)
Обратное преобразование Фурье дает
(2.82)
Так как B(τ) и G(ω) — четные, функции своих аргументов, то ф-лы (2.81) и (2.82) можно записать в другом виде:
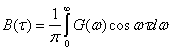
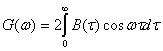
Физический смысл функции G(ω) легко выяснить на основании (2.82), если в последнем положить τ=0. При этом мы получаем
(2.85)
где Р — полная мощность процесса.
Формула (2.85) показывает, что функция G(ω) выражает спектральную плотность мощности процесса. Мощность в полосе — можно определить интегрированием G(ω) в пределах от
до
, т. е.
Энергетический спектр можно выразить и через текущий спектр реализации i(2.80). Согласно равенству Парсеваля энергия процесса x(t), выделяющаяся за время Т, равна:
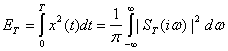
Средняя мощность процесса определится как предел ЕТ/Т при , т. е.
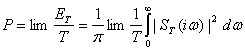
Сопоставляя (2.85) и (2.87), находим
(2.88)
Это соотношение устанавливает связь между энергетическим спектром процесса и текущим спектром его реализации.
Энергетический спектр характеризует поведение реализаций процесса в среднем. Так, если спектр G(ω) сосредоточен в области низких частот, то процесс этот — медленно изменяющийся по сравнению с тем процессом, у которого спектр сосредоточен в области. более высоких частот. Для узкополосного процесса G(ω) заметно отличается от нуля только в полосе Δω вокруг средней частоты ) причем Δω<<
. Такой процесс напоминает синусоиду с медленно меняющимися амплитудой и фазой.
Поскольку энергетический спектр и функция корреляции связаны между собой парой преобразований Фурье, то к ним можно применить известные теоремы спектрального анализа. Некоторые соотношения из этих теорем приведены в табл. 2.1. Здесь предполагается, что х=0, a и
— независимы.
Случайный процесс, у которого G(ω)= — постоянная величина, называется белым шумом.
Таблица 2.1
Корреляционная функция белого шума согласно (2.82) равна:
(2.89)
Для случайных процессов имеет место связь общего характера между шириной спектра Δf, и интервалом корреляции Δτ:
(2.90)
где μ — постоянная порядка единицы. Интервал корреляции вычисляется на основании выражения (2.24). Ширина энергетического спектра определяется аналогичным соотношением
(2.91)
Пусть, например, задан процесс, функция корреляции которого определяется выражением . Энергетический спектр такого процесса согласно (2.84)
Далее, , а согласно (2.24)
. Затем
отсюда
.
6
Сигналы и линейные системы
Тема 7: энергетические спектры сигналов
Математик
может говорить все, что взбредет ему в
голову, но физик обязан сохранять хотя
бы крупицу здравого смысла.
Джосайя
Гиббс. Американский физик, XIX в.
Хотела
бы я знать, где эта самая крупица здравого
смысла в энергии информационного
сигнала, если сама информация считается
понятием нематериальным.
Маргарита
Пястолова. Иркутский геофизик Уральской
школы, ХХ в.
Содержание:
Введение. 7.1.
Мощность и энергия сигналов. 7.2.
Энергетические спектры сигналов.
Скалярное
произведение сигналов. Взаимный
энергетический спектр. Энергетический
спектр сигнала. Литература.
Введение
Понятия
мощности и энергии
в теории
сигналов не относятся к характеристикам
каких-либо физических величин сигналов,
а являются их количественными
характеристиками, отражающими определенные
свойства сигналов и динамику изменения
их значений во времени, в пространстве
или по любым другим аргументам.
Для
произвольного, в общем случае комплексного,
сигнала мгновенная мощность по
определению
равна квадрату функции его модуля, для
вещественных сигналов — квадрату функции
амплитуд. Энергия сигнала, также по
определению, равна интегралу от мощности
по всему интервалу существования или
задания сигнала.
Энергия
сигналов может быть конечной или
бесконечной. Конечную энергию имеют
финитные сигналы и сигналы, затухающие
по своим значениям в пределах конечной
длительности, которые не содержат
дельта-функций и особых точек (разрывов
второго рода и ветвей, уходящих в
бесконечность). В противном случае их
энергия равна бесконечности. Бесконечна
также энергия периодических сигналов.
7.1. Мощность и энергия сигналов [1,3,16].
Частотное
представление применяется не только
для спектрального анализа сигналов, но
и для упрощения вычислений энергии
сигналов и их корреляционных характеристик.
Как
уже рассматривалось ранее, для
произвольного сигнала s(t) = a(t)+jb(t), где
а(t) и b(t) — вещественные функции, мгновенная
мощность сигнала (плотность распределения
энергии) определяется выражением:
w(t)
= s(t)s*(t) = a2(t)+b2(t)
= |s(t)|2.
Энергия сигнала
равна интегралу от мощности по всему
интервалу существования сигнала. В
пределе:
Еs
=
=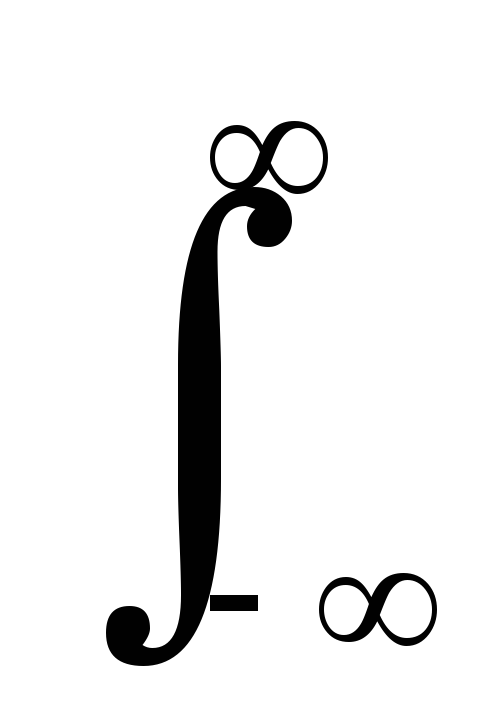
По
существу, мгновенная мощность является
плотностью мощности сигнала, так как
измерения мощности возможны только
через энергию, выделяемую на определенных
интервалах ненулевой длины:
w()
= (1/t)
Сигнал s(t) изучается,
как правило, на определенном интервале
Т (для периодических сигналов — в пределах
одного периода Т), при этом средняя
мощность сигнала:
WT()
= (1/T)w(t)
dt = (1/T)|s(t)|2
dt.
Понятие
средней мощности может быть распространено
и на незатухающие сигналы, энергия
которых бесконечно велика. В случае
неограниченного интервала Т строго
корректное определение средней мощности
сигнала производится по формуле:
Ws
=
w(t)
dt.
Энергия и норма
сигналов связаны соотношениями:
Es
= ||s(t)||2,
||s|| =
.
7.2. Энергетические спектры сигналов [1].
Скалярное
произведение сигналов.
Энергия суммы двух произвольных сигналов
u(t) и v(t) определяется выражением
E
=
[u(t)+v(t)]2
dt = Eu + Ev
+ 2
dt. (7.2.1)
Как
следует из этого выражения, энергии
сигналов, в отличие от самих сигналов,
в общем случае не обладают свойством
аддитивности. Энергия суммарного сигнала
u(t)+v(t), кроме суммы энергий составляющих
сигналов, содержит в себе и так называемую
энергию взаимодействия сигналов или
взаимную энергию
Euv
= 2
dt. (7.2.2)
Интеграл
выражения (7.2.2) для двух вещественных
сигналов является фундаментальной
характеристикой, пропорциональной
взаимной энергии сигналов. Его называют
скалярным
произведением
сигналов
Пuv
= (u(t),v(t)) =
dt = ||u||||v||
cos ,
(7.2.3)
Скалярное
произведение обладает следующими
свойствами
-
(u,v)
0; -
(u,v) = (v,u);
-
(au,v) = a(u,v), где а –
вещественное число; -
(u+v, a) = (u,a) + (v,a).
Линейное
пространство сигналов с таким скалярным
произведением называется гильбертовым
пространством
Н. С учетом того, что cos
1, в гильбертовом пространстве справедливо
неравенство Коши-Буняковского
|Пuv|
||u||||v||.
(7.2.4)
Для
комплексного гильбертова пространства
скалярное произведение также представляет
собой вещественное число и вычисляется
по формуле
Пuv
=
dt 
dt. (7.2.3′)
Из
выражения (7.2.3) следует, что косинус угла
между сигналами
cos
= Пuv/(||u||||v||).
(7.2.5)
При
полной тождественности сигналов
(равенстве амплитуд и временных координат)
имеем
= 0, cos
= 1, и скалярное произведение становится
равным энергии сигналов:
Пuv
=

dt 
dt
||u||2
||v||2
.
Дискретные
сигналы обычно рассматриваются в
пространстве Евклида
(обозначение пространства — R2).
Скалярное произведение двух сигналов
в пространстве Евклида:
Пuv
= (uk,vk)
=ukvk,
где n — размерность
пространства.
Взаимный
энергетический спектр.
Из очевидной однозначности энергии
взаимодействия сигналов независимо от
формы их математического представления
(в динамической и частотной модели)
следует выражение для скалярного
произведения произвольных вещественных
сигналов u(t) и v(t) через спектральные
плотности сигналов U()
и V()
в комплексном гильбертовом пространстве:
Пuv
= (1/2)
d(1/2)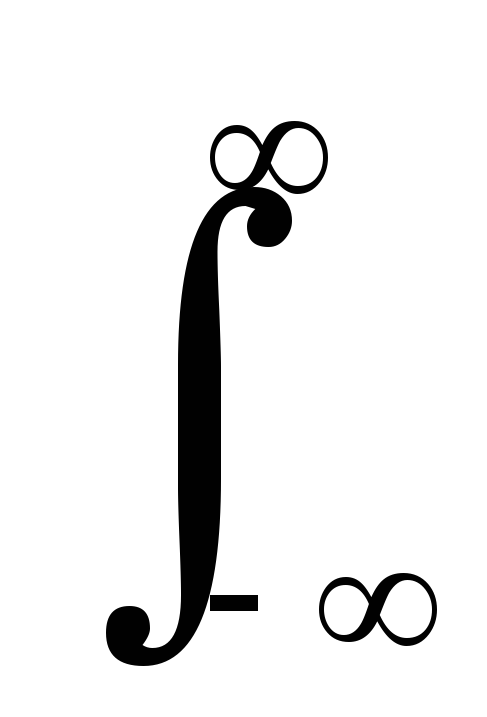
d.
(7.2.6)
Функции
Wuv()
= U()V*(),
Wvu()
= U*()V(),
Wuv()
= Wvu*(),
(7.2.7)
для
которых справедливо выражение (7.2.6),
называется взаимными
энергетическими спектрами
вещественных сигналов, и являются
функциями распределения плотности
энергии взаимодействия сигналов
(мощности взаимодействия) по частоте.
В
общем случае, за исключением спектров
четных функций, взаимные энергетические
спектры также являются комплексными
функциями:
U()
= Au()
+ j Bu(),
V()
= Av()
+ j Bv().
Wuv
= AuAv+BuBv+j
(BuAv
— AuBv)
= Re Wuv(w)
+ j Im Wuv().
(7.2.7′)
С
учетом четности реальной части и
нечетности мнимой части энергетических
спектров, интеграл мнимой части выражения
(7.2.7′) равен нулю, а, следовательно,
скалярное произведение сигналов всегда
является вещественным и неотрицательным,
как и энергия сигналов:
Пuv
= (1/2)
d
(1/)Re
Wuv()
d.2.8)
Рис.
7.2.1. Форма и энергетические спектры
сигналов.
На
рис. 7.2.1 приведена форма двух одинаковых
сдвинутых во времени и частично
перекрывающихся лапласовских импульсов
u(t) и v(t), а также суммарный импульс
z(t)=u(t)+v(t). Плотности энергии сигналов
W(f) приведены в относительных единицах
плотности энергии суммарного сигнала
Wz(f) на
нулевой частоте.
Как
видно из графиков, плотности энергии
сигналов являются вещественными
неотрицательными функциями и содержат
только реальные части. В отличие от них,
плотность взаимной энергии сигналов
является комплексной функцией, при этом
модуль плотности по своим значениям на
шкале частот соизмерим со средними
значениями плотности энергии сигналов
на этих частотах и не зависит от их
взаимного расположения на временной
оси. Для сигналов, одинаковых по форме,
модуль взаимной плотности равен значениям
плотности энергии сигналов.
Рис. 7.2.2. Взаимные
энергетические спектры сигналов.
На
рис. 7.2.2 приведены плотности взаимной
энергии тех же сигналов при разной
величине временного сдвига t
между сигналами. Однако при постоянном
значении модуля взаимной энергии
сигналов действительная и мнимая функции
спектра мощности существенно изменяются
при изменении сдвига между сигналами.
При незначительной величине временного
перекрытия сигналов частота осцилляций
реальной и мнимой части плотности
взаимной энергии достаточно велика, а
относительный коэффициент затухания
колебаний (уменьшение амплитудных
значений от периода к периоду) достаточно
мал. Соответственно, при вычислении
скалярного произведения по формуле
(7.2.8) положительные амплитудные значения
осцилляций Re(Wuv)
практически полностью компенсируются
отрицательными значениями и результирующий
интеграл, а равно и энергия взаимодействия
сигналов (удвоенное значение скалярного
произведения), близка к нулевой (стремится
к нулю по мере увеличения сдвига между
сигналами).
При
увеличении степени взаимного перекрытия
сигналов частота осцилляций плотности
взаимной энергии уменьшается (t
= 50 mkc на рис. 7.2.2) и основным по энергии
реальной части спектра становится
центральный низкочастотный пик, площадь
которого не компенсируется площадью
последующей отрицательной полуволны
осцилляции. Соответственно, возрастает
и энергия взаимодействия сигналов. При
полном перекрытии сигналов (при нулевом
фазовом угле между сигналами) осцилляции
исчезают, и энергия взаимодействия
сигналов максимальна.
Энергетический
спектр сигнала.
Если функция
s(t) имеет фурье-образ S(),
то плотность мощности сигнала
(спектральная
плотность энергии сигнала)
определяется выражением:
w(t) = s(t)s*(t) = |s(t)|2
|S()|2
= S()S*()
= W().
(7.2.9)
Спектр
мощности W()
— вещественная неотрицательная четная
функция, которую обычно называют
энергетическим
спектром.
Спектр мощности, как квадрат модуля
спектральной плотности сигнала, не
содержит фазовой информации о его
частотных составляющих, а, следовательно,
восстановление сигнала по спектру
мощности невозможно. Это означает также,
что сигналы с различными фазовыми
характеристиками могут иметь одинаковые
спектры мощности. В частности, сдвиг
сигнала не отражается на его спектре
мощности. Последнее позволяет получить
выражение для энергетического спектра
непосредственно из выражений (7.2.7). В
пределе, для одинаковых сигналов u(t) и
v(t) при сдвиге t
0, мнимая часть спектра Wuv()
стремится к нулевым значениям, а реальная
часть – к значениям модуля спектра. При
полном временном совмещении сигналов
имеем:
Wuv()
= U()V*()
= U()U*()
= |U()|2
= Wu().
(7.2.10)
Соответственно,
полная энергия сигнала:
Еu
=
= (1/2)
= (1/2)
d,
(7.2.11)
т.е.
энергия сигнала равна интегралу квадрата
модуля его частотного спектра — сумме
энергии его частотных составляющих, и
всегда является вещественной величиной.
Для произвольного
сигнала s(t) равенство
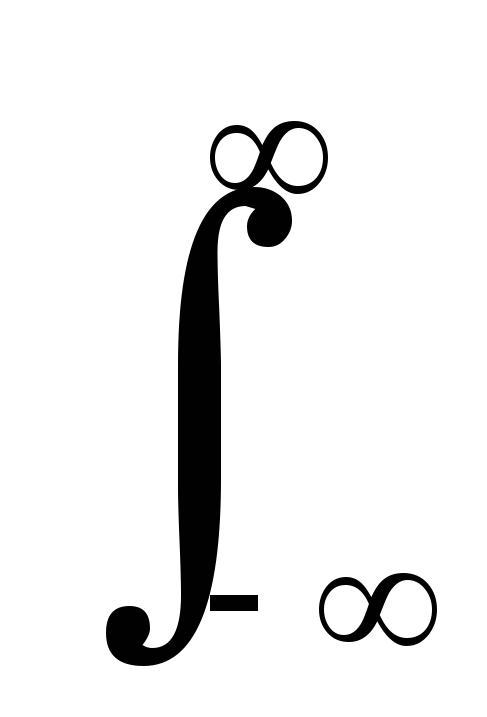
dt =
df
обычно называют
равенством Парсеваля (в математике –
теоремой Планшереля, в физике – формулой
Релея). Равенство очевидно, так как
координатное и частотное представления
по существу только разные математические
отображения одного и того же сигнала.
Аналогично для энергии взаимодействия
двух сигналов:
v*(t) dt =
V*(f) df.
Из равенства
Парсеваля следует инвариантность
скалярного произведения сигналов и
нормы относительно преобразования
Фурье:
(u(t),v(t))
= (U(f),V(f)), ||s(t)||2
= ||S(f)||2.
В
целом ряде чисто практических задач
регистрации и передачи сигналов
энергетический спектр сигнала имеет
весьма существенное значение.
Периодические
сигналы переводятся в спектральную
область в виде рядов Фурье. Запишем
периодический сигнал с периодом Т в
виде ряда Фурье в комплексной форме:
s(t)
=Sk
exp(j2kt/T),
и вычислим среднюю
мощность сигнала за один период:
WT
= (1/T)s2(t)
dt = (1/T)Sk
Smexp(j2k+m)t/T)
dt.
Интервал
0-Т содержит целое число периодов всех
подынтегральных экспонент, и равен
нулю, за исключением экспоненты при k =
-m, для которой интеграл равен Т.
Соответственно, средняя мощность
периодического сигнала равна сумме
квадратов модулей коэффициентов его
ряда Фурье:
WT
=|Sk|2.
Рис. 7.2.3. Энергетический
спектр
прямоугольного
импульса.
Как правило, спектры
сигналов с крутыми фронтами (например,
кодовых сигналов при передаче цифровых
данных) являются многолепестковыми с
постепенным затуханием энергии в
последовательных лепестках. Пример
нормированного энергетического спектра
прямоугольного импульса длительностью
и
приведен на рис. 7.2.3. Спектры выполнены
в линейном (сплошная линия) и логарифмическом
(пунктир) масштабе по оси значений. Для
четкого разделения лепестков функции
спектров приведены по безразмерной
частотной переменной fи.
Интегрированием
энергетического спектра по интервалам
лепестков спектра нетрудно вычислить,
что в пределах первого лепестка
сосредоточено 90.2% энергии всего сигнала,
в пределах второго – 4.8%, в пределах
третьего – 1.7%, и т.д. Если форма сигналов
в пункте их приема (детектирования)
существенного значения не имеет, а
регистрация сигналов идет на уровне
статистических шумов, равномерно
распределенных по всему частотному
диапазону, то такие сигналы целесообразно
пропускать через фильтр нижних частот
с выделением только первого энергетического
лепестка сигнала. Естественно, что при
этом фронты регистрируемого сигнала
будут сглажены. Но при расширении полосы
пропускания фильтра на два или три
лепестка энергия принимаемого сигнала
будет увеличена соответственно на 4.8
или 6.5%, в то время как энергия шумов в 2
или 3 раза.
Спектральное представление энергии сигнала легко получить из обобщенной формулы Рэлея, если в ней сигналы u(t) и v(t) считать одинаковыми. Формула (3.3), выражающая спектральную плотность энергии, приобретает вид
. (3.8)
Величина Wu(w) носит название спектральной плотности энергии сигнала u(t), или, короче, его энергетического спектра. Формула (3.2) при этом запишется так:
. (3.9)
Соотношение (3.9) известно в различных областях физики как формула Рэлея (в узком смысле), которая констатирует следующее: энергия любого сигнала есть результат суммирования вкладов от различных интервалов частотной оси. Каждый малый интервал положительных частот Dw обеспечивает вклад в общую энергию сигнала, равный
,
где w’ – некоторая внутренняя точка данного интервала.
Подход, основанный на спектральном представлении энергии сигнала, выгодно отличается относительной простотой. Действительно, энергии, отвечающие различным областям частотной оси, складываются так же, как вещественные числа. В то же время метод преобразования Фурье, применительно к самим сигналам, основан на том, что комплексные амплитуды, описывающие вклады малых частотных участков, складываются как комплексные числа, характеризующиеся модулями и фазами.
Изучая сигнал с помощью его энергетического спектра, мы неизбежно теряем информацию, которая заключается в фазовом спектре сигнала, поскольку в соответствии с формулой (3.8), энергетический спектр есть квадрат модуля спектральной плотности и не зависит от её фазы.
Тем не менее, понятие энергетического спектра оказывается очень полезным для получения различных инженерных оценок, устанавливающих реальную ширину спектра того или иного сигнала.
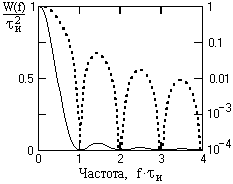
Пример 3.1. Энергетический спектр прямоугольного видеоимпульса.
Результат получается путём возведения в квадрат спектральной плотности вида (2.20):
. (3.10)
Соответствующий график приведён на рис. 3.2.
Рис. 3.2. Нормированный энергетический спектр прямоугольного видеоимпульса как функция безразмерной частотной переменной wtи
Рисунок наглядно показывает, что энергетический спектр данного сигнала имеет наибольшую величину в области низких частот. С ростом частоты вклад от соответствующих спектральных составляющих имеет немонотонный, колеблющийся характер, однако общая тенденция – уменьшение энергетического спектра по закону обратного квадрата: , при w®¥, (а не обратно пропорционально первой степени частоты, как для обычной спектральной плотности рассматриваемого сигнала).
Выражение (3.10) позволяет проверить формулу Рэлея прямым вычислением. Прежде всего, во временной области без труда находим энергию данного видеоимпульса:
. (3.11)
Чтобы определить энергию сигнала в частотной области, необходимо вычислить интеграл

Произведем замену переменной ,
тогда