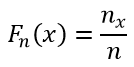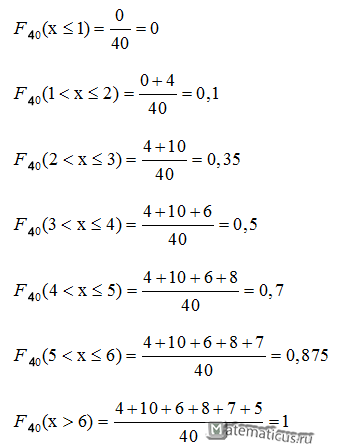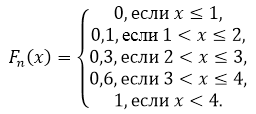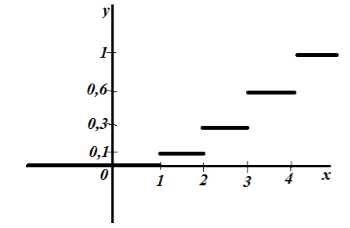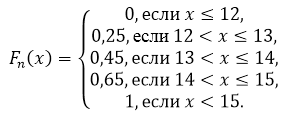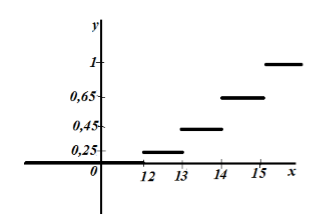Как найти эмпирическую функцию распределения по выборке - AvtoShod.ru

Эмпирической (опытной) функцией распределения или функцией распределения выборки называют такую функцию, которая определяет для каждого значения x частоту событий X<x и предназначена для оценке теоретической функции распределения генеральной совокупности в математической статистике.

Эмпирическая функция распределения находится по формуле:

n — объем выборки;

n_x — количество наблюдений (вариантов) меньше x.

Пример

Дана таблица функции распределения выборки. Требуется построить эмпирическую функцию распределения

x_i	1	2	3	4	5	6
n_i	4	10	6	8	7	5

Решение

Из таблицы n=40, т.е.
n=4+10+6+8+7+5=40
Вычислим функцию распределения выборки

Эмпирическая функция распределения имеет вид

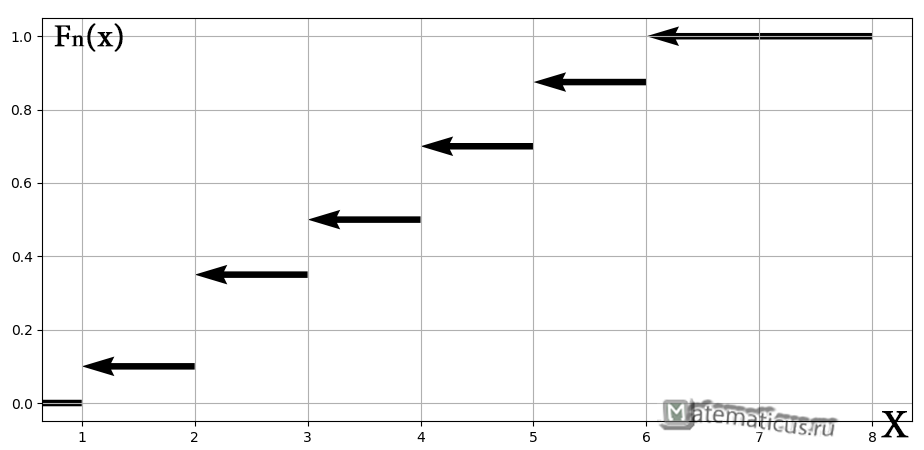
Построим график кусочно-постоянной эмпирической функции распределения

таким образом, по данным выборки можно приближенно построить функцию для неизвестной функции выборки.

74594

Источник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Определение эмпирической функции распределения

Пусть $X$ — случайная величина. $F(x)$ — функция распределения данной случайной величины. Будем проводить в одних и тех же независимых друг от друга условий $n$ опытов над данной случайной величиной. При этом получим последовательность значений $x_1, x_2 $, … ,$ x_n$, которая и называется выборкой.

Определение 1

Каждое значение $x_i$ ($i=1,2 $, … ,$ n$) называется вариантой.

Определение 2

Функция распределения $F(x)$ генеральной совокупности называется теоретической функцией распределения.

Одной из оценок теоретической функции распределения является эмпирическая функция распределения.

Определение 3

Эмпирической функцией распределения $F_n(x)$ называется функция, которая определяет для каждого значения $x$ относительную частоту события $X
[F_nleft(xright)=frac{n_x}{n}]

где $n_x$ — число вариант, меньших $x$, $n$ — объем выборки.

Отличие эмпирической функции от теоретической состоит том, что теоретическая функция определяет вероятность события $X

Свойства эмпирической функции распределения

Рассмотрим теперь несколько основных свойств функции распределения.

Область значений функции $F_nleft(xright)$ — отрезок $[0,1]$.
$F_nleft(xright)$ неубывающая функция.
$F_nleft(xright)$ непрерывная слева функция.
$F_nleft(xright)$ кусочно-постоянная функция и возрастает только в точках значений случайной величины $X$
Пусть $X_1$ — наименьшая, а $X_n$ — наибольшая варианта. Тогда $F_nleft(xright)=0$ при ${xle X}_1$и $F_nleft(xright)=1$ при $xge X_n$.

«Эмпирическая функция распределения» 👇

Введем теорему, которая связывает между собой теоретическую и эмпирическую функции.

Пусть $F_nleft(xright)$ — эмпирическая функция распределения, а $Fleft(xright)$ — теоретическая функция распределения генеральной выборки. Тогда выполняется равенство:

[{mathop{lim}_{nto infty } {|F}_nleft(xright)-Fleft(xright)|=0 }]

Примеры задач на нахождение эмпирической функции распределения

Пример 1

Пусть распределение выборки имеет следующие данные, записанные с помощью таблицы:

Рисунок 1.

Найти объем выборки, составить эмпирическую функцию распределения и построить её график.

Решение:

Объем выборки: $n=5+10+15+20=50$.

По свойству 5, имеем, что при $xle 1$ $F_nleft(xright)=0$, а при $x>4$ $F_nleft(xright)=1$.

Значение $x

Таким образом, получаем:

Рисунок 2.

Построим график эмпирического распределения:

Рисунок 3.

Пример 2

Из городов центральной части России случайным образом выбрано 20 городов, для которых получены следующие данные по стоимости проезда в общественном транспорте: 14, 15, 12, 12, 13, 15, 15, 13, 15, 12, 15, 14, 15, 13, 13, 12, 12, 15, 14, 14.

Составить эмпирическую функцию распределения данной выборки и построить её график.

Решение:

Запишем значения выборки в порядке возрастания и посчитаем частоту каждого значения. Получаем следующую таблицу:

Рисунок 4.

Объем выборки: $n=20$.

По свойству 5, имеем, что при $xle 12$ $F_nleft(xright)=0$, а при $x>15$ $F_nleft(xright)=1$.

Значение $x

Таким образом, получаем:

Рисунок 5.

Построим график эмпирического распределения:

Рисунок 6.

Оригинальность: $92,12%$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Как известно, закон
распределения случайной величины можно
задавать различными способами. Дискретную
случайную величину можно задать с
помощью ряда распределения или
интегральной функции, а непрерывную
случайную величину – с помощью или
интегральной, или дифференциальной
функции. Рассмотрим выборочные аналоги
этих двух функций.

Пусть имеется
выборочная совокупность значений
некоторой случайной величины
объемаи каждому варианту из этой совокупности
поставлена в соответствие его частость.
Пусть далее,– некоторое действительное число, а– число выборочных значений случайной
величины,
меньших.Тогда
числоявляется частостью наблюдаемых в выборке
значений величиныX,
меньших
,
т.е. частостью появления события
.
При измененииx
в общем случае будет изменяться и
величина
.
Это означает, что относительная частотаявляется функцией аргумента.
А так как эта функция находится по
выборочным данным, полученным в результате
опытов, то ее называют выборочной илиэмпирической.

Определение
10.15. Эмпирической
функцией распределения
(функцией распределения выборки) называют
функцию
,
определяющую для каждого значенияx
относительную частоту события
.

(10.19)

В отличие от
эмпирической функции распределения
выборки функцию распределения F(x)
генеральной совокупности называют
теоретической
функцией распределения.
Различие между ними состоит в том, что
теоретическая функция F(x)
определяет вероятность события
,
а эмпирическая – относительную частоту
этого же события. Из теоремы Бернулли
следует

,
(10.20)

т.е. при больших
вероятностьи относительная частота события,
т.е.мало отличаются одно от другого. Уже
отсюда следует целесообразность
использования эмпирической функции
распределения выборки для приближенного
представления теоретической (интегральной)
функции распределения генеральной
совокупности.

Функция
иобладают одинаковыми свойствами. Это
вытекает из определения функции.

Свойства
:

;
–неубывающая
функция;
;
.

Пример 10.4.
Построить эмпирическую функцию по
данному распределению выборки:

Варианты	2	6	10
Частоты	12	18	30

Решение:
Найдем объем выборки n=12+18+30=60.
Наименьшая варианта
,
следовательно,при.
Значение,
а именнонаблюдалось 12 раз, следовательно:

=при.

Значение x<10,
а именно
инаблюдались 12+18=30 раз, следовательно,=при.
При.

Искомая эмпирическая
функция распределения:

График
представлен на рис. 10.2

Р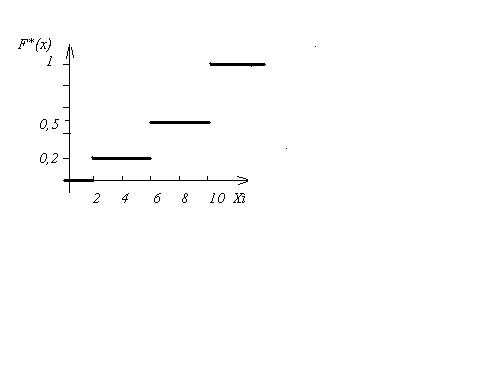ис.
10.2

Контрольные вопросы

1. Какие основные
задачи решает математическая статистика?
2. Генеральная и выборочная совокупность?
3. Дайте определение объема выборки. 4.
Какие выборки называются репрезентативными?
5. Ошибки репрезентативности. 6. Основные
способы образования выборки. 7. Понятия
частоты, относительной частоты. 8. Понятие
статистического ряда. 9. Запишите формулу
Стэрджеса. 10. Сформулируйте понятия
размаха выборки, медианы и моды. 11.
Полигон частот, гистограмма. 12. Понятие
точечной оценки выборочной совокупности.
13. Смещенная и несмещенная точечная
оценка. 14. Сформулируйте понятие
выборочной средней. 15. Сформулируйте
понятие выборочной дисперсии. 16.
Сформулируйте понятие выборочного
среднеквадратического отклонения. 17.
Сформулируйте понятие выборочного
коэффициента вариации. 18. Сформулируйте
понятие выборочной средней геометрической.

Соседние файлы в папке Лекции

Источник

Вычисление и построение эмпирических функций распределения

Пусть известно статистическое распределение частот количественного признака Х. Введем обозначения: n_х — число наблюдений, при которых наблюдалось значение признака меньшее x₁, n – общее число наблюдений (объем выборки). Ясно, что относительная частота события Х

_х/n. Если х будет изменяться, то, вообще говоря, будет, меняться и относительная частота, т.е. относительная частота n_х/n есть функция от х. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения х относительную частоту события Х

F*(x)=n_х/n

где n_х – число вариант, меньшее х, n – объем выборки

Таким образом, для того, чтобы найти, например F*(x₂), надо число вариант, меньшее x₂, разделить на объем выборки n: F*(x₂)=n_х₂/n

В отличие от эмпирической функции распределения выборки, интегральную функцию F(x) распределения генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F(x) определяет вероятность события Х Из определения функции F*(x) вытекают следующие ее свойства:
1. Значения эмпирической функции принадлежат отрезку [0;1]
2. F*(x) — неубывающая функция
3. Если х₁ – наименьшая варианта, то F*(x)=0 при х≤х₁; если х_k – наибольшая варианта, то F*(x)=1 при х>х_k.

Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

Пример 5. Построить эмпирическую функцию по данному распределению выборки:

Варианты	x_i	2	6	10
Частоты	n_i	12	18	30

Решение: Найдем объем выборки: 12+18+30=60. Наименьшая варианта равна 2, следовательно F*(x)=0 при x≤2. Значение х<6, а именно х₁= 2 наблюдалось 12 раз, следовательно, F*(x)=12/60=0.2 при 21=2 и х₂=6 наблюдались 12+18=30 раз, следовательно, F*(x)=30/60=0.5 при 6 Так как х=10 – наибольшая варианта, то F*(x)=1 при x>10.
Искомая эмпирическая функция:

эмпирическая функция, функция распределения, выборка, Высшая математика, лекция по высшей математике, теоретическая функция

Добавлять комментарии могут только зарегистрированные пользователи.

Регистрация Вход

Источник

Пусть Nх — число наблюдений, при которых значение признака Х меньше Х. При объеме выборки, равном П, относительная частота события Х < х равна Nx/N.

Определение 8. Функция

Определяющая для каждого значения Х относительную частоту события Х < х, называется Эмпирической функцией распределения, или функцией распределения выборки.

В отличие от эмпирической функции распределения F*(X) Выборки функция распределения F(X) генеральной совокупности называется Теоретической функцией распределения. Различие между ними состоит в том, что функция F(X) определяет вероятность события Х < х, a F*(X) — относительную частоту этого события. Из теоретических результатов общей теории вероятностей (закон больших чисел) следует, что при больших П вероятность отличия этих функций друг от друга близка к единице:

Нетрудно видеть, что F*(X) обладает всеми свойствами F(X), что вытекает из ее определения (18.49):

1) значения F*(X) принадлежат отрезку [0, 1];

2) F*(X) является неубывающей функцией;

3) если Х1 — наименьшая варианта, то F*(X) = 0 при Х ≤ Х1; если Xk — максимальная варианта, то F*(X) = 1 при X > XK.

Сама же функция F*(X) служит для оценки теоретической функции распределения F(X) генеральной совокупности.

Пример 3. Построить эмпирическую функцию по заданному распределению выборки:

Решение. Находим объем выборки: П = 10 + 15 + 25 = 50. Наименьшая варианта равна 2, поэтому F*(X) = 0 при Х ≤ 2. Значение Х < 4 (или X1 = 2) наблюдалось 10 раз, значит, F*(X) = 10/50 = 0,2 при 2 < Х < 4. Значения X < 6 (а именно X1 = 2 и X2 = 4) наблюдались 10 + 15 = 25 раз, значит, при 4 < Х < 6 функция F*(X) = 25/50 = 0,5. Поскольку X = 6 — максимальная варианта, то F*(X) = 1 при Х > 6. Напишем формулу искомой эмпирической функции: