Загрузить PDF
Загрузить PDF
Электрическая емкость характеризует способность проводника, такого как конденсатор, накапливать электрический заряд, используемый в электрической цепи. Единицей измерения емкости является фарад (Ф), который равен отношению 1 Кл (кулон) электрического заряда к 1 В (вольт) разности потенциалов. На деле же фарад является настолько большим значением, что емкость обычно измеряют в более мелких единицах, например, в микрофарадах, что составляют миллионную долю фарада, или нанофарадах – миллиардная доля фарада. И хотя для проведения точных замеров не обойтись без дорогостоящих приборов, с помощью цифрового мультиметра можно получить примерное значение.
Шаги
-
1
Выберите устройство. Как правило, даже самые дешевые цифровые мультиметры могут измерить электрическую емкость «–|(–». Они достаточно хороши для поверхностной проверки, но недостаточно точны для снятия точных измерений. Они показывают точные результаты у большинства пленочных конденсаторов, так как те больше всего похожи на идеальные конденсаторы, на которые рассчитан ваш мультиметр.[1]
Если вам важна точность, подумайте об использовании измерителя иммитанса. Стоимость этих приборов может достигать пары тысяч долларов (более ста тысяч рублей), но более надежного способа определения емкости вам не найти.- В этом руководстве речь пойдет о мультиметрах. Измеритель иммитанса должен поставляться вместе с инструкцией по его эксплуатации.
- ESR измеритель (Эквивалентное последовательное сопротивление) способен тестировать конденсаторы, пока те находятся в цепи, но не измеряет емкость напрямую.
-
2
Выключите питание. Отключите цепь от источника питания. Убедитесь, что питание выключено, переведя прибор в режим проверки напряжения. Приставьте щупы к противоположным сторонам источника питания электрической схемы. Если питание отключено, прибор должен показывать нулевое напряжение.
-
3
Осторожно разрядите конденсатор. Конденсатор может удерживать заряд в течение нескольких минут после отключения питания, а в редких случаях и того больше. Подключите резистор к коннекторам конденсатора, чтобы выпустить заряд. Убедитесь, чтобы резистор подходил для этой задачи:[2]
- Для небольших конденсаторов используйте резистор с сопротивлением (как минимум) 2,000Ω и рассчитанный на 5 Вт.
- Большие конденсаторы в источниках питания бытовых приборов, фотоаппаратах с фотовспышкой и двигателях могут удерживать в себе опасное или даже смертоносное количество заряда. Работы с подобным оборудованием настоятельно рекомендуем проводить под опытным надзором. Используйте резистор на 20,000Ω и 5 Вт, подключив его через кабель с сечением 3,30 мм2, рассчитанный на 600 вольт.
-
4
Отсоедините конденсатор. Тестирование конденсатора, пока он подключен к цепи, может дать весьма неточные результаты и даже привести к повреждению других элементов. Аккуратно вытащите конденсатор, при необходимости, распаивая коннекторы.
-
5
Переключите мультиметр на измерение емкости. Для обозначения емкости большинство цифровых мультиметров используют символ, похожий на –|(–. Переместите ручку регулятора на этот символ. Если в этом месте расположено сразу несколько символов, возможно, для переключения между ними необходимо нажать кнопку, пока на экране не появится символ емкости.[3]
- Если на устройстве есть несколько настроек для конденсатора, выберите наиболее вероятный диапазон его значения. Чтобы получить общее представление, осмотрите маркировку конденсатора. Если настройка лишь одна, ваш мультиметр автоматически определит диапазон.
-
6
Включите режим относительных измерений (REL), если он есть. Если на мультиметре есть кнопка REL, нажмите на нее, пока щупы разделены. Так вы обнулите емкость самих измерительных щупов, исключая ее из замеров.[4]
- В этом есть необходимость только при тестировании небольших конденсаторов.
- На некоторых моделях этот режим отключает автонастройку.[5]
-
7
Приложите щупы к коннекторам конденсатора. Обратите внимание, что электролитические конденсаторы (как правило, в форме бочонка) поляризованы, поэтому, прежде чем подключать мультиметр, вам нужно определить положительный и отрицательный коннекторы. Возможно, это не повлияет на тестирование, но вам определенно следует об этом знать, прежде чем вы используете конденсатор в цепи.[6]
Ищите любой из следующих признаков:[7]
- А + или — рядом с коннектором.
- Если из двух ножек одна окажется длиннее, она и будет положительным коннектором.
- Не стоит полагаться на цветную полосу рядом с коннектором, так как разные виды конденсаторов используют разные стандарты.[8]
-
8
Дождитесь результатов. Мультиметр пошлет электрический ток на зарядку конденсатора, измерит напряжение и с его помощью рассчитает емкость. Весь процесс может занять несколько секунд, во время которых кнопки и экран дисплея будут медленно реагировать на ваши команды.[9]
- Показатель «OL» или «overload» означает, что емкость слишком высока для измерения мультиметром. Если можно, настройте мультиметр на более высокий диапазон. Это также может означать, что конденсатор замкнуло.
- Если мультиметр с автонастройкой попадет на перегрузку, то начнет проверку с самого низкого диапазона и постепенно будет его повышать. Возможно, вы увидите, как на экране несколько раз появятся символы «OL», прежде чем узнаете результат проверки.
Реклама
Советы
- Человеческое тело также является конденсатором. Всякий раз, когда вы шаркаете ногами по ковру, скользите по сиденью автомобиля или расчесываете волосы, то создаете статический электрический заряд. Емкость человеческого тела зависит от его размеров и близости к другим электрическим проводникам.
- Большинство конденсаторов имеют цветовую маркировку, которая обозначает его уровень емкости. Сравните этот показатель с полученным значением, чтобы выяснить, работает ли ваш конденсатор на пределе своих возможностей.
- Аналоговые мультиметры (с игольчатым датчиком вместо экрана) не оборудованы источником питания, поэтому не могут отправить ток для проверки конденсатора. С его помощью можно проверить, работает ли конденсатор, но точно измерить его емкость у вас не получится.
- Некоторые мультиметры оснащены специальными щупами для работы с конденсаторами.
Реклама
Предупреждения
- Не подводите питание к конденсаторам с видимыми проколами или выпуклостями. Они могут загореться или даже взорваться.
Реклама
Об этой статье
Эту страницу просматривали 13 135 раз.
Была ли эта статья полезной?
Одним из важных параметров, учитываемых в электрических цепях, является электрическая емкость – способность проводников накапливать заряды. Понятие емкости применяется как для уединенного проводника, так и для системы, состоящей из двух и более проводников. В частности, емкостью обладают конденсаторы, состоящие из двух металлических пластин, разделенных диэлектриком или электролитом.
Для накопления зарядов широко применяютсяаккумуляторы, используемые в качестве источников постоянного тока для питания различных устройств. Количественной характеристикой, определяющей время работы аккумулятора, является его электроемкость.
Определение
Если диэлектрик, например, эбонитовую палочку, наэлектризовать трением то электрические заряды сконцентрируются в местах соприкосновения с электризующим материалом. При этом, другой конец палочки можно насытить зарядами противоположно знака и такая наэлектризованность будет сохраняться.
Совсем по-другому ведут себя проводники, помещенные электрическое поле. Заряды распределяются по их поверхности, образуя некий электрический потенциал. Если поверхность ровная, как у палочки, то заряды распределятся равномерно. Под действием внешнего электрического поля в проводнике происходит такое распределение электронов, чтобы внутри его сохранялся баланс взаимной компенсации негативных и позитивных зарядов.
Внешнее электрическое поле притягивает электроны на поверхность проводника, компенсируя при этом положительные заряды ионов. По отношению к проводнику имеет место электростатическая индукция, а заряды на его поверхности называются индуцированными. При этом на концах проводника плотность зарядов будет несколько выше.
На металлическом шаре заряды распределяются равномерно по всей поверхности. Наличие полости любой конфигурации абсолютно не влияет на процесс распределения.
Однако, если проводник убрать из зоны действия поля, то его заряды перераспределятся таким образом, что он снова станет электрически нейтральным.
На рисунке 1 изображена схема заряженного разнополюсного диэлектрика и проводника, удалённого из зоны действия электростатического поля. Благодаря тому, что диэлектрик сохраняет полученные заряды, уединенный проводник восстановил свою нейтральность.
Интересное явление наблюдается с двумя проводниками, разделенными диэлектриком. Если одному из них сообщить положительный заряд, а другому – отрицательный, то после убирания источника электризации заряды на поверхности проводников сохранятся. Заряженные таким образом проводники обладают разностью потенциалов.
Заряды, накопившиеся на диэлектрике, уравновешивают внутренние взаимодействие в каждом из проводников, не позволяя им разрядиться. Величина заряда зависит от площади поверхности параллельных проводников и от свойства диэлектрика, расположенного между ними.
Свойство сохранять накопленный заряд называется электроемкостью. Точнее говоря, – это характеристика проводника, физическая величина определяющая меру его способности в накоплении электрического заряда.
Накопленное электричество можно снять с проводников путем короткого замыкания их или через нагрузку. С целью увеличения емкости на практике применяют параллельные пластины или же длинные полоски тонкой фольги, разделённой диэлектриком. Полоски сворачивают в тугой цилиндр для уменьшения объема. Такие конструкции называют конденсаторами.
На рисунке 2 изображена схема простейшего конденсатора с плоскими обкладками.
Существуют конденсаторы других типов:
- переменные;
- электролитические;
- оксидные;
- бумажные;
- комбинированные и другие.
Важной характеристикой конденсатора, как и других накопительных систем, является его электрическая емкость.
Формулы
На рисунке 3 наглядно показано формулы для определения емкости, в т. ч. и для сферы.
По отношению к конденсатору, для определения его емкости применяют формулу: C = q/U. То есть, эта величина прямо пропорциональна заряду одной из обкладок и обратно пропорциональна разнице потенциалов между обкладками (см. рис. 4).
О других способах определения ёмкости конденсатора читайте в нашей статье: https://www.asutpp.ru/kak-opredelit-emkost-kondensatora.html
Единицы измерения
За единицу измерения величины электроемкости принято фараду: 1 Ф = 1 Кл/1В. Поскольку фарада величина огромная, то для измерения емкости на практике она мало пригодна. Поэтому используют приставки:
- мили (м) = 10-3;
- микро (мк) = 10-6;
- нано (н) = 10-9;
- пико (пк) = 10-12;
Например, электрическая емкость 1 мкф = 0,000001 Ф. Параметр зависит от геометрических размеров, конфигурации проводника и материала диэлектрика.
Уединенный проводник и его емкость
Уединенным называют проводник, влиянием на который других элементов цепей можно пренебречь. Предполагается, что все другие проводники бесконечно удалены от него, а как известно, потенциал точки, бесконечно удаленной в пространстве, равен 0.
Электрическую емкость C уединенного проводника, определяют как количество электричества q, которое требуется для повышения электрического потенциала на 1 В: С = q/ϕ. Параметр не зависит от материала, из которого изготовлен проводник.
Конденсаторы постоянной и переменной емкости
Эра накопителей электричества началась с воздушных конденсаторов. Благодаря плоскому конденсатору с большой площадью обкладок физики смогли понять, как взаимная емкость регулируется площадями пластин, что позволило им создать конденсаторы с переменной емкостью (см. рис. 5).
Идея изменения емкости состояла в том, чтобы путем поворота плоской обкладки изменять площадь поверхности, которая располагается напротив другой пластины. Если обкладки располагались точно друг против друга, то напряженность поля между ними была максимальной. При смещении одной из пластин на некоторый угол, напряженность уменьшалась, что приводило к изменению емкости. Таким образом, можно было плавно управлять накопительной способностью конденсатора.
Детали с переменной емкостью нашли применение в первых радиоприемниках для поиска частоты нужной станции. Данный принцип используется по сегодняшний день в различных аналоговых электрических схемах.
Большую популярность приобрели электролитические конденсаторы. В качестве одной из обкладок у них используется электролит, обладающий высокими показателями диэлектрической проницаемости. Благодаря диэлектрическим свойствам электролитов такие конденсаторы обладают большими емкостями.
Главные их преимущества электролитического конденсатора:
- высокие
показатели емкости при малом объеме; - применение в
цепях с постоянным током.
Недостатки:
- необходимо соблюдать полярность;
- ограниченный срок службы;
- чувствительность к повышенным напряжениям.
Высокую электрическую прочность имеют плоские конденсаторы, у которых в качестве диэлектрического материала применяется керамика. Они используются в цепях с переменным током и выдерживают большие напряжения.
Сегодня промышленность поставляет на рынок множество конденсаторов различных типов, с высокими показателями проницаемости диэлектриков.
Аккумуляторы и электроемкость
Накопители электричества большой емкости (аккумуляторы) состоят из положительных и негативных пластин, погруженных в электролит. Во время зарядки часть атомов электролита распадается на ионы, которые оседают на пластине. Образуется разность потенциалов между пластинами, что является причиной возникновения ЭДС при подключении нагрузки.
С целью увеличения напряжения аккумуляторы последовательно соединяют в батареи. Разница потенциалов одной секции около 2 В. Для получения аккумулятора на 6 В необходимо создать батарею из трех секций, а на 12 В – батарею из 6 секций.
Для характеристики аккумуляторов (батарей) используются параметры:
- емкости;
- номинального напряжения;
- максимального тока разряда.
Единицей емкости аккумулятора является ампер-час (А*ч) или кратные ей миллиампер-часы (мА*ч). Емкость аккумулятора зависит от площади пластин. Увеличить емкость можно путем параллельного подключения нескольких секций, но такой способ почти не применяется, так как проще и надежнее создать аккумулятор с большими пластинами.
Уединенным
называется проводник,
вблизи которого нет других заряженных
тел, диэлектриков, которые могли бы
повлиять на распределение зарядов
данного проводника.
Отношение
величины заряда к потенциалу для
конкретного проводника есть величина
постоянная, называемая электроемкостью
(емкостью)
С
,
.
Таким
образом,
электроемкость уединенного проводника
численно равна заряду, который необходимо
сообщить проводнику, чтобы изменить
его потенциал на единицу.
Опыт показал, что электроемкость
уединенного проводника зависит от его
геометрических размеров, формы,
диэлектрических свойств окружающей
среды и не зависит от величины заряда
проводника.
Рассмотрим
уединенный шар радиуса R,
находящийся в однородной среде с
диэлектрической проницаемостью .
Ранее было получено, что потенциал шара
равен
.
Тогда емкость шара,
т.е. зависит только от его радиуса.
За
единицу емкости принимается 1фарад (Ф).
1Ф — емкость такого уединенного
проводника, потенциал которого изменится
на 1В при сообщении заряда 1Кл. Фарад —
очень большая величина, поэтому на
практике используют дольные единицы
: миллифарад (мФ, 1мФ=10-3Ф),
микрофарад (мкФ, 1мкФ=10-6Ф),
нанофарад (нФ, 1нФ=10-9Ф),
пикофарад (пФ, 1пФ=10-12Ф).
Уединенные
проводники даже очень больших размеров
обладают малыми емкостями. Емкостью
в 1Ф обладал бы уединенный шар радиуса,
в 1500 раз большего радиуса Земли.
Электроемкость Земли составляет 0.7 мФ.
1. 18. Взаимная электроемкость. Конденсаторы
Пусть
вблизи заряженного проводника А
находятся незаряженные проводники
или диэлектрики. Под действием поля
проводника А в телах 1 и 2 возникают
индуцированные (если 1 и 2 проводники)
или связанные (если диэлектрики)
заряды, причем ближе к А будут располагаться
заряды противоположного знака (рис.1.25).
Индуцированные (или связанные) заряды
создают свое поле противоположного
направления, чем ослабляют поле
проводника А, уменьшая его потенциал и
увеличивая его электроемкость.

Взаимное влияние проводников.
На практике существует потребность
в устройствах, которые при относительно
небольшом потенциале накапливали
(конденсировали) бы на себе заметные по
величине заряды. В основу таких
устройств, называемыхконденсаторами,
положен факт, что емкость проводника
возрастает при приближении к нему других
тел. Простейший
плоский конденсатор состоит из двух
близко расположенных проводников,
заряженных равными по величине и
противоположными по знаку зарядами.
Образующие данную систему проводники
называются обкладками.
Для
того, чтобы поле, создаваемое заряженными
обкладками, было полностью сосредоточено
внутри конденсатора, обкладки должны
быть в виде двух близко расположенных
пластин, или коаксиальных цилиндров,
или концентрических сфер. Соответственно
конденсаторы называются плоскими,
цилиндрическими
или сферическими.
Разность
потенциалов между обкладками
пропорциональна абсолютной величине
заряда обкладки. Поэтому
отношение
есть величина постоянная для конкретного
конденсатора. Она обозначаетсяС
и называется взаимной
электроемкостью проводников или
емкостью конденсатора.
Емкость конденсатора численно равна
заряду, который нужно перенести с одной
обкладки конденсатора на другую, чтобы
изменить разность их потенциалов на
единицу.
Разность
потенциалов плоского конденсатора
равна
,
гдеповерхностная плотность заряда обкладки.S
— площадь обкладки конденсатора..
Отсюда
емкость плоского конденсатора
.Из этой
формулы следует, что С
плоского конденсатора зависит от
его геометрических размеров, т.е. от S
и d,
и диэлектрической проницаемости
диэлектрика, заполняющего межплоскостное
пространство. Применение в качестве
прослойки сегнетоэлектриков значительно
увеличивает емкость конденсатора,
т.к.
у них достигает очень больших значений.
В очень сильных полях (порядка Епр107
В/м) происходит разрушение диэлектрика
или «пробой», он перестает быть
изолятором и становится проводником.
Это «пробивное напряжение» зависит от
формы обкладок, свойств диэлектрика и
его толщины..
Для
получения устройств различной
электроемкости конденсаторы соединяют
параллельно и последовательно.
Параллельное
соединение конденсаторов (Рис. 1. 26).
В данном случае, так как соединенные
провода-проводники имеют один и тот же
потенциал, то разность потенциалов на
обкладках всех конденсаторов одинакова
и равна
.
Заряды конденсаторов будут
,
… ,
.
Рис.1.26. Параллельное
соединение конденсаторов.
Заряд, запасенный
всей батареей
.
Отсюда
видно, что полная
емкость системы из параллельно соединенных
конденсаторов
равнасумме
емкостей всех конденсаторов.
Последовательное
соединение конденсаторов (Рис. 1. 27).
В данном случае, вследствие электростатической
индукции,
заряды на всех обкладок q
будут равны по модулю, а общая разность
потенциалов складывается из разностей
на отдельных конденсаторах
.
Так как,
то.
Отсюда.
Рис.1.27. Последовательное
соединение конденсаторов.
При
последовательном соединении
конденсаторов обратная величина
результирующей емкости равна сумме
обратных величин емкостей всех
конденсаторов.
Соседние файлы в папке ЭЛЕКТРИЧ
- #
- #
- #
- #
- #
23.03.201699.84 Кб83КП.XLS
- #
|
Электрическая емкость. Конденсаторы. |
|
|
Емкость уединенного проводника. Уединенным будем называть проводник, размеры которого много меньше расстояний до окружающих тел. Пусть это будет шар радиусом r. Если потенциал на бесконечности принять за 0, то потенциал заряженного уединенного шара равен: эта величина не зависит ни от заряда, ни от потенциала и определяется только размерами шара (радиусом) и диэлектрической проницаемостью среды. Этот вывод справедлив для проводника любой формы. |
|
|
Электрической емкостью проводника наз. отношение заряда проводника к его потенциалу: |
|
|
Емкость определяется геометрической формой, размерами проводника и свойствами среды (от материала проводника не зависит). Чем больше емкость проводника, тем меньше меняется потенциал при изменении заряда. |
Емкость шара в СИ:
|
|
Единицы емкости. Емкостью 1Ф (фарад) обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда в 1 Кл. Емкостью 1Ф обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца. Емкость Земли 700 мкФ Если проводник не уединенный, то потенциалы складываются по правилу суперпозиции и емкость проводника меняется. |
1 мкФ=10-6Ф 1нФ=10-9Ф 1пФ=10-12Ф |
|
Конденсаторы (condensare — сгущение) . Можно создать систему проводников, емкость которой не зависит от окружающих тел. Первые конденсаторы — лейденская банка (Мушенбрук, сер. XVII в.). |
|
|
Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники наз. обкладками конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок. |
|
|
На рисунке — плоский и сферический конденсаторы. Поле плоского конденсатора почти все сосредоточено внутри (у идеального — все). Усферического — все поле сосредоточено между обкладками. |
|
|
Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками: |
|
|
При подключении конденсатора к батарее аккумуляторов происходит поляризация диэлектрика внутри конденсатора и на обкладках появляютсязаряды — конденсатор заряжается. Электрические поля окружающих тел почти не проникают через металлические обкладки и не влияют на разность потенциалов между ними. |
|
|
Емкость плоского конденсатора.
|
|
|
Емкость сферического конденсатора . Если зазор между обкладками мал по сравнению с радиусами, то формула переходит в формулу емкости плоского конденсатора. |
|
|
Виды конденсаторов |
|
|
При подключении электролитического конденсатора необходимо соблюдать полярность. |
|
|
Назначение конденсаторов
|
Проводники и системы, состоящие из нескольких проводников, обладают свойством накапливать электрический заряд. Какая физическая величина характеризует это свойство?
Электрическая ёмкость. Для характеристики свойства проводника накапливать электрический заряд ввели физическую величину — электрическую ёмкость С. Для объяснения физического смысла этой величины рассмотрим следующий опыт: присоединим тонким длинным проводником к стержню электрометра с заземлённым корпусом уединённый полый металлический шар.
Проводник считают уединённым, если он расположен вдали от возможных источников электрического поля как проводящих, так и непроводящих тел. Если вблизи заряженного проводника находятся другие тела, то вследствие явления электростатической индукции в проводниках происходит перераспределение свободных электрических зарядов — возникают индуцированные заряды, а в диэлектриках — смещение в противоположные стороны разноимённых зарядов, входящих в состав атомов вещества, приводящее к возникновению поляризационных зарядов. Поляризационные заряды, возникающие в диэлектриках, и заряды, индуцируемые на проводниках, создают дополнительное электростатическое поле, изменяющее потенциал заряженного проводника.
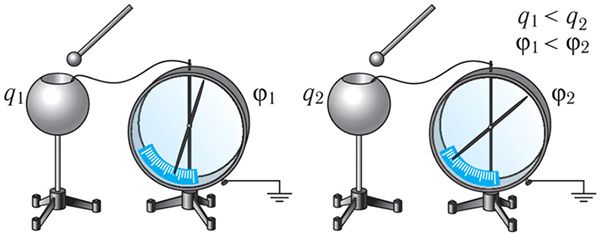
Касаясь наэлектризованным проводящим шариком, закреплённым на изолирующей ручке, внутренней поверхности полого металлического шара, будем последовательно сообщать ему одинаковые положительные электрические заряды, увеличивая его суммарный заряд в 2, 3 и т. д. раз (рис. 118.12). Чем больше сообщённый шару электрический заряд, тем больше его потенциал, так как , где R — радиус шара. Значит, во сколько раз увеличился заряд шара, во столько же раз увеличился и его потенциал, т. е. отношение электрического заряда к потенциалу остаётся величиной постоянной для данного уединённого шара:
.
Прямая пропорциональная зависимость между потенциалом и электрическим зарядом справедлива не только для уединённых шарообразных проводников, но и для любого уединённого проводника произвольной формы. Необходимо только, чтобы форма и размеры проводника, а также диэлектрические свойства среды, в которой он находится, оставались неизменными.
Электрическая ёмкость уединённого проводника — физическая скалярная величина, количественно характеризующая способность проводника накапливать электрический заряд и равная отношению заряда проводника к его потенциалу:
Отметим, что электрическая ёмкость является характеристикой уединённого проводника и не зависит ни от наличия избыточного заряда, ни от его потенциала. Поскольку заряды располагаются только на внешней поверхности проводника, то ни от вещества, из которого он изготовлен, ни от его массы электроёмкость проводника также не зависит. Она зависит только от формы и размеров проводника, а также от диэлектрической проницаемости среды, в которой этот уединённый проводник находится. Например, электроёмкость уединённого проводящего шара радиусом R, находящегося в безграничной однородной среде с диэлектрической проницаемостью ε, определяют по формуле
*.
Единицей электрической ёмкости в СИ является фарад (Ф).
1 Ф — очень большая электроёмкость. Электроёмкостью С = 1 Ф обладал бы находящийся в вакууме уединённый шар радиусом R = 9 ∙ 109 м (для сравнения: радиус земного шара RЗ = 6,4 ∙ 106 м). Поэтому на практике применяют дольные единицы: микрофарад (1 мкФ = 1 ∙ 10–6 Ф), нанофарад (1 нФ = 1 ∙ 10–9 Ф) и пикофарад (1 пФ = 1 ∙ 10–12 Ф).
Например, электроёмкость такого огромного проводника, как земной шар, равна С = 0,71 мФ, а электроёмкость человеческого тела примерно С = 50 пФ.
Из истории физики
В XVII-XVIII в. учёные рассматривали электричество как нематериальную жидкость. Эта жидкость могла вливаться в проводник и выливаться из него. Так появился термин «электрическая ёмкость».
1. Какой проводник можно считать уединённым?
2. Что называют электрической ёмкостью уединённого проводника?
3. От чего зависит электроёмкость уединённого проводника?
4. Обладает ли электроёмкостью незаряженный проводник?
5. Можно ли, проанализировав формулу для расчёта электроёмкости уединённого проводника, утверждать, что его электроёмкость зависит от заряда и потенциала проводника?
6. Два проводящих заряженных шара приводят в соприкосновение. Как распределятся заряды на шарах, если один из них алюминиевый, а другой стальной и радиусы шаров одинаковые?
* Это выражение можно получить в результате математических преобразований двух формул: для нахождения электроёмкости и потенциала заряженного шара
. ↑


















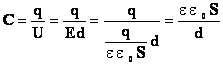 , т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.
, т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.