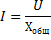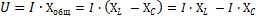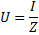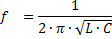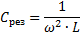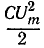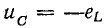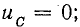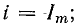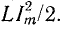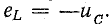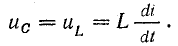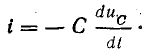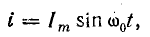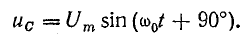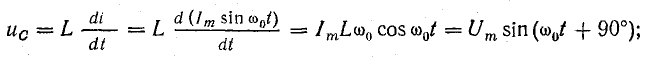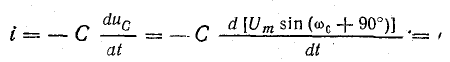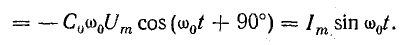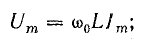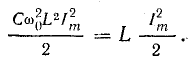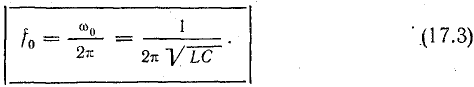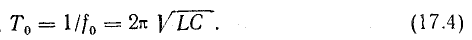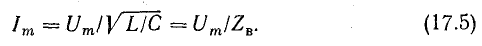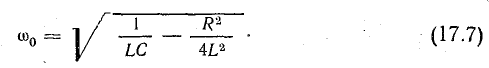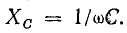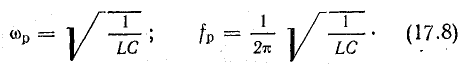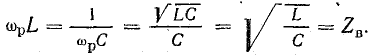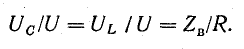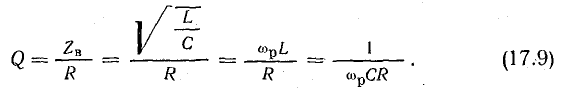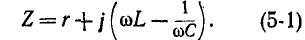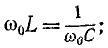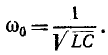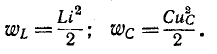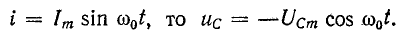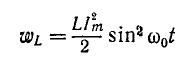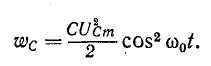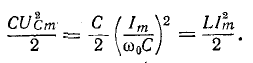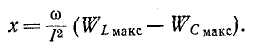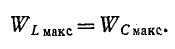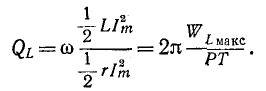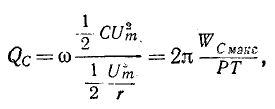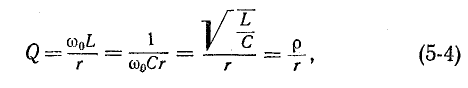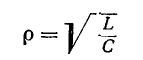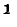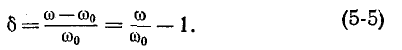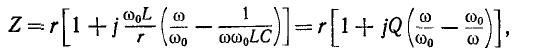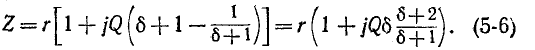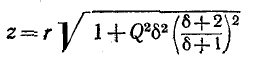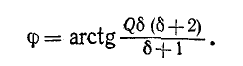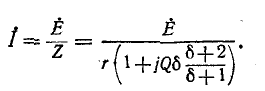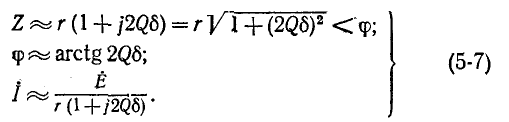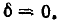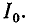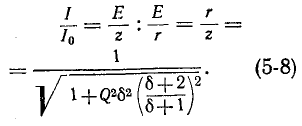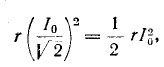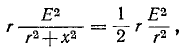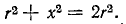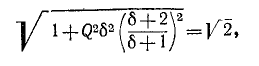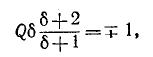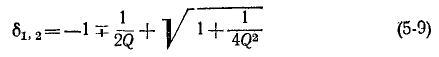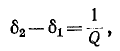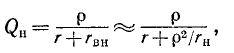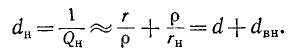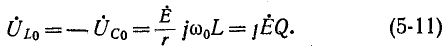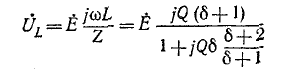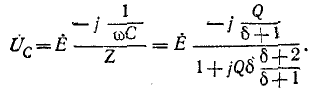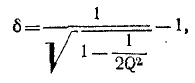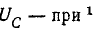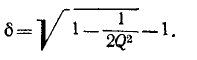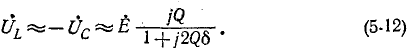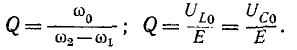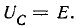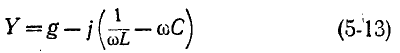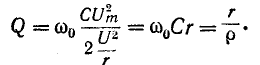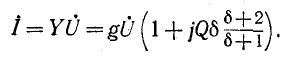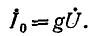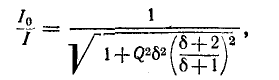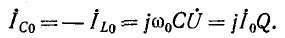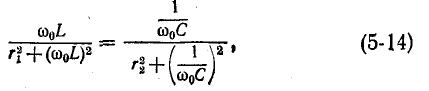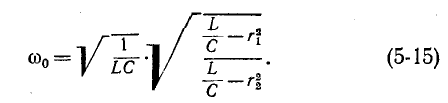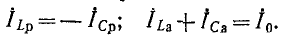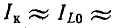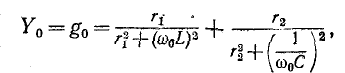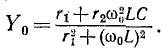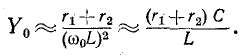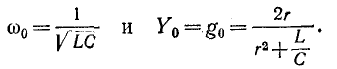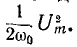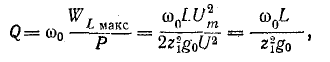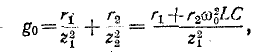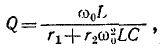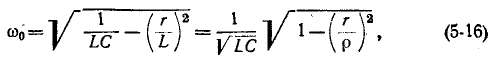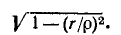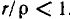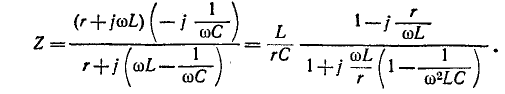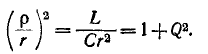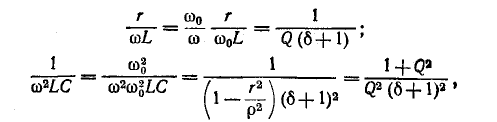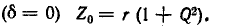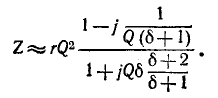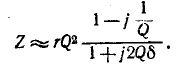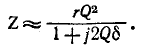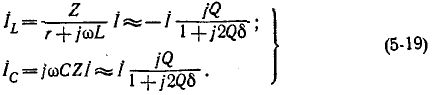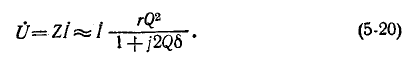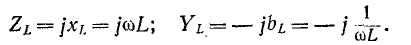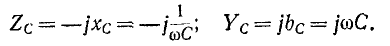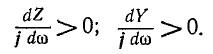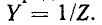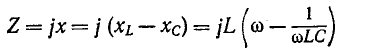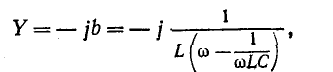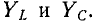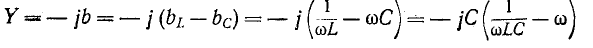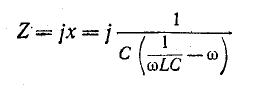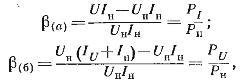Нахождение резонансной емкости
В общем
случае резонанс напряжений в цепи,
содержащей реактивные элементы, наступает
при равной нулю мнимой составляющей
комплексного сопротивления ZIm=0.
Рассмотрим это на примере простой цепи,
содержащей последовательно соединённые
резистор, катушку и конденсатор.
|
R |
C |
L |
|
|
Найдём
комплексное сопротивление ветви:
Таким
образом, в рассматриваемой цепи мнимая
составляющая комплексного сопротивления
равна нулю при равенстве сопротивлений
конденсатора и катушки:
Или,
если выразить реактивные сопротивления
через параметры LиC:
Нетрудно
увидеть, что при резонансе в рассматриваемой
цепи сопротивление минимально. В
соответствии с законом Ома:
,
ток при резонансе максимален.
Для
экспериментального определения величины
ёмкости, при которой в цепи наступит
резонанс, пользуются зависимостью тока
от ёмкости.
В
заданной цепи изменяют ёмкость в
определённых пределах, и снимают значение
величины тока в ветви с конденсатором.
Точка, в которой ток максимален показывает
резонансную ёмкость.
§2.9. Примеры и задачи
2.9.1. Синусоидальные величины и их символическое изображение
Мгновенные
значения синусоидальной величины
определяются выражением:
,
где
– амплитуда;
– действующее значение;
– угловая частота, [с-1];
– линейная частота, [Гц];
– период колебаний [c];
–
начальная фаза, [рад].
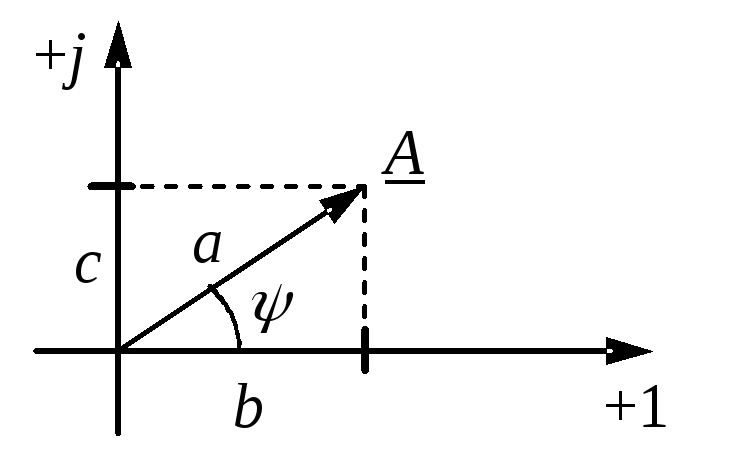
Расчет
цепей переменного тока облегчается,
если изображать гармонические токи,
напряжения и ЭДС векторами на комплексной
плоскости.
Совокупность
векторов, изображающих синусоидальные
функции в заданный момент времени,
называется векторной диаграммой.
Комплексное
число может быть представлено в
алгебраической и показательной форме:
.
Переход
из показательной формы в алгебраическую
форму осуществляется по формуле Эйлера:
.
При
обратном переходе:
,
если вещественная часть алгебраической
формы положительная, тоа если вещественная часть отрицательная,
то
.
Комплексная
синусоидальная функция представляется
в виде вращающегося вектора на комплексной
плоскости:
;
,
,
(при t
= 0).
Мгновенное
значение синусоидальной функции есть
проекция вращающегося вектора на мнимую
ось:
.
Обозначения:
i,
u, e
– мгновенные значения тока, напряжения,
ЭДС.
Im,Um,Em– комплексные амплитудные значения
тока, напряжения, ЭДС.
I,U,E– комплексные действующие значения
тока, напряжения, ЭДС.
Примеры
1.1. Дано
синусоидальное напряжение
.
Записать
выражения для комплексного амплитудного
и действующего значения.
Решение:
;
.
1.2.
Комплексное действующее значение тока
.
Записать
выражение для мгновенных значений тока.
Решение:
;
.
2.10.2. Расчет линейных цепей с гармоническими источниками электрической энергии
2.10.2.1. Закон Ома в комплексной форме
Таблица 2.1.
|
Элемент |
Связь между мгновенными значениями |
Связь между комплексными действующими |
Векторная диаграмма |
Применение |
|
|
|
|
|
Напряжение совпадает по фазе с током. |
|
|
|
|
|
Напряжение опережает ток на |
|
|
|
|
|
Напряжение отстает от тока на |
2.10.2.2. Комплексное сопротивление двухполюсника
–
активное сопротивление резистораR,
[Ом];
– реактивное сопротивление катушки,
[Ом];
–
индуктивность катушки, [Гн];
– угловая частота, [с -1];
– реактивное сопротивление конденсатора,
[Ом];
– емкость конденсатора, [Ф];
– комплексное сопротивление резистора;
– комплексное сопротивление катушки;
– комплексное сопротивление конденсатора.
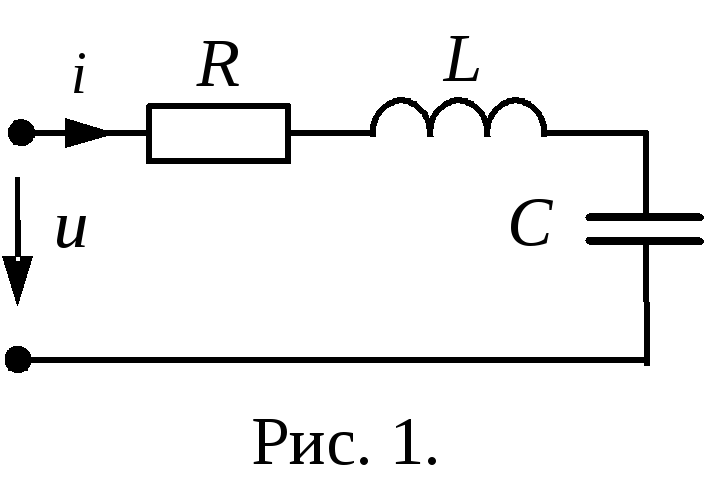
Для
цепи (рис. 1) комплексное сопротивление:
где
– модуль комплексного сопротивления
или полное сопротивление;
– угол сдвига фаз между напряжением и
током.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Резонанс напряжений
Катушка индуктивности вносит сдвиг фаз, при котором ток отстает от напряжения на четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Таким образом, действие индуктивного сопротивления на сдвиг фаз между током и напряжением в цепи противоположно действию емкостного сопротивления.
Это приводит к тому, что общий сдвиг фаз между током и напряжением в цепи зависит от соотношения величин индуктивного и емкостного сопротивлений.
Если величина емкостного сопротивления цепи больше индуктивного, то цепь носит емкостный характер, т. е. напряжение отстает по фазе от тока. Если же, наоборот, индуктивное сопротивление цепи больше емкостного, то напряжение опережает ток, и, следовательно, цепь носит индуктивный характер.
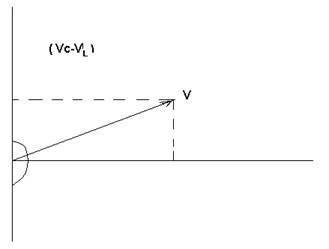
Общее реактивное сопротивление Хобщ рассматриваемой нами цепи определяется путем сложения индуктивного сопротивления катушки XL и емкостного сопротивления конденсатора ХС.
Но так как действие этих сопротивлений в цепи противоположно, то одному из них, а именно Хс приписывается знак минус, и общее реактивное сопротивление определяется по формуле:
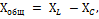
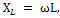
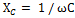
Применив к этой цепи закон Ома, получим:
Формулу эту можно преобразовать следующим образом:
В полученном равенстве I XL — действующее значение слагающей общего напряжения цепи, идущей на преодоление индуктивного сопротивления цепи, а I ХС — действующее значение слагающей общего напряжения цепи, идущей на преодоление емкостного сопротивления.
Таким образом, общее напряжение цепи, состоящей из последовательного соединения катушки и конденсатора, можно рассматривать как состоящее из двух слагаемых, величины которых зависят от величин индуктивного и емкостного сопротивлений цепи.
Мы считали, что такая цепь не обладает активным сопротивлением. Однако в тех случаях, когда активное сопротивление цепи не настолько уже мало, чтобы им можно было пренебречь, общее сопротивление цепи определяется следующей формулой:
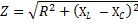
где R — общее активное сопротивление цепи, XL -ХС — ее общее реактивное сопротивление. Переходя к формуле закона Ома, мы вправе написать:
Резонанс напряжений в цепи переменного тока
Индуктивное и емкостное сопротивления, соединенные последовательно, вызывают в цепи переменного тока меньший сдвиг фаз между током и напряжением, чем если бы они были включены в цепь по отдельности.
Иначе говоря, от одновременного действия этих двух различных по своему характеру реактивных сопротивлений в цепи происходит компенсация (взаимное уничтожение) сдвига фаз.
Полная компенсация, т. е. полное уничтожение сдвига фаз между током и напряжением в такой цепи, наступит тогда, когда индуктивное сопротивление окажется равным емкостному сопротивлению цепи, т. е. когда XL = ХС или, что то же, когда ω L = 1 / ωС.
Цепь в этом случае будет вести себя как чисто активное сопротивление, т. е. как будто в ней нет ни катушки, ни конденсатора. Величина этого сопротивления определится суммой активных сопротивлений катушки и соединительных проводов. При этом действующее значение тока в цепи будет наибольшим и определится формулой закона Ома I = U / R , где вместо Z теперь поставлено R.
Одновременно с этим действующие напряжения как на катушке UL = I XL так и на конденсаторе Uc = I ХС окажутся равными и будут максимально большой величины. При малом активном сопротивлении цепи эти напряжения могут во много раз превысить общее напряжение U на зажимах цепи. Это интересное явление называется в электротехнике резонансом напряжений .
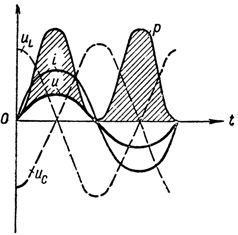
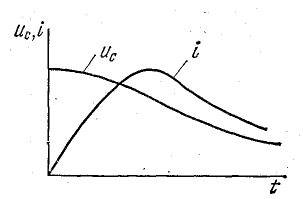
На рис. 1 приведены кривые напряжений, тока и мощности при резонансе напряжений в цепи.
График тока напряжений и мощности при резонансе напряжений
Следует твердо помнить, что сопротивления XL и ХС являются переменными, зависящими от частоты тока, и стоит хотя бы немного изменить частоту его, например, увеличить, как XL = ω L возрастет, а ХС = = 1 / ωС уменьшится, и тем самым в цепи сразу нарушится резонанс напряжений, при этом наряду с активным сопротивлением в цепи появится и реактивное. То же самое произойдет, если изменить величину индуктивности или емкости цепи.
При резонансе напряжений мощность источника тока будет затрачиваться только на преодоление активного сопротивления цепи, т. е. на нагрев проводников.
Действительно, в цепи с одной катушкой индуктивности происходит колебание энергии, т. е. периодический переход энергии из генератора в магнитное поле катушки. В цепи с конденсатором происходит то же самое, но за счет энергии электрического поля конденсатора. В цепи же с конденсатором и катушкой индуктивности при резонансе напряжений (XL = ХС) энергия, раз запасенная цепью, периодически переходит из катушки в конденсатор и обратно и на долю источника тока выпадает только расход энергии, необходимый для преодоления активного сопротивления цепи. Таким образом, обмен энергии происходит между конденсатором и катушкой почти без участия генератора.
Стоит только нарушить резонанс напряжений в цени, как энергия магнитного поля катушки станет не равной энергии электрического поля конденсатора, и в процессе обмена энергии между этими полями появится избыток энергии, который периодически будет то поступать из источника в цепь, то возвращаться ему обратно цепью.
Явление это очень сходно с тем, что происходит в часовом механизме. Маятник часов мог бы непрерывно колебаться и без помощи пружины (или груза в часах-ходиках), если бы не силы трения, тормозящие его движение.
Пружина же, сообщая маятнику в нужный момент часть своей энергии, помогает ему преодолеть силы трения, чем и достигается непрерывность колебаний.
Подобно этому и в электрической цепи, при явлении резонанса в ней, источник тока расходует свою энергию только на преодоление активного сопротивления цепи, тем самым поддерживая в ней колебательный процесс.
Итак, мы приходим к выводу, что цепь переменного тока, состоящая из генератора и последовательно соединенных катушки индуктивности и конденсатора, при определенных условиях XL = ХС превращается в колебательную систему . Такая цепь получила название колебательного контура.
Из равенства XL = ХС можно определить значения частоты генератора, при которой наступает явление резонанса напряжений:
Значение емкости и индуктивности цепи, при которых наступает резонанс напряжений :
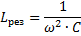
Таким образом, изменяя любую из этих трех величин ( f рез, L и С), можно вызвать в цепи резонанс напряжений, т. е. превратить цепь в колебательный контур.
Пример полезного применения резонанса напряжений : входной контур приемника настраивается конденсатором переменной емкости (или вариометром) таким образом, что в нем возникает резонанс напряжений. Этим достигается необходимое для нормальной работы приемника большое повышение напряжения на катушке по сравнению с напряжением в цепи, созданным антенной.
Наряду с полезным использованием явления резонанса напряжений в электротехнике технике часто бывают случаи, когда резонанс напряжений вреден. Большое повышение напряжения на отдельных участках цепи (на катушке или на конденсаторе) по сравнению с напряжением генератора может привести к порче отдельных деталей и измерительных приборов.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Что такое резонанс напряжений?
Резонансные явления наблюдаются в колебательных системах, когда частота собственных колебаний элементов системы совпадает с частотой внешних (вынужденных) колебательных процессов. Данное утверждение справедливо и для цепей с циркулирующим переменным током. В таких электрических цепях при наличии определённых условий возникает резонанс напряжений, что влияет на параметры тока. Явление резонанса в электротехнике может быть полезным или вредным, в зависимости от ситуации, в которой происходит процесс.
Описание явления
Если в некой электрической цепи (см. рис. 1) имеются ёмкостные и индуктивные элементы, которые обладают собственными резонансными частотами, то при совпадении этих частот амплитуда колебаний резко возрастёт. То есть происходит резкий всплеск напряжений на этих элементах. Это может вызвать разрушение элементов электрической цепи.

Давайте рассмотрим на этом примере, какие явления будут происходить при подключении генератора переменного тока к контактам схемы. Заметим, что катушки и конденсаторы обладают свойствами, которые можно сравнить с аналогом реактивного резистора. В частности, дроссель в электрической цепи создаёт индуктивное сопротивление. Конденсатор является причиной ёмкостного сопротивления.
Индуктивный элемент вызывает сдвиг фаз, характеризующийся отставанием тока от напряжения на ¼ периода. Под действием конденсатора ток, наоборот, на ¼ периода опережает напряжение.
Другими словами, действие индуктивности противоположно действию на сдвиг фаз ёмкостного сопротивления. То есть катушки индуктивности и ёмкостные элементы по-разному воздействуют на генератор и по-своему корректируют фазовые соотношения между электрическим током и напряжением.
Формула
Общее реактивное сопротивление рассматриваемых нами элементов равно сумме сопротивлений каждого из них. С учётом противоположности действий можно записать: Xобщ = XL — Xc , где XL = ωL — индуктивное реактивное сопротивление, выражение Xc = 1/ωC — это ёмкостное реактивное сопротивление.
На рисунке 2 изображены графики зависимости полного сопротивления цепи и связанной с ним силы тока, от реактивного сопротивления индуктивного элемента. Обратите внимание на то, как падает полное сопротивление при уменьшении реактивной сопротивляемости RL (график б) и как при этом возрастает ток (график в).

Электрические цепи, состоящие из последовательно соединённых конденсаторов, пассивный резисторов и катушек индуктивности называют последовательными резонансными (колебательными) контурами (см. рис. 2). Существуют также параллельные контуры, в которых R, L, C элементы подключены параллельно (рис. 3).


В режиме резонанса мощность источника питания будет рассеиваться только на активных сопротивлениях (в том числе на активном сопротивлении катушки). Для резонансных контуров характерны потери только активной мощности, которая израсходуется на поддержание колебательного процесса. Реактивная мощность на L C — элементах при этом не расходуется. Ток в резонансном режиме принимает максимальное значение:

Величину Q принято называть термином «Добротность контура». Данный параметр показывает, во сколько раз напряжение, возникшее на контактах реактивных элементов, превышает входное напряжение U электрической сети. Для описания соотношения выходного и входного напряжений часто применяют коэффициент K. При резонансе:
Формулировка
На основании вышеописанных явлений, сформулируем определение резонансного напряжения: «Если общее падение напряжения на ёмкостно-индуктивных элементах равно нулю, а амплитуда тока – максимальна, то такое особое состояние системы называется резонансом напряжений». Для лучшего понимания явления, немного перефразируем определение: резонансом напряжений является состояние, когда напряжение на CL — цепочке больше чем на входе электрической цепи.
Описанное явление довольно распространено в электротехнике. Иногда с ним борются, а иногда специально создают условия для образования резонанса. Основными характеристиками всякого резонансного контура являются параметры добротности и частоты [ 1 ].
В случае, если XL = Xc – справедливо равенство: ωL = 1/ωC , отсюда получаем:
Если ω = ω0 – возникает резонанс напряжений. Частоты совпадают в том случае, когда индуктивное сопротивление сравняется с ёмкостным сопротивлением конденсатора. В таких случаях в цепи будет действовать только активное сопротивление R. Наличие реактивных элементов в схеме приводит к увеличению полного сопротивления цепи (Z):
где R – общее активное сопротивление.
Учитывая, что по закону Ома U = I/Z, можно утверждать, что общее напряжение в цепи зависит, в том числе, и от слагаемых индуктивного и ёмкостного сопротивлений.
Если бы в рассматриваемой схеме (рис. 1) отсутствовало активное сопротивление R, то значение полного сопротивления Z стремилось бы к 0. Следовательно, напряжение на реактивных элементах при этом возрастает до критического уровня.
Поскольку XL и Xc зависят от частоты входного напряжения, то для возникновения резонанса следует подобрать соответствующую частоту сети, или изменять параметры катушки, либо конденсатора до тех пор, пока резонансные частоты не совпадут. Любое нарушение условий резонанса немедленно приводит к выходу системы из резонансного режима с последующим падением напряжения.
Условия наступления
Резонансные явления наступают только при наличии следующих условий:
- Наличие минимального активного сопротивления на участке электрической цепи.
- Равенство реактивных сопротивлений, возникших на цепочке LC.
- Совпадение входной частоты источника питания с резонансной частотой колебательного контура.
При резонансе в контуре напряжения на его элементах могут повышаться на порядок и больше.
Примеры применения на практике
Классическим примером применения резонанса колебательных контуров является настройка радиоприёмника на частоту соответствующей радиостанции. В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.
В момент совпадения резонансной частоты с рабочей частотой какой-либо радиостанции возникает резонанс напряжений, в результате которого резко возрастает амплитуда колебаний принятой радиоприёмником частоты. Специальные фильтры отделяют эти колебания от несущих радиочастот, а усилители усиливают полученные сигналы. В динамике появляются звуки, генерируемые передатчиком радиостанции.
Колебательные контуры, построенные на принципе последовательного соединения LC-элементов, применяются в цепях питания высокоомных нагрузок, потребляющих токи повышенного напряжения. Такие же устройства применяют в полосовых фильтрах.
Последовательный резонанс применяют при пониженных напряжениях сети. В этом случае используют реактивную энергию обмоток трансформатора, соединённых последовательно.
Конденсаторы и различные катушки индуктивности (рис. 5) входят в конструкцию практически всех аналоговых устройств. Они используются для настройки фильтров или для управления токами в отдельных узлах.
Важно знать, что резонансные контуры не увеличивают количество электрической энергии в цепях. Они лишь могут повышать напряжения, иногда до опасных значений. Постоянный ток не причиной резонансных явлений.
Наряду с полезными свойствами резонансных явлений, в практической электротехнике часто возникают ситуации, когда резонанс напряжений приносит вред. В основном это связано с нежелательным повышением параметров тока на участках цепей. Примером могут служить опасное резонансные явления в кабельных линиях без нагрузки, что может привести к пробоям изоляции. Чтобы этого не случилось, на концевых участках таких линий устанавливают балластные нагрузочные элементы.
Источник
Содержание:
Резонанс в электрических цепях:
Явление резонанса можно наблюдать в любых колебательных системах, в том числе механических и электрических. Электрический резонанс возникает при определенных условиях в электрических цепях переменного тока, содержащих индуктивности и емкости.
Изучение электрического резонанса
Изучение электрического резонанса необходимо, так как это явление широко используется в технике электросвязи, а в установках сильного тока, где его возникновение специально не предусматривается, резонанс может оказаться опасным (могут возникнуть перенапряжения и пробой изоляции).
Колебательный контур
Для того чтобы понять резонансные явления, переходные процессы в электрических цепях переменного тока, которые рассматриваются далее, важно иметь представление о процессах в колебательном контуре, состоящем из идеальных катушки и конденсатора, т. е. в контуре без потерь.
Колебательный процесс в таком контуре заключается во взаимном преобразовании электрического и магнитного полей. При этом изменяется энергия полей, поэтому колебательный процесс в контуре с количественной стороны будем, как и раньше, характеризовать изменением энергии.
Ток и напряжение в колебательном контуре
Предположим, что конденсатор с емкостью С получил от источника запас энергии
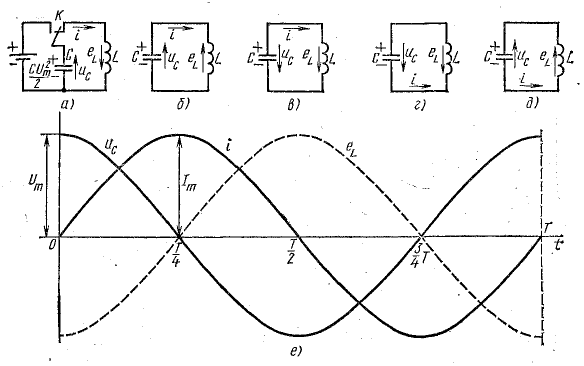
В первую часть периода (0 — T/4) конденсатор разряжается и в цепи существует ток. В это время в обособленной цепи конденсатор играет роль источника энергии (рис. 17.1, б). В начальный момент ток равен нулю, далее он увеличивается. Увеличение тока в цепи вызывает возникновение э. д. с. самоиндукции eL и накопление энергии в магнитном поле катушки. Э. д. с. самоиндукции уравновешивает напряжение на конденсаторе:
Напряжение на конденсаторе в процессе разрядки уменьшается, поэтому вызываемый в цепи ток растет все медленнее, соответственно с этим уменьшается и э. д. с. самоиндукции, которая пропорциональна скорости изменения тока. Таким образом, к концу разрядки конденсатора (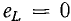
Рис. 17.1. К анализу колебательного контура
С этого момента ток начинает уменьшаться (но не прекращается), сохраняя свое направление. В следующую часть периода (от T/4 до T/2) направление тока сохраняется, потому что э. д. с. самоиндукции при уменьшении тока меняет свой знак, и роль источника энергии переходит к катушке. Уменьшающийся ток теперь является зарядным током конденсатора, заряжающегося в обратном направлении (рис. 17.1, в). Напряжение на конденсаторе увеличивается, уравновешивая теперь э. д. с. самоиндукции:
При увеличении напряжения на конденсаторе его зарядный ток уменьшается все быстрее, в результате чего э. д. с. eL увеличивается. Таким образом, к концу зарядки конденсатора напряжение на его обкладках достигает наибольшего значения, э. д. с. самоиндукции тоже максимальна, а ток становится равным нулю. Энергия магнитного поля снова перешла в энергию электрического поля . С этого момента рост э. д. с. самоиндукции прекращается и начинается ее уменьшение. Роль источника энергии снова переходит к конденсатору. Начинается третья часть периода (от Т/2 до 3T/4). В рассматриваемом процессе конденсатор второй раз становится источником энергии. Но по сравнению с первым он имеет обратную полярность, поэтому его разрядный ток изменяет направление и далее увеличивается. Снова энергия убывает в электрическом поле и накапливается в магнитном поле (рис. 17.1, г).
В момент времени t = 3T/4 напряжение на конденсаторе и э. д. с. самоиндукции становятся равными нулю, а ток — наибольшим. В последнем отрезке времени (от 3T/4 до Т) процесс протекает в том же порядке, что и во втором, но при обратном направлении тока (рис. 17.1, д).
В момент времени t = Т конденсатор заряжен в том же направлении и тем же количеством энергии, как и при t = 0. Ток переходит через нуль к положительным значениям и далее увеличивается. Процесс повторяется в порядке, рассмотренном ранее.
Характеристики колебательного контура
Энергетический процесс в колебательном контуре имеет периодический характер с периодом Т. Колебания в электрической цепи, не связанной с источником энергии, называют собственными или свободными.
Этот процесс рассмотрен по графикам изменения тока i, напряжения uC и э.д.с. eL, которые приняты синусоидальными функциями времени.
Для такого предположения имеется полное основание, так как эти величины взаимно связаны соотношением
Вместе с тем ток в контуре пропорционален скорости изменения заряда конденсатора, причем он увеличивается, когда конденсатор разряжается. Следовательно,
Такая взаимная связь переменных величин говорит о синусоидальном законе изменения тока и напряжения, но при наличии сдвига фаз между ними на 90°, т. е. при
Это можно проверить:
Величину ω0 в уравнениях тока и напряжения называют угловой частотой собственных колебаний в контуре. Найдем ее, используя равенство наибольшего количества энергии в конденсаторе и катушке:
и связь между амплитудами тока и напряжения:
Сокращая, получим
Частота собственных колебаний
Период собственных колебаний
Из равенства (17.1) вытекает еще одно важное соотношение
Величина, стоящая в знаменателе, имеет размерность сопротивления и называется волновым сопротивлением контура:
Колебательный контур с потерями энергии
Незатухающие колебания в контуре получаются в предположении, что потери энергии отсутствуют, т. е. R = 0.
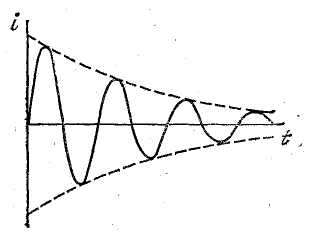
Если активное сопротивление контура не равно нулю, то запас энергии в контуре сокращается (энергия превращается в тепло), амплитуды тока и напряжения с каждым периодом убывают, как показано на рис. 17.2.
Более детальное исследование колебательного контура показывает, что частота собственных колебаний зависит от активного сопротивления:
При R = 0 это выражение совпадает с (17.2).
При 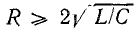
Рис. 17.2. График изменения тока в колебательном контуре с потерями
Рис. 17.3. Апериодический разряд конденсатора на катушку индуктивности
Резонанс напряжений
При рассмотрении различных режимов электрических цепей был отмечен случай равенства реактивных сопротивлений ХL = ХC при последовательном соединении элементов, содержащих индуктивность и емкость.
В этом случае электрическая цепь находится в режиме резонанса напряжений, который характеризуется тем, что реактивная мощность цепи равна нулю, ток и напряжение совпадают по фазе.
Условие возникновения резонанса
Резонанс напряжений возникает при определенной для данной цепи частоте источника энергии (частоте вынужденных колебании), которую называет резонансной частотой ωр.
При резонансной частоте, как будет показано далее, 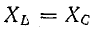
Режим электрической цепи при последовательном соединении участков с индуктивностью и емкостью, характеризующийся равенством индуктивного и емкостного сопротивлений, называют резонансом напряжений.
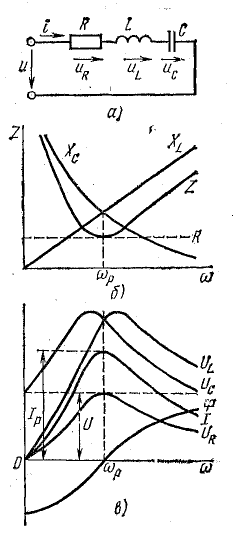
Резонанс напряжений рассмотрим, сначала на схеме идеализированной цепи (рис. 17.4, а), в которой последовательно с резистором R включены идеальные (без потерь) катушка L и конденсатор С.
Рис. 17.4. К вопросу о резонансе напряжений
Реактивные сопротивления ХL и ХC (рис. 17.4, б) зависят от частоты вынужденных колебаний ω:
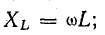
Приравнивая реактивные сопротивления и учитывая, что ω = ωр, получим
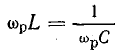
Отсюда резонансная частота
В данном случае выражение для резонансной частоты совпадает с формулой (17.3) для частоты собственных колебаний в контуре без потерь.
Основные соотношения между величинами, характеризующими режим электрической цепи и энергетические процессы. Нужно отметить, что в неразветвленной цепи обмен энергией между катушкой и конденсатором совершается через источник энергии, который восполняет потери энергии в активных сопротивлениях.
Резонансные кривые
Резонанс напряжений в цепи можно установить двумя путями: 1) изменением параметров L и С (одного из них или обоих вместе) при постоянной частоте источника или 2) изменением частоты источника энергии при постоянных L и С.
В связи с этим большой практический интерес представляют зависимости напряжений и токов на отдельных элементах цепи от частоты. Эти зависимости называют резонансными кривыми (рис. 17.4, в).
Реактивные сопротивления с изменением частоты меняются, как показано на рис. 17.4, б. При увеличении частоты ХL увеличивается пропорционально частоте, а ХC уменьшается по закону обратной пропорциональности.
Соответственно полное сопротивление Z цепи при резонансной частоте ωр оказывается наименьшим, равным активному сопротивлению R; при частоте 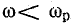
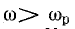
Такая зависимость полного сопротивления от частоты определяет характер изменения тока при постоянном напряжении в цепи (рис. 17.4, в). При 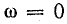
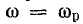
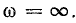
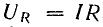
Напряжение на конденсаторе UC при 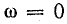
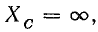
Индуктивное напряжение 

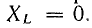
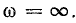
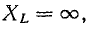
При частотах, меньших резонансной, реактивное сопротивление цепи имеет емкостный характер (отрицательно), поэтому и угол сдвига фаз в цепи отрицательный. Уменьшаясь с ростом частоты, он становится равным нулю при резонансе 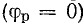
Добротность контура
При резонансе напряжений отношение напряжения на индуктивности или емкости к напряжению, приложенному к цепи (напряжению источника), равно отношению волнового сопротивления к активному. Действительно, при резонансе сопротивления реактивных элементов
Поэтому
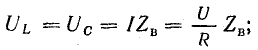
Из этого выражения следует, что при 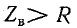
Такое превышение может оказаться значительным, если реактивные сопротивления много больше активного, и изоляция катушки или конденсатора может быть пробита. На практике подобный случай возможен, если на конце кабельной линии включается приемник, обладающий индуктивностью.
В радиотехнике качество резонансного контура считается тем выше, чем больше отношение 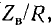
Чем меньше мощность потерь энергии в контуре (этому соответствует меньшая величина R), тем больше добротность контура.
Большей величине добротности соответствует больший ток Iр при резонансе и более острая резонансная кривая.
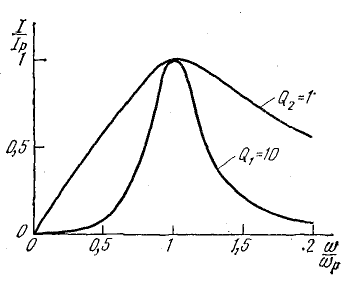
На рис. 17.5 показаны две резонансные кривые тока, построенные в относительных единицах при двух величинах добротности. По горизонтальной оси отложены отношения изменяющейся частоты источника энергии к резонансной частоте ω/ωр, а по вертикальной —отношения тока при данной частоте к току при резонансной частоте I/Iр.
Рис. 17.5. Резонансные кривые при двух значениях добротности контура
Все рассуждения о резонансе напряжений в идеализированной цепи можно распространить и на цепи, содержащие последовательно соединенные катушку и конденсатор с потерями. Как известно, реальные катушки и конденсатор могут быть представлены схемами последовательного соединения активного и реактивного сопротивлений (рис. 17.5). Активные сопротивления катушки и конденсатора можно рассматривать как часть общего активного сопротивления цепи R, тогда схема на рис. 17.4, а будет пригодна и в этом случае.
Резонанс в электрических цепях
Резонансные (колебательные) цепи:
Резонансными или колебательными цепями называются электрические цепи, в которых могут возникать явления резонанса напряжений или токов.
Резонанс представляет собой такой режим пассивной электрической цепи, содержащей индуктивности и емкости, при котором реактивное сопротивление и реактивная проводимость цепи равны нулю; соответственно равна нулю реактивная мощность на выводах цепи.
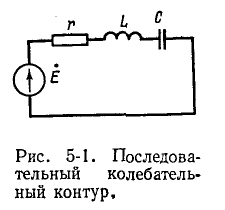
Резонанс напряжения наблюдается в электрической цепи с последовательным соединением участков, содержащих индуктивности и емкости. Неразветвленная цепь, состоящая из последовательно соединенных элементов r, L и С, рассмотренная, представляет собой один из простейших случаев такой цепи. В радиотехнике ее называют последовательным колебательным контуром.
При резонансе напряжений индуктивное сопротивление одной части цепи компенсируется емкостным сопротивлением другой ее части, последовательно соединенной с первой. В результате реактивное сопротивление и реактивная мощность на выводах цепи равны нулю.
В свою очередь резонанс токов наблюдается в электрической цепи с параллельным соединением участков, содержащих индуктивности и емкости. Один из простейших примеров такой цепи, состоящей из параллельно соединенных элементов r, L и С. В радиотехнике такую цепь называют параллельным колебательным контуром.
При резонансе токов индуктивная проводимость одной части цепи компенсируется емкостной проводимостью другой ее части, параллельно соединенной с первой. В результате реактивная проводимость и реактивная мощность на выводах цепи равны нулю.
Частоты, при которых наблюдается явление резонанса, называются резонансными частотами.
Исследование резонансных режимов в электрических цепях заключается в нахождении резонансных частот,
зависимостей различных величин от частоты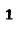
Резонансные цепи очень широко применяются в электротехнике и представляют собой неотъемлемую часть всякого радиотехнического устройства. Изучению явления резонанса, свойств и частотных характеристик простейших резонансных цепей посвящена данная глава.
Последовательный колебательный контур. Резонанс напряжений
Резонансная цепь с последовательным соединением r, L и С (рис. 5-1) является простейшей цепью для изучения явления резонанса напряжений и подробно рассматривается ниже. Комплексное сопротивление такой цепи зависит от частоты:
Резонанс напряжений наступает при частоте 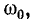
отсюда
Мгновенные энергии выражаются формулами:
Если принять
Поэтому
и
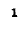
Максимальные значения этих энергий равны друг другу, так как
Это следует и из того, что реактивное сопротивление цепи, содержащей индуктивность и емкость, при любой схеме соединений пропорционально разности максимальных значений энергии, запасаемой в магнитном и электрическом полях:
Поэтому условию резонанса (х = 0) соответствует равенство
Мгновенные значения 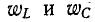
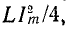
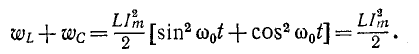
В рассматриваемом случае (резонанс напряжений, рис. 5-1) в цепи не происходит обмена энергии между источником и реактивными элементами цепи, а вся электрическая энергия, поступающая от источника, расходуется в сопротивлении r.
Мы уже встречались с понятием добротности индуктивной катушки 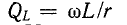
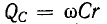
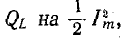
Здесь 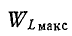
Аналогично рассуждая, т. е. умножив и разделив выражение 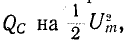
где 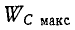
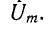
В случае резонансной цепи также пользуются понятием добротности цепи, подразумевая под этим в общем случае величину
здесь 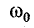
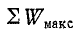
Знак 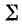
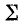
Для схемы рис. 5-1 на основании (5-3) получаем:
где
называется характеристическим (а также волновым) сопротивлением резонансного контура.
Условимся называть относительной расстройкой частоты по отношению к резонансной
частоте контура величину
Сопротивление контура согласно (5-1) и с учетом (5-2) и (5-4)
откуда, используя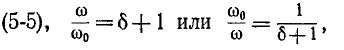
Следовательно, полное сопротивление цепи
и угол
Ток в цепи
При частоте, близкой к резонансной,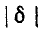
Выражения (5-7) практически достаточно точны при 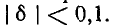
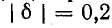
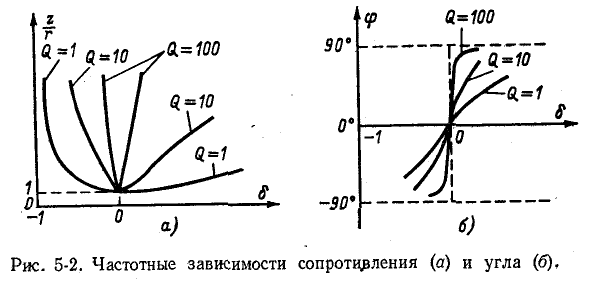
На рис. 5-2 кривые даны в относительных значениях: по оси абсцисс отложена относительная расстройка частоты 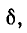
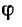
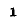
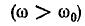
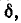
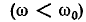
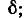
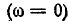
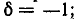
Полное сопротивление цепи минимально при резонансе напряжений при этом ток в цепи достигает своего максимального значения
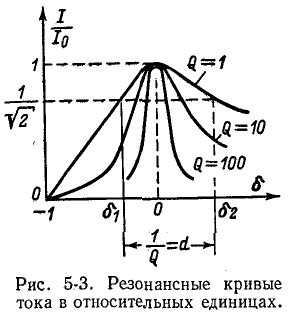
На рис. 5-3 изображены резонансные кривые тока в относительных значениях: по оси абсцисс, как и на предыдущих графиках, отложены значения 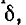
Чем выше добротность цепи Q, тем острее резонансные кривые. Таким образом, величина Q характеризует остроту резонансной кривой («остроту настройки»); согласно (5-3) чем больше отношение максимума энергии поля реактивного элемента к количеству теплоты, рассеиваемой за один период в резонансном контуре, тем острее резонансная кривая.
Резонансные кривые были построены здесь в зависимости от относительной расстройки частоты 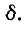
вывести расчетные выражения и построить резонансные кривые в зависимости от 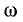
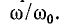
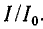
Полосу частот вблизи резонанса, на границах которой ток снижается до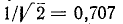
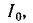
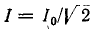
т. е. составляет половину мощности, расходуемой при резонансе. Поэтому полосу пропускания характеризуют как полосу, границы которой соответствуют половине максимальной мощности. На границах полосы пропускания резонансного контура активное и реактивное сопротивления равны 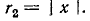
что дает
Соответственно и фазовый сдвиг между напряжением на выводах цепи и током составляет 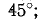
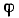
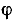
На основании (5-8) условие для границы полосы пропускания записывается в следующем виде:
или
откуда
(знак минус перед корнем, получающийся в результате решения квадратного уравнения, опускается, как не имеющий смысла). Индексы 1 и 2 и соответственно знаки минус и плюс в выражении (5-9) относятся к границам ниже и выше резонанса.
По определению полоса пропускания резонансного контура находится из условия
или
Величина d, обратная добротности контура, называется затуханием контура.
При достаточно высокой добротности резонансного контура 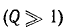
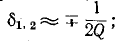
В радиотехнических устройствах к одному из реактивных элементов колебательного контура, например емкости, подключается нагрузка в виде сопротивления 
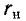
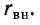
Так как обычно 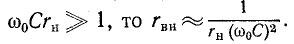
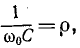
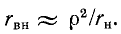
Таким образом, добротность нагруженного контура равна:
а затухание увеличивается на вносимое затухание
Если вносимое сопротивление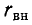
Внутреннее сопротивление источника э. д. с. 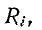
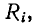
контура. Поэтому с точки зрения сокращения полосы пропускания последовательного колебательного контура выгоден источник напряжения с малым внутренним сопротивлением.
В условиях, близких к резонансу, напряжения на индуктивности и емкости могут быть весьма велики, что необходимо учитывать во избежание повреждения изоляции.
На рис. 5-4 показана векторная диаграмма тока и напряжений при резонансе. Напряжения на реактивных элементах при резонансе определяются из выражения
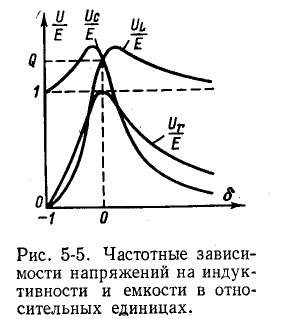
При Q > 1 эти напряжения превышают напряжение U — Е, приложенное к резонансному контуру. Однако значения, получаемые на основании (5-11), не являются максимальными: максимум напряжения 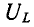
несколько выше (правее), а максимум Uc — ниже (левее) резонансной частоты (рис. 5-5).
Напряжение на индуктивности 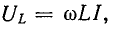
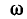
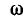
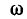
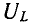
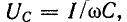
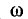
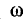
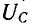
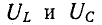
Эго также вытекает из анализа следующих ниже выражений, полученных с учетом (5-5) и (5-6):
и
Напряжение 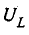
а напряжение
Пренебрегая 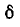
Возвращаясь к определению понятия добротности рассматриваемой резонансной цепи, мы видим, что наряду с формулами (5-3) и (5-4) добротность цепи характеризуется выражениями (5-10) и (5-11), а именно:
Последняя формула показывает, что добротность рассматриваемой цепи определяется как кратность перенапряжения на L и С при резонансной частоте.
Выше была рассмотрена неразветвленная электрическая цепь с последовательно соединенными r, L н С. Для исследования явления резонанса в более сложных разветвленных цепях, где резонанс напряжений может возникать на одной или нескольких частотах, наряду с аналитическим методом расчета, иллюстрированным выше, целесообразно также пользоваться методом геометрических мест.
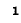
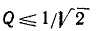
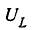
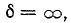
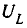
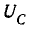
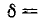

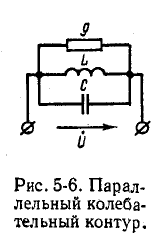
Параллельный колебательный контур и резонанс токов
Явление резонанса токов удобно изучать применительно к электрической цепи с параллельно соединенными r, L и С (рис. 5-6), так как при этом можно непосредственно воспользоваться результатами, полученными в предыдущем параграфе.
Действительно, выражение для комплексной проводимости такой цепи
по своей структуре аналогично выражению (5-1), причем резонансная частота определяется согласно (5-2).
Добротность резонансной цепи на основании (5-3)
По аналогии с предыдущим выражение (5-13) приводится к виду:
Сравнивая полученный результат с (5-6), убеждаемся в том, что выражение Y/g для схемы рис. 5-6 имеет тот же вид, что и выражение 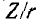
Поэтому кривые рис. 5-2 применимы и в данном случае: кривые рис. 5-2, а выражают зависимость от 6 Отношения y/g, а кривые рис. 5-2, б — зависимость угла —
Кривые рис. 5-2, а показывают, что при резонансе токов полная проводимость цепи минимальна, т. е. входное сопротивление достигает максимума.
При заданном напряжении 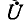
Этот ток достигает минимума при резонансной частоте, так как при этом
Следовательно, отношение. токов 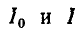
правая часть которого полностью совпадает с (5-8).
В связи с этим резонансные кривые рис. 5-3 выражают применительно к схеме рис. 5-6 зависимость
В случае резонанса токов токи в индуктивном и емкостном элементах схемы рис. 5-6 равны и противоположны по знаку:
Полученное выражение показывает, что добротность рассматриваемой цепи определяется как кратность токов в L и С по отношению к суммарному току
При Q > 1 эти токи превышают
Если параллельный колебательный контур питается от источника тока с внутренним сопротивлением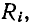
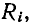
Для схемы рис. 5-6 при резонансе токов остается в силе вывод, сделанный в предыдущем параграфе о непрерывном обмене энергией между индуктивным и емкостным элементами при резонансе напряжений.
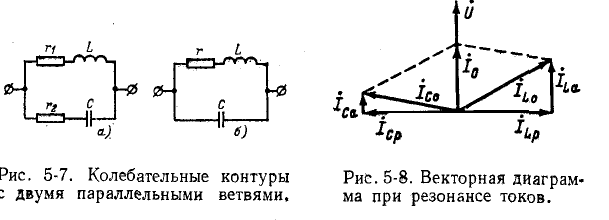
Схема рис. 5-6 является идеализированной, так как она не учитывает активных потерь в ветвях L и С. Поэтому рассмотрим другие схемы,’приняв во внимание активные сопротивления в ветвях L и С (рис. 5-7, а и б).
Условие резонанса токов для схемы рис. 5-7, а записывается в виде равенства реактивных проводимостей:
Откуда
Явление резонанса возможно при этом только в случае, если подкоренное выражение (5-15) имеет положительный
знак или, что то же, величины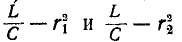
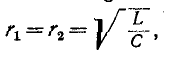
.
На рис. 5-8 показана векторная диаграмма при резонансе токов в цепи рис. 5-7, а. Токи в индуктивной и емкостной ветвях слагаются из активных 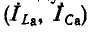
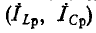
Чем меньше 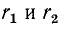
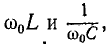
к 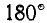
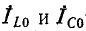
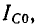
При резонансе вся цепь имеет только активную проводимость
откуда с учетом (5-14)
Для колебательного контура с малыми потерями можно пренебречь слагаемым 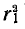
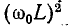
что 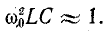
При 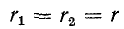
Кроме того, если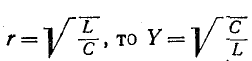
частоте (резонанс в такой цепи называют «безразличным» резонансом).
Легко убедиться в том, что и в. случае резонансной цепи с двумя параллельными ветвями (см. рис. 5-7) соблюдается условие 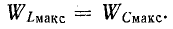
умножить обе части уравнения (5-14) на
Выше отмечалось, что в схеме с параллельно соединенными r, L и С (см. рис. 5-6) полная проводимость всей цепи имеет минимум при резонансной частоте.
Для схемы рис. 5-7, б нетрудно показать, что при изменении частоты о) или индуктивности L минимум полной проводимости цепи, а также минимум общего тока наступают не при резонансной частоте. В том же случае, когда переменным параметром является емкость С, проводимость и общий ток достигают минимума при резонансе токов.
Добротность параллельного колебательного контура рис. на основании (5-3) равна:
но
откуда
где резонансная частота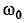
Часто в ветви с емкостью сопротивлением 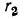
Рассмотрим этот случай (см. рис. 5-7, б).
Резонанасная частота такого контура согласно (5-15)
а добротность цепи в соответствии с полученным выше выражением
Из сопоставления (5-16) и (5-2) видно, что при одних и тех же параметрах r, L и С резонансные частоты для схем рис. 5-1 и 5-7, б отличаются множителем
При 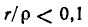
Общее сопротивление колебательного контура (см. рис, 5-7, б)
На основании соотношений (5-16) и (5-17) можно получить:
Учитывая также соотношения
получаем выражение для сопротивления колебательного контура:
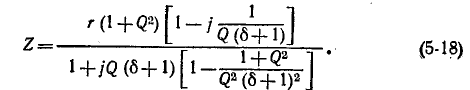
При резонансной частоте
В тех случаях, когда 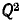
В режиме, близком к резонансу, когда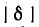
При высокой добротности колебательного контура
Приэтом токи в ветвях
Здесь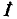
Напряжение на выводах цепи 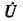
Приближенные выражения (5-19) и (5-20) аналогичны при заданном Q выражениям(5-12) и (5-7), выведенным для цепи рис. 5-1, при условии замены напряжений токами и обратно. Поэтому кривые сопротивлений, токов и напряжений, соответствующие схеме рис. 5-1, в известном масштабе приближенно выражают проводимости, напряжения и токи в схеме рис. 5-7, б.
Следует обратить внимание на то, что в схеме рис. 5-6 мгновенная мощность в цепи при резонансе токов равна мгновенной мощности, расходуемой в сопротивлении r; в схемах с двумя параллельными ветвями (рис. 5-7) мгновенная мощность на выводах цепи отлична от мгновенной мощности, расходуемой в сопротивлениях ветвей. Например, в тот момент, когда ток, входящий в цепь, проходит через нулевое значение, мгновенная мощность на выводах цепи равна нулю; в этот момент токи в ветвях, сдвинутые по фазе относительно суммарного тока цепи, отличны от нуля и поэтому мгновенная мощность, расходуемая в сопротивлениях ветвей, также не равна нулю. Объясняется это тем, что в схемах ~рис. 5-7, а и б энергия, накапливаемая реактивными элементами, периодически преобразуется частично в теплоту (в сопротивлениях ветвей), а затем вновь пополняется за счет энергии источника.
Для повышения крутизны резонансных характеристик, необходимой для более четкого разделения колебаний разных частот, в радиотехнике широко применяются двухконтурные резонансные цепи: два резонансных контура, настроенных каждый в отдельности на одну и ту же частоту, связываются индуктивно или электрически. В отличие от «одногорбой» резонансной кривой одиночного контура в связанных цепях получаются «двугорбые» кривые; например, ток в каждом контуре может иметь максимумы при двух частотах, расположенных ниже и выше резонансной частоты одиночного контура.
Частотные характеристики сопротивлений и проводимостей реактивных двухполюсников
Двухполюсником называется любая электрическая цепь или часть электрической цепи, имеющая два вывода. Ниже рассматриваются только линейные двухполюсники, т. е. такие, которые состоят из линейных элементов.
Различают двухполюсники активные и пассивные.
Активным называется двухполюсник, содержащий источники электрической энергии, которые не компенсируются взаимно внутри двухполюсника.
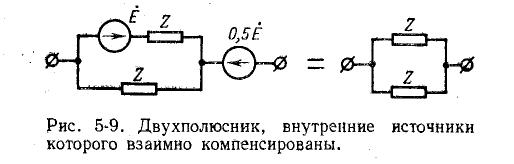
Пассивным называется двухполюсник, не содержащий источников электрической энергии; в случае линейного двухполюсника он может содержать источники электрической энергии, взаимно компенсирующиеся таким образом, что напряжение на его разомкнутых выводах равно нулю. Такой линейный двухполюсник относится к категории пассивных; его сопротивление, измеренное на выводах, не изменится, если источники электрической энергии внутри него заменить пассивными элементами — внутренними сопротивлениями источников э. д. с. или соответственно внутренними проводимостями источников тока. Пример двухполюсника, содержащего компенсированные источники, показан на рис. 5-9.
По числу элементов, входящих в двухполюсник, различают одноэлементный, двухэлементный и многоэлементный двухполюсники.
По характеру этих элементов двухполюсники делятся на реактивные, т. е. состоящие из индуктивностей и емкостей, и двухполюсники с потерями, содержащие активные сопротивления. Реактивные двухполюсники представляют собой идеализированные электрические системы, приближающиеся по своим свойствам к физически существующим цепям с малыми потерями.
Частотные характеристики сопротивлений или проводимостей двухполюсников, образующих электрическую цепь, предопределяют частотные и резонансные свойства цепи, т. е. зависимости амплитуд и фаз токов и напряжений от частоты.
Настоящий параграф посвящен изучению частотных характеристик пассивных реактивных двухполюсников.
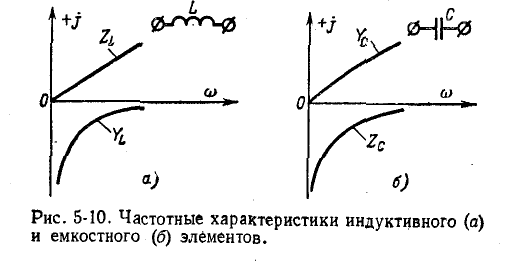
Одноэлементные реактивные двухполюсники
Индуктивность и емкость представляют собой простейшие одноэлементные реактивные двухполюсники. Знак комплексного сопротивления и комплексной проводимости каждого из этих двухполюсников не зависит от частоты; этим они существенно отличаются от других, более сложных реактивных двухполюсников, содержащих неоднородные реактивные элементы, т. е. индуктивность и емкость в разных сочетаниях.
Комплексное сопротивление индуктивного элемента во всем спектре частот имеет положительный знак, а комплексная проводимость — отрицательный:
Комплексное сопротивление емкостного элемента во всем спектре частот имеет отрицательный знак, а комплексная проводимость — положительный:
В рассматриваемом случае реактивных двухполюсников комплексные сопротивления и проводимости являются мнимыми. Поэтому для сохранения знаков частотные ха-рактернстнкн сопротивлений и проводимостей удобно рисовать в прямоугольной системе координат, в которой вверх откладываются мнимые величины со знаком плюс, а вниз — со знаком минус.
Частотные характеристики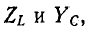
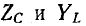
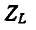
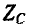
Следует заметить, что как сопротивления, так и проводимости рассматриваемых здесь одноэлементных реактивных двухполюсников возрастают (с учетом знака) по мере повышения частоты, т. е.
Это является общим свойством всех реактивных двухполюсников, а не только одноэлементных.
Двухполюсник, состоящий из последовательно или параллельно соединенных однородных элементов (индуктивностей или емкостей), относится к числу одноэлементных двухполюсников, так как последовательно или параллельно соединенные однородные элементы могут быть заменены одним эквивалентным реактивным элементом того же характера.
Двухэлементные реактивные двухполюсники
Двухэлементные двухполюсники, составленные из индуктивности и емкости, представляют собой простейшие резонансные цепи.
При последовательном соединении индуктивности и емкости алгебраически складываются комплексные сопротивления. На рис. 5-11, а жирной линией показана частотная характеристика двухполюсника, полученная в результате графического сложения кривых 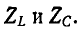
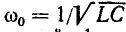
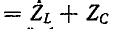
Частотная характеристика проводимости того же двухполюсника представляет собой функцию, обратную сопротивлению:
Кривая Y показана на рис. 5-11, б.
При резонансной частоте проводимость рассматриваемого двухполюсника обращается в бесконечность; эта точка носит название полюса функции Y и обозначается на чертеже крестиком
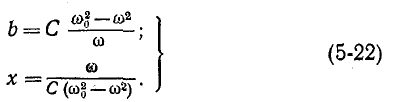
Частотные характеристики Z и Y, построенные таким образом1, соответствуют уравнениям:
и
или с учетом(5-2):
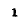
В области частот ниже резонансной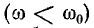
В области частот выше резонансной
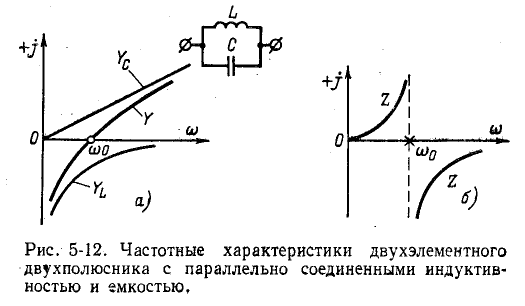
При параллельном соединении индуктивности и емкости алгебраически складываются их комплексные проводимости. На рис. 5-12, а жирной линией показана частотная
характеристика двухполюсника, полученная в результате графического сложения
Частотная характеристика сопротивления того же двухполюсника представляет собой функцию, обратную проводимости: Z — 1/Y. Кривая Z показана на рис. 5-12, б.
Частота, при которой характеристика Y пересекает ось абсцисс (нуль функции У), а характеристика Z уходит в бесконечность (полюс функции Z), является резонансной частотой (резонанс токов).
Частотные характеристики, построенные на рис. 5-12, соответствуют уравнениям:
И
или с учетом (5-22)
В области частот ниже резонансной проводимость индуктивного элемента перекомпенсирует проводимость емкостного элемента и сопротивление двухполюсника получается, индуктивным. В области частот выше резонансной наблюдается обратное явление и сопротивление двухполюсника имеет емкостный характер.
Таким образом, в зависимости от частоты двухэлементный реактивный двухполюсник может иметь либо индуктивное, либо емкостное сопротивление. При этом, так же как и в случае одноэлементного реактивного двухполюсника, кривые Z и Y возрастают, т. е. производные от 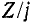
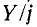
В отличие от сопротивлений одноэлементных двухполюсников, которые выражаются только через текущую частоту, сопротивления двухэлементных реактивных двухполюсников зависят также и от разности квадратов резонансной и текущей частот (формулы (5-21) и (5-22)1.
Как видно из выражений (5-21), для построения частотных характеристик двухполюсника, состоящего из последовательно соединенных элементов L и С, достаточно знать нуль функции Z или, что то же, полюс функции Y. Параметр L, входящий в (5-21), влияет только на выбор масштаба Z и Y по оси ординат.
Аналогично в соответствии с (5-22) для построения частотных характеристик двухполюсника, состоящего из параллельно соединенных элементов L и С, достаточно знать полюс Z или, что то же, нуль Y, причем параметр С влияет только на масштаб Z и Y.
Двухполюсники, имеющие одинаковые частотные характеристики Z или Y, эквивалентны.
Многоэлементный реактивный двухполюсник
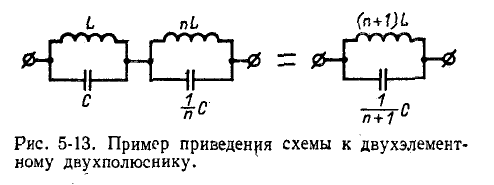
Многоэлементный реактивный двухполюсник может быть получен в результате различных сочетаний одноэлементных и двухэлементных двухполюсников. Пользуясь частотными характеристиками, приведенными выше, можно построить частотные характеристики для трех-, четырех- и много-элементных реактивных двухполюсников. При этом одно-
родные элементы (или группы элементов с одинаковыми резонансными частотами), соединенные параллельно или последовательно, должны быть сначала заменены одним элементом (или эквивалентной группой элементов, как это, например, показано на рис. 5-13).
Такие двухполюсники будем называть «приведенными».
Из свойства положительности производной 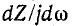
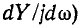
В общем случае, если при 
В противном случае порядок расположения резонансов обратный: первым наступает резонанс напряжений, вторым — резонанс токов и т. д.
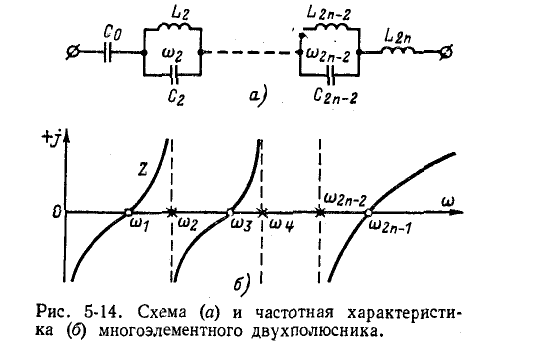
На рис. 5-14, а дана схема многоэлементного двухполюсника, а на рис. 5-14, б — соответствующая ему частотная характеристика сопротивления.
У реактивных двухполюсников сумма чисел полюсов и нулей (не считая точек 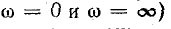
Расположение нулей и полюсов, как указывалось выше, поочередное, а все ветви частотной характеристики с увеличением 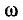
- Соединение звездой и треугольником в трехфазных цепях
- Принцип действия асинхронного и синхронного двигателей
- Метод симметричных составляющих
- Цепи периодического несинусоидального тока
- Расчет неразветвленной однородной магнитной цепи
- Энергия магнитного поля
- Синусоидальные Э.Д.С. и ток
- Электрические цепи с взаимной индуктивностью
Обновлено: 26.05.2023
Принцип резонансного метода заключается в определении резонансной частоты колебательного контура, состоящего из образцового и измеряемого элементов. Значение измеряемого параметра вычисляется из формулы
На основе резонансного метода разработаны и выпускаются приборы для измерения параметров элементов схем в диапазоне рабочих частот от 1 кГц до 300 МГц. К удобным и распространенным приборам относятся измерители добротности и измерители индуктивности и емкости с двумя генераторами.
Измерители добротности. Любой измеритель добротности (рис. 11-15) состоит из генератора высокой частоты измерительного контура и индикатора резонанса — электронного вольтметра Генератор позволяет устанавливать нужное значение частоты по шкале. Измерительный контур образуется исследуемой или вспомогательной (образцовой) катушкой и образцовым конденсатором с градуированной шкалой. В измерительный контур через делитель напряжения вводят последовательно небольшую известную часть выходного напряжения генератора На образцовом конденсаторе возникает напряжение отношение этих напряжений
В момент резонанса и отношение (11-9) достигает максимума:
Таким образом, если входное напряжение поддерживать во время измерений постоянным, то шкалу индикатора резонанса можно градуировать непосредственно в единицах добротности Поэтому измерители добротности часто называют куметрами. Применяя куметр для измерения добротности, путем вычислений можно определить индуктивность, емкость, сопротивление потерь, полные сопротивления двухполюсников, затухание и волновое сопротивление коаксиального кабеля и некоторые другие параметры. При измерении отсчет производят только в момент резонанса. На шкалах куметра получают связанные друг с другом значения частоты генератора, емкости образцового конденсатора и добротности.
Рис. 11-15. Схема измерителя добротности
Измерение индуктивности катушки. Катушку с индуктивностью и сопротивлением потерь присоединяют к зажимам 1, 2 (рис. 11-15). Изменением частоты генератора и емкости образцового конденсатора добиваются резонанса и считывают показания и . Полученное значение добротности здесь действующее, так как эквивалентная схема катушки соответствует рис. 11-3, б. Затем вычисляют реактивное сопротивление, индуктивность и сопротивление потерь:
Для определения истинных значений удобно пользоваться следующими формулами, вытекающими из формул (11-1) и (11-2):
Измерение собственной емкости катушки индуктивности. Для измерения используют схему рис. 11-15. Измерительный контур настраивают в резонанс дважды на частоте при максимальном значении емкости образцового конденсатора и на частоте при Запишем условия резонанса при этих настройках:
Разделим равенство для на возведем результат во вторую степень и решим полученное уравнение относительно предварительно положив
Измерение емкости конденсатора. Схема измерительного контура остается прежней (рис. 11-15), но вместо измеряемой катушки включают любую вспомогательную катушку. Если значение измеряемой емкости не выходит за пределы перекрытия емкости образцовым конденсатором, то, установив вблизи максимального значения, изменяя частоту генератора, настраивают контур в резонанс. Записывают точный отсчет по шкале . Затем параллельно образцовому конденсатору (к зажимам 3, 4) подключают измеряемый не меняя частоты генератора, настраивают контур в резонанс изменением емкости образцового конденсатора. Записывают значение . Очевидно, что при вторичной настройке неизвестная емкость замещена изменением емкости образцового конденсатора, поэтому
Если емкость измеряемого конденсатора больше максимальной емкости образцового, то измеряемый конденсатор включают последовательно с вспомогательной катушкой индуктивности; контур настраивают в резонанс изменением частоты генератора при максимальном значении Затем измеряемый конденсатор отключают и вновь настраивают контур образцовым конденсатором на ту же частоту записывают значение . Измеряемая емкость
Измерение параметров двухполюсников. Любой двухполюсник можно представить одной из эквивалентных схем,
приведенных на рис. 11-16. Последовательные двухполюсники (рис. 11-16, а, б, в) соответствуют малым сопротивлениям, т. е. большим емкостям и малым индуктивностям и малым активным сопротивлениям; параллельные (рис. 11-16, г, д, е) — малым емкостям и большим индуктивностям и сопротивлениям. Последовательные двухполюсники подключают последовательно с вспомогательной катушкой индуктивности (см. рис. 11-15), параллельные — к зажимам 3, 4 параллельно образцовому конденсатору.
Рис. 11-16. Эквивалентные схемы двухполюсников
Измерение выполняют в таком порядке. Предположим, что двухполюсник последовательный и соответствует схеме рис. 11-16, б. Сначала настраивают измерительный контур с вспомогательной катушкой на частоту и записывают значения
Затем включают двухполюсник последовательно с катушкой и восстанавливают настройку контура образцовым конденсатором, при этом получают новые значения
Подставляя сюда выражения для из формул (11-10), определяют искомые величины
Если окажется, что , то меняет знак, что означает соответствие двухполюсника схеме,
приведенной на рис. 11-16, в; тогда
Если предположить, что двухполюсник параллельный и соответствует рисунку то, аналогично, сначала измерительный контур настраивают на частоту и получают значения и , затем включают двухполюсник в зажимы 3, 4, т. е. параллельно образцовому конденсатору, и восстанавливают настройку. Получают значения Искомые величины определят так:
Если то двухполюсник соответствует схеме рис. 11-16, е. Тогда
Предположение о последовательном или параллельном соединении элементов двухполюсника подтверждается возможностью настройки измерительного контура при соответствующем включении двухполюсника.
Погрешность измерения с помощью куметра определяется нестабильностью и погрешностью установки частоты генератора, непостоянством его выходного напряжения, погрешностью градуировки шкал образцовых конденсаторов и вольтметров, а также неточностью настройки в резонанс. Погрешность измерения составляет Для повышения точности измерения индуктивности и емкости резонансным методом его сочетают с методами замещения и биений.
Сопротивление потерь в контуре при измерениях резонансными методами пренебрегают. Резонансные методы используются, как правило, на достаточно высоких частотах порядка сотен кГц и единиц МГц, т.к. на более низких частотах добротность контура бывает невысокой и трудно получить достаточно острую резонансную кривую, отчего точность измерения невысока.
На резонансной частоте , при этом ток в целом максимальный .
— круговая резонансная частота.
Добротность контура . При резонансе ток резко возрастает,
На использовании явления последовательного резонанса основаны приборы, называемые куметрами. Они служат для измерения добротности, а также могут использоваться для измерения индуктивности и емкости.
Примером может служить измеритель добротности Е4-11.
Этот прибор содержит источник напряжения калиброванных частот, ёмкостный делитель, состоящий из Сд1 и Сд2 , образцового переменного конденсатора С0, вольтметра. На корпусе он имеет клеммы для подключения исследуемой катушки индуктивности или исследуемого конденсатора.
I. Измерение ёмкости
В этом случае произвести измерение, как было сделано выше, невозможно, т.к. настроив контур в резонанс на определённой частоте в присутствии конденсатора Сх, мы не сможем получить резонанс в его отсутствие, т.к. не хватает ёмкости образцового конденсатора. Поэтому конденсатор с неизвестной ёмкостью Сх подключается последовательно к образцовой ёмкости. Куметр настраивается в резонанс. При этом
Затем куметр настраивается в резонанс без неизвестной емкости
Отсюда несложно определить неизвестную ёмкость
2. Измерение индуктивности и добротности
Значение определяется описанным ранее способом из формулы
Проводя измерения на двух частотах
или , где ; k=2, для удобства.
Погрешность измерения связанная с , т.к. , то С0 с точностью 10%
При измерении индуктивности катушку подключают к соответствующим клеммам, затем, используя ручки переключения образцовых частот и ручку управления образцовым конденсатором, добиваются резонанса.
-напряжение на образцовом конденсаторе,
— напряжение на всём контуре.
На результат измерения влияют потери в Собр.
поделив на резонансное сопротивление .
Самая существенная погрешность из-за измерений UС.
Измерительные приборы, основанные на использовании данного метода, содержат резонансный контур и используют явление чаще всего последовательного
L — индуктивность катушки индуктивности;
R — активное сопротивление катушки;
C — ёмкость конденсатора.
Сопротивление потерь в контуре при измерениях резонансными методами пренебрегают. Резонансные методы используются, как правило, на достаточно высоких частотах порядка сотен кГц и единиц МГц, т.к. на более низких частотах добротность контура бывает невысокой и трудно получить достаточно острую резонансную кривую, отчего точность измерения невысока.
На резонансной частоте , при этом ток в целом максимальный .
— круговая резонансная частота.
Добротность контура . При резонансе ток резко возрастает,
На использовании явления последовательного резонанса основаны приборы, называемые куметрами. Они служат для измерения добротности, а также могут использоваться для измерения индуктивности и емкости.
Примером может служить измеритель добротности Е4-11.
Этот прибор содержит источник напряжения калиброванных частот, ёмкостный делитель, состоящий из Сд1 и Сд2 , образцового переменного конденсатора С0, вольтметра. На корпусе он имеет клеммы для подключения исследуемой катушки индуктивности или исследуемого конденсатора.
I. Измерение ёмкости
В этом случае произвести измерение, как было сделано выше, невозможно, т.к. настроив контур в резонанс на определённой частоте в присутствии конденсатора Сх, мы не сможем получить резонанс в его отсутствие, т.к. не хватает ёмкости образцового конденсатора. Поэтому конденсатор с неизвестной ёмкостью Сх подключается последовательно к образцовой ёмкости. Куметр настраивается в резонанс. При этом
Затем куметр настраивается в резонанс без неизвестной емкости
Отсюда несложно определить неизвестную ёмкость
2. Измерение индуктивности и добротности
Значение определяется описанным ранее способом из формулы
Проводя измерения на двух частотах
или , где ; k=2, для удобства.
Погрешность измерения связанная с , т.к. , то С0 с точностью 10%
При измерении индуктивности катушку подключают к соответствующим клеммам, затем, используя ручки переключения образцовых частот и ручку управления образцовым конденсатором, добиваются резонанса.
Помимо измерения частоты электрических колебаний резонансные методы широко применяются для измерения малых ёмкостей и индуктивностей, добротности, собственной или резонансной частоты настройки и других параметров радиодеталей и колебательных систем.
Резонансная схема измерения ёмкостей (рис. 10) обычно включает в себя генератор высокой частоты, с контуром которого LС слабо связывается индуктивно (или через ёмкость) измерительный контур, состоящий из опорной катушки индуктивности Lо и испытуемого конденсатора Сх. Изменением ёмкости конденсатора С генератор настраивают в резонанс с собственной частотой fо измерительного контура по экстремальным показаниям индикатора резонанса, например электронного вольтметра V. При известной частоте настройки генератора fо измеряемая ёмкость определяется формулой
При фиксированном значении Lо конденсатор С можно снабдить шкалой с отсчётом в значениях ёмкостей Сх.
Пределы измерений ёмкостей определяются значением индуктивности Lо и диапазоном частот генератора. Например, при Lо = 100 мкГ и диапазоне генератора 160-3500 кГц прибор будет измерять ёмкости от десятков пикофарад до сотых долей микрофарад. Для расширения пределов измерений ёмкостей при ограниченном частотном диапазоне генератора применяют несколько сменных катушек Lо различной индуктивности, а также включают испытуемые конденсаторы в измерительный контур последовательно с конденсаторами известной ёмкости. Ёмкости более 0,01-0,05 мкФ резонансным методом обычно не измеряются, так как на низких частотах резонансные кривые колебательных контуров становятся тупыми, что затрудняет фиксацию резонанса.
В качестве индикаторов резонанса используют чувствительные высокочастотные приборы, реагирующие на ток или напряжение, действующие в измерительном контуре, например электронные вольтметры со стрелочным или электронно-световым индикатором, электроннолучевые осциллографы, термоэлектрические приборы и др. Индикатор резонанса не должен вносить в измерительный контур заметного затухания.
Погрешность измерения ёмкостей резонансным методом достигает 5-10% из-за воздействия паразитных связей, некоторого влияния контура генератора на параметры измерительного контура, трудности точной фиксации состояния резонанса; она также зависит от устойчивости частоты генератора и погрешности её измерения.
Рис. 10. Схема измерения ёмкостей резонансным методом
При сочетании резонансного метода с методом замещения устраняется зависимость результата измерения ёмкостей от точности измерения частоты генератора и паразитных связей, благодаря чему погрешность измерений можно снизить до 1% и менее. Для этого к измерительному контуру (рис. 10) подключают опорный конденсатор переменной ёмкости Со и при максимальной ёмкости его Со1 настраивают генератор на резонансную частоту контура. Затем параллельно конденсатору Со присоединяют конденсатор Сх; нарушенный резонанс восстанавливают при неизменной настройке генератора посредством уменьшения ёмкости Со до некоторого значения Со2. Измеряемая ёмкость, очевидно, определяется формулой Сх = Cо1-Cо2.
Верхний предел измеряемых подобным методом ёмкостей равен разности между максимальной См и начальной Сн ёмкостями конденсатора Со. Конденсаторы, ёмкость которых превышает значение См— Сн, можно подключать к контуру последовательно с постоянным конденсатором известной ёмкости Сх. При этом порядок измерений остаётся прежним, но измеряемая ёмкость подсчитывается по формуле
Например, при С1 = 600 пФ, Со1 = 500 пФ и Со2 = 100 пФ получаем Сx = 1200 пФ. Применяя несколько сменных конденсаторов С1 различных номиналов, можно получить ряд пределов измерений. Если задаться верхним пределом измеряемых ёмкостей Сп, то необходимая ёмкость Сx определится формулой:
Например, при Сп = 2000 пФ, См = 500 пФ и Сн = 20 пФ конденсатор должен обладать ёмкостью С1 = 630 пФ.
Различные варианты резонансных методов реализуются в специальных измерительных приборах или посредством малогабаритных приставок к типовой, имеющей частотные шкалы, радиоаппаратуре (к последним относятся высокочастотные измерительные генераторы, радиоприёмники и т. п.).
Рис. 11. Схема резонансного измерителя ёмкостей, использующего явление поглощения
На рис. 11 приведена схема резонансного измерителя ёмкостей, основанного на использовании явления поглощения (абсорбции). Прибор содержит маломощный генератор по схеме ёмкостной трёхточки, с колебательным контуром которого индуктивно связан измерительный контур L2, С6, С7. Связь между контурами устанавливается сравнительно сильной (например, посредством использования общего ферритового сердечника для катушек L1 и L2) с целью обеспечения заметного влияния измерительного контура на режим генератора. Индикатором резонанса служит микроамперметр постоянного токаmA, включённый в цепь базы транзистора Т. При настройке измерительного контура в резонанс с частотой генератора энергия, поглощаемая контуром, оказывается наибольшей. Это вызывает резкое уменьшение постоянной составляющей тока базы, измеряемой микроамперметром mA, что обеспечивает чёткую фиксацию состояния резонанса.
Для уменьшения погрешности измерения малых ёмкостей можно в измерительный контур включить два конденсатора переменной ёмкости (С6 и С7 на рис. 11) с максимальными ёмкостями, например, 500 и 50 пФ. Перед измерениями оба конденсатора устанавливаются на максимальную ёмкость и с помощью подстроечного сердечника одной из катушек добиваются резонансной настройки генератора и измерительного контура. Затем, присоединив к контуру конденсатор Сх, в зависимости от предполагаемой ёмкости последнего одним из конденсаторов С6 или С7 восстанавливают резонанс. Отсчёт по шкалам конденсаторов С6 и С7 желательно производить непосредственно в значениях ёмкостей Сх.
Рис 12. Схема измерения ёмкостей резонансным методом с помощью радиоприёмника
Рассмотренный вариант резонансного метода может быть реализован с помощью простейшей приставки к радиоприёмнику, имеющему внутреннюю магнитную антенну. Приставка (рис. 12) представляет собой измерительный контур L, Со, собственная частота которого при максимальном значении ёмкости Со должна находиться в пределах какого-либо частотного поддиапазона приёмника. Приёмник настраивают на частоту одной из хорошо принимаемых передающих радиостанций этого поддиапазона, а затем катушку L располагают вблизи приёмника, параллельно его магнитной антенне. При наибольшей ёмкости Со подстроечным сердечником катушки L контур настраивают в резонанс с частотой настройки приёмника, который обнаруживается по ослаблению слышимости звуковых сигналов радиостанции, а затем производят измерение ёмкости Сх методом замещения.
Высокая точность фиксации состояния резонанса достигается при гетеродинном методе (методе нулевых биений). В гетеродинном измерителе ёмкостей имеется два одинаковых высокочастотных гетеродина, колебания которых смешиваются в детекторном каскаде, нагруженном на телефоны. При максимальной ёмкости основных контурных конденсаторов переменной ёмкости оба гетеродина подстраиваются на одну и ту же частоту, что контролируется по нулевым биениям. Затем параллельно одному из этих конденсаторов включают конденсатор Сx, ёмкость которого определяют методом замещения.
Если оба гетеродина выполнить совершенно идентичными, то прибор можно успешно применить для выравнивания ёмкостей сдвоенных и строенных блоков конденсаторов переменной ёмкости. Для этого к контурам обоих гетеродинов одновременно подключают по одной секции проверяемого блока конденсаторов и при их максимально введённой ёмкости добиваются нулевых биений. Если обе секции одинаковы, то при сопряжённом уменьшении их ёмкостей нулевые биения должны сохраняться.
Однозначная связь между ёмкостью колебательного контура генератора и частотой возбуждаемых колебаний позволяет создать измеритель ёмкостей, состоящий из генератора, в контур которого включаются конденсаторы Cx, и частотомера, имеющего шкалу с непосредственным отсчётом значений Сx.
Во всех вариантах применения резонансного метода предварительную регулировку измерительной схемы следует выполнять при подключённых к ней проводниках связи с объектом измерений, длина которых должна быть возможно меньшей.
Измерение мощности.
Из выражения для мощности на постоянном токе Р = IU видно, что ее можно измерить с помощью амперметра и вольтметра косвенным методом. Однако в этом случае необходимо производить одновременный отсчет по двум приборам и вычисления, усложняющие измерения и снижающие его точность.
Для измерения мощности в цепях постоянного и однофазного переменного тока применяют приборы, называемые ваттметрами, для которых используют электродинамические и ферродинамические измерительные механизмы.
Электродинамические ваттметры выпускают в виде переносных приборов высоких классов точности (0,1 — 0,5) и используют для точных измерений мощности постоянного и переменного тока на промышленной и повышенной частоте (до 5000 Гц). Ферродинамические ваттметры чаще всего встречаются в виде щитовых приборов относительно низкого класса точности (1,5 -2,5).
Применяют такие ваттметры главным образом на переменном токе промышленной частоты. На постоянном токе они имеют значительную погрешность, обусловленную гистерезисом сердечников.
Для измерения мощности на высоких частотах применяют термоэлектрические и электронные ваттметры, представляющие собой магнитоэлектрический измерительный механизм, снабженный преобразователем активной мощности в постоянный ток. В преобразователе мощности осуществляется операция умножения ui = р и получение сигнала на выходе, зависящего от произведения ui, т. е. от мощности.
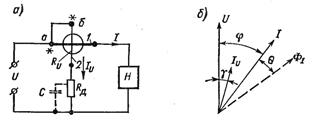
На рис. 1, а показана возможность использования электродинамического измерительного механизма для построения ваттметра и измерения мощности.
Рис. 1. Схема включения ваттметра (а) и векторная диаграмма (б)
Неподвижная катушка 1, включаемая в цепь нагрузки последовательно, называется последовательной цепью ваттметра, подвижная катушка 2 (с добавочным резистором), включаемая параллельно нагрузке — параллельной цепью.
Для ваттметра, работающего на постоянном токе:
Рассмотрим работу электродинамического ваттметра на переменном токе. Векторная диаграмма рис. 1, б построена для индуктивного характера нагрузки.Вектортока Iu параллельной цепи отстает от вектора U на угол γ вследствие некоторой индуктивности подвижной катушки.
Из этого выражения следует, что ваттметр правильно измеряет мощность лишь в двух случаях: при γ = 0 и γ = φ.
Условие γ = 0 может быть достигнуто созданием резонанса напряжений в параллельной цепи, например включением конденсатора С соответствующей емкости, как это показано штриховой линией на рис. 1, а. Однако резонанс напряжений будет лишь при некоторой определенной частоте. С изменением частоты условие γ = 0 нарушается. При γ не равном 0 ваттметр измеряет мощность с погрешностью βy, которая носит название угловой погрешности.
При малом значении угла γ (γ обычно составляет не более 40 — 50′), относительная погрешность
При углах φ, близких к 90°, угловая погрешность может достигать больших значений.
Второй, специфической, погрешностью ваттметров является погрешность, обусловленная потреблением мощности его катушками.
При измерении мощности, потребляемой нагрузкой, возможны две схемы включения ваттметра, отличающиеся включением его параллельной цепи (рис. 2).
Рис. 2. Схемы включения параллельной обмотки ваттметра
Если не учитывать фазовых сдвигов между токами и напряжениями в катушках и считать нагрузку Н чисто активной, погрешности β(а) и β(б), обусловленные потреблением мощности катушками ваттметра, для схем рис. 2, а и б:
где Рi и Рu — соответственно мощность, потребляемая последовательной и параллельной цепью ваттметра.
Из формул для β(а) и β(б) видно, что погрешности могут иметь заметные значения лишь при измерениях мощности в маломощных цепях, т. е. когда Рi и Рu соизмеримы с Рн.
Если поменять знак только одного из токов, то изменится направление отклонения подвижной части ваттметра.
Гомельский государственный технический университет
имени П.О.Сухого
Кафедра физики
Лабораторная работа № 2-8
Измерение емкости конденсатора методом резонанса.
Выполнил студент гр. Э-13
Колесников П.М.
Принял преподаватель
г. Гомель, 2002
Лабораторная работа № 2-8
Измерение емкости конденсатора методом резонанса.
Цель работы: Изучить закон Ома для цепей переменного тока при параллельном соединении реактивных и активных сопротивлений и явление резонанса тока.
Приборы и принадлежности: генератор переменной ЭДС, частотомер, катушка индуктивности, набор конденсаторов, осциллограф, соединительные провода и кабели.
Теоретическая часть
Резонансные методы измерений являются наиболее простыми и универсальными т.к. позволяют сравнивать с эталонами как индуктивности, так и емкости. Для получения количественных соотношений, нужно использовать закон Ома для цепи переменного тока с параллельным соединением различных элементов: R, C, L. Построим векторную диаграмму тока и напряжения для цепи, в которой к источнику переменной ЭДС параллельно подключены R, L ,C. Поскольку при параллельном соединении сопротивлений напряжение на них одинаково по величине и направлению, то это напряжение совмещается с осью проекций.
Разные по величине и направлению будут соответствующие токи ILICIR. Поскольку по фазе активный ток совпадает с напряжением на сопротивлении R, то вектор IR направлен по направлению напряжений VR=VL=VC. Емкостной ток IC по фазе па П/2 опережает напряжение VC на конденсаторе, а ток катушки индуктивности IL отстает от напряжения на индуктивности по фазе П/2. На рис. показана векторная диаграмма для случая когда IC>IL, поэтому эти токи противоположны по фазе и результирующий ток равен их разности, и направлен в сторону большего тока. Прибавляя к этому вектору еще и ток IR, получим результирующий ток всей цепи I, величина которого определяется по теореме Пифагора:
Выразив ток по закону Ома для однородного участка цепи (не одержащего ЭДС), получим:
Из этого закона Ома следует, что полное сопротивление цепи при параллельном соединении разных по природе сопротивлений выражается формулой:
Согласно формуле закона Ома минимальный ток от источника будет при условии что IL=IC и при этом же условии напряжение на параллельной группе будет максимальным. Поэтому реактивные токи катушки и конденсатора будут максимальными и могут существенно превосходить ток источника. Это явление резкого увеличения амплитуды реактивных токов в цепи параллельно включенных катушек и конденсаторов, при совпадении частоты источника с резонансной частотой контура определяется из условия: называется резонансом тока.
1. Включаем все приборы в сеть, изменяя частоту от 200 кГц до 20 кГц находим значение резонанса, нажав кнопку счет на частотомере измеряем значение частоты все полученные данные вносим в таблицу (R1=8,2(Ом), R2=15(Ом), К=0,01):
Читайте также:
- Каковы место и роль исполнительной власти в системе разделения властей кратко
- Москва город герой кратко презентация
- Основные концепции происхождения армии философия кратко и понятно самое важное
- Подвижные игры в системе физического воспитания кратко
- Русская философия отличается духовной проблематикой многообразием философских школ
Электрическая цепь, состоящая из соединеных в контур конденсатора емкостью С и катушки индуктивностью L,
обладающая сопротивлением R(сопротивление активных потерь в катушке), называется электрическим колебательным контуром.
В контуре возникает колебательный процесс ввиду перехода энергии электрического поля в энергию магнитного и наоборот.
Реактивные сопротивления индуктивности и емкости зависят от частоты переменного тока.
При увеличении частоты реактивное сопротивление индуктивности растет, а емкости падает.
При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное — растет.
При некоторой частоте ƒ0, емкостное сопротивление конденсатора и индуктивное сопротивление катушки
становятся численно равными: Xc = XL.
При этом токи индуктивной и емкостной ветвей также равны, что приводит к возрастанию амплитуды вынужденных колебаний.
Режим, возникающий в цепи, состоящей из генератора и параллельно включенных катушки и конденсатора, при равенстве
емкостного и индуктивного сопротивлений, называют режимом резонанса токов.
Явление резонанса токов используется в полосовых фильтрах для выделения определенной частоты.
Такая схема необходима для работы телевизора, радиоприемника, ёмкостного генератора и т.п.
Расчет частоты резонанса параллельного LC-контура описывается формулами:
XL
— индуктивное реактивное сопротивление, Ом;
XС
— ёмкостное реактивное сопротивление, Ом;
ƒ0
— резонансная частота, Гц;
Расчет частоты резонанса LC-контура
Введите значения индуктивности и ёмкости конденсатора, чтобы узнать резонансную частоту контура,
или введите резонансную частоту генератора, чтобы рассчитать необходимые значения индуктивности и емкости.
XL =
XC =
ƒ0 =
φ = °
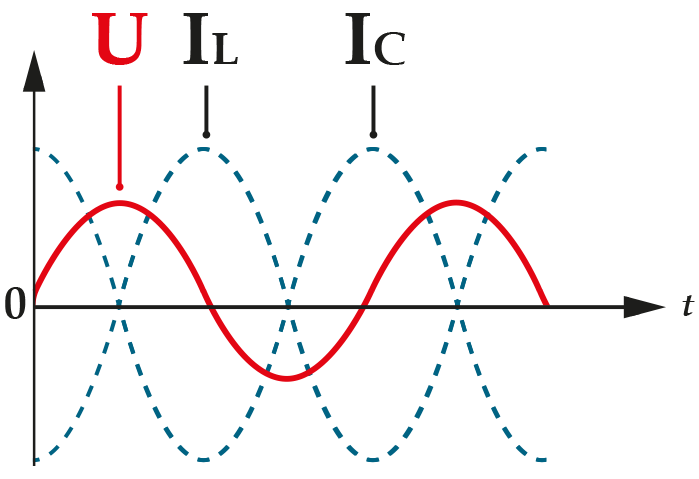
XL
>
XC
Цепь имеет емкостной характер,ее емкостное реактивное сопротивление меньше индуктивного.
Угол фазового сдвига между напряжением генератора и током в контуре приближается к 90°
Чем больше частота генератора отличается от собственной (резонансной) частоты контура, тем больше различаются токи IL и Іс,
тем больше реактивный ток в общей части цепи и меньше реактивное сопротивление контура.
Внимание! Производители объединяют элементы в серии или ряды: E6, E12, E24…
Для подбора компонентов будет использована серия E12.
Подбор конденсатора на сайте
Подбор катушки индуктивности на сайте
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!