Прямые
и переходные кривые должны плавно
сопрягаться с помощью переходных кривых.
Рисунок 3.1 — Схема разбивки переходных
кривых методом сдвижки
круговой кривой внутрь
Длину
переходной кривой определяем по формуле

где
i – уклон отвода
возвышения
h– возвышение наружного рельса, при
скоростях движения до 100км/ч приниматьi = 0,001;
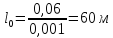
принимаемl0=60
м.
Параметр
кривой определяется как

Проверка
возможности разбивки переходной кривой
осуществляется по двум условиям:
Условие
1:

(3.7)
где
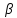
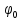
угол поворота на протяжении переходной
кривой;


Условие 2:

где

по формуле
(3.10)
Оба условия выполняются.
Определение вида переходной кривой.
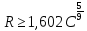
1100
> 475,9, следовательно, для разбивки
переходной кривой применяется кубическая
парабола.
Координаты
такой кривой определяют по формуле

Подсчет
ординат ведется с шагом 10 м.
Таблица
3.1 – Координаты переходной кривой по
кубической параболе
|
|
10 |
20 |
30 |
40 |
50 |
60 |
|
|
0,0025 |
0,02 |
0,068 |
0,161 |
0,315 |
0,545 |
Элементы
переходной кривой для разбивки на
местности:
Сдвижка
кривой внутрь:
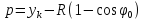
где
yk
– координата переходной кривой
приxk=l0
p=0,545-1100(1-0,855)=0,105м
Расстояние
от тангенсного столбика смещенной
круговой кривой до начала переходной
кривой подсчитывают по формуле

m=60-1100*0,026=30,31м
Расстояние
от тангенсного столбика бывшей круговой
кривой до начала переходной кривой
подсчитывают по формуле
, (3.15)
Полная
длина кривой:

(3.16)
Lкр=2*60+1100(0,505-2*0,027)=840
м
Суммарный
тангенс:

Ткр=30,31+(1100+0,105)*0,258=314,16м
Суммарная
биссектриса:

(3.18)
Расчет
числа укороченных рельсов:
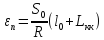
где

S0– расстояние между осями рельсов
(S0=1600 мм)
Число
укороченных рельсов определяется по
формуле:
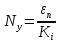
где
Ki–
стандартное укорочение, при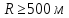
мм, при
мм.
4 Расчет и проектирование обыкновенного стрелочного перевода
4. 1 Основные параметры стрелки
Начальный
угол остряка:
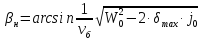
где

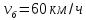
W0
– допустимый параметр потери
кинетической энергии при ударе (W0=0,225
м/с);

гребнем колеса и рамным рельсом (
j0– допустимая величина внезапно
появляющегося поперечного ускорения
, по заданиюj0=0,34
м/с2;

Полный
стрелочный угол:

где
y0– ордината
в корне остряка (y0=0,18
м);
R0– радиус остряка
Радиус
переходной кривой:

где

действующего непогашенного ускорения+
Длина
криволинейного остряка:
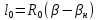
Передний
вылет рамного рельса:

где
с – расстояние между осями стыковых
брусьев (с=0,42 м);
z1– число пролетов между осями переводных
брусьев в зонеq(z1=5);
a– пролет между брусьями (а=0,5 м);
k– смещение начала остряка относительно
оси переводного бруса (k=0,041
м);
Длина
рамного рельса:

где

прямое направление,
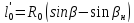

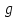

где
z2– число пролетов
в пределах заднего вылета (z2=2).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Круговые кривые. Железнодорожные линии (также и автомобильные дороги) в плане состоят из прямолинейных участков, сопряжённых между собой кривыми. Наиболее простой и распространённой формой кривой является дуга окружности. Такие кривые носят название круговых кривых. На железных дорогах применяют круговые кривые со следующими радиусами: 4000, 3000, 2000, 1800, 1500, 1200, 1000, 800, 700, 600, 500, 400 и 300 м. Радиус кривой выбирают при проектировании дороги, руководствуясь конкретными техническими условиями.
Главными точками кривой, определяющими её положение на местности, являются вершина угла ВУ, начало кривой НК, середина кривой СК и конец кривой КК (рис. 15.3).
![inj_geo_2-114.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-114.jpg)
Рис. 15.3 Схема круговой кривой
Основные элементы кривой – её радиус R и угол поворота a. К основным элементам относятся также:
– тангенс кривой Т (или касательная) — отрезок прямой между вершиной угла и началом или концом кривой;
– кривая К — длина кривой от начала кривой до её конца;
– биссектриса кривой Б — отрезок от вершины угла до середины кривой;
– домер Д — разность между длиной двух тангенсов и кривой.
Во время изысканий угол a измеряют, а радиус R назначают. Остальные элементы вычисляют по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НК, О (центр окружности):
Т = R×tg(a/2); К = R×a = p R a°¤180°; Б = R [sec(a/2) — 1], (15.1)
где a° — угол поворота в градусах.
Домер вычисляют по формуле
. (15.2)
Вместо вычислений по формулам можно воспользоваться таблицами для разбивки кривых на железных дорогах, где по заданным радиусу и углу поворота сразу находят значения Т, К, Б и Д.
В месте поворота трассы пикетаж ведётся по кривой. Пикетажное положение главных точек кривой определяют по формулам:
ПК НК = ПК ВУ — Т; ПК КК = ПК НК + К; ПК СК = ПК НК + К/2. (15.3)
Правильность вычислений контролируют по формулам:
ПК КК = ПК ВУ + Т — Д; ПК СК = ПК ВУ + Д/2. (15.4)
Пример.
Измерено a = 18°19¢ и задан радиус R = 600 м. Вершина угла расположена на пикете 6 + 36,00.
По формулам (15.1) и (15.2) или по таблицам находим элементы кривой: Т = 96,73 м; К = 191,81 м; Д = 1,65 м; Б = 7,75 м.
Вычислим пикетажное положение главных точек:
Контроль:
ПК ВУ 6 + 36,00 ПК ВУ 6 + 36,00
— Т 96,73 + Т 96,73
ПК НК 5 + 39,27 7 + 32,73
+ К 1 + 91,81 — Д 1,65
ПК КК 7 + 31,08 ПК КК 7 + 31,08
ПК НК 5 + 39,27 ПК ВУ 6 + 36,00
+ К/2 95,90 — Д/2 0,82
ПК СК 6 + 35,17 ПК СК 6 + 35,18
Переходные кривые. Непосредственное сопряжение прямого участка пути с круговой кривой приводит к тому, что во время движения поезда в месте сопряжения внезапно возникает центробежная сила F, прямо пропорциональная квадрату скорости движения v и обратно пропорциональная радиусу кривой . Чтобы обеспечить постепенное нарастание центробежной силы, между прямой и круговой кривой вставляют переходную кривую, радиус кривизны r которой плавно изменяется от ¥ до R. Если положить, чтобы центробежная сила менялась пропорционально расстоянию s от начала кривой, то получим
![inj_geo_2-117.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-117.jpg)
где s и r — текущие значения расстояния от начала переходной кривой и ее радиуса кривизны;
R – радиус кривизны в конце переходной кривой.
Индексом k отмечены значения переменных в конце переходной кривой.
Для радиуса кривизны переходной кривой в текущей точке i найдём:
r = lR/s, (15.5)
где через l обозначена длина переходной кривой sk. Кривая, описываемая уравнением (15.5), в математике называется клотоидой, или радиоидальной спиралью.
Угол поворота трассы на переходной кривой. На бесконечно малом отрезке кривой ds (рис. 15.4, а) происходит поворот трассы на угол
.
Подставляя выражение радиуса кривизны r из (15.5), получим
.
Выполним интегрирование от начала кривой НК, где j = 0 и s = 0, до текущей точки i:
![inj_geo_2-120.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-120.jpg)
откуда
Rlj = s2/2.
б)
а)
![inj_geo_2-121.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-121.jpg)
Рис. 15.4 Схема переходной кривой:
а – углы поворота трассы: φ – в текущей точке i, β – в конце
переходной кривой (точка КПК); б — приращения координат
Из полученного уравнения вытекают формулы:
![inj_geo_2-122.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-122.jpg)
![inj_geo_2-123.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-123.jpg)
где b — угол поворота трассы в конце переходной кривой;
l — длина переходной кривой;
R — радиус кривизны в конце переходной кривой, равный радиусу следующей за нею круговой кривой.
Координаты точки переходной кривой. Совместим начало координат с началом переходной кривой и направим ось x по касательной к ней (см. рис. 15.4, а). Бесконечно малому приращению дуги кривой соответствуют бесконечно малые приращения координат (рис. 15.4, б):
dx = cosj×ds; dy = sinj×ds. (15.7)
Разложим синус и косинус в ряд и, удержав в разложениях по два члена, подставим в них выражения для j из (15.6):
cosj = 1-j2/2 = 1 — s4/(8R2l2);
sinj = j — j3/6 = s2/(2Rl) — s6/(48R3l3).
Подставляя полученные выражения в (15.7) и выполняя интегрирование, найдём:
![inj_geo_2-124.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-124.jpg)
![inj_geo_2-125.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-125.jpg)
![inj_geo_2-126.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-126.jpg)
![inj_geo_2-127.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-127.jpg)
Смещение начала кривой (сдвижка). На рис. 15.5 дуга НК-КПК представляет собой переходную кривую, переходящую после точки КПК в круговую. Продолжим круговую кривую до точки Q, где её направление, параллельно оси x. Обозначим через m смещение, параллельное оси x, начала переходной кривой относительно точки Q, в которой начиналась бы круговая кривая при отсутствии переходной. Через p обозначим смещение в перпендикулярном направлении. Из рис. 15.5 видно:
,
где xКПК и yКПК — координаты конца переходной кривой, вычисляемые по формулам (15.8) и (15.9) с аргументом s = l .
Сочетание круговой кривой с переходными. На рис. 15.6 показана кривая, поворачивающая трассу на угол a и состоящая из круговой части с радиусом R и двух переходных кривых одинаковой длины l.
|
|
|
|
Рис. 15. 5 Смещение начала переходной кривой |
Рис. 15.6 Сопряжение круговой кривой с переходными |
Если бы не было переходных кривых, в образованный прямыми линиями трассы угол была бы вписана дуга окружности радиуса R, равная Q-СК-Q1 и имеющая длину K = Ra.
При наличии переходных кривых на каждой из них происходит поворот трассы на угол b, отчего на долю круговой кривой приходится поворот на угол a-2b. Поэтому суммарная длина кривой равна
Kc = R (a-2b) + 2l = Ra — 2Rb + 2l = K — l + 2l = K + l.
Тангенс и биссектриса определяются по формулам:
Тс = T + m + Tp; Бc = Б + Бp,
где Тp = ptg(a/2); Бp = psec(a/2).
Домер в этом случае равен
.
В полевых условиях значения m, Тp и Бp вычисляют на микрокалькуляторе или выбирают из таблиц для разбивки кривых на железных дорогах. Пикетажное положение главных точек кривой вычисляют по формулам, аналогичным (15.3) и (15.4).
Расчет закруглений с переходными кривыми плана трассы дороги
Страницы работы
Содержание работы
ПРАКТИЧЕСКАЯ РАБОТА №1
РАСЧЕТ
ЗАКРУГЛЕНИЙ С ПЕРЕХОДНЫМИ КРИВЫМИ
Тема
1.2 План трассы дороги
Цель: Получить умения и
навыки о порядке расчета переходных кривых, сокращенной круговой кривой,
составлению ведомости углов поворота, прямых и кривых и схемы плана трассы.
Исходные данные: 1
закругление
1.
Категория автомобильной дороги – IV;
2.
Угол поворота трассы αп
= 52º50´;
3.
Радиус закругления R = 400 м;
4.
Пикетажное положение вершины угла
поворота ВУ ПК 40+00;
5.
Уклон проезжей части iп = 25‰;
6.
Уклон обочины iо = 60‰;
2 закругление
1.
Угол поворота трассы
αл2 = 21º06´;
2.
Радиус закругления R2 = 1100 м;
3.
Пикетажное положение
вершины угла поворота ВУ2 пк 28 + 66;
4.
Пикетажное положение
конца трассы Ктр пк 35+00,00.
Задание:
1)
Рассчитать закругления с переходными
кривыми.
2)
Составить ведомость углов
поворота, прямых и кривых;
3)
Обозначить полученные расчетом
значения на схеме плана трассы.
Выполнение работы:
- Расчёт закругления №1
1.1 Из таблицы элементов круговых
кривых (т. 2.1 стр. 16[2]) для величины угла поворота α и радиуса R
определяем значения:
Т = 496,77 × 0,4 = 198,708 (м);
К = 922,12 × 0,4 = 368,848 (м);
Д = 71,42 × 0,4 = 28,568 (м);
Б = 116,59 × 0,4 = 46,637 (м);
Контроль 2Т – К = Д
2×198,708 – 368,848 = 28,568
28,568 = 28,568
1.2 Из таблицы переходных кривых
(т. 2.2 стр. 17[2]) определяем элементы переходных кривых (при R = 400 м).
L = 100
(м) – длина переходной кривой;
αmin = 2β = 14º19´;
t = 49,97
– добавочный тангенс;
ρ = 1,04 – сдвижка круговой кривой.
т.к. α > 2β (52º50´ > 14º19´), то разбивка
круговой кривой возможна.
1.3
Определим длину сокращённой кривой К0
Длина сокращённой кривой определяется по формуле:
К0
= (πRα0)/180º = (α0R)/57,3º
или
по таблицам:
вместо R применяется Rизм ,если ρ(сдвижка) ≥ 0,01 R
0,01R = 4(м).
1,04
< 4,00 то при определении сокращённой круговой кривой, берём то же значение
радиуса (в нашем случае R = 400м).
α0 = α — 2β; α0 =
52º50´ — 14º19´ = 38º31´;
по таблице Митина при α0 = 38º31´; R = 400м,
следовательно:
К0 = (38,51 × 400) / 57,05 = 270 (м) К0
= 270 (м).
1.4
Определим элементы полного закругления: Тп; Кп; Дп;
Бп
Тп = Т + t; Тп
= 198,708 + 49,97 = 248,678 (м);
Кп = К0 + 2L; Кп
= 270 + 100 × 2 = 470 (м);
Бп = Б + ρ; Бп
= 46,637 + 1,04 = 47,677 (м);
Дп = 2Тп — Кп; Дп
= 2 × 248,678 – 470 = 27,356 (м).
1.5
Определяем пикетажное положение главных точек закругления
_ВУ пк 16 + 20,00 Контроль:
Тп 2 + 48,68 +ВУ
пк 16 + 20,00
+НЗ пк 13 + 71,32
Тп 2 + 48,68
L 1 + 00,00 _пк 18
+ 68,68
+КПК,НПК 14 + 71,32
Дп 0 + 27,36
К0 2 + 70,00
КЗ пк 18 + 41,32
+НЗ пк 17 + 41,32
L 1 + 00,00
КЗ пк 18 + 41,32
- Расчёт
закругления №2
2.1 Из таблицы
элементов круговых кривых (т. 2.1 стр. 16[2]) для величины угла поворота α
и радиуса R определяем значения:
Т = 186,24 × 1,1 = 204,864 (м);
К = 368,26 × 1,1 = 405,086 (м);
Д = 4,22 × 1,1 = 4,642 (м);
Б = 17,20 × 1,1 = 18,92 (м);
Контроль 2Т – К = Д
2×204,864 – 405,086 = 4,642
4,642 = 4,642
2.2 Из таблицы
переходных кривых (т. 2.2 стр. 17[2]) определяем элементы переходных
кривых (при R = 1100 м).
L = 100 (м) – длина переходной кривой;
αmin = 2β = 5º12´;
t = 50 (м) – добавочный тангенс;
ρ = 0,38 (м) – сдвижка круговой кривой.
т.к. α > 2β (21º06´ > 5º12´), то
разбивка круговой кривой возможна.
2.3 Определим длину сокращённой кривой К0
Длина сокращённой кривой определяется по
формуле:
К0 = (πRα0)/180º
= (α0R)/57,3º
α0 = α — 2β, следовательно:
α0 = 21º06´ — 5º12´ = 15º54´;
К0 = (15,59 × 1100) / 57,05 =
306,57 (м).
2.4 Определим элементы полного закругления: Тп; Кп;
Дп; Бп
Тп = Т + t; Тп = 204,864 + 50 =
254,864 (м);
Кп = К0 + 2L; Кп = 306,57 + 100 × 2 =
506,57 (м);
Бп = Б + ρ; Бп =
4,642 + 0,38 = 5,022 (м);
Дп = 2Тп — Кп; Дп
= 2 × 254,864 – 506,57 = 3,158 (м).
Расчетная схема закругления показана на рисунке 1.1
2.5 Определяем пикетажное положение главных точек закругления
_ВУ пк 28 + 66,00 Контроль:
Тп 2
+ 54,86 +ВУ пк 28 + 66,00
+НЗ пк 26 + 11,14
Тп 2 + 54,86
Кп пк 5 + 06,57
_пк 31 + 20,86
КЗ пк 31 + 17,71
Дп 0 + 03,15
КЗ
пк 31 + 17,71
3
Составление ведомости углов поворота, прямых и кривых
3.1 Определение прямых участков – П;
а) П1 = пк НЗ1 = пк 13+71,32 = 1371,32 м
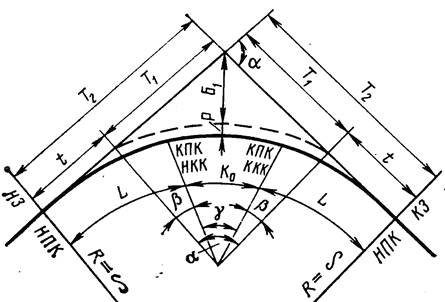
П2 = 2611,136 –1841,32 = 769,82 м
в)
П3 = пк КТ – пк КЗ2
П3
= 3500 – 3117,71 = 382,29 м
3.2 Определение расстояний между углами поворота – S;
а) S1 = пк ВУ1 S1 = 1620,0 м
б) S2 = пк ВУ2 28 + 66,00
пк ВУ1 16 + 20,00
12 + 46,50
Д 0 + 27,68
12 + 73,68
в) S3 = пк Ктр 35 + 00,00
пк ВУ2 28 + 66,00
6 + 34,00
Д2 3,98 Рисунок
2.1 Схема закругления с переходными
6 + 37,98 кривыми
3.3 Контроль составления ведомости
ΣП + ΣК = L
(1371,32 + 769,816 + 382,294) + (506,57 + 470) = 35000 (м)
ΣS – ΣД = L
(1620 + 1273,68 + 637,98) –(27,356 + 3,158) = 35000 (м)
Данные расчетов сведены в таблицу 1.1 Схема плана трассы
показана на рисунке 1.2
Похожие материалы
- Расчет отгона виража, определение поперечных уклонов, превышений, построение графика зависимости превышений
- Строительство участка автомобильной дороги Могилев-Чериков км72…км75 (расчетная интенсивность движения — 4000 авт./сутки, расчетная скорость движения — 100 км/час)
- Технический кодекс установившейся практики на автомобильные дороги и нормы их проектирования
Информация о работе
Тип:
Отчеты по лабораторным работам
На углах поворота трасс автомобильных дорог производим вставки кривых и пересчет по ним пикетажа. В качестве таких кривых применяем дуги окружностей больших радиусов. Главные точки кривой: начало, середина и конец кривой, далее НК, СК и КК соответственно (рис. 1.5).
Рис. 1.5 Элементы и главные точки горизонтальной круговой кривой
Элементы круговых кривых: угол поворота б, радиус кривой R, дорожный тангенс Т, длина кривой К, биссектриса Б, домер Д. При трассировании на кривых линейные измерения ведут по тангенсам, а длину трассы считают по кривой, домер показывает, насколько расстояние по двум тангенсам длиннее кривой.
Вычисление элементов горизонтальных кривых
Элементы кривых вычисляются по данным б, R и по формулам
, , , .
Вычисление пикетажных значений главных точек круговых кривых
Пикетажные значения главных точек кривых находят по формулам
ПК НК = ПК ВУ — Т, ПК К = ПК НК + К, ПК СК = ПК НК + К/2.
Контроль ПК КК = ПК ВУ + Т — Д, ПК СК = ПК КК — К/2 .
Составление ведомости прямых и кривых
По заданному азимуту начального направления трассы и углам поворота вычисляют азимуты последующих направлений
.
Вычисленные азимуты переводят в румбы.
Таблица 1.8 Перевод азимутов в румбы.
|
Азимут |
Определение румба по азимуту |
№ четверти, название румба |
|
I CB |
||
|
II ЮВ |
||
|
III ЮЗ |
||
|
IV СЗ |
Расстояние между вершинами углов:
.
Длина отрезка от ПК0 до первой вершины угла поворота ВУ1 равна пикетажному значению первой вершины угла.
Вычисляют длины прямых вставок
: .
Длина первой прямой вставки равна ПК НК первой кривой, последней разности ПК конца трассы и ПК КК последней кривой.
Переходные кривые
План трассы следует проектировать из условия наименьшего ограничения и изменения скорости движения автомобилей, обеспечения безопасности и удобства движения, а также возможной реконструкции дороги за пределами перспективного периода. При проектировании элементов плана, равно как и продольного и поперечного профилей, перспективный период следует принимать 20 лет. Начальным годом расчетного перспективного периода является год завершения разработки проекта дороги (или самостоятельного участка дороги).
Для обеспечения плавного въезда в круговую кривую малого радиуса и выезда из кривой последние сопрягают с прямыми участками трассы посредством переходных кривых.
В практике проектирования автомобильных дорог наибольшее распространение получили переходные кривые типа клотоиды, которые характеризуются линейным законом нарастания кривизны по длине и более, чем другие математические кривые, соответствуют фактической траектории движения автомобиля.
Клотоида (или радиоидальная спираль) как математическая кривая представляет собой спираль, радиус кривизны которой непрерывно изменяется от р = ? в начальной точке до р = 0 в бесконечном удалении от начала кривой (рис 1.9)
В качестве переходной кривой, как самостоятельного элемента трассы, применяется только начальный участок клотоиды от точки отхода от прямого участка, где р = ?, до точки на кривой, где р = R.
Уравнение клотоиды имеет вид:
,
где — радиус кривизны,
— расстояние от начала клотоиды до точки М на ней.
Параметр клотоиды — величина постоянная и выражается как произведение:
,
где R — радиус кривизны в конце клотоиды в конце отрезка клотоиды длиной L,
L — длина отрезка клотоиды от ее начала до точки на кривой, где радиус кривизны .
Рис. 1.9.1 Клотоида (переходная кривая)
Параметр А характеризует степень изменения кривизны клотоиды.
Наименьшая длина переходной кривой определяется по условию равномерного нарастания центробежной силы в пределах переходной кривой:
,
где Vp — расчетная скорость движения, принимаемая по СНиП- 2.05.02-85 для дороги соответствующей категории, км/ч;
I — допускаемая скорость нарастания центробежного ускорения, м/с3.
Для дорог 1- V категорий предельное значение 1= 0,3-0,1 м/с3. Чем выше расчетная скорость, тем меньшее значение I следует принимать.
Согласно СНиП [4] сопряжение прямых участков с круговыми кривыми посредством переходной кривой обязательно, если радиус круговой кривой R<3000 м — на дорогах / категории и R<2000 м — на дорогах прочих категорий. Наименьшая длина переходной кривой нормируется в зависимости от радиуса круговой кривой. Нормативную длину переходной кривой рекомендуется увеличить в 1,5 — 2 раза, если это позволяет расстояние между углами поворота трассы. Чем больше длина клотоиды, тем более плавно изменяется ее кривизна, а следовательно, условия движения для пассажиров и водителя более комфортны.


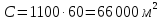





 ,
,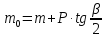



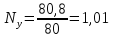
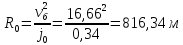

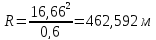




![inj_geo_2-129.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-129.jpg)
![inj_geo_2-130.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-130.jpg)






