|
0 / 0 / 0 Регистрация: 24.12.2009 Сообщений: 37 |
|
|
1 |
|
Найти минимальный элемент над главной диагональю и максимальный под главной диагональю матрицы02.06.2010, 21:30. Показов 7152. Ответов 8
Дан массив mas[1..n,1..n]. Найти минимальный элемент над главной диагональю и максимальный под главной диагональю…(предворительно выделив главную диагональ).
0 |
|
STGE 773 / 578 / 324 Регистрация: 17.06.2009 Сообщений: 1,188 |
||||
|
02.06.2010, 22:09 |
2 |
|||
0 |
|
0 / 0 / 0 Регистрация: 24.12.2009 Сообщений: 37 |
|
|
02.06.2010, 22:13 [ТС] |
3 |
|
хм??? шу-шуть не въеду…
0 |
|
STGE 773 / 578 / 324 Регистрация: 17.06.2009 Сообщений: 1,188 |
||||
|
02.06.2010, 22:44 |
4 |
|||
|
РешениеAltrex, я написал фрагмент программы поиска максимальных элементов над и под главной диагональю. Добавлено через 9 минут
Добавлено через 1 минуту
1 |
|
0 / 0 / 0 Регистрация: 24.12.2009 Сообщений: 37 |
|
|
02.06.2010, 22:44 [ТС] |
5 |
|
Кстати, а каким образом выделить диагональ (цвет, в отдельный вектор, заполнить нулями или ещё что-то) ? цветом
0 |
|
STGE 773 / 578 / 324 Регистрация: 17.06.2009 Сообщений: 1,188 |
||||
|
02.06.2010, 22:50 |
6 |
|||
|
Решение
0 |
|
Altrex 0 / 0 / 0 Регистрация: 24.12.2009 Сообщений: 37 |
||||
|
02.06.2010, 22:51 [ТС] |
7 |
|||
|
выводит только диагональ
0 |
|
773 / 578 / 324 Регистрация: 17.06.2009 Сообщений: 1,188 |
|
|
02.06.2010, 22:57 |
8 |
|
Так по условию сказано, что выделить только диагональ и надо.
0 |
|
AIEKCAH^P 105 / 102 / 89 Регистрация: 18.05.2009 Сообщений: 201 |
||||
|
03.06.2010, 08:14 |
9 |
|||
|
РешениеЭто же элементарно исправить
Миниатюры
1 |
Мы все знаем, как найти элементы выше главной диагонали в квадратной матрице. А что если матрица не квадратная, а просто прямоугольная и как найти в ней все элементы выше главной диагонали? Обычным if (i <= j) не обойдешься.
Допустим есть такой код, который делает все элементы выше диагонали 0, остальные — рандомные:
int n = 10;
int m = 16;
int** arr = (int**)malloc(sizeof(int*)*m);
for (int i = 0; i < m; i++)
{
arr[i] = (int*)malloc(sizeof(int)*n);
}
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
arr[i][j] = rand() % 9 + 1;
if (i <= j) //Какое-то корректное условие вместо данного
{
arr[i][j] = 0;
}
printf("%d ", arr[i][j]);
}
printf("n");
}
Как правильно решить такую задачу?
Kromster
13.5k12 золотых знаков43 серебряных знака72 бронзовых знака
задан 30 апр 2017 в 20:17
9
Если понимать искомую разделительную линию здесь, как диагональ прямоугольника, то можно предложить следующий подход:
if (i * n < j * m)
arr[i][j] = 2; //выше диагонали
else if (i * n == j * m)
arr[i][j] = 1; //точно на диагонали, таких элементов будет всего НОД(n,m)
else
arr[i][j] = 0; //ниже диагонали
для 6×6:
1 2 2 2 2 2
0 1 2 2 2 2
0 0 1 2 2 2
0 0 0 1 2 2
0 0 0 0 1 2
0 0 0 0 0 1
для 6×9:
1 2 2 2 2 2
0 2 2 2 2 2
0 0 2 2 2 2
0 0 1 2 2 2
0 0 0 2 2 2
0 0 0 0 2 2
0 0 0 0 1 2
0 0 0 0 0 2
0 0 0 0 0 0
ответ дан 14 окт 2018 в 15:28
MBoMBo
47.9k1 золотой знак17 серебряных знаков40 бронзовых знаков
следуя определению главной диагонали которая была дана в комментариях — следующий код напечатает все элементы стоящие выше главной диагонали (кроме самих элементов этой диагонали)
constexpr size_t n = 5, m = 4;
int mat[n][m] =
{
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{10, 11, 12, 13},
{14, 15, 16, 17}
};
for (size_t i = 0; i < n; i++)
{
for (size_t j = i + 1; j < m; j++)
{
cout << mat[i][j] << ' ';
}
cout << 'n';
}
ответ дан 1 мая 2017 в 18:52
ampawdampawd
3,6841 золотой знак14 серебряных знаков30 бронзовых знаков
1
Частным
случаем матрицы является квадратная
матрица,
т.е.
матрица, имеющая одинаковое количество
строк и столбцов (рис.43).
-
X[1,1]
X[1,2]
X[1,3]
X[2,1]
X[2,2]
X[2,3]
X[3,1]
X[3,2]
X[3,3]
Рис.43
Элементы
матрицы, выделенные на рис.43, называются
главной
диагональю.
Отличительной
особенностью этих
элементов является то, что они имеют
одинаковые
номера строки и столбца.
Поэтому в i-ой
строке индексы элемента
главной диагонали
матрицы Х будут X[i,i].
Для обработки
элементов главной
диагонали
требуется изменять только одну
переменную,
поэтому необходимо всего один
цикл, а не два,
как при обработке
всей матрицы.
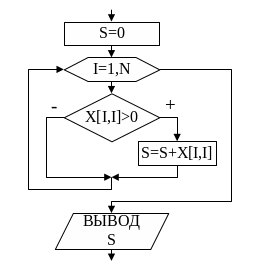
На рис.44 показан алгоритм
нахождения суммы положительных
элементов главной диагонали. Ниже
приведён фрагмент
программы к этому алгоритму.
•
• •
S:=0;
for
i:=1
to
N
do
if
X[i,i]>0 then
S:=S+X[i,i];
writeln(‘S=’
, S);
• • •
Рис.44
3.2.6. Обработка элементов побочной диагонали
Побочная
диагональ
(рис.45)
существует только в квадратной
матрице.
-
X[1,1]
X[1,2]
X[1,3]
X[2,1]
X[2,2]
X[2,3]
X[3,1]
X[3,2]
X[3,3]
Рис.45
Н
етрудно
заметить, что элемент побочной диагонали
матрицы Х в первой строке имеет индексы
Х[1,N],
во второй строке – Х[2, N-1], в третьей –
Х[3, N-2].
Отсюда можно заключить, что в i-ой
строке элемент побочной диагонали будет
иметь индексы Х[I,
N-I+1].
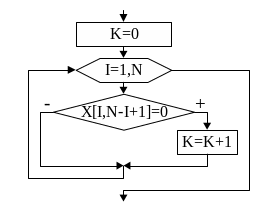
На
рис.46 показан алгоритм нахождения
количества равных
нулю элементов побочной диагонали. Ниже
представлен фрагмент
программы к этому алгоритму.
Рис.46
• • •
К:=0;
for
i:=1
to
N
do
if
X[i,N-i+1] = 0 then
K:=K+1
writeln(
‘K=’ , K) ;
• • •
3.2.7. Обработка элементов квадратных матриц, расположенных над и под главными и побочными диагоналями
На
рис. 47 приведена схема расположения
элементов относительно главной диагонали.
Г
лавная
диагональ (ГД) Элементы,
расположенные над ГД
-
гд
Гд
ГД
гд
Элементы,
расположенные под ГД
Рис.
47
Рассмотрим
элементы, расположенные над главной
диагональю матрицы. Для матрицы А
размером 4х4 эти элементы будут иметь
следующие индексы:
в
первой строке: A[1,2],
A[1,3],
A[1,4];
во
второй строке: A[2,3],
A[2,4];
в
третьей строке: A[3,4];
в
четвертой строке элементов нет.
Проанализировав
полученные индексы, можно определить,
что для элементов, расположенных выше
главной диагонали, номер столбца всегда
больше номера строки. Поэтому при
организации циклов для обработки этих
элементов нужно учитывать, что в первой
строке нужно рассматривать элементы,
начиная со второго столбца, во второй
строке – начиная с третьего столбца, в
третьей строке – начиная с четвертого
столбца. В общем случае элементы i-ой
строки нужно обрабатывать, начиная с
элемента из i+1
столбца и заканчивая элементом последнего
(N-го)
столбца.
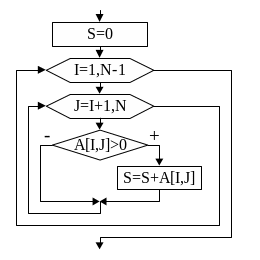
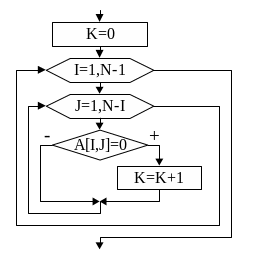
Для
примера рассмотрим алгоритм нахождения
суммы положительных элементов,
расположенных над главной диагональю
(рис.
48).
S:=0;
For
i :=1 to N-1 do
For
j:= I +1 to N do
If
A[I,j]>0 then
S:=S+A[I,j];
Рис.
48
Рассмотрим
элементы, расположенные под главной
диагональю матрицы. Для матрицы А
размером 4х4 эти элементы будут иметь
следующие индексы:
в
первой строке элементов нет;
во
второй строке: A[2,1],
в
третьей строке: A[3,1],
А[3,2];
в
четвертой строке: A[4,1],
A[4,2],
A[4,3].
Проанализировав
полученные индексы, можно определить,
что для элементов, расположенных ниже
главной диагонали, номер столбца всегда
меньше номера строки. Поэтому при
организации циклов для обработки этих
элементов нужно учитывать, что во второй
строке нужно рассматривать элементы
строки, заканчивая элементами из первого
столбца, в третьей строке – заканчивая
элементами из второго столбца, в четвертой
строке – заканчивая элементами из
третьего столбца. В общем случае элементы
i-ой
строки нужно обрабатывать, начиная с
элемента из первого столбца и заканчивая
рассмотрение элементами из i-1
столбца.
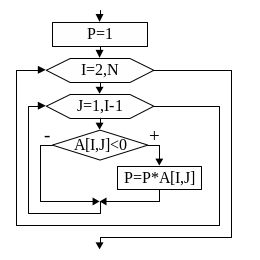
Для
примера рассмотрим алгоритм нахождения
произведения отрицательных элементов,
расположенных под главной диагональю
(рис.
49).
P:=1;
For
i :=2 to N do
For
j:= 1 to I-1 do
If
A[I,j]<0 then
P:=P+A[I,j];
Рис.
49
На
рис. 50 приведена схема расположения
элементов относительно побочной
диагонали.
Э
лементы,
Побочная диагональ(ПД)
р
асположенные
над ПД
-
пд
Пд
Пд
пд
Элементы,
расположенные под ПД
Рис.
50
Рассмотрим
элементы, расположенные над побочной
диагональю матрицы. Для матрицы А
размером 4х4 эти элементы будут иметь
следующие индексы:
в
первой строке: A[1,1],
A[1,2],
A[1,3];
во
второй строке: A[2,1],
A[2,2];
в
третьей строке: A[3,1];
в
четвертой строке элементов нет.
В
общем случае элементы i-ой
строки нужно обрабатывать, начиная с
элемента первого столбца и заканчивая
элементом из N-i
столбца.
Для
примера рассмотрим алгоритм нахождения
количества нулевых элементов, расположенных
над побочной диагональю (рис.
51).
K:=0;
For
i :=1 to N-1 do
For
j:= 1 to N-i do
If
A[I,j]=0 then
K:=K+1;
Рис.51
Теперь
рассмотрим элементы, расположенные под
побочной диагональю матрицы. Для матрицы
А размером 4х4 эти элементы будут иметь
следующие индексы:
в
первой строке элементов нет;
во
второй строке: A[2,4],
в
третьей строке: A[3,3],
А[3,4];
в
четвертой строке: A[4,2],
A[4,3],
A[4,4].
В
общем случае элементы i-ой
строки нужно обрабатывать, начиная с
элемента из столбца под номером N+2-I
и заканчивая элементом из последнего
(N-го
столбца).
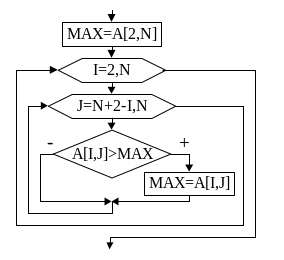
Для
примера рассмотрим алгоритм нахождения
максимального среди элементов,
расположенных под побочной диагональю
(рис. 52).
M
AX:=A[2,N];
{за начальное значения максимума берем
любой элемент, расположенный под побочной
диагональю}
For i :=2 to N do
For
j:= N+2-i to N do
If
A[I,j]>MAX then
MAX:=A[I,j];
Рис. 52
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Дана квадратная матрица размером nxn. Найти минимальный элемент среди элементов, расположенных ниже главной диагонали, найти максимальный элемент, среди элементов расположенных выше побочной диагонали. Найденные минимальный и максимальный элементы поменять местами и вывести их индексы.
// main_secondary_diagonal.cpp: определяет точку входа для консольного приложения.
#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;
int main(int argc, char* argv[])
{
srand(time(NULL));
int size_array; // размер квадратной матрицы
setlocale(LC_ALL, "rus");
cout << "Введите размер квадратной матрицы: ";
cin >> size_array;
// динамическое создание двумерного массива
int **arrayPtr = new int* [size_array];
for (int count = 0; count < size_array; count++)
arrayPtr[count] = new int [size_array];
for (int counter_rows = 0; counter_rows < size_array; counter_rows++)
{
for (int counter_columns = 0; counter_columns < size_array; counter_columns++)
{
arrayPtr[counter_rows][counter_columns] = rand() % 100; // заполнение массива случайными числами
cout << setw(2) << arrayPtr[counter_rows][counter_columns] << " "; // вывод на экран двумерного массива
}
cout << endl;
}
cout << endl;
int min = arrayPtr[1][0], // минимальный елемент массива, ниже главной диагонали
row_min = 1, // номер строки минимального элемента
column_min = 0; // номер столбца минимального элемента
// поиск минимального элемента в массиве, ниже главной диагонали
for (int counter_rows = 1; counter_rows < size_array; counter_rows++)
{
for (int counter_columns = 0; counter_columns < counter_rows ; counter_columns++)
{
if ( arrayPtr[counter_rows][counter_columns] < min )
{
min = arrayPtr[counter_rows][counter_columns];
row_min = counter_rows;
column_min = counter_columns;
}
}
}
cout << "min" << "[" << (row_min + 1) << "][" << (column_min + 1) << "]" << " = " << min << endl;
int max = arrayPtr[0][0], // максимальный элемнет массива, выше побочной диагонали
row_max = 0, // номер строки максимального элемента
column_max = 0; // номер столбца максимального элемента
for (int counter_rows = 0; counter_rows < size_array - 1; counter_rows++)
{
for (int counter_columns = 0; counter_columns < (size_array - counter_rows - 1); counter_columns++)
{
if ( arrayPtr[counter_rows][counter_columns] > max )
{
max = arrayPtr[counter_rows][counter_columns];
row_max = counter_rows;
column_max = counter_columns;
}
}
}
cout << "max" << "[" << (row_max + 1) << "][" << (column_max + 1) << "]" << " = " << max << endl;
//////////////////перестановка элементов////////////////////////////////////////////////
arrayPtr[row_min][column_min] = max;
arrayPtr[row_max][column_max] = min;
////////////////////////////////////////////////////////////////////////////////////////
cout << "nМассив после перестановки максимального и минимального элементов:n";
for (int counter_rows = 0; counter_rows < size_array; counter_rows++)
{
for (int counter_columns = 0; counter_columns < size_array; counter_columns++)
{
cout << setw(2) << arrayPtr[counter_rows][counter_columns] << " "; // вывод на экран двумерного массива
}
cout << endl;
}
cout << endl;
cout << "min" << "[" << (row_max + 1) << "][" << (column_max + 1) << "]" << " = " << min << endl;
cout << "max" << "[" << (row_min + 1) << "][" << (column_min + 1) << "]" << " = " << max << endl;
// удаление двумерного динамического массива
for (int count = 0; count < size_array; count++)
delete []arrayPtr[count];
system("pause");
return 0;
}
Результат работы программы показан ниже:
На занятии будет рассмотрен двумерный массив в Pascal и примеры работы с ним. Кроме того, предстоит знакомство с понятиями побочная диагональ матрицы в Паскаль и главная диагональ
Содержание:
- Двумерный массив в Pascal
- Описание, ввод и вывод элементов двумерного массива
- Главная и побочная диагональ при работе с двумерными матрицами в Pascal
Матрица или двумерный массив – это прямоугольная таблица чисел (или других элементов одного типа). Каждый элемент матрицы имеет два индекса (номер строки и номер столбца).
Исходные данные для решения многих задач можно представить в табличной форме:
Таблица результатов производственной деятельности нескольких филиалов фирмы может быть представлена так:
zavod1: array [1..4] of integer; zavod2: array [1..4] of integer; zavod3: array [1..4] of integer;
Или в виде двумерного массива так:
Объявление двумерного массива:
var A: array[1..3,1..4] of integer; begin {...}
begin var a := new integer[3,4]; {...} end.
Описание, ввод и вывод элементов двумерного массива
Варианты описания двумерного массива (традиционный pascal)
- Описание массива в разделе переменных:
- Описание массива через раздел type:
const N = 3; M = 4; var A: array[1..N,1..M] of integer;
const M=10; N=5; type matrix=array [1..M, 1..N] of integer; var A: matrix;
Ввод двумерного массива m x n с клавиатуры:
for i:=1 to N do for j:=1 to M do begin write('A[',i,',',j,']='); read ( A[i,j] ); end;
for var i:=0 to a.RowCount-1 do for var j:=0 to a.ColCount-1 do a[i,j]:=readinteger;
Заполнение случайными числами:
var a := MatrRandomInteger(3,4,0,10); // целые числа в диапазоне от 0 до 10 var a1 := MatrRandomReal(3,4,1,9) // веществ. числа в диапазоне от 1 до 9
«Красивый» вывод элементов двумерного массива m x n:
Следующий фрагмент программы выводит на экран значения элементов массива по строкам:
1 2 3 4 5 |
for i:=1 to N do begin for j:=1 to M do write ( A[i,j]:5 ); writeln; end; |
1 2 3 4 5 6 |
begin var a := MatrRandomInteger(3,4,0,10); var a1 := MatrRandomReal(3,4,1,9); a.Println; a1.Println(6,1) // 6 позиций всего на вывод, 1 знак после десят. запятой end. |
Результат:
8 2 1 3 5 8 0 8 6 3 9 3 3.3 4.7 3.7 5.4 2.9 1.7 2.3 4.0 8.3 3.7 8.4 1.4
Рассмотрим следующую задачу: Получены значения температуры воздуха за 4 дня с трех метеостанций, расположенных в разных регионах страны:
| Номер станции | 1-й день | 2-й день | 3-й день | 4-й день |
|---|---|---|---|---|
| 1 | -8 | -14 | -19 | -18 |
| 2 | 25 | 28 | 26 | 20 |
| 3 | 11 | 18 | 20 | 25 |
Т.е. запись показаний в двумерном массиве выглядела бы так:
| t[1,1]:=-8; | t[1,2]:=-14; | t[1,3]:=-19; | t[1,4]:=-18; |
| t[2,1]:=25; | t[2,2]:=28; | t[2,3]:=26; | t[2,4]:=20; |
| t[3,1]:=11; | t[3,2]:=18; | t[3,3]:=20; | t[3,4]:=25; |
Или в pascalabc.NET:
var t := Matr(3,4,-8,-14,-19,-18,25,28,26,20,11,18,20,25); t.Println;
Объявление двумерного массива:
var t: array [1..3, 1..4] of integer;
Задание array 1: Необходимо:
- Распечатать температуру на 2-й метеостанции за 4-й день и на 3-й метеостанции за 1-й день.
- Распечатать показания термометров всех метеостанций за 2-й день.
- Определить среднюю температуру на 3-й метеостанции.
- Распечатать, в какие дни и на каких метеостанциях температура была в диапазоне 24-26 градусов тепла.
Дополните код:
Показать решение:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
var t: array [1..3, 1..4] of integer; s,i,j:integer; begin t[1,1]:=-8; t[1,2]:=-14; t[1,3]:=-19; t[1,4]:=-18; t[2,1]:=25; t[2,2]:=28; t[2,3]:=26; t[2,4]:=20; t[3,1]:=11; t[3,2]:=18; t[3,3]:=20; t[3,4]:=25; {1. Распечатать показания термометров на 2-й метеостанции за 4-й день и на 3-й метеостанции за 1-й день} writeln('1-е задание: ',t[2,4] , ' и ',t[...,...]); {2. Показания термометров всех метеостанций за 2-й день} for i:=1 to ... do writeln ('2-е задание: ',t[...,...]); {3. Определим среднее значение температуры на 3-й метеостанции:} i:=3; s:=0; for j:=1 to 4 do s:=...; {сумматор} writeln('3-е задание: ', s/4); {распечатаем всю таблицу} for i:=1 to 3 do for j:=1 to 4 do writeln(t[i,j]); {4. Распечатаем станции и дни с температурой 24-26 гр} writeln('4-е задание: '); for i:=1 to 3 do for ... ... do if (...) and (...) then writeln('станция ', i, ' день ', j) end. |
Самостоятельно подумайте, как находится сумма элементов массива pascal.
Задание array 2. Найти сумму элементов массива (прямоугольной таблицы) размером [m x n]
Задание array 4.
Найти сумму всех элементов массива (переменная sum) 5 x 4, а также сумму элементов, составляющих столбцы таблицы (двумерного массива). Для хранения сумм столбцов чисел использовать одномерный массив (s). Дополните код.
Показать решение:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
const m = 5; n = 4; var a: array[1..m,1..n] of byte; s: array[1..n] of byte; i,j, sum: byte; begin randomize; for i := 1 to m do begin for j := 1 to n do begin ... {инициализация элементов массива случайными числами} ... {вывод элементов массива} end; writeln end; writeln ('------------'); {для оформления} {обнуление значений массива суммы s[]:} ... {поиск сумм элементов по столбцам:} for i := 1 to n do begin for j := 1 to m do begin s[i]:=...; end; write(...) ; end; {поиск общей суммы:} sum:=0; ... {вычисление суммы элементов массива значений сумм по столбцам:} for ... ... write (' | sum = ', sum); readln end. |
Задание array 4_1.
Найти сумму элементов двумерного массива [m x n] по строкам:
2 8 1 9 : sum = 20 3 1 7 2 : sum = 13 4 5 6 2 : sum = 17
Методы матриц для работы со строками и столбцами:
begin var a := MatrRandomInteger(3,4); a.Println; a.Row(0).Sum.Println(); a.Row(1).Average.Println; a.Row(2).Product.Println; a.Col(0).Min.Println; a.Col(1).Max.Println; end.
Результат:
86 62 80 33 51 4 36 65 78 30 5 16 261 39 187200 51 62
Главная и побочная диагональ при работе с двумерными матрицами в Pascal
Главная диагональ квадратной матрицы n x n (т.е. той, у которой количество строк равно количеству столбцов) проходит с верхнего левого угла матрицы (элемент 1,1) до правого нижнего угла матрицы (элемент n,n).
Побочная диагональ квадратной матрицы n x n проходит с нижнего левого угла матрицы (элемент n,1) до правого верхнего угла матрицы (элемент 1,n).
Формулу поиска элементов диагоналей проще всего искать, нарисовав элементы матрицы:
Если индексы начинаются с единицы (традиционный Паскаль):
| 1,1 | 1,2 | 1,3 | 1,4 |
| 2,1 | 2,2 | 2,3 | 2,4 |
| 3,1 | 3,2 | 3,3 | 3,4 |
| 4,1 | 4,2 | 4,3 | 4,4 |
Если индексы начинаются с нуля (pascalAbc.NET):
| 0,0 | 0,1 | 0,2 | 0,3 |
| 1,0 | 1,1 | 1,2 | 1,3 |
| 2,0 | 2,1 | 2,2 | 2,3 |
| 3,0 | 3,1 | 3,2 | 3,3 |
Учитывая, что первая цифра в программе будет соответствовать счетчику i, а вторая — счетчику j, то из таблицы можно вывести формулы:
Главная диагональ матрицы в Паскаль имеет формулу:
i=j
Побочная диагональ матрицы в Паскале традиционном имеет формулу:
n=i+j-1 (или j=n-i+1)
где n — размерность квадратной матрицы
Побочная диагональ матрицы в pascalAbc.Net имеет формулу:
n=i+j+1
где n — размерность квадратной матрицы
Пример: Вывести на экран сначала главную диагональ квадратной матрицы из N строк и N столбцов, а затем ее побочную диагональ.
Решение:
Пример: Заменить элементы главной и побочной диагонали квадратной матрицы нулями
Показать решение:
Паскаль:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
var i,j,n:integer; a: array[1..100,1..100]of integer; begin randomize; writeln ('введите размерность матрицы:'); readln(n); for i:=1 to n do begin for j:=1 to n do begin a[i,j]:=random(10); write(a[i,j]:3); end; writeln; end; writeln; for i:=1 to n do begin for j:=1 to n do begin if (i=j) or (n=i+j-1) then a[i,j]:=0; write(a[i,j]:3) end; writeln; end; end. |
PascalAbc.Net
1 2 3 4 5 6 7 8 9 10 11 12 |
begin var n := readinteger('введите размерность матрицы:'); var a := matrRandomInteger(n, n, -10, 10); a.Println(6); for var i := 0 to n - 1 do begin a[i, i] := 0; a[i, n - i - 1] := 0; end; writeln(); a.Println(6); end. |
Задание array 5:
Найти отдельно сумму элементов главной и побочной диагонали квадратной матрицы
1 7 3 7 2 1 8 3 5 7 6 4 8 2 3 1 ------- sum1 = 9 sum2 = 30
Пример:
Дана матрица 5х5. Найти сумму элементов, стоящих на двух соседних диагоналях с главной и параллельных ей.
Для решения задачи воспользуйтесь таблицей
Показать решение:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
var A:array[1..5,1..5] of integer; i,j:integer; sum,sum1,sum2:integer; begin randomize; for i:=1 to 5 do for j:=1 to 5 do A[i,j]:=random(10); write ('Исходный массив A: '); for i:=1 to 5 do begin writeln; for j:=1 to 5 do write (A[i,j]:2,' '); end; sum1:=0; for i:=1 to 5 do for j:=1 to 5 do if (i-j=1) then sum1:=sum1+A[i,j]; sum2:=0; for i:=1 to 5 do for j:=1 to 5 do if (j-i=1) then sum2:=sum2+A[i,j]; sum:=sum1+sum2; writeln; writeln('Сумма = ',sum); end. |
Задание array 6: Сформировать матрицу размерностью n. Вывести ее на экран. Затем преобразовать ее, заменив необходимые элементы на 0:

Задание array 7: Сформировать матрицу размерностью n. Вывести ее на экран. Затем преобразовать ее, заменив необходимые элементы на 0:

Задание array 8: Сформировать матрицу размерностью n. Вывести ее на экран. Затем преобразовать ее, заменив необходимые элементы на 0:

Задание array 9: Составить программу, позволяющую с помощью датчика случайных чисел сформировать матрицу размерностью N. Определить:
Рассмотрим еще один пример работы с двумерным массивом.
Пример: В двумерном массиве размером N х M определить среднее значение элементов. Найти индекс элемента массива, наиболее близкого к среднему значению.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
var index1,index2,i,j,N,M:integer; s,min,f:real; a:array[1..300,1..300] of real; begin N:=10; M:=5; for i:=1 to N do begin for j:=1 to M do begin a[i,j]:=random(20); s:=s+a[i,j]; write(a[i,j]:3); end; writeln; end; f:=s/(N*M); writeln('srednee znachenie ',f); min:=abs(a[1,1]-f); for i:=1 to N do begin for j:=1 to M do begin if abs(a[i,j]-f)<min then begin min:=abs(a[i,j]-f); index1:=i; index2:=j; end; end; end; writeln('naibolee blizkiy ',index1,' ',index2); end. |
Потренируйтесь в решении задач по теме, щелкнув по пиктограмме:


 Сообщение было отмечено Памирыч как решение
Сообщение было отмечено Памирыч как решение