Основные операции над матрицами (сложение, умножение, транспонирование) и их свойства.
В этой теме будут рассмотрены такие операции, как сложение и вычитание матриц, умножение матрицы на число, умножение матрицы на матрицу, транспонирование матрицы. Все обозначения, которые используются на данной странице, взяты из предыдущей темы «Матрицы. Виды матриц. Основные термины».
Содержание темы:
- Сложение и вычитание матриц.
- Умножение матрицы на число.
- Произведение двух матриц.
- Транспонированная матрица.
- Некоторые свойства операций над матрицами.
- Возведение матрицы в степень.
Сложение и вычитание матриц.
Суммой $A+B$ матриц $A_{mtimes n}=(a_{ij})$ и $B_{mtimes n}=(b_{ij})$ называется матрица $C_{mtimes n}=(c_{ij})$, где $c_{ij}=a_{ij}+b_{ij}$ для всех $i=overline{1,m}$ и $j=overline{1,n}$.
Аналогичное определение вводят и для разности матриц:
Разностью $A-B$ матриц $A_{mtimes n}=(a_{ij})$ и $B_{mtimes n}=(b_{ij})$ называется матрица $C_{mtimes n}=(c_{ij})$, где $c_{ij}=a_{ij}-b_{ij}$ для всех $i=overline{1,m}$ и $j=overline{1,n}$.
Пояснение к записи $i=overline{1,m}$: показатьскрыть
Стоит обратить внимание, что операции сложения и вычитания определены только для матриц одинакового размера. Вообще, сложение и вычитание матриц – операции, ясные интуитивно, ибо означают они, по сути, всего лишь суммирование или вычитание соответствующих элементов.
Пример №1
Заданы три матрицы:
$$
A=left(begin{array} {ccc} -1 & -2 & 1 \
5 & 9 & -8
end{array} right);;
B=left(begin{array} {ccc} 10 & -25 & 98 \
3 & 0 & -14
end{array} right); ;; F=left(begin{array} {cc} 1 & 0 \
-5 & 4
end{array} right).
$$
Можно ли найти матрицу $A+F$? Найти матрицы $C$ и $D$, если $C=A+B$ и $D=A-B$.
Решение
Матрица $A$ содержит 2 строки и 3 столбца (иными словами – размер матрицы $A$ равен $2times 3$), а матрица $F$ содержит 2 строки и 2 столбца. Размеры матрицы $A$ и $F$ не совпадают, поэтому сложить их мы не можем, т.е. операция $A+F$ для данных матриц не определена.
Размеры матриц $A$ и $B$ совпадают, т.е. данные матрицы содержат равное количество строк и столбцов, поэтому к ним применима операция сложения.
$$
C=A+B=left(begin{array} {ccc}
-1 & -2 & 1 \
5 & 9 & -8
end{array} right)+
left(begin{array} {ccc}
10 & -25 & 98 \
3 & 0 & -14
end{array} right)=\=
left(begin{array} {ccc}
-1+10 & -2+(-25) & 1+98 \
5+3 & 9+0 & -8+(-14)
end{array} right)=
left(begin{array} {ccc}
9 & -27 & 99 \
8 & 9 & -22
end{array} right)
$$
Найдем матрицу $D=A-B$:
$$
D=A-B=left(begin{array} {ccc}
-1 & -2 & 1 \
5 & 9 & -8
end{array} right)-
left(begin{array} {ccc}
10 & -25 & 98 \
3 & 0 & -14
end{array} right)=\=
left(begin{array} {ccc}
-1-10 & -2-(-25) & 1-98 \
5-3 & 9-0 & -8-(-14)
end{array} right)=
left(begin{array} {ccc}
-11 & 23 & -97 \
2 & 9 & 6
end{array} right)
$$
Ответ: $C=left(begin{array} {ccc}
9 & -27 & 99 \
8 & 9 & -22
end{array} right)$, $D=left(begin{array} {ccc}
-11 & 23 & -97 \
2 & 9 & 6
end{array} right)$.
Умножение матрицы на число.
Произведением матрицы $A_{mtimes n}=(a_{ij})$ на число $alpha$ называется матрица $B_{mtimes n}=(b_{ij})$, где $b_{ij}=alphacdot a_{ij}$ для всех $i=overline{1,m}$ и $j=overline{1,n}$.
Попросту говоря, умножить матрицу на некое число – означает умножить каждый элемент заданной матрицы на это число.
Пример №2
Задана матрица: $
A=left(begin{array} {ccc} -1 & -2 & 7 \ 4 & 9 & 0 end{array} right)$. Найти матрицы $3cdot A$, $-5cdot A$ и $-A$.
Решение
$$
3cdot A=3cdot left(begin{array} {ccc} -1 & -2 & 7 \ 4 & 9 & 0 end{array} right)
=left(begin{array} {ccc} 3cdot(-1) & 3cdot(-2) & 3cdot 7 \ 3cdot 4 & 3cdot 9 & 3cdot 0 end{array} right)=
left(begin{array} {ccc} -3 & -6 & 21 \ 12& 27 & 0 end{array} right).\
-5cdot A=-5cdot left(begin{array} {ccc} -1 & -2 & 7 \ 4 & 9 & 0 end{array} right)
=left(begin{array} {ccc} -5cdot(-1) & -5cdot(-2) & -5cdot 7 \ -5cdot 4 & -5cdot 9 & -5cdot 0 end{array} right)=
left(begin{array} {ccc} 5 & 10 & -35 \ -20 & -45 & 0 end{array} right).
$$
Запись $-A$ есть сокращенная запись для $-1cdot A$. Т.е., чтобы найти $-A$ нужно все элементы матрицы $A$ умножить на (-1). По сути, это означает, что знак всех элементов матрицы $A$ изменится на противоположный:
$$
-A=-1cdot A=-1cdot left(begin{array} {ccc} -1 & -2 & 7 \ 4 & 9 & 0 end{array} right)=
left(begin{array} {ccc} 1 & 2 & -7 \ -4 & -9 & 0 end{array} right)
$$
Ответ:
$3cdot A=left(begin{array} {ccc} -3 & -6 & 21 \ 12& 27 & 0 end{array} right)$;
$-5cdot A=left(begin{array} {ccc} 5 & 10 & -35 \ -20 & -45 & 0 end{array} right)$;
$-A=left(begin{array} {ccc} 1 & 2 & -7 \ -4 & -9 & 0 end{array} right)$.
Произведение двух матриц.
Определение этой операции громоздко и, на первый взгляд, непонятно. Поэтому сначала укажу общее определение, а потом подробно разберем, что оно означает и как с ним работать.
Произведением матрицы $A_{mtimes n}=(a_{ij})$ на матрицу $B_{ntimes k}=(b_{ij})$ называется матрица $C_{mtimes k}=(c_{ij})$, для которой каждый элемент $c_{ij}$ равен сумме произведений соответствующих элементов i-й строки матрицы $A$ на элементы j-го столбца матрицы $B$:
$$c_{ij}=sumlimits_{p=1}^{n}a_{ip}b_{pj}, ;; i=overline{1,m}, j=overline{1,n}.$$
Пошагово умножение матриц разберем на примере. Однако сразу стоит обратить внимание, что перемножать можно не все матрицы. Если мы хотим умножить матрицу $A$ на матрицу $B$, то сперва нужно убедиться, что количество столбцов матрицы $A$ равно количеству строк матрицы $B$ (такие матрицы часто называют согласованными). Например, матрицу $A_{5times 4}$ (матрица содержит 5 строк и 4 столбца), нельзя умножать на матрицу $F_{9times 8}$ (9 строк и 8 столбцов), так как количество столбцов матрицы $A$ не равно количеству строк матрицы $F$, т.е. $4neq 9$. А вот умножить матрицу $A_{5times 4}$ на матрицу $B_{4times 9}$ можно, так как количество столбцов матрицы $A$ равно количеству строк матрицы $B$. При этом результатом умножения матриц $A_{5times 4}$ и $B_{4times 9}$ будет матрица $C_{5times 9}$, содержащая 5 строк и 9 столбцов:
Пример №3
Заданы матрицы:
$
A=left(begin{array} {cccc}
-1 & 2 & -3 & 0 \
5 & 4 & -2 & 1 \
-8 & 11 & -10 & -5
end{array} right)$ и
$
B=left(begin{array} {cc}
-9 & 3 \
6 & 20 \
7 & 0 \
12 & -4
end{array} right)$. Найти матрицу $C=Acdot B$.
Решение
Для начала сразу определим размер матрицы $C$. Так как матрица $A$ имеет размер $3times 4$, а матрица $B$ имеет размер $4times 2$, то размер матрицы $C$ таков: $3times 2$:
Итак, в результате произведения матриц $A$ и $B$ мы должны получить матрицу $C$, состоящую из трёх строк и двух столбцов:
$
C=left(begin{array} {cc}
c_{11} & c_{12} \
c_{21} & c_{22} \
c_{31} & c_{32}
end{array} right)$. Если обозначения элементов вызывают вопросы, то можно глянуть предыдущую тему: «Матрицы. Виды матриц. Основные термины», в начале которой поясняется обозначение элементов матрицы. Наша цель: найти значения всех элементов матрицы $C$.
Начнем с элемента $c_{11}$. Чтобы получить элемент $c_{11}$ нужно найти сумму произведений элементов первой строки матрицы $A$ и первого столбца матрицы $B$:
Чтобы найти сам элемент $c_{11}$ нужно перемножить элементы первой строки матрицы $A$ на соответствующие элементы первого столбца матрицы $B$, т.е. первый элемент на первый, второй на второй, третий на третий, четвертый на четвертый. Полученные результаты суммируем:
$$
c_{11}=-1cdot (-9)+2cdot 6+(-3)cdot 7 + 0cdot 12=0.
$$
Продолжим решение и найдем $c_{12}$. Для этого придётся перемножить элементы первой строки матрицы $A$ и второго столбца матрицы $B$:
Аналогично предыдущему, имеем:
$$
c_{12}=-1cdot 3+2cdot 20+(-3)cdot 0 + 0cdot (-4)=37.
$$
Все элементы первой строки матрицы $C$ найдены. Переходим ко второй строке, которую начинает элемент $c_{21}$. Чтобы его найти придётся перемножить элементы второй строки матрицы $A$ и первого столбца матрицы $B$:
$$
c_{21}=5cdot (-9)+4cdot 6+(-2)cdot 7 + 1cdot 12=-23.
$$
Следующий элемент $c_{22}$ находим, перемножая элементы второй строки матрицы $A$ на соответствующие элементы второго столбца матрицы $B$:
$$
c_{22}=5cdot 3+4cdot 20+(-2)cdot 0 + 1cdot (-4)=91.
$$
Чтобы найти $c_{31}$ перемножим элементы третьей строки матрицы $A$ на элементы первого столбца матрицы $B$:
$$
c_{31}=-8cdot (-9)+11cdot 6+(-10)cdot 7 + (-5)cdot 12=8.
$$
И, наконец, для нахождения элемента $c_{32}$ придется перемножить элементы третьей строки матрицы $A$ на соответствующие элементы второго столбца матрицы $B$:
$$
c_{32}=-8cdot 3+11cdot 20+(-10)cdot 0 + (-5)cdot (-4)=216.
$$
Все элементы матрицы $C$ найдены, осталось лишь записать, что $C=left(begin{array} {cc}
0 & 37 \
-23 & 91 \
8 & 216
end{array} right)$. Или, если уж писать полностью:
$$
C=Acdot B =left(begin{array} {cccc}
-1 & 2 & -3 & 0 \
5 & 4 & -2 & 1 \
-8 & 11 & -10 & -5
end{array} right)cdot left(begin{array} {cc}
-9 & 3 \
6 & 20 \
7 & 0 \
12 & -4
end{array} right)=left(begin{array} {cc}
0 & 37 \
-23 & 91 \
8 & 216
end{array} right).
$$
Ответ: $C=left(begin{array} {cc}
0 & 37 \
-23 & 91 \
8 & 216
end{array} right)$.
Кстати сказать, зачастую нет резона расписывать подробно нахождение каждого элемента матрицы-результата. Для матриц, размер которых невелик, можно поступать и так:
$$
left(begin{array} {cc}
6 & 3 \
-17 & -2
end{array}right)cdot
left(begin{array} {cc}
4 & 9 \
-6 & 90
end{array} right)
=left(begin{array} {cc}
6cdot{4}+3cdot(-6) & 6cdot{9}+3cdot{90} \
-17cdot{4}+(-2)cdot(-6) & -17cdot{9}+(-2)cdot{90}
end{array} right)
=left(begin{array} {cc}
6 & 324 \
-56 & -333
end{array} right)
$$
Стоит также обратить внимание, что умножение матриц некоммутативно. Это означает, что в общем случае $Acdot Bneq Bcdot A$. Лишь для некоторых типов матриц, которые именуют перестановочными (или коммутирующими), верно равенство $Acdot B=Bcdot A$. Именно исходя из некоммутативности умножения, требуется указывать как именно мы домножаем выражение на ту или иную матрицу: справа или слева. Например, фраза «домножим обе части равенства $3E-F=Y$ на матрицу $A$ справа» означает, что требуется получить такое равенство: $(3E-F)cdot A=Ycdot A$.
Транспонированная матрица.
Транспонированной по отношению к матрице $A_{mtimes n}=(a_{ij})$ называется матрица $A_{ntimes m}^{T}=(a_{ij}^{T})$, для элементов которой $a_{ij}^{T}=a_{ji}$.
Попросту говоря, для того, чтобы получить транспонированную матрицу $A^T$, нужно в исходной матрице $A$ заменить столбцы соответствующими строками по такому принципу: была первая строка – станет первый столбец; была вторая строка – станет второй столбец; была третья строка – станет третий столбец и так далее. Например, найдем транспонированную матрицу к матрице $A_{3times 5}$:
Соответственно, если исходная матрица имела размер $3times 5$, то транспонированная матрица имеет размер $5times 3$.
Некоторые свойства операций над матрицами.
Здесь предполагается, что $alpha$, $beta$ – некоторые числа, а $A$, $B$, $C$ – матрицы. Для первых четырех свойств я указал названия, остальные можно назвать по аналогии с первыми четырьмя.
- $A+B=B+A$ (коммутативность сложения)
- $A+(B+C)=(A+B)+C$ (ассоциативность сложения)
- $(alpha+beta)cdot A=alpha A+beta A$ (дистрибутивность умножения на матрицу относительно сложения чисел)
- $alphacdot(A+B)=alpha A+alpha B$ (дистрибутивность умножения на число относительно сложения матриц)
- $A(BC)=(AB)C$
- $(alphabeta)A=alpha(beta A)$
- $Acdot (B+C)=AB+AC$, $(B+C)cdot A=BA+CA$.
- $Acdot E=A$, $Ecdot A=A$, где $E$ – единичная матрица соответствующего порядка.
- $Acdot O=O$, $Ocdot A=O$, где $O$ – нулевая матрица соответствующего размера.
- $left(A^T right)^T=A$
- $(A+B)^T=A^T+B^T$
- $(AB)^T=B^Tcdot A^T$
- $left(alpha A right)^T=alpha A^T$
В следующей части будет рассмотрена операция возведения матрицы в целую неотрицательную степень, а также решены примеры, в которых потребуется выполнение нескольких операций над матрицами.
Какой из векторов коллинеарен вектору -3;5
(1,5, -2.5)
Укажите каноническое уравнение прямой, проходящей через точки (2;-3;1) и (5;2;3).
х- 2 = y+ 3 z- 1
3 5 = 2
Вычислить произведение матриц:
A = 2 3 4 -5
1 2 -3 4
-1 -2 3 1
B = 3 2 1
4 1 -1
1 3 2
2 0 1
Ответ
12 19 2
16 -5 -3
-6 5 8
Какая из дробей является смешанной периодической дробью?
-3,25(1)
Вычислить определитель
-83
Векторы а и b взаимно перпендикулярны, причем |a|=6, |b|=8, тогда |a+b| будет равен …
14
Найти элемент c32 матрицы АВ, если:
A = ; B =
Решение. Элемент с32 равен сумме произведений элементов третьей строки матрицы А на соответствующие элементы второго столбца матрицы В, т. е.
c32 = (–1)•2 + (–5)•(–1) + 3•(–3) + 11•5 = 49.
49
Найдите -27 (КОРЕНЬ3)
-3
Вычислить определитель матрицы
1 1 1
2 -3 1
4 -1 -5
Ответ 40
Какое из чисел является иррациональным?
3,141592…
Сколько целых чисел удовлетворяет неравенству -3 < x < 12,5
15
Найти проекцию вектора b на ось вектора а, если а=(1,1,1), b=(2,3,1).
2(корень 3) 2√3
Вычислить определитель матрицы:
1 8
2 9
= 1•9 — 2•8 = 9 — 16 = -7
Определитель невырожденной матрицы умножается на 8, если
одна строка умножается на 2, другая на 4
какая-либо строка умножается на 8
Найдите ранг матрицы
A = 1-257301
21570-34
3-110143-35
4210140-68
2
Вычислите
5 12/17
Содержание:
- Матрицы: основные определения и понятия
- Умножение матрицы на число
- Сложение и вычитание матриц
- Умножение матриц
- Транспонирование матрицы
- Минор и алгебраическое дополнение
- Вычисление определителя
- Нахождение обратной матрицы
- Нахождение ранга матрицы
Матрицы широко применяются в математике для
компактной записи СЛАУ или систем дифференциальных уравнений. Тогда количество
строк матрицы соответствует количеству уравнений системы, а количество столбцов равно количеству неизвестных. Матричный
аппарат позволяет свести решение громоздких СЛАУ к компактным
операциям над матрицами.
На практике, они позволяют не делать лишних операций и сократить время выполнения задач.
Поэтому, будущим специалистам очень важно понять теорию матриц и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по матрицам, прочитать
все определения и свойства. Список тем находится в правом меню.
Примеры по темам:
- Матрицы: основные определения и понятия
- Умножение матрицы на число
- Сложение и вычитание матриц
- Умножение матриц
- Транспонирование матрицы
- Минор и алгебраическое дополнение
- Вычисление определителя
- Нахождение обратной матрицы
- Нахождение ранга матрицы
Матрицы: основные определения и понятия
Теоретический материал по теме — основные определения и понятия матриц.
Пример
Задание. Чему равен элемент $ a_{23} $
матрицы $ A=left( begin{array}{rrr}{1} & {4} & {0} \ {-1} & {3} & {7}end{array}right) $ ?
Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:
Таким образом, $a_{23}=7$.
Ответ. $a_{23}=7$
Умножение матрицы на число
Теоретический материал по теме — умножение матрицы на число.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Пусть $A=left( begin{array}{r}{3} \ {-1}end{array}right)$ .
Найти матрицу 2$A$.
Решение. $2 A=2 cdot left( begin{array}{r}{3} \ {-1}end{array}right)=left( begin{array}{c}{2 cdot 3} \ {2 cdot(-1)}end{array}right)=left( begin{array}{r}{6} \ {-2}end{array}right)$
Ответ. $2 A=left( begin{array}{r}{6} \ {-2}end{array}right)$
Сложение и вычитание матриц
Теоретический материал по теме — сложение и вычитание матриц.
Пример
Задание. Найти $A+B$, если
$A=left( begin{array}{rrr}{1} & {-2} & {4} \ {2} & {0} & {-1}end{array}right)$,
$B=left( begin{array}{lll}{5} & {2} & {3} \ {4} & {6} & {2}end{array}right)$
Решение. $C=A+B=left( begin{array}{rrr}{1} & {-2} & {4} \ {2} & {0} & {-1}end{array}right)+left( begin{array}{lll}{5} & {2} & {3} \ {4} & {6} & {2}end{array}right)=$
$=left( begin{array}{rrr}{1+5} & {-2+2} & {4+3} \ {2+4} & {0+6} & {-1+2}end{array}right)=left( begin{array}{lll}{6} & {0} & {7} \ {6} & {6} & {1}end{array}right)$
Ответ. $C=left( begin{array}{lll}{6} & {0} & {7} \ {6} & {6} & {1}end{array}right)$
Пример
Задание. Найти матрицу $C=A-3 B$,
если $A=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right), B=left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)$
Решение. $C=A-3 B=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-3 cdot left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)=$
$left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-left( begin{array}{rr}{-3} & {3} \ {3} & {6} \ {0} & {0}end{array}right)=left( begin{array}{cc}{1-(-3)} & {2-3} \ {2-3} & {-1-6} \ {3-0} & {0-0}end{array}right)=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right)$
Ответ. $C=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right)$
Умножение матриц
Теоретический материал по теме — умножение матриц.
Пример
Задание. Вычислить $A B$ и $B A$,
если $A=left( begin{array}{rr}{1} & {-1} \ {2} & {0} \ {3} & {0}end{array}right), B=left( begin{array}{ll}{1} & {1} \ {2} & {0}end{array}right)$
Решение. Так как $A=A_{3 times 2}$ , а
$B=B_{2 times 2}$ , то произведение возможно и результатом операции умножения будет матрица
$C=C_{3 times 2}$ , а это матрица вида $C=left( begin{array}{cc}{c_{11}} & {c_{12}} \ {c_{21}} & {c_{22}} \ {c_{31}} & {c_{32}}end{array}right)$ .
Вычисли элементы матрицы $C$ :
$ c_{11}=a_{11} cdot b_{11}+a_{12} cdot b_{21}=1 cdot 1+(-1) cdot 2=-1 $
$ c_{12}=a_{11} cdot b_{12}+a_{12} cdot b_{22}=1 cdot 1+(-1) cdot 0=1 $
$ c_{21}=a_{21} cdot b_{11}+a_{22} cdot b_{21}=2 cdot 1+0 cdot 2=2 $
$ c_{22}=a_{21} cdot b_{12}+a_{22} cdot b_{22}=2 cdot 1+0 cdot 0=2 $
$ c_{31}=a_{31} cdot b_{11}+a_{32} cdot b_{21}=3 cdot 1+0 cdot 2=3 $
$ c_{31}=a_{31} cdot b_{12}+a_{32} cdot b_{22}=3 cdot 1+0 cdot 0=3 $
Итак, $C=A B=left( begin{array}{rl}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$ .
Выполним произведения в более компактном виде:
$=left( begin{array}{rrr}{1 cdot 1+(-1) cdot 2} & {1 cdot 1+(-1) cdot 0} \ {2 cdot 1+0 cdot 2} & {2 cdot 1+0 cdot 0} \ {3 cdot 1+0 cdot 2} & {3 cdot 1+0 cdot 0}end{array}right)=left( begin{array}{rr}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$
Найдем теперь произведение $D=B A=B_{2 times 2} cdot A_{3 times 2}$. Так как
количество столбцов матрицы $B$ (первый сомножитель) не совпадает с
количеством строк матрицы $A$ (второй сомножитель), то данное произведение
неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $A B=left( begin{array}{rr}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$ .
В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы
$B$ не совпадает с
количеством строк матрицы $A$ .
Транспонирование матрицы
Теоретический материал по теме — транспонирование матрицы.
Пример
Задание. Найти матрицу $A^{T}$, если
$A=left( begin{array}{rl}{1} & {0} \ {-2} & {3}end{array}right)$
Решение. $A^{T}=left( begin{array}{rr}{1} & {0} \ {-2} & {3}end{array}right)^{T}=left( begin{array}{rr}{1} & {-2} \ {0} & {3}end{array}right)$
Ответ. $A^{T}=left( begin{array}{rr}{1} & {-2} \ {0} & {3}end{array}right)$
Минор и алгебраическое дополнение
Теоретический материал по теме — минор и алгебраическое дополнение.
Пример
Задание. Найти минор
$M_{23}$ к элементу
$a_{23}$ определителя
$left| begin{array}{rrr}{1} & {2} & {-1} \ {1} & {0} & {3} \ {7} & {8} & {4}end{array}right|$ .
Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
тогда $M_{23}=left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Ответ. $M_{23}=left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Пример
Задание. Найти алгебраическое дополнение
$A_{23}$ к элементу
$a_{23}$ определителя
$left| begin{array}{rrr}{1} & {2} & {-1} \ {1} & {0} & {3} \ {7} & {8} & {4}end{array}right|$ .
Решение. $A_{23}=(-1)^{2+3} cdot M_{23}=(-1)^{5} cdot left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|=-left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Ответ. $A_{23}=-left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Вычисление определителя
Теоретический материал по теме — методы вычисления определителей.
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{cccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$
$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$
$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$
Ответ. $Delta=-80$
Нахождение обратной матрицы
Теоретический материал по теме — нахождение обратной матрицы.
Пример
Задание. Для матрицы $A=left( begin{array}{ll}{7} & {4} \ {5} & {3}end{array}right)$
найти обратную методом присоединенной матрицы.
Решение. Приписываем к заданной матрице
$A$ справа единичную матрицу второго порядка:
$Aleft|E=left( begin{array}{ll|ll}{7} & {4} & {1} & {0} \ {5} & {3} & {0} & {1}end{array}right)right.$
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):
$Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {5} & {3} & {0} & {1}end{array}right)right.$
От второй строки отнимаем две первых:
$Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {1} & {1} & {-2} & {3}end{array}right)right.$
Первую и вторую строки меняем местами:
$Aleft|E sim left( begin{array}{rr|r|rr}{1} & {1} & {-2} & {3} \ {2} & {1} & {1} & {-1}end{array}right)right.$
От второй строки отнимаем две первых:
$Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {0} & {-1} & {5} & {-7}end{array}right)right.$
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:
$Aleft|E sim left( begin{array}{rr|rr}{1} & {0} & {3} & {-4} \ {0} & {1} & {-5} & {7}end{array}right)right.$
Итак, слева получили единичную матрицу, а значит матрица, стоящая в
правой части (справа от вертикальной черты), является обратной к исходной.
Таким образом, получаем, что $A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right)$
Ответ. $A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right)$
Пример
Задание. Найти обратную матрицу для $A=left( begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right)$
Решение. Шаг 1. Находим определитель: $Delta=left| begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right|=2-1=1 neq 0$
Шаг 2. $A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Шаг 3. $A^{-1}=frac{1}{Delta} cdot A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Ответ. $A^{-1}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Пример
Задание. Найти обратную матрицу к матрице $A=left( begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right)$
Решение. Вычисляем определитель матрицы:
$Delta=left| begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right|=1 cdot(-1) cdot(-1)+2 cdot 3 cdot 2+0 cdot 1 cdot 1-$
$-1 cdot(-1) cdot 2-3 cdot 1 cdot 1-2 cdot 0 cdot(-1)=1+12+0+2-3+0=12 neq 0$
Так как определитель не равен нулю, то матрица имеет обратную.
Обратная матрица $A^{-1}$ к матрице
$A$ находится по формуле:
$A^{-1}=frac{1}{Delta} cdot widetilde{A}^{T}$
Найдем союзную матрицу $check{A}$ , для этого вычислим алгебраические
дополнения к элементам матрицы $A$ :
$A_{11}=(-1)^{1+1} left| begin{array}{rr}{-1} & {1} \ {3} & {-1}end{array}right|=(-1) cdot(-1)-3 cdot 1=1-3=-2$
$A_{12}=(-1)^{1+2} left| begin{array}{rr}{2} & {1} \ {1} & {-1}end{array}right|=-[2 cdot(-1)-1 cdot 1]=-(-2-1)=3$
$A_{13}=(-1)^{1+3} left| begin{array}{rr}{2} & {-1} \ {1} & {3}end{array}right|=2 cdot 3-1 cdot(-1)=6+1=7$
$A_{21}=(-1)^{2+1} left| begin{array}{rr}{0} & {2} \ {3} & {-1}end{array}right|=-[0 cdot(-1)-3 cdot 2]=-(0-6)=6$
$A_{22}=(-1)^{2+2} left| begin{array}{rr}{1} & {2} \ {1} & {-1}end{array}right|=1 cdot(-1)-1 cdot 2=-1-2=-3$
$A_{23}=(-1)^{2+3} left| begin{array}{cc}{1} & {0} \ {1} & {3}end{array}right|=-[1 cdot 3-1 cdot 0]=-(3-0)=-3$
$A_{31}=(-1)^{3+1} left| begin{array}{rr}{0} & {2} \ {-1} & {1}end{array}right|=0 cdot 1-(-1) cdot 2=0+2=2$
$A_{32}=(-1)^{3+2} left| begin{array}{cc}{1} & {2} \ {2} & {1}end{array}right|=-[1 cdot 1-2 cdot 2]=-(1-4)=3$
$A_{33}=(-1)^{3+3} left| begin{array}{rr}{1} & {0} \ {2} & {-1}end{array}right|=1 cdot(-1)-2 cdot 0=-1-0=-1$
Таким образом, $tilde{A}=left( begin{array}{rrr}{-2} & {3} & {7} \ {6} & {-3} & {-3} \ {2} & {3} & {-1}end{array}right)$
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
$widetilde{A}^{T}=left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Итак, $A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Ответ. $A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Нахождение ранга матрицы
Теоретический материал по теме — нахождение ранга матрицы.
Пример
Задание. Найти ранг матрицы $A=left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {10} & {18} & {40} & {17} \ {1} & {7} & {17} & {3}end{array}right)$
Решение. С помощью элементарных преобразований над ее строками приведем матрицу $A$ к
ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:
$A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {2} & {2} & {4} & {3} \ {1} & {7} & {17} & {3}end{array}right)$
От второй строки отнимаем четвертую строку, умноженную на 4; от третьей — две четвертых:
$A sim left( begin{array}{rrrr}{0} & {4} & {10} & {1} \ {0} & {-20} & {-50} & {-5} \ {0} & {-12} & {-30} & {-3} \ {1} & {7} & {17} & {3}end{array}right)$
Ко второй строке прибавим пять первых, к третьей — три третьих:
$A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right)$
Меняем местами первую и вторую строчки:
$A sim left( begin{array}{cccc}{0} & {0} & {0} & {0} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right)$
Далее четвертую и первую строки:
$A sim left( begin{array}{cccc}{1} & {7} & {17} & {3} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0}end{array}right) Rightarrow r a n g A=2$
Ответ. $operatorname{rang} A=2$
Пример
Задание. Найти ранг матрицы $A=left( begin{array}{rrrr}{1} & {2} & {-1} & {-2} \ {2} & {4} & {3} & {0} \ {-1} & {-2} & {6} & {6}end{array}right)$ ,
используя метод окаймления миноров.
Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам
матрицы $A$ . Рассмотрим, например, минор
$M_{1}=1 neq 0$ . расположенный в первой строке и первом
столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор
$M_{2}^{1}=left| begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right|=0$ ; рассмотрим еще один минор второго
порядка, для этого минор $M_{1}$ окаймляем при
помощи второй строки и третьего столбца, тогда имеем минор $M_{2}^{2}=left| begin{array}{rr}{1} & {-1} \ {2} & {3}end{array}right|=5 neq 0$ ,
то есть ранг матрицы не меньше двух. Далее рассматриваем миноры третьего порядка, которые окаймляют минор
$M_{2}^{2}$ . Таких миноров два: комбинация
третьей строки со вторым столбцом или с четвертым столбцом. Вычисляем эти миноры:
$M_{3}^{1}=left| begin{array}{rrr}{1} & {2} & {-1} \ {2} & {4} & {3} \ {-1} & {-2} & {6}end{array}right|=0$
так как содержит два пропорциональных столбца (первый и второй); второй минор
$M_{3}^{2}=left| begin{array}{rrr}{1} & {-1} & {-2} \ {2} & {3} & {0} \ {-1} & {6} & {6}end{array}right|$
преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:
$M_{3}^{2}=left| begin{array}{rrr}{0} & {5} & {4} \ {0} & {15} & {12} \ {-1} & {6} & {6}end{array}right|=0$
И так как первая и вторая строки пропорциональны, то минор равен нулю.
Таким образом, все окаймляющие миноры третьего порядка равны нулю. А, значит, ранг матрицы $A$
равен двум: $operatorname{rang} A=2$
Ответ. $operatorname{rang} A=2$
Читать первую тему — основные определения и понятия матриц,
раздела матрицы.
Нами были рассмотрены действия сложения, вычитания и умножения матриц на число. Еще одним действием над ними является умножение. Выполняется оно сложнее, а само правило может показаться немного странным. При его выполнении важно уметь определять размер матриц. Это понятие было рассмотрено в теме «Что такое матрица».
Онлайн-калькулятор
Как умножать матрицы
Приступим к рассмотрению умножения матриц.
Нам известно, что складывать и вычитать можно матрицы, которые имеют одинаковый размер. С умножением дела обстоят немного сложнее.
Какие матрицы можно умножать
Матрицу P можно умножить на матрицу K только в том случае, если число столбцов матрицы P равняется числу строк матрицы K. Матрицы, для которых данное условие не выполняется, умножать нельзя.
Пример 1
Определим, можно ли умножить матрицу
K=(15271810)K=begin{pmatrix}15&27\18&10end{pmatrix} на матрицу L=(3516)L=begin{pmatrix}35\16end{pmatrix}.
Матрица KK состоит из 2 строк и 2 столбцов, а матрица LL — из 2 строк и 1 столбца. Число столбцов матрицы KK равно числу строк матрицы LL, значит, матрицу KK можно умножить на матрицу LL.
Пример 2
Переставим матрицы местами и определим, можно ли умножить матрицу
F=(3516)F=begin{pmatrix}35\16end{pmatrix} на матрицу C=(15271810)C=begin{pmatrix}15&27\18&10end{pmatrix}.
Матрица FF состоит из 2 строк и 1 столбца, а матрица CC — из 2 строк и 2 столбцов. Число столбцов матрицы FF не равно числу строк матрицы CC, значит, матрицу FF нельзя умножить на матрицу CC.
Произведение матрицы AA размера m×nmtimes n и матрицы BB размера n×kntimes k — это матрица CC размера m×kmtimes k, в которой элемент cijc_{ij} равен сумме произведений элементов ii строки матрицы AA на соответствующие элементы jj столбца матрицы B:cij=ai1b1j+ai2b2j+…+ainbnjB: c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+…+a_{in}b_{nj}.
Умножение матриц осуществляется путем умножения строки на столбец. Находятся произведения первого элемента строки и первого элемента столбца, второго элемента строки и второго элемента столбца и т.д. Затем полученные произведения суммируются.
Алгоритм нахождения произведения матриц
- определить размеры матриц;
- если число столбцов первой матрицы совпадает с числом строк второй матрицы, то выполнять умножение.
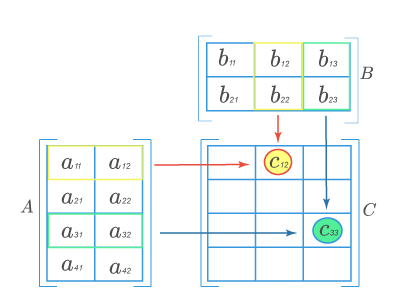
Рассмотрим пример умножения матрицы
A=(a11a12a21a22a31a32a41a42)A=begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}\a_{41}&a_{42}end{pmatrix}
на матрицу
B=(b11b12b13b21b22b23)B=begin{pmatrix}b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}end{pmatrix}.
Матрица AA состоит из 4 строк и 2 столбцов, а матрица BB — из 2 строк и 3 столбцов. Число столбцов матрицы AA равно числу строк матрицы BB, значит, можно найти произведение C=A⋅BC=Acdot B. Причем матрица CC будет иметь размер 4×34times 3. Найдем элементы c12c_{12} (выделен красными стрелками) и c33c_{33} (выделен синими стрелками):
Для того чтобы найти элемент c12c_{12} нужно перемножать соответствующие элементы 1 строки матрицы AA и 2 столбца матрицы B:c12=a11⋅b12+a12⋅b22B: c_{12}=a_{11}cdot b_{12}+a_{12}cdot b_{22}. Для того чтобы найти элемент c33c_{33} нужно перемножать соответствующие элементы 3 строки матрицы AA и 3 столбца матрицы BB: c33=a31⋅b13+a32⋅b23c_{33}=a_{31}cdot b_{13}+a_{32}cdot b_{23}. Так находят все элементы.
Таким образом, матрица CC может быть найдена следующим образом:
A⋅B=(a11a12a21a22a31a32a41a42)⋅(b11b12b13b21b22b23)=Acdot B=begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}\a_{41}&a_{42}end{pmatrix}cdot begin{pmatrix}b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}end{pmatrix}=
=(a11⋅b11+a12⋅b21a11⋅b12+a12⋅b22a11⋅b13+a12⋅b23a21⋅b11+a22⋅b21a21⋅b12+a22⋅b22a21⋅b13+a22⋅b23a31⋅b11+a32⋅b21a31⋅b12+a32⋅b22a31⋅b13+a32⋅b23a41⋅b11+a42⋅b21a41⋅b12+a42⋅b22a41⋅b13+a42⋅b23)=begin{pmatrix}a_{11}cdot b_{11}+a_{12}cdot b_{21}&a_{11}cdot b_{12}+a_{12}cdot b_{22}&a_{11}cdot b_{13}+a_{12}cdot b_{23}\a_{21}cdot b_{11}+a_{22}cdot b_{21}&a_{21}cdot b_{12}+a_{22}cdot b_{22}&a_{21}cdot b_{13}+a_{22}cdot b_{23}\a_{31}cdot b_{11}+a_{32}cdot b_{21}&a_{31}cdot b_{12}+a_{32}cdot b_{22}&a_{31}cdot b_{13}+a_{32}cdot b_{23}\a_{41}cdot b_{11}+a_{42}cdot b_{21}&a_{41}cdot b_{12}+a_{42}cdot b_{22}&a_{41}cdot b_{13}+a_{42}cdot b_{23}end{pmatrix}
Произведение B⋅ABcdot A нельзя найти, поскольку число столбцов матрицы BB неравно числу строк матрицы AA.
Найти произведение матрицы C=(15271810)C=begin{pmatrix}15&27\18&10end{pmatrix} на матрицу F=(3516)F=begin{pmatrix}35\16end{pmatrix}.
Матрица CC имеет размер 2×22times 2, матрица FF имеет размер 2×12times 1, значит, размер матрицы произведения будет 2×12times 1.
C⋅F=(15271810)⋅(3516)=(15⋅35+27⋅1618⋅35+10⋅16)=(957790)Ccdot F=begin{pmatrix}15&27\18&10end{pmatrix}cdot begin{pmatrix}35\16end{pmatrix}=begin{pmatrix}15cdot 35+27cdot 16\18cdot 35+10cdot 16end{pmatrix}=begin{pmatrix}957\790end{pmatrix}.
Как отмечалось выше, произведение матриц F⋅CFcdot C невозможно.
Найти произведение матриц K⋅LKcdot L и L⋅KLcdot K, если K=(12171314)K=begin{pmatrix}12&17\13&14end{pmatrix} на матрицу L=(18111210)L=begin{pmatrix}18&11\12&10end{pmatrix}.
Матрица KK имеет размер 2×22times 2, матрица LL имеет размер 2×22times 2, значит, размер матрицы произведения будет 2×22times 2.
K⋅L=(12171314)⋅(18111210)=(12⋅18+17⋅1212⋅11+17⋅1013⋅18+14⋅1213⋅11+14⋅10)=(420302402283)Kcdot L=begin{pmatrix}12&17\13&14end{pmatrix}cdot begin{pmatrix}18&11\12&10end{pmatrix}=begin{pmatrix}12cdot 18+17cdot 12&12cdot 11+17cdot 10\13cdot 18+14cdot 12&13cdot 11+14cdot 10end{pmatrix}=begin{pmatrix}420&302\402&283end{pmatrix}
Произведение L⋅KLcdot K существует и его размер — 2×22times 2.
L⋅K=(18111210)⋅(12171314)=(18⋅12+11⋅1318⋅17+11⋅1412⋅12+10⋅1312⋅17+10⋅14)=(359460274344)Lcdot K=begin{pmatrix}18&11\12&10end{pmatrix}cdot begin{pmatrix}12&17\13&14end{pmatrix}=begin{pmatrix}18cdot 12+11cdot 13&18cdot 17+11cdot 14\12cdot 12+10cdot 13&12cdot 17+10cdot 14end{pmatrix}=begin{pmatrix}359&460\274&344end{pmatrix}
Произведение двух матриц в общем случае зависит от порядка сомножителей, т.е. оно некоммутативно: A⋅B≠B⋅AAcdot Bneq Bcdot A.
Так, для матриц K=(12171314)K=begin{pmatrix}12&17\13&14end{pmatrix} и L=(18111210)L=begin{pmatrix}18&11\12&10end{pmatrix} из рассмотренного примера K⋅L≠L⋅KKcdot L neq Lcdot K.
Перестановочные матрицы
Перестановочные, или коммутирующие, матрицы – матрицы, для которых выполняется равенство A⋅B=B⋅AAcdot B=Bcdot A. Они обязательно квадратные.
Проверить, являются ли перестановочными матрицы CC и DD, если C=(2342)C=begin{pmatrix}2&3\4&2end{pmatrix}, D=(3343)D=begin{pmatrix}3&3\4&3end{pmatrix}.
Найдем произведения этих матриц C⋅DCcdot D и D⋅CDcdot C.
C⋅D=(2342)⋅(3343)=(2⋅3+3⋅42⋅3+3⋅34⋅3+2⋅44⋅3+2⋅3)=(18152018)Ccdot D=begin{pmatrix}2&3\4&2end{pmatrix}cdot begin{pmatrix}3&3\4&3end{pmatrix}=begin{pmatrix}2cdot 3+3cdot 4&2cdot 3+3cdot 3\4cdot 3+2cdot 4&4cdot 3+2cdot 3end{pmatrix}=begin{pmatrix}18&15\20&18end{pmatrix},
D⋅C=(3343)⋅(2342)=(3⋅2+3⋅43⋅3+3⋅24⋅2+3⋅44⋅3+3⋅2)=(18152018)Dcdot C=begin{pmatrix}3&3\4&3end{pmatrix}cdot begin{pmatrix}2&3\4&2end{pmatrix}=begin{pmatrix}3cdot 2+3cdot 4&3cdot 3+3cdot 2\4cdot 2+3cdot 4&4cdot 3+3cdot 2end{pmatrix}=begin{pmatrix}18&15\20&18end{pmatrix}.
Таким образом, для заданных матриц выполняется равенство C⋅DCcdot D и D⋅CDcdot C, поэтому они являются перестановочными.
Проверить, являются ли перестановочными матрицы FF и HH, если F=(3421)F=begin{pmatrix}3&4\2&1end{pmatrix}, H=(0593)H=begin{pmatrix}0&5\9&3end{pmatrix}.
Найдем произведения этих матриц F⋅HFcdot H и H⋅FHcdot F.
F⋅H=(3421)⋅(0593)=(3⋅0+4⋅93⋅5+4⋅32⋅0+1⋅92⋅5+1⋅3)=(3627913)Fcdot H=begin{pmatrix}3&4\2&1end{pmatrix}cdot begin{pmatrix}0&5\9&3end{pmatrix}=begin{pmatrix}3cdot 0+4cdot 9&3cdot 5+4cdot 3\2cdot 0+1cdot 9&2cdot 5+1cdot 3end{pmatrix}=begin{pmatrix}36&27\9&13end{pmatrix},
H⋅F=(0593)⋅(3421)=(0⋅3+5⋅20⋅4+5⋅19⋅3+3⋅29⋅4+3⋅1)=(1053339)Hcdot F=begin{pmatrix}0&5\9&3end{pmatrix}cdot begin{pmatrix}3&4\2&1end{pmatrix}=begin{pmatrix}0cdot 3+5cdot 2&0cdot 4+5cdot 1\9cdot 3+3cdot 2&9cdot 4+3cdot 1end{pmatrix}=begin{pmatrix}10&5\33&39end{pmatrix}.
Таким образом, для заданных матриц не выполняется равенство F⋅HFcdot H и H⋅FHcdot F, поэтому они не являются перестановочными.
Контрольные работы на заказ онлайн от практикующих исполнителей!
ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ
Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде
прямоугольной таблицы из m
строк и n столбцов. Эту таблицу
обычно заключают в круглые скобки. Например, матрица может иметь вид:
Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.
В общем виде матрицу размером m×n записывают так

Числа,
составляющие матрицу, называются элементами
матрицы. Элементы матрицы удобно снабжать двумя индексами aij: первый указывает номер
строки, а второй – номер столбца. Например, a23 – элемент стоит во 2-ой строке, 3-м столбце.
Если в матрице
число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше
примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая
матрица – её порядок 1.
Матрица, в
которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.
Различаются также
матрицы, имеющие только одну строку или один столбец.
Матрица, у
которой всего одна строка , называется матрицей –
строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.
Матрица, все
элементы которой равны нулю, называется нулевой
и обозначается (0), или просто 0. Например,

Главной диагональю квадратной матрицы назовём диагональ, идущую
из левого верхнего в правый нижний угол.
Квадратная
матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю,
называется треугольной матрицей.

Квадратная
матрица, у которой все элементы, кроме, быть может, стоящих
на главной диагонали, равны нулю, называется диагональной матрицей. Например, 
.
Диагональная
матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой
E. Например, единичная матрица 3-го порядка имеет вид 
ДЕЙСТВИЯ НАД МАТРИЦАМИ
Равенство матриц. Две матрицы A и B называются равными, если
они имеют одинаковое число строк и столбцов и их соответствующие элементы равны
aij = bij. Так если 

если a11 = b11, a12 = b12, a21 = b21 и a22 = b22.
Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно
сопоставить такую матрицу B из
n строк и m столбцов, у которой каждая
строка является столбцом матрицы A с
тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак,
если 

Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.
Таким образом, транспонирование – это
перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают AT.
Связь между матрицей A и её транспонированной
можно записать в виде .
Например. Найти матрицу транспонированную данной.
Сложение матриц. Пусть матрицы A и B состоят из одинакового
числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры.
Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах.
Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по
правилу, например,
или
Примеры. Найти сумму матриц:
.
— нельзя, т.к. размеры матриц различны.
.
Легко проверить,
что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).
Умножение матрицы на число. Для того чтобы умножить
матрицу A на число k нужно каждый элемент
матрицы A умножить на это число.
Таким образом, произведение матрицы A на
число k есть новая матрица, которая
определяется по правилу 
.
Для любых чисел a и b и
матриц A и B выполняются равенства:
.
Примеры.
.
- Найти 2A-B, если
,
.
.
Найти C=–3A+4B.
Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.
Умножение матриц. Эта операция осуществляется по своеобразному
закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть
согласованы. Перемножать можно только те матрицы, у которых число столбцов
первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки
первой равна высоте столбца второй). Произведением
матрицы A не матрицу B называется новая матрица C=AB,
элементы которой составляются следующим образом:

Таким образом,
например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой
строке и 3-м столбце c13, нужно в 1-ой матрице взять
1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на
соответствующие элементы столбца и полученные произведения сложить. И другие
элементы матрицы-произведения получаются с помощью аналогичного произведения
строк первой матрицы на столбцы второй матрицы.
В
общем случае, если мы умножаем матрицу A = (aij) размера m×n на
матрицу B = (bij) размера n×p, то получим матрицу C
размера m×p, элементы которой вычисляются следующим образом: элемент cij получается в результате
произведения элементов i-ой строки матрицы A на соответствующие элементы j-го
столбца матрицы B и их сложения.
Из этого правила следует,
что всегда можно перемножать две квадратные матрицы одного порядка, в
результате получим квадратную матрицу того же порядка. В частности, квадратную
матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.
Другим важным
случаем является умножение матрицы–строки на матрицу–столбец, причём ширина
первой должна быть равна высоте второй, в результате получим матрицу первого
порядка (т.е. один элемент). Действительно,

Примеры.
- Пусть
Найти элементы c12, c23 и c21 матрицы C.
- Найти произведение матриц.
.
.
— нельзя, т.к. ширина
первой матрицы равна 2-м элементам, а высота второй – 3-м.- Пусть
Найти АВ и ВА.
Найти АВ и ВА.
, B·A – не имеет смысла.
Таким образом,
эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении
матриц нужно тщательно следить за порядком множителей.
Можно
проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному
законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.
Легко также
проверить, что при умножении квадратной матрицы A на единичную матрицу E
того же порядка вновь получим матрицу A, причём AE=EA=A.
Можно
отметить следующий любопытный факт. Как известно произведение 2-х отличных от
нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение
2-х не нулевых матриц может оказаться равным нулевой матрице.
Например, если 
.
ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ
Пусть дана
матрица второго порядка – квадратная матрица, состоящая из двух строк и двух
столбцов 
Определителем второго порядка, соответствующим данной
матрице, называется число, получаемое следующим образом: a11a22 – a12a21.
Определитель обозначается
символом 
Итак, для того
чтобы найти определитель второго порядка нужно из произведения элементов
главной диагонали вычесть произведение элементов по второй диагонали.
Примеры. Вычислить определители второго порядка.
.
- Вычислить определитель матрицы D, если D= -А+2В и
Аналогично можно
рассмотреть матрицу третьего порядка и соответствующий ей определитель.
Определителем третьего порядка, соответствующим данной
квадратной матрице третьего порядка, называется число, обозначаемое и
получаемое следующим образом:

Таким образом,
эта формула даёт разложение определителя третьего порядка по элементам первой
строки a11, a12, a13 и сводит вычисление определителя третьего порядка к вычислению
определителей второго порядка.
Примеры. Вычислить определитель третьего порядка.
.
.
- Решите уравнение.
.
.
(x+3)(4x-4-3x)+4(3x-4x+4)=0.
(x+3)(x-4)+4(-x+4)=0.
(x-4)(x-1)=0.
x1 = 4, x2 = 1.
Аналогично можно ввести понятия определителей
четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам
1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.
Итак, в отличие
от матрицы, которая представляют собой таблицу чисел, определитель это число,
которое определённым образом ставится в соответствие матрице.







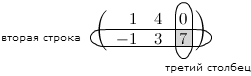
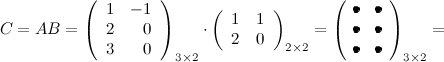
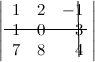





 .
. .
. Найти C=–3A+4B.
Найти C=–3A+4B.

 .
. .
.



 .
. .
. .
.