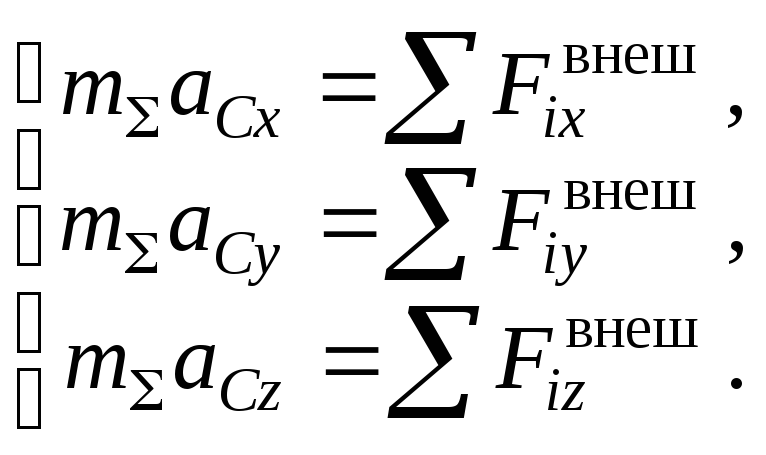Как найти эквивалентную жесткость пружин - AvtoShod.ru

Последовательные и параллельные пружины

редактировать

В механике две или более пружины называются последовательно, когда они соединены встык или точка-точка, и говорят, что параллельно, когда они соединены стороной рядом; в обоих случаях, чтобы действовать как одна пружина:

В более общем случае, две или более пружины включены последовательно при приложении любого внешнего напряжения к ансамблю применяется к каждой пружине без изменения величины, а величина деформации (деформации) ансамбля представляет собой сумму деформаций отдельных пружин. И наоборот, они считаются параллельными, если деформация ансамбля равна их общее напряжение, и напряжение Ансамбль — это сумма их напряжений.

Любая комбинация пружин Гука (линейного отклика), включенных последовательно или параллельно, ведет себя как одиночная пружина Гука. Формулы для объединения их физических атрибутов аналогичны тем, которые применяются к конденсаторам, подключенным последовательно или параллельно в электрической цепи.

Содержание

1 Формулы
- 1.1 Эквивалентная пружина
2 Формулы перегородки
- 2.1 Вычисление формулы пружины (эквивалентная жесткость пружины)
3 См. Также
4 Ссылки

Формулы

Эквивалентная пружина

В следующей таблице приведены формулы для пружины, которая эквивалентна системе из двух пружин, последовательно или параллельно, у которых постоянные пружины равны k 1 { displaystyle k_ {1}} $k_ {1}$ и k 2 { displaystyle k_ {2}} $k_ {2}$ . (соответствие c { displaystyle c}пружины является обратной величиной 1 / k { displaystyle 1 / k} 1 / k от его жесткость пружины.)

Количество	Параллельно	Последовательно

Эквивалентная жесткость пружины	keq = k 1 + k 2 { displaystyle k _ { mathrm {eq }} = k_ {1} + k_ {2}} ${ displaystyle k _ { mathrm {eq}} = k_ {1} + k_ {2}}$	1 keq = 1 k 1 + 1 k 2 { displaystyle { frac {1} {k _ { mathrm {eq}}}} = { frac {1} {k_ {1}}} + { frac {1} {k_ {2}}}} ${ displaystyle { frac {1} {k _ { mathrm {eq}}}} = { frac {1} {k_ {1}}} + { frac {1} {k_ {2}}}}$
Эквивалентное соответствие	1 ceq = 1 c 1 + 1 c 2 { displaystyle { frac { 1} {c _ { mathrm {eq}}}} = { frac {1} {c_ {1}}} + { frac {1} {c_ {2}}}} ${ displaystyle { frac {1} {c _ { mathrm {eq}}}} = { frac {1} {c_ {1}}} + { frac {1} { c_ {2}}}}$	ceq = c 1 + c 2 { displaystyle c _ { mathrm {eq}} = c_ {1} + c_ {2}} ${ displaystyle c _ { mathrm {eq}} = c_ {1} + c_ {2}}$
Прогиб (удлинение)	xeq = x 1 = x 2 { displaystyle x _ { mathrm {eq }} = x_ {1} = x_ {2}} ${ displaystyle x _ { mathrm {eq}} = x_ {1} = x_ {2} }$	xeq = x 1 + x 2 { displaystyle x _ { mathrm {eq}} = x_ {1} + x_ {2}} ${ displaystyle x _ { mathrm {eq}} = x_ {1} + x_ {2}}$
Force	F экв = F 1 + F 2 { Displaystyle F _ { mathrm {eq}} = F_ {1} + F_ {2}} ${ displaystyle F _ { mathrm {eq}} = F_ {1} + F_ {2}}$	F экв = F 1 = F 2 { Displaystyle F _ { mathrm {eq}} = F_ {1} = F_ {2}} ${ displaystyle F _ { mathrm {eq}} = F_ {1} = F_ {2}}$
Накопленная энергия	E eq = E 1 + E 2 { displayst yle E _ { mathrm {eq}} = E_ {1} + E_ {2}} ${ displaystyle E _ { mathrm {eq}} = E_ {1} + E_ {2}}$	E eq = E 1 + E 2 { displaystyle E _ { mathrm {eq}} = E_ {1} + E_ { 2}} ${ displaystyle E _ { mathrm {eq}} = E_ {1} + E_ {2}}$

Формулы разделения

Количество	Параллельно	Последовательно

Прогиб (удлинение)	x 1 = x 2 { displaystyle x_ {1} = x_ {2} ,}	x 1 x 2 = k 2 k 1 = c 1 c 2 { displaystyle { frac {x_ {1}} {x_ {2}}} = { frac {k_ {2}} {k_ {1}}} = { frac {c_ {1}} {c_ {2}}}} $frac {x_1} {x_2} = frac {k_2} {k_1} = frac {c_1} {c_2}$
Сила	F 1 F 2 = k 1 k 2 = c 2 c 1 { displaystyle { frac {F_ {1}} {F_ {2}}} = { frac {k_ {1}} {k_ {2}}} = { frac {c_ {2}} {c_ {1) }}}} $frac {F_1} {F_2} = frac { k_1} {k_2} = frac {c_2} {c_1}$	F 1 = F 2 { displaystyle F_ {1} = F_ {2} ,}
Накопленная энергия	E 1 E 2 = k 1 k 2 = c 2 c 1 { Displaystyle { frac {E_ {1}} {E_ {2}}} = { frac {k_ {1}} {k_ {2}}} = { frac {c_ {2}} {c_ {1} }}} $frac {E_1} {E_2} = frac {k_1} {k_2} = frac {c_2} {c_1}$	E 1 E 2 = k 2 k 1 = c 1 c 2 { displaystyle { frac {E_ {1}} {E_ {2}}} = { frac {k_ {2}} { k_ {1}}} = { frac {c_ {1}} {c_ {2}}}} $frac {E_1} {E_2} = frac {k_2} {k_1} = frac {c_1} {c_2}$

Вывод формулы пружины (эквивалентная жесткость пружины)

Эквивалентная постоянная пружины (серия)
При установке две пружины в их положениях равновесия последовательно прикрепленные на конце к блоку, а затем смещая его из этого равновесия, каждая из пружин испытывает соответствующие смещения x 1 и x 2 для общего смещения x 1 + х 2. Мы будем искать уравнение силы, действующей на блок, которое выглядит так: F b = — k e q (x 1 + x 2). { displaystyle F_ {b} = — k _ { mathrm {eq}} (x_ {1} + x_ {2}). ,} ${ displaystyle F_ {b} = - к _ { mathrm {eq}} (x_ {1} + x_ {2}). ,}$ Сила, которую испытывает каждая пружина, должна быть одинаковой, иначе пружины будет прятаться. Кроме того, эта сила будет такой же, как F b. Это означает, что F 1 = — k 1 x 1 = F 2 = — k 2 x 2. { displaystyle F_ {1} = — k_ {1} x_ {1} = F_ {2} = — k_ {2} x_ {2}. ,} Используя абсолютные значения, мы можем решить для x 1 { displaystyle x_ {1} ,}и x 2 { displaystyle x_ {2} ,}: x 1 = F 1 k 1, x 2 = F 2 К 2 { Displaystyle x_ {1} ~ = ~ { frac {F_ {1}} {k_ {1}}} ,, qquad x_ {2} ~ = ~ { frac {F_ { 2}} {k_ {2}}}} ${ displaystyle x_ {1} ~ = ~ { frac {F_ {1}} {k_ {1}}} ,, qquad x_ {2} ~ = ~ { frac {F_ {2}} {k_ {2}}}}$ , и аналогично, x 1 + x 2 = F bkeq { displaystyle x_ {1} ~ + ~ x_ {2} ~ = ~ { frac {F_ {b}} {k _ { mathrm {eq}}}}} ${ displaystyle x_ {1} ~ + ~ x_ {2} ~ = ~ { frac {F_ {b}} {k _ { mathrm {eq}}}}}$ . Подставляя x 1 { displaystyle x_ {1} ,}и x 2 { displaystyle x_ {2} ,}в последнем уравнении находим F 1 k 1 + F 2 k 2 = F bkeq { displaystyle { frac {F_ {1}} {k_ { 1}}} ~ + ~ { frac {F_ {2}} {k_ {2}}} ~ = ~ { frac {F_ {b}} {k _ { mathrm {eq}}}}} ${ displaystyle { frac {F_ {1}} {k_ {1}}} ~ + ~ { frac { F_ {2}} {k_ {2}}} ~ = ~ { frac {F_ {b}} {k _ { mathrm {eq}}}}}$ . Теперь, вспоминая, что F 1 = F 2 = F b { displaystyle F_ {1} ~ = ~ F_ {2} ~ = ~ F_ {b}} ${ displaystyle F_ {1} ~ = ~ F_ {2} ~ = ~ F_ {b}}$ , мы приходим к 1 keq знак равно 1 к 1 + 1 к 2. { displaystyle { frac {1} {k _ { mathrm {eq}}}} = { frac {1} {k_ {1}}} + { frac {1} {k_ {2}}}. ,} ${ displaystyle { frac {1} {k _ { mathrm {eq}}}} = { frac { 1} {k_ {1}}} + { frac {1} {k_ {2}}}. ,}$

Эквивалентная постоянная пружины (серия)

При установке две пружины в их положениях равновесия последовательно прикрепленные на конце к блоку, а затем смещая его из этого равновесия, каждая из пружин испытывает соответствующие смещения x 1 и x 2 для общего смещения x 1 + х 2. Мы будем искать уравнение силы, действующей на блок, которое выглядит так:

F b = — k e q (x 1 + x 2). { displaystyle F_ {b} = — k _ { mathrm {eq}} (x_ {1} + x_ {2}). ,} ${ displaystyle F_ {b} = - к _ { mathrm {eq}} (x_ {1} + x_ {2}). ,}$

Сила, которую испытывает каждая пружина, должна быть одинаковой, иначе пружины будет прятаться. Кроме того, эта сила будет такой же, как F b. Это означает, что

F 1 = — k 1 x 1 = F 2 = — k 2 x 2. { displaystyle F_ {1} = — k_ {1} x_ {1} = F_ {2} = — k_ {2} x_ {2}. ,}

Используя абсолютные значения, мы можем решить для x 1 { displaystyle x_ {1} ,} x_1 , и x 2 { displaystyle x_ {2} ,} x_2 , :

x 1 = F 1 k 1, x 2 = F 2 К 2 { Displaystyle x_ {1} ~ = ~ { frac {F_ {1}} {k_ {1}}} ,, qquad x_ {2} ~ = ~ { frac {F_ { 2}} {k_ {2}}}} ${ displaystyle x_ {1} ~ = ~ { frac {F_ {1}} {k_ {1}}} ,, qquad x_ {2} ~ = ~ { frac {F_ {2}} {k_ {2}}}}$

и аналогично,

x 1 + x 2 = F bkeq { displaystyle x_ {1} ~ + ~ x_ {2} ~ = ~ { frac {F_ {b}} {k _ { mathrm {eq}}}}} ${ displaystyle x_ {1} ~ + ~ x_ {2} ~ = ~ { frac {F_ {b}} {k _ { mathrm {eq}}}}}$

Подставляя x 1 { displaystyle x_ {1} ,} x_1 , и x 2 { displaystyle x_ {2} ,} x_2 , в последнем уравнении находим

F 1 k 1 + F 2 k 2 = F bkeq { displaystyle { frac {F_ {1}} {k_ { 1}}} ~ + ~ { frac {F_ {2}} {k_ {2}}} ~ = ~ { frac {F_ {b}} {k _ { mathrm {eq}}}}} ${ displaystyle { frac {F_ {1}} {k_ {1}}} ~ + ~ { frac { F_ {2}} {k_ {2}}} ~ = ~ { frac {F_ {b}} {k _ { mathrm {eq}}}}}$

Теперь, вспоминая, что F 1 = F 2 = F b { displaystyle F_ {1} ~ = ~ F_ {2} ~ = ~ F_ {b}} ${ displaystyle F_ {1} ~ = ~ F_ {2} ~ = ~ F_ {b}}$ , мы приходим к

1 keq знак равно 1 к 1 + 1 к 2. { displaystyle { frac {1} {k _ { mathrm {eq}}}} = { frac {1} {k_ {1}}} + { frac {1} {k_ {2}}}. ,} ${ displaystyle { frac {1} {k _ { mathrm {eq}}}} = { frac { 1} {k_ {1}}} + { frac {1} {k_ {2}}}. ,}$

Эквивалентная постоянная пружины (параллельная)

В этом случае обе пружины касаются блока, и независимо от расстояния, сжимаемого пружиной 1, должна быть одинаковая величина сжатия пружины 2.

Тогда сила, действующая на блок, равна:

F b { displaystyle F_ {b} ,}	= F 1 + F 2 { displaystyle = F_ {1} + F_ {2} , }
	= — k 1 x — k 2 x { displaystyle = -k_ {1} x-k_ {2} x ,}

Таким образом, сила, действующая на блок, равна

F b = — ( к 1 + к 2) х. { displaystyle F_ {b} = — (k_ {1} + k_ {2}) x. ,}

Вот почему мы можем определить эквивалентную жесткость пружины как

k e q = k 1 + k 2. { displaystyle k _ { mathrm {eq}} = k_ {1} + k_ {2}. ,} ${ displaystyle k _ { mathrm {eq}} = k_ {1} + k_ {2}. ,}$

Расстояние в сжатом состоянии

В случае, когда две пружины включены последовательно, сила пружин на каждую остальные равны:

F 1 = F 2 { displaystyle F_ {1} = F_ {2} ,}

— k 1 x 1 = — k 2 x 2. { displaystyle -k_ {1} x_ {1} = — k_ {2} x_ {2}. ,}

Отсюда мы получаем соотношение между сжатыми расстояниями для случая in series :

х 1 х 2 = k 2 k 1. { displaystyle { frac {x_ {1}} {x_ {2}}} = { frac {k_ {2}} {k_ {1}}}. ,} $frac {x_1} {x_2} = frac {k_2} {k_1}. ,$

Накопленная энергия
Для series case, соотношение энергии, запасенной в пружинах, равно: E 1 E 2 = 1 2 k 1 x 1 2 1 2 k 2 x 2 2, { displaystyle { frac {E_ { 1}} {E_ {2}}} = { frac {{ frac {1} {2}} k_ {1} x_ {1} ^ {2}} {{ frac {1} {2}} k_ {2} x_ {2} ^ {2}}}, ,} $frac {E_1} {E_2} = frac { frac {1} {2} k_1 x_1 ^ 2} { frac {1} {2} k_2 x_2 ^ 2}, ,$ , но существует связь между x 1 и x 2, полученными ранее, поэтому мы можем подключить что в: E 1 E 2 = k 1 k 2 (k 2 k 1) 2 = k 2 k 1. { displaystyle { frac {E_ {1}} {E_ {2}}} = { frac {k_ {1}} {k_ {2}}} left ({ frac {k_ {2}} {k_ {1}}} right) ^ {2} = { frac {k_ {2}} {k_ {1}}}. ,} $frac {E_1} {E_2} = frac {k_1} {k_2} left ( frac {k_2} {k_1} right) ^ 2 = frac {k_2} {k_1}. ,$ Для случая параллельного, E 1 E 2 знак равно 1 2 К 1 Икс 2 1 2 К 2 Икс 2 { Displaystyle { frac {E_ {1}} {E_ {2}}} = { frac {{ frac {1} {2} } k_ {1} x ^ {2}} {{ frac {1} {2}} k_ {2} x ^ {2}}} ,} $frac {E_1} {E_2} = frac { frac {1} {2} k_1 x ^ 2} { frac {1} {2} k_2 x ^ 2} ,$ потому что сжатое расстояние пружин такое же, это упрощается до E 1 E 2 = k 1 k 2. { displaystyle { frac {E_ {1}} {E_ {2}}} = { frac {k_ {1}} {k_ {2}}}. ,} $frac {E_1} {E_2} = frac {k_1} {k_2}. ,$

Накопленная энергия

Для series case, соотношение энергии, запасенной в пружинах, равно:

E 1 E 2 = 1 2 k 1 x 1 2 1 2 k 2 x 2 2, { displaystyle { frac {E_ { 1}} {E_ {2}}} = { frac {{ frac {1} {2}} k_ {1} x_ {1} ^ {2}} {{ frac {1} {2}} k_ {2} x_ {2} ^ {2}}}, ,} $frac {E_1} {E_2} = frac { frac {1} {2} k_1 x_1 ^ 2} { frac {1} {2} k_2 x_2 ^ 2}, ,$

, но существует связь между x 1 и x 2, полученными ранее, поэтому мы можем подключить что в:

E 1 E 2 = k 1 k 2 (k 2 k 1) 2 = k 2 k 1. { displaystyle { frac {E_ {1}} {E_ {2}}} = { frac {k_ {1}} {k_ {2}}} left ({ frac {k_ {2}} {k_ {1}}} right) ^ {2} = { frac {k_ {2}} {k_ {1}}}. ,} $frac {E_1} {E_2} = frac {k_1} {k_2} left ( frac {k_2} {k_1} right) ^ 2 = frac {k_2} {k_1}. ,$

Для случая параллельного,

E 1 E 2 знак равно 1 2 К 1 Икс 2 1 2 К 2 Икс 2 { Displaystyle { frac {E_ {1}} {E_ {2}}} = { frac {{ frac {1} {2} } k_ {1} x ^ {2}} {{ frac {1} {2}} k_ {2} x ^ {2}}} ,} $frac {E_1} {E_2} = frac { frac {1} {2} k_1 x ^ 2} { frac {1} {2} k_2 x ^ 2} ,$

потому что сжатое расстояние пружин такое же, это упрощается до

E 1 E 2 = k 1 k 2. { displaystyle { frac {E_ {1}} {E_ {2}}} = { frac {k_ {1}} {k_ {2}}}. ,} $frac {E_1} {E_2} = frac {k_1} {k_2}. ,$

См. также

Ссылки

Последняя правка сделана 2021-06-08 01:10:08

Содержание доступно по лицензии CC BY-SA 3.0 (если не указано иное).

Источник

При
описании колебательного движения
систему пружин, действующих на материальную
точку, заменяют одной пружиной, жесткость
которой равна жесткости системы. Эту
пружину называют эквивалентной.
Рассмотрим три основные схемы соединения
пружин.

1 Параллельное соединение(рисунок
8.1).

Рисунок
8.1

араллельно соединенные пружины,
если их деформации одинаковы, можно
заменить эквивалентной пружиной,
коэффициент жесткости которой равен
сумме коэффициентов жесткости соединенных
пружин,

2 Последовательное соединение(рисунок 8.2).

При
последовательном соединении нескольких
пружин они могут быть заменены
эквивалентной пружиной, податливость
которой равна сумме податливостей
соединенных пружин (податливостью
пружины называют величину, обратную
коэффициенту жесткости). Следовательно,
коэффициент жесткости эквивалентной
пружины в данном случае определяется
следующим образом:

Рисунок
8.2

«Двухстороннее» соединение(рисунок 8.3).

П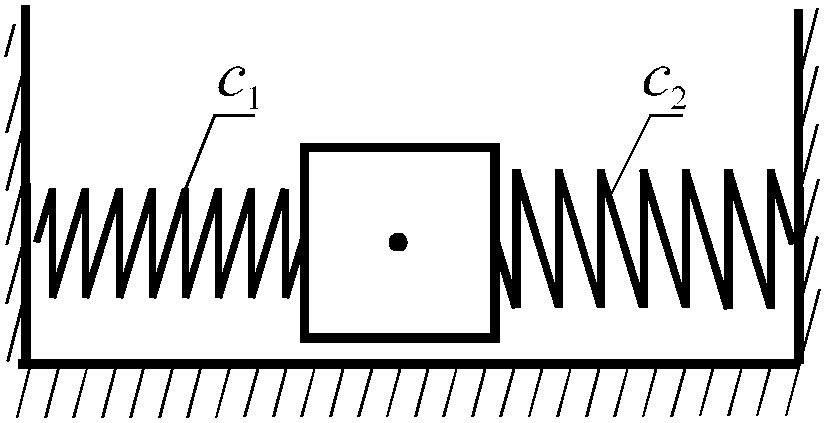ри
движении исследуемой материальной
точки деформации обоих пружин будут
одинаковы. Результирующая сила,
действующая со стороны этих пружин на
точку, будет равна сумме сил упругости
в пружинах 1 и 2. Следовательно, коэффициент
жесткости эквивалентной пружины будет
равен сумме коэффициентов жесткости
пружин 1 и 2:

Любую систему пружин можно представить
как набор рассмотренных схем.

Рисунок
8.3

Лекция 9 Динамика материальной
системы.

(2 часа, 1 семестр, 2 курс)

Вопрос 9.1Теорема о движении центра масс материальной системы.

Центром масс материальной системы
называют точку, радиус-вектор
которой определяется по формуле

где
– масса материальной системы;

m_i,– масса и радиус-векторi-й
материальной точки.

Координаты центра масс системы:

где x_i,y_i,z_i– координаты центра массi-го
тела системы.

При решении задач динамики материальной
системы часто оказывается полезной
теорема о движении центра масс:произведение массы материальной
системы
на ускорение ее центра массa_C
равно геометрической сумме внешних
сил, приложенных к системе:

В ходе решения выражение теоремы
проецируют на оси координат. При этом
получается система уравнений

Использование теоремы о движении центра
масс материальной системы для решения
задач динамики рекомендуется осуществлять
по следующей методике:

1 Изображается материальная система, и
указываются все внешние силы, действующие
на нее.

2 Выбираются оси координат.

3 Внешние силы, действующие на систему,
проецируются на выбранные оси.

4 Записываются выражения координат
центра масс системы через координаты
центров масс одного из тел системы.

5 Дифференцируя выражения координат
центра масс по времени, получают
зависимости для скорости и ускорения
центра масс системы.

6 Полученные выражения подставляются
в систему динамических уравнений.

7 Решается дифференциальное уравнение
относительно искомой координаты с
учетом заданных начальных условий.

Вопрос 9.2Динамические уравнения движения твердого тела.

Динамические уравнения движения твердого
тела устанавливают связь между
кинематическими характеристиками
движения тела и действующими на него
силами.

Поступательное движение тела.В
этом случае динамическое уравнение
представляет собой следствие из теоремы
о движении центра масс:

где m– масса тела;

– ускорение центра масс тела;

–i-тая сила, действующая
на тело.

При решении задач динамическое уравнение
поступательного движения тела проецируют
на оси координат.

Вращательное движение тела. Для
него динамическое уравнение имеет вид:

где J_z– момент инерции тела относительно оси
вращенияz;

 – угловое ускорение тела;

M_iz– моментi-й силы
относительно оси вращения.

При составлении динамического уравнения
вращательного движения тела выбирается
направление отсчета угла поворота .
Моменты сил, вращающих тело против
выбранного направления, принимаются
отрицательными, а по выбранному
направлению – положительными.

Момент инерции J_z
является мерой инертности тела при
вращательном движении. Момент инерции
материальной системы относительно
данной осиOzопределяется
как сумма произведений масс всех точек
системы на квадраты их расстояний от
этой оси:

Для абсолютно твердого тела суммирование
по точкам системы заменяется интегрированием
по объему

где ρ – плотность материала тела;

h– расстояние от
точки с координатамиx,y,zдо осиOz.

Момент инерции J_Cтела относительно осиCz,
проходящей через центр массC,
называютцентральным моментом инерции.
Если для тела известенрадиус инерцииi, то центральный
момент

Центральные моменты инерции некоторых
тел:

1 Тонкий однородный стержень с массой
mи длинойl:

2 Тонкое круглое однородное кольцо с
массой mи радиусомR:

3 Круглый однородный диск с массой mи радиусомR:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Эквивалентная жесткость двух последовательно соединенных пружин Калькулятор

Search
Дом	физика ↺
физика	Механические колебания ↺
Механические колебания	Незатухающая свободная вибрация ↺

✖Жесткость пружины 1 — это сила на единицу длины, необходимая для отклонения первой пружины.ⓘ Жесткость пружины 1 [K₁]

+10%

-10%

✖Жесткость пружины 2 — это сила на единицу длины, необходимая для отклонения второй пружины.ⓘ Жесткость пружины 2 [K₂]

+10%

-10%

✖Эквивалентная жесткость пружины — это единая жесткость пружины, полученная путем объединения различных констант пружины.ⓘ Эквивалентная жесткость двух последовательно соединенных пружин [K_eq]

⎘ копия

Эквивалентная жесткость двух последовательно соединенных пружин Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Жесткость пружины 1: 14 Ньютон на миллиметр —> 14000 Ньютон на метр (Проверьте преобразование здесь)
Жесткость пружины 2: 11 Ньютон на миллиметр —> 11000 Ньютон на метр (Проверьте преобразование здесь)

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

6160 Ньютон на метр —>6.16 Ньютон на миллиметр (Проверьте преобразование здесь)

4 Незатухающая свободная вибрация Калькуляторы

Эквивалентная жесткость двух последовательно соединенных пружин формула

Эквивалентная жесткость пружин = (Жесткость пружины 1*Жесткость пружины 2)/(Жесткость пружины 1+Жесткость пружины 2)

K_eq = (K₁*K₂)/(K₁+K₂)

Что такое жесткость?

Жесткость — это степень сопротивления объекта деформации в ответ на приложенную силу. Чем более гибкий объект, тем он менее жесткий.

Источник

В механике говорят , что две или более пружины включены последовательно, когда они соединены встык или точка в точку, и говорят, что они параллельны, когда они соединены бок о бок; в обоих случаях, чтобы действовать как одна пружина:

В более общем смысле, две или более пружины включены последовательно, когда любое внешнее напряжение, приложенное к ансамблю, прикладывается к каждой пружине без изменения величины, а величина деформации (деформации) ансамбля является суммой деформаций отдельных пружин. И наоборот, они считаются параллельными, если деформация ансамбля является их общей деформацией, а напряжение ансамбля является суммой их напряжений.

Любая комбинация пружин Гука (линейного отклика), включенных последовательно или параллельно, ведет себя как одна пружина Гука. Формулы для объединения их физических характеристик аналогичны тем, которые применяются к конденсаторам, включенным последовательно или параллельно в электрическую цепь .

Формулы

Эквивалентная пружина

В следующей таблице приведены формулы для пружины, которая эквивалентна системе из двух последовательно или параллельно установленных пружин, постоянные пружины которых равны и . ( Податливость пружины является обратной величиной ее жесткости.)
$к_ {1}$ $к_ {2}$ 1 / к

Количество	Последовательно	В параллели

Эквивалентная жесткость пружины	${ displaystyle { frac {1} {k _ { mathrm {eq}}}} = { frac {1} {k_ {1}}} + { frac {1} {k_ {2}}}}$	${ Displaystyle к _ { mathrm {eq}} = k_ {1} + k_ {2}}$
Эквивалентное соответствие	${ displaystyle c _ { mathrm {eq}} = c_ {1} + c_ {2}}$	${ displaystyle { frac {1} {c _ { mathrm {eq}}}} = { frac {1} {c_ {1}}} + { frac {1} {c_ {2}}}}$
Прогиб (удлинение)	${ displaystyle x _ { mathrm {eq}} = x_ {1} + x_ {2}}$	${ displaystyle x _ { mathrm {eq}} = x_ {1} = x_ {2}}$
Сила	${ Displaystyle F _ { mathrm {eq}} = F_ {1} = F_ {2}}$	${ Displaystyle F _ { mathrm {eq}} = F_ {1} + F_ {2}}$
Накопленная энергия	${ displaystyle E _ { mathrm {eq}} = E_ {1} + E_ {2}}$	${ displaystyle E _ { mathrm {eq}} = E_ {1} + E_ {2}}$

Формулы разбиения

Количество	Последовательно	В параллели

Прогиб (удлинение)	$frac {x_1} {x_2} = frac {k_2} {k_1} = frac {c_1} {c_2}$
Сила		$frac {F_1} {F_2} = frac {k_1} {k_2} = frac {c_2} {c_1}$
Накопленная энергия	$frac {E_1} {E_2} = frac {k_2} {k_1} = frac {c_1} {c_2}$	$frac {E_1} {E_2} = frac {k_1} {k_2} = frac {c_2} {c_1}$

Вывод формулы пружины (эквивалент жесткости пружины)

Эквивалентная постоянная пружины (серия)
При установке двух пружин в их положения равновесия последовательно, прикрепленных на конце к блоку, а затем смещении их из этого положения равновесия, каждая из пружин будет испытывать соответствующие смещения x ₁ и x ₂ для общего смещения x ₁ + x ₂ . Мы будем искать уравнение силы, действующей на блок, которое выглядит так: ${ displaystyle F_ {b} = - k _ { mathrm {eq}} (x_ {1} + x_ {2}). ,}$ Сила, которую испытывает каждая пружина, должна быть одинаковой, в противном случае пружины изгибаются. Причем эта сила будет такой же, как F _b . Это означает, что ${ Displaystyle F_ {1} = - k_ {1} x_ {1} = F_ {2} = - k_ {2} x_ {2} = F_ {b}. ,}$ Используя абсолютные значения, мы можем решить для и : ${ displaystyle x_ {1} ~ = ~ { frac {F_ {1}} {k_ {1}}} ,, qquad x_ {2} ~ = ~ { frac {F_ {2}} {k_ { 2}}}}$ , и аналогично, ${ displaystyle x_ {1} ~ + ~ x_ {2} ~ = ~ { frac {F_ {b}} {k _ { mathrm {eq}}}}}$ . Подставляя и в последнее уравнение, находим ${ displaystyle { frac {F_ {1}} {k_ {1}}} ~ + ~ { frac {F_ {2}} {k_ {2}}} ~ = ~ { frac {F_ {b}} {к _ { mathrm {eq}}}}}$ . Теперь, вспомнив это , мы приходим к ${ Displaystyle F_ {1} ~ = ~ F_ {2} ~ = ~ F_ {b}}$ ${ displaystyle { frac {1} {k _ { mathrm {eq}}}} = { frac {1} {k_ {1}}} + { frac {1} {k_ {2}}}. ,}$

Эквивалентная постоянная пружины (серия)

При установке двух пружин в их положения равновесия последовательно, прикрепленных на конце к блоку, а затем смещении их из этого положения равновесия, каждая из пружин будет испытывать соответствующие смещения x ₁ и x ₂ для общего смещения x ₁ + x ₂ . Мы будем искать уравнение силы, действующей на блок, которое выглядит так:

${ displaystyle F_ {b} = - k _ { mathrm {eq}} (x_ {1} + x_ {2}). ,}$

Сила, которую испытывает каждая пружина, должна быть одинаковой, в противном случае пружины изгибаются. Причем эта сила будет такой же, как F _b . Это означает, что

${ Displaystyle F_ {1} = - k_ {1} x_ {1} = F_ {2} = - k_ {2} x_ {2} = F_ {b}. ,}$

Используя абсолютные значения, мы можем решить для и :
x_1 , х_2 ,

${ displaystyle x_ {1} ~ = ~ { frac {F_ {1}} {k_ {1}}} ,, qquad x_ {2} ~ = ~ { frac {F_ {2}} {k_ { 2}}}}$

и аналогично,

${ displaystyle x_ {1} ~ + ~ x_ {2} ~ = ~ { frac {F_ {b}} {k _ { mathrm {eq}}}}}$

Подставляя и в последнее уравнение, находим
x_1 , х_2 ,

${ displaystyle { frac {F_ {1}} {k_ {1}}} ~ + ~ { frac {F_ {2}} {k_ {2}}} ~ = ~ { frac {F_ {b}} {к _ { mathrm {eq}}}}}$

Теперь, вспомнив это , мы приходим к
${ Displaystyle F_ {1} ~ = ~ F_ {2} ~ = ~ F_ {b}}$

${ displaystyle { frac {1} {k _ { mathrm {eq}}}} = { frac {1} {k_ {1}}} + { frac {1} {k_ {2}}}. ,}$

Эквивалентная постоянная пружины (параллельная)

В этом случае обе пружины соприкасаются с блоком, и независимо от того, сжимается ли пружина 1, должна быть одинаковая величина сжатия пружины 2.

Тогда сила на блоке равна:

Итак, сила на блоке

Вот как мы можем определить эквивалентную жесткость пружины как

${ Displaystyle к _ { mathrm {eq}} = k_ {1} + k_ {2}. ,}$

Сжатое расстояние

В случае, если две пружины установлены параллельно, сразу же:

${ displaystyle F_ {1} = - k_ {1} x_ {1}}$

а также ${ Displaystyle F_ {2} = - k_ {2} x_ {2}. ,}$

В случае, когда две пружины включены последовательно, силы пружин друг на друга равны:

Отсюда мы получаем соотношение между сжатыми расстояниями для случая in series :

$frac {x_1} {x_2} = frac {k_2} {k_1}. ,$

Накопленная энергия
Для последовательного случая отношение энергии, запасенной в пружинах, составляет: $frac {E_1} {E_2} = frac { frac {1} {2} k_1 x_1 ^ 2} { frac {1} {2} k_2 x_2 ^ 2}, ,$ но существует связь между x ₁ и x _2, полученная ранее, поэтому мы можем подключить ее: $frac {E_1} {E_2} = frac {k_1} {k_2} left ( frac {k_2} {k_1} right) ^ 2 = frac {k_2} {k_1}. ,$ Для параллельного случая $frac {E_1} {E_2} = frac { frac {1} {2} k_1 x ^ 2} { frac {1} {2} k_2 x ^ 2} ,$ поскольку сжатое расстояние пружин такое же, это упрощает $frac {E_1} {E_2} = frac {k_1} {k_2}. ,$

Накопленная энергия

Для последовательного случая отношение энергии, запасенной в пружинах, составляет:

$frac {E_1} {E_2} = frac { frac {1} {2} k_1 x_1 ^ 2} { frac {1} {2} k_2 x_2 ^ 2}, ,$

но существует связь между x ₁ и x _2, полученная ранее, поэтому мы можем подключить ее:

$frac {E_1} {E_2} = frac {k_1} {k_2} left ( frac {k_2} {k_1} right) ^ 2 = frac {k_2} {k_1}. ,$

Для параллельного случая

$frac {E_1} {E_2} = frac { frac {1} {2} k_1 x ^ 2} { frac {1} {2} k_2 x ^ 2} ,$

поскольку сжатое расстояние пружин такое же, это упрощает

$frac {E_1} {E_2} = frac {k_1} {k_2}. ,$

Смотрите также

Ферма
Двойственность (машиностроение)

использованная литература

Источник

Последовательные и параллельные пружины

Содержание

Формулы

Эквивалентная пружина

Формулы разделения

Вывод формулы пружины (эквивалентная жесткость пружины)

См. также

Ссылки

Вопрос 9.1Теорема о движении центра масс материальной системы.

Вопрос 9.2Динамические уравнения движения твердого тела.

Эквивалентная жесткость двух последовательно соединенных пружин Калькулятор

Эквивалентная жесткость двух последовательно соединенных пружин Решение

4 Незатухающая свободная вибрация Калькуляторы

Эквивалентная жесткость двух последовательно соединенных пружин формула

Что такое жесткость?

Формулы

Эквивалентная пружина

Формулы разбиения

Вывод формулы пружины (эквивалент жесткости пружины)

Смотрите также

использованная литература

Не пропустите также: